Разрешение матрицы. Цифровая фотография. Трюки и эффекты

Разрешение матрицы. Цифровая фотография. Трюки и эффекты

ВикиЧтение

Цифровая фотография. Трюки и эффекты
Гурский Юрий Анатольевич

Содержание

Разрешение матрицы

Мы знаем, что матрица состоит из мельчайших светочувствительных элементов. Количество таких элементов в матрице – это и есть ее разрешение. Разрешение матрицы получают умножением количества элементов по горизонтали и вертикали. Самые распространенные пиксельные значения разрешения камеры соответствуют тем, которые применяются в компьютерных мониторах: 1024 х 768, 1280 х 1024, 1600 х 1200 и т. д. Первое число означает количество пикселов по горизонтали, второе – по вертикали. Перемножив их, получим разрешение камеры. К примеру, трехмегапиксельная цифровая фотокамера позволяет получить снимок с разрешением 2000 х 1500 точек.

Недостаточное разрешение камеры означает недостаток информации для правильного отображения снимка: если такую фотографию увеличить до определенных размеров, то она «распадется» на точки (вернее, на квадратики-пикселы). Округлые и искривленные границы предметов при этом окажутся как бы состоящими из ступенек (рис. 3.2). Недостаточное разрешение также может вызывать искажение цветов.

Рис. 3.2. В случае недостаточного разрешения цифровое изображение распадается на пикселы

Значит, чем больше мегапикселов, тем лучше камера и фотографии? И да, и нет. Если разрешение вашей камеры невелико и вы предполагаете разместить сделанную этой камерой картинку в Интернете, то проблем, скорее всего, не будет. Другое дело, если вы хотите увеличить изображение и распечатать. Снимки, сделанные шестимегапиксельной камерой, сохраняют хорошее качество в формате 21 х 16 см. Тому, кто покупает свою первую цифровую камеру, за количеством пикселов гнаться не стоит – для обычного семейного фотоальбома, для отпускных фотографий или съемки вечеринок достаточно четырех или пяти миллионов пикселов (то есть четырех или пяти мегапикселов).

Но для того, чтобы распечатать изображение большего размера, разрешения камеры может оказаться недостаточно (табл. 3.1).

Таблица 3.1. Зависимость максимальных размеров выводимого на печать изображения от разрешения цифровой камеры

В последнее десятилетие разработка матриц стремительно развивается и столь же быстро дешевеют цифровые камеры. На рынке уже давно идет «мегапиксельная гонка». Камеры с разрешением меньше пяти мегапикселов сегодня уже практически не выпускают. Рынок цифровых камер и диапазон их характеристик изменяются так стремительно, что восьми– и даже десятимегапиксельные камеры, совсем недавно считавшиеся полупрофессиональными, сегодня относят к потребительскому классу.

И все же чем больше мегапикселов, тем больше возможностей! Одних возможностей больше, а других – меньше. Гонясь за высоким разрешением, не следует забывать, что с ростом количества пикселов матрицы увеличивается объем создаваемого камерой файла изображения. Если снимки, сделанные четырехмегапиксельной камерой, «весят» около 1940 Кбайт, то из шестимегапиксельной камеры выходят фотографии размером примерно 3800 Кбайт – почти в 2 раза больше! Разница же в качестве изображения ощущается только при печати большого формата.

Секрет

Одинаковых матриц не бывает, как не бывает одинаковых человеческих глаз. А это значит, что не бывает совершенно одинаковых камер. Попрактиковавшись, вы постепенно изучите «характер» своей камеры и будете знать ее особенности гораздо лучше, чем разработчик и производитель.

Разрешением матрицы ее характеристики не исчерпываются. Есть еще три не менее важных показателя: физический размер матрицы, ее динамический диапазон и уровень шумов.

Данный текст является ознакомительным фрагментом.

6.

1. Разрешение экрана

6.1. Разрешение экрана Если не знаете, что такое разрешение экрана и зачем оно вообще нужно, то в данном разделе мы проведем теоретическую подготовку.Под разрешением экрана следует понимать то количество точек по горизонтали и вертикали, с помощью которых формируется

§ 69. Разрешение картинок

§ 69. Разрешение картинок 16 июня 2001Попробуем разобраться в одном из самых больших заблуждений человечества за всю историю существования экранной графики.Дело в том, что у электронного изображения вообще нет разрешения. Разрешение (точнее, разрешающая способность) может

§ 132. Низкое разрешение

§ 132. Низкое разрешение 28 мая 2006Применительно к человеку понятие разрешение может означать способность различать стили, объекты, здания, цвета, шрифты, голоса и так далее.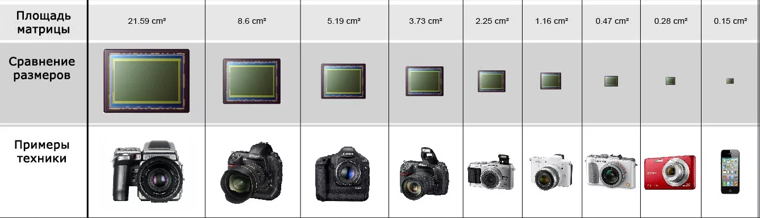 Любое образование ставит целью повысить разрешение в выбранной области. Художники долго рисуют

R.6.8 Разрешение неоднозначности

R.6.8 Разрешение неоднозначности Существует неоднозначность в грамматике языка, касающаяся оператора-выражения и описания, а именно, оператор-выражение, содержащий как самое левое подвыражение явное преобразование типа, заданное в функциональном стиле (§R.5.2.3), может быть

8.1.8. Реализация разреженной матрицы

8.1.8. Реализация разреженной матрицы Иногда бывает нужен массив, в котором определена лишь небольшая часть элементов, а остальные не определены вовсе или (даже чаще) равны 0. Подобная разреженная матрица потребляет так много памяти зря, что были найдены способы более

9.4.1. Реализация графа в виде матрицы смежности

9. 4.1. Реализация графа в виде матрицы смежности Нижеприведенный пример основан на двух предыдущих. В листинге 9.3 неориентированный граф реализован в виде матрицы смежности с помощью класса ZArray (см. раздел 8.1.26). Это нужно для того, чтобы новые элементы по умолчанию получали

11.14. Реализация динамической матрицы

11.14. Реализация динамической матрицы ПроблемаТребуется реализовать числовые матрицы, размерности которых (количество строк и столбцов) неизвестны на этапе компиляции.РешениеВ примере 11.28 показана универсальная и эффективная реализация класса динамической матрицы,

11.15. Реализация статической матрицы

11.15. Реализация статической матрицы ПроблемаТребуется эффективно реализовать матрицу, когда ее размерность (т.е. количество строк и столбцов) постоянна и известна на этапе компиляции. РешениеКогда размерность матрицы известна на этапе компиляции, компилятор может легко

Разрешение

Разрешение Величина под названием «разрешение» является «связующим звеном» между логическим и физическим размером. Она определяет соотношение между ними и позволяет судить о качестве изображения.Измеряя разрешение, мы фактически измеряем размер одного пиксела.

Физический размер матрицы

Физический размер матрицы Выбирая цифровую камеру, неплохо поинтересоваться физическим размером ее матрицы, ведь именно эта характеристика определяет качество камеры. Чем сенсор больше, тем больше он содержит ПЗС-элементов, тем выше его разрешение и, следовательно,

Динамический диапазон матрицы

Динамический диапазон матрицы Динамический диапазон светочувствительной матрицы – это ее способность воспринимать градации каждого из цветов. Говоря проще, динамический диапазон определяет, сколько ступеней разности контраста может увидеть и зафиксировать матрица.

Облет повисшего объекта, или Эффект «Матрицы»

Облет повисшего объекта, или Эффект «Матрицы» Несмотря на современные достижения компьютерной техники, для получения некоторых визуальных эффектов используются старые проверенные методы фотографии. Казалось бы, что общего может иметь фотография с таким современным

Чистка матрицы зеркальной камеры

Чистка матрицы зеркальной камеры У владельцев зеркальных камер к радости от возможности смены объективов прибавляется забота о чистоте матрицы. Что делать, если вы заметили на снимках ровной светлой поверхности соринки и пятна? В некоторых моделях зеркальных камер

Чистка матрицы зеркальной камеры

Чистка матрицы зеркальной камеры В зеркальной камере, в отличие от компактной, приходится чистить матрицу.

Хотите вы или нет, но рано или поздно на матрицу попадает пыль, мелкие соринки. Насколько скоро это произойдет, зависит от частоты смены объективов, условий

ТЕМА НОМЕРА: Реформирование матрицы

ТЕМА НОМЕРА: Реформирование матрицы Автор: Леонид Левкович-МаслюкГде-то в конце 1980-х или начале 1990-х я читал в «Независимой газете» обзор событий в мире книг. Автор отмечал, что на прилавках появилось оригинальнейшее сочинение по истории древнего мира, которое написал

виды матриц и их возможности

Матрица – сердце фотоаппарата. Именно от нее зависит качество изображения и простота процесса. Поэтому важно, чтобы вид сенсора подходил под задачи и стиль фотографа. Инженеры сервисного центра Фотоблик предлагают разобраться, какие возможности дают разные виды матриц.

Что такое матрица?

По факту речь идет о микросхеме, которая состоит из фотодиодов (это самый дорогой компонент камеры).

В процессе создания фотографии свет попадает через оптику на матрицу, преобразовывается в изображение и передается на карту памяти уже полноценной фотографией. То есть, сенсор – это современный аналог пленки. У каждого вида свои характеристики и возможности.

Среднеформатные матрицы

Размер таких сенсоров составляет от 45х60 мм до 60х90 мм (больше, чем фулфрейм). Сам компонент состоит из нескольких более простых матриц.

Такой сенсор позволяет создавать очень детальные и большие по площади кадры, дает плавный переход тонов. Однако в производстве он дороже, поэтому часто встречается в топовых профессиональных камерах.

Полнокадровые матрицы

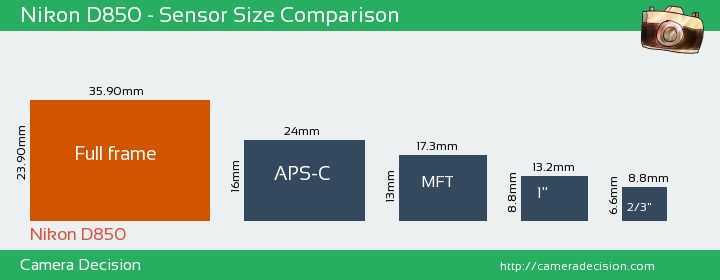
Размер сенсора – 36х24 мм (совпадает с размером негативов пленки). Разрешение таких матриц достигает 50 мегапикселей.

Полный кадр способен принять больше света, чем матрицы меньшего размера. В итоге получаются очень качественные изображения. Еще один плюс: к фулфрейму могут подходить объективы, созданные под APS-C.

Эти сенсоры используются и в любительской, и в профессиональной фототехнике, и считаются эталоном.

APS-C матрицы

Размер такого сенсора зависит от производителя, однако средним значения считается 23,5х15,6 мм. Именно такой размер предлагает компания Nikon (кроп-фактор – 1,5). Его прямой конкурент Canon устанавливает матрицы размером 22.3×14.9 мм (кроп-фактор — 1,6).

* Кроп-фактор обозначает, во сколько раз размер матрицы меньше полного кадра.

Этот вид светочувствительного элемента можно встретить как в профессиональных, так и в любительских камерах. APS-C дает неплохое качество изображения и сочетается со многими объективами. Хорошо подходит для съемок репортажей и природы.

Micro 4/3

Эти матрицы почти в два раза меньше (17.3×13.0 мм), чем полнокадровые. Такие сенсоры часто встречаются в компактных зеркальных и беззеркальных камерах.

Таким образом, кадры сделанные с помощью матрицы микро 4/3 имеют соотношение сторон 4 к 3. Этот сенсор позволяет добиться резкости для всех объектов на кадре. Однако на высоких ISO будет много шумов.

Маленькие матрицы

Речь идет о матрицах размером от 6,16×4,62 до 12,8×9,6 мм. Такие сенсоры используются в бюджетных компактах. За их счет получается создать небольшую камеру с длиннофокусной оптикой.

Разрешение матрицы чаще всего составляет 16-20 мегапикселей.

На что влияет размер матрицы?

● Количество шумов. Маленькие матрицы при недостатке света дают больше шума.

● Динамический диапазон. Этот показатель определяет интервал яркости, на который способен фотоаппарат без ущерба самым светлым и самым темным тонам. И, конечно, у полного кадра он выше.

● Глубина цвета. Фулфрейм способен передать больше полутонов и создать плавный переход между ними. А кроп дает возможность сыграть на контрастах.

● Глубина резко изображаемого пространства. Полный кадр позволит сделать качественное фото с плавным размытие, а с кропнутой матрицей для такого результата придется сильно повозиться.

● Размер камеры. Чем меньше матрица, тем меньше фотоаппарат.

● Стоимость аппарата. Чем меньше сенсор, тем ниже цена.

Для того чтобы определить, какой вид матрицы больше всего подходит именно вам, нужно четко понимать задачу фотоаппарата. Если вы хотите просто заполнить семейный альбом, нет смысла тратиться на полный кадр или средний формат. Если же планируете сделать фотографию своей профессией, стоит задуматься о камерах с большой матрицей.

Поделиться с друзьями

Что такое внутренние и внешние параметры камеры в компьютерном зрении? | by Aqeel Anwar

Photo by ShareGrid on Unsplash

Подробное объяснение внутренних и внешних параметров камеры с помощью визуализаций

Изображения являются одним из наиболее часто используемых данных в последних моделях глубокого обучения. Камеры — это датчики, используемые для захвата изображений. Они берут точки мира и проецируют их на двумерную плоскость, которую мы видим как изображения. В этой статье мы рассмотрим полную трансформацию, которая происходит в этом процессе.

Это преобразование обычно делится на две части: Внешняя и Внутренняя. Внешние параметры камеры зависят от ее расположения и ориентации и не имеют ничего общего с ее внутренними параметрами, такими как фокусное расстояние, поле зрения и т. д. С другой стороны, внутренние параметры камеры зависят от того, как она захватывает изображения. Такие параметры, как фокусное расстояние, апертура, поле зрения, разрешение и т. д., определяют внутреннюю матрицу модели камеры.

Эти внешние и внешние параметры являются матрицами преобразования, которые преобразуют точки из одной системы координат в другую. Чтобы понять эти преобразования, нам сначала нужно понять, какие системы координат используются при построении изображений.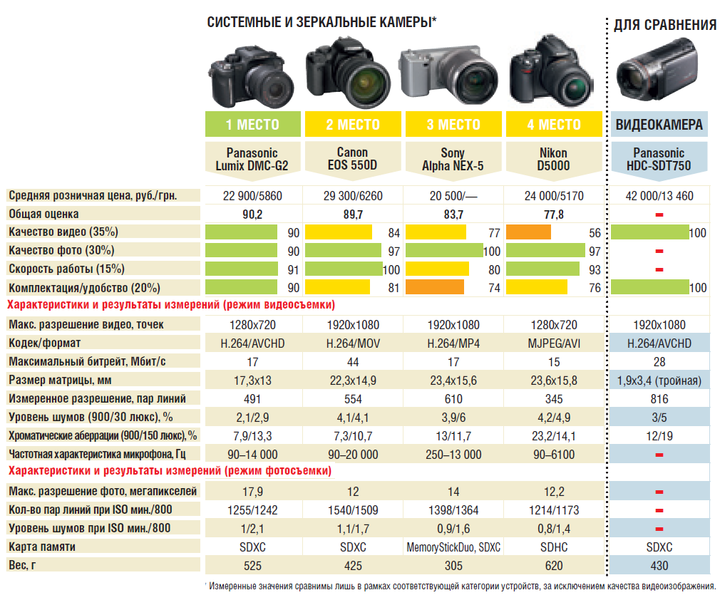

Image By Author

Обычно используемые системы координат в Computer Vision:

1. Мировая система координат (3D)
2. Система координат камеры (3D)
3. Система координат изображения (2D)
4. Система координат пикселей (2D)

Внешняя матрица представляет собой матрицу преобразования из мировой системы координат в систему координат камеры, а внутренняя матрица является матрицей преобразования который преобразует точки из системы координат камеры в пиксельную систему координат.

Мировая система координат (3D):

[Xw, Yw, Zw]: Это трехмерная базовая декартова система координат с произвольным началом. Например, определенный угол комнаты. Точку в этой системе координат можно обозначить как Pw = (Xw, Yw, Zw).

Изображение Автор

Система координат объекта/камеры (3D):

[Xc, Yc, Zc]: Это система координат, которая измеряется относительно начала координат/ориентации объекта/камеры. Ось Z системы координат камеры обычно направлена ​​наружу или внутрь объектива камеры (главная ось камеры), как показано на изображении выше (ось Z направлена ​​внутрь объектива камеры). Можно перейти от мировой системы координат к системе координат объекта (и наоборот) с помощью операций вращения и перемещения.

Image By Author

Матрица преобразования 4×4, которая преобразует точки из мировой системы координат в систему координат камеры, известна как внешняя матрица камеры . Внешняя матрица камеры изменяется, если изменяется физическое расположение/ориентация камеры (например, камера на движущемся автомобиле).

Изображение Автор

Система координат изображения (2D) [Модель пинхола]:

[Xi, Yi]: 2D система координат, в которой 3D точки в системе координат камеры спроецированы на 2D плоскость (обычно перпендикулярную ось z системы координат камеры — показана желтой плоскостью на рисунках ниже) камеры с моделью обскуры.

Image By Author

Лучи проходят через центр отверстия камеры и проецируются на 2D-плоскость на другом конце. 2D-плоскость — это то, что камера захватывает в виде изображений. Это преобразование с потерями, что означает, что проецирование точек из системы координат камеры на 2D-плоскость не может быть обращено (информация о глубине теряется. Следовательно, глядя на изображение, снятое камерой, мы не можем определить фактическую глубину). из точек). Координаты X и Y точек проецируются на 2D-плоскость. 2D-плоскость находится в f (фокусное расстояние) расстояние от камеры. Проекции Xi, Yi можно найти по закону подобных треугольников (луч, входящий и выходящий из центра камеры, имеет одинаковый угол с осью x и y, альфа и бета соответственно).

Image By AuthorImage By AuthorImage By Author

Следовательно, в матричной форме у нас есть следующая матрица преобразования из системы координат камеры в систему координат изображения.

Изображение Автор

Это преобразование (от камеры к системе координат изображения) является первой частью внутренняя матрица камеры .

Пиксельная система координат (2D):

[u, v]: Представляет целочисленные значения путем дискретизации точек в системе координат изображения. Пиксельные координаты изображения — это дискретные значения в диапазоне, который можно получить, разделив координаты изображения на ширину и высоту пикселя (параметры камеры — единицы измерения: метр/пиксель).

Image By Author

Система координат пикселей имеет начало в левом верхнем углу, поэтому наряду с дискретизацией требуется оператор перевода (c_x, c_y).

Изображение Автора

Полное преобразование из системы координат изображения в пиксельную систему координат может быть показано в матричной форме, как показано ниже. Ось X и Y не 90 градусов. В этом случае необходимо выполнить еще одно преобразование для перехода от прямоугольной плоскости к наклонной плоскости (перед выполнением преобразования из изображения в пиксельную систему координат). Если угол между осями x и y равен тета, то преобразование, которое переводит точки из идеальной прямоугольной плоскости в наклонную плоскость, можно найти, как показано ниже.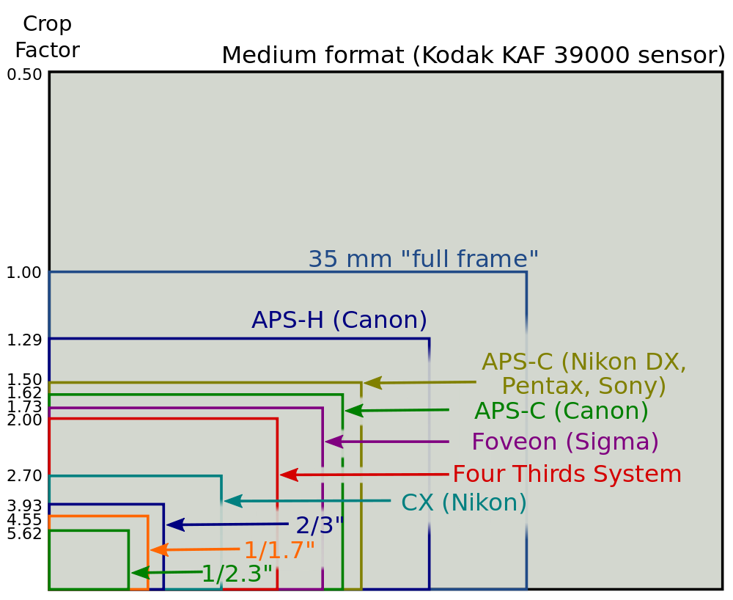 0005 Изображение Автор

Эти две матрицы преобразования, т. е. преобразования из прямоугольной системы координат изображения в систему координат перекошенного изображения и из системы координат перекошенного изображения в пиксельную систему координат, образуют вторую часть внутренней матрицы камеры .

Объединение трех матриц преобразования дает внешнюю матрицу камеры, как показано ниже0012 3D-3D проекция. Вращение, масштабирование, перемещение

Камера-изображение: 3D-2D-проекция. Потеря информации. Зависит от модели камеры и ее параметров (пинхол, f-тета и т.д.)

Изображение в пиксель: 2D-2D проекция. От непрерывного к дискретному. Квантование и сдвиг начала координат.

Матрицы камеры — изображение автора

Внешняя матрица камеры (от мира к камере):

Преобразует точки из мировой системы координат в систему координат камеры. Зависит от положения и ориентации камеры.

Внутренняя матрица камеры (камера-изображение, изображение-пиксель):

Преобразует точки из системы координат камеры в пиксельную систему координат. Зависит от свойств камеры (таких как фокусное расстояние, размеры в пикселях, разрешение и т. д.)

C++ Opencv Калибровка камеры с другим разрешением

спросил 5 лет, 8 месяцев назад

Изменено 5 лет, 7 месяцев назад

Просмотрено 5к раз

Моя камера имеет другое разрешение 1280*480 640*240 320*120

Я использовал алгоритм Opencv3 для калибровки камеры с разрешением 1280*480 и получил матрицу камеры (fx fy cx cy) и матрицу искажения (k1 k2 p1 p2 k3) для этого разрешения .

Но теперь я хочу использовать эту матрицу камеры и матрицу дисторсии для калибровки камеры с разрешением 320*120. Я не знаю, как применить эти две матрицы разрешения 1280*480 к разрешению 320*120. PS Я не калибровал камеру с разрешением 320*120 напрямую, потому что изображение слишком маленькое и алгоритм Opencv не может найти шахматную доску.

Я хочу знать, как изменится матрица камеры (fx fy cx cy) и матрица искажения (k1 k2 p1 p2 k3), если я изменю разрешение 1280*480 на 320*120.

Алгоритм opencv следующий: http://docs.opencv.org/3.0-beta/doc/tutorials/calib3d/camera_dication/camera_dication.html

• c++
• opencv
• матрица
• камера

7

Матрицу искажения менять не нужно. Что касается матрицы камеры (та, что содержит fx, fy, cx, cy ), в вашем случае их просто нужно разделить на 4. Общая формула:

 fx' = (dimx' / dimx) * fx
фу' = (димы' / димы) * фу
 

fx' — это значение вашего нового разрешения, fx — это значение, которое у вас уже есть для исходного разрешения, dimx' — это новое разрешение по оси X, dimx — это исходное разрешение.