5 секретов кадрирования фотографий в Photoshop: cdyu — LiveJournal

? LiveJournal

• Main
• Ratings
• Interesting
• iOS & Android
• Disable ads

Login

• Login
• CREATE BLOG Join
• English (en)
  • English (en)
  • Русский (ru)
  • Українська (uk)
  • Français (fr)
  • Português (pt)
  • español (es)
  • Deutsch (de)
  • Italiano (it)
  • Беларуская (be)

Свет и освещение – Обзор новинок фототехники, видеотехники. Советы по фотосъемке.

Эта статья не посвящена специально вопросам освещения, но, когда речь идет о вопросах экспозиции, владеть основными понятиями, относящимися к свету в фотографических процессах, необходимо. По сути, экспонирование — это управление светом.

Есть два важных фактора, относящихся к свойствам света, которые вы должны учитывать:

1. То, что вы видите, это совсем не то, что есть на самом деле.

2. Вы видите совсем не то, что видит камера.

Рассмотрим первый из этих факторов. Когда наши глаза видят свет, мозг обрабатывает получаемую глазами информацию во многом так же, как камера может обрабатывать информацию, зарегистрированную матрицей. Например, «встроенный» в нас природой баланс белого (ББ) сводит весь свет, который мы видим, к нейтральному белому независимо от цветовой температуры источника.

Так, когда мы видим свет настольной лампы, мы воспринимаем его как свет в середине дня при солнечном освещении. Кроме того, люди способны видеть только очень малый участок полного диапазона световых волн, которые присутствуют вокруг нас. Эти волны мы называем видимым светом.

Рисунок 1. Закон обратных квадратов утверждает, что освещенность увеличивается вчетверо, когда расстояние от вспышки до объекта уменьшается вдвое, и уменьшается вчетверо, когда оно удваивается.

По этим и другим причинам важно помнить и второй из упомянутых факторов: люди и камеры «видят» свет по-разному. Например, для того чтобы удалить цветовой опенок с данной цветовой температурой, вы должны указать камере, как сбалансировать свет относительно шкалы Кельвина при настройке ББ. Также мы можем не видеть свет, выходящий за пределы видимой части спектра, а камера регистрирует ультрафиолетовый (УФ) свет, если не применен светофильтр, задерживающий его.

Другое очень важное различие между человеком и камерой, о котором следует помнить, заключается в том, что мы видим контраст в значительно большем диапазоне яркостей (динамическом диапазоне), чем цифровая камера. Когда мы смотрим на высококонтрастную сцену, мы в состоянии различать детали и в ярких, и в темных местах, а камера этого не может. В результате на фото окажутся без деталей черные или белые участки, или и то, и то.

По этим причинам любой фотограф, желающий освоить мастерство фотографии, должен представлять себе освещение сцены или объекта не так, как воспринимает его человек, а как «видит» его камера.

Интенсивность светового потока и закон обратных квадратов

Интенсивность освещения непосредственно влияет на экспозицию. Чем ярче освещение, тем меньше должна быть экспозиция за счет уменьшения выдержки или проходящего в камеру количества света. Когда освещение становится слабее, экспозицию приходится увеличивать, увеличивая выдержку или количество света. Со съемкой на улице ситуация более понятная. Однако когда применяется искусственное освещение (вспышка) в качестве основного источника, положение меняется. Это происходит потому, что вспышка представляет собой почти точечный источник света. Когда освещается один объект, все в порядке: чем дальше источник света, тем большая экспозиция требуется.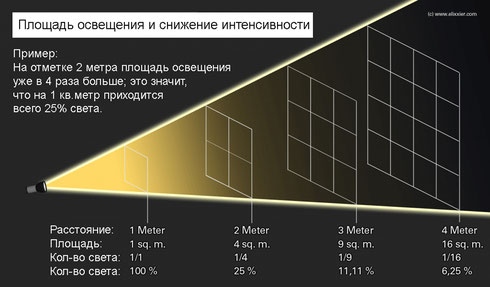 Но если надо осветить два или больше объектов на разном расстоянии, возникает проблема. Требуемая экспозиция становится разной для разных объектов.

Рисунок 2. Недодержка может быть преодолена путем перемещения источника света ближе к модели.

Например, вы снимаете сцену в студии. Модель расположена в 3 м от вспышки на фоне автомобиля, находящегося в 6 м от вспышки. В этом примере автомобиль получит вчетверо (т.е. на 2 ступени) меньше света по сравнению с моделью.

В этих условиях срабатывает закон обратных квадратов, который гласит, что интенсивность освещения уменьшается в четыре раза, если расстояние от вспышки до объекта станет в два раза больше (и увеличится в четыре раза, если уменьшить расстояние между вспышкой и объектом вдвое).

Задача снижения влияния закона обратных квадратов может быть решена следующими способами:

1. Перенесение источника света дальше от объектов, при этом уменьшится отношение расстояний ближайшего объекта и дальнего объекта до источника света. Например, в приведенном примере, если отодвинуть источник на 10 футов (3 м) назад, отношение расстояний станет 2:3 вместо 1:2.

2. Применение источника более рассеянного света, который снизит эффект влияния расстояния.

Хотя закон обратных квадратов применим в основном к искусственным источникам освещения, аналогичная проблема возникает и при солнечном освещении, когда свет попадет в студию через небольшое окно. Такое освещение сходно с источником искусственного освещения.

Разумеется, существуют ситуации, когда закон обратных квадратов работает в пользу фотографа. Например, снижение света требует увеличения экспозиции для объектов фона по отношению к объектам переднего плана. Если компенсацию не вводить, то детали заднего плана останутся недодержанными. Это будет давать преимущество, когда предпочтительно спрятать отвлекающие детали фона, которые иначе скрыть трудно.

Направление и качество света

Направление и качество света играют важную роль в фотографии.

Объект может быть освещен сверху и снизу, сзади и спереди, с боков. Направленность освещения сказывается в расположении теней. Например, при переднем освещении экспозиция будет правильной для всей поверхности объекта. Однако при встречном освещении объект оказывается в тени, хотя фон может быть ярко освещенным. Разная направленность освещения требует различной экспозиции.

Рисунок 3. Переднее освещение идеально для выявления деталей объектов, таких как здания.

Часто боковое освещение считается лучшим, так как позволяет устранить несоразмерность между полностью и частично освещенными сторонами объекта. За счет этого лучше воспринимаются объемы, объекты получают на фотографии форму и глубину.

Качество света зависит от его источника. Прямое (солнечное или искусственное) освещение считается жестким, поскольку формирует плотные хорошо различимые тени. Рассеянный свет (свет солнца, закрытого облаками, отраженный искусственный свет, свет вспышки, рассеянный софтбоксом) считается мягким, неконтрастным.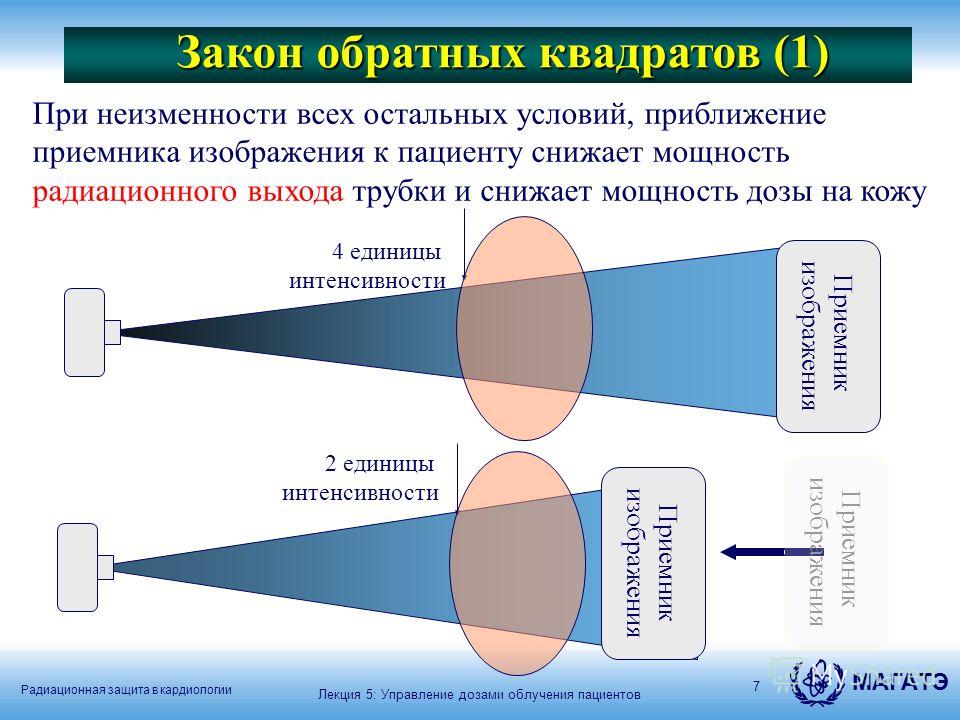

При выборе экспозиции важным свойством света оказывается уровень результирующего контраста. Поскольку жесткий свет (от прямого источника) создает резкие тени, контраст оказывается большим, иногда превышающим ДА матрицы. Сниженный контраст теней получается при мягком рассеянном освещении, при котором легче управлять одновременно и тенями, и светами изображения.

Цветовая температура и баланс белого

Цветовая температура естественного света непостоянна в течение дня и неодинакова для искусственного света в зависимости от типа используемых ламп. Влияют на нее и другие факторы, такие как погода и место съемки.

Рисунок 4. Мягкое освещение снижает контраст, так как уменьшается плотность теней.

В отличие от вариаций интенсивности реальная цветовая температура света мало влияет на экспозицию в цифровой фотографии, хотя изменения ББ могут приводить к коррекции экспозиционных параметров. Об этом стоит упомянуть, поскольку цифровые камеры оборудованы управлением ББ, что позволяет фотографу согласовать реакцию матрицы с цветовой температурой источника света, чтобы нейтрализовать нежелательный цветовой опенок. Это напоминает реакцию человека на цветовой характер освещения.

Известно, что наиболее точный способ установки ББ состоит в измерении его по фотографируемой сцене с последующей ручной установкой соответствующей температуры на камере. Однако этот метод часто трудно применить, в особенности при съемках вне помещения при естественном свете, когда условия могут очень быстро изменяться. Гораздо удобнее так снимать в студии и вне помещений при искусственном свете, например на стадионах при прожекторах.

Для компенсации этого неудобства цифровые камеры имеют предустановки для большинства распространенных источников света (см. в прошлой статье). Выбирая любой из подходящих источников, можно получить сбалансированное или почти нейтральное по цвету изображение. Однако этот способ получить нейтральное свободное от цветного тона изображение не всегда дает удовлетворительный результат. Например, пейзажисты ловят прекрасный золотистый оттенок рано утром или поздно вечером, который может быть сведен на нет неверной установкой ББ.

По этой причине стоит поэкспериментировать с ББ. Это легко сделать, снимая в формате RAW, когда установки камеры можно менять при последующей обработке снимков. Например, недавно я выполнял проект по съемке пейзажа при лунном свете, а затем экспериментировал с различными установками ББ и заметил, что наилучший баланс цвета оказался при задании цветовой температуры на 4100 К (аналогично предустановке для люминесцентных ламп), при котором идеальными оказались глубокие тона синего неба.

Рисунок 5. Жесткий боковой свет хорошо выявляет длинные тени.

Будьте осторожны, используя автоматический баланс белого (АББ) камеры. В большинстве ситуаций АББ камеры позволяет получить приемлемые результаты и часто дает хорошую основу для после съемочной обработки, особенно для RAW-формата. Однако если ваша задача — получить точные результаты в камере, то надо учесть два обстоятельства. Первое связано с диапазоном АББ, который обычно простирается от 3500 до 8000 К. Если реальная цветовая температура источника света выходит за границы этого диапазона, то в выходном изображении будет присутствовать цветовой оттенок.

Второе замечание относится к определенным моделям цифровых камер, у которых имеется измеритель ББ внешнего освещения, работающий в комплексе с обычным TTL-измерителем ББ. К ним относятся Nikon D2X и D2H и их варианты. Такой измеритель ББ окружающего освещения устанавливается над корпусом видоискателя и может оказаться перекрытым полями шляпы или козырьком, например, бейсболки. Это может привести к неточности результатов АББ.

ЦВЕТОВАЯ ТЕМПЕРАТУРА ПРЕДУСТАНОВОК ББ
Установка ББ Цветовая температура (в Кельвинах)
Лампы накаливания                      3,000
Люминесцентные                          4,200
Прямой солнечный свет             5,200
Вспышка                                           5,400
Облачно                                            6,000
Тень                                                   8.000

Применение оптических фильтров

Большинство оптических фильтров может использоваться с цифровыми камерами точно так же, как и с пленочными. Например, поляризационный фильтр будет работать эффективно и одинаково и на цифровой камере, и на пленочной. Некоторые оптические фильтры тоже будут работать, но они меньше подходят для цифровой съемки, например УФ-фильтры. Это связано с тем, что они в меньшей степени влияют на матрицы, чем на пленку.

Рисунок 6. Выбор установки ББ для люминесцентных ламп позволил усилить голубые тона на этом снимке, снятом при свете луны.

Надо быть внимательным, когда вы применяете корректирующие фильтры в сочетании с ББ. Например, если ББ установлен на камере в режиме АББ, а на объективе использован корректирующий фильтр теплого опенка серии 81, АББ сведет к нулю влияние этого фильтра. То же справедливо при холодном фильтре серии 80 и для любого другого корректирующего фильтра.

Аналогично если включена предустановка ББ и применен оптический цветной фильтр, то их эффекты сложатся. Влияние фильтра добавится к установке ББ, что приведет к наложению поправок на изображение.

закон обратных квадратов — со всех языков на все языки

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАканАлтайскийАрагонскийАрабскийАстурийскийАймараАзербайджанскийБашкирскийБагобоБелорусскийБолгарскийТибетскийБурятскийКаталанскийЧеченскийШорскийЧерокиШайенскогоКриЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийВаллийскийДатскийНемецкийДолганскийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГэльскийГуараниКлингонскийЭльзасскийИвритХиндиХорватскийВерхнелужицкийГаитянскийВенгерскийАрмянскийИндонезийскийИнупиакИнгушскийИсландскийИтальянскийЯпонскийГрузинскийКарачаевскийЧеркесскийКазахскийКхмерскийКорейскийКумыкскийКурдскийКомиКиргизскийЛатинскийЛюксембургскийСефардскийЛингалаЛитовскийЛатышскийМаньчжурскийМикенскийМокшанскийМаориМарийскийМакедонскийКомиМонгольскийМалайскийМайяЭрзянскийНидерландскийНорвежскийНауатльОрокскийНогайскийОсетинскийОсманскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПортугальскийКечуаКвеньяРумынский, МолдавскийАрумынскийРусскийСанскритСеверносаамскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиШумерскийСилезскийТофаларскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийТувинскийТвиУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВьетнамскийВепсскийВарайскийЮпийскийИдишЙорубаКитайский

 

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАлтайскийАрабскийАварскийАймараАзербайджанскийБашкирскийБелорусскийБолгарскийКаталанскийЧеченскийЧаморроШорскийЧерокиЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийДатскийНемецкийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГалисийскийКлингонскийЭльзасскийИвритХиндиХорватскийГаитянскийВенгерскийАрмянскийИндонезийскийИнгушскийИсландскийИтальянскийИжорскийЯпонскийЛожбанГрузинскийКарачаевскийКазахскийКхмерскийКорейскийКумыкскийКурдскийЛатинскийЛингалаЛитовскийЛатышскийМокшанскийМаориМарийскийМакедонскийМонгольскийМалайскийМальтийскийМайяЭрзянскийНидерландскийНорвежскийОсетинскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПуштуПортугальскийКечуаКвеньяРумынский, МолдавскийРусскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиТамильскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВодскийВьетнамскийВепсскийИдишЙорубаКитайский

Закон обратных квадратов — Энциклопедия по машиностроению XXL

Использование закона обратных квадратов. Коротко остановимся на некоторых методах определения фотометрических величин.  [c.18]

При использовании этого метода следует принять во внимание, что закон обратных квадратов применим для точечных источников. Кроме того, этот метод практически менее выгоден при сравнении источников, мощности которых резко отличаются, так как в этом случае и будут также сильно отличаться друг от друга.  [c.18]

Пересчетом по закону обратных квадратов определяют мощность дозы на расстоянии / [м] от мишени для тока / [ма]  [c.238]

По закону обратных квадратов, исходя из планировки помещения, определяют плотность потоков нейтронов на расстоянии R [м] от мишени  [c.239]

Глава 9 (Силы, действующие по закону обратных квадратов). Задачу о планетных орбитах легко можно изложить в том виде, как она дана в тексте. Это классическая задача классической механики. Ее следует пропустить, если уже использованы две трети всего учебного времени. В демонстрации  [c.15]

Однако положение не безнадежно, так как мы знаем, что значение любой силы, действующей между двумя телами, должно довольно быстро уменьшаться по мере увеличения расстояния между этими телами. Если бы силы не уменьшались достаточно быстро с увеличением расстояний между взаимодействующими телами, то мы никогда не смогли бы изолировать взаимодействие двух тел от взаимодействий их со всеми другими телами во Вселенной. Значение всех известных сил, действующих между частицами, убывает по крайней мере не менее быстро, чем по закону обратных квадратов. Мы, как и всякое другое тело на Земле, испытываем притяжение главным образом к центру Земли и только в ничтожной степени — к ка-какой-либо удаленной части Вселенной. Если бы мы не опирались о пол, то получили бы ускорение 980 см/с по направлению к центру Земли. Менее сильно нас притягивает Солнце согласно уравнению (7) мы движемся с направленным к нему ускорением 0,6 см/с . Если разумно оценивать возможное ускорение, то следует ожидать, что на тело, значительно удаленное от всех других тел, вероятно, не будут действовать силы, и поэтому оно не будет иметь ускорения. Типичная звезда удалена от ближайших соседних небесных тел на расстояние не менее 10 см ), и поэтому следует ожидать, что она имеет лишь маленькое ускорение. Таким образом, мы пришли к утверждению, что с хорошей степенью приближения можно определить связанную с неподвижными звездами систему координат как удобную систему, не имеющую ускорения.  [c.80]

Если известно, что значение силы обратно пропорционально квадрату расстояния, то какие особые заключения следуют из этого Какие принципиальные свойства Вселенной являются следствиями закона обратных квадратов Займемся теперь этими важными вопросами. Мы будем чаще иметь дело с потенциальной энергией, а не силой. При решении задач на определение потенциальной энергии или силы студенту почти всегда легче  [c.269]

Из закона обратных квадратов можно вывести важное следствие сила, действующая на материальную точку с массой М (пробную массу), находящуюся на расстоянии г от центра однородного тонкого шарового слоя радиусом R, имеет при r >R (т. е. если эта материальная точка находится вне шара) такую величину и направление, как если бы вся масса слоя была сконцентрирована в его центре. Второе следствие сила, действующая на материальную точку, находящуюся внутри слоя, т. е. при г специальный метод решения, в котором используется геометрическая симметрия условий задачи.  [c.269]

Таким образом, на находящуюся внутри слоя пробную массу не действует никакая сила. Это свойство характерно только для сил, подчиняющихся закону обратных квадратов. Вне слоя сила изменяется пропорционально l/r , причем г отсчитывается от центра слоя.  [c.272]

Силы, действующие по закону обратных квадратов, и статическое равновесие  [c.279]

В т. II мы покажем, что группа материальных точек (или точечных электрических зарядов), силы взаимодействия между которыми подчиняются закону обратных квадратов, не может  [c. 279]

Рассмотрим теперь задачу Кеплера требуется найти орбиты двух тел, силы взаимодействия между которыми определяются законом обратных квадратов. Классическим примером объекта для этой задачи является движение планет Солнечной системы. Другие важные примеры — это движение спутников вокруг планет и относительное движение компонентов двойной звезды. Уравнение движения F = М для i-й материальной точки из системы N таких точек имеет следующий вид  [c.280]

Выше мы привели без доказательства следующий важный вывод невозможно устойчивое равновесие системы материальных точек, взаимодействующих по закону обратных квадратов. Это означает, что в системе, где дей-  [c.298]

Применение теоремы о вириале ) дает нам возможность определить среднюю (за большой промежуток времени) кинетическую энергию системы ча-ч тиц, движущихся в ограниченной области пространства под влиянием сил, действующих по закону обратных квадратов  [c. 299]

Докажем теперь теорему о вириале для сил, действующих по закону обратных квадратов. Сначала рассмотрим движение одной материальной точки в поле центральных сил, описываемых следующим уравнением для потенциальной энергии  [c.299]

Область применения теоремы о вириале не ограничивается силами, действующими по закону обратных квадратов. Однако только для сил, подчиняющихся закону обратных квадратов, коэффициент в правой части уравнения (93) равен —1/2.  [c.299]

Средняя кинетическая энергия материальной точки, совершающей пространственно ограниченное движение под действием сил притяжения, подчиняющихся закону обратных квадратов, равна половине ее средней потенциальной энергии с обратным знаком.  [c.300]

Та же теорема справедлива и для любого числа материальных точек, удерживаемых внутри некоторого ограниченного объема взаимными силами притяжения, действующими по закону обратных квадратов, если даже не все массы этих точек одинаковы и если некоторые из сил являются силами отталкивания (например, в молекуле, представляющей собой систему из электронов и атомных ядер). Чтобы доказать это, рассмотрим N материальных точек (обозначим их 1, 2,. ..,. V) с массами Mi, Мг,. .., Мц. Мы можем выразить потенциальную энергию взаимодействия между i-й и /-й материальными точками в следующем виде  [c.300]

Для движения одной материальной точки вириалом называется величина— (1/2), которая, согласно уравнению (96), -равна — (1/2), если силе F определяется по закону обратных квадратов. Прим. ред.]  [c.300]

Половина среднего по времени значения этой двойной суммы, взятая С обратным знаком, называется вириалом системы материальных точек, между которыми действуют силы, подчиняющиеся закону обратных квадратов. фрим. ред.)  [c.301]

Из теоремы о вириале в ее общем виде (112) следует не только то, что материальные точки, связанные между собой силами, действующими по закону обратных квадратов, должны иметь кинетическую энергию, но и то, что кинетическая и потенциальная энергии такой системы всегда сравнимы по величине. Даже если часть материальных точек в начальный момент не движется, силы притяжения, значения которых обратно пропорциональны квадрату расстояния, сближают эти точки друг с другом, увеличивая как потенциальную, так и кинетическую энергии до тех пор, пока средняя кинетическая энергия не станет равной с обратным знаком половине средней потенциальной энергии. В приводимом ниже примере мы воспользуемся теорем ой. о вириале, чтобы оценить температуру внутри Солнца, представляющего собой, как почти все звезды, массу сжатого раскаленного газа.  [c.302]

Теорема о вириале служит ключом к пониманию строения любого вещества, в котором силы сцепления обусловлены главным образом притяжением частиц по закону обратных квадратов. Среднее расстояние между атомами рли атомными ядрами в типичной звезде, по-видимому, всегда больше 10- см, так как плотность такой звезды не превышает 10- г/см . Такие расстояния слишком велики для сильных ядерных взаимодействий, эффективных в пределах около 10 з см поэтому только силы гравитационного притяжения соединяют звезду в единое целое.  [c.302]

Любая достаточно большая газовая туманность, соединенная в одно целое собственным взаимным гравитационным притяжением, превратится в ходе эволюции в звезду или в несколько звезд это является необходимым следствием того факта, что зависимость сил притяжения от расстояния подчиняется закону обратных квадратов.  [c.305]

Полученное выражение показывает, что освещенность, создаваемая точечным источником ), обратно пропорциональна квадрату расстояния от источника до поверхности и прямо пропорциональна косинусу угла, составляемого направлением светового потока (осью узкого конуса, внутри которого распространяется поток) с нормалью к освещаемой поверхности. Это есть основной закон освещенности, создаваемой точечным источником (закон обратных квадратов).  [c.46]

Для протяженных источников мы можем разбить поверхность источников на элементарные участки (достаточно малые по сравнению с Д) и, определив освещенность, создаваемую каждым из них по закону обратных квадратов, проинтегрировать затем по всей площади источника, приняв, конечно, во внимание зависимость силы света от направления. Зависимость освещенности от R окажется при этом более сложной. Однако при достаточно больших (по отношению к величине источника) расстояниях можно пользоваться и законом обратных квадратов, т. е. считать источник точечным. Этот упрощенный расчет дает практически хорошие результаты, если линейные размеры источника не превышают /ю расстояния от источника до освещаемой поверхности. Так, если источником служит равномерно освещенный диск диаметром 50 см, то в точке, лежащей на нормали к центру диска, ошибка в расчете по упрощенной формуле для расстояния 50 см достигает приблизительно 25%, для расстояния 2 м не превышает 1,5%, а для расстояния 5 м составляет всего лишь 0,25%.  [c.46]

Применение всех этих приспособлений требует тех или иных предосторожностей. Закон обратных квадратов справедлив лишь для точечных источников (см. 7) фильтры должны в одинаковой степени поглощать свет различной длины волны (нейтральные фильтры) сетки не должны отбрасывать теней и поэтому употребляются предпочтительно в соединении с линзами, вблизи которых они распола-  [c. 56]

Освещенность 45, 345 —, закон обратных квадратов 46 Осциллятор ангармонический 570  [c.924]

ЗАДАЧА КЕПЛЕРА. Пусть точка притягивается к началу координат согласно закону обратных квадратов  [c.154]

Инфракрасные лучи следуют тем же законам, что и видимый свет, и подчиняются, в частности, закону распространения по прямой линии и закону обратных квадратов. Это важно запомнить в связи с практикой их применения.  [c.20]

Пределы измерения фотоэлектрического калориметра можно, почти не снижая точности, расширять при помощи рассеиваю-щего ослабителя. Яркость лазерного пучка можно уменьшать за счет ослабления по закону обратных квадратов (фиг. 4.18). Излучение, диффузно отраженное от рассеивающей поверхности, падает на фотоэлемент, расположенный на расстоянии R от рассеивателя в направлении, близком к нормали. Перед катодом фотоэлемента помещена диафрагма с отверстием площадью S. Отношение энергии излучения, падающего на фотоэлемент, к энергии лазерного пучка равно  [c.181]

При исследовании наиболее ярких линий наблюдалось насыщение пространственного заряда в фотоумножителях. Пользуясь законом обратных квадратов и стабилизированной лампой, можно определить, при каком выходном токе умножителя наступает насыщение. (Отметим, что при импульсной подаче избытка напряжения увеличивается усиление, уменьшается разрешающее время и насыщение пространственного заряда при данном выходном токе). Выходной сигнал умножителя развертывают на экране осциллографа, фотографируют и затем анализируют при помощи аналоговой вычислительной машины, которая сравнивает экспериментальные кривые с несколькими кривыми затухания, форму которых можно менять.  [c.282]

Можно доказать, что для расчета работы сил всемирного тяготения, подчиняющихся закону обратных квадратов, правильным будет брать значение силы F, соответствующее среднему геометрическому значению г, т. е. соответствующее г = К такими средними геометрическими значениями величины вы знакомились в курсе математики. Итак, для расчета работы при малом перемещении мы можем использовать выражение для силы всемирного тяготения в виде  [c.234]

Поверхность сферической волны, излучаемой баллоном, увеличивается по. мере удаления от баллона соответственно интенсивность звука уменьшается. Каждому увеличению расстояния вдвое соответствует увеличение поверхности звуковой волны в 4 раза, что приводит к снижению интенсивности звука, а следовательно и уровня звукового давления, на 6 дБ. Другими словами, интенсивность звука обратно пропорциональна квадрату расстояния от источника — это так называемый закон обратных квадратов.  [c.128]

Поэтому почти весь звук излучается в направлении, перпендикулярном пластине закон обратных квадратов здесь неприменим.  [c.130]

На распространение звука на открытом воздухе влияют не только градиенты ветра и температуры. На больших расстояниях для высоких частот очень существен другой фактор — вязкость воздуха. Так как частицы воздуха непрерывно совершают колебательные движения, то между соседними частицами возникают силы трения. Тренне всегда приводит к поглощению энергии на высоких частотах, когда соседние частицы колеблются друг относительно друга с большой скоростью, влияние трения -может стать заметным. В результате трения звук частотой 10 кГц на расстоянии в 1 км затухает примерно на 40 дБ, это помимо ослабления, обусловленного законом обратных квадратов. Земля также поглощает звуковую энергию. Об этом мы узнаем в следующей главе. Если местность холмистая, заросшая лесом или покрыта снегом, поглощение может оказаться очень существенным.  [c.134]

Рассмотрим сферический источник звука с уровнем звуковой мощности 100 дБ. Согласно закону обратных квадратов, в открытом пространстве уровень интенсивности звука на расстоянии 3 м от такого источника составит 79 дБ. Внесем этот источник в большое помещение размерами, скажем, ЮХ ХЗ м. Допустим, что коэффициент поглощения стен, потолка и пола в этом помещении равен 0,05 (так будет, если помещение построено, например, из оштукатуренного кирпича или бетона). Что мы услышим теперь Во-первых, по-прежнему прямой звук будет приходить непосредственно от источника к уху, и, если мощность источника не изменилась и между ним и ухом не поставили какого-либо препятствия, уровень интенсивности этого звука по-прежнему составит 79 дБ. Однако, после того как мы услышали прямой звук, волна пробежит далее и упадет на стены, пол и потолок. Эти поверхности поглотят 5% звуковой энергии, а 95% отразят обратно к нам. Звуковые волны снова пробегут мимо нас, и этот процесс будет повторяться снова и снова. Чтобы звук потерял 20% своей энергии, то есть чтобы его уровень упал на 1 дБ, он должен испытать более четырех отражений. В результате добавления всех последовательных отражений, следующих друг за другом, пока они совершенно не затухнут, интенсивность первой отраженной волны окажется увеличенной в 18 раз. Можно показать, что в результате от сложения всех отражений интенсивность звука увеличивается в  [c.181]

На основании очень точных измерений установлено, что показатель степени при г в уравнении (1а) равен 2,000. .. для электростатических сил это проверено вплоть до расстояний порядка 10- см. Имеется большое число результатов измерений, выполненных настолько точно, что они позволили бы обнаружить даже небольшие отклонения от закона обратных квадратов. Основные данные этих измерений излагаются в т. II в связи с обсуждением электростатических сил. В качестве экспериментального подтверждения справедливости закона обратных квадратов для сил тяготения можно прежде всего указать на превос-  [c.267]

Закон обратных квадратов, определяющий центральные силы, может быть также выражен в виде соотношения, согласно-которому потенциальная энергия обратно пропорциональна первой степени расстояния. Как мы видели в гл. 5, абсолютная величина силы F равна —dVIdr. Тогда, согласно уравнению (1а),  [c.268]

Рис. 9.1. Потенциал сил гравитацион ного прнтяжения, как н потенциал сил электростатического притяжения, нропорционален величине -г . При больших расстояниях эта функция убывает с увеличением расстояния относительно медленно таким образом, сила, действующая по закону обратных квадратов, является силой дальнего порядка (дальнодействия). Потенциал ядерных сил притяжения пропорционален величине -ехр(-г/го)г-1

Через несколько лет Эдмунд Г аллей на основе третьего закона Кеплера пришел к выводу, что сила притяжения Солниа тоже должна уменьшаться обратно пропорционально квадрату расстояния планет от него, и пытался определить их пути. Не сумев этого сделать и не получив помощи от Гука и Рена, он поехал к Ньютону, у которого с удивлением обнаружил не только уже гото вое решение, но и еще немало важных материалов. Галлей предложил немедленно опубликовать их, но Ньютон, боясь новых споров и скандалов, только в 1686 г. представил их в Королевское общество. Гук немедленно заявил, что Ньютон использовал его результаты. Ньютон ответил резким письмом Галлею, указав, что Гук сам черпает свои данные у Борелли, а возможно, и у него, поскольку еще в 1673 г. он писал о законе обратных квадратов Гюйгенсу через Королевское общество, секретарем которого был Гук. Наконец конфликт уладили, и в 1687 г. труд Ньютона в трех книгах вышел в свет под названием Математические начала натуральной философии . В нем упоминались имена Гука, Рена и Галлея. Первые две книги посвящены классической механике, в третьей законы механики применяются для описания системы мира — это небесная механика, неизбежно затрагивающая интересы официальной христианской идеологии. Ньютон долга не соглашался на издание третьей книги. 22 мая 1686 г. он писал Третью книгу я намерен теперь устранить, философия — это такая наглая и сутяжная дама, что иметь с ней дело — это все равно, что быть вовлеченным в судебную тяжбу .  [c.85] Иногда утверждают, что отсутствие Г. п. в ОТО обусловлено тем, что в этой теории скорость распространения тяготения конечна (ур-ния ОТО — гиперболич. типа), в отличие от ньютоновской теории (ур-ние Пуассона — эллиптическое). Такое объяснение некорректно. Согласно ОТО, со скоростью света распространяется только изменение гравитац. поля. Сама же ку-лоиовская часть , соответствующая ньютоновскому закону обратных квадратов расстояния, с самого начала простираясь в бесконечность, никуда не распространяется. Математически это выражается в том, что в ОТО нач. данные для решений ур иий поля, задаваемые в иек-рый момент времени (i= onst), должны удовлетворять системе ур-иий, в к-рую входит и ур-ние эллиптич. типа, аналогичное ур-нию Пуассона ньютоновской теории. В действительности причиной отсутствия Г. п. в ОТО является то, что ур-ния пишутся ера-зу для наблюдаемых величин и кол-во ур-ний достаточно для определения всех этих величин.  [c.532]

По мере удаления от пластины, а также с увеличением длинььволны взаимное уничтожение волн по краям пластины становится менее полным. Поэтому на расстоянии нескольких метров от нее, в так называемой дальней зоне, форма волн снова приближается к сферической, а закон обратных квадратов опять входит в силу, однако лишь для каждого направления в отдельности, поскольку в разных направлениях интенсивность звука может быть различной. Зависимость доли излученной интенсивности от направления называют коэффициентом направленности Qв.  [c.130]

---

Визуальный подход к закону обратных квадратов и его влияние на фотографов

Закон обратных квадратов (ISL) — один из тех принципов фотографии, которые сводят людей с ума. Это довольно простая концепция, которую можно разбить на довольно запутанные предложения. В нем говорится, что интенсивность такого эффекта, как освещение или гравитационная сила, изменяется обратно пропорционально квадрату расстояния от источника. Для большинства людей это абсолютно ничего не значит.

Итак, в этом видео фотограф Джо Эдельман здесь, чтобы объяснить это прямо.Как обычно, у Джо есть множество диаграмм и практических примеров, чтобы проиллюстрировать, что это такое. Поначалу может быть сложно осознать ISL. Однако, как только вы это поймете, все обретет смысл. Вы удивитесь, как вы вообще жили, не зная об этом.

Проблема с ISL в том, что это физика. Это математика. И кто хочет с этим заниматься? Люди не хотят думать об этом каждый раз, когда идут снимать фото. Но как только вы это разберетесь, с этим довольно легко справиться.И вам не нужно носить с собой калькулятор. Это определенно не то, чего вам следует бояться.

Начинается с ослабления света. Насколько быстро (или медленно) свет темнеет, чем дальше он удаляется от источника. Источник — вспышка. Джо выстраивает свои яйца в шести дюймах друг от друга для иллюстрации. Вы можете видеть, что существует большая разница в выдержке между экспозицией в 6 дюймов от вспышки и в 12 дюймах. Всего в шести дюймах друг от друга. Однако между ними очень мало различий между 42 и 48 дюймами, которые также находятся на расстоянии шести дюймов друг от друга.

Следующий шаг этой демонстрации показывает, почему ISL сбивает людей с толку. Люди, естественно, просто предполагают, что удвоив расстояние, вы получите половину света, но это не так. Когда вы удваиваете расстояние, вы фактически получаете только четверть света, падающего на ваш объект. Это целых две остановки. Итак, в то время как Джо нуждался в диафрагме f / 22, чтобы адекватно экспонировать яйцо на 6 дюймов, f / 11 (не f / 16) выставляет яйцо на 12 дюймов.

Более простой и легкий пример, показывает портретный объект в 3 футах на среднем сером фоне.Свет также находится на расстоянии 3 фута перед объектом. При съемке с f / 16 объект хорошо экспонируется, на довольно темно-сером фоне.

Обратите внимание на то, что происходит, когда свет перемещается еще на 3 фута от объекта. Удвоение расстояния с 3 футов до 6 футов означает, что диафрагма должна быть увеличена с f / 16 до f / 8, чтобы снова получить хорошую экспозицию. Помните, когда вы удваиваете расстояние, вы теряете две остановки.

А вы замечаете, как фон стал светлее? Это потому, что расстояние между светом и фоном не увеличилось вдвое.Итак, две остановки не потеряны. Объект увеличился вдвое, увеличившись с 3 до 6 футов. Фон только увеличился с 6 футов до 9 футов. Значит, потеряна только остановка. Когда вы настраиваете диафрагму для компенсации объекта, фон становится примерно на стоп ярче.

Когда вы снова удваиваете расстояние, увеличивая расстояние от источника света до объекта с 6 до 12 футов, вы теряете еще две остановки. Это на четыре ступени ниже нашей исходной экспозиции. Теперь, при f / 4, фон стал еще ярче по сравнению с нашим объектом.

Когда вы видите все три рядом, вы действительно замечаете разницу. И помните, что для всех трех снимков установлен одинаковый уровень мощности вспышки. Единственное, что изменилось, — это расстояние до объекта (и фона).

Это только один из способов воздействия ISL на вашу фотографию. И это довольно простой пример. Где это начинает усложняться и где понимание этого является наиболее важным, — это когда вы начинаете фотографировать несколько объектов вместе.Когда вы фотографируете пары или группы, меньше всего вам нужно, чтобы один объект был хорошо освещен, а другие — недоэкспонированы.

Джо на протяжении всего видео показывает, что важно помнить визуальные эффекты. Как свет, расположенный ближе или дальше от объекта, влияет на его представление. Вам не нужно запоминать точное расстояние или апертуру. Как говорит Джо, именно поэтому у нас есть люксметры.

Эта диаграмма показывает визуальное представление того, как и почему работает ISL.И, опять же, помните, что числа не важны. Как расстояние влияет на свет.

Джо приводит в своем видео еще несколько примеров, которые иллюстрируют типичные ошибки, которые делают новые фотографы со вспышкой. Он также объясняет, как их решать. Поэтому, если на ваших портретах были переэкспонированные элементы или групповые снимки, на которых одни люди ярче других, обратите внимание.

А для тех, кто хочет математику, ну…

Возможно, вам захочется посмотреть видео пару раз, чтобы понять его.И вам почти наверняка придется пойти и попробовать это на себе и поэкспериментировать. Но как только вы это поймете, вы будете очень рады, что сделали это.

Закон обратных квадратов | Что это значит для фотографов

Что это значит для фотографов

Хотя для физика закон обратных квадратов распространяется на все виды излучения, как фотографы мы заинтересованы в том, что мы можем видеть. Таким образом, вы можете рассматривать нашу версию как закон обратных квадратов света .

Полезно немного узнать о законе обратных квадратов. особенно при использовании вспышки или студийного освещения.В основном все Закон обратных квадратов говорит, что объект, который вдвое больше расстояние от точечного источника света получит четверть освещения. Для нас, фотографов, это значит, что если вы переместите объект с трех до шести метров, Вам понадобится в четыре раза больше света для той же экспозиции. Проще всего этого добиться, открыв диафрагму объектива. две диафрагмы (см. диафрагму для объяснения) или с помощью вспышки, которая четыре раза такой же мощный.

Что мы подразумеваем под точечным источником света? Хорошо по физике может быть очень строгое определение, но для наших целей Точечным источником можно считать любую вспышку или лампу. В Другая переменная, о которой следует помнить, — это то, что закон работает для «несфокусированные» источники света. Свет от лазера или другого сфокусированный источник не исчезнет так быстро.

Здравый смысл?

Ну … да и нет. Причина, по которой сила света так быстро уменьшается не потому, что у него «заканчивается энергия» или что-то в этом роде это, но поскольку он распространяется на и поэтому меньший и меньшая часть света попадает на объект.Вот небольшая диаграмма, чтобы проиллюстрировать точку.

Как видно из схемы луч света довольно быстро рассеивается, и объект дальше всего от света получает лишь небольшую часть света большая часть луча не попадает в цель.

Чем больше сфокусирован луч, тем выше доля свет упадет на объект. С театральным прожектором например, у которого очень узкий луч, гораздо больше света упадет на объект.

В фотографии мы не склонны использовать лучи, так как они дают очень резкий свет, слишком контрастный для наших целей.Итак, закон обратных квадратов, как правило, большого пальца, работает для нас очень хорошо. Если вы хотите узнать больше о математике, попробуйте эту статью в Википедии о законе обратных квадратов.

Как можно использовать закон обратных квадратов для улучшения своих фотографий?

Если вы используете вспышку на камере, и все происходит автоматически тогда вам не нужно беспокоиться о правильной экспозиции. Кроме вас может «закончиться свет», потому что ваша вспышка не мощная достаточно, чтобы охватить

Закон обратных квадратов для чайников и практическое правило фотографии

Я любил уроки физики в средней школе.В колледже я изучал математику и инженерию. Но когда я впервые прочитал о том, как объясняется закон обратных квадратов для съемки со вспышкой, я остался чесать голову. Это объяснение, график и калькулятор сделают это намного проще, чем многие другие объяснения.

Объяснение закона обратных квадратов

Математик скажет вам, что закон обратных квадратов гласит, что интенсивность силы обратно пропорциональна квадрату расстояния от этой силы .

Вы скажете: что?

Затем математик попытается прояснить это, записав формулу закона обратных квадратов: Интенсивность = 1 / D ² .

Самое простое объяснение закона обратных квадратов с помощью манекена пещерного человека состоит в том, что сила будет иметь резкое падение силы по мере того, как она удаляется от источника, а затем отступает. Это объяснение no math , а вот как выглядит график закона обратных квадратов пещерного человека:

Калькулятор основного закона обратных квадратов

Поэкспериментируйте с ползунком, чтобы увидеть, что произойдет.Обратите внимание на то, что первое снижение силы на 75%, а затем только на 14%.

Как закон обратных квадратов применим к фотографии?

В фотографии — что буквально означает «письмо светом» — закон обратных квадратов описывает поведение света.

Несмотря на то, что он описывает поведение всего света, он наиболее полезен при съемке со вспышкой.

В следующем калькуляторе закона обратных квадратов мы рассмотрим вспышку с ведущим числом 60. Ведущие числа являются темой этого поста.Сейчас это не важно, просто знайте, что в этом примере вы наберете 100% силы на дистанции 60 метров.

Поэкспериментируйте с ползунком, чтобы увидеть, что происходит с мощностью вспышки на вашем объекте, когда вы изменяете расстояние с шагом 30 метров.

Классные интерактивные ползунки, но что можно сделать с практическим применением закона обратных квадратов в фотографии?

Представьте, что вы делаете групповой портрет с одной мощной вспышкой. Вам понадобится широкоугольный объектив, потому что они пятнадцать человек в поперечнике.Они, конечно, подсвечены, потому что никогда не бывает легко. Вы уменьшаете масштаб головки вспышки и кладете перед ней зонтик, чтобы обеспечить охват всех на фотографии.

А теперь расположите вспышку как можно ближе к объектам или подальше от них? Как вы обосновываете свой ответ?

Улучшите свои фотографии с помощью свежих советов, вдохновения и скидок на онлайн-курсы, доставленные на вашу электронную почту.

Нажмите здесь, чтобы подписаться

Посмотрите на следующие диаграммы.

В первом мы разместили нашу вспышку в 10 футах от центра группы, шириной 30 футов. Я сделаю для вас тригонометрию, но люди на концах находятся в 18 футах от вспышки — почти вдвое больше, чем в центре.

Если люди в центре получают правильную экспозицию вспышки, люди на концах будут получать только приблизительно 25% этой мощности. Они будут темными, недоэкспонированными на две целых ступени.

На второй диаграмме мы перемещаем вспышку дальше от центра нашей группы.В тридцати футах. Тригонометрия говорит нам, что люди на концах находятся на расстоянии 33 футов от вспышки — чуть дальше центра.

Люди на концах получают 83% света, который получают люди в центре. Это разница всего в треть остановки — разница, незаметная для большинства людей.

Фактическая настройка мощности вспышки не имеет ничего общего с соотношением света, падающего на все ваши объекты.

Правило большого пальца по закону обратных квадратов

Если вы хотите, чтобы объекты были равномерно освещены с одной стороны на другую, увеличьте мощность и сделайте расстояние до вспышки не меньше ширины объекта .Чем дальше, тем лучше.

• Если ширина объекта десять футов, поместите вспышку на расстоянии не менее десяти футов от центра.
• Если объект шириной тридцать футов, поместите вспышку на расстоянии не менее тридцати футов.
• И так далее.

Сделайте треугольник похожим на второй рисунок выше, а не на первый.

Если вы ищете резкое падение , например, если вы просто хотите осветить объект, но не фон, уменьшите мощность и поместите источник света как можно ближе к объекту.Чем ближе, тем резче спад.

После того, как у вас все получится (каламбур?), Остается лишь настроить мощность вспышки для правильной экспозиции.

Закон обратных квадратов зависит от расстояния, а не от настроек мощности вспышки.

Теперь все имеет смысл?

Ознакомьтесь с этим видео от Марка Уоллеса из AdoramaTV:

Понимание закона обратных квадратов для значимого фотографического освещения

Освещение + математика = скучно?

На первый взгляд тема статьи выглядит суховатой, да и скучной.Или, по крайней мере, ничего, что, по вашему мнению, вам необходимо знать, чтобы создавать привлекательные фотографии, верно?

Ну вот и далеко!

Йоханнес Даунер, генеральный директор и основатель программного обеспечения elixxier (которое изобрело SAL3D) написал краткий, подробный, (почти) легкий для понимания дискурс о мощности источника света, распределении света, размещении света (= расстояние) и воздействии / соотношение качества света, диафрагмы (и / или) выдержки.

Следующая экскурсия — безусловно, наиболее точно написанная статья о законе обратных квадратов , которую я видел за долгое время.И это, конечно, проиллюстрировано и подтверждено симуляциями, выполненными в SAL3D.

Я взял на себя смелость добавить несколько реальных примеров, материал, который был взят из моей электронной книги ESSENTIALS Lighting… .

Как закон обратных квадратов улучшает ваш дизайн освещения

В общем, закон обратных квадратов объясняет непропорциональное ослабление света с увеличением расстояния от объекта до источника света. Эти знания помогают нам лучше понять, как соотносить свет и освещение с расстоянием до объекта и его яркостью.

Давайте начнем с того, что вернемся к корням и сначала объясним диафрагму (диафрагму)…

Диафрагма (= диафрагма)

• Переключение с максимальной диафрагмы на следующую меньшую уменьшает количество падающих частиц света, попадающего в ваш объектив.
• Диаметр апертуры каждый раз уменьшается в 1 / √2 раза, что также сокращает поверхность линзы и, следовательно, количество света вдвое.
• Благодаря этой градации мы просто настраиваем выдержку и диафрагму в соответствии с существующим освещением: каждое число диафрагмы (диафрагма) является результатом предыдущего, умноженного на √2 = 1,414…
• В то же время , округляем результат так, чтобы, например, апертура 4 — согласно расчету 4 x 1.4 — переходит в следующее большее значение диафрагмы 5,6.
• Вот отрывок из этой хорошо известной последовательности, который гласит:
  f / 1> f / 1,4> f / 2> f / 2,8> f / 4> f / 5,6> f / 8> f / 11> f / 16> f / 22> f / 32

Закон обратных квадратов

Предположим, у нас есть точечный источник света. Он распространит свою энергию равномерно во всех направлениях .Поэтому, если вы хотите найти все точки в пространстве, в которых энергия имеет одинаковую интенсивность, вам придется нарисовать сферу вокруг точки источника. Чем больше радиус сферы, тем больше «поверхность», по которой распространяется энергия.

Связь между радиусом и площадью поверхности сферы является обратной квадратной зависимостью. Это означает, что интенсивность будет зависеть от 1 / r ² . Если вы удвоите расстояние от источника, интенсивность не уменьшится вдвое, а упадет до четверти своего значения, утроение расстояния приведет к падению интенсивности до девятой и так далее.

————————————————- ——

Любой точечный источник, который распространяет свое влияние равномерно во всех направлениях без ограничений до его диапазона будет подчиняться закону обратных квадратов. Просто эксперимент может проиллюстрировать это.

Это исходит от строго геометрические соображения. Интенсивность воздействия на любом заданном радиусе r — мощность источника, деленная на площадь поверхность сферы на этом радиусе.

Строгое геометрические по своему происхождению, закон обратных квадратов применим ко многим различным явления.

Точечные источники гравитационной силы, электрического поля, света, звука, электромагнитного или ядерного излучения подчиняются закону обратных квадратов.

Как одно из полей, подчиняющихся общему закону обратных квадратов, гравитация можно поместить в форму, показанную ниже, показывая, что ускорение силы тяжести, g, является выражением напряженности гравитационного поля.

Как одно из полей, подчиняющихся общему закону обратных квадратов, электрическое поле точечного заряда можно записать в виде, показанном ниже, где точка заряд Q является источником поля.Электрическая сила в кулоновской закон следует закону обратных квадратов.

Как одно из полей, подчиняющихся общему закону обратных квадратов, точка источник излучения можно охарактеризовать следующим соотношением: вы говорите о беккерелях, рентгенах, радах или ремах. Все меры воздействия уменьшатся по закону обратных квадратов.

Щелкните здесь, чтобы перейти на интерактивную страницу Java-Script, которая позволяет вам провести «киберэксперимент»

.