3 4 или 1 2 что больше: Что больше 1/2 или 3/4? Решение и ответ!
Как правильно сравнивать дроби?
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше. |
А теперь на примерах.
Пример 1. Сравните дроби:
- Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
8 < 12
12 > 8 - Это значит, что < Изи!
Пример 2. Сравните дроби:
- Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
9 > 10
1 < 10 - Это значит, что >
Пример 3.
- Знаменатели дробей снова равны. Сравниваем числители:
3 > 1
1 < 3 - Это значит, что >
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
- Запишем в виде дробей: и
- А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
6 > 5
5 < 6. - Это значит, что >
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой.
Запишитесь и участвуйте в розыгрыше 8 уроков
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Запомните правило:
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем. |
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
9 > 7
7 < 9 - Значит, дробь с меньшим знаменателем — больше:
Пример 2. Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
10 < 11
11 > 10 - Значит дробь с меньшим знаменателем — больше:
Пример 3.
Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3 < 6 - Значит, дробь с меньшим знаменателем — больше.
Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка.
А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:
Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение😉.
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями.
Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Запоминаем
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю, а затем сравнить числители.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
- Нужно подобрать число, которое будет делиться на 7 и на 2, например, 14. Проверим:
14:7 = 2 - Первую дробь умножаем на дополнительный множитель 2:
- Вторую дробь умножаем на дополнительный множитель 7:
- Дроби приведены к общему знаменателю:
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
- Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
30 : 15 = 2
30 : 2 = 15 - Первую дробь умножаем на дополнительный множитель 2:
- Вторую дробь умножаем на дополнительный множитель 15:
- Дроби приведены к общему знаменателю:
- Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
- 6/5 — неправильная дробь.
- Выделим целую часть:
- Значит, что
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
- 12 — 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
Вычитаемая дробь меньше уменьшаемой
- Выполняем вычитание:
Пример 2.
Найдите разность:
- Смешанные дроби превращаем в неправильные:
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю:
- Наименьшее общее кратное — 40
40 : 8 = 5
40 : 5 = 8 - Умножаем первую дробь на дополнительный множитель 5:
- Умножаем вторую дробь на дополнительный множитель 8:
- Дроби приведены к общему знаменателю:
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше.
Это значит, что
Пример 3. Сравните дроби:
Как решаем:
Ответ:.
- По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
- Наименьшее общее кратное — 15:
15 : 15 = 1
15 : 5 = 3 - Умножаем первую дробь на дополнительный множитель 1:
- Умножаем вторую дробь на дополнительный множитель 3:
- Дроби приведены к общему знаменателю:
- Сравниваем числители получившихся дробей: 3 < 6
Пример 4. Найдите разность:
Как решаем:
- Смешанные дроби превращаем в неправильные:
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю.
- Наименьшее общее кратное — 42:
42 : 7 = 6
42 : 6 = 7 - Умножаем первую дробь на дополнительный множитель 6:
- Умножаем вторую дробь на дополнительный множитель 7:
- Дроби приведены к общему знаменателю.
- Теперь можно вычитать:
Ответ:
Что больше 1 или 3 4? – Обзоры Вики
Как вы видели, если у двух или более дробей один и тот же знаменатель, вы можете сравнить их, посмотрев на их числители. Как вы можете видеть ниже, 3/4 больше 1/4.
Следовательно, 1/8 больше или меньше 1 4? 1 8 < 1 4 Четвертые больше восьмых, поэтому одна четвертая больше одной восьмой.
Что такое 7/8 в виде десятичной дроби? Найти больше дробей до десятичных дробей
| 1 / 1 = 1 | 1 / 8 = 0.125 | 7 / 8 = 0.875 |
|---|---|---|
| 1 / 4 = 0.25 | 1 / 11 = 0.09 | 4 / 11 = 0.36 |
| 1 / 5 = 0.2 | 1 / 12 = 0.083 | 7 / 16 = 0.4375 |
| 1 / 6 = 0.16 | 1 / 16 = 0.0625 | 15 / 16 = 0.9375 |
| 1 / 7 = 0.142857 | 2 / 3 = 0.6 | 19 / 32 = 0.5937 |
• 1 декабря 2021 г.
Дополнительно Что больше ½ или ¼? Дробь 1/4 меньше чем 1/2 . Это может показаться странным, поскольку число 4 больше числа 2.
Что больше 1/4 или 3/8 дюйма? Отвечать: 3/8 больше 1/4
Давайте найдем значение дробей в следующем разделе. Объяснение: 3/8 выражается как 0.375 в десятичной форме, а 1/4 выражается как 0.25 в десятичной форме. Понятно, что значение 3/8 больше, чем 1/4.
1/4 это четверть?
Доля одной четверти, одна четверть, 25% золото 0.25; см. Квартал (значения)
Какая дробь наименьшая? Чай дробь с наименьшим числителем является самым маленьким. Дробь с наибольшим числителем и есть самая большая.
Что такое 7 16 в виде десятичной дроби? Ответ: 7/16 в виде десятичной дроби равно 0.4375.
Что такое 57 220 в виде десятичной дроби?
Это буквально все, что нужно сделать! 57/220 в виде десятичной дроби 0.25909090909091.
Также Что такое 15 на 16 в виде десятичной дроби? Ответ: 15/16 записывается как 0.
9375 в десятичной форме.
Какая дробь меньше 1 4?
| Таблица преобразования дробей | ||
|---|---|---|
| Доля | Десятичная дробь | Миллиметры |
| 7/32 | 0.21875 | 5.556 |
| 15/64 | 0.234375 | 5.953 |
| 1/4 | 0.25 | 6.35 |
Это больше или меньше? Равно, больше или меньше чем
| = | Когда два значения равны, мы используем знак «равно». | пример: 2 + 2 = 4 |
|---|---|---|
| < | Когда одно значение меньше чем другой, мы используем знак «меньше» | пример: 3 <5 |
| > | Когда одно значение больше другого, мы используем знак «больше». | пример: 9> 6 |
Какой размер больше 5/16 или 3 8?
Сравнение дробей: Дроби можно сравнивать, если они имеют общий знаменатель.
Например, 5/16 дюйма и 3/8 дюйма — это два измерения на линейке. Чтобы сравнить две дроби, у них должен быть общий знаменатель 16. 3/8 больше, чем 5/ 16.
Какое число больше?
Число, которое занимает первое место с большей цифрой, находится дальше от 0 на числовой прямой. Самое дальнее правое число на числовой прямой это большее число.
Это больше или меньше, чем? Равно, больше или меньше чем
| = | Когда два значения равны, мы используем знак «равно». | пример: 2 + 2 = 4 |
|---|---|---|
| < | Когда одно значение меньше чем другой, мы используем знак «меньше» | пример: 3 <5 |
| > | Когда одно значение больше другого, мы используем знак «больше». | пример: 9> 6 |
Какая дробь больше 1 2? Ответ: Да, 3/4 больше 1/2.
В этом можно убедиться, переведя обе дроби в десятичные.
Десятичное число 0.75 больше 0.5, поэтому 3/4 больше 1/2.
Что означает ¼?
одна из четырех равных или эквивалентных частей, на которые что-либо делится или может быть разделено. 2. четвертая часть, сп. из одного (¼).
Как называется ¼? Мы пишем одна четвертая есть ¼. … Когда целое разделено на 4 равные части, и каждая часть называется одной четвертью. Четверть — это одна из четырех равных частей. Пишется как 14. Читается как одна четверть или одна четвертая.
Чему равно ¼ разделить на 4?
Другими словами – одна четверть, деленная на четыре = одна шестнадцатая.
Какая дробь самая большая? Как известно, разница между знаменателем и числителем равна 1, тогда дробь с наибольшим числителем является наибольшей дробью. ∴ 7/8 является наибольшей дробью. Следовательно, 7/8 — самая большая дробь.
Что такое 7 16 как число?
Таблицы преобразования дробей в десятичные
| дробь = десятичная | ||
|---|---|---|
8 / 11 = 0. 72 | 10 / 11 = 0.90 | |
| 1 / 12 = 0.083 | 5 / 12 = 0.416 | 11 / 12 = 0.916 |
| 1 / 16 = 0.0625 | 3 / 16 = 0.1875 | 7 / 16 = 0.4375 |
| 11 / 16 = 0.6875 | 15 / 16 = 0.9375 |
Как перевести 7/16 в проценты? Что это? Теперь мы видим, что наша дробь равна 43.75/100, что означает, что 7/16 в процентах составляет 43.75%.
Сколько в миллиметрах 7 16?
Таблица перевода дюймов в мм
| Размеры — дюймы в метрические единицы | ||
|---|---|---|
| 0.438 « | 7 / 16 « | 11.13 мм |
| 0.500 « | 1 / 2 « | 12.70 мм |
| 0.563 « | 9 / 16 « | 14.30 мм |
| 0.625 « | 5 / 8 « | 15.88 мм |
Дроби — как объяснить ребенку действия с дробями
Тема дробей — одна из самых непростых для школьников.
Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей.
Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь.
С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные.
Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
- 15/4,
- 22/12,
- 30/7.
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1.
Преобразовать в смешанное число неправильную дробь:
- 27/4,
- 18/5,
- 45/7.
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
- 3 4/5;
- 12 7/11.
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07.
Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
- 8/10,
- 4/100,
- 7/1000.
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2.
Сократить дробь 10/25Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
- 6/18,
- 20/40;
- 7/21.
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное.
Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
Вычитание дробей
Эта операция проводится аналогично сложению.
Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением.
Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число.
В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби.
Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- Таблица умножения для детей
- Как объяснить ребенку состав числа?
NumberNut.com: дроби и десятичные дроби: дроби: больше или меньше
Числа и счет|Арифметика| Дроби и десятичные дроби |Предварительная алгебра|Карта сайта
В этом разделе мы будем составлять много «подобных дробей» (дроби с общими знаменателями ). Помните, что 1 можно представить дробью, если числитель и знаменатель совпадают. 2/2 соответствует 1. 9/9 соответствует 1. 52/52 соответствует единице. Если это сбивает с толку, подумайте об этом как о проблеме деления. 2÷2=1. 9÷9=1.
52÷52=1. Кроме того, помните, что при умножении все, что умножается на 1, дает одно и то же значение. 2*1=2. 9*1=9. 52*1=52. Этот математический факт называется тождественным свойством умножения. Мы собираемся использовать этот трюк, чтобы сделать похожие дроби.
Мы знаем, что 1/3 * 1 = 1/3. Допустим, нашей задаче о дробях нужно было решить, чтобы знаменатель был равен 18 (нижнее число). Используйте концепцию, согласно которой 1 равно , что эквивалентно до 6/6. Это означает…
• Начало: 1/3 * 1 = 1/3
• Поменять местами: 1/3 * 6/6 = 1/3
• Умножить дроби: (1*6)/(3*6) = 6/18
• Упростить для проверки Ответ: 6/18 = 1/3
Мы использовали свойство идентичности для создания эквивалентных дробей. Мы создали один и тот же знаменатель для всех наших терминов.
Вы получите много задач, где вас попросят сравнить дроби. 1/2 больше или меньше 1/3? Вы уже должны знать о символах « больше » и « меньше ».
С целыми числами проще…
• Сравните 2 и 1. Вы знаете, что два больше, чем один.
• Сравните 13 и 27. Вы знаете, что тринадцать меньше двадцати семи.
• Сравните -40 и -2. Мы уже работали с отрицательными целыми числами. -40 меньше -2.
А дроби? Один несколько уровней это так же просто. Дроби с большими знаменателями (нижнее число) имеют больше возможных частей. Когда у вас есть больше частей, которые можно разместить в одном и том же пространстве, они должны быть меньше. Если количество штук (числитель) в каждой дроби одинаково, то та, у которой знаменатель больше, всегда будет меньше другой. Это работает только тогда, когда вы можете сравнить одинаковое количество штук.
Примеры:
Сравните 1/2 и 1/5.
Подумай о пироге. Один пирог разрезается на две части, а другой на пять частей. Какой кусок больше? Половина пирога больше одной пятой части пирога. Таким образом, 1/2 больше, чем 1/5.
Сравните 5/8 и 5/10.
Для начала заметьте, что у вас есть по пять штук каждого. Поскольку это одно и то же число, мы можем их игнорировать. Затем посмотрите на знаменатели и подумайте о кусках пирога. Восьмая часть пирога больше, чем десятая часть пирога. По сути, у вас есть пять больших частей по сравнению с пятью меньшими частями. Так что 5/8 больше, чем 5/10.
Когда числители одинаковы, нам не нужно беспокоиться о преобразовании каких-либо чисел. Давайте посмотрим на одинаковые дроби (с одинаковыми знаменателями). Они легкие. Вам нужно только сосредоточиться на значениях числителей, ничего не конвертируя.
Примеры:
Сравните 2/9 и 6/9.
У вас одинаковые знаменатели, поэтому и размер фигур одинаковый. Теперь посмотрите на числители. Две штуки по сравнению с шестью штуками. У вас есть этот. Если 2 < 6, то...
2/9< 6/9
Сравните 17 августа с 17 марта
И снова у вас одинаковые знаменатели. Кусочки одинакового размера. Сравните восемь с тремя.
Так как восемь больше трех…
17/8 > 17/3
Легкие теперь не нужны. Но что происходит, когда у вас разные дроби (разные знаменатели) с разными числителями? Вам нужно будет сделать их «подобными дробям», чтобы действительно сравнить их. Это означает, что вам понадобятся одни и те же нижние числа (общие знаменатели) для каждой дроби. Вам понадобится небольшое умножение, чтобы сделать это.
Примеры:
Сравните 5/6 и 17/18
У нас есть шестые и восемнадцатые для знаменателей. Нам нужно сделать их похожими на дроби. У них общий делитель 6 (6×3=18). Это хорошо, нам нужно иметь дело только с термином 5/6. 17/18 может остаться таким, какой он есть. Поскольку мы знаем, что 6×3=18, давайте умножим числитель и знаменатель на 3. Воспользуемся описанным выше процессом «начало-перестановка-умножение».
5/6 = 5/6 * 1 = 5/6 * 3/3 = (5*3)/(6*3) = 15/18
Теперь можно сравнить 15/18 и 17/18. Без проблем.
15/18 < 17/18
Сравните 6/9 и 3/4.
Обратите внимание, что у нас есть девятые и четвертые для знаменателей. В этой проблеме нет общих факторов. Быстрый способ — создать эквивалентные дроби для каждого термина и сравнить их. Как? Умножьте первый член на 4/4, а второй на 9/9. Другими словами, мы будем умножать верхние и нижние числа одного члена на знаменатель другого. Используйте описанный выше процесс start-swap-multiply для обоих терминов.
6/9 = 6/9* 1 = 6/9 * 4/4 = (6*4)/(9*4) = 24/36
3/4 = 3/4 * 1 = 3/4 * 9/9 = (3*9) /(4*9) = 27/36
Вы это видели? Когда вы умножаете на знаменатель другого члена, вы получаете одинаковые дроби. Теперь мы можем сравнить 24/36 и 27/36. Проще простого.
24/36 < 27/36
► СЛЕДУЮЩАЯ СТРАНИЦА ПО ДРОБЯМ И ДЕСЯТИЧНЫМ ЗНАЧЕНИЯМ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или выполните поиск на сайтах…
- Обзор
- Типы номеров
- Факторы
- Дроби
- Структура
- Уменьшение
- Более или менее
- Смешанные номера
- Смешанные номера 2
- Дополнение
- Вычитание 1
- Вычитание 2
- Умножение
- Подразделение
- Проблемы со словами
- Реальный мир
- Десятичные числа
- Проценты
- Оценка
- Коэффициенты
- Деньги
- Виды деятельности
- Дополнительные темы по математике
Википедия:
https://en.
wikipedia.org/wiki/Fraction_%28mathematics%29
Британская энциклопедия:
http://www.0150
Университет Делавэра:
https://sites.google.com/a/udel.edu/fractions/
Калькулятор дробей
Этот калькулятор дробей выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 .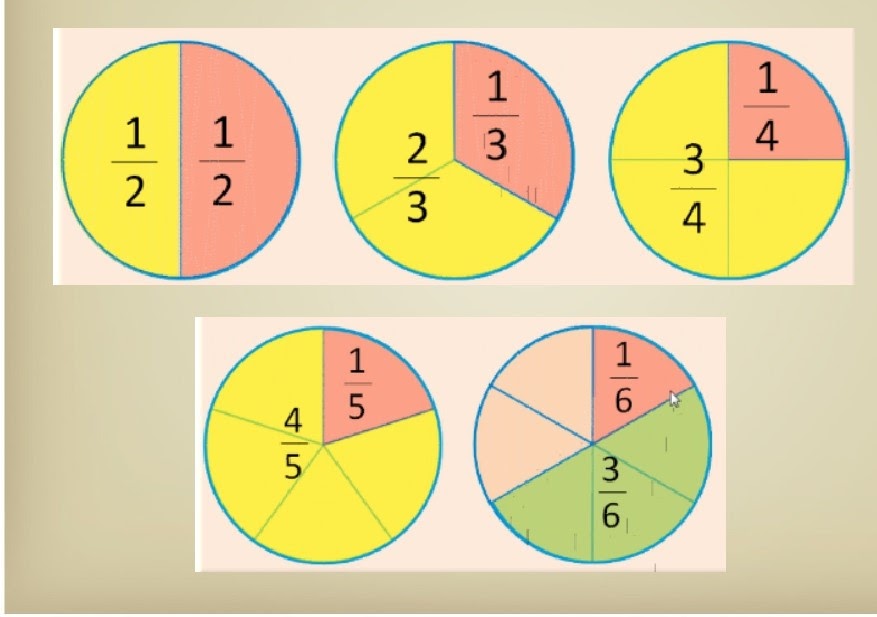
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс знак | Дополнение | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | Минус. | multiplication | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2/3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Использовала 1/3 яйца. Какая часть яиц использовалась?
Какая часть карандашей не имеет ластика на конце?
