Частотное разложение на 3 частоты: Метод частотного разложения. Разложение на три частоты
Метод частотного разложения. Разложение на три частоты
Автор: Сергей Бунин. Дата публикации: . Категория: Обработка фотографий в фотошопе.
Метод частотного разложения
Разложение на три частоты
Приветствую Вас уважаемые коллеги!
В этой заключительной части материала о методе частотного разложения мы с Вами познакомимся еще с одним приемом – это разложение на три частотные составляющие изображений для ретуши.
Я думаю, Вы уже разобрались с предыдущим материалом и научились раскладывать изображение на две пространственные частоты.
Попробовали все прелести работы на разных слоях, с отдельно выделенной формой и фактурой.
Разложение же на три составляющие облегчит нам работу, т.к. мы выделим слой средних частот «СЧ», на котором будем оставлять все основные неприятности и так называемые «некрасивости» в виде родинок, прыщей, пигментных пятен, оспин и целлюлита.
Слой «НЧ» организуем только для работы со светотеневым рисунком и цветом, а на слое «ВЧ» оставим самую мелкую и необходимую фактуру. Такая структура частотного разложения обеспечит нам большую гибкость, более эффективный и профессиональный подход к ретуши фотографий, нежели метод с двумя полосами, особенно когда требуются высокое качество обработки.
Предыдущий материал:
- Урок «Метод частотного разложения. Разложение на две частоты»
- Урок «Метод частотного разложения. Инструменты для ретуши»
Итак, рассмотрим принцип разложения на три пространственные частоты.
Открываем исходное изображение в программе. Фотография была сделана на китовый объектив, потому светопередача не лучшая, но идейно она мне нравится: «Через три поколения – три полосы частот». Сделаем три копии изображения и сразу переименуем их в «НЧ» — низкие частоты, «СЧ» — средние частоты, «ВЧ» — высокие частоты.
Проводим анализ и видим, что у правнучки необходимо убрать дефект от простуды под нижней губой, прабабушке, хоть она и не молодая, удалить пигментные возрастные пятна, чуток разгладить кожу и поправить светотеневой рисунок.
Начнем с нижних частот, отключив временно видимость двух верхних слоев, и будем, как принято по технологии применять к ним фильтр «Размытие по Гауссу». Примерно при радиусе =12 пикселей детали, от которых мы хотим избавиться пропали. Нажимаем «Ок».
Далее переместимся на слой «ВЧ», включаем его видимость. Применяя к нему фильтр «Цветовой контраст постараемся оставить на нем только аккуратную и необходимую нам фактуру, но при этом следить за тем, чтобы не проявились те дефекты, от которых надо избавиться. В результате при разложении на три полосы частот радиус фильтра «Цветовой контраст» получается маленьким, и иметь примерное соотношение 1/3÷1/4 к радиусу фильтра «Размытие по Гауссу». Нажимаем «Ок».
Отключим временно видимость слоя «ВЧ». После этого начинаем формировать среднюю полосу частот. Переходим на слой «СЧ» и включим его видимость. Для того чтобы вычесть из этого слоя низкочастотную составляющую по аналогии со слоем «ВЧ» применяем фильтр «Цветовой контраст» с радиусом равным радиусу размытия по Гауссу, т. е. =12 пикселям.
е. =12 пикселям.
Для того чтобы избавиться от высокочастотной фактуры, ее просто надо размыть, применив фильтр «Размытие по Гауссу» с радиусом равным радиусу фильтра «Цветовой контраст» применяемого при отделении ВЧ составляющей. Радиус =3,5 пикселя.
Теперь надо сложить наше изображение в единое целое. Сначала к низкочастотному слою прибавляем слой с полосой средних частот. Вызываем корректирующий слой «Кривые», понижаем контрастность в два раза.
Применяем Кривые непосредственно к слою «СЧ», отсекая все нижележащие слои, нажав на кнопку с изображением угловой стрелки направленной вниз.
Меняем режим наложения слоя «СЧ» на «Линейный свет».
Осталось еще прибавить высокочастотные составляющие к общему изображению. Также создаем корректирующий слой «Кривые», понижающий контрастность в два раза, но уже применительно к слою «ВЧ».
Также меняем режим наложения слоя «ВЧ» на «Линейный свет».
Вот если сейчас выключить видимость слоя со средними частотами можно увидеть предварительный результат Вашей работы. Выглядит он немного странно, но по нему можно на промежуточном этапе оценить правильность подбора радиусов применяемых фильтров. Так как вместе с отключением слоя «СЧ» отключается видимость тех «некрасивостей», которые были вынесены на этот слой. В связи с этим и можно оценить правильность выделения нежелательных дефектов.
Выглядит он немного странно, но по нему можно на промежуточном этапе оценить правильность подбора радиусов применяемых фильтров. Так как вместе с отключением слоя «СЧ» отключается видимость тех «некрасивостей», которые были вынесены на этот слой. В связи с этим и можно оценить правильность выделения нежелательных дефектов.
Приступаем к ретуши нашего изображения.
Для наглядности можно создать вспомогательный корректирующий слой «Микширование каналов» на самом верху структуры слоев. Он не будет оказывать никакого воздействия на результат Вашей работы, но поможет проявить те дефекты, неравномерности кожи и пятна, которые не сразу можно различить на некоторых фотографиях.
На панели «Свойства» полученного корректирующего слоя включаем режим отображения «Монохромный». Снижаем процент наличия КРАСНОГО цвета в изображении на -150%, процент СИНЕГО цвета, так как в нем содержатся основные дефекты кожи, наоборот увеличиваем до +200%, ну а ЗЕЛЕНЫМ цветом можно подобрать оптимальную на Ваш взгляд яркость.
Изображение выглядит страшновато, но зато на нем как уже отмечалось, явно видны все дефекты кожи.
Начинают ретушь, как правило, на слое со средними частотами. Работают на нем так же, как и на слое «НЧ», т.е. с применением инструмента «Штамп» с мягкими краями, непрозрачность для постепенного воздействия понижают примерно до 70÷80%, но можно и сразу применять 100%-ную непрозрачностью. Образец для Штампа берется с рабочего слоя в режиме «Активный слой».
Также можно устранять дефекты и на маске, созданной для слоя «СЧ».
Тогда возможно применение обычной кисти с мягкими краями и равной либо приближенной к 100% непрозрачности.
Вычищая средний слой, начинаем наслаждаться своей работой, наблюдать какой гладкой становится кожа. Но работать надо аккуратно и постепенно, может даже точечно, т.е. подчищать только определенные участки, имеющие дефекты, не трогая остальные. Это позволяет сохранить имеющиеся неоднородности и рельеф в полосе средних частот, создающие натуральность изображения.
Продемонстрирую Вам основные участки, которые подверглись воздействию на «СЧ» слое.
Отключаем вспомогательный слой «Микширование каналов» и видим, какой более мягкой и бархатистой стала кожа.
Далее есть смысл перейти к высокочастотному слою и, используя инструмент «Штамп» с жесткими краями и 100%-ной непрозрачностью.
Устраняем дефекты мелкой фактуры.
Не поддайтесь соблазну вылизать фактуру кожи при включенном вспомогательном слое, не забывайте о нем, иначе получите двадцати летнюю прабабушку.
Некоторые детали изображения могут находиться не только в средней полосе частот, но в двух или даже в трех частотных диапазонах. Обратите внимание на представленные ниже скриншоты. Выделенная часть изображения присутствует во всех частотных полосах.
Данная морщина, конечно, имеет право на существование у пожилой женщины, но я покажу, как можно устранить данный дефект. В таких случаях работая на слое «ВЧ» при всех включенных слоях, т.е. имея в окне просмотра композитное изображение, можно использовать обычные инструменты такие как, например «Заплатка».
В таких случаях работая на слое «ВЧ» при всех включенных слоях, т.е. имея в окне просмотра композитное изображение, можно использовать обычные инструменты такие как, например «Заплатка».
Выделяем данным инструментом область, требующую исправления. Потом наводим курсор на выделенную область и, зажав левую кнопку мышки (ЛКМ), перетягиваем ее на участок с более ровной кожей. Отпускаем ЛКМ и получаем уже не такой глубокий залом. Для оценки результата, нажав комбинацию клавиш «Ctrl+H», временно скрываем выделение.
Но иногда, как в нашем случае, это может выглядеть не совсем естественно, поэтому в меню «Редактирование» выбираем команду «Ослабить: Выделение заплатки».
Снижаем непрозрачность и получаем более приемлемый результат. Таким образом, можно исправить все нежелательные неровности: морщины, оспы, шрамы т.д.
В итоге подправим светотеневой рисунок на низкочастотном слое.
На личике правнучки, подправим нижнюю губу и посмотрим на результат, как мы омолодили прабабушку.
Метод разложения изображения на три частотные полосы имеет преимущество перед двух полосным в том, что вынося цвет и свет на нижние частоты, а фактуру на верхние, мы имеем возможность работать с дефектами на среднем слоя не обращая внимание ни на цвет, ни на мелкую детализацию.
Этим материалом мы заканчиваем рассматривать метод частотного разложения. Если у Вас остались какие-либо вопросы не стесняйтесь, задавайте их, постараемся в них разобраться.
Приятных творческих успехов!
Если Вы не хотите пропустить интересные уроки по обработке фотографий — подпишитесь на рассылку.
Форма для подписки находится ниже.
Временно закрыто комментирование для гостей, нужна обязательная регистрация, ввиду засилья спамботов.
зарегистрируйтесь на сайте, что бы оставлять комментарии!
Частотное разложение пошагово: суть метода, этапы, настройки | Статьи | Фото, видео, оптика
Как незаметно и качественно убрать с кожи дефекты, но сохранить текстуру? Как аккуратно выровнять пигмент и неровности лица? Для таких задач простых инструментов вроде штампа или восстанавливающей кисти будет мало. Вам потребуется частотное разложение.
Вам потребуется частотное разложение.
Рассказываем, что такое ретушь методом частотного разложения, как делать её качественно, быстро и при этом не превратить лицо в пластиковую маску.
Частотное разложение отталкивает новичков из-за кажущейся сложности, но, запомнив алгоритм, вы будете владеть мощнейшим и одним из самых быстрых приёмов работы с кожей / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Что такое частотное разложение в Photoshop
Ретушь частотным разложением — это когда фотографию по специальному алгоритму раскладывают на несколько частот. Обычно снимок делят на две частоты — верхнюю и нижнюю.
Верхняя частота отвечает за детали и текстуру. К ним относятся прыщики, морщинки, небольшие шрамы, родинки, отдельные волосинки, чёрные точки, пыль, осыпавшаяся тушь. Нижние частоты — это светотеневой рисунок и цвет. Они отвечают за форму, крупные элементы снимка.
Визуалзиация высоких и низких частот.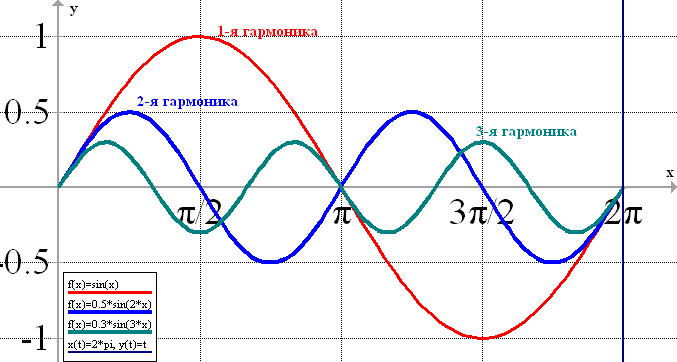 Слева — высокие частоты, текстура, справа — низкие, светотень / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Слева — высокие частоты, текстура, справа — низкие, светотень / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Разложив фотографию на две частоты, фотограф работает отдельно с мелкой текстурой и светотенью. Это позволяет аккуратно разгладить кожу, но оставить поры; убрать прыщики, но сохранить нетронутым цвет.
Как сделать частотное разложение
В ретуши кожи частотным разложением невероятно важно соблюдать точный порядок действий, не пропускать ни один из этапов. Изначально это кажется сложным, но после 5-10 повторений с конспектом под рукой процесс запоминается.
Алгоритм нужно выучить — это неизбежность. Но вы получаете невероятно мощный и быстрый способ ретуши кожи, который ускорит обработку и выведет её на новый уровень.
Этапы частотного разложения. Подготовка слоёв
1. Создайте две копии исходного слоя.
Для этого кликните правой кнопкой мыши и нажмите Дублировать слой / Duplicate Layer. Вариант быстрее — сочетание клавиш Ctrl + J. Сделать это нужно два раза. Верхний слой будет для высоких частот, текстуры, нижний — для низких — светотени.
Сделать это нужно два раза. Верхний слой будет для высоких частот, текстуры, нижний — для низких — светотени.
Чтобы лучше ориентироваться, кликните по названиям слоёв дважды и переименуйте их. Так и назовите — высокая частота и низкая / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
2. Проявите низкие частоты.
– Отключите видимость слоя с высокими частотами — нажмите на иконку глаза слева от слоя.
– Кликните мышью по слою с низкими частотами.
Нажмите на иконку глаза, чтобы отключить видимость слоя. После этого встаньте на слой с низкими частотами, чтобы начать работу с ними / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
– Примените к нему фильтр Размытие по Гауссу / Guassian Blur.
Найти его можно наверху в меню Фильтр / Filter — Размытие / Blur — Размытие по Гауссу / Guassian Blur.
Где найти фильтр Размытие по Гауссу / Guassian Blur для размытия низких частот / Иллюстрация: Елизавета Чечевица, Фотосклад.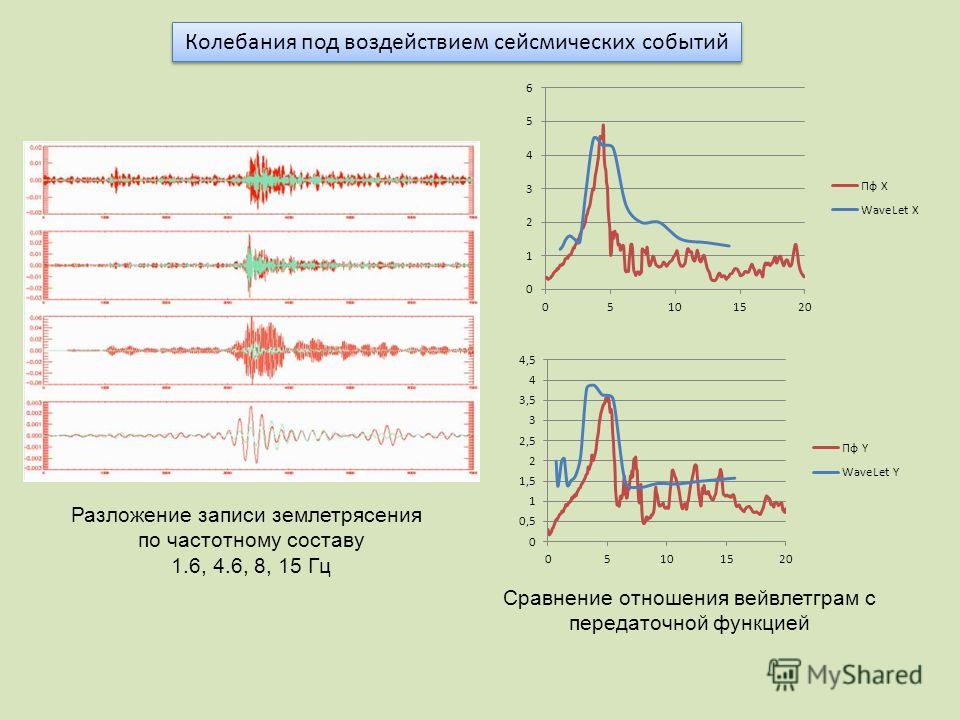 Эксперт
Эксперт
– Выберете радиус размытия.
Нужно, чтобы на коже пропали мелкие детали, и вы не могли разглядеть текстуру — поры, отдельные волосинки, мелкие морщины / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Чем крупнее в кадре лицо, тем больше значение радиуса. Обычно это диапазон от 3 до 20 пикселей. Групповые и ростовые портреты, где лица моделей маленькие, размывайте примерно на 3-5 пикселей, а портреты, где всё пространство фотографии занимает лицо, на 15-20 пикселей. Эти числа — не аксиома, но удобная отправная точка для собственных экспериментов.
3. Проявите высокие частоты.
– Включите видимость слоя с высокими частотами.
–Встаньте на слой с высокими частотами, кликнув на него левой кнопкой мыши.
Чтобы включить видимость слоя, верните значок с глазом в красном круге. То, на каком вы слое находитесь в данный момент, видно по его цвету. Активный слой — с верхними частотами — сейчас тёмно-серый / Иллюстрация: Елизавета Чечевица, Фотосклад.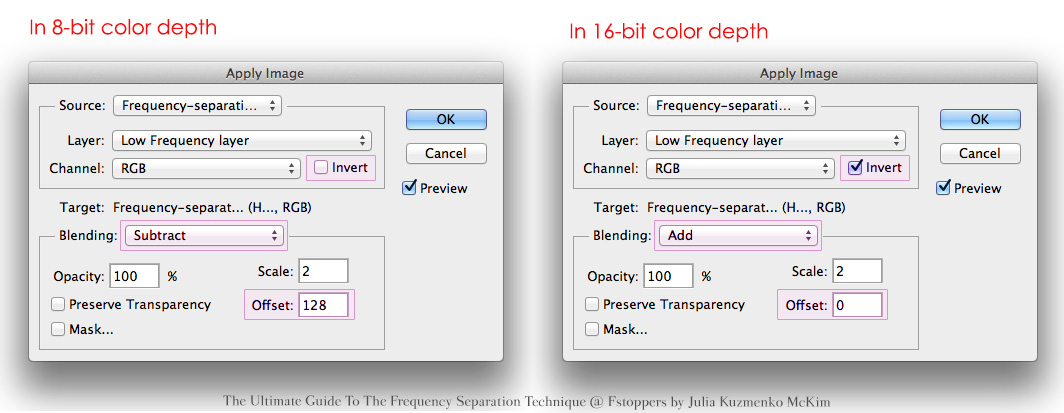 Эксперт
Эксперт
– Откройте Изображение / Image — Внешний канал / Apply Image.
Здесь мы «вытащим» на слой с верхними частотами текстуру. Для этого из исходника вычитается размытый слой с низкими частотами.
Где найти функцию Внешний канал / Apply Image в Photoshop / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Здесь важно лишь одно — поставить следующие настройки:
— Во вкладке Слой / Layer выберете слой с низкими частотами, который вы размывали (ещё одна причина, по которой новичку полезно переименовывать слои).
Чтобы из слоя с высокими частотами вычесть нижние, нужно выбрать размытый слой в выпадающем списке Слой / Layer / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
— Для 8-битного режима: Наложение / Blending — Вычитание / Subtract. Масштаб / Scale — 2. Сдвиг / Offset — 128.
Настройки частотного разложения для 8-битного режима / Иллюстрация: Елизавета Чечевица, Фотосклад. Эксперт
Эксперт
Если изображение стало серым — не пугайтесь! Так и надо. Значит, вы на верном пути.
— Для 16-битного режима: Наложение / Blending — Добавление / Add. Масштаб / Scale — 2. Сдвиг / Offset — 0. Галочку Инвертировать / Invert.
Настройки частотного разложения для 16-битного режима / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
– Нажмите Ок или клавишу Enter, чтобы применить настройки.
Чтобы понять, какой битности у вас фотография, посмотрите на цифру в скобочках рядом с названием / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
– Поставьте серый слой с высокими частотами в режим наложение Линейный свет / Linear Light.
После применения Линейного света / Linear Light картинка должна выглядеть, как выглядел исходник, когда вы только открыли файл. Это значит, вы разложили фотографию на частоты правильно / Иллюстрация: Елизавета Чечевица, Фотосклад. Эксперт
Эксперт
Частотное разложение — настройки инструментов
В частотном разложении работа идёт попеременно с двумя частотами. Можно постоянно переключаться между слоями, либо ретушировать поэтапно — сначала полная чистка от прыщиков, волосков, а потом правка светотени. Порядок не принципиален. Важно — не путать инструменты и слои, на которых вы работаете.
Для ретуши мы будем использовать инструменты Штамп / Clone Stamp Tool, Восстанавливающая кисть / Healing Brush Tool и Микс-кисть / Mixer Brush Tool. Подробно о том, как работают эти инструменты, читайте в тексте про базовую ретушь.
Настройки инструментов для высоких частот
На слое для ретуши текстуры (прыщи, морщинки, шрамики, волосы) работу можно проводить двумя инструментами:
- Штамп / Clone Stamp Tool.
Настройки штампа для частотного разложения / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
- Восстанавливающая кисть / Healing Brush Tool.

Главное, также как и для Штампа, — в выпадающем списке Образец / Sample выбрать Текущий слой / Current Layer.
Это нужно для того, чтобы инструмент брал заплатку с того слоя, на котором находится, не задействуя слои под собой. В противном случае заплатка будет сильно выбиваться по цвету. В остальном можно оставить настройки по умолчанию.
Вот что происходит, если НЕ поставить в графе Образец / Sample настройку Текущий слой / Current Layer. Это актуально и для Штампа и для Восстанавливающей кисти. Чтобы ретушь работала, ставьте Текущий слой / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Секреты частотного разложения: работа на слое с высокими частотами
- Размер кисти должен соответствовать или быть чуть больше дефекта.
Не стоит вымерять, чтобы радиус кисти пиксель в пиксель совпадал с прыщиком или толщиной волоса, но также сложнее работать аккуратно, если заплатка сильно больше недостатка.
- Ищите для заплаток участки с похожими текстурами.
На разных участках лица у кожи разная текстура. Например, кожа под глазами более нежная и тонкая, чем на щеках. Визуально кожа на лбу и на носу также отличаются между собой. Чтобы ретушь была незаметной, ищите заплатку неподалёку. Если ретушируете щеку, берите образец для штампа или восстанавливающей кисти также со щеки.
- Берите заплатки с участков с одинаковой яркостью.
Например, если попытаться на блик перенести заплатку, которую вы взяли с участка кожи в тени, в глаза бросится несовпадение по текстурам.
Вот что происходит, если заплатка не совпадает по яркости и текстуре / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Настройки инструментов для низких частот
Чтобы выровнять светотень, разгладить пигментные пятна, нужно встать на слой с низкими частотами и использовать инструмент Микс-кисть / Mixer Brush Tool.
Микс-кисть / Mixer Brush Tool — это попытка разработчиков Photoshop имитировать эффект обычной кисти в реальности, когда художник рисует по бумаге.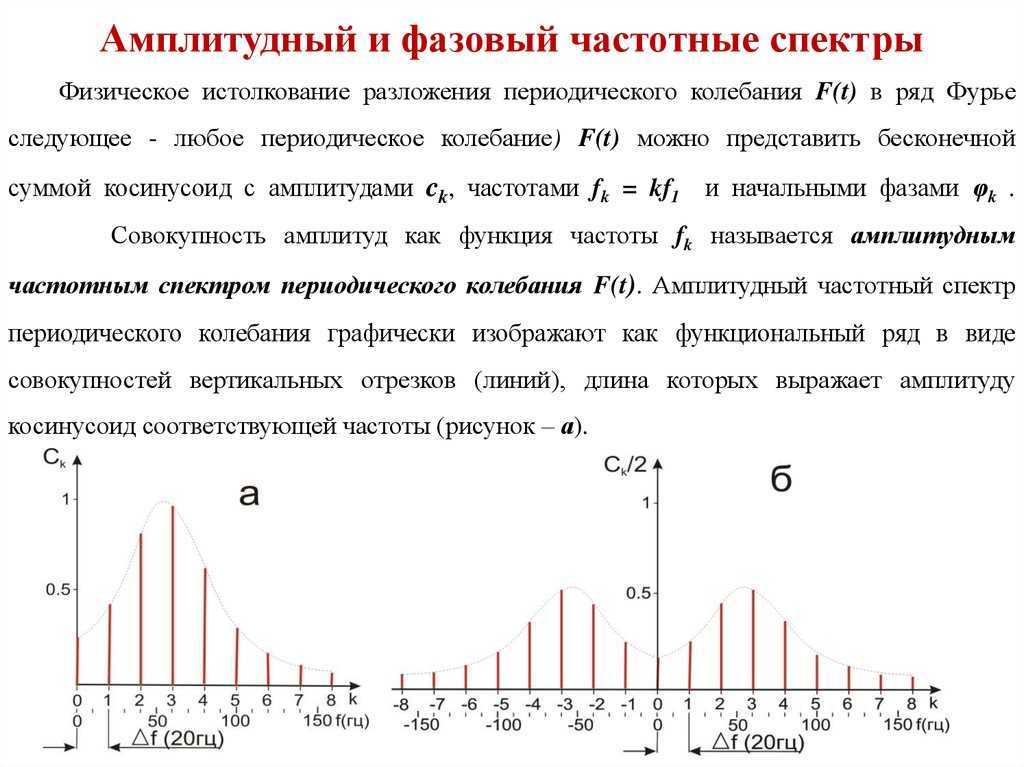 Она переносит цвет из одной области картинки в другую мазками, а также смешивает цвета между собой, как если бы вы пытались смешать два цвета на палитре.
Она переносит цвет из одной области картинки в другую мазками, а также смешивает цвета между собой, как если бы вы пытались смешать два цвета на палитре.
Настройки микс-кисти для частотного разложения. Если хотите, чтобы воздействие было более сильным, регулируйте только один параметр — Нажим / Flow / Иллюстрация: Елизавета Чечевица, Фотосклад.Эксперт
Принципы работы с микс-кистью при частотном разложении
Если тон лица нужно разгладить, водите кистью небольшими круговыми движениями. Так цвета будут смешиваться.
Если задача поправить или продлить тень, слегка осветлить синяки под глазами, то нужно работать штрихами, перенося цвет из одной части картинки в другую.
Микс-кисть — мощный инструмент, с помощью которого легко можно «убить» анатомию лица. Например, следует помнить, что наиболее выпуклые части лица (лоб, кончик носа, подбородок, столбик носа, скулы) должны быть светлее всего остального. Тени же лежат под скулами, под нижней губой, под челюстью.
Ещё один секрет — ни в коем случае нельзя полностью убирать носогубную складку. Чтобы этого избежать, постоянно смотрите на светотень исходника. Это поможет вовремя заметить неестественность и вернуться на пару шагов назад.
Лайфхак: если вы сделали что-то не то, отмените последние команды с помощью сочетания клавиш Ctrl + Z.
После ретуши частотным разложением результат может показаться слишком сильным — кожа в таких случаях кажется «пластиковой», слишком гладкой. В таком случае добавьте слои в группу (иллюстрация ниже) и понизьте непрозрачность получившейся папки. Тогда сквозь ретушь проступит естественная текстура. С практикой вы всё реже будете прибегать к этому — научитесь аккуратно ретушировать, не перебарщивая.
Чтобы добавить слои в группу, кликните по ним, зажав Ctrl, а после на значок с папкой. Кликните на папку и понизьте непрозрачность с помощью ползунка Непрозрачность / Opacity / Иллюстрация: Елизавета Чечевица, Фотосклад. Эксперт
Эксперт
Частотно-временное разложение — SEG Wiki
Содержание
- 1 Преобразование Фурье
- 2 Частотно-временное представление
- 3 Продолжить изучение
- 4 Автор, ответственный за переписку
- 5 Благодарностей
- 6 Внешние ссылки
Рассмотрим форму волны или сигнала s как функцию времени t . Например, синусоида с некоторой амплитудой a и с некоторой частотой f может быть определен как
s (t) = asin (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.
Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией , на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:
по определению sine_wave(f, a, продолжительность, частота дискретизации):
t = np.arange(0, продолжительность, 1/sample_rate)
вернуть * np. sin (2 * np.pi * f * t), т
sin (2 * np.pi * f * t), т Теперь мы можем вызвать эту функцию, передав ей частоту f = 261,63 Гц. Мы попросим 0,25 с с частотой дискретизации 10 кГц.
с, t = sine_wave(f=261,63,
а=1,
продолжительность=0,25,
sample_rate=10e3) Это приводит к следующему сигналу, обычно называемому временным рядом , который мы визуализируем путем построения графика s в зависимости от времени t :
Я изобразил результирующий массив в виде линии, но на самом деле это ряд дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:
array([ 0. , 0.1636476 , 0.32288289, 0.47341253])
Построим первые 80 точек:
Когда воздух вибрирует на этой частоте, мы слышим среднее До или До4. Вы можете прослушать примечание для себя в Jupyter Notebook, сопровождающем эту статью, по адресу https://github.com/seg/tutorials-2018.
(Блокнот также содержит весь код для создания графиков. ) Код для вывода массива s в виде звука очень короткий:
) Код для вывода массива s в виде звука очень короткий:
из IPython.display import Audio фс = 10e3 Аудио(и, скорость=fs)
Этот сигнал длится всего 0,25 с, а покачиваний уже много. Мы бы хотели иметь сейсмические данные на этой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20–30 клавишах 88-клавишного фортепиано — действительно, самая нижняя клавиша — это A0, что на частоте 27,5 Гц превышает пиковую частоту многих старых съемок.
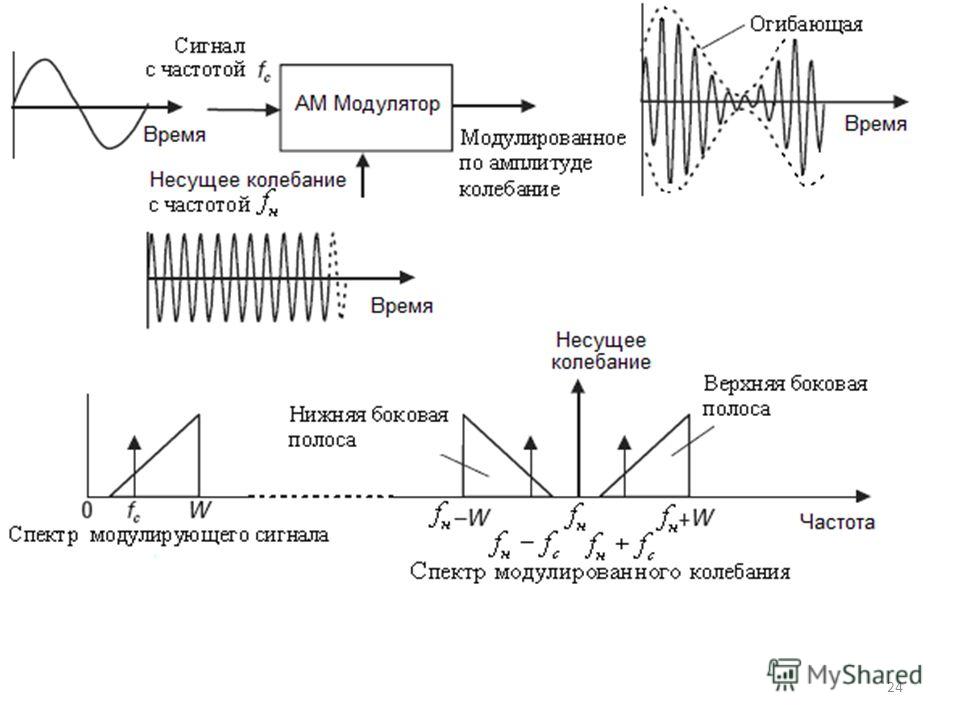
Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто подсчитать количество циклов в единицу времени. Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
f = np.массив ([261,6, 329,6, 392,0]) а = np.массив ([1,5, 0,5, 1]) s, t = sine_wave (f = f.reshape (3, 1), а=а.изменить(3, 1), продолжительность=0,25, sample_rate=10e3)
Результатом является набор из трех синусоидальных кривых длиной 0,25 с:
Общий сигнал определяется суммой трех кривых:
s = np.sum(s, axis=0)
Преобразование Фурье
Хотя это смешанное или политонный сигнал представляет собой просто сумму трех чистых тонов, разобраться в компонентах уже не тривиально. Здесь в дело вступает преобразование Фурье.
Мы не будем вдаваться в подробности того, как работает преобразование Фурье. Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Сначала мы конусность сигнала путем умножения его на функцию окна . Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
s = s * np.blackman(s.size)
Оконная функция (зеленая) оказывает сужающее действие на сигнал:
Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временем 9(е) {\ Displaystyle {\ шляпа {s}} (е)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :
S = np.fft.fft(s)
Вспомогательная функция fftfreq() возвращает массив частот, соответствующих коэффициентам. Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
freq = np.fft.fftfreq(s.size, d=1/10e3)
Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.
Частотно-временное представление
Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одно усложнение — сигналы, компоненты которых меняются со временем. Такие сигналы называются нестационарный . Например, подумайте о монотонном сигнале, тон которого меняется в какой-то момент (см. Блокнот для кода, который генерирует этот сигнал):
Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:
с *= np.blackman(s.size) S = np.fft.fft(s) freq = np.fft.fftfreq(s.size, d=1/10e3)
И постройте амплитуду S в зависимости от массива частот freq :
Он очень похож на спектр, который мы сделали раньше, но без средней частоты. Пики немного более рассредоточены, потому что продолжительность каждого сигнала вдвое меньше, чем была. (Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
(Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени (мы делаем!), это проблема. Одним из решений является обращение к частотно-временным представлениям . Пытаясь разделить сигнал одновременно по времени и частоте, они предлагают способ одновременного использования преимуществ обеих областей.
Библиотека для построения графиков Python matplotlib предлагает удобный способ построения графика время-частота, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
_ = plt.specgram(s, Fs=1/10e3,
NFFT=512, noverlap=480) Немного поработав, мы можем получить очень богатое представление наших данных:
График использует алгоритм, называемый кратковременным преобразованием Фурье, или STFT. Это просто делает преобразование Фурье в скользящем окне длиной
Это просто делает преобразование Фурье в скользящем окне длиной NFFT с перекрытием точек, перекрывающихся в предыдущем окне. Мы хотим NFFT должен быть длинным, чтобы получить хорошее разрешение по частоте, и мы хотим, чтобы nooverlap был большим, чтобы получить хорошее разрешение по времени.
Обратите внимание, что мы не можем точно увидеть точную частоту компонентов — они не служат достаточно долго, чтобы их можно было зафиксировать. И есть некоторая неопределенность в отношении сроков перехода, потому что для получения приличного разрешения по частоте нам нужен длинный сегмент сигнала (в данном случае 512 отсчетов) — поэтому мы теряем информацию о времени. Но в целом этот сюжет лучше, чем только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.
Фрагмент фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:
Существует большое сходство между этим частотно-временным разложением и нотной записью:
Оказывается, самые интересные сигналы — и, возможно, все естественные сигналы — политонны и нестационарны. По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот некоторые примеры; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот некоторые примеры; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
Человеческий голос произносит «SEG». Сонорные гласные имеют гармоники (горизонтальные полосы), а шипящие звуки «С» и первой части «Г» — шумоподобные. спектральные отклики.
На этой спектрограмме показана 5-секундная серия чириканий летучих мышей. Я указал 18 кГц, приблизительный предел человеческого слуха, оранжевой линией, и если вы слушаете звук этого сигнала в Ноутбук, можно убедиться, что чириканье еле слышно при нормальной скорости воспроизведения; только при замедлении клипа они могут быть отчетливо слышны.
Наконец, вот вулканический «крик» — гармонический толчок, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года.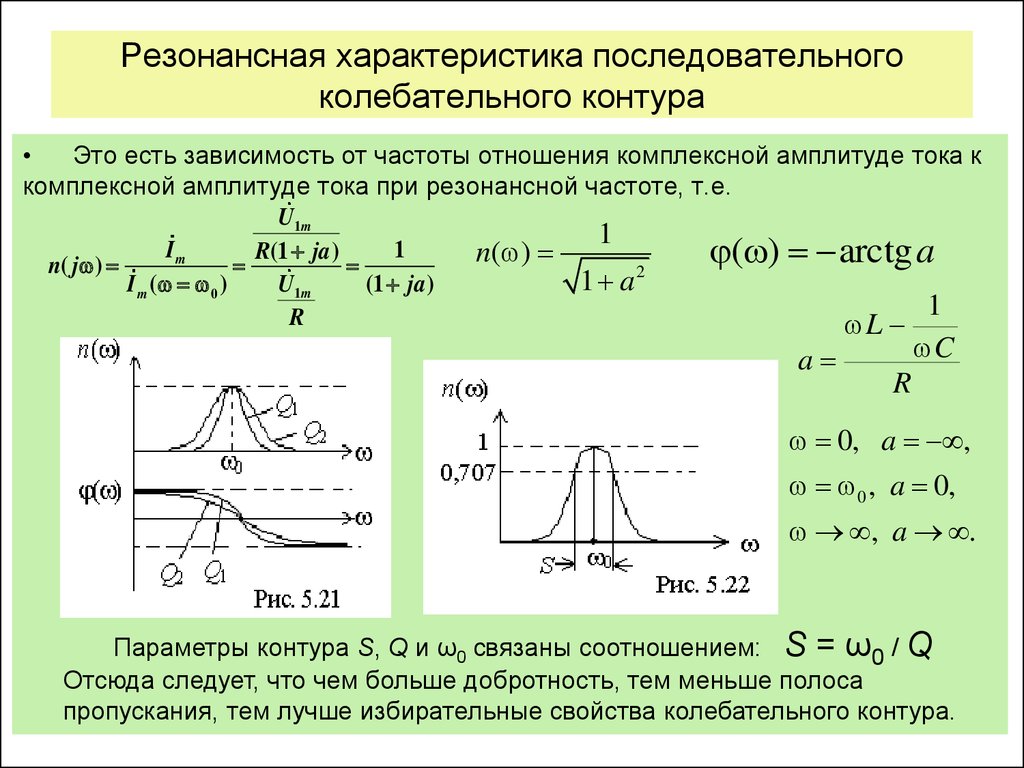 На слух это звучит невероятно, но спектрограмма
тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
На слух это звучит невероятно, но спектрограмма
тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
Продолжить изучение
Все рисунки в этой записной книжке можно воспроизвести с помощью кода в записной книжке Jupyter, прилагаемой к этой статье, на https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь — не волнуйся!
В хранилище вы также найдете больше сигналов, синтетических и естественных, от сердцебиения и загадочного подводного щебетания до гравитационных волн и сейсмических следов. Мало того, есть записная книжка, показывающая, как использовать другой алгоритм — непрерывное вейвлет-преобразование — для проведения частотно-временного анализа другого типа.
Счастливого разложения!
Автор, ответственный за переписку
- Автор, ответственный за переписку: Matt Hall, Agile Scientific, Mahone Bay, Новая Шотландия, Канада.
 Электронная почта:
Электронная почта: mattagilescientific.com
Благодарности
Фортепианная запись из BWV846 Баха лицензирована Кимико Ишизака CC-BY на http://welltemperedclavier.org. Данные чириканья летучих мышей лицензированы CC-BY-NC пользователем http://freesound.org klankschap. Спасибо Алисии Хотовек-Эллис за ее помощь с данными о горе Редут, записанными вулканической обсерваторией Геологической службы США на Аляске.
Внешние ссылки
| найти литературу о Частотно-временное разложение |
- Мадагаскарский рабочий процесс — воспроизводимый с помощью Мадагаскарского программного обеспечения с открытым исходным кодом Зеленым цветом показаны области, настроенные на частоту 30 Гц, а красным — настройка на частоту 18 Гц. После того, как Лафлин и др. (2002)
Спектральное разложение или частотно-временной анализ (также частотно-временное разложение) — это метод, используемый для облегчения интерпретации сейсмических данных.
 Спектральное разложение может быть выполнено по множеству атрибутов (частота, угол наклона, азимут…), хотя чаще всего используется частота. Это также может быть выполнено с данными, мигрированными во времени, или данными, мигрированными по глубине, и приводит к настройке частот с единицами измерения в Гц и циклах/расстоянии соответственно. Результатом спектрального разложения данных являются частотная и фазовая составляющие, из которых первая является прямой мерой относительной сейсмической амплитуды в полосе частот [1] [2] . Основное использование атрибута заключается в помощи в стратиграфической интерпретации за счет улучшения разрешения тонких слоев и демонстрации временной изменчивости толщины слоев. Это необходимо, потому что вейвлет часто охватывает несколько подповерхностных слоев, что приводит к сложному настроенному отражению, являющемуся результатом сверточной модели. По этой причине считается, что спектральное разложение удаляет вейвлет-наложение из сейсмических данных [3] .
Спектральное разложение может быть выполнено по множеству атрибутов (частота, угол наклона, азимут…), хотя чаще всего используется частота. Это также может быть выполнено с данными, мигрированными во времени, или данными, мигрированными по глубине, и приводит к настройке частот с единицами измерения в Гц и циклах/расстоянии соответственно. Результатом спектрального разложения данных являются частотная и фазовая составляющие, из которых первая является прямой мерой относительной сейсмической амплитуды в полосе частот [1] [2] . Основное использование атрибута заключается в помощи в стратиграфической интерпретации за счет улучшения разрешения тонких слоев и демонстрации временной изменчивости толщины слоев. Это необходимо, потому что вейвлет часто охватывает несколько подповерхностных слоев, что приводит к сложному настроенному отражению, являющемуся результатом сверточной модели. По этой причине считается, что спектральное разложение удаляет вейвлет-наложение из сейсмических данных [3] . Рисунок 1 слева хорошо иллюстрирует окончательный результат спектральной декомпозиции (вариации мощности в пределах стратиграфического тела). Первая из двух дискретных частот составляет 30 Гц (зеленый цвет) и освещает самую тонкую часть канала на карте. Красным цветом показаны 18 Гц и показаны более толстые части канала (тальвеги).
Рисунок 1 слева хорошо иллюстрирует окончательный результат спектральной декомпозиции (вариации мощности в пределах стратиграфического тела). Первая из двух дискретных частот составляет 30 Гц (зеленый цвет) и освещает самую тонкую часть канала на карте. Красным цветом показаны 18 Гц и показаны более толстые части канала (тальвеги).Содержание
- 1 Методы
- 1.1 Методы спектрального разложения:
- 2 Визуализация
- 3 Применение
- 4 выпуска
- 5 примеров
- 5.1 Интерпретация заполнения врезанной долины
- 5.2 Интерпретация непрерывности канала
- 6 Каталожные номера
- 7 Внешние ссылки
Методы
Несмотря на то, что в записанных сейсмических данных вейвлет наложился, тонкие пласты все же обладают уникальными частотными выражениями. Таким образом, если записанные трассы преобразуются из временной (или глубинной) в частотную область (анализ Фурье), спектры могут быть извлечены.
 Существует множество методов для выполнения этого преобразования и создания временных срезов и объемов спектральной декомпозиции (перечисленных ниже), каждый из которых вычисляется на основе трассировки 9.0254 [4] . Один из этих методов называется дискретным преобразованием Фурье с коротким окном (SWDFT). По сути, этот метод берет вертикальные срезы или целые объемы и присваивает вес трассам (или взаимную корреляцию с заостренными синусами и косинусами) в течение фиксированного временного окна [1] . Это временное окно сосредоточено вокруг каждой точки анализа в данный момент времени. Обычно длина окна находится в диапазоне от 50 до 100 мс с конусностью около 20 % от длины окна [1] . Непрерывное вейвлет-преобразование (CWT) — еще один распространенный метод, используемый для спектральной декомпозиции. Он похож на SWDFT, однако CWT имеет переменную длину окна (конусность), которая пропорциональна центральной частоте: она короче для более высоких частот и длиннее для более низких частот [1] .
Существует множество методов для выполнения этого преобразования и создания временных срезов и объемов спектральной декомпозиции (перечисленных ниже), каждый из которых вычисляется на основе трассировки 9.0254 [4] . Один из этих методов называется дискретным преобразованием Фурье с коротким окном (SWDFT). По сути, этот метод берет вертикальные срезы или целые объемы и присваивает вес трассам (или взаимную корреляцию с заостренными синусами и косинусами) в течение фиксированного временного окна [1] . Это временное окно сосредоточено вокруг каждой точки анализа в данный момент времени. Обычно длина окна находится в диапазоне от 50 до 100 мс с конусностью около 20 % от длины окна [1] . Непрерывное вейвлет-преобразование (CWT) — еще один распространенный метод, используемый для спектральной декомпозиции. Он похож на SWDFT, однако CWT имеет переменную длину окна (конусность), которая пропорциональна центральной частоте: она короче для более высоких частот и длиннее для более низких частот [1] . Результатом этих различий в длине окна является разрешение. SWDFT будет иметь фиксированное частотно-временное разрешение, в то время как CWT не будет иметь [5] .
Результатом этих различий в длине окна является разрешение. SWDFT будет иметь фиксированное частотно-временное разрешение, в то время как CWT не будет иметь [5] .Methods for Spectral Decomposition:
- Fourier Transform
- Short-time Discrete Fourier Transform
- S transform or Stockwell Transform
- Continuous-Wavelet Transform
- Matching pursuit and other dictionary-based трансформирует
- Эмпирическое разложение режима
- Распределение Wigner-ville
- Синхросезинг преобразование
Визуализация
Рисунок 2: Изображение показано три отдельных спектральных спектра. с градационными цветовыми схемами и двумя комбинированными изображениями d) смешивание RGB (красный = 30 Гц, зеленый = 40 Гц, синий = 50 Гц) и e) смешивание HLS. После Холла и Труйо (2004).

Отдельные частотные срезы или объемы спектрального разложения (на одной частоте) могут отображаться в различных программах и с множеством цветовых схем. Однако есть два часто используемых варианта цвета, которые эффективно смешивают несколько спектрально разложенных изображений. Это RGB и HLS оттенок-яркость-насыщенность). В RGB пользователь выбирает три дискретные частоты и наносит их на красный, зеленый и синий цвета. HLS означает оттенок (длина волны цвета), легкость (яркость цвета) и насыщенность (оттенок цвета) [[1]]. На этом дисплее три сгенерированных амплитудных среза представлены этими тремя величинами, а затем объединены для получения единого изображения 9.0254 [1] . Представление этих цветовых схем показано на рисунке 2. На рисунке a, b и c представляют собой отдельные спектральные компоненты, где белый соответствует яркому цвету. Часть d представляет собой смесь RGB трех частотных срезов, а e представляет собой изображение HLS, на котором ярко-красным цветом показаны места, где все три частоты являются яркими [1] .
 Рисунок 3 представляет собой изображение спектральной декомпозиции RGB с более высоким разрешением, которое показывает одну большую извилистую речную систему и несколько меньших, менее извилистых каналов. Самые толстые каналы отображаются оранжевым цветом, зелено-желтые участки менее толстые, а синие участки тонкие (в основном илистые надбережные отложения).
Рисунок 3 представляет собой изображение спектральной декомпозиции RGB с более высоким разрешением, которое показывает одну большую извилистую речную систему и несколько меньших, менее извилистых каналов. Самые толстые каналы отображаются оранжевым цветом, зелено-желтые участки менее толстые, а синие участки тонкие (в основном илистые надбережные отложения).Рис. 3: Изображение выше представляет собой смесь RGB в стратиграфически сложном резервуаре у побережья Западной Африки. Высокая частота — синий, средняя частота — зеленый, низкая частота — красный. После того, как Бахорич и соавт. (2002).
Применение
Спектральная декомпозиция стала широко использоваться в нефтяной промышленности как часть геофизических рабочих процессов для интерпретации трехмерных сейсмических данных. В сочетании с дисперсией (также известной как подобие, когерентность) каналы легче идентифицировать и анализировать. Когерентность освещает края канала, а спектральное разложение представляет толщину канала.
 Кроме того, этот метод может дать лучшее представление о непрерывности тела канала, изменчивости заполнения и возможном качестве резервуара 9.0254 [6] .
Кроме того, этот метод может дать лучшее представление о непрерывности тела канала, изменчивости заполнения и возможном качестве резервуара 9.0254 [6] .Помимо традиционного использования спектрального разложения в виде частотных срезов, его можно комбинировать с традиционным анализом изменения амплитуды со смещением для расчета спектрального AVO. В этом методе сейсмические сейсмограммы спектрально разлагаются на различные интересующие частоты, а затем выполняется AVO. Преимущество этого метода заключается в том, что с помощью этого метода можно легко прогнозировать сложенные тонкие газообразные пески, которые обычно не видны в традиционном AVO [7] .
Другим применением является включение спектральной декомпозиции в другие сейсмические атрибуты, такие как SPICE или голосовые компоненты. SPICE (спектральная визуализация коррелятивных событий) — это атрибут, улучшающий сходимость сигналов. В этом методе используются коэффициенты вейвлет-преобразований и показатель Гёльдера, который является мерой сингулярности функции [1] .
 Результатом является объем, который подчеркивает разрывы и позволяет автопикерам отслеживать горизонты в стратиграфически сложных областях. Пример SPICE показан на рисунке 4, который показывает его эффективность при оценке сингулярности. В амплитудных данных (рис. 4а) наблюдается схождение отражателей, которые трудно разделить. Однако в части б) атрибут SPICE более отчетливо показывает неоднородность между отражателями. Компоненты голоса — это функция спектральной амплитуды и фазы в каждой частотно-временной выборке, взятой из спектрального разложения. Сам атрибут представляет собой отфильтрованную версию входных сейсмических данных, которая обычно освещает неоднородности [8] .
Результатом является объем, который подчеркивает разрывы и позволяет автопикерам отслеживать горизонты в стратиграфически сложных областях. Пример SPICE показан на рисунке 4, который показывает его эффективность при оценке сингулярности. В амплитудных данных (рис. 4а) наблюдается схождение отражателей, которые трудно разделить. Однако в части б) атрибут SPICE более отчетливо показывает неоднородность между отражателями. Компоненты голоса — это функция спектральной амплитуды и фазы в каждой частотно-временной выборке, взятой из спектрального разложения. Сам атрибут представляет собой отфильтрованную версию входных сейсмических данных, которая обычно освещает неоднородности [8] .Рис. 4. На изображениях выше показан а) вертикальный срез данных амплитуды и б) вертикальный срез объема SPICE. После того, как Лайнер и др. (2004).
Проблемы
Одной из проблем, которая становится все более распространенной при интерпретации сейсмических данных, является проблема чрезмерных данных (особенно атрибутов).
 Спектральное разложение вносит большой вклад в эту проблему. Часто генерируются многочисленные фазовые и спектральные объемы или срезы, в зависимости от выбранного приращения частоты [2] . Решением этой проблемы является уменьшение размерности с помощью анализа главных компонентов, который анализирует атрибуты и дает несколько объемов, представляющих максимальное изменение входных атрибутов [9] .
Спектральное разложение вносит большой вклад в эту проблему. Часто генерируются многочисленные фазовые и спектральные объемы или срезы, в зависимости от выбранного приращения частоты [2] . Решением этой проблемы является уменьшение размерности с помощью анализа главных компонентов, который анализирует атрибуты и дает несколько объемов, представляющих максимальное изменение входных атрибутов [9] .Другая проблема связана с визуальным отображением. Как упоминалось ранее, существуют методы смешивания дискретных частот для более последовательной интерпретации. Однако частотные спектры очень изменчивы, и поэтому трех компонентов может быть недостаточно для детализации. Одним из способов решения этой проблемы является оптическое суммирование большего диапазона частот 9.0254 [10] .
Примеры
Интерпретация засыпки врезанной долины
Широко известное исследование спектрального разложения было выполнено Peyton et al. в 1999 г.
 В своем исследовании группа использовала комбинацию спектральной декомпозиции и когерентности, чтобы очертить и интерпретировать врезанные долины интервала Верхний Ред-Форк в северной части бассейна Анадарко. Спектральная декомпозиция и когерентность применялись в трехмерной сейсморазведке Amoco mega merge. Цель состояла в том, чтобы идентифицировать прерывистые тела канала и, возможно, интерпретировать этапы заполнения канала. Используя два атрибута, группа смогла достичь обоих. На рис. 5 показан один из результатов исследования, отображающий срез спектральной составляющей на частоте 36 Гц. В части 5а показан канал, очерченный когерентностью, а также разности амплитуд в его пределах. Используя информацию об интервале Верхнего Ред-Форка и каротажных диаграммах (часть 5b), они смогли интерпретировать различные этапы заполнения долины по всему каналу 9.0254 [11] .
В своем исследовании группа использовала комбинацию спектральной декомпозиции и когерентности, чтобы очертить и интерпретировать врезанные долины интервала Верхний Ред-Форк в северной части бассейна Анадарко. Спектральная декомпозиция и когерентность применялись в трехмерной сейсморазведке Amoco mega merge. Цель состояла в том, чтобы идентифицировать прерывистые тела канала и, возможно, интерпретировать этапы заполнения канала. Используя два атрибута, группа смогла достичь обоих. На рис. 5 показан один из результатов исследования, отображающий срез спектральной составляющей на частоте 36 Гц. В части 5а показан канал, очерченный когерентностью, а также разности амплитуд в его пределах. Используя информацию об интервале Верхнего Ред-Форка и каротажных диаграммах (часть 5b), они смогли интерпретировать различные этапы заполнения долины по всему каналу 9.0254 [11] .Рис. 5: На приведенном выше изображении показан срез спектрального компонента на частоте 36 Гц с а) без интерпретации б) интерпретированными этапами заполнения долины.
 После того, как Пейтон и др. (1999).
После того, как Пейтон и др. (1999).Интерпретация непрерывности канала
Более свежий пример — Othman et al. 2016 г., в котором спектральное разложение использовалось для картирования мощности пласта, изображения геологических неоднородностей и очерчивания каналов в глубоководной нефтяной провинции Западной пустыни в 110 км к северо-востоку от Александрии, Египет [6] . В амплитудных данных были обнаружены два канала (обозначенные как Красный и Желтый), оба из которых падают на север и выклиниваются вбок. Красный канал был легко идентифицирован и сопровождался данными амплитуды с двумя четкими внутренними разрывами (обозначены на рисунках 6 и 7). Однако желтый канал был более тусклым и затруднял отслеживание отражателя. Поскольку было доказано, что спектральное разложение помогает в интерпретации каналов, было принято решение использовать этот метод. Таким образом, вокруг интерпретируемых горизонтов генерировались объемы спектрального разложения, и интерпретировались различные частотные объемы.
 Для красного канала были выбраны частоты 5, 25 и 65 Гц, так как они выявляли разные особенности каналов. На рис. 7 показан результат смешивания RGB, выполненного с тремя отдельными частотными объемами. Изображение отображает большую часть канала яркой окраской, что означает, что оно содержит все три частоты и соответствует самой толстой части канала. Два разрыва, видимые как низкие амплитуды на рисунке 6, видны на рисунке 7 как низкочастотные зоны (5 Гц) между областями смешанных частот. Это было истолковано как указание на то, что канал был подключен в этих регионах. Кроме того, там, где фарватер канала не был определен на картах амплитуд, его можно четко увидеть на частоте 65 Гц в частотных данных (рис. 7). Аналогичный процесс был также выполнен для Желтого канала, который выявил многоэтажный комплекс каналов.
Для красного канала были выбраны частоты 5, 25 и 65 Гц, так как они выявляли разные особенности каналов. На рис. 7 показан результат смешивания RGB, выполненного с тремя отдельными частотными объемами. Изображение отображает большую часть канала яркой окраской, что означает, что оно содержит все три частоты и соответствует самой толстой части канала. Два разрыва, видимые как низкие амплитуды на рисунке 6, видны на рисунке 7 как низкочастотные зоны (5 Гц) между областями смешанных частот. Это было истолковано как указание на то, что канал был подключен в этих регионах. Кроме того, там, где фарватер канала не был определен на картах амплитуд, его можно четко увидеть на частоте 65 Гц в частотных данных (рис. 7). Аналогичный процесс был также выполнен для Желтого канала, который выявил многоэтажный комплекс каналов.Рис. 6: Атрибут средней абсолютной амплитуды, извлеченный из верхней поверхности красного канала. Канал отчетливо проявляется в целом высокой средней абсолютной амплитудой.
 Изображение было аннотировано для освещения особенностей канала. После того, как Отман и др. (2016)
Изображение было аннотировано для освещения особенностей канала. После того, как Отман и др. (2016)Рис. 7: Смешанное изображение спектральных частот 5 Гц, 25 Гц и 65 Гц, извлеченное на верхнюю поверхность красного канала. После того, как Отман и др. (2016)
Ссылки
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 Чопра, С., и Марфурт, К. Дж. (2007). «Глава 6: Спектральная декомпозиция и вейвлет-преобразования» Сейсмические атрибуты для идентификации объектов и определения характеристик резервуаров (том ISBN 978-1-56080-141-2, ISBN 978-0-931830-41-9). Дои: https://doi.org/10.1190/1.9781560801900
- ↑ 2,0 2,1 Чопра, С., и Марфурт, К. Дж. (2015). Повышение интерпретируемости сейсмических данных с фазовыми компонентами спектрального разложения. Чтение представлено на ежегодном собрании SEG в США, Новый Орлеан.
- ↑ Партика, Г.
 , Гридли, Дж., и Лопес, Дж. (1999). Интерпретационные применения спектральной декомпозиции в характеристике коллектора. Передовой край, 18 (3), 353-360. дои: 10.1190/1.1438295
, Гридли, Дж., и Лопес, Дж. (1999). Интерпретационные применения спектральной декомпозиции в характеристике коллектора. Передовой край, 18 (3), 353-360. дои: 10.1190/1.1438295 - ↑ Tengfei Lin, Bo Zhang, Shiguang Guo, Kurt Marfurt, Zhonghong Wan, and Yi Guo (2013) Спектральная декомпозиция данных, мигрированных во времени и по глубине. Расширенные тезисы технической программы SEG 2013: стр. 1384-1388. https://doi.org/10.1190/segam2013-1166.1
- ↑ Синха, С., Раут, П.С., Анно, П.Д., и Кастанья, Дж.П. (2005). Спектральная декомпозиция сейсмических данных с непрерывным вейвлет-преобразованием. Геофизика, 70(6), 19-25. дои: 10.1190/1.2127113
- ↑ 6,0 6,1 , А. А., Фати М. и Махер А. (2016). Использование метода спектральной декомпозиции для оконтуривания каналов при открытии солнечного газа на шельфе дельты Западного Нила, Египет. Египетский нефтяной журнал, 25(1), 45-51. doi:10.1016/j.ejpe.2015.03.005
- ↑ Сапутро, Дж., Дж., Самудра, А.
 Б., Лестари, Э.П., С., Рамадан, А., и Хиросиади, Ю. (2016). Комбинированный анализ AVO и спектрального разложения для определения характеристик резервуара с газообразным песком ниже условия настройки толщины. проц. Индонезийский бензин. Assoc., 40th Ann. Конв. дои: 10.29118/ипа.0.16.136.г
Б., Лестари, Э.П., С., Рамадан, А., и Хиросиади, Ю. (2016). Комбинированный анализ AVO и спектрального разложения для определения характеристик резервуара с газообразным песком ниже условия настройки толщины. проц. Индонезийский бензин. Assoc., 40th Ann. Конв. дои: 10.29118/ипа.0.16.136.г - ↑ Чопра С. и Марфурт К. Дж. (2016). Спектральная декомпозиция и спектральная балансировка сейсмических данных. Передовой край, 35 (2), 176-179. дои: 10.1190/tle35020176.1
- ↑ Чопра С. и Марфурт К. Дж. (2014). Перемешивание сейсмических атрибутов с анализом главных компонент. Расширенные тезисы технической программы SEG, 2014 г. doi: 10.1190/segam2014-0235.1
- ↑ Иоганн, П., Г. Рагинин и М. Спинола, 2003, Спектральная декомпозиция выявляет скрытые геологические особенности на картах амплитуд из глубоководного резервуара в бассейне Кампос: 73-я ежегодная международная встреча, SEG, Expanded Abstracts, 1740 –1743.
- ↑ Пейтон, Л., Ботджер, Р., и Партика, Г. (1998).

- 1 Методы

 sin (2 * np.pi * f * t), т
sin (2 * np.pi * f * t), т  массив ([1,5, 0,5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
а=а.изменить(3, 1),
продолжительность=0,25,
sample_rate=10e3)
массив ([1,5, 0,5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
а=а.изменить(3, 1),
продолжительность=0,25,
sample_rate=10e3)  Электронная почта:
Электронная почта:  Спектральное разложение может быть выполнено по множеству атрибутов (частота, угол наклона, азимут…), хотя чаще всего используется частота. Это также может быть выполнено с данными, мигрированными во времени, или данными, мигрированными по глубине, и приводит к настройке частот с единицами измерения в Гц и циклах/расстоянии соответственно. Результатом спектрального разложения данных являются частотная и фазовая составляющие, из которых первая является прямой мерой относительной сейсмической амплитуды в полосе частот [1] [2] . Основное использование атрибута заключается в помощи в стратиграфической интерпретации за счет улучшения разрешения тонких слоев и демонстрации временной изменчивости толщины слоев. Это необходимо, потому что вейвлет часто охватывает несколько подповерхностных слоев, что приводит к сложному настроенному отражению, являющемуся результатом сверточной модели. По этой причине считается, что спектральное разложение удаляет вейвлет-наложение из сейсмических данных [3] .
Спектральное разложение может быть выполнено по множеству атрибутов (частота, угол наклона, азимут…), хотя чаще всего используется частота. Это также может быть выполнено с данными, мигрированными во времени, или данными, мигрированными по глубине, и приводит к настройке частот с единицами измерения в Гц и циклах/расстоянии соответственно. Результатом спектрального разложения данных являются частотная и фазовая составляющие, из которых первая является прямой мерой относительной сейсмической амплитуды в полосе частот [1] [2] . Основное использование атрибута заключается в помощи в стратиграфической интерпретации за счет улучшения разрешения тонких слоев и демонстрации временной изменчивости толщины слоев. Это необходимо, потому что вейвлет часто охватывает несколько подповерхностных слоев, что приводит к сложному настроенному отражению, являющемуся результатом сверточной модели. По этой причине считается, что спектральное разложение удаляет вейвлет-наложение из сейсмических данных [3] .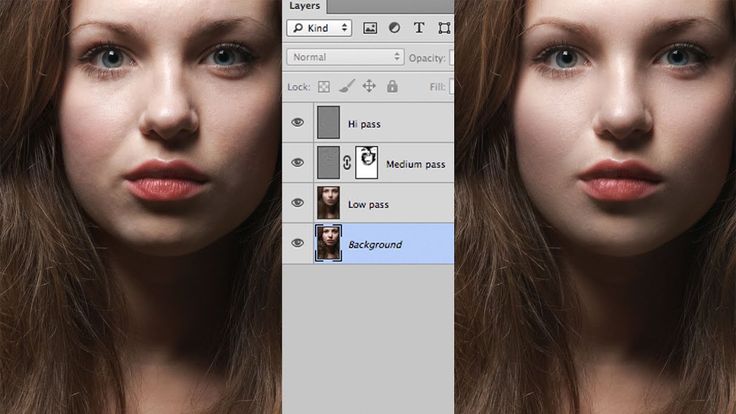 Рисунок 1 слева хорошо иллюстрирует окончательный результат спектральной декомпозиции (вариации мощности в пределах стратиграфического тела). Первая из двух дискретных частот составляет 30 Гц (зеленый цвет) и освещает самую тонкую часть канала на карте. Красным цветом показаны 18 Гц и показаны более толстые части канала (тальвеги).
Рисунок 1 слева хорошо иллюстрирует окончательный результат спектральной декомпозиции (вариации мощности в пределах стратиграфического тела). Первая из двух дискретных частот составляет 30 Гц (зеленый цвет) и освещает самую тонкую часть канала на карте. Красным цветом показаны 18 Гц и показаны более толстые части канала (тальвеги). Существует множество методов для выполнения этого преобразования и создания временных срезов и объемов спектральной декомпозиции (перечисленных ниже), каждый из которых вычисляется на основе трассировки 9.0254 [4] . Один из этих методов называется дискретным преобразованием Фурье с коротким окном (SWDFT). По сути, этот метод берет вертикальные срезы или целые объемы и присваивает вес трассам (или взаимную корреляцию с заостренными синусами и косинусами) в течение фиксированного временного окна [1] . Это временное окно сосредоточено вокруг каждой точки анализа в данный момент времени. Обычно длина окна находится в диапазоне от 50 до 100 мс с конусностью около 20 % от длины окна [1] . Непрерывное вейвлет-преобразование (CWT) — еще один распространенный метод, используемый для спектральной декомпозиции. Он похож на SWDFT, однако CWT имеет переменную длину окна (конусность), которая пропорциональна центральной частоте: она короче для более высоких частот и длиннее для более низких частот [1] .
Существует множество методов для выполнения этого преобразования и создания временных срезов и объемов спектральной декомпозиции (перечисленных ниже), каждый из которых вычисляется на основе трассировки 9.0254 [4] . Один из этих методов называется дискретным преобразованием Фурье с коротким окном (SWDFT). По сути, этот метод берет вертикальные срезы или целые объемы и присваивает вес трассам (или взаимную корреляцию с заостренными синусами и косинусами) в течение фиксированного временного окна [1] . Это временное окно сосредоточено вокруг каждой точки анализа в данный момент времени. Обычно длина окна находится в диапазоне от 50 до 100 мс с конусностью около 20 % от длины окна [1] . Непрерывное вейвлет-преобразование (CWT) — еще один распространенный метод, используемый для спектральной декомпозиции. Он похож на SWDFT, однако CWT имеет переменную длину окна (конусность), которая пропорциональна центральной частоте: она короче для более высоких частот и длиннее для более низких частот [1] . Результатом этих различий в длине окна является разрешение. SWDFT будет иметь фиксированное частотно-временное разрешение, в то время как CWT не будет иметь [5] .
Результатом этих различий в длине окна является разрешение. SWDFT будет иметь фиксированное частотно-временное разрешение, в то время как CWT не будет иметь [5] .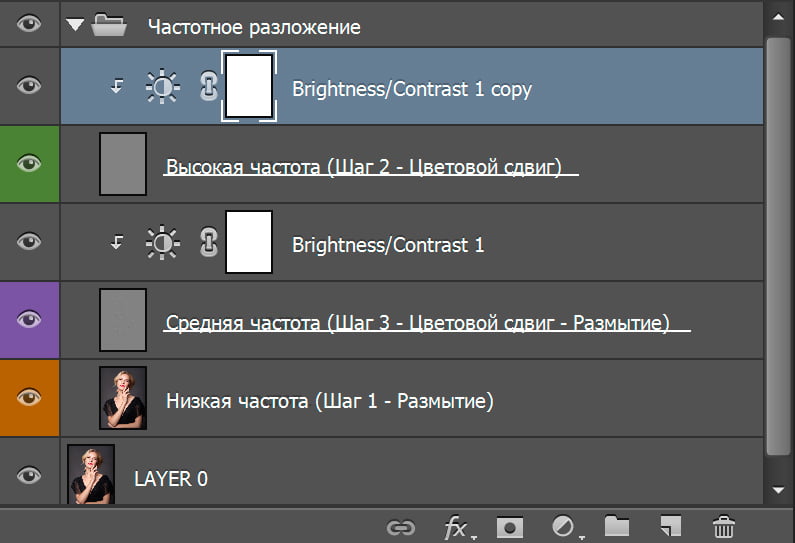
 Рисунок 3 представляет собой изображение спектральной декомпозиции RGB с более высоким разрешением, которое показывает одну большую извилистую речную систему и несколько меньших, менее извилистых каналов. Самые толстые каналы отображаются оранжевым цветом, зелено-желтые участки менее толстые, а синие участки тонкие (в основном илистые надбережные отложения).
Рисунок 3 представляет собой изображение спектральной декомпозиции RGB с более высоким разрешением, которое показывает одну большую извилистую речную систему и несколько меньших, менее извилистых каналов. Самые толстые каналы отображаются оранжевым цветом, зелено-желтые участки менее толстые, а синие участки тонкие (в основном илистые надбережные отложения). Кроме того, этот метод может дать лучшее представление о непрерывности тела канала, изменчивости заполнения и возможном качестве резервуара 9.0254 [6] .
Кроме того, этот метод может дать лучшее представление о непрерывности тела канала, изменчивости заполнения и возможном качестве резервуара 9.0254 [6] . Результатом является объем, который подчеркивает разрывы и позволяет автопикерам отслеживать горизонты в стратиграфически сложных областях. Пример SPICE показан на рисунке 4, который показывает его эффективность при оценке сингулярности. В амплитудных данных (рис. 4а) наблюдается схождение отражателей, которые трудно разделить. Однако в части б) атрибут SPICE более отчетливо показывает неоднородность между отражателями. Компоненты голоса — это функция спектральной амплитуды и фазы в каждой частотно-временной выборке, взятой из спектрального разложения. Сам атрибут представляет собой отфильтрованную версию входных сейсмических данных, которая обычно освещает неоднородности [8] .
Результатом является объем, который подчеркивает разрывы и позволяет автопикерам отслеживать горизонты в стратиграфически сложных областях. Пример SPICE показан на рисунке 4, который показывает его эффективность при оценке сингулярности. В амплитудных данных (рис. 4а) наблюдается схождение отражателей, которые трудно разделить. Однако в части б) атрибут SPICE более отчетливо показывает неоднородность между отражателями. Компоненты голоса — это функция спектральной амплитуды и фазы в каждой частотно-временной выборке, взятой из спектрального разложения. Сам атрибут представляет собой отфильтрованную версию входных сейсмических данных, которая обычно освещает неоднородности [8] . Спектральное разложение вносит большой вклад в эту проблему. Часто генерируются многочисленные фазовые и спектральные объемы или срезы, в зависимости от выбранного приращения частоты [2] . Решением этой проблемы является уменьшение размерности с помощью анализа главных компонентов, который анализирует атрибуты и дает несколько объемов, представляющих максимальное изменение входных атрибутов [9] .
Спектральное разложение вносит большой вклад в эту проблему. Часто генерируются многочисленные фазовые и спектральные объемы или срезы, в зависимости от выбранного приращения частоты [2] . Решением этой проблемы является уменьшение размерности с помощью анализа главных компонентов, который анализирует атрибуты и дает несколько объемов, представляющих максимальное изменение входных атрибутов [9] . В своем исследовании группа использовала комбинацию спектральной декомпозиции и когерентности, чтобы очертить и интерпретировать врезанные долины интервала Верхний Ред-Форк в северной части бассейна Анадарко. Спектральная декомпозиция и когерентность применялись в трехмерной сейсморазведке Amoco mega merge. Цель состояла в том, чтобы идентифицировать прерывистые тела канала и, возможно, интерпретировать этапы заполнения канала. Используя два атрибута, группа смогла достичь обоих. На рис. 5 показан один из результатов исследования, отображающий срез спектральной составляющей на частоте 36 Гц. В части 5а показан канал, очерченный когерентностью, а также разности амплитуд в его пределах. Используя информацию об интервале Верхнего Ред-Форка и каротажных диаграммах (часть 5b), они смогли интерпретировать различные этапы заполнения долины по всему каналу 9.0254 [11] .
В своем исследовании группа использовала комбинацию спектральной декомпозиции и когерентности, чтобы очертить и интерпретировать врезанные долины интервала Верхний Ред-Форк в северной части бассейна Анадарко. Спектральная декомпозиция и когерентность применялись в трехмерной сейсморазведке Amoco mega merge. Цель состояла в том, чтобы идентифицировать прерывистые тела канала и, возможно, интерпретировать этапы заполнения канала. Используя два атрибута, группа смогла достичь обоих. На рис. 5 показан один из результатов исследования, отображающий срез спектральной составляющей на частоте 36 Гц. В части 5а показан канал, очерченный когерентностью, а также разности амплитуд в его пределах. Используя информацию об интервале Верхнего Ред-Форка и каротажных диаграммах (часть 5b), они смогли интерпретировать различные этапы заполнения долины по всему каналу 9.0254 [11] . После того, как Пейтон и др. (1999).
После того, как Пейтон и др. (1999). Для красного канала были выбраны частоты 5, 25 и 65 Гц, так как они выявляли разные особенности каналов. На рис. 7 показан результат смешивания RGB, выполненного с тремя отдельными частотными объемами. Изображение отображает большую часть канала яркой окраской, что означает, что оно содержит все три частоты и соответствует самой толстой части канала. Два разрыва, видимые как низкие амплитуды на рисунке 6, видны на рисунке 7 как низкочастотные зоны (5 Гц) между областями смешанных частот. Это было истолковано как указание на то, что канал был подключен в этих регионах. Кроме того, там, где фарватер канала не был определен на картах амплитуд, его можно четко увидеть на частоте 65 Гц в частотных данных (рис. 7). Аналогичный процесс был также выполнен для Желтого канала, который выявил многоэтажный комплекс каналов.
Для красного канала были выбраны частоты 5, 25 и 65 Гц, так как они выявляли разные особенности каналов. На рис. 7 показан результат смешивания RGB, выполненного с тремя отдельными частотными объемами. Изображение отображает большую часть канала яркой окраской, что означает, что оно содержит все три частоты и соответствует самой толстой части канала. Два разрыва, видимые как низкие амплитуды на рисунке 6, видны на рисунке 7 как низкочастотные зоны (5 Гц) между областями смешанных частот. Это было истолковано как указание на то, что канал был подключен в этих регионах. Кроме того, там, где фарватер канала не был определен на картах амплитуд, его можно четко увидеть на частоте 65 Гц в частотных данных (рис. 7). Аналогичный процесс был также выполнен для Желтого канала, который выявил многоэтажный комплекс каналов. Изображение было аннотировано для освещения особенностей канала. После того, как Отман и др. (2016)
Изображение было аннотировано для освещения особенностей канала. После того, как Отман и др. (2016) , Гридли, Дж., и Лопес, Дж. (1999). Интерпретационные применения спектральной декомпозиции в характеристике коллектора. Передовой край, 18 (3), 353-360. дои: 10.1190/1.1438295
, Гридли, Дж., и Лопес, Дж. (1999). Интерпретационные применения спектральной декомпозиции в характеристике коллектора. Передовой край, 18 (3), 353-360. дои: 10.1190/1.1438295 Б., Лестари, Э.П., С., Рамадан, А., и Хиросиади, Ю. (2016). Комбинированный анализ AVO и спектрального разложения для определения характеристик резервуара с газообразным песком ниже условия настройки толщины. проц. Индонезийский бензин. Assoc., 40th Ann. Конв. дои: 10.29118/ипа.0.16.136.г
Б., Лестари, Э.П., С., Рамадан, А., и Хиросиади, Ю. (2016). Комбинированный анализ AVO и спектрального разложения для определения характеристик резервуара с газообразным песком ниже условия настройки толщины. проц. Индонезийский бензин. Assoc., 40th Ann. Конв. дои: 10.29118/ипа.0.16.136.г