1. Что называют дифракцией света? Физика 11 класс Громов, Шаронова. Вопросы к параграфу 10 – Рамблер/класс

1. Что называют дифракцией света? Физика 11 класс Громов, Шаронова. Вопросы к параграфу 10 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

1. Что называют дифракцией света?

ответы

1 .Дифракция света — это огибание световыми волнами непрозрачных тел и проникновение света в область геометрической теня.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

Компьютерные игры

похожие вопросы 5

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№33. Зад.№14.Под руководством Ященко. Помогите поставить в соответствие.

   Здравствуйте! На рисунке изображён график функции у =f(х). Точки a, b, с, d и е задают на оси х четыре интервала. Помогите пользуясь (Подробнее…)

ГДЗЭкзаменыМатематикаЯщенко И.В.

2. В чем заключается принцип Ферма? Громов, Шаронова 11 класс Физика.

Вопросы к параграфу 1

2. В чем заключается принцип Ферма?

ГДЗФизикаГромов С.В.11 класс

ГДЗ по Физике Громов 10 класс, вопросы Гл.1§6№7.

Если не затруднит помогите ответить на вопрос Гл.1§6№7.
Что нужно знать для того, чтобы можно было решить основную за-
дачу (Подробнее…)

ГДЗФизика10 классГромов С.В.

ГДЗ Русский язык 11 класс Греков В. Ф. §91 Вопрос 490 Составьте и запишите шесть предложений с прямой речью.

Привет!!! Помогите срочно! Завтра самостаялка будет…нужно знать ответ….
Составьте и запишите шесть предложений с прямой (Подробнее…)

ГДЗРусский язык11 классШколаГреков В.Ф.

ГДЗ информатика 9 класс Босова, рабочая тетрадь, упр. 36. Переведите число 1010 из десятичной системы счисления в двоичную

Переведите число 1010 из десятичной системы счисле-

ния в двоичную систему счисления. Сколько единиц со-
держит полученное (Подробнее. ..)

ГДЗИнформатика9 классБосова Л.Л

Дифракция — Всё для чайников

Подробности

Категория: Оптика

ДИФРАКЦИЯ

 

 

 

Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.

Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.

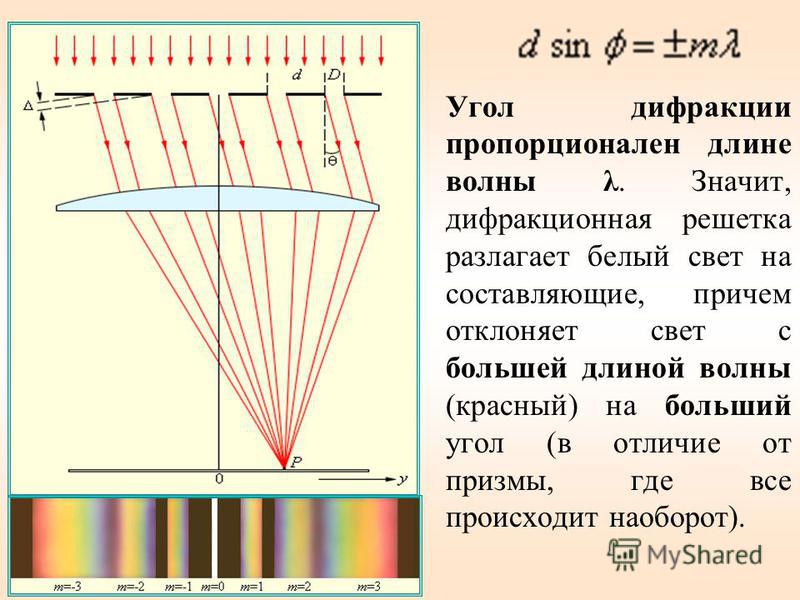
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.

Явление дифракции волн на поверхности воды можно наблюдать, если поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны (рис. 128). Хорошо будет видно, что за экраном распространяется круговая волна, как если бы в отверстии экрана располагалось колеблющееся тело -источник волн. Согласно принципу Гюйгенса так и должно быть. Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.

Если размеры щели велики по сравнению с длиной волны, то картина распространения волн за экраном совершенно иная (рис. 129). Волна проходит сквозь щель, почти не меняя своей формы. Только по краям можно заметить небольшие искривления волновой поверхности, благодаря которым волна частично проникает и в пространство за экраном. Принцип Гюйгенса позволяет понять, почему происходит дифракция. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.

 

 

ДИФРАКЦИЯ СВЕТА

Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.

Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.

Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.

 Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.

Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.

Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.

Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.

Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).

Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.

Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.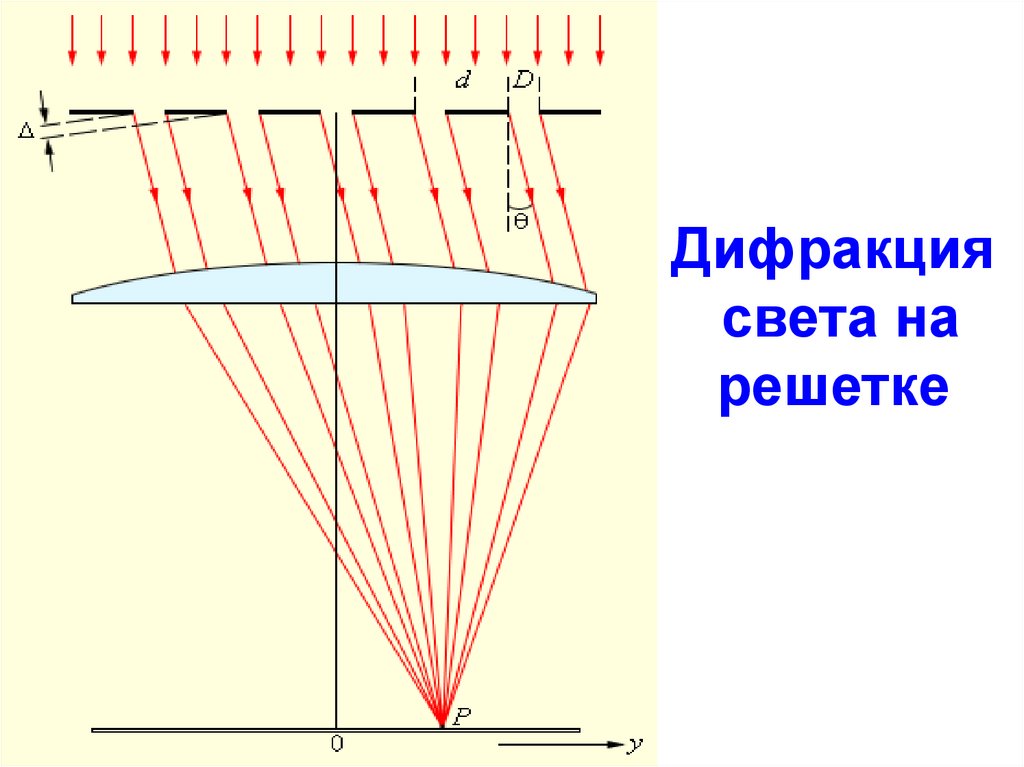

Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.

Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.

На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.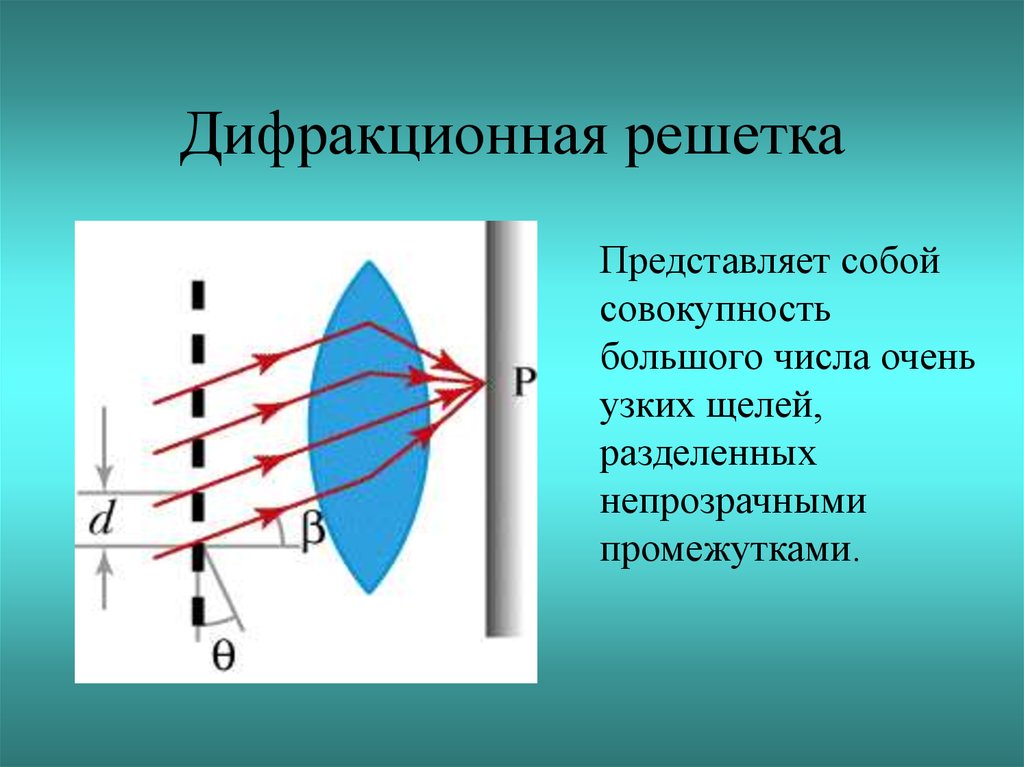

Зоны Френеля для трехсантиметровой волны       

 

Зонная пластинка для трехсантиметровых волн      

 

Трёхсантиметровые волны: пятно Пуассона       

 

Трёхсантиметровые волны: фазовая зонная пластинка      

 

Круглое отверстие. Геометрическая оптика — дифракция Френеля     

 

Круглое отверстие. Дифракция Френеля — дифракция Фраунгофера     

 

Сравнение картин дифракции: ирисовая диафрагма и круглое отверстие      

 

Пятно Пуассона      

 

Дифракция Френеля на краю полуплоскости      

 

Трехсантиметровые волны: дифракция Френеля на двух щелях       

Дифракция Фраунгофера. Щель и полоска    

 

Дифракция Фраунгофера. Две щели     

 

Дифракционные решетки с разными периодами      

 

Двумерные дифракционные решетки      

 

Трёхсантиметровые волны и очень узкая щель      

 

Модель спирали Корню       

Разница между BJT и FET в табличной форме

Электроника

BJT и FET

BJT и FET являются электронными устройствами. Основное различие между BJT и FET заключается в том, что транзистор с биполярным переходом является биполярным устройством управления током, а FET (полевой транзистор) является однопереходным транзистором. Это устройство контроля напряжения.

1: BJT (биполярный переходной транзистор) является биполярным устройством.	1:FET (полевой транзистор) — однопереходный транзистор.
2: Его работа зависит как от основных, так и от неосновных носителей заряда.	2: Его работа зависит от основных носителей заряда, которыми могут быть дырки или электроны.
3: Входной импеданс биполярного транзистора очень мал, т.е. (1 кОм -3 кОм)	3: Входной импеданс полевого транзистора очень большой.
4: это текущее устройство управления.	4: Это устройство, управляемое напряжением.
5: Шумнее.	5:Меньше шума.
6: Изменения частоты влияют на их производительность.	6:Высокочастотный отклик.
7:Это устройство, зависящее от температуры.	7: Обладает лучшей термостойкостью.
8: Это дешевле.	8:Это дороже, чем бджт.
9:Больше по размеру, чем полевой транзистор.	9: меньше по размеру, чем BJT.

10: Имеет напряжение смещения.	10: Напряжение смещения отсутствует.
11: Больше усиления.	11:Меньшее усиление.
12: Имеет высокое выходное сопротивление из-за высокого коэффициента усиления.	12: Имеет низкий выходной импеданс из-за меньшего коэффициента усиления.
13: Его коллектор и база более положительны, чем эмиттер.	13:Сток положительный, ворота отрицательные по отношению к истоку.
14: Его база отрицательна по отношению к эмиттеру.	14:Его врата более негативны по отношению к источнику.
15:Bjt состоит из трех частей (основа, излучатель и коллектор).	15:Fet состоит из трех частей (Drain, Source и Gate).
16: Имеет высокий коэффициент усиления по напряжению.	16: Низкий коэффициент усиления по напряжению.
17: Низкий коэффициент усиления по току.	17: Имеет высокий коэффициент усиления по току.
18: Среднее время переключения.	18: Быстрое время переключения.
19:Легко поддается смещению.	19: Его смещение затруднено.

20: Предпочтительны для слаботочных приложений.	20: предпочтительнее для приложений с низким напряжением.
21: Для поддержания требуется небольшой ток.	21:Для их работы требуется небольшое напряжение.
22: потребляет больше энергии. 23: Имеет отрицательный температурный коэффициент.	22:Потребляет меньше энергии. 23: Имеет положительный температурный коэффициент.

Похожие статьи

Емкость конденсатора Формула

Электричество и магнетизмЭлектроника

емкость конденсатора0167 напряжение на его обкладках конденсатора. Емкость находится путем деления электрического заряда на напряжение по формуле C=Q/V. Его единицей является Фарада.

Формула

Его формула выглядит следующим образом:

C=Q/V

Где C — емкость, Q — напряжение, а V — напряжение. Мы также можем найти заряд Q и напряжение V, переформулировав приведенную выше формулу следующим образом:

Q=CV

V=Q/C

  Фарад — единица измерения емкости. Один фарад — это величина емкости, когда один кулон заряда хранится с одним вольтом на его пластинах.

Большинство конденсаторов, используемых в электронике, имеют емкость, указанную в микрофарадах (мкФ) и пикофарадах (пФ). Микрофарад — это одна миллионная часть фарада, а пикофарад — одна триллионная часть фарада.

Какие факторы влияют на емкость конденсатора?

Зависит от следующих факторов:

Площадь пластин

Емкость прямо пропорциональна физическому размеру пластин, определяемому площадью пластин, A. Большая площадь пластины дает большую емкость и меньшую емкость. На рис. (а) показано, что площадь пластины конденсатора с параллельными пластинами равна площади одной из пластин. Если пластины перемещаются относительно друг друга, как показано на рис. (b), площадь перекрытия определяет эффективную площадь пластины. Это изменение эффективной площади пластины является основным для определенного типа переменного конденсатора.

Разделение пластин

`Емкость обратно пропорциональна расстоянию между пластинами. Разделение пластин обозначено буквой d, как показано на рис. (а). Чем больше расстояние между пластинами, тем меньше емкость, как показано на рис. (b). Как обсуждалось ранее, напряжение пробоя прямо пропорционально расстоянию между пластинами. Чем дальше разнесены пластины, тем больше напряжение пробоя .

Диэлектрическая проницаемость материала

Как известно, изоляционный материал между обкладками конденсатора называется диэлектриком. Диэлектрические материалы имеют тенденцию уменьшать напряжение между пластинами для данного заряда и, таким образом, увеличивать емкость. Если напряжение фиксировано, из-за присутствия диэлектрика может быть сохранено больше заряда, чем без диэлектрика. Мера способности материала создавать электрическое поле называется диэлектрической проницаемостью или относительной диэлектрической проницаемостью, обозначаемой символом ∈ _р .

Емкость прямо пропорциональна диэлектрической проницаемости. Диэлектрическая проницаемость вакуума определяется как 1, а диэлектрическая проницаемость воздуха очень близка к 1. Эти значения используются в качестве справочных, и все другие материалы имеют значения εr, указанные по отношению к вакууму или воздуху. Например, материал с εr=8 может иметь емкость, в восемь раз превышающую емкость воздуха, при прочих равных условиях.

Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала,∈r, к абсолютной диэлектрической проницаемости вакуума,∈ ₀ , что выражается следующей формулой:

∈ _r =∈/∈ ₀

Ниже приведены некоторые распространенные диэлектрические материалы и типичные диэлектрические постоянные для каждого из них. Значения могут варьироваться, поскольку зависят от конкретного состава материала.

Материал Типичные значения ∈R

• воздух 1.0
• Тефлон 2.0
• Бумага 2.5
• Масло 4.0
• MICA 5,0
• Стекло 7,5
• Ceramic 1200

Диэлектрическая проницательность ∈R является безразмерной, поскольку она является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала,∈r, к абсолютной диэлектрической проницаемости вакуума,∈0, выражаемое следующей формулой:

∈r=∈/∈0

8,85×10-12 Ф/м.

Формула емкости в пересчете на физические параметры

Вы видели, что емкость напрямую связана с площадью пластины, A, и диэлектрической проницаемостью,εr, и обратно пропорциональна расстоянию между пластинами, d. Точная формула для расчета емкости с точки зрения этих трех величин: m)

Производная емкость конденсатора с плоскими пластинами

Рассмотрим конденсатор с плоскими пластинами. Размер пластины большой, а расстояние между пластинами очень маленькое, поэтому электрическое поле между пластинами однородно.

Электрическое поле ‘E’ между плоским конденсатором составляет:

отношение плоского конденсатора

Емкость цилиндрических конденсаторов физика

Рассмотрим цилиндрический конденсатор длиной L, образованный двумя коаксиальными цилиндрами радиусов ‘a’ и ‘b ‘.Предположим, что L >> b такое, что на концах цилиндров нет окантовывающего поля.

Пусть «q» — заряд конденсатора, а «V» — разность потенциалов между пластинами. Внутренний цилиндр заряжен положительно, а внешний цилиндр заряжен отрицательно.