Что такое размерность матрицы: Как найти размерность матрицы

Содержание

Как найти размерность матрицы

Матрица записывается в виде прямоугольной таблицы, состоящей из некоторого количества строк и столбцов, на пересечении которых располагаются элементы матрицы. Основное математическое применение матриц – решение систем линейных уравнений.

Число столбцов и строк задают размерность матрицы. К примеру, таблица размерностью 5×6 имеет 5 строк и 6 столбцов. В общем случае, размерность матрицы записывается в виде m×n, где число m указывает на количество строк, n – столбцов.

Размерность матрицы важно учитывать при совершении алгебраических операций. Например, складывать можно матрицы только одного и того же размера. Операция сложения матриц с разной размерностью не определена.

Если массив имеет размерность m×n, его можно умножить на массив n×l. Число столбцов первой матрицы должно равняться числу строк второй, иначе операция умножения не будет определена.

Размерность матрицы указывает на число уравнений в системе и количество переменных. Число строк совпадает с количеством уравнений, а за каждым столбцом закреплена своя переменная. Решение системы линейных уравнений «записано» в действиях над матрицами. Благодаря матричной системе записи становится возможным решать системы высоких порядков.

Если число строк равно числу столбцов, матрица называется квадратной. В ней можно выделить главную и побочную диагонали. Главная идет от левого верхнего угла к правому нижнему, побочная – от правого верхнего к левому нижнему.

Массивы размерностью m×1 или 1×n являются векторами. Также в виде вектора можно представить любую строку и любой столбец произвольной таблицы. Для таких матриц определены все операции над векторами.

Поменяв в матрице A строки и столбцы местами, можно получить транспонированную матрицу A(Т). Таким образом, при транспонировании размерность m×n перейдет в n×m.

В программировании для прямоугольной таблицы задается два индекса, один из которых пробегает длину всей строки, другой – длину всего столбца. При этом цикл для одного индекса помещен внутрь цикла для другого, за счет чего обеспечивается последовательное прохождение всей размерности матрицы.

Матрицы размерность — Справочник химика 21

Рассмотрим некоторые свойства и связи в матрицах Г и В. Напомним, что рангом матрицы называется максимальное Число линейно-независимых векторов — строк матрицы, и численно ранг матрицы равен порядку ее наивысшего ненулевого минора. Матрица размерности (В х X М) имеет полный ранг, если ее ранг совпадает с минимальным из чисел В, М, т. е. если выполняется условие rg Г = ш п(Д, М), Важнейшее свойство такой матрицы заключается в том, что она сохраняет свой ранг при любых достаточно малых возмущениях, а ее нормальное решение имеет непрерывный характер. Ранг стехиометрической матрицы Г никогда не может быть выше М — I), где [c.130]
Техника нахождения элементов матрицы Г достаточно проста [12, 63]. В уравнении (3.28) разобьем атомную матрицу В по столбцам на две матрицы В и В так, чтобы их размерность была соответственно (ТУ X М— )] и т -1) X I].

Для дальнейших преобразований удобно представить для матрицы В условие сохранения в виде = 0. В свою очередь В х можно разбить еще на две матрицы и перегруппировать столбцы так, чтобы получить неособенную квадратную матрицу размерности [(ТУ — —I) X М — I)]. Тогда размерность оставшейся матрицы есть [(Л/ — I) X ]. Аналогично для матрицы получим две матрицы размерностей [(ЛГ — /) X П и [/ х Л соответственно. В матричной записи имеем [c.132]

Показатели степеней у размерностей переменных объединяются в матрицу размерностей [c.88]

Последовательный подход. Вначале рассмотрим эту проблему применительно к последовательному подходу. Здесь уменьшение размерности задачи расчета ХТС достигается методами структурного анализа [47]. При этом решаются следующие задачи 1) в схеме выделяются комплексы — совокупности блоков охваченных обратными связями [3, с. 33] 2) определение внутри каждого комплекса оптимальной с точки зрения какого-либо критерия совокупности итерируемых переменных (II, 5).

Обычно совокупность итерируемых переменных (II, 5) выбирается из условия, чтобы их суммарная размерность была минимальной. Положительные и отрицательные стороны такого выбора переменных (II, 5) обсуждаются в работе [3, с. 85]. Отметим здесь, что применительно к квазиньютоновским методам это более или менее оправдано, поскольку, как мы уже отмечали, можно считать при применении этих методов, что число итераций растет пропорционально размерности системы нелинейных уравнений. Уменьшаются требования и к размеру памяти, поскольку приходится хранить одну или две матрицы размерности fix/г. При использовании ориентированного на уравнения подхода так же, как и в предыдущем случае определяются комплексы, а внутри комплексов — оптимальные совокупности разрываемых потоков [48 17 18, с. 258]. [c.61]

Матрица, содержащая одну строку, т. е. размерности 1 X и, называется вектор-строкой, а матрица размерности и X 1, т. е. состоящая из одного столбца, называется вектор-столбцом. [c.229]

Отличительной особенностью большинства соотношений, используемых для расчета коэффициентов активности многокомпонентной смеси, является то, что они являются обобщением соответствующих соотношений для бинарных смесей. Поэтому коэффициенты этих соотношений определяются по экспериментальным равновесным данным соответствующих бинарных пар. Очевидно, для системы, содержащей к компонентов, коэффициенты будут представляться в простейшем случае матрицей размерности к X к. [c.410]

Для решения покомпонентного материального баланса применяются те же алгоритмы, что и при решении задачи линеаризации, однако здесь элементы являются скалярными величинами, а не матрицами размерностью (2С + I) х (2С + 1).

[c.262]

Базисной матрицей называется невырожденная матрица размерности т хт, образованная из т столбцов матрицы ограничений А. [c.183]

Пусть (/ = 1, 2 г = 1,. . га) есть -обратные матрицы размерности I X га, удовлетворяющие соотношениям [c. 67]

Пусть Nq = щ,. . Пд) — матрица размерности (п X д), столбцы которой образованы векторами и, (г = 1,. . д ). Примем, что ранг ее равен а. Алгоритм движения надо строить таким образом, чтобы поисковые направления р1 лежали внутри линейного многообразия Ьд. Очевидно, что этого можно достигнуть, образуя направления по формуле [c.192]

Здесь С = Фп, т+1-Ф , т+1 — матрица размерности (т + 1 X X т + 1) 5 = II Я,. . Я — матрица размерности (т + 1 X 1) а = 0,. . — матрица размерности (т + 1 X 1). [c.39]

Таким образом, в представлении (XI,2) векторы г/( ) и являются клеточными матрицами размерностей соответственно и х1 и т х1. Как обычно, уравнения блоков должны быть дополнены уравнениями связей [c.230]

Пусть I — матрица размерности (2/7 Хт), столбцы которой являются базисом подпространства V. Тогда нужно вычислять матрицу V I, т.е. применять оператор V к /п векторам. [c.84]

Всиомним теперь, что часть компонент вектора 6 — заданные величины, равные перемещениям на и перенесем произведения их на соответствующие элементы матрицы К в правую часть системы уравнений (4. 204) вспомним также, что уравнения, соответствующие узлам на незаконны и вычеркнем их из системы (4.203). В результате этих преобразований получим вторую систему уравнений с матрицей размерности 2Х (Л/в—М в), где Мин — количество лежащих на 8и вершин. Обозначим эту матрицу через [ ], она получается вычеркиванием строк и столбцов матрицы [X] с номерами 21—1 и 21, где I пробегает номера вершин на 5 (заметим, что программная реализация этого процесса достаточно проста).

[c.189]

Матрица [К], называемая глобальной матрицей жесткости, или просто матрицей жесткости системы, получается сложением локальных матриц жесткости [Я ] по следующему правилу сначала к нулевой матрице размерности МХМ добавляется матрица, в левом верхнем углу которой стоит локальная матрица жесткости 1-го элемента, к получившейся матрице добавляется матрица размерности NXN, ненулевые элементы которой расположены на пересечении 2-го и 3-го столбцов и 2-й и 3-й строк и равны соответствующим элементам локальной матрицы жесткости для [c. 181]

Для группы Сав существует только четыре разных набора матриц размерности 1 X 1, т. е. четыре НП типа Л а, В (табл. 19). [c.114]

Таким образом, матрицы представления Г суть унитарные матрицы. Можно доказать, что все возможные представления каждой группы О (в том числе и не обязательно группы точечной симметрии) эквивалентны ее унитарным представлениям, другими словами, при подходящем выборе базиса матрицы любого представления переходят в унитарные матрицы, а потому при рассмотрении представлений достаточно ограничиться лишь унитарными представлениями. Среди всех унитарных представлений всегда есть единичное, или полносимметричное, в котором каждому элементу группы отвечает одна и та же матрица размерности 1 х 1, а именно единица. [c.201]

Отсюда следует, что любой объект gi е Охарактеризуется матрицей размерности [т X 1]. Каждый элемент этой матрицы принимает значение из отрезка [О, 1]. Примером таких объектов могут служить отдельные изделия выпускаемой продукции, а свойствами — характеристики качества изделий.

[c.25]

I — единичная матрица размерности 3 х 3), согласно соотношению [c.346]

Представлением группы называется гомоморфное ютображение данной группы на группу квадратных матриц. Размерность матриц называется размерностью представления. [c.20]

Допустим, что матрицы компенсации можно представить в виде В( = (Е( где Et — единичная матрица размерности/и fXWf. Разо- [c.81]

Следовательно, проатранство решений (2) представляет собой матрицу размерностью 6 х 4. [c.143]

В результате полного цикла моделирования за время Т будет получена симуляционная матрица размерности (N 5), где N-общее число повторов, возникших с самого качала работы модели. [c.69]

Изменение размерности матриц, выбор значений из NumPy массивов по условию

До этого момента индексы и срезы использовать для извлечения подмножеств. В этих методах используются числовые значения.

Но есть альтернативный путь получения элементов — с помощью условий и булевых операторов.

Предположим, что нужно выбрать все значения меньше 0,5 в матрице размером 4х4, которая содержит случайные значения между 0 и 1.

>>> A = np.random.random((4, 4))
>>> A
array([[ 0.03536295, 0.0035115 , 0.54742404, 0.68960999],
       [ 0.21264709, 0.17121982, 0.81090212, 0.43408927],
       [ 0.77116263, 0.04523647, 0.84632378, 0.54450749],
       [ 0.86964585, 0.6470581 , 0.42582897, 0.22286282]])

Когда матрица из случайных значений определена, можно применить оператор условия. Результатом будет матрица из булевых значений: True, если элемент соответствовал условию и False — если нет. В этом примере можно видеть все элементы со значениями меньше 0,5.

>>> A < 0.5
array([[ True, True, False, False],
       [ True, True, False, True],
       [False, True, False, False],
       [False, False, True, True]], dtype=bool)

На самом деле, булевы массивы используются для неявного извлечения частей массивов. Добавив прошлое условие в квадратные скобки, можно получить новый массив, который будет включать все элементы меньше 0,5 из предыдущего.

>>> A[A < 0.5]
array([ 0.03536295, 0.0035115 , 0.21264709, 0.17121982, 0.43408927,
        0.04523647, 0.42582897, 0.22286282])

Управление размерностью

Вы уже видели, как можно превращать одномерный массив в матрицу с помощью функции reshape().

>>> a = np.random.random(12)
>>> a
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
        0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
        0.41894881, 0.73581471])
>>> A = a.reshape(3, 4)
>>> A
array([[ 0.77841574, 0.39654203, 0.38188665, 0.26704305],
       [ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
       [ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])

Функция reshape() возвращает новый массив и таким образом может создавать новые объекты. Но если необходимо изменить объект, поменяв его форму, нужно присвоить кортеж с новыми размерностями атрибуту shape массива.

>>> a.shape = (3, 4)
>>> a
array([[ 0.77841574, 0.39654203, 0.38188665, 0.26704305],
       [ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
       [ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])

Как видно на примере, в этот раз оригинальный массив изменил форму, и ничего не возвращается. Обратная операция также возможна. Можно конвертировать двухмерный массив в одномерный с помощью функции ravel().

>>> a = a.ravel()
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
        0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
        0.41894881, 0.73581471])

Или прямо повлиять на атрибут shape самого массива.

>>> a.shape = (12)
>>> a
array([ 0. 77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
        0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
        0.41894881, 0.73581471])

Еще одна важная операция — транспонирование матрицы. Это инверсия колонок и рядов. NumPy предоставляет такую функциональность в функции transpose().

>>> A.transpose()
array([[ 0.77841574, 0.27519705, 0.52008642],
       [ 0.39654203, 0.78115866, 0.10862692],
       [ 0.38188665, 0.96019214, 0.41894881],
       [ 0.26704305, 0.59328414, 0.73581471]])

Основы программирования в R

Создание матрицы

Матрицы в R можно создавать разными способами. Выбор способа зависит от того, какую матрицу мы хотим создать: пустую матрицу (чтобы потом заполнять ее нужными значениями) или матрицу, составленную из уже имеющихся значений, например, из векторов.

Для того чтобы создать пустую матрицу, нужно определить, матрицу какой размерности мы хотим. Размерность матрицы – число строк и число столбцов в ней. Создадим для начала матрицу $2 \times 3$, состоящую из нулей:

M <- matrix(0, nrow = 2, ncol = 3)
M

##      [,1] [,2] [,3]
## [1,]    0    0    0
## [2,]    0    0    0

Можем посмотреть на ее размерность:

dim(M)

## [1] 2 3

Заполнять эту матрицу другими значениями мы пока не будем – это будет интереснее делать, когда мы узнаем про циклы. А сейчас посмотрим, как собрать матрицу из “готовых” векторов.
Пусть у нас есть три вектора

x <- c(1, 2, 3, 0)
y <- c(4, 5, 6, 0)
z <- c(7, 8, 9, 0)

и мы хотим объединить их в матрицу. Векторы будут столбцами матрицы:

M_cols <- cbind(x, y, z) # c - от columns
M_cols

##      x y z
## [1,] 1 4 7
## [2,] 2 5 8
## [3,] 3 6 9
## [4,] 0 0 0

А теперь векторы будут строками матрицы:

M_rows <- rbind(x, y, z) # r - от rows
M_rows

##   [,1] [,2] [,3] [,4]
## x    1    2    3    0
## y    4    5    6    0
## z    7    8    9    0

Другой способ создавать матрицы — разбивать на строки один длинный вектор. Возьмем вектор:

long_vec <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 5, 0)

Посиотрим, сколько в нем элементов:

length(long_vec)

## [1] 12

А теперь превратим вектор в матрицу из трех строк и четырех столбцов:

m1 <- matrix(long_vec, 3, 4) # получим матрицу с 3 строками и 4 столбцами
m1

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7    0
## [2,]    2    5    8    5
## [3,]    3    6    9    0

Конечно, если бы потребовали от R невозможное – матрицу, произведение числа строк и столбцов которой не равно длине вектора, из которого мы пытаемся эту матрицу создать – мы бы получили ошибку:

# m2 <- matrix(long_vec, 4, 5)

Столбцам и строкам матрицы можно дать названия. Посмотрим еще раз на матрицу m1:

m1

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7    0
## [2,]    2    5    8    5
## [3,]    3    6    9    0

А теперь дадим столбцам этом матрицы названия.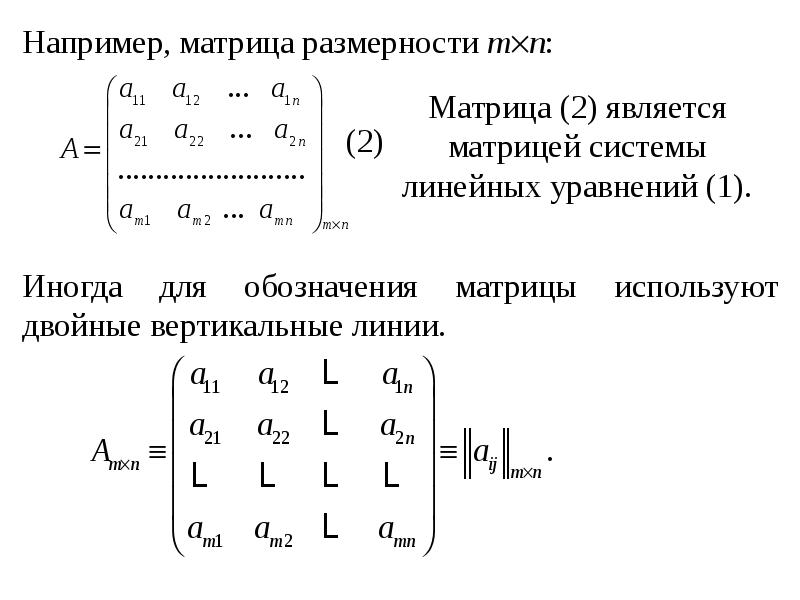

colnames(m1) <- c("A", "B", "C", "D")
m1

##      A B C D
## [1,] 1 4 7 0
## [2,] 2 5 8 5
## [3,] 3 6 9 0

А теперь назовем строки матрицы:

rownames(m1) <- c("r1", "r2", "r3")
m1

##    A B C D
## r1 1 4 7 0
## r2 2 5 8 5
## r3 3 6 9 0

Можно, конечно, присваивать названия сразу и строкам, и столбцам. Проделаем это с матрицей M_cols.

dimnames(M_cols) <- list(c("r1", "r2", "r3", "r4"), c("X", "Y", "Z")) # сначала названия строк, затем -- столбцов

О том, что такое list – поговорим чуть позже.

Маркировка и размер матриц

Исторически сложилось, что маркировка матриц соответствует маркировке видиконов по внешнему диаметру с равным матрице размером чувствительной к свету области. Примерно, диагональ матрицы равна 2/3 от значения маркировки. Ниже приведена сводная таблица для наиболее ходовых типов матриц. В графе Размер приведены ширина и высота реальных матриц, используемых в аппаратах и которые производитель отнес к данному типу. Для APS-C у разных фирм размер может немного различаться.

Тип	Размер	Диагональ	Площадь	Комментарий
	мм	мм	мм²
Mysterium* Monstro**	186х56	194,25	10416	RED Epic 617
Mysterium Monstro	56х42	70	2352	RED Epic 645
Средний формат	48х36	60	1728	Mamiya RZ22
	44х33	55	1452	Pentax 645D, Leaf Capture
	45х30	54	1350	Leica S2
Полный кадр	36х24	43,27	864
APS-H	27,9х18,6	33,53	519	Canon EOS-1D Mark IV
Mysterium-X	27,7х14,6	31,31	404	RED Epic X
APS-C	23,6х15,8	28,4	373
Mysterium	24,2х12,5	27,24	302,5	RED One
APS-C(Canon)	22,3х14,9	26,82	332
1,5″(25,4)***	18,7х14	23,36	262	Canon G1 X
4/3	17,3×13	21,64	225
1″(16,9)	12,8х9,6	16	123
Nikon CX	13,2х8,8	15,86	116
2/3″(11,3)	8,8х6,6	11	58
1/1,7″(10)	7,44х5,58	9,3	41,5
1/1,8″(9,4)	7,18х5,35	8,95	38,4
1/2″(8,5)	6,4х4,8	8	30,7
1/2,3″(7,4)	6,17х4,55	7,67	28,1	Pentax Q
1/2,7″(6,3)	5,27×3,96	6,59	20,9
1/3,2″(5,3)	4,54×3,42	5,68	15,5

*Матрицы Mysterium используются в видеокамерах фирмы RED.
** Mysterium Monstro, вероятно, существуют в единичных экземплярах и сейчас на сайте фирмы RED камеры с их использованием не упоминаются.
*** В скобках после типа матрицы указана ожидаемая диагональ.

Установите проигрыватель Flash

Облако тегов:

…

Матрицы в видеорегистраторах. Что это?

В этой статье, мы подробно расскажем вам, за что отвечает матрица в видеорегистраторе и какие её параметры влияют на качество записываемого видео.

Матрица, также известная как видеосенсор, это безусловно один из важнейших элементов абсолютно любого видеорегистратора. Вместе с объективом, они образуют тандем, который отвечает за качество видеозаписи. Естественно, что многих автомобилистов интересует именно получаемое изображение, его четкость и детализация, однако многие не совсем понимают, на какие характеристики стоит обратить свое внимание.

Итак, для матрицы существуют два главных параметра, это её размер и количество пикселей.

Физический размер матрицы, определяет расположение и размер пикселя. В свою очередь площадь пикселя определяет светочувствительность и улучшает динамический диапазон, а также снижает количество видео-шумов в кадре.

Иными словами, физический размер матрицы определяет общее качество изображения, ведь чем больше матрица, тем больше размер пикселя, а чем больше пиксель, тем он чувствительнее. Матрицы с маленькой площадью неизбежно «шумят» во время ночной съемки. На первый взгляд, может показаться, что размер матрицы и количество пикселей, для улучшения качества записи, должно стремиться к увеличению, это так, но во всем необходимо знать меру.

Если переводить все в конкретные значения, то выходит следующее. Матрица 1/1,6 больше матрицы 1/2,5 по площади примерно в 2,44 раза. Теоретически туда можно поместить и 15-17 мегапикселей. Реклама говорит нам, что, чем больше мегапикселей, тем лучше. Но это не совсем так. Да, чем их больше, тем детальнее картинка. Но не в ущерб размерам каждого отдельного пикселя. Матрица 1/1,6 с 15-17 мегапикселями «на борту» по качеству то же самое, что и матрица 1/2,5 с 6-7 Мп. А вот если в первом случае оставить «всего» 10 Мп, то картинка окажется уже значительно лучше.

Из этого следует, что чем матрица больше, тем качественнее будет картинка в условиях плохой освещенности. Но увеличение матрицы – это увеличение и самого прибора, и его стоимости. А так как видеорегистратор должен быть компактен и незаметен, приходится искать «золотую середину». Сейчас у всех регистраторов матрицы примерно одного размера. Качество теперь заключается в нюансах настроек и параметров.

Размер матрицы фотоаппарата все, что нужно знать | leopard2021

Раньше было вполне логичным, что покупая компактную камеру, вы получали небольшую матрицу, а если выбирали крупногабаритную зеркалку со сменными объективами, матрица на ней была значительно больше. Это сказывалось на качестве фотографий, поскольку чем больше матрица, тем более детализированы были изображения.

Сейчас это в принципе, тоже в какой-то мере актуально, матрица — это самая дорогая часть камеры в плане производства, и чем больше матрица, тем и камера, соответственно, дороже. Потому на дорогие камеры обычно не устанавливаются матрицы 1/2.3 дюймовые, а на дешевых, соответственно, не найти полнокадровую.

Но надо сказать, что сейчас многие производители стали предлагать компактные камеры с относительно большими матрицами, точно так же как и камеры под сменные объективы с меньшими матрицами. Так что разобраться в ситуации, пожалуй, стало сложнее. Небольшие матрицы способны отлично срабатывать в различных условиях, и даже имеют некоторые преимущества перед большими.

За последние годы и сама технология создания матриц значительно продвинулась вперед, так что сегодня большое количество предлагаемых вариантов может смутить даже опытного пользователя, что уж говорить о тех, кто приобретает первую фотокамеру. А ведь размер матрицы еще и на фокусном расстоянии сказывается, так что учитывать при выборе камеры действительно нужно очень многое.

Итак, мы решили разобраться в различных типах матриц, чтобы расставить все по местам. Но для начала нужно уточнить, как именно размер матрицы влияет на эффективное фокусное расстояние.

Фокусное расстояние

Итак, мы уже выяснили, что размер матрицы связан с фокусным расстоянием, то есть с тем, какой именно объектив подойдет вашей камере. Если вы приобретаете компактный девайс с не съемным объективом, проблема сама собой отпадает, то есть с позиции покупателя это гораздо проще. Но не просто так профессионалы выбирают именно те камеры, где объективы можно менять. Любой объектив должен иметь поле (круг) изображения или диаметр света, который существует в объективе и который покрывает размер матрицы. Есть одно исключение, к которому мы вернемся позже.

Итак, встроенные или нет, объективы всегда помечены реальным фокусным расстоянием, а не эффективным фокусным расстоянием, которое вы получите при использовании на той или иной камере. Но проблема в том, что различные объективы с различной маркировкой могут в итоге обеспечить одно и то же фокусное расстояние для работы. Почему? Потому что они предназначены для разных матриц. Именно поэтому производители помимо маркировки указывают эквивалент, где основным расстоянием считается 35мм или полнокадровая матрица.

Вот — один из примеров: камера с матрицей меньше чем полнокадровая вполне может использоваться с 18-55мм объективом, но на деле фокусное расстояние, которое вы получите будет ближе к 27-82мм. Это все происходит потому, что матрица не достаточно велика, чтобы использовать объектив точно так же как смог бы полнокадровый. Из-за того, что периферическое пространство внутри объектива не принимается в расчет, получается тот же эффект как от использования объектива с большим фокусным расстоянием.

В компактных камерах может был установлен 19мм объектив, но из-за размера матрицы, который меньше фуллфрейма, вы получите в итоге большее фокусное расстояние, около 28мм. Точная длина определяется кроп-фактором, то есть числом, на которое нужно увеличить данное под фуллфрейм фокусное расстояние, чтобы выяснить какое расстояние получится на той или иной камере.

Размеры матриц

/2.3 дюйма

Размер такой матрицы примерно 6.3 x 4.7 мм. Это — самая маленькая матрица, которую можно найти в современных камерах, и чаще всего — в бюджетных компактных моделях. Разрешение такой матрицы составляет, как правило, 16-20 Мп.

По крайней мере такой расклад был самым популярным какое-то время назад. Сегодня многие производители стали делать больший упор на любительские фотоаппараты с большими матрицами, так что и размер такой не так распространен как ранее.

Однако, преимущество в том, что такой размер позволяет получить компактную камеру и использовать ее с длиннофокусными объективами, например компактными суперзумами. А большая матрица значит, что и объектив понадобится больший.

При хорошем освещении такие камеры могут предоставить неплохой результат, но для более придирчивых фотографов они точно не подойдут, поскольку при низкой освещенности будут зернить.

1/1.7 дюймов

Размер этих матриц 7.6 x 5.7мм. С такой матрицей гораздо проще выделить объект съемки из фона, и соответственно, производительность в плане деталей как в тени, так и на свету. Так что использовать их можно уже в более разнообразных условиях. Раньше такие камеры были самыми распространенными среди любителей, но сейчас их место стремительно занимают дюймовые матрицы, о которых речь и пойдет дальше.

А вот 1/1.7 дюймовые матрицы используются в некоторых относительно устаревших камерах Q-серии Pentax.

Дюймовые матрицы

Размер дюймовой матрицы 13.2мм x 8.8мм. Сегодня такие матрицы очень популярны на различных типах камер, размер позволяет им оставаться легкими и компактными. Логично, что самый популярный способ применения для дюймовой матрицы — это карманные любительские камеры, на которых объектив будет лимитирован 24-70мм или 24-100мм (если брать эквивалент 35мм). Однако, на некоторых суперзум камерах он тоже используется?, примеры — это Sony RX 10 III и Panasonic FZ2000.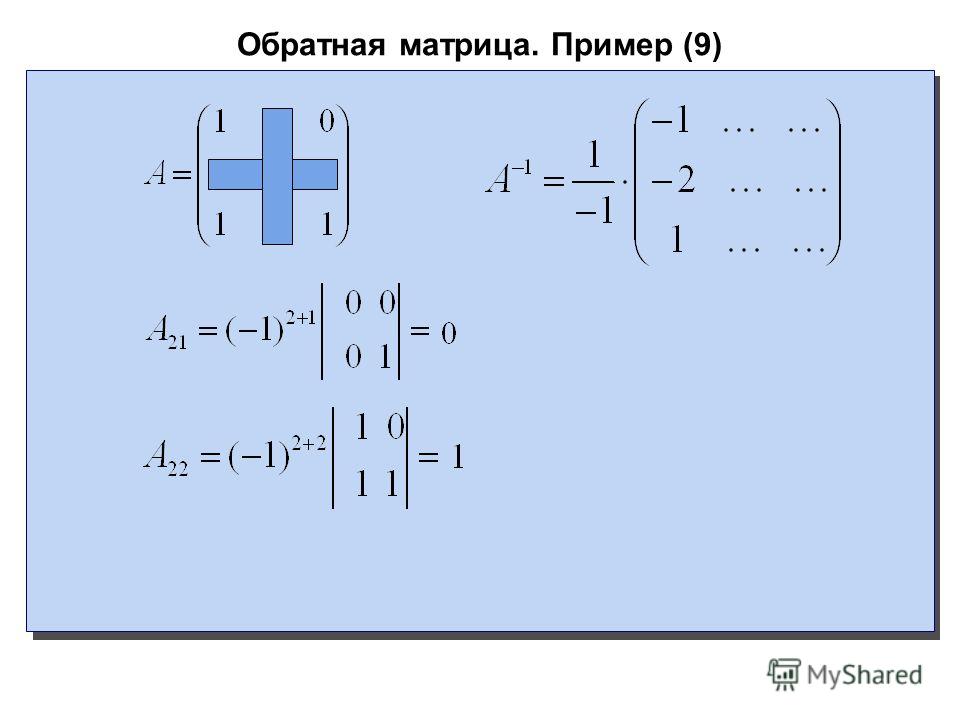

Гораздо лучше дюймовая матрица нам знакома по камерам Nikon серии 1, например Nikon 1 J5 — отличной и легкой камере, которая способна делать отличные фото и снимать 4К видео. Такую матрицу можно встретить даже среди смартфонов — Panasonic CM1.

Камеры с дюймовой матрицей способны показать результаты, значительно отличные от предыдущих вариантов. Качество их будет высоким, а даже компактные камеры, как правило, имеют широкую максимальную апертуру, так что на матрицу попадает достаточно света, потому и фотографии выходят четкими и резкими.

Частично, это результат технологии, а не только размера матрицы. Матрицы современного производства могут более эффективно захватывать свет.

k} \\ \ верт & & \ верт \ end {pmatrix} \ ,. $$ Пусть $ [s] $ обозначает $ \ {1, \ ldots, s \} $ для всех $ s \ in \ mathbb {N} $. Пусть $ C \ in \ mathcal {M} _ {k \ times n} (\ mathbb {K}) $ — матрица с вышеупомянутыми коэффициентами: $$ C = (\ lambda_ {ij}) _ {(i, j) \ in [k] \ times [n]} = \ begin {pmatrix} \ lambda_ {11} & \ cdots & \ lambda_ {1n} \\ \ vdots & \ ddots & \ vdots \\ \ lambda_ {k1} & \ cdots & \ lambda_ {kn} \ end {pmatrix} \ ,.

\ mathrm {t}) \ iff \ dim (\ mathrm {colsp} \ A) \ le \ dim (\ mathrm {rowsp} \ A) \ ,.$$ Поскольку у нас есть как $ \ dim (\ mathrm {rowsp} \ A) \ le \ dim (\ mathrm {colsp} \ A) $, так и $ \ dim (\ mathrm {colsp} \ A) \ le \ dim (\ mathrm {rowsp} \ A) $, заключаем, что $$ \ dim (\ mathrm {colsp} \ A) = \ dim (\ mathrm {rowsp} \ A) \ ,. \ квад \ квадрат

$ Размер

(функции MATLAB) Размер

(функции MATLAB)

Справочник функций MATLAB

размер

Размеры массива

Синтаксис

 d = размер (X)
[m, n] = размер (X)
m = размер (X , размер )
[d1, d2, d3 ,..., dn] = размер (X)

Описание

d = размер (X) возвращает размеры каждого измерения массива X в векторе d с ndims (X) элементами.

[m, n] = размер (X) возвращает размер матрицы X в отдельных переменных m и n .

м = размер (X, тусклый) возвращает размер измерения X , заданный скаляром dim .

[d1, d2, d3, ..., dn] = размер (X) возвращает размеры первых n измерений массива X в отдельных переменных.

Если количество выходных аргументов n не равно ndims (X) , то для:


`n> ndims (X)`	`size` возвращает единицы в «дополнительных» переменных, т. Е. Выводит от `ndims (X) +1` до `n` .
`n`	`dn` содержит произведение размеров остальных размеров `X,` i.е., размеры от `n + 1` до `ndims (X)` .

Примечание Для массива Java size возвращает длину массива Java как количество строк. Количество столбцов всегда равно 1. Для массива массивов Java результат описывает только массив верхнего уровня.

Примеры

Пример 1. Размер второго измерения rand (2,3,4) равен 3.

 м = размер (ранд (2,3,4), 2)

m =
     3

Здесь размер выводится как один вектор.

Здесь размер каждого измерения присваивается отдельной переменной.

 [m, n, p] = размер (rand (2,3,4))
m =
     2

п =
     3

p =
     4

Пример 2. Если X = единицы (3,4,5), то

Но когда количество выходных переменных меньше ndims (X):

«Дополнительные» измерения свернуты в единый продукт.

Если n> ndims (X), все «дополнительные» переменные представляют собой одноэлементные измерения:

 [d1, d2, d3, d4, d5, d6] = размер (X)

d1 = d2 = d3 =
     3 4 5

d4 = d5 = d6 =
     1 1 1

См. Также

существующие , длина , whos

sinh

размер (серийный)

Пространство строк и столбцов матрицы

Пусть A будет матрицей m на n .Пространство, охватываемое строками A , называется пространством строк A , обозначается RS (A) ; это подпространство R ⁿ. Пространство, охватываемое столбцами A , называется пространством столбцов A , обозначается CS (A) ; это подпространство R ^м.

Набор { r ₁, r ₂,…, r _m}, состоящий из рядов A , не может служить основой для RS (A) , потому что коллекция не может быть линейно независимой. Однако максимальное линейно независимое подмножество { r ₁, r ₂,…, r _m} не дает основу для пространства строк. Поскольку максимальное количество линейно независимых строк A равно рангу A ,

Аналогично, если c ₁, c ₂,…, c _n обозначают столбцы A , то максимальное линейно независимое подмножество { c _{1 9027 , c ₂,…, c _n} дает основу для пространства столбцов A .Но максимальное количество линейно независимых столбцов также равно рангу матрицы, поэтому}

Следовательно, хотя RS (A) является подпространством R ⁿ и CS (A) является подпространством R ^m, уравнения (*) и (** ) означает, что

, даже если m ≠ n .

Пример 1 : Определение размера и основы для пространства строк матрицы

Последовательность операций с элементарной строкой сводит эту матрицу к эшелонированной матрице

Ранг B равен 3, поэтому dim RS (B) = 3.Базис для RS (B) состоит из ненулевых строк в приведенной матрице:

Другая основа для RS (B) , состоящая из некоторых исходных строк B , -

Обратите внимание, что, поскольку пространство строк является трехмерным подпространством R ³, оно должно быть полностью из R ³.

Критерии принадлежности к пространству столбцов . Если A - это матрица mxn и x - вектор n , записанный как матрица столбцов, то произведение A x равно линейной комбинации столбцов A :

По определению вектор b в R ^m находится в пространстве столбцов A , если его можно записать как линейную комбинацию столбцов A . То есть b ∈ CS (A) именно тогда, когда существуют скаляры x ₁, x ₂,…, x _n так, что

Таким образом, объединение (*) и (**) приводит к следующему выводу:

Пример 2 : Для какого значения b находится вектор b = (1, 2, 3, b ) ^T в пространстве столбцов следующей матрицы?

Сформируйте расширенную матрицу [ A / b ] и сократите:

Из-за нижней строки нулей в A ′ (сокращенная форма A ) нижняя запись в последнем столбце также должна быть 0, что дает полную строку нулей внизу [ A ′ / b ′] - чтобы система A x = b имела решение.Устанавливая (6-8 b ) - (17/27) (6-12 b ) равным 0 и решая для b , получаем

Следовательно, b = (1, 2, 3, b ) ^T находится в CS (A) тогда и только тогда, когда b = 5.

Поскольку элементарные операции со строками не изменяют ранг матрицы, ясно, что в приведенном выше вычислении ранг A = ранг A 'и ранг [ A / b ] = ранг [ A ′ / b ′].(Так как нижняя строка A ′ состояла полностью из нулей, ранг A ′ = 3, подразумевая также ранг A = 3.) При b = 5 нижняя строка [ A ′ / b ′] также полностью состоит из нулей, что дает ранг [ A ′ / b ′] = 3. Однако, если b не было равно 5, то нижняя строка [ A ′ / b ′] не будет полностью состоять из нулей, и ранг [ A ′ / b ′] будет равен 4, а не 3.Этот пример иллюстрирует следующий общий факт: когда b находится в CS (A) , ранг [ A / b ] совпадает с рангом A ; и, наоборот, когда b не находится в CS (A) , ранг [ A / b ] не совпадает с рангом A (он строго больше). Следовательно, эквивалентный критерий принадлежности к пространству столбцов матрицы выглядит следующим образом:

Пример 3 : Определение размера и основы для пространства столбцов матрицы

из Примера 1 выше.

Поскольку размерность пространства столбцов матрицы всегда равна размерности пространства ее строк, CS (B) также должен иметь размерность 3: CS (B) является трехмерным подпространством R ⁴. Поскольку B содержит только 3 столбца, эти столбцы должны быть линейно независимыми и, следовательно, составлять основу:

Пример 4 : Найдите основу для пространства столбцов матрицы

Поскольку пространство столбцов A состоит в точности из тех векторов b , так что A x = b является разрешимой системой, одним из способов определения основы для CS (A) было бы сначала найдите пространство всех векторов b так, чтобы A x = b было согласованным, затем построите основу для этого пространства. Однако элементарное наблюдение предлагает более простой подход: Поскольку столбцы A являются строками A ^T, поиск основы для CS (A) эквивалентен поиску основы для RS (A ^T) . Редуктор рядов A ^T дает

Поскольку в сокращенной форме A ^T остались две ненулевые строки, ранг A ^T равен 2, поэтому

Кроме того, поскольку { v ₁, v ₂} = {(1, 2, −3), (0, −4, 7)} является основой для RS (A ^T), коллекция

является основой для CS (A) , двумерного подпространства R ³.

Основы линейной алгебры

Этот документ представляет собой список некоторых материалов по линейной алгебре. с которым вы должны быть знакомы. В дальнейшем мы будем считать A матрицей 3 x 4.

Я предполагаю, что вы знакомы со сложением и умножением матриц и векторов.

Все векторы будут столбцов векторов.
Учитывая вектор v , если мы так говорим, мы имеем в виду, что v имеет хотя бы один ненулевой составная часть.
Транспонирование вектора или матрицы обозначается надстрочным индексом T . Например,
Внутренний продукт или скалярное произведение двух векторов u и v в можно написать u ^T v ; это означает . Если u ^T v = 0, то u и v являются ортогональными .
Нулевое пространство из A - это набор всех решений x для матрично-векторное уравнение Ax = 0.
Чтобы решить систему уравнений Ax = b , используйте метод исключения Гаусса. Например, если , затем решаем Ax = b следующим образом: (Мы настраиваем расширенную матрицу и уменьшаем строку (или сводим) к верхнему треугольная форма.)

Таким образом, решениями являются все векторы x вида

для любых номеров s и t .
Диапазон набора векторов - это набор всех линейных комбинаций векторов. Например, если а также тогда диапазон v ¹ и v ² является набором все векторы вида sv ¹ + tv ² для некоторых скаляров s и t .
Диапазон набора векторов в дает подпространство из. Любое нетривиальное подпространство можно записать как оболочку любого из несчетное количество наборов векторов.
Набор векторов линейно независимый если единственное решение векторного уравнения является для всех и . Если набор векторов не является линейно независимым, тогда это линейно зависимый . Например, строки A являются , а не линейно независимыми, поскольку

Чтобы определить, является ли набор векторов линейно независимым, запишите векторы как столбцы матрицы C , скажем, и решите Cx = 0.Если есть какие-либо нетривиальные решения, то векторы линейно зависимый; в противном случае они линейно независимы.
Если линейно независимый набор векторов охватывает подпространство тогда векторы образуют базис для этого подпространства. Например, v ¹ и v ² образуют основу для диапазона строк A . Учитывая подпространство S , каждый базис S содержит одинаковое количество векторы; это число является размером подпространства.Чтобы найти основу для диапазона набора векторов, запишите векторы как строки матрицы, а затем уменьшите матрицу по строкам.
Промежуток строк матрицы называется пространством строк матрица. Размерность строки - это ранг матрицы.
Диапазон столбцов матрицы называется диапазоном или диапазоном пространство столбцов матрицы. Пространство строки и пространство столбца всегда имеют одинаковое измерение.
Если M является матрицей m x n , то пустое пространство и пространство строки M подпространства и диапазон M является подпространством.
Если u находится в пространстве строк матрицы M и v находится в нулевом пространстве из M , то векторы ортогональны. Размерность пустого пространства матрицы - это null . матрицы. Если M имеет n столбцов, то ранг ( M ) + недействительность ( M ) = n . Любая основа для пространства строк вместе с любой основой для нулевого пространства дает основу для.
Если M квадратная матрица, - скаляр, а x - вектор удовлетворение тогда x - это собственный вектор из M с соответствующим собственным значением . Например, вектор является собственным вектором матрицы

с собственным значением.
Собственные значения симметричной матрицы всегда действительны. Несимметричная матрица может иметь комплексные собственные значения.
Дана симметричная матрица M , следующие эквивалентны:
1.
Все собственные значения M положительны.
2.
x ^T Mx > 0 для любого.
3.
M - положительно определенный .
Дана симметричная матрица M , следующие эквивалентны:
1.
Все собственные значения M неотрицательны.
2.
для любых х .
3.
M - это положительное полуопределенное значение .

Джон Э. Митчелл
2004-08-31

Размер матрицы

Имя: Тип: Цель:

Описание:

920,000 / 3 = 306666 элементов временных матриц. при выполнении матричных манипуляций. По умолчанию используйте 3000 строк и 100 столбцов. Самая большая квадратная матрица примерно 550 x 550 пикселей.

РАЗМЕР МАТРИЦЫ позволяет изменять строки и столбцы для временных матриц.Количество строк не может быть установлено больше, чем максимальное количество строк для переменной (по умолчанию установлено значение 20 000).

Поскольку эта команда измеряет только временные матрицы во время вычислений, вы можете вводить эту команду так часто, как вы желание во время одного сеанса Dataplot.

Синтаксис 1:

, где - число или параметр, определяющий максимальное количество столбцов для временного матрицы.

Синтаксис 2:

Примеры:

По умолчанию:

По умолчанию 3000 строк на 100 столбцов. Синонимы: Связанные команды:

ИЗМЕРЕНИЕ	= Измерьте рабочее пространство Dataplot.
СТАТУС	= Отображает размер, переменные, параметры, функции и т. д.
НАБОР	= Устанавливает значение внутренней переменной.

Приложения: Дата реализации: Программа:

Конфиденциальность Уведомление о политике / безопасности
Заявление об ограничении ответственности | FOIA

NIST - агентство США. С. Департамент торговли.

Дата создания: 05.06.2001
Последнее обновление: 11.03.2015
Отправьте комментарии на этой странице в Интернете по адресу [email protected].

Векторы и матрицы

Марко Табога, доктор философии

Эта лекция представляет собой неформальное введение в матрицы и векторы.

Матрица

Матрица - это двумерный массив с фиксированным количеством строк и столбцы и содержит число на пересечении каждой строки и столбца.А матрица обычно ограничивается квадратными скобками.

Пример Ниже приведен пример матрицы, состоящей из двух строк и двух столбцы:

Размерность матрицы

Количество строк и столбцов матрицы составляет ее размерность. Если матрица имеет ряды и столбцы, мы говорим, что это матрица, или что она имеет размерность .

Элементы матрицы

Числа, содержащиеся в матрице, называются элементами матрицы (или записи или компоненты).Если матрица, элемент на пересечении строки и столбец обычно обозначается (или же ) и мы говорим, что это -го элемент .

Векторы

Если матрица имеет только одну строку или только один столбец, она называется вектором.

Матрица, имеющая только одну строку, называется вектором-строкой .

Пример В матрица вектор-строка, потому что он имеет только одну строку.

Матрица, имеющая только один столбец, называется вектором-столбцом .

Пример В матрица вектор-столбец, потому что он имеет только один столбец.

Скаляры

Матрица, имеющая только одну строку и один столбец, называется скаляром.

Пример В матрица скаляр. Другими словами, скаляр - это одно число.

Равные матрицы

Равенство между матрицами определяется очевидным образом. Два матрицы а также имеющие одинаковую размерность, считаются равными тогда и только тогда, когда все их соответствующие элементы равны каждому Другие:

Нулевые матрицы

Матрица является нулевой матрицей , если все ее элементы равны нулю, и мы пишем

Пример Если это матрица и , тогда

Матрицы квадратные

А Матрица называется квадратной матрицей , если количество ее строк равно то же, что и количество его столбцов, то есть .

Пример В матрица квадратная матрица.

Диагональные и недиагональные элементы

Позволять - квадратная матрица. Диагональ (или главная диагональ ) это набор всех элементов такой, что . Элементы, принадлежащие диагонали, называются диагональными элементами, и все остальные элементы называются недиагональными.

Матрица идентичности

Квадратная матрица называется единичной матрицей , если все ее диагональные элементы равны и все его недиагональные элементы равны . Обычно обозначается буквой .

Пример В матрица в единичная матрица.

Транспонирование матрицы

Если это матрица, ее транспонирует , обозначается , это матрица такая, что -го элемент равно -го элемент для любой а также удовлетворение а также .Другими словами, столбцы равны строкам (эквивалентно, строки равны столбцам ).

Симметричные матрицы

Квадратная матрица называется симметричной , если она равна ее транспонировать.

Решенные упражнения

Ниже вы можете найти несколько упражнений с объясненными решениями.

Упражнение 1

Позволять быть матрица определена byFind его транспонировать.

Решение

Транспонирование матрица такая, что ее столбцы равны строкам :

Упражнение 2

Позволять быть вектор-столбец определен byShow что его транспонирование является вектором-строкой.

Решение

Упражнение 3

Позволять быть матрица определена по он симметричный?

Решение

Как цитировать

Укажите как:

Табога, Марко (2017).«Векторы и матрицы», Лекции по матричной алгебре. https://www.statlect.com/matrix-algebra/vectors-and-matrices.

The Dimension of a Numpy Array

Numpy - популярная библиотека Python для науки о данных, ориентированная на массивы, векторы и матрицы. Если вы работаете с данными, вам просто не избежать NumPy.

Задача : Как получить количество измерений массива NumPy?

Решение : Используйте атрибут array.ndim для доступа к количеству измерений массива NumPy.Обратите внимание, что это атрибут, а не функция.

Одномерный массив имеет одно измерение:

 import numpy as np

a = np.array ([1, 2, 3])
печать (а.ндим)
# 1

Двумерный массив имеет два измерения:

 import numpy as np

a = np.array ([[1, 2, 3],
              [4, 5, 6]])
печать (а.ндим)
# 2

И трехмерный массив имеет три измерения:

 import numpy as np

a = np.array ([[[1, 2, 3],
               [4, 5, 6]],
              [[0, 0, 0],
               [1, 1, 1]]])
печать (a.ндим)
# 3

Предпосылки : Прежде чем мы двинемся дальше, вы можете спросить: Какое в любом случае определение измерений в массиве?

Numpy не просто хранит кучу значений данных в произвольном порядке (для этого вы можете использовать списки). Вместо этого NumPy устанавливает строгий порядок данных - он создает оси фиксированного размера.

Не путайте ось с размером. Точка в трехмерном пространстве, например [1, 2, 3] имеет три измерения, но только одну ось. Вы можете думать об оси как о глубине вложенных данных.Если вы хотите узнать количество осей в NumPy, подсчитайте количество открывающих скобок '[' , пока не достигнете первого числового значения.

Статья по теме: NumPy Shape

NumPy Puzzle Dimensionality

Можете ли вы решить следующую головоломку NumPy, которая проверяет то, что вы уже узнали?

 импортировать numpy как np

# зарплата в (1000 долларов США) [2015, 2016, 2017]
dataScientist = [133, 132, 137]
productManager = [127, 140, 145]
дизайнер = [118, 118, 127]
softwareEngineer = [129, 131, 137]

а = нп.массив ([dataScientist,
              productManager,
              дизайнер
              программист])
print (a.ndim)

Упражнение : Что дает эта головоломка?

Вы можете решить эту задачу в нашем интерактивном приложении-головоломке Finxter.com:

В этой головоломке мы используем данные о зарплатах четырех рабочих мест: специалистов по обработке данных, менеджеров по продуктам, дизайнеров и инженеров-программистов. Мы создаем четыре списка, в которых хранится среднегодовая зарплата четырех рабочих мест в тысячах долларов за три года, 2015, 2016 и 2017.

Затем мы объединяем эти четыре списка в двумерный массив (обозначенный как матрица). Вы можете представить себе двумерную матрицу как список списков. Трехмерная матрица будет списком списков списков. Вы уловили идею.

В головоломке каждый список заработной платы отдельной работы становится строкой двумерной матрицы. В каждой строке есть три столбца, по одному на каждый год. Головоломка печатает размер этой матрицы. Поскольку наша матрица двумерна, решение этой головоломки равно 2.

Связанное видео NumPy

Вы хотите стать мастером NumPy? Загляните в нашу интерактивную книгу-головоломку Coffee Break NumPy и улучшите свои навыки в области анализа данных! (ссылка Amazon открывается в новой вкладке.