Дефект матрицы: Ранг, дефект линейного оператора.

Содержание

Ранг, дефект линейного оператора.

Образ нуля равен нулю. Действительно, , отсюда.

Множество векторов из W, образ которых равен 0, называется ядром линейного оператора. Ядро линейного преобразования обозначим (). Ядро является подпространствомW (докажите) и его размерность называют дефектом и обозначают .

Множество всех образов векторов из W обозначают (). Множество образов является подпространствомV (докажите), его размерность называют рангом линейного оператора и обозначают .

Теорема 6.21..

Доказательство. Пусть – базис . По определению для каждого вектора существует прообразизW. Система векторов является линейно независимой. Действительно, из равенства, выводим, или

. В силу линейной независимости, все коэффициенты равны 0, и система является линейно независимой.

Аналогично показывается, что пересечение линейной оболочки векторови состоит только из нулевого вектора. Действительно, из включения , выводим, и далее,. Для любого вектораx из W найдутся коэффициенты, что , и. Таким образомW представляется в виде прямой суммы линейной оболочки векторов и . Теорема вытекает из свойства прямой суммы.

Следствие 6.15. Можно выбрать базисы в пространствахW и V так, чтобы матрица линейного оператора имела диагональный вид, причем по диагонали расположены 1 и 0. Количество ненулевых элементов на диагонали равно рангу оператора.

Доказательство. Пусть иимеют тот же смысл, что и в доказательстве предыдущей теоремы. Дополним векторыдо базисаV, а векторы до базисаW векторами из . Полученные базисы обозначим через и, соответственно. Построим матрицу линейного оператора в этих базисах. Заметим,, а координаты векторав базисеравны (0,…,0,1,0,…,0), где 1 стоит на

i-ом месте.

Таким образом, матрица линейного оператора в этих базисах имеет диагональный вид, причем по диагонали расположены 1 и 0. Количество 1 равно рангу оператора.

Линейное преобразование
1. Линейное преобразование. Его матрица

Однозначное отображение линейного пространстваV над числовым полем P в себя называется линейным преобразованием, если оно сохраняет линейность, то есть для любыхи.

Линейное преобразование полностью определяется своими значениями на базисных векторах. Действительно, пусть базисV. Вектор x разложим по базису , где- координаты вектораx. По свойству линейного преобразования имеем . Перейдем в последнем равенстве от равенства векторов к равенству их координат, которое можно записать используя матричное умножение следующим образом. Матрицаназывается

матрицей линейного преобразования и обозначается . Матрица линейного преобразования связывает координаты образа с координатами исходного вектора.

Изменение матрицы линейного преобразования при изменении базиса.

Поскольку линейное преобразование частный случай линейного оператора, то можно воспользоваться полученной ранее формулой , гдеP – матрица перехода. Матрицы A и B называются подобными, если существует невырожденная матрица P, что . Вопрос о подобии матриц сводится к решению системы линейных уравнений, где в роли неизвестных выступают элементы матрицыP, с дополнительным нелинейным условием .

Алгебра линейных преобразований.

На множестве всех линейных преобразований пространства V расмотрим операции:

Умножение на число: .
Сложение (вычитание)
Умножение .

Легко проверить линейность всех этих преобразований и вывести следующие формулы, связывающие их матрицы

Линейное преобразование, переводящее каждый вектор в себя, называется тождественным преобразованием и обозначается . В любом базисе матрица тождественного преобразования равна единичной.

Пусть — некоторый многочлен,- линейное преобразование пространстваV. Сопоставим многочлену линейное преобразование. Будем говорить, что преобразованиеполучено подстановкойв многочлен. Матрицаможет быть вычислена по формуле.

Свойство 7.14. Пусть. Тогда.

ПОЛЕЗНОСТИ » Возможные дефекты экрана

Экран является наиболее хрупким компонентом ноутбука. Он требует замены в следующих случаях: физическое повреждение; вертикальные или горизонтальные полосы; вышла из строя подсветка.

БИТЫЕ ПИКСЕЛЫ

Проблема:

На экране есть черные или белые точки либо точки, постоянно светящиеся красным или зеленым или синим цветом.

Решение:

Мертвые (битые) пикселы – это, как правило, дефект производства. В некоторых случаях возможно исправить пиксел либо используя специальную программу, либо механически. Программа может выводить на экран последовательность специальных картинок со сменой цветов в попытке заставить пиксел функционировать корректно. Можно попробовать мягко надавить на поврежденную область чем-то вроде карандашной резинки. Это приведет к сдвигу жидкости внутри панели.

ПРИМЕЧАНИЕ: Этот метод может привести к повреждению экрана и не гарантирует положительного результата.

ТУСКЛЫЙ ЭКРАН:

Проблема:

Картинка слабо видна, но она слишком темна, чтобы ноутбуком можно было пользоваться. Регулировка яркости не помогает.

Решение:

Вышла из строя подсветка либо вышел из строя инвертер, подающий питание на подсветку. Имеет смысл попробовать заменить инвертер перед тем, как заказывать новый экран.

РАЗБИТЫЙ (РАСКОЛОТЫЙ) ЭКРАН:

Проблема:

На экране могут быть видны пятна, напоминающие чернильные потеки. Поверхность выглядит ровной, но стекло внутри экрана расколото.

Решение:

Надо менять экран (матрицу).

ПОЛОСЫ (ЛИНИИ) НА ЭКРАНЕ:

Проблема:

На экране тонкие горизонтальные

либо вертикальные полосы. Перед заменой экрана необходимо убедиться, что эта проблема вызвана не видеокартой.

Решение:

Подключите к ноутбуку внешний монитор. Если полосы остались, вероятно, проблема вызвана НЕ экраном ноутбука, а, например, видеокартой.

ЧЕРНЫЙ ЭКРАН:

Проблема:

Экран абсолютно черный, нет никакой картинки.

Решение:

Убедитесь, что яркость не установлена на самый низкий уровень. Подключите ноутбук к внешнему монитору, чтобы убедиться, что проблема не вызвана видеокартой. Если картинка видна на внешнем мониторе, вероятно, вышла из строя подсветка.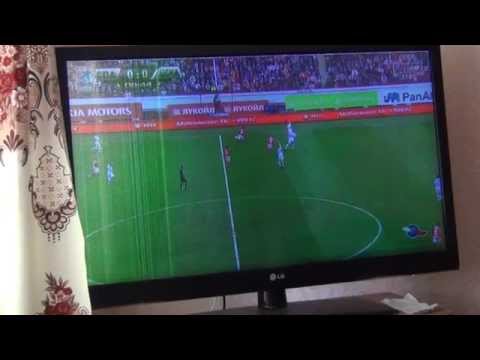

МЕРЦАЮЩИЙ (МИГАЮЩИЙ) ЭКРАН:

Проблема:

Картинка на экране мигает.

Решение:

Имеет смысл вскрыть ноутбук, чтобы проверить, насколько надежно подсоединен кабель данных к

экрану ноутбука. То же относится к кабелю инвертора. Проверьте, нет ли повреждений на самом кабеле. Если с кабелями все нормально, скорее всего, надо менять экран.

linear алгебра — Интуитивно понятно, почему у дефектных матриц есть лишние собственные значения?

$\begingroup$

Недавно я видел пример того, как сдвиг $$\begin{bmatrix} 1 & 1\\ 0 & 1\end{bmatrix}$$ является примером дефектной матрицы, так как она имеет собственные значения $1,1 $, но только один независимый собственный вектор $\mathbf{v}_1 = (1,0)$.

Итак, в этом случае я вижу, что алгебраическая кратность больше, чем геометрическая кратность, но мне интересно, что почему система создала «два» собственных значения, когда только одно из них было «фактически собственным значением» — (Дело даже не в том, что было два собственных вектора, каждый из которых соответствовал $1$, $1$).

Есть ли какая-то основная причина, по которой система выдала два собственных значения? (Если бы я интуитивно догадался, что произойдет, чисто с геометрической точки зрения, я бы предположил, что характеристический полином будет просто линейным: $\lambda — 1$. Хотя это невозможно для $2 \times 2$, Мне было интересно, есть ли какое-то другое значение для второго собственного значения?)

линейная алгебра
матрицы
собственные значения-собственные векторы
линейные преобразования
интуиция

$\endgroup$

$\begingroup$

Ну, я бы сказал, что есть только одно собственное значение: $1$. Дело в том, что мы обычно говорим, что оно «повторяется» или что оно имеет «(алгебраическую) кратность $2$». Подумайте о том, что значит «повторить» собственное значение; при каких обстоятельствах мы перечисляем его дважды или больше? И когда мы это сделаем, сколько раз мы должны перечислять это?

Похоже, вы считаете, основываясь на размерности собственного пространства для собственного значения (или, что то же самое, на максимальном количестве линейно независимых собственных векторов, которое вы можете найти). n$, и, как следствие, мы всегда можем сформировать базис обобщенных собственных векторов. Есть особенно хороший класс таких оснований, называемых основаниями Джордана; это следующие лучшие вещи, которые мы можем найти после баз собственных векторов. Вместо того, чтобы диагонализовать матрицу, они превращают ее в нормальную форму Жордана — отличный утешительный приз, когда нам отказывают в диагональном представлении. Нормальные формы Жордана существуют для каждая матрица , в отличие от диагональных форм!

Алгебраические кратности также соответствуют показателям соответствующих множителей в характеристических полиномах. Фактически, некоторые определяют характеристический многочлен по этой характеристике, и его детерминантное представление становится теоремой.

В случае представленной матрицы $2 \times 2$ собственное пространство $\operatorname{ker} (M — I)$ равно просто $\operatorname{span}\{(1, 0)\}$. Однако, если мы вычислим $$\operatorname{ker} \left(\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} — \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\right) ^2 = \operatorname{ker} \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}^2 = \operatorname{ker} \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{ bmatrix} = \Bbb{C}^2,$$ мы видим, что обобщенное собственное пространство $2$-мерно, а алгебраическая кратность равна $2$. n=0$ для некоторого $n$, существует некоторый базис $\mathcal{B}=\{b_1, …,b_n\}$ такой, что матрица в этом базисе имеет вид матрицы сдвига (т.е. $A b_i= b_{i+1}$ или $A b_i=0$ для любого $i$).

Существует еще одна теорема, утверждающая, что любая матрица является суммой нильпотентной матрицы и матрицы, которую можно диагонализовать (при условии, что ваши скаляры принадлежат алгебраически замкнутому полю, такому как $\mathbb{C}$). Следовательно, возьмем вашу общую $M=D+A,$, где $D$ диагонализируема, а $A$ нильпотентна. Затем приведенные выше наблюдения позволяют нам найти базис, такой, что $D$ является диагональным, и другой базис, такой, что $A$ является матрицей сдвига.

Однако магия обычной формы Джордана в том, что это можно делать одновременно. То есть существует единственный базис, относительно которого $D$ диагональна, а $A$ является матрицей сдвига. Таким образом, препятствием к геометрической кратности каждого собственного значения, соответствующего их алгебраической кратности, является именно эта матрица сдвига $A$. Если $A=0,$, то $D$ диагонализируема и, конечно, наоборот.

В вашем случае у вас есть что-то, что является почти собственным вектором, а именно $(0,1),$, но вместо того, чтобы просто производить скаляр, кратный самому себе, он производит и честный собственный вектор , $(1,0)$. Они называются обобщенными собственными векторами.

Итак, резюмируем: с геометрической точки зрения у вас не так много реальных собственных векторов, как хотелось бы, потому что происходит некоторый сдвиг.

$\endgroup$

1 9кх = 0 $$ для некоторого натурального $k$. Для каждого собственного значения $\lambda$ вы получаете соответствующее подпространство, где $B-\lambda I$ действует как нильпотентная матрица. Его размерность равна алгебраической кратности $\lambda$ (и, таким образом, алгебраическая кратность и обобщенная геометрическая кратность совпадают). Если алгебраическая кратность и геометрическая кратность $\lambda$ совпадают, то $B-\lambda I$ действует как нулевая матрица на этом подпространстве.

Если вы используете это, чтобы «диагонализировать» $B$ как можно лучше, вы получите так называемую Нормальная форма Жордана (с $\lambda$ по диагонали и $1$ по супердиагонали в подходящих местах).

В вашем случае матрица уже находится в жордановой нормальной форме, и вся плоскость (за вычетом начала координат) представляет собой обобщенные собственные векторы с собственным значением $1$.

$\endgroup$

$\begingroup$

Полезнее думать, что дефектные матрицы не имеют лишних собственных значений, а имеют меньше «правильных» собственных векторов. Любая матрица размера n x n имеет n собственных значений (включая кратность корней характеристического уравнения), но любые идентичные собственные значения (кратности m) могут иметь общий собственный вектор. Инвариантное подпространство оператора, связанного с этим собственным значением, по-прежнему имеет основу из m независимых векторов, но они не являются чистыми участками, как определяются собственные векторы. Вместо этого они образуют цепочку обобщенных собственных векторов, которые преобразуются от одного к другому с помощью нильпотентной части оператора, как это диктуется нормальной формой Жордана.

$\endgroup$

Направленная регенеративная терапия 203 последовательно пролеченных внутрикостных дефектов с использованием биорассасывающегося матричного барьера. Клинические и рентгенологические данные

Клинические испытания

. 1997 июнь; 68 (6): 571-81.

doi: 10.1902/jop.1997.68.6.571.

Х Фальк ¹ , Л. Лорелл, Н. Равальд, А. Тейвик, Р. Перссон

Принадлежности

принадлежность

¹ Государственная специализированная стоматологическая клиника пародонтологии, Нэссё, Швеция.

PMID: 9203101
DOI: 10.1902/jop.1997.68.6.571

Клинические испытания

H Фальк и др. J Пародонтол. 1997 июнь

. 1997 июнь; 68 (6): 571-81.

doi: 10.1902/jop.1997.68.6.571.

Авторы

Х Фальк ¹ , Л. Лорелл, Н. Равальд, А. Тейвик, Р. Перссон

принадлежность

¹ Государственная специализированная стоматологическая клиника пародонтологии, Нэссё, Швеция.

PMID: 9203101
DOI: 10.1902/jop.1997.68.6.571

Абстрактный

ЦЕЛЬ ЭТОГО РЕТРОСПЕКТИВНОГО трехцентрового исследования заключалась в оценке терапии направленной регенерацией тканей (НТР) в клинических пародонтологических условиях. Материал состоял из 203 последовательно обработанных внутрикостных дефектов > или = 4 мм у 143 пациентов с использованием биорассасывающегося матричного барьера. Каждый центр следовал одному и тому же протоколу для предоперационных, интраоперационных и последующих обследований. Начальная терапия, хирургическое и последующее лечение проводились в соответствии с рутиной каждого центра. Лечение оценивали через 1 год по клиническим оценкам уменьшения глубины зондирования (PD) и увеличения уровня клинического прикрепления (CAL), а также по наполнению кости по компьютерным оцифрованным рентгенограммам. Исходная глубина внутрикостного дефекта составила в среднем 6,3 ± 1,0 мм клинически и 5,7 ± 1,8 мм рентгенологически. Среднее значение PD было снижено с 9от 0,0 +/- 1,0 мм до 3,3 +/- 1,0 мм. Среднее увеличение CAL составило 4,8 +/- 1,5 мм, что соответствует 79 +/- 13% исходной глубины внутрикостного дефекта; 78% дефектов показали прирост CAL > или = 4 мм. Костное наполнение в среднем составило 3,2+2-1,8 мм. Вместе с резорбцией гребня 1,1 ± 1,4 мм это привело к разрешению дефекта 4,3 ± 1,9 мм или 72%. Сорок семь процентов (47%) вариабельности прироста CAL можно объяснить глубиной дефекта, шириной дефекта, ранним обнажением барьера и наличием зубного налета в обрабатываемой области. Прирост CAL и костное заполнение положительно коррелировали с глубиной внутрикостного дефекта; т. е. чем глубже дефект, тем больше прирост CAL и наполнение кости. На участках с барьерным воздействием в течение первых 2 недель заживления наблюдалось значительно меньшее увеличение CAL, чем на участках, на которых воздействие произошло на более позднем этапе или не произошло вовсе. Наличие зубного налета в обработанной области оказало значительное негативное влияние как на прирост CAL, так и на заполнение костной ткани. Был сделан вывод, что GTR-лечение внутрикостных дефектов > или = 4 мм в практике специалиста-пародонтолога приведет к увеличению уровня клинического прикрепления и костного заполнения, сравнимому с тем, что было продемонстрировано в тематических исследованиях и контролируемых клинических испытаниях. Предсказуемость получения прироста CAL > или = 4 мм при дефектах > или = 4 мм составила 78%.

Цитируется

Влияние морфологии костного дефекта на исход реконструктивного лечения периимплантита.
Агазаде А., Перссон Р.Г., Ренверт С. Агазаде А. и др. Int J Implant Dent. 2020 17 июня; 6 (1): 33. дои: 10.1186/s40729-020-00219-5. Int J Implant Dent. 2020. PMID: 32548733 Бесплатная статья ЧВК.
Влияние воздействия мембраны на увеличение латерального гребня: исследование случай-контроль.
Эскан М.А., Жируар М.Е., Мортон Д., Гринвелл Х. Эскан М.А. и соавт. Int J Implant Dent. 2017 дек;3(1):26. doi: 10.1186/s40729-017-0089-z. Epub 2017 22 июня. Int J Implant Dent. 2017. PMID: 28643223 Бесплатная статья ЧВК.
Лечение внутрикостных дефектов с направленной тканевой регенерацией при агрессивном пародонтите: клинические результаты через 6 и 12 мес.
Ракмани Т., Гриффитс Г. С., Ауплиш Г., Дарбар У., Петри А., Олсен И., Донос Н. Ракмани Т. и др. Clin Oral Investig. 2016 июль; 20(6):1217-25. doi: 10.1007/s00784-015-1608-z. Epub 2015 28 сентября. Clin Oral Investig. 2016. PMID: 26411859 Клиническое испытание.
Клиническая и радиографическая оценка биорезорбируемой коллагеновой мембраны рыбного происхождения при лечении пародонтальных внутрикостных дефектов: предварительное исследование.
Сантош Кумар Б.Б., Аруна Д.Р., Гауда В.С., Галагали С.Р., Прашанти Р., Наванита Х. Сантош Кумар Б.Б. и др. J Indian Soc Periodontol. 2013 сен; 17 (5): 624-30. doi: 10.4103/0972-124X.119279. J Indian Soc Periodontol. 2013. PMID: 24174757 Бесплатная статья ЧВК.
Оценка биорезорбируемой коллагеновой мембраны рыбного происхождения при лечении пародонтальных внутрикостных дефектов: проспективное клиническое исследование.
No related posts.