Дифракция пример – Дифракция света
Дифракция света
Определение 1
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.
В классической физике, явление дифракции описывается как интерференция волны в соответствии с принципом Гюйгенса-Френеля. Эти характерные модели поведения проявляются, когда волна встречает препятствие или щель, которая сравнима по размерам с ее длиной волны. Подобные эффекты возникают, когда световая волна проходит через среду с изменяющимся показателем преломления, или когда звуковая волна проходит через среду с изменением акустического импеданса. Дифракция происходит со всеми видами волн, в том числе звуковыми волнами, ветровыми волнами и электромагнитными волнами, а также с видимым светом, рентгеновскими лучами и радиоволнами.
Поскольку физические объекты имеют волновые свойства (на атомном уровне), дифракция происходит также с веществами и может быть изучена в соответствии с принципами квантовой механики.
Примеры
Эффекты дифракции часто встречаются в повседневной жизни. Наиболее яркими примерами дифракции являются те, которые связаны со светом; например, близко расположенные дорожки на CD или DVD дисках выступают в качестве дифракционной решетки. Дифракция в атмосфере мелких частиц может привести к яркому кольцу, которое видно возле яркого источника света, такого как солнце или луна. Спекл, который наблюдается, когда лазерный луч падает на оптически неровную поверхность, также является дифракцией. Все эти эффекты являются следствием того факта, что свет распространяется в виде волны.
Замечание 1
Дифракция может произойти с любым видом волны.
Океанские волны рассеивают вокруг пристаней и других препятствий. Звуковые волны могут преломляться вокруг объектов, поэтому можно услышать, что кто-то зовет, даже когда он прячется за деревом.
История
Эффекты дифракции света были хорошо известны во времена Гримальди Франческо Марии, который также ввел термин дифракции. Результаты, полученные, Гримальди были опубликованы посмертно в $1665 $году. Томас Юнг провел знаменитый эксперимент в $1803$ году, демонстрируя интерференцию от двух близко расположенных щелей. Объясняя свои результаты с помощью интерференции волн, исходящих от двух разных щелей, он сделал вывод, что свет должен распространяться в виде волн. Френель сделал более точные исследования и расчеты дифракции, которые были опубликованы в $1815$ г. В основу своей теории Френель использует определение света, разработанное Христианом Гюйгенсом, дополнив его идеей об интерференции вторичных волн. Экспериментальное подтверждение теории Френеля стало одним из главных доказательств волновой природы света. В настоящее время эта теория известна как принцип Гюйгенса-Френеля.
Дифракция света
Дифракция на щели
Длинная щель бесконечно малой ширины, которая освещается светом, преломляет свет в серию круговых волн и в волновой фронт, который выходит из щели и является цилиндрической волной однородной интенсивности. Щель, которая шире, чем длина волны производит эффекты интерференции в пространстве на выходе из щели. Их можно объяснить тем, что щель ведет себя так, как будто она имеет большое количество точечных источников, которые распределены равномерно по всей ширине щели. Анализ этой системы упрощается, если рассматривать свет одной длины волны. Если падающий свет является когерентным, эти все источники имеют одинаковую фазу.
Дифракционная решетка
Дифракционная решетка представляет собой оптический компонент с периодической структурой, который расщепляет и дифрагирует свет на несколько лучей, распространяющихся в разных направлениях.
Свет, дифрагированный на решетке определяется путем суммирования света, дифрагированного от каждого из элементов, и по существу является сверткой дифракционных и интерференционных картин.
spravochnick.ru
Примеры дифракции в физике, теория и онлайн калькуляторы
ОпределениеОтклонение от прямолинейного распространения волны, огибание волной препятствия называют дифракцией.
Дифрагировать могут любые волны (волны света, акустические волны и др.). Явление дифракции проявляется особенно четко, если размеры препятствий сравнимы или меньше длины волны. При дифракции поверхность волны искривляется около краев препятствия.
Дифракцию объясняют с помощью принципа Гюйгенса. Каждую точку волнового поля нужно рассматривать в качестве источника вторичных волн. Эти волны распространяются во всех направлениях, попадая в область геометрической тени препятствия.
Дифракция механических волн
Рассмотрим дифракцию волн на поверхности воды. На пути распространения волн поместим экран, имеющий узкую щель. Размер щели меньше длины волны. За экраном будет распространяться круговая волна так, как будто в щели находится источник волн, как и следует из принципа Гюйгенса. Вторичные источники в узком отверстии экрана находятся близко друг к другу и их можно считать единым точечным источником.
Увеличим размер отверстия в экране до величины много большей длины волны. Картина распространения волн за экраном станет иной. Волна будет проходить через щель, не изменяя своей формы. На краях отверстия экрана можно заметить только небольшое искривление поверхности волны, волна частично попадает в пространство позади экрана.
Дифракция световых волн
Исторически явление дифракции начали исследовать при изучении свойств света.
Дифракция света — это совокупность явлений, которые связаны с волновой природой света. Дифракцию света можно получить при распространении его в веществе, имеющем неоднородности. Примерами дифракции света являются: отклонение света от распространения по прямой линии при прохождении через отверстие в непрозрачном экране, огибание границ непрозрачных тел.
Наблюдать дифракцию света — это непростая задача, так как длина световой волны
www.webmath.ru
Пути света | Проекты
Предмет: Физика
Класс: 11 классы.
Тема: Дифракция света
Основной вопрос: Может ли свет огибать препятствия и как это будет происходить.
Гипотеза:
Свет распространяется прямолинейно и следовательно, обходить препятствия не может.
Цели:
Изучение световых явлений на примере дифракции и выявление условий её возникновения и ограничения , которые она накладывает на применение законов геометрической оптики.
Задачи:
- Изучить из теории явление дифракции, условия её возникновения и условия при которых она накладывает ограничение на применение законов геометрической оптики .
- Провести опыты наглядно показывающие/объясняющие явление дифракции.
Этапы:
- Ознакомиться с теорией и информацией в сети интернет.
- Провести консультацию у учителей физики и проанализировать видео ранее найденных опытов в сети интернет.
- Провести собственные эксперименты (опыты с бумагой, с булавкой и CD-диском).
- Проанализировать полученные результаты.
- Сделать выводы.
Результаты изучения научной литературы
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.
Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени.
Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец.
Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом.
Явление дифракции накладывает ограничения на применение законов геометрической оптики:
Закон прямолинейного распространения света, законы отражения и преломления света выполняются достаточно точно только , если размеры препятствий много больше длины световой волны.
Дифракция накладывает предел на разрешающую способность оптических приборов:
— в микроскопе при наблюдении очень мелких предметов изображение получается размытым
— в телескопе при наблюдении звезд вместо изображения точки получаем систему светлых и темных полос.
Постановка опытов:
ОПЫТ С БУМАГОЙ
Можно увидеть дифракцию света и на круглом отверстии в листе черной бумаги.
Сделайте большое отверстие, например, при помощи дырокола. Тогда под лупой будет видна легкая цветная кайма по его краям снаружи. У луча света, выходящего из большого отверстия, дифракционная картина почти незаметна. В большинстве случаев ее можно вообще не учитывать, полагая, что свет распространяется исключительно прямолинейно. Дифракционная картина крохотного отверстия, проколотого в бумаге иглой, гораздо больше, чем оно само, и выглядит как система колец.
В этом случае отверстие выступает как источник света с малыми угловыми размерами. Его можно заменить светящейся точкой любого происхождения.
Взяв, например, отражение солнца в шарике от подшипника, лежащем на черном фоне, можно увидеть отчетливую картину, состоящую из колец, как дифракция на отверстии.
Отражение солнца в шарике — не что иное, как его оптически уменьшенное изображение! Так, например, в шарике диаметром 3 мм мы видим солнце таким, каким бы оно виделось с очень далекой планеты. Поэтому звезды, находящиеся от нас гораздо дальше, предстают перед окуляром обычного телескопа как крохотные светящиеся точки, при увеличении которых можно видеть лишь их дифракционные картины.
ОПЫТ С БУЛАВКОЙ
Обычная булавка с колечком укреплена на кусочке дерева и освещена лампой карманного фонари с расстояния 1 — 1,5 м. Если на булавку посмотреть через лупу, то станет отчетливо видна дифракционная картина.
Точно так же рассмотрение мелких предметов через микроскоп с очень большим увеличением позволяет отчетливо видеть их дифракционные картины, и их нередко принимают за реальные детали, иногда приводило к ложным открытиям.
Примеры дифракции в природе и в быту:
Тонкий слой облаков из водяных капелек, закрывающий солнце или месяц, действует как дифракционная решетка. Светило кажется окруженным разноцветным венцом (радужным ореолом) . В случае игольчатых, ледяных облаков получается другое явление: узкое кольцо большого радиуса вокруг солнца или луны. Оно возникает вследствие преломления света.
Если рассматривать пламя свечи через запотевшее стекло, посыпанное очень мелким порошком, то пламя кажется окруженным радужным ореолом.
Радуга возникает в основном вследствие преломления и полного отражения солнечных лучей в шарообразных каплях дождя. Радуга состоит из спектра, расположенного таким образом, что внешняя сторона радуги окрашена в красный цвет, а внутренний край – в фиолетовый цвет; от внешнего края до фиолетового располагаются все остальные цвета спектра. Радиус полукруга виден под углом зрения в 42,5º. Побочная радуга имеет внутренний радиус, видный под углом в 51º, и окрашена изнутри в красный цвет, а снаружи в фиолетовый.
Выводы:
- Изучив теорию и проведя опыты, мы сделали вывод, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным.
- При этом световая волна также может огибать препятствие, но размеры препятствия должны быть сравнимы с длинной её волны, следовательно наша гипотеза была не верна.
- Мы выяснили, что явление дифракции накладывает ограничения на применение законов геометрической оптики: закон прямолинейного распространения света, законы отражения и преломления света выполняются достаточно точно только , если размеры препятствий много больше длины световой волны.
-
Дифракция накладывает предел на разрешающую способность оптических приборов: в микроскопе при наблюдении очень мелких предметов изображение получается размытым; в телескопе при наблюдении звезд вместо изображения точки получаем систему светлых и темных полос.
Ссылки на ресурсы:
http://www.physics.ru Информационный портал о физике «ФИЗИКОН»
https://ru.wikipedia.org/wiki/Дифракция «Википедия» – Энциклопедия.
http://class-fizika.spb.ru/ «Класс!ная физика – занятные страницы»
http://www.scienceforum.ru/ Научный форум
Презентация
Дифракция
iteach.vspu.ru
Дифракция света и дифракционная решетка: определение простыми словами

Содержание:
Первые опыты и активные исследования природы света начались еще в далеком XVII веке, когда итальянский ученый Франческо Гримальди впервые открыл такое интересное физическое явление как дифракция света. Что же такое дифракция света? Это отклонение света от прямолинейного распространения в силу определенных препятствий на его пути. Более научное объяснение причинам дифракции света было дано в начале XIX века английским ученым Томасом Юнгом, согласно нему дифракция света возможна благодаря тому, что свет представляет собой волну, идущую от своего источника и естественным образом искривляющуюся при попадании на определенные препятствия. Им же была изобретена первая дифракционная решетка, представляющая собой оптический прибор, работающий на основе дифракции света, то есть специально искривляющий световую волну.
Дифракция и интерференция света
Изучая поведение монохроматического пучка света, Томас Юнг, разделив его пополам, получил дифракционную картину, которая представляла собой последовательное чередование ярких и темных полос на экране. Волновая теория природы света, сформированная Юнгом, прекрасно объясняла это явление. Будучи волной, пучок света при попадании на непрозрачное препятствие искривляется, меняет траекторию своего движения. Так появляется дифракция света, при которой свет может, как целиком огибать препятствия (если длина световой волны больше размеров препятствия) или искривлять свою траекторию (когда размеры препятствий сопоставимы с длиной световой волны). Примером тут может быть попадание света через узкие щели или небольшие отверстия, как на фото ниже.

Луч света в пещере, наглядная иллюстрация дифракции света в природе.
А тут на картинке показано более схематическое изображение дифракции.

Физическое явление дифракции света дополняет еще одно важное свойство световой волны – интерференция света. Суть интерференции света заключается в накладывании одних световых волн на другие. В результате может происходить искривление синусоидальной формы результирующей волны.

Так схематически выглядит интерференция.
При этом, волны, которые накладываются, могут, как усиливать мощь общей световой волны (при совпадении амплитуд), так и наоборот погасить ее.
Дифракционная решетка
Как мы писали выше, дифракционная решетка представляет собой простой оптический прибор, который искривляет световую волну.

Вот так она выглядит.

Или еще чуть более маленький экземпляр.
Также дифракционную решетку можно охарактеризовать тремя параметрами:
- Период d. Он представляет собой расстояние между двумя щелями, через которые проходит свет. Так как длина световой волны обычно находится в диапазоне нескольких десятых микрометра, то величина d обычно имеет 1 микрометр.
- Постоянная решетка а. Это количество прозрачных щелей на длине 1 мм поверхности решетки. Эта величина обратно пропорциональна периоду дифракционной решетки d. Обычно имеет 300-600 мм-1
- Общее количество щелей N. Высчитывается путем умножения длины дифракционной решетки на ее постоянную а. Обычно длина решетки имеет несколько сантиметров, а количество щелей при этом составляет 10-20 тысяч.
Виды дифракционных решеток
На самом деле есть целых два вида дифракционных решеток: прозрачная и отражающая.
Прозрачная решетка представляет собой прозрачную тонкую пластину из стекла или прозрачного пластика, на которую нанесены штрихи. Штрихи эти как раз и являются препятствиями для световой волны, сквозь них она не может пройти. Ширина штриха – это и есть, по сути, период дифракционной решетки d. А оставшиеся между штрихами прозрачные зазоры – это щели. Такие решетки наиболее часто применяются при выполнении лабораторных работ.
Отражающая дифракционная решетка – это металлическая либо пластиковая и отполированная пластина. Вместо штрихов на нее нанесены бороздки определенной глубины. Период d соответственно это расстояние между этими бороздками. Простым примером отражающей дифракционной решетки может быть оптический CD диск.

Такие решетки часто используют при анализе спектров излучения, так как благодаря их дизайну можно удобно распределить интенсивность максимумов дифракционной картины на пользу максимумов более высокого порядка.
Принцип работы дифракционной решетки
Представим, что на нашу решетку падает свет, имеющий плоский фронт. Это важный момент, так как классическая формула будет верна при условии, что волновой фронт является плоским и параллельным самой пластинке. Штрихи решетки будут вносить в этот световой фронт возмущение и как результат на выходе из решетки создаться ситуация будто бы работает множество когерентных (синхронных) источников излучения. Эти источники и являются причиной дифракции.
От каждого источника (по сути щели между штрихами решетки) будут распространяться световые волны, которые будут когерентными (синхронными) друг другу. Если на некотором расстоянии от решетки поместить экран, то мы сможем увидеть на нем яркие полосы, между которыми будет тень.
Формула дифракционной решетки
Яркие полосы, которые мы увидим на экране можно также назвать максимумами решетки. Если рассматривать условия усиления световых волн, то можно вывести формулу максимума дифракционной решетки, вот она.
sin(θm) = m*λ/d
Где θm это углы между перпендикуляром к центру пластинки и направлением на соответствующую линию максимума на экране. Величина m называется порядком дифракционной решетки. Она принимает целые значения и ноль, то есть m = 0, ±1, 2, 3 и так далее. λ – длина световой волны, а d – период решетки.
Таким образом, можно рассчитать положение всех максимумов решетки.
Разрешающая способность дифракционной решетки
Разрешающей способностью называют способность решетки разделить две волны с близкими значениями длины λ на два отдельных максимума на экране.
Применение дифракционной решетки
Какое же практическое применение дифракционной решетки, в чем ее конкретная польза? Дифракционная решетка является важным и незаменимым инструментов в спектроскопии, так с ее помощью можно узнать, например, химический состав далекой звезды. Свет, идущий от этой звезды, собирают зеркалами и направляют на решетку. Измеряя значения θm можно узнать все длины волн спектра, а значит и химические элементы, которые их излучают.
Дифракция света и дифракционная решетка, видео
И в завершение интересное образовательное видео по теме нашей статьи от заслуженного учителя Украины – Павла Виктора, на наш взгляд его видео лекции на Ютубе по физике могут быть очень полезными для всех, кто изучает этот предмет.
www.poznavayka.org
Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля
Определение 1Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.
Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.
Принцип Гюйгенса-Френеля
Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.
Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

Рисунок 3.8.1 Принцип Гюйгенса-Френеля. ∆S1 и ∆S2– элементы волнового фронта, n1→ и n2→ — заданные нормали.
Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновы
zaochnik.com
Дифракция света
7
Л3-4Дифракция света
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшое отверстие в экранах и т.д.
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн. Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн.
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения P по линзе так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы (рис.).
Принципиально дифракция Фраунгофера
не отличается от дифракции Френеля.
Количественный критерий, позволяющий
установить, какой вид дифракции имеет
место, определяется величиной безразмерного
параметра  ,
где b – характерный
размер препятствия, l – расстояние между препятствием и
экраном, на котором наблюдается
дифракционная картина,
– длина волны. Если
,
где b – характерный
размер препятствия, l – расстояние между препятствием и
экраном, на котором наблюдается
дифракционная картина,
– длина волны. Если

Явление дифракции качественно объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Для монохроматической волны волновая поверхность есть поверхность, на которой колебания совершаются в одинаковой фазе.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис.). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. огибает края отверстия.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности на фронте волны. Из повседневного опыта известно, что в большом числе случаев лучи света не отклоняются от их прямолинейного распространения. Так, предметы, освещенные точечным источником света, дают резкую тень. Таким образом, принцип Гюйгенса нуждается в дополнении, позволяющем определять интенсивность волны.
Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых малыми элементами некоторой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому источники вторичных волн действуют синфазно. В аналитическом виде для точечного источника этот принцип записывается в виде
 , (1)
где E – световой
вектор, включающий в себя временную
зависимость
, (1)
где E – световой
вектор, включающий в себя временную
зависимость  , k – волновое число, r – расстояние
от точки P на
поверхности S до точки P, K – коэффициент, зависящий от ориентации
площадки по отношению к источнику и
точке P. Правомерность
формулы (1) и вид функции K устанавливается в
рамках электромагнитной теории света
(в оптическом приближении).
, k – волновое число, r – расстояние
от точки P на
поверхности S до точки P, K – коэффициент, зависящий от ориентации
площадки по отношению к источнику и
точке P. Правомерность
формулы (1) и вид функции K устанавливается в
рамках электромагнитной теории света
(в оптическом приближении).
В том случае, когда между источником S и точкой наблюдения P имеются непрозрачные экраны с отверстиями, действие этих экранов может быть учтено следующим образом. На поверхности непрозрачных экранов амплитуды вторичных источников считаются равными нулю; в области отверстий амплитуды источников такие же, как при отсутствии экрана (так называемое приближение Кирхгофа).
Метод зон Френеля. Учет амплитуд и фаз вторичных волн позволяет в принципе найти амплитуду результирующей волны в любой точке пространства и решить задачу о распространении света. В общем случае расчет интерференции вторичных волн по формуле (1) довольно сложный и громоздкий. Однако ряд задач можно решить, применив чрезвычайно наглядный прием, заменяющий сложные вычисления. Метод этот получил название метода зон Френеля.
Суть метода разберем на примере точечного
источника света S.
Волновые поверхности представляют
собой в этом случае концентрические
сферы с центром в S.
Разобьем изображенную на рисунке
волновую поверхность на кольцевые зоны,
построенные так, что расстояния от краев
каждой зоны до точки P отличаются на  .
Обладающие таким свойством зоны
называются зонами Френеля. Из рис.
видно, что расстояние
.
Обладающие таким свойством зоны
называются зонами Френеля. Из рис.
видно, что расстояние  от внешнего края – m-й
зоны до точки P равно
от внешнего края – m-й
зоны до точки P равно
 ,
где b – расстояние
от вершины волновой поверхности O до точки P.
,
где b – расстояние
от вершины волновой поверхности O до точки P.
Колебания, приходящие в точку P от аналогичных точек двух соседних зон (например, точек, лежащих в середине зон или у внешних краев зон), находятся в противофазе. Поэтому колебания от соседних зон будут взаимно ослаблять друг друга и амплитуда результирующего светового колебания в точке P
 , (2)
где
, (2)
где  ,
,  ,
… – амплитуды колебаний, возбуждаемых
1-й, 2-й, … зонами.
,
… – амплитуды колебаний, возбуждаемых
1-й, 2-й, … зонами.
Для оценки амплитуд колебаний найдем
площади зон Френеля. Пусть внешняя
граница m-й
зоны выделяет на волновой поверхности
сферический сегмент высоты  .
Обозначив площадь этого сегмента через
.
Обозначив площадь этого сегмента через  ,
найдем, что, площадь m-й
зоны Френеля равна
,
найдем, что, площадь m-й
зоны Френеля равна 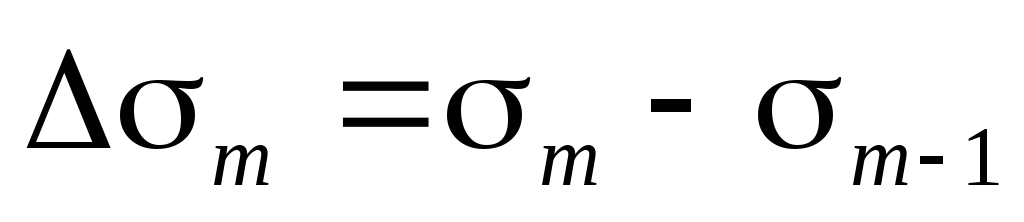 .
Из рисунка видно, что
.
Из рисунка видно, что 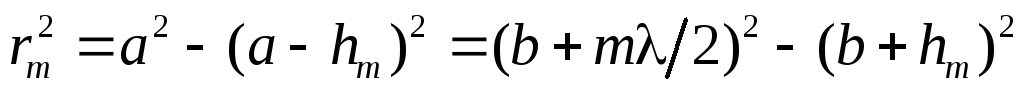 .
После несложных преобразований,
учитывая
.
После несложных преобразований,
учитывая 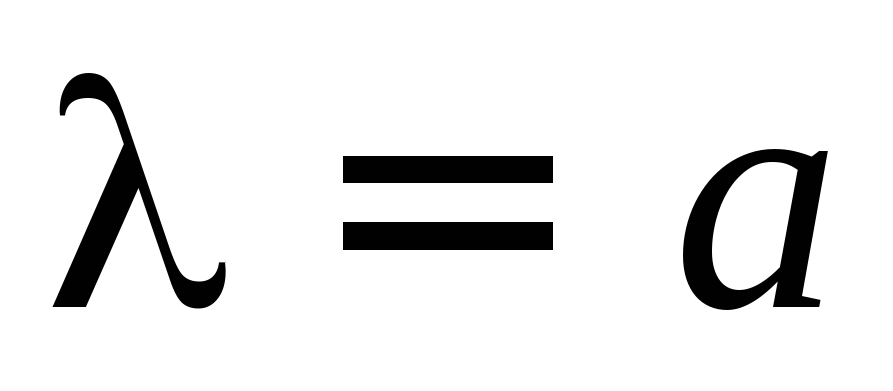 и
и 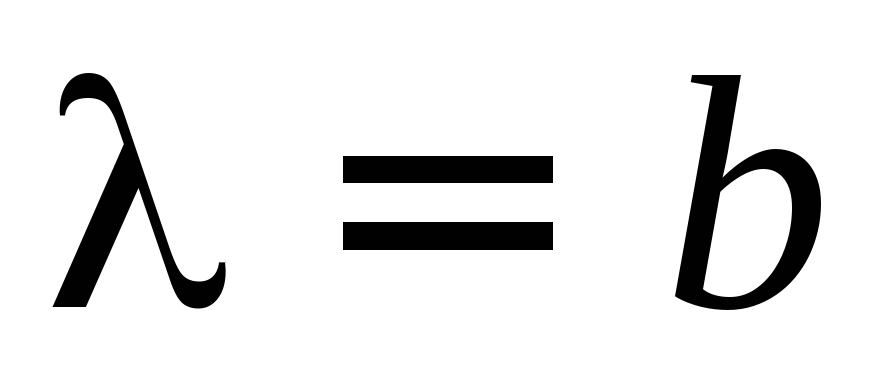 ,
получим
,
получим
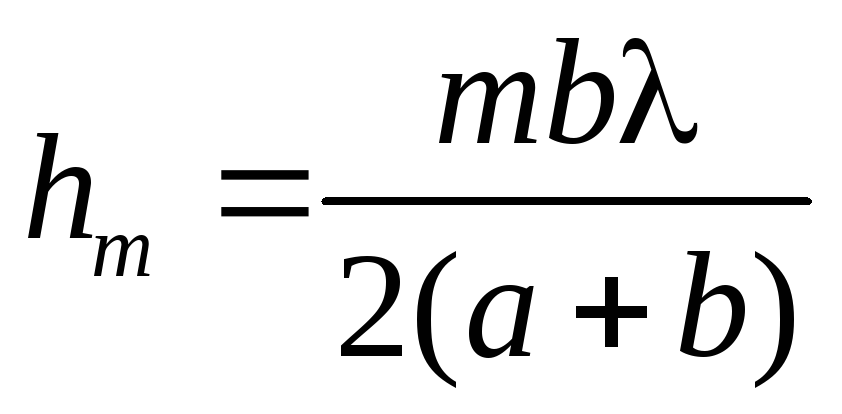 .
Площадь сферического сегмента и
площадь m-й
зоны Френеля соответственно равны
.
Площадь сферического сегмента и
площадь m-й
зоны Френеля соответственно равны
 ,
,  . (3)
Таким образом, при не слишком
больших m площади зон
Френеля одинаковы. Согласно предположению
Френеля, действие отдельных зон в точке P тем меньше, чем больше
угол
. (3)
Таким образом, при не слишком
больших m площади зон
Френеля одинаковы. Согласно предположению
Френеля, действие отдельных зон в точке P тем меньше, чем больше
угол  между нормалью n к поверхности зоны и направлением
на P, т.е. действие зон
постепенно убывает от центральной к
периферийным. Кроме того, интенсивность
излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от
зоны до точки P.
Таким образом, амплитуды колебаний
образуют монотонно убывающую
последовательность
между нормалью n к поверхности зоны и направлением
на P, т.е. действие зон
постепенно убывает от центральной к
периферийным. Кроме того, интенсивность
излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от
зоны до точки P.
Таким образом, амплитуды колебаний
образуют монотонно убывающую
последовательность
 .
.
Общее число зон Френеля, умещающихся
на полусфере, очень велико; например,
при  и
и 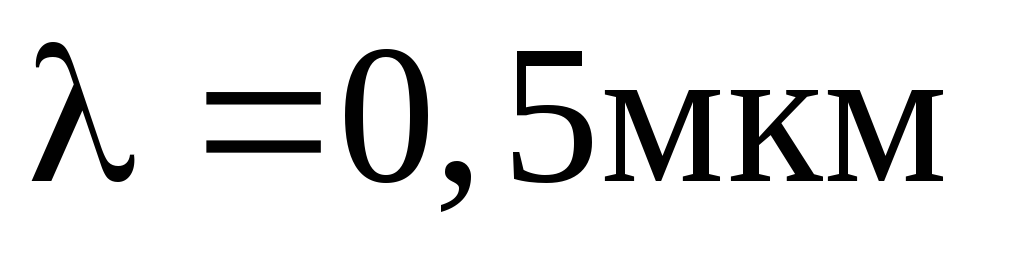 число зон достигает ~106.
Это означает, что амплитуда убывает
очень медленно и поэтому можно приближенно
считать
число зон достигает ~106.
Это означает, что амплитуда убывает
очень медленно и поэтому можно приближенно
считать
 . (4)
Тогда выражение (2) после перегруппировки
суммируется
. (4)
Тогда выражение (2) после перегруппировки
суммируется
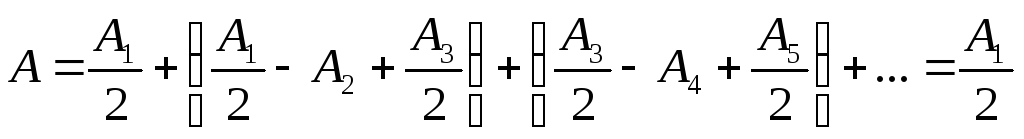 , (5)
так
как выражения в скобках, согласно (4),
равны нулю, а вклад последнего слагаемого
ничтожно мал. Таким образом, амплитуда
результирующих колебаний в произвольной
точке P определяется
как бы половинным действием центральной
зоны Френеля.
, (5)
так
как выражения в скобках, согласно (4),
равны нулю, а вклад последнего слагаемого
ничтожно мал. Таким образом, амплитуда
результирующих колебаний в произвольной
точке P определяется
как бы половинным действием центральной
зоны Френеля.
При не слишком больших m высота сегмента  ,
поэтому можно считать, что
,
поэтому можно считать, что  .
Подставив значение для
.
Подставив значение для  ,
получим для радиуса внешней границы m-й
зоны
,
получим для радиуса внешней границы m-й
зоны
 . (6)
При
. (6)
При  и
и 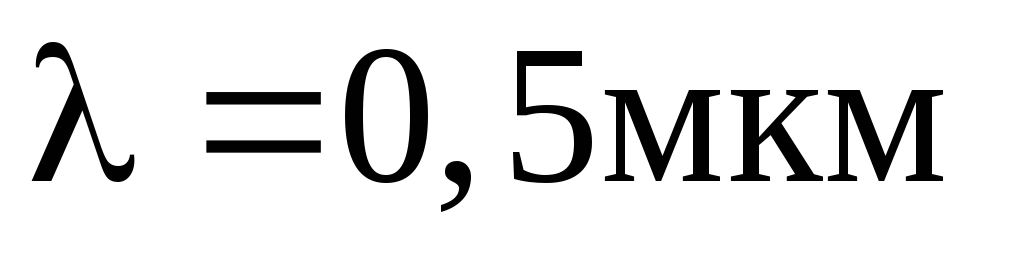 радиус первой (центральной) зоны
радиус первой (центральной) зоны  .
Следовательно, распространение света
от S к P происходит так, как если бы световой
поток шел внутри очень узкого канала
вдоль SP, т.е. прямолинейно.
.
Следовательно, распространение света
от S к P происходит так, как если бы световой
поток шел внутри очень узкого канала
вдоль SP, т.е. прямолинейно.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонная пластинка – в простейшем случае стеклянная пластинка, состоящая из системы чередующихся прозрачных и непрозрачных концентрических колец, с радиусами зон Френеля заданной конфигурации. Если поместить зонную пластинку в строго определенном месте (на расстоянии a от точечного источника и на расстоянии b от точки наблюдения), то результирующая амплитуда будет больше, чем при полностью открытом волновом фронте.
Дифракция Френеля на круглом отверстии. Дифракция Френеля наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, в данном случае экрана с отверстием. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути экран с отверстием. Дифракционная картина наблюдается на экране, параллельном экрану с отверстием. Ее вид зависит от расстояния между отверстием и экраном (для данного диаметра отверстия). Проще определить амплитуду световых колебаний в центре картины. Для этого разобьем открытую часть волновой поверхности на зоны Френеля. Амплитуда колебания, возбуждаемая всеми зонами равна
 , (7)
где знак плюс отвечает нечетным m и минус – четным m.
, (7)
где знак плюс отвечает нечетным m и минус – четным m.
Когда отверстие открывает нечетное
число зон Френеля, то амплитуда
(интенсивность) в центральной точке
будет больше, чем при свободном
распространении волны; если четное то
амплитуда (интенсивность) будет равна
нулю. Например, если отверстие открывает
одну зону Френеля, амплитуда  ,
то интенсивность (
,
то интенсивность ( )
больше в четыре раза.
)
больше в четыре раза.
Расчет амплитуды колебания на внеосевых участках экрана более сложен, так как соответствующие зоны Френеля частично перекрываются непрозрачным экраном. Качественно ясно, что дифракционная картина будет иметь вид чередующихся темных и светлых колец с общим центром (если m четное, то в центре будет темное кольцо, если m нечетное – то светлое пятно), причем интенсивность в максимумах убывает с расстоянием от центра картины. Если отверстие освещается не монохроматическим светом, а белым светом, то кольца окрашены.
Рассмотрим предельные случаи. Если
отверстие открывает лишь часть
центральной зоны Френеля, на экране
получается размытое светлое пятно;
чередования светлых и темных колец в
этом случае не возникает. Если отверстие
открывает большое число зон, то  и амплитуда в центре
и амплитуда в центре 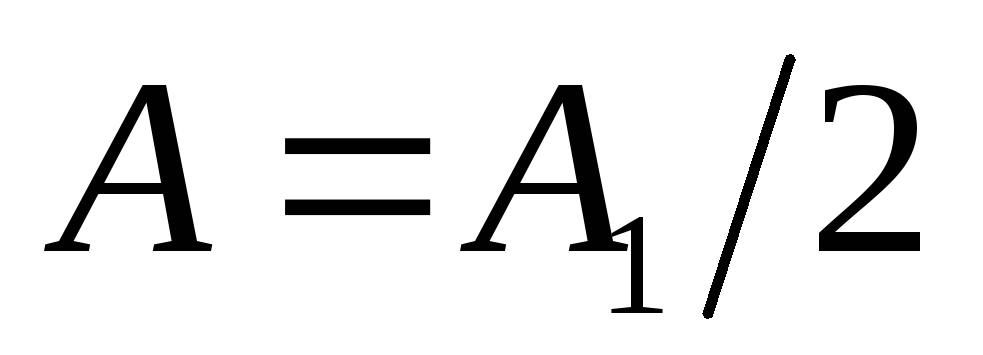 ,
т.е. такая же, как и при полностью открытом
волновом фронте; чередование светлых
и темных колец происходит лишь в очень
узкой области на границе геометрической
тени. Фактически дифракционная картина
не наблюдается, и распространение света,
по сути, является прямолинейным.
,
т.е. такая же, как и при полностью открытом
волновом фронте; чередование светлых
и темных колец происходит лишь в очень
узкой области на границе геометрической
тени. Фактически дифракционная картина
не наблюдается, и распространение света,
по сути, является прямолинейным.
Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.). Дифракционная картина, наблюдаемая на экране, является центрально симметричной. Определим амплитуду световых колебаний в центре. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда колебаний равна
 или
или  , (8)
так как выражения, стоящие в скобках,
равны нулю. Следовательно, в центре
всегда наблюдается дифракционный
максимум (светлое пятно), соответствующий
половине действия первой открытой зоны
Френеля. Центральный максимум окружен
концентрическими с ним темными и светлыми
кольцами. При небольшом числе закрытых
зон амплитуда
, (8)
так как выражения, стоящие в скобках,
равны нулю. Следовательно, в центре
всегда наблюдается дифракционный
максимум (светлое пятно), соответствующий
половине действия первой открытой зоны
Френеля. Центральный максимум окружен
концентрическими с ним темными и светлыми
кольцами. При небольшом числе закрытых
зон амплитуда  мало отличается от
мало отличается от  .
Поэтому интенсивность в центре будет
почти такая же, как при отсутствии диска.
Изменение освещенности экрана с
расстоянием от центра картины изображено
на рис.
.
Поэтому интенсивность в центре будет
почти такая же, как при отсутствии диска.
Изменение освещенности экрана с
расстоянием от центра картины изображено
на рис.
Рассмотрим предельные случаи. Если диск
закрывает лишь небольшую часть центральной
зоны Френеля, он совсем не отбрасывает
тени – освещенность экрана всюду
остается такой же, как при отсутствии
диска. Если диск закрывает много зон
Френеля, чередование светлых и темных
колец наблюдается только в узкой области
на границе геометрической тени. В этом
случае 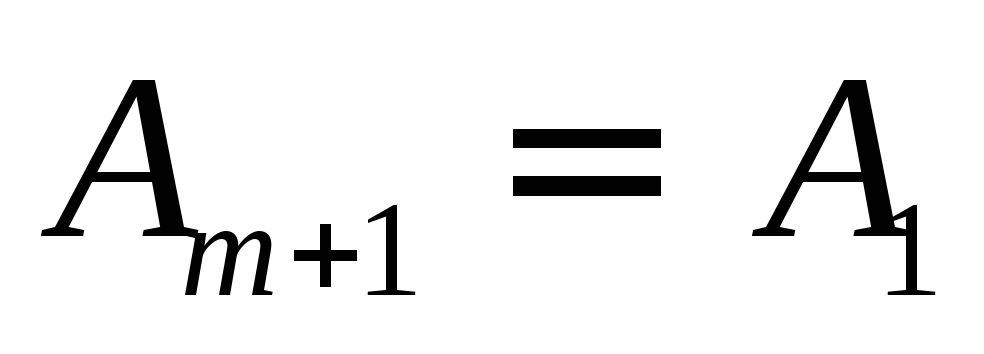 ,
так что светлое пятно в центре отсутствует,
и освещенность в области геометрической
тени практически всюду равна нулю.
Фактически дифракционная картина не
наблюдается, и распространение света
является прямолинейным.
,
так что светлое пятно в центре отсутствует,
и освещенность в области геометрической
тени практически всюду равна нулю.
Фактически дифракционная картина не
наблюдается, и распространение света
является прямолинейным.
Дифракция Фраунгофера на одной щели. Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной a. Оптическая разность хода между крайними лучами, идущими от щели в некотором направлении
 .
.
Разобьем открытую часть волновой
поверхности в плоскости щели на зоны
Френеля, имеющие вид равновеликих полос,
параллельных щели. Так как ширина каждой
зоны выбирается такой, чтобы разность
хода от краев этих зон была равна  ,
то на ширине щели уместится
,
то на ширине щели уместится  зон. Амплитуды вторичных волн в плоскости
щели будут равны, так как зоны Френеля
имеют одинаковые площади и одинаково
наклонены к направлению наблюдения.
Фазы колебаний от пары соседних зон
Френеля отличаются на ,
поэтому, суммарная амплитуда этих
колебаний равна нулю.
зон. Амплитуды вторичных волн в плоскости
щели будут равны, так как зоны Френеля
имеют одинаковые площади и одинаково
наклонены к направлению наблюдения.
Фазы колебаний от пары соседних зон
Френеля отличаются на ,
поэтому, суммарная амплитуда этих
колебаний равна нулю.
Если число зон Френеля четное, то
 , (9а)
и в точке B наблюдается минимум освещенности
(темный участок), если же число зон
Френеля нечетное, то
, (9а)
и в точке B наблюдается минимум освещенности
(темный участок), если же число зон
Френеля нечетное, то
 (9б)
и
наблюдается близкая к максимуму
освещенность, соответствующей действию
одной нескомпенсированной зоны Френеля.
В направлении
(9б)
и
наблюдается близкая к максимуму
освещенность, соответствующей действию
одной нескомпенсированной зоны Френеля.
В направлении  щель действует, как одна зона Френеля,
и в этом направлении наблюдается
наибольшая освещенность, точке
щель действует, как одна зона Френеля,
и в этом направлении наблюдается
наибольшая освещенность, точке  соответствует центральный или главный
максимум освещенности.
соответствует центральный или главный
максимум освещенности.
Расчет освещенности в зависимости от направления дает
 , (10)
где
, (10)
где 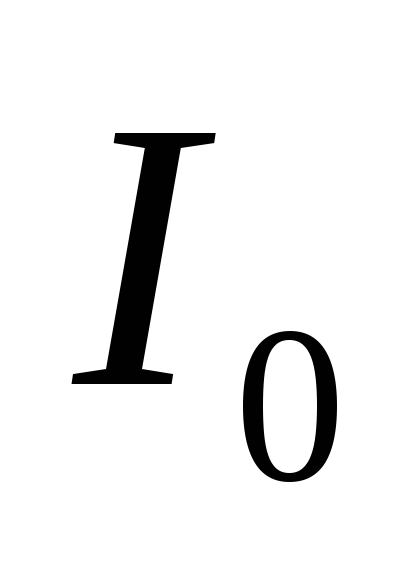 – освещенность в середине дифракционной
картины (против центра линзы),
– освещенность в середине дифракционной
картины (против центра линзы),  – освещенность в точке, положение
которой определяется направлением .
График функции (10) изображен на рис.
Максимумы освещенности соответствуют
значениям ,
удовлетворяющие условиям
– освещенность в точке, положение
которой определяется направлением .
График функции (10) изображен на рис.
Максимумы освещенности соответствуют
значениям ,
удовлетворяющие условиям
 ,
,  ,
,  и т.д.
Вместо этих условий для максимумов
приближенно можно пользоваться
соотношением (9б), дающим близкие значения
углов. Величина вторичных максимумов
быстро убывает. Численные значения
интенсивностей главного и следующих
максимумов относятся как
и т.д.
Вместо этих условий для максимумов
приближенно можно пользоваться
соотношением (9б), дающим близкие значения
углов. Величина вторичных максимумов
быстро убывает. Численные значения
интенсивностей главного и следующих
максимумов относятся как
 и т.д.,
т.е. основная часть световой
энергии, прошедшей через щель, сосредоточена
в главном максимуме.
и т.д.,
т.е. основная часть световой
энергии, прошедшей через щель, сосредоточена
в главном максимуме.
Сужение щели приводит к тому, что
центральный максимум расплывается, а
его освещенность уменьшается. Наоборот,
чем щель шире, тем картина ярче, но
дифракционные полосы уже, а число самих
полос больше. При  в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
studfile.net
Интерференция и дифракция, с примерами решений
Определение интерференции
Или немного иначе: Интерференцией называют сложение в пространстве волн, при этом возникает неизменное во времени амплитудное распределение суммарных колебаний.
Интерференцией волн света называют сложение волн, при котором можно наблюдать устойчивую во времени картину усиления или ослабления суммарных колебаний света в разных пространственных точках. Термин интерференция в науку ввел Т. Юнг.
Условия возникновения интерференции
Для того чтобы при наложении волн образовывалась устойчивая интерференционная картина необходимо, чтобы источники волн обладали одинаковой частотой и постоянной разностью фаз. Подобные источники называют когерентными (согласованными). Когерентными называют волны, которые созданы когерентными источниками.
Так, исключительно при наложении когерентных волн возникает устойчивая интерференционная картина.
В оптике для создания интерференционной картины когерентные волны получают:
- делением амплитуды волны;
- делением фронта волны.
Условие минимумов интерференции
Амплитуда колебаний интерферирующих волн в рассматриваемой точке будет минимальной, если разность хода () волн в этой точке содержит нечетное число длин полуволн ():
Допустим, что на отрезке укладывается , тогда получается, одна волна отстает от другой на половину периода. Разность фаз этих волн оказывается равна , что означает – колебания происходят в противофазе. При сложении таких колебаний, амплитуда суммарной волны получится равной нулю.
Условие максимумов интерференции
Амплитуда колебаний интерферирующих волн в рассматриваемой точке будет максимальной, если разность хода () волн в этой точке содержит целое число длин волн ():
Определение дифракции
Слово дифракция с латинского языка означает разломанный.
Явление дифракции объясняют при помощи принципа Гюйгенса. Вторичные волны, которые испускаются участками вещества (среды), попадают за края препятствия, которое находится на пути движения волны. Согласно теории Френеля поверхность волны в любой произвольный момент времени – это не только огибающая вторичных волн, а результат их интерференции.
Условия, при которых наблюдается дифракция
Особенно явно дифракция проявляется тогда, когда размеры препятствия меньше или сравнимы с длиной волны.
Дифрагировать могут волны любой природы, как и интерферировать.
Условие минимумов интенсивности
При дифракции световой волны на одной щели при нормальном падении лучей условие минимума интенсивности записывается как:
где a – ширина щели; – угол дифракции; k – номер минимума; – длина волны.
Условие максимумов интенсивности
При дифракции световой волны на одной щели при нормальном падении лучей условие максимума интенсивности записывается как:
где – приближенная величина угла дифракции.
Условие главных максимумов интенсивности при дифракции на дифракционной решетке
Условие главных максимумов интенсивности дифракция света на дифракционной решетке при нормальном падении лучей записывают:
где d – период (постоянная) решетки; k – номер главного максимума; – угол между нормалью к плоскости решетки и направлением дифрагированных волн.
Значение дифракции
Дифракция не дает возможности получать четкие изображения мелких предметов, так как не всегда можно считать, что свет распространяется строго по прямой. Вследствие этого, изображения могут быть размытыми, при этом увеличение не помогает увидеть детали предмета, если его размер сравним с длиной волны света. Явление дифракции накладывает границы на применимость законов геометрической оптики и определяет предел разрешающей способности оптических приборов.
Примеры решения задач
ru.solverbook.com
