Дифракции света: 3.8. Дифракция света
Дифракция волн. Дифракция света | Частная школа. 9 класс
Конспект по физике для 9 класса «Дифракция волн. Дифракция света». Что такое дифракция волн. При каких условиях волны изменяют направление своего распространения. Каковы особенности дифракции световых волн.
Конспекты по физике Учебник физики Тесты по физике
На предыдущих уроках вы познакомились с интерференцией волн, которая характерна для всех волновых процессов. Вместе с тем существует ещё одно явление, которое также присуще только волнам.
ДИФРАКЦИЯ МЕХАНИЧЕСКИХ ВОЛН
Вероятно, вам не раз приходилось наблюдать за поведением волн на поверхности воды, когда волна встречает на своём пути различные препятствия. При этом, если размеры препятствия малы по сравнению с длиной волны, например, торчащий из воды прутик, небольшой камень и т. п., то волны его свободно огибают, смыкаясь за ним.
Совсем другая картина наблюдается, когда размеры препятствия существенно превосходят длину волны. В этом случае за препятствием (например, большим камнем) образуется область невозмущённой водной поверхности.
В этом случае за препятствием (например, большим камнем) образуется область невозмущённой водной поверхности.
Особенно наглядно способность огибать препятствия наблюдается у звуковых волн. Например, мы отчётливо слышим шум работающего двигателя автомобиля за углом здания, хотя автомобиля не видим.
Когда мы работаем в комнате, то обычно закрываем дверь в шумный коридор. Если же дверь открыть настежь, то шум мешает работать. А как вы думаете, будет ли в комнате по-прежнему тихо, если дверь немного открыть и оставить узкую щель? Может быть, это почти то же самое, что и полностью закрытая дверь? Однако повседневный опыт убеждает нас в обратном: в этом случае шум из коридора так же проникает в комнату, как и при широко открытой двери.
Явление отклонения волн от прямолинейного распространения, огибание волнами препятствий называют дифракцией (от лат. diffraction — разломанный).
Рассмотрим опыт, наглядно демонстрирующий явление дифракции.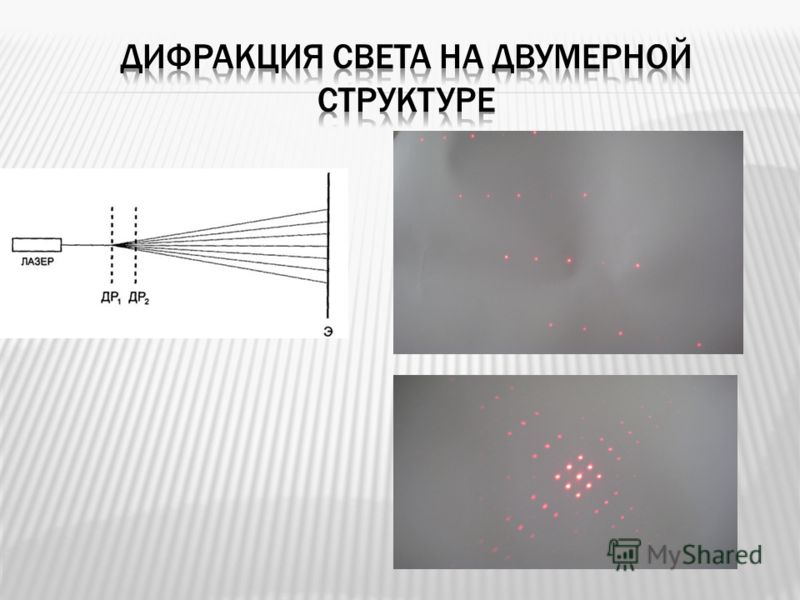
Возбудим с помощью узкой дощечки волны на поверхности воды, налитой в прямоугольную кювету, снабжённую экраном со щелью. Для этого придадим дощечке периодически колебательные движения в направлении, перпендикулярном её продольной оси. В результате по поверхности воды будут последовательно R распространяться гребни со впадинами между ними.
Опыт показывает, что если на пути волн установлен экран со щелью, размеры которой велики по сравнению с длиной волны, то волны проходят сквозь щель, почти не меняя своей формы и направления распространения. Лишь на значительном расстоянии за щелью имеет место некоторое расширение фронта волны.
Совершенно иная картина распространения волн наблюдается в случае, когда размеры щели меньше длины волны. При этом кардинально меняется форма волн за щелью — они становятся круговыми, а колебания охватывают всю поверхность воды за экраном. В данном случае дифракция волн полностью аналогична дифракции звуковых волн на щели, образованной неплотно закрытой дверью, о чём говорилось выше.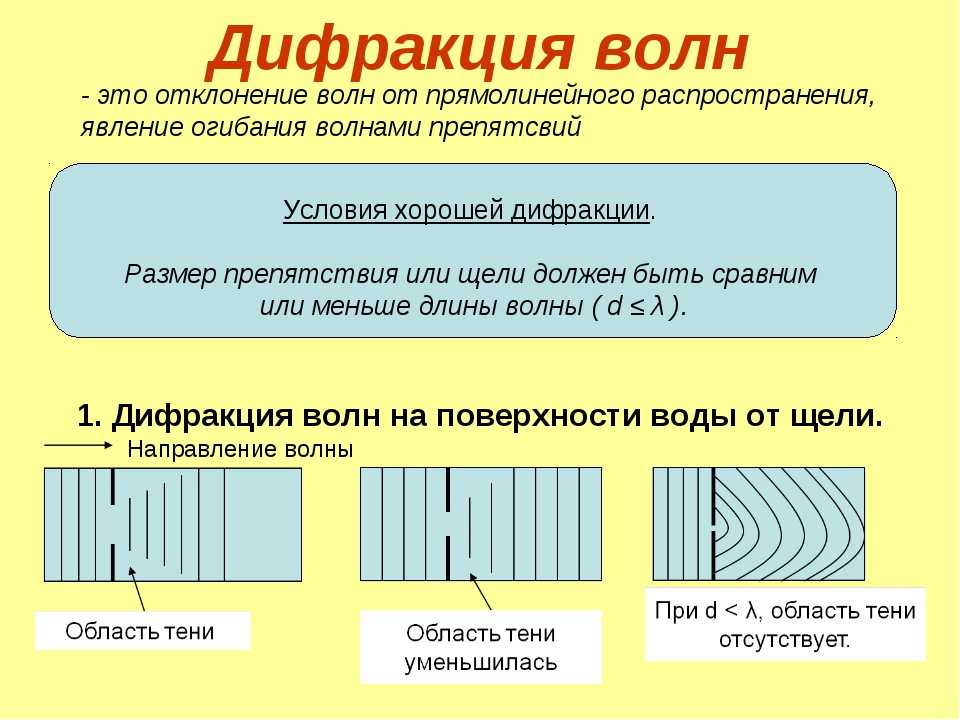
ДИФРАКЦИЯ СВЕТА
Рассмотренные ранее опыты по интерференции света убедительно свидетельствуют о его волновой природе. Поэтому для света должна также наблюдаться и дифракция, которая присуща любому волновому процессу. Но в отличие от дифракции механических волн, наблюдать дифракцию света много сложнее. Дело в том, что световые волны дифрагируют заметным образом только в том случае, когда размеры препятствия сравнимы с длиной волны, а она у света очень мала.
Первые опыты по дифракции света выполнил в XVII в. итальянский учёный Ф. Гримальди. В частности, пропуская узкий пучок света через малое отверстие, Гримальди обнаружил отступление от закона прямолинейного распространения света: размер светлого пятна на экране, расположенном против отверстия, оказался больше размера самого отверстия. Опыты также показали, что если диаметр отверстия (размер щели) в ширме достаточно велик, а расстояние от ширмы до экрана не очень велико, то закон прямолинейного распространения света выполняется с высокой точностью. Поскольку Гримальди разделял 4 точку зрения Гюйгенса на природу света, то наблюдаемые особенности в распространении света он объяснял как следствие его волновой природы.
Поскольку Гримальди разделял 4 точку зрения Гюйгенса на природу света, то наблюдаемые особенности в распространении света он объяснял как следствие его волновой природы.
Классический опыт по дифракции света был осуществлён в 1802 г. Т. Юнгом, открывшим явление интерференции света. Схема опыта по наблюдению дифракции была практически полностью аналогична опыту по интерференции света, подробно описанному выше. Световой пучок, исходивший из узкой щели первой ширмы, освещал две близко расположенные щели во второй ширме. Вследствие дифракции из этих щелей выходили два расходящихся световых пучка, которые частично перекрывались, при этом на экране, установленном за ширмой, наблюдалась интерференционная картина.
Таким образом, на основе опыта Т. Юнг продемонстрировал два важнейших свойства света — интерференцию и дифракцию. Кроме того, опираясь на результаты своего опыта, Юнг впервые получил точную оценку длины световой волны. Последовательную теорию дифракции света развил в своих работах современник Юнга французский учёный О. Френель.
Френель.
Вы смотрели Конспект по физике для 9 класса «Дифракция волн. Дифракция света». Что такое дифракция волн. При каких условиях волны изменяют направление своего распространения. Каковы особенности дифракции световых волн. ВСПОМНИТЕ: Какие виды механических волн существуют? В чём заключается главная идея опыта Юнга?
Вернуться к Списку конспектов по физике (Оглавление).
Изучение дифракции света от дифракционной решетки
38
Работа 42
Цель
работы. Изучение
дифракционной картины от дифракционной
решетки в проходящем свете; определение
постоянной дифракционной решетки и
длины волны монохроматического света.
Встречая на своем пути препятствия, световые волны могут отклоняться от прямолинейного направления распространения в область геометрической тени. Любые отклонения при распространении волн от законов геометрической оптики называются
Явление
дифракции света, как и интерференции
(интерференция волн
— взаимное усиление или ослабление двух
или более волн при их наложении друг на
друга при одновременном распространении
в пространстве), связано с перераспределением
энергии волн (или интенсивности светового
потока, пропорциональной энергии волны)
в пространстве. Для объяснения результатов
перераспределения интенсивности волн
в пространстве в результате дифракции
в волновой теории используется принцип
Гюйгенса—Френеля. Согласно этому принципу каждый элемент
волновой поверхности можно рассматривать
как источник вторичных элементарных
волн, огибающая которых будет волновой
поверхностью в дальнейшие моменты
времени.
Большое практическое значение имеет дифракция света при падении его на дифракционную решетку. В простейшем случае дифракционная решетка представляет собой систему параллельных друг другу щелей, разделенных непрозрачными промежутками равной ширины. Распределение интенсивности света в дифракционной картине определяется интерференцией вторичных волн, приходящих в точку наблюдения от различных щелей дифракционной решетки. Чаще всего для наблюдения дифракции на дифракционной решетке создаются условия, когда на дифракционную решетку падает плоская
 В этом случае наблюдается дифракция в
параллельных лучах.
В этом случае наблюдается дифракция в
параллельных лучах. На
рисунке 1 изображен ход параллельных
лучей до и после дифракционной решетки.
Световой пучок падает нормально к
плоскости дифракционной решетки (ДР).
В результате дифракции световые лучи
отклоняются на некоторый угол
(угол
дифракции),
собираются линзой Л, а на экране Э,
расположенном в фокальной плоскости
линзы Л, образуется дифракционная
картина, представляющая собой систему
максимумов и минимумов света. При
визуальном наблюдении роль линзы играет
хрусталик глаза. В направлении
первоначального распространения света
будет располагаться центральный максимум
(или максимум нулевого порядка) М.
Максимумы 1-го, 2-го, 3-го и других более
высоких порядков (М,
М,
М… соответственно) располагаются
симметрично относительно максимума
нулевого порядка по обе стороны от него.
Положение максимумов определяется
такими значениями углов дифракции(k=1, 2, 3 …), для которых волны, приходящие
в точку наблюдения ото всех щелей
усиливают друг друга.
В случае нормального падения света на решетку с шириной прозрачный штрихов (щелей) a и шириной непрозрачных штрихов (непрозрачных промежутков между щелями) b положение максимумов определяется из условия:
(a+b)sin=2k(четное число длин полуволн) (1)
или dsin=2k,
где — угол дифракции, т.е. угол между нормалью к решетке и направлением отклонения лучей на решетке;- длина дифрагирующей волны; k — порядок максимума (k=1, 2, 3 …).
Условием минимума является:
(a+b)sin=(2k+1)(нечетное число длин полуволн).
Величина (a+b)=d называется периодом или постоянной дифракционной решетки.
Как
следует из условий (1) углы, под которыми
наблюдаются световые максимумы, зависят
от длины волны. Таким образом, дифракционная
решетка представляет собой спектральный
прибор: если на дифракционную решетку
падает не монохроматический свет, а
свет сложного спектрального состава,
то после дифракции на решетке на экране
наблюдается спектр, причем фиолетовые
лучи отклоняются решеткой на меньшие
углы, чем красные (<).
В месте расположения нулевого максимума
(k=0,=0)
находятся нулевые максимумы всех длин
волн дифрагирующего света, накладывающиеся
друг на друга. При попадании на
дифракционную решетку белого света
нулевой максимум остается белым
(неокрашенным), а по обе стороны от него
симметрично относительно нулевого
максимума располагаются максимумы
более высоких порядков, причем
последовательность их окраски подчиняется
условиям (1). Дифракционная решетка
поэтому может использоваться как
диспергирующий элемент в спектральных
приборах. Условия (1) позволяют рассчитать
длину волныдифрагирующего света, если измерить
все другие величины, входящие в формулы
(1).
Таким образом, дифракционная
решетка представляет собой спектральный
прибор: если на дифракционную решетку
падает не монохроматический свет, а
свет сложного спектрального состава,
то после дифракции на решетке на экране
наблюдается спектр, причем фиолетовые
лучи отклоняются решеткой на меньшие
углы, чем красные (<).
В месте расположения нулевого максимума
(k=0,=0)
находятся нулевые максимумы всех длин
волн дифрагирующего света, накладывающиеся
друг на друга. При попадании на
дифракционную решетку белого света
нулевой максимум остается белым
(неокрашенным), а по обе стороны от него
симметрично относительно нулевого
максимума располагаются максимумы
более высоких порядков, причем
последовательность их окраски подчиняется
условиям (1). Дифракционная решетка
поэтому может использоваться как
диспергирующий элемент в спектральных
приборах. Условия (1) позволяют рассчитать
длину волныдифрагирующего света, если измерить
все другие величины, входящие в формулы
(1).
Растянутость
спектра зависит от порядка спектра и
постоянной дифракционной решетки
(растянутость увеличивается с увеличением
порядка спектра и уменьшением дифракционной
решетки).
При увеличении числа щелей на дифракционной решетке через нее проходит больше света, и, следовательно, увеличивается интенсивность света в направлении главных максимумов.
Дифракция света — Физика — Презентации
Дифракция света
Характерным проявлением волновых свойств света является дифракция света —
отклонение от прямолинейного распространения
на резких неоднородностях среды
Дифракция была открыта Франческо Гримальди в конце XVII в. Объяснение явления дифракции света дано Томасом Юнгом и Огюстом Френелем, которые не только дали описание экспериментов по наблюдению явлений интерференции и дифракции света, но и объяснили свойство прямолинейности распространения света с позиций волновой теории
Биографии
Принцип Гюйгенса — Френеля
Для вывода законов отражения и преломления мы использовали принцип Гюйгенса. Френель дополнил его формулировку для объяснения явления дифракции
Френель дополнил его формулировку для объяснения явления дифракции
Определите, какое дополнение ввел Френель?
Принцип Гюйгенса:
каждая точка волновой поверхности является источником вторичных сферических волн
Принцип Гюйгенса-Френеля:
каждая точка волновой поверхности является источником вторичных сферических волн ,
которые интерферируют между собой
Дифракция от различных препятствий: а) от тонкой проволочки; б) от круглого отверстия; в) от круглого непрозрачного экрана.
Дифракционные картины от одного препятствия с разным числом открытых зон
Если разность хода от двух соседних зон равна половине длины волны , то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум , если разность хода равна длине волны , то наблюдается интерференционный максимум
Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно)
Если нечетное число полуволн, то наблюдается максимум (светлое пятно)
Зонные пластинки
На этом принципе основаны т.н. зонные пластинки
Условия наблюдения дифракции
- Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны
Условия наблюдения дифракции
- Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максимумы располагаются очень близко друг к другу, а их интенсивность быстро убывает
Границы применимости геометрической оптики
- Дифракция наблюдается хорошо на расстоянии
- Если , то дифракция невидна и получается резкая тень ( d — диаметр экрана).
- Эти соотношения определяют границы применимости геометрической оптики
Границы применимости геометрической оптики
- Если наблюдение ведется на расстоянии , где d — размер предмета, то начинают проявляться волновые свойства света
Соотношения длины волны и размера препятствия
- На рис.
 показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны.
показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны.
Интерференционные картины от разных точек предмета перекрываются, и изображение смазывается, поэтому прибор не выделяет отдельные детали предмета. Дифракция устанавливает предел разрешающей способности любого оптического прибора
Разрешающая способность человеческого глаза приблизительно равна одной угловой минуте: , где D — диаметр зрачка; телескопа =0 ,02 »; у микроскопа увеличение не более 2 . 10 3 раз. Можно видеть предметы, размеры которых соизмеримы с длиной световой волны
Дифракционная решетка
Дифракционные решетки, представляющие собой точную систему штрихов некоторого профиля, нанесенную на плоскую или вогнутую оптическую поверхность, применяются в спектральном приборостроении, лазерах, метрологических мерах малой длины и т. д
д
Дифракционная решетка
Дифракционная решетка
Дифракционная решетка
- Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части
Дифракционная решетка
- Угол — угол отклонения световых волн вследствие дифракции.
- Наша задача — определить, что будет наблюдаться в произвольном направлении — максимум или минимум
Дифракционная решетка
- Оптическая разность хода
- Из условия максимума интерференции получим:
Дифракционная решетка
- Следовательно:
— формула дифракционной решетки.
Величина k — порядок дифракционного максимума
( равен 0, 1, 2 и т.д.)
Определение с помощью дифракционной решетки
https://www.youtube.com/watch?v=S8orh4bft0c&list=RDCMUCqKclh3n8KxqtUaBOfXsavA&index=2
Гримальди Франческо 2. IV.1618 — 28.XII.1663
Итальянский ученый. С 1651 года — священник.
Открыл дифракцию света, систематически ее изучал и сформулировал некоторые правила. Описал солнечный спектр, полученный с помощью призмы. В 1662 г. определил величину поверхности Земли.
Френель Огюст Жан (10.V.1788 — 14.VII.1827)
Французский физик. Научные работы посвящены физической оптике.
Дополнил известный принцип Гюйгенса, введя так называемые зоны Френеля (принцип Гюйгенса — Френеля). Разработал в 1818 году теорию дифракции света
Разработал в 1818 году теорию дифракции света
Юнг Томас 13 .IV.1773-10.V.1829
Английский ученый. Полиглот. Научился читать в 2 года. Объяснил аккомодацию глаза, обнаружил интерференцию звука, объяснил интерференцию света, и ввел этот термин. Измерил длины волн световых лучей. Исследовал деформацию
Араго Доменик Франсуа (26. II.1786-2.X.1853)
Французский физик и политический деятель. Автор многих открытий по оптике и электромагнетизму: хроматическую поляризацию света, вращение плоскости поляризации, намагничивание железных опилок вблизи проводника с током. Установил связь полярных сияний с магнитными бурями. По его указаниями А.Физо и У.Фуко измерили скорость света, а У.Леверье открыл планету Нептун
Фраунгофер Йозеф (6.III.1787- 7.VI.1826)
Немецкий физик.
Научные работы относятся к физической оптике. Внёс существенный вклад в исследование дисперсии и создание ахроматических линз. Фраунгофер изучал дифракцию в параллельных лучах (так называемая дифракция Фраунгофера).Сначала от одной щели, а потом от многих. Большой заслугой учёного является использование(с 1821 года) дифракционных решеток для исследования спектров (некоторые исследователи считают его даже изобретателем первой дифракционной решетки)
Фраунгофер изучал дифракцию в параллельных лучах (так называемая дифракция Фраунгофера).Сначала от одной щели, а потом от многих. Большой заслугой учёного является использование(с 1821 года) дифракционных решеток для исследования спектров (некоторые исследователи считают его даже изобретателем первой дифракционной решетки)
Пуассон Семион Дени (21.VI.1781 — 25.IV.1840)
Французский механик, математик, физик, член Парижской академии наук (с 1812 года). Физические исследования относятся к магнетизму, капиллярности, теории упругости, гидромеханике, теории колебаний, теории света. Член Петербургской академии наук (с 1826 года)
КОНЕЦ
свет | Определение, свойства, физика, характеристики, типы и факты
видимый спектр света
Смотреть все СМИ
- Ключевые люди:
- Исаак Ньютон Альберт Эйнштейн Джеймс Клерк Максвелл Птолемей Роджер Бэкон
- Похожие темы:
- цвет Солнечный лучик фотон интенсивность света скорость света
Просмотреть весь связанный контент →
Популярные вопросы
Что такое свет в физике?
Свет — это электромагнитное излучение, воспринимаемое человеческим глазом.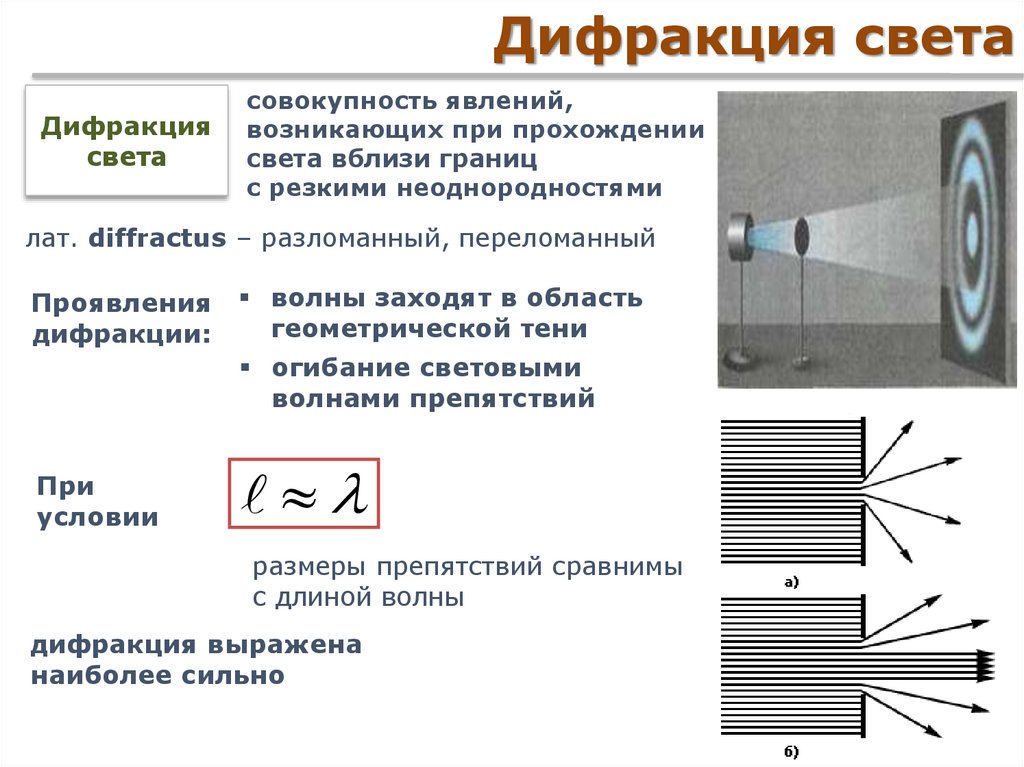 Электромагнитное излучение возникает в чрезвычайно широком диапазоне длин волн, от гамма-лучей с длиной волны менее примерно 1 × 10 −11 метров до радиоволн, измеряемых в метрах.
Электромагнитное излучение возникает в чрезвычайно широком диапазоне длин волн, от гамма-лучей с длиной волны менее примерно 1 × 10 −11 метров до радиоволн, измеряемых в метрах.
Какова скорость света?
Скорость света в вакууме является фундаментальной физической константой, и в настоящее время принято значение 29.9 792 458 метров в секунду, или около 186 282 миль в секунду.
Что такое радуга?
Радуга образуется при преломлении солнечного света сферическими каплями воды в атмосфере; два преломления и одно отражение в сочетании с хроматической дисперсией воды создают первичные цветовые дуги.
Почему свет важен для жизни на Земле?
Свет является основным инструментом восприятия мира и взаимодействия с ним для многих организмов. Солнечный свет согревает Землю, определяет глобальные погодные условия и запускает поддерживающий жизнь процесс фотосинтеза; около 10 22 джоулей солнечной лучистой энергии достигает Земли каждый день. Взаимодействие света с материей также помогло сформировать структуру Вселенной.
Взаимодействие света с материей также помогло сформировать структуру Вселенной.
Каково отношение цвета к свету?
В физике цвет ассоциируется именно с электромагнитным излучением определенного диапазона длин волн, видимым человеческому глазу. Излучение таких длин волн составляет часть электромагнитного спектра, известную как видимый спектр, т. е. свет.
Сводка
Прочтите краткий обзор этой темы
свет , электромагнитное излучение, воспринимаемое человеческим глазом. Электромагнитное излучение возникает в чрезвычайно широком диапазоне длин волн, от гамма-лучей с длиной волны менее примерно 1 × 10 −11 метров до радиоволн, измеряемых в метрах. В этом широком спектре длины волн, видимые человеку, занимают очень узкую полосу, от примерно 700 нанометров (нм; миллиардных долей метра) для красного света до примерно 400 нм для фиолетового света. Области спектра, примыкающие к видимому диапазону, часто также называют световыми, инфракрасными с одной стороны и ультрафиолетовыми с другой. Скорость света в вакууме — фундаментальная физическая константа, принятое в настоящее время значение которой равно ровно 299 792 458 метров в секунду, или около 186 282 миль в секунду.
Скорость света в вакууме — фундаментальная физическая константа, принятое в настоящее время значение которой равно ровно 299 792 458 метров в секунду, или около 186 282 миль в секунду.
Нет однозначного ответа на вопрос «Что такое свет?» удовлетворяет множеству контекстов, в которых свет воспринимается, исследуется и используется. Физик интересуется физическими свойствами света, художник — эстетической оценкой визуального мира. Благодаря зрению свет является основным инструментом восприятия мира и общения в нем. Солнечный свет согревает Землю, определяет глобальные погодные условия и запускает поддерживающий жизнь процесс фотосинтеза. В самом большом масштабе взаимодействие света с материей помогло сформировать структуру Вселенной. Действительно, свет дает окно во Вселенную, от космологических до атомных масштабов. Почти вся информация об остальной Вселенной достигает Земли в виде электромагнитного излучения. Интерпретируя это излучение, астрономы могут заглянуть в самые ранние эпохи Вселенной, измерить общее расширение Вселенной и определить химический состав звезд и межзвездной среды. Подобно тому, как изобретение телескопа значительно расширило возможности исследования Вселенной, так и изобретение микроскопа открыло сложный мир клетки. Анализ частот света, испускаемого и поглощаемого атомами, явился основным толчком к развитию квантовой механики. Атомная и молекулярная спектроскопия по-прежнему остается основным инструментом для исследования структуры вещества, обеспечивая сверхчувствительные тесты атомных и молекулярных моделей и способствуя изучению фундаментальных фотохимических реакций.
Подобно тому, как изобретение телескопа значительно расширило возможности исследования Вселенной, так и изобретение микроскопа открыло сложный мир клетки. Анализ частот света, испускаемого и поглощаемого атомами, явился основным толчком к развитию квантовой механики. Атомная и молекулярная спектроскопия по-прежнему остается основным инструментом для исследования структуры вещества, обеспечивая сверхчувствительные тесты атомных и молекулярных моделей и способствуя изучению фундаментальных фотохимических реакций.
Свет передает пространственную и временную информацию. Это свойство лежит в основе областей оптики и оптических коммуникаций, а также множества связанных с ними технологий, как зрелых, так и новых. Технологические приложения, основанные на манипулировании светом, включают лазеры, голографию и волоконно-оптические телекоммуникационные системы.
В большинстве повседневных обстоятельств свойства света можно вывести из теории классического электромагнетизма, в которой свет описывается как связанные электрические и магнитные поля, распространяющиеся в пространстве в виде бегущей волны. Однако эта волновая теория, разработанная в середине 19 в.го века недостаточно для объяснения свойств света при очень низкой интенсивности. На этом уровне квантовая теория необходима для объяснения характеристик света и взаимодействия света с атомами и молекулами. В своей простейшей форме квантовая теория описывает свет как состоящий из дискретных пакетов энергии, называемых фотонами. Однако ни классическая волновая модель, ни классическая модель частиц не описывают свет правильно; свет имеет двойственную природу, которая раскрывается только в квантовой механике. Этот удивительный корпускулярно-волновой дуализм характерен для всех первичных составляющих природы (например, электроны имеют как корпускулярный, так и волновой аспекты). С середины 20-го века физики считали законченной более полную теорию света, известную как квантовая электродинамика (КЭД). КЭД объединяет идеи классического электромагнетизма, квантовой механики и специальной теории относительности.
Однако эта волновая теория, разработанная в середине 19 в.го века недостаточно для объяснения свойств света при очень низкой интенсивности. На этом уровне квантовая теория необходима для объяснения характеристик света и взаимодействия света с атомами и молекулами. В своей простейшей форме квантовая теория описывает свет как состоящий из дискретных пакетов энергии, называемых фотонами. Однако ни классическая волновая модель, ни классическая модель частиц не описывают свет правильно; свет имеет двойственную природу, которая раскрывается только в квантовой механике. Этот удивительный корпускулярно-волновой дуализм характерен для всех первичных составляющих природы (например, электроны имеют как корпускулярный, так и волновой аспекты). С середины 20-го века физики считали законченной более полную теорию света, известную как квантовая электродинамика (КЭД). КЭД объединяет идеи классического электромагнетизма, квантовой механики и специальной теории относительности.
Викторина «Британника»
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какова единица измерения циклов в секунду? Проверьте свою физику с помощью этого теста.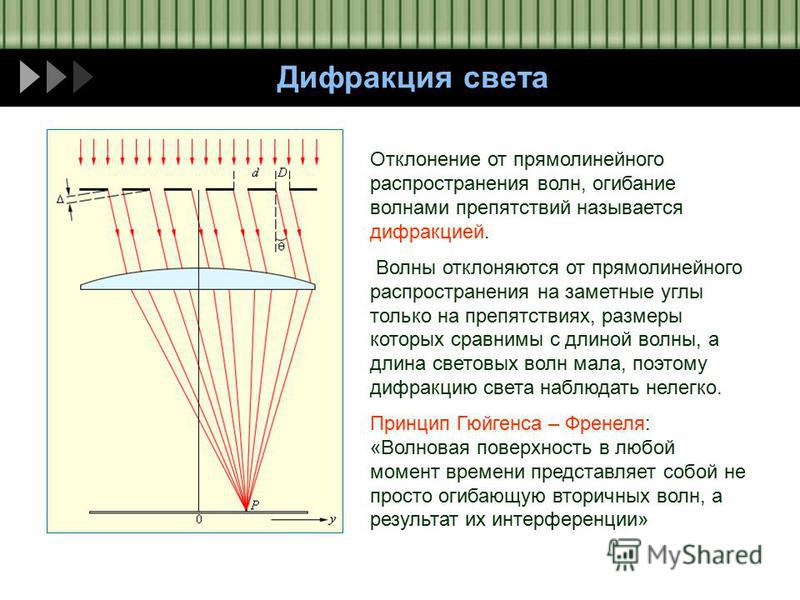
В этой статье основное внимание уделяется физическим характеристикам света и теоретическим моделям, описывающим природу света. Его основные темы включают введение в основы геометрической оптики, классические электромагнитные волны и эффекты интерференции, связанные с этими волнами, а также основные идеи квантовой теории света. Более подробные и технические презентации этих тем можно найти в статьях «Оптика, электромагнитное излучение, квантовая механика и квантовая электродинамика». См. также относительность для получения подробной информации о том, как рассмотрение скорости света, измеренной в различных системах отсчета, сыграло решающую роль в развитии специальной теории относительности Альберта Эйнштейна в 1905 году. world
Хотя есть явные свидетельства того, что ряд ранних цивилизаций использовали простые оптические инструменты, такие как плоские и криволинейные зеркала и выпуклые линзы, древнегреческим философам обычно приписывают первые формальные рассуждения о природе света. Концептуальное препятствие, заключающееся в том, чтобы отличить человеческое восприятие визуальных эффектов от физической природы света, препятствовало развитию теорий света. В этих ранних исследованиях преобладало созерцание механизма зрения. Пифагор ( с. 500 до н.э.) предположил, что зрение вызывается визуальными лучами, исходящими из глаза и ударяющими по предметам, тогда как Эмпедокл ( ок. 450 до н.э.), по-видимому, разработал модель зрения, в которой свет излучался как предметами, так и глазом. Эпикур ( г. ок. г. 300 г. до н.э.) считал, что свет излучается другими источниками, помимо глаза, и что зрение возникает, когда свет отражается от объектов и попадает в глаз. Евклид ( ок. 300 г. до н.э.) в своей книге Оптика представил закон отражения и обсудил распространение световых лучей по прямым линиям. Птолемей ( с. 100 н.э.) предпринял одно из первых количественных исследований преломления света при переходе из одной прозрачной среды в другую, сведя в таблицу пары углов падения и пропускания для комбинаций нескольких сред.
Концептуальное препятствие, заключающееся в том, чтобы отличить человеческое восприятие визуальных эффектов от физической природы света, препятствовало развитию теорий света. В этих ранних исследованиях преобладало созерцание механизма зрения. Пифагор ( с. 500 до н.э.) предположил, что зрение вызывается визуальными лучами, исходящими из глаза и ударяющими по предметам, тогда как Эмпедокл ( ок. 450 до н.э.), по-видимому, разработал модель зрения, в которой свет излучался как предметами, так и глазом. Эпикур ( г. ок. г. 300 г. до н.э.) считал, что свет излучается другими источниками, помимо глаза, и что зрение возникает, когда свет отражается от объектов и попадает в глаз. Евклид ( ок. 300 г. до н.э.) в своей книге Оптика представил закон отражения и обсудил распространение световых лучей по прямым линиям. Птолемей ( с. 100 н.э.) предпринял одно из первых количественных исследований преломления света при переходе из одной прозрачной среды в другую, сведя в таблицу пары углов падения и пропускания для комбинаций нескольких сред.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
С упадком греко-римского царства научный прогресс переместился в исламский мир. В частности, аль-Махмун, седьмой аббасидский халиф Багдада, основал Дом Мудрости (Байт аль-Хикма) в 830 г. н.э. для перевода, изучения и улучшения эллинистических научных и философских трудов. Среди первых ученых были аль-Хорезми и аль-Кинди. Известный как «философ арабов», аль-Кинди расширил концепцию прямолинейно распространяющихся световых лучей и обсудил механизм зрения. К 1000 г. от пифагорейской модели света отказались, и возникла лучевая модель, содержащая основные концептуальные элементы того, что сейчас известно как геометрическая оптика. В частности, Ибн аль-Хайтам (латинизированный как Альхазен) в Китаб аль-маназир ( ок. 1038; «Оптика») правильно приписал зрение пассивному восприятию световых лучей, отраженных от предметов, а не активному излучению световых лучей глазами. Он также изучал математические свойства отражения света от сферических и параболических зеркал и нарисовал подробные изображения оптических компонентов человеческого глаза. Работа Ибн аль-Хайтама была переведена на латынь в 13 веке и оказала побудительное влияние на францисканского монаха и естествоиспытателя Роджера Бэкона. Бэкон изучал распространение света через простые линзы и считается одним из первых, кто описал использование линз для коррекции зрения.
Он также изучал математические свойства отражения света от сферических и параболических зеркал и нарисовал подробные изображения оптических компонентов человеческого глаза. Работа Ибн аль-Хайтама была переведена на латынь в 13 веке и оказала побудительное влияние на францисканского монаха и естествоиспытателя Роджера Бэкона. Бэкон изучал распространение света через простые линзы и считается одним из первых, кто описал использование линз для коррекции зрения.
Дифракция света на фазовой решетке при наклонном падении в промежуточном режиме дифракции
Введение
Стандартный подход к явлениям дифракции основан на следующих двух простых случаях: во-первых, рассматривается дифракция света на оптически тонких решетках при нормальном падении. Многочисленные наблюдаемые дифракционные максимумы, мало зависящие от угла падения, обычно объясняют многоволновой интерференцией, когда углы дифракции определяются уравнением решетки (см., например, [1]). Во-вторых, брэгговская дифракция на толстых решетках вводится в контексте определения кристаллических структур. В этом случае нормальное падение не приводит ни к какой дифракции. Вместо этого условие, при котором возникает конструктивная интерференция и может наблюдаться резкий дифракционный максимум, задается законом Брэгга [1].
В этом случае нормальное падение не приводит ни к какой дифракции. Вместо этого условие, при котором возникает конструктивная интерференция и может наблюдаться резкий дифракционный максимум, задается законом Брэгга [1].
Ясно, что приведенные выше два случая являются двумя достаточно простыми крайностями более общих и сложных ситуаций в физике дифракции. Теории практически для любых мыслимых конфигураций, отличных от двух упомянутых выше, рассматриваются в литературе (см., например, [2, 3]), но остаются малоизвестными большинству неспециалистов. Здесь мы экспериментально выясняем один из таких общих случаев: наклонное падение на (голографическую) фазовую решетку, проявляющую дифракцию в так называемом промежуточном дифракционном режиме [4], который находится между режимом Рамана-Ната для оптически тонких решеток [5, 6 ] и режим Брэгга для оптически толстых решеток. Мы используем плоскую одномерную ненаклонную решетку, дифракционные свойства которой не могут быть описаны ни одним из двух крайних случаев, описанных выше. Сначала опишем измерения угловой зависимости дифрагированных интенсивностей для простого и обычного случая плоскостной дифракции, т. е. для входящего и выходящего пучков, лежащих в одной плоскости. Для изменения угла падения решетку ступенчато поворачивают на углы \(\theta\) вокруг оси, перпендикулярной последней плоскости (см. рис. 1). В качестве следующего шага, начиная снова с нормального падения, мы наклоняем решетку вокруг ее вектора решетки на угол \(\дзета\), чтобы получить наклонное падение, и измеряем угловую зависимость также для этой более сложной ситуации. Концепция использования экстремально наклонного падения («внеплоскостной установки») важна не только для нейтронной оптики [7, 8], но и для рентгеновских лучей [9].] при разработке спектрометров для космических приложений [10], например, а также для экстремального УФ-излучения при скользящем падении [11, 12].
Сначала опишем измерения угловой зависимости дифрагированных интенсивностей для простого и обычного случая плоскостной дифракции, т. е. для входящего и выходящего пучков, лежащих в одной плоскости. Для изменения угла падения решетку ступенчато поворачивают на углы \(\theta\) вокруг оси, перпендикулярной последней плоскости (см. рис. 1). В качестве следующего шага, начиная снова с нормального падения, мы наклоняем решетку вокруг ее вектора решетки на угол \(\дзета\), чтобы получить наклонное падение, и измеряем угловую зависимость также для этой более сложной ситуации. Концепция использования экстремально наклонного падения («внеплоскостной установки») важна не только для нейтронной оптики [7, 8], но и для рентгеновских лучей [9].] при разработке спектрометров для космических приложений [10], например, а также для экстремального УФ-излучения при скользящем падении [11, 12].
Система координат xyz закреплена на лабораторной раме таким образом, что световая волна падает в положительном направлении z . Чтобы установить наклонное падение, решетка (серые и зеленые пластины) наклоняется вокруг вектора решетки \({\mathbf {G}}\) (направление, сделанное видимым по оси CD; прикрепленное к образцу) на угол \(\zeta \) ( 9{\circ }\)
Чтобы установить наклонное падение, решетка (серые и зеленые пластины) наклоняется вокруг вектора решетки \({\mathbf {G}}\) (направление, сделанное видимым по оси CD; прикрепленное к образцу) на угол \(\zeta \) ( 9{\circ }\)
Изображение в натуральную величину
В настоящей работе исследуются два конкретных вопроса: сколько возникает порядков дифракции и где располагаются дифракционные максимумы при вращении или наклоне? В предшествующих исследованиях уже были в определенной степени даны ответы на поставленные выше вопросы [13, 14]: они находят — как теоретически, так и экспериментально — положения дифракционных максимумов в зависимости от углов, измеренных относительно четко определенных осей вращения, которые крепятся к дифракционной решетке. Однако их теоретический подход не зависит от расстояния между решетками и используемой длины волны падающего света: интенсивность дифрагированных лучей оценивается с использованием формализма Френеля-Кирхгофа. Таким образом, в пределе дальнего поля (дифракция Фраунгофера) амплитуды дифрагированных лучей пропорциональны преобразованию Фурье апертурной функции решетки. Реализуемый таким образом подход эквивалентен применению первого борновского приближения [15], справедливого, когда показатель преломления среды не слишком сильно отличается от единицы, без учета процессов многократной дифракции. В качестве естественного продолжения предыдущих исследований в настоящей работе мы даем простое аналитическое выражение для положения дифракционных максимумов при вращении и наклоне фазовой решетки на основе условия Флоке [16], т.е. на основе закона сохранения энергии и импульса Только. Кроме того, в отношении интенсивностей дифрагированных пучков и их угловой зависимости мы придерживаемся более общего подхода: хотя теория Френеля–Кирхгофа хорошо обоснована для ситуации, изученной в [10]. [14] (шаг решетки \(\varLambda \приблизительно 83\,\upmu\)м, длина волны падающего света \(\lambda =532\) нм, при которой дифракция явно ограничивается режимом Рамана-Ната [5, 6] ), в нашей работе мы используем строгий анализ связанных волн (RCWA, [16,17,18]) для решения задачи дифракции для комбинации длины волны/решетки/геометрии, в которой угловые зависимости дифрагированных интенсивностей не могут быть рассмотрены в режим Рамана-Ната, ни теорией толстых решеток (режим Брэгга).
Реализуемый таким образом подход эквивалентен применению первого борновского приближения [15], справедливого, когда показатель преломления среды не слишком сильно отличается от единицы, без учета процессов многократной дифракции. В качестве естественного продолжения предыдущих исследований в настоящей работе мы даем простое аналитическое выражение для положения дифракционных максимумов при вращении и наклоне фазовой решетки на основе условия Флоке [16], т.е. на основе закона сохранения энергии и импульса Только. Кроме того, в отношении интенсивностей дифрагированных пучков и их угловой зависимости мы придерживаемся более общего подхода: хотя теория Френеля–Кирхгофа хорошо обоснована для ситуации, изученной в [10]. [14] (шаг решетки \(\varLambda \приблизительно 83\,\upmu\)м, длина волны падающего света \(\lambda =532\) нм, при которой дифракция явно ограничивается режимом Рамана-Ната [5, 6] ), в нашей работе мы используем строгий анализ связанных волн (RCWA, [16,17,18]) для решения задачи дифракции для комбинации длины волны/решетки/геометрии, в которой угловые зависимости дифрагированных интенсивностей не могут быть рассмотрены в режим Рамана-Ната, ни теорией толстых решеток (режим Брэгга).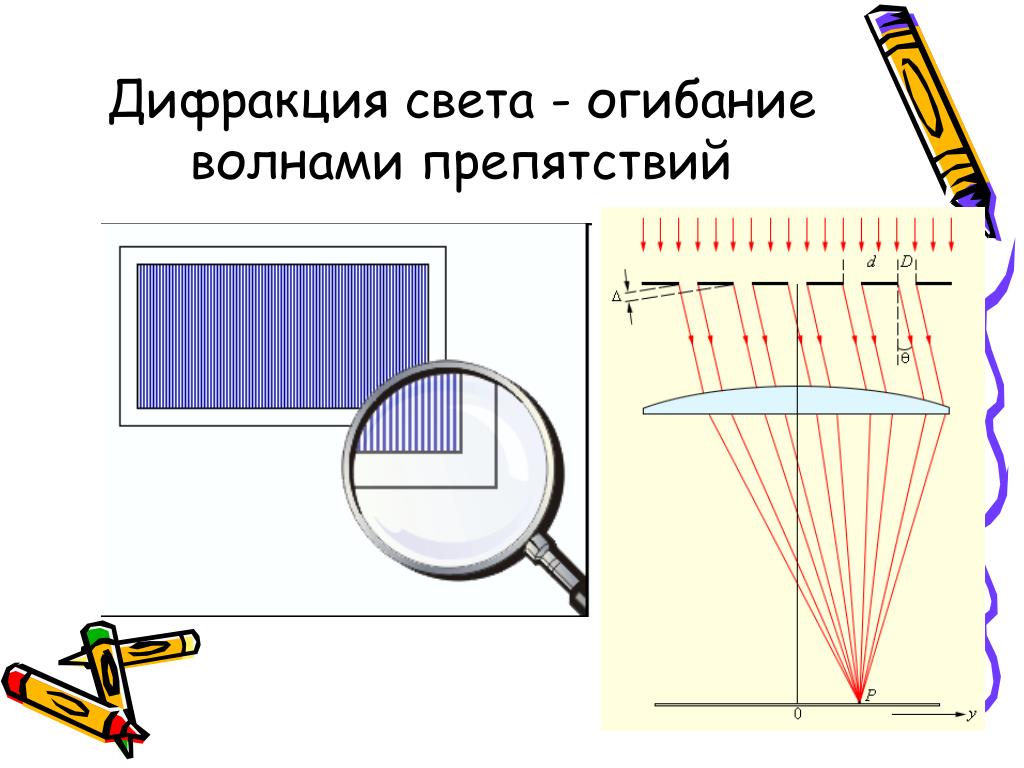 Наконец, мы также обсудим возможность подобного измерения с помощью нейтронных волн материи.
Наконец, мы также обсудим возможность подобного измерения с помощью нейтронных волн материи.
Моделирование
Рассмотрим одномерную фазовую решетку с пространственно-модулированным показателем преломления n ( x ), определяемым выражением
$$\begin{aligned} n({\mathbf {x}})= n_0+n_1\cos ({\mathbf {G}}\cdot {\mathbf {x}})+ n_2\cos (2{\mathbf {G}}\cdot {\mathbf {x}})+\cdots , \end{aligned}$$
(1)
где \({\mathbf {G}}\) — вектор решетки, \(n_0\) — средний показатель преломления решетки, а \(n_{ 1,2,\ldots }\) — амплитуды различных компонент Фурье, сводится к решению соответствующей краевой задачи. Точные решения были даны в терминах модальной теории (часто называемой динамической теорией дифракции, см., например, [19].]) или, альтернативно, теория связанных волн [17]. Стратегия состоит в том, чтобы решить уравнения Максвелла в каждой из областей (вход, решетка, выход) и согласовать тангенциальные компоненты полей на границах. Теорема Флоке выделяет разрешенные поля в периодической решетке. Требуется \({\mathbf {q}}_m={\mathbf {q}}_0-m{\mathbf {G}}\), где \({\mathbf {q}}_m\) и \({ \mathbf {q}}_0\) — волновые векторы m -го порядка дифракции на решетке (при \(\vert {\mathbf {q}}_m\vert =2\pi n_0/\lambda\) ) и падающий волновой вектор соответственно. В самом деле, для пространственно ограниченной решетки с периодичностью только вдоль x -направлении (см. рис. 1), достаточно, чтобы составляющая волнового вектора, параллельная поверхности образца и вдоль вектора решетки, удовлетворяла условию Флоке [16]. Кроме того, на границах эта параллельная компонента \({\mathbf {q}}_{||}\) совпадает с параллельной компонентой в ограничивающей среде (здесь: свободное пространство) \({\mathbf {k}}_{| |}\), так что разрешенные волновые векторы дифракции вне решетки равны:
Требуется \({\mathbf {q}}_m={\mathbf {q}}_0-m{\mathbf {G}}\), где \({\mathbf {q}}_m\) и \({ \mathbf {q}}_0\) — волновые векторы m -го порядка дифракции на решетке (при \(\vert {\mathbf {q}}_m\vert =2\pi n_0/\lambda\) ) и падающий волновой вектор соответственно. В самом деле, для пространственно ограниченной решетки с периодичностью только вдоль x -направлении (см. рис. 1), достаточно, чтобы составляющая волнового вектора, параллельная поверхности образца и вдоль вектора решетки, удовлетворяла условию Флоке [16]. Кроме того, на границах эта параллельная компонента \({\mathbf {q}}_{||}\) совпадает с параллельной компонентой в ограничивающей среде (здесь: свободное пространство) \({\mathbf {k}}_{| |}\), так что разрешенные волновые векторы дифракции вне решетки равны:
$$\begin{aligned} {\mathbf {k}}_m= {\mathbf {k}}_0-m{\mathbf {G}}-\varDelta k{{\шляпа{s}}} \end{выровнено}$$
(2)
$$\begin{align} |{\mathbf {k}}_m|= 2\pi /\lambda \rightarrow \beta , \end{align}$$
(3)
где \({{\hat{s}}}\) обозначает единичный вектор нормали к поверхности образца, а \(\varDelta k\) — параметр небрегговской дефазировки [20], который мы получим ниже. {\circ }\) (см. рис. 1). Искривленная поверхность является частью сферы Эвальда. Вершины векторов \({\mathbf {k}}_0\), \({\mathbf {k}}_3\) и \(\varDelta k {{\hat{s}}}\) касаются сферы Эвальда поверхность. Обратите внимание, что \(\vert {\mathbf {k}}_0\vert =\vert {\mathbf {k}}_3\vert\)
{\circ }\) (см. рис. 1). Искривленная поверхность является частью сферы Эвальда. Вершины векторов \({\mathbf {k}}_0\), \({\mathbf {k}}_3\) и \(\varDelta k {{\hat{s}}}\) касаются сферы Эвальда поверхность. Обратите внимание, что \(\vert {\mathbf {k}}_0\vert =\vert {\mathbf {k}}_3\vert\)
Изображение в натуральную величину
Уравнение (2) представляет собой условие дифракции или уравнение Лауэ (см., например, [21]). Последнее эквивалентно вышеупомянутому закону Брэгга, заданному формулой \(2\varLambda \sin \theta _{m}=m\lambda\).
Далее мы приводим аналитические выражения для дифрагированных волновых векторов для геометрии в наших экспериментах. Как показано на рис. 1а, фазовая решетка помещается на держатель образца, что позволяет наклонять ее вокруг вектора решетки \({\mathbf {G}}\) (коллинеарно оси CD) на угол наклона \(\zeta \). Держатель образца закреплен на поворотном столике, с помощью которого осуществляется поворот решетки на углы \(\theta\) вокруг оси вращения и (см. рис. 1б). Ось y перпендикулярна вектору решетки и зафиксирована в лабораторной системе отсчета, независимо от угла наклона \(\дзета\). Сноска 1 Кроме того, здесь векторы \({\mathbf {k}}_0\), \({\mathbf {G}}(\theta)\) и \({{\hat{s}} }(\theta ,\zeta )\) даны в лабораторной рамке. Без ограничения общности мы можем выбрать нашу систему координат так, чтобы входящий луч соответствовал волновому вектору \({\mathbf {k}}_0=(0,0,\beta)\). Вектор решетки остается в плоскости \(x{-}z\) и может быть записан как \({\mathbf {G}}=G(\cos\theta,0,-\sin\theta)\) ( см. рис. 1b), где \(G=|{\mathbf {G}}|=2\pi /\varLambda\). Обращаясь к рис. 1b, c, можно увидеть, что нормаль к поверхности решетки может быть задана выражением \({{\hat{s}}}=(-\cos \zeta \sin \theta ,\sin \zeta ,-\cos \дзета \cos \тета )\). Таким образом, путем объединения уравнений. (2) и (3), \(\varDelta k\) можно выразить через углы \(\theta\) и \(\zeta\) как 92}\right] , \end{aligned}$$
рис. 1б). Ось y перпендикулярна вектору решетки и зафиксирована в лабораторной системе отсчета, независимо от угла наклона \(\дзета\). Сноска 1 Кроме того, здесь векторы \({\mathbf {k}}_0\), \({\mathbf {G}}(\theta)\) и \({{\hat{s}} }(\theta ,\zeta )\) даны в лабораторной рамке. Без ограничения общности мы можем выбрать нашу систему координат так, чтобы входящий луч соответствовал волновому вектору \({\mathbf {k}}_0=(0,0,\beta)\). Вектор решетки остается в плоскости \(x{-}z\) и может быть записан как \({\mathbf {G}}=G(\cos\theta,0,-\sin\theta)\) ( см. рис. 1b), где \(G=|{\mathbf {G}}|=2\pi /\varLambda\). Обращаясь к рис. 1b, c, можно увидеть, что нормаль к поверхности решетки может быть задана выражением \({{\hat{s}}}=(-\cos \zeta \sin \theta ,\sin \zeta ,-\cos \дзета \cos \тета )\). Таким образом, путем объединения уравнений. (2) и (3), \(\varDelta k\) можно выразить через углы \(\theta\) и \(\zeta\) как 92}\right] , \end{aligned}$$
(4)
где \(\rho _m:=m G/\beta\). Следовательно, уравнения (2) и (4) полностью определяют направления \({\mathbf {k}}_m/\beta\) дифрагированных лучей для m -го порядка дифракции. Обратите внимание, что этот результат был получен только из закона сохранения импульса и энергии (\(\vert {\mathbf {k}}_0\vert =\vert {\mathbf {k}}_m\vert\)). Ожидается, что из уравнения. (2) что при увеличении \(\varDelta k\) углы дифракции быстро отклоняются от \(2\theta _{m}\). Обратите внимание, что уравнение (4) дает ноль для \(m=0\), что означает, что не ожидается, что дифрагированный вперед луч будет испытывать какое-либо отклонение от плоскости падения.
Следовательно, уравнения (2) и (4) полностью определяют направления \({\mathbf {k}}_m/\beta\) дифрагированных лучей для m -го порядка дифракции. Обратите внимание, что этот результат был получен только из закона сохранения импульса и энергии (\(\vert {\mathbf {k}}_0\vert =\vert {\mathbf {k}}_m\vert\)). Ожидается, что из уравнения. (2) что при увеличении \(\varDelta k\) углы дифракции быстро отклоняются от \(2\theta _{m}\). Обратите внимание, что уравнение (4) дает ноль для \(m=0\), что означает, что не ожидается, что дифрагированный вперед луч будет испытывать какое-либо отклонение от плоскости падения.
Эксперименты
Подготовка фазовой решетки пропускания
Голографическая фазовая решетка для экспериментов по дифракции была изготовлена с использованием фотополимеризуемого композиционного материала с наночастицами, используемого для голографических приложений [8]. Наночастицы \(\hbox {SiO}_2\) со средним диаметром 13 нм и объемным показателем преломления 1,46, диспергированные в растворе метилизобутилкетона, смешивали с метакрилатными мономерами (2-метилакриловая кислота 2-4- [2-(2-метил-акрилоилокси)-этилсульфанилметил]-бензилсульфанил-этиловый эфир) [22]. Показатель преломления образовавшегося полимера составил 1,59.при 589 нм. Показатель преломления однородно отвержденных полимерных пленок без дисперсии наночастиц измеряли с помощью рефрактометра Аббе. Концентрация легирования наночастиц \(\hbox {SiO}_2\) составляла 34 об.%. Фотоинициатор титаноцен (Irgacure 784, Ciba) смешивали в количестве 1 % масс. по отношению к мономеру для обеспечения светочувствительности в зеленом цвете. Химическую смесь отливали на стеклянную пластину, сушили и накрывали другой стеклянной пластиной, отделенной от первой прокладками известной толщины. Для записи голограммы, обеспечивающей ненаклонная фазовая решетка пропускания с \(\varLambda =5~\upmu\)м и толщиной решетки \(d\приблизительно 13~\upmu\)м: В ярких областях интерференционной картины, облучающей образец, срабатывает фотоинициатор процесс полимеризации. Мономер расходуется в светлых областях на образование полимера. Вследствие возникающей разности химических потенциалов между светлыми и темными областями взаимная диффузия мономера в темных областях и наночастиц в светлых областях в конечном итоге приводит к увеличению концентрации наночастиц в темных областях и образующегося полимера в светлых областях.
Показатель преломления образовавшегося полимера составил 1,59.при 589 нм. Показатель преломления однородно отвержденных полимерных пленок без дисперсии наночастиц измеряли с помощью рефрактометра Аббе. Концентрация легирования наночастиц \(\hbox {SiO}_2\) составляла 34 об.%. Фотоинициатор титаноцен (Irgacure 784, Ciba) смешивали в количестве 1 % масс. по отношению к мономеру для обеспечения светочувствительности в зеленом цвете. Химическую смесь отливали на стеклянную пластину, сушили и накрывали другой стеклянной пластиной, отделенной от первой прокладками известной толщины. Для записи голограммы, обеспечивающей ненаклонная фазовая решетка пропускания с \(\varLambda =5~\upmu\)м и толщиной решетки \(d\приблизительно 13~\upmu\)м: В ярких областях интерференционной картины, облучающей образец, срабатывает фотоинициатор процесс полимеризации. Мономер расходуется в светлых областях на образование полимера. Вследствие возникающей разности химических потенциалов между светлыми и темными областями взаимная диффузия мономера в темных областях и наночастиц в светлых областях в конечном итоге приводит к увеличению концентрации наночастиц в темных областях и образующегося полимера в светлых областях. регионов [8]. Такое различие их концентраций обеспечивает пространственно-периодическую модуляцию показателя преломления, т. е. голографическую фазовую решетку. 9{\circ}\) были измерены путем размещения Si-фотодиодов в положениях дифрагированных лучей. Для чисто фазовой решетки дифракционная эффективность для дифракционного порядка m может быть получена из измеренных данных по формуле
регионов [8]. Такое различие их концентраций обеспечивает пространственно-периодическую модуляцию показателя преломления, т. е. голографическую фазовую решетку. 9{\circ}\) были измерены путем размещения Si-фотодиодов в положениях дифрагированных лучей. Для чисто фазовой решетки дифракционная эффективность для дифракционного порядка m может быть получена из измеренных данных по формуле
$$\begin{aligned} \eta _m=I_m/\sum I_m. \end{aligned}$$
На рис. 3 показан график дифракционной эффективности, полученный с помощью гелий-неонового лазера (633 нм). Хорошо видно, что дифракция для нашей решетки не может быть должным образом описана комбинационным методом. -Ната, так как процесс дифракции обладает значительной угловой селективностью, т. е. эффективность дифракции существенно падает при \(\тета\) не слишком далеко от угла Брэгга. Пренебрегая более низкими сигналами ± 3-го порядка, подгонка RCWA к сигналам другого порядка показана кривыми на рис. 3. В частности, приблизительный расчет RCWA был выполнен только для 5 порядков дифракции чистой фазовой решетки. Оценки параметров подгонки оказались равными \(n_1=(4,9{-6}\) соответственно. Учитывая величины \(n_1\) и \(n_2\), мы считаем, что профиль показателя преломления решетки не является полностью синусоидальным, так как \(|n_2|\) имеет тот же порядок величины, что и \(| n_1|\). Знак минус перед \(n_2\) указывает на то, что существует фазовый сдвиг \(\pi\) между первой и второй компонентами Фурье [ср. уравнение (1)] профиля показателя преломления этой решетки. Установлено, что установка RCWA хорошо согласуется с данными.
Оценки параметров подгонки оказались равными \(n_1=(4,9{-6}\) соответственно. Учитывая величины \(n_1\) и \(n_2\), мы считаем, что профиль показателя преломления решетки не является полностью синусоидальным, так как \(|n_2|\) имеет тот же порядок величины, что и \(| n_1|\). Знак минус перед \(n_2\) указывает на то, что существует фазовый сдвиг \(\pi\) между первой и второй компонентами Фурье [ср. уравнение (1)] профиля показателя преломления этой решетки. Установлено, что установка RCWA хорошо согласуется с данными.
Увеличенное изображение
Рис. 4 Схема установки с решеткой (зеленая плита, центр) и падающим справа пучком (красный). Исходящие дифрагированные лучи (красные) проходят от решетки к полупрозрачному экрану (синий, слева), где положения дифракционных пятен формируют дифракционную картину. {\circ }\). 9{\circ }\)
{\circ }\). 9{\circ }\)
Изображение в натуральную величину
Видно, что при наклонном падении дифракция происходит вне плоскости падения, как только нарушается условие Брэгга, как и ожидается из уравнения (1). (2), который предсказывает внеплоскостную дифракцию для порядка м (с \(m\ne 0\)) при \(\varDelta k\) в уравнении. (4) отличен от нуля. Отклонения направлений дифрагированных лучей от плоскости падения различны для различных порядков дифракции с индексом м . Например, на рис. 5 положения лучей, соответствующие порядкам дифракции \(+1,+2\) и \(+3\), расположены справа от положения луча нулевого порядка (последнее легко распознается здесь как самое яркое пятно). ), показывают небольшую разницу в их вертикальных координатах вне плоскости (9{\circ}\) показаны. Сноска 2 Хорошо видно, что максимумы порядков дифракции проявляются в широком диапазоне положений в соответствии с соответствующими значениями \(\varDelta k\) (и векторами \({{\hat{s}}}\)) в диапазоне от положительного к отрицательному, в то время как \(\theta\) изменяется при заданном \(\zeta\). Как и ожидалось, вертикальная внеплоскостная составляющая увеличивается с увеличением \(\zeta\). Дифракционные пятна можно было наблюдать только до \(\pm\, 4\)-го порядка из-за очень низких дифракционных сигналов более высоких порядков. Система уравнений
Как и ожидалось, вертикальная внеплоскостная составляющая увеличивается с увеличением \(\zeta\). Дифракционные пятна можно было наблюдать только до \(\pm\, 4\)-го порядка из-за очень низких дифракционных сигналов более высоких порядков. Система уравнений
$$\begin{align} h = L\frac{\varDelta k(\theta ,\zeta )\cos \zeta \sin \theta -m G \cos \theta}{\beta +\varDelta k(\ theta ,\zeta )\cos \zeta \cos \theta +m G\sin \theta } \end{aligned}$$
(5)
$$\begin{aligned} v= & {} -L\ frac{\varDelta k(\theta,\zeta)\sin\zeta}{\beta +\varDelta k(\theta,\zeta)\cos\zeta\cos\theta+m G\sin\theta} \end{ выровненный}$$
(6)
, описывающий горизонтальное и вертикальное положения дифракционных пятен, был получен с использованием уравнений. (2) и (4). Здесь, L — расстояние от решетки до экрана. Уравнения (5) и (6) были подобраны к данным с \(\zeta , \varLambda\) и L , установленными в качестве свободных параметров. Оценки параметров хорошо согласуются с измеренными значениями. {\circ }\) в виде слабой пунктирной желтой линии на рис. 6 (вторая сверху) . Незакрашенные кружки соответствуют измеренным положениям пятен для \(-4\ldots +2\) порядков дифракции. 9{\circ }\), для сравнения (см. текст)
{\circ }\) в виде слабой пунктирной желтой линии на рис. 6 (вторая сверху) . Незакрашенные кружки соответствуют измеренным положениям пятен для \(-4\ldots +2\) порядков дифракции. 9{\circ }\), для сравнения (см. текст)
Изображение в полный размер
На рис. 6 видно, что чем больше | м |, при изменении \(\theta\) наблюдаются меньшие дифракционные максимумы: Далекие левый и правый «следы» максимумов на рис. 6 содержат очень мало точек по сравнению с низко-| м | заказы. Есть несколько возможных причин такой тенденции: Одна из них – полное внутреннее отражение от границы стекло-воздух на задней поверхности решетки под большими углами \(\zeta\) и \(\theta\). Еще одной менее тривиальной причиной такого поведения являются нераспространяющиеся дифрагированные лучи, как объясняется в следующем: Уравнение. (4) предсказывает, что для данного индекса порядка дифракции м , дифракция наблюдается только в определенных угловых пределах при \(\theta\) и \(\zeta\), так как — при выходе за эти пределы — \(\varDelta k\), а значит, и волновой вектор сам дифрагированный пучок становится сложным. 2\theta \cos (2\zeta )-\cos (2\theta )}\right) }\right\rceil \end{aligned}$$
2\theta \cos (2\zeta )-\cos (2\theta )}\right) }\right\rceil \end{aligned}$$
где \(\left\lceil {x}\right\rceil\) и \(\left\lfloor {x}\right\rfloor\) обозначают функции потолка и пола соответственно. Приведенные выше уравнения для \(m_\pm\) утверждают, что при данных \(\theta\) и \(\zeta\) возбуждаются распространяющиеся волны (с вещественными волновыми векторами), соответствующие порядкам дифракции м , при условии, что их индекс m лежит между двумя крайними точками, т. е. \(m_{-}\le m\le m_+\).
Обсуждение
Отметим, что поведение дифракционных картин (положения дифракционных пятен) хорошо согласуется с уравнениями. 5 и 6, как видно на рис. 6. Наш вывод соответствующих уравнений [уравнения. (4)–(6)] основано только на сохранении энергии и импульса с использованием теоремы Флоке. Однако, решая уравнение (17) связанной предыдущей работы Jetty et al. В работе [14] для получения вертикального положения пятен на экране в зависимости от горизонтального положения мы находим, что последнее точно соответствует зависимости наших уравнений. (5) и (6) в пределе высоты щели (см. [14]), стремящейся к нулю. Интересно и несколько неожиданно, что даже если их работа [14] и наш эксперимент исследуют внеплоскостную дифракцию в контексте очень разных дифракционных режимов, предсказания и данные совпадают и находятся в хорошем согласии. Эксперимент Джетти и др. явно регулировался режимом Рамана-Натха, в отличие от нашего, управляемого промежуточным режимом, где необходим RCWA.
(5) и (6) в пределе высоты щели (см. [14]), стремящейся к нулю. Интересно и несколько неожиданно, что даже если их работа [14] и наш эксперимент исследуют внеплоскостную дифракцию в контексте очень разных дифракционных режимов, предсказания и данные совпадают и находятся в хорошем согласии. Эксперимент Джетти и др. явно регулировался режимом Рамана-Натха, в отличие от нашего, управляемого промежуточным режимом, где необходим RCWA.
Было бы интересно посмотреть, происходит ли внеплоскостная дифракция для массивных частиц, в отличие от фотонов. Учитывая экспериментальную проверку внеплоскостной дифракции и для массивных квантовых объектов, таких как, например, нейтроны, оценим отклонение от плоскостной дифракции для случая медленных нейтронов с длиной волны де Бройля \(\lambda _N=5\) нм и шаг решетки \(\varLambda =500\) нм. Расстояние L между образцом и детектором обычно составляет, скажем, пару метров. Кривая угловой зависимости решетки с \(d=30~\upmu\)м при \(\zeta \приблизительно 70^{\circ}\) показывает угловую ширину (область вокруг дифракционного максимума с приемлемой интенсивностью) около \(0,6^{\circ }\) (см. , например, [23]). Использование уравнения. (6) ожидаются вертикальные смещения дифрагированных пучков в диапазоне около 100 \(\upmu\)м, которые могут быть обнаружены с помощью имеющейся нейтронной аппаратуры и разрешения детектора.
, например, [23]). Использование уравнения. (6) ожидаются вертикальные смещения дифрагированных пучков в диапазоне около 100 \(\upmu\)м, которые могут быть обнаружены с помощью имеющейся нейтронной аппаратуры и разрешения детектора.
Резюме
Мы выполнили эксперименты по дифракции света на композитной плосковолновой решетке из наночастиц и полимера. Угловая зависимость положений дифракционных пятен при нескольких углах косого падения была приспособлена только к теоретическому предсказанию, полученному из сохранения энергии и импульса и правильных граничных условий. Сравнение с предыдущим опубликованным исследованием Jetty et al. Работа [14], основанная на формуле дифракции Френеля–Кирхгофа, дает в некотором частном случае полное соответствие. Последнее несколько удивительно, так как здесь мы также показываем, что за пределами приближения Френеля-Кирхгофа [15] или приближений, таких как теория пропускания Рамана-Ната [5, 6], невозможно объяснить угловую зависимость дифракционной эффективности в удовлетворительным образом. Напротив, угловые зависимости дифракционной эффективности, рассчитанные по измеренным интенсивностям, могут быть успешно объяснены с помощью RCWA [18].
Напротив, угловые зависимости дифракционной эффективности, рассчитанные по измеренным интенсивностям, могут быть успешно объяснены с помощью RCWA [18].
Наконец, мы дали оценку величины эффекта для нейтронов, которая предполагает, что проверка этого явления для волн материи возможна с помощью современных технологий.
Список литературы
Д. Холлидей, Р. Резник, Дж. Уокер, Основы физики (Wiley, 2007)
МАТЕМАТИКА Google ученый
Е.Г. Loewen, E. Popov, Дифракционные решетки и приложения Оптическая наука и техника. (Тейлор и Фрэнсис, 1997).
Google ученый
C. Palmer, Справочник по дифракционным решеткам , 7-е изд. (Корпорация Ньюпорт, 2014 г.). http://www.gratinglab.com/. По состоянию на 25 апреля 2021 г.
«>C.V. Раман, Н.С.Н. Нат, проц. Инд. акад. науч. (A) A 2 , 406–412 (1935)
Артикул Google ученый
C.V. Раман, Н.С.Н. Нат, проц. Инд. акад. науч. (A) A 2 , 413–420 (1935)
Артикул Google ученый
J. Klepp, C. Pruner, Y. Tomita, P. Geltenbort, J. Kohlbrecher, M. Fally, Materials 5 , 2788 (2012). https://doi.org/10.3390/ma5122788
ОБЪЯВЛЕНИЕ Статья Google ученый
Ю. Томита, Э. Хата, К. Момосе, С. Такаяма, X. Лю, К. Чикама, Дж. Клепп, К. Прунер, М. Фалли, Дж. Мод. Опц. 63 , S1 (2016). https://doi.org/10.1080/09500340.
 2016.1143534
2016.1143534РЕКЛАМА Статья Google ученый
Дж.Ф. Сили, Л.И. Горай, Б. Кьорнраттанаванич, Дж. М. Лэминг, Г.Е. Холланд, К.А. Фланаган, Р.К. Хайльманн, К.Х. Чанг, М.Л. Schattenburg, A.P. Rasmussen, Appl. Опц. 45 (8), 1680 (2006). https://doi.org/10.1364/AO.45.001680
ОБЪЯВЛЕНИЕ Статья Google ученый
Р. Л. Макентаффер, В. Кэш, А. Шипли, Решетки отражения вне плоскости для Constellation-X, в Space Telescopes and Instrumentation 2008: Ultraviolet to Gamma Ray , vol. 7011, изд. М.Дж.Л. Тернер, К.А. Фланаган (SPIE Proc., 2008), с. 75–82. ШПАЙ. https://doi.org/10.1117/12.789543
L. Poletto, P. Villoresi, Appl. Опц. 45 (34), 8577 (2006). https://doi.org/10.1364/AO.45.008577
ОБЪЯВЛЕНИЕ Статья Google ученый
«>Л.Г. Фадке, Дж. Аллен, Ам. Дж. Физ. 55 (6), 562 (1986)
АДС Статья Google ученый
Н.Р. Джетти, А. Суман, Р. Б. Хапарде, Ам. Дж. Физ. 80 (11), 972 (2012). https://doi.org/10.1119/1.4737854
ОБЪЯВЛЕНИЕ Статья Google ученый
М. Борн, Э. Вольф, Принципы оптики , 7-е изд. (Издательство Кембриджского университета, Кембридж, 2002 г.)
МАТЕМАТИКА Google ученый
Т.К. Гейлорд, М.Г. Мохарам, заявл. физ. Б 28 , 1 (1982). https://doi.org/10.1007/BF00693885
ОБЪЯВЛЕНИЕ Статья Google ученый
«>М.Г. Мохарам, Э.Б. Гранн, Д.А. Поммет, Т.К. Гейлорд, Дж. Опт. соц. Являюсь. А 12 (5), 1068 (1995). https://doi.org/10.1364/JOSAA.12.001068
РЕКЛАМА Статья Google ученый
П.С.Дж. Рассел, физ. 71 (4), 209 (1981). https://doi.org/10.1016/0370-1573(81)
-4
ОБЪЯВЛЕНИЕ Статья Google ученый
Дж.Т. Шеридан, Дж. Мод. Опц. 39 , 1709 (1992). https://doi.org/10.1080/713823578
РЕКЛАМА Статья Google ученый
СЗ Эшкрофт, Д. Н. Мермин, Физика твердого тела (Издательство Saunders College Publishing, Филадельфия, 1976)
МАТЕМАТИКА Google ученый
«>М. Фалли, Дж. Клепп, Ю. Томита, Т. Накамура, К. Прунер, М.А. Эллаббан, Р.А. Rupp, M. Bichler, I. Drevenšek Olenik, J. Kohlbrecher, H. Eckerlebe, H. Lemmel, H. Rauch, Phys. Преподобный Летт. 105 , 123904 (2010). https://doi.org/10.1103/PhysRevLett.105.123904
ОБЪЯВЛЕНИЕ Статья Google ученый
Т.К. Гейлорд, М.Г. Мохарам, заявл. Опц. 20 , 3271 (1981)
АДС Статья Google ученый
Л.И. Goray, G. Schmidt, J. Opt. соц. Являюсь. А 27 (3), 585 (2010)
АДС Статья Google ученый
М.Г. Мохарам, Т.К. Гейлорд, Дж. Опт. соц. Являюсь. 71 , 811 (1981). https://doi.org/10.1364/JOSA.71.000811
РЕКЛАМА Статья Google ученый
Н. Судзуки, Ю. Томита, заявл. Опц. 43 , 2125 (2004). https://doi.org/10.1364/AO.43.002125
ОБЪЯВЛЕНИЕ Статья Google ученый
Ссылки на скачивание
Дифракция, объяснение RP Photonics Encyclopedia; Фраунгофер, Френель, дифракционная оптика, интерференция, дифракционные характеристики
| Главная | Викторина | (With this you move over to the Buyer’s guide section.)»> Руководство покупателя | |
| Поиск | Категории | Глоссарий | Реклама |
| Прожектор фотоники | Учебники |
| Показать статьи A-Z |
Примечание: поле поиска по ключевому слову статьи и некоторые другие функции сайта требуют Javascript, который, однако, отключен в вашем браузере.
Дифракция — это общий термин для явлений, которые могут возникать, когда световые волны (или другие волны) сталкиваются с определенными структурами. Некоторые типичные примеры эффектов дифракции обсуждаются в следующих разделах.
Хотя в повседневной жизни редко встречаются значительные эффекты дифракции света, такие эффекты очень распространены в оптике и лазерной технике. На самом деле принципы работы различных оптических устройств по существу основаны на дифракции (→ дифракционная оптика ). Дифракция также играет решающую роль во многих других устройствах, таких как оптические резонаторы и волокна.
Дифракция на одной щели
Обычная ситуация состоит в том, что узкая оптическая щель равномерно освещается пространственно-когерентным излучением монохроматического лазера. За щелью можно наблюдать дифракционную картину (см. рис. 1) со следующими особенностями:
- Для каждой длины волны есть главный максимум посередине, и они гораздо слабее боковых максимумов под большими углами.

- Для более длинных волн центральный пик шире, а боковые пики появляются под большими углами.
Для данной длины волны первый минимум интенсивности возникает там, где разность фаз вкладов от двух краев щели достигает 2π. Профили интенсивности можно описать с помощью sinc 2 функции.
Дифракция на двойной щели
В своем знаменитом эксперименте с двумя щелями 1803 года Томас Юнг использовал две близко расположенные узкие оптические щели. Поскольку у него не было лазера, ему пришлось добиться пространственно-когерентного освещения двух щелей, используя перед ними третью узкую щель.
На рис. 2 показан расчетный профиль интенсивности для одной конкретной длины волны.
Первая установка возникает из-за интерференции полевых вкладов от двух разных щелей.
Профиль интенсивности далее медленно модулируется функцией, определяемой конечной шириной каждой щели.
На рис. 3 в цветовой шкале показаны интерференционные картины для разных длин волн. Картины для более длинных волн включают соответственно большие углы дифракции.
Рисунок 3: Дифракционные картины на одной щели для всех цветов.Дифракция на круглых апертурах
Если световой луч (например, лазерный луч) сталкивается с какой-либо апертурой, которая пропускает свет в одних областях и блокирует его в других случаях, непосредственным воздействием на прошедший свет является только соответствующее усечение профиля интенсивности. Лишь на некотором расстоянии за апертурой можно наблюдать характерные эффекты дифракции.
На рис. 4 показан смоделированный пример, в котором исходный гауссовский луч был усечен в центрированной круглой жесткой апертуре.
При дальнейшем распространении в воздухе профиль интенсивности приобретает сложную структуру за счет дифракции. Для мягкой апертуры (рис. 5), вызывающей плавное падение интенсивности на краю, дифракционная картина получается более гладкой.
Для мягкой апертуры (рис. 5), вызывающей плавное падение интенсивности на краю, дифракционная картина получается более гладкой.
Такие дифракционные эффекты можно хорошо понять и рассчитать на основе оптики Фурье. Жесткая апертура вводит высокие оптические частоты, соответствующие быстрым пространственным изменениям интенсивности.
Подобные эффекты также могут возникать, например, при попытке принудительно перевести лазер в режим одной поперечной моды (для оптимального качества луча) путем установки твердой апертуры в резонатор лазера.
Хотя такая апертура может обеспечить значительно более высокие потери на полное распространение для мод резонатора более высокого порядка по сравнению с потерями для основной моды, она также вносит эффекты дифракции. Поэтому метод часто не работает так хорошо.
Поэтому метод часто не работает так хорошо.
Угловое разрешение многих оптических инструментов, таких как телескопы, также ограничено из-за дифракции, т.е. на входном отверстии. Этот предел разрешения можно приблизительно оценить как длину волны, деленную на диаметр апертуры.
Отверстия не всегда круглые. На рисунках 6 и 7 показан пример, когда лазерный луч усекается лезвием.
Рисунок 6: Профиль интенсивности лазерного луча, усеченного лезвием, показан на расстоянии 10 мм после лезвия. Рисунок 7: То же, что и на рис. 6, но через 100 мм.Большинство лазеров и лазерной оптики сконструированы таким образом, что из-за жестких апертур возникают лишь незначительно слабые дифракционные эффекты. Это означает, что, например, все лазерные зеркала должны быть настолько большими, чтобы можно было отразить практически весь профиль луча.
Обратите внимание, что дифракционные эффекты неразрывно зависят от длины волны оптического излучения.
Для полихроматических лучей результирующие пространственные картины могут существенно отличаться для различных компонентов длины волны.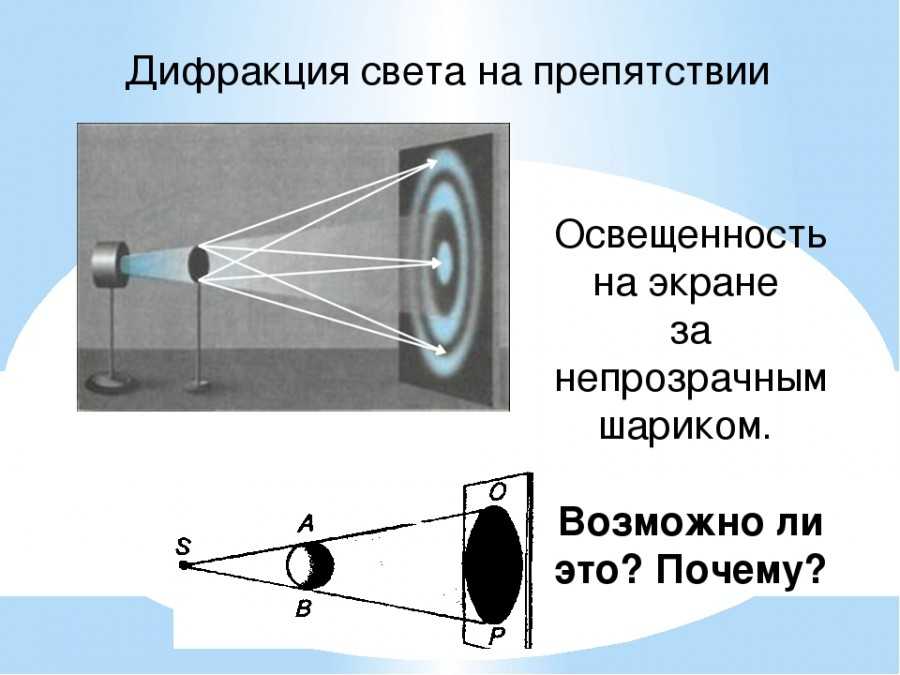 Следовательно, можно наблюдать цвета, например, для белого входного луча.
Классический случай — дифракционная решетка, который обсуждается ниже.
Следовательно, можно наблюдать цвета, например, для белого входного луча.
Классический случай — дифракционная решетка, который обсуждается ниже.
Расхождение лазерных лучей
Даже без апертуры лазерный луч всегда демонстрирует некоторую степень дифракции в соответствии с его поперечным пространственным ограничением. Для гауссовых пучков форма профиля интенсивности сохраняется, т. е. остается гауссовой; только радиус луча постепенно увеличивается. Это свойство сохраненных форм профиля интенсивности также применимо к другим типам мод в свободном пространстве, например. к модам Эрмита–Гаусса. Однако в целом дифракция приводит к изменению формы профиля интенсивности, как это можно видеть, например. на рис. 1.
Лазерные лучи часто имеют дифракционное ограничение, т. е. их расширение при распространении не сильнее, чем вызванное одной лишь дифракцией.
Для света с большими длинами волн возникают сильные эффекты дифракции.
Например, производительность генерации длинноволновых пучков на разностной частоте может быть сильно ограничена из-за дифракции генерируемого луча, что ограничивает длину взаимодействия или приводит к более слабой фокусировке луча.
Дифракционная и резонаторная или волноводная моды
Дифракционные эффекты также играют решающую роль в формировании некоторых видов мод. Например, существуют моды оптических волокон, для которых (по определению) профиль интенсивности остается постоянным при распространении. Такие моды формируются двумя противодействующими эффектами:
- Одна только дифракция имеет тенденцию к расширению луча, как обсуждалось выше.
- Волноводные эффекты от профиля показателя преломления волокна обеспечивают своего рода фокусировку.
Для мод волокна эти два эффекта точно уравновешивают друг друга. Точно так же моды резонатора демонстрируют баланс эффектов дифракции и фокусировки, только последние обычно сосредоточены, а не распределены в резонаторе.
Хорошая стабильность таких мод достигается, когда два противодействующих эффекта относительно сильны, так что любые дополнительные эффекты (например, дефекты структуры волокна, изгиб волокна или несоосность элемента резонатора) оказывают сравнительно слабое влияние. Плохая стабильность возникает в ситуациях, когда оба эффекта слабы, например, в лазерном резонаторе, где релеевская длина луча намного больше длины резонатора.
Такие ситуации могут возникать, например. при разработке лазеров с модуляцией добротности с большими радиусами мод и короткими лазерными резонаторами.
Плохая стабильность возникает в ситуациях, когда оба эффекта слабы, например, в лазерном резонаторе, где релеевская длина луча намного больше длины резонатора.
Такие ситуации могут возникать, например. при разработке лазеров с модуляцией добротности с большими радиусами мод и короткими лазерными резонаторами.
Дифракция на периодических и непериодических структурах
Рисунок 8: Выходные лучи всех возможных порядков дифракции на дифракционной решетке. Эффекты дифракции также могут возникать, когда световой луч сталкивается со структурой, которая вызывает периодические в пространстве изменения оптической интенсивности (через переменное поглощение) или оптической фазы (например, из-за переменного показателя преломления или высотного профиля).
Такие структуры называются дифракционными решетками, а явление называется .Дифракция Брэгга .
Если решетка демонстрирует большое количество колебаний в профиле луча, может быть несколько дифрагированных выходных лучей (см. Рисунок 8), каждый из которых имеет такую же пространственную форму, что и входной луч.
Направление выходных лучей (за исключением луча нулевого порядка) зависит от длины волны оптического излучения.
Этот эффект используется, например. в решетчатых спектрометрах.
Рисунок 8), каждый из которых имеет такую же пространственную форму, что и входной луч.
Направление выходных лучей (за исключением луча нулевого порядка) зависит от длины волны оптического излучения.
Этот эффект используется, например. в решетчатых спектрометрах.
Дифракция также может быть вызвана модуляциями показателя преломления в некотором объеме среды. Например, существуют объемные брэгговские решетки, которые можно использовать в качестве отражателей, зависящих от длины волны. Также возможна дифракция Брэгга на основе звуковых волн в среде; это используется в акустооптических модуляторах.
Дифракционные эффекты также могут возникать при отражении. Фактически большинство дифракционных решеток являются отражающими элементами.
Конечно, дифракционные эффекты возникают и на непериодических структурах.
Например, явление лазерного спекла возникает, когда лазерный луч рассеивается на шероховатой поверхности, что фактически вызывает сложную картину фазовой модуляции луча. Очень заметные спекл-эффекты можно наблюдать в квазимонохроматическом свете, полученном от лазеров.
Это не относится к широкополосному (временно некогерентному) свету, потому что полученные картины имеют сильную зависимость от длины волны, так что усреднение интенсивностей по некоторому диапазону длин волн эффективно размывает такие картины.
Очень заметные спекл-эффекты можно наблюдать в квазимонохроматическом свете, полученном от лазеров.
Это не относится к широкополосному (временно некогерентному) свету, потому что полученные картины имеют сильную зависимость от длины волны, так что усреднение интенсивностей по некоторому диапазону длин волн эффективно размывает такие картины.
Дифракционная оптика
Существуют и другие виды оптических элементов, в которых используются эффекты дифракции. Например, существуют дифракционные светоделители с несколькими выходами, а аналогичные устройства используются для когерентного объединения лучей. Подробнее читайте в статье о дифракционной оптике.
Дифракция и интерференция
Эффекты дифракции можно объяснить на основе интерференции различных вкладов профиля поля в результирующие поля в удаленных местах ( принцип Гюйгенса-Френеля ).
На самом деле четкой границы между дифракцией и интерференцией нет.
Например, прохождение света через узкую щель (апертуру) обычно описывают в терминах дифракции, а явления за двойной щелью называют явлениями интерференции. Однако основной принцип интерференции можно применить к обоим случаям.
Однако основной принцип интерференции можно применить к обоим случаям.
Различные режимы дифракции
Различают разные режимы дифракции, которые можно трактовать разными математическими методами. Дифракция Фраунгофера актуальна при рассмотрении дальнего поля, т. е. дифракционных картин вдали от преломляющей структуры; этот режим характеризуется значениями числа Френеля значительно ниже 1. С другой стороны, концепция дифракции Френеля с большими числами Френеля может применяться к случаям, когда важно ближнее поле.
Дифракционные характеристики оптических приборов
Характеристики различных видов оптических инструментов, таких как микроскопы, существенно ограничены эффектами дифракции.
По существу, ограниченный поперечный размер входного отверстия или внутренних элементов вызывает дифракционные эффекты, которые задают минимальный размер пятна так называемой функции рассеяния точки.
Поэтому оптические микроскопы (в том числе и лазерные микроскопы) обычно имеют разрешающую способность порядка половины длины волны оптического излучения. Есть несколько исключений из этого ограничения, например микроскопы ближнего поля (использующие оптический наконечник субволнового размера для сканирования объектов) или некоторые виды флуоресцентной микроскопии (STED).
Есть несколько исключений из этого ограничения, например микроскопы ближнего поля (использующие оптический наконечник субволнового размера для сканирования объектов) или некоторые виды флуоресцентной микроскопии (STED).
Аналогичные ограничения производительности применяются к оптическим телескопам. Ограничение дифракционных эффектов (для оптимального углового разрешения) требует использования больших оптических апертур.
Вопросы и комментарии от пользователей
Здесь вы можете задать вопросы и комментарии. Если они будут приняты автором, они появятся над этим абзацем вместе с ответом автора. Автор принимает решение о принятии на основе определенных критериев. По существу, вопрос должен представлять достаточно широкий интерес.
Пожалуйста, не вводите здесь личные данные; в противном случае мы бы удалили его в ближайшее время. (См. также нашу декларацию о конфиденциальности.) Если вы хотите получить личную обратную связь или консультацию от автора, свяжитесь с ним, например. по электронной почте.
по электронной почте.
Ваш вопрос или комментарий:
Проверка на спам:
(Пожалуйста, введите сумму тринадцати и трех в виде цифр!)
Отправляя информацию, вы даете свое согласие на возможную публикацию ваших материалов на нашем веб-сайте в соответствии с нашими правилами. (Если вы позже отзовете свое согласие, мы удалим эти материалы.) Поскольку ваши материалы сначала просматриваются автором, они могут быть опубликованы с некоторой задержкой.
См. также: дифракционные решетки, дифракционно-ограниченные пучки, резонаторные моды, моды, лазерный спекл, Фурье-оптика, ближнее и дальнее поле
и другие статьи в категории общая оптика
Если вы хотите разместить ссылку на эту статью на каком-либо другом ресурсе (например, на своем сайте, в социальных сетях, на дискуссионном форуме, в Википедии), вы можете получить необходимый код здесь.
HTML-ссылка на эту статью:
Статья о дифракции
в

 показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны.
показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны. 2016.1143534
2016.1143534