Дифракционный предел: размер пикселя, диафрагма и кружок рассеивания
Таблица дифракционного предела | БЛОГ ДМИТРИЯ ЕВТИФЕЕВА
к содержанию ↑
к содержанию ↑
Теория
У нас есть оптическая система, называемая объектив. В ней наличествует диафрагма, при прохождении которой в объективе возникает дифракция световых волн.
Зеленой линией помечено распределение интенсивности света.
Дифракционный предел был открыт 1873 году Эрнстом Аббе. Дифракционный предел — минимально возможный размер светового пятна, которое можно получить, фокусируя электромагнитное излучение (свет) заданной длины волны в среде с показателем преломления n:
В нашем случае мы получаем на матрице камеры так называемый диск Эйри.
диск Эйри, Airy disc
Размер диска и в частности его радиус, который нам понадобится для вычислений, принято мерить по первому световому кольцу, на которое приходится около 80% интенсивности света.
λ — длина волны света. Если у нас белый свет, то все длины волн будут создавать диски разного размера, ухудшая ситуацию (видимый свет от 400 nm синий до 700 nm красный).
D — диаметр диафрагмы
F — фокусное расстояние
Это явление накладывает на нас два ограничения.
1. Каждая точка объекта съемки на матрице камеры создаёт такой рисунок. Если два диска Эйри будут расположены слишком близко друг к другу, то 2 точки будут восприниматься, как одна.
По формуле видно, что при увеличении значения диафрагмы, растёт радиус диска Эйри.
И происходит сливание дисков Эйри в один объект. Т.е. точка перестает быть точкой на изображении. Это явление дифракции, которое и снижает разрешение объектива при достижении определенной диафрагмы. Оно называется DLA (Diffraction Limited Aperture).
Оно существует для каждого оптического прибора, но если результат мы проецируем на некий носитель (пленку или матрицу или глаз), то накладывается еще одно ограничение.
 Если расстояние между их центрами меньше радиуса, то разрешение объектива падает.
Если расстояние между их центрами меньше радиуса, то разрешение объектива падает.И в принципе это явление не имеет отношения к матрице камеры. Совсем не имеет, пока мы не начали разделять получившуюся картинку на цифровые пиксели.
И вот если мы начали оцифровывать сигнал с помощью пикселей, то получаем такие правила.
Если пиксель больше диска Эйри, то значит сенсор не способен использовать всё разрешение, которое предоставляет ему объектив и считается, что система ограничена разрешением.
Если пиксель меньше диска Эйри, то дополнительного разрешения мы не получаем, а вот система становится ограниченной явлением дифракции, которая возникает в объективе.
Размер диска Эйри существенно уменьшается при открытии диафрагмы, но там вступают в силу ХА ( хроматические аберрации), которые тоже существенно снижают разрешение объектива.
к содержанию ↑
Пример
Для примера возьмем камеру Canon 5D mark II.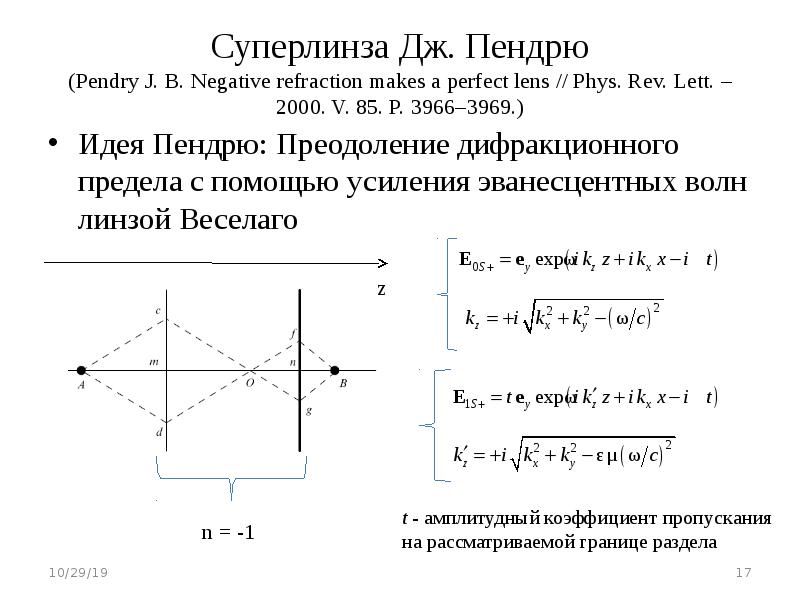
При длине волны 555nm (жёлто-зеленый свет к которому глаз наиболее чувствителен и который лучше всего воспринимает камера) и диафрагме F11 диаметр диска Эйри составит 14.8 микрон.
При этом размер пикселя у Canon 5D mark II составляет 36мм / 5616пикс * 1000 = 6.4 микрона
Но! Для того, чтобы различить хоть какие-то детали нам нужен не один пиксель, а, как минимум, два пикселя.
Скажем, для того, чтобы увидеть черную полоску, нам нужна одна черная и одна белая.
Один пиксель показывает черный цвет, другой белый — мы можем установить, что видим переход с черного на белый.
Частота Найквиста — в цифровой обработке сигналов частота, равная половине частоты дискретизации. Названа в честь Гарри Найквиста. Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если спектр (спектральная плотность) сигнала равна или ниже частоты Найквиста.
 В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть (теоретически) продискретизирован и затем восстановлен без искажений. Фактически «оцифровка» сигнала (превращение аналогового сигнала в цифровой) сопряжена с квантованием отсчётов — каждый отсчёт записывается в виде цифрового кода конечной разрядности, в результате чего к отсчетам добавляются ошибки квантования (округления), при определенных условиях рассматриваемые как «шум квантования».
В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть (теоретически) продискретизирован и затем восстановлен без искажений. Фактически «оцифровка» сигнала (превращение аналогового сигнала в цифровой) сопряжена с квантованием отсчётов — каждый отсчёт записывается в виде цифрового кода конечной разрядности, в результате чего к отсчетам добавляются ошибки квантования (округления), при определенных условиях рассматриваемые как «шум квантования».
© Википедия
Замечу к цитате, что фильтр слишком высоких частот в фотокамерах это фильтр антиалиасинга. Без него мы получали бы муар на снимках с повторяющейся текстурой (например, ткань).
В идеале это (2px на одну линию) так, но в основном для ЧБ сенсора без АА (антиалиасинг) фильтра. Такой сенсор, например, у Leica M-Monochrom.
У цветного сенсора разрешение будет ниже.
Т.е. реальное разрешение сенсора Canon 5D mark II — 12.8 микрон (2 пикселя).
Диаметр диска Эйри на F8 — 10.7 микрон
Диаметр диска Эйри на F11 — 14.8 микрон
Значит, для того, чтобы система камера Canon 5D mark II + объектив была ограничена разрешением сенсора камеры, нужно снимать на диафрагме более открытой, нежели F11 (F8->F1.2).
Теоретически — F8,F11 оптимальные диафрагмы для камер Canon 5D mark II, при которых разрешение сенсора не ограничено дифракцией, а разрешение объектива не ограничено сенсором камеры.
Камера Canon 60D (сенсор APS-C), объектив Canon 100/2.8L
Сделать с этим ничего нельзя тк это закон природы Дифракция и зависит он только от диаметра дырки-диафрагмы и длины волны света. Можете попробовать снимать в ультрафиолете (шутка 🙂 )
Для чего я тут всё расписывал и вас утомлял теорией?
Сколько бы пикселей не было на матрице — разрешение будет падать, начиная с F (относительное отверстие) = DLA. Для обычного режима съемки относительное отверстие равно «значению диафрагмы камеры». Для макросъемки это не так, смотрите данные к своему объективу (относительное отверстие объектива указывается для режима фокусировки на бесконечность). Например, для макрообъектива Nikon 105mm f/2.8G IF-ED AF-S VR Micro-Nikkor показывается реальное относительное отверстие в режиме макросъемки — F4.8 вместо 2.8, заявленных на оправе объектива. Для Canon EF 100/2.8L IS USM реальное относительное отверстие на камере не показывается (остается якобы 2.
На данный момент нельзя добавлять мегапиксели без потери попиксельной резкости на закрытых диафрагмах, ухудшения соотношения сигнал/шум (SNR) и уменьшения динамического диапазона (ДД).
к содержанию ↑
Расчётный дифракционный предел (DLA)
к содержанию ↑
Таблица дифракционного предела
DLA — Дифракционно ограниченная диафрагма (Difraction Limited Aperture)
Расчётная DLA — значение диафрагмы, получаемое по формуле
Фактическая DLA — значение диафрагмы, получаемое в результате тестов (в частности программой Reikan Focal)
Если вашей камеры нет в таблице — посчитайте её плотность пикселей, найдите ближайшее к нему значение другой камеры и посмотрите DLA.
Mpix (35mm) — сколько мегапикселей было бы на сенсоре с такой плотностью пикселей, если бы его увеличили до размера сенсора 35×24мм.
q, pix/mm — плотность пикселей на матрице
Res, lp/mm — разрешение матрицы при допущении, что она линия это одна черная и одна белая линия (идеальный случай). Вменяемого ответа как считать разрешение матрицы в lp/mm нет. Кто-то считает, что только из 3-х пикселей можно различить переход черный/белый.
| Наименование камеры | Sens | Tech | Размер сенсора, мм | Res, Mpix | Разрешение, пикс | Размер сенселя, мкм | Q, pix/mm | Res матрицы, lp/mm | Расчётная DLA | фактическая DLA | Mpix (35mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Canon 1D X | Canon | CMOS | 36 x 24 | 18 | 5184 x 3456 | 6,9 | 144 | 72 | 11,1 | 18 | |
| Canon EOS 1Ds Mark III | Canon | CMOS | 36 x 24 | 21 | 5616 x 3744 | 6,9 | 156 | 78 | 10,3 | 21 | |
| Canon EOS 1Ds Mark II | Canon | CMOS | 36 x 24 | 16 | 4992 x 3328 | 7,2 | 11. 8 8 | ||||
| Canon EOS 1Ds | Canon | CMOS | 35,8 x 23,8 | 11 | 4064 x 2704 | 8,8 | 14,2 | 11,1 | |||
| Canon EOS 1D Mark IV | Canon | CMOS | 27,9 x 18,6 | 16 | 4896 x 3264 | 5,7 | 175 | 87 | 7,4 | 26,6 | |
| Canon EOS 1D Mark III | Canon | CMOS | 28,1 x 18,7 | 10 | 3888 x 2592 | 138 | 69 | 9,3 | |||
| Canon EOS 1D Mark II N, Canon EOS 1D Mark II | Canon | CMOS | 28,7 x 19,1 | 8 | 3520 x 2336 | 8,2 | 122 | 61 | 10,4 | ||
| Canon EOS 1D | Kodak | CCD | 28,7 x 19,1 | 4 | 2464 x 1648 | 11,6 | 14,8 | 6,4 | |||
| Canon 5Ds / Canon 5DsR | Canon | CMOS | 36 x 24 | 50 | 8688 x 5792 | 4,14 | 241 | 121 | 6,7 | 16 | 50 |
| Canon EOS 5D Mark III | Canon | CMOS | 36 x 24 | 21 | 5760 x 3840 | 6,25 | 156 | 78 | 10,3 | 22 | 21 |
| Canon EOS 5D mark II | Canon | CMOS | 36 x 24 | 21 | 5616 x 3744 | 6,4 | 156 | 78 | 10,3 | 22 | 21 |
| Canon EOS 6D | Canon | CMOS | 35,8 x 23,9 | 20 | 5472 x 3648 | 6,54 | 152 | 76 | 10,3 | 22 | 21 |
| Canon 5D | Canon | CMOS | 35,8 x 23,9 | 12 | 4368 x 2912 | 8,2 | 122 | 61 | 13,6 | 12 | |
| Canon 7D mark II | Canon | CMOS | 22,5 x 15,0 | 20 | 5472 x 3648 | 4,11 | 243 | 122 | 6,6 | ||
| Canon 7D | Canon | CMOS | 22,3 x 14,9 | 18 | 5184 x 3456 | 4,3 | 232 | 116 | 7 | ||
| Canon EOS 70D | Canon | CMOS | 22,5 x 15,0 | 20 | 5472 x 3648 | 4. 1 1 | 243 | 122 | 6,6 | ||
| Canon 550D, 600D, 650D, 700D, 1200D | Canon | CMOS | 22,3 x 14,9 | 18 | 5184 x 3456 | 4,3 | 232 | 116 | 7 | ||
| Canon 500D / 50D | Canon | CMOS | 22,3 x 14,9 | 15 | 4752 x 3168 | 4,7 | 213 | 106 | 7,6 | ||
| Canon 450D, 1100D | Canon | CMOS | 22,2 x 14,8 | 12 | 4272 x 2848 | 5,2 | 8,5 | ||||
| Canon 400D, 1000D | Canon | CMOS | 22,2 x 14,8 | 10 | 3888 x 2592 | 5,7 | 9,3 | ||||
| Canon 350D / 20D / 30D | Canon | CMOS | 22,5 x 15 | 8 | 3504 x 2336 | 6,4 | 156 | 78 | 10,4 | 20,9 | |
| Canon 300D / 10D / D60 | Canon | CMOS | 22,7 x 15,1 | 6 | 3072 x 2048 | 7,4 | 12,4 | 15,5 | |||
| Canon EOS M | Canon | CMOS | 22,3 x 14,9 | 18 | 5184 x 3456 | 4,3 | 232 | 116 | |||
| Canon PowerShot G1 X | Canon | CMOS | 18,7 x 14,0 | 14 | 4352 x 3264 | 4,3 | 232 | 116 | 6,9 | ||
| Canon PowerShot G12 | Canon | CMOS | 7,4 x 5,6 | 10 | 3648 x 2048 | 2,7 | 493 | 246 | 4,3 | ||
| Canon PowerShot G9 | Canon | CMOS | 7,6 x 5,7 | 12 | 4000 x 3000 | 2,5 | 526 | 263 | 4,0 | ||
| Nikon D4 | ? | CMOS | 36 x 24 | 16 | 4928 x 3280 | 7,3 | 137 | 68 | 16 | ||
| Nikon D3X | ? | CMOS | 35,9 x 24 | 24 | 6048 x 4032 | 5,9 | 9,9 | 24,4 | |||
| Nikon D800 | Sony | CMOS | 35,9 x 24 | 36 | 7360 x 4912 | 4,9 | 205 | 103 | 36 | ||
| Nikon D700 / D3 / D3s | ? | CMOS | 36,0 x 23,9 | 12 | 4256 x 2832 | 8,4 | 14,1 | 12,2 | |||
| Nikon D7100 | ? | CMOS | 23,5 x 15,6 | 24 | 6000 x 4000 | 3,9 | 255 | 128 | 5,9 | ||
| Nikon D7000 | ? | CMOS | 23,6 х 15,6 | 16 | 4928 x 3264 | 4,79 | 209 | 104 | 7,1 | ||
| Nikon D5000 / D90 / D300 / D300s / D2X / D2Xs | Sony | CMOS | 23,7 x 15,6 | 12 | 4288 x 2848 | 5,4 | 9 | 28,8 | |||
| Nikon D3000 / D40x / D60 / D80 / D200 | Sony | CCD | 23,6 x 15,8 | 10 | 3872 x 2592 | 6,1 | 10,3 | 23,4 | |||
| Nikon D1/D1H | Sony | CCD | 23,7 x 15,5 | 2,6 | 2000 x 1312 | 11,9 | 20 | 6,2 | |||
| Nikon D40 / D50 / D70 / D100 | Sony | CCD | 23,7 x 15,5 | 6 | 3008 x 2000 | 7,8 | 13,1 | 14,0 | |||
| Nikon D2H | Nikon | JFET | 23,7 x 15,5 | 4 | 2464 x 1632 | 9,6 | 16,1 | 9,3 | |||
| Sony A900 / A850 | Sony | CMOS | 35,9 x 24 | 24 | 6048 x 4032 | 5,9 | 9,9 | 24 | |||
| Sony A7 | Sony | CMOS | 35,8 x 23,9 | 24 | 6000 x 4000 | 5,97 | 168 | 84 | 24 | ||
| Sony NEX 5R | Sony | CMOS | 23,5 x 15,6 | 16 | 4912 x 3264 | 4,78 | 209 | 105 | |||
| Olympus E-5 | ? | 17,3 x 13,0 | 12 | 4032 x 3024 | 4,3 | 233 | 117 | ||||
| Olympus OM-D E-M10 Mark II | ? | 17,3 x 13,0 | 16 | 4608 x 3456 | 3,75 | 266 | 133 | 61 | |||
| FUJIFILM GFX 100 | Sony | CMOS | 43,8 x 32,9 | 102 | 11648 x 8736 | 3,76 | 266 | 133 | 5,6 | 61 | |
| FUJIFILM GFX 50s | Sony | CMOS | 43,8 x 32,9 | 50 | 8256 x 6192 | 5,3 | 188 | 94 | 8 | 31 | |
| Fuji X-E2 | ? | 23,6 x 15,6 | 16 | 4896 x 3264 | 4,82 | 207 | 104 | ||||
| PhaseOne P65+ | ? | 54,9 x 40,4 | 60 | 8984 x 6732 | 6,1 | 164 | 82 | ||||
| Leica S2 | Kodak | 45 x 30 | 37 | 7500 x 5000 | 6,0 | 10,0 | 22 | ||||
| Leica M9 | Kodak | 36 x 24 | 18 | 5212 x 3472 | 6,9 | 145 | 72 | 18 | |||
| Leica M8 | Kodak | 26,8 x 17,9 | 10 | 3936 x 2630 | 6,8 | 11,4 | 18 | ||||
| Hasselblad h4DII-50 | Kodak | 49,1 x 36,8 | 50 | 8176 x 6132 | 6,0 | 10,0 | 22 | ||||
| Hasselblad h4DII-39 | Kodak | 49,1 x 36,8 | 39 | 7212 x 5412 | 6,8 | 11,4 | 18 | ||||
| Hasselblad h4DII-31 | Kodak | 44,2 x 33,1 | 31 | 6496 x 4872 | 6,8 | 11,4 | 18 | ||||
| Hasselblad H6D-100c | Sony | CMOS | 53,4 x 40 | 100 | 11600 x 8700 | 4,6 | 217 | 109 | 7 | 41 |
aperture — Какой-то «дифракционный предел и»?
думаю, что сцены как состоит из многих В небольших дискретных точек света.
 Вы понимаете, что каждый из этих точек, когда сфокусирован объектив, создает свой собственный Эйри на средних изображений.
Что Касается Среднего Изображения
Вы понимаете, что каждый из этих точек, когда сфокусирован объектив, создает свой собственный Эйри на средних изображений.
Что Касается Среднего ИзображенияОно также должно быть четко указано, что дифракция ограничения на самом деле не ограничение объектива. Как отмечалось выше, линзы всегда в создании дифракционной картины, только отчасти, что изменения в модели в качестве объектива остановился вниз. В «лимит» из дифракции является функцией среднего визуализации. Датчик с меньшим фотосайты, или пленки с меньшим зерном, будет иметь нижний предел дифракции, чем те, с более крупными светочувствительными элементами/зерновые. Это связано с тем, что меньше собирают крышки меньше площади диска Эйри чем более крупной ячейкой. Когда Эйри увеличивается в размерах и интенсивности как линза остановлена вниз, диска Эйри влияет на соседние ячейки.
В дифракционного предела — это точка, где диска Эйри расти достаточно большой, что они начинают влиять более чем на одну ячейку. Другой способ смотреть на это, когда диска Эйри от двух точечных источников света разрешимое датчика начинают сливаться. На широкой диафрагмой, два точечных источников света изображается с помощью датчика может затронуть только один соседних ячеек. Когда диафрагма закрывается, диска Эйри, созданных каждым точечным источником света растет, причем наружные кольца каждого Эйри начинают сливаться. Это та точка, где датчиком является «дифракционное» и, поскольку отдельные точечные источники света не разрешается в один фотоэлемент…они сливаются и охватывают более, чем одну ячейку. Точка, в которой центр каждого воздушного сливает диске-разрешение, и вы не сможете решить любую мелкую деталь, независимо от используемой диафрагмы. Это дифракция частоты среза. Следует отметить, что это возможно для объектива для устранения небольших пятна пиксели в среде визуализации. Это тот случай, когда диска Эйри сосредоточены крышкой объектива только доля фотоэлемент. В этом случае, даже если два высокого разрешения точечных источников света генерировать светлые диски, которые сливаются в один фотоэлемент, конечный результат будет тот же.
Другой способ смотреть на это, когда диска Эйри от двух точечных источников света разрешимое датчика начинают сливаться. На широкой диафрагмой, два точечных источников света изображается с помощью датчика может затронуть только один соседних ячеек. Когда диафрагма закрывается, диска Эйри, созданных каждым точечным источником света растет, причем наружные кольца каждого Эйри начинают сливаться. Это та точка, где датчиком является «дифракционное» и, поскольку отдельные точечные источники света не разрешается в один фотоэлемент…они сливаются и охватывают более, чем одну ячейку. Точка, в которой центр каждого воздушного сливает диске-разрешение, и вы не сможете решить любую мелкую деталь, независимо от используемой диафрагмы. Это дифракция частоты среза. Следует отметить, что это возможно для объектива для устранения небольших пятна пиксели в среде визуализации. Это тот случай, когда диска Эйри сосредоточены крышкой объектива только доля фотоэлемент. В этом случае, даже если два высокого разрешения точечных источников света генерировать светлые диски, которые сливаются в один фотоэлемент, конечный результат будет тот же. ..датчик будет определять только одну точку света, независимо от диафрагмы. В «дифракционный предел» у такого датчика будет выше (скажем, на F/16), чем на датчик, который способен четко решить обе точечных источников света (что может быть дифракционный предел на F/8). Это также возможно, и скорее всего ссылки источники света не будут вполне сосредоточены на центре фотоэлемент. Вполне правдоподобно для Эйри быть сосредоточены на границе между двумя фотосайты, или на перекрестке четырех ячеек. В черно-белом или датчик факты следует учитывать (наборный цвет sensels), это было единственной причиной размягчения. В датчик цвета «Байера», где квадратный узел 4 фотосайты будет захватывать чередование цветов GRGB, как Эйри могут повлиять на конечный цвет с помощью четырех фотоэлементов, а также причиной размягчения или ненадлежащее разрешение.
Мой Кэнон 450Д, на 12,2 Мп APS-C сенсор, имеет дифракционный предел на F/8.4. В отличие от канона 5D Марк II, в 21.1 Мп полнокадровый сенсор, имеет дифракционный предел на F/10.
..датчик будет определять только одну точку света, независимо от диафрагмы. В «дифракционный предел» у такого датчика будет выше (скажем, на F/16), чем на датчик, который способен четко решить обе точечных источников света (что может быть дифракционный предел на F/8). Это также возможно, и скорее всего ссылки источники света не будут вполне сосредоточены на центре фотоэлемент. Вполне правдоподобно для Эйри быть сосредоточены на границе между двумя фотосайты, или на перекрестке четырех ячеек. В черно-белом или датчик факты следует учитывать (наборный цвет sensels), это было единственной причиной размягчения. В датчик цвета «Байера», где квадратный узел 4 фотосайты будет захватывать чередование цветов GRGB, как Эйри могут повлиять на конечный цвет с помощью четырех фотоэлементов, а также причиной размягчения или ненадлежащее разрешение.
Мой Кэнон 450Д, на 12,2 Мп APS-C сенсор, имеет дифракционный предел на F/8.4. В отличие от канона 5D Марк II, в 21.1 Мп полнокадровый сенсор, имеет дифракционный предел на F/10. 3. Более крупный сенсор, несмотря на то, что почти в два раза больше мегапикселей, может идти лишнюю остановку, прежде чем она встречает своего дифракционного предела. Это происходит потому, что физический размер фотосайты на 5Д II больше, чем на 450Д. (Хороший пример одного из многочисленных преимуществ больше датчиков.) Гайковерты в смеси Вы часто можете встретить таблицы в интернете, что указать определенный дифракционный предел диафрагмы для определенных форматов. Я часто вижу Ф/16 используется для APS-C сенсоров, и F/22 для полного кадра. В цифровом мире, эти цифры, как правило, бесполезно. Дифракционного ограничения диафрагмы (дла) является в конечном счете функцией отношения величины целенаправленной точка света (в том числе картина Эйри) размер один источник света, чувствительный элемент на датчике. Для любого заданного размера датчик APS-C и полный кадр, дифракционный предел будет меняться в зависимости от размера ячейки. Пример этого можно увидеть с Canon’ы ЭОС повстанческие линии камер на протяжении многих лет:
3. Более крупный сенсор, несмотря на то, что почти в два раза больше мегапикселей, может идти лишнюю остановку, прежде чем она встречает своего дифракционного предела. Это происходит потому, что физический размер фотосайты на 5Д II больше, чем на 450Д. (Хороший пример одного из многочисленных преимуществ больше датчиков.) Гайковерты в смеси Вы часто можете встретить таблицы в интернете, что указать определенный дифракционный предел диафрагмы для определенных форматов. Я часто вижу Ф/16 используется для APS-C сенсоров, и F/22 для полного кадра. В цифровом мире, эти цифры, как правило, бесполезно. Дифракционного ограничения диафрагмы (дла) является в конечном счете функцией отношения величины целенаправленной точка света (в том числе картина Эйри) размер один источник света, чувствительный элемент на датчике. Для любого заданного размера датчик APS-C и полный кадр, дифракционный предел будет меняться в зависимости от размера ячейки. Пример этого можно увидеть с Canon’ы ЭОС повстанческие линии камер на протяжении многих лет:
Создан оптический микроскоп, преодолевающий дифракционный предел для видимого света
Ученые создали оптический микроскоп, который способен преодолеть дифракционный предел для видимого света — фундаментальное ограничение, которое накладывает запрет на минимальный размер разрешаемых при помощи микроскопа объектов. Работа исследователей появилась в журнале Nature Communications, а коротко о ней пишет Wired.
Работа исследователей появилась в журнале Nature Communications, а коротко о ней пишет Wired.Из-за дифракционного предела в микроскоп нельзя рассмотреть объекты, размер которых меньше половины длины волны используемого излучения. Для оптической микроскопии — то есть длин волн, различимых человеческим глазом, предельный размер объекта составляет около 200 нанометров. Примерно таков размер крупных вирусов и самых мелких бактерий. Для того чтобы изучать более миниатюрные объекты, ученые используют электронную и рентгеновскую микроскопию, а также новые методы, основанные на использовании метаматериалов (так называемые суперлинзы). Третий метод пока не вошел в повседневную практику, а первые два не позволяют исследовать живые объекты in situ — во время подготовки препарата они неизбежно погибают.
Для усиления «зоркости» оптического микроскопа авторы новой работы использовали так называемые исчезающие волны. Этим термином обозначают волны, испускаемые освещенным объектом, которые чрезвычайно быстро затухают с расстоянием.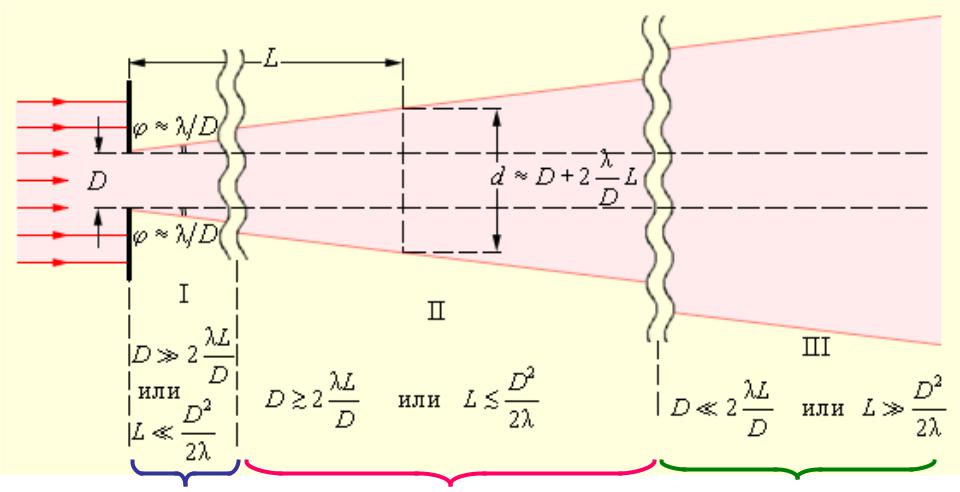 Чтобы получить большое количество таких волн, физики размещали на поверхности изучаемого объекта большое количество крошечных гранул из оксида кремния размером от 2 до 9 микрометров (микрометр — это одна миллионная часть метра).
Чтобы получить большое количество таких волн, физики размещали на поверхности изучаемого объекта большое количество крошечных гранул из оксида кремния размером от 2 до 9 микрометров (микрометр — это одна миллионная часть метра).
Гранулы собирают свет, проходящий сквозь образец, а возникающие на их поверхности исчезающие волны фокусируются таким образом, чтобы они собирались при помощи стандартных линз, используемых в оптической микроскопии. Детали эксперимента уточняет BBC News.
Такая стратегия позволила ученым разглядеть объекты размером до 50 нанометров. Так, исследователи получили четкие изображения желобков, остающихся после записи информации на дисках Blu-ray, а также отверстия в золотой фольге диаметром около 50 нанометров.
Коллеги исследователей отнеслись к их работе с большим энтузиазмом, однако отметили, что пока ее нельзя назвать завершенной. Так, специалисты отмечают, что авторы не продемонстрировали возможности своего микроскопа для изучения живых систем — например, вирусов или бактерий. Эти объекты постоянно движутся, поэтому к задаче получить собственно изображение добавляется необходимость сфокусироваться.
Эти объекты постоянно движутся, поэтому к задаче получить собственно изображение добавляется необходимость сфокусироваться.
Источник: Lenta.ru
Дифракционный предел разрешения оптических инструментов
Для практики наиболее интересен случай дифракции света, когда препятствие оставляет открытой лишь малую часть 1-й зоны Френеля. Этот случай реализуется при условии
то есть дифракционную картину от препятствий небольшого размера следует в этом случае наблюдать на очень больших расстояниях. Например, если R = 1 мм, λ = 550 нм (зеленый свет), то расстояние L до плоскости наблюдения должно быть значительно больше 2 метров (то есть минимум 10 метров или больше). Лучи проведенные в далекую точку наблюдения от различных элементов волнового фронта, практически можно считать параллельными. Этот случай дифракции так и называется – дифракция в параллельных лучах или дифракция Фраунгофера – по имени немецкого физика И. Фраунгофера, современника Френеля. Если на пути лучей за препятствием поставить собирающую линзу, то параллельный пучок лучей, дифрагировавший на препятствии под углом θ, соберется в некоторой точке фокальной плоскости (рис. 6.9.1). Следовательно, любая точка в фокальной плоскости линзы эквивалентна бесконечно удаленной точке в отсутствие линзы.
Этот случай дифракции так и называется – дифракция в параллельных лучах или дифракция Фраунгофера – по имени немецкого физика И. Фраунгофера, современника Френеля. Если на пути лучей за препятствием поставить собирающую линзу, то параллельный пучок лучей, дифрагировавший на препятствии под углом θ, соберется в некоторой точке фокальной плоскости (рис. 6.9.1). Следовательно, любая точка в фокальной плоскости линзы эквивалентна бесконечно удаленной точке в отсутствие линзы.
| 1 |
| Рисунок 6.9.1. Дифракция в параллельных лучах. Зеленая кривая – распределение интенсивности в фокальной плоскости (масштаб по оси x сильно увеличен). |
В фокальной плоскости линзы наблюдается дифракционная картина Фраунгофера. Но согласно геометрической оптике, в фокусе линзы должно располагаться точечное изображение удаленного точечного предмета. На самом деле изображение точечного предмета оказывается размытым из-за дифракции. В этом проявляется волновая природа света. Никакая оптическая система не может дать точечного изображения. В случае дифракции Фраунгофера на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец (рис. 6.9.2). Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен
В этом проявляется волновая природа света. Никакая оптическая система не может дать точечного изображения. В случае дифракции Фраунгофера на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец (рис. 6.9.2). Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен
Если лучи света от удаленного источника падают на линзу непосредственно, то роль экрана, на котором дифрагирует свет, выполняет оправа линзы. В этом случае под D нужно понимать диаметр линзы.
| 2 |
Рисунок 6.9. 2. Дифракционное изображение точечного источника (дифракция на круглом отверстии). В центральное пятно попадает приблизительно 85 % энергии света. 2. Дифракционное изображение точечного источника (дифракция на круглом отверстии). В центральное пятно попадает приблизительно 85 % энергии света. |
Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Во многих оптических устройствах (фотоаппараты, проекторы и т. д.) дифракционное размытие изображений маскируется значительно более сильными искажениями из-за несовершенства оптики. Но в высокоточных астрономических приборах реализуется дифракционный предел качестваизображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимы от изображения одной точки. Рассмотрим в качестве примера объектив астрономического телескопа, нацеленного на две близкие звезды, находящиеся на угловом расстоянии ψ друг от друга. Предполагается, что все дефекты и аберрации устранены, и в фокальной плоскости объектива наблюдаются дифракционные изображения звезд (рис.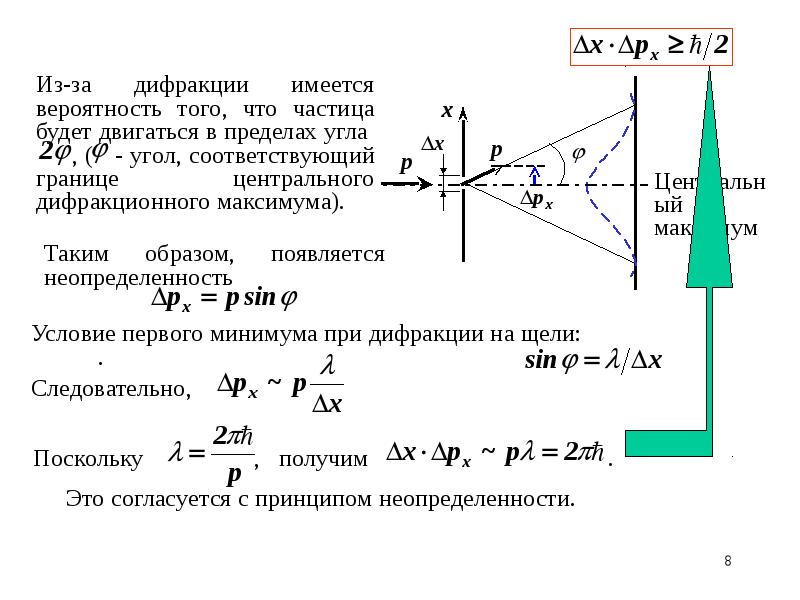 6.9.3).
6.9.3).
| 3 |
| Рисунок 6.9.3. Дифракционные изображения двух близких звезд в фокальной плоскости объектива телескопа. |
На рис. 6.9.3 расстояние Δl между центрами дифракционных изображений звезд превышает радиус r центрального светлого пятна – в этом случае изображения звезд воспринимаются наблюдателем раздельно и, следовательно, объектив телескопа позволяет разрешить две близкие звезды. При уменьшении углового расстояния ψ между звездами дифракционные изображения могут сильно перекрыться и перестанут отличаться от изображения одиночной звезды. В этом случае объектив телескопа не разрешает близкие звезды. Английский физик Дж. Релей в конце XIX в. предложил условно считать разрешение полным, когда расстояния Δl между центрами изображений равно (или превышает) радиус r диска Эйри (рис. 6.9.4). Условие Δl = r называют критерием разрешения Релея. Из этого критерия следует:
Телескоп с диаметром объектива D = 1 м способен разрешать две звезды, находящиеся на угловом расстоянии ψmin = 6,7·10–7 рад (для λ = 550 нм).
| 4 |
| Рисунок 6.9.4. Предел разрешения по Релею. Красная кривая – распределение суммарной интенсивности света. |
Космический телескоп Хаббла, выведенный на орбиту в 1990 году, имеет зеркало диаметром D = 2,40 м. Предельное угловое разрешение этого телескопа по длине волны λ = 550 нм равно: ψmin = 2,8·10–7 рад. На работу космического телескопа не оказывают влияния атмосферные возмущения. Для характеристики объектива телескопа можно ввести величину R, обратную предельному углу ψmin. Эту величину называютразрешающей силой телескопа:
Для увеличения разрешающей способности телескопа следует увеличивать диаметр объектива (либо переходить к более коротким волнам). Все сказанное выше о разрешающей способности телескопа применимо и к невооруженному глазу. Глаз при рассматривании удаленных предметов действует так же, как и объектив телескопа. Роль D играет диаметр зрачка глаза dзр. Полагая dзр = 3 мм, λ = 550 нм, найдем для предельного углового разрешения глаза
Глаз при рассматривании удаленных предметов действует так же, как и объектив телескопа. Роль D играет диаметр зрачка глаза dзр. Полагая dзр = 3 мм, λ = 550 нм, найдем для предельного углового разрешения глаза
Этот результат хорошо согласуется с физиологической оценкой разрешающей способности глаза, выполненной исходя из размеров светочувствительных элементов сетчатки (палочек и колбочек). Теперь можно сделать один общий вывод: световой пучок диаметром D и длиной волны λ вследствие волновой природы света испытывает дифракционное уширение. Угловая полуширина φ пучка оказывается порядка λ / D, так что полная ширина d пучка на расстоянии L приблизительно равна
Рис.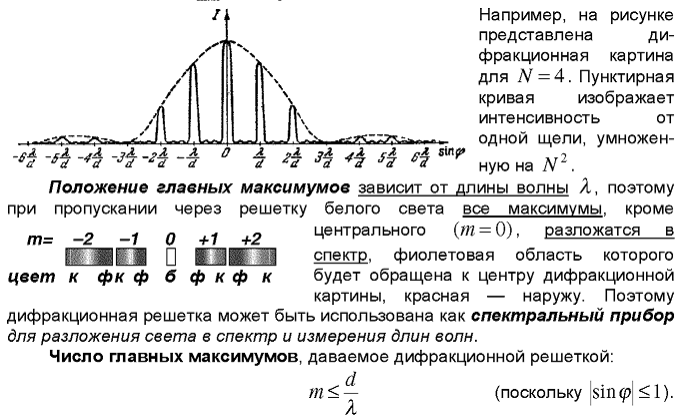 6.9.5 качественно показывает, как по мере удаления от препятствия трансформируется пучок света.
6.9.5 качественно показывает, как по мере удаления от препятствия трансформируется пучок света.
| 5 |
| Рисунок 6.9.5. Пучок света, расширяющийся вследствие дифракции. Область I – понятие луча света, законы геометрической оптики. Область II – зоны Френеля, пятно Пуассона. Область III – дифракция в параллельных лучах. |
Оценки, выполненные на рис. 6.9.5, показывают, что угловое расхождение пучка уменьшается при увеличении его первоначального поперечного размера D. Этот вывод справедлив для волн любой физической природы. Чтобы, например, послать «узкий» пучок лазерного излучения на Луну, нужно сначала его расширить. Это достигается с помощью телескопа, когда лазерный пучок направляется в окуляр и затем, пройдя через телескоп, выходит из объектива, имея диаметр D (рис. 6.9.6).
| 6 |
Рисунок 6.9.6. Расширение лазерного пучка с помощью телескопической системы. |
Такой расширенный пучок, дойдя до Луны, «засветит» на ее поверхности пятно радиусом где L – расстояние до Луны. Приняв D = 2,5 м (телескоп-рефлектор Крымской обсерватории), λ = 550 нм, L = 4·106 м, получим R ≈ 90 м. Если бы на Луну был направлен первоначальный пучок лазерного света, имеющий диаметр порядка 1 см, то он «засветил» бы на Луне пятно, радиус которого оказался бы в 250 раз больше. Разрешающая способность микроскопа. С помощью микроскопа наблюдают близко расположенные объекты, поэтому его разрешающаяся способность характеризуется не угловым, а линейным расстоянием между двумя близкими точками, которые еще могут восприниматься раздельно. Наблюдаемый объект располагается вблизи переднего фокуса объектива. Часто пространство перед объективом заполняется специальной прозрачной жидкостью – иммерсией (рис. 6.9.7). В плоскости, геометрически сопряженной объекту, располагается его увеличенное изображение, которое рассматривается глазом через окуляр.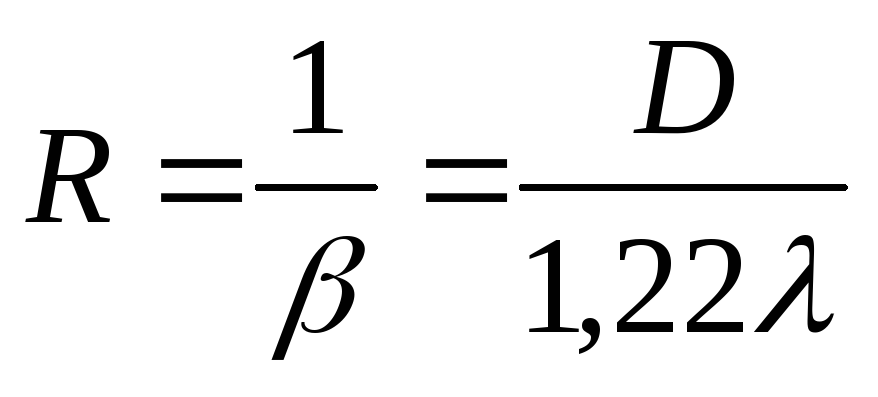 Изображение каждой точки оказывается размытым вследствие дифракции света.
Изображение каждой точки оказывается размытым вследствие дифракции света.
| 7 |
| Рисунок 6.9.7. Иммерсионная жидкость перед объективом микроскопа. |
Впервые предел разрешения объектива микроскопа был определен немецким физиком Г. Гельмгольцем (1874 г.). Формула Гельмгольца имеет вид:
Здесь λ – длина волны, n – показатель преломления иммерсионной жидкости, α – так называемый апертурный угол (рис. 6.9.7). Величина n sin α называется числовой апертурой. У хороших микроскопов апертурный угол α близок к своему пределу: α ≈ π / 2. Как видно из формулы Гельмгольца, применение иммерсии несколько улучшает предел разрешения. Полагая для оценок sin α ≈ 1, n ≈ 1,5, получим:
lmin ≈ 0,4 λ. Таким образом, с помощью микроскопа принципиально невозможно рассмотреть какие-либо детали, размер которых значительно меньше длины света. Волновые свойства света определяют предел качества изображения объекта, полученного с помощью любой оптической системы.
Волновые свойства света определяют предел качества изображения объекта, полученного с помощью любой оптической системы.
Лазерная наногравировка позволяет преодолеть дифракционный предел
В лаборатории нанобиофотоники Института химической физики РАН получены многообещающие результаты в области микро- и наногравировки поверхностей с использованием импульсного лазерного излучения.
Во многих областях техники возникает необходимость создать заданный микрорельеф. Это бывает нужно для схем микрофлюидики, при производстве оптических микросенсоров, оптических интегральных микросхем или их элементов: фотонных кристаллов, волноводов, микролазеров.
Сложность такой работы в том, что при нанесении гравировки и при контроле результата оптическими методами их точность (пространственное разрешение) ограничена так называемым дифракционным пределом.
Дифракционный пределВ обыденной жизни видимые нами предметы имеют более или менее контрастные очертания, а распределение света и тени дает представление о форме предмета и даже о фактуре его поверхности. Все это возможно только потому, что свет, играющий роль «щупа» в нашем визуальном восприятии, имеет чрезвычайно малую длину волны.
Все это возможно только потому, что свет, играющий роль «щупа» в нашем визуальном восприятии, имеет чрезвычайно малую длину волны.
Сталкиваясь с препятствием, размеры которого сравнимы с длиной волны, свет будет огибать его, проникая в область геометрической тени (именно это явление первоначально и называлось дифракцией). Попадая на узкую щель, свет будет расходиться по разным направлениям, а не только в направлении первоначального движения. Две точки, от которых идет свет, будут практически неразличимы, если расстояние между ними меньше половины длины волны. Именно это расстояние и называется дифракционным пределом.
Иными словами, возможность отличить друг от друга две близко расположенных точки определяется не свойствами оптического прибора, а свойствами самого света. Кстати, это одна из причин, по которой в физических исследованиях часто используют коротковолновое излучение — в ультрафиолетовом или рентгеновском диапазоне. Для видимого же света предел пространственного разрешения около 200-400 нм.
Описанная проблема, таким образом, возникает из-за наличия у света волновых свойств. При переходе к мелким пространственным масштабам свет оказывается не совокупностью бесконечно тонких прямолинейных лучей, отражаемых и преломляемых под четко определенными углами, а волнами, расходящимися во все стороны, как круги по воде.
В физике это называют переходом от геометрической оптики к оптике волновой. Однако волновая оптика тоже является предельным случаем общего электромагнитного описания явлений. Она работает на больших расстояниях от источника излучения, в так называемом дальнем поле. В непосредственной же близости от источника (а таковым в оптике будет любая отражающая свет поверхность), в так называемом ближнем поле, распределение электрического и магнитного полей будет подчиняться совсем иным закономерностям.
Ближнее поле хорошо изучено в радиофизике, где оно может составлять метры и более вокруг излучающей антенны и относительно легко доступно для исследования.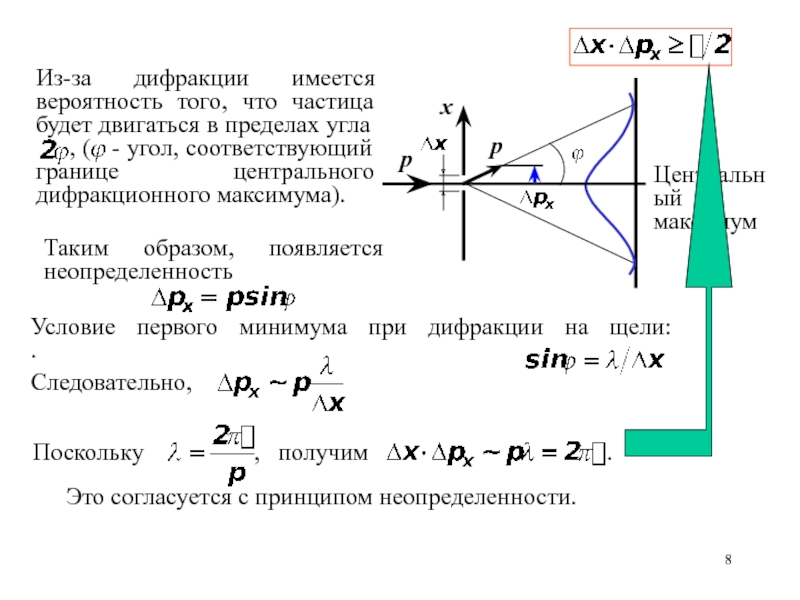 Сама идея использовать принципы физики ближнего поля в оптической микроскопии возникла еще в 1920-х годах. Но лишь в начале 1980-х годов были получены первые оптические изображения с разрешением в 20 раз меньше длины волны.
Сама идея использовать принципы физики ближнего поля в оптической микроскопии возникла еще в 1920-х годах. Но лишь в начале 1980-х годов были получены первые оптические изображения с разрешением в 20 раз меньше длины волны.
Принципы ближнепольной оптики можно применить не только для получения микроскопических изображений поверхности, но и, наоборот, для создания на ней нужного нам распределения электромагнитных полей — для ее обработки. Для этой цели в качестве микролинз ближнего поля мы применили кварцевые микрошарики размером порядка 1 микрона.
Производство кварцевых микрошариков (glass microspheres) началось еще в 1950-х годах. Простые и дешевые в изготовлении, сейчас они используются в разных целях в нефте- и горнодобывающей промышленности, при производстве красок и строительных материалов, косметики и разнообразных потребительских товаров. Небольшие вариации в диаметре и сферичности микрошариков не сказываются на разрешении и точности получаемых изображений.
Замечательно то, что эти шарики можно захватить лазерным излучением: при высокочастотном (более 80 МГц) импульсном лазерном излучении диэлектрическая кварцевая частица втягивается в область наиболее интенсивного электромагнитного поля в лазерном луче. Этот эффект в последние годы широко используется в самых разных областях науки и техники и известен как «лазерный пинцет» или «оптическая ловушка». В нашем случае один и тот же лазерный луч может использоваться и для воздействия на вещество поверхности, и для управления кварцевой частицей.
Ближнепольная фотохимияРаспределение интенсивности излучения в световом пятне, полученном в ближнем поле такой микролинзы, будет иметь заметный градиент (см. рис.). Можно подобрать параметры излучения (интенсивность, длительность воздействия импульса и некоторые другие) так, что в нужной нам области лазерное излучение окажет нужное нам тепловое, термохимическое или фотохимическое действие на материал. Причем размер этой области может быть гораздо меньше, чем дифракционный предел.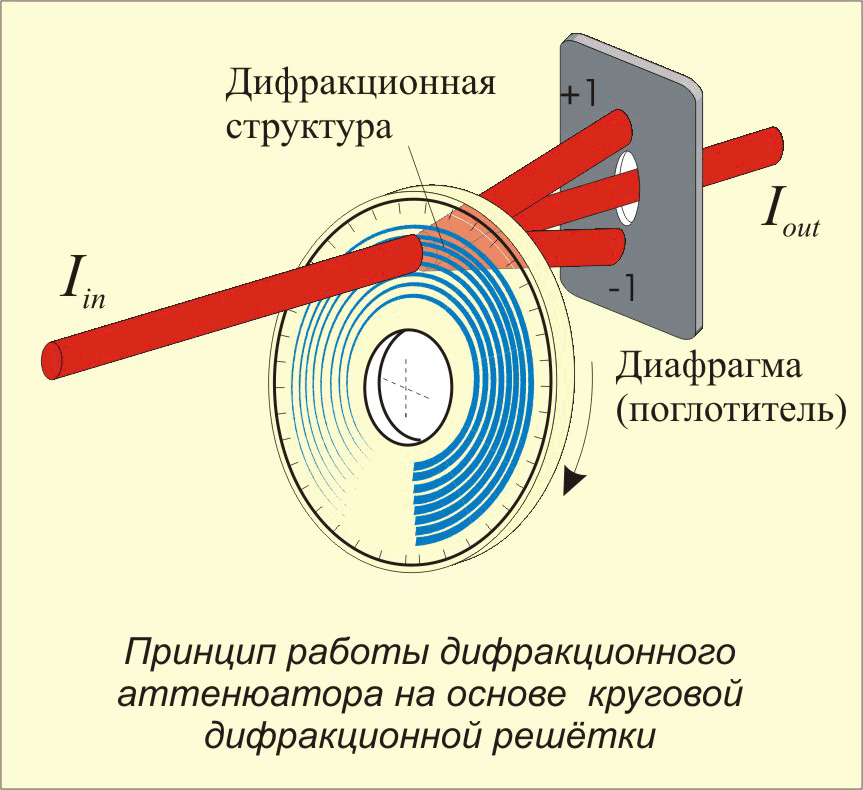 Нам уже удалось уменьшить размер области, которую мы способны обработать лазерным излучением, до 1/8-1/11 длины волны, вместо «стандартного» предела в 1/2.
Нам уже удалось уменьшить размер области, которую мы способны обработать лазерным излучением, до 1/8-1/11 длины волны, вместо «стандартного» предела в 1/2.
При этом лазер отнюдь не прожигает освещаемый им участок поверхности, а вызывает его химическую модификацию. Например, если мы воздействуем излучением на поверхность кварца (представляющего собой оксид кремния, SiO2), то она теряет кислород. Сначала после обработки поверхности кварца лазером на ней возникают микропики (в месте точечного воздействия лазерного луча) или микровалы (по ходу лазерного луча). Происходит это из-за теплового расширения кварца и его «вскипания» при выделении кислорода. И лишь после последующего травления щелочью, вымывающей кремний, на микрорельефе кварца на месте пиков возникают ямки, а на месте валов — траншеи (см. рис.).
С учетом пространственного разрешения (десятки нанометров) наш метод следовало бы назвать наногравировкой (в научном лексиконе чаще используется термин наноструктурирование поверхности). В настоящее время структурирование поверхности в таких пространственных масштабах возможно только с помощью ионной или ультрафиолетовой литографии, однако эти технологии несравнимо дороже и сложнее в использовании. Технология, описанная здесь, открывает широкие возможности для развития целого нового направления, известного как Lab-on-a-chip («лаборатория на чипе») и чрезвычайно востребованного в последнее время не только в научных, но и, например, в медицинских задачах.
В настоящее время структурирование поверхности в таких пространственных масштабах возможно только с помощью ионной или ультрафиолетовой литографии, однако эти технологии несравнимо дороже и сложнее в использовании. Технология, описанная здесь, открывает широкие возможности для развития целого нового направления, известного как Lab-on-a-chip («лаборатория на чипе») и чрезвычайно востребованного в последнее время не только в научных, но и, например, в медицинских задачах.
Василий Птушенко, кандидат физико-математических наук;
Александр Шахов, кандидат физико-математических наук;
Артем Астафьев, кандидат физико-математических наук;
Виктор Надточенко, доктор химических наук, профессор, Институт химической физики РАН
Ультрафиолетовая литография
— нанесение на поверхность полимерного светочувствительного материала (фоторезиста), который под воздействием ультрафиолетового излучения становится растворимым и удаляется растворителем. Используются «глубокое» (deep ultra violet, DUV) или «жесткое» (extreme ultra violet, EUV) ультрафиолетовое излучение с длинами волны около 200 нм или 13,5 нм соответственно. Технология обеспечивает разрешение до нескольких нанометров. Есть и ряд недостатков: сложность и дороговизна получения EUV достаточно высокой мощности, поглощение EUV практически любыми материалами, в том числе и компонентами оптических схем, необходимость работы в вакууме.
Технология обеспечивает разрешение до нескольких нанометров. Есть и ряд недостатков: сложность и дороговизна получения EUV достаточно высокой мощности, поглощение EUV практически любыми материалами, в том числе и компонентами оптических схем, необходимость работы в вакууме.
Ионная (или ионно-лучевая) литография — нанесение изображения на поверхность с помощью пучков ионов, как правило, протонов или альфа-частиц. В силу высокой чувствительности материалов к облучению потоком относительно тяжелых заряженных частиц позволяет отказываться от использования полимерного фоторезиста. Обеспечивает разрешение до 10 нм.
Микрофлюидика (микрогидродинамика) — наука о поведении жидкостей на микро- и нанопространственных масштабах. Основные области применения — технические устройства малых размеров (например, устройства струйной печати), медицина и молекулярная биология.
Дифракция в фотографии. Избегаем падения резкости на фото
С таким оптическим явлением, как дифракция, фотографы встречаются довольно часто. В отличие от прочих искажений, таких как дисторсия или хроматические аберрации, дифракция свойственна в равной мере любому объективу и полностью устранить её невозможно. В этой статье мы рассмотрим проблему дифракции на практике.
В отличие от прочих искажений, таких как дисторсия или хроматические аберрации, дифракция свойственна в равной мере любому объективу и полностью устранить её невозможно. В этой статье мы рассмотрим проблему дифракции на практике.
Дифракция — это оптический эффект, при котором снижается резкость фотографии независимо от того, сколько у вашей камеры мегапикселей и какова резкость используемого объектива. Если обычно лучи света распространяются по прямой, то проходя через маленькое отверстие (закрытая диафрагма объектива), они начинают рассеиваться. При этом луч формирует на фото не точку, а круг — так называемый диск Эйри. Чем сильнее закрываем диафрагму, тем заметнее становится дифракция, поскольку каждая точка изображения перестает быть точкой.
Заметить дифракцию невооружённым глазом можно тогда, когда размер диска Эйри станет сопоставим с размером одного пикселя на матрице — это дифракционный предел.
Концентрические круги вокруг фонарей — диск Эйри, следствие дифракции. Он особенно заметен вокруг точечных источников света.
Изучим серию тестовых фотографий, снятых на Nikon D3400. Этот недорогой аппарат с матрицей формата APS-C имеет высокое разрешение (24 Мп), поэтому мы сможем оценить все детали на фото, а заодно отчётливо увидим появление дифракции. Ниже приведены фрагменты снимка со 100% увеличением.
Удобно оценивать резкость кадров, например, по знаку пешеходного перехода. Видно, что детализация начинает снижаться уже после f/8 и критически падает к f/14. Чем сильнее закрыта диафрагма, тем меньше деталей остаётся на снимке.
NIKON D3400 / 18.0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F5.6, 1 с, 27.0 мм экв. NIKON D3400 / 18-35 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F8, 2 с, 27.0 мм экв. NIKON D3400 / 18.0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F11, 4 с, 27.0 мм экв. NIKON D3400 / 18-35 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F14, 6 с, 27.0 мм экв. NIKON D3400 / 18. 0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F16, 8 с, 27.0 мм экв.
NIKON D3400 / 18.0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F22, 15 с, 27.0 мм экв.
0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F16, 8 с, 27.0 мм экв.
NIKON D3400 / 18.0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 100, F22, 15 с, 27.0 мм экв.По тестовым фото видно, что дифракционный предел на Nikon D3400 находится в районе f/8; далее заметна дифракция.
Рассмотрим на примере Nikon Z 7, как в подобных ситуациях ведут себя полнокадровые матрицы. Казалось бы, на 45-мегапиксельной матрице Nikon Z 7 дифракция должна сказываться очень серьёзно — ведь у неё очень высокое разрешение. Однако плотность пикселей у этой матрицы всё ещё ниже, чем у 24-мегапиксельного кропа. Рассчитать это легко — достаточно разделить количество мегапикселей на площадь матрицы.
Итак, сравним на практике пары тестовых изображений, сделанных при f/8 и при f/16 на кропе и на 45-мегапиксельном полном кадре.
Видно, что даже на закрытых диафрагмах полнокадровый аппарат обеспечивает лучшую детализацию. Особенно показателен пример на f/16: на кроп-матрице картинка уже фактически нерабочая, а полнокадровый снимок ещё вполне можно использовать.
Nikon Z 7 и объектив Nikon Nikkor Z 85mm F1.8 S
Дифракция и практика съёмки
Начинающему фотографу может быть непонятно, зачем вообще закрывать диафрагму настолько сильно, чтобы на фото начинала влиять дифракция. Однако есть ряд причин, по которым приходится пользоваться закрытыми диафрагмами.
Первая и основная — увеличение глубины резкости. Во многих направлениях фотографии необходимо показать резкими все объекты на фото, уложив их в ГРИП. Глубина резкости регулируется диафрагмой, и подчас приходится её сильно закрывать, чтобы, например, в кадре резко показать цветок на переднем плане и горы на заднем. В таких случаях лучше небольшое снижение резкости из-за дифракции, чем просто не резкий передний или задний план.
Для достижения максимальной глубины резкости использована наводка на гиперфокальное расстояние и диафрагма f/16.
Но не спешите закрывать диафрагму до упора. Научитесь сначала рассчитывать и рационально использовать её значения.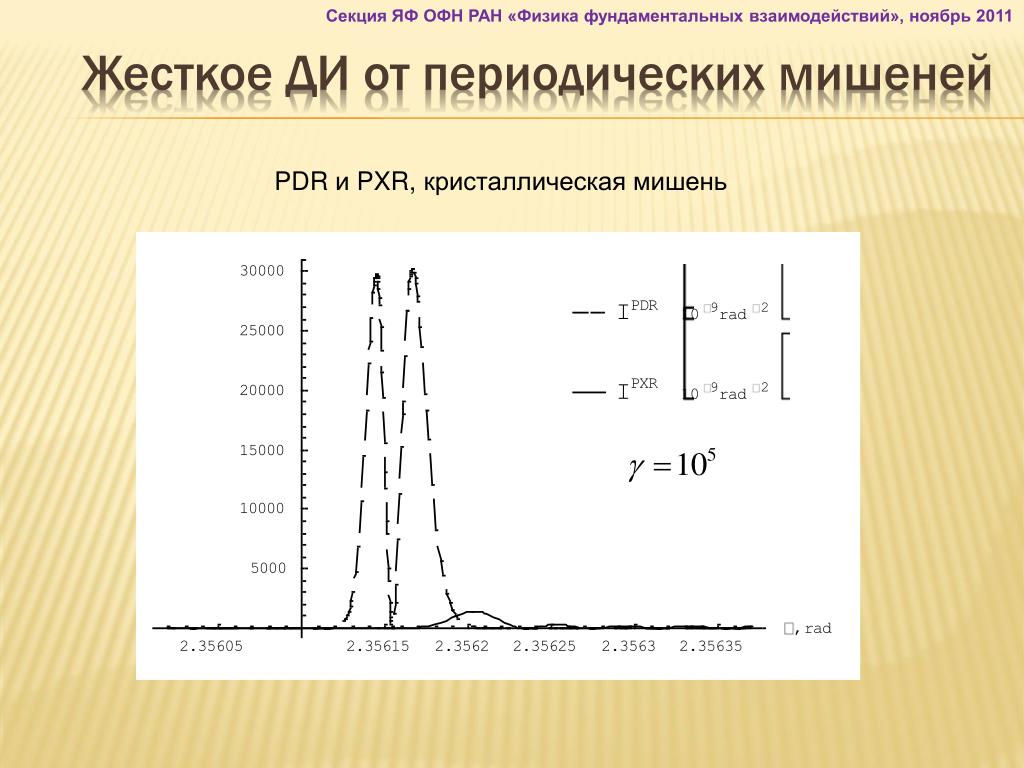 Так, в пейзажной, архитектурной и интерьерной фотографии используются различные приёмы фокусировки и работы с ГРИП. Один из них — наводка на гиперфокальное расстояние.
Так, в пейзажной, архитектурной и интерьерной фотографии используются различные приёмы фокусировки и работы с ГРИП. Один из них — наводка на гиперфокальное расстояние.
Пожалуй, каждый фотограф сам для себя должен определить тот уровень снижения резкости, на который он готов пойти. Я, например, фотографируя на полнокадровую 45-мегапиксельную камеру, определил для себя в качестве максимального значения f/16. Снимая на кроп, где дифракция сказывается раньше, я предпочитаю не закрываться более чем на f/11.
Аналогичная проблема возникает при съёмке небольших предметов и в макросъёмке, где после f/8 только начинается рабочий диапазон диафрагм. Поскольку съёмка ведётся на малой дистанции, глубина резкости также крайне мала. Поэтому, чтобы показать объект полностью резким, приходится серьёзно закрывать диафрагму. Тут лучше пренебречь дифракцией, но добиться нужной ГРИП, чем получить просто нерезкий кадр из-за недостатка глубины резкости.
Лучше закрыть диафрагму, пренебрегая дифракцией, чтобы поместить снимаемый объект в глубину резкости.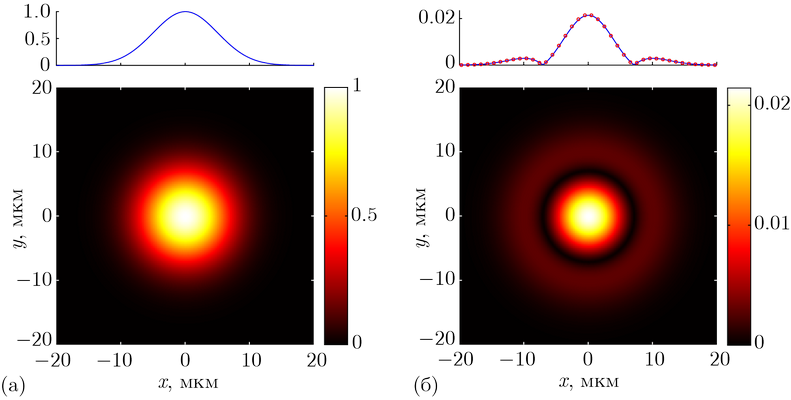 ..
..
…чем получить в кадре нерезкий по краям предмет.
Но глубину резкости невозможно расширять бесконечно. Часто при съёмке небольших предметов, вместо того, чтобы сильно закрывать диафрагму, пользуются фокус-стекингом. Иногда этот приём применяют и при съёмке интерьеров, пейзажа. Суть его в том, что делается несколько кадров с фокусировкой на разных дистанциях, а потом результат сводится воедино на компьютере. Этот приём помогает избежать негативного влияния дифракции и при этом расширить глубину резкости вплоть до бесконечности. Фотокамеры Nikon D850, Nikon Z 7 и Nikon Z 6 имеют встроенную функцию фокус-стекинга. О ней и о самом приёме отдельная статья на нашем сайте.
При фокус-стекинге в пейзаже, как правило, хватает 3–5 кадров с фокусировкой на разных дистанциях. В случае макросъемки, могут потребоваться десятки снимков.
Вторая причина, по которой сильно закрывают диафрагму, — стремление добиться идеальной резкости и отсутствия искажений в кадре. На открытых диафрагмах объективы могут давать далёкую от идеала картинку — с нерезкими краями и обилием хроматических аберраций. Победить это легко — достаточно прикрыть диафрагму. Если же объектив изначально имеет светосилу, скажем, f/5,6, что характерно для бюджетной оптики, то его придётся крутить до f/8– f/11, чтобы получить достойную резкость. Уж лучше пусть на фото немного скажется дифракция, но при этом мы уберём все искажения со стороны объектива.
На открытых диафрагмах объективы могут давать далёкую от идеала картинку — с нерезкими краями и обилием хроматических аберраций. Победить это легко — достаточно прикрыть диафрагму. Если же объектив изначально имеет светосилу, скажем, f/5,6, что характерно для бюджетной оптики, то его придётся крутить до f/8– f/11, чтобы получить достойную резкость. Уж лучше пусть на фото немного скажется дифракция, но при этом мы уберём все искажения со стороны объектива.
Когда не стоит закрывать диафрагму. Часто фотографы закрывают до упора диафрагму в стремлении поснимать на длинных выдержках размытые огни автомобилей или воду в горном ручье… И получают некачественные изображения. Да, выдержка удлиняется, когда диафрагма закрыта, но даже при f/22 при дневном освещении она вряд ли станет достаточно длинной, чтобы можно было эффективно работать с размытием движения. Чтобы эффективно работать с длинными выдержками, необходимы нейтрально-серые фильтры. Также очень помогает, когда в камере есть очень низкие ISO. Например в Nikon D810, Nikon D850 и Nikon Z 7 есть возможность опустить светочувствительность до ISO 32.
Также очень помогает, когда в камере есть очень низкие ISO. Например в Nikon D810, Nikon D850 и Nikon Z 7 есть возможность опустить светочувствительность до ISO 32.
Использован нейтрально-серый светофильтр ND1000. Он позволил снимать при дневном освещении на выдержке в 100 секунд.
NIKON D850 / 18.0-35.0 mm f/3.5-4.5 УСТАНОВКИ: ISO 64, F14, 100 с, 18.0 мм экв.А ещё не надо чрезмерно закрывать диафрагму в погоне за звездами вокруг точечных источников света — фонарей, солнца, так как эффектные лучи на большинстве объективов формируются уже при f/11–f/14.
NIKON D850 / 18-35 mm f/3.5-4.5 УСТАНОВКИ: ISO 64, F11, 60 с, 18.0 мм экв.Подытожим. На современных кропах резкость изображения снижается уже после f/11, на полном кадре — после f/14–f/16. Из-за меньшей плотности пикселей на матрице полнокадровые камеры (даже многомегапиксельные) дают качественное, детализированное изображение даже на закрытых диафрагмах, поэтому бояться какой-то особенно страшной дифракции в практической работе не стоит. Работать на закрытых диафрагмах можно и иногда необходимо. Просто делать это надо осознанно и не злоупотреблять съёмкой на закрытой до предела диафрагме.
Работать на закрытых диафрагмах можно и иногда необходимо. Просто делать это надо осознанно и не злоупотреблять съёмкой на закрытой до предела диафрагме.
Дифракционный предел разрешающей способности — Энциклопедия по машиностроению XXL
Здесь следует сделать следующее замечание. Угловую неопределенность, так же как и дифракционный предел разрешающей способности, нельзя указать точно. Критерий Релея (согласно которому Аа=1,22 X/D, где D — диаметр отверстия) можно превысить, и неопределенность угла можно уменьшить по сравнению с той, которая следует из приведенной формулы. Как показано в ряде работ, например [24], для некоторых типов предметов можно получить разрешение, превышающее предел Релея. Если передаваемый предмет пространственно ограничен и может быть представлен точно конечной частью спектра, то полный снектр такого предмета [c.64]Путем построения более сложных систем можно добиться совпадения фокусов для трех различных цветов.
 Таковы наиболее совершенные объективы микроскопов (апохроматы), разработанные Аббе. Геометрооптические качества 10-линзового апохромата Аббе настолько высоки, что он позволяет достичь теоретического дифракционного предела разрешающей способности, обусловленного волновой природой света (см. 7.6).
[c.359]
Таковы наиболее совершенные объективы микроскопов (апохроматы), разработанные Аббе. Геометрооптические качества 10-линзового апохромата Аббе настолько высоки, что он позволяет достичь теоретического дифракционного предела разрешающей способности, обусловленного волновой природой света (см. 7.6).
[c.359]Дифракционный предел разрешающей способности [c.144]
Предел разрешения микроскопа определяется дифракционными явлениями, возникающими в плоскости предметов, микроструктура которых действует на световые волны подобно дифракционной решетке. Разрешающая способность микроскопа вычисляется по формуле [c.134]
Прослеживается процесс превращения дифракционной картины в изображение предмета. Обсуждается предел разрешающей способности оптических приборов. [c.239]
Применение увеличений больше нормального не может выявить новые детали рассматриваемого объекта. Увеличения, значительно превосходящие нормальное, приносят только вред, поскольку чрезмерное сужение выходящего пучка может внести в изображение значительные дифракционные искажения. Однако по физиологическим причинам иногда бывает полезно брать увеличения, превосходящие нормальное в 2—4 раза. Рассматривая детали на пределе разрешающей способности, глаз работает с напряжением и быстро утомляется, его чувствительность и разрешающая способность понижаются. Применение увеличений, несколько превышающих нормальное, не выявляет новых подробностей в строении рассматриваемых объектов, но позволяет рассматривать их с меньшим напряжением. К таким же выводам мы пришли в 23 из фотометрических соображений.
[c.365]
Однако по физиологическим причинам иногда бывает полезно брать увеличения, превосходящие нормальное в 2—4 раза. Рассматривая детали на пределе разрешающей способности, глаз работает с напряжением и быстро утомляется, его чувствительность и разрешающая способность понижаются. Применение увеличений, несколько превышающих нормальное, не выявляет новых подробностей в строении рассматриваемых объектов, но позволяет рассматривать их с меньшим напряжением. К таким же выводам мы пришли в 23 из фотометрических соображений.
[c.365]
Открытие голографии и получение первых голограмм было встречено с восторгом. И действительно, большая хорошо сделанная голограмма выглядит как чудо. При виде ее трудно удержаться от возгласа восхищения. В открытии голографии есть одна замечательная черта. Дело в том, что физические принципы, используемые в этой новой науке, были известны давно, но как-то вошло в привычку считать, что дифракционные (волновые) явления света определяют предел разрешающей способности оптического прибора. И физики долго не задавали себе простого вопроса, который сейчас кажется вполне естественным Куда девается информация о предмете (источнике света), дающем дифракционную картину, и как восстановить изображение Развитие интерференционных методов приучило к тому, что эта информация никуда не исчезает и, если правильно распорядиться установкой, то количество информа-
[c.126]
И физики долго не задавали себе простого вопроса, который сейчас кажется вполне естественным Куда девается информация о предмете (источнике света), дающем дифракционную картину, и как восстановить изображение Развитие интерференционных методов приучило к тому, что эта информация никуда не исчезает и, если правильно распорядиться установкой, то количество информа-
[c.126]
Условие (63.1), полученное с помощью качественных соображений, мало отличается от результатов строгого рассмотрения разрешающей способности микроскопа (см. 97). Этого и следовало ожидать, так как специфические черты голографирования, такие, как наличие опорной волны, ее геометрия, просвечивание и т. п., совершенно не существенны в вопросе о дифракционном пределе разрешения. [c.257]
Рядом авторов [15, 102, 160, 164—172, 174, 184, 185, 188, 195] проведены подробные экспериментальные исследования схемы касательного синхронизма, позволившие авторам [31, 32] проанализировать возможности практического использования преобразователей.
 В [160] при Я1г = 1,06 мкм и [195] при Я.1Г = 10,6 мкм реализована разрешающая способность, близкая к теоретическому дифракционному пределу. Авторы [192—194] продемонстрировали возможность формирования корреляционных функций изображения в реальном масштабе времени.
[c.134]
В [160] при Я1г = 1,06 мкм и [195] при Я.1Г = 10,6 мкм реализована разрешающая способность, близкая к теоретическому дифракционному пределу. Авторы [192—194] продемонстрировали возможность формирования корреляционных функций изображения в реальном масштабе времени.
[c.134]Подобное утверждение подтверждается как теоретически [24], так и экспериментальными результатами. Так, в работе [40] показано, что разрешающая способность голографической системы достигает дифракционного предела. В той же работе приводится сравнение частотно-контрастной характеристики голографической системы с характеристикой почти безаберрационного [c.121]
Лазерный локатор испытывался как в непрерывном, так и в импульсном режимах работы. В непрерывном режиме эксперименты проводились в лабораторных условиях на дальностях 60 и 100 м. Изображение тестовой таблицы, сфотографированное с экрана видеоконтрольного устройства, показано на рис. 7.8. Разрешающая способность лучше 0,1 мрад, что близко к дифракционному пределу для апертуры диаметром 2,5 см, равному 0,05 мрад. В импульсном режиме при пиковой мощности излучения передатчика 2 кВт дальность действия локатора возрастала до нескольких километров.
[c.256]
В импульсном режиме при пиковой мощности излучения передатчика 2 кВт дальность действия локатора возрастала до нескольких километров.
[c.256]
Так же как и чувствительность, разрешающая способность является только качественным понятием, связанным с предельно разрешимым контрастом, который должен определяться условно. Поскольку общепринятого способа определения предельного контраста не существует, отдельные данные относительно предельного разрешения часто являются несопоставимыми. Для определения предельного разрешения можно было бы воспользоваться критерием Рэлея для разрешающей способности оптических приборов, в соответствии с которым две точки разрешаются субъективно, если интенсивность света между центрами дифракционных пятен отличается не менее чем на 20% от значения интенсивности в центрах пятен. В этом случае имеем / ах = 1 mm = 0,8 откуда для контраста получаем К = 0,11. Поэтому иногда за предел разрешения принимают значение пространственной частоты, при которой контраст снижается до 10% от своего максимального значения. [c.145]
[c.145]
Отсюда следует, что пятно должно перемещаться в пределах 1% от своего собственного размера. Следовательно, дифракционную решетку следует выбирать так, чтобы ее разрешающая способность приблизительно равнялась [c.518]
Второе достоинство методов термометрии ФЛ и КР — наиболее высокая среди всех других методов пространственная разрешающая способность, не превышающая дифракционного предела для зондирующего света ( 0,5 мкм). Это позволяет надеяться на дальнейшее [c.193]
Разрешающая способность глаза. Возьмите миллиметровую шкалу или сделайте метки на листе белой бумаги и найдите расстояние от бумаги до глаза, на котором метки покажутся совпадающими друг с другом, т. е. неразрешимыми. Обычно, если расстояние между метками равно 1 мм, то они плохо разрешимы на расстоянии в2 м и совсем неразрешимы на расстояния 4 м. Таким образом, если глаз находится в центре поля зрения (т. е. когда вы смотрите прямо на линии), то предельное значение углового разрешения близко к А9л 1 лш/2 м = 1/2000. Теперь посмотрите в зеркало и с помощью линейки, расположенной близко к глазу, измерьте диаметр О вашего зрачка. Обычно мм. Дифракционный предел углового раз-
[c.436]
Теперь посмотрите в зеркало и с помощью линейки, расположенной близко к глазу, измерьте диаметр О вашего зрачка. Обычно мм. Дифракционный предел углового раз-
[c.436]
В заключение рассмотрим случай, когда размеры объекта меньше предела разрешения оптической системы. Такой случай типичен при наблюдении звезд невооруженным глазом и в телескоп. В этом случае оптическое изображение не передает формы предмета, а представляет собой дифракционный кружок, окруженный темными и светлыми кольцами (см. рис. 180, стр. 300), причем почти весь свет сконцентрирован в центральном кружке. Назначение телескопа при наблюдении звезд состоит не в том, чтобы различать детали рассматриваемого объекта (они находятся за пределами его разрешающей способности), а в том, чтобы увеличить световой поток, попадающий в глаз наблюдателя, и тем самым обнаруживать все более и более слабые звезды. [c.161]
Типичная ширина спектральной линии в видимой области спектра Av — Гц (см.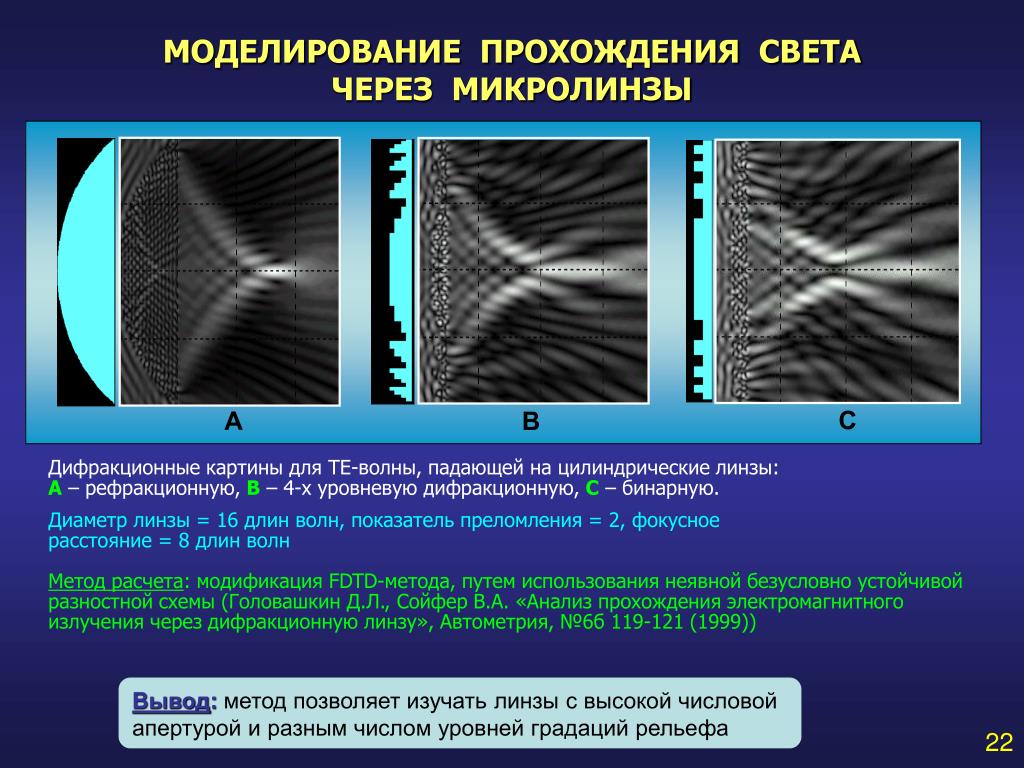 главу 13), что соответствует АХ = Av/ — 0,008 /ш. Для того чтобы эта ширина могла быть зарегистрирована прибором, последний должен иметь разрешающую силу Х/АХ — 60 ООО. Эта величина достигается и далее перекрывается современными интерференционными и дифракционными спектральными приборами высокого разрешения. Таким образом, классические спектральные приборы достигли фактического предела разрешения. Дальнейшее увеличение разрешающей способности возможно только на основе принципиально новых физических идей, реализуемых, например, в лазерной спектроскопии.
[c.114]
главу 13), что соответствует АХ = Av/ — 0,008 /ш. Для того чтобы эта ширина могла быть зарегистрирована прибором, последний должен иметь разрешающую силу Х/АХ — 60 ООО. Эта величина достигается и далее перекрывается современными интерференционными и дифракционными спектральными приборами высокого разрешения. Таким образом, классические спектральные приборы достигли фактического предела разрешения. Дальнейшее увеличение разрешающей способности возможно только на основе принципиально новых физических идей, реализуемых, например, в лазерной спектроскопии.
[c.114]
Разрешающая способность микроскопа характеризуется величиной, обратной линейному пределу разрешения. Согласно дифракционной теории Аббе линейный предел разрешения микроскопа, т. е. минимальное расстояние между точками предмета, которые изображаются как раздельные, определяется по формуле [c.195]
Предел разрешения двух самосветящихся точек. На практике разрешающая способность оптического прибора определяется исходя из критерия Рэлея, согласно которому два изображения светящихся точек (линий) находятся на пределе разрешения в том случае, когда центральный дифракционный максимум одной из точек (линий) совмещен с первым минимумом другой, т.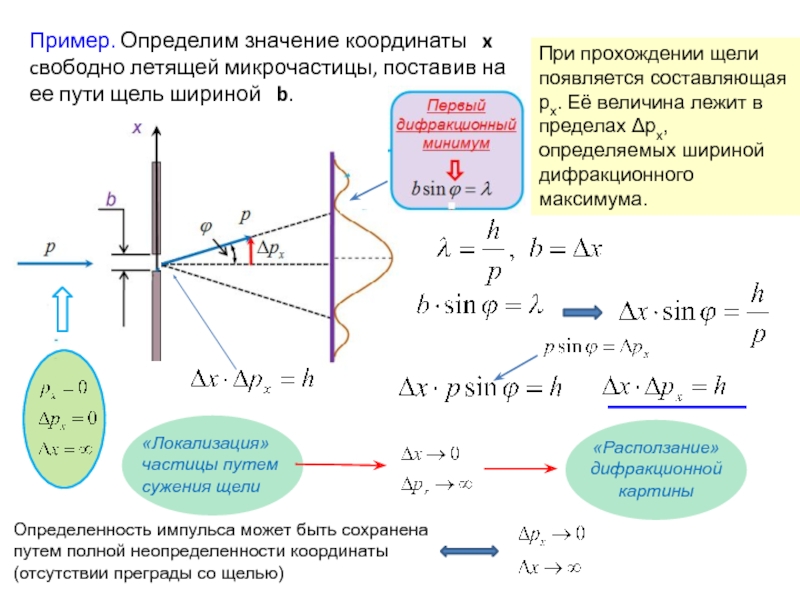 е. если
[c.25]
е. если
[c.25]
Теоретическая разрешающая способность оптической системы определяется на основе дифракционной теории построения изображений. Если две светящиеся точки з и 1 (рис. 4.3) находятся на определенном расстоянии друг от друга, то их изображения, созданные оптической системой, будут иметь вид не точек з и 5/, а дифракционных кружков рассеивания, состоящих из концентрических темных и светлых колец. Распределение облученности в пределах таких -колец схематично показано на рис. 4.3, в, причем в центральной части облученность будет максимальной. Раздельно обнаружить с помощью любой анализирующей системы эти два изображения х и 5/ можно только при условии, что расстояние [c.85]
Получаемые действительные и мнимые изображения обладают трехмерными свойствами. Трудность использования этих свойств заключается в том, что большая разница между длинами волн света и звука приводит к несоответствию в геометрических размерах между восстановленным изображением объекта и самим объектом.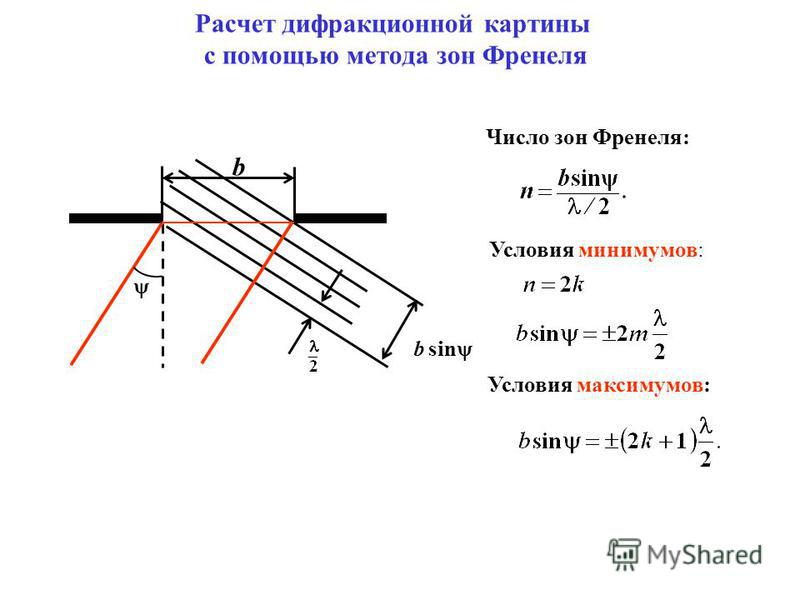 В сообщении [28] говорится, что в опытах были использованы фигурки из пенопласта размером в несколько сантиметров, расположенные на расстоянии 10—25 см от приемной апертуры. Частота ультразвука была выбрана 10 Мец при размере апертуры 4X5 см. Достигнутая при этом разрешающая способность равнялась дифракционному пределу, определяемому длиной волны и размером апертуры.
[c.99]
В сообщении [28] говорится, что в опытах были использованы фигурки из пенопласта размером в несколько сантиметров, расположенные на расстоянии 10—25 см от приемной апертуры. Частота ультразвука была выбрана 10 Мец при размере апертуры 4X5 см. Достигнутая при этом разрешающая способность равнялась дифракционному пределу, определяемому длиной волны и размером апертуры.
[c.99]
Точное изображение плоского объекта теоретически мохсет быть получено лишь с помощью неограниченных пучков света. При наличии диафрагмы каждая точка объекта изображается дифракционной картиной диафрагмы. Это ограничивает предел разрешающей способности оптических приборов. [c.241]
Качество полученных в результате изображений зависит от качества схемы измерения, полноты проекционных данных, размеров приемной матрицы, помех при измерениях и Т.Д. Наилучшая разрешающая способность определяется разрешающей способностью матрицы приемников. Предел разрешающей способности дифракционной томографии стремится к дифракционному пределу (порздка длины волны звука).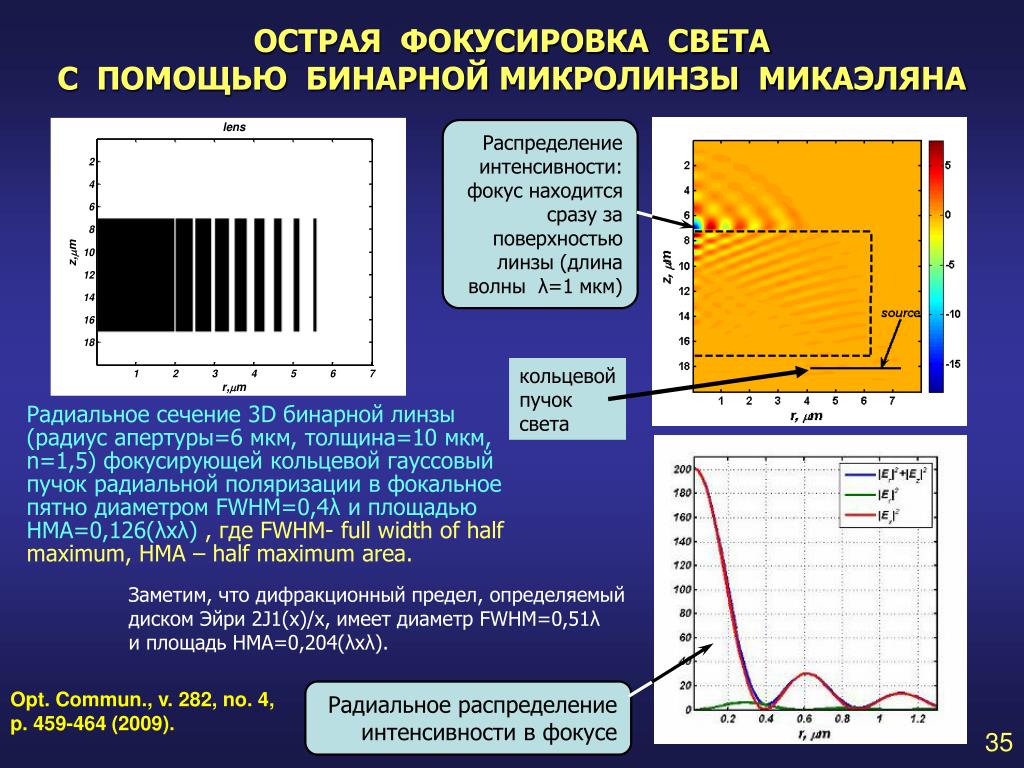 [c.375]
[c.375]
Оптическая система выступает как фильтр пространственных частот и, в частности, всегда пропускает низкие частоты, а верхний предел частот определяется пределом разрешающей способности и зависит для безаберрацион-ного объектива от диаметра дифракционного кружка рассеяния, и в частности, применяя формулу (379), для положения предмета в Оесконечности (6 = / tg 115) будем иметь [c.194]
Хотя история лазеров началась с использования плоского резонатора, его теория оказалась весьма крепким орешком . Особенно сложно дело обстояло с методами оценки дифракционных потерь. Правда, еще Шавлов и Таунс в своей основополагающей работе [197] попытались выполнить такудо оценку. По аналогии с известным приемом, позволяющим учесть влияние конечного размера зеркал интерферометра Фабри —Перо на его разрешающую способность [110], они отождествляли время, затрачиваемое наклонными световыми пучками до их выхода за пределы зеркал, со средним временем жизни фотонов в резонаторе. Благодаря своей наглядности такой упрощенный подход принес поначалу определенную пользу, однако уже расчеты Фокса и Ли [164] показали полную его несостоятельность.
[c.92]
Благодаря своей наглядности такой упрощенный подход принес поначалу определенную пользу, однако уже расчеты Фокса и Ли [164] показали полную его несостоятельность.
[c.92]
В голографическом варианте факторами, ограничивающими разрешающую способность, также являются ограниченность апертуры голограммы и ее аберрации. Однако создание практически безаберрационных голограмм не встречается с такими трудностями, как при исправлении аберраций объективов. Коррекция аберраций объективов является, как правило, чрезвычайно трудоемкой задачей, которая до конца не решается. В голографии же, как показывает эксперимент, удается сравнительно легко достигнуть дифракционного предела разрешения при определенных размерах голограммы. Кроме того, создание голограмм большего размера является более простой задачей, чем создание объективов с большой апертурой. Следовательно, возможности голографии в отношении достижения высокой разрешающей способности выше, чем возможности лиизовой оптики. [c.121]
[c.121]
До сих пор при рассмотрении задачи восстановления истинного распределения интенсивности на объекте не учитывалось влияние шума. Между тем именно шум является основным ограничивающим фактором при повышении разрешающей способности оптических систем выше дифракционного предела путем апостериорной обработки формируемых ими изображений. В действительности регистрируемое изображение не является чистой сверткой распределения интенсивности на объекте с импульсной характеристикой оптической системы, а представляет собой аддитивную смесь этой свертки с шумом. Если уровень шума значителен, то использование инверсного пространственного фильтра не обеспечит получения желаемого результата из-за искажения шумом изображения на выходе схемы пространственной фильтрации. Дело в том, что корректируемые передаточные характеристики в большинстве случаев являются осциллирующими знакопеременными функциями, принимающими нулевое значение. Так, например, передаточная характеристика дефокусированной оптической системы имеет вид
[c. 248]
248]
Вот как спустя 23 года после своих первых работ высказался Габор о своей идее, ее реализации и последствиях Для ученого нет большей радости, чем быть свидетелем того, как одна из его идей открывает собой новую, стремительно развивающуюся отрасль науки. Мне выпало счастье высказать одну такую идею. В тот период я много занимался электронной микроскопией. Волны де Бройля были достаточно короткими для разрешения атомных решеток, но из-за несовершенства электронных линз разрешающая способность оказывалась ограниченной практически. При апертуре, обеспечивающей необходимый дифракционный предел разрушения, можно было получить только размытое изображение. Тем не менее, если исходить из принципа Гюйгенса, пучок должен содержать всю необходимую информацию. Что мешает ее расшифровать Очевидно то, что на пластинке регистрируется только половина информации мы пренебрегаем фазой волны. Нельзя ли ее вы51вить с помощью интерференции, налагая когерентный фон. Немного математики и несколько опытов позволили быстро проверить идею о восстановлении волн. Достаточно было осуществить суперпозицию комплексной волны, приходящей от объекта, с простой волной (плоской или сферической), сделать фотографию, затем, осветив ее простой волной, восстановить исходную картину. Возникающее при этом изображение было трехмерным. Мешало одно незначительное обстоятельство одновременно восстанавливалось еще одно изображение — двойник объекта.
[c.49]
Достаточно было осуществить суперпозицию комплексной волны, приходящей от объекта, с простой волной (плоской или сферической), сделать фотографию, затем, осветив ее простой волной, восстановить исходную картину. Возникающее при этом изображение было трехмерным. Мешало одно незначительное обстоятельство одновременно восстанавливалось еще одно изображение — двойник объекта.
[c.49]
Предел разрешения микроскопа определяется дифрахщюнными явлениями, возникающими в плоскости предмета,, микроструктура которого действует на световые волны подобно дифракционной решетке. >5аксимальная разрешающая способность микроскопа при еосогл осве-щепин определяется по формуле [iOO [c.89]
Таким образом, разрешающая способность фурье-спектрометра определяется максимальной разностью хода, а спектральный предел разрешения пропорционален обратной величине максимальной разности хода. В уникальных приборах величина Дщах достигает 100—200 см, что для области вблизи Я = 10 мкм (V = 1000 см ) дает Дv яа 3 10 см . Эта величина намного превышает предел разрешения классических дифракционных спектрометров для указанной области спектра.
[c.430]
В уникальных приборах величина Дщах достигает 100—200 см, что для области вблизи Я = 10 мкм (V = 1000 см ) дает Дv яа 3 10 см . Эта величина намного превышает предел разрешения классических дифракционных спектрометров для указанной области спектра.
[c.430]
Ширина изображения точки на вашей сетчатке примерно равна произведению фокусного расстояния линзы (хрусталика) вашего глаза на угловую ширину изображения точки. Фокусное расстояние f приблизительно раЕно внутреннему диаметру глаза. Когда вы смотрите на удаленный объект, этот диаметр равен примерно 3 см. Поэтому ширина изображения пятна на сетчатке от удаленной точки близка к/(Я/D) = 3-5-10 V0.2 8Тотфакт, что разрешающая способность нашего глаза ограничена дифракционным пределом, говорит о том, что фоторецепторы в центре сетчатки отделены друг от друга расстоянием, не большим чем 8 мкм. [c.437]
Физ. основу методов Р. т. составляет дифракц. контраст в изображении разл. областей кристалла в пределах одного дифракционного пятна. Этот контраст формируется вследствие различий интенсивностей или направлений лучей от разных точек кристалла в соответствии с совершенством или ориентацией крист, решётки в этих точках. Эфiфeкт, вызываемый изменением хода лучей, позволяет оценивать размеры и дезориентации элементов субструктуры в кристаллах (фрагментов, блоков), а различие в интенсивностях пучков используется для выявления дефектов упаковки, дислокаций, сегрегаций примесей и напряжений. Р. т. отличается от др. рентг. структурных методов (см. Рентгеновский структурный анализ. Рентгенография материалов) высокой разрешающей способностью и чувствительностью, а также возможностью исследования объёмного расположения дефектов в сравнительно крупных (до десятков см), почти совершенных кристаллах.
[c.637]
Этот контраст формируется вследствие различий интенсивностей или направлений лучей от разных точек кристалла в соответствии с совершенством или ориентацией крист, решётки в этих точках. Эфiфeкт, вызываемый изменением хода лучей, позволяет оценивать размеры и дезориентации элементов субструктуры в кристаллах (фрагментов, блоков), а различие в интенсивностях пучков используется для выявления дефектов упаковки, дислокаций, сегрегаций примесей и напряжений. Р. т. отличается от др. рентг. структурных методов (см. Рентгеновский структурный анализ. Рентгенография материалов) высокой разрешающей способностью и чувствительностью, а также возможностью исследования объёмного расположения дефектов в сравнительно крупных (до десятков см), почти совершенных кристаллах.
[c.637]
Дифракционные явления в реальной антенной системе весьма значительны. Например, параболическая антенна, направленная на бесконечно удаленный точечный источник, будет иметь ширину луча около 2,4 Xld радиан между нулями диаграммы направленности. Боковые лепестки будут существенно зависеть от деталей конструкции облучателя антенны. Чтобы получить хорошую разрешающую способность параболического зеркала, необходимо, чтобы отношение djX было как можно больше. В существующих системах управления величина этого отношения колеблется в пределах от 10 до 100. В настоящее время для Национальной радиоастрономической обсерватории планируется создание антенны диаметром 140 футов, предназначенной для работы на волнах длиной 3 см. Для этой днтенны отношение dlX составит около 1400.
[c.640]
Боковые лепестки будут существенно зависеть от деталей конструкции облучателя антенны. Чтобы получить хорошую разрешающую способность параболического зеркала, необходимо, чтобы отношение djX было как можно больше. В существующих системах управления величина этого отношения колеблется в пределах от 10 до 100. В настоящее время для Национальной радиоастрономической обсерватории планируется создание антенны диаметром 140 футов, предназначенной для работы на волнах длиной 3 см. Для этой днтенны отношение dlX составит около 1400.
[c.640]
Диск Эйри и предел дифракции
Авторы: Грегори Холлоуз, Николас Джеймс
Это раздел 2.4 Руководства по работе с изображениями.
Воздушный диск
Когда свет проходит через апертуру любого размера (каждая линза имеет конечную апертуру), возникает дифракция. Результирующая дифракционная картина, яркая область в центре, вместе с серией концентрических колец уменьшающейся интенсивности вокруг нее, называется диском Эйри (см. , рис. 1, ).Диаметр этого рисунка связан с длиной волны (λ) освещающего света и размером круглой апертуры, что важно, поскольку диск Эйри является наименьшей точкой, в которую может быть сфокусирован луч света. По мере того, как сфокусированные узоры Эйри из разных деталей объекта приближаются друг к другу, они начинают накладываться друг на друга (см. Контраст). Когда перекрывающиеся узоры создают достаточно конструктивных помех, чтобы уменьшить контраст, они в конечном итоге становятся неотличимыми друг от друга. На рисунке 1 показана разница в размерах пятна между объективами, установленными на f / 2.8 и объектив с диафрагмой f / 8. Этот эффект становится все более серьезной по мере того, как пиксели продолжают уменьшаться в размере. Диск Эйри $ \ left (\ varnothing _ {\ small {\ text {Airy Disk}}} \ right) $ или минимальный размер пятна можно оценить с помощью f / # и длины волны (λ):
, рис. 1, ).Диаметр этого рисунка связан с длиной волны (λ) освещающего света и размером круглой апертуры, что важно, поскольку диск Эйри является наименьшей точкой, в которую может быть сфокусирован луч света. По мере того, как сфокусированные узоры Эйри из разных деталей объекта приближаются друг к другу, они начинают накладываться друг на друга (см. Контраст). Когда перекрывающиеся узоры создают достаточно конструктивных помех, чтобы уменьшить контраст, они в конечном итоге становятся неотличимыми друг от друга. На рисунке 1 показана разница в размерах пятна между объективами, установленными на f / 2.8 и объектив с диафрагмой f / 8. Этот эффект становится все более серьезной по мере того, как пиксели продолжают уменьшаться в размере. Диск Эйри $ \ left (\ varnothing _ {\ small {\ text {Airy Disk}}} \ right) $ или минимальный размер пятна можно оценить с помощью f / # и длины волны (λ):
(1) $$ \ varnothing _ {\ small {\ text {Airy Disk}}} \ примерно 2,44 \ times \ lambda \ times \ left (\ text {f} / \ # \ right) $$
(1)$$ Ø _ {\ small {\ text {Airy Disk}}} \ примерно 2,44 \ times \ lambda \ times \ left (\ text {f} / \ # \ right) $$
Рис. 1: Дифракция увеличивается при закрытии диафрагмы объектива (f / # увеличивается).Верхний объектив установлен на f / 2,8; нижняя линза на f / 8.
1: Дифракция увеличивается при закрытии диафрагмы объектива (f / # увеличивается).Верхний объектив установлен на f / 2,8; нижняя линза на f / 8.Таблица 1 показывает диаметр диска Эйри для различных значений f / # с использованием зеленого света (520 нм). Наименьший достижимый размер пятна может быстро превысить размер маленьких пикселей. Это приводит к трудностям в получении полной разрешающей способности сенсора с любым используемым уровнем контрастности. Кроме того, при этом не учитываются какие-либо ограничения конструкции линзы или производственные ошибки, связанные с изготовлением линзовых элементов или оптических сборок, которые могут привести к снижению способности создавать наименьшее физически достижимое пятно и, таким образом, уменьшать уровни разрешения и контрастности.
| f / # | Диаметр диска Эйри [мкм] при длине волны 520 нм |
|---|---|
| 2 | 2,54 |
| 2,8 | 3,55 |
| 4 | 5,08 |
| 6,6 | 7,11 |
| 8 | 10,15 |
| 11 | 13,96 |
| 16 | 20.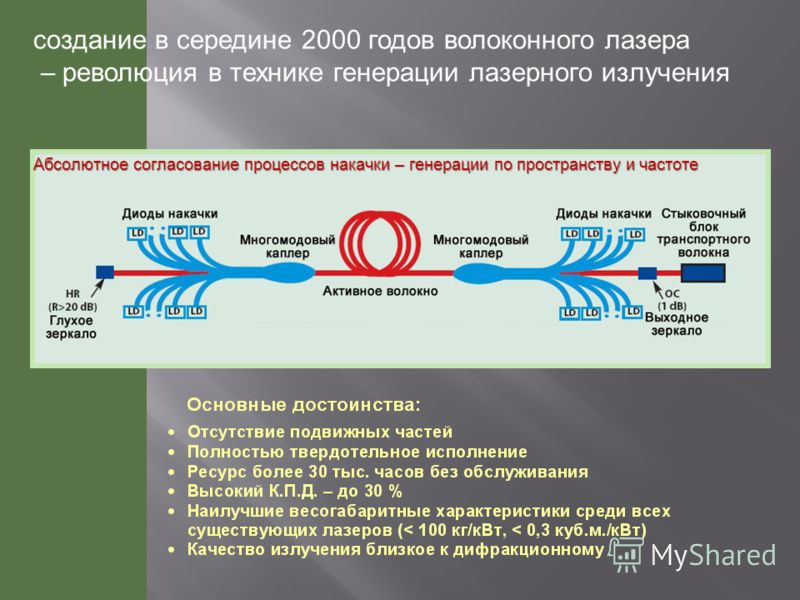 30 30 |
Примечание: Это все теоретически и является отправной точкой для ограничений в оптической системе.
Предел дифракции
Каждая линза имеет верхний предел характеристик, определяемый законами физики и диском Эйри, известный как предел дифракции.Этот предел представляет собой теоретическую максимальную разрешающую способность линзы, указанную в парах линий на миллиметр $ \ left [\ small {\ tfrac {\ text {lp}} {\ text {mm}}} \ right] $. Идеальный объектив, не ограниченный конструкцией, по-прежнему будет ограничен дифракцией.
Это предел — точка, в которой два паттерна Эйри больше не различимы друг от друга (, рис. 2, в контрасте). Ограниченное дифракцией разрешение, часто называемое частотой среза линзы, рассчитывается с использованием линзы f / # и длины волны света. Узнайте больше о f / # в f / # (настройка диафрагмы объектива / диафрагмы).
Узнайте больше о f / # в f / # (настройка диафрагмы объектива / диафрагмы).
(2) $$ \ xi _ {\ small {\ text {Предел дифракции}}} = \ frac {1} {\ left (\ text {f} / \ # \ right) \ times \ lambda} \ times \ left (\ frac {1000 \ large {\ unicode [Cambria Math] {x03BC}} \ normalsize {\ text {m}}} {1 \ text {mm}} \ right) $$
(2)$$ \ xi _ {\ small {\ text {Предел дифракции}}} = \ frac {1} {\ left (\ text {f} / \ # \ right) \ times \ lambda} \ times \ left (\ frac {1000 \ large {\ unicode [Cambria Math] {x03BC}} \ normalsize {\ text {m}}} {1 \ text {mm}} \ right) $$
Когда достигается предел дифракции, линза не может разрешить более высокие частоты. Таблица 2 показывает дифракционный предел для контраста при 0% при заданном значении f / # s. Таблица 2 показывает дифракционный предел для контраста при 0% при заданном значении f / # s. Эти числа могут показаться большими, но являются теоретическими; необходимо также учитывать несколько других факторов. Как правило, из-за собственного фонового шума датчики изображения не могут воспроизводить информацию с контрастом 0% или близким к нему. Контраст, как правило, должен составлять 10% или больше, чтобы его можно было обнаружить стандартными датчиками изображения. Чтобы избежать осложнений при визуализации, рекомендуется установить контраст 20% или выше при критическом разрешении для конкретного приложения.Кроме того, аберрации линз и отклонения, связанные с производственными допусками, также снижают производительность.
Как правило, из-за собственного фонового шума датчики изображения не могут воспроизводить информацию с контрастом 0% или близким к нему. Контраст, как правило, должен составлять 10% или больше, чтобы его можно было обнаружить стандартными датчиками изображения. Чтобы избежать осложнений при визуализации, рекомендуется установить контраст 20% или выше при критическом разрешении для конкретного приложения.Кроме того, аберрации линз и отклонения, связанные с производственными допусками, также снижают производительность.
| f / # | Предел контрастности 0% $ \ bf {\ left [\ small {\ tfrac {\ text {lp}} {\ text {mm}}} \ right]} $ @ 0,520 мкм |
|---|---|
| 1,4 | 1374 |
| 2 | 962 |
| 2,8 | 687 |
| 4 | 481 |
| 5.6 | 343 |
| 8 | 240 |
| 11 | 175 |
| 16 | 120 |

Рекомендуемые ресурсы
Указания по применению
Указания по применению
Нарушая дифракционный предел света: революция в флуоресцентной микроскопии?
Идентификация и каталогизация
все последовательности генов и соответствующие им белки высокого разрешения
конструкции послужат лишь прелюдией к реальным вызовам будущего
биологическое исследование — расшифровка клеточной схемы и ее
подробные зависящие от времени ответы на различные раздражители.Большинство из
центральные функции клетки выполняют высокоорганизованные
самосборные клеточные машины, которые контролируются и регулируются
сложный набор динамических взаимодействий между множеством молекулярных построек
блоки. Потребуется разработать аналитические инструменты для выявления и
измерить эти молекулярные взаимодействия. Наряду с традиционными методами
молекулярной биологии, электронной и рентгеновской микроскопии,
кристаллография, иммуноцитохимия и многие другие, оптические
микроскопия, и в частности флуоресцентная микроскопия, будет играть важную роль. жизненно важная роль в этом начинании.
жизненно важная роль в этом начинании.
Флуоресцентная микроскопия предлагает множество преимуществ для исследования живых организмов.
клетки. Это неинвазивно; он обеспечивает трехмерное изображение; Это
имеет высокую чувствительность вплоть до уровня одной молекулы, что позволяет
наблюдение за сигналами, специфичными для молекул и органелл. В
развитие зеленых (и других цветных) флуоресцентных белков как
специфические генетически модифицированные молекулярные маркеры и другие
сложные индикаторы флуоресценции вместе с улучшением
методы визуализации произвели революцию в флуоресцентной визуализации живых
клетки.Применение новых спектроскопических методов и передовых
методы анализа изображений теперь предоставляют количественные аналитические инструменты
для изучения клеточной динамики. Однако обычные оптические
микроскопия не имеет необходимого нанометрового разрешения, необходимого для поставленной задачи.
описано выше. Как было показано Аббе более 100 лет назад, волна
природа света налагает фундаментальные ограничения на достижимые
пространственное разрешение, известное как «дифракционный предел света» (1).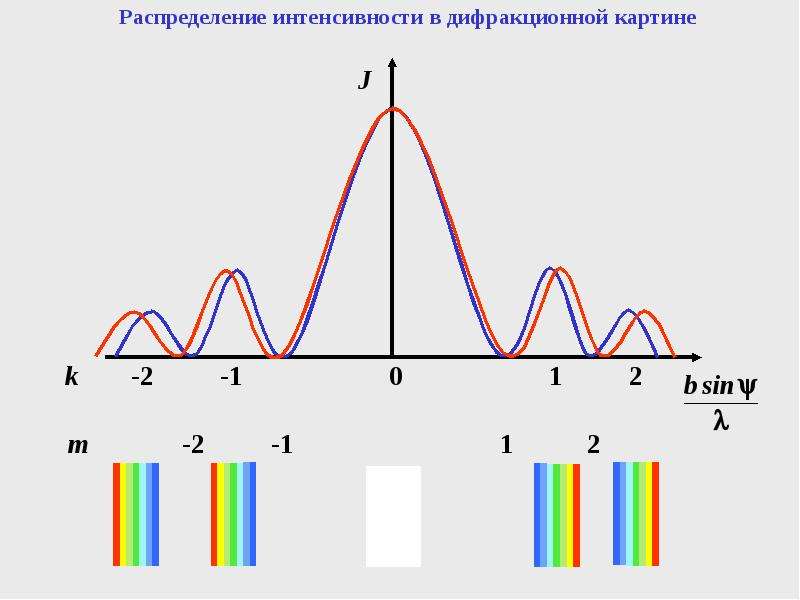 Для часто используемых красителей и масляной иммерсии с высокой числовой апертурой
Для объективов этот предел разрешения составляет порядка 250–300 нм.В
в последние годы мы стали свидетелями того, как в ответ на этот вызов
изобретательские решения, которые успешно преодолевают дифракционный предел
светлый. К ним относятся поверхностно-зависимая двумерная апертура (2) и
безапертурная (3) сканирующая оптическая микроскопия в ближнем поле, широкое поле
восстановление трехмерного изображения вычислительными методами (4) и
трехмерное неоднородное периодическое возбуждение (и излучение)
паттерны, содержащие высокочастотные компоненты, как в 4PI (5),
некогерентная интерференционная подсветка, интерференция изображения (6),
флуоресценция полного внутреннего отражения стоячей волны (7) и гармоническая
возбуждающая световая (8) микроскопия.В предыдущем выпуске PNAS Клар et al. продемонстрировал новый и умный подход к
сверхразрешение изображения, которое сильно отличается от предыдущего
подходы, имеющие большие перспективы для будущего применения (9).
Для часто используемых красителей и масляной иммерсии с высокой числовой апертурой
Для объективов этот предел разрешения составляет порядка 250–300 нм.В
в последние годы мы стали свидетелями того, как в ответ на этот вызов
изобретательские решения, которые успешно преодолевают дифракционный предел
светлый. К ним относятся поверхностно-зависимая двумерная апертура (2) и
безапертурная (3) сканирующая оптическая микроскопия в ближнем поле, широкое поле
восстановление трехмерного изображения вычислительными методами (4) и
трехмерное неоднородное периодическое возбуждение (и излучение)
паттерны, содержащие высокочастотные компоненты, как в 4PI (5),
некогерентная интерференционная подсветка, интерференция изображения (6),
флуоресценция полного внутреннего отражения стоячей волны (7) и гармоническая
возбуждающая световая (8) микроскопия.В предыдущем выпуске PNAS Клар et al. продемонстрировал новый и умный подход к
сверхразрешение изображения, которое сильно отличается от предыдущего
подходы, имеющие большие перспективы для будущего применения (9).
Хотя самые последние методы сверхразрешения, перечисленные выше, полагаются только
от объемного формирования возбуждающего света (через ближнее поле
диафрагма / острие или периодические световые градиенты, вызванные интерференцией),
Были также предприняты попытки улучшить разрешение с помощью
нелинейная связь между возбуждением и флуоресценцией
эмиссия (10, 11).Сочетание сильных световых градиентов и сильных
нелинейный отклик может еще больше уменьшить пространственную протяженность
функция рассеяния точки (PSF), как схематично показано на рис.
1. К сожалению, часто используемые нелинейные
двух- и многофотонные возбуждения страдают двумя основными недостатками.
Для эффективного обнаружения необходимы флуорофоры, излучающие в видимом диапазоне.
Многофотонное возбуждение видимых флуорофоров требует более длительного
длина волны (удвоенная или утроенная) основная. Поскольку дифракция
предел света линейно масштабируется с длиной волны, это приводит к
удвоение или утроение размера пятна возбуждения. Фактически,
уменьшение PSF, полученной нелинейным откликом, не может даже полностью
компенсировать набухание PSF в результате более длительного
длина волны возбуждения. Во-вторых, потому что многофотонные возбуждения
нерезонансные процессы высших порядков, их сечения поглощения равны
на много порядков меньше, чем у линейного однофотонного
процесс. Для эффективного
возбуждение. Однако такие импульсы фототоксичны для клетки, потому что
они ускоряют радикальное производство, тем самым ограничивая доступный
время наблюдения до повреждения клеток.
Фактически,
уменьшение PSF, полученной нелинейным откликом, не может даже полностью
компенсировать набухание PSF в результате более длительного
длина волны возбуждения. Во-вторых, потому что многофотонные возбуждения
нерезонансные процессы высших порядков, их сечения поглощения равны
на много порядков меньше, чем у линейного однофотонного
процесс. Для эффективного
возбуждение. Однако такие импульсы фототоксичны для клетки, потому что
они ускоряют радикальное производство, тем самым ограничивая доступный
время наблюдения до повреждения клеток.
Нелинейная зависимость между испусканием флуоресценции (F)
а возбуждающий свет (I ex ) «сжимает»
выброс PSF. «Вход» возбуждения PSF (синий, Left ) будет преобразован в «выход» излучения
PSF (зеленый, , правый ) через «нелинейную флуоресценцию».
ящик »( Центр ). Диаграмма Яблонского вверху справа
«ящика флуоресценции» описывает произвольную нелинейную
процесса возбуждения (хотя для
I ex , он может описывать многофотонный процесс). Выходной PSF
нормализуется и сравнивается с входным PSF.
Выходной PSF
нормализуется и сравнивается с входным PSF.
Осознание недостатков многофотонного возбуждения для сверхразрешения
визуализации, адская группа искала альтернативу
«Умные» нелинейности, использующие видимый, а не инфракрасный
возбуждения и имеют большие эффективные сечения. Хотя предыдущие
подходы к флуоресценции как к линейному процессу, группа Ада
искали способы использовать спектроскопические свойства
флуорофоры для создания таких нелинейностей.Они предложили и
теоретически исследовали возможность торможения
резонансный перенос энергии флуоресценции при насыщении донора
условия для донорно-акцепторной пары красителей (12, 13). Более
недавно они предложили схему, основанную на многократном возбуждении
зонд накачки с короткими импульсами для эффективного продления флуоресценции
время жизни молекул в центре PSF (по сравнению с молекулами
на окраине) (14). Оба предложения пока ждут экспериментального
проверка.Их третье и более раннее предложение (15) теперь было
экспериментально продемонстрировано (9, 16).
Концепция, получившая название «инжиниринг функции распределения точки (PSFE)»
истощение стимулированных выбросов (STED) »опирается на два основных
ингредиенты: ( и ) флуорофоры, которые действуют как эффективные
четырехуровневые системы и демонстрируют очень эффективное стимулированное излучение (как
хорошие лазерные красители делают), и ( ii ) невырожденный (разные
длина волны) схема накачка-зонд, возбуждающая флуорофоры одним
балка и закаливает их с другой.Короткий (200 фс) видимый импульс
фокусируется в ограниченное дифракцией фокусное пятно и возбуждает все
флуорофоры в этом томе. Второй ближний инфракрасный и более длинный импульс
(40 пс) стимулирует излучение молекул во внешней части
фокус, переводя их в основное состояние сразу после того, как они
взволнованный. Большая длительность этого второго импульса гарантирует полное
закалка без реабсорбции. Прелесть такого подхода в
использование двух конструктивных эффектов: во-первых, закалка
эффективность экспоненциально масштабируется с интенсивностью STED (в отличие от
степенной зависимости в многофотонных процессах) и, следовательно, требует
только умеренные мощности.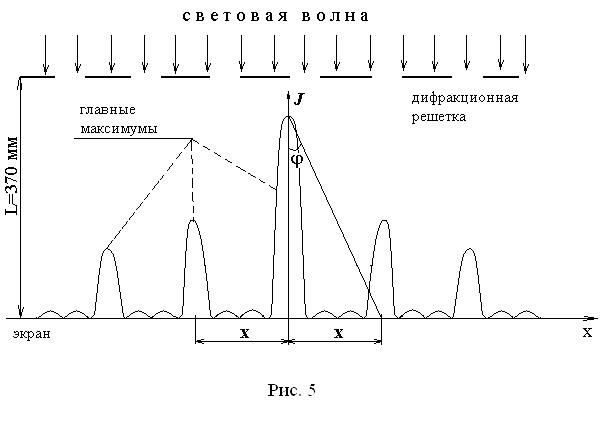 Во-вторых, сечение вынужденного излучения
велико и сравнимо с сечением однофотонного возбуждения. В
вырезание и изменение формы PSF достигается с помощью фазовой маски, которая
вставлен в путь луча STED. Фазовая маска перераспределяет STED
энергии, давая нулевую интенсивность (узел) в точном фокусе, но
сохранение крыльев балки СТЭД. Эти крылья являются «резьбой по дереву».
нож », который гасит флуоресценцию и сжимает обнаруженные
(эмиссия) PSF. Рис. 2 иллюстрирует
основы техники.На рис.2 a показан Jablonski.
(энергетический уровень), спектры поглощения и излучения
флуорофор и спектральное выравнивание возбуждения и STED
импульсы. На рис. 2 b показано, как сужается размер PSF.
одно измерение с помощью этого метода (иллюстрация в одном измерении
только для демонстрации; усадка эффективна во всех трех
Габаритные размеры).
Во-вторых, сечение вынужденного излучения
велико и сравнимо с сечением однофотонного возбуждения. В
вырезание и изменение формы PSF достигается с помощью фазовой маски, которая
вставлен в путь луча STED. Фазовая маска перераспределяет STED
энергии, давая нулевую интенсивность (узел) в точном фокусе, но
сохранение крыльев балки СТЭД. Эти крылья являются «резьбой по дереву».
нож », который гасит флуоресценцию и сжимает обнаруженные
(эмиссия) PSF. Рис. 2 иллюстрирует
основы техники.На рис.2 a показан Jablonski.
(энергетический уровень), спектры поглощения и излучения
флуорофор и спектральное выравнивание возбуждения и STED
импульсы. На рис. 2 b показано, как сужается размер PSF.
одно измерение с помощью этого метода (иллюстрация в одном измерении
только для демонстрации; усадка эффективна во всех трех
Габаритные размеры).
PSFE фирмы STED. ( a Левый ) Диаграмма Яблонского, показывающая
земля (S 0 ) и первый возбужденный синглет (S 1 )
состояния флуорофора с соответствующими колебательными многообразиями. Флуорофор действует как эффективная четырехуровневая система, поскольку
колебательные релаксации S 1 и S 0 происходят быстро
по сравнению со временем жизни флуоресценции. Короткий пульс
(I ex , 200 фс) возбуждает флуорофор в
колебательное состояние S 1 . Медленный импульс STED (STED, 40 пс)
стимулирует излучение из низшего колебательного состояния S 1 в высокое колебательное состояние S 0 . Стимулированный
Эмиссия истощает S 1 и гасит флуоресценцию.( Справа ) Диаграмма эквивалентных длин волн, показывающая
кривая поглощения (пунктирная черная линия), кривая излучения (сплошная черная линия)
линия), а также позиции I ex , STED и фильтра (F).
Фильтр блокирует два лазера и пропускает сигнал (заштрихованный зеленым).
( b ) Комбинация возбуждения PSF (синий) с
инженерное распределение интенсивности STED (красный) действует как вход для
PSFE от STED «нелинейный ящик».
Флуорофор действует как эффективная четырехуровневая система, поскольку
колебательные релаксации S 1 и S 0 происходят быстро
по сравнению со временем жизни флуоресценции. Короткий пульс
(I ex , 200 фс) возбуждает флуорофор в
колебательное состояние S 1 . Медленный импульс STED (STED, 40 пс)
стимулирует излучение из низшего колебательного состояния S 1 в высокое колебательное состояние S 0 . Стимулированный
Эмиссия истощает S 1 и гасит флуоресценцию.( Справа ) Диаграмма эквивалентных длин волн, показывающая
кривая поглощения (пунктирная черная линия), кривая излучения (сплошная черная линия)
линия), а также позиции I ex , STED и фильтра (F).
Фильтр блокирует два лазера и пропускает сигнал (заштрихованный зеленым).
( b ) Комбинация возбуждения PSF (синий) с
инженерное распределение интенсивности STED (красный) действует как вход для
PSFE от STED «нелинейный ящик». Выходной PSF (зеленый)
сжался.
Выходной PSF (зеленый)
сжался.
Используя очень простую неоптимизированную фазовую маску, Klar et al. смогли преодолеть дифракционный предел и уменьшить ФРТ в раз
в шесть раз по оптической оси и в два раза по радиальной
направления, уменьшая объем конфокального пятна в раз
2 × 2 × 6 ≈ 18 (математика немного усложняется из-за
эффект преображения!). Что очень важно, они показали, что их
Метод сверхразрешения совместим с визуализацией живых клеток (9). В
фундаментальные ограничения методики пока не ясны. В
В принципе, по мере увеличения интенсивности пучка STED степень
PSF следует дополнительно уменьшить.Однако фотофизические
свойства флуорофоров (квантовые выходы, скорости межсистемного пересечения,
времена жизни триплетных состояний, скорости безызлучательного распада, насыщение
интенсивности, скорости фотообесцвечивания) и других физических факторов, таких как
концентрация зонда в фокусном объеме, несовершенство фильтров и
утечка возбуждающего и СТЭД-лучей в полосу детектирования,
определит пределы разрешения техники. Теоретические и
экспериментальные исследования, посвященные этим вопросам, будут необходимы для
оценить конечные возможности техники.Независимо от
результаты этих исследований, совершенно ясно, что многие улучшения могут
можно себе представить.
Теоретические и
экспериментальные исследования, посвященные этим вопросам, будут необходимы для
оценить конечные возможности техники.Независимо от
результаты этих исследований, совершенно ясно, что многие улучшения могут
можно себе представить.
Объединение PSFE от STED с одним или несколькими другими сверхразрешениями
техники, вероятно, последуют. Восстановление трехмерного изображения
деконволюция очевидно совместима. СТЭД в сочетании с неоднородной
схемы периодического возбуждения обеспечат сложный контроль
световые нанометрические схемы возбуждения в трех измерениях.
Гибридный подход, сочетающий двухфотонное возбуждение с однофотонным STED.
может предложить улучшение отношения сигнал / шум (за счет более высокого
интенсивности).Кроме того, возможно, можно будет использовать адаптивную оптику.
методы улучшения формы пучка STED. Управляемый компьютером
пространственный модулятор света или деформируемое зеркало могут заменить неподвижное
фазовая маска. Адаптивные алгоритмы, такие как генетическая эволюция (17), могут
позволяют контролировать и оптимизировать амплитуду импульса STED,
фазовое и пространственное распределение в фокусном пятне, обеспечивающее
контроль, манипулирование и оптимизация формы
пятно сверхвысокого разрешения.
Разработка оптимизированных датчиков для PSFE компанией STED в значительной мере
принесут пользу будущим приложениям.Технику будет нелегко расширить
к многоцветным зондам, потому что импульсы STED с разной длиной волны будут
нужный. Тем не менее, должна быть возможность мультиплексировать несколько
сигналы с помощью пробников одного цвета, но с разным сроком службы.
Поскольку этот метод основан на импульсном возбуждении, флуоресценция
пожизненная визуализация (FLIM) (18) с помощью таймерного обнаружения или
коррелированный по времени подсчет одиночных фотонов может производиться одновременно
реализовано. Сочетание FLIM с PSFE от STED позволит динамично
колокализация клеточных факторов с точностью сверхразрешения в
живая клетка.Еще одна интересная область для будущих исследований — это
комбинация PSFE от STED с резонансным переносом энергии флуоресценции
торможение (13). Наконец, уменьшенный объем PSF должен улучшиться.
эксперименты с одной молекулой, объединяющие сверхвысокое разрешение с
сверхчувствительное обнаружение.
Работа Клара и др. . имеет потенциал преобразовать
флуоресцентная микроскопия «Возрождение» мы в настоящее время
переживать «Тысячелетие Просвещения». Наше восприятие
идей, выдвинутых Аббе более века назад, безусловно, будут
преобразованный.Мощная концепция свадебных нелинейных микроскопов
с индивидуальными фотофизическими свойствами флуорофоров продолжит
создавать инновационные методологии и открывать новые окна в сотовых
динамика. Перечисленные выше несколько предсказаний — лишь небольшая часть
что будет дальше, и эта красивая история на этом не закончится:
эта техника может предложить даже больше, чем визуализацию живых клеток и
биология. Пространственные и временные манипуляции амплитудой и фазой
коротких импульсов может обеспечить когерентный контроль химических реакций на
нанометровая шкала.Такие возможности могут найти применение, например, в
контроль химического состава фоторезиста для литографии сверхвысокого разрешения,
электрооптика, магнитооптика для хранения данных и многое другое.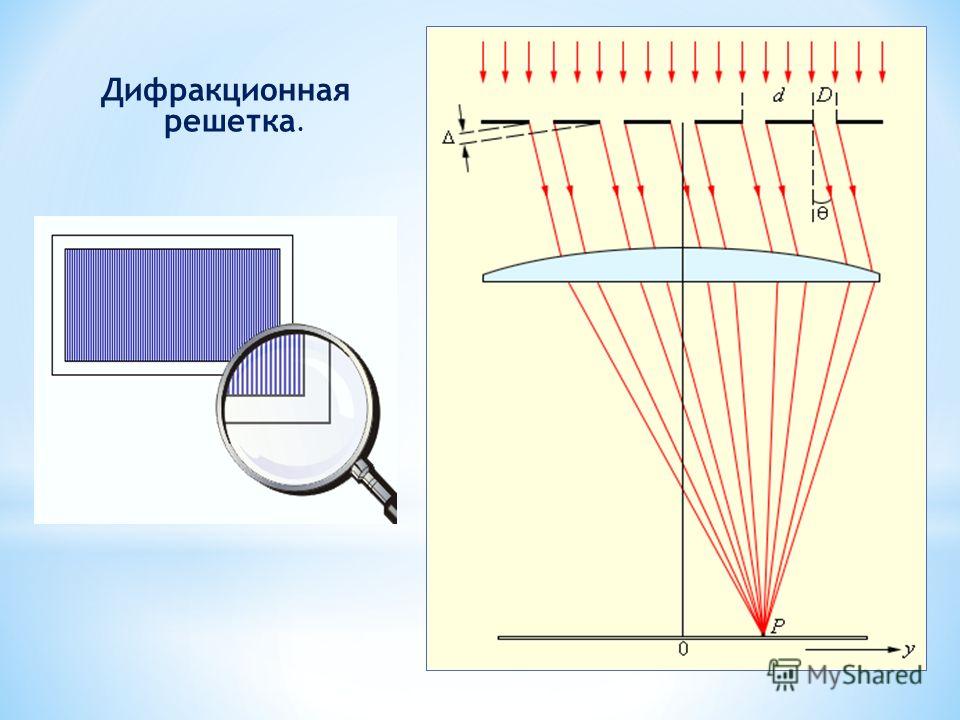 приложения нанотехнологий. Держать глаза открытыми!
приложения нанотехнологий. Держать глаза открытыми!
Благодарности
Благодарю Дженнифер Гласс, Тило Лакоста, Теда Лоуренса и Ксавьера. Мишале за критическое чтение и содержательные комментарии. Исследование из этой лаборатории поддерживается Лабораторией направленного исследования и Программа развития Национальной лаборатории Лоуренса Беркли и Директор, Управление науки, Управление биологии и окружающей среды Исследования U.S. Министерство энергетики по контракту № DE-AC03–76SF00098 и контракт Управления военно-морских исследований N0001498F0402.
Сноски
↵ * Эл. Почта: sweiss {at} lbl.gov.
См. Сопутствующую статью на странице 8206 в выпуске 15 тома 97.
- Авторские права © 2000, Национальная академия наук
Получение изображений с ограничением дифракции
Если изображение создается через маленькую апертуру, есть точка, в которой разрешение изображения ограничено дифракцией апертуры. Обычно в фотографической оптике использование меньшей диафрагмы (большее число f) дает большую глубину резкости и, как правило, более резкое изображение. Но если сделать апертуру слишком маленькой , эффекты дифракции будут достаточно большими, чтобы начать уменьшать эту резкость, и вы достигли точки формирования изображения с ограничением дифракции.
Обычно в фотографической оптике использование меньшей диафрагмы (большее число f) дает большую глубину резкости и, как правило, более резкое изображение. Но если сделать апертуру слишком маленькой , эффекты дифракции будут достаточно большими, чтобы начать уменьшать эту резкость, и вы достигли точки формирования изображения с ограничением дифракции.
Если вы визуализируете две световые точки, то наименьшее расстояние, на котором вы можете различить, что есть две точки, можно разумно использовать в качестве предела разрешения процесса визуализации.Если предположить, что дифракция является определяющим фактором, то общепринятым критерием минимальной разрешаемой детали является критерий Рэлея.
Здесь показаны кривые интенсивности радиального распределения дифрагированного света для различных расстояний. Ваш глаз видит характерное распределение света «мишень», как показано ниже.
Хотя идеальное изображение источника представляло бы собой идеальные круги света меньшего размера, это показывает размытие света за счет дифракции в образцах «яблочко».
Для современной цифровой фотографии, когда изображения проецируются на ПЗС, информация собирается на пикселях цифрового детектора. Слева — попытка показать влияние дифракции на такое изображение в тех случаях, когда дифракция является явлением, ограничивающим разрешение. Если изображение находится в фокусе и на нем нет видимых эффектов аберраций объектива, возможно, оно уместится на один пиксель. Но если апертура достаточно мала, то дифракция может распространить изображение на соседние пиксели и ограничить разрешение изображения. |
Ссылки:
На сайте Cambridge in Color есть расчеты и демонстрации дифракционного расплывания при различных f-числах.
Предел дифракции света
Предел дифракции в контексте микроскопии сверхвысокого разрешения
Существует множество факторов, которые могут повлиять на конечное разрешение оптической системы визуализации, такой как микроскоп, но наиболее важным из них является дифракционный предел свет .
Разрешение микроскопа обратно пропорционально длине волны наблюдаемого света и прямо пропорционально размеру самого объектива.
Еще в 1873 году немецкий физик Эрнст Аббе обнаружил, что у микроскопов есть ограничения из-за дифракции света. Его исследование показало, что разрешение микроскопа связано не с качеством самих компонентов микроскопа, а с длиной волны используемого света и апертурой оптики.
Из-за этого явления микроскоп не может разрешить два объекта, если они расположены на расстоянии, меньшем, чем λ / 2NA, где λ — длина волны света, а NA — числовая апертура объектива, формирующего изображение.Это означает, что дифракционный предел света не позволяет микроскопу различать два объекта, разделенных поперечным расстоянием, которое меньше половины длины волны света, который использовался для изображения образца [2-3].
Аббе обнаружил, что изображения состоят из массива из дифракционно-ограниченных пятен с изменяемой интенсивностью, которые перекрывают друг друга для получения окончательного изображения. Есть несколько вариантов перекрытия этих ограничений и максимального увеличения пространственного разрешения и контрастности изображения, чтобы уменьшить размер пятен, которые ограничены дифракцией света .Например, можно уменьшить длину волны изображения, увеличить числовую апертуру или использовать среду формирования изображения, которая имеет большой показатель преломления [4].
Рисунок 2: Схема, показывающая разницу между хорошим и плохим разрешением с учетом дифракционного предела света
Как преодолеть дифракционный предел света
?Микроскопия со структурированным освещением сверхвысокого разрешения увеличивает пространственное разрешение в два раза по сравнению с микроскопией с широким полем.В 2D / 3D -SIM поперечное и осевое разрешение улучшены на 100 нм и 250 нм соответственно.
Преимущества SR-SIMSR-SIM также позволяет получать 4D-изображения с высокой частотой кадров. Обычно для фильтрации необработанных изображений необходимо девять для 2D / 3D- SIM , в то время как для STORM / PALM необходимо иметь не менее тысячи.
Возможно использование обычных флуорофоров, открывающих доступ к существующим биологическим мутированным клеточным линиям.
До четырех различных длин волн [1] можно использовать с микроскопом с подсветкой структуры , что делает этот метод очень полезным для совместной локализации или доступа к множественной информации с высоким разрешением внутри клеток и органелл.
Наконец, подготовка образцов для наблюдений SR-SIM проще, чем другие методы сверхвысокого разрешения, такие как STED или STLM [2].
Ограничения SR-SIMЭтот метод микроскопии со сверхвысоким разрешением очень чувствителен к расфокусированному свету, и его очень трудно сфокусировать на толстых образцах или образцах с плотной меткой [3].
Кроме того, в то время как методы PALM / STORM или STED могут достигать 20 нм бокового дифракционного предела , микроскопия со структурированным освещением ограничена 200 нм [4].
Наконец, во время реконструкции изображения могут возникать некоторые артефакты, которые могут ухудшить качество изображения [5].
Рисунок 3: Схема различных этапов до, во время и после наблюдений SR-SIM, которая включает подготовку образца, наблюдение и реконструкцию изображений [5].
За дифракционным пределом | Природа Фотоника
Появление схем визуализации, способных преодолеть дифракционный барьер Аббе, произвело революцию в оптической микроскопии.
В 1873 году немецкий физик Эрнст Аббе понял, что разрешающая способность оптических приборов для получения изображений, включая телескопы и микроскопы, в основном ограничена дифракцией света.Его открытие показало, что в конечном итоге разрешение визуализирующего прибора ограничивается не качеством прибора, а длиной волны используемого света и апертурой его оптики. Это означало, что микроскоп не мог разрешить два объекта, расположенных ближе, чем λ / 2NA, где λ — длина волны света, а NA — числовая апертура объектива, формирующего изображение.
Это ограниченное дифракцией явление препятствовало работе оптической микроскопии более века и считалось фундаментальным, нерушимым правилом.Однако недавно появилось несколько новых интересных подходов к визуализации, которые могут «нарушить» это правило при определенных обстоятельствах. Теперь кажется, что нет фундаментальных ограничений в достижении пространственного разрешения; используя видимый свет, с помощью этих подходов можно разрешить до нескольких нанометров.
Чтобы отметить эти достижения, в этом выпуске особое внимание уделяется методам получения изображений сверхвысокого разрешения, которые работают за пределами дифракционного предела. Здесь можно найти сборник статей о различных методах визуализации — от флуоресценции в дальней зоне до плазмоники.Сборник состоит из обзорной статьи, статьи о прогрессе, двух комментариев и интервью.
Предоставлено: XIAOWEI ZHUANG / HARVARD UNIVERSITY
В интервью на странице 368 W. E. Moerner подчеркивает некоторые невероятные преимущества визуализации, когда она не ограничивается дифракцией 1 . Такие методы не только позволяют неинвазивным образом исследовать внутреннюю часть биологических клеток, но и обещают наноизображение полупроводниковых устройств в электронной промышленности.Мёрнер элегантно резюмирует преимущества и недостатки различных подходов к визуализации с ограничением субдифракции, разработанных на сегодняшний день, а также обсуждает перспективы использования таких методов в будущем.
Читая эти статьи, вы обнаружите, что методы можно разделить на несколько групп. Во-первых, существуют подходы ближнего и дальнего поля: первые работают рядом с образцом, часто собирая быстро затухающие сигналы, которые содержат дополнительную информацию о образце, тогда как последний собирает оптические сигналы (обычно флуоресценцию) на нормальном рабочем расстоянии. .Затем методы визуализации на основе флуоресценции можно разделить на отдельные категории в зависимости от того, как они видят природу образца — либо как набор отдельных молекулярных меток, либо как флуорофор с постоянно изменяющейся плотностью. Методы, включающие переключение оптических сигналов, также можно разделить на категории по способам разделения сигналов — либо целевым переключением сигналов, либо стохастическим переключением одиночных молекул.
Подход, который, несомненно, вызвал большой интерес в сообществе специалистов по визуализации дальнего поля, — это микроскопия истощения с использованием стимулированного излучения, впервые примененная Стефаном Хеллом.На странице 381 Хелл и его коллеги рассматривают недавний прогресс в создании трехмерных изображений прозрачных флуоресцентных объектов с помощью наноскопии в дальней зоне 2 . Они объясняют, как две противоположные линзы в сочетании с включением (включением и выключением) флуоресценции между соседними маркерами могут преодолеть дифракционный барьер. Хотя приведенные примеры представляют собой микроскопию истощения с помощью стимулированного излучения и микроскопию локализации фотоактивации, авторы предполагают, что схемы с двумя линзами могут быть применены к другим подходам и, в конечном итоге, станут центральными для трехмерной оптической визуализации в дальней зоне на наноуровне.
В биологии микроскопия стохастической оптической реконструкции — методика, в которой используются детектирование одиночных молекул и фотопереключаемые зонды для получения флуоресцентных изображений с высоким разрешением — теперь позволяет визуализировать внутреннюю часть клеток с беспрецедентным уровнем детализации. На странице 365 Сяовей Чжуан объясняет, как с помощью этого подхода можно достичь пространственного разрешения в несколько десятков нанометров. 3 . Она также описывает, как многоцветную трехмерную микроскопию стохастической оптической реконструкции можно найти хорошее применение для визуализации молекулярных структур в клетках.
На странице 362 Райнер Хайнцманн и Матс Густафссон рассматривают проблему субдифракционного изображения шире и обсуждают, что необходимо для того, чтобы это стало возможным. Они объясняют, как использование пространственно-неоднородного освещения и образца с нелинейным фотоответом являются единственными двумя фундаментальными требованиями для визуализации пространственно непрерывного распределения флуоресценции со сверхвысоким разрешением 4 .
Помимо флуоресценции, поверхностные плазмоны (те, которые возбуждаются на металлической поверхности или локализованы в небольшом металлическом наконечнике) также обеспечивают метод преодоления дифракционного предела света.В обзорной статье Сатоши Кавата и его коллег на странице 388 комментируется потенциал плазмоники для улучшения визуализации 5 .
Как объясняет Мёрнер в интервью, все эти различные подходы к изображению за «дифракционным пределом» дополняют друг друга. Ясно одно: достижения в области визуализации сверхвысокого разрешения сокращают разрыв между оптической микроскопией и схемами получения изображений сверхвысокого разрешения (такими как рентгеновская или электронная микроскопия), которые используют гораздо более короткие длины волн, чем видимый свет.Появление оптических микроскопов сверхвысокого разрешения позволит с новой степенью ясности наблюдать за окружающим миром. Это почти наверняка приведет к появлению очень интересной новой науки, особенно в области биологии, но не ограничиваясь ею.
Ссылки
- 1
Вон, Р. Nature Photon. 3 , 368–369 (2009).
Артикул Google Scholar
- 2
Ад, С.W., Schmidt, R. & Egner, A. Nature Photon. 3 , 381–387 (2009).
ADS Статья Google Scholar
- 3
Zhuang, X. Nature Photon. 3 , 365–367 (2009).
ADS Статья Google Scholar
- 4
Heintzmann, R. & Gustafsson, M. G. L. Nature Photon. 3 , 362–364 (2009).
ADS Статья Google Scholar
- 5
Кавата, С., Иноуе, Ю. и Верма, стр. Nature Photon. 3 , 388–394 (2009).
ADS Статья Google Scholar
Скачать ссылки
Об этой статье
Цитировать эту статью
За пределами дифракционного предела. Nature Photon 3, 361 (2009).https://doi.org/10.1038/nphoton.2009.100
Скачать цитату
Поделиться этой статьей
Все, с кем вы поделитесь следующей ссылкой, смогут прочитать это содержание:
Получить ссылку для совместного использованияИзвините, ссылка для совместного использования в настоящее время недоступно для этой статьи.
Предоставлено инициативой по обмену контентом Springer Nature SharedIt
Дополнительная литература
Определение характеристик проводящих тонких пленок ZnO, легированных алюминием, для плазмонных приложений
- F.Ф. Масуле
- И. Синно
- К. П. Мур
Прикладная физика A (2018)
Белок, ингибирующий апоптоз (NAIP), локализуется в цитокинетическом аппарате во время деления клеток.
- Франсиско Абадиа-Молина
- Вирджиния Морон-Кальвенте
- Алекс Маккензи
Научные отчеты (2017)
Какой дифракционный предел? | Nature Materials
Веселаго, В.Г. сов. Phys. Усп. 10 , 509–514 (1968).
Артикул Google Scholar
Smith, D. R. et al. Phys. Rev. Lett. 84 , 4184–4187 (2000).
CAS Статья Google Scholar
Riikonen, S., Romero, I. & García de Abajo, F. J. Phys. Ред. B 71 , 235104 (2005).
Артикул Google Scholar
Alù, A., Silveirinha, M.G., Salandrino, A. & Engheta, N. Phys. Ред. B 75 , 155410 (2007).
Артикул Google Scholar
Schwanecke, A. S. et al. J. Opt. A 9 , L1 – L2 (2007).
Артикул Google Scholar
Alù, A. & Engheta, N. Phys. Ред. E 72 , 016623 (2005).
Артикул Google Scholar
Федотов В.А., Младёнов П. Л., Просвирнин С. Л., Желудев Н. И. Phys. Ред. E 72 , 056613 (2005).
CAS Статья Google Scholar
Леонхардт, У. Наука 312 , 1777–1780 (2006).
CAS Статья Google Scholar
Schurig, D. et al. Наука 314 , 977–980 (2006).
CAS Статья Google Scholar
Федотов В.А. и др. Phys. Rev. Lett. 97 , 167401 (2006).
CAS Статья Google Scholar
Леонхардт У. и Филбин Т. Г. New J. Phys. 9 , 254 (2007).
Артикул Google Scholar
Пендри, Дж.B. Phys. Rev. Lett. 85 , 3966–3969 (2000).
CAS Статья Google Scholar
Чао, В., Хартенек, Б. Д., Лиддл, Дж. А., Андерсон, Э. Х. и Эттвуд, Д. Т. Nature 435 , 1210–1213 (2005).
CAS Статья Google Scholar
Synge, E.H. Phil Mag. 6 , 356–362 (1928).
CAS Статья Google Scholar
Чжан, X. и Лю, З. Nature Mater. 7 , 435–441 (2008).
CAS Статья Google Scholar
Blaikie, R. J. & Melville, D. O. S. J. Opt. A 7 , S176 – S183 (2005).
CAS Статья Google Scholar
Фанг, Н.и другие. Наука 308 , 534–537 (2005).
CAS Статья Google Scholar
Toraldo di Francia, G. Suppl. Nuovo Cim. 9 , 426–438 (1952).
Артикул Google Scholar
Oseen, C. W. Annln Phys. (Лейпц.) 374 , 202–204 (1922).
Артикул Google Scholar
Щелкунов, С.A. Bell Syst. Tech. J. 22 , 80–107 (1943).
Артикул Google Scholar
Bouwkamp, C. J. & de Bruijn, N. G. Philips Res. Rep. 1 , 135–158 (1945/1946).
Google Scholar
Woodward, P. M. & Lawson, J. D. J. Inst. Избрать. Англ. III 95 , 363–370 (1948).
Google Scholar
Берри, М.V. & Popescu, S. J. Phys. А 39 , 6965–6977 (2006).
Артикул Google Scholar
Феррейра, П. Дж. С. Г. и Кемпф, А. IEEE Trans. Сигнальный процесс. 54 , 3732–3740 (2006).
Артикул Google Scholar
Хуанг, Ф. М., Желудев, Н., Чен, Ю. и Гарсия де Абахо, Ф. Дж. , заявл. Phys.Lett. 90 , 091119 (2007).
Артикул Google Scholar
Хуанг Ф. М., Чен Ю., Гарсия де Абахо Ф. Дж. И Желудев Н. И. J. Opt. A 9 , S285 – S288 (2007).
Артикул Google Scholar
Предел дифракции — обзор
4.10.2.4 Near-Field CL
Основная идея преодоления дифракционного предела в микроскопии обсуждалась Synge (1928, 1932).Чтобы понять предложение Synge, мы должны ввести два понятия, которые не применимы к обычной оптике: дальнее поле и ближнее поле. Что касается источника света, наблюдатель остается в дальней зоне, когда расстояние между ним и источником света больше, чем длина волны λ излучаемого света ( d > λ). Следовательно, ближнее поле описывает диапазон в пределах длины волны света ( d <λ).
Когда наблюдатель остается в ближнем поле, теория Аббе о дифракционном пределе (Abbe, 1873), также известная как критерий Рэлея, больше не применима, и разрешение определяется только размером источника света и его удалением от поверхность.Следовательно, если тонкий образец освещается падающей плоской волной через апертуру, меньшую длины волны, возможно разрешение за пределами дифракционного предела. Для формирования изображения с разрешением, функционально зависящим только от размера зонда и расстояния между зондом и образцом, каждая из которых может быть намного меньше длины волны света, не требуется линзы с ограничением дифракции.
Сканирующий микроскоп ближнего поля обычно состоит из зонда, который может индуцировать или обнаруживать взаимодействия ближнего поля с образцом.В зависимости от того, какое свойство следует анализировать, взаимодействия в ближнем поле могут быть вызваны различными полями или волнами, такими как оптические, магнитные, электрические, тепловые, акустические или механические. Публикуемых приложений и статей так много, что их невозможно здесь процитировать. Итак, ниже мы кратко сосредоточимся только на применении к полупроводникам модифицированной сканирующей ближнепольной оптической микроскопии (СБОМ), а именно сканирующей ближнепольной электронной микроскопии, с особым вниманием к сканирующей ближнепольной катодолюминесцентной микроскопии ( SNCLM) (также называемая катодолюминесценцией ближнего поля).
Новаторские работы в этой области были выполнены Cramer et al. (1998) и Troyon et al. (1998).
Вкратце, чтобы получить исследования SNCLM в нанометровом масштабе, была разработана гибридная система, созданная с помощью SNOM, реализованного в камере SEM. Система позволяет нам отображать образец в обычном режиме SEM, исследовать местную топографию и одновременно выполнять визуализацию CL в ближнем поле.
На практике область контакта зонд-образец равномерно облучается первичными электронами, и результирующая люминесценция улавливается непосредственно над центрами рекомбинации зондом SNOM с расстоянием между зондом и образцом в несколько нанометров.Наконечник АСМ используется для дифракции затухающих волн на поверхности, а сбор света осуществляется с помощью оптического волокна. Возбуждение КЛ осуществляется непосредственно под острием с помощью обычного сфокусированного электронного пучка с помощью SEM. Было доказано улучшение пространственного разрешения по крайней мере на один порядок по сравнению с классической КЛ в дальней зоне.
