kapankov.ru — Дифракция и резкость

Полагаю, нет никакого секрета в том, что на средних диафрагмах (f4-f8) снимки получаются более резкими. В качестве подтверждения приведу результаты независимых измерений с сайта photozone.de для объектива Canon EF 50/1.2 USM L.

На графике отчетливо видно, что наилучшая резкость в центре достигается на диафрагме 4, а по всему полю кадра на диафрагме 5.6. При этом диафрагма 1.2 дает существенное снижение качества. Изменение резкости неизбежно происходит при смене диафрагмы при прочих равных условиях. Причина заключается в явлении дифракции. Разберемся с этим подробнее.

Свет имеет корпускулярно-волновую природу, схожую со звуком, жидкостями и т.п. Что происходит со звуком, который проходит через небольшое отверстие, при полной звукоизоляции препятствия? Звуковые волны распространяются так, словно отверстие является источником звука. И действительно, в соответствии с принципом Гюйгенса-Френеля, при прохождении волн через отверстие в препятствии, отверстие можно рассматривать как источник вторичных волн, которые распространяются во все стороны с той же скоростью, что и первичные волны.

Свет не является исключением. Свет имеет свойство как бы огибать препятствия при их прохождении. Это называется Дифракцией — явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Причем при уменьшении размера отверстия волны рассеиваются и накладываются друг на друга сильнее. При сильной закрытой диафрагме лучи рассеиваясь проходят разное расстояние до фокальной плоскости и часть лучей, соответственно, оказываются в другой фазе. В результате наблюдается эффект получения дифракционного рисунка, показанного на рисунке выше. Для идеально круглого отверстия плоский дифракционный рисунок называется «диском Эйри», в честь его первооткрывателя Джорджа Эйри. Размер кружка рассеивания (определяется как диаметр первого тёмного круга) используется в качестве определения теоретического предела разрешающей способности объектива.

Диаметр диска Эйри определяется формулой:

D = 1. 22*λ*f

где

λ — длина волны света, прошедшей через объектив (в фотографических расчетах используют 546 нм)
f — диафрагменное число

А теперь, представьте, что свет проходя через объектив создает на матрице две рядом находящиеся точки (два диска Эйри), которые мы можем различить. Закрывая диафрагму, происходит расширение дисков Эйри и в какой то момент эти точки сливаются друг с другом, т.е. различие между ними исчезает. Это определяется критерием Релея: два диска Эйри воспринимаются зрением как два в том случае, если между их максимумами имеется минимум с интенсивностью на 20% меньше. Иначе наш глаз не способен их видеть как два, и говорят, что они не разрешаются.

А теперь вспомним, что в фотоаппарате разрешение определяется системой объектив-сенсор. То есть за величину принимается наибольшее значение разрешающей способности. Другими словами, пока диск Эйри меньше размера пикселя, разрешающую способность определяет разрешение матрицы, а как только диск Эйри превысит размер пикселя, то соответственно за разрешающую способность уже отвечает объектив. Так вот дифракционным пределом для системы объектив-камера принято считать размер пикселя. Когда диск Эйри становится соизмеримым с размером пикселя говорят, что достигнут дифракционный предел. Вот почему на кроп-камерах с маленьким размером пикселей так важно использовать объективы высокого качества.

Можно рассчитать теоретический дифракционный предел для камеры. Например, возьмем сенсор камеры Canon EOD 5D Mark III. Размер пикселя 6.08 мкм.

f = D/(1.22*λ)=6.08/(1.22*0.546)=9.1

Обратите внимание на то, что это теоретический дифракционный предел, которые не учитывает множество факторов, таких как, аберрации, освещенность сцены и т.п. Кроме того формула подразумевают идеально круглое отверстие, тогда как диафрагма формирует в действительности многоугольник. Также нужно помнить, что в камерах используется фильтр низких частот, размывающий изображение для борьбы с муаром.

А как же быть с открытыми диафрагмами? Ведь казалось бы, чем шире отверстие, тем резче должно быть изображение, а в самом начале статьи мы обратили внимание на то, что это вовсе на так. Дело в том, что чем больше отверстие диафрагмы, тем больше света попадает на сенсор, и свет этот собирается с большей поверхности линз и чем ближе к краям, тем больше искажений происходит при этом. Взгляните на самый первый график, приемлемая резкость у Canon EF 50/1.2 USM L начинается где-то f2.

Что же это получается? Объективы имеют предельные диафрагмы f1.2 и f22, а пользоваться ими нельзя? Да нет, можно и даже нужно при определенных условиях, когда фотограф готов пожертвовать некоторой потерей детализации для увеличения глубины резкости, например. Вопрос лишь в том, насколько готов пожертвовать фотограф резкостью. И этот момент точно нельзя доверять автоматическим режимам, по крайней мере на сегодняшний день.

Еще один замечательный вывод можно сделать, что дальнейшее увеличение мегапиксельности камер не будет приводить к увеличению детализации, поскольку не существует объективов с требуемой разрешающей способностью. Потому, можно купить хоть теоретическую 100 мегапиксельную камеру, изображения четче не станут.

В заключении хочется привести слова Энсела Адамса: «Нет ничего хуже, чем резкая фотография с нечёткой идеей». Не следует гнаться за сверхрезкими фотографиями. Во многих случаях, особенно в портретной съемке некоторая мыльность снимка только улучшит восприятие. Так или иначе, знания о влиянии различных факторов на качество снимка не являются лишними.

Практическое задание

Распечатайте две мишени: отсюда и отсюда. Снимайте их со штатива, полностью заполнив кадр с ISO 100 или 200. Меняя диафрагму изучите при каких диафрагмах резкость начинает ухудшаться для вашего объектива. Сравните результаты с тестами на photozone.de.

Твитнуть

воздушный диск

---

В оптике диск Эйри ( или диск Эйри ) и узор Эйри — это описания наиболее сфокусированного светового пятна , которое может создать идеальная линза с круглой апертурой , ограниченной дифракцией света . Диск Эйри имеет важное значение в физике , оптике и астрономии .

Дифракционная картина, полученная от равномерно освещенной круглой апертуры, имеет яркую центральную область , известную как диск Эйри, который вместе с серией концентрических колец вокруг называется картиной Эйри.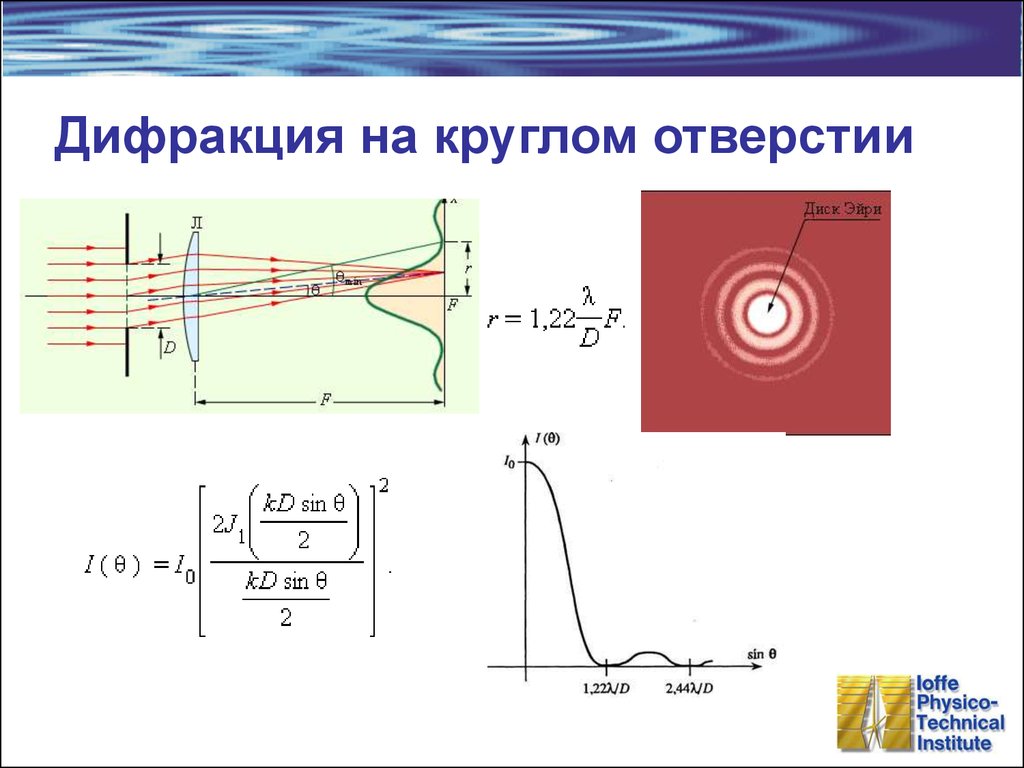 Оба названы в честь Джорджа Бидделла Эйри . Феномен диска и колец был известен еще до Эйри; Джон Гершель описал появление яркой звезды , видимой в телескоп под большим увеличением, в статье 1828 года о свете для Encyclopedia Metropolitana :

… звезда тогда видна (при благоприятных условиях спокойной атмосферы, одинаковой температуры и т. д.) как идеально круглый, четко очерченный планетарный диск, окруженный двумя, тремя или более попеременно темными и яркими кольцами, которые, если при внимательном рассмотрении видны слегка окрашенные края. Они сменяют друг друга почти через равные промежутки вокруг центрального диска…. ^[1]

Эйри написал первое полное теоретическое рассмотрение, объясняющее это явление (его 1835 г. «О дифракции предметного стекла с круглой апертурой»). ^[2]

Математически дифракционная картина характеризуется длиной волны света, освещающего круглое отверстие, и размером отверстия. Внешний вид дифракционной картины дополнительно характеризуется чувствительностью глаза или другого детектора, используемого для наблюдения картины.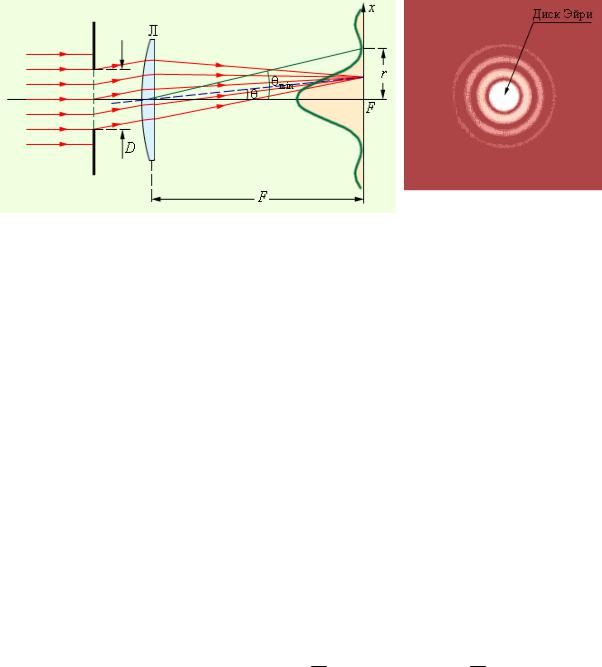

Наиболее важным применением этой концепции являются камеры , микроскопы и телескопы. Из-за дифракции наименьшая точка, в которую линза или зеркало могут сфокусировать пучок света, равна размеру диска Эйри. Даже если бы удалось сделать совершенный объектив, все равно существует предел разрешающей способности изображения, создаваемого таким объективом. Оптическая система, в которой разрешение больше не ограничено несовершенствами линз, а только дифракцией, называется дифракционно-ограниченной .

---

Компьютерное изображение диска Эйри. Интенсивность оттенков серого была скорректирована для повышения яркости внешних колец узора Эйри.

Сгенерированный компьютером диск Эйри из дифрагированного белого света ( спектр D65 ). Обратите внимание, что красный компонент дифрагирует больше, чем синий, так что центр кажется слегка голубоватым.

Настоящий диск Эйри, созданный путем пропускания красного лазерного луча через отверстие диаметром 90 микрометров с дифракцией 27 порядков.

Диск Эйри, снятый объективом камеры с фокусным расстоянием 2000 мм и диафрагмой f/25. {2} / \ лямбда}

Дифракция от отверстия с линзой. Изображение в дальней зоне будет (только) формироваться на экране на расстоянии одного фокусного расстояния, где R=f (f=фокусное расстояние). Угол обзора остается таким же, как и в безлинзовом случае.θ{\ Displaystyle \ тета}

Паттерн Эйри на интервале ka sin θ  = [−10, 10]

Обведенная мощность отображается на графике рядом с интенсивностью.

Радиальное поперечное сечение модели Эйри (сплошная кривая) и ее аппроксимация гауссовым профилем (штриховая кривая). Абсцисса дана в единицах длины волны, умноженной на f-число оптической системы.λ{\ Displaystyle \ лямбда}

Онлайн-кампус микроскопии ZEISS | Interactive Tutorials

Когда изображение формируется в плоскости сфокусированного изображения оптического микроскопа, каждая точка образца представляется дифракционной картиной Эйри с конечным разбросом. Это происходит потому, что световые волны, излучаемые точечным источником, не фокусируются объективом в бесконечно малую точку, а сходятся вместе и интерферируют вблизи плоскости промежуточного изображения, создавая трехмерную дифракционную картину Фраунгофера.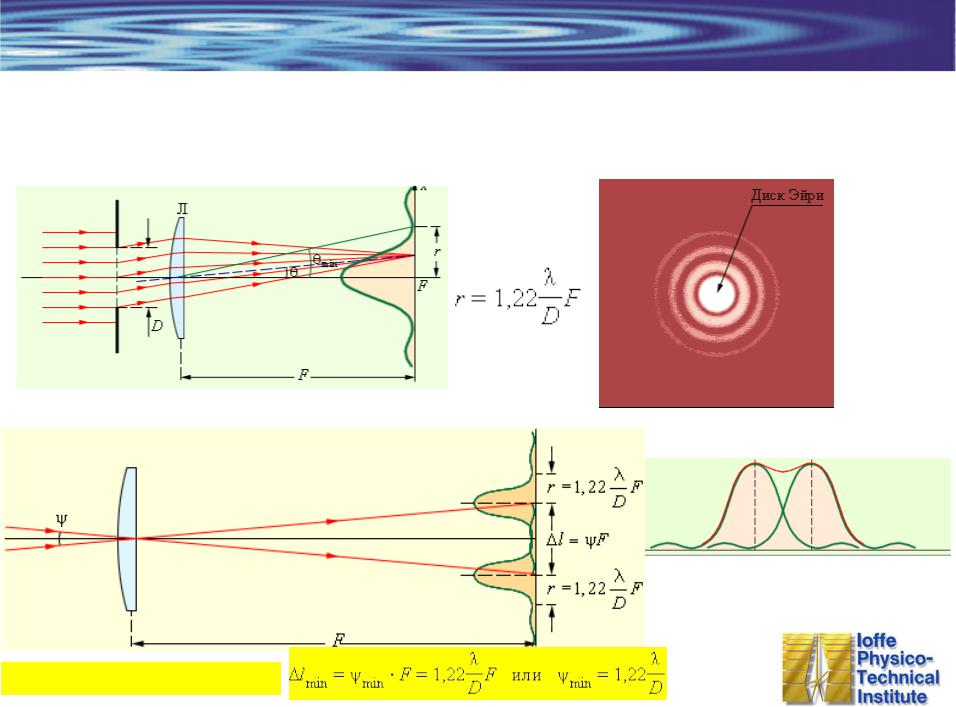 В этом интерактивном учебном пособии исследуется происхождение дифракционных картин Эйри, формируемых задней апертурой объектива микроскопа и наблюдаемых в плоскости промежуточного изображения.

Формирование паттерна Эйри Плоскость изображения Распространение вейвлета

A’ ₀

A’ ₀

Плоскость изображенияSpherical WavefrontObjectiveSpherical WavefrontPoint SourceAAngular Apertureθ 9000 3 м _-1 м ₁ м ₀

А’ ₀

Image PlaneIntensityImage Plane

В учебном пособии анимированный рисунок слева представляет собой схематическую иллюстрацию оптической системы микроскопа, в которой одна линза (обозначенная цифрой 9)0031 Объектив ) представляет собой объектив микроскопа. Монохроматический свет излучается точечным источником на воображаемый образец (помеченный точкой A ), размер которого меньше, чем можно разрешить с помощью оптики микроскопа. Предполагая, что показатель преломления среды изображения равен n , а угловая апертура объектива равна θ , числовая апертура равна:

Числовая апертура (NA) = n(sinθ)(1)

В плоскости промежуточного изображения, точка A’ ₀ представляет собой распределение света, излучаемого точечным источником A .

Сферическая волновая поверхность, исходящая от объектива, состоит из ряда точечных источников, каждый из которых излучает сферическую волну (называемую вейвлетом Гюйгенса), которые создают соответствующие волновые поверхности в плоскости изображения с центрами в точке A’ ₀ . Для целей этого интерактивного руководства вейвлеты изображены возникающими из трех точек на сферическом волновом фронте ( M ₀ , M ₁ и M _-1 ), которые приходят в точку A’ ₀ в фазе и подвергаться конструктивной интерференции, чтобы получить яркое изображение апертуры.

Ползунок Wavelet Spread можно использовать для преобразования вейвлетов, исходящих из точек M ₀ , M ₁ и M _{-1 900 08} от точки A’ ₀ в плоскости изображения. При перемещении ползунка слева направо вейвлеты, разбросанные по плоскости изображения, проходят через точки

A’ _n и A’ _-n . Эти вейвлеты, испускаемые из всех точек вдоль сферического волнового фронта, должны двигаться дальше, прежде чем достигнут плоскости изображения, и становятся все более несовпадающими по фазе, формируя распределение интенсивности света, которое спадает по колоколообразной кривой. Распределение света в плоскости изображения можно математически описать функцией Бесселя в виде:

Распределение света = (sinθ/θ)

² (2)

, где θ — угол A’ ₀ -M ₀ -A’ _n . Когда вейвлеты достигают точек A’ ₁ и A’ _-1 , они сдвинуты по фазе на 180 градусов, что приводит к деструктивной интерференции, которая отменяет каждый вейвлет. Если вклад вейвлетов, исходящих из всех точек апертуры (а не только

M ₀ , M ₁ и M _-1 ), соответствующая сумма, полученная в результате деструктивной интерференции, равна нулю, а в точках A’ ₁ и A’ _-1 света нет. Это показано графически с помощью диаграммы Эйри, представленной справа от оптической цепочки. Чередующийся концентрический узор из светлых и темных (красных) полос показан в верхней части узора Эйри, который нарисован плоскостью узора, параллельной плоскости промежуточного изображения. Синяя линия, пересекающая центр трехмерного паттерна Эйри, представляет собой точку 9.0031 A’ ₀ в плоскости изображения. Когда распространение вейвлета просматривается в плоскости изображения в учебном пособии по оптическому поезду, синяя линия, наложенная на шаблон Эйри, разделяется на два компонента ( A’ _n и A’ _-n ), которые отслеживают прогресс интенсивности центрального диска Эйри. Когда вейвлеты достигают A’ ₁ и A’ _-1 на плоскости изображения, синие линии на паттерне Эйри располагаются в первом минимуме (нулевая интенсивность).

Когда вейвлеты проходят мимо точек A’ ₁ и A’ _-1 на плоскости изображения (не показано), функция Бесселя снова поднимается выше нуля, формируя второй максимум с резко уменьшенной амплитудой. Перемещая вейвлеты еще дальше от плоскости изображения, где они продолжают интерферировать как конструктивно, так и деструктивно, функция Бесселя колеблется с постепенно уменьшающейся амплитудой, пока интенсивность не упадет до нуля. В результате получается паттерн Эйри, показанный справа в учебнике, где центральный диск Эйри окружен чередующимися чередующимися темными и светлыми зонами убывающей интенсивности, где вейвлеты взаимодействуют как конструктивно (светлые зоны), так и деструктивно (темные зоны). ). Они представляют собой дифракционные картины как нулевого, так и более высокого порядка, образованные точечным источником света в плоскости изображения идеальной (без аберраций) линзы.

---

Соавторы

Руди Роттенфуссер — консультант по микроскопии Zeiss, 46 Landfall, Falmouth, Massachusetts, 02540.

Tiehu Jiang и Майкл В. Дэвидсон — Национальная лаборатория сильного магнитного поля, 1800 г., Ист-Пол Доктор Дирак, Университет штата Флорида, Таллахасси, Флорида, 32310.

Вернуться к основам микроскопии

Вернуться к интерактивным учебным пособиям

Образцы Эйри и критерии разрешения (трехмерная версия) — Учебник по Java

Диаграммы Эйри и критерии разрешения (трехмерная версия) — Учебное пособие по Java для освещения образца используется монохроматический свет). Для хорошо скорректированного объектива с равномерной круглой апертурой две соседние точки разрешаются только тогда, когда центры их диаграмм Эйри разнесены на минимальное расстояние ( D ), равный радиусу ( r ) центрального диска в узоре Эйри. В этом учебном пособии показано, как размеры диска Эйри на пределе оптического разрешения изменяются в зависимости от числовой апертуры объектива и длины волны освещения, а также как эти изменения влияют на разрешение (

r ) и контрастность объектива по отношению к спектру Рэлея и Спэрроу. пределы, когда два точечных изображения сливаются вместе.

Учебное пособие инициализируется с помощью ползунка Длина волны , установленного на 450 нанометров в области синего цвета спектра видимого света. Также при инициализации виртуальный 9Ползунок 0031 Числовая апертура установлен на значение 0,75, а расстояние между двумя шаблонами Эйри (ползунок Степень разделения ) составляет 2,0 микрометра. Размер светового конуса будет увеличиваться с числовой апертурой (при фиксированной длине волны) и вызывать соответствующее уменьшение размера дисков Эйри (и увеличение разрешения). Уменьшение длины волны при фиксированной числовой апертуре приведет к уменьшению размера диаграммы Эйри. Узоры Airy представлены в виде трехмерной сетки под названием 9.0031 Airy Functions

и как График интенсивности в отдельном окне. Под окном Intensity Plot находится вычисление в реальном времени контраста изображения и критерия разрешения Рэлея в соответствии с теорией дифракции Аббе. Когда два шаблона Эйри достаточно разделены, чтобы удовлетворялись критерии Рэлея и Спарроу, это указывается в полях, расположенных под ползунками.

Для работы с учебным пособием используйте ползунок Длина волны для регулировки длины волны освещения.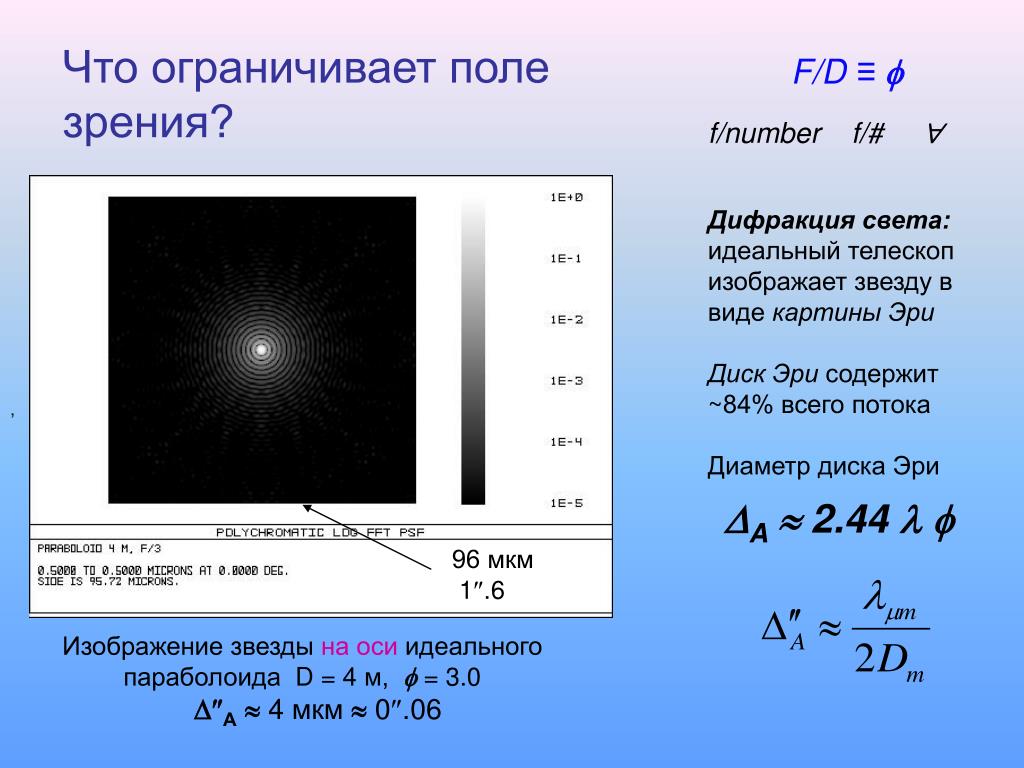 По мере уменьшения этого значения обратите внимание, как увеличивается размер диска Эйри вместе с расстоянием Рэлея при фиксированной числовой апертуре. Числовая апертура Ползунок также можно использовать для регулировки размера шаблона Эйри путем изменения числовой апертуры объектива виртуального микроскопа. По мере того как шаблоны Эйри приближаются друг к другу, путем перемещения ползунка

Степень разделения , они в конечном итоге достигают предела разделения по критерию Рэлея (обсуждается ниже), за которым следует предел Спарроу, и результирующее изображение теряет контраст. В этом учебном пособии предполагается, что линзы виртуального объектива полностью свободны от аберраций с узорами Эйри одинаковой яркости и что единичная дифракционная картина, создаваемая образцом через круглое отверстие, на самом деле является диском Эйри. Картины Эйри преобразуются в альтернативные картины дифракции из-за аберраций объектива или нестандартных условий диафрагмы.

Объекты в оптическом микроскопе, которые либо самосветятся, либо освещаются конусом света под большим углом, образуют узоры Эйри в плоскости промежуточного изображения, которые некогерентны и не мешают друг другу. Это позволяет определить минимальное разделяющее расстояние между соседними узорами Эйри путем изучения распределения общей интенсивности (суммы интенсивностей), когда эти узоры расположены близко друг к другу или перекрываются. В случае узоров Эйри, произведенных

когерентного освещения, минимальное расстояние разделения должно быть определено путем сложения амплитуд диаграммы направленности, а не их интенсивности.

Когда разделительное расстояние ( D ) между соседними узорами Эйри больше радиуса центрального диска ( r ), сумма интенсивностей дает два отдельных пика. Когда диски приближаются друг к другу, расстояние разделения достигает значения, равного центральному радиусу диска, условие, известное как критерий Рэлея. При еще большем сближении разделяющее расстояние меньше радиуса центрального диска, и сумма двух пиков сливается в один пик. В последнем случае говорят, что два паттерна Эйри не разрешены.

В идеальном случае, когда объектив свободен от аберраций и обеспечивает равномерную круглую апертуру, две соседние точки разрешаются только тогда, когда центры их дисков Эйри разнесены на

r (центральный радиус диска Эйри). Когда числовая апертура объектива совпадает с числовой апертурой предметного столика, r определяется из уравнения как иммерсионная среда и NA(obj) — числовая апертура объектива (и конденсора). Согласно теории дифракции Аббе числовая апертура объектива определяется выражением :

NA(obj) = n(sin(θ))

, где n — показатель преломления среды, разделяющей переднюю линзу объектива. и образец, и представляет собой полуконус света, захваченный объективом. Если образец не является самосветящимся или когда числовые апертуры объектива и конденсора не совпадают, уравнение для r определяется как :

r = 1,22λ/(NA(obj) + NA(cond))

где определяется рабочая числовая апертура конденсора ( NA(cond) ) от :

NA(cond) = n(sin(θ))

Рисунок 1 иллюстрирует расчетное влияние числовой апертуры конденсора на разрешение и включает значения, при которых числовая апертура объектива меньше, чем у конденсора.