Для чего предназначена гистограмма: Что такое гистограмма и как построить этот график: когда используется, какие есть виды и типы
Электронный учебник — Словарь 2М
Электронный учебник — Словарь 2М2М гистограммы. Этот термин был впервые использован Пирсоном в 1895 г.) 2М гистограммы являются графическими представлениями распределения частот выбранных переменных, на которых для каждого интервала (класса) рисуется столбец, высота которого пропорциональна частоте класса.
2М гистограммы
— Висячие столбцы. Гистограмма висячих
столбцов является «наглядным критерием
проверки на нормальность распределения»,
который помогает определить области
распределения, где возникают расхождения между
наблюдаемыми и ожидаемыми нормальными
частотами. В то время как стандартным способом
представления подогнанного к наблюдаемому
распределению нормального распределения
является наложение на гистограмму наиболее
подходящей нормальной кривой, гистограмма
висячих столбцов предлагает противоположный
способ: столбцы, представляющие наблюдаемые
частоты для последовательных диапазонов
значений, «подвешиваются» к наиболее
подходящей нормальной кривой.
Если исследуемое распределение хорошо
приближается нормальной кривой, то нижние ребра
всех столбцов должны образовать прямую
горизонтальную линию.
2М гистограммы -
Простые. Эта гистограмма представляет
собой столбчатую диаграмму распределения частот
для выбранной переменной (если выбрано более
одной переменной, то для каждой из них будет
построен отдельный график).
2М гистограммы -
С двойной осью Y. Гистограмму с двойной осью
Y можно считать комбинацией двух по-разному
масштабированных составных гистограмм. Для этой
гистограммы можно выбрать две различные группы
переменных. Для каждой из выбранных переменных
будет изображено распределение частот, но
частоты переменных из первого списка
(называемого Левая ось Y) будут
откладываться по левой оси Y, а частоты
переменных из второго списка (называемого Правая
ось Y) будут откладываться по правой оси Y.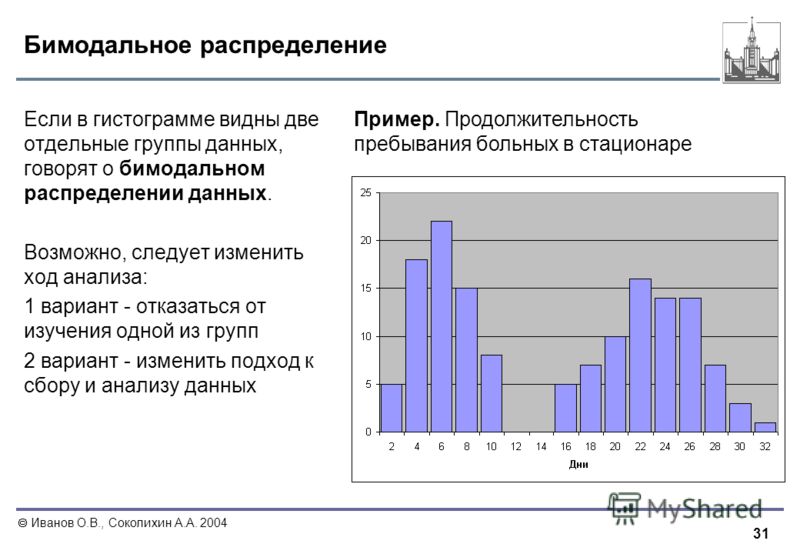 Имена всех переменных из двух списков будут
внесены в условные обозначения и будут
сопровождаться буквами Л или П,
обозначающими соответственно левую или правую
ось Y.
Имена всех переменных из двух списков будут
внесены в условные обозначения и будут
сопровождаться буквами Л или П,
обозначающими соответственно левую или правую
ось Y.
Этот график полезен для сравнения
распределений переменных с разными частотами.
2М гистограммы - Составные. Составные гистограммы изображают распределение частот для нескольких переменных на одном 2М графике. В отличие от гистограмм с двойной осью Y частоты для всех переменных откладываются по левой оси Y.
Значения всех исследуемых переменных
откладываются по одной оси
2М диаграммы
диапазонов — Отрезки.
На диаграмме диапазонов такого типа диапазоны
представлены «отрезками» с горизонтальными
черточками на обоих концах (см. следующий
рисунок).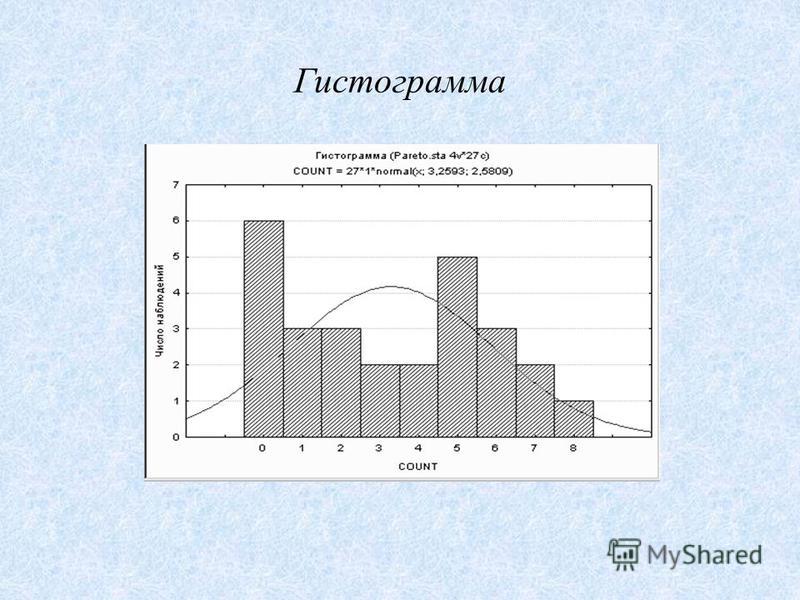 Средние точки обозначены маркерами
точек.
Средние точки обозначены маркерами
точек.
2М диаграммы
диапазонов — Прямоугольники.
На диаграмме такого типа диапазон
изображается в виде прямоугольника (верхняя
сторона которого соответствует верхней границе
диапазона, а нижняя сторона — нижней). Средние
точки изображаются либо маркерами точек, либо
горизонтальными линиями, «пересекающими»
прямоугольник.
2М диаграммы
диапазонов — Столбцы.
На диаграмме диапазонов такого типа средняя
точка представлена столбцом (т.е. верх столбца
задается значением средней точки), а диапазон
(представленный «отрезком»)
накладывается на столбец.
2М
диаграммы диапазонов — Столбцы ошибок. На
двумерной диаграмме диапазонов такого типа
диапазоны или столбцы ошибок определяются
исходными значениями выбранных переменных.
Средние точки изображаются маркерами точек. Для
каждого наблюдения строится один диапазон или
столбец ошибок. В простейшем случае нужно
выбрать три переменные, одна из которых будет
соответствовать средним точкам, другая — верхним
границам, а оставшаяся — нижним границам.
В простейшем случае нужно
выбрать три переменные, одна из которых будет
соответствовать средним точкам, другая — верхним
границам, а оставшаяся — нижним границам.
2М диаграммы
размаха. На диаграммах размаха (этот термин
был впервые использован Тьюки в 1970 г.) диапазоны
или характеристики распределения значений
выбранной переменной (или переменных)
изображаются отдельно для групп наблюдений,
заданных значениями категориальной
(группирующей) переменной. Для каждой группы
наблюдений вычисляется центральная тенденция
(например, медиана или среднее) и вариационные
статистики или статистики диапазона (например, квартили, стандартные
ошибки или стандартные
отклонения), и выбранные значения изображаются
на диаграмме размаха выбранного типа. Также
могут быть изображены точки выбросов.
2М
диаграммы размаха/медианы (блоковые
статистические графики). Этот тип блоковых
статистических графиков представляет собой диаграмму размаха для медиан (а
также минимаксных значений и 25-й и 75-й
процентилей) для столбцов или строк блока. Каждый
прямоугольник отображает данные из одного
столбца или строки.
Каждый
прямоугольник отображает данные из одного
столбца или строки.
2М диаграммы размаха — Отрезки. На диаграмме размаха такого типа диапазон (т.е. стандартная ошибка, стандартное отклонение, минимум-максимум или константа) представлен в виде отрезка (с горизонтальными черточками на обоих концах, как на показанном ниже рисунке).
2М диаграммы
размаха — Прямоугольники. На диаграмме
размаха такого типа вокруг средней точки (т.е.
среднего или медианы) рисуется прямоугольник,
который отражает выбранный диапазон (т.е.
стандартную ошибку, стандартное отклонение,
минимум-максимум или константу).
2М
диаграммы размаха — Прямоугольники — Отрезки.
На диаграммах размаха этого типа вокруг средней
точки (т.е. среднего или медианы) рисуются
прямоугольник, представляющий выбранный
диапазон (т.е. стандартную ошибку, стандартное
отклонение, минимум-максимум или константу), и
отрезок, также отражающий выбранный диапазон,
концы которого расположены вне прямоугольника
(см.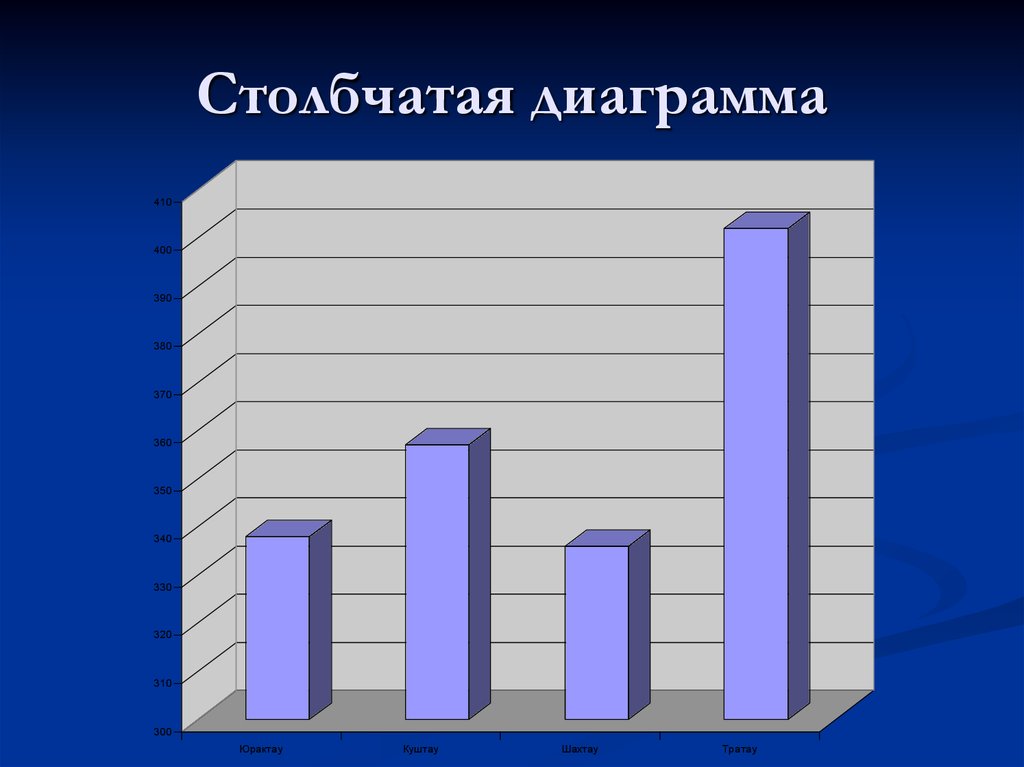
2М диаграммы размаха/средние (блоковые статистические графики). Этот тип блоковых статистических графиков представляет собой диаграмму размаха для средних (а также стандартных ошибок и стандартных отклонений) для столбцов или строк блока. Каждый прямоугольник отображает данные из одного столбца или строки.
2М диаграммы размаха — Столбцы ошибок. На статистических 2М диаграммах размаха такого типа диапазоны или столбцы ошибок вычисляются по данным. Центральная тенденция (например, медиана или среднее) и диапазон или вариационные статистики (например, значения минимума и максимума, квартили, стандартные ошибки или стандартные отклонения) вычисляются для каждой переменной, и выбранные значения представляются в виде столбцов ошибок.
На показанном выше рисунке диапазоны выбросов и крайних точек представлены
на «классической» диаграмме
размаха (о диаграммах размаха см.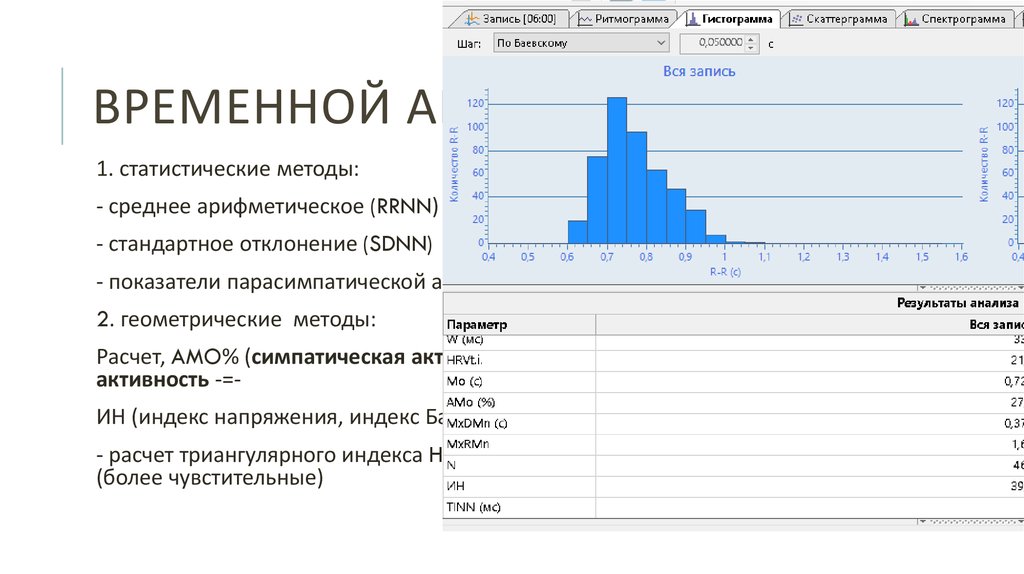 в работе
Тьюки — Tukey, 1977).
в работе
Тьюки — Tukey, 1977).
2М диаграммы рассеяния. Диаграмма рассеяния визуализирует зависимость между двумя переменными X и Y (например, весом и высотой). Данные изображаются точками в двумерном пространстве, где оси соответствуют переменным (X — горизонтальной, а Y — вертикальной оси).
Две координаты, которые определяют положение каждой точки, соответствуют значениям двух переменных.
См. также раздел Сокращение объема выборки
2М диаграммы
рассеяния Вороного. Эта особая диаграмма
рассеяния одной переменной является в большей
степени аналитическим средством, нежели просто
методом графического представления данных.
Предлагаемые ею решения помогают моделировать
множество явлений в естественных и социальных
науках (см. Coombs, 1964 г.; Ripley, 1981 г.). Программа
разделяет пространство между точками данных,
представленными координатами X, Y в двумерном
пространстве. Пространство между отдельными
точками данных делится границами на такие
области, каждая точка которых находится ближе к
заключенной внутри точке данных, чем к любой
другой соседней точке данных.
Пространство между отдельными
точками данных делится границами на такие
области, каждая точка которых находится ближе к
заключенной внутри точке данных, чем к любой
другой соседней точке данных.
Использование этого метода сильно зависит от области исследования; однако во многих случаях к этой диаграмме полезно добавлять дополнительные измерения, используя категоризацию (см. следующий рисунок).
См. также раздел Сокращение
объема выборки.
2М диаграммы
рассеяния — Простая. Простая диаграмма
рассеяния визуализирует зависимость между двумя
переменными X и Y (например, весом и высотой). Точки
данных изображаются точками в двумерном
пространстве, где оси соответствуют переменным.
Две координаты (X и Y), которые определяют
положение каждой точки, соответствуют значениям
двух переменных для этой точки.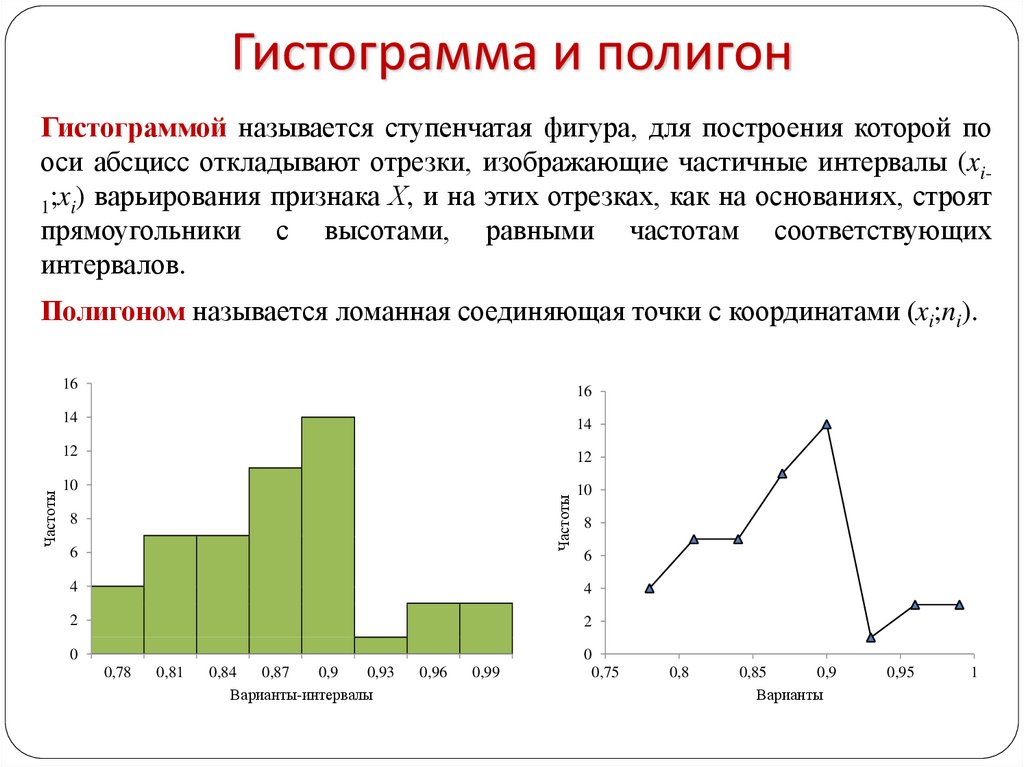 Если две
переменные сильно связаны, то множество точек
данных принимает определенную форму (например,
прямой линии или кривой). Если же переменные не
связаны, то точки образуют «облако» (на
следующем рисунке показан каьегоризованный
график для двух типов данных).
Если две
переменные сильно связаны, то множество точек
данных принимает определенную форму (например,
прямой линии или кривой). Если же переменные не
связаны, то точки образуют «облако» (на
следующем рисунке показан каьегоризованный
график для двух типов данных).
Подгонка функций к диаграмме рассеяния позволяет выявить структуру связей между переменными (см. следующий рисунок).
Другие примеры диаграмм рассеяния можно найти
в разделах Выбросы и Закрашивание. См. также
раздел Сокращение
объема выборки.
2М диаграммы
рассеяния — С двойной осью Y. Диаграмму
рассеяния такого типа можно рассматривать как
комбинацию двух составных
диаграмм рассеяния для одной переменной X и
двух различных наборов (списков) переменных Y.
Для переменной X и каждой из переменных Y будет
построена диаграмма рассеяния, но переменные из
первого списка (называемого Левая ось Y)
будут откладываться по левой оси Y, в то
время как переменные из второго списка
(называемого Правая ось Y), будут
откладываться по правой оси Y. Имена всех
переменных Y из двух списков будут включены
в условные обозначения, сопровождаемые буквой (Л)
или (П), обозначающей левую или правую ось Y
соответственно.
Имена всех
переменных Y из двух списков будут включены
в условные обозначения, сопровождаемые буквой (Л)
или (П), обозначающей левую или правую ось Y
соответственно.
Диаграммы рассеяния с двойной осью Y можно использовать для сравнения структуры нескольких корреляционных зависимостей путем изображения их на одном графике. При этом в силу независимости масштабов, используемых для двух списков переменных, этот график облегчает сравнение переменных, значения которых принадлежат разным диапазонам.
См. также раздел Сокращение
объема выборки.
2М диаграммы
рассеяния — Составная. В отличие от простой
диаграммы рассеяния, на которой одна переменная
представлена по горизонтальной, а вторая — по
вертикальной оси, составная диаграмма рассеяния
состоит из нескольких зависимостей и изображает
несколько корреляций : значения одной переменной
(X) откладываются по горизонтальной оси, а по
вертикальной оси откладываются значения
нескольких переменных (Y).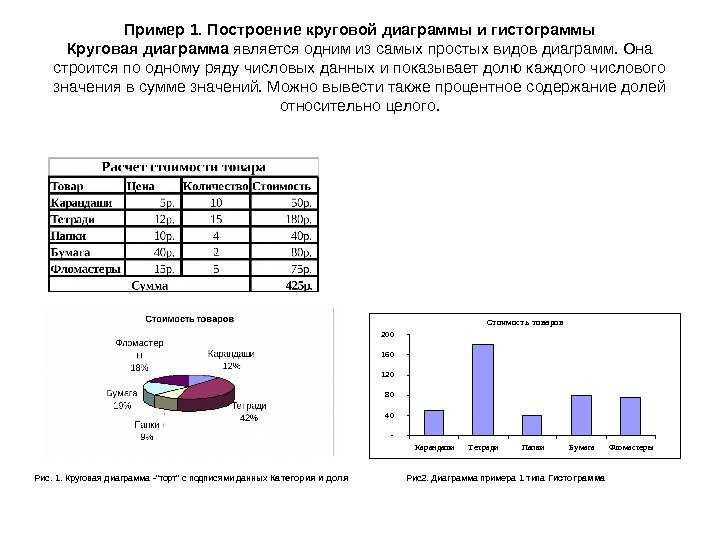 Для каждой переменной Y
используется разный цвет и вид точек, который
указан в условных обозначениях, так что на
графике можно отличить зависимости для
различных переменных.
Для каждой переменной Y
используется разный цвет и вид точек, который
указан в условных обозначениях, так что на
графике можно отличить зависимости для
различных переменных.
Диаграмма рассеяния составного типа используется для сравнения структуры нескольких корреляционных зависимостей путем изображения их на одном графике, использующем один общий масштаб (например, для выявления основной структуры факторов или измерений при анализе дискриминантных функций).
См. также раздел Сокращение
объема выборки.
2М диаграммы рассеяния — Частоты . На диаграммах частот изображаются частоты перекрывающихся точек для двух переменных, чтобы наглядно представить веса точек данных или другие измеряемые параметры.
См. также раздел Сокращение
объема выборки.
2М круговая
диаграмма. Термин «круговые
диаграммы» впервые был использован Хаскеллом
в 1922 году. На этих графиках пропорции отдельных
значений переменной X представлены в виде
круговых секторов.
Термин «круговые
диаграммы» впервые был использован Хаскеллом
в 1922 году. На этих графиках пропорции отдельных
значений переменной X представлены в виде
круговых секторов.
2М линейные графики. На линейных графиках отдельные точки данных соединены линией.
Эти графики являются простым способом
представления и исследования
последовательностей значений. Графики
трассировочного типа можно использовать для
воспроизведения следа (а не последовательности).
Также линейные графики применяются для
изображения непрерывных функций, теоретических
распределений и т.п.
2М линейные графики — Агрегированные. Агрегированные линейные графики изображают последовательность средних для последовательных подмножеств выбранной переменной.
Можно выбрать число последовательных
наблюдений, по которым будет вычислено среднее, а
при необходимости диапазон значений в каждом
подмножестве будет выделен значками типа
отрезков.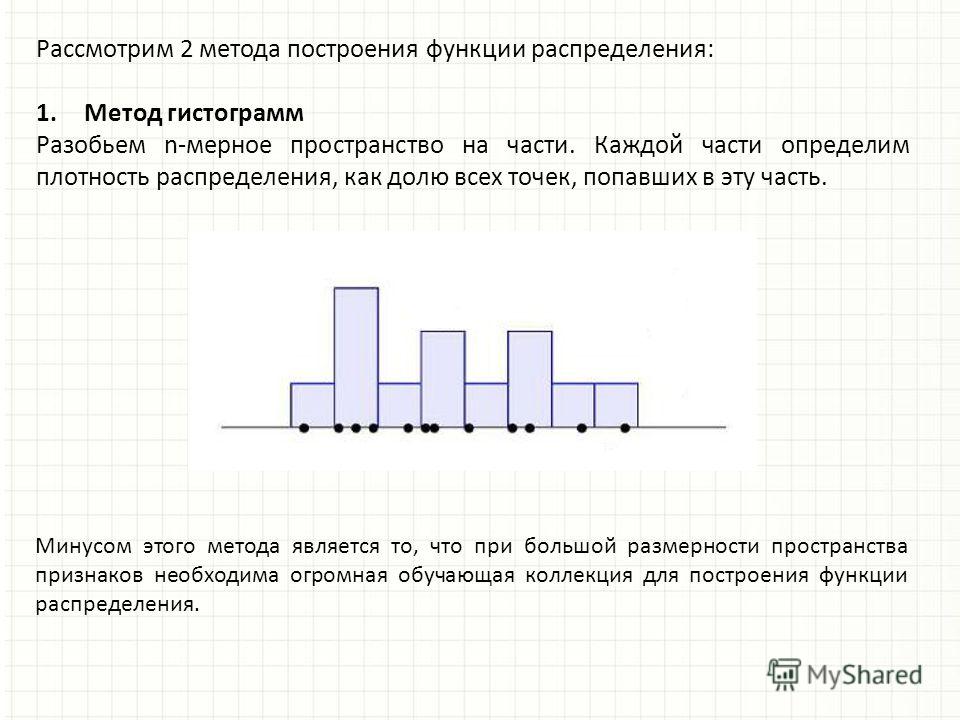 Агрегированные линейные графики
используются для представления и исследования
последовательностей большого числа значений.
Агрегированные линейные графики
используются для представления и исследования
последовательностей большого числа значений.
2М линейные графики — Простые. Простые линейные графики используются для представления и исследования последовательностей значений (обычно когда порядок значений является существенным).
Кроме того, линейные последовательные графики
применяются при построении графиков непрерывных
функций, таких как функции подгонки или
теоретические распределения. Заметьте, что
пустая ячейка данных (т.е. пропущенные данные)
«разрывает» линию.
2М линейные
графики — С двойной осью Y. Линейный
график с двойной осью Y можно рассматривать
как комбинацию двух по-разному масштабированных составных линейных
графиков. Для каждой выбранной переменной
используется свой шаблон линии; и при этом все
переменные, выбранные в списке Левая ось Y,
будут откладываться по левой оси Y, а
переменные, выбранные в списке Правая ось Y,
будут откладываться по правой оси Y.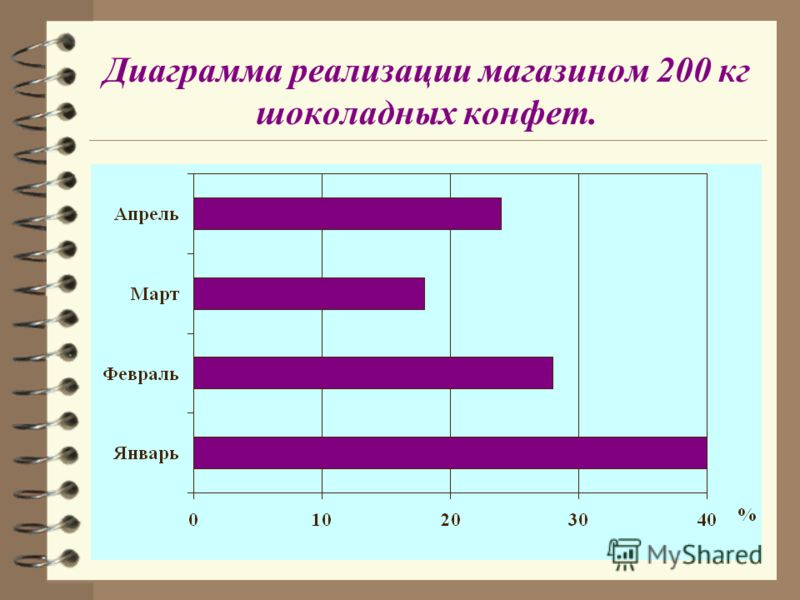 Имена
всех переменных будут указаны в условных
обозначениях вместе с буквой Л для
переменных, относящихся к левой оси Y, и с
буквой П для переменных, относящихся к
правой оси Y.
Имена
всех переменных будут указаны в условных
обозначениях вместе с буквой Л для
переменных, относящихся к левой оси Y, и с
буквой П для переменных, относящихся к
правой оси Y.
Линейный график с двойной осью Y можно
использовать для сравнения последовательностей
значений нескольких переменных, накладывая их
линейные представления на один график. В то же
время в силу независимости шкал, используемых
для двух осей, этот график может облегчить
сопоставление переменных трудно поддающихся
сравнению (т.е. имеющих значения в разных
диапазонах).
2М линейные
графики — Составные. В отличие от простых линейных
графиков, на которых представлена
последовательность значений одной переменной,
на составном линейном графике изображаются
несколько последовательностей значений
(переменных). Для каждой переменной используется
и указывается в условных обозначениях свой
шаблон и цвет линии.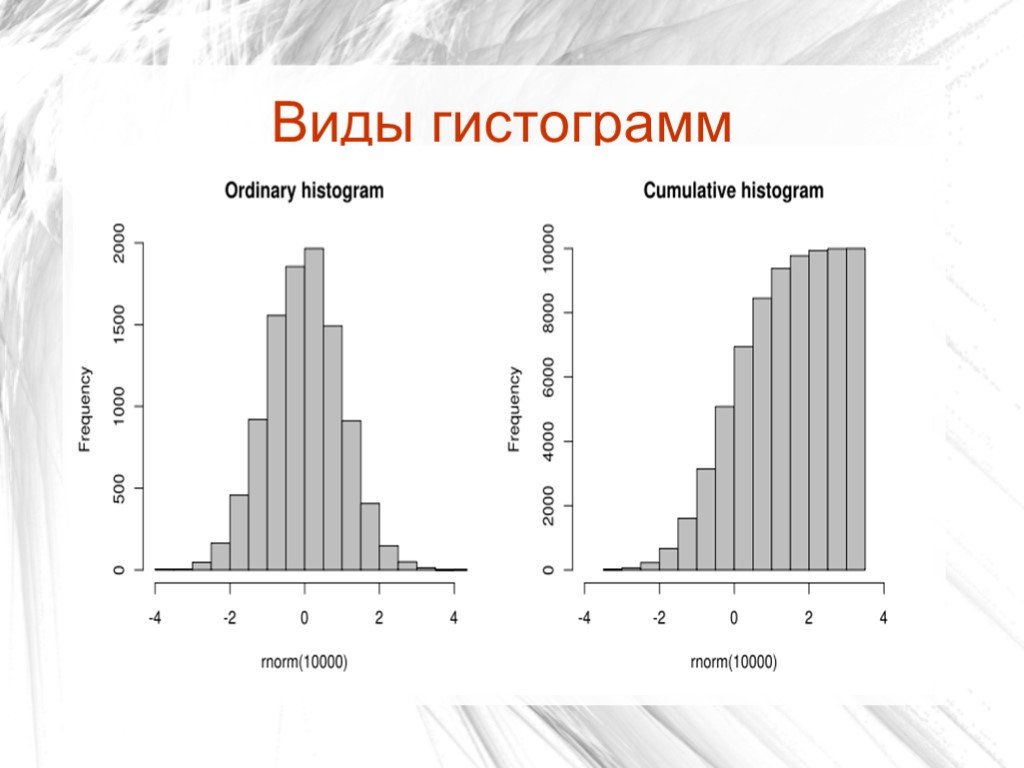
Этот тип линейных графиков используется для
сравнения последовательностей значений
нескольких переменных (или нескольких функций)
путем изображения их на одном графике,
использующем один общий масштаб (например, для
сравнения нескольких одновременных
экспериментальных процессов, социальных
явлений, цен акций или товаров, форм кривых
текущих характеристик и т.п.).
2М линейные
графики — Трассировочные XY. На
трассировочных графиках сначала строится
диаграмма рассеяния двух переменных, а затем
отдельные точки данных соединяются линией (в
порядке их считывания из файла данных). В этом
смысле трассировочные графики визуализируют
«путь» последовательного процесса
(движение, изменение явления во времени и т.п.).
2М
линейные графики (профили наблюдений). В
отличие от простых
линейных графиков, на которых значения одной
переменной изображаются в виде одной линии
(точки данных соединяются линией), на линейных
графиках профилей наблюдений одна линия
рисуется для значений выбранных переменных для
одного наблюдения (строки), т. е. для каждого из
выбранных наблюдений строится один линейный
график. Линейные графики профилей наблюдений
являются простым способом наглядного
представления значений одного наблюдения
(например, результатов нескольких тестов).
е. для каждого из
выбранных наблюдений строится один линейный
график. Линейные графики профилей наблюдений
являются простым способом наглядного
представления значений одного наблюдения
(например, результатов нескольких тестов).
2М линейный график (или категоризованный
линейный график) медиан с квантилями и
минимаксными диапазонами
С помощью диалогового окна Статистические 2М
диаграммы размаха можно построить 2М линейный
график медиан с квантилями и минимаксными
столбцами диапазонов. В этом окне нужно выбрать
медиану в качестве средней точки, процентили (с
коэффициентом 25) для прямоугольника, и мин-макс
для отрезка. Наконец, остается пометить поле
Соединить средние точки, чтобы медианы на
графике были соединены линией.
Таким же образом можно построить
категоризованный 2М линейный график медиан с
квантилями и минимаксными диапазонами, выбирая
те же пункты в диалоговом окне Статистические
категоризованные диаграммы размаха.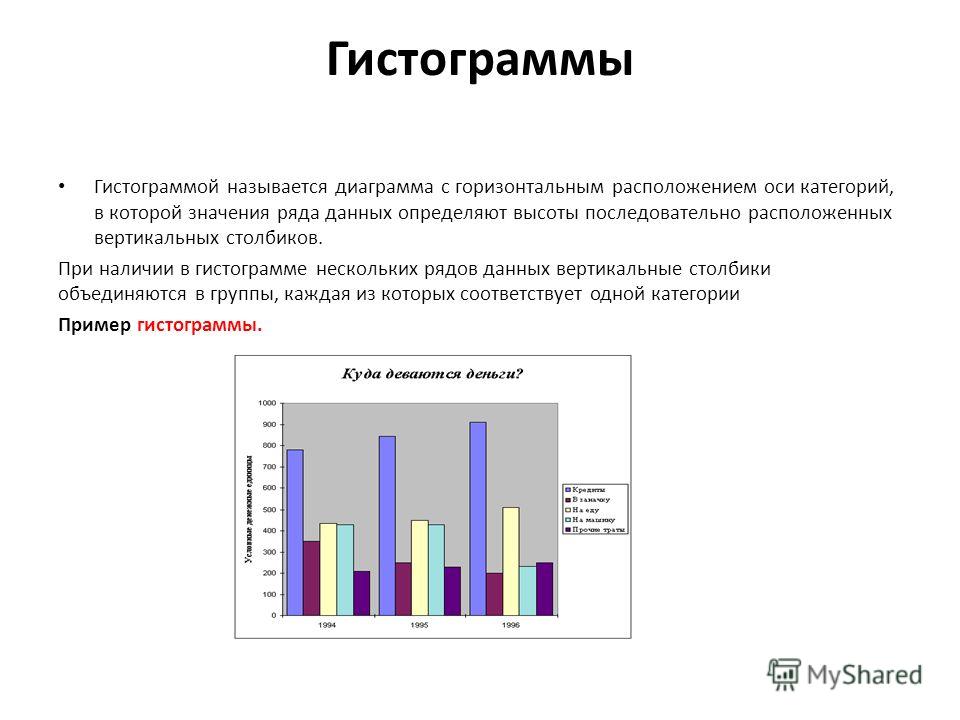
2М
последовательные/наложенные графики — Зонные.
На графике этого типа последовательности
значений каждой выбранной переменной будут
представлены последовательными областями,
расположенными одна над другой.
2М
последовательные/наложенные графики — Линейные.
На графике этого типа последовательности
значений каждой выбранной переменной будут
представлены последовательными линиями,
расположенными одна над другой.
2М
последовательные/наложенные графики — Смешанные
ступенчатые. На графике этого типа
последовательности значений переменных,
выбранных в первом списке, будут представлены
последовательными ступенчатыми областями,
расположенными одна на другой, а
последовательности значений переменных,
выбранных во втором списке, -
последовательными ступенчатыми линиями,
расположенными одна над другой (над областью,
отвечающей последней переменной из первого
списка).
2М
последовательные/наложенные графики — Смешанные
линейные. На графике этого типа
последовательности значений переменных,
выбранных в первом списке, будут представлены
последовательными областями, расположенными
одна на другой, а последовательности значений
переменных, выбранных во втором списке, -
последовательными линиями, расположенными
одна над другой (над областью, отвечающей
последней переменной из первого списка).
2М
последовательные/наложенные графики -
Столбчатые диаграммы. На графике
этого типа последовательности значений каждой
выбранной переменной будут представлены
последовательными сегментами вертикальных
столбцов, расположенных друг над другом.
2М
последовательные/наложенные графики -
Ступенчатые. На графике этого типа
последовательности значений каждой выбранной
переменной будут представлены ступенчатыми
линиями, расположенными одна над другой.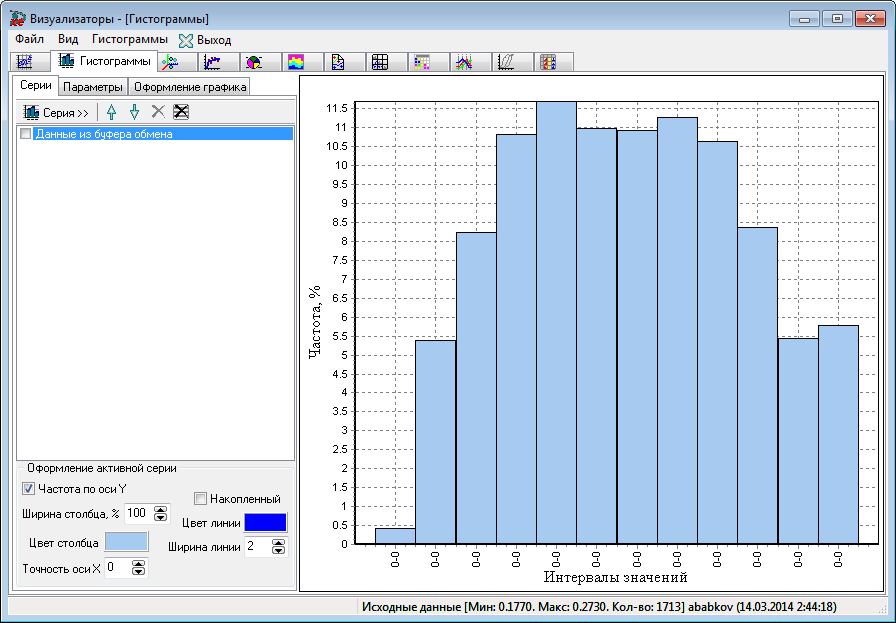
2М
последовательные/наложенные графики -
Ступенчатые зонные. На графике этого
типа последовательности значений каждой
выбранной переменной будут представлены
ступенчатыми областями, расположенными одна над
другой.
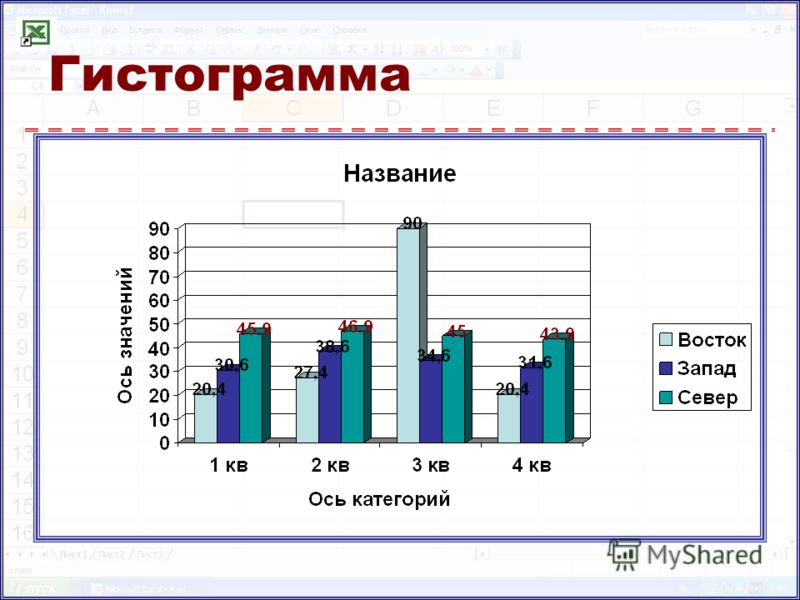
2М столбчатые диаграммы. На столбчатой диаграмме последовательность значений представлена в виде столбцов (одному наблюдению соответствует один столбец). Если выбрано несколько переменных, то для каждой из них будет построен отдельный график. Можно построить составную диаграмму, где все переменные будут отображены одновременно в виде групп столбцов (одна группа для каждого наблюдения, как на следующем рисунке).
Столбчатые диаграммы: виды, сферы применения
Что это? Столбчатая диаграмма – один из популярных методов визуализации данных. Отличается понятной и читаемой структурой, простыми принципами построения.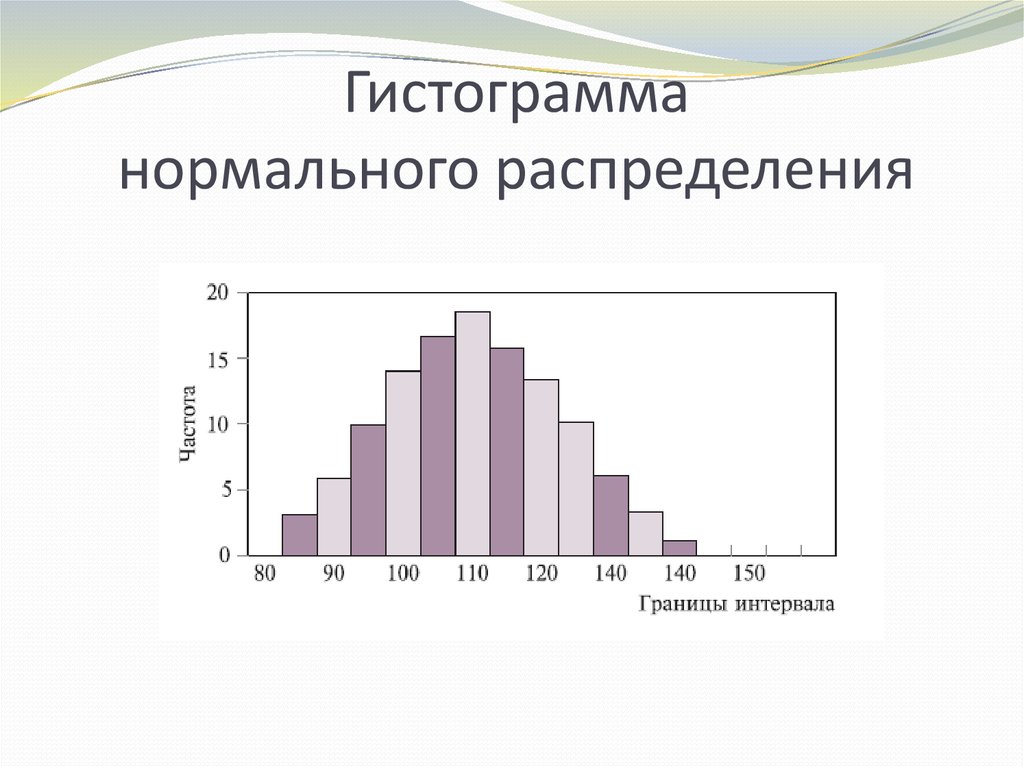 Столбики с данными могут быть расположены как горизонтально, так и вертикально.
Столбики с данными могут быть расположены как горизонтально, так и вертикально.
Где используются? Подходит для отображения категориальных данных, анализа рейтинговых значений, отслеживания динамики изменения показателей. Подробнее о видах, применении столбчатых диаграмм читайте в нашем материале.
В статье рассказывается:
- Описание столбчатой диаграммы
- Сферы применения столбчатых диаграмм
- Преимущества и недостатки построения столбчатых диаграмм
- Виды столбчатых диаграмм
- Как сделать столбчатую диаграмму в Excel
- Общие правила визуализации данных
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Описание столбчатой диаграммы
Диаграмму, где отображаемые величины оформлены в виде столбцов или вертикальных прямоугольников, пропорциональных по длине или высоте своему значению, называют столбчатой. Эти прямоугольные зоны располагают как горизонтально, так и вертикально.
Эти прямоугольные зоны располагают как горизонтально, так и вертикально.
График в виде столбчатой диаграммы предназначен для сравнения ряда дискретных категорий: по одной её оси расположены сравниваемые категории, по второй — измеряемая величина. По каждой категории можно отобразить несколько разных величин.
Описание столбчатой диаграммыВо многих источниках изобретателем столбчатых диаграмм называют Уильяма Плейфера, жившего в 1759-1824 гг. Именно он в своём «Коммерческом и политическом атласе» построил диаграмму импорта и экспорта товаров в Шотландии за конкретный год из различных регионов земного шара. До него никто не строил гистограмм, хотя тремястами годами ранее трактат «Широта форм» был проиллюстрирован прото-гистограммой скорости равноускоряющегося тела за определённый промежуток времени.
Сферы применения столбчатых диаграмм
С помощью столбчатых диаграмм удобно визуально оформлять категориальные данные — информацию, распределённую по дискретным группам (категориям). Например, возрастные группы людей, месяцы, размеры, виды животных и т. д.
Например, возрастные группы людей, месяцы, размеры, виды животных и т. д.
Столбчатая диаграмма позволяет решать различного рода аналитические задачи, а именно:
- Показать рейтинг величин, чтобы сравнить их друг с другом и выделить лучшие и худшие.
- Проиллюстрировать динамику — изменение значения во времени.
Оба вида графиков широко используются в корпоративных отчётах и презентациях, и это делает гистограммы столь популярными в бизнес-кругах. Столбчатая диаграмма позволяет визуализировать такие данные, как, например:
- разница прибылей нескольких торговых точек;
- соотношение фактической прибыли и плановых значений;
- рейтинг менеджеров по количеству заключённых сделок;
- спрос на различные товары;
- причины ухода клиентов, и т. д.
У любой столбчатой диаграммы область категорий дискретна и, как правило, имеет такой масштаб, чтобы все данные поместились и были хорошо различимы. Если нет какого-либо естественного способа упорядочить зоны на диаграмме, то они могут идти в любом порядке.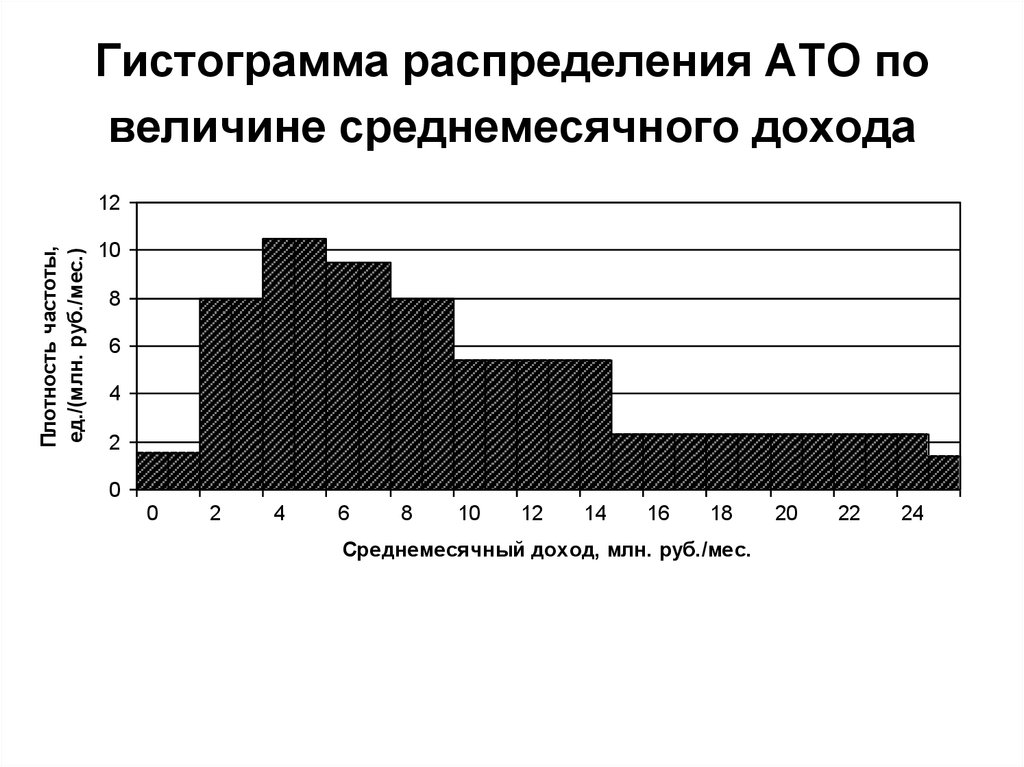 А если категории в гистограмме следуют в порядке уменьшения значений — от самых больших к самым маленьким — то это диаграмма Парето.
А если категории в гистограмме следуют в порядке уменьшения значений — от самых больших к самым маленьким — то это диаграмма Парето.
С помощью столбчатых диаграмм можно сравнивать данные и более изощрёнными способами. Например, группированная диаграмма содержит не одно сравниваемое значение, а два или несколько, и у каждого из них — своя зона на графике. Одни и те же параметры разных категорий окрашены в один оттенок.
Как правило, параметры в таких группированных столбчатых диаграммах имеют одинаковую последовательность в каждой из категорий.
В стековой столбчатой диаграмме зоны, символизирующие параметры каждой категории, наложены друг на друга, чтобы удобно было сравнивать их в рамках этой категории. При наличии хотя бы у одного свойства отрицательного значения этот тип диаграмм не подходит, и лучше использовать группированную.
Преимущества и недостатки построения столбчатых диаграмм
Любой способ визуализации данных в области аналитики (и не только) имеет свои преимущества и ограничения.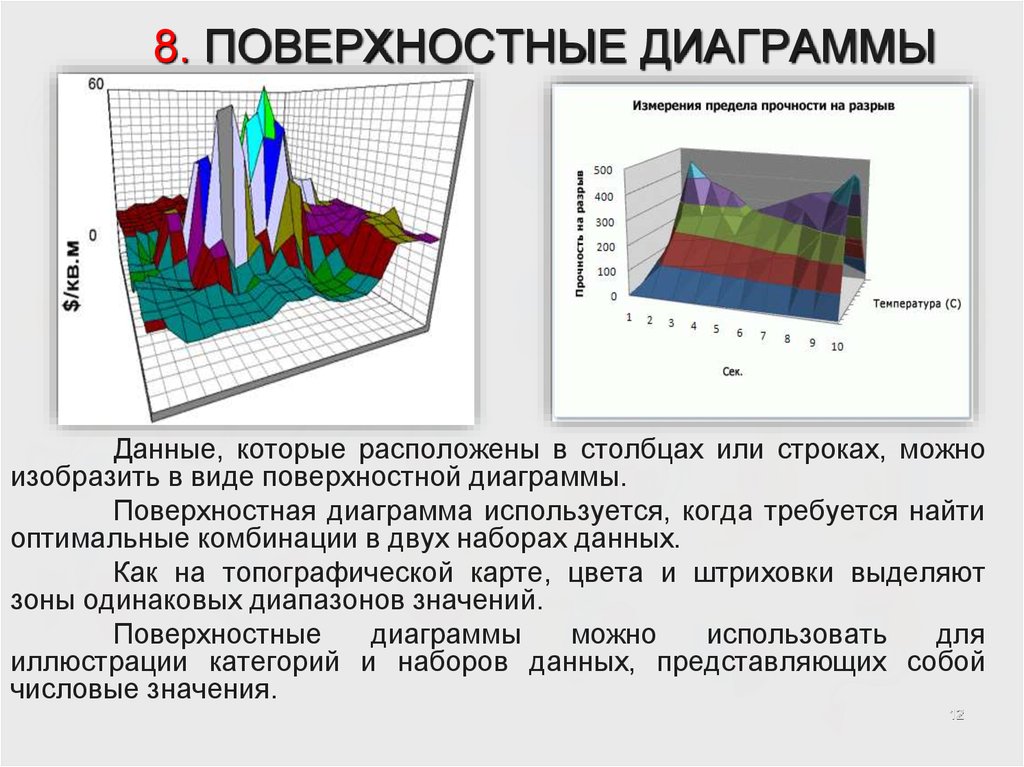 Нет какого-то универсального вида диаграмм. Как линейная, так и столбчатая, и прочие разновидности диаграмм предназначены для разных задач.
Нет какого-то универсального вида диаграмм. Как линейная, так и столбчатая, и прочие разновидности диаграмм предназначены для разных задач.
Достоинства гистограмм:
- они максимально ясны и наглядны;
- их легко построить в любой программе;
- можно менять визуальные настройки, чтобы оформить диаграмму самым подходящим способом;
- столбчатые диаграммы прекрасно комбинируются с другими видами.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
pdf 3,7mb
doc 1,7mb
Уже скачали 20110
Недостатки:
- если категорий много, диаграмма будет перегружена данными;
- нет возможности отобразить непрерывную переменную;
- широкое распространение гистограмм превращает их в избитое, банальное решение.

Виды столбчатых диаграмм
Столбчатые диаграммы делятся на несколько видов, и их постоянно путают. Давайте посмотрим, чем они отличаются и каковы их особенности.
Гистограмма
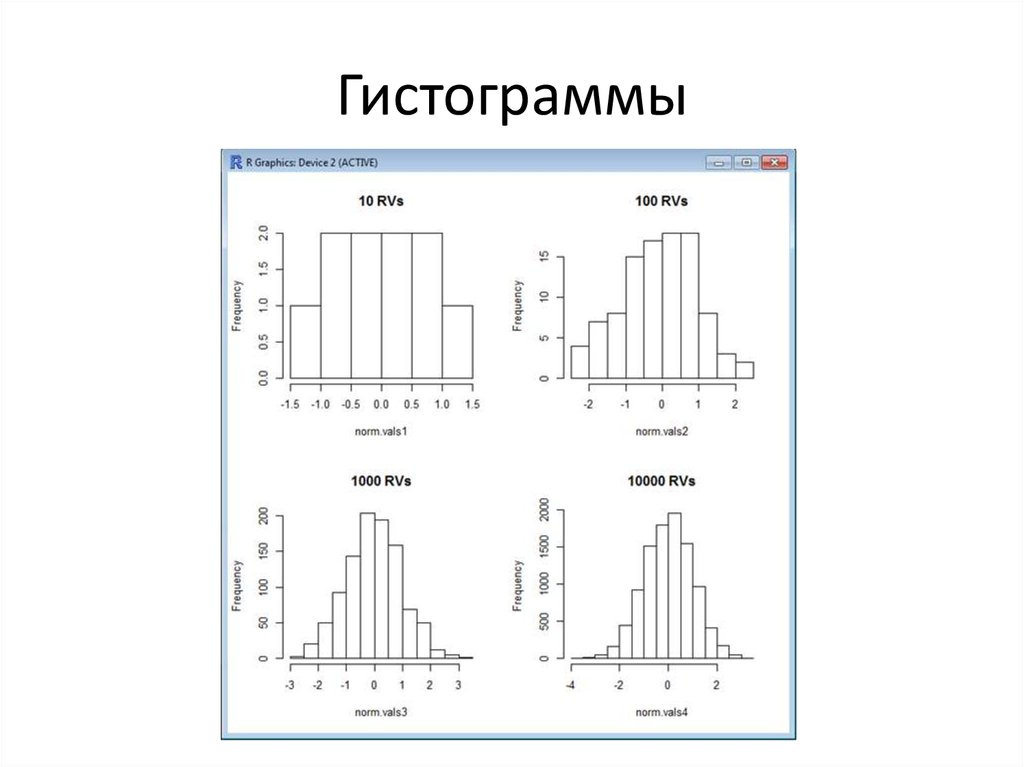
Термин был взят из математической статистики. Этот вид диаграмм изначально был придуман для распределения значений случайной величины и показывал, насколько часто встречается та или иная подгруппа в рамках одной категории. К примеру, если исследовать возраст читателей, то можно наглядно отобразить гистограммой, скольким из них от 15 до 20 лет, скольким — 20-25 лет, и т. п. Это и называется распределением аудитории по возрасту.
Постепенно гистограммы вышли за пределы статистического анализа, и этим термином стали называть и другие похожие диаграммы. Сейчас под гистограммой понимается просто столбчатый график, где столбцы ориентированы вертикально.
ГистограммаКроме столбцов, есть и иные подвиды столбчатых диаграмм. Два из них особенно популярны.
- Гистограмма с группировкой
Этот вариант удобен для группирования параметров. К примеру, можно таким образом визуализировать показатели продаж каждой ассортиментной группы товара для разных городов. Или, например, изменение показателей продаж за год для двух или нескольких товаров (возобновляемой и невозобновляемой энергии).
К примеру, можно таким образом визуализировать показатели продаж каждой ассортиментной группы товара для разных городов. Или, например, изменение показателей продаж за год для двух или нескольких товаров (возобновляемой и невозобновляемой энергии).
Гистограмма с группировкой прекрасно подходит для того, чтобы представить отклонение фактических величин от плановых. Неопытные аналитики пытаются вместо гистограммы задействовать круговую диаграмму, но это неудачное решение.
- Гистограмма с накоплением
В одном столбике можно собрать несколько разных категорий, и он в этом случае разделится на цветовые зоны. Тут требуются внимание и аккуратность, ошибку допустить очень легко.
Гистограммы с накоплением подходят лишь для тех случаев, когда в одном столбце все варианты суммируются, а его высота — это сумма всех компонентов. Сохраняется возможность сравнить его с соседними, у которых — собственная высота.
Удобно визуализировать таким образом, например, каналы коммуникации, актуальные для разных категорий опрошенных, либо продажи за месяц по каждой торговой марке. Но нельзя в одном прямоугольнике складывать плановые и фактические показатели выручки — эти величины не суммируются в принципе.
Но нельзя в одном прямоугольнике складывать плановые и фактические показатели выручки — эти величины не суммируются в принципе.
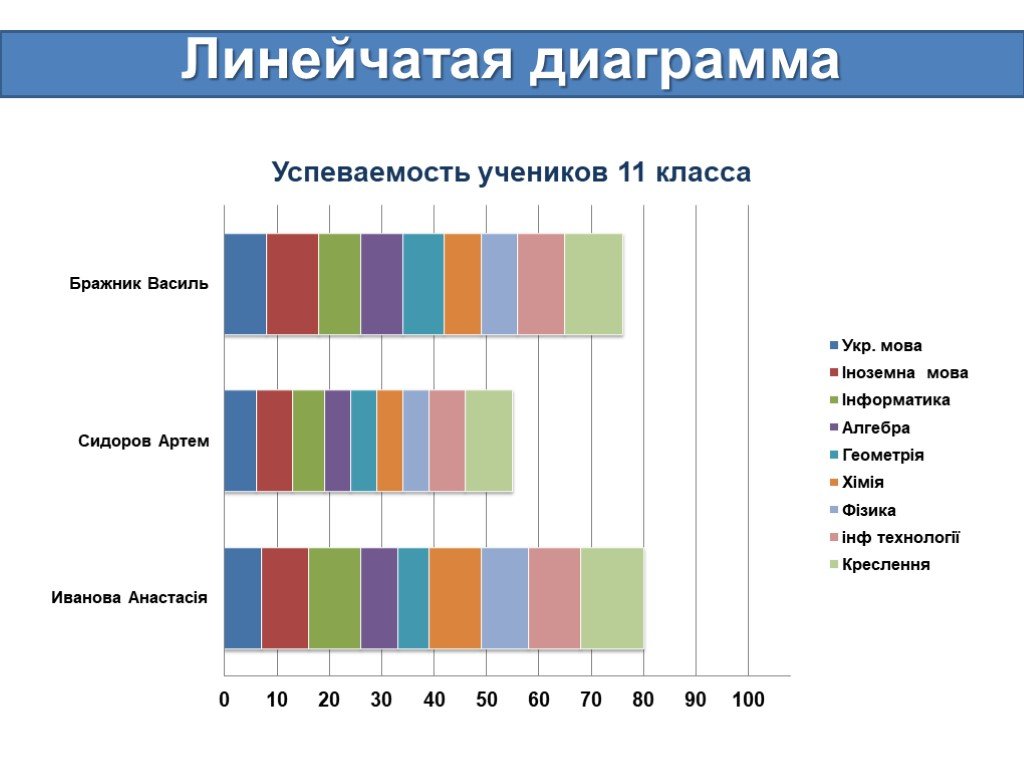
Линейчатая диаграмма
Ещё одна распространённая разновидность барчарта. Это горизонтальная столбчатая диаграмма, отличающаяся только направлением следования столбцов. Прекрасно подходит для случаев, когда надо отобразить много элементов или когда у них длинные подписи.
Есть один общий принцип для графиков, включая столбчатые диаграммы: распределение текста допускается только горизонтальное. Не заставляйте читателя вертеть головой, чтобы прочесть текст, расположенный под 90о или ещё более сложным углом. Если нет возможности сократить названия столбцов, просто положите их горизонтально и увеличьте пространство для подписей.
- Линейчатая с группировкой
Здесь всё то же, что и в аналогичной гистограмме, но элементы расположены горизонтально. А что касается назначения и правил построения таких диаграмм, то они не отличаются от таковых для вертикальных столбчатых.
Точный инструмент «Колесо компетенций»
Для детального самоанализа по выбору IT-профессии
Список грубых ошибок в IT, из-за которых сразу увольняют
Об этом мало кто рассказывает, но это должен знать каждый
Мини-тест из 11 вопросов от нашего личного психолога
Вы сразу поймете, что в данный момент тормозит ваш успех
Регистрируйтесь на бесплатный интенсив, чтобы за 3 часа начать разбираться в IT лучше 90% новичков.
Только до 27 марта
Осталось 17 мест
- Линейчатая с накоплением
Ещё один горизонтально ориентированный вариант линейчатой гистограммы. В ней тоже суммируются внутренние элементы каждой категории. Будьте осторожны с любыми столбчатыми диаграммами, предполагающими накопление: если сомневаетесь, можно ли суммировать показатели, лучше не делайте этого и просто сгруппируйте их.
Трёхмерные и другие нестандартные варианты
3D-эффекты придают графику объём. Многие считают, что такие диаграммы более солидные, выглядят дорого, стильно, впечатляюще. Практически во всех программах можно вместо плоских столбцов изобразить цилиндры и даже более интересные фигуры, сделать заливку рисунком или пиктограммой (главное, чтобы их размер соответствовал значению столбца).
Практически во всех программах можно вместо плоских столбцов изобразить цилиндры и даже более интересные фигуры, сделать заливку рисунком или пиктограммой (главное, чтобы их размер соответствовал значению столбца).
Но это порочная практика, и без крайней необходимости добавлять диаграмме объём нежелательно. Трёхмерные столбцы смотрятся немодно, устарело, выдают плохой вкус автора и существенно затрудняют понимание информации на графике.
Если вы выбираете, оставить ли столбчатую диаграмму двухмерной или добавить ей объём, то плоский вариант всегда предпочтительнее. Есть ситуации, когда подход к оформлению должен быть более креативным, и можно даже поиграть с 3D. Но надо соблюдать основное требование — корректность интерпретации информации.
Как сделать столбчатую диаграмму в Excel
В табличном редакторе Excel столбчатые диаграммы не выделены в самостоятельный тип, ищите их в общем списке, ориентируясь на объекты схожей структуры. Откройте перечень всех видов графиков, внимательно посмотрите на них.
- Если нужно, сразу выделите таблицу, на основе которой будете формировать график. Но если она единственная на листе, то можно сразу зайти во вкладку «Вставка».
- Кликните по кнопке «Рекомендуемые диаграммы», чтобы добраться до требуемого списка шаблонов диаграмм.
- Этот перечень неполон, так что лучше открыть вкладку «Все диаграммы» — там вы найдёте больше шаблонов. Присмотритесь к типу «Гистограмма», он больше всего подходит под ваши цели.
- Определитесь с тем, будет ли столбчатая диаграмма, построенная на основе таблицы, плоской, состоящей из линий или трёхмерной.
- Подведите мышь к интересующему шаблону. Посмотрите представление диаграммы. Она подходит вам?
- Кликните двойным щелчком по понравившейся диаграмме. Она тут же добавится на лист, и вы сможете её отредактировать как надо.
Выбирая тип диаграммы, в первую очередь смотрите на то, как отобразятся на ней числа из таблицы. Её содержимое должно быть ясным и понятным с первого взгляда. Возможно, придётся выбрать другую разновидность диаграмм (к примеру, «Биржевую», чтобы отразить курсы валют, акций).
Возможно, придётся выбрать другую разновидность диаграмм (к примеру, «Биржевую», чтобы отразить курсы валют, акций).
Для сложных случаев, когда, помимо столбчатых зон, нужно показать горизонтальные линии или точки, в Excel есть тип диаграмм «Комбинированная».
Общие правила визуализации данных
Чтобы построить понятную для пользователя столбчатую диаграмму, соблюдайте несколько нехитрых правил:
- Для сравнения данных за текущий и прошлый год можно окрасить столбцы или сегменты прошлого года в более бледный оттенок, а текущего — в более насыщенный. Придерживайтесь одного и того же цвета, который символизирует тот или иной показатель.
- Форматировать числа на графике нужно правильно. Для больших чисел — использовать разделитель (согласитесь, ведь 2 000 000 читается лучше, чем 2000000), сократить лишние знаки после запятой. Ваша цель — сделать числа как можно более читабельными.
- Название диаграммы тоже имеет значение. Оно должно выражать её суть и содержать полную легенду — все пояснения и подписи.
 У читателя не должно возникать сомнений по поводу единиц измерений и периода времени, за который представлены данные.
У читателя не должно возникать сомнений по поводу единиц измерений и периода времени, за который представлены данные.
И, наконец, последние рекомендации. Однотипные данные не следует визуализировать с помощью графиков разных типов, выбирайте всегда один и тот же тип диаграмм для того или иного вида данных. Читатель, видя графики, ещё должен разобраться, что означает та или иная линия, столбец, сегмент и т. д., и привыкнуть к формату.
Кстати, цветовой гаммы это тоже касается: отчёт или презентация не должны пестрить всеми цветами радуги на графиках, оформляйте их в едином стиле. Оптимально — в корпоративных цветах.
Рейтинг: 5
( голосов 1 )
Поделиться статьей
Определение, типы, графики и примеры
В статистике гистограмма представляет собой графическое представление распределения данных. Гистограмма представлена набором прямоугольников, примыкающих друг к другу, где каждый столбец представляет тип данных. Статистика — это поток математики, который применяется в различных областях. Когда цифры повторяются в статистических данных, это повторение известно как частота и может быть записано в виде таблицы, называемой частотным распределением. Частотное распределение можно показать графически с помощью различных типов графиков, и гистограмма является одним из них. В этой статье давайте подробно обсудим что такое гистограмма , как создать гистограмму для заданных данных, различные типы гистограммы и подробное различие между гистограммой и гистограммой.
Гистограмма представлена набором прямоугольников, примыкающих друг к другу, где каждый столбец представляет тип данных. Статистика — это поток математики, который применяется в различных областях. Когда цифры повторяются в статистических данных, это повторение известно как частота и может быть записано в виде таблицы, называемой частотным распределением. Частотное распределение можно показать графически с помощью различных типов графиков, и гистограмма является одним из них. В этой статье давайте подробно обсудим что такое гистограмма , как создать гистограмму для заданных данных, различные типы гистограммы и подробное различие между гистограммой и гистограммой.
Содержание:
|
Что такое гистограмма?
Гистограмма представляет собой графическое представление сгруппированного частотного распределения с непрерывными классами.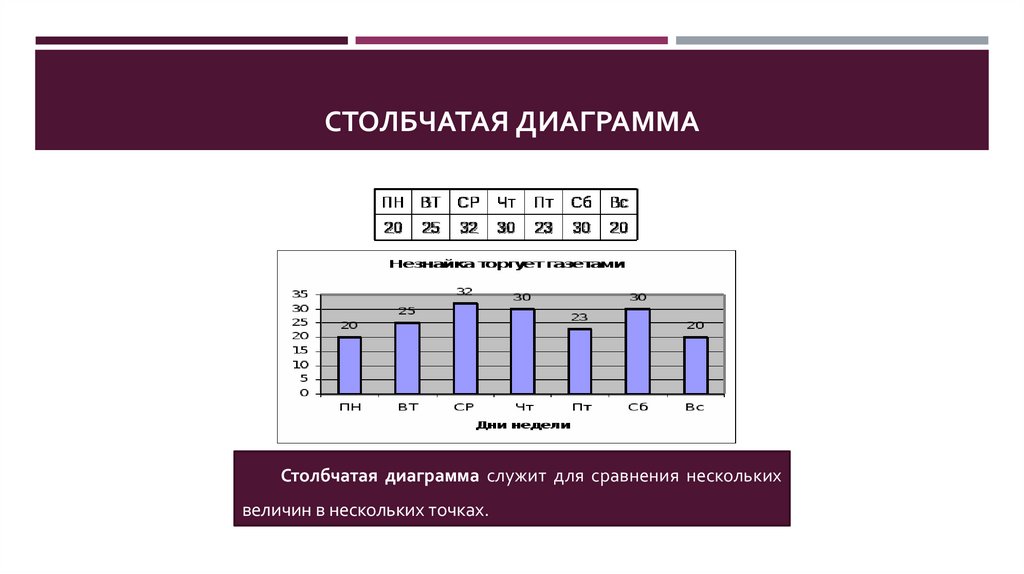 Это диаграмма с площадями, которую можно определить как набор прямоугольников с основаниями вместе с интервалами между границами классов и с площадями, пропорциональными частотам в соответствующих классах. В таких представлениях все прямоугольники являются смежными, так как основание покрывает интервалы между границами классов. Высота прямоугольников пропорциональна соответствующим частотам подобных классов, а для разных классов высоты будут пропорциональны соответствующим плотностям частот.
Это диаграмма с площадями, которую можно определить как набор прямоугольников с основаниями вместе с интервалами между границами классов и с площадями, пропорциональными частотам в соответствующих классах. В таких представлениях все прямоугольники являются смежными, так как основание покрывает интервалы между границами классов. Высота прямоугольников пропорциональна соответствующим частотам подобных классов, а для разных классов высоты будут пропорциональны соответствующим плотностям частот.
Другими словами, гистограмма представляет собой диаграмму, состоящую из прямоугольников, площадь которых пропорциональна частоте переменной, а ширина равна интервалу класса.
Как построить гистограмму?
Для построения гистограммы необходимо выполнить следующие шаги.
- Начните с отметки интервалов классов по оси X и частот по оси Y.
- Масштабы для обеих осей должны быть одинаковыми.
- Интервалы классов должны быть эксклюзивными.
- Нарисуйте прямоугольники с основаниями в качестве интервалов классов и соответствующими частотами в качестве высот.

- На каждом интервале классов строится прямоугольник, так как по горизонтальной оси отмечены границы классов, а по вертикальной – частоты.
- Высота каждого прямоугольника пропорциональна частоте соответствующего класса, если интервалы равны.
- Площадь каждого отдельного прямоугольника пропорциональна частоте соответствующего класса, если интервалы не равны.
Хотя гистограммы кажутся похожими на графики, между ними есть небольшая разница. Гистограмма не содержит пробелов между двумя последовательными барами.
Когда использовать гистограмму?
График гистограммы используется при определенных условиях. Они:
- Данные должны быть числовыми.
- Гистограмма используется для проверки формы распределения данных.
- Используется для проверки изменения процесса от одного периода к другому.
- Используется, чтобы определить, отличаются ли выходные данные, если они включают два или более процессов.

- Используется для анализа соответствия данного процесса требованиям заказчика.
Разница между гистограммой и гистограммой
Гистограмма является одним из наиболее часто используемых графиков для отображения частотного распределения. Как мы знаем, частотное распределение определяет, как часто каждое отдельное значение встречается в наборе данных. Гистограмма больше похожа на гистограмму, но между ними есть разница. Список отличий гистограммы от гистограммы приведен ниже:
| Гистограмма | Гистограмма |
| Это двумерная фигура | Это одномерная фигура |
| Частота показана площадью каждого прямоугольника | Высота показывает частоту, а ширина значения не имеет. |
| Показывает касающиеся друг друга прямоугольники | Состоит из прямоугольников, отделенных друг от друга равными промежутками. |
Вышеуказанные различия видны на рисунках ниже:
Гистограмма (промежутки между столбцами)
Гистограмма (без промежутков между столбцами)
Типы гистограмм
Гистограмму можно разделить на различные типы в зависимости от частотного распределения данных.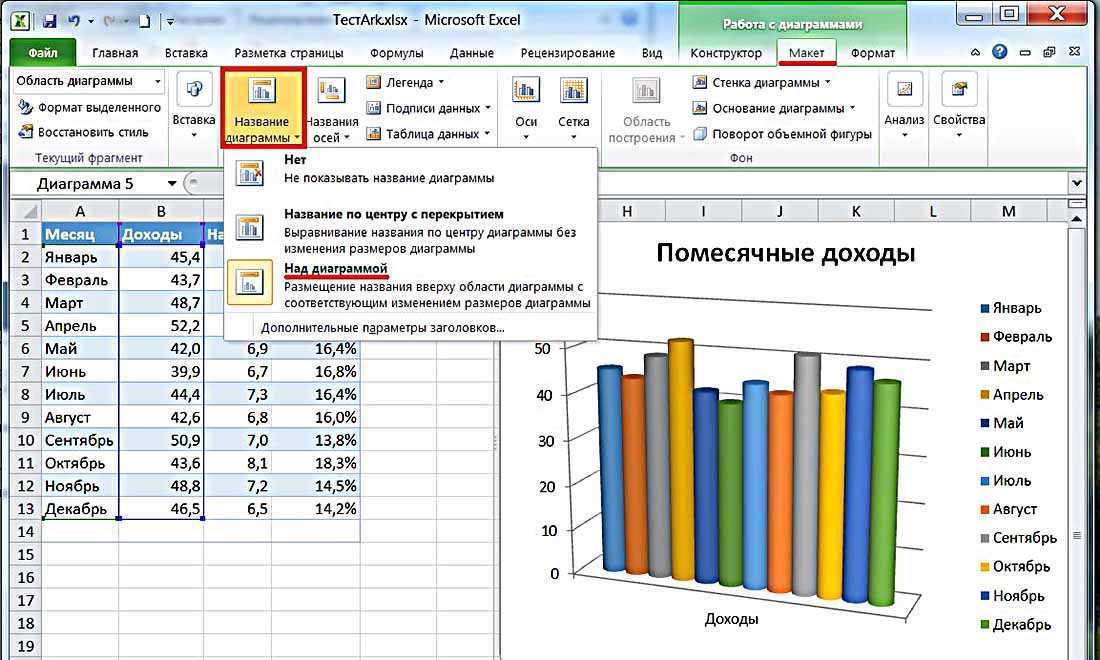 Существуют различные типы распределений, такие как нормальное распределение, асимметричное распределение, бимодальное распределение, мультимодальное распределение, гребенчатое распределение, распределение краевых пиков, распределение собачьего корма, распределение сердцевины и так далее. Гистограмму можно использовать для представления этих различных типов распределений. Различные типы гистограммы:
Существуют различные типы распределений, такие как нормальное распределение, асимметричное распределение, бимодальное распределение, мультимодальное распределение, гребенчатое распределение, распределение краевых пиков, распределение собачьего корма, распределение сердцевины и так далее. Гистограмму можно использовать для представления этих различных типов распределений. Различные типы гистограммы:
- Равномерная гистограмма
- Симметричная гистограмма
- Бимодальная гистограмма
- Гистограмма вероятности
Единая гистограмма
Равномерное распределение показывает, что количество классов слишком мало, и каждый класс имеет одинаковое количество элементов. Это может быть распределение, имеющее несколько пиков.
Бимодальная гистограмма
Если гистограмма имеет два пика, она называется бимодальной. Бимодальность возникает, когда в наборе данных есть наблюдения за двумя разными типами людей или объединенными группами, если центры двух отдельных гистограмм достаточно далеки от изменчивости в обоих наборах данных.
Симметричная гистограмма
Симметричная гистограмма также называется гистограммой в форме колокола. Когда вы проводите вертикальную линию по центру гистограммы, а две стороны одинаковы по размеру и форме, говорят, что гистограмма симметрична. Диаграмма совершенно симметрична, если правая половина изображения похожа на левую половину. Гистограммы, которые не являются симметричными, известны как асимметричные.
Гистограмма вероятности
Гистограмма вероятности показывает графическое представление дискретного распределения вероятности. Он состоит из прямоугольника, центром которого является каждое значение x, а площадь каждого прямоугольника пропорциональна вероятности соответствующего значения. Диаграмма гистограммы вероятности начинается с выбора классов. Вероятности каждого исхода — это высоты столбцов гистограммы.
Применение гистограммы
Применение гистограмм можно увидеть, когда мы узнаем о различных распределениях.
Нормальное распределение
Обычная картина, имеющая форму колоколообразной кривой, называется нормальным распределением. В нормальном распределении точки данных, скорее всего, появятся как на одной стороне среднего, так и на другой. Следует отметить, что другие распределения выглядят так же, как нормальное распределение. Расчеты в статистике используются для доказательства нормальности распределения. Необходимо отметить, что термин «нормальный» объясняет конкретное распределение процесса. Например, в различных процессах они обладают пределом, естественным для стороны, и будут создавать искаженные распределения. Это нормально, что означает для процессов, в случае, когда распределение не считается нормальным.
Искаженное распределение
Распределение, которое перекошено, является асимметричным, поскольку предел, который естественно противостоит конечным результатам с одной стороны. Пик распределения — это смещенный от центра в направлении предела и хвост, уходящий далеко от него.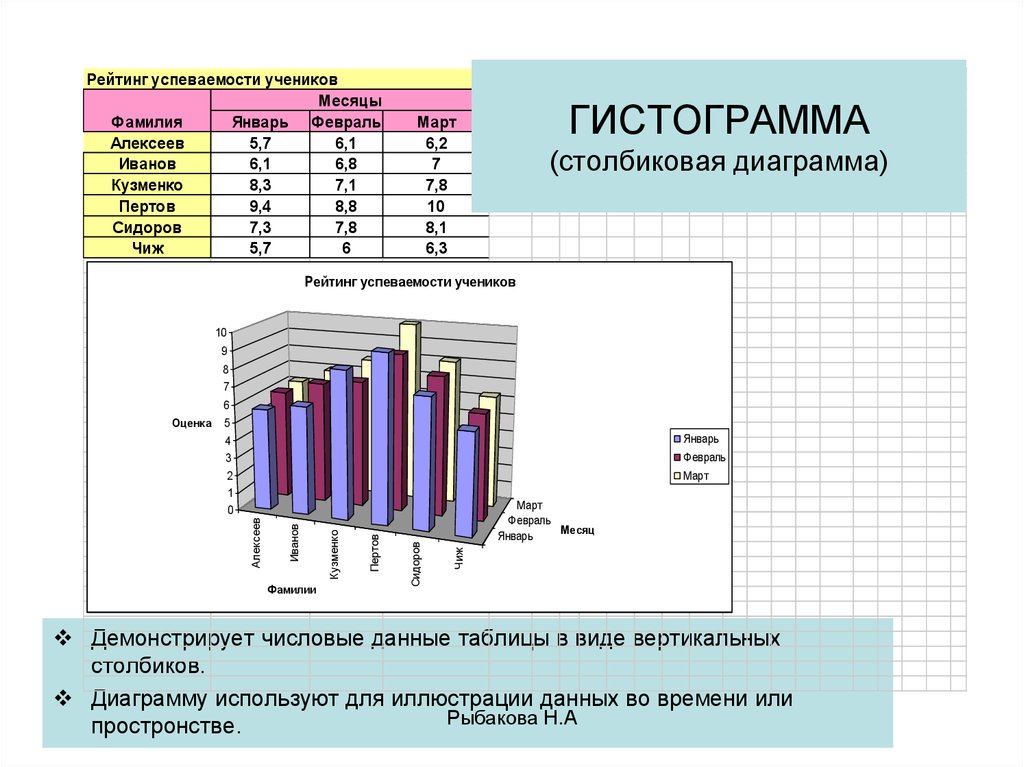 Например, распределение, состоящее из анализов продукта, который не содержит фальсификации, будет искажено, поскольку продукт не может иметь более чем 100-процентную чистоту. Другими примерами естественных ограничений являются отверстия, которые не могут быть меньше диаметра сверла, или время приема звонков, которое не может быть меньше нуля. Вышеуказанные распределения называются правыми или левыми в зависимости от направления хвоста.
Например, распределение, состоящее из анализов продукта, который не содержит фальсификации, будет искажено, поскольку продукт не может иметь более чем 100-процентную чистоту. Другими примерами естественных ограничений являются отверстия, которые не могут быть меньше диаметра сверла, или время приема звонков, которое не может быть меньше нуля. Вышеуказанные распределения называются правыми или левыми в зависимости от направления хвоста.
Мультимодальные перевозки
Альтернативное название мультимодального распределения — распределение плато. Различные процессы с нормальным распределением объединяются. Поскольку имеется много пиков, расположенных рядом друг с другом, вершина распределения имеет форму плато.
Краевой пик Распределение
Это распределение похоже на нормальное распределение, за исключением того, что оно имеет больший пик на одном хвосте. Как правило, это связано с неправильным построением гистограммы, когда данные объединяются в коллекцию под названием «больше».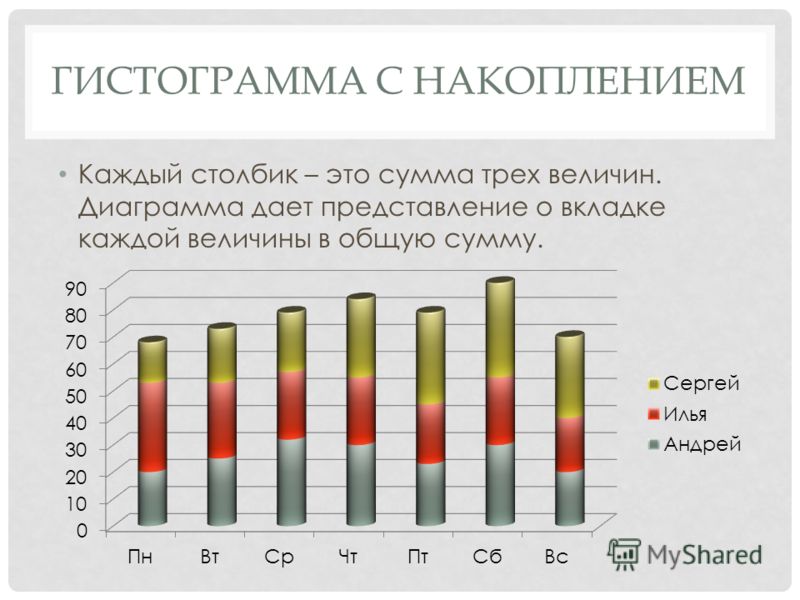
Распределитель гребенки
В этом распределении существуют столбцы, которые поочередно высокие и короткие. Чаще всего это результат округления данных и/или неправильно нарисованной гистограммы. Например, температура, округленная до ближайших 0,2 o , будет иметь форму гребенки при условии, что ширина столбца гистограммы равна 0,1 o .
Усеченное или неполное распределение
Приведенное выше распределение напоминает нормальное распределение с обрезанными хвостами. Производитель может производить нормальное распределение продукта, а затем, в зависимости от инспекции, отделять то, что находится в пределах спецификации, а что — нет. Полученная посылка для конечного пользователя из спецификаций является сердцем.
Раздача корма для собак
В этом дистрибутиве чего-то не хватает. Результат близок к среднему. Если конечный пользователь получает эту раздачу, кто-то другой получает раздачу в форме сердца, а оставшийся конечный пользователь получает корм для собак, остатки, оставшиеся после трапезы хозяина. Даже если конечный пользователь получает в пределах спецификаций, товар делится на 2 кластера, а именно: один ближе к верхнему пределу спецификации, а другой ближе к меньшему пределу спецификации. Это различие вызывает проблемы в процессе конечных пользователей.
Даже если конечный пользователь получает в пределах спецификаций, товар делится на 2 кластера, а именно: один ближе к верхнему пределу спецификации, а другой ближе к меньшему пределу спецификации. Это различие вызывает проблемы в процессе конечных пользователей.
Связанные статьи
- Графическое представление
- Гистограмма
- Линейный график
- Круговые диаграммы
Пример решения гистограммы
Вопрос: В следующей таблице указан срок службы 400 неоновых ламп. Нарисуйте гистограмму для приведенных ниже данных.
| Срок службы (в часах) | Количество ламп |
| 300 – 400 | 14 |
| 400 – 500 | 56 |
| 500 – 600 | 60 |
| 600 – 700 | 86 |
| 700 – 800 | 74 |
| 800 – 900 | 62 |
| 900 – 1000 | 48 |
Решение:
Гистограмма для данных:
Видео урок
Часто задаваемые вопросы по гистограмме
Гистограмма и гистограмма — это одно и то же?
Нет, гистограммы и гистограммы разные. На гистограмме каждый столбец представляет группу, которая определяется категориальной переменной, тогда как на гистограмме каждый столбец определяется непрерывной и количественной переменной.
На гистограмме каждый столбец представляет группу, которая определяется категориальной переменной, тогда как на гистограмме каждый столбец определяется непрерывной и количественной переменной.
Какая гистограмма представляет согласованные данные?
Гистограмма однородной формы показывает согласованные данные. В однородной гистограмме частота каждого класса похожа друг на друга. В большинстве случаев значения данных в гистограмме однородной формы могут быть мультимодальными.
Можно ли построить гистограмму для нормально распределенных данных?
Да, гистограмму можно построить для нормального распределения данных. Нормальное распределение должно быть идеально симметричным относительно своего центра. Это означает, что правая сторона должна быть зеркальным отражением левой стороны относительно ее центра и наоборот.
Когда гистограмма смещена вправо?
Гистограмма скошена вправо, если большинство значений данных находится в левой части гистограммы, а хвост гистограммы скошен вправо.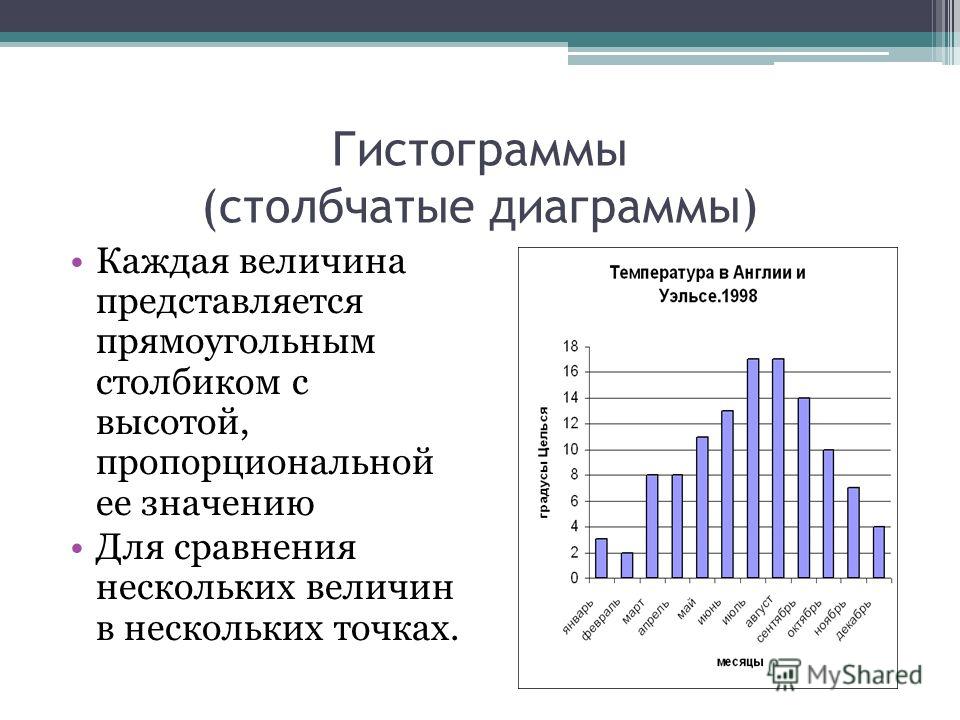 Когда данные смещены вправо, среднее значение больше, чем медиана набора данных.
Когда данные смещены вправо, среднее значение больше, чем медиана набора данных.
Когда гистограмма скошена влево?
Гистограмма скошена влево, если большинство значений данных приходится на правую часть гистограммы, а хвост гистограммы скошен влево. В этом случае среднее значение меньше медианы набора данных.
Чтобы узнать больше о гистограммах, графиках и других статистических концепциях, посетите BYJU’S — The Learning App сегодня!
Что такое гистограмма? | Определение, использование и примеры
Гистограмма позволяет увидеть частотное распределение набора данных. Он предлагает «с первого взгляда» картину распределения, представленную в виде диаграммы в определенных категориях. Гистограммы — один из наиболее часто используемых методов построения графиков исторических данных.
Данные обычно отображаются в виде гистограммы, что позволяет зрителям быстро усваивать информацию. Главное — представить информацию в логическом порядке.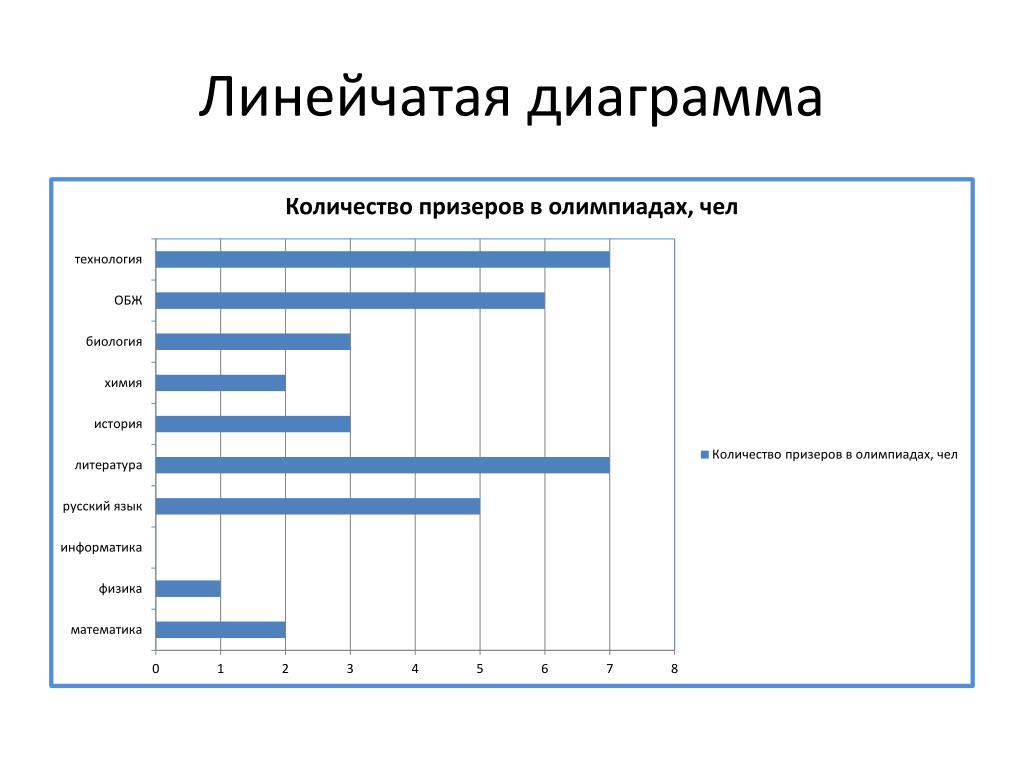 Это простая диаграмма, в которой используются горизонтальная и вертикальная оси.
Это простая диаграмма, в которой используются горизонтальная и вертикальная оси.
Когда используется гистограмма?
Основными преимуществами гистограммы являются ее простота и универсальность. Его можно использовать во многих различных ситуациях, чтобы предложить глубокий взгляд на частотное распределение. Например, его можно использовать в продажах и маркетинге для разработки наиболее эффективных планов ценообразования и маркетинговых кампаний.
В программе «Шесть сигм» используется для поиска изменений в процессе. Гистограмма используется, чтобы показать, например, где происходят задержки, путем определения частоты задержек на каждом этапе процесса. Используя данные, руководители проектов могут затем найти лучшие способы уменьшить вариативность.
Преимущества гистограммы
С течением времени гистограммы могут показать, каково нормальное распределение для процесса, который работает бесперебойно. Однако при регулярном построении гистограмм любое изменение быстро обнаруживается. Это большое преимущество для организаций, поскольку оно помогает быстро находить и устранять отклонения в процессах.
Это большое преимущество для организаций, поскольку оно помогает быстро находить и устранять отклонения в процессах.
Колоколообразная кривая на гистограмме обычно указывает на нормальное распределение. Всплески на графике указывают на вариации, на которые следует обратить внимание. Такие всплески также могут указывать на возможность извлечь выгоду из тренда, как это видно на примере ресторана ниже.
Примеры использования гистограммы
Менеджеры ресторанов могут построить гистограмму, чтобы определить, сколько клиентов приходит в ресторан в разное время в течение дня. Количество посетителей отложено по вертикальной оси, а временные интервалы — по горизонтальной оси. Диаграмма покажет частотное распределение прихода посетителей в ресторан (25 приходят в 9 часов).являюсь.; 77 в полдень и др.). Если в определенное время дня наблюдаются огромные всплески, менеджеры могут найти способы извлечь выгоду из этого увеличения трафика (специальные товары, корректировка цен).
Аналогичным образом гистограмма может показать, сколько товаров розничный магазин продает за один день. Допустим, это карандаши. Количество проданных карандашей будет указано по вертикали, а временные интервалы — по горизонтали. Опять же, корректировки в ценообразовании и маркетинговых усилиях могут быть скорректированы в зависимости от того, когда товар наиболее популярен.
При оценке процесса пики на гистограмме указывают на проблему. Если построить гистограмму времени ожидания в амбулаторной клинике, высокие пики будут указывать на то, что время ожидания слишком велико в определенные периоды дня (интервалы времени ожидания будут отложены по вертикальной оси, а временные интервалы — по горизонтальной оси). . Затем необходимо более глубоко изучить процесс, чтобы определить, какие решения являются лучшими для сглаживания вариаций.
Гистограммы обеспечивают простое, но эффективное решение многих технологических проблем. Они предлагают способ визуализации частотного распределения, предоставляя отличный первый шаг, отображая исторические данные, которые дают представление о том, как работает процесс.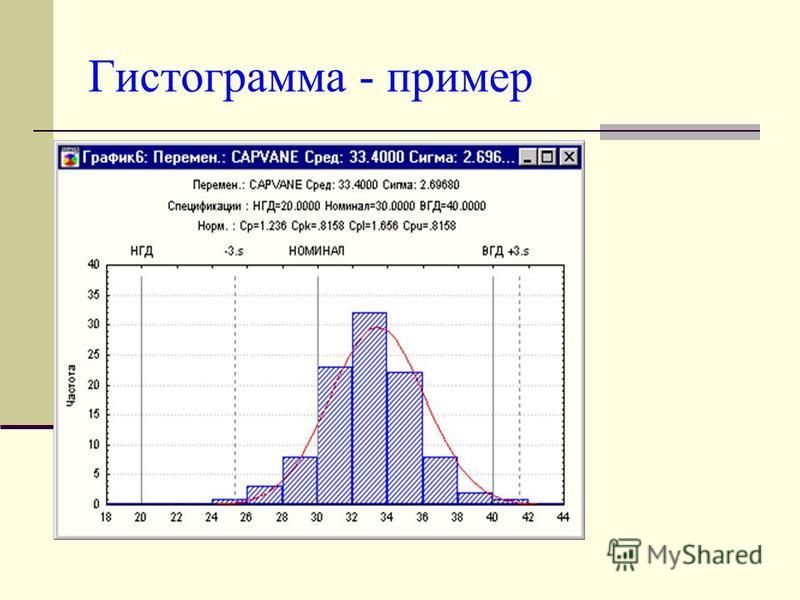

 У читателя не должно возникать сомнений по поводу единиц измерений и периода времени, за который представлены данные.
У читателя не должно возникать сомнений по поводу единиц измерений и периода времени, за который представлены данные.