Dx что это: код | это… Что такое DX-код?
код | это… Что такое DX-код?
DX-код на кассете. ISO 125, 24 кадра, регулировка экспозиции +3 -1 Штрих-код на краю плёнки Считыватель DX-кода в камере.DX-код (от англ. Digital indeX — цифровое обозначение) — стандарт ANSI для маркировки плёнок и кассет типа 135 или APS. Стандартная маркировка состоит из 3 частей, описываемых ниже.
Содержание
|
Штрих-код на кассете
Находится рядом с щелью для выхода плёнки.
Представляет собой штрих-код (кодирование 2/5) и читаемый номер, в котором зашифрованы следующие данные:
- DX-номер
- количество кадров
- код производителя
DX-номер, присваиваемый организацией I3A, обозначает конкретного производителя и тип плёнки. Исходя из этих данных, фотолабы выясняют необходимые условия процесса проявки отснятой плёнки [1].
Штрих-код на краю плёнки
Находится на краю каждого кадра ниже уровня перфорации.
Штрих-код невидим до процесса проявки, он оптически запечатлён как скрытое изображение на этапе производства. Используется фотолабами для определения границ кадра и правильной ориентации перед печатью.
Состоит из двух параллельных линейных штрих-кодов
- синхронизация
- кодирование типа плёнки, кода производителя, номера кадра
Код на кассете
Находится на кассете, выглядит как таблица 6×2, составленная из черных и белых прямоугольников.
Белые прямоугольники представляют собой открытый металл кассеты и проводят электрический ток. Чёрные прямоугольники являются закрашенными областями и не проводят ток. Таким образом возможно организовать двоичное кодирование некоторой информации, которая передаётся в фотоаппарат посредством электрического считывающего устройства.
Из этой таблицы фотоаппарат может получить данные о чувствительности плёнки, количестве кадров и фотографической широте.
Общий вид таблицы:
| З | Ч1 | Ч2 | Ч3 | Ч4 | Ч5 |
| З | Д1 | Д2 | Д3 | К1 | К2 |
- З — земля, два самых левых контакта в каждом ряду
- Ч — чувствительность, поле длиной 5 бит, кодирующее 32 варианта чувствительности плёнки, из которых используются только 24 (в единицах ISO от 25 до 5000), при этом порядок двоичного исчисления не соблюдается
- Д — длина плёнки в кадрах, поле длиной 3 бита, кодирует 8 вариантов длины плёнки, из которых обычно используются 4 (от 12 до 36)
- К — фотографическая широта, поле длиной 2 бита, кодирует 4 диапазона фотографической широты
| Чувствительность ISO | 1-й ряд контактов DX | |||||
|---|---|---|---|---|---|---|
| 25/15° | ||||||
| 32/16° | ||||||
| 40/17° | ||||||
| 50/18° | ||||||
| 64/19° | ||||||
| 80/20° | ||||||
| 100/21° | ||||||
| 125/22° | ||||||
| 160/23° | ||||||
| 200/24° | ||||||
| 250/25° | ||||||
| 320/26° | ||||||
| 400/27° | ||||||
| 500/28° | ||||||
| 640/29° | ||||||
| 800/30° | ||||||
| 1000/31° | ||||||
| 1250/32° | ||||||
| 1600/33° | ||||||
| 2000/34° | ||||||
| 2500/35° | ||||||
| 3200/36° | ||||||
| 4000/37° | ||||||
| 5000/38° | ||||||
| custom 1 | ||||||
| custom 2 | ||||||
| custom 3 | ||||||
| custom 4 | ||||||
| custom 5 | ||||||
| custom 6 | ||||||
| custom 7 | ||||||
| custom 8 | ||||||
| Кадров | 2-й ряд контактов DX | |||||
|---|---|---|---|---|---|---|
| нестандартная | ||||||
| 12 | ||||||
| 20 | ||||||
| 24 | ||||||
| 36 | ||||||
| 48 | ||||||
| 60 | ||||||
| 72 | ||||||
| Значение регулировки (в f-стопах) | 2-й ряд контактов DX | |||||
|---|---|---|---|---|---|---|
| ±½ | ||||||
| ±1 | ||||||
| +2 -1 | ||||||
| +3 -1 | ||||||
Примечания
Ссылки
- (рус.
) DX-код. Научно-технический центр Красногорского завода имени С. А. Зверева. - (англ.) Java-апплет для создания и расшифровки DX-кодов
) DX-код. Научно-технический центр Красногорского завода имени С. А. Зверева.Дифференциал функции
- Понятие и геометрический смысл дифференциала
- О разных формах записи дифференциала
- Свойства дифференциала
- Применение дифференциала в приближенных вычислениях
- Абсолютная и относительная погрешности приближенных вычислений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
или
или же
Геометрический смысл дифференциала.
Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину (см. рисунок).
Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал, является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
Дифференциал функции в точке x и обозначают
или
Следовательно,
(1)
или
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а — наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
(3)
или
(4)
Пример 1. Найти дифференциалы функций:
1) ;
2) ;
3) ;
4) .
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) ;
2) ;
3) ;
4) .
Найти дифференциалы самостоятельно, а затем посмотреть решения
Пример 2. Найти дифференциал функции
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции
в точке x.
Пример 4. Найти дифференциал функции
в точках x = 0 и x = 1.
Посмотреть правильные решения примеров 2, 3, 4.
В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
(С – постоянная величина) (5)
(6)
(7)
(8)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .
Одно из особеннейших свойств дифференциала — инвариантность формы дифференциала в случае сложных функций.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Установленное во втором параграфе приближенное равенство
или
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
а
то
или
(11)
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x .
Формула (11) в данном случае примет вид
Положим
тогда
Следовательно,
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 6. Пользуясь понятием дифференциала, вычислить приближенно
Решение. Число
является одним из значений функции
Так как производная этой функции
то формула (11) примет вид
Полагая
и
получаем
(табличное значение
).
Вычислить приближенно самостоятельно, а затем посмотреть решение
Пример 7.
Вычислить приближенно:
1) ;
2) .
Посмотреть правильное решение и ответ.
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:
(12)
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
(13)
Если точное число неизвестно, то
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях.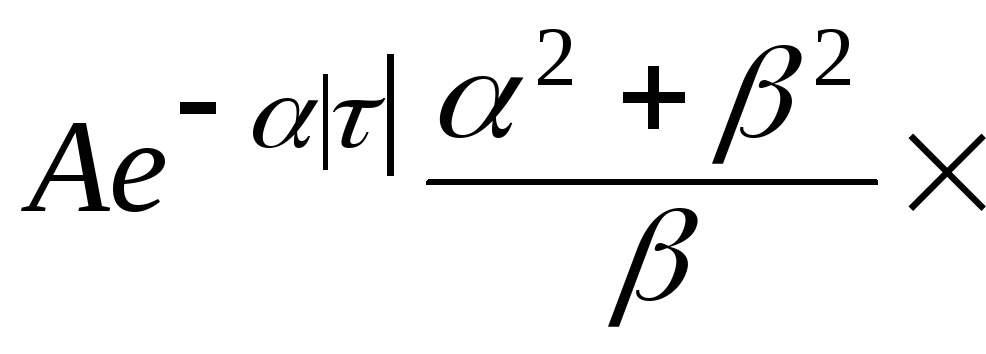
Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.
Решение. Рассмотрим функцию
Её производная равна
а формула (11) примет вид
В данном случае было бы нерационально вычислять приближенно следующим образом:
так как значение
не является малым по сравнению со значением производной в точке
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
Теперь, полагая
получим
Умножая на 4/3, находим
Принимая табличное значение корня
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Правило Лопиталя
- Частные производные
Поделиться с друзьями
Исчисление— Что означает dx в интеграле?
$\begingroup$ Я знаю, что dy/dx, например, означает «производное y по отношению к x «, но меня смущает другой контекст.
Обычно вы просто видите термин dx в конце интегрального уравнения, и я просто не знаю точно, что он означает и почему он там.
Например, если я введу в Wolfram Alpha «интеграл от 2x», он напишет:
Там dx ! Я предполагаю, что он говорит «интеграл 2x по отношению к x»? Но зачем это вообще нужно? Разве это не подразумевается? Это раздражает, потому что это похоже на умножение, как будто это означает «2 * x * dx», и это просто вводящая в заблуждение запись.
- вычисления
- интеграция
Если вы хотите узнать, что на самом деле означает $dx$, этот вопрос задавался здесь много раз. См., например, Что означает $dx$?
$\endgroup$ 1 $\begingroup$ Это потому, что интеграл означает, что вы суммируете множество очень тонких прямоугольников под кривой.
Высота прямоугольника равна f(x), а ширина называется $\delta x$ (эти два символа следует читать как один символ, это не означает $\delta \times x$). Таким образом, вы бы написали это так:
$\sum f(x) \delta x$
Знак $\Sigma$ означает сигму и означает «сумма». В интеграле вы берете предел, когда $\delta x$ стремится к нулю. Поэтому мы заменяем сигму другим типом s: $\int$. И $\delta$ меняется на d. Итак, теперь написано:
$\int f(x) dx $
и это «интеграл от f(x) по x». Но dx сам по себе ничего не значит.
$\endgroup$ $\begingroup$Лично мне нравится думать о знаке $\int$ и «d» в $dx$ как о левой и правой скобках: они ограничивают размер подынтегральной функции. «x» в $dx$ указывает вам переменную интегрирования.
Существует также интуитивное понятие, заключающееся в том, что вы суммируете значения подынтегральной функции при изменении $x$ и умножаете каждое значение на маленькую «ширину», чтобы получить площадь прямоугольника, а суммируя эти площади, получаете интеграл .
.. если вы берете предел, поскольку «крошечная ширина $\Delta x$ становится все меньше и меньше». «$dx$» позволяет людям неформально думать, что вы умножаете высоту $f(x)$ на «бесконечно малую ширину» $dx$, а затем получаете бесконечную сумму. 9n f(x_k)\Delta x_k$$
Что имеет смысл, если вы знакомы с аппроксимацией площади под кривой фигурой, похожей на прямоугольник (суммы Римана). Вы находите сумму площадей прямоугольников, длина которых уменьшается. Когда вы берете предел, когда количество прямоугольников увеличивается до бесконечности, вы получаете площадь под кривой. Вот полезная анимация, показывающая процесс перехода $\Delta x_k$ к 0,
. $\endgroup$ $\begingroup$ 9{k-1}$», «$2x$» означает то же, что и «$\left(2\frac{i}{k}\right)$», а $dx$ означает то же, что и «$\ left(\frac{i+1}{k}-\frac{i}{k}\right)$».Этот ход мыслей, конечно, не совсем правильный, поскольку $\lim\limits_{k\rightarrow\ infty}\left(\frac{i+1}{k}-\frac{i}{k}\right)=0$, но передает идею о том, что $dx$ просто относится к произвольно малому изменению $x $
$\endgroup$ $\begingroup$ Предположим, $x$ — константа, тогда 92+1)у+С$$.
Что такое DX? 10 ответов на вопросы о DX в области медицины и здравоохранения
Сокращенный термин «DX», означающий «цифровое преобразование», получил широкое распространение по мере продвижения и развития цифровых и ИТ-технологий. Хотя цифровая трансформация (DX) явно связана с цифровыми технологиями, что на самом деле означает этот термин? Мы смотрим на основу DX через призму медицины и здравоохранения, знакомой области, имеющей отношение к нашей повседневной жизни. Масаки Исигуро, руководитель отдела развития бизнеса отдела здравоохранения Sojitz 3, отвечает на 10 вопросов о DX.
Text_Kayo Yabushita (оригинал на японском языке)
Photograph_Kaoru Yamada
Illustration_Saki Obata
Edit_Shota Kato (оригинал на японском языке)
В чем разница между «DX» и «оцифровкой»?
1. Хотя термин DX часто используется в наши дни, что именно он означает? DX означает революционную трансформацию, ставшую возможной благодаря применению ИТ-технологий в бизнесе и повседневной жизни.
Мы наблюдаем глобальную тенденцию, когда компании реагируют на меняющиеся потребности клиентов и общества с помощью продуктов, услуг и бизнес-моделей, которые по-новому используют данные и цифровые технологии.
2. В чем разница между «DX» и «оцифровкой»?
Оцифровка — преобразование аналоговой информации в цифровую форму. Например, офис, который распространяет печатные документы, может повысить эффективность работы за счет преобразования этих документов в цифровые файлы посредством оцифровки. Проще говоря, оцифровка повышает производительность существующей работы. Напротив, DX — это более широкое обновление, которое переосмысливает то, как существующая работа может быть фундаментально улучшена за счет применения цифровых технологий. В логистическом бизнесе обновление DX выходит за рамки повышения эффективности за счет оцифровки логистических процессов, но также включает создание новых планов доставки на основе аналитики, предоставляемой большими данными.
3.
Какие успешные проекты DX в настоящее время привлекают внимание в Японии или за рубежом?
Лично мне было интересно наблюдать за развитием новой службы онлайн-обучения Try Group «Try It». Это сервис видеообучения, доступный на платформах смартфонов для учащихся средних и старших классов, с уроками, которые можно смотреть в любом месте в любое время. Try Group использовала свой опыт отправки преподавателей на очные занятия при добавлении новых онлайн-лекций к своим очным занятиям. Добавляя дополнительные возможности для учащихся, Try Group теперь предлагает учащимся средних и старших классов как очное, так и онлайн-обучение. Этот новый сервис онлайн-репетиторства помогает уравнять возможности учащихся, устраняя неравенство, основанное на географических и экономических факторах. В будущем Try Group, вероятно, будет анализировать и использовать информацию, полученную из данных онлайн-обучения студентов.
4. Чем Япония отличается от других стран, когда речь идет о DX? Япония отстает от Европы и США?
Не думаю, что это так.
В то время как Uber является типичным зарубежным примером услуги, определяемой его цифровыми технологиями, в Японии также появляются предприятия DX, такие как Try Group, особенно в отраслях, совместимых с цифровыми технологиями. Ожидается, что в будущем Япония создаст больше DX-бизнесов, использующих преимущества опыта на местах.
Будущий переход от централизованной стационарной помощи к индивидуальной помощи
5. Одним из достоинств DX является повышение эффективности. При этом есть ли какие-либо недостатки или проблемы, связанные с DX?
Одной из серьезных проблем является обеспечение того, чтобы осуществимость системы соответствовала реальным операциям. Например, в учреждениях здравоохранения в Японии все большее распространение получают электронные медицинские карты. Однако эти записи может быть сложно интегрировать в другие системы без стандартизированного формата электронных медицинских карт пациентов.
6. Какие тенденции DX можно увидеть на месте в медицинских учреждениях?
Телемедицина находится на подъеме.
Раньше нужно было находить время, чтобы посетить медицинское учреждение, когда заболел, чтобы пройти обследование, а затем вернуться домой. В дальнейшем можно будет принимать врачей дистанционно в тех случаях, когда не требуется срочная очная помощь. Однако после назначения врача следующим шагом является лечение. Одна из проблем, с которой сталкиваются некоторые страны при использовании телемедицины, заключается в том, как доставить рецептурные лекарства на дом пациенту. Реальное и цифровое должны быть эффективно интегрированы, иначе пользователи могут столкнуться с трудностями при использовании системы.
7. Что необходимо для облегчения DX?
Во-первых, оцифровка должна быть реализована, чтобы служить основой для DX. Учитывая тот факт, что DX предполагает более широкое обновление существующей работы посредством применения цифровых технологий, оцифровка является важной предпосылкой. Также важно, чтобы компании и системы были интегрированы и совместимы, чтобы служить основой для DX.
Никто из нас не застрахован от внезапного приступа болезни. Когда мы думаем о DX, а также о медицине и здравоохранении, мы осознаем необходимость оказания помощи как онлайн, так и офлайн. Эта концепция интеграции онлайн- и офлайн-сервисов называется «онлайн-слияние в автономном режиме (OMO)». Одной из основных идей DX сейчас является необходимость расширения охвата услуг за счет интеграции как онлайн, так и офлайн.
8. Какую пользу могут получить медицинские учреждения и пользователи от реализации DX?
В Японии здравоохранение всегда было сосредоточено в больницах, где сосредоточены медицинские знания и оборудование. Если вы заболели, вы посещаете больницу, где есть врачи, медсестры и необходимое медицинское оборудование и приборы для осмотра, лечения, а затем обеспечения вас лекарствами. Тем не менее, DX децентрализует эту помощь, предоставляя пользователям дополнительные возможности, такие как онлайн-консультации для предотвращения заболеваний, онлайн-посещения телемедицины по мере необходимости и последующие встречи с прогнозом в рамках оптимизированной услуги.
Телемедицина может быть полезна для тех, кто живет в отдаленных районах, и позволяет родителям и опекунам, не выходя из дома, обращаться за медицинской помощью к врачам. В будущем мы увидим переход от централизованной помощи в больницах к более индивидуальной модели ухода за пациентами.
DX открывает захватывающее будущее для здравоохранения
9. Как вы думаете, как будет развиваться DX в разгар пандемии Covid-19?
Из-за последствий пандемии медицинские телевизиты стали обычным явлением для среднего пациента за границей. Мы видим, что телемедицина, естественно, не может охватить все условия, и что есть ситуации, требующие личного ухода. Я уверен, что в будущем появится спрос на ориентированную на пользователя модель OMO, оптимизирующую как цифровую, так и реальную информацию. Подход OMO в здравоохранении может широко применяться, и я думаю, что мы сохраним как цифровые, так и личные варианты, поскольку эта интегрированная бизнес-модель продолжает развиваться.
10. Какое будущее ждет нас с DX?
В настоящее время в Sojitz мы участвуем в ряде медицинских DX-проектов посредством инвестиций в медицинские компании как в Японии, так и за рубежом. Если вы посмотрите на глобальный ландшафт здравоохранения, вы заметите, что сети клиник растут по всей Азии. Это может показаться чрезмерным сравнением, но сети медицинских клиник могут стать такими же легко доступными и широко распространенными, как японские круглосуточные магазины. Учитывая растущую осведомленность о здоровье во всем мире и высокий интерес к профилактическим мерам для здоровья, Sojitz стремится расширять сети клиник с помощью многогранного подхода, а также предлагать новые услуги через DX. Я думаю, что мы можем рассчитывать на некоторые захватывающие будущие возможности, которые появятся в медицинской отрасли.
Как обычная торговая компания, мы не являемся больницей или поставщиком медицинских услуг, но мы традиционно выполняем свою миссию по предоставлению товаров и услуг первой необходимости там, где это необходимо.
Мы будем использовать опыт и сети, которые мы создали за более чем 140 лет, и применим этот опыт в медицинском мире. Мы поможем связать медицинские учреждения с компаниями, владеющими необходимыми DX-технологиями и сервисами, для создания новых сервисов. Глобальная сеть связей Sojitz дает компании уникальную возможность внести свой вклад в медицинскую отрасль.
Хотя термин «DX» может пугать многих людей, будущее цифровой трансформации — это будущее всеобщего процветания. Конечно, Sojitz — не единственная компания, занимающаяся DX-инициативами, и многие компании в самых разных отраслях внедряют DX. Если вы посмотрите на DX в интересующей вас области, вы увидите, что цифровая трансформация не такая уж чуждая концепция.
ПРОФИЛЬ
Масаки Исигуро
Исигуро работает менеджером отдела развития бизнеса в отделе здравоохранения Sojitz 3. Отдел развития бизнеса занимается новыми разработками в Департаменте здравоохранения, которые зависят от таких ключевых слов, как здоровье и DX.
