Физический размер матрицы: Размер матрицы. Что это такое?

Содержание

Типы и размеры матриц камер видеонаблюдения

Разберем характеристику первой попавшейся камеры.

Матрица	1/4″ Progressive Scan CMOS
Эффективных пикселей	1Мп, 1280 х 720

Такую таблицу вы встретите на странице каждой камеры, меняются лишь значения, подставляемые к перечню характеристик. Как понять, что вам нужно и на какие данные стоит обратить внимание в первую очередь? Ведь матрица – это и есть та главная часть камеры, которая получает изображение, как фотопленка в старых фотоаппаратах.

Рассмотрим типы матриц. И начнем от обратного. Матрицы, не использующиеся Hikvision – CCD-матрицы.

По сравнению с технологией CMOS, которую применяет в своих камерах Hikvision, CCD-матрицы позволяют создавать высококачественное изображение. В процессе съемки возникает гораздо меньше шумов, а бороться с все же возникшими намного легче, чем в матрицах CMOS.

Еще одним важным показателем является их высокая эффективность. Например, коэффициент заполнения у матриц CCD приближается к 100%, а соотношение зарегистрированных матрицей фотонов к их общему числу – 95%. Если сравнивать с нашими глазами, то при расчёте в тех же единицах соотношение составит только 1%.

К недостаткам CCD-матриц можно отнести сложность процесса. Для фиксации изображения в камере необходимо дополнительное наличие целого перечня устройств. Это приводит к более высокому энергопотреблению, делает их дороже в производстве и “капризнее” в эксплуатации.

Теперь о CMOS-матрицах.

Главное достоинство CMOS-матриц – более низкое энергопотребление и возможность произвольного считывания ячеек, а это CCD-матрице недоступно, там считывание происходит одновременно. Благодаря произвольному считыванию в CMOS-матрицах нет размазывания изображения.

Еще одно достоинство – расположение значительной части электроники непосредственно на ячейке, благодаря этому появляются широкие возможности управления матрицей и изображением.

При всех имеющихся достоинствах данной технологии, недостатков хватает. Главный – незначительный размер светочувствительного элемента в соотношении к общей площади пикселя. Одно из основных достоинств – расположения электроники на ячейке. Но из него вытекает еще один недостаток – значительная часть площади пикселя занята электроникой, а значит, уменьшена площадь светочувствительного элемента.

В то же время нельзя не отметить, что CMOS был модифицирован несколько лет назад, и для видеонаблюдения CMOS-матрицы действительно подходят лучше (благодаря чёткому изображению, низкому энергопотреблению и возможности уменьшать битрейт видео.

Физический размер матрицы | panoramist.ru

Физический размер матрицы

Одной из ключевых характеристик матрицы является её физический размер (не путайте с разрешением). Физический размер — это размер самой поверхности микросхемы, на которой расположены фотоэлементы в миллиметрах. Если физический размер матрицы мал, то даже высокое разрешение в мегапикселях не гарантирует получение качественных снимков.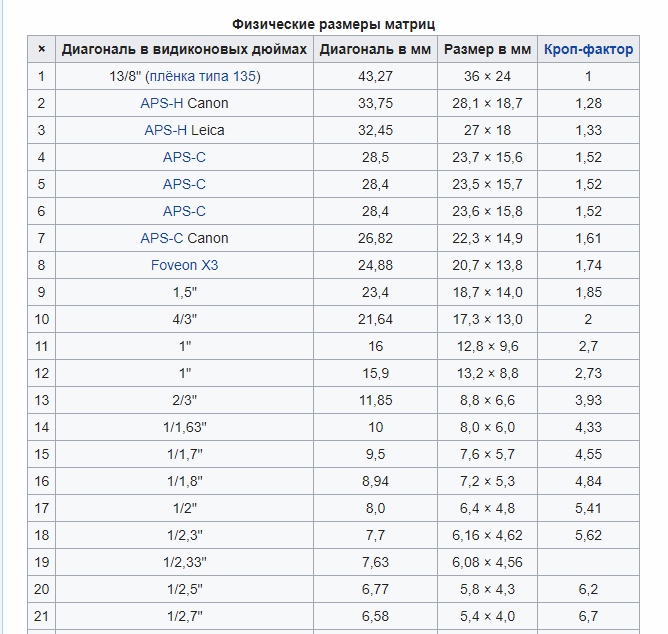 Виной этому так называемые цифровые шумы, о которых будет рассказано в отдельной статье. Таким образом, чем больше физические размеры матрицы, тем лучше и качественней будут снимки. Идельным считается размер матрицы, соответствующий размеру полного плёночного кадра 35×24мм. Однако, чем больше матрица, тем она сложнее в изготовлении и дороже. Поэтому матрицы, имеющие размер полного каждра ставятся только в очень дорогие зеркальные камеры. Даже матрицы размером в половину плёночного кадра, ещё слишком дороги, чтобы ставить их в недорогие фотокамеры, поэтому в мыльницах как правило физический размер матрицы не превышает нескольких миллиметров.

Вроде бы очевидный факт про физический размер матрицы становится очень даже неочевидным, когда мы читаем характеристики цифрового фотоаппарата в паспорте. Мы видим напротив слов «размер матрицы» какие-то странные цифры: 1/2.3″, 1/2.5″, 1/1.8″, 2/3″ и т.д. и начинаем недоумевать — что это? Это странное обозначение является размером матрицы в обратном количестве дюймов. Чем такое соотношение больше, тем крупнее матрица. Однако, каким именно образом этот размер отражает физический размер матрицы в миллиметрах, понять совершенно невозможно. Имеются лишь сведения, что данное обозначение пошло от размеров электронно-лучевых трубок телевизоров и дисплеев, когда с его помощью показывали эффективную площадь поверхности этих самых трубок, которая использовалась при формировании изображения. Учитывая полную непригодность самих цифр для нужной нам оценки физического размера матрицы, всё-таки можно воспользоваться данной ниже картинкой, чтобы понять как эти цифры относятся между собой и получить представление о нужном нам размере.

Как можно заметить на рисунке, кроме размера в миллиметрах и обратных дюймах, на рисунке есть загадочное обозначение KF. Это так называемый кроп-фактор, который показывает во сколько раз физический размер матрицы фотоаппарата меньше размера плёночного кадра 35×24мм. Таким образом, это ещё один параметр, ориентируясь на который можно судить о физическом размере матрицы. Чем больше кроп-фактор, тем меньше матрица и тем она хуже. Идеальный кроп-фактор, соответствующий полному кадру, размером в 35×24мм — это 1. Кроп-фактор соответствующий размеру полвины кадра равен 1.92 и т.д.

Но даже кроп-фактор, не даёт точного представления о том каков всё-таки точный физический размер матрицы в миллиметрах, давая лишь приблизительное представление.

Sony HDR-CX405B технические характеристики видеокамеры Sony HDR-CX405B

Общая информация

Производитель

Sony

Общие характеристики

Тип носителя

перезаписываемая память (Flash)

Поддержка видео высокого разрешения (Full HD)

есть

Максимальное разрешение видеосъемки

1920×1080

Режим ночной съемки

есть

Широкоформатный режим видео

есть

Фокусное расстояние объектива

1. 9 — 57 мм

Эквивалентное фокусное расстояние

26.8 — 804 мм

Zoom оптический/цифровой

30x / 350x

Выдержка

1/10000 — 1/6 сек

Диафрагма

F1. 8 — F4

Ручная установка экспозиции

есть

Ручная фокусировка

есть

Фоторежим

есть

Фотосъемка в режиме видеосъемки

есть

Широкоформатный режим фото

есть

Тип матрицы

CMOS

Количество матриц

Матрица

2. 29 Мпикс

Физический размер матрицы

1/5.8″

Функциональные возможности

Стабилизатор изображения

оптический

ЖК-экран

есть (2. 7″, 230400 пикс.)

Видоискатель

нет

Баланс белого

авто, предустановки, ручная установка

Форматы записи

720p, 1080i, 1080p

Автоэкспозиция

есть

Режимы съемки

портретная, восход и закат, пейзаж, пляж, снег, фейерверк

Фокусировка по лицу

есть

Интерфейсы и носители

Интерфейсы ?

AV-выход, HDMI-выход, USB-интерфейс

Запись на карту памяти

есть

Поддержка карт памяти

MS Duo

Дополнительная информация

Минимальная освещенность

3 люкс

Физические параметры (нетто)

Размеры (ШxВxГ)

128x60x54 мм

Вес (нетто)

215 г

Вес (брутто, кг)

0. 5_

Матрица для лучшего видеорегистратора и скорость записи

Первая часть статьи — вступление, какое разрешение записи лучше для видеорегистратора

2 часть

Качественная матрица в видеорегистраторе обеспечивает отличную первичную картинку

Это специализированная микросхема, на которую проецируется изображение через линзы объектива. Матрица считывает картинку и преобразует её в цифровой сигнал, который обрабатывается процессором и записывается в память. Эти приборы обладают множеством характеристик, большинство из которых понятны только инженерам, но рядовому покупателю все характеристики матрицы и не нужны. Для того, чтобы выбрать видеорегистратор лучший из множества моделей по качеству матрицы достаточно знать и понимать только те параметры, которые указываются в технических характеристиках – тип матрицы, её размер и количество пикселей.

- Тип матрицы В большинстве видеорегистраторов применяется CMOS матрица (на полевых транзисторах), выпускаются также регистраторы оснащенные CCD матрицей (технология приборов с зарядовой связью на фотодиодах). Изначально CCD матрицы давали лучшее видеоизображение, чем CMOS-матрицы, однако инженеры довели технологию CMOS до совершенства и теперь, по большому счету, нет разницы, какой матрицей оснащен видеорегистратор – качество видео (применительно к автомобильным видеорегистраторам) практически одинаковое. Гораздо большее значение имеет не тип матрицы, а её производитель. Например, неплохие матрицы делает SONY и CANON.

Если Вы хотите купить лучший видеорегистратор — смотрите в характеристиках физический размер матрицы

Физический размер матрицы. Обозначается обычно в дюймах, например 1/3,2″ — матрица имеет размер 3,4х3,5 мм. Чем физические размеры матрицы больше, тем лучше – меньше шум и больше чувствительность (хорошо для видеосъемки в условиях недостаточной освещенности). Естественно, большие матрицы и дороже стоят.
- Для справки — Матрица 1/3,2″ — меньше размерами, чем 1/2,7″.
Количество пикселей. В названии матрицы это отражается например так: 0,3 МП (мегапикселя) или 5 МП. Простой арифметический подсчет показывает, что для формата FULL HD разрешение 1920х1080 пикселей (самое высокое качество, которое на данный момент поддерживают автомобильные видеорегистраторы), нужно 2073600 пикселей. То есть, матрицы 3-5 МП хватит с лихвой. Большие размеры матриц – 8 или 12 МП, ничего к качеству видеозаписи не добавляют. Обычно это рекламный ход или нужно для режима фотоаппарата.

Скорость видеосъемки измеряется частотой кадров в секунду

Стандартной считается скорость записи (частота кадров в секунду) 25 к/с для видео стандарта PAL (европейский стандарт) и 30 к/с для NTSC (американский и японский стандарт). Однако в последнее время появились видеорегистраторы поддерживающие более высокие скорости 50 и 100 к/сек для PAL и 60 и 120 к/сек для NTSC. Это очень полезная функция. В экстремальной ситуации автомобиль на дороге может совершать довольно резкие маневры и не всегда по желанию водителя. В этот момент смена картинки в объективе видеорегистратора может превысить скорость видеозаписи, и, если смотреть запись по кадрам, видеокартинка получится смазанной, нечеткой.

Отдельный кадр записи видеорегистратором автомобиля на большой скорости со стандартной частотой кадров (30 к/сек)

Другое дело, если видеозапись велась со скоростью кадров в два (60 к/сек), а то и в четыре раза (120 к/сек) быстрее. Без всяких приборов Вы сразу же заметите разницу – кадры будут намного четче. Также, если снять видео с ускоренной частотой кадров, а потом просматривать его на стандартной частоте, то Вы увидите высококачественное замедленное видео – без рывков и резких переходов. Минус ускоренной видеосъемки – увеличенный расход памяти для записи соответственно в 2 или 4 раза больше.

Отдельный кадр записи видеорегистратором автомобиля на большой скорости с учетверенной частотой кадров (120 к/сек)

Также режим с ускоренной частотой кадров создает дополнительную нагрузку на видеопроцессор, поэтому обычно видеозапись с ускоренной частой кадров не применяется в разрешении 1920х1080 (процессор не тянет), а обычно в более низких разрешениях – 848х480 или 1280х720 пикселей. Однозначно, если Вам попадется видеорегистратор, который пишет с ускоренной частотой кадров в режиме FULL HD (1920х1080 пикс.) – можете не сомневаться – в нем установлен самый современный и мощный видеопроцессор.

Читать третью часть — оптика -стекло или пластик?

Видеокамера Sony FDR-AX700 Black

Общие
Тип	Видеокамера
Производитель ?	Sony
Основные характеристики
Размеры (ШxВxТ) (см)	197x90x116 мм
Вес (кг)	935 г
Цвет	Black
Экран
Тип экрана ?	ЖК-экран, сенсорный
Диагональ (дюйм) ?	3.5
Разрешение экрана ?	1555000 пикс.
Видоискатель	есть, цветной
Число пикселов видоискателя	2359296 пикс.
Процессор и память
Процессор	Процессор обработки изображения BIONZ X
Мультимедийные возможности
Макс. разрешение фото	5024×2824 пикс
Широкоформатный режим фото	есть
Фоторежим	есть
Другие функции
Управление	дистанционное управление
Дополнительные возможности	есть индикация пересвета, поддержка ExifPrint, возможность записи 5.1-канального звука, запись в H.264, запись в MPEG4
Интерфейсы
Интерфейсы	AV-выход, HDMI-выход, USB-интерфейс, выход на наушники, микрофонный вход, Wi-Fi, NFC
Тип карт памяти	SD, SDHC, SDXC, microSD, MS Duo
Объектив
Выдержка	1/10000 — 1/8 сек
Фокусное расстояние ?	9. 3 — 111.6 мм
Zoom цифровой	192x
Диафрагма	F2.8 — F4.5
Оптический зум	12x
Диаметр фильтра	62 мм
Эквивалентное фокусное расстояние	29 — 348 мм
Ручная установка экспозиции	есть
Ручная фокусировка	есть
Матрица
Размер	14.20 Мпикс
Тип матрицы	CMOS
Физический размер матрицы	1″
Количество матриц	1
Видеосъемка
Стабилизация изображения	оптический
Баланс белого	авто, предустановки, ручная установка
Поддержка видео высокого разрешения	UHD 4K
Максимальное разрешение видеосъемки	2160×3840
Режим ночной съемки	есть
Широкоформатный режим видео	есть
Максимальная частота кадров при съемке HD-видео	60 кадров/с при разрешении 1280×720, 120 кадров/с при разрешении 1920×1080, 30 кадров/с при разрешении 4K
Форматы записи	720p, 1080i, 1080p
Режимы съемки	портретная, восход и закат, пейзаж, пляж, прожектор, снег, фейерверк
Дополнительная информация
Комплектация	аккумулятор, сетевой адаптер электропитания, шнур питания, руководство по эксплуатации, пульт дистанционного управления, бленда объектива, крышка объектива, большой наглазник
Гарантия	24 мес

Маркировка матрицы видеокамеры и значения её параметров

При выборе видеокамеры важными параметрами являются физический размер матрицы, разрешение и использованные в ней технологии

В описании камеры видеонаблюдения производитель сообщает информацию об установленной в неё матрице. Обычно это физический размер диагонали сенсора в дюймах, чувствительность в Лк и число эффективных пикселей (точек). Некоторые производители видеокамер, например, AltCam, дополнительно указывают изготовителя сенсора: Sony, OmniVision или Aptina. В этой статье мы расскажем, на какие параметры нужно обращать внимание в первую очередь.

Физический размер матрицы

Размер диагонали сенсора указывается в дюймах. Исторически принято использовать обратный способ обозначения: 1/2,7”, 1/4” и так далее. Чтобы понять, как соотносится размер сенсора с полноценным кадром плёнки 35 мм, мы приводим следующую схему из справочников для любителей фотографии.

Так, 1/3,2” соответствует прямоугольнику 3,4 на 4,5 мм. В видеокамерах такие крупные матрицы, как 4/3” применяются только в профессиональных дорогих моделях. Сенсоры бюджетных камер и устройств среднего ценового диапазона не превышают 1/2,7 дюйма. По ряду причин, они обеспечивают оптимальное соотношение стоимости и качества изображения при разрешении до 2 и даже 4 Мп.

Матрицы меньшего, чем 1/2,7”, размера имеют следующие недостатки.

Высокий уровень цифровых шумов. Особенно сильно проявляется это на маленьких сенсорах с разрешением 2 Мп и выше. Пиксели расположены слишком плотно и дают наводки на соседей.
Относительно узкий угол обзора. Чем больше матрица, тем шире угол обзора камеры.
Искажение картинки. Маленьким сенсорам в большей степени свойственны аберрации, дисторсия и виньетирование. В причины их образования вдаваться в данной статье не будем, но профессионалы от фотографии подтвердят справедливость этого суждения.

Вывод. При покупке старайтесь выбирать видеокамеры с матрицей размером 1/2,7” и более для получения качественной разборчивой картинки при видеонаблюдении.

Чувствительность матрицы

В принципе, чем меньше значение чувствительности, тем лучше сенсор работает при плохом освещении. Показатель иногда отдельно указывается для чёрно-белой и цветной съёмки. Хороший показатель для цветного режима – 0,01 Лк.

Чтобы наглядно понять уровень освещения при разных сценах, снова обратимся к картинке из справочника для фотографов.

Надпись «0 Лк при включённой ИК-подсветке» означает лишь то, что камера отлично снимает при полной темноте в ИК-диапазоне. В этом случае картинка всегда будет монохромной.

Вывод. Выбирайте видеокамеры со значением чувствительности матрицы 0,01 Лк в цвете, чтобы получать цветную картинку в сумерках. ИК-подсветка в данном случае не используется.

Разрешение сенсора

В настоящее время наиболее популярны доступные аналоговые видеокамеры высокого разрешения 1 и 2 Мп. Их обозначают 720p и 1080p. Для IP-устройств приемлемые по стоимости решения есть и с 4 Мп. А со временем качество картинки в видеонаблюдении обещает выйти на уровень 4K.

На рисунке ниже приведено сравнение размеров изображения в пикселях.

Вывод. Выбирая видеокамеру, ориентируйтесь на разрешение 2 Мп, как на обеспечивающее детализированную картинку. Чем больше пикселей, тем более информативный зум можно получить. Но не покупайте видеокамеры с разрешением 2 Мп и матрицей, меньше 1/3 дюйма. Причины изложены выше.

Производитель матрицы видеокамеры

В устройствах Hikvision и HiWatch упоминания о марке сенсора вы не найдёте. Указывается размер, чувствительность, разрешение, но не чип. Если же вы выбираете видеокамеру от CTV или AltCam, купить которую в Москве можно в БэстСБ, то там производитель матрицы указан.

По качеству картинки, на основе мнения экспертов, расположить их можно следующим образом.

Sony. Дорогой, но обеспечивающий наиболее качественную картинку чип. В современных сенсорах серии IMX реализован ряд технологий, которых нет у конкурентов.
Aptina. Уверенный середняк, как по стоимости, так и по качеству изображения.
OmniVision. Сенсоры этого бренда выигрывают у конкурентов по цене. Используются в бюджетных видеокамерах высокого разрешения.

Вывод. Если не хотите экономить на качестве картинки, выбирайте более дорогие чипы от Sony или Aptina. Тем не менее, для многих задач видеонаблюдения чипы OmniVision также справляются неплохо, а стоят дешевле конкурентов.

По любым вопросам, связанных с выбором видеокамеры, смело обращайтесь к менеджерам БэстСБ. Их профессиональное мнение основано на опыте эксплуатации сотен моделей камер от самых бюджетных до дорогих специализированных моделей. Мы поможем сделать верный выбор!

Размер матрицы — обзор

■

Мы используем одну (или в нижнем индексе) жирную заглавную букву для обозначения матрицы (например, A , B , C ₁, C ₂) в отличие от строчных полужирных букв, используемых для обозначения векторов. Заглавные буквы I и O обычно зарезервированы для специальных типов матриц, обсуждаемых позже.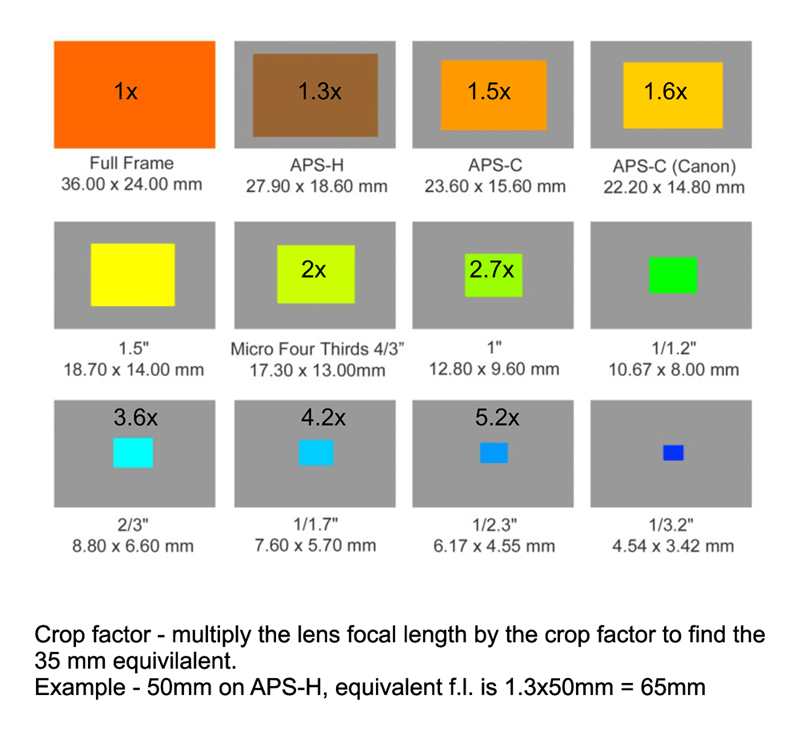

■

Размер матрицы всегда указывается первым числом строк.Например, матрица 3 × 4 всегда имеет три строки и четыре столбца, а не четыре строки и три столбца.

■

Матрица m × n может рассматриваться как набор векторов-строк m , каждый из которых имеет координаты n , или как набор векторов-столбцов n , каждый имеющий координаты м . Матрица с одной строкой (или столбцом) по существу эквивалентна вектору с координатами в виде строки (или столбца).

■

Мы часто пишем a _ij для представления записи в строке i и j -м столбце матрицы A . Например, в предыдущей матрице , , , , _{, 23,} — это запись -5 во второй строке и третьем столбце. Типичная матрица 3 × 4 C имеет элементы, обозначенные как

C = [c11c12c13c14c21c22c23c24c31c32c33c34].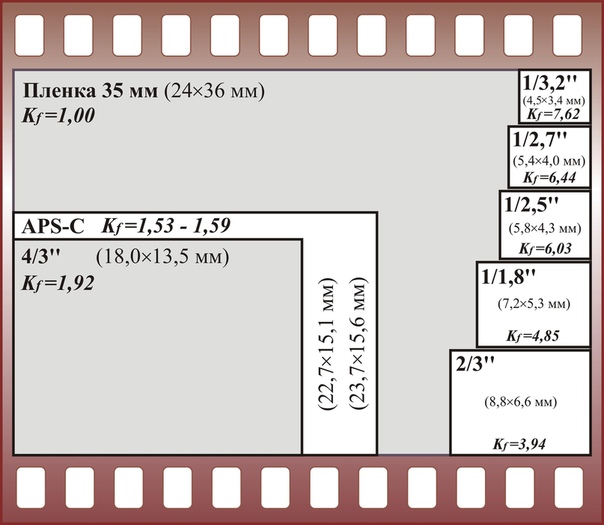

■

ℳ _mn представляет собой набор всех матриц с записями действительных чисел, имеющими m строк и n столбцов.Например, ℳ ₃₄ — это набор всех матриц, имеющих три строки и четыре столбца. Типичная матрица в ℳ ₃₄ имеет форму предшествующей матрицы C .

■

главная диагональ элементов матрицы A — это a ₁₁, a ₂₂, a ₃₃,…, те, которые лежат на диагональной линии рисуются вправо, начиная с верхнего левого угла матрицы.

Матрицы и матричная алгебра — Статистика Как к

Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):

Матричная алгебра: введение
Добавление матрицы: дополнительные примеры
Умножение матриц
Определение сингулярной матрицы
Матрица идентичности
Что такое обратная матрица?
Собственные значения и собственные векторы
Расширенные матрицы
Определитель матрицы
Диагональная матрица
Что такое симметричная и кососимметричная матрицы?
Что такое матрица транспонирования?
Что такое матрица дисперсии-ковариации?
Корреляционные матрицы
Идемпотентная матрица.

Матрица — это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:

Преобразование в матричную алгебру в основном включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):

Числа, которые появляются в матрице, называются элементами матрицы .

Матрицы

: Обозначение

Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список, подобный этому: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы придерживаться соглашения.

Некоторые из наиболее распространенных терминов, с которыми вы встретитесь при работе с матрицами:

Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
Элементы : числа, которые появляются внутри матрицы.
Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы.
Скаляр : любое действительное число.
Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.

Матрицы идентичности. Изображение: Википедия.com.

Матричная алгебра: сложение и вычитание

Размер матрицы (т.е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерностей должно быть точно так же, как . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одно и то же место (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).

Примечание к обозначениям: на листе (например, в Excel) буквы столбцов (ABCD) и номера строк (123) используются для определения местоположения ячейки, например A1 или D2. Для матриц типично использование обозначений типа g _ij, что означает i-ю строку и j-й столбец матрицы G.

Вычитание матриц работает точно так же.
Наверх

Дополнение Matrix — это всего лишь серия дополнений. Для матрицы 2 × 2:

Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
Сложите верхние правые числа и запишите сумму в правом верхнем углу.
Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
Сложите нижние правые числа вместе и запишите сумму в правом нижнем углу:

Используйте ту же процедуру для матрицы 2 × 3:

Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.

Матрица с 4 строками и 2 столбцами может быть добавлена  к матрице с 4 строками и 2 столбцами.
Матрица с 4 строками и 2 столбцами не может быть добавлена  к матрице с 5 строками и 2 столбцами.

Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.

Другой способ подумать…

Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.

Добавление матрицы для неравных размеров

Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов — прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):

Например:

К началу

Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:

Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14

Результат четырех умножений дает числа в новой матрице справа.

Умножение матриц: две матрицы

Если вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.

Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:

Вы можете выполнить матричное умножение двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице.Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).

Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете умножить несколько матриц вместе.

Microsoft Excel также может выполнять матричное умножение с использованием функций «массива».Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
Наверх

Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):

Есть и другие типы сингулярных матриц, некоторые из них не так-то легко обнаружить.Следовательно, необходимо более формальное определение.

Следующие три свойства определяют сингулярную матрицу:

Матрица квадратная и
Не имеет обратного.
Имеет определитель 0.

1. Квадратная матрица

Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица — это квадратная матрица, но не все квадратные матрицы сингулярны.

Необратимые матрицы

Если квадратная матрица не имеет обратной, то это особая матрица.

Обратная матрица — это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.

Матрицы идентичности. Изображение: Wikipedia.com.

Если вы не знакомы с поиском инверсий, вы можете посмотреть это короткое видео:

Определитель нуля

Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.

Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:

К началу

Единичная матрица — это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах. Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:

По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным.Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x. По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .

В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I _{n * n}. На главной диагонали всегда будут единицы, а оставшиеся пробелы — нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:

Матрица аддитивной идентичности

Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности.Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей .

Аддитивная единичная матрица для матрицы 3 * 3.

Вернуться к началу

Обратные матрицы — это то же самое, что и обратные. В элементарной алгебре (а может быть, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.

Изображение предоставлено LTU

Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая в основном представляет собой матрицу с единицами и нулями.

Поиск обратной матрицы состоит из нескольких шагов. Посмотрите это короткое видео о том, как найти обратную матрицу, или выполните следующие действия:

Шаг 1: Найдите адъюгат матрицы.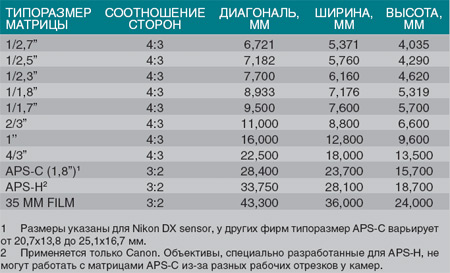 Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:

Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.

Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) — (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .

Проверка ответа

Вы можете проверить свой ответ с помощью умножения матриц. Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
Наверх

Собственное значение (λ) — это специальный скаляр, используемый при умножении матриц и имеет особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем.Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его по вектору x .

Пример собственного значения

В следующем примере 5 — собственное значение A, а (1,2) — собственный вектор:

Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):

Что, если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?

Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в разложении на собственные числа . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.

Расчет

Найдите собственные значения для следующей матрицы:

Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:

Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:

Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) — (3) (3)
Упрощая, получаем:
-5 — 5λ + λ + λ ² — 9
= λ ² — 4λ — 14

Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ ² — 4λ — 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2

Ответ : 2 + 3√2 и 2-3√2

Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.

Наверх

На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений, и именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.

Например, следующая система линейных уравнений:

x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11

Можно поместить в следующую расширенную матрицу:

После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.

У вас не , а , чтобы использовать вертикальную полосу в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.

Написание системы уравнений

Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.

Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, а затем укажите «z.«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y — 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце со знаком равенства.
-1x + 7y + 3 = 0
2x + 4y — 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом шаге стоит отрицательный знак, просто сделайте константу отрицательным числом.
Наверх

Определитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:

Это действительное число. Сюда входят отрицательные числа.
Определители существуют только для квадратных матриц.
Обратная матрица существует только для матриц с ненулевыми определителями.

Символ для определителя матрицы A — это | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два понятия не имеют ничего общего друг с другом.

Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.

Определитель матрицы 2 × 2

Формула определителя матрицы 2 × 2 — ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.

Определитель матрицы 3 × 3

Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:

= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.

Определитель матрицы 4 × 4

Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые входят в матрицу 4 × 4.В виде формулы:

Наверх

Диагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.

Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.

Единичная матрица, которая имеет все 1 по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е. 2,2,2 или 9,9,9) является скалярным кратным единичной матрице и также может быть классифицирована как диагональная.

Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n — порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.

Обозначение

Обозначение, обычно используемое для описания диагональной матрицы, — diag (a, b, c) , где abc представляет числа в первой диагонали. Для приведенной выше матрицы это обозначение будет diag (3,2,4)..

Верхняя и нижняя треугольные матрицы

Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. Нижнетреугольная матрица имеет числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.

Диагональная матрица — это матрица с нижней диагональю и матрица с нижней диагональю.

Прямоугольные диагональные матрицы

Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n .Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.

Наверх

Транспонирование матрицы (или транспонирование матрицы) — это как раз то место, где вы переключаете все строки матрицы в столбцы. Матрицы транспонирования полезны при комплексном умножении.

Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r».Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.

Симметричная матрица — это частный случай транспонированной матрицы; он равен своей транспонированной матрице.

Формально A = A ^{T ^.}

Символы для транспонированной матрицы

Обычный символ для транспонированной матрицы — A ^T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ^‘ и.

Свойства матриц транспонирования

Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:

(A ^T) ^T = A: транспонированная матрица транспонирования является исходной матрицей.
(A + B) ^T = A ^T + B ^T: Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
(rA) ^T = rA ^T: когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, которая может умножать матрицу).
(AB) ^T = B ^T A ^T: транспонирование двух матриц, умноженных вместе, совпадает с произведением их транспонированных матриц в обратном порядке.
(A ^-1) T = (A ^T) ^-1: транспонирование и инверсия матрицы могут выполняться в любом порядке.

Наверх

Симметричная матрица — это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:

Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.

Альтернативное определение

Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.

Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M ^T, где M ^T — матрица транспонирования.

Максимальное количество номеров

Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.

Диагональные матрицы

Диагональная матрица — это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.

Что такое асимметричная матрица?

Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:

Математически асимметричная матрица удовлетворяет условию a _ij = -a _ji.Например, возьмите запись в строке 3, столбец 2, которая равна 4. Его симметричный аналог — -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A ^T = — А. Другими словами, матрица является кососимметричной, только если A ^T = -A, где A ^T — транспонированная матрица.

Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что из _{i, i} = −a _{i, i} следует _{i, i} = 0.

Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:

Добавление двух кососимметричных матриц все вместе.

Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг — убедиться, что все элементы на ведущей диагонали равны нулю (что невозможно «доказать» математически!).Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a _ij = — a _ji.

Косоэрмитский

Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.

Косоэрмитова матрица, показывающая комплексные числа.

Фактически, кососимметричный и кососимметричный эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).
Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу

Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) — это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Дисперсия — это мера того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины перемещаются вместе в одном направлении.

Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариантной матрицы, потому что в основном эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.

Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.

Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.

Создание матрицы дисперсии-ковариации

Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.

Если вы хотите сделать один вручную:
Шаг 1: Вставьте дисперсии для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A). На следующей диаграмме показано, где каждая ковариация и дисперсия появляются для каждого варианта.

Наверх

См. Также:
Что такое матрица неточностей?

Следующий : Форма эшелона строк / Форма сокращенного эшелона строк

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

пикселей и таблицы цветов

Цифровая обработка изображений

Оцифровка изображения приводит к формированию элементов изображения, обычно называемых пикселей

Большинство систем формирования изображений имеют аналого-цифровые преобразователи (АЦП), которые принимают данные, полученные от ФЭУ, а затем оцифровывают информацию в матрицу с координатами X и Y
Чем больше пикселей в изображении, тем выше разрешение
В ядерной медицине ключевым фактором лучшего разрешения является количество пикселей в изображении
Размер матрицы определяет количество пикселей в изображении.Чтобы упростить это обсуждение, давайте посмотрим на матрицу 3 x 3, которая содержит 9 пикселей

Приведенная выше матрица показывает значение счетчика в каждой ячейке, замечающее, что оно уменьшается в порядке убывания, при этом нижний правый угол содержит 50 пунктов, а верхний левый — 0 пунктов.

Это изменение количества отсчетов показывает изменение серой шкалы, где увеличение оттенков серого относится к уменьшению количества отсчетов

Шкала серого имеет 256 оттенков (2 ⁸) серого, что соответствует количеству отсчетов в изображении
При отображении счетчиков из сбора данных компьютер применяет справочную таблицу (LUT), которая назначает количество / пиксель с координатами XY
С учетом приведенной выше шкалы серого пиксель (ы) с максимальным количеством отсчетов является белым (или чистым), а пиксели с наименьшим количеством отсчетов — черными
Серая шкала также может быть инвертирована, когда самый горячий пиксель становится черным, а белый цвет означает отсутствие подсчета.Это называется обратным видео

LUT также может быть назначена многим типам цветовых шкал, которые могут дополнительно улучшить отображаемые данные и могут улучшить диагностическое качество исследования.
1. комбинации LUT используют до трех основных цветов: R ed, G reen и B lue (помните ограбление?)
2. Смешение цветов увеличивает разницу между количеством отсчетов в пикселях и количеством цветовых оттенков на отсчет (а)
3. Это дополнительно увеличивает возможность обнаружения незначительных изменений в счетах, когда используются все три основных цвета.Согласно Perigees, можно использовать 262000 оттенков или комбинаций, однако, если каждый цвет представляет 2 ⁸ оттенков, тогда будет 2 ⁸ x 2 ⁸ x 2 ⁸ = 1,67 x 10 ⁷ (красный, зеленый, и синий) комбинации
4. Пример того, как разные цветовые шкалы влияют на то, как мы визуально видим сканирование костей
Какие детали мы действительно можем видеть?

В отношении оттенков серого человеческий глаз может видеть только изменение яркости примерно на 2%.Следовательно, учитывая 256 оттенков серого, требуется 5 оттенков в любом направлении, чтобы реализовать небольшое изменение шкалы
Человеческий глаз может видеть более 1 миллиона типов цветов, поэтому глаз более «чувствителен» к трехцветной шкале
Однако человеческий глаз более чувствителен к зеленому и желтому, чем к синему и красному
Понимая «ограниченное» разрешение наших шлюх и НМ, можно сказать, что незначительные изменения в количестве отсчетов на пиксель могут быть не заметны
Проверьте нашу способность замечать незначительные изменения цвета (оттенка).Всего 4 ряда. Первый и последний блоки в каждой строке нельзя перемещать. Расставьте поля в ряду, чтобы они соответствовали тонким изменениям цвета. Нажмите Test
Вот множество примеров LUT, используемых в ядерной медицине и диагностической радиологии. Щелкните изображение для увеличения

Глядя на ядерную кардиологию с отображением LUT, какую шкалу вы бы выбрали?

Размер матрицы — с плоской точки зрения (двухмерные изображения)

Размер пикселя
1. Определение размера пикселя указано выше для матрицы 128 и камеры с квадратом 15 дюймов
2. Эта информация полезна не только для оценки разрешения, но и для возможности измерить размер поражения, зная количество пикселей, которые оно покрывает
Размеры матриц ядерной медицины различаются и составляют следующие

32 x 32 (исследование потока)
64 x64 (исследование потока)
128 x 128 (потоковые или статические изображения)
256 x 256 (статические изображения)
512 x 512 (статические изображения)
256 x 1024 (сканирование всего тела)
512 x 1048 (сканирование всего тела)

Возникает вопрос: какая матрица лучше всего подходит для конкретной процедуры? Хотя примеры приведены выше, все же есть некоторые различия в различных вариантах выбора
При обдумывании матрицы вам необходимо включить количество приобретаемых отсчетов
Другой проблемой, вызывающей озабоченность, является режим байта-слова-слова пикселя.
1. Считайте, что 16 бит = 2 байта = 8 = 1 слово.Сколько отсчетов может содержать пиксель?
2. Если размер матрицы составляет 128 x 128 x 1 байт, это означает, что каждый пиксель может содержать 2 ⁸ отсчетов или до 256 отсчетов. Сколько там пикселей?
3. Что произойдет, если пиксель станет насыщенным или количество отсчетов превысит 256?
  1. Изображение перестает копироваться (это мой личный опыт) или
  2. Пиксель перестает получать, но остальная часть системы продолжает считать или
  3. Счетчики в насыщенном пикселе откатываются и начинаются снова с нуля и снова нарастают
4. Пиксель также может находиться в режиме слова, что соответствует 2 ⁸ x 2 ⁸ = 65.5 тыс. Отсчетов на пиксель. Шансы на насыщение пикселей практически отсутствуют. Большинство современных фотоаппаратов имеют возможность собирать в текстовом режиме
5. Вот пример того, как на разрешение влияют размер и глубина матрицы
Эффект частичного объема (PVE) ¹

Это лучше всего объяснить, посмотрев на край круга (вверху), где только часть пикселя собирает счетчики
Результат — потеря счета на краю получения изображения
На экзамене фактическое изображение круглое, но пиксели квадратные.
1. Это означает, что определенные области цилиндра собирают меньше отсчетов на основании того факта, что только часть пикселя собирает данные
2. Активность перетекает из цилиндра в частичный пиксель (пиксели)
3. Аналогичным образом активность также распространяется на пиксели, находящиеся за пределами цилиндра, области фона
Чистый результат обозначается как PVE
Вот как PVE может фактически сбить с толку полученные данные.На приведенном выше изображении ПЭТ-сканирование определяет опухоль, которая может прикрепляться или не прикрепляться к грудной стенке. КТ показывает, что это не часть стены, а объединенная ПЭТ / КТ-сканирование помогает врачу свести на нет эффект ПВЭ. Другой интересный момент заключается в том, что матрица для приведенного выше изображения в ПЭТ составляет 128, тогда как изображение КТ имеет матрицу 512

Размер матрицы и статистический шум

Предположим, вы собрали 1 миллион счетчиков за одно наводнение.Что такое процентный коэффициент вариации?
Что произойдет с резюме, если вы соберете такое же количество отсчетов в матрице 256?
Сколько отсчетов нужно сделать в 256-м матричном порядке, чтобы иметь такое же изменение, что и в 128-м?
Слишком много ошибок ~ шума вызывают проблемы с качеством изображения?

Регулировка изображения и дисплеи

Изображения можно настраивать в различных форматах — вверху графическое отображение, внизу — визуальные результаты
1. Необработанные данные отображаются на линейной кривой по мере увеличения числа, так же как и шкала серого
2. В изображении с большим количеством элементов может быть выполнена логарифмическая корректировка, которая улучшает пиксели с низким количеством пикселей, в то время как пиксели с большим количеством пикселей имеют меньшую вариацию
3. При экспоненциальной регулировке пиксели с меньшим количеством пикселей имеют небольшие вариации, однако пиксели с большим количеством пикселей показывают большее изменение серого
4. Вычитание фона дает каждому пикселю один и тот же серый цвет (ноль), пока кривая не начнет подниматься
5. Повышение контрастности дает значение самого горячего пикселя для всех пикселей на плато, где происходит изменение серого цвета по мере того, как кривая начинает опускаться
6. Вот что на самом деле делают с изображением различные настройки.На крайнем левом изображении , а не , корректировка
7. Изображения также можно корректировать с помощью различных типов фильтров
Свернутое ядро (термин, используемый при фильтрации изображения)

Первый взгляд на сглаживающий фильтр
Компоненты — необработанные данные + свернутый фильтр = вывод измененных подсчетов. Другими словами, необработанные данные обрабатываются путем добавления мини-матрицы (свернутое ядро) с числовым значением, которое в той или иной форме изменяет исходную матрицу
Свернутое ядро умножает каждый пиксель на 1, а затем делит центральный пиксель на 9
Эта операция выполняется для каждого пикселя в исходной матрице (необработанные данные)

http: // www.slideshare.net/brucelee55/processing-methods-of-nuclear-medicine-images

Выше результаты сглаживающего фильтра

Фильтр улучшения края (ядро)

В варианте фильтрации взвешенное ядро, как показано выше, имеет разные значения в своей мини-матрице, которая изменяет необработанные данные совершенно другим способом
Обратите внимание, что центральный пиксель в ядре — единственное положительное значение, все остальные отрицательные
Конечный результат приводит к тому, что пиксели с большим количеством пикселей значительно улучшаются

Фильтрация нашла множество применений в ядерной медицине, а также в других областях цифровой обработки изображений.В Wiki есть интересная ссылка, касающаяся многих типов приложений-фильтров и связанных с ними запутанных ядер

Разрешение

Размер

Чтобы определить разрешение, вы должны сначала определить зону сбора данных или размер головки детектора
Если область изображения составляет 400 мм и вы используете матрицу 32 x 32, каков размер каждого пикселя?

Это можно рассчитать следующим образом: 400 мм / 32 пикселя = 12.5 мм или 1,25 см / пиксель
Это означает, что каждый пиксель соответствует размеру 1,25 см.
Если размер области с дефицитом фотонов составляет 3,0 см, то гипотетически вы сможете разрешить ее, поскольку размер вашего пикселя меньше, чем область с дефицитом отсчетов
Однако, если размер области дефицита фотонов составлял 6 мм, вы ее пропустите, потому что процесс болезни меньше, чем разрешение системы
Следовательно, увеличение размера матрицы становится критичным для разрешения меньшей области (холодной или горячей)

Разрешение и 64 x 64 при условии, что наша область изображения составляет 400 мм x 400 мм

400 мм / 64 = 6.25 мм / пиксель
На этом этапе способность визуализировать холодное пятно размером 6 мм почти не отличается от пикселя
На самом деле вам следует применить матрицу 128 x 128, чтобы вы могли еще больше улучшить свое разрешение. Это дает размер пикселя 3,25 мм
Примечание: та же логика, описанная выше, может применяться, если в рассматриваемой области жарко или холодно.

Подробнее о размере матрицы

Каждый раз, когда вы увеличиваете матрицу, вы увеличиваете необходимое пространство для хранения на жестком диске.Время обработки также увеличивается в 4 раза
Ключевой момент — Определение наилучшего разрешения изображения для системы

Как указано в ваших материалах для чтения, типичный размер детектора может составлять 15 x 20 дюймов или 400 x 500 мм.
Использование коллиматора LEHR, который может разрешить объект диаметром 8 мм на глубине 10 см (это означает, что FWHM составляет 8 мм)
Гипотетически предлагается уменьшить разрешающую способность системы в мм / пиксель.
Однако разрешение выборки определило, что требуется втрое больше
Итак, если FWHM составляет 8 мм, то мм / пиксель должно быть 8 мм / 3 = 2.7

Если используется матрица 128, какой мм / пиксель? 500 мм (детектор) / 128 (матрица) = 3,9 мм / пиксель. Технически это недостаточно
Рекомендуется использовать матрицу 256 500 мм / 256 = 2,0 мм / пиксель
Следовательно, матрица 256 x 256 — это то, что необходимо для разрешения до 8-миллиметрового объекта. Какой размер пикселя?

Домашнее задание: пиксели и разрешение — это задание использует вышеуказанные данные для определения разрешения системы.

Режимы получения цифровых изображений
1. Режим кадра
  1. Считайте это статическим режимом, в котором счетчики адресованы координате пикселя XY в матрице
  2. Во время получения изображение сохраняется в буфере изображений, а затем сохраняется после остановки получения на жестком диске
  3. В динамическом режиме компьютер обычно имеет два буфера изображений, в которых счетчики регистрируются в первом, затем, когда время на каждый кадр заканчивается, полученное изображение сохраняется, в то время как следующее полученное изображение продолжается с буфером №2.
    1. Размер матрицы также важен, поскольку для хранения матрицы большего размера потребуется больше времени
    2. Следовательно, динамические изображения обычно получаются в матрице 64
    3. Сбалансируйте концепции — динамическое изображение, количество отсчетов и размер матрицы
2. Режим закрытого кадра
  1. В этом случае количество буферов равно количеству собираемых кадров
  2. Состояние кадра запускается зубцом R и собирается за очень короткий период времени
  3. Каждый зубец R запускает состояние кадра, и счет ведется до тех пор, пока не будет достигнут определенный уровень
  4. Если есть колебания в частоте сердечных сокращений, то обычно в конечных кадрах не будет активности в конце зубца R, что приведет к эффекту мигания.
  5. Стробированные исследования могут быть настроены на отклонение нерегулярных сокращений, и когда это происходит, буферы возвращаются к нулевым счетам в ожидании следующего хорошего зубца R
3. Режим списка
  1. Это не помещает счетчики в буфер, а вместо этого сохраняет все счетчики с местоположением XY и сохраняет их индивидуально
  2. Хороший пример, где это может быть применено, — это кардиостробирование, когда каждый кадр собирается индивидуально
  3. Если применяется, все подсчеты, положения XY, с каждым зубцом R.Затем технолог выбирает, какие зубцы R допустимы, составляя правильный сердечный цикл. Это те, у которых есть нормальные сокращения
  4. Этот тип приобретения используется редко
4. Цифровой зум (после или до)
  1. В этом случае масштабирование после получения изображения
    1. Если вы получили изображение с матрицей 128, а затем увеличили изображение в 2 раза, в результате получилось бы изображение, которое теперь находилось в матрице 64
    2. Результат в потере разрешения
  2. Масштабирование перед захватом улучшает разрешение
    1. Считайте, что получаемая матрица 128 имеет увеличение x2.По сравнению с обычным масштабированием, предварительное масштабирование отображает 1/2 области изображения с тем же количеством пикселей
    2. Это улучшает разрешение
Устройства отображения
1. Существует множество типов дисплеев, о которых вы можете прочитать в своей книге
2. Ключевые моменты, о которых следует помнить:
  1. Разрешение ядерной медицины ограничено
  2. Разрешение устройства отображения должно быть не ниже разрешения изображения

Вернуться к началу документа
Вернуться к оглавлению

2/18

1.Эффект частичного объема в визуализации опухоли с помощью ПЭТ. Авторы M Soret, L Stephen, JNMT, Vol.48 # 66/07
2. Свертка изображений Дж. Людвига, Государственный университет Портленда,

Basic Introduction to Matrix Product States — документация TensorNetwork

В этом руководстве мы дадим базовое введение в матричные состояния продукта (MPS) и покажем как эффективно вычислять тензорные компоненты MPS и перекрытия между двумя MPS.

Мы будем использовать следующие библиотеки:

импортировать тензорную сеть как tn импортировать numpy как np import matplotlib.{s_1 \ cdots s _ {\textf {N}}} \), где каждый \ (s_i \ in \ {1, \ ldots d_i \} \) и где \ (d_i \) называется физическим размером а \ (N \) - ранг тензора. В приложениях для конденсированных сред или квантовых вычислений \ (N \) обычно - это размер системы или количество кубитов. Стандартное графическое представление этого тензора выглядит так:

, где каждая линия представляет один индекс тензора.

Теперь давайте создадим тензор со случайными записями, с рангами и физическими размерами, которые проходят в небольших диапазонах, и проанализируем их требования к памяти:

 def create_tensor (измерение, ранг):
  '' 'Строит тензор заданного ранга со случайными целыми числами' ''
  dim_list = кортеж ([измерение для _ в диапазоне (ранг)])
  вернуть нп.random.random_sample (dim_list)

ранги = диапазон (2,6)
размеры = диапазон (2,40)

для звания в чинах:
  память = []
  для тусклых размеров:
      тензор = create_tensor (тусклый, ранг)
      компонент = кортеж (np.random.randint (0, dim, rank))
      memory.append (np.sum ([x.nbytes для x в тензоре]))
      данные = тензор [компонент]
  plt.loglog (размеры, память, 'o', ls = ':', label = f'N = {rank} ')

plt.legend ()
plt.xlabel ("Размер")
plt.ylabel ('Стоимость памяти')
plt.show ()

Это дает следующий результат:

Мы видим, что память, необходимая для хранения тензора, масштабируется как \ (\ sim d ^ {\textf {N}} \).Это экспоненциальный рост на , который быстро насыщает наши вычислительные ресурсы.

Введение в матричные состояния продукта

Один из способов обойти эту «катастрофу размерности» - сосредоточиться на определенном виде тензоров: те, которые могут быть записаны как состояние произведения матриц (слово состояние здесь связано с квантовым состоянием, сформированным из коэффициентов тензора). Состояния произведения матриц - это особый класс тензоров, которые можно записать как произведения над многими тензорами ранга 3.{s_j} \):

Вертикальные линии, как и раньше, представляют физические индексы. Новые горизонтальные линии называются вспомогательными индексами, с физическими и вспомогательными индексами на каждом сайте \ (j \), помеченными как \ (s_j, \ alpha_j \) соответственно. Линия, соединяющая два тензора (квадраты), представляет собой сокращение общего индекса двух тензоров. Различная ширина вспомогательных опор свидетельствует о том, что каждый размер может быть разным (их метки серого цвета). {s_N} _ {\ alpha_ {N-1}} \]

, где \ (\ {\ alpha \} = \ {\ alpha_1, \ ldots, \ alpha_ {N-1} \} \) и \ (\ alpha_i \ in \ {1 \ cdots D_i \} \).

В этом уроке мы возьмем все \ (D_i \) (также называемые размерностью связи ) равными одному \ (D \). Любой тензор можно записать как MPS с помощью Разложения по сингулярным значениям (хотя и ценой очень высоких размеров облигаций - экспоненциально высоки как \ (N \ to \ infty \))

Начнем с создания непосредственно узловой структуры MPS. Сначала мы определяем функции для построения каждого блока MPS, а затем сам MPS:

 # Получение компонента

блок def (* размеры):
  '' 'Построить новую матрицу для MPS со случайными числами от 0 до 1' ''
  size = tuple ([x для x в размерах])
  вернуть нп.mps [k + 1] [0]
      connected_edges.append (соединение)

  вернуть mps, connected_edges

Мы рассчитаем объем памяти MPS различных размеров и рангов (обратите внимание, мы можем пойти намного дальше, чем раньше)

 размеров = диапазон (2,9,2)
MPS_ranks = диапазон (2150)
MPS_memory = []

для тусклых размеров:
    bond_dim = 2
    MPS_memory = []
    для i в диапазоне (len (MPS_ranks)):
        rank = MPS_ranks [i]

        # Создание состояния MPS:
        ########################################################################### ################
        mps_nodes, mps_edges = create_MPS (ранг, размер, размер связи)
        MPS_memory.append (np.sum ([x.tensor.nbytes для x в mps_nodes]))

    # Результаты графика
    plt.loglog (MPS_ranks, MPS_memory, 'o', ls = ':', label = f'd = {dim} ')

plt.legend ()
plt.xlabel ('Тензорный ранг')
plt.ylabel ('память MPS')

plt.show ()

Получаем следующие результаты:

Мы видим, что требования к памяти значительно снижаются: теперь масштабирование составляет \ (\ sim N \) (что является полиномиальным). Мы можем исследовать более высокие физические измерения с меньшим объемом памяти.

Извлечение компонентов MPS

Теперь найдем компонент системы физической размерности \ (2 \) и ранга \ (N = 20 \).Это эквивалентно доступу к компонентам волновой функции одномерной квантовой цепочки \ (20 \) кубитов! Основными вычислительными затратами будет сокращение облигаций MPS. Здесь мы используем простой алгоритм для выполнения расчета: сжимаем каждую облигацию последовательно, пока весь MPS не рухнет до желаемого компонента тензора.

С помощью этой схемы можно вычислить компонент тензора за линейное время по \ (N \).

 ################################################################################## #######################
# ----- Извлечение компонента из MPS путем сжатия его краев ----- #
#################################################################################################### ######################
dim = 2
bond_dim = 2
ранг = 20
компоненты = кортеж (np.random.randint (0, dim, rank)) # произвольно выбираем компоненты, которые мы будем получать
print (f'компоненты: {компоненты} ')

mps_nodes, mps_edges = create_MPS (ранг, размер, размер связи)
для k в диапазоне (len (mps_edges)):
    A = tn.contract (mps_edges [k])

# последний узел теперь имеет все ребра, соответствующие компонентам тензора.

print (f 'коэффициент тензора при выбранных компонентах: {A.tensor [components]}')

Использование библиотеки TensorNetwork

TensorNetwork предлагает простой встроенный класс MPS, который можно использовать для вычислений тензорной сети, который мы будем использовать в дальнейшем.Получение компонента снова просто выполняется путем заключения контракта на вспомогательные индексы MPS. Мы напишем весь алгоритм для \ (\textf {N} = 24 \) и \ (d = d_i = 2 \) (опять же, чтобы сделать ссылку на спины):

 # Алгоритм поиска компонентов:

ранг = 24
Phys_dim = 2
bond_dim = 6

# построить мпс:
# состояние канонически нормализовано, когда мы определяем класс FiniteMPS
mpstate = tn.FiniteMPS.random (
  d = [Phys_dim для _ в диапазоне (ранг)],
  D = [размер_связи для _ в диапазоне (ранг-1)],
  dtype = np.узлы [k + 1] .edges [0] для k в диапазоне (-1, ранг-1)]

для x в connected_bonds:
 contract_node = tn.contract (x) # обновление для каждой контрактной облигации

# оценить желаемый компонент
компонент = кортеж (np.random.randint (0, Phys_dim, rank))

print (f 'Выбранные компоненты тензора: {component}')
print (f'Соответствующий коэффициент тензора: {Contracted_node.tensor [component]} ')

MPS образуют особый класс одномерных квантовых волновых функций, которые слабо запутаны. В одном пространственном измерении есть строгое доказательство что основные состояния локальных гамильтонианов с щелью могут быть аппроксимированы с произвольной точностью МПС с конечной размерностью связи \ (D \).И наоборот, для любого MPS можно построить локальный гамильтониан с разрывом, который имеет этот MPS в качестве основного состояния (называемого родительским гамильтонианом).

Внутренний продукт MPS

Все внутренние произведения появляются при вычислении математических ожиданий и норм квантовых состояний. Иногда их называют перекрытиями . Обратите внимание, что структура MPS делает внутреннее произведение тензоров графически интуитивно понятным, включая сокращение всех связанных ребер и связей:

Эффективный алгоритм использует свойства факторизации результирующих матриц после того, как тензоры были помещены в форму MPS.Мы делаем сокращения в последовательности «ребро-связь-связь», перемещаясь по графику:

 np.random.seed (3) # исправить seed для построения одинаковых тензоров каждый раз при вызове random

Phys_dim = 2
bond_dim = 2
ранги = диапазон (2, 60)

for Phys_dim in range (2, 11, 2): # проверить, как физический dim меняет масштаб
  перекрытие = []
  для звания в чинах:
      mpstateA = tn.FiniteMPS.random (d = [Phys_dim для _ в диапазоне (ранг)], D = [bond_dim для _ в диапазоне (ранг-1)], dtype = np.complex128)
      mpstateB = tn.FiniteMPS.nodeB [k] [1] для k в диапазоне (ранг)]
      сокращение = nodesA [0] @ nodesB [0]
      для i в диапазоне (1, len (nodesA)):
          сокращение = сокращение @ nodesA [i] @ nodesB [i]
      overlap.append (np.abs (сокращение.tensor))

  plt.loglog (ранги, перекрытие, 'o', ls = ':')
plt.show ()

Обратите внимание, как перекрытие исчезает по мере роста ранга тензора. Если мы возьмем скалярное произведение MPS на себя, мы получим квадрат нормы, который равен \ (1 \) для нормализованное состояние.

Умножение матриц

Умножение матриц: дальше по кроличьей норе

До сих пор мы имели дело с достаточно простыми операциями: сложение и вычитание матриц ограничено матрицами одинакового размера, а скалярное умножение просто запускает одно число через всю матрицу.

Но поймите: фактические матрицы также можно перемножать друг на друга. Это немного сложнее, но в основном вам просто нужно запомнить самое важное: размер имеет значение - по крайней мере, для умножения матриц.

Размеры задействованных матриц являются здесь наиболее важным фактором, поэтому будьте осторожны: для перемножения матриц количество столбцов в первой матрице должно быть таким же, как количество строк во второй . И это сделает вашу жизнь намного проще, если вы на секунду освежите в памяти разницу между строкой и столбцом.Помните, строк - это по горизонтали (слева направо), а столбцов - это по вертикали (сверху вниз).

Пример задачи

Скажем, у нас есть матрица A и матрица B :

И размер матриц, и порядок их умножения в значениях.

AB - это то, что мы не можем сделать, потому что в A есть два столбца и три строки в B . Игра окончена, чувак.

BA мы можем сделать, потому что B имеет два столбца, а A имеет две строки. Идеально. Следующее, что следует помнить, это то, что матрица продукта будет иметь такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая матрица . Да, это так важно, что мы выделили всю эту проклятую штуку курсивом.

Далее на BA . Вот как это выглядит:

Мы знаем, что у продукта будет три строки, такие как B, и два столбца, например, A :

Мы уже знаем, что первая матрица здесь B , а второй - A .Назовем наш продукт P . В этом случае записи в матрицах могут быть помечены следующим образом:

Вы захотите пройтись и спуститься, чтобы решить это:

P ₁₁ = ( B ₁₁) ( A ₁₁) + ( B ₁₂) ( A ₂₁)

Мы умножаем и складываем элементы первой строки первой матрицы с элементами первого столбца вторая матрица.Поэтому размеры должны совпадать, чтобы ничего не осталось. Затем для следующей записи в нашем продукте:

P ₁₂ = ( B ₁₁) ( A ₁₂) + ( B ₁₂) ( A ₂₂)

Теперь переходим к следующей части. Вы умножаете и складываете элементы второй строки первой матрицы с элементами первого столбца второй матрицы. Пристегнитесь.

P ₂₁ = ( B ₂₁) ( A ₁₁) + ( B ₂₂) ( A ₂₁)

Затем вы разбиваете вторую строка первой матрицы со вторым столбцом второй матрицы.Это дает вам вторую строку вашего продукта.

P ₂₂ = ( B ₂₁) ( A ₁₂) + ( B ₂₂) ( A ₂₂)

Почти готово. Еще одна строка, и вы, вероятно, можете догадаться, как это происходит:

P ₃₁ = ( B ₃₁) ( A ₁₁) + ( B ₃₂) ( A ₂₁)

P ₃₂ = ( B ₃₁) ( A ₁₂) + ( B ₃₂) ( A ₂₂)

Вставляя весь этот мусор в общую картину, мы получаем следующее:

Вот еще один способ взглянуть на это.Мы знаем из правил, что P будет иметь три строки, например B , и два столбца, например A . Попробуйте представить себе три из них вместе следующим образом:

Глядя на пересечения, мы можем увидеть, какая строка из B и какой столбец из A сталкиваются, чтобы получить одну из P записи. Ниже мы видим, что X отмечает место, где первая строка B и первый столбец A сбой:

Мы знаем, что эти четыре числа должны слиться в одно.Как они это делают? Ну, читаем строки слева направо, как книгу. Читаем столбцы сверху вниз. Следовательно, мы умножаем первое число из первой строки B на первое число из первого столбца A :

(1) (2) = 2

Затем мы умножаем второе число из B первая строка со вторым номером из первого столбца A :

(3) (3) = 9

И мы складываем их вместе:

(1) (2) + (3) (3) = 2 + 9 = 11

Затем мы проверяем конфликт между первой строкой B и вторым столбцом A :

Ага; X отмечает точку, и мы делаем то же самое.Читаем строки слева направо, как книгу. И читаем столбцы сверху вниз. Мы умножаем первое число из первой строки B на первое число из второго столбца A : (1) (1) = 1. Затем мы умножаем второе число из первой строки B на второе число из второго столбца A : (3) (2) = 6. Сложите их вместе, чтобы получить нашу запись для X:

(1) (1) + (3) (2) = 1 + 6 = 7

Мы знаем, мы знаем.Мы как побитый рекорд, но X снова отмечает точку, и мы делаем то же самое. Мы читаем строку слева направо, а столбец - сверху вниз. На этот раз мы делаем вторую строку в продукте, поэтому мы умножаем первое число из второй строки B на первое число из первого столбца A : (2) (2) = 4. Затем умножьте второе число из второй строки B на второе число из первого столбца A : (1) (3) = 3. Теперь добавьте их:

(2) (2) + (1 ) (3) = 4 + 3 = 7

Мы действительно куда-то идем.Почти на месте.

Теперь это выглядит так, и мы можем видеть, что дальше:

X отмечает точку, друг, и мы делаем то же самое. Строка идет слева направо, столбец сверху вниз. На этот раз мы по-прежнему делаем вторую строку продукта, но переходим ко второй позиции. Мы умножаем первое число из второй строки B на первое число из второго столбца A : (2) (1) = 2. Затем мы умножаем второе число из второй строки B на второе число из второго столбца A : (1) (2) = 2.Сложите этих парней:

(2) (1) + (1) (2) = 2 + 2 = 4

И мы проделываем это снова, на этот раз с третьей строкой в B , один раз для каждой записи в первом столбце A .

(4) (2) + (2) (3) = 8 + 6 = 14

И, наконец, мы соединяем третью строку B со вторым столбцом A :

(4) (1) + (2) (2) = 4 + 4 = 8

Woohoo! Мы сделали это!

Мы не теряем головы, и это становится только легче, если мы помним самые важные правила:

Для перемножения матриц количество столбцов в первой матрице должно быть таким же, как количество строк в второй.
Матрица произведения будет иметь такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая матрица.

Эй, помните, когда мы сказали, что даже когда у нас есть две матрицы одинакового размера, порядок имеет значение? Конечно, вы можете умножать в любом порядке, но ответ будет неодинаков. Часы:

Пример задачи

Сначала мы можем выполнить это в следующем порядке:

(2) (1) + (4) (4) = 2 + 16 = 18
(2) (0) + (4 ) (2) = 0 + 8 = 8
(3) (1) + (3) (4) = 3 + 12 = 15
(3) (0) + (3) (2) = 0 + 6 = 6

Итак, это наш продукт:

А если перевернуть столы?

Расположим так, чтобы было легче видеть:

(1) (2) + (0) (3) = 2 + 0 = 2
(1) (4) + (0) ( 3) = 4 + 0 = 4
(4) (2) + (2) (3) = 8 + 6 = 14
(4) (4) + (2) (3) = 16 + 6 = 22

Это наш продукт:

Совершенно разные.Странно, правда?

Но подержите прессы. Помните единичную матрицу и нулевую матрицу? Theeeey're baaaack ...

Двоичное мышление

Единственный раз, когда число можно умножить и остаться неизменным, - это умножить его на число 1.

3 × 1 = 3
100 × 1 = 100
457,820 × 1 = 457 820

В Matrix Land единичная матрица - это матричная версия 1. Все матрицы идентичности равны нулю, за исключением диагональной линии единиц, идущей от верхнего левого до нижнего правого углов.Они могут быть любых размеров, если они квадратные:

Вот в чем суть: всякий раз, когда матрица умножается на единичную матрицу, произведение совпадает с неединичной матрицей. И мы можем это доказать.

Пример задачи

Мы действуем так же, как и раньше при умножении. Мы назовем единичную матрицу I , произведение P , а другую матрицу мы назовем T для Теда. Нам просто нравится название, хорошо? Попробуйте визуализировать три из них вместе следующим образом:

Итак, мы объединяем первую строку T с первым столбцом I , чтобы найти X:

(2) (1) + (3 ) (0) + (2) (0) = 2 + 0 + 0 = 2

Мы продолжаем работу по этому шаблону и получаем продукт, точно такой же, как T , потому что умножение матрицы на I похоже на умножение числа на число 1.

Правило: Всякий раз, когда мы умножаем матрицу на единичную матрицу, ответ всегда такой же, как и на неединичную матрицу. Ага, мы вернули курсив для этого очень важного правила.

А нулевая матрица? Что ж, мы помним, что любое число, умноженное на ноль, равно нулю. Нулевая матрица работает и при умножении матриц точно так же. Это все нулевые матрицы:

Правило: Всякий раз, когда мы умножаем матрицу на нулевую матрицу, ответом всегда будет нулевая матрица, которая имеет такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая. матрица.

Пример задачи

Мы знаем, что их можно перемножить, потому что количество столбцов в первой матрице (3) совпадает с количеством строк во второй (также 3). Мы также знаем, что матрица продукта будет матрицей 3 × 3, потому что матрица продукта будет иметь такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая матрица.

Стрела:

Ага, это так просто. Все, умноженное на ноль, равно нулю, даже в Matrix Land.

Создание матрицы | Руководства по поддержке Erply

Создание измерения
Во-первых, вам нужно создать матричные измерения для создания матричных продуктов. Это нужно сделать только при первом использовании, все размеры матрицы будут сохранены для следующего продукта.
Шаг 1: Выберите размеры матрицы из модуля PIM .
Шаг 2: Выберите Новый , чтобы добавить новое измерение.
Шаг 3: Дайте вашему измерению имя и нажмите Сохранить .
Шаг 4: Определите варианты, сложив значения. Перед добавлением каждый вариант должен иметь новое значение и код .
Вы создали новое измерение и определили его варианты. Теперь вы готовы создать родительский продукт.
Создание родительского продукта
Примечание: Убедитесь, что группы продуктов для этого продукта построены наиболее оптимальным образом для вашего предприятия.Дополнительная информация о группах продуктов: Группы продуктов.
Шаг 1: Щелкните модуль PIM и выберите + рядом с Каталог продуктов , чтобы открыть новую карточку продукта.
Шаг 2: Заполните соответствующую информацию, такую как Название, Группа продуктов, Цена и т. Д. Не забудьте поместить продукт в соответствующую группу продуктов, которая была создана ранее.
Шаг 3: Измените Тип с _Product _ на Matrix Product
Шаг 4: Щелкните Сохранить .Вверху карточки продукта появится зеленое уведомление о необходимости создания вариантов матрицы
Производство детских товаров
Примечание: Если вы еще не создали размер (-а) матрицы и варианты, тогда: Создание размеров
Шаг 1: Перейдите на карточку продукта родительского продукта и нажмите кнопку MATRIX , которая теперь появилась на нижней черной полосе экрана. Если эта полоса не отображается, нажмите желтую кнопку в левом нижнем углу экрана, чтобы отобразить ее.
Совет: Матрицу можно выполнять по трем измерениям.
Шаг 2: Щелкните вкладку Создать
Шаг 3: Выберите каждое измерение, используемое для этого конкретного продукта в раскрывающемся меню, затем щелкните Создать варианты продукта внизу.
После завершения генерации вы увидите список всех вариантов.
Шаг 4: Отметьте варианты.Внизу вы также можете добавить разделитель. По завершении нажмите Создать внизу.
Шаг 5: Обзор и апрель. Чтобы не применять никаких вариантов, снимите флажок. Вы успешно создали Матрицу «детей» (размеры и цвета) этого «родительского» продукта.
После утверждения вы сможете просматривать каждый дочерний продукт на вкладке Варианты продукта . Вы можете щелкнуть код или имя, чтобы открыть карточку продукта дочерних продуктов.
Каждому дочернему продукту будет присвоен уникальный код. Этот код является родительским продуктом, за которым следует измерение. В первом примере это (123456794), за которым следует цвет (RD), а затем размер (L).
Обновить инвентарь
Шаг 1: Перейдите на карточку продукта родительского продукта и нажмите кнопку MATRIX на нижней черной полосе экрана. Если эта полоса не отображается, нажмите желтую кнопку в левом нижнем углу экрана, чтобы отобразить ее.
Шаг 2: Переключите вид с Варианты продукта с на Количественный просмотр .
Шаг 3: Выберите из раскрывающегося списка, что вы хотите отредактировать.
Примечание: Невозможно изменить уровни запасов с Сумма запасов . Чтобы изменить уровень запасов, необходимо выбрать конкретное Местоположение . Здесь вы можете изменить доступную сумму, выбрать точку пополнения и уровень пополнения.
Шаг 4: Чтобы добавить коды UPC, выбрав UPC CODE в раскрывающемся списке Quantity view Вы можете вручную ввести код UPC или отсканировать его.
Размеры матрицы теперь применены. Вы можете увидеть продукт со всеми вариациями матрицы, количествами на складе и кодами EAN в каждом магазине из инвентаря, выполнив поиск по родительскому продукту и щелкнув M + , чтобы развернуть его.
Все продукты теперь добавлены в систему и готовы к сканированию (если был добавлен код EAN) в представлении POS.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера на прием файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с вашим системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
No related posts.

Физический размер матрицы: Размер матрицы. Что это такое?

Типы и размеры матриц камер видеонаблюдения

Физический размер матрицы | panoramist.ru

Физический размер матрицы

Sony HDR-CX405B технические характеристики видеокамеры Sony HDR-CX405B

Матрица для лучшего видеорегистратора и скорость записи

2 часть

Качественная матрица в видеорегистраторе обеспечивает отличную первичную картинку

Скорость видеосъемки измеряется частотой кадров в секунду

Видеокамера Sony FDR-AX700 Black

Маркировка матрицы видеокамеры и значения её параметров

Физический размер матрицы

Чувствительность матрицы

Разрешение сенсора

Производитель матрицы видеокамеры

Размер матрицы — обзор

Матрицы и матричная алгебра — Статистика Как к

: Обозначение

Матричная алгебра: сложение и вычитание

Другой способ подумать…

Добавление матрицы для неравных размеров

Умножение матриц: две матрицы

1. Квадратная матрица

Необратимые матрицы

Определитель нуля

Матрица аддитивной идентичности

Проверка ответа

Пример собственного значения

Расчет

Написание системы уравнений

Определитель матрицы 2 × 2

Определитель матрицы 3 × 3

Определитель матрицы 4 × 4

Обозначение

Верхняя и нижняя треугольные матрицы

Прямоугольные диагональные матрицы

Символы для транспонированной матрицы

Свойства матриц транспонирования

Альтернативное определение

Максимальное количество номеров

Диагональные матрицы

Что такое асимметричная матрица?

Косоэрмитский

Создание матрицы дисперсии-ковариации

пикселей и таблицы цветов

http://en.wikibooks.org/wiki/Basic_Physics_of_Nuclear_Medicine/Computers_in_Nuclear_Medicine

http: // www.slideshare.net/brucelee55/processing-methods-of-nuclear-medicine-images

2/18

Basic Introduction to Matrix Product States — документация TensorNetwork

Введение в матричные состояния продукта

Извлечение компонентов MPS

Использование библиотеки TensorNetwork

Внутренний продукт MPS

Умножение матриц

Умножение матриц: дальше по кроличьей норе

Пример задачи

Пример задачи

Двоичное мышление

Пример задачи

Пример задачи

Создание матрицы | Руководства по поддержке Erply

Произошла ошибка при настройке пользовательского файла cookie

Настройка вашего браузера на прием файлов cookie

Почему этому сайту требуются файлы cookie?

Что сохраняется в файле cookie?

alexxlab

Простые раскраски для детей 2 лет: развиваем мелкую моторику и творческие способности

Почему грудничок психует во время кормления: причины и решения

Кишечная инфекция при беременности: причины, симптомы, лечение

Компот из чернослива для грудничка: польза, рецепты и советы по приготовлению

Двойня: особенности родов и выбор между естественными и кесаревым сечением

Физиологический насморк у грудничка: симптомы, причины и особенности

Добавить комментарий Отменить ответ