Фокальное расстояние: Фокальное расстояние гиперболы. Гипербола и ее каноническое уравнение
Фокальное расстояние гиперболы. Гипербола и ее каноническое уравнение
Определение 7.2. Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой .
Замечание 7.2. Говоря о разности расстояний, подразумевают, что из большего расстояния вычитается меньшее. Это значит, что на самом деле для гиперболы постоянным является модуль разности расстояний от любой ее точки до двух фиксированных точек. #
Определение гиперболы аналогично определению эллипса . Различие между ними лишь в том, что для гиперболы постоянна разность расстояний до фиксированных точек, а для эллипса — сумма тех же расстояний. Поэтому естественно, что у этих кривых много общего как в свойствах, так и в используемой терминологии.
Фиксированные точки в определении гиперболы (обозначим их F 1 и F 2) называют фокусами гиперболы . Расстояние между ними (обозначим его 2с) называют фокальным расстоянием , а отрезки F 1 M и F 2 M, соединяющие произвольную точку M на гиперболе с ее фокусами, —

Вид гиперболы полностью определяется фокальным расстоянием |F 1 F 2 | = 2с и значением постоянной величины 2а, равной разности фокальных радиусов, а ее положение на плоскости — положением фокусов F 1 и F 2 .
Из определения гиперболы следует, что она, как и эллипс, симметрична относительно прямой, проходящей через фокусы, а также относительно прямой, которая делит отрезок F 1 F 2 пополам и перпендикулярна ему (рис. 7.7). Первую из этих осей симметрии называют действительной осью гиперболы , а вторую — ее мнимой осью . Постоянную величину а, участвующую в определении гиперболы, называют действительной полуосью гиперболы .
Середина отрезка F 1 F 2 , соединяющего фокусы гиперболы, лежит на пересечении ее осей симметрии и поэтому является центром симметрии гиперболы, который называют просто центром гиперболы .
Для гиперболы действительная ось 2а должна быть не больше, чем фокальное расстояние 2с, так как для треугольника F 1 MF 2 (см. рис.
Уравнение гиперболы . Рассмотрим на плоскости некоторую гиперболу с фокусами в точках F 1 и F 2 и действительной осью 2а. Пусть 2с — фокальное расстояние, 2c = |F 1 F 2 | > 2а. Согласно замечанию 7.2, гипербола состоит из тех точек M(х; у), для которых | |F 1 M| — — |F 2 M| | = 2а. Выберем прямоугольную систему координат Oxy так, чтобы центр гиперболы находился в начале координат , а фокусы располагались на оси абсцисс (рис. 7.8). Такую систему координат для рассматриваемой гиперболы называют
В канонической системе координат фокусы гиперболы имеют координаты F 1 (c; 0) и F 2 (-с; 0). Используя формулу расстояния между двумя точками, запишем условие ||F 1 M| — |F 2 M|| = 2а в координатах |√((х — с) 2 + у 2) — √((х + с) 2 + у 2)| = 2а, где (x; у) — координаты точки M. Чтобы упростить это уравнение, избавимся от знака модуля: √((х — с) 2 + у 2) — √((х + с) 2 + у 2) = ±2а, перенесем второй радикал в правую часть и возведем в квадрат: (х — с) 2 + у 2 = (х + с) 2 + у 2 ± 4а √((х + с) 2 + у 2) + 4а 2 . После упрощения получим -εх — а = ±√((х + с) 2 + у 2), или
Чтобы упростить это уравнение, избавимся от знака модуля: √((х — с) 2 + у 2) — √((х + с) 2 + у 2) = ±2а, перенесем второй радикал в правую часть и возведем в квадрат: (х — с) 2 + у 2 = (х + с) 2 + у 2 ± 4а √((х + с) 2 + у 2) + 4а 2 . После упрощения получим -εх — а = ±√((х + с) 2 + у 2), или
√((х + с) 2 + у 2) = |εх + а| (7.7)
где ε = с/а. Возведем в квадрат вторично и снова приведем подобные члены: (ε 2 — 1)х 2 — у 2 = с 2 — а 2 , или, учитывая равенство ε = с/а и полагая b 2 = c 2 — a 2 ,
x 2 /a 2 — y 2 /b 2 = 1 (7.8)
Величину b > 0 называют мнимой полуосью гиперболы .
Итак, мы установили, что любая точка на гиперболе с фокусами F 1 (с;0) и F 2 (-с; 0) и действительной полуосью а удовлетворяет уравнению (7.8). Но надо также показать, что координаты точек вне гиперболы этому уравнению не удовлетворяют. Для этого мы рассмотрим семейство всех гипербол с данными фокусами F 1 и F 2 . У этого семейства гипербол оси симметрии являются общими. Из геометрических соображений ясно, что каждая точка плоскости (кроме точек, лежащих на действительной оси симметрии вне интервала F1F2, и точек, лежащих на мнимой оси симметрии) принадлежит некоторой гиперболе семейства, причем только одной, так как разность расстояний от точки до фокусов F 1 и F 2 меняется от гиперболы к гиперболе. Пусть координаты точки M(х; у) удовлетворяют уравнению (7.8), а сама точка принадлежит гиперболе семейства с некоторым значением ã действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению Следовательно, система
двух уравнений с двумя неизвестными
Пусть координаты точки M(х; у) удовлетворяют уравнению (7.8), а сама точка принадлежит гиперболе семейства с некоторым значением ã действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению Следовательно, система
двух уравнений с двумя неизвестными
имеет хотя бы одно решение. Непосредственной проверкой убеждаемся, что при ã ≠ а это невозможно. Действительно, исключив, например, x из первого уравнения:
после преобразований получаем уравнение
которое при ã ≠ а не имеет решений, так как . Итак, (7.8) есть уравнение гиперболы с действительной полуосью а > 0 и мнимой полуосью b = √(с 2 — а 2) > 0. Его называют каноническим уравнением гиперболы .
Вид гиперболы. По своему виду гипербола (7.8) заметно отличается от эллипса. Учитывая наличие двух осей симметрии у гиперболы, достаточно построить ту ее часть, которая находится в первой четверти канонической системы координат. В первой четверти, т.е. при x ≥ 0, у ≥ 0, каноническое уравнение гиперболы однозначно разрешается относительно у:
у = b/a √(x 2 — а 2). (7.9)
(7.9)
Исследование этой функции y(x) дает следующие результаты.
Область определения функции — {x: x ≥ а} ив этой области определения она непрерывна как сложная функция, причем в точке x = а она непрерывна справа. Единственным нулем функции является точка x = а.
Найдем производную функции y(x): y»(x) = bx/a√(x 2 — а 2). Отсюда заключаем, что при x > а функция монотонно возрастает. Кроме того, , а это означает, что в точке x = a пересечения графика функции с осью абсцисс существует вертикальная касательная. Функция y(x) имеет вторую производную y» = -ab(x 2 — а 2) -3/2 при x > а, и эта производная отрицательна. Поэтому график функции является выпуклым вверх, а точек перегиба нет.
Указанная функция имеет наклонную асимптоту, это вытекает из существования двух пределов:
Наклонная асимптота описывается уравнением y = (b/a)x.
Проведенное исследование функции (7.9) позволяет построить ее график (рис. 7.9), который совпадает с частью гиперболы (7. 8), содержащейся в первой четверти.
8), содержащейся в первой четверти.
Так как гипербола симметрична относительно своих осей, вся кривая имеет вид, изображенный на рис. 7.10. Гипербола состоит из двух симметричных ветвей, расположенных по разные
стороны от ее мнимой оси симметрии. Эти ветви не ограничены с обеих сторон, причем прямые у = ±(b/a)x являются одновременно асимптотами и правой и левой ветвей гиперболы.
Оси симметрии гиперболы различаются тем, что действительная пересекает гиперболу, а мнимая, будучи геометрическим местом точек, равноудаленных от фокусов, — не пересекает (поэтому ее и называют мнимой). Две точки пересечения действительной оси симметрии с гиперболой называют вершинами гиперболы (точки A(a; 0) и B(-a; 0) на рис. 7.10).
Построение гиперболы по ее действительной (2a) и мнимой (2b) осям следует начинать с прямоугольника с центром в начале координат и сторонами 2a и 2b, параллельными, соответ-ственно, действительной и мнимой осям симметрии гиперболы (рис. 7.11). Асимптоты гиперболы являются продолжениями диагоналей этого прямоугольника, а вершины гиперболы — точками пересечения сторон прямоугольника с действительной осью симметрии.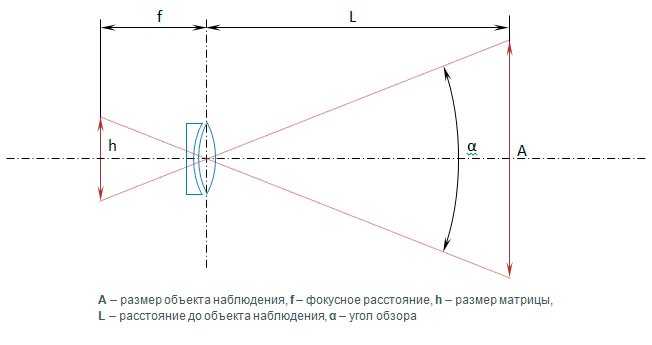 Отметим, что прямоугольник и его положение на плоскости однозначно определяют форму и положение гиперболы. Отношение b/a сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε. Для гиперболы, описываемой уравнением (7.8), ε = c/a. Отметим, что если
Отметим, что прямоугольник и его положение на плоскости однозначно определяют форму и положение гиперболы. Отношение b/a сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε. Для гиперболы, описываемой уравнением (7.8), ε = c/a. Отметим, что если
фокусное расстояние, уравнение, свойства и эксцентриситет фигуры
О чем статья
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и . Допустим, что расстояние = – фокусное расстояние.
Рис. 1
– фокусы .
; ,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, . Так как по определению сумма – постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим и на оси симметричной к началу координат. Тогда у фокусов будут такие координаты и (см. рис. 2).
Тогда у фокусов будут такие координаты и (см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через и – расстояние от точки к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) , и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается . Так как , тогда , и поэтому .
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.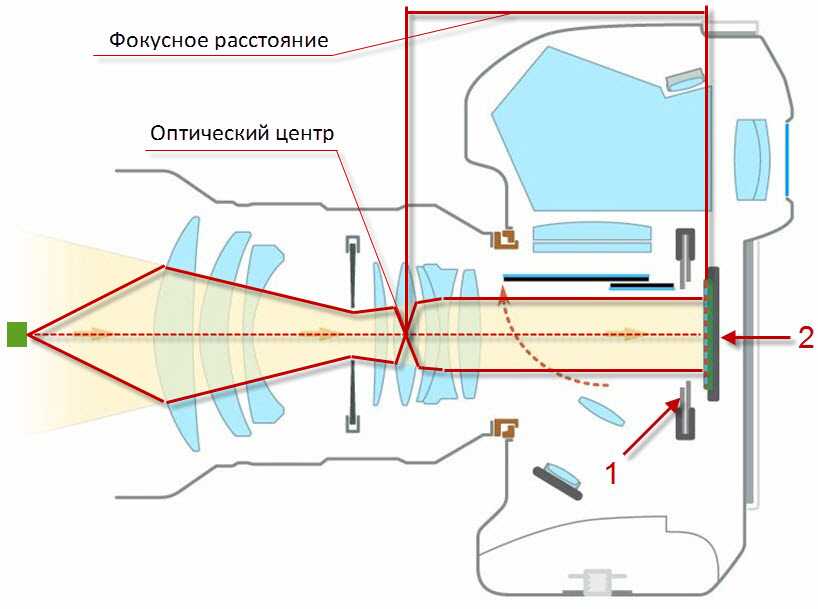
Из уравнения (2) находим , для первой четверти .
Если , тогда . Если же , тогда . Точки и , а также симметричные с ними , – вершины эллипса, точка – центр эллипса, = большая ось, – малая ось эллипса.
Если первой четверти, тогда из получается, что при возрастании от к значение падает от к . (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом .
2. Уравнение касательной к эллипсу в точке с координатами :
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и у треугольника , тогда выполняется соотношение:
=
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим – полуфокусное расстояние.
Строим фокусы и на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках и . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию.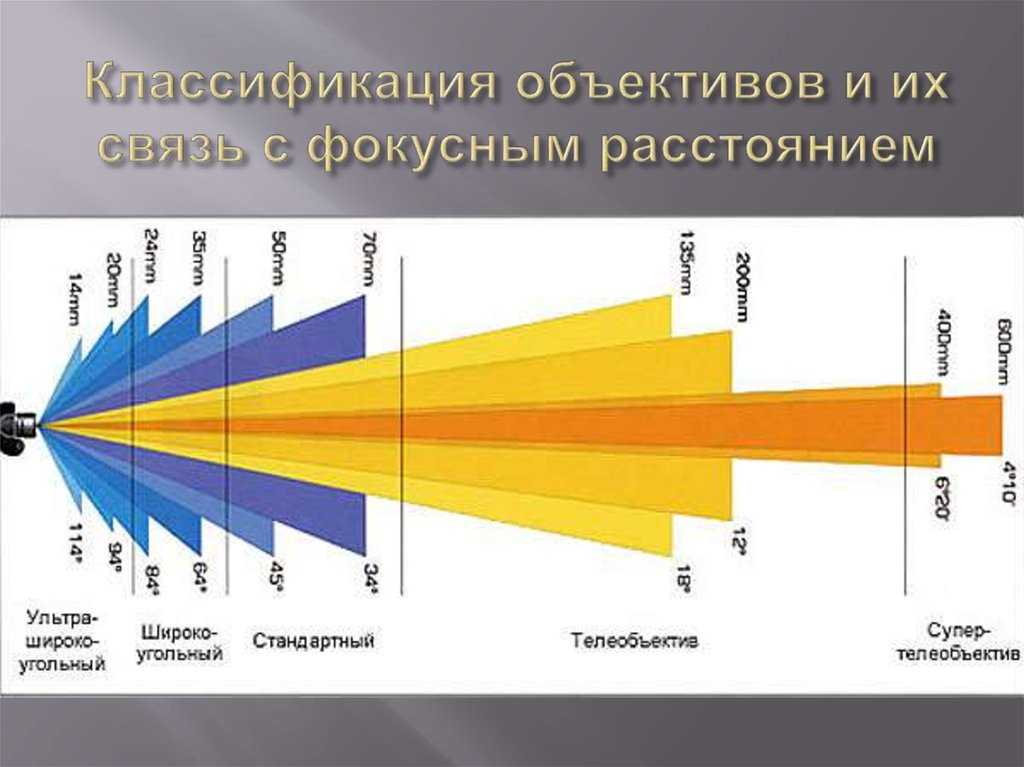 Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Пример 1
Задача
Задан эллипс уравнением и точки . Необходимо:
- убедиться, что точки и лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты точки в левую часть уравнения эллипса:
– точка лежит на эллипсе. Аналогично для :
точка лежит на эллипсе.
2. С канонического и данного уравнения эллипса выходит: Из равенства получается:
– полуфокусное расстояние. Координаты фокусов и .
3. Найдём фокальные радиусы точки :
4. Найдём сумму , что отвечает определению эллипса.
5. Эксцентриситет находится по формуле .
Эксцентриситет находится по формуле .
Пример 2
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
, . Вершины эллипса в точках , , , . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние .
Фокусы в точках и . (см. рис. 3)
Рис. 4
Пример 3
Найти оси, вершины и фокусы эллипса или . Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
, . Откуда находим оси эллипса: , и координаты вершин: , , , . Дальше из формулы:
. Значит, фокусами эллипса есть точки: и . Для построения эллипса отложим на осях и вершины соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда .
Фокусное расстояние глаза. Какое же оно? / Хабр
Перед началом статьи обращаюсь к маленьким фотографам — запасайтесь огнетушителями.
Поехали!
В этой статье я постараюсь обойтись без аналогий глаза с фотоаппаратом и мозга с компьютером. Почему?
С самых первых попыток изучения мозга человеком люди искали аналогии для облегчения понимания/объяснения его работы. Для каждой эпохи были свои примеры — человек сравнивал мозг с самым сложным устройством своего времени:
— паровые машины,
— ламповая техника,
— сегодня это компьютеры,
— в будущем…
Обратимся за материалом к учебникам по физиологии, дабы избежать ненужных заблуждений.
Глаз как оптическая система
На этом рисунке добавил пояснения для удобства.
Начнём с руководства по офтальмологии.
Суммарная преломляющая сила всей оптической проводящей системы глаза называется физической рефракцией.
Диоптрии всех оптических сред глазного яблока:
— роговица ~ 43 дптр,
— передняя камера ~ 3 дптр,
— хрусталик ~ 19-33 дптр,
— стекловидное тело ~ 6 дптр.
Передняя камера заполнена водянистой влагой — жидкостью по оптическим свойствам близкой к воде. (Ремизов А.Н. «Медицинская и биологическая физика» с.384)
Необходимо понимать, что первые три среды являются собирающими свет, а стекловидное тело рассеивает его, поэтому при расчёте мы отнимаем это значение.
Сила преломления рассчитывается в диоптриях по простой формуле из геометрической оптики:
Д=Др+Дп.к+Дхр-Дст.т.= 43+3+19-6=59 дптр
Значение хрусталика в этом расчёте принято 19 дптр, так как оно соответствует его рефракции в расслабленном состоянии, когда мы смотрим в даль.
Дальше переводим диоптрии в миллиметры:
F=1/Д=1/59=0,0169 м=17 мм.
Вывод: фокусное расстояние глаза человека ~17 мм.
На этапе изучения оптических свойств глаза мы имеем значение ~17 мм.
Цитата — «Возьмем случай, где средняя физическая рефракция (60,0D) в глазном яблоке с передне-задним размером средней величины (23 мм). Нетрудно подсчитать, что при толщине роговицы около 1 мм, глубине передней камеры около 3 мм и отрезке от переднего полюса хрусталика до узловой точки 2 мм, от последней до сетчатки остается как раз 17 мм, что и обеспечит фокусировку параллельных лучей в центральной ямке желтого пятна, так как совпадает с главным фокусным расстоянием.»
С.А.Рухлова «Основы офтальмологии» 2006 г.
Но, думаю, кто-то возразит — фокусное расстояние должно быть около 50мм!
Почему должно и почему некоторым так кажется? Для ответа на этот вопрос мы двинемся дальше — в зрительную кору.
Зрительная кора
Дэвид Хьюбел и Торстен Визель в своих знаменитых работах по физиологии зрения установили, что путь сетчатка->ЛКТ->первичная зрительная кора имеет топографическую организацию.
Это говорит нам о том, что порядок, в котором волокна зрительного нерва выходят из сетчатки сохраняется и в коре V1.
А визуализировать это утверждение смог Р. Тутелл. Для этого он взял макака, нашпиговал его транквилизаторами и в течение 45 минут показывал мишень с тремя радиальными кружками. Обезьян смотрел на рисунок только одним глазом. Перед всей этой затеей животному сделали инъекцию радиоактивной 2-дезоксиглюкозы.
Так как нейроны питаются исключительно глюкозой, то можно легко отследить самые активные клетки — они потребляют больше всего сахара.
После этого первичную зрительную кору макаки растянули, заморозили и проявили радиоактивные метки.
Результат на рисунке ниже.
Самый маленький кружок в центре мишени на топографической проекции в коре занимает площадь совсем немного меньше, чем площадь внешнего круга. У человека этот эффект ещё более выражен — центральная часть поля зрения проецируется на бОльшие площади в коре.
Для облегчения понимания был создан такой рисунок:
Здесь прекрасно видно, как увеличивается изображение с центра сетчатки.
Сделаю ударение на том, что это не оптическое, а кортикальное увеличение.
Подведём итог:
— фокусное расстояние ~17 мм,
— охват поля зрения одного глаза по горизонтали 140 – 160˚,
— изображение с центральной части сетчатки создаёт в коре ощущение(феномен) увеличенной картинки, хотя оптически проекция равномерная.
UPD:
И всё же, для успокоения тех, у кого подгорает от 17 мм — выше была дана цифра фокусного расстояния для ВСЕГО глаза и для ВСЕГО поля зрения.
Чёткое зрение у нас только в центральной части сетчатки, которая называется Fovea. Угловое разрешение этой части сетчатки 1˚40′. Когда мы смотрим на мир вокруг(читаем текст, разглядываем пейзаж), то практически всегда наше внимание находится в этой маленькой точке с угловым разрешением около 1 градуса. Да, сознательно мы можем сместить внимание хоть на край сетчатки — там, где картинка совсем нечёткая. Но расширить зону внимания невозможно — такова физиология зрительной коры и феноменология построения той картинки, которую мы видим в итоге. И исходя из этого зрительного опыта создаётся впечатление о более узком поле зрения(длинном фокусном расстоянии), чем есть на самом деле.
Но расширить зону внимания невозможно — такова физиология зрительной коры и феноменология построения той картинки, которую мы видим в итоге. И исходя из этого зрительного опыта создаётся впечатление о более узком поле зрения(длинном фокусном расстоянии), чем есть на самом деле.
Литература:
В.В.Вит «Строение зрительной системы человека» 2003 г.
Е.А.Егоров «Офтальмология» 2010 г.
С.А.Рухлова «Основы офтальмологии» 2006 г.
Новохатский А.Г. «Клиническая периметрия», 1973 г.
Дэвид Хьюбел — «Глаз, мозг, зрение»
Стивен Палмер — «От фотонов к феноменологии»
Баарс Б., Гейдж Н. — «Мозг, познание, разум»
Джон Николлс, А. Мартин, Б. Валлас, П. Фукс — «От нейрона к мозгу»
Майкл Газзанига — «Кто за главного?»
Ссылки:
https://www.sciencedirect.com/science/article/pii/S089662730700774X
https://www.ncbi.nlm.nih.gov/books/NBK10944/
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5446894/
https://books. google.com/books?id=_yYrIBT42BkC&pg=PA414
google.com/books?id=_yYrIBT42BkC&pg=PA414
: почему это важно?
Последнее обновление: 11 июня 2020 г.
Фокусное расстояние — это один из немногих важных параметров телескопа, который может сильно повлиять на ваши визуальные впечатления и качество изображения, которое вы увидите через окуляр. Технические термины могут поначалу пугать любого, кто плохо знаком с наблюдением за звездами, но важно понимать влияние фокусного расстояния на характеристики телескопа. Это позволит вам сделать более осознанный выбор при покупке или обновлении телескопа.
Что означает фокусное расстояние?
Телескоп работает следующим образом: свет собирается через апертуру телескопа и затем передается к фокальной точке (фокусировщику), где он фокусируется, чтобы вы могли видеть через окуляр.
Фокусное расстояние — это, по существу, расстояние (в миллиметрах), которое свет проходит внутри телескопа от его точки входа (апертуры) до точки выхода (фокусера, куда вы помещаете окуляр или цифровую зеркальную камеру, также называемого изображением с основным фокусом) .
В рефракторе или телескопе-рефлекторе фокусное расстояние начинается от апертуры (главного зеркала или объектива) и заканчивается в фокусере, где собираются световые лучи. Как правило, глядя на телескоп, можно с уверенностью предположить, что длинная трубка означает большое фокусное расстояние, а короткая труба означает более короткое фокусное расстояние.
Однако телескопы некоторых типов, такие как телескоп Шмидта-Кассегрена, имеют совершенно другую настройку оптики и оснащены вторичными зеркалами, от которых отражается свет, прежде чем попасть в фокусер. Это означает, что у них гораздо большее фокусное расстояние, даже несмотря на то, что их труба выглядит намного меньше, чем у ньютоновского телескопа.
Воспроизвести видео
Телескопы с коротким фокусным расстоянием пользуются большой популярностью у астрофотографов.
Можете ли вы рассчитать фокусное расстояние вашего телескопа?
Не существует формулы для расчета фокусного расстояния вашего телескопа. Это фиксированная мера, которая уникальна для вашего телескопа и указана на этикетке, обычно размещаемой на трубе. Однако его можно уменьшить, добавив редуктор фокусного расстояния , полезный для астрофотографии, или даже увеличить его, поместив в фокусер линзу Барлоу, но это тема для другой статьи.
Это фиксированная мера, которая уникальна для вашего телескопа и указана на этикетке, обычно размещаемой на трубе. Однако его можно уменьшить, добавив редуктор фокусного расстояния , полезный для астрофотографии, или даже увеличить его, поместив в фокусер линзу Барлоу, но это тема для другой статьи.
Фокусное расстояние, однако, является важным элементом для двух основных формул телескопа . Первое, что вы можете рассчитать, это увеличение (или мощность) вашего телескопа. Второе, что вы можете рассчитать, это фокусное отношение (яркость и поле зрения).
Фокусное расстояние и увеличение
Чтобы рассчитать увеличение телескопа , вам просто нужно разделить фокусное расстояние телескопа на фокусное расстояние установленного на нем окуляра.
Помните, это все в миллиметрах. Итак, если у вас есть телескоп с фокусным расстоянием 2000 мм и окуляром 20 мм, то ваше увеличение будет 2000/20=100!
Фокусное расстояние и апертура
Фокусное расстояние является частью другой формулы, которая позволяет рассчитать фокусное расстояние телескопа. На этот раз вам нужно будет разделить фокусное расстояние на апертуру телескопа.
На этот раз вам нужно будет разделить фокусное расстояние на апертуру телескопа.
Допустим, у вас есть телескоп-рефлектор с апертурой 6 дюймов (152,4 мм) и фокусным расстоянием 1000 мм, ваше фокусное отношение 1000/152,4 = 6,56! На астрономическом жаргоне это будет называться f/6.5.
Влияет ли это на поле зрения?
Да, это так! Более длинное фокусное расстояние сократит поле зрения, но увеличит увеличение, что идеально подходит для наблюдения за планетами и луной. Более короткое фокусное расстояние обеспечивает большее поле зрения, что лучше для астрофотографии и наблюдения за галактиками, туманностями и другими объектами глубокого космоса, поскольку они являются более крупными, но более тусклыми целями.
В астрономическом сообществе ведутся вечные споры «короткое или длинное фокусное расстояние», но, в конце концов, все зависит от личных предпочтений и того, что подходит именно вам. Перфекционист захочет идеально настроить все параметры телескопа, в то время как астроном-любитель будет совершенно счастлив увидеть галактики с «неоптимизированным» фокусным расстоянием. Вам нравится астрономия как личное и случайное хобби или вы планируете публиковать свои работы по астрофотографии в книгах, журналах и онлайн-изданиях?
Вам нравится астрономия как личное и случайное хобби или вы планируете публиковать свои работы по астрофотографии в книгах, журналах и онлайн-изданиях?
Фокусное расстояние на самых мощных телескопах
Несмотря на то, что размер космического телескопа Хаббл составляет 13,3 метра, его фокусное расстояние составляет 57,3 метра, потому что это телескоп-рефлектор Кассегрена. Вторичное зеркало эффективно увеличивает фокусное расстояние и обеспечивает большее увеличение.
Космический телескоп Джеймса Уэбба имеет впечатляющее фокусное расстояние 131,4 метра, что более чем в два раза больше, чем у Хаббла!
Самый большой телескоп на Земле, Gran Telescopio Canaria в Испании, имеет рекордное фокусное расстояние 1690,9 метра (почти такой же высоты, как монумент Вашингтона)! Обратите внимание, что это не размер телескопа… Свет эффективно отражается от нескольких зеркал, так что путь, по которому проходит свет, увеличивается внутри телескопа.
Часто задаваемые вопросы
Какое хорошее фокусное расстояние для телескопа?
Все зависит от того, что вы хотите видеть в ночном небе, для планет и луны полезно большее фокусное расстояние, потому что оно увеличивает силу увеличения телескопа. Для объектов глубокого космоса, таких как галактики, лучше использовать более короткое фокусное расстояние, так как поле зрения будет шире.
Как фокусное расстояние влияет на телескопы?
Фокусное расстояние напрямую влияет на силу увеличения вашего телескопа, а также на поле зрения: два очень важных фактора для наблюдения за звездами и астрофотографии.
Как узнать фокусное расстояние моего телескопа?
Обычно фокусное расстояние указано на этикетке на трубе телескопа или внутри инструкции по эксплуатации.
Телескопы представляют собой сложные оптические системы, и может потребоваться некоторое время, чтобы научиться их оптимально использовать. Я надеюсь немного облегчить этот процесс обучения, предоставив некоторые из моих советов и мой опыт о том, как получить максимальную отдачу от вашего телескопа.
Я надеюсь немного облегчить этот процесс обучения, предоставив некоторые из моих советов и мой опыт о том, как получить максимальную отдачу от вашего телескопа.
Рекомендуемая литература
Если вы не знаете, с чего начать, вот самые важные вещи, которые нужно знать и сделать перед покупкой своего первого телескопа.
Объективы камеры и фокусное расстояние. Какие цифры на объективе?
Объективы играют важную роль в фотографии — некоторые могут даже утверждать, что они не менее, если не более важны, чем выбор камеры.
Как мы уже говорили в первой главе этого курса, разные объективы дают разные результаты в зависимости от конфигурации корпуса объектива. Эти конфигурации определяют увеличение и угол обзора и позволяют создавать различные эффекты в зависимости от объектива.
Как работают объективы фотоаппаратов
Линзы фокусируют свет на носитель записи, что позволяет записывать изображение. Как видно из иллюстрации цифровой зеркальной камеры ниже, свет попадает в объектив и проходит через передний элемент (2), прежде чем достичь нескольких элементов объектива (3, 5 и 6). Эти элементы служат для направления света в одну фокусную точку, чтобы он мог точно регистрироваться датчиком (9) после того, как зеркало (7) поднимется (что срабатывает при нажатии кнопки спуска затвора). Беззеркальные камеры работают так же, но без зеркала или призмы.
Эти элементы служат для направления света в одну фокусную точку, чтобы он мог точно регистрироваться датчиком (9) после того, как зеркало (7) поднимется (что срабатывает при нажатии кнопки спуска затвора). Беззеркальные камеры работают так же, но без зеркала или призмы.
Качество объектива определяется такими факторами, как его максимальная светосила (число диафрагмы, указанное на объективе), его разрешающая способность (насколько резкие получаемые изображения), цвета, которые он может сфокусировать (качество стекла), достигаемый контраст (а также качество стекла) и тип материала, из которого изготовлен объектив, — все это часть конструкции объектива.
Что означают цифры на объективе
Теперь, когда вы понимаете основы работы объектива, вам может быть интересно, что означают все цифры (и буквы) на объективе. Обычно объективы пишут в таком формате: Canon EF 24-70mm f/2.8L II USM Lens или Nikon AF-S 50mm f/1.8G. Каждая из этих цифр и букв сообщает вам важную информацию, такую как фокусное расстояние, максимальная диафрагма, версия объектива и мотор фокусировки. Другие указанные характеристики могут включать стабилизацию, диаметр фильтра и расстояние фокусировки.
Другие указанные характеристики могут включать стабилизацию, диаметр фильтра и расстояние фокусировки.
При покупке объектива важно учитывать каждый из этих пунктов, поскольку они частично расскажут вам о характеристиках и возможностях объектива.
Типы объективов для фотоаппаратов
Что касается объективов, то недостатка в них нет. Проще говоря, объективы можно разделить на две основные группы — объективы с фиксированным фокусным расстоянием и объективы с переменным фокусным расстоянием, оба из которых имеют разное фокусное расстояние.
Фикс-объективы и зум-объективы
Фикс-объективы (или фиксированные) имеют фиксированное фокусное расстояние. Доступные в различных фокусных расстояниях, объективы с фиксированным фокусным расстоянием известны тем, что обеспечивают высокое качество изображения. Они также обычно предлагают гораздо более широкую апертуру по сравнению с зум-объективами.
Зум-объективы, с другой стороны, обеспечивают различные фокусные расстояния в одном объективе. Это делает их очень универсальными, а также снижает потребность в нескольких объективах.
Это делает их очень универсальными, а также снижает потребность в нескольких объективах.
Фокусное расстояние
Фокусное расстояние является одной из определяющих характеристик объектива, поскольку оно определяет угол обзора, а также увеличение. То, как определяется фокусное расстояние, требует понимания физики света и вогнутых или выпуклых линз, но очень просто, когда свет попадает в линзу, стеклянные элементы внутри линзы служат для сведения света в одну точку, известную как «фокус». Расстояние между этой точкой и центром линзы и есть фокусное расстояние.
Фокусное расстояние обычно указывается сбоку на оправе объектива, а иногда и на передней части объектива вместе с диаметром объектива. В диапазоне от 8 мм до 2000 мм фотографы могут выбирать из множества фокусных расстояний, каждое из которых лучше подходит для разных жанров фотографии. Объективы с более коротким фокусным расстоянием обеспечивают гораздо более широкий угол обзора и поэтому лучше подходят для съемки пейзажей, чем для предметной фотографии, а также имеют меньшее увеличение. Противоположное также верно для более длинных фокусных расстояний, которые могут лучше подходить для съемки спорта или дикой природы, чем для архитектурной фотографии. Объективы с меньшим фокусным расстоянием также обеспечивают меньшее увеличение, чем объективы с большим фокусным расстоянием.
Противоположное также верно для более длинных фокусных расстояний, которые могут лучше подходить для съемки спорта или дикой природы, чем для архитектурной фотографии. Объективы с меньшим фокусным расстоянием также обеспечивают меньшее увеличение, чем объективы с большим фокусным расстоянием.
Фокусное расстояние влияет не только на угол обзора и увеличение, но и на дрожание камеры. Объективы с большим фокусным расстоянием более подвержены дрожанию камеры из-за большего увеличения — малейшие движения увеличиваются, что может привести к размытым фотографиям. Как правило, я рекомендую снимать с выдержкой, равной фокусному расстоянию или превышающей ее, так как это может помочь предотвратить это.
Диафрагма
Хотя это и не тип объектива, апертура является еще одной важной характеристикой объектива.
Как вы уже знаете из предыдущих глав, диафрагма — это отверстие в линзе, которое определяет количество света, попадающего на матрицу. Это указывается в формате 1:2,8, например, второй набор цифр указывает на максимальную апертуру. Некоторые объективы будут иметь две максимальные диафрагмы (показаны как 1:4-5,6). Это означает, что при увеличении диафрагма изменяется. Таким образом, при самом коротком фокусном расстоянии вы сможете снимать на f4, но как только вы увеличите фокусное расстояние до самого длинного, самая широкая диафрагма, с которой вы сможете снимать, будет f5,6. Как правило, объективы с более широкой апертурой предпочтительнее из-за их повышенных возможностей улавливания света.
Некоторые объективы будут иметь две максимальные диафрагмы (показаны как 1:4-5,6). Это означает, что при увеличении диафрагма изменяется. Таким образом, при самом коротком фокусном расстоянии вы сможете снимать на f4, но как только вы увеличите фокусное расстояние до самого длинного, самая широкая диафрагма, с которой вы сможете снимать, будет f5,6. Как правило, объективы с более широкой апертурой предпочтительнее из-за их повышенных возможностей улавливания света.
Существует также категория объективов с фиксированной диафрагмой. Катадиоптрические или зеркальные линзы, которые раньше были довольно распространены, обычно имеют большее фокусное расстояние, например 500 мм при фиксированной диафрагме f6,3. Большинство телескопов являются катадиоптрическими.
Пример лепестков диафрагмы, частично закрытых примерно до f8. © Karl Taylor. Однако на данный момент важно отметить, что на самом деле их может быть пять. Это связано с тем, что изображения можно записывать без объектива. Эти камеры известны как камеры-обскуры (или камеры-обскуры). Однако запись изображения без объектива гораздо сложнее и не дает фотографу такой же творческой свободы, как при использовании объективов. По сути, без объектива вы снимаете с очень маленькой фиксированной диафрагмой. Объективы из-за различий в увеличении позволяют нам снимать много разных объектов, что просто невозможно с камерой-обскурой. Дополнительные сведения об этом см. в руководстве в формате PDF.
Эти камеры известны как камеры-обскуры (или камеры-обскуры). Однако запись изображения без объектива гораздо сложнее и не дает фотографу такой же творческой свободы, как при использовании объективов. По сути, без объектива вы снимаете с очень маленькой фиксированной диафрагмой. Объективы из-за различий в увеличении позволяют нам снимать много разных объектов, что просто невозможно с камерой-обскурой. Дополнительные сведения об этом см. в руководстве в формате PDF.
Все содержимое © Copyright Karl Taylor Education.
Как фокусное расстояние влияет на психологическое воздействие ваших изображений
Различные фокусные расстояния могут полностью изменить ваши изображения и дать им новую интерпретацию. Давайте изучим основы концепции.
Если вы не слишком хорошо знакомы с фокусным расстоянием, у нас есть для вас информация. Вкратце: короткое фокусное расстояние будет иметь широкое поле зрения, а длинное фокусное расстояние будет иметь узкое поле зрения.
Объективы
Обычно группы объективов делятся на следующие группы:
- Чрезвычайно широкоугольный : Менее 21 мм (короткое фокусное расстояние)
- Широкоугольный : 21 мм – 7010 мм 9018ard : 35–70 мм
- Короткий/средний телефото : 70–135 мм
- Телефото : 135–500 мм+ (длинное фокусное расстояние)
Так как разные камеры имеют разные размеры сенсора, соответственно. Этот удобный калькулятор сообщит вам, какое поле зрения у вас есть на большинстве потребительских и профессиональных камер.
Этот удобный калькулятор сообщит вам, какое поле зрения у вас есть на большинстве потребительских и профессиональных камер.
Эффекты
Вот три снимка с одним и тем же относительным кадрированием и предметом: Женщина, сидящая в кресле, занимает почти две трети композиции.
Широкоугольный: 24 мм
Стандартный: 50 мм
Телефото: 180 мм
Каждый объектив изменил динамику композиции и, самое главное, изменил психологическую ценность изображения. Чтобы понять, как использовать это в своих интересах, давайте сначала посмотрим на то, что произошло.
Каждая линза имеет уникальный голос и меняет то, как зрители воспринимают изображение, которое они видят.
В широкоугольном объективе объекты кажутся более удаленными друг от друга, восприятие глубины сильно преувеличено, а движение по оси Z усилено. Чем короче фокусное расстояние, тем больше искажение восприятия объектов, особенно объектов, которые кажутся ближайшими к объективу.
Фовеальное зрение человека (это угол зрения, при котором мы можем четко видеть детали) простирается примерно до 40°. Стандартная линза (обычно 50 мм) — это линза, которая дает наиболее близкое представление к нашему полю зрения. Объектив 50 мм имеет около 39Поле зрения 0,6° при использовании с 35-мм сенсором, отсюда и термин стандартный объектив .
Телеобъективы, что неудивительно, имеют эффект, противоположный широкоугольным объективам. Вся композиция сжимается, объекты переднего плана расплываются, а удаленные объекты кажутся ближе. Меньше внимания уделяется движению объектов, движущихся к камере или от нее.
Телеобъективы Изображение через B&H.
Сжатие пространства за счет использования телеобъектива может быть применено для вдохновляющих случаев. Телеобъектив усилит интенсивность действия и движения в лоб. Он сжимает пространство по оси Z и заставляет объекты на переднем, среднем и заднем плане казаться ближе друг к другу.
Например, при правильном расположении камеры автомобиль, сворачивающий, чтобы не попасть в человека, стоящего посреди дороги, может выглядеть так, будто он промахнулся всего в нескольких дюймах, хотя на самом деле он промахнулся на безопасном расстоянии. Взгляните на следующий снимок из Tinker Tailor Soldier Spy (показан в этом клипе от Васи Недоманского):
Этот снимок был сделан благодаря использованию DP Hoyte Van Hoytema телеобъектива 2000 мм. Сжатие всей композиции сохраняет относительный размер актеров и самолета и уменьшает пространство между актерами и самолетом, создавая ощущение напряжения и страха. Похоже, что самолет вот-вот столкнется с двумя персонажами. Мужчина слева также разделяет эту озабоченность нервным языком тела. На самом деле самолет находился на безопасном расстоянии.
Как было сказано ранее, сжатие по оси Z замедляет все, что движется к камере или от нее.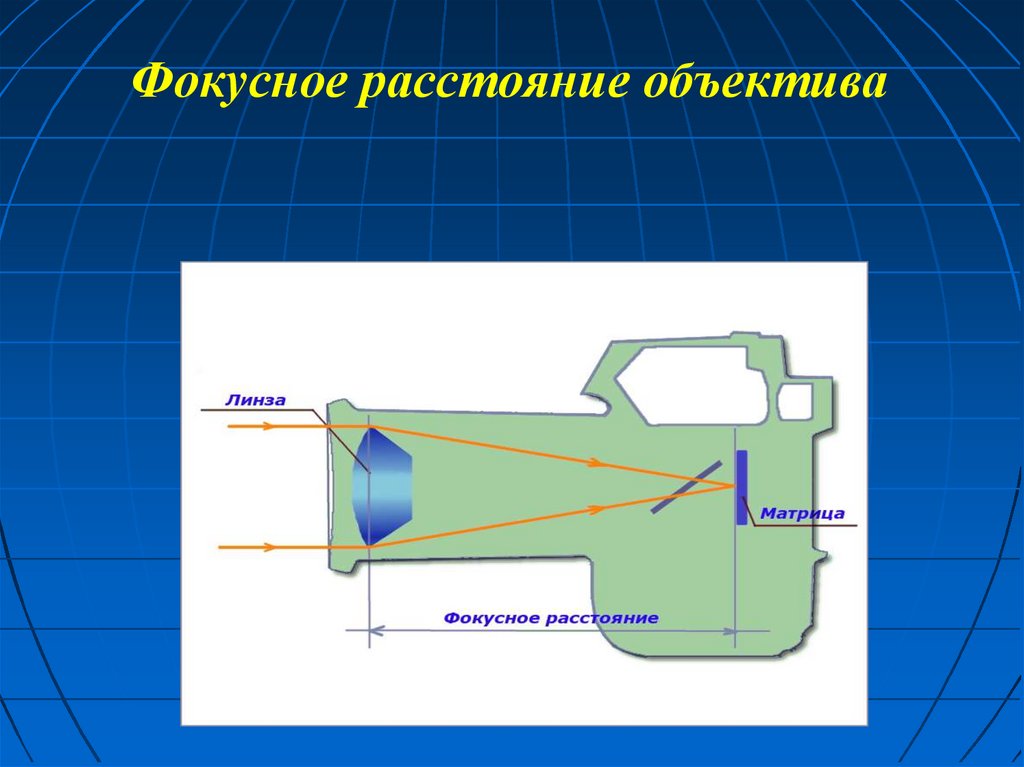 Это идеально подходит для выделения персонажа, который движется к камере.
Это идеально подходит для выделения персонажа, который движется к камере.
Возьмите сцену ниже из Выпускник . Бенджамин Брэддок бежит в церковь, чтобы остановить свадьбу. У него мало времени, и ему нужно поторопиться.
Использование телеобъектива визуально увеличивает расстояние, которое должен преодолеть Брэддок, и вызывает психологическое напряжение у зрителей. 902:30 Успеет ли он туда вовремя или потерпит неудачу? Если вы просто сосредоточитесь на голове Бенджамина в течение первых нескольких секунд, то создастся впечатление, что он вообще ничего не покрывает.
Телеобъектив идеально подходит для выделения и остановки объектов. Давайте использовать примеры изображений. Изображение, снятое на 24-миллиметровую камеру, намного более личное и привлекательное. Хотя изображение, снятое на 180 мм, имеет такое же обрамление, оно изолирует героиню и отдаляет ее от зрителей.
Хотя изображение, снятое на 180 мм, имеет такое же обрамление, оно изолирует героиню и отдаляет ее от зрителей.
С широким углом мы как будто участвуем в разговоре с персонажем; мы в ее ближайшем окружении. Изображение, снятое на телеобъектив, полностью отсекает нас как зрителей. Мы больше не являемся частью внутреннего круга этого персонажа. Мы почти вторгаемся в ее пространство, и 902:30 нас там быть не должно .
Пространство вокруг нее тоже стало клаустрофобным; мы больше не можем видеть окрестности или местоположение. Изменение поля зрения внезапно сделало этого персонажа очень одиноким, несмотря на то, что ее размер и расположение оставались неизменными на каждом изображении.
Широкоугольные объективы Изображение через B&H.
Широкоугольный объектив имеет более широкое поле зрения, что преувеличивает размер и расстояние объектов вблизи и вдали. Увеличение объектов, расположенных ближе к объективу, может добавить значимости объектам на переднем плане. В то же время из-за искажения перспективы это может быть отличным инструментом для добавления сюрреалистических характеристик лицу актера, когда камера находится очень близко. (См. ниже: Город потерянных детей ).
В то же время из-за искажения перспективы это может быть отличным инструментом для добавления сюрреалистических характеристик лицу актера, когда камера находится очень близко. (См. ниже: Город потерянных детей ).
Многое из того, что мы обсудили с широкими углами, приходится на использование психологических методов воздействия на аудиторию. Как насчет практических приложений на съемочной площадке?
Использование 11 мм вместо 50 мм может сильно помочь вам с движением камеры. Возможно, вы не всегда сможете использовать гусеницу и тележку; возможно, локация маловата или вы физически не можете ее привезти, но метровый слайдер не помешает.
Поскольку широкоугольный объектив искажает расстояние до объектов вблизи и вдали, он также увеличивает количество движений с помощью ползунка. Внезапно метровый ползунок становится хорошим отслеживанием на несколько секунд. Стандартный объектив покажет небольшое движение, но широкоугольный объектив (чем шире, тем лучше) покажет заметное движение с помощью ползунка на один метр. Телеобъектив практически не покажет движения.
Телеобъектив практически не покажет движения.
Важно помнить, что если вы будете двигаться по направлению к объекту или персонажу, есть шанс, что вы увидите ползунок в кадре. Поэтому лучше всего работает, когда вы отслеживаете слева направо или справа налево.
Объективы — это больше, чем просто инструменты, помогающие приблизиться к объекту или уместить больше пейзажа в кадре. Другой объектив может придать вашему изображению совершенно новый смысл при правильном применении.
Если у вас есть три минуты свободного времени, я настоятельно рекомендую просмотреть фрагменты во встроенном видео ниже. Это из документального фильма Cinematographer Style (2006), а в разделе ниже есть отрывок из работы маэстро кинематографии Роджера Дикинса.
У меня очень сильное предчувствие по поводу линз.