Геометрическая композиция в рисунке: Композиция в рисунке. Основы композиции в учебном рисунке. — Ghenadie Sontu Fine Art
Композиция в рисунке. Основы композиции в учебном рисунке. — Ghenadie Sontu Fine Art
Любой рисунок начинается с композиционного размещения изображений на листе бумаги. От того, как скомпоновано то или иное изображение, во многом зависит общее впечатление от рисунка.
Одним из главных требований в учебном рисунке является умение правильно размещать изображения предметов на листе бумаги.
Композиция в переводе с латинского означает «составлять, сочинять». Компоновка — составлять целое из частей. Композиция как термин имеет двоякое смысловое значение. В учебном рисунке слово «композиция» означает выполнение элементарных начальных упражнений. В художественном творчестве оно имеет более широкое смысловое значение. Разделение понятий «композиция» и «компоновка» носит весьма условный характер, так как одно незаметно переходит в другое, сливаясь в процессе работы над рисунком. Термин «композиция» употребляется в различных сферах и областях искусства: в кино, музыке, театральных постановках, балете, литературе, различных видах изобразительного искусства и в архитектуре. В творческом понимании «композиция» — это общий художественный замысел, структура произведения искусства, наиболее полно выражающая его идею. В учебном рисунке — это правильный выбор размера и расположения предмета в пределах заданного формата.
Термин «композиция» употребляется в различных сферах и областях искусства: в кино, музыке, театральных постановках, балете, литературе, различных видах изобразительного искусства и в архитектуре. В творческом понимании «композиция» — это общий художественный замысел, структура произведения искусства, наиболее полно выражающая его идею. В учебном рисунке — это правильный выбор размера и расположения предмета в пределах заданного формата.
Для общего представления о композиции в изобразительном искусстве необходимо знать следующее. Композиции бывают станковые, декоративные, монументально-декоративные, монументально-скульптурные, театрально-декорационные, объемно-пространственные. Существуют композиции предметов прикладного искусства и дизайна. К станковым относятся композиции в графическом, скульптурном и живописном исполнении. Это портреты, пейзажи, картины сюжетного характера, гравюры, эстампы, литографии и скульптурные композиции. К декоративным и декоративно-прикладным композициям относятся всевозможные эскизы росписей по ткани, стеклу, фарфору, дереву, керамике, резьбы по дереву и многое другое.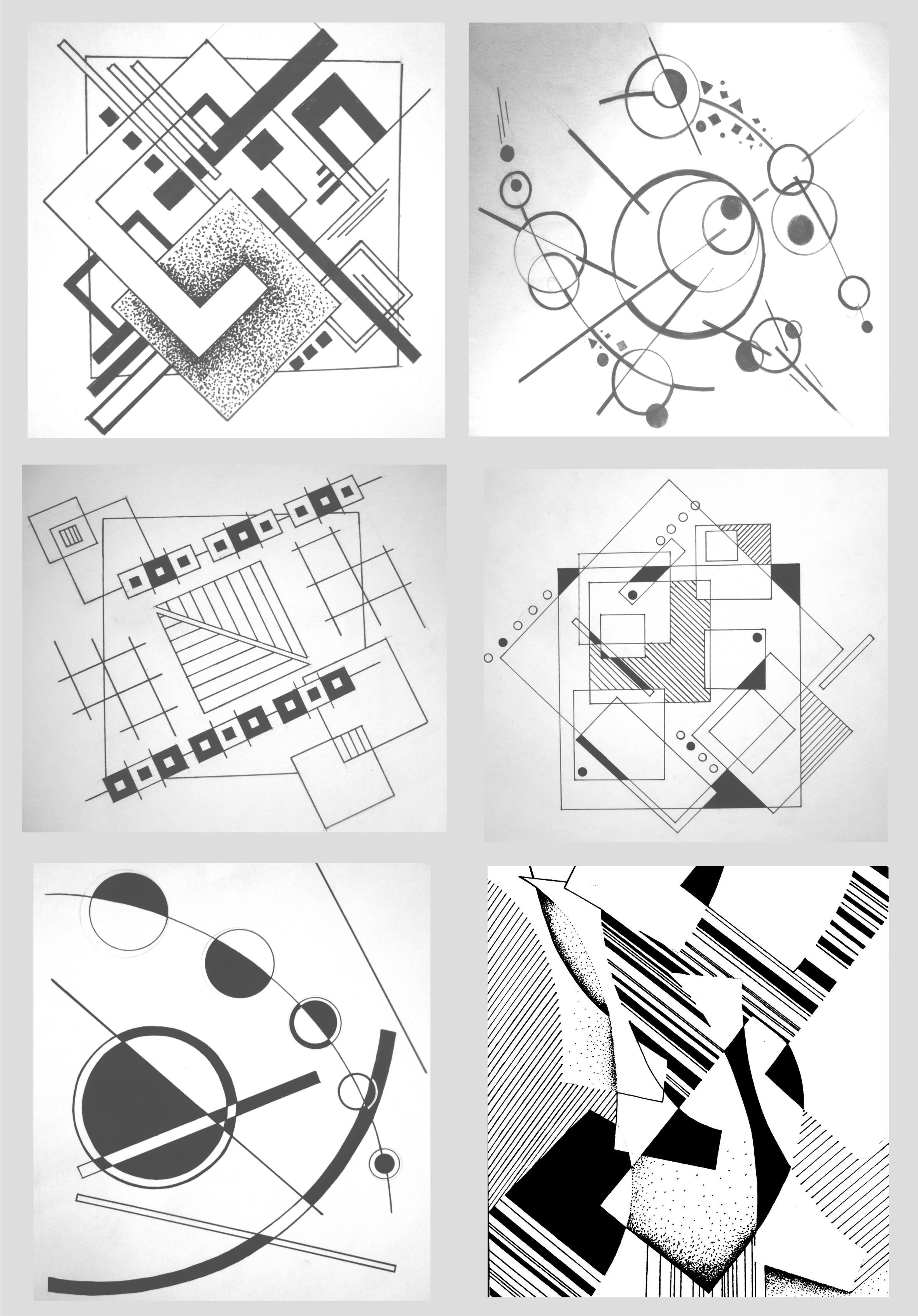
Композиция как отдельный специальный предмет не входит в число учебных дисциплин программы курса по рисунку в архитектурных вузах; тем не менее имеет важное значение для представления о композиции вообще, а также для будущей творческой деятельности, требующей решения сложных разнообразных композиционных задач. Композиция воспитывает образное мышление, является признаком, определяющим профессиональную зрелость, мастерство и творчество, умение воплощать идеи и образы.
Главной задачей композиции в учебном рисунке является умение размещать предметы и их части так, чтобы создать единое гармоническое выразительное целое.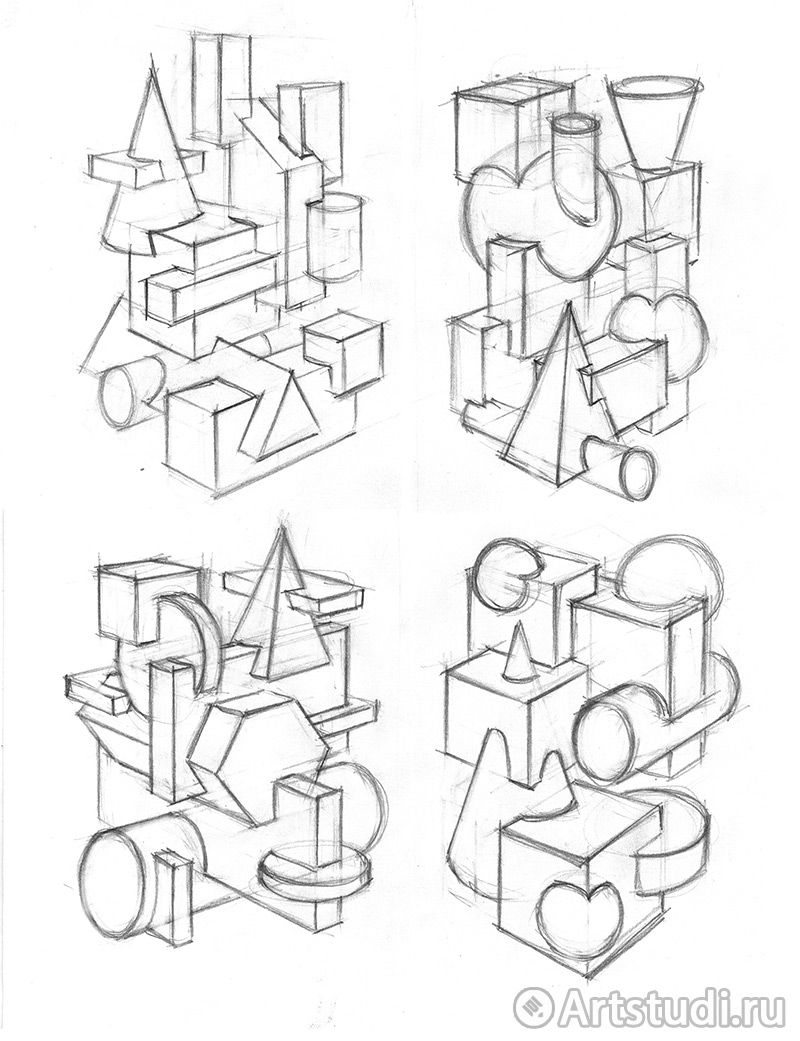
При решении композиционных задач нельзя пренебрегать такими понятиями, как масштаб, пропорции, соразмерность, равновесие, тема, сюжет, образ, тон, форма, объем, конструкция, пространство (перспектива), симметрия, контраст, ритм, динамика, статика, а также главное и второстепенное, единство и целостность, и, разумеется, выразительность и гармония.
Композиция — это система правил и приемов взаимного расположения частей в единое гармоническое целое. Умение точно и выразительно размещать изображение в пределах формата листа является непременным условием в учебном рисунке. Умение составлять композиции — это тоже искусство. Поэтому для овладения искусством компоновки потребуется развитие композиционного видения, чутья.
Благодаря существующему природному таинству, человеческому глазу присуще видеть и воспринимать окружающий нас мир в пропорциях и соразмерностях, т.е. сама природа позаботилась, положила в основу нашего зрения великолепные качества, позволяющие определять прекрасные пропорции. Выразительные композиции — это наличие гармоничности, т.е. такого качества художественных произведений, при котором глаз не ощущает несоответствия размеров частей и целого, а сочетания цветов не раздражают глаз. Гармония обязывает рисующего компоновать изображенные предметы и их части так, чтобы ни одна часть не казалась чужеродной или несоразмерной. Вот что писал о гармонии выдающийся теоретик Возрождения Леон Баттиста Альберти: «Есть нечто большее, слагающееся из сочетания и связи этих трех вещей (числа, ограничения и размещения) нечто, чем чудесно озаряет весь лик красоты. Ведь назначение и цель гармонии — упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту… И нет у природы большей заботы, чем та, чтобы произведенное ею было вполне совершенным. Этого нельзя никак достичь без гармонии, ибо без нее распадается внешнее согласие частей». Из слов Альберти понятно, что основа прекрасного — это гармония.
Выразительные композиции — это наличие гармоничности, т.е. такого качества художественных произведений, при котором глаз не ощущает несоответствия размеров частей и целого, а сочетания цветов не раздражают глаз. Гармония обязывает рисующего компоновать изображенные предметы и их части так, чтобы ни одна часть не казалась чужеродной или несоразмерной. Вот что писал о гармонии выдающийся теоретик Возрождения Леон Баттиста Альберти: «Есть нечто большее, слагающееся из сочетания и связи этих трех вещей (числа, ограничения и размещения) нечто, чем чудесно озаряет весь лик красоты. Ведь назначение и цель гармонии — упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту… И нет у природы большей заботы, чем та, чтобы произведенное ею было вполне совершенным. Этого нельзя никак достичь без гармонии, ибо без нее распадается внешнее согласие частей». Из слов Альберти понятно, что основа прекрасного — это гармония.
В работе над композицией нужно научиться композиционному видению. Такое видение можно развить следующим образом. К примеру, рассматривать с балкона многочисленные частные строения внизу, сравнивая с ними заинтересовавший вас объект. В данном случае главный объект вашего интереса находится в центре вашего внимания, а окружение служит для определения объекта и его места в этом окружении. Посредством такого зрительного восприятия окружающей среды можно развивать композиционное видение. Подобные упражнения можно проделывать дома, на улице, в транспорте, на работе, словом — везде.
Рис.28
Хорошим упражнением для развития композиционного видения может послужить такой прием. Кляксу или любое пятно на бумаге можно ограничить рамкой, прочерченной вокруг пятна на определенном расстоянии, сообразно его размеру и форме (рис. 28). Тогда вы получите композицию пятна. Любое абстрактное пятно, мысленно или буквально ограниченное рамкой таким образом, будет называться композицией или компоновкой. Вопрос в том, как соблюдены правила и приемы размещения предметов на листе. Наиболее полезное упражнение для развития композиционного видения: представив какой-либо предмет по памяти или воображению, впишите его в воображаемую рамку (формат листа) или, наоборот, в воображаемую рамку поместите рисунок предмета.
28). Тогда вы получите композицию пятна. Любое абстрактное пятно, мысленно или буквально ограниченное рамкой таким образом, будет называться композицией или компоновкой. Вопрос в том, как соблюдены правила и приемы размещения предметов на листе. Наиболее полезное упражнение для развития композиционного видения: представив какой-либо предмет по памяти или воображению, впишите его в воображаемую рамку (формат листа) или, наоборот, в воображаемую рамку поместите рисунок предмета.
По мере усвоения этих приемов, можно попытаться усложнить задачу по принципу «от простого к сложному», включив в компоновку два и более предметов. Таким образом закладываются и воспитываются основы понимания композиции, необходимые для выполнения более сложных композиционных задач в будущем. Хорошо технически выполненные рисунки с плохой компоновкой заметно теряют свои достоинства, тем самым снижается общее впечатление от работы в целом. Хорошая композиция придает художественному произведению цельность, выразительность и гармонию, что является главным признаком любого художественного произведения.
При работе над композицией в учебном рисунке необходимо:
1. Определить задачи и цели (смысловое содержание учебной постановки).
2. Изучить натурную постановку и определить точку зрения.
3. Определить масштаб и характер предмета (предметов) и правильно расположить лист бумаги (вертикально или горизонтально).
4. Разместить и уравновесить предметы на листе бумаги.
5. Определить центр композиции.
6. Построить предметы с учетом перспективы, пропорции и передачи характера.
7. Выявить объем предметов посредством светотени.
8. Обобщить и завершить работу над композицией.
1. Определить задачи и цели (смысловое содержание учебной постановки).
Прежде чем приступить к работе над композицией, необходимо определить смысловое содержание и задачи данной постановки. Предметы для учебной постановки, как правило, подбираются в соответствии с определенным сюжетом или темой. По тому, как составлена учебная постановка, можно предопределить будущую композицию, ибо сама постановка, в некотором смысле, уже есть композиция.
2. Изучить натурную постановку и определить точку зрения.
Отсутствие достаточной информации о предмете изображения и о его расположении, пропорции и других изобразительных моментах в процессе рисования чревато лишь срисовыванием или механическим переносом предметов постановки на бумагу. Постановка предметов, включенных в композицию, может быть не совсем удачной. В одном случае они могут располагаться слишком близко друг к другу или быть одинаковыми в размерах, в другом — плохо просматриваться в глубине постановки (т.е. за крупным предметом) или предмет может иметь незнакомую конструкцию и т.
Рис.29
3. Определить масштаб и характер предмета и правильно расположить лист бумаги (вертикально или горизонтально).
Правильность компоновки предметов изображения прежде всего зависит от формы предметов, составляющих постановку, и их размерных величин (рис.29). В данном случае имеется в виду один предмет. Если возьмем, к примеру, кувшин по его вертикальной оси, формат бумаги располагается вертикально. Для изображения же предметов типа кастрюли или таза с большими горизонтальными размерами бумагу следует располагать скорее горизонтально, чем вертикально. Это связано с закономерностью зрительного восприятия. В каждом отдельном случае расположение листа к модели выбирают в зависимости от конкретных предметов и их постановки. Во всяком случае, формат листа должен быть соразмерен предмету или группе предметов в целом.
Для изображения же предметов типа кастрюли или таза с большими горизонтальными размерами бумагу следует располагать скорее горизонтально, чем вертикально. Это связано с закономерностью зрительного восприятия. В каждом отдельном случае расположение листа к модели выбирают в зависимости от конкретных предметов и их постановки. Во всяком случае, формат листа должен быть соразмерен предмету или группе предметов в целом.
4. Разместить и уравновесить предметы на плоскости листа.
Композиционное размещение предметов начинается с работы над поиском эскизных вариантов композиции в рисунке (на полях или отдельном листочке). Для этого необходимо определить место предполагаемого изображения предметов на листе, размер и, следовательно, масштаб. При компоновке группы предметов важно умение увидеть в постановке предметы не по отдельности, а в целом. После чего намечаются крайние точки будущего изображения сверху, снизу, справа и слева. Они нужны для размещения изображения натурных постановок. Вместе с тем, крайние точки и их контуры не должны касаться краев листа бумаги. Также и наоборот, нельзя оставлять на листе неоправданное пустое пространство. В обоих этих случаях нарушается композиция.
Вместе с тем, крайние точки и их контуры не должны касаться краев листа бумаги. Также и наоборот, нельзя оставлять на листе неоправданное пустое пространство. В обоих этих случаях нарушается композиция.
Рис.30
5. Определить центр композиции.
Под композиционным центром понимается середина ограниченного зрительного поля группы предметов, составляющих одно целое, т.е. серединная часть целого. Под зрительным центром понимается наиболее выделяющаяся часть предмета, которая останавливает наш взгляд. Композиционный центр не всегда может совпадать со зрительным, во многом это зависит от расположения главного, основного предмета, вокруг которого группируются остальные, а также от выбора точки зрения. Композиционный центр на листе определяется так называемым центральным лучом (крестообразной пометкой), полученным условным симметричным делением формата путем проведения вертикальных и горизонтальных линий.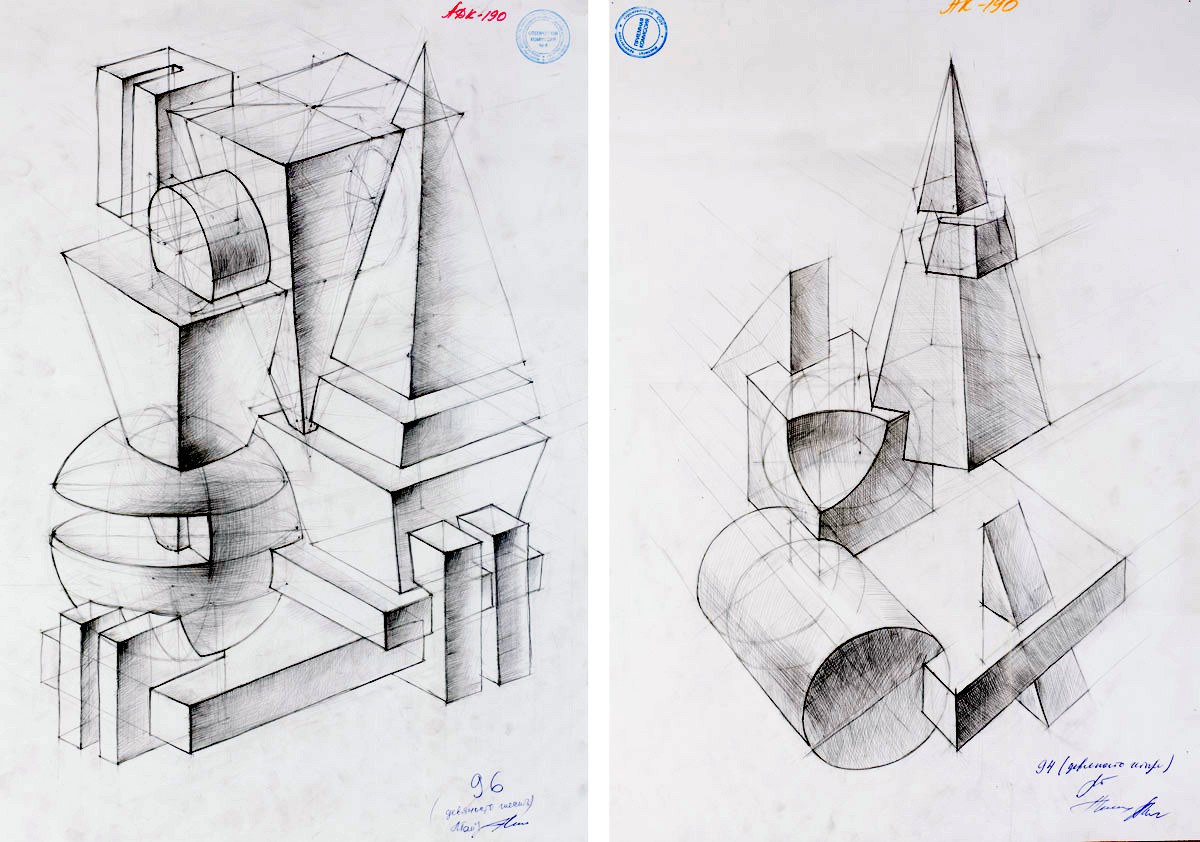 Пересечение двух линий можно считать центром композиции, заключенным в пределах зрительного поля. Что касается предметов с падающими тенями, то композиционный центр в этом случае располагается примерно посередине, между предметом и тенью, в зависимости от освещенности предмета, контраста, масштаба и направления тени. При компоновке отдельных предметов с незначительными падающими тенями композиционный центр попадает на середину предмета.
Пересечение двух линий можно считать центром композиции, заключенным в пределах зрительного поля. Что касается предметов с падающими тенями, то композиционный центр в этом случае располагается примерно посередине, между предметом и тенью, в зависимости от освещенности предмета, контраста, масштаба и направления тени. При компоновке отдельных предметов с незначительными падающими тенями композиционный центр попадает на середину предмета.
Одним из наиболее распространенных и удобных в работе над композицией инструментов является видоискатель, изготовленный из клочка бумаги с вырезанным в нем прямоугольным отверстием с отношениями сторон, соответствующими пропорциям листа бумаги, предназначенного для рисунка. Пользоваться им нужно следующим образом. Держа видоискатель перед собой, направьте его к постановке. Перемещая рамочное отверстие, размещайте видимые сквозь него предметы так, чтобы было «ни убавить, ни прибавить» в пределах отверстия (рамки «формата»). Тем самым упрощается и облегчается решение композиционной задачи (рис. 30).
30).
6. Построить предметы с учетом перспективы, пропорции и передачи характера.
Построение предметов на плоскости бумаги следует начать с определения их мест в пределах границ, отведенных им ранее. Определение этих мест осуществляется легким касанием карандаша, при этом намечаютобщими овалами места расположения предметов с учетом масштаба и пропорций будущих предметов (рис.31). Затем на листе намечают общий характер формы предметов, их пропорции и расположение в пространстве. В последующем, при построении конструктивной основы форм предметов, необходимо обратить особое внимание на перспективное изображение оснований предметов, т.е. на расположение их следков на плоскости стола и расстояние между ними. При этом следки оснований не должны накладываться, а края выступающих поверхностей предметов врезаться друг в друга. Кроме того, расстояния между предметами должны быть логически выдержаны.
Рис.31
7. Выявление объема предметов посредством светотени.
Выявление объема предметов посредством светотени.
Для выявления объема предметов вначале следует определить их светотеневые контрасты, а затем — полутона. Легким касанием карандаша на бумаге помечаются границы собственных и падающих теней, после чего приступают к прокладыванию тоном теневых участков. После этого можно проложить полутона, одновременно усиливая как границы собственных теней, так и сами тени. Нельзя забывать, что работа над выявлением объема предмета тоном — это, прежде всего, лепка формы предметов с его помощью. Об этом, к сожалению, часто забывают, находясь в плену у натуры. Падающие тени всегда темнее собственных, особенно от наиболее близко расположенных к вам предметов. Работая тоном, необходимо постоянно сравнивать светотеневые отношения предметов друг с другом, уточнять их пропорции, следить за смещением предметов (компоновкой) и перспективными изменениями. Главное в работе тоном ~ это выявление формы предметов и умение работать тональными отношениями.
Рисование тоном требует развитого чувства формы и цельного видения. При штриховке целесообразно класть тон штрихами по форме предмета. Такое направление штриховки в рисунке дает хорошую рис 31 возможность добиться объемности формы предмета.
Переходя к детальной проработке формы предметов, нельзя забывать, что детали подчинены общему целому, в противном случае они будут раздробленными. Такой подход не означает, что деталями полностью пренебрегают. Не следует также делать их «камнем преткновения». Работу следует вести в совокупности, продвигаясь от общего к частному и от частного к общему, т.е. методически последовательно.
8. Завершение и обобщение работы над рисунком, т.е. рисунок следует привести к общему соподчинению всех тонов в соответствии с общим зрительным впечатлением и композиционной целостностью.
Схемы поиска композиционного равновесия на примере пятна-окружности на листе бумаги
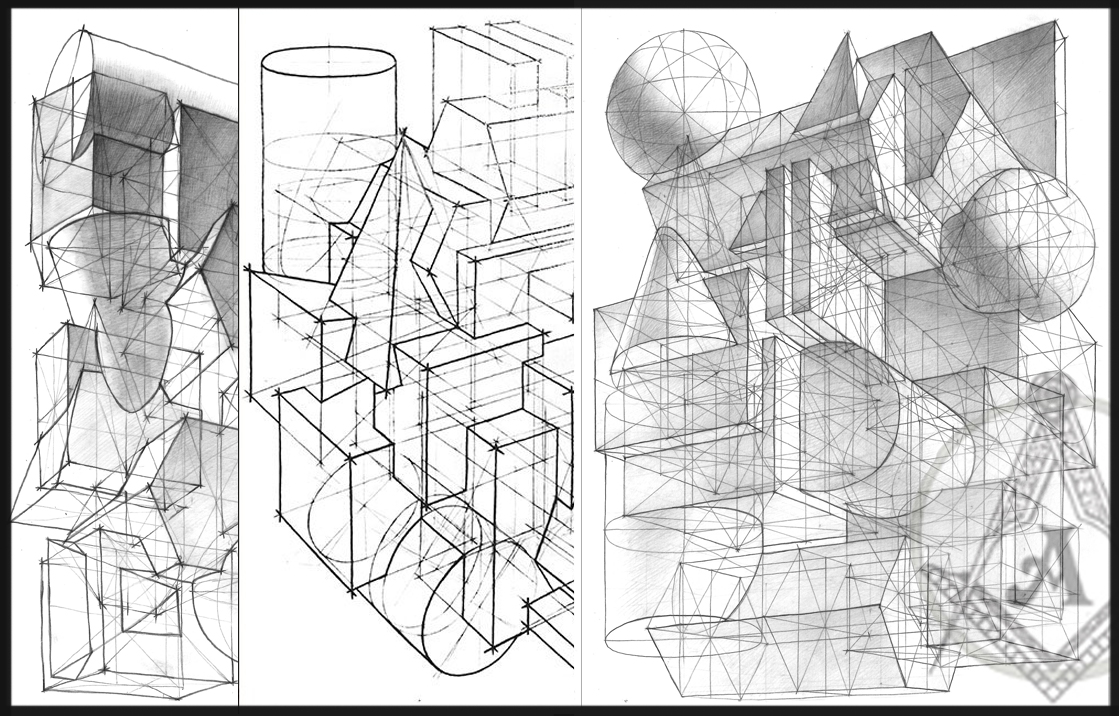
Рис.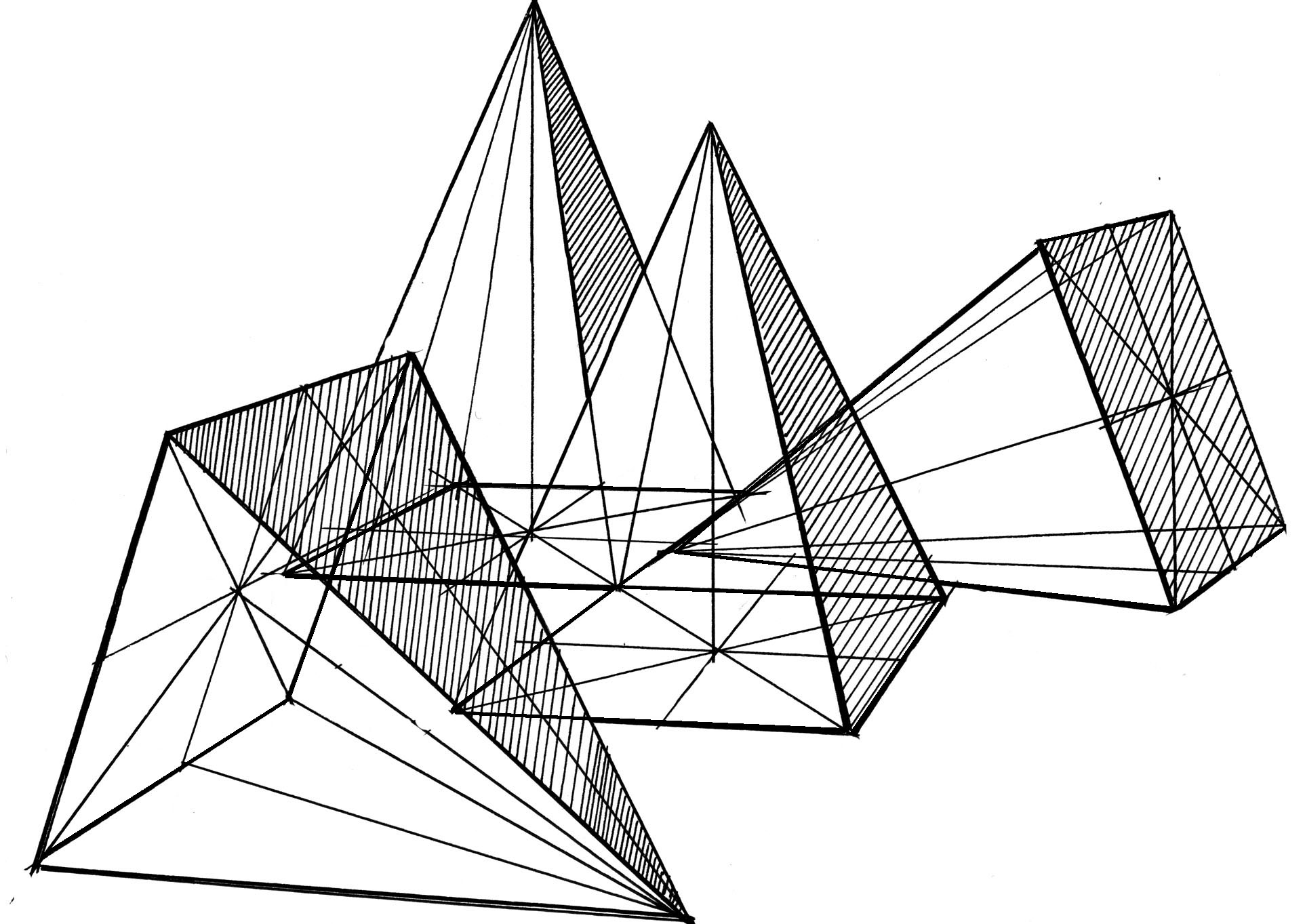 32. Плоскостные композиции из геометрических фигур
32. Плоскостные композиции из геометрических фигур
Рис.33. Объемно-пространственные архитектурные композиции
In Art, Академический рисунок, Обучение искусству, Рисунок*, Школа Искусств Tags учебный академический рисунок, учебные пособия, Композиция, изображение предметов на листе бумаги, Основы композиции, композиция рисунок, Методическое пособие, Учебное пособие, Компоновка, композиционный центр рисунок, Композиция в рисунке, Основы композиции в учебном рисунке, рисунок живопись композиция, композиция карандашом рисунок, школа рисунок, картина композиция, композиция основа, объемно пространственная композиция рисунок, построение рисунка композиция
Композиционный рисунок — 82 фото
Врезки МАРХИ пирамида в шар
Геометрический натюрморт
Врезка фигур МАРХИ
Archineo
Композиция из геометрических фигу
Натюрморт из геометрических фигур (куб, Призма)
Линейно-конструктивный рисунок геометрических тел МАРХИ
МАРХИ черчение вступительный экзамен
Компоновка предметов в натюрморте
Композиция в рисунке примеры
Композиция для поступления в МАРХИ
МАРХИ композиция Асейкина
Композиция рисунок
Объемно-пространственная композиция рисунок
Статика и динамика беспредметная композиция
МАРХИ черчение вступительный экзамен
МАРХИ объемно пространственная композиция
Архитектурная композиция из геометрических фигур
Врезки геометрических тел аксонометрия
Фигуры карандашом
Московский архитектурный институт МАРХИ : «архитектура»
Объемная архитектурная композиция вступительный экзамен СПБГАСУ
Врезки геометрических фигур МАРХИ
Объемно-пространственная композиция рисунок
Врезки композиция МАРХИ
Композиция из объемных фигур
Объемно-пространственная композиция рисунок
МАРХИ архитектура вступительные экзамены
Геометрические фигуры для экзамена МАРХИ
Гризайль Академия художеств Репина
Статика динамика ритм
Натюрморт с овощами карандашом
Варианты композиции в рисунке
Бионика клаузура
Композиция эмоции
Контрастность в композиции
Светотень шар, конус, цилиндр, куб
Пропедевтика основы композиции
Линейная композиция
Композиция для скетча
Композиция из геометрических фигур
Компоновка натюрморта на листе
Композиция из геометрических фигу
Композиция из линий и пятен
Композиционные зарисовки
Человек ракурс снизу референс
Вступительные в архитектурный
Глубинно пространственная композиция эскиз
Графическая композиция
Академический натюрморт
Врезки геометрических фигур МАРХИ
Композиционные Наброски будущего рисунка
Построение композиции
Основы графической композиции
ТГАСУ олимпиада по рисунку
Экзамены на архитектурный Факультет
Вдохновение для рисования
Этапы построения натюрморта
Композиция из геометрических тел МАРХИ
Врезка фигур МАРХИ
Перспективная композиция
Средства композиции симметрия асимметрия статика динамика ритм
Осенние скетчи акварелью
Композиция в архитектуре для поступления
Геометрическая композиция
Графический натюрморт
Рисование геометрических тел
Архитектурная композиция
Академический Строгановка линейно конструктивный натюрморт
МАРХИ вступительные экзамены
Арт композиция
Геометрические фигуры в перспективе
Этапы рисования натюрморта
Композиция из геометрических фигур
Горизонтальная композиция из геометрических фигур
Врезки композиция МАРХИ
Простые предметы для рисования
Комментарии (0)
Написать
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Значение, операторы, правила и методы
Мы изучили концепцию функций и то, как мы можем выразить их в виде уравнений. Но задумывались ли вы когда-нибудь, что, если две функции даны вместе и их комбинация образует совершенно новую функцию? И если такое сочетание возникает и при обработке фигур с помощью Geometry, то как с этим бороться? Эти виды сложных функций и преобразований формы могут быть решены с использованием концепции композиции. В этом разделе мы поймем, что такое состав и как он применяется и используется.
Значение композиции
В математике мы можем создать единственную более сложную функцию из нескольких простых функций. Этот процесс известен как композиция, когда мы рассматриваем выходные данные одной функции как входные данные другой функции.
A композиция функций представляет собой математический процесс, в котором две функции объединяются для создания составной функции. Выход одной функции используется как вход другой.
Составные функции можно обозначать как f∘g или T∘S, где f и g — функции, а T и S — преобразования. Композицию также можно обозначить как f(g(x)). Композиция двух функций f и g дает новую функцию h. Важно знать порядок функций, так как это влияет на создание новой составной функции. Например, использование выходных данных функции f в качестве входных данных функции g для получения составной функции h равно , а не , то же самое, что использовать функцию g в качестве входа функции f.
Мы также можем использовать концепцию композиции в геометрии, называемую композицией преобразований, которая происходит с формами (или фигурами), а не с функциями. Преобразования в геометрии включают перемещения, отражения, повороты и т. д.
композиция преобразований представляет собой процесс, при котором комбинация преобразований последовательно выполняется над формой или фигурой, при этом результирующая форма, преобразованная в результате одного преобразования, используется в качестве отправной точкой в следующем преобразовании.
В этой статье мы исследуем композицию с точки зрения преобразований и функций.
Композиция преобразований
Рассмотрим преобразование T, которое отображает из точки A в B, а также другое преобразование S, которое отображает из точки B в C. Из этих преобразований T и S мы можем произвести новое составное преобразование . которая может отображать непосредственно из точки A в C, называемую композицией S и T. Мы обозначаем ее как S ∘ T и формулируем как «S of T».
Композиция преобразований, StudySmarter Originals
Здесь мы сначала применяем преобразование T, а затем применяем преобразование S. Таким образом, мы можем представить эту композицию как: C=S(B)=S(T(A))=( S∘T)(A)
Примером композиции преобразований является скользящее отражение. Это композиция отражения и перевода.
Утверждения о композиции преобразований
Рассмотрим некоторые теоремы о композиции преобразований.
Теорема 1 : Теорема о композиции
Композиция двух изометрий является изометрией.
Теорема 2 : Отражения в параллельных прямых Теорема
Композиция отражений в двух параллельных прямых является переносом. То есть для двух параллельных прямых l и m отражение в l, а затем отражение в m — это то же самое, что и перенос.
Теорема 3 : Отражение в пересекающихся прямых Теорема
Композиция отражений в двух пересекающихся линиях представляет собой вращение вокруг точки пересечения этих двух линий. Другими словами, если l и m — две прямые, пересекающиеся в точке O, то отражение в l, а затем и в m — это то же самое, что и вращение вокруг точки O.
Композиция отражений в перпендикулярных линиях представляет собой пол-оборота вокруг точки пересечения линий.
Теорема 5 : Композиция вращения
Композиция двух вращений относительно одной и той же точки снова является вращением.
Теорема 6 : Композиция перевода
Композиция двух переводов также является переводом.
Композиция примеров перевода
Давайте посмотрим на рабочий пример композиции переводов.
Состав вращения, StudySmarter Originals
Найти композицию в заданном вращении.
Решение: Здесь угол поворота дуги PP’ равен 90°, а угол поворота дуги P’P» равен 45°. Тогда для угла поворота дуги PP» мы использовать состав вращения. Это просто означает, что мы добавляем градусы вращения для обоих из двух вращений, чтобы получить нашу композицию вращения.
⇒(RC,90°∘RC,45°)=(RC,135°)
Композиция функций
Если заданы две функции f(x) и g(x), мы можем объединить функции, чтобы создать новая составная функция. Это означает, что мы берем функцию g и используем ее в качестве входных данных для другой функции f. Тогда композиция этих функций обозначается как f(g(x)) или (f∘g)(x). Мы называем это «f от g от x».
Мы также можем сформировать составную функцию, используя обратный порядок, где мы рассматриваем функцию f как вход для функции g.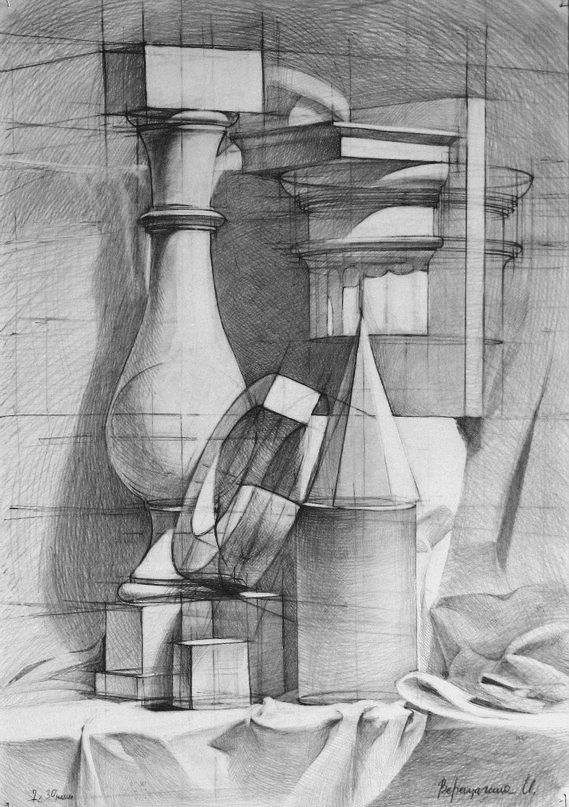 В этом случае мы представляем составную функцию как g(f(x)) или (g∘f)(x).
В этом случае мы представляем составную функцию как g(f(x)) или (g∘f)(x).
Обратите внимание, что g(f(x)) и f(g(x)) дадут разные функции, если только они не являются совершенными обратными (противоположными) друг другу, в которых f(g(x))=g(f(x) )=х.
Порядок композиции функций
При работе с композицией важно помнить о порядке функций f и g. Здесь представлен пример, чтобы лучше понять эту концепцию.
Рассмотрим две функции f(x)=x2 и g(x)=x+2. Теперь найдем композиции f∘g и g∘f и проверим, дают ли они одинаковые ответы или разные.
f∘g(x)=f(g(x))=f(x+2)=(x+2)2=x2+2x+4
В приведенном выше уравнении мы используем функцию g в качестве входных данных для функции f. Теперь давайте рассмотрим составную функцию, в которой мы используем функцию f в качестве входных данных для функции g.
g∘f(x)=g(f(x))=g(x2)=x2+2
Мы видим разницу между обеими композициями. Другими словами, f∘g(x) не равно g∘f(x).
Домен составных функций
Все значения, которые принимает конкретная функция, называются доменом этой функции. Однако для композиции функций мы имеем дело с двумя разными функциями. Таким образом, при работе с областью определения составной функции необходимо учитывать обе функции.
Однако для композиции функций мы имеем дело с двумя разными функциями. Таким образом, при работе с областью определения составной функции необходимо учитывать обе функции.
Бывают случаи, когда мы не можем составить отдельные функции для всех значений x. Итак, в этой ситуации мы ограничим некоторые значения x, чтобы использовать композицию. Эти ограниченные значения становятся доменом для этой функции. В композициях область определения второй функции может либо совпадать с первой функцией, либо лежать в ее пределах.
Рассмотрим две функции f(x)=4x-6,g(x)=x. Здесь найдем область определения композиции g(f(x)).
Поскольку функция g представляет собой квадратный корень, мы можем рассматривать только значения x, большие или равные нулю.
Теперь для функции f он станет входом функции g. Таким образом, значение f должно быть больше или равно нулю.
Таким образом, f(x)≥0 будет возможно только тогда, когда значение x рассматривается как x≥32.
Здесь значение x получается как:
f(x)≥0⇒4x-6≥0⇒4x≥6⇒x≥64⇒x≥32
Следовательно, функция композиции g(f(x)) имеет область значений x≥32.
Диапазон составных функций
Диапазон функции касается выходных значений этой функции. Мы можем вычислить диапазон составной функции точно так же, как мы делаем это для диапазона любой другой функции. Диапазон составной функции может быть таким же, как у второй функции (т. е. внешней функции), или лежать в ее пределах.
Пусть f(x)=x-8,g(x)=x2. Найдем композицию g(f(x)). Здесь функция f может принимать любые значения. Но вторая функция g имеет форму квадрата. Таким образом, значения будут больше, чем равны нулю. Теперь для композиции g(f(x)) имеем:
g(f(x))=g(x-8)=(x-8)2=x2-16x+64
Так как f может быть чем угодно и применить к нему g, где g может быть больше или равно до нуля, диапазон композиции g(f(x)) будет больше или равен нулю.
Примеры композиции функций
Давайте лучше разберемся с композицией функций на некоторых примерах работы.
Даны две функции f(x)=3x и g(x)=2×2-5. Найдите композицию (g∘f)(x).
Решение: Здесь нам нужно найти g∘f. Итак, мы сначала рассмотрим функцию, а затем будем использовать ее в качестве входных данных для функции g. Таким образом, мы можем записать это как:
Итак, мы сначала рассмотрим функцию, а затем будем использовать ее в качестве входных данных для функции g. Таким образом, мы можем записать это как:
(g∘f)(x)=g(f(x))=g(3x)=2(3x)2+5=2(9×2)+5=18×2+5
Найти f(g(- 1)) для функций f(x)=x2-2x и g(x)=x-5.
Решение: Нас просят вычислить состав f и g, когда значение x задано как (-1). Во-первых, мы используем функцию g в качестве входных данных для функции f. Для этого мы заменим переменную x в функции f на всю функцию g, то есть role=»math» g(x)=x-5.
Примечание : Функция ввода входит в каждое значение x, а не только в первое значение.
f(x-5)=(x-5)2-2(x-5)=x2-10x+25-2x+10=x2-12x+35
На последнем этапе мы просто вводим значение x, -1, в приведенном выше составном уравнении.
f(g(x))=x2-12x+35∴f(g(-1))=(-1)2-12(-1)+35=48
В качестве альтернативы мы также можем использовать следующее подход к решению композиции. Во-первых, мы оцениваем g(x):
⇒g(x)=x-5∴g(-1)=-1-5=-6
Затем мы продолжаем дальше, используя рассчитанное выше значение в качестве входных данных.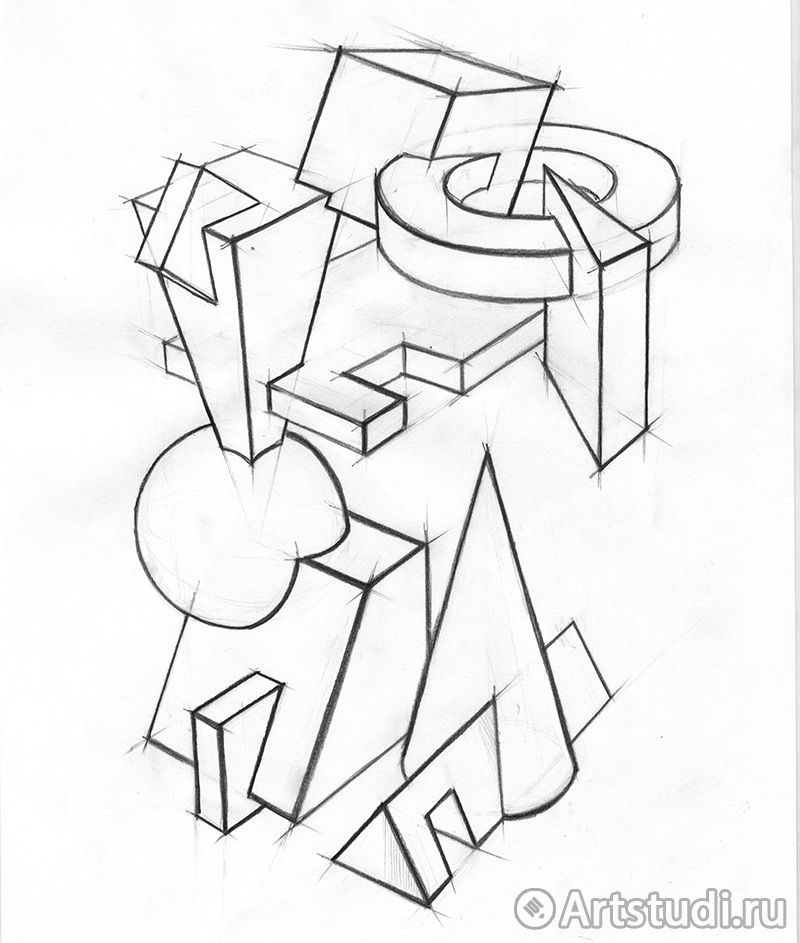 для функции f.
для функции f.
f(g(-1))=f(-6)=x2-2x=(-6)2-2(-6)=36+12=48
∴f(g(-1))=48
Композиция – основные выводы
- композиция функций представляет собой математический процесс, в котором две функции объединяются для создания составной функции. Выход одной функции используется как вход другой.
- A композиция трансформаций — процесс, при котором комбинация трансформаций (перемещений, поворотов, отражений и т. д.) последовательно выполняется над формой или фигурой, при этом результирующая форма, преобразованная в результате одного преобразования, используется в качестве отправной точки в следующем преобразовании.
- При работе с композицией важен порядок функций f и g.
- По составу область определения второй функции может либо совпадать с первой функцией, либо лежать в ее пределах.
- Диапазон составной функции может быть таким же, как у второй функции (т. е. внешней функции), или лежать в ее пределах.

Плакат с геометрическими фигурами Royalty Free Vector
Плакат с геометрическими фигурами Royalty Free Vector- лицензионные векторы
- Геометрические векторы
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный / редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и модифицировать | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по запросу |
Владение Узнать больше
Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже: Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.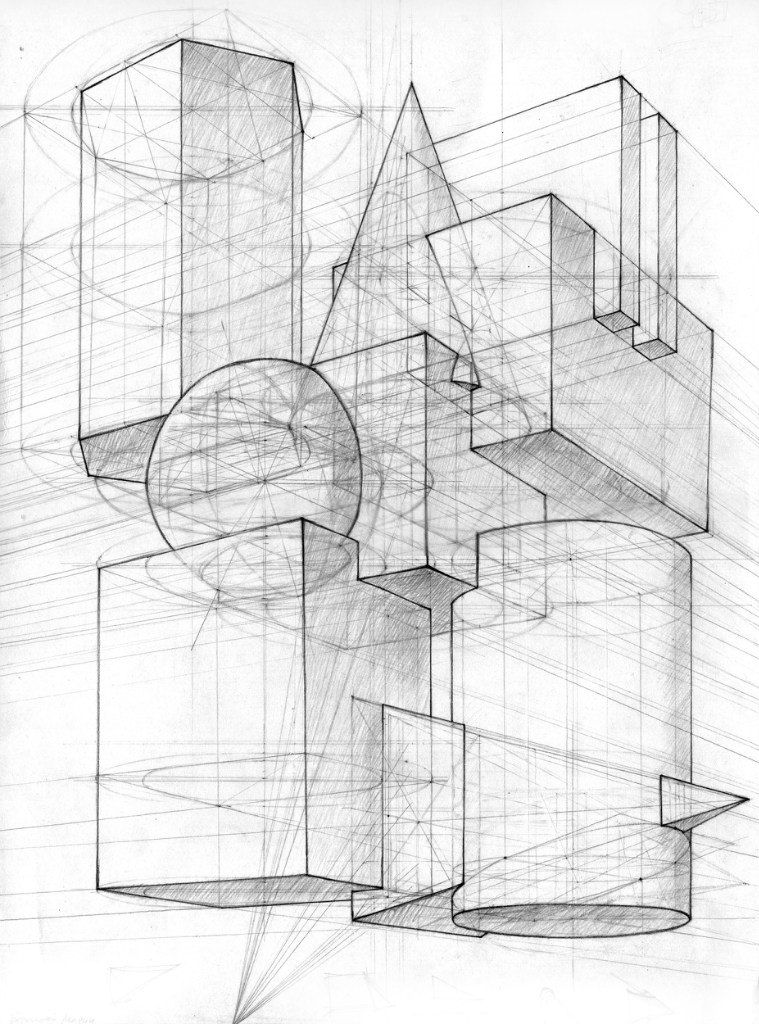
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69Оплатить стандартные лицензии можно тремя способами. Цены $ $ .
| Оплата с | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00 Существует два способа оплаты расширенных лицензий.