Гистограмма это: Гистограммы. Что это? Как построить? Как представить данные? Как провести анализ? | Бережливые шесть сигм | Статьи | База знаний
Гистограмма — QUORACE
Гистограммы позволяют сделать при контроле качества предварительную оценку закона распределения случайной величины, т.е. понять, как происходит разброс значений, есть ли влияющие факторы и как они влияют на измеряемый результат.
Гистограмма является столбчатым графиком и позволяет наглядно представить характер распределения случайной величины
Построение гистограммы происходит следующим образом
1. Создаётся план исследования, проводятся измерения, результаты заносятся в таблицу. Результатом может быть, как фактическое измеренное значение, например, момент затяжки 20 Н*м, так и отклонение от требуемого значения, например, запись отклонения в 0,05 мм при оценке диаметра изделия.
В Таблице 1 приведён пример для 40 результатов измерений момента силы (Н*м).
Заданный момент силы равен 25,5 Н*м, отклонения ±1,5 Н*м. Он будет рассмотрен для построения гистограмм.
Таблица 1.
2. В полученной выборке находят минимальное и максимальное значение
3. Вычисляют разницу R=Xmax-Xmin (Таблица 2).
4. Разницу R разбивают на z равных интервалов (L), где z=√N, N – объём всей выборки (количество измеренных значений параметра) (Таблица 2). Для точного анализа выборка должна быть представительной, т.е. быть достаточной для проведения анализа и его точной интерпретации. Представительной считается выборка от 35 до 100 значений, обычно N=100. Длина интервала L=R/x должна быть больше цены деления шкалы измерительного устройства, которым выполнялись измерения.
Таблица 2.
5. Подсчитываются частоты попадания значений в интервалы, составляется таблица распределения и строится его графическое изображение. При этом частоты значений, оказавшиеся на границе интервалов, поровну распределяют между соседними интервалами (Рис.
Рис.1
Имея таблицу распределения значения X(среднее арифметическое) и S2 (стандартное отклонение) можно рассчитать по формулам
Где xi – среднее значение i-го интервала
Или воспользовавшись соответствующими функциями в MS Excel
СРЗНАЧ() для X
СТАНДОТКЛОН.В() или СТАНДОТКЛОН.Г() для S2
Зная X и S2 можно оценить индекс воспроизводимости процесса (Ср), который будет рассмотрен в другой статье.
Исходя из гистограммы, рассмотренной в примере, можно сделать вывод о том, что часть значений находится вне допусков и большинство значений уходят в сторону двух пиков по левую и правую границу допусков, что характерно для выборки, объединяющей результаты двух процессов, когда происходит смешивание двух распределений с далеко отстоящими средними значениями. В данном случае необходимо применить метод стратификации и провести анализ ещё раз. В данном случае можно предположить, что измерения проводились двумя различными ключами, что и дало такой результат. Разделение данных по различным ключам позволит исключить двойные пики в гистограмме.
Существует восемь основных типов гистограмм:
- Нормальное распределение. Обычный тип. Форма колокола.
Симметричная форма с пиком примерно в центре интервала характерна для нормального распределения. Отклонения от данной формы могут указывать на наличие различных причин, влияющих на распределение. - Распределение с двумя пиками.
В центре интервала низкая частота попадания, зато есть два пика по левую и правую стороны интервала. Подобное распределение говорит о том, что в выборку включены значения, объединяющие различные процессы, например, смешаны результаты контроля двух станков или была произведена различная настройка контролирующего инструмента.
- Плато
При подобном распределении можно говорить о влиянии условий, аналогичных предыдущей гистограмме, отличие в том, что средние значения нескольких распределений отличаются незначительно. Необходимо провести расслоение данных, снизить вариабельность процессов. - Распределение гребенчатого типа.
Чередующиеся высокие и низки значения обычно указывают на ошибки измерений или ошибки в способе группировки данных, также на систематическую погрешность в способе округления данных. Существуют незначительная вероятность того, что это распределение типа плато. Если значения в таблицу заносятся человеком, то наличие пиков на целых числах может быть обусловлено влиянием человека при округлении значений. Человеку свойственно отдавать предпочтения при записи круглым числам - Положительно или отрицательно скошенное распределение.
Среднее значение гистограммы локализовано слева или справа от центра размаха. Частоты резко спадают к противоположному от пика концу. Форма ассиметрична. Подобное распределение возможно, когда невозможно получение значений больше или меньше определённой величины, либо при наличии одностороннего поля допуска, также это может быть влияние точности заготовок при их механической обработке. - Усечённое распределение, с обрывом справа или слева.
Среднее арифметическое гистограммы локализовано далеко слева или справа от центра размаха, частоты резко спадают в противоположном от пика направлении. Подобные распределения встречаются при стопроцентном просеивании изделий из-за плохой воспроизводимости процессов, т.е., например, часть распределения изъята при контроле качества. - Распределение с изолированным пиком.
На ряду с обычным распределением любого типа по одну сторону от распределения находится маленький пик. Причиной может быть включение данных из другого распределения или появление ошибки измерения. Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика.
Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика. - Распределение с пиком на краю.
Имеется большой пик по одну из сторон размаха. Подобное распределение может быть при объединении всех несоответствий, близких к одному из концов размаха в одну категорию, либо на неаккуратную запись данных.
Если существуют границы допуска, то следует нанести их на гистограммы. Исходя из положения распределения относительно границ допуска на гистограмме можно делать выводы о необходимости принятия решений.
Есть пять типичных случаев расположения распределения относительно границ допуска
- Гистограмма находится в допуске.
Состояние процесса стабильно, необходимо поддерживать процесс в данном состоянии - Гистограмма находится в допуске, но вплотную к границам.
Необходимо уменьшить разброс до меньшего значения. - Гистограмма за границами допуска слева (или справа).
Необходимо сместить среднее значение ближе к центру. - Гистограмма за границами допуска слева и справа.
Необходимы действия, направленные на снижение вариаций процесса. - Гистограмма за границами допуска слева и справа, пик смещён вправо (или влево).
Необходимо провести действия, аналогичные для 3 и 4 случая одновременно, для снижения вариаций и смещения среднего.
гистограмма
Алгоритм раскладывания в виде одного из значений в этой таблице.
Значение | Описание |
|---|---|
|
|
| Целочисленное правило полезно с целочисленными данными, когда это создает интервал для каждого целого числа. Это использует ширину интервала 1 и помещает границы интервала на полпути между целыми числами. Чтобы постараться не случайно создавать слишком много интервалов, можно использовать это правило, чтобы создать предел 65 536 интервалов (216). Если область значений данных больше 65536, то целочисленное правило использует более широкие интервалы вместо этого. Примечание
|
| Правило Стерджеса популярно из-за его простоты. Это выбирает количество интервалов, чтобы быть |
| Правило Квадратного корня широко использовано в других пакетах программного обеспечения. Это выбирает количество интервалов, чтобы быть |
histogram не всегда выбирает количество интервалов с помощью этих точных формул. Иногда количество интервалов настроено немного так, чтобы границы интервала упали на «хорошие» числа.
Для данных о datetime метод интервала может быть одним из этих модулей времени:
'second' | 'month' |
'minute' | 'quarter' |
'hour' | 'year' |
'day' | 'decade' |
'week' | 'century' |
Для данных о длительности метод интервала может быть одним из этих модулей времени:
'second' | 'day' |
'minute' | 'year' |
'hour' |
Если вы задаете BinMethod с datetime или данными о длительности, затем histogram может использовать максимум 65 536 интервалов (или 216). Если заданная длительность интервала требует большего количества интервалов, то histogram использует большую ширину интервала, соответствующую максимальному количеству интервалов.
Эта опция не применяется к гистограммам категориальных данных.
Примечание
Если вы устанавливаете BinLimitsNumBins BinEdges , или BinWidth свойство, затем BinMethod свойство установлено в 'manual'.
Пример: histogram(X,'BinMethod','integers') создает гистограмму с интервалами, сосредоточенными на целых числах.
Динамическая гистограмма или график распределения частот в Excel
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
=ЧАСТОТА(tblData[Age];C13:C22)=FREQUENCY(tblData[Age],C13:C22)
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных – rngGroups (столбец Frequency) и второй для подписей горизонтальной оси – rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать.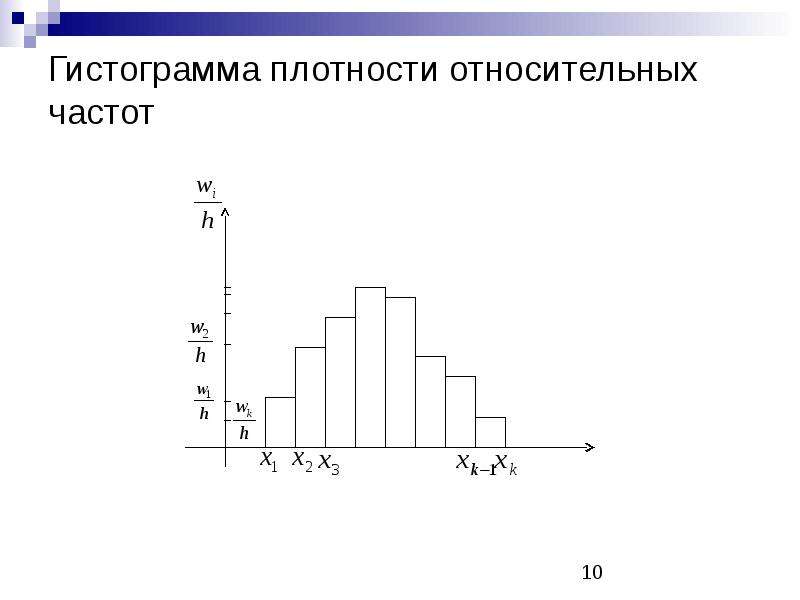 Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Оцените качество статьи. Нам важно ваше мнение:
Двумерная гистограмма
Когда двумерная гистограмма отображает ячейки, цвет каждой ячейки отображает значение плотности вероятности не относительно всей двумерной плоскости значений, а только относительно текущего интервала оси X.
Имя – Имя гистограммы. По этому имени гистограмма будет доступна из кода.
Исключить – Если опция выбрана, то гистограмма будет исключена из модели.
Отображается на верхнем агенте – Если опция выбрана, то гистограмма будет видна на презентации типа агента, в который будет вложен данный агент.
Отображать вложения — Если опция выбрана, то данные на двумерной гистограмме будут отображаться в виде вложений («конвертов»).
Отображать ячейки — Если опция выбрана, то данные на двумерной гистограмме будут отображаться в виде ячеек.
– С помощью этой кнопки вы можете добавить новый объект данных гистограммы на гистограмму. Щелкнув по ней, вы откроете новую секцию свойств, в которой вы должны будете задать свойства нового объекта данных:
Заголовок – Заголовок этого объекта данных, который будет отображаться в легенде гистограммы.
Данные
– Имя этого
объекта данных двумерной гистограммы.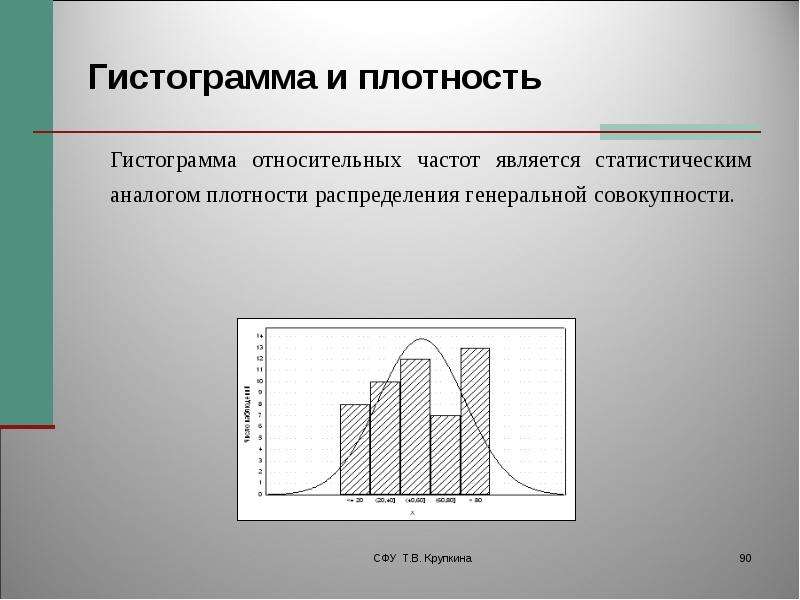
Цвет – Цвет, которым будут отображаться значения этого объекта данных на гистограмме. Щелкните мышью внутри элемента управления и выберите нужный цвет из списка наиболее часто используемых цветов или же выберите любой другой цвет с помощью диалога Цвета.
Чтобы удалить объект данных с гистограммы, щелкните мышью по кнопке внизу этой секции свойств. Используйте кнопки и , чтобы изменять порядок расположения элементов данных.
Обновлять данные автоматически — Если опция выбрана, то гистограмма будет производить обновление значений отображаемых на ней объектов данных с периодичностью, указанной в поле Период. Так же здесь вы можете выбрать, хотите ли вы Использовать модельное время, чтобы задать Время первого обновления, или вы хотите Использовать календарные даты, чтобы задать Дату обновления.
Не обновлять данные автоматически — Если опция выбрана, то гистограмма не будет самостоятельно производить обновление значений отображаемых на ней объектов данных.
Метки по оси X – С помощью данного выпадающего списка вы можете задать расположение меток, отображаемых для оси X, относительно области гистограммы (Снизу или Сверху). Если вы не хотите, чтобы у оси X отображались метки, выберите из списка Нет.
Метки по оси Y
– С помощью данного выпадающего списка вы можете задать расположение
меток, отображаемых для оси Y, относительно области гистограммы (Слева
или
Справа). Если вы не хотите, чтобы у оси Y отображались метки, выберите из списка
Нет.
Если вы не хотите, чтобы у оси Y отображались метки, выберите из списка
Нет.
Цвет фона – Фоновый цвет гистограммы.
Цвет границы – Цвет, которым будет отображаться граница гистограммы.
Цвет меток – Цвет, которым будут отображаться метки по оси Y. Если вы не хотите, чтобы метки были видны, выберите Нет цвета.
Цвет сетки – Цвет, которым будет отображаться сетка гистограммы. Если вы не хотите, чтобы сетка была видна, выберите Нет заливки.
Уровень – Уровень, на котором расположена эта гистограмма.
X – X-координата верхнего левого угла гистограммы.
Y – Y-координата верхнего левого угла гистограммы.
Ширина – Ширина гистограммы (в пикселах).
Высота – Высота гистограммы (в пикселах).
Легенда – Если опция выбрана, то у данной гистограммы будет отображаться легенда. Вы можете управлять местоположением легенды относительно области гистограммы с помощью группы кнопок Расположение. Размер области, выделенной под легенду, задается с помощью элемента управления Ширина (или Высота, в зависимости от того, какое задано Расположение легенды). Также вы можете изменить Цвет текста легенды.
Свойства, расположенные в секции Область диаграммы, задают визуальные свойства области диаграммы:
Смещение по оси X
– Смещение области диаграммы по оси X относительно левой границы всей
области, выделенной в графическом редакторе под диаграмму.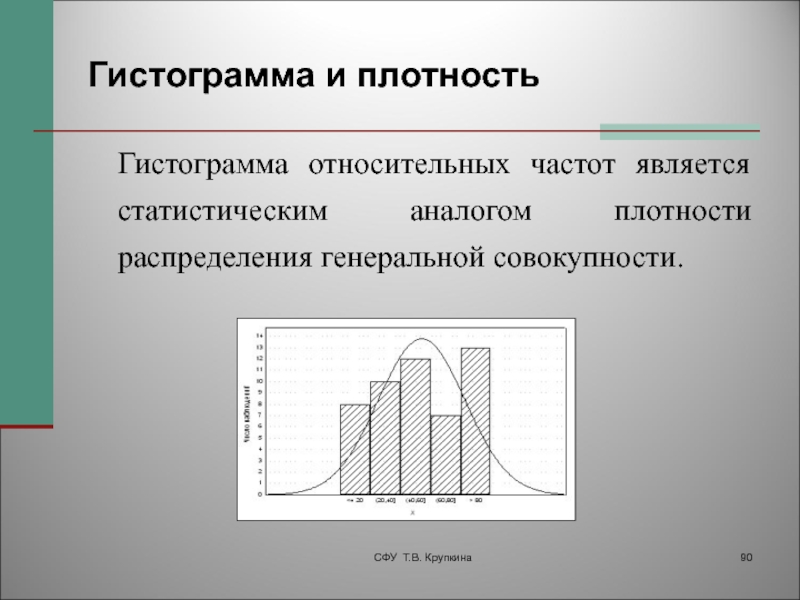
Смещение по оси Y – Смещение области диаграммы по оси Y относительно верхней границы всей области, выделенной в графическом редакторе под диаграмму.
Ширина – Ширина области диаграммы (в пикселах).
Высота – Высота области диаграммы (в пикселах).
Цвет фона – Фоновый цвет области диаграммы.
Цвет границы – Цвет, которым будет отображаться граница области диаграммы.
Видимость – Видимость гистограммы. Гистограмма будет видна, если заданное здесь выражение будет истинно (true), в противном случае гистограмма отображаться не будет.
Количество – Количество экземпляров данной гистограммы. Если вы оставите это поле пустым, то будет создана только одна такая гистограмма.
Действие при изменении выделения
– Код, который будет выполняться, когда пользователь выделит на
гистограмме какой-то один (или несколько) элемент(ов) данных. Код будет
вызываться как в том случае, если пользователь выделит элементы,
щелкнув мышью по их заголовкам в легенде, так и в том случае, если он
выделит их программно путем вызова метода selectItem().
Вы можете использовать в этом коде две переменные:
int[] selectedIndices
— номера выделенных в текущий момент элементов данных.
boolean programmatically
— определяет, были ли элементы выделены программно (true) или нет (false).
Отображать имя
– Если опция выбрана, то имя фигуры будет отображаться в графическом редакторе.
Чтобы изменить способ отображения данных на гистограмме
Закончив создание гистограммы, последовательно добавьте на нее те объекты сбора данных двумерной гистограммы, которые вы хотите отображать на данной гистограмме.
Новая гистограмма уже содержит элемент данных. Если вы хотите добавить еще один элемент данных, выполните следующие шаги:
Если по какой-то причине вам больше не нужно отображать тот или иной объект данных на гистограмме, вы можете удалить его с гистограммы.
ГистограммаНаглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма. Гистограмма — это способ графического изображения интервальных распределений вариант при непрерывном варьировании признака. Гистограмма распределения применяется только для изображения интервального вариационного ряда. Гистограмма представляет собой столбчатый график, построенный по полученным за определенный период (например, за неделю или за месяц) данным, которые разбиваются на несколько интервалов; число данных, попадающих в каждый из интервалов (частота), выражается высотой столбика. Данные для построения гистограммы собирают в течение длительного периода — недели, месяца, года и т. д. Гистограмма
– это серия столбиков одинаковой ширины, но разной высоты, показывающая
рассеяние и распределение данных. Ширина столбика – это интервал в диапазоне
наблюдений, высота – количество данных, приходящихся на тот или иной интервал,
т.е. частость. По существу, гистограмма отображает
распределение исследуемого показателя. Гистограмма позволяет оценить характер
рассеивания показателя и разобраться в том, на чём следует сосредоточить усилия
по улучшению. Гистограмму используют для изображения только интервальных рядов. Признак называется непрерывно варьирующим, если его значения отличаются друг от друга на сколь угодно малую величину, т.е. признак может принимать любые значения в некотором интервале. Непрерывный вариационный ряд такого признака называется интервальным (см. табл. 3 и 4). Таблица 3 Общий вид интервального вариационного ряда частот
Таблица 4 Общий вид интервального вариационного ряда частостей
Просматривая результаты проведенных наблюдений,
определяют, сколько значений вариантов попало в каждый конкретный интервал. Для того чтобы интервальный вариационный ряд не был громоздким и в то же время позволял выявить характерные черты изменения значений случайной величины, обычно число частичных интервалов выбирают от 7 до 10. Длина частичного интервала (интервальная разность) зависит от размаха варьирования и выбранного числа интервалов Если окажется, что h – дробное число, то за длину частичного интервала следует брать либо ближайшее целое число, либо ближайшую простую дробь. Для упрощения последующих расчетов интервальный вариационный ряд можно заменить условно дискретным. В этом случае серединное значение i-го интервала принимают за вариант xi, а соответствующую интервальную частоту mi– за частоту этого интервала. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению (плотность частоты). Площадь частичного i-го прямоугольника равна — сумме частот вариант, попавших в i-ый интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n Если
соединить середины верхних оснований прямоугольников отрезками прямой, то можно
получить полигон того же распределения, который будет являться выборочным
аналогом дифференциальной функции распределения f(x). Гистограммой относительных частотназывают ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению (плотность относительной частоты). Площадь частичного i-го прямоугольника равна — сумме относительных частот вариант, попавших в i — ый интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. Характерные типы гистограмм показаны на рис. .
Рис. Характерные типы гистограмм На рис.,а показан обычный тип гистограммы с двусторонней симметрией, что указывает на стабильность процесса. На рис.,б в распределении имеется два пика (двугорбая гистограмма). Такая гистограмма получается при объединении двух распределений, например, в случае двух видов сырья, изменения настройки процесса или объединения в одну партию изделий, обработанных на двух разных станках. Требуется расслоение продукции. На рис.,в показана гистограмма с обрывом. Такое распределение получается, когда невозможно получить значение ниже (или выше) некоторой величины. Подобное распределение имеет место также, когда из партии исключены все изделия с показателем ниже (и/или выше) нормы, т.е. изначально это была партия с большим количеством дефектных изделий. Такое же распределение получается, когда измерительные приборы были неисправны. На рис.,г показана гистограмма с островком. Получается при ошибках в измерениях, или когда некоторое количество дефектных изделий перемешано с доброкачественными. На рис. На рис.,е показана гистограмма в форме плато. Получается, когда объединяются несколько распределений при небольшой разнице средних значений. В этом случае требуется расслоение. Гистограмма строится в следующем порядке. Систематизируют данные, собранные, например, за 10 дней или за месяц. Число данных должно быть не менее 30-50, оптимальное число — порядка 100. Если их оказывается более 300, затраты времени на их обработку оказываются слишком большими. Следующий шаг — определение наибольшего L и наименьшего S значений данных. При большом числе значений (порядка 100) определение L и S затруднительно, поэтому вначале определяют наибольшее и наименьшее значения в каждом десятке значений, а затем среди полученных значений определяют L и S. Интервал между наибольшим и наименьшим значениями делят на соответствующие участки. Число участков должно примерно соответствовать корню квадратному из числа данных. При числе данных З0-50 число участков должно быть равно 5-7, при числе данных 50-100-6-10; при числе данных 100-2008-15. Далее определяют ширину участка h. Разность между L и S делят на число участков и полученное число округляют. Например, для анализа результатов контроля толщины пластин при L=11,8 мм,S=7,1 мм и числе участков 10 получим h=(11,8-7,1):10=0,47 мм. Округляют это число до 0,5 мм и получают ширину участка h=0,5 мм. Значения границ участков определяют следующим образом. Вначале находят наименьшее граничное значение для первого участка из условия S — единица измерения/2. В приведенном примере S=7,1 мм; единица измерения составляет 0,1 мм . Таким образом, наименьшее граничное значение для первого участка оказывается равным 7,1 мм — 0,1 мм/2 = 7,05 мм Прибавляя к полученному значению ширину участка h=0,5 мм, находим что первый участок занимает интервал на оси абсцисс от 7,05 мм до 7,55 мм . В интервал последнего участка (11,55-12,05) входит наибольшее значение L. Следующий шаг — определение центральных значений для участков. Центральное значение для участка определяют по формуле Сумма граничных значений участка/2=нижнее граничное значение участка+верхнее граничное значение участка/2 В приведенном примере центральное значение для первого участка равно 7,05+7,55/2=7,3 мм Центральные значения последующих участков находятся прибавлением ширины участка h=0,5 мм к значению для предыдущего участка. В размеченные описанным выше образом интервалы участков размещают данные измеренных значений толщины пластин в каждом интервале, которые составляют частоту f попадания этих данных в соответствующий интервал (табл. 9). Таблица 9
Сумма (f)100 Последним шагом является построение графика гистограммы. Поскольку гистограмма выражает условия процесса за период, в течение которого были получены данные, важную информацию может дать форма распределения гистограммы в сравнении с контрольными нормативами. Режим «Гистограмма» Пакета Анализа Excel сслужит для вычисления частот попадания данных в указанные границы интервалов, а также для построения гистограммы интервального вариационного ряда распределения.
в начало |
Изучаем Гистограмму Гистограмма –… — Фотостудия Pandora
Изучаем Гистограмму
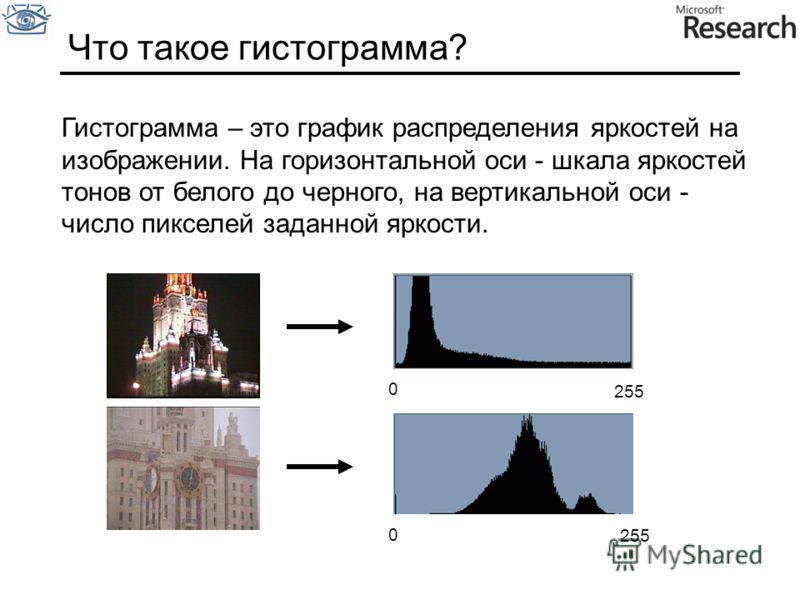
Гистограмма – это диаграмма по тоновому распределению пикселей на снимке.
Слева направо (по горизонтали) указана яркость, а снизу вверх (по вертикали) количества площади фотографии той или иной тональности. Часто говорят, что вертикальные столбцы просто показывают соотношения количества пикселов той или иной тональности. То есть, диаграмма показывает сколько на снимке преобладает светлых или темных оттенков, сколько зеленых или красных или других оттенков цветов на снимке больше. Гистограммы бывают разные. В фотографии, в основном, используют трех типов:
Гистограммы бывают разные. В фотографии, в основном, используют трех типов:
1. Общая гистограмма экспозиции
2. Гистограмма по каждому из трех основных цветов, такую гистограмму часто называют RGB — red, green, blue — красный, зеленый, синий
3. Гибридная гистограмма для общей экспозиции и для основных цветов (часто, просто на гистограмму по экспозиции налаживают гистограму RGB)
Гистограмму часто разделяют на 3-4 части. Часть гистограммы с самого левого края называют «тенями» или темными тонами, так как эта область показывает на сколько сильны темные участки изображения. Крайнюю правую часть «светАми» или светлыми тонами, так эта часть показывает сколько количество светлых участков на гистограмме. Середину – «полутенями» или средними тонами. Самую крайнюю правую часть иногда называют областью засветки, если в самом крайнем правом углу имеется всплеск на гистограмме, то, скорее всего, фотография переекспонированная.
Чем полезна гистограмма?
1. С ее помощью легко контролировать недодержки (недоэкспонированное изображение) и пересветы (переэкспонированное). При переэкспонировании пик (вершина на диаграмме) будет виден в правой стороне гистограммы, а при недоэкспонировании пик будет наблюдаться в левой стороне гистограммы.
2. Точно подстраивать экспозицию
3. Контролировать цветовые каналы на фотографии. С помощью гистограммы можно определить цветовую насыщенность снимка.
4. Контролировать контраст. По гистограмме можно легко угадать на сколько контрастная картинка.
Когда я использую гистограмму?
Лично я использую гистограмму всего в двух случаях – когда нужно проверить экспозицию снимка при ярком освещении, когда самого снимка на дисплее камеры практически не видно. Это могут быть условия летнего пляжа или яркого солнца в горах. При таких условиях просто не видно того, что на снимке, потому, я смотрю на гистограмму, чтобы приблизительно прикинуть отклонения экспозиции. И, во-вторых я использую гистограмму при редактировании фотографий, очень удобно определять ключ, в котором сделана фотография по гистограмме, а иногда подгонять фото с помощью корректировки части кривой гистограммы. Например, иногда я просто беру «света» в гистограмме и ползунком двигаю их влево – двигаю в тени, фотография получается без пересветов.
Например, иногда я просто беру «света» в гистограмме и ползунком двигаю их влево – двигаю в тени, фотография получается без пересветов.
Тональный Диапазон
Область, в которой находится большинство значений яркости, называется «тональным диапазоном». Тональный диапазон может радикально отличаться от изображения к изображению, и потому выработать ощущение того, как числа соотносятся с яркостями, зачастую критически важно, как до съёмки, так и по её результатам. Не существует «идеальной гистограммы», которой должны соответствовать все изображения; гистограммы должны соответствовать тональному диапазону сцены и замыслу фотографа.
Контраст
Гистограмма может также описать степень контраста в изображении. Контраст является измерением разницы яркостей между светлыми и тёмными частями изображения. Широкие гистограммы отражают сцены со значительным контрастом, тогда как узкие гистограммы означают, что контраст снижен, и изображение может оказаться плоским или скучным. Это может быть вызвано любой комбинацией предметов съёмки и условий освещения. Снимки, сделанные в тумане, будут иметь малый контраст, тогда как те, что были сняты в ярком дневном свете, окажутся высококонтрастными.
Контраст может иметь значительное визуальное влияние на изображение, выделяя текстуры, как показано на снимке выше. На высококонтрастной воде тени глубже, а свет более выраженный, порождая текстуру, которая «торчит» из снимка.
Выводы:
Гистограмма – полезный инструмент фотографа. Пользоваться гистограмой или нет – решать Вам, можно прекрасно обходиться и без нее, или все же разобраться в ее свойствах и использовать ее при обработке фотографии или корректировке точной экспозиции.
Игорь Бурба
Представляйте данные исследования с использованием блочных диаграмм и гистограмм
Гистограммы и блочные диаграммы часто используются для визуального представления данных исследований. Поэтому важно понимать разницу между ними. Использование блочной диаграммы или гистограммы зависит от характера данных и интерпретации, которую исследователь хотел бы предоставить.
Поэтому важно понимать разницу между ними. Использование блочной диаграммы или гистограммы зависит от характера данных и интерпретации, которую исследователь хотел бы предоставить.
Блочные диаграммы и как их читать
Блочная диаграмма используется для построения графика распределения данных. Блочные диаграммы также называются диаграммами размаха. Эти графики кодируют пять характеристик распределения данных, показывая читателю их положение и длину. Блок варьирует от Q1 (первый квартиль) распределения до Q3 (третий квартиль) распределения, а диапазон представлен IQR (межквартильный диапазон). Медиана обозначена линией поперек блока. Размахи на блочных диаграммах простираются от Q1 и Q3 до самых крайних точек данных. В свою очередь, каждое из этих выпадающих значений отмечено знаком. Как альтернатива, максимальные и минимальные значения могут быть использованы в качестве конечных точек размаха.
Чтение блочных диаграмм не так сложно, как может показаться. Медиана, представленная линией, проходящей через блок, является серединой набора данных. Это означает, что 50% данных больше медианы. Верхний размах представляет значения выше среднего. Выпадающие значения – это точки над верхним размахом. Аналогичная интерпретация применяется к нижнему размаху и выпадающим значениям. Блочные диаграммы также могут представлять ассиметричные распределения в наборе данных. Положение медианы на блоке показывает, насколько много данных находится над или под ней.
Благодарим за представление изображения: Натан Яу из Flowing Data
Гистограммы и как их читать
Гистограммы предназначены для представления категориальных переменных и подходят для подсчета. Гистограммы отображают и сравнивают частоту, число или другие показатели (например, среднее) для разных категорий данных. Однако непрерывные данные лабораторных исследований, исследований на людях и исследований на животных часто представлены в виде гистограмм. Гистограммы – это часто используемые графики, потому что их легко интерпретировать и просто создавать. Они полезны для отображения номинальных или порядковых категорий. Порядковые категории – это данные, которые ранжируются (например, от очень хорошего до очень плохого), в то время как номинальные данные представляют качественные или описательные данные (например, страна рождения, предмет, изучаемый в университете). Существуют различные типы гистограмм, такие как горизонтальные гистограммы, сгруппированные гистограммы и гистограммы с накоплением. Исследователи должны создавать свои графики, соблюдая несколько правил, чтобы представить свои работы в четкой и эффективной форме.
Они полезны для отображения номинальных или порядковых категорий. Порядковые категории – это данные, которые ранжируются (например, от очень хорошего до очень плохого), в то время как номинальные данные представляют качественные или описательные данные (например, страна рождения, предмет, изучаемый в университете). Существуют различные типы гистограмм, такие как горизонтальные гистограммы, сгруппированные гистограммы и гистограммы с накоплением. Исследователи должны создавать свои графики, соблюдая несколько правил, чтобы представить свои работы в четкой и эффективной форме.
Интерпретация гистограмм начинается с наблюдения высоты гистограммы относительно соответствующего значения на оси Y. Различия в высотах столбцов можно определить, обратившись к оси Y. Второй шаг – сравнить группировки столбцов. Некоторые гистограммы могут иметь столбцы, сгруппированные в кластеры. В этом случае сравните столбцы внутри кластеров, чтобы понять, как каждый набор данных в подкатегории сравнивается с другими наборами данных. Кроме того, вы также можете проверить диапазон, вычитая самое низкое значение (обозначенное самым коротким столбцом) из наибольшего значения (обозначенного самым длинным столбцом).
Какой из этих графиков следует использовать?
Какой тип данных вы будете представлять? Как вы хотите представить свои данные? Вам нужно ответить на такие вопросы, прежде чем выбирать между этими двумя типами.
Некоторые авторы утверждают, что гистограммы не должны использоваться, в то время как другие утверждают, что должны появиться новые форматы для представления данных. Сгруппированные гистограммы полезны, например, для отображения бюджетов для двух домохозяйств. Одно из распространенных применений гистограмм – показать соотношение одного значения к другому.
С другой стороны, блочные диаграммы полезны для построения различных наборов данных из независимых источников. Пример включает в себя сравнение результатов тестов между различными университетами, изменение данных (до и после) в результате процесса или данные с разных машин, производящих один и тот же продукт. Блочные диаграммы – это хороший способ представить распределение ваших данных, особенно если вы стремитесь показать другие значения помимо среднего.
Блочные диаграммы – это хороший способ представить распределение ваших данных, особенно если вы стремитесь показать другие значения помимо среднего.
Связывание данных ваших исследований
Это просто, если вы решите, какой тип графика лучше всего подходит для ваших данных. Например, если ваши данные ассиметричны, можно использовать блочную диаграмму. Ваш читатель сможет определить, смещены ли данные влево или вправо, в зависимости от блока полосы выше и ниже средней линии. Данные из ANOVA также могут быть показаны с помощью блочной диаграммы. Если ваши данные, в основном, носят описательный характер, и вы хотите показать пропорции, то гистограмма – ваш лучший выбор.
Какой бы путь вы ни выбрали, важно понимать полезность этих графиков. Ваш анализ данных исследования является основной частью отчета об исследовании – делайте это эффективно! Дайте нам знать, что вы думаете об использовании блочной диаграммы и гистограммы при представлении результатов!
Определение гистограммы
Что такое гистограмма?
Гистограмма — это графическое представление, которое упорядочивает группу точек данных в определенные пользователем диапазоны. По внешнему виду похожая на гистограмму, гистограмма уплотняет ряд данных в легко интерпретируемый визуальный элемент, беря множество точек данных и группируя их в логические диапазоны или интервалы.
Ключевые выводы
- Гистограмма — это представление данных в виде гистограммы, которое объединяет диапазон результатов в столбцы по оси x.
- Ось Y представляет количество или процент вхождений в данные для каждого столбца и может использоваться для визуализации распределения данных.
- В торговле гистограмма MACD используется техническими аналитиками для обозначения изменений импульса.
Как работают гистограммы
Гистограммы обычно используются в статистике, чтобы продемонстрировать, сколько переменных определенного типа встречается в определенном диапазоне. Например, перепись населения, ориентированная на демографию страны, может использовать гистограмму, чтобы показать, сколько людей находится в возрасте от 0 до 10, от 11 до 20, 21-30, 31-40, 41-50 и т. Д.Эта гистограмма будет похожа на приведенный ниже пример.
Например, перепись населения, ориентированная на демографию страны, может использовать гистограмму, чтобы показать, сколько людей находится в возрасте от 0 до 10, от 11 до 20, 21-30, 31-40, 41-50 и т. Д.Эта гистограмма будет похожа на приведенный ниже пример.
Аналитик может настраивать гистограммы несколькими способами. Первый — изменить интервал между ведрами. В приведенном выше примере есть 5 сегментов с интервалом в десять. Это можно было бы изменить, например, на 10 сегментов с интервалом 5.
Другое соображение — как определить ось y. Самая простая метка — использовать частоту встречаемости, наблюдаемую в данных, но вместо этого можно также использовать процент от общего количества или плотность.
Изображение Джули Банг © Investopedia 2019Гистограммы и столбчатые диаграммы
И гистограммы, и гистограммы обеспечивают визуальное отображение с использованием столбцов, и люди часто используют эти термины как синонимы. С технической точки зрения гистограмма представляет собой частотное распределение переменных в наборе данных. С другой стороны, гистограмма обычно представляет собой графическое сравнение дискретных или категориальных переменных.
Пример: гистограмма MACD
Технические трейдеры могут быть знакомы с гистограммой расхождения конвергенции скользящих средних (MACD), популярным техническим индикатором, который показывает разницу между линией MACD и сигнальной линией.
Например, если разница между двумя линиями составляет 5 долларов, гистограмма MACD графически представляет эту разницу. Гистограмма MACD нанесена на график, чтобы трейдеру было легко определить импульс конкретной ценной бумаги.
Полоса гистограммы является положительной, когда линия MACD находится выше сигнальной линии, и отрицательной, когда линия MACD находится ниже сигнальной линии. Возрастающая гистограмма MACD указывает на увеличение восходящего импульса, в то время как убывающая гистограмма используется для обозначения нисходящего импульса.
Торговля с гистограммой MACD
Трейдеры часто упускают из виду гистограмму MACD при использовании этого индикатора для принятия торговых решений. Слабость использования индикатора MACD в его традиционном понимании, когда линия MACD пересекает сигнальную линию, заключается в том, что торговый сигнал отстает от цены. Поскольку две линии являются скользящими средними, они не пересекаются до тех пор, пока не произойдет движение цены. Это означает, что трейдеры отказываются от части этого начального движения.
Гистограмма MACD помогает решить эту проблему, генерируя более ранние сигналы входа.Трейдеры могут отслеживать длину столбцов гистограммы по мере их удаления от нулевой линии. Индикатор генерирует торговый сигнал, когда столбец гистограммы короче предыдущего бара. После того, как меньшая полоса гистограммы завершится, трейдеры открывают позицию в направлении снижения гистограммы.
Другие технические индикаторы следует использовать вместе с гистограммой MACD, чтобы повысить надежность сигнала. Более того, трейдеры должны разместить стоп-лосс, чтобы закрыть сделку, если цена ценной бумаги не изменится, как ожидалось.
| 1.
Исследовательский анализ данных 1,3. Методы EDA 1.3.3. Графические методы: алфавитный | |
| Назначение: Обобщение одномерного набора данных | Назначение гистограммы
(Камеры)
графически суммировать распределение одномерного
набор данных. Гистограмма графически показывает следующее:
Эти особенности ясно указывают на то, что
правильная модель распределения данных. Примеры В разделе показан внешний вид ряда общих функций выявляется по гистограммам. |
| Образец участка | |
| Приведенный выше график представляет собой гистограмму скорость света Майкельсона набор данных. | |
| Определение | Наиболее распространенный вид гистограммы получается путем разбиения
диапазон данных в бункерах равного размера (называемых классами).
Затем для каждого бина количество точек из набора данных, которые
попадают в каждую корзину.То есть
Кумулятивная гистограмма — это вариант гистограммы на которой по вертикальной оси отложены не только значения отдельная корзина, но дает подсчет для этой корзины плюс все ячейки для меньших значений переменной ответа. И гистограмма, и кумулятивная гистограмма имеют дополнительный вариант, при котором подсчеты заменены нормализованными счетчиками. Названия этих вариантов относительная гистограмма и относительная кумулятивная гистограмма. Есть два распространенных способа нормализовать счет.
|
| Вопросы | Гистограмма может быть использована для ответа на следующие вопросы:
|
| Примеры |
|
| Связанные методы | Коробчатая диаграмма Вероятностная диаграмма Приведенные ниже методы не обсуждаются в Руководстве.Однако по назначению они похожи на гистограмму. Дополнительная информация о них содержится в Палаты и Ссылки Скотта. График частот |
| Пример использования | Гистограмма представлена в счетчик теплового потока тематическое исследование данных. |
| Програмное обеспечение | Гистограммы доступны в большинстве статистических программное обеспечение.Они также поддерживаются в большинстве случаев. программы для построения графиков, электронных таблиц и бизнес-графики. |
| Обсуждение Унимодальных и Бимодальных | Гистограмма, показанная выше, иллюстрирует данные бимодального (2 пика)
распределение. В отличие от предыдущего примера, этот пример иллюстрирует бимодальность из-за не лежащей в основе детерминированной модели, а бимодальность из-за смеси вероятностных моделей.В этом случае каждый мод имеет грубую колоколообразную составляющую. Можно было легко представить, что гистограмма выше генерируется процессом состоящий из двух нормальных распределений с одинаковым стандартным отклонением но с двумя разными местоположениями (одно с центром примерно на 9,17 а другой — около 9,26). Если это так, тогда задача исследования состоит в том, чтобы физически определить, почему два похожих, но отдельных подпроцесса. | Рекомендуемые дальнейшие действия | Если гистограмма показывает, что данные могут быть подходящими
со смесью двух нормальных распределений рекомендуется следующий
шаг: Подобрать модель нормальной смеси, используя метод наименьших квадратов или максимальная вероятность.Общая модель нормального перемешивания:
Независимо от того, используется ли максимальное правдоподобие или наименьшие квадраты, качество посадки зависит от хороших начальных значений. Для смеси двух нормалей можно использовать гистограмму для первоначальной оценки местоположения и масштаба параметры двух нормальных распределений. И код Dataplot, и Код R можно использовать для смесь двух нормалей. |
Примеры, типы и способы построения гистограмм
Что такое гистограмма?
Гистограмма используется для суммирования дискретных или непрерывных данных.Другими словами, он обеспечивает визуальную интерпретацию данных. Представление данных Аналитики передают результаты финансового анализа руководству, инвесторам и деловым партнерам. Это требует сосредоточения внимания на основных моментах, фактах числовых данных, показывая количество точек данных, которые попадают в указанный диапазон значений (называемый «ячейками»). Он похож на вертикальную гистограмму. Однако гистограмма, в отличие от вертикальной гистограммы, не показывает промежутков между столбцами.
Части гистограммы
- Заголовок: Заголовок описывает информацию, содержащуюся в гистограмме.
- Ось X: Ось X — это интервалы, показывающие шкалу значений, под которую попадают измерения.
- Ось Y: Ось Y показывает, сколько раз значения встречались в пределах интервалов, установленных осью X.
- Полосы: Высота полосы показывает, сколько раз значения встречались в пределах интервала, а ширина полосы показывает покрытый интервал. Для гистограммы с одинаковыми ячейками ширина должна быть одинаковой для всех столбцов.
Важность гистограммы
Создание гистограммы обеспечивает визуальное представление распределения данных. Гистограммы могут отображать большой объем данных и функцию частоты. Функция частоты. Функция частоты относится к категории статистических функций Excel. Функция рассчитает и вернет частотное распределение. Мы можем использовать его, чтобы получить частоту значений в наборе данных. значений данных. Функция medianMEDIAN Функция MEDIAN относится к категории Статистических функций Excel.Функция вычислит среднее значение заданного набора чисел. Медиана может быть определена как среднее число группы чисел. То есть половина чисел возвращает значения, которые больше медианы, и распределение данных можно определить с помощью гистограммы. Кроме того, он может отображать любые выбросы или пробелы в данных.
Распределения гистограммы
Нормальное распределение: При нормальном распределении точки на одной стороне от среднего Функция AVERAGE Расчет среднего значения в Excel.Функция СРЕДНИЙ относится к Статистическим функциям. Он вернет среднее значение аргументов. Он используется для вычисления среднего арифметического заданного набора аргументов. Финансовому аналитику эта функция полезна для определения среднего числа. с такой же вероятностью, как и на другой стороне среднего.
Бимодальное распределение: В бимодальном распределении есть два пика. При бимодальном распределении данные следует разделять и анализировать как отдельные нормальные распределения.
Скошенное вправо распределение: Скошенное вправо распределение также называется положительно смещенным распределением. В распределении со смещением вправо большое количество значений данных находится в левой части с меньшим количеством значений данных в правой части. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в левой части гистограммы. Например, граница 0.
Скошенное влево распределение: Скошенное влево распределение также называется отрицательно скошенным распределением.В распределении со смещением влево большое количество значений данных находится в правой части, а меньшее количество значений данных — в левой. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в правой части гистограммы. Например, граница, такая как 100.
Случайное распределение: Случайное распределение не имеет видимой закономерности и имеет несколько пиков. В гистограмме случайного распределения может быть случай, когда были объединены разные свойства данных.Поэтому данные следует разделять и анализировать отдельно.
Пример гистограммы
Джефф — менеджер филиала в местном банке. Недавно Джефф получил отзывы клиентов, в которых говорилось, что время ожидания обслуживания клиента представителем службы поддержки слишком велико. Джефф решает наблюдать и записывать время, потраченное каждым клиентом на ожидание. Вот его результаты наблюдения и записи времени ожидания, потраченного 20 клиентами:
Соответствующая гистограмма с 5-секундными ячейками (5-секундные интервалы) будет выглядеть следующим образом:
Мы видим, что:
- Есть 3 клиента ожидают между 1 и 35 секундами
- Есть 5 клиентов ожидают между 1 и 40 секундами
- Есть 5 клиентов ожидают между 1 и 45 секунд
- Есть 5 клиентов ожидают между 1 и 50 секундами
- Есть 2 клиента ожидают между 1 и 55 секундами
Джефф может заключить, что большинство клиентов ждут между 35.1 и 50 секунд.
Как создать гистограмму
Давайте создадим нашу собственную гистограмму. Загрузите соответствующий файл шаблона Excel для этого примера.
Шаг 1: Откройте окно анализа данных. Это можно найти на вкладке данных как Анализ данных :
Шаг 2: Выбрать гистограмму :
Введите соответствующий шаг диапазон ввода и диапазон бункера.В этом примере диапазоны должны быть:
- Диапазон ввода: $ C $ 10: $ D $ 19
- Диапазон корзины: $ F $ 9: $ F $ 24
Убедитесь, что «Вывод диаграммы» отмечен и нажмите «ОК».
Загрузите пример шаблона, чтобы создать его самостоятельно!
Ссылки по теме
CFI является официальным поставщиком глобальной сертификации финансового моделирования и оценки (FMVA) ™ FMVA® Certification Присоединяйтесь к более 850 000 студентов, которые работают в таких компаниях, как Amazon, J.П. Морган и программа сертификации Ferrari, призванная помочь любому стать финансовым аналитиком мирового уровня. Чтобы продолжить продвижение по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:
- Типы графиков в Excel Типы графиков 10 типов графиков для представления данных, которые вы должны использовать — примеры, советы, форматирование, как использовать эти различные графики для эффективного общение и в презентациях. Загрузите шаблон Excel с гистограммой, линейной диаграммой, круговой диаграммой, гистограммой, водопадом, диаграммой рассеяния, комбинированной диаграммой (столбчатая и линейная), измерительной диаграммой,
- Создание информационной панели в Excel Создание информационной панели в ExcelЭто руководство по созданию приборной панели в Excel научит вас, как создать красивую дашборд в Excel, используя приемы визуализации данных от профессионалов.В
- Ярлыки Excel Ярлыки ПК и MacExcel Ярлыки MacExcel ПК — Список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета. Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
- Список функций Excel ФункцииСписок наиболее важных функций Excel для финансовых аналитиков.Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel.
Гистограмма — краткое введение
сообщить об этом объявлении Рубен Герт ван ден Берг в разделе «Диаграммы и статистика» от А до Я Гистограмма — это диаграмма, показывающая частоты для
интервалов значений метрической переменной.
Такие интервалы называются «ячейками», и все они имеют одинаковую ширину. В приведенном выше примере ширина корзины составляет 25 долларов. Таким образом, он показывает, сколько людей зарабатывают от 800 до 825 долларов, от 825 до 850 долларов и так далее.
Обратите внимание, что режим этого частотного распределения составляет от 900 до 925 долларов, что встречается примерно 150 раз.
Гистограмма — пример
Компания хочет знать, как ежемесячная заработная плата распределяется между 1110 сотрудниками, имеющими рабочие места на уровне оперативного, среднего или высшего руководства. На скриншоте ниже показано, как выглядят их необработанные данные.
Поскольку эти зарплаты частично основаны на комиссионных, в основном у каждого сотрудника немного разная зарплата. Теперь, как мы можем получить представление о распределении заработной платы?
Гистограммаи столбчатая диаграмма
Сначала мы пробуем построить гистограмму месячных зарплат.Результат показан ниже.
Наша гистограмма бесполезна. Единственное, что мы извлекаем из этого, это то, что большинство зарплат выплачиваются только один раз, а некоторые — дважды. Основная проблема здесь в том, что гистограмма показывает частоту , с которой каждое отдельное значение встречается в данных .
Важно отметить, что первый интервал имеет ширину (832 доллара — 802 доллара =) 30 долларов. Последний интервал представляет (1206 — 1119 долларов =) 87 долларов. Но оба имеют одинаковую ширину в миллиметрах на вашем экране. Это говорит нам о том, что
ось x не имеет линейного масштаба
что делает эту диаграмму непригодной для такой метрической переменной, как ежемесячная зарплата.
Гистограмма — базовый пример
Поскольку наша гистограмма не очень хороша, мы теперь пытаемся запустить гистограмму на наших данных. Результат показан ниже.
Эта диаграмма выглядит намного полезнее, но как она была создана? Итак, мы распределили зарплату каждого сотрудника с интервалом в 25 долларов (800-825 долларов, 825-850 долларов и так далее). Затем мы посмотрели количество сотрудников, попадающих в каждый такой интервал. Мы визуализируем эти частоты в виде столбцов на графике.
Важно отметить, что ось нашей диаграммы имеет линейный масштаб : каждый интервал в 25 долларов соответствует одинаковой ширине в миллиметрах, даже если он не содержит сотрудников.График, который мы получили, известен как гистограмма, и, как мы увидим через минуту, она очень полезна.
Гистограмма — ширина ячейки
Ширина бина — это ширина интервалов
, частоты которых мы визуализируем на гистограмме.
В нашем первом примере использовалась корзина шириной 25 долларов; первая полоса представляет собой количество зарплат от 800 до 825 долларов и так далее. Эта ширина бункера в 25 долларов — это скорее , произвольный выбор . На рисунке ниже показаны гистограммы для одних и тех же данных с использованием разной ширины бинов.
Хотя разная ширина бинов кажется разумной, мы считаем, что 10 долларов — это довольно мало, а 100 долларов — довольно много для имеющихся данных. Кажется, больше подходят 25 или 50 долларов.
Гистограммы — почему они так полезны?
Почему гистограммы так полезны? Во-первых, диаграммы намного нагляднее, чем таблицы; посмотрев на диаграмму в течение 10 секунд, вы сможете узнать о своих данных гораздо больше, чем после 10 секунд просмотра соответствующей таблицы. Как правило, диаграммы передают информацию о наших данных быстрее, чем таблицы, , хотя и менее точно.
Вдобавок к этому гистограммы также дают нам более более полную информацию о наших данных. Помните, что вы можете разумно оценить среднее значение переменной, стандартное отклонение, асимметрию и эксцесс по гистограмме. Однако вы не можете оценить гистограмму переменной на основе вышеупомянутой статистики. Проиллюстрируем это на примере.
Гистограмма и описательная статистика
Допустим, мы находим в наших данных две возрастные переменные и не уверены, какую из них следует использовать.Мы сравниваем базовую описательную статистику для обеих переменных, и они выглядят почти одинаково.
Итак, можем ли мы сделать вывод, что обе возрастные переменные имеют примерно одинаковое распределение? Если вы так думаете, взгляните на их гистограммы, показанные ниже.
Разделенная гистограмма — частоты
Каждый из 1110 сотрудников в наших данных имеет уровень должности: операционный, средний менеджмент или высшее руководство. Если мы хотим сравнить распределение заработной платы между этими тремя группами, мы можем проверить разделенную гистограмму: мы создаем отдельную гистограмму для каждого уровня должности, и эти три гистограммы имеют идентичных оси .Результат показан ниже.
Наша разделенная гистограмма — отстой. Проблема в том, что размеры групп очень неравны, и они линейно связаны с площадями поверхности наших гистограмм. В результате площадь для высшего руководства (n = 10) составляет только 1% от площади для «оперативного» (n = 1000). Гистограмма для высшего руководства настолько мала, что ее больше не видно.
Разделенная гистограмма — проценты
Мы только что видели, что разделенная гистограмма с частотами бесполезна для имеющихся данных.Означает ли это, что мы не можем сравнивать распределение заработной платы по уровням должностей? Неа. Если мы выберем процентное соотношение внутри групп уровня должностей, то каждая гистограмма будет иметь одинаковую площадь поверхности 100%. Результат показан ниже.
Гистограмма — Заключительные примечания
Этот учебник был направлен на объяснение того, что такое гистограммы и чем они отличаются от гистограмм. На наш взгляд, гистограммы — одни из самых полезных диаграмм для метрических переменных. С помощью подходящего программного обеспечения (такого как SPSS) вы можете очень быстро создавать и проверять гистограммы, и это отличный способ познакомиться с вашими данными.
Статистика: Сила из данных! Типы графиков: гистограммы и гистограммы
Архивный контент
Информация, помеченная как архивная, предназначена для справочных, исследовательских или учетных целей. Он не регулируется веб-стандартами правительства Канады и не изменялся и не обновлялся с момента его архивирования. Свяжитесь с нами, чтобы запросить формат, отличный от доступных.
Гистограмма — популярный инструмент построения графиков. Он используется для суммирования дискретных или непрерывных данных, измеренных в интервальной шкале.Его часто используют для иллюстрации основных особенностей распределения данных в удобной форме. Гистограмма делит диапазон возможных значений в наборе данных на классы или группы. Для каждой группы создается прямоугольник с базовой длиной, равной диапазону значений в этой конкретной группе, и площадью, пропорциональной количеству наблюдений, попадающих в эту группу. Это означает, что прямоугольники будут нарисованы неодинаковой высоты. Гистограмма выглядит как вертикальная гистограмма, но когда переменные непрерывны, между столбцами нет промежутков.Однако, когда переменные дискретны, между полосами следует оставлять промежутки. Рисунок 1 — хороший пример гистограммы.
Вертикальная гистограмма и гистограмма различаются следующим образом:
- На гистограмме частота измеряется областью столбца.
- На вертикальной гистограмме частота измеряется высотой полосы.
Характеристики гистограммы
Обычно гистограмма имеет столбцы одинаковой ширины, хотя это не тот случай, когда интервалы классов различаются по размеру.Выбор подходящей ширины полосок для гистограммы очень важен. Как вы можете видеть в приведенном выше примере, гистограмма состоит просто из набора вертикальных полос. Значения изучаемой переменной измеряются в арифметической шкале по горизонтальной оси абсцисс. Полосы имеют одинаковую ширину и соответствуют равным интервалам классов, а высота каждой полоски соответствует частоте класса, который она представляет.
Гистограмма используется для переменных, значения которых являются числовыми и измеряются в интервальной шкале.Обычно он используется при работе с большими наборами данных (более 100 наблюдений). Гистограмма также может помочь обнаружить любые необычные наблюдения (выбросы) или любые пробелы в данных.
Гистограммы
Гистограмма или многоугольник частот — это граф, образованный соединением средних точек вершин столбцов гистограммы. Эти графики используются только при отображении данных из непрерывных переменных, показанных на гистограмме.
Гистограмма сглаживает резкие изменения, которые могут появиться на гистограмме, и полезна для демонстрации непрерывности изучаемой переменной.Рисунки 2 и 3 являются хорошими примерами гистограмм.
В отличие от рисунка 2, на этой гистограмме есть промежутки между полосами. Просто взглянув на эту иллюстрацию, читатель может сразу сказать, что пробелы означают, что переменные дискретны. Таким образом, гистограммы помогают читателям определить, какой тип переменных использовался.
Что такое гистограмма и как ее использовать?
Гистограмма — это тип графика, который имеет широкое применение в статистике.Гистограммы обеспечивают визуальную интерпретацию числовых данных, указывая количество точек данных, лежащих в пределах диапазона значений. Эти диапазоны значений называются классами или ячейками. Частота данных, попадающих в каждый класс, отображается с помощью столбца. Чем выше полоса, тем выше частота значений данных в этой ячейке.
Гистограммы и гистограммы
На первый взгляд гистограммы очень похожи на гистограммы. Оба графика используют вертикальные полосы для представления данных.Высота полосы соответствует относительной частоте количества данных в классе. Чем выше полоса, тем выше частота данных. Чем ниже полоса, тем ниже частота данных. Но внешность обманчива. На этом сходство между двумя видами графов заканчивается.
Причина того, что эти виды графиков различаются, связана с уровнем измерения данных. С одной стороны, гистограммы используются для данных на номинальном уровне измерения.Гистограммы измеряют частоту категориальных данных, и классы для гистограммы являются этими категориями. С другой стороны, гистограммы используются для данных, которые находятся, по крайней мере, на порядковом уровне измерения. Классы гистограммы — это диапазоны значений.
Еще одно ключевое различие между гистограммами и гистограммами связано с порядком столбцов. На гистограмме принято менять расположение полос в порядке убывания высоты. Однако столбцы на гистограмме не могут быть переставлены.Они должны отображаться в том порядке, в котором происходят классы.
Пример гистограммы
Диаграмма выше показывает нам гистограмму. Предположим, что четыре монеты подброшены и результаты записаны. Использование соответствующей таблицы биномиального распределения или простых вычислений с помощью биномиальной формулы показывает, что вероятность того, что ни одна голова не отображается, равна 1/16, вероятность того, что одна голова отображается, равна 4/16. Вероятность выпадения двух орлов — 6/16. Вероятность выпадения трех решек — 4/16.Вероятность выпадения четырех решек — 1/16.
Всего мы построим пять классов шириной один. Эти классы соответствуют количеству возможных голов: ноль, один, два, три или четыре. Над каждым классом рисуем вертикальную полосу или прямоугольник. Высота этих столбцов соответствует вероятностям, упомянутым в нашем вероятностном эксперименте подбрасывания четырех монет и подсчета орлов.
Гистограммы и вероятности
Приведенный выше пример не только демонстрирует построение гистограммы, но также показывает, что дискретные распределения вероятностей могут быть представлены с помощью гистограммы.Действительно, и дискретное распределение вероятностей можно представить гистограммой.
Чтобы построить гистограмму, представляющую распределение вероятностей, мы начинаем с выбора классов. Это должны быть результаты вероятностного эксперимента. Ширина каждого из этих классов должна составлять одну единицу. Высота столбцов гистограммы — это вероятности для каждого из результатов. Если гистограмма построена таким образом, площади столбцов также являются вероятностями.
Поскольку такая гистограмма дает нам вероятности, она зависит от нескольких условий.Одно из условий состоит в том, что только неотрицательные числа могут использоваться для шкалы, которая дает нам высоту данного столбца гистограммы. Второе условие состоит в том, что, поскольку вероятность равна площади, сумма всех площадей столбцов должна составлять единицу, что эквивалентно 100%.
Гистограммы и другие приложения
Столбцы на гистограмме не обязательно должны быть вероятностями. Гистограммы полезны не только в вероятностных областях, но и в других областях. Каждый раз, когда мы хотим сравнить частоту появления количественных данных, можно использовать гистограмму для отображения нашего набора данных.
.
 Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика.
Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика. (-1/3), где
(-1/3), где 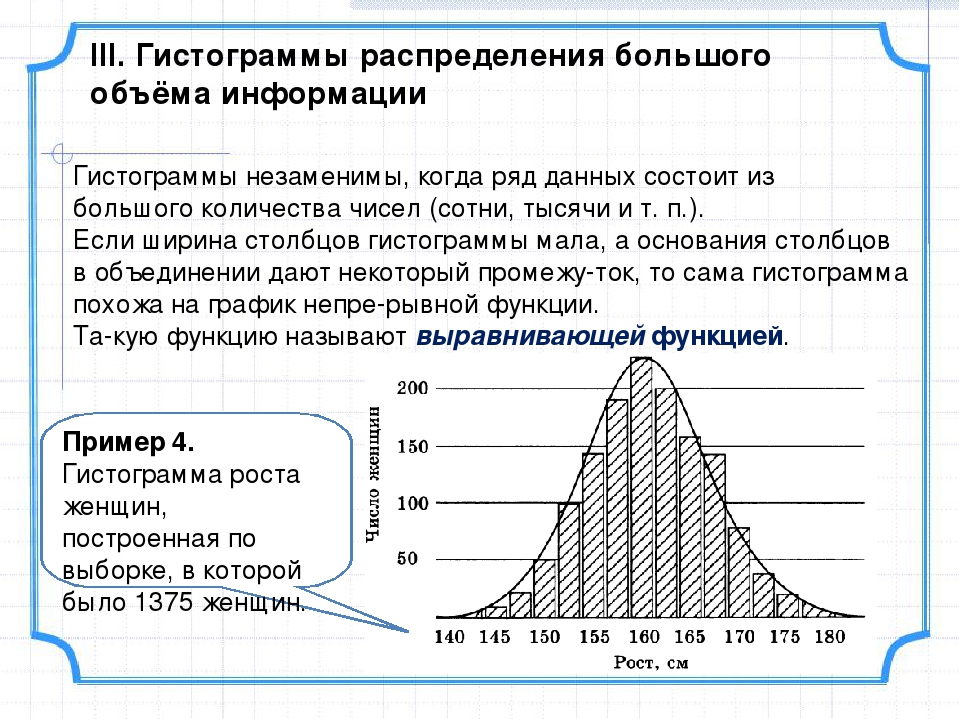
 Предполагается, что каждому интервалу принадлежит один из его концов: либо во
всех случаях левые (чаще), либо во всех случаях правые, а частоты или частости
показывают число вариантов, заключенных в указанных границах. Разности (ai-ai+1) называются частичными
интервалами или интервальными разностями.
Предполагается, что каждому интервалу принадлежит один из его концов: либо во
всех случаях левые (чаще), либо во всех случаях правые, а частоты или частости
показывают число вариантов, заключенных в указанных границах. Разности (ai-ai+1) называются частичными
интервалами или интервальными разностями.
 ,д показана гистограмма с прогалами («гребёнка»). Получается, когда ширина интервала
не кратна единице измерения или при ошибках оператора.
,д показана гистограмма с прогалами («гребёнка»). Получается, когда ширина интервала
не кратна единице измерения или при ошибках оператора. Аналогично, прибавляя 0,5 мм к 7,55 мм, получим интервал второго участка (7,55 мм- 8,05 мм ), и т. д.
Аналогично, прибавляя 0,5 мм к 7,55 мм, получим интервал второго участка (7,55 мм- 8,05 мм ), и т. д. По оси абсцисс откладывают значения параметров качества, по оси ординат — частоту. Для каждого участка строят прямоугольник (столбик) с основанием, равным ширине интервала участка; высота его соответствует частоте попадания данных в этот интервал (см. рис. 20). Если на гистограмме от руки провести кривую распределения данных по частоте, а также верхнее и нижнее предельные значения нормы, то легко можно понять вид распределения гистограммы и соотношение значений контрольных нормативов. Анализ гистограммы позволяет сделать заключение о состоянии процесса, однако если неясны условия контроля процесса или временные изменения, необходимо в комбинации с гистограммой использовать также контрольные карты и график, представляемый ломаной линией. Полученная в результате анализа гистограммы информация может быть легко использована для построения и исследования причинно-следственной диаграммы, что повысит обоснованность мер, намеченных для улучшения процесса.
По оси абсцисс откладывают значения параметров качества, по оси ординат — частоту. Для каждого участка строят прямоугольник (столбик) с основанием, равным ширине интервала участка; высота его соответствует частоте попадания данных в этот интервал (см. рис. 20). Если на гистограмме от руки провести кривую распределения данных по частоте, а также верхнее и нижнее предельные значения нормы, то легко можно понять вид распределения гистограммы и соотношение значений контрольных нормативов. Анализ гистограммы позволяет сделать заключение о состоянии процесса, однако если неясны условия контроля процесса или временные изменения, необходимо в комбинации с гистограммой использовать также контрольные карты и график, представляемый ломаной линией. Полученная в результате анализа гистограммы информация может быть легко использована для построения и исследования причинно-следственной диаграммы, что повысит обоснованность мер, намеченных для улучшения процесса. В
вероятностный график или
проверка соответствия может быть
используется для проверки модели распределения.
В
вероятностный график или
проверка соответствия может быть
используется для проверки модели распределения.