Измерение высоты объекта по изображению—ArcGIS Pro

Измерения высот можно получить при наличии модели сенсора. Информация о угле вектора на Солнце необходима для проведения измерений с использованием теней.

Подсказка:

Единицы для этих измерений можно изменить в окне Результаты измерений.

Лучше всего получать измерения высот из пространства изображения, использующего систему координат изображения (ICS), поскольку такое изображение не искажено каким-либо образом. Система координат изображения поддерживается в дополнительном модуле ArcGIS Image Analyst, в приложении Анализ пространства изображения.

Измерение высоты наземного объекта

Инструмент Высота от основания до верха рассчитывает высоту конструкции путем измерения от основания конструкции до ее вершины. Измерения выполняются перпендикулярно основанию объекта; поэтому предполагается, что это здание не коническое и построено без наклона. Измеряемая линия идет вдоль здания и её конечная точка должна находиться непосредственно над исходной точкой на основании.

В примере ниже есть несколько местоположений вдоль каждого из этих зданий, по которым можно легко определить основание здания и местоположение вершины.

1. Щелкните на слое на панели Содержание.
2. Щелкните вкладку Изображения.
3. В группе Измерение щелкните стрелку ниспадающего списка с раскрывающейся галереей измерений и выберите инструмент Высота от основания до верха.
4. Щёлкните точку в основании конструкции.
5. Щёлкните соответствующую точку на вершине конструкции.

Измерения высоты здания отображаются на панели Результаты измерения, в единицах, заданных пользователем.

Измерение высоты конструкции только по тени

Инструмент Высота от основания до верхней точки тени рассчитывает высоту конструкции путем измерения от основания конструкции до верхней точки ее тени. Точка на тени должна представлять точку на конструкции, перпендикулярную основанию.

Вычисление будет уточнено топографией, если задать набор данных Высот на панели Опции измерения.

В данном примере изображение было улучшено, чтобы сделать тень более видимой. Используя инструмент Высота от основания до верхней точки тени, можно вычислить высоту опоры уличного освещения, измерив длину тени от основания опоры лампы до верхней точки ее тени. Лучше использовать именно этот инструмент, а не инструмент Высота от основания до верха, поскольку в этом примере затруднительно различить верхнюю точку лампы.

1. Щелкните на слое на панели Содержание.
2. Щелкните вкладку Изображения.
3. В группе Измерение щелкните стрелку ниспадающего списка с раскрывающейся галереей измерений и выберите инструмент Высота от основания до верха.
4. Щёлкните точку в основании конструкции.
5. Щёлкните точку, соответствующую верхней точке тени конструкции.

Измерение высоты конструкции по конструкции и тени

Инструмент Высота от вершины до верхней точки тени рассчитывает высоту конструкции путем измерения от вершины конструкции до верхней точки ее тени. Точки на конструкции и ее тени должны быть представлены одной точкой.

Вычисление будет передано в учетную запись для топографии, когда набор данных Высот будет определен на панели Опции замера.

В представленном ниже примере точка, в которой тень пересекается со зданием (основание тени) загорожена деревом и, следовательно, использоваться не может. Чтобы правильно рассчитать высоту этого здания, необходимо определить точку на вершине здания, которую можно определить в верхней части тени, в нашем случае она отмечена синей стрелкой.

Этот инструмент можно использовать при расчете высоты части конструкции или конструкции, не являющейся прямоугольником. В следующем примере высоту остроконечной крыши можно измерить только от вершины крыши до верхней точки тени, так как нет возможности установить точку основания, которая должна находиться непосредственно под вершиной крыши.

Данный инструмент также оптимален для расчета высоты объекта на вершине конструкции. Например, чтобы измерить подсобное помещение на крыше здания, вы можете определить верхнюю точку этого объекта на изображении, а затем определить ту же точку в тени.

1. Щелкните на слое на панели Содержание.
2. Щелкните вкладку Изображения.
3. В группе Измерение щелкните стрелку ниспадающего списка с раскрывающейся галереей Измерение и выберите инструмент Высота от вершины до верхней точки тени.
4. Щёлкните на точке на вершине конструкции.
5. Щёлкните точку, соответствующую верхней точке тени конструкции.

Ограничения измерений

Инструменты измерения обеспечивают интерактивные методы для измерения высоты объектов на снимках. Отметьте опцию Ограничить направление движения курсора для инструментов измерения высоты в диалоговом окне Опции измерения, чтобы ограничить движения курсора и упростить процесс измерения высоты.

Эти три инструмента измерения высоты работают таким образом, что начальная точка измерения становится конечной точкой линии для данного ограничения. Курсор будет перемещаться только по линии, предназначенной для данного измерения. Например, при выборе инструмента измерения Высота от основания до верха первой точкой должна быть точка на основании объекта. Затем движение курсора ограничивается вертикальным направлением. Это важно при измерении объектов, когда местоположение основания трудно отличить от верхней части объекта. Например, вы можете легко найти ребро основания объекта пирамидального типа, но затрудняетесь при определении центра этого основания. Бывают случаи, когда трудно увидеть другие конечные точки измерений, а ограничение может помочь пользователю определить эти точки.

Измерение от основания до верха с ограничением направления движения курсора с использованием инфракрасного изображения с целью отличить детали башни от растений. Изображение Quickbird-2 представлено DigitalGlobe.

Для инструмента Высота от основания до верха тени начальной точкой должно служить основание объекта. Затем курсор будет вынужден двигаться по пути тени на поверхности земли.

Для инструмента Высота тени от вершины до вершины начальной точкой должна быть вершина объекта. Этот инструмент заставляет курсор перемещаться по пути солнечных лучей, которые образуют верхний край тени от вершины объекта.

Ограничения измерений — это удобный способ использования инструментов измерения высоты, который помогает делать корректные измерения, используя метаданные изображений.

Связанные разделы

---

Отзыв по этому разделу?

Высота здания определение термина по нормативным документам, ФЗ, ГОСТ

 

 

Предлагаю Вашему вниманию видеолекцию на тему «Пожарно-техническая высота здания»

 

 

 

Определение	Источник
высота расположения верхнего этажа, не считая верхнего технического этажа, определяемая:  — максимальной разностью отметок поверхности проезда для пожарных машин и нижней границы открывающегося проема (окна) в наружной стене;  — полу суммой отметок пола и потолка этажа при отсутствии открывающихся окон (проемов).   Примечания:   1. При наличии эксплуатируемого покрытия высота здания определяется по максимальному значению разницы отметок поверхности проезда для пожарных машин и верхней границы ограждений покрытия.  2. При определении высоты здания покрытие не следует считать эксплуатируемым, если на нем не предусмотрено постоянное пребывание людей.  3. При наличии балконов (лоджий) или ограждений окон высота определяется по максимальному значению разницы отметок поверхности проезда для пожарных машин и верхней границы ограждения.	пункт 3.1  Свода правил СП 1.13130.2020 «Системы противопожарной защиты. Эвакуационные пути и выходы»
Высота здания определяется высотой расположения верхнего этажа, не считая верхнего технического этажа, а высота расположения этажа определяется разностью отметок поверхности проезда для пожарных машин и нижней границы открывающегося проема (окна) в наружной стене. При отсутствии открывающихся окон (проемов) высота расположения этажа определяется полусуммой отметок пола и потолка этажа. При наличии эксплуатируемого покрытия высота здания определяется по максимальному значению разницы отметок поверхности проездов для пожарных машин и верхней границы ограждений покрытия.	пункт 3.1  Свода правил СП 1.13130.2009 «Системы противопожарной защиты. Эвакуационные пути и выходы»
Высота здания: расстояние от отметки поверхности проезда для пожарных машин до нижней границы открывающегося проема в наружной стене верхнего этажа. Примечания: 1. Чердак или верхний технический этаж принимаются в расчет высоты здания при условии обращения и/или хранения на чердаке или в помещениях верхнего технического этажа горючих веществ и материалов и/или применения в конструкциях горючих материалов (Г1 — Г4), даже если эти конструкции подвергнуты огнезащитной обработке. 2. При наличии эксплуатируемой кровли высота здания принимается выше отметки кровли на 1,35 м.	пункт 3.11 Свода правил СП 10.13130.2020 «Системы противопожарной защиты.Внутренний противопожарный водопровод. Нормы и правила проектирования»
Высота здания определяется высотой расположения верхнего этажа, не считая верхнего технического этажа, а высота расположения этажа определяется разностью отметок поверхности проезда для пожарных машин и нижней границы открывающегося проема (окна) в наружной стене.	примечание к пункту 1.4 *, 1.5 *, 1.6 *, 1.7 * СНиП 21-01-97*
Высота здания в таблицах 6.1, 6.2, 6.3  измеряется от пола 1-го этажа до потолка верхнего этажа, включая технический этаж. При переменной высоте потолка принимается средняя высота этажа.	примечание к таблицам 6.1, 6.2, 6.3  СП 2.13130.2020 «Системы противопожарной защиты. Обеспечение огнестойкости объектов защиты»
Вертикальный размер, измеряемый от проектной отметки земли до верхней отметки самого высокого конструктивного элемента здания (парапет кровли; карниз, конек кровли, верх фронтона; купол; шпиль; башня). Примечания 1 Верхними конструктивными элементами здания могут быть надстройки для выхода на кровлю и для размещения технического оборудования, трубы и т.п.; подкрестное яблоко — в православных храмах, колокольнях и звонницах. 2 Высота здания для определения условий обеспечения требований пожарной безопасности принимается в соответствии с СП 1.13130. 3 Антенны на кровле, молниеотводы и другие электротехнические и инженерные устройства при определении высоты здания не учитываются.	пункт 3.5 СП 118.13330.2012 «Общественные здания и сооружения»

 

 

 

---

---

 

 

 

Формально высота зданий не относится к пожарно-техническим классификационным характеристикам. Она не указана в статье 29 Федерального закона от 22 июля 2008 года № 123-ФЗ «Технический регламент о требованиях пожарной безопасности». Но фактически такая классификация существует и исходя из этой фактической классификационной характеристики принимаются решения о том, какие требования пожарной безопасности должны соблюдаться в отношении зданий той или иной высоты.

 

Кроме того здания по высоте прямо классифицируются на: 

 

здания повышенной этажности

высотные здания

 

И хотя здание «повышенной этажности» определяется в большинстве источников именно в зависимости от количества этажей, правильнее было бы опрделять их в зависимости от высоты, так как «стандартная» пожарно-техническая высоты 9 этажного здания — и составляет те самые 28 метров, которые используются в большинстве нормативных документов как критерий перехода с большую на меньшую опасность.

 

Если исследовать взялись эти «28» метров, то можно сделать вывод о фактическом смысле пожарно-технической высоты здания.. Как сообщил мне лучший знаток истории пожарной техники — Александр Владимирович Карпов. Эта величина появилась в нормах тогда, когда на вооружение пожарной охраны практически повсеместно использовался пожарный автомобиль Faszination Feuerwehr 43, Magirus DL 26, т.е. еще в 30-е — 40-е годы XX века. Этот автомобиль имел максимальную высоту подъема 26 метров и оснащелся 2-х метровой надставной лестницей

 

 

 

После этого из года в год величина 28 метров переписывалась из нормы в норму, хотя ее фактический смысл сейчас безусловно устарел, так как современные пожарные автолестницы обладают куда большими возможностями. .

 

Это не единственный пример того, что пожарно-техническая высота здания связана прежде всего с профилактической целью, которую в определении пожарной профилактики я сформулировал как «создание условий для тушения пожара пожарными подразделениями». От высоты здания, по логике пожарного нормирования зависит доступ для пожарных подразделений, как мы увидели из примера который я приводил касательно 28 метров это легло в основу пожарно-технической классификации зданий по высоте.

 

История вопроса высоты зданий крайне важна, так как она отображает суть противодействия «пожарные» vs. «строители».

 

Мой друг, историк пожарной охраны Москвы, Николай Борисович Рогачков нашел крайне интересный материал, связанный именно с понятием пожарно-техническая высота зданий и полезный для понимания сути этой нормы. Приведем касающиеся пожарной безопасности выдержки из этой статьи 1912 года адаптировав ее современному русскому языку.

 

Далее, вопрос о пожарной опасности.

Пожарная опасность таится во всяком доме, какой-бы высоты он не был.

От пожара одноэтажного дома соседние здания могут затронуть с тем-же усилием, как и от пожара 7-этажного дома.

 

---

---

Главное, что нужно иметь ввиду, это то, что стремление к «небоскребу» строительству,  не досужая фантазии того или другого строителя.  Строить многоэтажные дома стало насущной необходимостью.

Такое требование диктуется жизнью, а налагать основы на жизнь — пустое занятие :жизнь сумеет их бросить.

 

В самом деле:

 

Население Москвы растёт со страшной быстротой. Вся интенсивность домостроителей, наблюдающаяся в последние годы, не в состоянии разрешить
капитальный кризис.

Свободные участки земли, особенно центральных районах, осталось очень немного.

Цены на землю подняли чрезмерно. Цены на строительные материалы в рабочие руки ещё того больше. При таких условиях, — как прикажите строить дома?

 

Если в 3-4 этажа это, то при существенной норме расценки квартиры ни в каком случае не окупятся.  Если-же повышают квартирную плату, то толком тот-же квартирант, которому за якобы «светлую» квартиру, придётся платить дорога.

Единственный выход-строить многоэтажные дома, квартиры, в которых будут доступны средства обывателя и дадут известность его дохода владельцу.

---

 

 

.Таким образом мы можем сделать вывод о том, что высота здания — его важная характеристика, и несмотря на довольно архаичную классификацию, основанную на тактико-технических характеристиках автомобилей, которых давно нет на вооружении, высота здания напрямую влияет на различные аспекты пожарной профилактки в этом здании, на вопросы распространения пожара и эвакуации людей, но исторически, традиционно основной фактический смысл введения понятия «пожарно-техническая высота здания» — это обеспечение деятельности пожарных подразделений.

 

В связи с тем, что пожарно-техническая высота здания крайне редко указывается в проектной документации на здание, для пожарного специалиста особенно важно уметь ее определять.  

 

---

---

 

Вариант 1 — проемы (окна) на верхнем этаже здания открываются

 

Вариант 2 проемы (окна с ограждениями)

 

Вариант 3 балкон и лоджия — ограждения былконов и лоджий

 

Вариант 4 при наличии эксплуатируемого покрытия (примечание 1) и примечание 2)

 

 Вариант 5 — при отсутствии открывающихся окон

Вариант 6  для целей определения степени огнестойкости, класса констурктивной опжарной опансости и площади этажа в пределах пожарного отсека здавний классов ФПО Ф5

 

 

Во всех вариантах, кроме варианта 5 высота здания определяется именно по логике, которая описана в параграфе посвященном истории этого вопроса. Т.е. начало измерения идет от планировочной отметки проезда для пожарных автомобилей. М в этом на первый взгляд простом деле есть немало сложных моментов.

 

---

---

 

 на этапе жизненного цикла — проектирование

 

на этапе жизненного цикла эксплуатация

 

---

статью подготовил:

инженер пожарной безопасности

П. Ю. Князев

Размещено 05 мая 2020 года 

 

Все права на текст статьи принадлежат автору. Копирование, распространение, использование и иные действия, за исключением ознакомления на данной странице сайта ptm01.ru  запрещены.

Разрешено: копировать ссылку (url) на данную страницу и направлять скопированную ссылку неограниченному кругу лиц.

В случае сомнений, руководствуйтесь правилом: всё, что не разрешено — запрещено

 

Измерение высоты здания Детчинской школы необычными способами

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Балан Н.И. 1

---

1МОУ Детчинская средняя общеобразовательная школа

Никонорова Л.А. 1Панина И.Ю. 1

---

1МОУ Детчинская средняя общеобразовательная школа, Малоярославецкого района, Калужской области

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителяСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

«Кто с детских лет занимается математикой,

тот развивает внимание, тренирует свой мозг,

свою волю, воспитывает на­стойчивость и

упорство в достижении цели»

(А. Маркушевич)

Введение

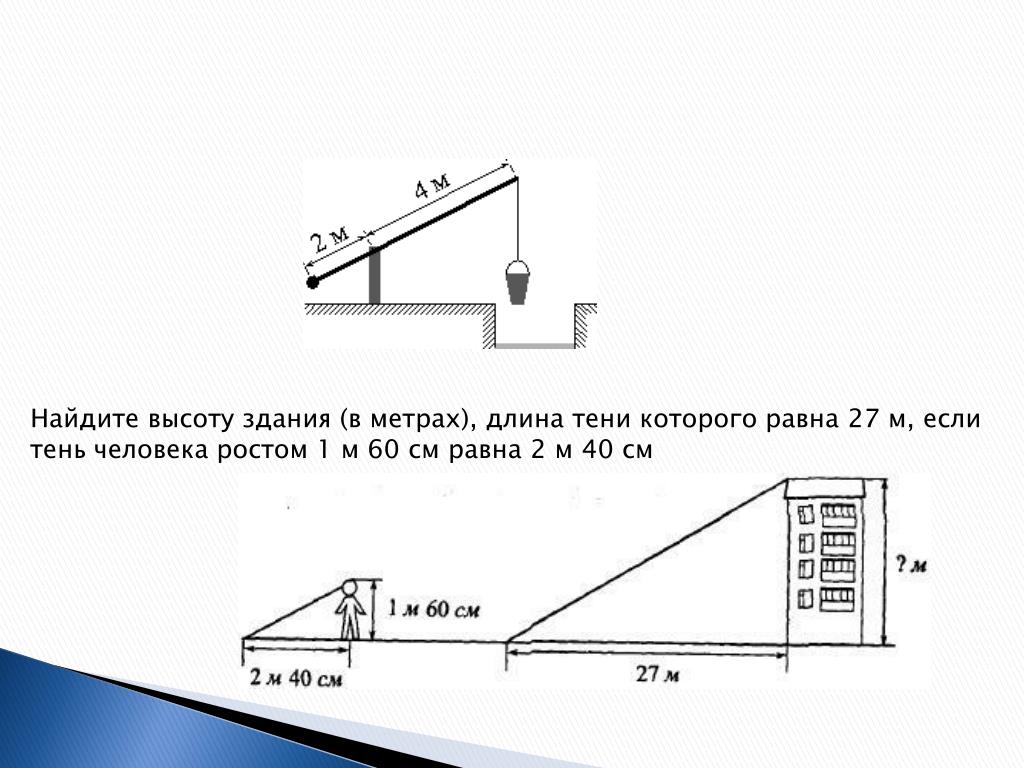
Однажды в интернете я прочитала интересный случай о том, как один студент сдавал экзамен по физике. Преподаватель задал вопрос: «Объясните, каким образом можно измерить высоту здания с помощью барометра».
Ответ студента был таким: «Нужно подняться с барометром на крышу здания, спустить барометр вниз на длинной веревке, а затем втянуть его обратно и измерить длину веревки, которая и покажет точную высоту здания». После чего этот студент был выгнан из аудитории, но после подал на апелляцию, основываясь на том, что ответ был абсолютно правильным.

На пересдаче студент заявил, что у него есть несколько решений проблемы, и он просто выбирал лучшее. И представил 25 решений этой задачи.

 Студентом этим был Нильс Бор, впоследствии — великий датский физик, лауреат Нобелевской премии 1922г.

Актуальность темы:

В жизни иногда необходимо умение оценивать расстояние до предмета. Например, до леса, до другого берега реки, высоту скалы, дерева, здания. Каждому человеку, научившемуся писать и считать, неоднократно приходилось что-либо измерять. При этом не всегда под рукой мы имеем сантиметровую линейку или специальные приборы. Поэтому необходимо знать и косвенные методы измерения объектов, дающие неплохой результат. К тому жеповторение элементов алгебры и геометрии, таких как подобие треугольников и пропорция будет очень полезным.

Объект исследования:

высота здания Детчинской средней общеобразовательной школы

Предмет исследования: методы измерения высоты предметов

Цель – определить высоту здания средней общеобразовательной школы разными методами без специальных приборов

Задачи:

изучить интернет ресурсы и литературу по проблеме исследования;

провести анкетирование среди учащихся моего класса;

изучить различные методы измерения высоты зданий;

провести практическое исследование по измерению высоты школы разными способами;

найти наиболее точный способ измерения высоты зданий применимый на практике;

Гипотеза: предполагаю, что косвенные методы измерения дают близкие результаты к фактической высоте здания школы

На различных этапах моей исследовательской работы мною использовались следующие методы исследования:

анализ литературы и материалов сети интернет, счет, измерение, сравнение.

Историческая справка:

Строительство современного здания школы начато в IV квартале 1975 года, окончено в конце 1977 года. Школа сдана в эксплуатацию с оценкой «Отлично». Занятия в этом здании начались 11 января 1978 года.

Основная часть

1.Теоретическое исследование проблемы

1.1 Обзор литературы

Треугольники знакомы нам с детства. Эта геометрическая фигура таит в себе много интересного и загадочного. И чтобы измерить высоту школы мне пришлось повторить для своей работы такие понятиями как подобные треугольники, пропорция

Что такое подобные треугольники?

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Коэффициент подобия равен отношению сходственных сторон подобных треугольников.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Признаки подобных треугольников.

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Подобие треугольников в жизни.

Подобие треугольников можно применять для разных целей. Например, для измерения высоты дерева или дома.

Пропорция

Если у двух отношений одинаковое частное, то их можно соединить знаком равенства, тогда это равенство будет уже пропорцией.

Определение: Равенство двух отношений называется пропорцией.

Буквенная запись пропорции a:b = c:d — это общий вид пропорции, где:

a и d — это крайние члены пропорции; b и c — это средние члены пропорции.

Основное свойство пропорции: а*d = b*c

Правило 1. Произведение средних членов истинной пропорции равно произведению ее крайних членов.

Правило 2. Средние и крайние члены пропорции можно менять местами, от этого пропорция не изменится.

1.2 Описание методов измерения высоты предметов

При проведении исследования я познакомилась с различными методами измерения высоты зданий, их довольно много, но я выбрала наиболее простые и интересные для меня.

Метод при помощи фотографии

Надо сфотографировать человека возле здания. Человек должен стоять вплотную к измеряемому зданию. Затем надо узнать сколько раз человек может поместиться на фотографии вертикально. Это количество надо умножить на рост человека, это и будет высота здания.

Формула:

Н= Рост человека кол-во размноженных человек на фото

Метод при помощи шеста

П ри отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, который был описан в книге Жюль Верна «Таинственный остров».

Решение:

Нужно вбить в землю шест, лечь на землю так, чтобы было видно верхний конец шеста и верхушку измеряемого предмета. Измерить расстояние от шеста до предмета, измерить высоту шеста и расстояние от макушки человека до основания шеста.

Формула: H=

Припомощизеркала

Этот способ можно удачно применять после дождя, когда на земле появляются лужи.

Р ешение:

Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например, дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас. Вместо лужицы можно пользоваться положенным горизонтально зеркальцем.

Формула:

H =

Метод Фалеса (при помощи тени)

Как по длине тени, падающей от дерева в солнечный день, определить высоту дерева?

Решение: так как лучи солнца можно считать практически параллельными, то тень от дерева во столько же раз длиннее тени от какого либо шеста, во сколько раз дерево выше шеста. Поэтому, установив вертикально шестизвестной высоты и измерив отношение длины тени от дерева к длине тени от шеста, мы вычислим искомую (примерную) высоту дерева.

Формула:

H=

_{Более распространенным способом является метод, с помощью которого еще Фалес, по преданию, измерил высоту египетских пирамид. Когда жрецы, желая испытать Фалеса, предложили учёному измерить высоту пирамиды, он дождался, когда длина его собственной тени стала равна его росту, и в этот момент измерил длину тени, которую отбрасывала пирамида. Эта измеренная длина тени и равна высоте пирамиды.}

При помощи воздушного шарика

Привязали нитку к шарику, размотали нитку до подъёма шарика до крыши школы. Смотали веревку и замерили ее длину.

Припомощи барометра

Барометр (с др.-греч. «тяжесть» и «измеряю») – прибор для измерения атмосферного давления. Ртутный барометр был изобретен итальянским математиком и физиком Торричелли в 1644 году, это была тарелка с налитой в неё ртутью и пробиркой (колбой), поставленной отверстием вниз. Когда атмосферное давление повышалось, ртуть поднималась в пробирке, когда же оно понижалось – ртуть опускалась. Из-за неудобства такая конструкция перестала применяться и уступила место барометру — анероиду, но метод, по которому такой барометр был изготовлен, стал применяться в термометрах. Барометр нужен для определения погоды и для определения высоты.

Припомощиравнобедренноготреугольника

Приближаясь к предмету (например, к дереву) или удаляясь от него, установить треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с вершиной дерева. Высота дерева будет равна расстоянию до дерева (в шагах) плюс высота до глаз наблюдателя.

Практическое исследование проблемы

И зучив данные методы измерения я решила провести эксперимент: измерение высоты нашей школы перечисленными способами. Результаты представлены в рассчетной таблице.

Метод измерения с помощью фотографии.

Оборудование: фотоаппарат и программа Paint.

На этой фотографии я помещаюсь приблизительно 5,9 раз.

Мой рост равен 1 ,67 + 0,05=1,72

Результат: Н =5,9*1,72=10,1 м

Метод измерения с помощью шеста.

Пусть Н — это высота школы.

Оборудование: рулетка и шест.

В роли шеста была я, а в роли лежащего на земле человека мой одноклассник.

H=

Высота шеста – 1м 67 см

Расстояние от макушки до школы – 11,27м

Расстояние от макушки до шеста – 1,70 м

Высота школы-Н

Результат : Высота школы = 11м 07см

Метод измерения с помощью зеркала.

H =

Оборудование: зеркало и рулетка.

Расстояние от школы до зеркала- 23м

Мой рост – 1м 67 см

Мой рост до уровня глаз -1 м 57см

Высота школы – Н

Результат : Высота школы = 11м 64 см

Метод измерения при помощи тени.

Моя тень – 3,5м

Тень школы — 24,8м

Мой рост – 1,67м

Результат : Высота школы = 11м 83 см

Метод при помощи шарика

На мой взгляд, самый простой и веселый метод. Привязали нитку к шарику, размотали нитку до подъёма шарика до крыши школы. Смотали веревку и замерили ее размер. Высота школы получилась 11м 67 см.

Метод «Барометр»

С помощью барометра я измерила атмосферное давления на 1,2 и 3 этажах здания. Измерения высоты школы с помощью барометра — анероида не дал результатов — показания на улице и на третьем этаже школы были одинаковыми. По всей видимости, высота школы меньше 12 м.

Метод припомощиравнобедренноготреугольника

Удаляясь от здания школы, установили треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с крышей школы. Высота школы равна расстоянию до школы плюс высота до глаз наблюдателя.

Мой рост до уровня глаз -1 м 57см

Высота школы – Н

Расстояние от меня до школы 10,5м

Результат: Высота школы 12,07м

Н=1,57+10,5=12,07м

3. Социальный опрос одноклассников

Я провела социальный опрос одноклассников по данной проблеме. Вопросы, на которые они отвечали:

Знаете ли вы, какова высота нашей школы?

Какая на ваш взгляд высота нашей школы?

Какой способ измерения высоты вы знаете?

Как, используя знания геометрии можно определить высоту удаленного предмета?

Как, используя знания физики определить высоту здания школы?

Результаты анкетирования

В опросе участвовало 20 учащихся 9б класса

Вывод:

Познакомившись с моим исследованием, многие ученики, на вопрос о необходимости изучать математику, ответят положительно. Моя работа может быть использована школьниками для повышения своего образовательного уровня, а также научит применять полученные в школе знания на практике, что сегодня очень актуально.

Заключение

В ходе исследования я изучила и проанализировала различную литературу и материалы сети интернет и выяснила, что существует много способов для измерения высоты различных предметов.

Измерение высоты школы я проводила 7 методами. Измерение высоты здания с помощью тени не всегда выполнимо, так как необходима солнечная погода. Методы дают примерно одинаковый результат.

Сравнив результат моих измерений с взятой информацией из Технического паспорта школы – 11,9м , можно прийти к выводу, что наиболее точным методом является «Метод измерения при помощи тени» и «Метод измерения при помощи равнобедренного треугольника» , но и остальные методы показали близкие результаты.

Конечно, измерение высоты удаленного предмета удобнее делать, когда в наличии имеется специальное измерительное оборудование. Но не каждый раз удается предугадать ситуацию, которая может возникнуть на прогулке или в туристическом походе. Вот тогда такие простые знания пригодятся и даже помогут выйти из затруднительного положения.

Оригинальность моей работы была в создании лучшей модели измерения высоты здания, в интеграции предметов (физики и математики).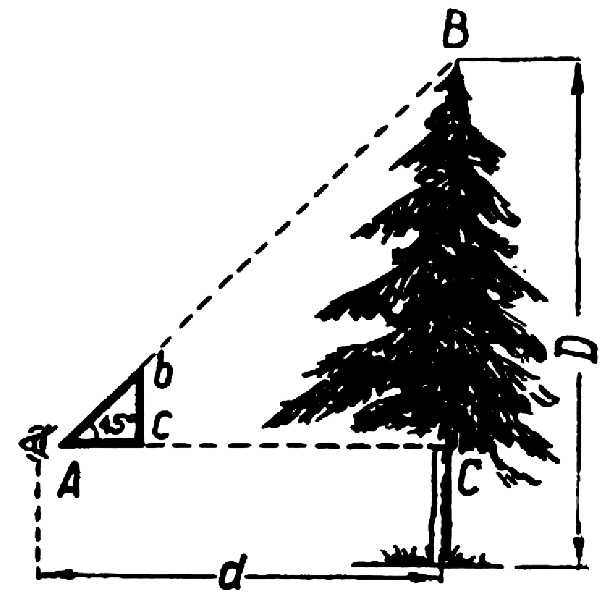 Создав модель, и проводя эксперименты, я более глубоко изучила подобие треугольников и применение подобия на практике; соотношения в прямоугольном треугольнике; более детально изучили некоторые физические явления (угол падения равен углу отражения). То есть была доказана взаимосвязь теории с практикой. По результатам измерений был проведен сравнительный анализ, составлены таблицы.

Гипотеза о том, что косвенные методы измерения высоты здания дают близкий результат подтвердилась. Таким образом, задачи исследовательской работы решены, поставленная цель достигнута, выдвинутая проблема выяснена.

Список используемой литературы

Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняков, И. И. Юдина. Геометрия. М. Просвещение. 2005г. 138с.

http://shkolo.ru/proportsiya/

И. Баврин. Большой справочник школьника. Математика. М. дрофа. 2006г. 435с.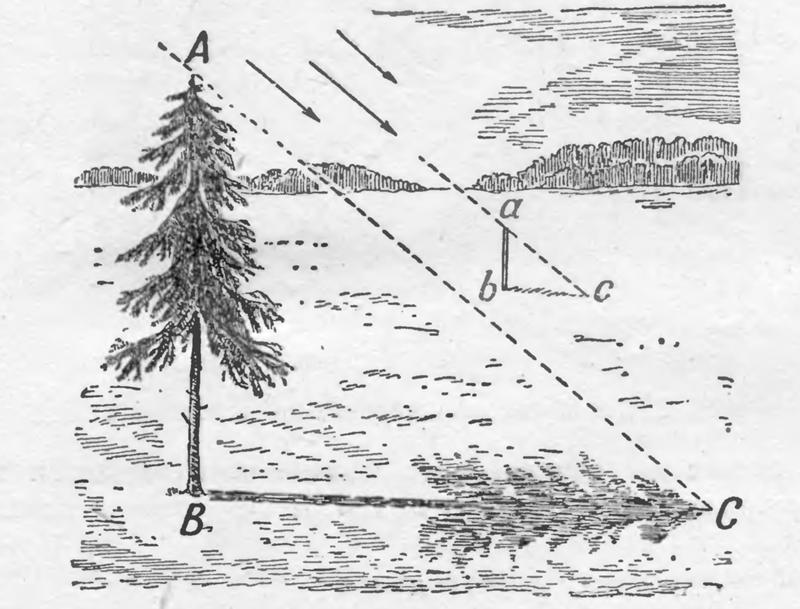

Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику. – М.: Наука. Гл. ред. физ.-мат. лит.,1989. – 240с.

газета: Гумеров И. Измеряем высоту // Математика №3, 2007.

газета: Каменева Т. Измерение высоты здания Пермэнерго // Физика в школе №9, 2008.

http://nsportal.ru/ap/library/drugoe/2013/03/21/izmerenie-vysoty-zdaniya-maksimalnym-kolichestvom-neobychnykh-sposobov

http://ru.calameo.com/books/0012979861d005ab16a9f

http://project.1september.ru/works/596940

https://ru.wikipedia.org

Приложение 1

Таблица «Измерение высоты школы»

Метод	Формула	Измерения(М)
1.При помощи фото	————————————————	Н= 10,1
2. При помощи шеста	Формула: H=
3.При помощи зеркала.	H =
4.При помощи тени.	H=
5. При помощи шарика.	—————————————————-	Н= 11,67м
6 .При помощи барометра	—————————————————	Результат показал Н меньше12м
7.При помощи равнобедренного треугольника	Н=рост человека до глаз+расстояние от челов. до здания	Н=1,57+10,5=12,07м

№	Метод	Результат	Ошибка
1	По фотографии	11,52м	3%
2	При помощи шеста	11,07м	7%
3	Припомощизеркала	11,64м	2%
4	При помощи тени	11,83м	0,5 %
5	При помощи шарика	11,67м	2%
6	Припомощи барометра	меньше 12м
7	При помощи равнобедренного треугольника	12,07	1,4 %

Приложение 2

Просмотров работы: 299

4 способа измерения высоты здания

Содержание

Как измерить высоту здания

Мы можем измерить высоту здания различными способами, когда невозможно измерить высоту напрямую. Таким образом, для измерения высоты здания или дерева также используются различные инструменты в зависимости от различных условий. Методы определения высоты здания или дерева следующие:

1. Использование только линейки и рулетки.
2. Использование тени здания или дерева.
3. Использование клинометра.
4. Использование транзитного теодолита.

Использование только линейки и ленты-

Условия: Этот метод подходит, когда земля ровная.

Необходимые инструменты: Две линейки и измерительная лента.

Процедура:  Предположим, что высота здания равна PT, которую необходимо определить. T — основание, P — вершина здания. Два дальномера закреплены в точках А и В на ровной поверхности на некотором расстоянии друг от друга. На этих дальномерных вехах C и D отмечены таким образом, что AC = BD.

Теперь точка E отмечена на здании, если смотреть через линию CD. Затем из точки С визирована точка Р, сохраняя при этом точки С, F и Р на одной прямой. Затем измеряются AT, AB и DF.

Из ΔPEC и ΔFDC мы можем сказать:

PE/CE = DF/CD

или PE= (FD/CD) x CE

, т. е. PE = (FD/AB) x AT.

мы можем легко измерить ЕТ рулеткой.

Высота здания = PE +ET.

Использование тени здания или дерева

Условия: Этот метод подходит для ровной поверхности.

Необходимые инструменты: Одна линейка и измерительная лента.

Процедура:  Предположим, что высота здания равна EF, а длина его тени равна DE. Теперь ставим рейку на некотором расстоянии. Высота дальномера равна BC, а длина его тени равна BC.

длину AB, BC и DE можно легко измерить рулеткой.

Таким образом, из Δ ABC и Δ DEF мы можем сказать, что

(BC/AB)=(EF/DE)

или, EF = (BC/AB) x DE = высота здания.

Использование тени здания или дерева

Условия: Этот метод подходит, когда земля находится на склоне.

Требуемые инструменты: Одна линейка и клинометр.

Клинометр

Клинометр — это прибор, используемый для измерения угла наклона. Клинометр в основном подобен градуированному полукруглому протектору. Рядом с прямым краем есть два штифта для наведения на объекты. Отвес подвешен к центру клинометра. Отвесная линия совпадает с 0 °, когда нет наклона (т. Е. Горизонтали).

При измерении любого уклона клинометр наклоняется, но отвес остается вертикальным. В этом наклонном состоянии отвесная линия совпадает с делением на клинометре. Эта градуировка указывает на наклон объекта.

Процедура

Клинометр может использоваться для измерения высоты здания или дерева. Сначала в точке, откуда будет измеряться угол, закрепляется дальномерная рейка. Теперь геодезист измеряет наклон верхней части здания. Допустим, угол равен Θ°. На следующем этапе измеряется расстояние между дальномером, например, расстояние равно L.

Таким образом, мы можем сказать, что высота = основание x tanΘ° = LtanΘ°.

Таким образом, высота здания равна TP = (LtanΘ°+ высота клинометра).

Использование транзитного теодолита.

Необходимые инструменты : Одна дальномерная рейка и транзитный теодолит

Теодолит.

Теодолит – универсальный геодезический прибор. Этот прибор может измерять различные типы измерений. С его помощью мы можем измерять различные типы горизонтальных и вертикальных углов. Мы также можем измерить расстояние с помощью теодолита, когда это невозможно. По сути, теодолит может измерять0003

1.  горизонтальный угол
2. вертикальный угол
3. угол отклонения
4. магнитный пеленг
5. дальность и удлинение линии
6. горизонтальное расстояние
7. вертикальная высота.

Теодолит подразделяется на два типа:

1. транзитный теодолит
2. нетранзитный теодолит

Что такое транзитный и качающийся?

Вращение зрительной трубы теодолита вокруг горизонтальной оси в вертикальной плоскости называется транзитным. Другими терминами перехода являются разворот или погружение.

Если теодолит может проходить, то он называется транзитным теодолитом.

Вращение зрительной трубы в горизонтальной плоскости вокруг вертикальной оси называется качанием.

Процедура

Измерение высоты здания с помощью теодолита происходит следующим образом.

1. Нахождение вертикального угла вершины здания.
2. Измерение горизонтального расстояния между теодолитом и зданием.
3. расчет вертикальной высоты здания.

Нахождение вертикального угла вершины здания.

1. Сначала теодолит устанавливается, центрируясь в точке, откуда должен быть измерен угол.
2. Затем необходимо выровнять теодолит с помощью ножного винта и проверить пузырьковые трубки.
3. Приблизительно увидеть объект. Затем ограничили горизонтальное вращение теодолита, зафиксировав нижний и верхний зажимные винты.
4. После этого совместите ноль вертикального круга с нулем вертикальной нониусной шкалы.
5. Теперь разделите верхнюю часть здания пополам, отрегулировав вертикальный прижимной винт и касательные винты.

Измерение горизонтального расстояния между теодолитом и зданием

Если поверхность земли ровная, мы можем легко измерить расстояние с помощью цепи или рулетки. Но если поверхность земли крутая с неровностями, то мы не можем измерить цепью или рулеткой. В этом случае мы должны измерить расстояние с помощью тахеометра.

Тахеометр представляет собой транзитный теодолит, снабженный дополнительным объективом и диафрагмой.

Расчет вертикальной высоты здания.

Предположим, что угол, измеренный геодезистом с помощью теодолита, равен Θ°. Расстояние равно L. Таким образом, высота здания над линией обзора равна H= L x tanΘ°.

Общая высота здания равна высоте прибора + LtanΘ°.

Заключение

Среди этих четырех методов косвенного измерения высоты здания метод с теодолитом дает наиболее точные результаты. В случае отсутствия теодолита можно использовать клинометр.

Как измерить высоту башни здания или небоскреба

Сегодня в этой статье мы поговорим о том, как измерить высоту здания | как измерить высоту здания | калькулятор угла депрессии | как измерить здание | высота дома  | измерение высоты здания | высота здания | Как измеряется высота здания | Метод метлы

Как рассчитать высоту здания или башни: Как измерить высоту здания

Иногда нам может понадобиться найти высоту здания до или после строительства . Существует несколько способов расчета высоты здания . В этой статье я буду использовать два метода: как измерить высоту здания

Метод тригнометрии для расчета высоты здания/башни (метод 1):

Это самый простой метод. Вы можете использовать этот метод, чтобы узнать высота любого объекта, такого как здание или башня, резервуар для воды, дерево, световой шланг и т.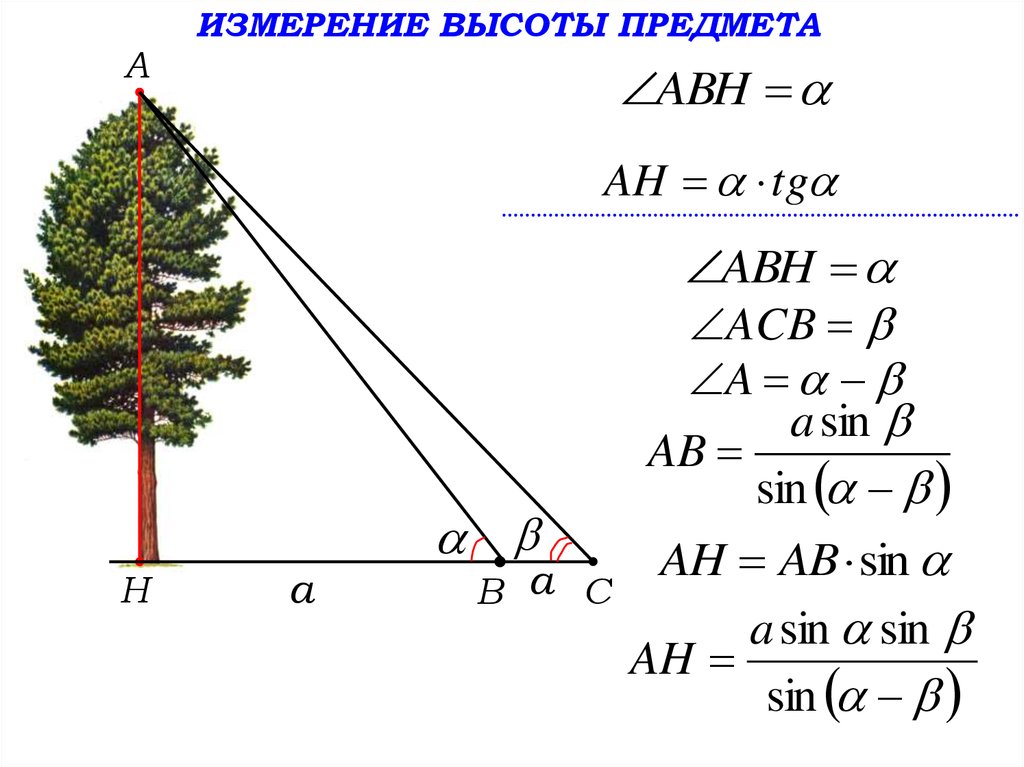 д. калькулятор угла наклона

Необходимые данные:

Расстояние и угол (как показано на рис.)

Дано :

Угол = Ɵ = 30 ^o Расстояние – d – 5000 футов

Процедура:

Мы знаем, Высота дома

Отношение касательной к противоположной стороне.

что означает tanƟ = Противоположная сторона / Смежная сторона

здесь Ɵ = 30 ^o

Таким образом, Tan = 30 ^o = Противоположная сторона / Смежная сторона = x/d = x/5000

x

2 ^o x 5000 = 0,577 x 5000 = 2885 футов

Следовательно, высота здания/башни составляет 2885 футов. высота дома

---

Метод метлы (Метод 2):

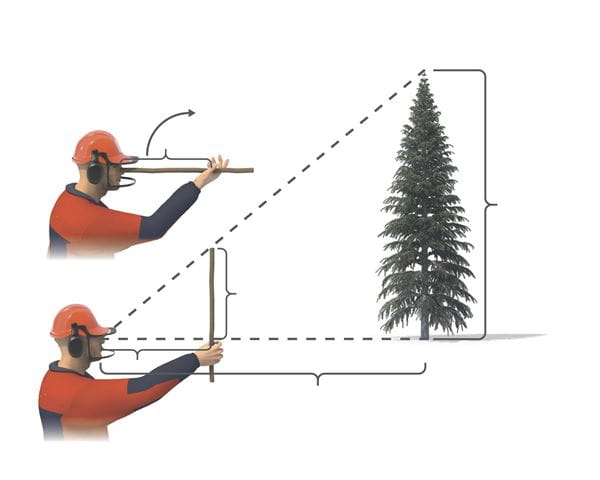
Не всегда возможно использовать вышеуказанный метод из-за наличия места или времени. Этот метод измерения также использует тени, но вам не нужно ждать, пока длина тени от метлы сравняется с ее высотой.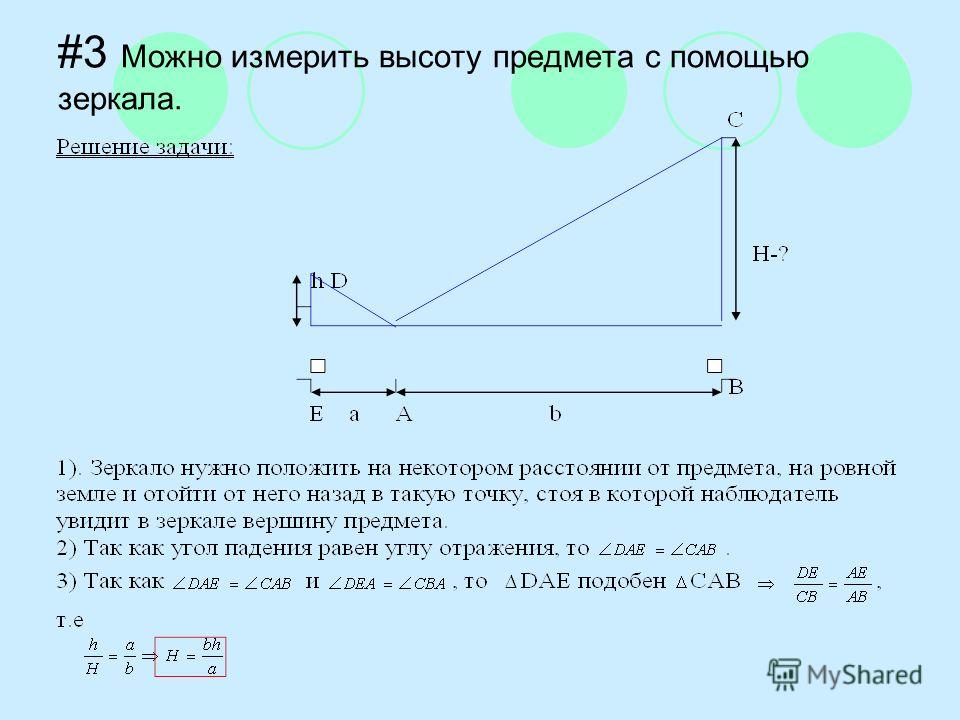 Положите метлу на пол лицевой стороной вверх. Теперь измерьте высоту метлы и длину тени. Быстро измерьте длину тени, создаваемой структурой. Такими же треугольниками мы можем достичь высоты здания. измерение высоты здания

Чтобы понять свойства подобных треугольников, см. изображение ниже. Структура и ее форма образуют прямоугольный треугольник. А метла и ее тень образуют один и тот же треугольник прямых углов. Поскольку оба треугольника имеют прямые углы, они равны.

Таким образом, высота конструкции может быть рассчитана из приведенных ниже соотношений.

(длина тени метлы/высота метлы) = (длина тени здания/высота здания) Согласно приведенной выше формуле; h/x = a/b

Необходимые данные:

Предположим, x = 600 футов и a = 100 футов, b = 60 футов, тогда найдите x = ?

Процедура:

Как мы знаем,

h/x = a/b

Итак, h = (a/b) * x = 100/60 x 600 = 1000 футов

3 9002 Отсюда Высота Здания/Башни составляет 1000 футов.

---

Как измерить высоту объекта/здания с помощью теодолита (метод 3):

Теперь давайте рассчитаем высоту здания с помощью теодолита , как показано ниже. Во-первых, вы должны измерить теодолит по прямой оси и установить угол на 0 ° по горизонтальной оси, например, показанной пунктирной линией. Вы должны измерить расстояние (L) здания от места расположения канала теодолита, как показано на схеме.

Поместите весы в верхний угол здания с помощью теодолита и запишите значение угла θ1. Аналогичным образом разделите пополам нижний краевой угол здания и запишите значение угла θ2.

Нарисуем треугольники выше с целью расчета значений измеренного угла. Метод метлы

Допустим, треугольник 1 подобен АВС, где А — точка канала теодолита.

Треугольник ABC : Угол θ1 = 34° 7′

Длина AB = L = 72 м.

Из тригонометрии,

Tan θ1

= противоположная сторона ÷ смежная сторона.

= сторона BC ÷ сторона AB

Tan 34° 7′

= ч2 ÷ 72м.

h2 = tan 34° 7′ × 72 м.

= 0,67747 × 72 м

= 48,778 м.

Треугольник 2 обозначим как ABD, где A – точка станции теодолита.

Треугольник ABD. Приведенные данные :

Угол θ2 = 1° 12′

Длина AB = L = 72 м.

Из тригонометрии,

Tan θ2 =

противоположная сторона ÷ смежная сторона.

= сторона BD ÷ сторона AB

Tan 1° 12′

= h3 ÷ 72m.

h3 = тангенс 1° 12′ × 72 м.

= 0,02094 × 72 м

= 1,508 м.

Теперь высота здания

H = h2 + h3

= 48,778м. + 1.508м.

 =  50,286 м.

---

ДРУГИЕ СООБЩЕНИЯ:

Расчет нагрузки на колонну, балку, стену и перекрытие

Основные правила расчета колонны | Основные правила проектирования колонн

Основные компоненты дорожной конструкции и метод строительства

Как создать отчет с координатами трассы дороги XML XLS в AutoCAD Civil 3D

Разница между гибким и жестким покрытием | Типы дорожного покрытия

---

Вывод:

Полная статья о как измерить высоту здания | как измерить высоту здания | калькулятор угла депрессии | как измерить здание | высота дома  | измерение высоты здания | высота здания | как измеряется высота здания | Как измеряется высота здания | Метод метлы .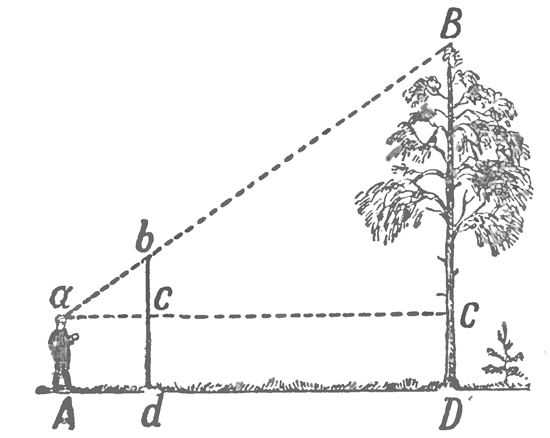  Благодарим вас за полное прочтение этой статьи на платформе « Гражданское строительство » на английском языке. Если вы считаете этот пост полезным, помогите другим, поделившись им в социальных сетях. Если какая-либо формула BBS отсутствует в этой статье, сообщите мне об этом в комментариях.    

10 различных способов измерения высоты небоскреба

10 различных способов измерения высоты небоскреба

Слева направо: One World Trade Center, изображение © James Ewing; Бурдж-Халифа, изображение © пользователя Wikimedia Donaldytong, лицензия CC BY-SA 3.0; Тайбэй 101, изображение © пользователя Викимедиа Peellden под лицензией CC BY-SA 3.0; Шанхайская башня, фото © Gensler/Shen Zhonghai.

• Автор: Линдси Леарди
• 12 октября 2017 г.

Как определить фактическую высоту здания? Где разместить размерную линию? История измерения небоскребов восходит к 1885 году, задолго до создания AutoCAD или Revit, когда Дом страхования жилья в Чикаго был одним из первых, кто мог похвастаться тем, что является самым высоким зданием в мире, но Совет по высотным зданиям и городской среде обитания (CTBUH)— или Объединенный комитет по высотным зданиям, как он первоначально назывался, — не был сформирован до 1969. CTBUH, признанный многими авторитетом в области высотных зданий, часто упоминается при определении самого высокого здания в мире (или в стране, или в городе). Однако CTBUH — не единственная организация, занимающаяся измерением зданий; глобальная база данных информации о зданиях Emporis также является крупным игроком. Между собой эти две организации предлагают 10 различных способов определения высоты небоскреба, которые мы суммировали ниже.

Методы измерения CTBUH

CTBUH признает три способа измерения небоскреба, каждый из которых использует уровень чистового пола за пределами самого низкого входа на уровне земли в качестве базовой линии.

via CTBUH

1. Архитектурный топ

Это наиболее распространенный способ измерения здания. Архитектурная вершина здания включает в себя любую строительную конструкцию или украшения, такие как шпили или парапеты, но не включает в себя то, что CTBUH считает «функционально-техническим оборудованием». Функционально-техническое оборудование — это все, что может быть изменено, например, флагшток, антенны или вывески. Метод архитектурной вершины используется для определения самых высоких зданий в мире, хотя из-за субъективности того, что является «архитектурным», а что просто «функционально-техническим оборудованием», он иногда может вызывать некоторые разногласия.

via CTBUH

2. Самый высокий занимаемый этаж

Чтобы считаться самым высоким пригодным для проживания этажом, он должен представлять собой кондиционированное помещение, предназначенное для постоянного проживания людей на законных основаниях. Механические места не в счет. Это измерение проводится до уровня пола.

via CTBUH

3. Наконечник

Наконечник здания – это самая высокая точка, независимо от материала и назначения. Например, архитектурная вершина Уиллис-Тауэр — это уровень крыши на высоте 1451 фута (442 метра), но ее верхушка имеет высоту 1729 метров.футов (527 метров).

через CTBUH

Методы измерения Emporis

В дополнение к трем вышеперечисленным методам глобальная информационная база данных зданий Emporis определяет несколько других способов определения высоты здания. Чтобы легко предоставлять данные о здании, Emporis определяет различные категории информации в своих стандартах. Некоторые из них предназначены для обеспечения фактической точности, в то время как другие используются для предоставления оценок, когда невозможно найти более точные данные. Еще больше предназначено для обеспечения внутренних измерений здания, а не для определения общей высоты здания. Emporis также использует несколько иную базовую линию для многих своих измерений: в то время как CTBUH использует уровень пола у самого нижнего входа, Emporis использует самую низкую точку, в которой здание встречается с землей, независимо от ее отношения к уровням пола.

4. Предполагаемая архитектурная высота

Чтобы оценить архитектурную высоту здания, Emporis может рассчитать высоту на основе списка известных значений. Например, приблизительная высота конструкции с учетом высоты этажей зданий с аналогичным расположением и назначением.

5. От пола до потолка

Это говорит само за себя. В базе данных Emporis указано среднее расстояние от пола до потолка. Высоту здания можно оценить (очень приблизительно) путем вычисления суммы измерений от верха плиты пола до потолка для каждого уровня.

6. От пола до пола

Еще один пример, в котором Emporis обеспечивает среднее измерение для здания, высота от пола до этажа вычисляет пространство между верхней частью двух соседних плит пола. Для оценки общей высоты от пола до пола является более точным, чем от пола до потолка, поскольку он учитывает пространство между уровнями.

7. Главная крыша

В зданиях со значительными уровнями крыши можно использовать этот метод для измерения до основной плиты крыши. Это измерение не включает пентхаусы или башни.

8. Смотровая площадка

От базового уровня до открытой смотровой площадки. Смотровая площадка определяется как самое высокое внешнее смотровое пространство, подобное тому, которое Меганом спроектировал для сверхвысокого роскошного небоскреба на Манхэттене.