Как определить размерность матрицы: основные определения, обозначение, формулы и элементы матрицы

Содержание

7.4.4. Вывод размера матрицы MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1763 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

Главная
База знаний
CAD / CAM
org/Breadcrumb»>MathCAD 12

Линейная алгебра
7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
7.2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.2.2. Скалярное произведение
- 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
7.3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
7.4. Вспомогательные матричные функции
- 7.4.1. Автоматическая генерация матриц
- 7.4.2. Разбиение и слияние матриц
- 7. 4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы

Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции (листинги 7.28 и 7.29 соответственно):

rows (A) — число строк;
cols (А) — число столбцов;
length (v) — число элементов вектора;
last (v) — индекс последнего элемента вектора:

А — матрица или вектор;
v — вектор.

ПРИМЕЧАНИЕ

Если матричные индексы нумеруются с 1, т. е. системная константа ORIGIN равна не о (по умолчанию), а 1, то число элементов вектора и индекс его последнего элемента совпадают.

Листинг 7.28. Размер матриц

Листинг 7.29. Размер векторов

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

10107 0

Глава 10 Работа с информационными ресурсами Mathcad 11

7088 0

Глава 2 Работа с файлами Mathcad 11

12841 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2322 s

Вычисление размера размерности массива MatLab

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

1763 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

org/Breadcrumb»>Главная
База знаний
CAD / CAM
MatLab

Урок 13. Многомерные массивы Понятие о многомерных массивах
Применение оператора «:» в многомерных массивах

Доступ к отдельному элементу многомерного массива
Удаление размерности в многомерном массиве
Создание страниц, заполненных константами и случайными числами
Использование функций ones, zeros, rand и randn
Объединение массивов
Работа с размерностями
Вычисление числа размерностей массива
Вычисление размера размерности массива
Перестановки размерностей массивов
Сдвиг размерностей массивов
Удаление единичных размерностей
Что нового мы узнали?

Для вычисления размера каждой размерности массива используется функция size:

М = size(A. DIM) возвращает размер размерности, указанной скаляром DIM, в виде вектора-строки размером 2. Для двумерного или одномерного массива А size(A.l) возвращает число рядов, a size (А, 2) — число столбцов;

Для N-мерных массивов А при n>2 size(A) возвращает N-мерный вектор-строку, отражающий страничную организацию массива, последняя составляющая этого вектора равна N. В векторе отсутствуют данные о единичных размерностях (тех, где расположены вектор-строка или вектор-столбец, т. е. size(A,DIM)==l). Исключение представляют N-мерные массивы Java массивов javaarray, которые возвращают размер массива самого высокого уровня.

Вообще, когда входным аргументом size является javaarray, то возвращаемое число столбцов всегда 1, а число рядов (строк) равно размеру (длине) javarray.

[Ml, М2 ,МЗ,. .., MN] = si ze(A) возвращает размер первых N размерностей массива А;

D = size (А), для mxn матрицы А возвращает двухэлементный вектор-строку, в котором первая составляющая — число строк т, а вторая составляющая — число столбцов n;

[m.n] = size(A) возвращает число рядов и столбцов в разных выходных параметрах (выходных аргументах в терминологии MATLAB) тип.

Нравится

Твитнуть

Теги MatLab САПР

Сюжеты MatLab

Знакомство с матричной лабораторией MATLAB MatLab

8268 0

Визуализация и графические средства MatLab

9818 0

Техническая документация по системе MatLab

6314 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.

1$ количество векторов в базисе соответствует количеству свободных переменных.

Нам говорят, что все решения $\mathbf{x}$ данного матричного уравнения

$$A\mathbf{x} = \mathbf{b}\tag1$$, где

$$\mathbf{b} = \begin{bmatrix}1\\2\\3\\4\\5\end{bmatrix}$$

имеют вид $\mathbf{x} = \mathbf{p} + s\mathbf{q }$ для $s \in \mathbb{R}$, где

$$\mathbf{p} = \begin{bmatrix}1\\2\\3\\4\end{bmatrix} \qquad \text{и } \qquad \mathbf{q} = \begin{bmatrix}2\\3\\4\\5\end{bmatrix} \tag2$$

[Вектор $\mathbf{p}$ называется частное решение уравнения (1).]

Пусть $X$ обозначает множество решений уравнения (1), то есть $X = \{\mathbf{x} : \mathbf{x} = \mathbf{p} + s\mathbf{q} \text{ for } s \in \mathbb{R}\}$, и напомним, что нулевое пространство $A$ — это множество

всех векторов $\mathbf{x}$, которые удовлетворяют уравнению

$$A\mathbf{x} = \mathbf{0} \tag3$$

Существует тесная связь между векторами в $X$ и векторами в $\mathrm{Nul}\, A$ . Обозначим множество $Z = X — X = \{\mathbf{z} : \mathbf{z} = \mathbf{x} — \mathbf{y} \text{ для }\mathbf{x}, \mathbf{y } \in X\}$ и заметим, что любой $\mathbf{z} \in Z$ является решением (3).

$$A\mathbf{z} = A(\mathbf{x} — \mathbf{y}) = A\mathbf{x} — A\mathbf{y} = \mathbf{b} — \mathbf{b } = \mathbf{0} \qquad \text{где $\mathbf{x},\mathbf{y} \in X$} $$

Таким образом, $Z \subset \mathrm{Nul}\, A$.

Поскольку $\mathbf{x} = \mathbf{p} + r\mathbf{q}$ и $\mathbf{y} = \mathbf{p} + s\mathbf{q}$ для некоторых $r,s \in \mathbb{R}$ имеем $\mathbf{z} = \mathbf{x} — \mathbf{y} = (r-s)\mathbf{q}$. Таким образом, любой $\mathbf{z} \in Z$ можно записать в виде $t\mathbf{q}$ (выбираем $t = r -s$), и каждому вектору $t\mathbf{q}$ соответствует вектору $\mathbf{z} \in Z$ (выберите $r-s =t$). Другими словами, $Z = \mathrm{Span}\{\mathbf{q}\}$, поэтому аналогично имеем $\mathrm{Span}\{\mathbf{q}\} \subset \mathrm{Nul} \, А$.

Далее мы покажем, что каждый вектор в нуль-пространстве $A$ находится в $\mathrm{Span}\, \{\mathbf{q}\}$.

Пусть $\mathbf{x} = \mathbf{p} + r\mathbf{q}$, где $r \in \mathbb{R}$ (то есть $\mathbf{x} \in X$), и пусть $\mathbf{u} \in \mathrm{Nul}\, A$. Тогда имеем

$$A(\mathbf{x} + \mathbf{u}) = A(\mathbf{p} + r\mathbf{q} + \mathbf{u}) = A(\mathbf{ p} + \mathbf{u}) + A(r\mathbf{q}) = A(\mathbf{p} + \mathbf{u}) = \mathbf{b} + \mathbf{0} = \mathbf{ b}$$

Таким образом, $\mathbf{p} + \mathbf{u}$ является решением (1) и должно иметь вид $\mathbf{p} + s\mathbf{q}$. то есть

$$\mathbf{p} + \mathbf{u} = \mathbf{p} + s\mathbf{q} \quad \text{или эквивалентно} \quad \mathbf{u} = s\mathbf{q} \quad \text{для некоторого $s \in \mathbb{R}$}$$

Таким образом, если $\mathbf{u} \in \mathrm{Nul}\, A$, $\mathbf{u}$ является скалярным числом, кратным $\mathbf{q}$, что по определению означает, что $\mathbf{u} \in \mathrm{Span}\{\mathbf{q}\}$.

Как мы показали, $\mathrm{Nul}\, A \subset \mathrm{Span} \{\mathbf{q}\}$ и $\mathrm{Span} \{\mathbf{q}\} \ подмножество \mathrm{Nul}\, A$, мы имеем, что $\mathrm{Span} \{\mathbf{q}\} = \mathrm{Nul}\, A$. 9n s_i \mathbf{q}_i$$

, где $\mathbf{p} \ne \mathbf{0}$ обозначает частное решение неоднородной системы, $s_i$ обозначает свободную переменную, а каждая $\mathbf{ q}_i$ аналогичен $\mathbf{q}$ из (2). Отсюда мы покажем, что каждый $\mathbf{q}_i \in \mathrm{Nul}\, A$ и что если $\mathbf{x} \in \mathrm{Nul}\, A$, то $\ mathbf{x} \in \mathrm{Span}\{\mathbf{q}_1,\dotsc,\mathbf{q}_n\}$. Подтверждение линейной независимости множества $\{\mathbf{q}_1,\dotsc,\mathbf{q}_n\}$ устанавливает $\{\mathbf{q}_1,\dotsc,\mathbf{q}_n\ }$ в качестве основы для $\mathrm{Nul}\, A$ с $n$ векторами, так что мы можем заключить, что $\mathrm{dim}(\mathrm{Nul}\, A) = n$.

Как найти размерность, недействительность и ранг векторного пространства — Криста Кинг Математика

Определение размерности векторного набора

В этом уроке мы хотим поговорить о размерности векторного набора, который, начнем с того, что он полностью отличается от размерности матрицы.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

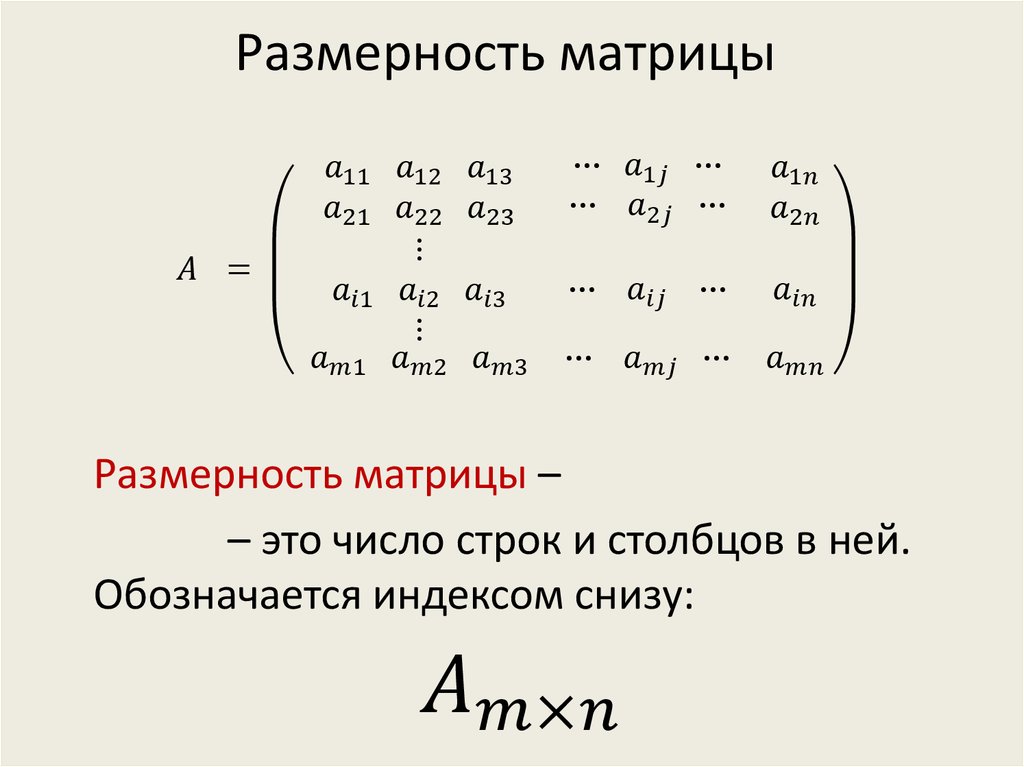
Как мы уже знаем, размеры матрицы всегда определяются количеством строк и столбцов, как

???\text{dimensions}=\text{\#rows}\times\text{\#columns} ???

Но размерность векторного пространства относится совсем к другому. Существует множество различных способов описания размерности, и мы можем сделать множество выводов о пространстве, зная его размерность, но сейчас давайте просто скажем, что размерность векторного пространства определяется количеством базисных векторов, необходимых для охвата этого пространства. космос.

Говоря о векторных пространствах, мы только что рассмотрели два очень важных: нулевое пространство и пространство столбцов. Итак, давайте уделим немного времени, чтобы поговорить о измерении каждого из этих пространств.

Размерность пустого пространства (недействительность)

Размерность нулевого пространства матрицы ???A??? также называется ничтожностью ???A??? и может быть записан как ???\text{Dim}(N(A))??? или ???\text{недействительность}(A)???.

Недействительность матрицы всегда определяется количеством свободных переменных (неосновных переменных) в системе. Таким образом, если мы поместим матрицу в сокращенную ступенчатую форму, мы сможем быстро идентифицировать как опорные столбцы (с опорными переменными), так и свободные столбцы (со свободными переменными). Количество свободных переменных равно нулю матрицы.

Причина, по которой мы можем получить нулевое значение из свободных переменных, заключается в том, что каждая свободная переменная в матрице связана с одним линейно независимым вектором в пустом пространстве. Это означает, что нам понадобится один базисный вектор для каждой свободной переменной, так что количество базисных векторов, необходимых для покрытия нулевого пространства, определяется количеством свободных переменных в матрице.

Как найти размерность, недействительность и ранг любой матрицы

Пройти курс

Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого.

🙂

Нахождение неравенства матрицы

Пример

Нахождение неравенства ???K???.

Чтобы найти нулевую матрицу, нам нужно сначала найти нулевое пространство, поэтому мы настроим расширенную матрицу для ???K\vec{x}=\vec{O}???, затем поместим матрица в редуцированной строчно-эшелонной форме.

Обычно на этом этапе мы бы переписали эту матрицу в виде системы уравнений на пути к поиску нулевого пространства. Но на самом деле мы можем найти недействительность непосредственно из матрицы rref. Мы видим, что первый столбец — это сводной столбец, а остальные три столбца — свободные столбцы со свободными переменными. Поскольку есть три свободных переменных, значение nullity равно

???\text{Dim}(N(K))=\text{nullity}(K)=3???

Мы можем подтвердить это, если найдем нулевое пространство. Матрица rref может быть записана просто как уравнение

???x_1-2x_2+x_3+3x_4=0???

, которые мы можем решить для одной опорной переменной.

???x_1=2x_2-x_3-3x_4???

Мы можем переписать это как линейную комбинацию.

???\begin{bmatrix}x_1\\ x_2\\ x_3\\ x_4\end{bmatrix}=x_2\begin{bmatrix}2\\ 1\\ 0\\ 0\end{bmatrix}+x_3\ begin{bmatrix}-1\\ 0\\ 1\\ 0\end{bmatrix}+x_4\begin{bmatrix}-3\\ 0\\ 0\\ 1\end{bmatrix}???

Тогда нулевое пространство ???K??? является размахом векторов в этом линейном комбинационном уравнении.

???N(K)=\text{Span}\Big(\begin{bmatrix}2\\ 1\\ 0\\ 0\end{bmatrix},\begin{bmatrix}-1\\ 0\ \ 1\\ 0\end{bmatrix},\begin{bmatrix}-3\\ 0\\ 0\\ 1\end{bmatrix}\Big)???

Пустое пространство подтверждает то, что мы уже узнали о размерности нулевого пространства. Мы нашли ???3??? связующие векторы, которые образуют основу для нулевого пространства, которое соответствует размерности нулевого пространства, ???\text{Dim}(N(K))=\text{nullity}(K)=3???.

Размер пространства столбца (ранг)

Аналогично размерность пространства столбцов матрицы ???A??? также называется рангом ???A??? и может быть записан как ???\text{Dim}(C(A))??? или ???\text{ранг}(A)???.

Ранг матрицы всегда определяется количеством опорных переменных в системе. Таким образом, если мы поместим матрицу в сокращенную ступенчатую форму, мы сможем быстро идентифицировать опорные столбцы (с опорными переменными). Количество опорных переменных является рангом матрицы.

Причина, по которой мы можем получить ранг по опорным переменным, заключается в том, что каждая опорная переменная в матрице связана с одним линейно независимым вектором в пространстве столбцов. Это означает, что нам понадобится один базисный вектор для каждой сводной переменной, так что количество базисных векторов, необходимых для охвата пространства столбца, определяется количеством сводных переменных в матрице.

Давайте посмотрим на пример, где мы возвращаем матрицу из урока о пространстве столбцов матрицы.

Пример

Найти ранг ???A???.

Чтобы найти ранг матрицы, нам нужно сначала представить матрицу в сокращенном строково-эшелонном виде. Мы уже делали это в предыдущем уроке, поэтому здесь мы сократим шаги.

Теперь, когда матрица представлена в сокращенной ступенчато-строковой форме, мы можем найти ранг непосредственно из матрицы. Мы видим, что первые три столбца — это сводные столбцы (с опорными переменными), а последний столбец — свободный столбец. Поскольку есть три опорных переменных, ранг равен 9.0005

???\text{Dim}(C(A))=\text{rank}(A)=3???

Тогда пространство столбца ???A??? является диапазоном первых трех векторов-столбцов ???A???, так как это были столбцы, которые стали опорными столбцами, когда мы поместили матрицу в rref.

И это подтверждает то, что мы уже узнали о размерности пространства столбца. Мы говорим, что есть ???3??? связующие векторы, которые образуют основу для пространства столбцов, которое соответствует размерности пространства столбцов, ???\text{Dim}(C(A))=3???.