Как выглядит прямая: Точка, прямая линия, кривая и отрезок — урок. Математика, 1 класс. — Primelens.ru-Зеркальные Фотоаппараты,Компактные Фотоаппараты,Видеокамеры,Объективы,Фотовспышки, и Аксессуары в Москве.

Как выглядит прямая: Точка, прямая линия, кривая и отрезок — урок. Математика, 1 класс.

Содержание

1 класс, прямая, отрезок, точка, урок и презентация по математике луч, ломанная

Дата публикации: 08 апреля 2017.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Скачать:Точка, прямая и кривая линии, отрезок, луч, ломаная (PPTX)

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 1 класса
Тренажер по Дорофееву Г.В. Тренажер по Демидовой Т.Е.

Точка

Дорогие ребята, сегодня вместе с нашими героями мы будем изучать простейшие геометрические фигуры.

Начнем с точки. В математике точка обозначается буквой алфавита, например, буквой А. В тетради это выглядит так.

Если у вас на рисунке есть несколько точек, то их необходимо называть разными буквами, чтобы не путаться.

Линии

Вжик нарисовал линию.

В математике линию принято обозначать строчными латинскими буквами, например, буквой b.

Если на рисунке несколько линий, то разные линии нужно обозначать разными буквами.

Прямая линия
Линия называется прямой, если она нигде не искривляется.
Вжик нарисовал несколько прямых линий разного цвета.
В математике прямая линия бесконечная, а это значит, что у неё нет ни начала, ни конца.

Кривая линия
Чип нарисовал несколько кривых линий. Каждый может их нарисовать от руки.

Отрезок
Если отрезать от прямой линии некоторую часть, то получится отрезок с началом и концом, что мы попробуем сделать. Получится отрезок AB. У данного отрезка есть длина, и обозначается она так, АB = 4 см.

На этом рисунке нарисовано 2 отрезка: АВ и СЕ.

Луч
Луч – часть прямой, которая имеет начало, но не имеет конца. Обозначается, как показано на рисунке.

Ломаная линия
Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.

Ломаная на рисунке обозначается $A_1A_2A_3A_4A_5A_6$.

Ребята, определите, какие фигуры изображены на рисунке? Назовите каждую фигуру.

Методические указания по теме:

По программе ученики начальных классов знакомятся с плоскостными фигурами, именуемыми вообще многоугольниками; в частности с различного вида треугольниками, прямоугольниками и другими видами четырех-угольников, фигурами с большим числом сторон: пятиугольниками, шестиугольниками, которые легко можно разбить на треугольники и четырехугольники.
При ознакомлении с указанными фигурами необходимо с самых первых шагов (когда дети пользуются различными фигурами как дидактическим материалом) дать практически понятие детям о том, что треугольник, четырехугольник, прямоугольник, квадрат и вообще многоугольник— это часть плоскости (поверхность бумаги, картона, фанеры, ткани), ограниченная сторонами — отрезками прямых линий, как в прямоугольнике или треугольнике, или кривой линией, как в круге, или кривой и прямой, как в полукруге.

Надо избегать обычной, повторяющейся и в пособиях, и в учебниках ошибки, заключающейся в том, что вместо понятия о треугольнике, четырехугольнике и вообще о всяком многоугольнике детям внедряется понятие о контуре этой фигуры. Например, ученика спрашивают, сколько нужно взять палочек, что-бы сложить квадрат (вместо того чтобы спросить, сколько надо взять палочек, чтобы составить контур, границы квадрата). После таких вопросов ученик начинает думать, что квадрат, треугольник, прямоугольник можно сделать из палочек.
Чтобы избежать этих ошибок, мы предлагаем знакомство с треугольником, прямоугольником и любым многоугольником начинать путем вырезывания этой фигуры из бумаги (контур фигуры очерчивается по линейке карандашом, а затем по начерченному контуру ножницами или ножичком вырезывается фигура). Вторым этапом ознакомления с такими фигурами являются чертежи на бумаге с обязательной затушевкой. Пусть ученик знает, что когда он начертил только стороны треугольника или квадрата, то это только контур (границы) фигуры, а когда он сделает затушевку, то будет видеть всю фигуру.

Если же учитель желает провести с учениками практическую работу с палочками, то им можно предложить примерно такие вопросы:
1) Сколько надо взять палочек и каких, чтобы из них сложить все стороны (или границы) квадрата? треугольника с равными сторонами?
2) Какая получится линия из сторон квадрата, если убрать одну сторону квадрата, т. е. одну палочку? (Получится ломаная линия из трех равных отрезков.) И т. п.
При изучении сотни ученики I класса знакомятся с мерами длины — сантиметром, дециметром и метром, а также с мерой массы — килограммом и с мерой емкости— литром. С мерой длины сантиметром желательно познакомить детей раньше, лучше в самом начале за¬нятий, так как знакомство с этой мерой даст возможность разнообразить занятия различными задачами практического характера.
Практика:
52. Начертите три прямые линии: одну —слева направо (по строке), другую — снизу вверх, третью — наискось. Подумайте и скажите, можно ли каждую из этих линий продолжить в обе стороны.

Чертите хорошо отто-ченным карандашом по линейке слева направо. Линейку придерживайте левой рукой, а карандаш — наклонно.
Указание. Надо показать, как правильно проводить прямую линию. Для этого можно листок клетчатой бумаги при¬крепить кнопками к доске и по¬казать, как держать линейку и вести карандаш. После этого необходимо проследить, как каждый из учеников выполняет это задание, и тем, кто делает неправильно, показать в тетради, как надо держать линейку и карандаш. Если этого не сделать вначале, то потом уйдет больше времени на поправки и указания.

53. Отметьте в тетради точку и проведите через нее две прямые линии. Подумайте, можно ли через эту же точку провести еще прямые линии. Проведите еще две прямые через эту точку и скажите, сколько еще можно провести прямых линий через ту же точку.
Указание. Дети должны сделать вывод, что через одну точку можно провести сколько угодно прямых.
54. Отметьте две точки и проведите через них прямую линию. Можно ли через эти две точки провести еще прямую линию, чтобы она не слилась с первой? Теперь попробуйте провести кривую линию, чтобы она прошла через те же две точки.

Можно ли еще через те же две точки провести кривую линию? А сколько кривых линий можно провести через две точки?

55. Начертите 6 пар прямых линий. Всмотритесь в них внимательно и скажите, чем отличаются друг от друга 1, 3 и 6-я пары линий от 2, 4 и 5-й пар.
Найдите у себя в тетрадях и в классе такие пары прямых линий, как 1, 3, 6-я. Такие линии не пересекаются друг с другом. Их много в окружающей нас обстановке (две противоположных стороны тетради, окна, двери и т. п.). Найдите теперь такие две пары линий, которые пересекаются, как 2, 4, 5-я. Их тоже можно найти в тетрадях и в классе.
56. Начертите пару непересекающихся прямых и пару пересекающихся прямых. Все прямые линии на бумаге или на доске чертятся не полностью, они могут быть продолжены в обе стороны сколько угодно.
57. На этом чертеже даны две прямые линии. Какие они — пересекающиеся или непересекающиеся? Как это узнать? Как найти точку их пересечения?
Указание. Ученики должны догадаться, что обе эти прямые надо продолжить вправо.

58. Начертите две такие прямые линии, которые на чертеже не пересекаются, но должны пересечься при продолжении, и найдите точку их пересечения.
59. Начертите прямую линию и пересеките ее в двух местах черточками (штрихами). Этими черточками мы ограничиваем (отрезаем) кусочек прямой линии, и эта часть прямой линии от одной черточки до другой называется отрезком прямой линии или просто отрезком. Вокруг вас много отрезков: ребра (стороны) тетради, стекла, доски, двери — все это части прямых линий, которые ограничены с двух концов, значит, они являются отрезками.
60. Отметьте на бумаге две точки и проведите через них прямую линию. Как можно назвать ту часть линии, которая находится между точками? Можно ли провести другой отрезок между теми же точками, который не сов-пал бы с первым отрезком?

Отрезок — что это такое

Обновлено 30 января 2023 Просмотров: 176 938 Автор: Дмитрий Петров

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.

Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.

Отрезок — это геометрическая фигура

Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.

На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.

В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.

Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.

Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.

Разница между отрезком, лучом и прямой

Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:

Прямой называется линия, которая не искривляется, а также не имеет начала и конца.
Луч — это часть прямой, ограниченная одной точкой. Он имеет начало и не имеет конца.
Отрезок ограничивается двумя точками. Он имеет и начало, и конец.

Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.

Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.

Направленный отрезок — это вектор

Отрезки бывают двух видов:

Ненаправленные.
Направленные.

Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.

Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ^➜ и ВА^➜ — разные отрезки, так как они противоположно направленные.

Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.

Модулем вектора называется длина направленного отрезка. Обозначается как АВ^➜. Модули векторов АВ^➜ и ВА^➜ равны.

Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.

Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.

Ломаная линия — это множество соединенных отрезков

Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.

Вершинами ломаной являются следующие точки:

Точка, с которой началась ломаная.
Точка, которой ломаная закончилась.
Точки, в которых соединяются смежные звенья (отрезки ломаной).

Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.

Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.

Любая замкнутая ломаная является геометрической фигурой — многоугольником.

Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.

Отрезок времени

Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.

Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.

Время в целом в таком случае определяется как временная прямая.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Математика

Прямая линия — уравнения, определение, свойства, примеры

Прямая линия — это бесконечная одномерная фигура, не имеющая ширины. Это комбинация бесконечных точек, соединенных по обе стороны от точки. Прямая линия не имеет в себе никакой кривой. Он может быть горизонтальным, вертикальным или наклонным. Если мы начертим угол между любыми двумя точками на прямой линии, мы всегда получим 180 градусов.

В этом мини-уроке мы будем исследовать мир прямых линий, разбираясь в уравнениях прямых линий в различных форматах и как решать вопросы, основанные на прямых линиях.

1.	Что такое прямая линия?
2.	Типы прямых линий
3.	Свойства прямой линии
4.	Уравнение прямой
5.	Типы уклонов
6.	Часто задаваемые вопросы (FAQ)

Что такое прямая линия?

Прямая линия — это линия бесконечной длины, на которой нет кривых. Прямую можно провести и между двумя точками, но оба ее конца уходят в бесконечность. Прямая линия – это фигура, образованная двумя точками А (х

1 , у ₁) и В (х ₂, у ₂) соединенными кратчайшим расстоянием между ними, а концы прямой продолжены до бесконечности.

На изображении ниже показана прямая линия между двумя точками A и B. Прямая линия AB представлена: $\overleftrightarrow{A B}$

Хотя прямые линии не имеют определенного начала или конца, в нашей повседневной жизни они представлены такими примерами, как железнодорожные пути или Автострада.

Типы прямых линий

Прямые линии могут быть различных типов. Как правило, прямые линии классифицируются на основе их выравнивания. Их выравнивание относится к углу, который они образуют с осью x или осью y. По расположению прямых линий они бывают следующих видов:

Горизонтальные линии
Вертикальные линии
Косые или наклонные линии

Давайте рассмотрим их один за другим.

Горизонтальные линии

Линии, проведенные горизонтально и параллельные оси X или перпендикулярные оси Y, называются горизонтальными линиями. Они образуют угол 0 ^o или 180 ^o с осью x и угол 90 ^o или 270 ^o с осью y.

На данном рисунке $\overleftrightarrow{\text{AB}}$ — горизонтальная линия.

Вертикальные линии

Линии, проведенные вертикально и параллельные оси Y или перпендикулярные оси X, называются вертикальными линиями. Они образуют угол 90 ^o или 270 ^o с осью x и угол 0 ^o или 180 ^o с осью y.

На данном рисунке $\overleftrightarrow{\text{CD}}$ — вертикальная линия.

Наклонные или наклонные линии

Линии нарисованы под наклоном или образуют угол, отличный от 0 ^o , 90 ^o , 180 ^o , 270 ^o , 360 ^o с горизонтальными или вертикальными линиями называются косыми или наклонными линиями.

На данном рисунке $\overleftrightarrow{\text{EF}}$ и $\overleftrightarrow{\text{GH}}$ — наклонные линии.

Свойства прямой линии

Свойства прямых описаны ниже.

Прямая имеет бесконечную длину. Мы никогда не сможем вычислить расстояние между двумя крайними точками линии.
Прямая линия имеет нулевые площади, нулевой объем. но имеет бесконечную длину.
Прямая линия – это одномерная фигура.
Через одну точку может проходить бесконечное количество линий, но только одна уникальная линия проходит через две точки.

Уравнение прямой

Уравнение прямой является линейным уравнением. Прямая линия на декартовой плоскости может иметь различные представления, основанные на известных переменных, углах и константах. Наклон прямой линии определяет направление прямой линии и говорит о том, насколько она крутая. Он рассчитывается как разница в координатах y/разница в координатах x, что также называется превышением пробега. Уравнение прямой имеет различные формы. Они следующие:

Общее уравнение прямой линии

Общее уравнение прямой линии можно представить как ax + by + c = 0, где

a, b, c — константы, а
x, y — переменные.
Наклон -a/b

Наклон и точка пересечения с Y Форма

Прямая линия, имеющая наклон m = tanθ, где θ — угол, образованный линией с положительной осью x, и точка пересечения с осью y, поскольку b определяется как: y = mx + b, где m — наклон.

Форма точки наклона

Прямая линия, имеющая наклон m = tanθ, где θ — угол, образованный линией с положительной осью x и проходящая через точку (x ₁ , y ₁ ), равна определяется как: Форма точки наклона как y — y ₁ = m(x — x ₁ )

Форма двух точек

Прямая линия, проходящая через точки (x ₁ , y ₁ ) и (x ₂ , y ₂ ) задается в двухточечной форме как: y — y ₁ = [(у ₂ — у ₁ ) / (х ₂ — х ₁ )] (х — х ₁ ).

Форма точки пересечения

Прямая линия, имеющая точку пересечения x как a и точку пересечения y как b, как показано на рисунке ниже, где точка A находится на оси x (здесь вертикальная), а точка B находится на оси y. оси (здесь горизонтальной), задается в виде точки пересечения как x/a + y/b = 1

Уравнение прямых, параллельных оси X или оси Y

Уравнение прямой, параллельной оси x- ось определяется как: y = ± a, где

a — расстояние линии от оси x. Значение a равно +ve, если оно лежит выше оси x, и n-ve, если оно лежит ниже оси x.

Уравнение прямой, параллельной оси Y. определяется как: x = ± b, где

b — расстояние линии от оси y. Значение b равно +ve, если оно лежит справа от оси y, и -ve, если оно лежит слева от оси y.

Ниже приведено изображение линий, параллельных оси x и оси y соответственно.

Типы уклонов

Угол, образованный линией с положительной осью x, является наклоном линии. Разные линии образуют разные углы с осью x. У линии могут быть наклоны, меняющиеся от положительного, отрицательного, нулевого или даже бесконечного наклона. Давайте посмотрим на некоторые случаи.

Нулевой наклон

Если линия образует угол 0 ^o с осью x, наклон линии равен 0. Наклон линии представлен m = tanθ

Здесь θ = 0 ^или . Следовательно, m = tan0 = 0. Следовательно, линия с наклоном 0 параллельна оси x.

Положительный наклон

Если линия образует угол между 0 ^o и 90 ^o с осью x, наклон линии положительный.

Отрицательный наклон

Если линия образует угол между 90 ^o и 180 ^o с осью x, наклон линии отрицательный.

Бесконечный наклон

Если линия образует угол 90 ^o с осью x или линия параллельна оси y, наклон линии не определен или бесконечен.

Как известно, наклон прямой m = tan θ

Здесь θ = 90 ^o . уклон m = tan 90 ^o не определен. Следовательно, линия с бесконечным наклоном параллельна оси у.

Важные замечания о прямой линии

Вот несколько пунктов, которые следует помнить при изучении прямой линии:

Прямая не может проходить через три точки, не лежащие на одной прямой.
Если две прямые l и m совпадают, они следуют соотношению l = k × m, где k — действительное число.
Острый угол θ между двумя линиями, имеющими наклоны m ₁ и m ₂ , где m ₂ > m ₁, можно вычислить по формуле tanθ =(m ₂ — m _{1 9 0052 )/ (1 + m ₂ × m ₁ ).}

☛Связанные темы

Вот список тем, связанных с прямой линией:

Расстояние между двумя линиями
Калькулятор уравнения прямой
Форма уклона точки

Примеры прямых линий

Пример 1: Для прямой линии y = -3x + 2, что такое:
а) склон
б) y-перехват?
Раствор
Для общей прямой линии y = mx + b координата y точки пересечения с осью y представляет b, а наклон равен m.
В этом случае m = -3 и b = 2
Ответ:
Пример 2: Пол рисует прямую на декартовой плоскости с уравнением y = 2x — 1, а его сестра рисует прямую 2y = x + 1, Пол говорит, что прямые пересекаются во 2-м квадранте, а его сестра говорит, что прямые пересекаются в 1-м квадранте, кто прав.
Решение
Дано:
Прямая, проведенная Полом, равна y = 2x — 1
Его сестра нарисовала прямую 2y = x +1
Давайте решим эти два уравнения одновременно, чтобы найти точку пересечения.
у = 2х — 1
2у = х + 1
Когда мы решим эти два уравнения одновременно, мы получим
х = 1 и у = 1
Обе прямые пересекаются в точке (1, 1)
Точка пересечения лежит в первом квадранте
Ответ: Сестра Пола права.
Пример 3: Колония расположена на декартовой плоскости, дом Мэтью расположен в точке (4, 3) и дом Джима расположен в точке (7, -2) две дороги должны быть построены из квадрата, расположенного в точке ( 3, 2), выяснить, перпендикулярны ли эти две дороги друг другу или нет (при условии, что дороги образуют прямую линию).
Решение
Предположим, что дом Мэтью находится в точке P (4, 3)
Дом Джима расположен в точке Q (7, -2)
Квадрат расположен в точке R (3, 2)
применение формулы для расчета наклона прямой между двумя точками
м = (у ₂ — у ₁ ) / (х ₂ — х ₁ )
Наклон линии между точками P и R равен
. м ₁ =(3 — 2)/(4 — 3)
м ₁ = 1
Наклон линии между точками Q и R равен
. м ₂ =(-2 — 2}{7 — 3}
м ₂ =(-4}{4}
м ₂ = -1
Если две прямые перпендикулярны друг другу, то произведение их наклонов равно -1.
м ₁ × м ₂ = 1 × -1
m ₁ × m ₂ = -1
Ответ: Дороги перпендикулярны друг другу.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по прямым линиям

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о прямых линиях

Что вы понимаете под прямой линией в геометрии?

Прямая линия представляет собой бесконечную фигуру без ширины. Это комбинация бесконечных точек, соединенных с обоих концов. Он не имеет кривых или вообще не имеет кривых. Он может быть вертикальным, горизонтальным или наклонным. Проще говоря, для детей дошкольного возраста мы используем прямую линию для сна или стоящую прямую линию.

Что вы используете для рисования прямой линии?

Прямую линию можно провести с помощью линейки, таврового угольника и т. д. Для проведения прямой линии между двумя точками можно также использовать различные геометрические инструменты, имеющие гладкую и плоскую поверхность. Прямая линия, проведенная между двумя точками, называется отрезком. Линейки — это широко используемый инструмент для проведения прямой линии между двумя точками или прямой линии в целом.

В чем разница между параллельными и перпендикулярными прямыми линиями?

Угол между двумя параллельными прямыми равен 0 градусов, а угол между двумя перпендикулярными прямыми равен 90 ^∘ . Параллельные линии выровнены в направлении друг друга, тогда как перпендикулярные линии выровнены под углом 90 ^∘ друг к другу. Наклоны параллельных линий равны друг другу, тогда как наклоны перпендикулярных линий не равны друг другу, а наклон одной линии равен отрицательной обратной величине наклона другой линии.

Каков наклон прямой линии?

Угол, образованный линией с положительной осью x, представляет собой наклон линии, состоящей из разных линий под разными углами с осью x. У линии могут быть наклоны, меняющиеся от положительного, отрицательного, нулевого или даже бесконечного наклона. Наклон линии специально измеряется по оси X или по горизонтальной линии. Чтобы измерить наклон любой линии, мы проводим горизонтальную линию из любой точки на данной линии и измеряем угол против часовой стрелки от горизонтальной линии до данной линии, а затем вычисляем тангенс θ данного угла.

Какое общее уравнение прямой линии?

Общее уравнение прямой может быть представлено как ax + by + c = 0, где

a, b, c — константы, а
x, y — переменные.

Какой угол между двумя перпендикулярными прямыми?

Угол между двумя перпендикулярными линиями равен 90 градусов. Две перпендикулярные прямые выровнены таким образом, что произведение наклонов двух прямых равно -1. Везде видны перпендикулярные линии, например угол стола, угол комнаты и т. д., и мы можем измерить угол между сторонами и узнать, что угол между перпендикулярными линиями равен 90 градусов.

Что такое параллельные прямые?

Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются. Параллельные линии имеют отклонение друг от друга на 0 или 180 градусов. Они выровнены в одном направлении друг с другом. Если у нас есть две параллельные прямые, где нам известен наклон одной прямой, то мы можем приравнять наклон другой прямой, равной первой прямой, и узнать наклон другой прямой.

Что такое прямая линия? (Определение, видео и примеры)

Автор:

Малкольм МакКинзи

11 января 2023 г.

Факт проверен

Пол Маццола

Что такое прямая линия? (Определение, видео и примеры)

Хорошо, давайте проясним одну вещь… то есть прямую линию.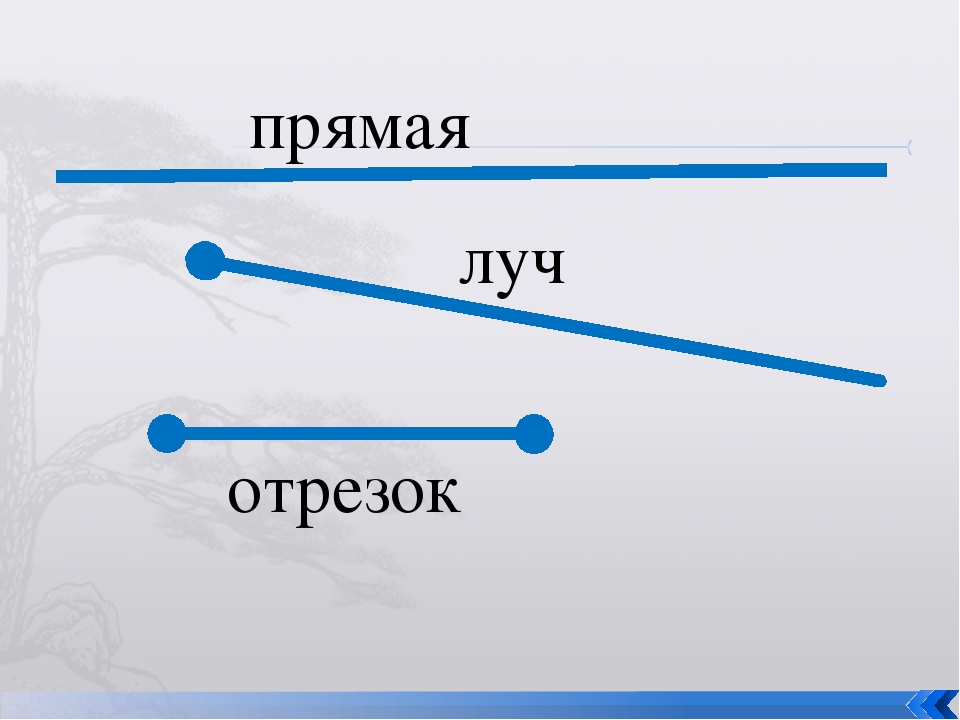 Что может быть проще в геометрии, чем изящная, редкая, прямая линия? (Честно говоря, точка 90 527 — это 90 528 проще; совокупность точек образует прямую линию.) Прямая линия может показаться банальной, но она немного сложнее и может даже замаскироваться.

Что такое прямая?

По определению, прямая – это множество всех точек между двумя точками и за их пределами. В большинстве геометрий линия представляет собой примитивный объект, который не имеет формальных свойств, кроме длины, своего единственного измерения.

Два свойства прямых линий в евклидовой геометрии заключаются в том, что они имеют только одно измерение, длину, и всегда тянутся в двух направлениях.

Свойства прямых линий

Одномерный
Может быть горизонтальным, вертикальным или диагональным
Оба конца продолжаются в двух направлениях навсегда

Что такое точка?

точка это простейшая фигура в геометрии. Это место в пространстве, без измерения. У него нет ни ширины, ни объема, ни толщины, ни длины, ни глубины. Но когда у вас есть две точки, если вы соедините каждую точку между этими двумя точками, у вас получится прямая линия.

Точки на линии коллинеарны (столбцы = «с», или «вместе» и линейные = «строка», или «линия» ).

Для определения линии нужны только две точки.

Именование и определение прямых линий

Прямые линии называются любыми двумя точками на их длине. Обычно вы называете их слева направо.

Чтобы обозначить линию на письме, вы пишете две точки заглавными буквами и рисуете крошечную двустороннюю линию над двумя буквами, например, AB↔\overleftrightarrow{AB}AB.

Как построить прямую линию

Прямая линия — одно из самых простых построений в геометрии. С помощью листа чистой бумаги, карандаша и линейки вы можете легко провести линию:

Начертите на бумаге две точки на некотором расстоянии друг от друга; это Точки
Используйте линейку, чтобы соединить две Точки карандашной линией, и продлите линию далеко за обе Точки
Нарисуйте стрелки на концах нарисованной линии

Отрезки и лучи

Прямые линии считаются бесконечными в двух направлениях по их длине. Из-за этого вы редко используете чистые линии в повседневной геометрии. Вы берете фрагменты прямых линий:

Отрезок линии — Отрезок линии — это сегмент или конечная часть бесконечной прямой линии
Луч — Луч — это бесконечный участок прямой линии ; имеет одну точку начала, но всегда продолжается в одном направлении

Отрезки линий используются для построения сторон всех многоугольников. Лучи используются для создания углов. Отрезки и лучи являются частями или сегментами прямых линий.

А кривые?

Кривая не является прямой линией, так же как прямая линия не является кривой. Кривая линия содержит точки, которые не являются линейными относительно двух заданных точек. Кривая движется в других направлениях от прямой линии, созданной путем соединения коллинеарных точек.

Направление прямых

Прямые линии могут быть горизонтальными , то есть перемещаться влево и вправо от точки обзора навсегда.