Кривая — Википедия

Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».

По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.

Отображение отрезка[править | править код]

Чаще всего кривая определяется как непрерывное отображение из отрезка в топологическое пространство:

γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют

параметризованными кривыми или, если [a,b]=[0,1]{\displaystyle [a,b]=[0,1]}, путями.

Отношение эквивалентности[править | править код]

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

γ1:[a1,b1]→X{\displaystyle \gamma _{1}\colon [a_{1},b_{1}]\to X} и γ2:[a2,b2]→X{\displaystyle \gamma _{2}\colon [a_{2},b_{2}]\to X}

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h{\displaystyle h} из отрезка [a1,b1]{\displaystyle [a_{1},b_{1}]} на отрезок [a2,b2]{\displaystyle [a_{2},b_{2}]}, такая что

γ1≡γ2∘h.{\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Комментарий[править | править код]

Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.

Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Кривая Жордана[править | править код]

Кривая Жордана на плоскости с положительной мерой Лебега.

Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется

замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.

Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.

Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом^[1]. .

В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R2{\displaystyle \mathbb {R} ^{2}}). Пусть x(t){\displaystyle x(t)} и y(t){\displaystyle y(t)} — функции на отрезке [a,b]{\displaystyle [a,b]}, непрерывно дифференцируемые на этом отрезке, и такие, что (x′(t))2+(y′(t))2{\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ:[a,b]→R2,t↦(x(t),y(t)){\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле

L(γ)=∫ab(x′(t))2+(y′(t))2dt.{\displaystyle {\text{L}}(\gamma )=\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt.}

Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.

Определение в дифференциальной геометрии[править | править код]

Если X{\displaystyle X} — гладкое многообразие, можно определить гладкую кривую на X{\displaystyle X} как гладкое отображение γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}, дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия X{\displaystyle X} равен k{\displaystyle k}, то Ck{\displaystyle C_{k}}-кривая вводится как кривая, для которой γ{\displaystyle \gamma } — k{\displaystyle k} раз непрерывно дифференцируемое отображение. Если X{\displaystyle X} — аналитическое многообразие (например, евклидово пространство) и γ{\displaystyle \gamma } — аналитическое отображение, кривую называют аналитической.

Гладкие кривые γ1:I→X{\displaystyle \gamma _{1}\colon I\to X} и γ2:J→X{\displaystyle \gamma _{2}\colon J\to X} называются эквивалентными, если существует диффеоморфизм p:I→J{\displaystyle p\colon I\to J} (замена параметра), такой что γ1=γ2∘p{\displaystyle \gamma _{1}=\gamma _{2}\circ p}. Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.

Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она назывется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x² + y² + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.

Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.

Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен

zd⋅f(x/z,y/z){\displaystyle z^{d}\cdot f(x/z,y/z)}

после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xⁿ + yⁿ = zⁿ в аффинной форме принимает вид xⁿ + yⁿ = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.

Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:

Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:

Типы точек на кривой[править | править код]

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L{\displaystyle L}, она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L′{\displaystyle L’}, гомеоморфное L{\displaystyle L}. Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

Впоследствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство C{\displaystyle C} топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

1. ↑ W. F. Osgood. A Jordan curve of positive area (англ.) // Trans. Am. Math. Soc.. — 1903. — Vol. 4. — P. 107–112.

ru.wikipedia.org

Кривые — это… Что такое Кривые?

Всякая линия, за исключением прямой, называется К. Если через все точки К. можно провести одну общую плоскость, то К. называется плоской. В противном случае К. называется К. двоякой кривизны. К. может быть рассматриваема или как геометрическое место точек, или как путь, пройденный движущейся точкой, или как граница поверхности. По Плюкеру, К. образуется следующим образом: точка движется по прямой, которая в это время вращается около движущейся точки в некоторой плоскости, плоскость же эта вращается около упомянутой прямой. В этом образовании движущаяся точка есть точка К., вращающаяся прямая — касательная, а вращающаяся плоскость — плоскость соприкосновения. В математике особенное внимание обращается на К., определяемые каким-нибудь законом. Закон, определяющий К., выражается уравнением между координатами точки К. Если уравнение, определяющее К., выражено в Декартовых координатах (см.), то порядок уравнения (степень высшего члена уравнения, освобожденного от радикалов над переменными и от переменных в знаменателях) показывает во скольких точках К. пересекается прямой, причем точки пересечения могут быть действительными или мнимыми. Законом образования К. называются свойства ее, достаточные для определения и изучения. Например: геометрическое место точек, сумма расстояний которых от двух данных точек есть величина постоянная, есть эллипс (фиг. 1, табл. I), который может быть выражен уравнением: x²/a²+y²/b²=1.

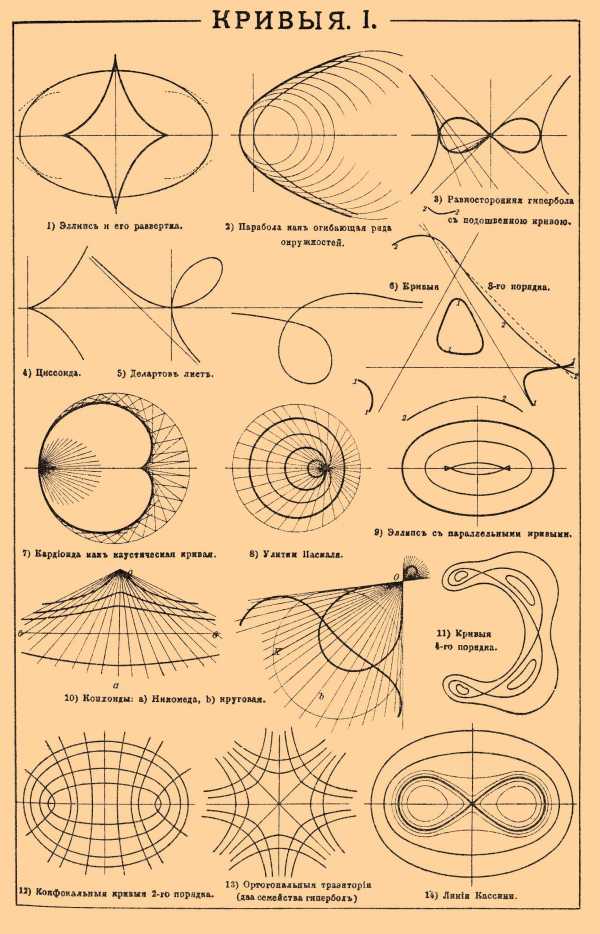
КРИВЫЕ I.

1) Эллипс и его развертка. 2) Парабола как огибающая ряда окружностей. 3) Равносторонняя гипербола с подошвенной кривой. 4) Циссоида. 5) Декартов лист. 6) Кривые 3-го порядка. 7) Кардиоида как каустическая кривая. 8) Улитки Паскаля. 9) Эллипс с параллельными кривыми. 10) Конхоиды: a) Никомеда, b) круговая. 11) Кривые 4-го порядка. 12) Конфокальные кривые 2-го порядка. 13) Ортогональные траектории (два семейства гипербол). 14) Линии Кассини.

Геометрическое место точек, равно удаленных от некоторой данной точки и от некоторой прямой, есть парабола (фиг. 2), которая может быть выражена уравнением: у²=2рх.

Геометрическое место точек, разность расстояний которых от двух данных точек есть величина постоянная, есть гипербола

(фиг. 3), которая может быть выражена уравнением: x²/a²-y²/b²=1 На фиг. 3-ей изображена также подошвенная К. гиперболы; подошвенной К. данной К. называется геометрическое место оснований перпендикуляров, опущенных из данной точки на касательные данной К. Некоторые К. удобнее выражаются в каких-либо иных координатах, например — в полярных. Если из какой-либо точки окружности будем проводить секущие и на них, начиная от пересечения с окружностью, будем откладывать одну и ту же длину, то получим ряд точек, образующих улитку Паскаля (фиг. 7 и 8), выражаемую уравнением r = а + bcosφ где: а = длина, откладываемая от окружности, b = диаметр окружности, r и φ — полярные координаты (см. Координаты). Если из какой-либо точки будем проводить прямые, пересекающие данную прямую, и на них, начиная от пересечения с данной прямой, будем откладывать одну и ту же длину, то получим ряд точек, образующих К., называемую

конхоидой (фиг. 10 а). Поступая также не с данной прямой, а с данной окружностью, получим круглую конхоиду (фиг. 10b). На фигуре 11-й изображены некоторые К. 4-го порядка. На фигуре 12-й изображена сеть, состоящая из ряда эллипсов и гипербол, имеющих одни и те же фокусы. Такая сеть конфокольных эллипсов и гипербол может служить координатной сетью для определения положения точки. Кривые, уравнения которых содержат тригонометрические функции или высшие трансцендентные функции переменных, называются трансцендентными. К ним относится между прочим: синусоида (фиг. 1, табл. II), выражаемая уравнением: у=sinx.

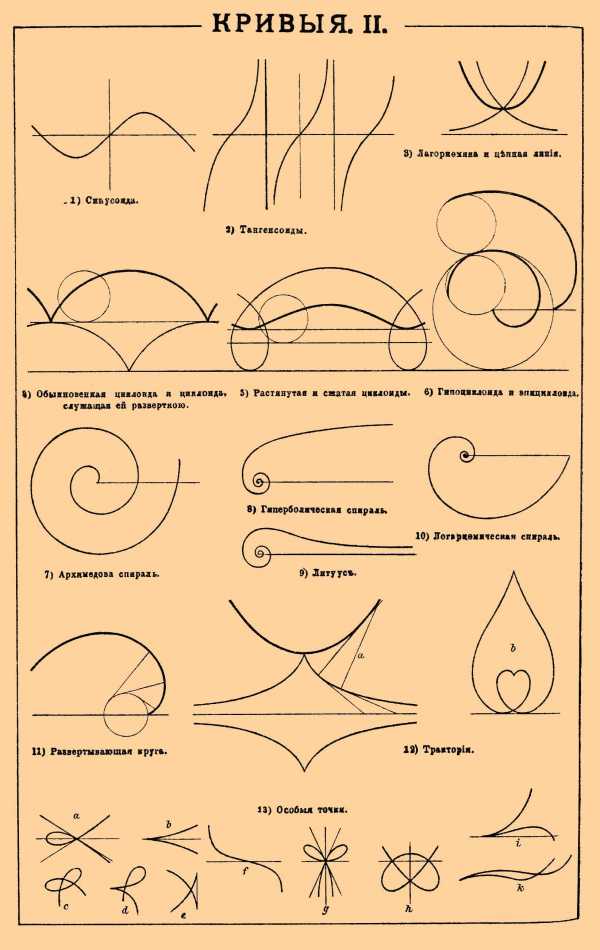
КРИВЫЕ II.

1) Синусоида. 2) Тангенсоиды. 3) Логарифмика и ценная линия. 4) Обыкновенная циклоида и циклоида, служащая ей разверткой. 5) Растянутая и сжатая циклоиды. 6) Гипоциклоида и эпициклоида. 7) Архимедова спираль. 8) Гиперболическая спираль. 9) Литуус. 10) Логарифмическая спираль. 11) Развертывающая круга. 12) Трактория. 13) Особые точки.

Тангенсоида (фиг. 2, табл. II) выражается уравнением: y =tgx. На фиг. 3-й табл. II изображены две логарифмики, из которых левая выражается уравнением x = mlgy, и цепная линия, выражаемая уравнением у=a/2[l^x/a+l^—x/a] и представляет собою вид тяжелой цепи, подвешенной за концы. На фиг. 4-й табл. II изображена циклоида, описываемая точкой обода колеса, катящегося по плоскости (точнее говоря — точкой окружности, катящейся по прямой). На фиг. 5-й табл. II изображена растянутая циклоида, описываемая точкой колеса, находящейся между ободом и центром, и сжатая циклоида, описываемая точкой, прикрепленной к колесу на расстоянии от центра большем радиуса колеса. На фиг. 6-й изображена эпициклоида,

описываемая точкой окружности, катящейся по внешней стороне неподвижной окружности, и гипоциклоида, описываемая точкой окружности катящейся по внутренней стороне неподвижной окружности. На фиг. 7-й изображена Архимедова спираль, имеющая уравнение p = аω. Гиперболическая спираль (фиг. 8) имеет уравнение рω = а. Уравнение спирали логарифмической есть p = а^ω. Точка нити, развертываемой с окружности, на которую она была намотана, описывает развертывающие окружности (фиг. 11). Каждая К., рассматриваемая как развертывающая, имеет свою развертку, то есть такую К., развертывая с которой нить можно описать данную К. Развертка эллипса (фиг. 1, табл. I). Развертка циклоиды есть циклоида (фиг. 4, табл. II). Цепная линия есть развертка трактрисы (трактории) (фиг. 12). На ф. 13 изображены особые точки К.: двойные точки (а, с, d, е, h), в которых К. пересекается сама с собой. Точка с узлом а — крунодольная. Точки возврата b — куспидольная. Точка перегиба f. Важнейшие свойства главнейших К. излагаются в курсах аналитической геометрии, дифференциального и интегрального исчислений.

Н. Д.

dic.academic.ru

Кривые и основные понятия

Понятие простой кривой.

Пусть в трехмерном пространстве выбрана прямоугольная система координат \(Oxyz\), и пусть на отрезке \([\alpha,\beta]\) заданы непрерывные функции \(x=x(t),y=y(t),z=z(t)\). Тогда говорят, что задано непрерывное отображение отрезка \([\alpha,\beta]\) в трехмерное пространство.

Рис. 22.1

Числа \(x(t),y(t),z(t)\) можно рассматривать как координаты точки M (рис. 22.1), где \(M=M(t)\), или как координаты вектора \(r(t)\) с началом в точке \(O\) и концом в точке \(M\), то есть
$$
\overrightarrow{OM}=r(t)=(x(t),y(t),z(t)).\nonumber

$$
Если считать, что переменное \(t\) есть время, то уравнения
$$
x=x(t),\quad y=y(t),\quad z=z(t),\quad \alpha\leq t\leq\beta,\label{ref1}
$$
определяют закон движения точки \(M(t)\), а множество точек \(M(t)\), соответствующих всевозможным значениям \(t\) на отрезке \([\alpha,\beta]\), можно рассматривать как след (путь) точки, движущейся по закону \eqref{ref1}.

Замечание 1.

В общем случае закон движения может быть очень сложным. Например, существуют такие непрерывные на отрезке \([\alpha,\beta]\) функции \(x(t),y(t),z(t)\), что точка \(M(t)\), движущаяся в соответствии с законом \eqref{ref1}, пройдет через каждую точку некоторого куба.

Предположим, что любым двум различным значениям \(t_{1}\) и \(t_{2}\) из отрезка \([\alpha,\beta]\) соответствуют различные точки \(M(t_1)\) и \(M(t_2)\) пространства, и обозначим через \(K\) множество всех точек \(M(x,y,z)\) пространства, координаты которых определяются формулами \eqref{ref1}.

Будем говорить, что точка \(M(t_2)\in K\) следует за точкой \(M(t_{1})\in K\) или точка \(M(t_1)\) предшествует точке \(M(t_{2})\), если \(\alpha\leq t_{1} < t_{2}\leq\beta\). Введенное правило следования точек устанавливает порядок на множестве \(K\). Упорядоченное указанным способом множество \(K\) будем называть простой кривой \(\Gamma\) и записывать уравнение этой кривой либо в координатной форме
$$
\Gamma={x=x(t),\ y=y(t),\ z=z(t),\ \alpha\leq t\leq\beta},\label{ref2}
$$
либо в векторной форме
$$
\Gamma={\textbf{r}=\textbf{r}(t),\ \alpha\leq t\leq\beta},\label{ref3}
$$
где
$$
\textbf{r}=(x,y,z),\quad \textbf{r}(t)=(x(t),y(t),z(t)).\nonumber
$$
Условимся переменное \(t\) в уравнениях \eqref{ref2}, \eqref{ref3} называть параметром кривой \(\Gamma\). Точки \(M(\alpha)\) и \(M(\beta)\), соответствующие значениям \(\alpha\) и \(\beta\) параметра кривой \(\Gamma\), будем называть начальной точкой (началом) кривой и конечной точкой (концом) кривой.

Согласно определению простой кривой отображение \eqref{ref1} является взаимно однозначным: каждому значению \(t\in[\alpha,\beta]\) соответствует единственная точка \(M(t)\in\Gamma\), и наоборот, каждой точке \( M\in\Gamma\) соответствует единственное значение \(t\in[\alpha,\beta]\).

Если простая кривая \(\Gamma\) лежит в некой плоскости \(\mathcal{P}\), то эту кривую называют плоской. В частности, если плоскость \(\mathcal{P}\) совпадает с плоскостью \(Oxy\), то уравнение кривой \(\Gamma\) имеет вид
$$
\Gamma={x=x(t),\ y=y(t),\ z=0,\ \alpha\leq t\leq\beta}.\nonumber
$$
Обычно в этом случае опускают уравнение \(z=0\) и записывают уравнение кривой в виде
$$
\Gamma={x=x(t),\ y=y(t),\ \alpha\leq t\leq\beta}.\nonumber
$$
Например, уравнением
$$
\Gamma={x=R\cos t,\ y=R\sin t,\ 0\leq t\leq\pi},\nonumber
$$
где \(R > 0\), задается полуокружность радиуса \(R\), лежащая в верхней полуплоскости (\(y\geq 0\)) и «пробегаемая» против часовой стрелки. График функции \(y=f(x)\), непрерывной на отрезке \([\alpha,\beta]\), можно рассматривать как простую плоскую кривую \(\Gamma\), заданную уравнением
$$
\Gamma={x=t,\ y=f(t),\ \alpha\leq t\leq\beta}.\nonumber
$$

---

Параметризуемые кривые.

Если существуют два различных значения \(t_1\) и \(t_2\) из отрезка \([\alpha,\beta]\) таких, что \(M(t_{1})=M(t_{2})\), то отображение \eqref{ref1} отрезка в трехмерное пространство не является взаимно однозначным.

Предположим, что отрезок \([\alpha,\beta]\) можно разбить на отрезки \(\delta_{k}=[t_{k-1},t_{k}],\ k=\overline{1,n}\), где \(\alpha=t_{0} < t_{1} < \ldots < t_{n-1} < t_{n}=\beta\), такие, что каждое из непрерывных отображений
$$
x=x(t),\quad y=y(t),\quad z=z(t),\quad t\in\delta_{k},\quad k=\overline{1,n},\nonumber
$$
является однозначным и, следовательно, определяет простую кривую
$$
\Gamma_{k}={x=x(t),\ y=y(t),\ z=z(t),\ t\in\delta_{k}}.\nonumber
$$
Тогда будем говорить, что уравнения \eqref{ref2} задают параметризуемую кривую \(\Gamma\), или, что кривая \(\Gamma\) параметризована при помощи уравнений \eqref{ref2}, где под кривой \(\Gamma\) упорядоченную совокупность (\(\Gamma_{1},\ldots,\Gamma_{n}\)) простых кривых таких, что конечная точка кривой \(\Gamma_{k}\) совпадает с начальной точкой кривой \(\Gamma_{k+1},\ k=\overline{1,n-1}\). В этом случае говорят также, что «кривая \(\Gamma\) разбита на простые кривые \(\Gamma_{1},\ldots\Gamma_{n}\)» или что «кривая \(\Gamma\) составлена из простых кривых \(\Gamma_{k},\ k=\overline{1,n}\)» и пишут \(\Gamma=\Gamma_{1}\Gamma_{2}\ldots\Gamma_{n}\), а каждую из кривых \(\Gamma_{k}\) называют частью кривой \(\Gamma\) или простой дугой кривой \(\Gamma\).

Замечание 2.

Одна и та же кривая \(\Gamma\) может быть параметризована различными способами. Мы будем рассматривать только такие параметризации, которые получаются из данной параметризации \eqref{ref2} путем представления параметра \(t\) в виде непрерывной строго возрастающей функции другого параметра.

Это означает, что если наряду с представлением кривой \(\Gamma\) через параметр \(t\) уравнением \eqref{ref3} эта кривая представлена через параметр \(s\) уравнением
$$
\Gamma={\rho=\rho(s),\ \alpha_{1}\leq s\leq\beta_{1}},\label{ref4}
$$
то должно выполняться условие: \(s=s(t)\) —  непрерывная строго возрастающая функция на отрезке \([\alpha,\beta]\), причем
$$
s(\alpha)=\alpha_{1},\quad s(\beta)=\beta_1,\quad \rho(s(t))=\textbf{r}(t)\quad для\ всех\ t\in [\alpha,\beta].\label{ref5}
$$

В этом случае на отрезке \([\alpha_{1},\beta_{1}]\) определена непрерывная и строго возрастающая функция \(t=t(s)\), обратная к функции \(s=s(t)\), и для всех \(s\in[\alpha_{1},\beta_{1}]\) выполняется равенство
$$
\rho(s)=\textbf{r}(t(s)).\label{ref6}
$$

Замечание 3.

Условимся в дальнейшем, если не оговорено противное, для записи уравнений кривых использовать, только параметризации, указанные в замечании 2, и называть их допустимыми.

Пусть параметризуемая кривая \(\Gamma\) задана уравнением \eqref{ref3}, и пусть существуют значения \(t_{1}\) и \(t_{2}\) (\(t_{1}\neq t_{2}\)) из отрезка \([\alpha,\beta]\) такие, что \(\textbf{r}(t_1)=\textbf{r}(t_2)\). Тогда говорят, что точка \(M_{1}(x_{1},y_{1},z_{1})\), где \(x_{1}=x(t_1)=x(t_2),\ y_{1}=y(t_{1})=y(t_2),\ z_1=z(t_1)=z(t_{2})\), является точкой самопересечения (кратной точкой) кривой \(\Gamma\).

Если равенство \(\textbf{r}(t_1)=\textbf{r}(t_2\)) выполняется при \(t_{1}=\alpha,\ t_{2}=\beta\), то кривую \(\Gamma\) называют замкнутой. Замкнутую кривую, не имеющую точек самопересечения, отличных от точки \(M_{1}(x(\alpha),y(\alpha),z(\alpha))\), будем называть простым контуром.

Например, кривая
$$
\Gamma=\{x=\cos t,\ y=\sin t,\ 0\leq t\leq 2\pi\}\nonumber
$$
является простым контуром. При изменении \(t\) от 0 до \(2\pi\) точка \(M(\cos t,\sin t)\) «описывает» единичную окружность, двигаясь против часовой стрелки. Точка плоскости \(Oxy\) с координатами \((0,1)\) является одновременно начальной и конечной точкой кривой \(\Gamma\).

---

Касательная к кривой.

Пусть кривая \(\Gamma\) задана уравнением \eqref{ref3}, где \(\textbf{r}(t)\) — вектор-функция, дифференцируемая в точке \(t_{0}\in [\alpha,\beta]\), причем \(\textbf{r}'(t_{0})\neq 0\). Тогда
$$
\Delta \textbf{r}=\textbf{r}(t_0+\Delta t)-\textbf{r}(t_0)=r'(t_0)\Delta t+\Delta t\alpha(\Delta t),\label{ref7}
$$
где \(\alpha(\Delta t)\rightarrow 0\) при \(\Delta t\rightarrow 0\). Из условия \(\textbf{r}'(t0)\neq 0\) и равенства \eqref{ref7} следует, что при всех достаточно малых \(\Delta t\neq 0\) правая часть \eqref{ref7} есть ненулевой вектор, и поэтому \(\Delta \textbf{r} \neq 0\), то есть существует число \(\delta > 0\) такое, что если
$$
0 < |\Delta t| < \delta,\quad t_{0}+\Delta t\in[\alpha,\beta],\label{ref8}
$$
то \(r(t_0+\Delta t)\neq r(t_0)\).

Пусть \(M_{0}\) и \(M\) — точки кривой \(\Gamma\), соответствующие значениям параметра \(t_0\) и \(t_0+\Delta t\). Проведем через эти точки прямую и назовем ее секущей.

Рис. 22.2

Если \(\textbf{r}'(t_{0})\neq 0\), то при всех значениях \(\Delta t\), удовлетворяющих условиям \eqref{ref8}, ненулевой вектор \(\Delta \textbf{r}=\textbf{r}(t_0+\Delta t)-\textbf{r}(t_0)\) параллелен секущей, и поэтому вектор \(\displaystyle \frac{\Delta r}{\Delta t}\) также параллелен секущей. Уравнение секущей имеет вид
$$
r=r(t_0)+\frac{\Delta r}{\Delta t}\lambda,\qquad \lambda \in\mathbb{R}.\label{ref9}
$$

Пусть существует предельное положение секущей, то есть существует \(\displaystyle \lim_{\Delta t\rightarrow 0}\frac{\Delta r}{\Delta t}\neq 0\). Тогда прямая, уравнение которой получается из уравнения \eqref{ref9} заменой отношения \(\displaystyle \frac{\Delta r}{\Delta t}\) его пределом, называется касательной к кривой \(\Gamma\) в точке \(M_{0}\).

Утверждение 1.

Если \(r'(t_0)\neq 0\), то существует касательная к кривой \(\Gamma\) в точке \(M_{0}\), и уравнение этой касательной можно записать в виде
$$
\textbf{r}=\textbf{r}(t_{0})+\textbf{r}'(t_{0})\lambda,\qquad\lambda\in\mathbb{R}.\label{ref10}
$$\(\circ\) Если функция \(\textbf{r}(t)\) дифференцируема при \(t=t_0\) и \(\textbf{r}'(t_{0})\neq 0\), то существует \(\displaystyle \lim_{\Delta t\rightarrow 0}\frac{\Delta \textbf{r}}{\Delta t}=\textbf{r}'(t_0)\), и по определению прямая \eqref{ref10} является касательной к кривой \(\Gamma\) в точке \(M_{0}\). \(\bullet\)В координатной форме уравнение \eqref{ref10} имеет вид
$$
x=x(t_{0})+\lambda x'(t_{0}),\quad y=y(t_0)+\lambda y'(t_0),\quad z=z(t_{0})+\lambda z'(t_{0}),\quad \lambda\in \mathbb{R},\nonumber
$$
a в канонической форме уравнение касательной записывается в виде
$$
\frac{x-x(t_{0})}{x'(t_{0})}=\frac{y-y(t_{0})}{y'(t_{0})}=\frac{z-z(t_{0})}{z'(t_{0})}.\quad\bullet\nonumber
$$

Доказательство

---

Понятие гладкой кривой.

Пусть кривая \(\Gamma\) задана уравнением \eqref{ref3}, где \(\textbf{r}(t)\) — дифференцируемая на отрезке \([\alpha,\beta]\) функция, тогда говорят, что \(\Gamma\) — дифференцируемая кривая.

Если \(r'(t_0)\neq 0\), то точку \(M_{0}\in\Gamma\), где \(\overrightarrow{OM}=r(t_0)\), называют неособой точкой кривой \(\Gamma\); если же \(\textbf{r}'(t_0)=0\), то говорят, что \(M_{0}\) — особая точка кривой \(\Gamma\).

Пусть \(\textbf{r}(t)=(x(t),y(t),z(t))\), тогда \(r'(t_0)=(x'(t_{0}),y'(t_{0}),z'(t_{0}))\), и поэтому точка \(M_0\) является неособой точкой кривой \(\Gamma\) тогда и только тогда, когда \((x'(t_0))^2+(y'(t_0))^2+(z'(t_0))^2 > 0\). из определения неособой точки и утверждения 1 следует, что во всякой неособой точке кривой \(\Gamma\) существует касательная.

Если функция \(r'(t)\) непрерывна на отрезке \([\alpha,\beta]\), то будем говорить, что кривая \(\Gamma\), заданная уравнением \eqref{ref3}, непрерывно дифференцируема.

Условимся называть кривую гладкой, если она является непрерывно дифференцируемой и не имеет особых точек. Следовательно, кривая \(\Gamma\), заданная уравнением \eqref{ref3}, является гладкой, если функция \(\textbf{r}'(t)\neq 0\) при всех \(t\in[\alpha,\beta]\). Если кривая составлена из конечного числа гладких кривых, то такую кривую будем называть кусочно гладкой.

Замечание 4

Для непрерывно дифференцируемой кривой \(\Gamma\) в качестве допустимых преобразований параметра (см. замечания выше) рассматриваются функции \(s(t)\), непрерывно дифференцируемые и такие, что \(s'(t) > 0\).

В этом случае на отрезке \([\alpha,\beta]\) определена непрерывно дифференцируемая функция \(t=t(s)\), обратная к функции \(s=s(t)\), причем \(t'(s) > 0\) и выполняется равенство \eqref{ref6}.

univerlib.com

Кривая — Википедия

Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

Элементарная геометрия

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».

По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.

Определение в топологии

Отображение отрезка

Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:

γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,b]=[0,1]{\displaystyle [a,b]=[0,1]}, путями.

Отношение эквивалентности

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

γ1:[a1,b1]→X{\displaystyle \gamma _{1}\colon [a_{1},b_{1}]\to X} и γ2:[a2,b2]→X{\displaystyle \gamma _{2}\colon [a_{2},b_{2}]\to X}

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h{\displaystyle h} из отрезка [a1,b1]{\displaystyle [a_{1},b_{1}]} на отрезок [a2,b2]{\displaystyle [a_{2},b_{2}]}, такая что

γ1≡γ2∘h.{\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Комментарий

Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.

Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Кривая Жордана

Кривая Жордана на плоскости с положительной мерой Лебега.

Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.

Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.

Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом^[1]. .

Определение в анализе

В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R2{\displaystyle R^{2}}). Пусть x(t){\displaystyle x(t)} и y(t){\displaystyle y(t)} — функции на отрезке [a,b]{\displaystyle [a,b]}, непрерывно дифференцируемые на этом отрезке, и такие, что (x′(t))2+(y′(t))2{\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ:[a,b]→R2,t↦(x(t),y(t)){\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле

L(γ)=∫ab(x′(t))2+(y′(t))2dt.{\displaystyle {\text{L}}(\gamma )=\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt.}

Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.

Определение в дифференциальной геометрии

Если X{\displaystyle X} — гладкое многообразие, можно определить гладкую кривую на X{\displaystyle X} как гладкое отображение γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}, дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия X{\displaystyle X} равен k{\displaystyle k}, то Ck{\displaystyle C_{k}}-кривая вводится как кривая, для которой γ{\displaystyle \gamma } — k{\displaystyle k} раз непрерывно дифференцируемое отображение. Если X{\displaystyle X} — аналитическое многообразие (например, евклидово пространство) и γ{\displaystyle \gamma } — аналитическое отображение, кривую называют аналитической.

Гладкие кривые γ1:I→X{\displaystyle \gamma _{1}\colon I\to X} и γ2:J→X{\displaystyle \gamma _{2}\colon J\to X} называются эквивалентными, если существует диффеоморфизм p:I→J{\displaystyle p\colon I\to J} (замена параметра), такой что γ1=γ2∘p{\displaystyle \gamma _{1}=\gamma _{2}\circ p}. Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.

Алгебраические кривые

Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она назывется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x² + y² + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.

Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.

Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен

zd⋅f(x/z,y/z){\displaystyle z^{d}\cdot f(x/z,y/z)}

после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xⁿ + yⁿ = zⁿ в аффинной форме принимает вид xⁿ + yⁿ = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.

Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:

Трансцендентные кривые

Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:

Типы кривых

Типы точек на кривой

Обобщённые кривые

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L{\displaystyle L}, она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L′{\displaystyle L’}, гомеоморфное L{\displaystyle L}. Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

Впоследствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство C{\displaystyle C} топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

См. также

Примечания

1. ↑ W. F. Osgood. A Jordan curve of positive area (англ.) // Trans. Am. Math. Soc.. — 1903. — Vol. 4. — P. 107–112.

Литература

Ссылки

wikipedia.green

Кривая — Википедия. Что такое Кривая

Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

Элементарная геометрия

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».

По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.

Определение в топологии

Отображение отрезка

Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:

γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,b]=[0,1]{\displaystyle [a,b]=[0,1]}, путями.

Отношение эквивалентности

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

γ1:[a1,b1]→X{\displaystyle \gamma _{1}\colon [a_{1},b_{1}]\to X} и γ2:[a2,b2]→X{\displaystyle \gamma _{2}\colon [a_{2},b_{2}]\to X}

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h{\displaystyle h} из отрезка [a1,b1]{\displaystyle [a_{1},b_{1}]} на отрезок [a2,b2]{\displaystyle [a_{2},b_{2}]}, такая что

γ1≡γ2∘h.{\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Комментарий

Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.

Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Кривая Жордана

Кривая Жордана на плоскости с положительной мерой Лебега.

Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.

Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.

Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом^[1]. .

Определение в анализе

В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R2{\displaystyle R^{2}}). Пусть x(t){\displaystyle x(t)} и y(t){\displaystyle y(t)} — функции на отрезке [a,b]{\displaystyle [a,b]}, непрерывно дифференцируемые на этом отрезке, и такие, что (x′(t))2+(y′(t))2{\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ:[a,b]→R2,t↦(x(t),y(t)){\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле

L(γ)=∫ab(x′(t))2+(y′(t))2dt.{\displaystyle {\text{L}}(\gamma )=\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt.}

Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.

Определение в дифференциальной геометрии

Если X{\displaystyle X} — гладкое многообразие, можно определить гладкую кривую на X{\displaystyle X} как гладкое отображение γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}, дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия X{\displaystyle X} равен k{\displaystyle k}, то Ck{\displaystyle C_{k}}-кривая вводится как кривая, для которой γ{\displaystyle \gamma } — k{\displaystyle k} раз непрерывно дифференцируемое отображение. Если X{\displaystyle X} — аналитическое многообразие (например, евклидово пространство) и γ{\displaystyle \gamma } — аналитическое отображение, кривую называют аналитической.

Гладкие кривые γ1:I→X{\displaystyle \gamma _{1}\colon I\to X} и γ2:J→X{\displaystyle \gamma _{2}\colon J\to X} называются эквивалентными, если существует диффеоморфизм p:I→J{\displaystyle p\colon I\to J} (замена параметра), такой что γ1=γ2∘p{\displaystyle \gamma _{1}=\gamma _{2}\circ p}. Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.

Алгебраические кривые

Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она назывется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x² + y² + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.

Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.

Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен

zd⋅f(x/z,y/z){\displaystyle z^{d}\cdot f(x/z,y/z)}

после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xⁿ + yⁿ = zⁿ в аффинной форме принимает вид xⁿ + yⁿ = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.

Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:

Трансцендентные кривые

Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:

Типы кривых

Типы точек на кривой

Обобщённые кривые

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L{\displaystyle L}, она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L′{\displaystyle L’}, гомеоморфное L{\displaystyle L}. Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

Впоследствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство C{\displaystyle C} топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

См. также

Примечания

1. ↑ W. F. Osgood. A Jordan curve of positive area (англ.) // Trans. Am. Math. Soc.. — 1903. — Vol. 4. — P. 107–112.

Литература

Ссылки

wiki.sc

Длина кривой — Википедия

Материал из Википедии — свободной энциклопедии

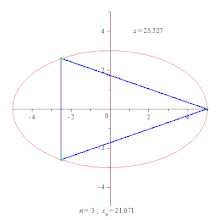Приближение длины дуги эллипса с помощью ломаных

Длина кривой (или, что то же, длина дуги кривой) — числовая характеристика протяжённости этой кривой^[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление).

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных.

Например, пусть непрерывная кривая γ{\displaystyle \gamma } в трёхмерном пространстве задана параметрически:

x=x(t),y=y(t),z=z(t){\displaystyle x=x(t),\quad y=y(t),\quad z=z(t)}

(1)

Приближение кривой ломаными

где a⩽t⩽b{\displaystyle a\leqslant t\leqslant b}, все три функции непрерывны и нет кратных точек, то есть разным значениям t{\displaystyle t} соответствуют разные точки кривой. Построим всевозможные разбиения параметрического интервала [a,b]{\displaystyle [a,b]} на m{\displaystyle m} отрезков: a=t0<t1<⋯<tm=b{\displaystyle a=t_{0}<t_{1}<\dots <t_{m}=b}. Соединение точек кривой γ(t0),…,γ(tm){\displaystyle \gamma (t_{0}),\dots ,\gamma (t_{m})} отрезками прямых даёт ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных^[2].

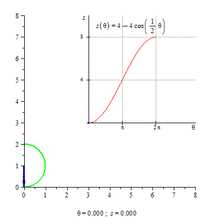Длина дуги циклоиды (s) в зависимости от её параметра (θ)

Связанные определения[править | править код]

• Всякая кривая имеет длину, конечную или бесконечную. Если длина кривой конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая. Снежинка Коха — классический пример ограниченной, но неспрямляемой кривой; более того, любая, сколь угодно малая её дуга неспрямляема^[3].
• Параметризация кривой длиной её дуги называется естественной.
• Кривая есть частный случай функции из отрезка в пространство. Вариация функции, определяемая в математическом анализе, является обобщением длины кривой (см. ниже).

s=∫abx′2(t)+y′2(t)+z′2(t)dt{\displaystyle s=\int \limits _{a}^{b}{\sqrt {{x’}^{2}(t)+{y’}^{2}(t)+{z’}^{2}(t)}}\,dt}

(2)

Формула подразумевает, что a⩽b{\displaystyle a\leqslant b} и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

s=∫ab∑k=1nfk′2(t)dt{\displaystyle s=\int \limits _{a}^{b}{\sqrt {\sum \limits _{k=1}^{n}{f’_{k}}^{2}(t)}}\,dt}.

• Если плоская кривая задана уравнением y=f(x),{\displaystyle y=f(x),} где f{\displaystyle f} — гладкая функция на отрезке значений параметра [a,b]{\displaystyle [a,b]}, то длина кривой определяется по формуле:

s=∫ab1+(f′(x))2dx.{\displaystyle s=\int \limits _{a}^{b}{\sqrt {1+(f'(x))^{2}}}\,dx.}

В полярных координатах (r,φ){\displaystyle (r,\varphi )}:

s=∫abr2+(drdφ)2dφ.{\displaystyle s=\int \limits _{a}^{b}{\sqrt {r^{2}+\left({\frac {dr}{d\varphi }}\right)^{2}}}\,d\varphi .}

• Формула Крофтона позволяет связать длину кривой на плоскости и интеграл числа её пересечений с прямыми по естественной мере на пространстве прямых.

Задача спрямления оказалась гораздо сложнее, чем вычисление площади, и в античные времена единственное успешное спрямление было выполнено для окружности. Декарт даже высказывал мнение, что «отношение между прямыми и кривыми неизвестно и, даже, думаю, не может быть познано людьми»^[4][5].

Первым достижением стало спрямление параболы Нейла (1657), выполненное Ферма и самим Нейлом. Вскоре была найдена длина арки циклоиды (Рен, Гюйгенс). Джеймс Грегори (ещё до открытия математического анализа) создал общую теорию нахождения длины дуги, которая немедленно была использована для различных кривых.

Риманово пространство[править | править код]

В n-мерном римановом пространстве с координатами x1⋯xn{\displaystyle x^{1}\cdots x^{n}} кривая задаётся параметрическими уравнениями:

xi=xi(t){\displaystyle x^{i}=x^{i}(t)\qquad \qquad },

((3))

Длина кривой в римановом пространстве задаётся формулой:

s=∫abgijdxidtdxjdtdt{\displaystyle s=\int \limits _{a}^{b}{\sqrt {g_{ij}{dx^{i} \over dt}{dx^{j} \over dt}}}\,dt},

где : gij{\displaystyle g_{ij}} — метрический тензор. Пример: кривая на поверхности в R3{\displaystyle \mathbb {R} ^{3}}.

Общее метрическое пространство[править | править код]

В более общем случае произвольного метрического пространства (X,ρ){\displaystyle (X,\rho )} длиной S{\displaystyle S} кривой называется вариация задающего кривую отображения, то есть длина кривой γ:[a,b]→X{\displaystyle \gamma :[a,b]\to X} определяется согласно формуле:

s=sup∑k=0mρ(γ(xk+1),γ(xk)),{\displaystyle s=\sup \sum \limits _{k=0}^{m}\rho (\gamma (x_{k+1}),\gamma (x_{k})),}

где верхняя грань берётся, как и ранее, по всем разбиениям a=x0<x1<⋯<xm=b{\displaystyle a=x_{0}<x_{1}<\dots <x_{m}=b} отрезка [a,b]{\displaystyle [a,b]}.

1. ↑ Длина // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
2. ↑ Шибинский, 2007, с. 199.
3. ↑ Шибинский, 2007, с. 201—202.
4. ↑ Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М.—Л.: Гостехиздат, 1938. — С. 49. — 297 с. — (Классики естествознания).
5. ↑ Оригинал цитаты на французском языке: «la proportion qui est entre les droites et les courbes n’étant pas connue, et même, je crois, ne le pouvant être par les hommes», см. Descartes, René. Discours de la méthode…. — 1637. — С. 340.

ru.wikipedia.org

кривая — Викисловарь

Морфологические и синтаксические свойства[править]

кри-ва́·я

Существительное, неодушевлённое, женский род, адъективное склонение (тип склонения <п 1b> по классификации А. А. Зализняка).

Корень: -крив-; окончание: -ая.

Произношение[править]

• МФА: ед. ч. [krʲɪˈvaɪ̯ə]  мн. ч. [krʲɪˈvɨɪ]

Семантические свойства[править]

Значение[править]

1. геометр. непрерывная линия, которая не является прямой ◆ Из его писем видно, что он понимал свойства некоторых кривых, называемых трансцендентными, применение которых к тангенсу даёт формулу, содержащую начатки дифференциального и интегрального исчислений. Мераб Мамардашвили, «Картезианские размышления», 1981—1993 г. (цитата из Национального корпуса русского языка, см. Список литературы)
2. перен. путь, имеющий вид такой линии ◆ Показания кофейной гущи она сопоставляла с картинами своих снов, соединяла их, мысленно прочерчивая кривую судьбы. Ф. А. Искандер, «Сандро из Чегема», 1989 г. (цитата из Национального корпуса русского языка, см. Список литературы)
3. спец. графическое изображение соотношения количественных показателей какого-либо процесса посредством такой линии ◆ У некоторых больных кривые запоминания имеют зигзагообразную форму, что говорит о неустойчивости, истощаемости мнестических процессов больных. Б. В. Зейгарник, «Патопсихология», 1986 г. (цитата из Национального корпуса русского языка, см. Список литературы)

Синонимы[править]

1. частичн.: линия
2. частичн.: функция

Антонимы[править]

1. прямая
2. —

Гиперонимы[править]

1. линия
2. график, зависимость

Гипонимы[править]

1. гипербола, дуга, загогулина, окружность, парабола, синусоида, спираль, тангенсоида, эвольвента, эволюта, экспонента, каустика
2. гипербола

Родственные слова[править]

Список всех слов с корнем «крив-»	[править]
имена собственные: Кривой Рог пр.  существительные: кривая, кривизна, кривило, искривление, кривляние, кривляка прилагательные: кривой, кривенький, кривильный, кривоватый глаголы: кривить, кривиться, кривлять, кривляться, скривить, скривиться, искривлять, искривляться наречия: криво, кривенько, кривовато, вкривь

Этимология[править]

Происходит от прил. кривой, далее из праслав. *krivъ, от кот. в числе прочего произошли: др.-русск., церк.-слав. кривъ (др.-греч. σκολιός). Ср.: укр. криви́й, белор. крывы́, болг. крив, сербохорв. кри̑в, кри́ва, кри̑во «левый», словенск. krȋv, kríva, чешск. křivý «кривой, неправильный, лживый», словацк. krivý, польск. krzywy, в.-луж. křiwy, н.-луж. kśiwy, полаб. kreivė. Родственно лит. kreĩvas «кривой», латышск. krievs — то же, лит. krìvis «кособокий, кривой», вост.-лит. kraivas «кривой, косой», apýkraivis «искривленный», далее латышск. krèiss «левый», krails «изогнутый, искривленный», kreĩlis «левша», kraitȃt «шататься»; вероятно родство с греч. κροιός ̇νοσώδης, ἀσθενής (Гесихий), атт. (337 г. до н. э.), κροιός «имеющий изъян». Возможна связь с лат. curvus «кривой», греч. κυρτός — то же. Френкель относит к *kreivos также лит. kairỹs «левая рука», по его мнению, происходящее из *krair-. Использованы данные словаря М. Фасмера. См. Список литературы.

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Библиография[править]

Для улучшения этой статьи желательно: Добавить все семантические связи (отсутствие можно указать прочерком, а неизвестность — символом вопроса) Добавить хотя бы один перевод для каждого значения в секцию «Перевод»

• форма именительного падежа женского рода единственного числа прилагательного кривой ◆ Отсутствует пример употребления (см. рекомендации).

ru.wiktionary.org