Матрица 3 на 4: Определитель матрицы 2×2, 3×3, 4×4…
Определитель матрицы 2×2, 3×3, 4×4…
Определитель (детерминант) квадратной матрицы A — это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.
Обозначения
Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$
Свойства определителя
- Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$ - Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$ - Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то
Пример 14
$\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)
или
$\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны) - Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или$ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
- При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 16
$3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:
В определителе
$\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:
$6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$ - При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.
Пример 17
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
Пример 18
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$ - При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$Пример 20
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$ - Определитель матрицы равен определителю транспонированной матрицы.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
Один из миноров матрицы A есть $\begin{vmatrix} 1 & 4\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
Другим минором является $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)
Пример 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $
Один из миноров матрицы B есть $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)
Другим минором является $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Пусть $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & .
Можно определить минор $\Delta_{i,j}$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_{i,j}$ квадратной матрицы A. Такой минор называется дополнительным.
Пример 23
$ A = \begin{pmatrix} 4 & 7\\ 2 & 9 \end{pmatrix}$
Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_{2,1}$.
Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем
Минор, дополнительный к элементу 2, есть $\Delta_{2,1} = 7$.
Пример 24
$B=\begin{pmatrix} 1 & 4 & 2\\ 5 & 3 & 7\\ 6 & 2 & 1\\ \end{pmatrix}$
Нужно найти минор, дополнительный к элементу 7.
Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_{2,3}$.
Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем
Минор, дополнительный к элементу 7, — это $\Delta_{2,3}= \begin{vmatrix} 1 & 4\\ 6 & 2 \end{vmatrix}$
Пример 25
$C=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix}$
Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_{1,2}$.
Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем
Минор, дополнительный к элементу 5, — это $\Delta_{1,2}= \begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$
Алгебраическое дополнение элемента матрицы
Пусть $A=\begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & .
{7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $a_{2,5}$.
Порядок определителя
Порядок определителя матрицы равен числу ее строк и столбцов.
Пример 26
$\begin{vmatrix} 1 & 4\\ 6 & 2\\ \end{vmatrix}$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)
Пример 27
$\begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)
Вычисление определителя матрицы
Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.
$\left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & .
$\Delta_{1,1}= \begin{vmatrix} a_{2,2} & a_{2,3}\\ a_{3,2} & a_{3,3} \end{vmatrix} = a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2}$
$\Delta_{1,2}= \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3} \end{vmatrix} = a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1}$
$\Delta_{1,3}= \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{vmatrix} = a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1}$
$\left| A\right| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot(a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1,2}\cdot a_{2.1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$
Упростить получение последней формулы можно следующим образом.
Начнем с того, что перепишем первые две строки под определителем как показано ниже.
$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}}$
$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm} \begin{array}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{array}$
Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:
$\color{blue}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$
Вычитая вторую сумму из первой, получаем формулу определителя:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$
Пример 30
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{pmatrix}$
$\begin{vmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 1 & 4 & 3\\ 2 & 1 & 5\\ \end{array}$
$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 -(3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $ 1 + 12 + 60 -(9 + 10 + 8)=73-27=46$
Пример 31
$A=\begin{pmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{pmatrix}$
$\begin{vmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 3 & 5 & 1\\ 1 & 4 & 2\\ \end{array} $
$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 -(1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$
Элементы матрицы могут быть обозначены буквами.
{2} \end{vmatrix}= $
$\begin{vmatrix} a-c & b-c \\ (a-c)(a+c) & (b-c)(b+c) \end{vmatrix}=$ $(a-c)(b-c)\begin{vmatrix} 1 & 1\\ a+c & b+c \end{vmatrix}=$
$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$
Вычисление определителя матрицы 4×4
Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.
Но сначала надо использовать свойства определителей:
- Проверим, не выполняется ли одно из условий того, что определитель равен 0.
- Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
- Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.
В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение.
В этом случае, алгебраическое дополнение — это определитель матрицы 3×3, который считается по уже известной формуле.
Пример 33
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 0 & 0 & 0 & 0\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.
Пример 34
$\begin{vmatrix} 1 & 3 & 1 & 2\\ 5 & 8 & 5 & 3\\ 0 & 4 & 0 & 0\\ 2 & 3 & 2 & 8 \end{vmatrix}$
Замечаем, что $C_{1}$ равно $C_{3}$, следовательно, определитель равен 0.
Пример 35
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 10 & 16 & 18 & 4\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.
Пример 36
$\begin{vmatrix} \color{red}{4} & 3 & 2 & 2\\ 0 & 1 & -3 & 3\\ 0 & -1 & 3 & 3\\ 0 & 3 & 1 & 1 \end{vmatrix}$
Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец.
Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.
=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot(-3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$
Пример 37
$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix}$
Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением.
Заметим, что в строке 2 уже есть два нулевых элемента. Достаточно обратить лишь еще один элемент в 0, чтобы осталось посчитать только одно алгебраическое дополнение единичного элемента.
$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix} \xlongequal{C_{4}+2C_{2}}$ $\begin{vmatrix} 4 & 3 & 2 & 8\\ 0 & \color{red}{1} & 0 & 0\\ 1 & -1 & 3 & 1\\ 2 & 3 & 1 & 7 \end{vmatrix}=$ $=$br />
$= 1\cdot(-1)^{2+2}\cdot \begin{vmatrix} 4 & 2 & 8\\ 1 & 3 & 1\\ 2 & 1 & 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$
Пример 38
$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 3 & 3 & 3 & 3\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$
Можно вынести множитель 3 из строки 3:
$3\cdot \begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$
Поскольку в строке 3 все элементы равны 1, легко обратить получить нули.
{4+1}\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}$
Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 — (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3\cdot 1)]=$ $-(180+12+117-24-195-54)=36$
Пример 40
$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$
Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули.
$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 & 1 & 2 & -1\\ 0 & 0 & \color{red}{1} & 0 \\ -1 & -4 & 3 & -2\\ -1 & -2 & 2 & -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 & 1 & -1\\ -1 & -4 & -2\\ -1 & -2 & -1 \end{vmatrix}$
Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $-[2\cdot 4\cdot 1 + 1\cdot 2\cdot (-1)+ 1\cdot 1\cdot 2 — ((-1)\cdot 4\cdot 1 + 2\cdot 2\cdot 2 + 1\cdot 1\cdot 1)]=$ $-(8-2+2+4-8-1)=-3$
Пример 41
$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3\\ \end{vmatrix}$
Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы.
$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{L_{1}+L_{2}+L_{3}+L_{4}} \begin{vmatrix} 10 & 10 & 10 & 10\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix} =$ $10\cdot \begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{C_{1} — C_{4},C_{2}-C_{4},C_{3}-C_{4}}10\cdot \begin{vmatrix} 0 & 0 & 0 & \color{red}{1}\\ -1 & 1 & 2 & 2\\ 2 & 3 & 1 & 1\\ 1 & -1 & -2 & 3 \end{vmatrix}=$
$=10\cdot1\cdot(-1)^{1+4}$
$ = (-10)\cdot \begin{vmatrix} -1 & 1 & 2\\ 2 & 3 & 1\\ 1 & -1 & -2 \end{vmatrix}=$ $(-10)\cdot((-1)\cdot 3\cdot (-2) +2 \cdot (-1)\cdot2 + 1\cdot 1\cdot 1$ $-(2\cdot 3\cdot 1 + 1\cdot (-1)\cdot (-1) + (-2)\cdot1\cdot2))$ $= -10\cdot(6 -4 +1 -6 — 1 + 4) =0$
Матрицы Умножение матриц Ранг матрицы Обратные матрицы Матричные уравнения Системы уравнений Калькуляторы для матриц
Определитель матрицы 3 на 3.
КалькуляторНайти определитель матрицы 3*3 можно быстро по правилу треугольника
Определители обозначают следующими знаками
Примеры вычисления определителей
Пример 1. Найти определитель матрицы
Решение: Применяем правило треугольника для нахождения определителя
Определитель равен 11.
Приведенная схема пригодиться Вам для вычисления определителя матрицы 3 * 3. Все что Вам нужно — подставить свои значения.
Пример 2. Вычислить определитель матрицы
Решение: В целях научить Вас чему-то новому, найдем определитель матрицы по правилу Саррюса.
Схема вычислений приведена выше поэтому копировать ее не будем, а лишь распишем в деталях. Для этого дописываем к стандартному определителю два первых столбца и выполняем следующие расчеты.
В результате вычислений определитель равен нулю.
Пример 3. Найти определитель матрицы 3*3
Решение: Применяем правило треугольника для нахождения определителя
Определитель равен -161.
Пример 4. Вычислить определитель матрицы
Решение: Находим определитель матрицы 3*3 по правилу треугольников
Пример 5. Найти определитель матрицы
Решение: Матрица имеет несколько нулевых элементов. Такие матрицы называют разреженными. Для уменьшения количества операций вычислим определитель через алгебраические дополнения ко второму строки или столбца.
Проще уже не может быть.
Пример 6. Доказать что определитель матрицы А равен 3
Решение: Матрица содержит два нулевых элементы, поэтому можем найти определитель через алгебраические дополнения. Разложим определитель по элементам первого столбца.
Определитель равен 3 что и требовалось доказать.
Пример 7. Найти определитель матрицы
Решение:По предварительной схеме определитель матрицы вычисляем через алгебраические дополнения первой строки или третьего столбца. выполняем вычисления
Определитель равен 39.
Пример 8. При каких значениях параметра а определитель матрицы равен нулю
Решение: По правилу треугольников находим определитель
По условию приравниваем определитель к нулю и находим параметр
Параметры при которых определитель обращается в нуль уровне a=-3;a=3.
Пример 9. Найти определитель матрицы
Решение: Найдем определитель матрицы по правилу треугольников и через алгебраические дополнения. По первой схеме получим
Теперь разложим с помощью алгебраических дополнений, например, третьим столбцом. Он удобен тем, что содержит самые элементы матрицы. Находим определитель
Сравнением количества расчетов убеждаемся, что в таких случаях целесообразнее использовать правило треугольников. Вычисления проще и меньше вероятность сделать ошибку.
Для разреженных матриц или большего порядка блочных стоит применять расписание определителя по строке или столбцу.
И напоследок бонус от нас — калькулятор YukhymCalc.
С его помощью Вы легко проверите правильность исчисления основных операций с матрицами, а также сможете найти определитель матрицы и обратную матрицу. Для матриц 3*3 используется правило треугольников, для 4*4 — расписание определителя через элементы первой строки. Меню довольно простое и интуитивно понятное.
Определитель 7 задачу через матричный калькулятор иметь следующий вид
Как видите преимущество матричного калькулятора перед другими, в том числе онлайн калькуляторами, в том, что Вы видите все промежуточные операции. А это важно для проверки и контроля ошибок.
Используйте приведенные схемы вычислений определителей в обучении. Если возникают трудности в вычислениях и есть возможность, то можете проверить найдены определители калькулятором. Скачать матричный калькулятор YukhymCalc Вы можете без регистрации по этой ссылке.
4. Умножение матриц
Важно: Мы можем перемножать матрицы, только если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Пример 1
а) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно и дает в качестве ответа матрицу 2 × 4.
b) Умножение матрицы 7 × 1 на матрицу 1 × 2 допустимо; это дает матрицу 7 × 2
c) Матрица 4 × 3, умноженная на матрицу 2 × 3, НЕвозможна.
Как умножить 2 матрицы
Сначала мы используем буквы, чтобы понять, что происходит. После этого мы увидим пример с числами.
В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.
`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]`
Ответом будет матрица 2 × 2.
Умножаем и складываем элементы следующим образом. Мы работаем через 1-й строки первой матрицы, умножая на 1-й столбец второй матрицы, элемент за элементом. Мы добавить полученных продуктов. Наш ответ занимает позицию a 11 (вверху слева) матрицы ответов.
Проделываем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы.
Результат помещается в позицию a 12 .
Теперь о 2-й -й строке первой матрицы и 1-м -м столбце второй матрицы. Результат помещается в позицию а 21 .
Наконец, делаем 2-ю строку первой матрицы и 2-й столбец второй матрицы. Результат помещается в позицию a 22 .
Таким образом, результат умножения двух наших матриц выглядит следующим образом:
`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]` `=[(au+bw+cy,av +bx+cz),(du+ew+fy,dv+ex+fz)]`
Теперь давайте рассмотрим числовой пример.
Пользователи телефона
ПРИМЕЧАНИЕ. Если вы разговариваете по телефону, вы можете прокручивать любые широкие матрицы на этой странице вправо или влево, чтобы увидеть все выражение.
Пример 2
Умножить:
`((0,-1,2),(4,11,2))((3,-1),(1,2),(6,1))`
Ответить
Это 2×3 умножить на 3×2, что даст нам 2×2
отвечать.
`((0,-1,2),(4,11,2)) ((3,-1),(1,2),(6,1))`
`=((0xx3+ — 1xx1 + 2xx6,0xx-1+ -1xx2 + 2xx1), (4xx3+11xx1+2xx6,4xx -1 + 11xx2 + 2xx1))`
` = ((0-1+12,0-2+2), (12+11+12,-4+22+2))`
` = ((11,0),(35,20)) `
Наш ответ — матрица 2×2.
Умножение матриц 2 × 2
Процесс одинаков для матрицы любого размера. Мы умножаем на строк первой матрицы и на столбцов второй матрицы, элемент за элементом. Затем мы добавляем продукты:
`((a,b),(c,d))((e,f),(g,h))` `=((ae+bg,af+bh),(ce+dg,cf+dh ))`
В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.
Пример 3
Умножить:
`((8,9),(5,-1))((-2,3),(4,0))`
Ответить
` ((8,9),(5,-1))((-2,3),(4,0)) `
`= ((8 xx -2+9xx4,8xx3+9xx0),( 5xx-2+ -1xx4,5xx3 + -1xx0))`
` = ((-16+36,24+0),(-10+ -4,15 + 0)) `
` = ((20 ,24),(-14,15)) `
Матрицы и системы одновременных линейных уравнений
Теперь мы видим, как написать систему линейных уравнений, используя матричное умножение.
Пример 4
Система уравнений
−3 х + y = 1
6 х — 3 у = -4
можно записать как:
`((-3,1),(6,-3))((x),(y))=((1),(-4))`
Матрицы идеально подходят для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру для решения системы требуются только первая и последняя матрицы, как мы увидим в разделе «Матрицы и линейные уравнения».
Примечание 1 — Обозначение
Уход с записью умножение матриц.
Следующие выражения имеют различных значения:
AB это умножение матриц
A × B является произведением перекрестного , которое возвращает вектор
A * B используется в компьютерной записи, но не на бумаге
А • B Произведение точек , которое возвращает скаляр .
[Дополнительную информацию о векторных и скалярных величинах см. в главе «Вектор».]
Примечание 2. Коммутативность умножения матриц
`AB = BA`?
Давайте посмотрим, так ли это на примере.
Пример 5
Если
`А=((0,-1,2),(4,11,2))`
и
`В=((3,-1),(1,2),(6,1))`
найти AB и ВА.
Ответить
Мы выполнили AB выше, и ответ был:
`AB = ((0,-1,2),(4,11,2)) ((3,-1),(1,2), (6,1))`
` = ( (11,0),(35,20) )`
Теперь BA равно (3 × 2)(2 × 3), что даст 3 × 3:
`BA= ((3,-1),(1,2),(6,1))((0,-1,2),(4,11,2))`
`= ((0 -4,-3-11,6-2),(0+8,-1+22,2+4),(0+4,-6+11,12+2))`
` = (( -4,-14,4),(8,21,6),(4,5,14)) `
Итак, в этом случае AB НЕ равно BA.
На самом деле, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.
В общем случае при перемножении матриц перестановочный закон не выполняется, т.е. AB ≠ BA . Есть два общих исключения из этого:
- Матрица идентичности: IA = AI = A .
- обратная матрица: A -1 А = АА -1 = I.
В следующем разделе мы узнаем, как найти обратную матрицу.
Пример 6. Умножение на матрицу идентичности
Учитывая, что
`А=((-3,1,6),(3,-1,0),(4,2,5))`
найти AI .
Ответить
`AI = ((-3,1,6),(3,-1,0),(4,2,5)) ((1,0,0),(0,1,0),(0 ,0,1))`
`=((-3+0+0,0+1+0,0+0+6),(3+0+0,0+ -1+0,0+0 +0),(4+0+0,0+2+0,0+0+5))`
`=((-3,1,6),(3,-1,0),(4,2,5))`
`=A`
Мы видим, что умножение на единичную матрицу не изменить значение исходной матрицы.
То есть
АИ = А
Упражнения
1.
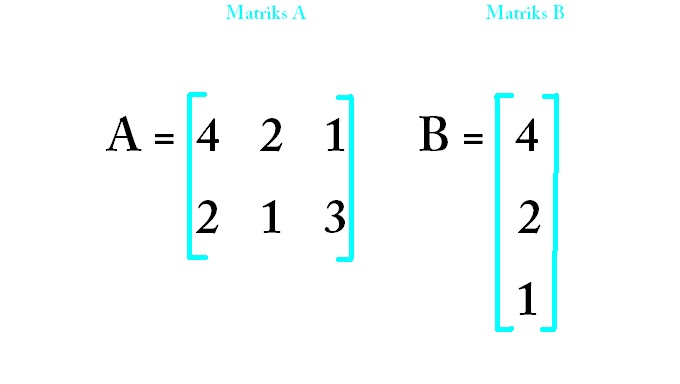Если возможно, найдите BA и AB .
`А=((-2,1,7),(3,-1,0),(0,2,-1))`
`В=(4\\-1\\\5)`
Ответить
`BA=(4\ \ -1\ \ \ 5)((-2,1,7),(3,-1,0),(0,2,-1))`
`=(-8+(-3)+0\ \ \ 4+1+10\ \ \ 28+0+(-5))`
`=(-11\ \ 15\ \ 23)`
AB невозможно. (3 × 3) × (1 × 3).
2. Определить, если B = A -1 , учитывая:
`А=((3,-4),(5,-7))`
`В=((7,4),(5,3))`
Ответить
Если B = A -1 , то `AB = I`.
`AB=((3,-4),(5,-7))((7,4),(5,3))`
`=((21-20,12-12),( 35-35,20-21))`
`=((1,0),(0,-1))`
` !=I`
Итак, B НЕ является обратным A.
3. При изучении движения электронов, одна из спиновых матриц Паули равна
`s=((0,-j),(j,0))`
где
`j=sqrt(-1)`
Покажите, что с 2 = I.
[Если вы никогда раньше не видели j , перейдите в раздел, посвященный комплексным числам].
92+0))``= ((1,0),(0,1))`
`=I`
4. Оцените следующее матричное умножение, которое используется при управлении движением роботизированного механизма .
`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`
Ответить
`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`
`=((2(0,5)-4(0,866)+0),(2(0,866)+4(0,5)+0),(0+0+0))`
`= ((-2.464),(3.732),(0))`
Интерпретация этого заключается в том, что рука робота перемещается из позиции (2, 4, 0) в позицию (-2,46, 3,73, 0). То есть это движется в x-y плоскость, но ее высота остается равной z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят ему, на сколько градусов двигаться.
Интерактивы Matrix Multiplication
- Другие примеры умножения матриц
- Интерактивные операции с матрицами
Умножение матриц
Умножение матриц Рассмотрим произведение матрицы 2×3 и матрицы 3×4.
Умножение
определяется, поскольку внутренние размеры (3) одинаковы. Продукт будет
быть матрицей 2×4, внешние размеры.
Так как в первой матрице три столбца и три строки во второй матрица (внутренние размеры которой должны быть одинаковыми), каждый элемент в произведении будет сумма трех продукты.
Строка 1, Столбец 1
Чтобы найти элемент в строке 1, столбце 1 произведения, мы возьмем строку 1 из первой матрицы и столбец 1 из второй матрицы. Мы соединяем эти значения вместе, умножаем пары значений, а затем добавляем к прибыть в 25.
Р 1 : 1 -2 3
×С 1 : 1 -3 6
---------------
1 +6 +18 = 25 Строка 2, Столбец 3
Чтобы найти элемент в строке 2, столбце 3 произведения, возьмем строку 2 из первой матрицы и столбец 3 из второй матрицы. Соединяем эти значения вместе, перемножьте пары значений, а затем добавьте к прибыть на 53.
Р 2 : 4 5 -2
×С 3 : 4 7 -1
---------------
16 +35 +2 = 53 Понимание того, откуда взялось каждое число в произведении, полезно, когда
вам нужно только определенное значение.
Вам не нужно умножать полностью, если вы
нужны только определенные элементы. Просто возьмите строку из первой матрицы и
столбец из второй матрицы.
Процесс можно завершить для остальных элементов матрицы.
| Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | ||
|---|---|---|---|---|---|
| значения | [1, -3, 6] | [-8, 6, 5] | [4, 7, -1] | [-3, 2, 4] | |
| Ряд 1 | [1, -2, 3] | 1(1) — 2(-3) + 3(6) = 1 + 6 + 18 = 25 | 1(-8) -2(6) + 3(5) = -8 — 12 + 15 = -5 | 1(4) -2(7) +3(-1) = 4 — 14 — 3 = -13 | 1(-3) -2(2) + 3(4) = -3 -4 + 12 = 5 |
| Ряд 2 | [4, 5, -2] | 4(1) + 5(-3) -2(6) = 4 — 15 — 12 = -23 | 4(-8) + 5(6) — 2(5) = -32 + 30 — 10 = -12 | 4(4) + 5(7) -2(-1) = 16 + 35 + 2 = 53 | 4(-3) + 5(2) -2(4) = -12 + 10 — 8 = -10 |
Итак, конечный продукт
| 25 | -5 | -13 | 5 | ||
| -23 | -12 | 53 | -10 |
Обратите внимание, что умножение не определяется другим способом.
