Пленка тонировочная MTF Original Premium 5% Сharcol в тубе (0.5м х 3м)

Описание Свойства Отзывы (0) Похожие товары (9)

Особенности тонировочной пленки MTF Film Original Premium

• Защищает от ярких солнечных лучей.
• Защищает от ультрафиолетового и теплового излучения.
• Сохраняет прохладу в салоне солнечную погоду.
• Защищает интерьер и внутреннюю отделку салона от выцветания.
• Повышает ударопрочность стекол и обеспечивает безопасность при ДТП.
• Устойчивость к механическим повреждениям (обладает антицарапным покрытием).
• Устойчива к большому диапазону температур.
• Повышенный коэффициент светоотражения.
• Повышенный уровень подавления бликов.
• Легкая установка.
• Увеличивает эффективность работы «климат-контроля» или кондиционера
• Создает атмосферу уюта в салоне и улучшает внешний вид автомобиля (стильность).
• Гарантия качества производителя (от выцветания пленки) – 7 лет.

Тонировочная пленка MTF Film Original Premium 5% charcoal отличается весьма высоким качеством и отлично подходит для всех типов автомобилей. С ее помощью вы не только повысите безопасность и комфортабельность, но и улучшите эксплуатационные свойства своего автомобиля. К тому же, тонирование стекол позволяет придать уникальность внешнему виду машины.

Создание оригинального цвета стекол — не единственная польза пленки. Благодаря ей отражаются инфракрасные лучи, и все пассажиры и салон авто надежно ограждены от ультрафиолетового излучения (защита до 99%). Тонировочная пленка для авто MTF Film Premium делает стекло безосколочным, что в обычном виде ему несвойственно. А это существенно повышает безопасность пассажиров в случае разбития окон.

Производитель оставляет за собой право вносить изменения в дизайн упаковки продукта без предварительного уведомления.

Эта модель пленки имеет 2 варианта размера: маленький и большой (0,5х3 метра и 0,75х3 метра) – выберите наиболее подходящий размер в соответствии с высотой стекол вашего автомобиля.
Чтобы определить, сколько рулонов пленки вам потребуется, достаточно измерить длину всех стекол, которые вы планируете затонировать, и разделить на длину рулона (3 метра).
Инструкция по установке – внутри упаковки.
Внимание! Шпатель для установки пленки в комплекте не прилагается, его нужно приобрести отдельно!

Технические характеристики

Название: Premium 5%
Прохождение видимого света: 6%
Пропускание УФ лучей: <1%
Отражение солнечной энергии: 6%
Поглощение солнечной энергии: 52%
Пропускание солнечной энергии: 42%
Стойкость к царапинам: 2H<

Адгезия: 5В
Толщина 1ply: 1.5mil
Тип пленки: 1-слойная неметаллизированая
Цвет: Charcoal (Древесный уголь)
Размер рулона: 0.5м х 3м

Сделано в Корее.

Написать отзыв

Ваше Имя:

Ваш отзыв: Внимание: HTML не поддерживается! Используйте обычный текст.

Оценка:

Файл MTF – чем открыть, описание формата

Чем открыть, описание – 5 форматов файла

1. Файл темы Motorola — Файлы настроек
2. Файл минусовки Multi Tracker — Аудио-файлы
3. Подсказки MasterCook — Другие файлы
4. Файл поддержки быстрого перевода в памяти переводов Trados — Другие файлы
5. Файл таблицы смертности XLActuary — Файлы данных

1. Файл темы Motorola

Motorola Theme File

Тип данных: Неизвестно

Разработчик: Motorola

Подробное описание

Файл MTF — это файл темы для настройки интерфейса мобильного телефона Motorola. В файле хранятся параметры обоев, заставки и мелодии звонка. Пользователи могут создавать собственные темы и загружать их в телефон с помощью приложения Motorola Media Manager.

Как, чем открыть файл .mtf?

Инструкция — как выбрать программу из списка, скачать и использовать ее для открытия файла

2. Файл минусовки Multi Tracker

Multi Tracker File

Тип данных: Двоичный файл

Разработчик: Song Galaxy

Подробное описание

Фонограмма, созданная в программе Song Galaxy Multi Tracker. Файл содержит минусовку — песню с удаленной партией вокала или инструмента, что позволяет музыкантам исполнить их самостоятельно.

Как, чем открыть файл .mtf?

Инструкция — как выбрать программу из списка, скачать и использовать ее для открытия файла

3. Подсказки MasterCook

MasterCook Tips

Тип данных: Неизвестно

Разработчик: Неизвестно

Подробное описание

Файл содержит подсказки по приготовлению блюд и используется ValuSoft MasterCook, программой с функциями кулинарной книги, которая позволяет управлять коллекцией кулинарных рецептов. Файл MTF сохранен в собственном формате MasterCook и может быть открыт данным приложением.

Как, чем открыть файл .mtf?

Инструкция — как выбрать программу из списка, скачать и использовать ее для открытия файла

4. Файл поддержки быстрого перевода в памяти переводов Trados

Translation Memory Translations File

Тип данных: Неизвестно

Разработчик: SDL

Подробное описание

Вспомогательный файл, используемый модулем памяти переводов (Translation Memory) программы автоматизированного перевода Trados. Память переводов представляет собой базу данных, включающую набор ранее переведенных частей текста. Файл MTF обеспечивает быстрый перевод слов и фраз, содержащихся в памяти переводов.

Как, чем открыть файл .mtf?

Инструкция — как выбрать программу из списка, скачать и использовать ее для открытия файла

5. Файл таблицы смертности XLActuary

Mortality Table File

Тип данных: Неизвестно

Разработчик: ARMON Technologies

Подробное описание

Файл статистических данных о смертности населения. Содержит показатели смертности для таблиц, используемых расширением XLActuary в Microsoft Excel. Данное расширение служит для проведения статистических расчетов, определения факторов риска и страховых коэффициентов.

Как, чем открыть файл .mtf?

Инструкция — как выбрать программу из списка, скачать и использовать ее для открытия файла

Для более точного определения формата и программ для открытия файла используйте функцию определения формата файла по расширению и по данным (заголовку) файла.

МТФ-это хутор? Немного об Умарове и Дугучиеве… —

«Объявить благодарность от лица Президента Российской федерации, В.В. Путина, в адрес Дугучиева Ислама Бетрсултановича — старшего тренера спортивной сборной команды Российской Федерации по греко-римской борьбе федерального государственного бюджетного учреждения «Центр спортивной подготовки сборных команд России», город Москва«, так сообщается в официальном сообщении.

Ислам Бетрсултанович, старший тренер юношеской сборной России по греко-римской борьбе. «Первые шаги» в греко-римской борьбе начинал в Наурском районе (Чеченской Республики) под началом Заслуженного тренера СССР и России — Пазлу Саидовича Умарова.

Надо отметить, что вся многочисленная семья Дугучиевых «прошла» через заботливые руки Пазлу Саидовича. Очень много теплых и немного смешных воспоминаний бережно хранит Пазлу Умаров, о своем легендарном воспитаннике.

Вот одна из них:

— В далекие 80 годы, когда Ислам Дугучиев еше не был Легендой борьбы, будучи школьником, принимал участие в Спартакиаде. В заявках участников было указано место проживания, в данном случае было указано -МТФ. А так как, несведущему человеку это формулировка малопонятна, то один из непосредственных участников и задал вопрос тренеру: » МТФ — это хутор?»

Для справки: МТФ -молочно-товарная ферма, где трудились и жили родители Ислама, а он учился и тренировался в интернате, в котором и работал, начинающий тогда тренер, Пазлу Умаров.

В одном из интервью, Ислам Дугучиев, вспоминая своего первого тренера, отметил, что база, заложенная им, является залогом надежности, дальнейшего роста и как будущего спортсмена, а также и личности. «Если фундамент плохой, то дом стоять не будет«, добавил он.

Сегодня, когда Саидовичу уже слегка за 70, и за его плечами множество спортсменов, которым он дал путевку в жизнь, свою тренерскую деятельность он продолжает уже в стенах школы имени своего легендарного ученика.

Фото из личного архива

Поделиться страницей:

Что такое MTF-диаграмма

На упаковке , при его покупке объектива, вы можете наблюдать загадочный график или диаграмму. Какие данные изображают эти графики? Что полезное можно из них узнать?

Диаграмма эта называется MTF (Modular Transfer Function). Если говорить по-русски, то это частотно-контрастная характеристика, которая определяет качество объектива.

Оценка, которую дают подобные графики, позволяет узнать способность объектива передавать детализацию, которая зависит от расстояния до центра объектива. По горизонтальной оси откладывается расстояние, а по вертикальной — детализация, которая измеряется в процентах. Цифра 1 для детализации обозначает 100%.

Для определения резкости используют два набора линий, которые перпендикулярны друг другу.

Детализацию оценивают на различном удалении этих линий от центра объектива. Чем график выше, тем резкость сильнее. Если с удалением от центра график опускается, значит, резкость ближе к углам плохая.

Вот как выглядит светящаяся точка при просмотре через различные объективы.

Белый квадрат – это пиксель на сенсоре камеры. Рисунок № 1 демонстрирует светосильный объектив с открытой диафрагмой. Рисунки 2 — 4 демонстрируют не очень хорошие широкоугольные объективы. У объективов №5 и 6 видны проблемы с фокусом. Объектив № 7можно назвать идеальным, но такого не бывает из-за фильтра, который стоит перед сенсором и делает из седьмого номера восьмой. Фильтра, который избавляет снимки от муара, нет только на камере Nikon D800E.

У различных производителей толщина линий может отличаться, но принцип у всех один. Перво-наперво оцениваются толстые линии. Они более важные, хотя на тонкие тоже смотрят. Они определяют более мелкую детализацию.

График MTF зависит от множества параметров. Диафрагма, расстояние до объекта, освещенность — всё это может повлиять на результат измерения. Именно поэтому на графике должно быть указано, при каких условиях выполнялись измерения. Наиболее полный график должен выглядеть примерно вот так:

Есть два способа расчета графика. Немецкие производители предпочитают выполнять исследования каждого объектива и строить для него подробный график. Для массового производства такой подход не приемлем. Именно поэтому такие компании как Nikon делают все расчеты на компьютере, не исследуя реальный объектив. График строится ля всех объективов определенной модели. Из-за сложности конструкции даже объективы одной модели будут меть различные оптические характеристики, поэтому в большинстве случаев такой график отображает приблизительные значения резкости.

Исследования одного и того же объектива пи различных условиях освещения дадут различный результат. На следующих графиках можно увидеть хороший (слева) и плохой (справа) объективы.

На правом графике наблюдаются очевидные проблемы с резкостью в углах. Умение читать MTF графики всегда может пригодиться, но желательно иметь подробную информацию об условиях измерения. В противном случае возникает очень много вопросов. Кроме того полезны реально измеренные значения графиков, а не построенные на компьютере усреднено для всей серии объективов.

На основе материалов с сайта: http://review.lospopadosos.com

MTF

Пользователи также искали:

лампы mtf h21 отзывы, лампы mtf h5, mtf light отзывы, лампы, отзывы, light, ксенон, лампы mtf h, лампы mtf h отзывы, mtf light отзывы, mtf лампы, mtf это, mtf h, mtf light h, mtf ксенон отзывы, лампы mtf h5, лампы mtf h21 отзывы, mtf h7, mtf light h21, mtf, move-to-front. mtf,

…

что означает RIH на графике MTF

Если присмотреться к документу, можно увидеть, что он может не быть ‘RIH’, а скорее может быть ‘R | H’ внутри каждого набора скобок.

Вот урожай из pdf:

И еще одна культура просматривалась точно на 100%:

Исходный документ, на который дается ссылка в данном вопросе, принадлежит компании Lomographische AG, расположенной в Вене, Австрия. официальный язык Вены — немецкий. R | H может быть аббревиатурой немецких слов, которые не встречаются в поиске в английском google, но я нигде не могу найти ссылку на ‘R | H’ или ‘RIH’ в сочетании с измерениями MTF. Поскольку размеры измерений довольно велики, в диапазоне от 0 мм до 11 мм до 22 мм, а расстояние по диагонали кадра 36×24 мм от центра до угла составляет 21,633 мм, я предполагаю (при поддержке наблюдения @ scottbb), что измерение в миллиметрах — это расстояние от центра оптической оси объектива, где оно пересекает плоскость изображения камеры, до места измерения каждой кривой.

Сначала я подумал, что это может быть высота определенного тестового шаблона, обозначенного как «R» (во многом так же, как шаблон представлен в различных размерах на других графиках, таких как стандартная диаграмма USAF 1951), но ближе проверка графиков в связанных PDF-файлах доказывает, что это неверно. Если бы это было так, то ‘R | H’ было бы обозначением высоты различных размеров шаблона ‘R’ на используемой тестовой карте.

Диаграмма испытаний USAF 1951 года, в которой используется система счисления для обозначения разных размеров одного и того же образца испытаний:

‘R’ или ‘T’ перед каждым набором скобок предназначены для линий ‘Radial’ (чаще всего называемых ‘Sagittal’ в англоязычных кругах) или линий ‘Tangential’ (иногда называемых ‘Meridional’) (подробнее ниже) ,

Я думал (это так), что график MTF будет показывать кривые линия / мм

Подавляющее большинство графиков MTF точно не показывают пары линий на миллиметр (lp / mm) кривых. Они показывают, в какой степени сохраняется контраст, когда система визуализации используется для просмотра диаграммы с определенным рисунком, представляющим собой определенное количество пар линий на миллиметр. Роджер Цикала объяснил это так же просто, как я когда-либо видел в записи блога под названием « MTF — английский перевод »

Теперь я покажу вам формулу MTF без математики: MTF = контраст. Мы можем сделать его немного сложнее и точнее, не прибегая к математическим данным: MTF = самый черный-белый / черный + белый.

Остальная часть записи в блоге также стоит прочитать.

Если чистый черный цвет на тестовой диаграмме имеет значение «1», а чистый белый — «0», то (1-0) / (1 + 0) = 1. Объектив, который может поддерживать одинаковые уровни чистого черного и чистого белого, теоретически имеет идеальный MTF, равный 1. Такой объектив не существует. Если бы «черные» линии на изображении были только 70% чистого черного, а «белые» линии были на 25% черными, то MTF была бы (70-25) / (70 + 25) = 0,47. Более подробное математическое объяснение см. В « Zeiss: Как читать кривые MTF ». Кривые, указанные в абзаце между двумя непосредственно предшествующими кавычками, относятся к типу, описанному на страницах 20-23. Но они не являются типом кривых в документе Lomographische AG.

Кривая «30 мм / lp» на обычной диаграмме MTF показывает контраст, создаваемый системой, когда размер тестового шаблона , проецируемый на плоскость изображения камеры , составляет 30 lp / мм. Кривые показывают, в какой степени сохраняется контраст между более яркими и темными линиями на тестовой диаграмме. Как правило, левая сторона диаграммы показывает значение, измеренное в центре объектива, а правая сторона показывает значение, измеренное около края круга изображения или в углу кадра камеры. Кривая показывает контраст в каждой точке вдоль линии между центром и краем / углом круга изображения кадра камеры. Значение 30 lp / mm 0,85 при 40% расстояния от центра до края означает, что при измерении на расстоянии 40% от центра до края система создает контраст между белой и черной частями 30 пар линий на миллиметр это составляет 85% от степени контрастности между каждой половиной пар линий на самом графике. Значение 50 lp / mm, равное 0,20, означает, что система создает контраст между белыми и черными участками, контрастность которого составляет всего 20% между каждой половиной рисунка 50 lp / mm и т. Д.

Обратите внимание, что «MTF50» — это не то же самое, что измерение «50 lp / mm». Это даже близко не одно и то же. «MTF50» — это способ измерения того, сколько lp / мм может быть отображено при сохранении как минимум 50% контраста между темными и светлыми участками каждой пары линий. Есть графики, которые показывают кривую для такого измерения, которая обычно помечена как «MTF by Frequency». График имеет вертикальную ось, которая указывает контраст, и горизонтальную ось, которая указывает lp / мм. Такая кривая не показывает различный контраст вдоль линии от центра к краю поля зрения объектива. Скорее, такая диаграмма покажет процент контрастности, измеренный в одной точке (обычно в центре), или покажет несколько кривых с каждой кривой, измеренной в конкретной точке между центром и краем, по мере увеличения числа пар линий на миллиметр , MTF30 — это показатель того, сколько lp / мм можно отобразить с контрастностью не менее 30%, MTF20 — это показатель того, сколько lp / мм можно отобразить с контрастом не менее 20% и т. Д.

Кривые в документе Lomographische AG, по-видимому, представляют собой этот тип графика «MTF by Frequency». Обратите внимание на очень светлый «Пространственная частота (циклы / мм)», напечатанный сбоку справа от каждого графика который, вероятно, должен быть расположен вдоль оси х в верхней или нижней части графика, чтобы было яснее, что шкала 0 — 50 — 100 на горизонтальной оси графика является ссылкой на lp / мм, а не на процент расстояния от центра до края круга объектива или рамки камеры.

При нормальных измерениях MTF контраст измеряется в двух направлениях, которые находятся под прямым углом друг к другу: сагиттальный / радиальный и тангенциальный / меридиональный. Тестовые таблицы ориентируют сагиттальные и тангенциальные линии относительно центра оптической оси. Сагиттальные линии проходят вдоль линии, проведенной от центра к краю рамки, в то время как тангенциальные линии расположены под прямым углом к ​​сагиттальным линиям. Результирующие числа показывают разрешение частей формы «колес фургона», где центр рамы — это ступица оси, сагиттальные линии — спицы, а тангенциальные линии — обод. Zeiss (см. Стр. 19 связанного документа) и многие другие лаборатории тестирования используют эту систему. Другие диаграммы ориентируют сагиттальные и меридиональные линии только относительно диагональной линии, идущей от нижнего левого до верхнего правого угла рамки. Сагиттальные линии проходят параллельно диагонали, а меридиональные линии — перпендикулярно диагонали. Nikon использует эту систему для своих собственных графиков MTF. Обратите внимание, что по диагонали, описанной выше, обе системы одинаковы. Но система, используемая Nikon, измеряет только по этой диагонали, в то время как система, используемая большинством всех остальных, также измеряет по другим линиям, проходящим через центр, и усредняет результаты по каждой линии. Также обратите внимание, что большинство производителей публикуют «теоретические» графики MTF, которые представляют собой не измерения реальных объективов, а то, что MTF имеет теоретически идеальная копия рассматриваемой конструкции объектива. В случае симметричных конструкций линз теоретическая MTF идеальной копии конструкции линзы будет одинаковой вдоль любой линии, проходящей через центр кадра.

Многие диаграммы показывают несколько кривых. Каждая кривая может быть для переменной частоты пары линий или высоты / ширины пары линий, так как изображение проверяется от центра к краю кадра, или каждая кривая может соответствовать количеству контрастности, сохраняемой в одной точке, как число lp / мм увеличивается. Диаграммы в документе Lomographische AG, связанном с вопросом, показывают пять таких наборов кривых последнего типа. Существует тангенциальная и радиальная кривая для каждого из четырех наборов. Кажется, что каждый набор Тангенциальной и Радиальной кривых был измерен на расстоянии от центра кадра, обозначенном расстояниями, указанными в F3, F5, F7 и F9. Поскольку F1 был измерен в центре, ни у одной из линий нет ни тангенциальной, ни радиальной ориентации. F1: Дифф. предел представляется кривой MTF для теоретически совершенной дифракционной линзы с ограниченным фокусным расстоянием. F1: (R | H) представляется измеренным контрастом в центре кадра для числа lp / мм на шкале по горизонтальной оси диаграммы.

Значения (R | H) для Тангенциальной и Радиальной линий выражены в миллиметрах от центра кадра. F3: T (R | H) 11,000000 мм — тангенциальное измерение, выполненное на расстоянии 11 мм от центра рамы. Левая сторона графика начинается с 0 lp / мм, а правая сторона графика заканчивается при 100 lp / мм. F9: R (R | H) 22,000001 мм — радиальное (сагиттальное) измерение, выполненное на расстоянии 22 мм от центра рамы. Поскольку половина диагонали датчика полной рамки 36×24 мм составляет 21,633 мм от центра рамки до самого угла, F9, по-видимому, была измерена на круге изображения объектива в точке, которая находится сразу за той частью, которая упала бы в самый угол 35-мм пленки или датчика полной рамки.

Как читать MTF-графики. Брошюра от Carl Zeiss

Перевод брошюры Как читать MTF-графики на русский язык осуществлён Николаем Мыльниковым. За что ему большое спасибо!

к содержанию ↑

By H. H. Nasse
Carl Zeiss Camera Lens Division December 2008
Скачать брошюру Как читать MTF-графики. Брошюра от Carl Zeiss на английском
[lock][download id=43][/lock]

к содержанию ↑

к содержанию ↑

Предисловие

Из интернетовской дискуссии «Как читать кривые MTF» был сделан хороший честный вывод, показывающий нам, как трудно фотографам понять этот мир цифр. Тем не менее, на последующих страницах будет показано, что дело не так и плохо, и вполне возможно представить основные закономерности без экскурсии в высшую математику оптики Фурье. После прочтения этой статьи вы сможете делать заключения о характеристиках объективов на основании данных MTF, публикуемых производителями или тестирующими институтами. Вместе с тем, вы поймете пределы использования MTF, и это позволит вам критически относиться к обзорам объективов. А те, кто мало обращает внимания на цифры и графики могут утвердиться в своей уверенности, что для хорошего фотографа это действительно не нужно, т.к. фотография основывается, гл. обр. на опыте. Но есть люди, желающие лучше понимать работу своих инструментов, и именно этого они смогут достичь при чтении этой первой части. Во второй – мы покажем вам несколько иллюстраций.
к содержанию ↑

Функция рассеяния точки

Когда фотограф намеревается получить точное соответствие снимка объекту он должен пожелать получить на свою камеру идеальный объектив, тот, что позволяет всем лучам света, исходящим из одной точки объекта снова в точности сойтись в одной точке снимка. Сейчас мы знаем, что с реальными объективами мы прошли лишь часть пути для достижения идеала. Точка изображения, в геометрическом смысле слова, в действительности не существует. Абберации в системе линз объектива, производственные допуски, волновая природа света, в конечном счете, приводят к тому, что свет, исходящий из одной точки объекта всегда распределяется по области, лежащей вокруг идеальной точки изображения. До определенной степени, эта область является «минимально возможной окружностью возмущения». Однако вокруг области свет распределяется неодинаково, и его интенсивность снижается от центра к краям, а форма редко бывает округлой. Этот эффект известен как «Функция рассеяния точки» (point spread function). Её форма и размеры характеризуют качество изображения объектива. Если возможно сравнить фотографию с полотном, то функция рассеяния точки будет мазком. Подобно тому, как кисти бывают широкие, узкие, точечные или даже лохматые, объективы тоже имеют различные «стили письма».

Тогда почему до сих пор не используются количественные методы описания качества изображения? Для этого имеются три причины:
1. Форма области иногда очень сложная и не поддается простому количественному описанию. Это показано на следующих картинках, полученных с помощью микроскопа. Первые шесть точек, показанных на следующей странице, являются примером реальных, но средних по качеству изображений, типичных для светосильных объективов на полной диафрагме, широкоугольных объективов на краю изображений или объективов слегка расфокусированных. Маленькие белые квадратики в каждом изображении помещены для сравнения и представляют 8,5 мкм пиксель, подобный тому, что находится на 12 МР полнокадровой матрице 35 мм камеры. Все эти области рассеяния точки, как можно видеть, значительно больше, чем площадь (относительно большая) пикселя.

Рассеяние точки №7 – пример выдающегося качества изображения. Однако цифровой сенсор обычно не видит такое маленькое рассеяние точки. На изображении №8 показано то же самое рассеяние помещенное за низкочастотный (low pass) фильтр, к-рый обычно помещают перед сенсором для подавления муара. Качество изображения, таким образом, намеренно ухудшают, значительно увеличивая рассеяние точки при помощи нескольких дисков с двойным лучепреломлением.
2. Вы почти никогда не увидите такое одиночное, изолированное точечное рассеяние. Только сфотографировав звезду темной ночью, можно достичь эффекта, приведенного здесь и полученного в лаборатории. Большинство изображений создаются в камере путем сложной комбинации частей большого количества единичных рассеяний точек. Т.к. небольшой участок объекта состоит из многих близко стоящих точек, что соответствует многим плотно стоящим идеальным точкам изображения, получаемым позади объектива. Поскольку реальные рассеяния точек не могут быть бесконечно малыми, то это означает, что индивидуальные рассеяния точек перекрываются. Интенсивность единичной точки изображения (можно даже сказать единичного пикселя) создаются взаимодействием (сложением) многих рассеяний точек. Т.е. являются математически трудно описуемой связью между «мазком кистью» и изображением, которое мы видим.
3. Состоит в том, что целостная воображаемая цепь от объектива до глаза может быть более просто описана с помощью метода, который я собираюсь сейчас объяснить.
к содержанию ↑

Поскольку в первую очередь нас интересует получение изображений протяженных объектов, объектов не похожих на звезду и состоящих из неопределенного числа точек, то нам необходимо найти другой способ количественного описания качества изображения. Для того, чтобы изучить как выглядит простой, насколько это возможно, объект на изображении мы используем синусоидальное распределение яркости. Синусоидальное распределение яркости – это последовательность светлых и темных полос, между которыми переход между яркостью и темнотой происходит постоянно и постепенно, т. е. синусоидально. Синусоидальный полосатый образец используется потому, что получаемое изображение, неизменно, тоже является синусоидальным, независимо от того, каким бы сложным ни было рассеяние точки. Некоторые его свойства остаются неизменными, или, по крайней мере, не оказывают влияния на качество изображения: не изменяются направление полосок и их частота, т.е. количество на единицу длины. Эти показатели изменяются только с изменением образца. Что не идентично более оригиналу, так это различие в яркости между светлыми и темными полосками. Это происходит потому, что из-за протяженного рассеяния точки часть света не попадает на яркие полоски, а попадает на области, которые в действительности должны быть абсолютно черными.

На приведенном графике показан синусоидальный профиль яркостей последовательности темных и светлых полос (черная кривая) в виде профиля интенсивности (сечение перпендикулярное направлению полос). На один миллиметр приходится 20 периодов, т.е. 1 период равен 50 микрометрам (мкм). Красная и синяя кривые – поперечные сечения распределения яркостей в рассеяниях точек. Яркость точки, лежащей на кривой и обозначенной синим, которая отобразится на идеальном изображении, распределится на окружающей поверхности в соответствии с синей кривой. Видно, что часть света подает в темные «долины» на 25 мкм отстоящие от синей точки. Свет также падает сюда и от точки кривой, обозначенной красным цветом. Хотя красная точка лежит на боку кривой и, следовательно, темнее, значительная часть света достигает точки -25мкм т.к. красная точка ближе к темной «долине». Т.о. освещенность темных областей образца является суммой добавочного света, поступающего с соседних участков. В результате изображение будет характеризоваться кривой с ослабленной модуляцией (помеченной «image»). Яркость темных полос изображения возрастает из-за отклонения света, а яркие полосы становятся темнее. В оптике различия между ярким и темным определяется как контраст. С более общей точки зрения, различия между максимальным и минимальным значениями, для любого синусоидального периодически изменяющегося показателя называется «модуляция». Если мы сравним модуляцию объекта с модуляцией изображения, просто разделив эти цифры одна на другую, мы получим число, характеризующее изобразительные свойства объектива: воспроизведение модуляции (modulation transfer). Т.о. мы уже понимаем, что обозначают первые две буквы в термине «MTF». Это число от 0 до 1 или от 0% до 100%. Фотографы для отражения различий между светом и тенью используют шаги диафрагмы, которые отражают логарифмическую шкалу чувствительности наших глаз. Но, для примера, что означает воспроизведение модуляции 50%, если различия между темными и светлыми точками нашего образца составляют 6 шагов диафрагмы? Не означает ли это, что соотношение яркостей составляет 1:26 = 1:64? Может быть, различия между яркостями в изображении составляют 3 шага диафрагмы, или м.б. 1:32, т.е. 5 шагов диафрагмы? И то и другое неверно. В действительности в этом случае мы имеем примерно 1,5 шага диафрагмы. Это потому, что в оптике параметр «контраст» определяется следующим образом:

Поэтому в нашем случае контраст объекта приблизительно 0,97 (63:65). После получения изображения с воспроизведением модуляции (modulation transfer) 50% контраст снизился в 2 раза, приблизительно до 0,48. Минимум и максимум, т.о составили 1:2,9 (1,9/3,9 = 0,48). Следующий график показывает как контраст объекта и контраст изображения связаны для различных воспроизведений модуляции (modulation transfers) если измерять их в шагах диафрагмы.

График демонстрирует 3 важных свойства MTF, которые мы должны помнить, изучая кривые MTF:
1. Небольшие различия между высокими показателями MTF становятся особенно заметными при высоком контрасте объекта.
2. С другой стороны, слабая изменчивость в тонах – менее одного шага диафрагмы – не требует высоких значений MTF. Различия более 70-80% вполне уместны.
3. При очень низких значениях MTF контраст объекта практически не имеет значения. Контраст изображения будет всегда низким.
Именно поэтому в спецификации пленки всегда также указывается разрешение при низком контрасте 1:1,6. Контраст в 1:1000 может быть измерен только методом контактной экспозиции. Ни один объектив в мире не способен передать изображение очень мелких структур (например, очень высокую частоту полос) с контрастом в 10 шагов диафрагмы. Желание получить на пленке такое высокое разрешение, т.о., слишком оптимистично.
к содержанию ↑

Очевидно, что образец, состоящий из одной полоски недостаточен для характеристики объектива. Образец с широкими промежутками м-ду светлыми и темными полосками, конечно, может быть хорошо воспроизведен объективом с большой областью рассеяния точки. Если же мы уменьшим расстояние м-ду полосками до такой степени, что оно приближается к величине функции рассеяния точки, то часть света ярких зон будет попадать на темные и контраст изображения сильно упадет. Продолжая сравнение с кистями, можно сказать, что крупные структуры можно изобразить толстой кистью, для изображения же тонких деталей требуется тонкая точечная кисть. Т.о. нам требуется исследовать, как объектив передает изображения образов с различной толщиной полос, т.е. мы должны определить воспроизведение частот (modulation transfer — МТ) для каждого из этих образцов. При этом мы получаем целостную последовательность чисел и если затем мы представим их в виде функции, описывающей толщину линий образца, то последовательность этих чисел будет представлять кривую, называемую функцией воспроизведения колебаний (modulation transfer function) – MTF.
Толщину полос можно измерять, подсчитывая их кол-во (периодов: белый-черный) на 1 мм изображения. Период – это расстояние между двумя яркими или двумя темными полосками, ширина пары линий состоящей из одной яркой и одной темной. Кол-во периодов в 1 мм на плоскости изображения – частота полос. Она характеризуется показателем пара линий на 1 мм, сокращенно л/мм (lp/mm).

MTF 50 мм объектива в 35 мм формате в центре изображения, измеренная при диафрагме 2 и диафрагме 5,6 для сравнения. Так же приводится воспроизведение модуляции ограниченное дифракцией для диафрагмы 5,6 и диафрагмы 16 (сплошная линия без кружков). Самая лучшая картинка – ограниченная только дифракцией. По горизонтальной оси отложена частота пар линий на мм.

Если изображение ограничено только явлением дифракции, то MTF представляет почти прямую линию, снижающуюся пропорционально возрастанию частоты полос. MTF = 0 достигается при этом в т.н. точке предела частоты полос, которая определяется диафрагменным числом и длиной волны света. Приближенно можно считать, что для средней длины волны видимого света ширина области рассеяния точки в мкм соответствует диафрагменному числу, а предельная частота полос приблизительно равна 1500, деленное на диафрагменное число.

У реальных объективов, имеющих остаточные абберации, значения MTF сначала быстро снижаются, а затем очень медленно приближаются к 0. Т.е кривая явно провисает. В вышеприведенном примере это явно наблюдается для кривой апертуры 2; при диафрагме 5,6 характеристика объектива не слишком отличается от физически возможного оптимума. Частота линий, при которой значение MTF достигает 0, или опускается ниже предельного порога (н-р 10%) называют разрешающей способностью объектива в воздухе. Образцы с чередующимися полосами могут содержать всё более тонкие линии, прежде, чем их изображение сделается сплошным серым. Кривая для диафрагмы 2, в частности, показывает, что предел разрешения здесь трудно измерить. Очень слабый наклон кривой при высоком значении частоты полос означает, что результат определяется минимумом требуемого контраста. Измерения поэтому очень неточны. Исходя из этого, оказывается, что недостаточно характеризовать объектив только разрешающей способностью. И уж совсем не следует путать этот показатель с разрешающей способностью, достигаемой при взаимодействии объектива и сенсора. Это снова возвращает нас к 3-ей причине, по которой мы описываем качество изображения с помощью MTF: мы никогда не воспринимаем изображение, получаемое объективом непосредственно глазами, всегда требуется еще одно звено в цепи формирования изображения, Мы всегда нуждаемся в приемнике изображения: сенсоре – цифровом или аналоговом, или сканере, принтере, или проецирующем устройстве. Каждый из этих компонентов, наряду с глазом человека имеет свои изобразительные св-ва, каждое из к-рых м. б. описано функцией воспроизведения. И хорошие показатели MTF, как MTF целостной цепочки формирования изображения является продуктом всех индивидуальных MTF.

Рассмотрим несколько типичных примеров:

Две MTF: очень хорошего 35-мм форматного объектива и цветной негативной пленки. Результат всегда слабее, чем самый слабый фактор в цепи формирования изображения. В данном случае, общее качество изображения существенно ограничено свойствами пленки. Если принять минимальное воспроизведение модуляции в 10%, то разрешающую способность следует ожидать на уровне 80-100 л/мм. Если принимать во внимание наличие других элементов — глаз или оптика проектора – результат будет существенно хуже.

Результат сложения двух функций воспроизведения модуляции: 35-мм объектив среднего качества и цветной негативной пленки. В этом случае, суммарная кривая почти в равной степени определяется св-вами объектива и пленки.

Если рассматривать кривую образованную только двумя функциями воспроизведения, имея в виду, что в действительности этих функций может быть больше и они могут только ухудшать результат, то станет ясно, что нет необходимости использовать много образцов с очень высокой плотностью линий на 1 мм. Цифровой сенсор в 24 МП в 35мм формате, или 15 МП в APS-C формате имеют разрешение около 90 л/мм. Теоретически их разрешение можно сравнить с разрешением цветной негативной пленки. Поэтому при этих форматах обычно бывает достаточным рассматривать частотный образец до 40 л/мм. Если кол-во пикселей больше, то 40 л/мм становится более важным показателем, чем обычно.
Другое соображение в пользу того, что это достаточный предел заключается в следующем: если рассматривать изображение в формате А4 с расстояния 25 см и видя т.о. изображение под углом 60о, то глаз способен различить до 1600 линий на изображение по высоте. Т.е. его максимальное разрешение в этом случае составляет 8 л/мм. Это расстояние «наименьшая дистанция ясного видения». Для формата 35мм с 24 мм по высоте это соответствует 66 л/мм. Частота полос важная для глаза находится, т.о. тоже в пределах до 40 л/мм.
Если увеличить изображение, то с короткой дистанции будут видны более мелкие детали, и можно увидеть погрешности изображения незаметные при нормальном рассматривании изображения. Это похоже на то, когда цифровое изображение рассматривают на большом мониторе при 100% увеличении. Изображение в 12 МП при этом будет более 1 м в ширину. Сенсор способный воспроизводить разрешение обеспечиваемое объективом – это низкочувствительная черно-белая пленка.

Хороший объектив в сочетании с черно-белой пленкой высокого разрешения (Из Т-Мах-100)

На следующей картинке графически показано, что 40 л/мм достаточно высокая частота, по крайней мере, для 35мм формата. Это хорошо известные звезды Сименса, часто используемые для испытания камер. Полная картинка для 12 МП камеры в 35мм формате содержит 9 звезд.

Сильно увеличенное изображение центра звезды Сименса показывает, как близко к центру располагаются линии, частота которых 40 л/мм.

к содержанию ↑

Мы уже знаем почему модуляция синусоидального полосатого образца на оптическом изображении понижается по мере увеличения частоты полос, а также на дальнейших стадиях образования изображения вплоть до его восприятия. Но что могут сказать нам эти цифры о качестве реальной картинки? Каковы отношения между такими терминами как: четкость, яркость, разрешение деталей etc. и этими числами? Наш объект съемки, конечно, не содержит синусоидальных деталей. Они могут быть приблизительно созданы только в условиях лаборатории, поэтому используются другие тест-объекты, по которым синусоидальная модуляция рассчитывается математически. В специальных тестах для оценки объективов и камер и определения эффективной разрешающей способности используются образцы с прямоугольным профилем интенсивности, резким переходом между черным и белым. Передача модуляции для прямоугольного образца, обычно несколько лучше, чем для синусоидального той же частоты. Однако такие резко прямоугольные формы тоже редко встречаются в реальной фотографии. Тонкие периодические структуры, которые наш глаз использует для оценки качества картинки, присутствуют лишь на небольших фрагментах снимка. На самом деле наиболее важными являются переходы, границы между двумя областями, различающимися по яркости или цвету. Хотелось бы понять каковы взаимоотношения между MTF и воспроизводством переходов. Это опять приводит нас к функции рассеяния точки.
Ниже, слева направо представлены рисунки:
1. Профиль интенсивности функции рассеяния точки в логарифмической шкале вплоть до 1/1000 от максимальной интенсивности, находящейся в центре. Ширина функции рассеяния точки представлена в мкм, 1 мкм = 1/1000 мм.
2. Профиль интенсивности двух границ в изображении с большим и малым переходами яркостей. Вертикальная шкала – логарифмическая шкала диафрагм знакомая фотографам. Каждое деление отражает имеющуюся освещенность. Горизонтальная шкала – опять же мера расстояния на изображении в мкм. Яркая и темная стороны перехода находятся, соответственно, слева и справа.
3. Воспроизведение модуляции для 5 частотных образцов: 5, 10, 20, 40 и 80 л/мм представлено в виде столбиков на соответствующей диаграмме.

Пример очень хорошего изображения в 35 мм формате: рассеяние точки узкое, переход между белым и черным узкий – не шире 10 мкм, т. е. очень крутой. Фотографы говорят в таких случаях: границы резкие. На языке передачи модуляции на такие характеристики указывает тот факт, что показатели воспроизведения всех частот очень высокие и не сильно снижаются при возрастании частот. Для объективов с такими параметрами изображения качество получаемой картинки ограничивается обычно свойствами сенсора, аккуратностью фокусировки, движением камеры etc.

Если диаметр функции рассеяния точки значительно больше, то изображение переходов от белого к черному не назовешь резким. Профиль границы плоский, т.к. переход от максимальной яркости к черному составляет 30-50 мкм в зависимости от величины изменения яркостей. Тем не менее, абсолютно черный на этом изображении присутствует и контраст м-ду вершинами и концами кривых высокий. Значения MTF быстро падают с возрастанием частоты образца, что объясняет предшествующие показатели. При 10 л/мм MTF незначительно отличается от предыдущего примера (высокий контраст).

Профиль рассеяния точки в виде прямоугольника естественным образом приводит к ослаблению способности видеть границу. Показатели MTF на низких и средних – до 20 л/мм — частотах нормальные. Даже при 60л/мм воспроизведение модуляции остается на приемлемом уровне. Если учитывать только эти значения частот, то можно думать, что изображение будет вполне приличным.
Но: здесь нет контраста при 40 л/мм! Кривая воспроизведения модуляции может упасть до 0, а затем вновь подняться. Такое явление называется «фальшивым разрешением», что не совсем удачно, поскольку структуры с частотой 60 л/мм заметно воспроизводятся. Обычно остается незаметным, что черное и белое меняются местами (за исключением звезды Сименса) и следующая точка 0 придется на частоту 80 л/мм, затем изображение вновь появится с черным и белым на своих местах. Термин «фальшивое разрешение» подчеркивает, что отдельная демонстрация высокого разрешения в одной особо предпочитаемой частоте может создавать впечатление высокого качества картинки, которое в действительности отсутствует. В публикуемых MTF вы не найдете такого рода изображений, но в практике они имеют место и приводят к ошибкам фокусировки и блюру, вызываемому движением.

Следующая функция рассеяния точки такая же узкая, как и в первом примере, но окружена слабым ореолом (halo). Определение границ на части графика четкое, но в тоже время широкие. Яркие лучи протягиваются в зону темноты. Фотограф скажет, что объектив подсвечивает. Контраст между светом и тенью слабый.

Величина MTF этого четвертого типа характеризуется тем, что с повышением частоты снижается слабо, как и в 1-м случае, но при низких значениях частот: 5 и 10 л/мм невысокая. Изобразительные качества объектива с такими характеристиками могут быть до некоторой степени непостоянными и проявляться различно в зависимости от содержания изображения. Границы низкого и среднего контраста воспроизводятся с одинаковой резкостью, в частности, если выдержка короткая. Тонкие структуры со слабым контрастом становятся несколько плоскими, а границы с достаточным контрастом и света подсвечиваются или становятся более широкими при обычных выдержках.
Многие светосильные стандартные объективы 60-х годов на больших диафрагмах были откорректированы именно таким образом. При 10 л/мм они имели только 60-70% MTF, у современных объективов это значение обычно 80-90%.
Иногда говорят, что такие объективы «оптимизированы по разрешению». Это не совсем верно, т.к. они просто хорошо воспроизводят границы, а разрешающая способность для тонких периодических структур не лучше, чем у объективов с другими техническими характеристиками. Во времена доминирования черно-белой фотографии низкий контраст таких объективов можно было компенсировать, используя высококонтрастную бумагу. При цветной фотографии с ее менее гибким процессом лабораторной обработки позже требовались изменения в способах коррекции для получения нужного контраста. Впрочем такие объективы до сих пор находят своих поклонников. Поэтому следует быть осмотрительным, высказывая свое мнение об объективах. Например, знаменитый мягкий портретник ‘IMAGON’ имеет следующую MTF:

Между прочим, это не значит, что при расчете объективов приходится делать выбор между высокой разрешающей способностью и хорошим контрастом изображения: у объективов с хорошей коррекцией есть и то и другое.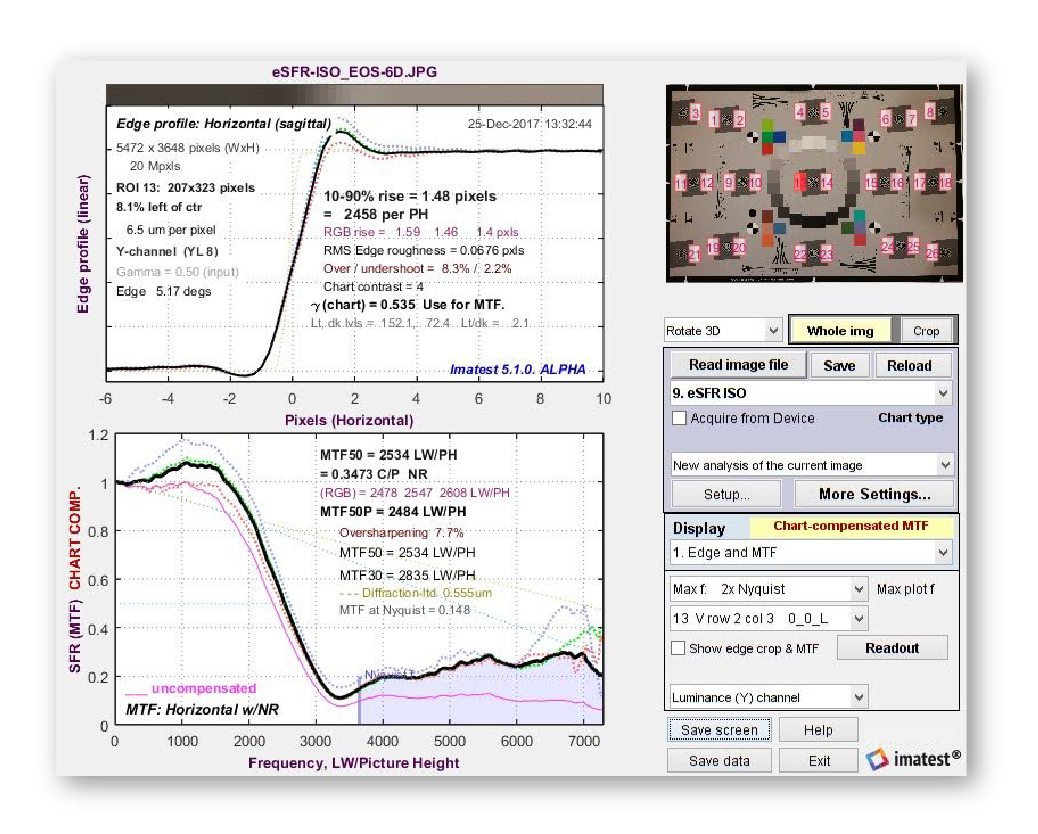
Но что обозначает «контрастное изображение»? Мы не должны забывать, что когда мы говорим о «контрасте», мы всегда имеем в виду микроконтраст, т.е. структуры, которые, например, на слайде — еще видны или уже не видны невооруженным глазом. А когда мы фотографируем, например, шахматную доску, так, чтобы она полностью занимала площадь снимка, с контрастом между белыми и черными квадратами ничего не происходит. Измерения MTF ничего не говорят о таком макроконтрасте. Они оценивают только степень коррекции объектива, т.е. небольшие отклонения световых лучей, тогда как макроконтраст зависит от замутненности чистоты, непросветленности объектива, т.е. от больших отклонений. Последние – результат нежелательных отражений между оптическими поверхностями и рассеяния света на внутренних бочкообразных компонентах. Поэтому свет обычно достигает поверхности изображения более длительным путем, чем напрямую. Эти характеристики обычно смешивают между собой в термине «яркость картинки». Васокие показатели MTF при низких частотах линий необходимы, но недостаточны для получения «яркой картинки» (звенящей?).

Увеличенные изображения фрагмента шахматной доски. Слева – совершенное качество изображения; середина – слабый микроконтраст; справа – значительная степень замутненности.

Свойства изображений приведенных выше, иллюстрируют их гистограммы: у картинки, полученной объективом со слабым микроконтрастом правый пик значительно шире, чем левый, т.к. светлые тона на границах частично заходят на области черного. Тем не менее, расстояние между пиками на шкале серого точно такое же, как и для левого отличного изображения. На правой картинке с высоким уровнем замутненности пик темных тонов на гистограмме перемещен в сторону светлых, т.к. черный осветлен замутнением объектива по всему полю изображения.

Основные четыре типа функций рассеяния точки, приведенные выше, и, соответствующие им кривые MTF, можно обнаружить в характеристиках всех объективов, не всегда в виде примеров, показанных здесь, но обычно, как их комбинация. Эти примеры также показывают, что MTF следует изучать для нескольких пространственных частот. Показатель 75% для 10 л/мм будет недвусмысленным только для изображения синусоидного образца. Для реального изображения он всегда также зависит от величин показателей для 20 и 40 л/мм. Если они очень высокие, то объектив отлично прорисовывает границы, дает прекрасный контраст и хорошо передает света, как в нашем 4-ом примере. Если эти показатели ниже, то объектив теряет резкость, может быть слегка расфокусирован и у него нет «звона».
Тесты, оценивающие только одну точку MTF, например разрешение или частоту линий при к-рых MTF достигает 50% стоят немного. Это можно сравнить с оценкой HI-FI системы: я знаю, какую частоту лучше всего воспроизводят динамики или как воспроизводится частота 400Hz, но не знаю как звучит в них музыка.
к содержанию ↑

При преобразовании реального изображения в цифровое большое значение имеет MTF камеры. Путем легкого осветления светлого края границы и притенения темного, производится подчеркивание границ. Этот прием повышает микроконтраст, резкость перехода границ и при этом субъективное восприятие резкости значительно улучшается без увеличения разрешения в деталях. Это убедительно доказывает, что четкость и разрешение не одно и то же. На MTF такие манипуляции можно обнаружить по кривой, которая частично или полностью прерывается, как это происходит у объективов, рисующих очень резкие переходы, хотя нормально должна понижаться с повышением частоты образцов.
При построении цифрового изображения можно даже усилить контрастность границ и создать функцию, которая возрастает с увеличением частоты полос. На языке теории воспроизведения она т.о. имеет характер high-pass, а такие системы способны создавать искусственные границы.

Модуляция в изображении Зеркальной 24 МП камеры 35 мм формата при различных режимах усиления переходов при внутрикамерном преобразовании в JPEG. Кривая с плоской вершиной в район 50 л/мм относится к изображению с наиболее высоким усилением границ.

Модуляция в изображении 2/3» камеры при минимальном, среднем и максимальном усилении границ. При горбатой кривой следует ожидать сильных артефактов. За границей темной зоны при этой кривой обычно наблюдаются дополнительные яркие линии.
к содержанию ↑

До сих пор мы рассматривали отношения между функцией воспроизведения и функцией рассеяния точки. Мы увидели, как форма функции рассеяния точки и распределение интенсивности света в ее пределах влияет на функцию воспроизведения при различных частотах полос. Здесь мы рассмотрим MTF как функцию параметров частоты полос.
Функция верна только для одной единичной точки изображения, тем не менее, даже для этой точки мы должны иметь несколько кривых, т.к. из наших примеров мы видели, что области рассеяния точки не обязательно округлые. Некоторые можно сравнить с плоской кистью, которой можно рисовать тонкие линии лишь в одном направлении. Если мы повернем частотный образец, то можем ожидать, что увидим другую MTF-кривую, которая зависит от того, короткая или длинная ось области рассеяния точки перпендикулярна направлению полосок образца.

Главные направления, т.е. короткая или длинная сторона функции рассеяния точки всегда параллельна или перпендикулярна радиусу окружности изображения, т.к. объектив имеет вращательную симметрию. Образец полоски которого длинной стороной направлены к центру в оптике принято называть радиальными или сагиттальными (sagitta — лат. стрела). Это направление обычно обладает лучшим воспроизведением модуляции. Полоски перпендикулярные им ориентированы так же как касательные к окружностям, лежащим вокруг центра изображения. Такую ориентацию полосок называют тангенциальной или меридиональной.

к содержанию ↑

Поскольку качество изображения объективов изменяется, в общем, от центра к краям, и поскольку именно эти различия представляют для нас особый интерес, то, естественно, что для тангенциального и сагиттального направлений нам требуется больше, чем 2 кривые. Для описания частотных изменений свойств изображения с удовлетворительной точностью между центром и углом требуется полдюжины или около того точек измерения. Это будет в целом 12 кривых – не слишком ясная и четкая картина.
Кривые MTF, которые мы уже хорошо знаем, и для построения которых на вертикальной оси мы откладываем воспроизведение модуляции, а на горизонтальную – частоту полос, на самом деле удобны только для сенсоров, т.к. его характеристики не изменяются по площади. Для объективов такое представление результатов неудобно. Поскольку кривая MTF, являясь функцией частоты полос, всегда более или менее быстро падает вправо, становится достаточным выделить 3 различных значения для каждой кривой, обычно это 10, 20 и 40 л/мм. Если показать как кривые MTF для этих частот изменяются по площади изображения, то мы получим графики более удобные для объективов.
Именно поэтому на кривых MTF, приводимых в наших данных, воспроизведение модуляции приводится на Y-оси, а высота изображения – сечение оптической оси – на X-оси. На диаграмме показано 6 кривых, т.е. тангенциальная (прерывистая линия ) и сагитальная (непрерывная линия) для каждой из 3 частот. Верхняя из 6-ти кривая всегда относится к само низкой частоте, а нижняя, конечно, к самой высокой.

Кривая MTF объектива Planar 1.4/50 ZF для 10, 20 и 40 л/мм; белый свет, фокусировка на бесконечность

В центре этот объектив достигает при 10 л/мм более чем 80% MTF даже при полностью открытой диафрагме, но при 40л/мм MTF падает ниже 40%. Это означает хорошее воспроизведение контраста и среднюю степень детализации, которая проявляется в слабом эффекте размытия при большом увеличении картинки. Дальше от центра MTF при 10 л/мм падает до 70%, возрастает склонность к размытию при высоком контрасте границ. В углах изображения сагиттальные кривые тесно сближается при низком значении MTF поэтому следует ожидать значительного засвечивания углов открытыми источниками света.

Если диафрагму прикрыть все показатели MTF сильно возрастают: кривые сближаются друг с другом и сильно поднимаются. Т.е. значения MTF снижаются относительно медленно с возрастанием пространственной частоты. Это означает отличное воспроизведение границ и очень хороший микроконтраст. В углу изображения все кривые несколько падают: для 10 л/мм немного, для более высоких частот – сильнее. Это указывает на хорошую плоскость поля зрения до, примерно, 18 мм высоты картинки, а затем о расфокусировке изображения в углах картинки из-за внезапно возникающей кривизны поля зрения. Не следует принимать слишком серьезно небольшие изменения кривой при 40 л/мм, они будут заметны лишь при очень большом увеличении картинки и когда фотографируют плоский объект; на большинстве изображений они просто не видны. Они вызваны кривизной поля зрения и сдвигом фокуса. Почему это происходит, мы узнаем в разделе о трехразмерных характеристиках MTF.

Сравнение двух объективов при одном фокусном расстоянии для 35 мм формата, на диафрагме 5,6. Слева высококачественный объектив (Planar 1.4/85 ZF), справа – недорогой 5-х зум объектив. Качество картинки первого по всему кадру ограничивается практически только свойствами сенсора и допускает самое большое увеличение. Зум-объектив достаточно хорош в центре, но значительно хуже у краев кадр. За исключением углов здесь можно ожидать хороший контраст, но у объектива отсутствует четкая резкость, т.к. MTF высоких частот падает быстрее. Изображения объектива могут быть рекомендованы только для небольшого увеличения.

Сравнение двух широкоугольных объективов, которые значительно труднее в изготовлении, при диафрагме 5,6. Слева данные для Distagon 2.8/21 ZF, справа объектив, у которого боковые хроматические абберации устранены не так хорошо. У него объектив показывает некоторый сдвиг фокуса и, тем не менее, он не так и плох. Но тангенциальные MTF очень низки по краям кадра. Что это значит можно видеть на приведенных изображениях (200×200 пикс. с 12 МП картинки, высота изображения около 12 мм).

к содержанию ↑

Очевидно, что разрешение картинки зависит от того, правильно ли была произведена фокусировка. Т.е. этот параметр можно описать кривой MTF. Сейчас мы познакомимся с мало известным типом кривых MTF. Этот показатель не является функцией частоты по высоте картинки, а описывает параметры фокуса. Для этого мы измеряем как MTF изменяется в продольном направлении плоскости изображения объектива и получили такие кривые:

Значения MTF для 10, 20 и 40 л/мм вновь откладываются по вертикальной оси. Точка 0 на горизонтальной оси соответствует наилучшему фокусу; т.е. значение MTF для средней частоты — 20 л/мм здесь максимальна и именно здесь надо размещать сенсор или пленку, что обозначено желтой линией. Влево мы приближаемся к объективу, вправо мы отодвигаемся за сенсор.
Можно видеть, что приемлемые границы значения MTF для этой диафрагмы всего несколько сотых миллиметра. Два черных треугольничка показывают глубину фокусировки в плоскости изображения, подсчитанную чисто геометрически для круга смешения диаметром 0,03 мм. В соответствии с этим критерием, глубина области, находящейся в фокусе, ограничивается значением MTF равным 20% при 40 л/мм. Т.е. допускается, что максимальные значения для различных частот находятся в разных положениях, а кривые часто ассиметричны. Это означает, что тип размытия будет различным впереди и сзади фокуса. Что произойдет если уменьшить диафрагму? Мы уменьшили диафрагму на 3 ступени и повторили измерения, фокусировку не меняли, т.е. точка 0 все еще означает: MTF максимальна в центре картинки при 20 л/мм и диафрагме 1,4.

Максимальное значение MTF существенно возросло, т.к. снижение апертуры сильно снижает остаточную абберацию. В то же время мы отмечаем сдвиг всех кривых вправо, т.е. дальше от объектива. Объектив сейчас больше не фокусируется оптимально, т.е. в месте размещения сенсора (желтая линия), повышение MTF произошло, но не на этом месте. Геометрически рассчитанная глубина фокуса на плоскости изображения плохая, его длина вполне нормальная, а положение неверное. Такое явление называется «сдвиг фокуса», обычно оно свойственно объективам с большой апертурой и связано со сферической абберацией, что означает, что пучки света, проходящие через область диафрагмы на различном расстоянии от оптической оси, имеют разный фокус. В нашем случае сдвиг фокуса около 0,05 мм. Черные точки на вышеприведенном графике показывают, как этот сдвиг в пространстве изображения связан с расстоянием в пространстве объекта перед камерой (шкала с правой стороны графика). Если, например, первоначально при f/1,4 объектив был сфокусирован на расстояние 3 м, то сейчас, если другие настройки объектива не изменились, точка наилучшего фокуса сдвинулась на 3,25 м.
Следует ли вводить поправку на этот сдвиг фокуса при фотографировании? Вовсе нет, несмотря на то, что лучшее качество изображения в центре. 0,05 мм составляют около 20% расстояния между крайними точками глубины резкости для f/4 и поэтому трудно поддается точной корректировке. Кроме того, все равно в другой точке кадра картина будет совсем иной. Поэтому мы вновь измеряем MTF в продольном направлении, но не в центре, а на расстоянии 10 мм.

Здесь для наглядности мы приведем только тангенциальную и сагиттальную кривые для 40 л/мм, кривые для 10 и 20 л/мм не показаны. Мы видим, что обе кривые сдвинулись влево. Таким образом, положение максимума сдвигается, если мы перемещаемся по площади изображения.

Здесь мы достигли края изображения на расстоянии 18 мм от центра и видно, что сагиттальная кривая возвращается к точке вблизи 0 нашей шкалы фокусировки. Т.е. по площади изображения кривая изменяется не единообразно, но могут быть и точки возврата. Комбинация остаточной кривизны плоскости и сдвиг фокуса приводят к тому, что MTF для объектива может выглядеть совершенно иначе, если мы не будем искать локальный максимум для каждой точки изображения, а будем регистрировать ее точно по плоскости изображения.

Потому эти два графика не означают: что левый объектив несколько хуже в центре, чем по полю, а правый объектив, напротив, отличный в центре, но в области дальше 15 мм имеет значительные нарушения. Оба графика получены на одном объективе, но с чуть разным фокусом. Отличия в 0,05 мм фокусировки того же порядка, как допуски обычной механической камеры, как установки АF на фокусировочном экране.
к содержанию ↑

Явления, рассмотренные в предшествующей главе, являются удобным поводом поговорить об ограничениях этого мира цифр. Если форма кривой столь чувствительна к малейшим изменениям фокусировки, то, конечно, нельзя предсказать форму кривой для каждого изображения, если объект съемки трехмерный, т.е. когда изменение расстояния вызывает улучшение изображения одних деталей и ухудшение других. Условия измерения MTF можно сравнить с контактной печатью снимков, когда плоскость, в которой произведен один отпечаток, не отличается от плоскости, в которой произведен другой. Другим примером этого служат фотографии очень удаленного объекта, сделанные на коротком фокусном расстоянии.
Шкала измерения качества MTF не соответствует нашему восприятию. Требуется определенный опыт, для того чтобы, анализируя кривые MTF, предвидеть
субъективное восприятие изображения. Необходимо учитывать при этом и условия, в которых рассматривается изображение: рассматриваемое с одинакового расстояния, изображение в формате А4 будет значительно отличаться от такового на большом мониторе при 100% увеличении. Графически важная часть изображения обычно находится ниже кривой MTF для 40л/мм и выше кривой MTF для 10 л/мм. Почему же тогда количественную шкалу измерения MTF не подогнать под возможности нашего восприятия? Потому, что кривые MTF объективов характеризуют только первое звено в цепи формирования изображения и не принимают во внимание те, что следуют за ними. Сенсор, сканер, проектор, глаз, короче все последующее также всегда имеет свою функцию воспроизведения, которая снижается с увеличением пространственной частоты. И, т.о. приводит к ухудшению качества изображения объектива при высоких частотах, т.к. все функции воспроизведения перемножаются. Если, например, находиться сзади проектора, то глаз не сможет различить 40 л/мм.
Еще одной причиной является то, что во внимание не принимается логарифмическое восприятие яркости глазом. Проведено множество исследований, направленных на построение соответствия шкалы нашего восприятия и измерений MTF. Карл Цейс, например, пользуется числами Хейнахера (Heynacher numbers). Находят применение и другие психофизиологические факторы; н-р: SQF (subjective quality factor — субъективный количественный фактор), MTFA (modulation transfer area — область воспроизведения модуляции), SQRI (square root integral — сумма квадратных корней). Их общей чертой является то, что они подсчитывают площадь под кривой «модуляции предельной пространственной частоты». Общим у них является и то, что все они пытаются описать качество одной точки изображения одной цифрой. Выше мы уже видели, что иногда это приводит к неуместному упрощению данных.
к содержанию ↑

Желание упростить объясняет, почему до сих пор я не касался вопроса: как величина MTF соотносится с общими характеристиками корректированных объективов. Не секрет, что такую сложную систему как объектив нельзя описать несколькими цифрами. Описание изобразительных свойств объектива (компьютерное или лабораторное) занимает небольшую папку. Упрощение необходимо для того, чтобы сделать его понятным и ясным, при этом можно столкнуться с фактом, что четкость описания страдает.
Этого достаточно для введения, вернемся к деталям. Возможно, что два объектива, имеющие одинаковые MTF, формируют изображения заметно различающиеся в деталях. Например:

Детали края изображения, формируемые двумя короткофокусными светосильными объективами при полностью открытой диафрагме.

На картинке изображены крыша дома и дерево на фоне яркого неба, т.е. типичная картина горизонта с большим контрастом. MTF низкочастотных образцов важна, в частности, на границе темных объектов, т.к. она определяет степень засвечивания перехода к этим объектам. На левой картинке крыша не засвечивается, а дерево засвечивается. На правой картинке – наоборот. Если бы не дерево, то можно было бы считать, что левая картинка лучше (в черно-белом варианте, во всяком случае). Между тем, на этом расстоянии от центра кадра MTF обоих объективов одинаковы для всех пространственных частот. MTF ничего не говорит нам об этих различиях, т.к. не полностью описывает характеристики функции рассеяния точки. Действительно, полная функция оптического воспроизведения OTF (optical transfer function) – имеет вторую составляющую – функцию воспроизведения фазы – PTF (phase transfer function), которой обычно пренебрегают. Она в некоторой степени связана с симметрией функции рассеяния точки. Мы учитываем, что функция рассеяния точки может быть протяженной, иметь различные распределения в сагиттальном и тангенциальном направлениях. Поэтому мы измеряем по 2 MTF для каждой точки изображения. В предшествующих примерах мы мысленно предполагали, что распределения яркостей симметричны в каждом из перпендикулярных направлений функции рассеяния точки. На самом деле часто это не так. Функция рассеяния точки может быть ассиметричной, как это показано на следующем рисунке. Наиболее частой причиной этого являются запятовидные искажения, в результате которых функция рассеяния точки формируется с «хвостом» в радиальном направлении.

Для таких ассиметричных профилей яркости функции рассеяния точки ориентация границ в изображении, конечно, очень важна. Приведенная функция рассеяния точки слева имеет гало около 1% от максимальной яркости, справа она внезапно исчезает. Если яркая сторона границы в изображении будет справа, она будет давать подсветку влево (нижний рис.). Если же имеет место обратное, и левая сторона границы изображения яркая (верхн. рис.), тогда контраст на границе будет высокий, т.к. вправо функция рассеяние точки распространяется на очень короткое расстояние.
Величина MTF не учитывает этой зависимости от ориентации. Она учитывается функцией воспроизведения фазы, изменения которой зависят от ориентации «хвоста» функции рассеяния точки. Такое название происходит оттого, что такая ассиметричная функция рассеяния точки сдвигает фазу, т.е. положение ее максимума и минимума на синусоидальном образце.
к содержанию ↑

То, что оптические характеристики стекла зависят от длины волны света, можно также видеть на наших рисунках. Объективы имеют цветовые абберации. Хотя каждый объектив имеет подходящую систему компенсаций, использующую комбинацию различных типов стекла, приводящую к тому, что этот тип аббераций не представляет в настоящее время большой проблемы, некоторые остаточные абберации все-таки еще присутствуют. Есть объективы, где они более заметны, главным образом на длинном фокальном отрезке, где только сравнительно недавно удалось значительно улучшить качество изображения, благодаря появлению совершенно новых типов стекла. Длиннофокусные объективы, не обладающие линзами такого типа, т.е. с экстремально низкой дисперсией или аномальной остаточной дисперсией – достигают лишь посредственных величин MTF. Для многих объектов, тем не менее, с ними можно добиться очень хорошего качества изображения. Это происходит потому, что MTF таких объективов сильно зависит от спектрального состава света. Если произвести измерения с зеленым светом в сравнении с обычным белым, где в определенном соотношении присутствуют все длины волн видимого спектра, то кривые MTF будут разительно отличаться.

Кривые MTF длиннофокусного 300 мм объектива: слева измеренные в белом свете, справа в зеленом с длиной волны 100 нм

Именно поэтому зеленый фильтр был важной принадлежностью во времена черно-белой фотографии, Тот же эффект может быть достигнут в цветной фотографии, если объект съемки преимущественно одноцветный (фотографии природы, красных крыш).
Это еще одна причина, по которой свойства изображений не полностью отражаются с помощью кривых MTF.
Но не во всех случаях кривые MTF оценивают объективы так пессимистично. Напротив, возможно, когда недостаточная цветовая коррекция объектива не видна на MTF-данных для белого цвета. Другими словами: MTF мало говорит о цветной кайме. Сравнение MTF в белом и окрашенном свете помогает понять причины появления цветной каймы на изображении высококонтрастных переходов и светов. Следующие кривые иллюстрируют продольную хроматическую абберацию светосильного среднефокусного объектива путем измерения MTF как функции фокуса.

Фокусы MTF на полностью открытой диафрагме объектива Planar 1.4/85 ZA для белого (черная кривая), синего, зеленого и красного светов. Крестики связывают положение на стороне изображения (горизонтальная шкала) с расстоянием до объекта съемки (вертикальная правая шкала), объектив сфокусирован в белом свете на расстояние 5 м.

Значение MTF для окрашенных светов выше, чем для белого света, в тоже время их максимумы находятся в разных местах и не имеют единого фокуса. При лучшем фокусе для белого света ( положение 0) MTF для красного света вообще самая низкая. Из этого следует, что рассеяние красной линии имеет самый большой диаметр, а изображение, т.о. будет иметь слабую красноватую кайму. Это будет проявляться сильнее, если объект съемки будет находиться чуть ближе, там, где MTF зеленого света максимальна. Поэтому светосильные объективы такого типа дают кайму красного или пурпурного цвета на ярких деталях, если последние находятся перед плоскостью фокусировки и зеленую кайму — если за ней. Насыщенность этих цветов, называемых вторичным спектром, зависит от расстояния между пиками и пологости фокуса кривых MTF. Если у объективов имеются преимущественно монохроматические абберации (как у старых объективов), то кривые более плоские, а цвета тусклые. Современные хорошо откорректированные светосильные объективы склонны к образованию более насыщенных цветов. Поскольку расстояние между положениями пиков нельзя сделать неопределенно малым, единственным способом устранения каймы остается уменьшение диафрагмы. Глубина резкости при этом становится значительно больше, чем продольная хроматическая абберация, а различия MTF кривых окрашенных светов становятся малыми.

Фокусы MTF объектива Planar 1.4/85 ZA при f/5.6
к содержанию ↑

Кривые, у которых величины тангенциального и сагиттального направлений близки по всему полю видимости часто называют идеальными кривыми MTF, т.к. в этих случаях « боке», т.е. изображение сильно расфокусированного заднего плана – особенно красивое.
Такие заявления следует принимать с осторожностью. MTF только дает представление о фокальной плоскости или ее непосредственном окружении. А в вышеупомянутом случае действительно преобладает округлая форма функции рассеяния точки, которая воспроизводит мелкие детали изображения настолько близко к оригиналу насколько это возможно, с наилучшим соответствием форме. Это важно для четкости письма, например.
Вместе с тем, невозможно использовать данные MTF для обоснования выводов о распределении яркости в пределах сильно расфокусированной точки рассеяния. Есть объективы с прекрасно параллельными тангенциальными и сагиттальными кривыми MTF, но которые сферически сильно перекорректированы. Это состояние коррекции вызывает кольцеобразную при расфокусировке функцию рассеяния точки, которая выглядит как круг света и как двойная линия, что дает беспокойно-выглядящий фон. Эту неприятную характеристику нельзя предсказать на основании кривых MTF.
к содержанию ↑

Данные MTF публикуются во многих изданиях производителями объективов, а в настоящее время и независимыми испытателями. Несомненно, при сравнении этих данных следует быть осторожным, т.к. условия измерений могут сильно варьировать.
Наименее существенной и зачастую незамечаемой проблемой может быть разная частота образцов. Невозможность сравнения часто вызвана различной шириной спектра видимого света используемой в тестах.
Есть производители, которые не брезгуют публиковать данные, превышающие ограничения, накладываемые дифракцией, т.е. физически невозможные. Это говорит, что параметры получены просто путем расчета, и что в расчет принималась только геометрическая оптика, без учета волновых свойств света. Если такие объективы хорошо откорректированы, то значение MTF приближается к 100%. Но, пожалуйста, не верьте, что эти цифры реальны. Реальные объективы всегда немножко хуже, чем рассчитанные по программам проектирования оптики.
Величины MTF, публикуемые Zeiss, всегда основаны на результатах оценки объективов.

Как измерить MTF — Optikos

Передаточная функция модуляции

(ответ черного ящика на известные входные данные)

Разрешение и контраст

Понятия разрешения и контраста часто путают и неправильно меняют местами.

Разрешение относится к обнаруживаемости. Разрешение, необходимое для визуальной оптической системы, отличается, например, от фотографической оптической системы. Поэтому спецификации разрешения указываются для каждого приложения.

Спецификация разрешения для визуальной оптической системы часто определяется с использованием «точки, в которой радиальные и касательные линии не разрешаются наблюдателем» в визуальной оптической системе.

В своей простейшей форме тестирование разрешения принимает форму офтальмологической диаграммы — ряд цифр, каждая из которых представляет различные уровни пространственной детализации, помещается на страницу и просматривается. Помимо уровней детализации, ориентация фигур (например, большая буква «E» на офтальмологической карте) может предоставить информацию об астигматизме наблюдателя.

Рисунок 1 — Глазковая диаграмма (без масштабирования)

Разрешение реальной оптической системы формирования изображения (например, объектива микроскопа или окуляра) снова задается путем запроса наблюдателя определить точку, в которой гистограмма становится неразрешимой.

Диаграмма разрешения аэрофотоснимков, более известная как Карта ВВС 1951 года, представляет собой серию вертикальных и горизонтальных полос, расположенных с интервалом в 50% светлого-темного рабочего цикла, намотанных на группы групп и элементов. Маска этой карты используется как объект в оптической скамейке. Тестируемый объектив устанавливается так, чтобы создать реальное изображение диаграммы разрешения, которое оператор исследует под большим увеличением.

Рисунок 2 — Цель разрешения USAF 1951 (без масштабирования)

Пространственная частота связана с номером группы и номером элемента на диаграмме соотношением:

, где Частота измеряется парами линий (циклы темный-светлый) на миллиметр. Оператор просто выделяет точку (в терминах групп и элементов), в которой разрешение становится ложным или теряется (когда полосы и пробелы неопознанно смешиваются), умножает его на увеличение тестируемого объектива и вычисляет предельное разрешение с воздуха в lp / мм.

Целевое разрешение предоставляет ценную информацию о разрешающих характеристиках объектива. К сожалению, он не предоставляет дискретных методов определения относительных уровней контрастности. Высокое разрешение не всегда означает высокую контрастность! Контрастность или «модуляция» — это соотношение между максимальной интенсивностью и минимальной интенсивностью изображения (темный-светлый) или степенью серого.

Разрешение отсечки определяется как частота, при которой контраст изображения уменьшается до нуля.Другими словами, это частота, на которой MTF падает до нуля.

Контрастность является синонимом модуляции и чаще всего определяется как:

Здесь I _max — максимальная интенсивность изображения, а I _min — минимальная интенсивность. Интенсивность измеряется как Вт / см ² (энергетическая освещенность) детектором или видеоизображением с цифровой камеры.

Рассмотрим, например, объект «штакетник» (чередующиеся светлые и темные полосы с острыми краями) и человеческий глаз как оптическую систему.Пикеты расположены в 50% рабочем цикле со 100% контрастом — наполовину включены и выключены, полностью белые и черные. При уменьшении ширины пикетов с 3 дюймов до меньших значений изображение, создаваемое на сетчатке, не только станет меньше, но и начнут размываться резкие края между белыми и черными полосами, белые полосы станут темнее и черные полосы светлее. В определенный момент наблюдатель больше не может различать белые и черные полосы; изображение забора — однородно-серого цвета.Частота, на которой это происходит, является предельной пространственной частотой или пределом разрешения.

Рисунок 3 — Уменьшение контрастности изображения

При небольшом интервале штакетник «размывается» до однородного серого цвета. На этой частоте глубина модуляции равна нулю. Это предел обнаруживаемости или разрешения.

Теория МОГ

Оптическая передаточная функция (OTF) описывает реакцию оптических систем на известные источники и состоит из двух компонентов: функции передачи модуляции и функции передачи фазы.

MTF можно описать как карту модуляции в зависимости от пространственной частоты пространственно изменяющегося источника. Пространственная частота определяется как величина, обратная пространственному периоду синосоиды.

MTF и передаточная функция для некогерентного света

Когда оптическая система создает изображение с использованием совершенно некогерентного света, тогда функция, которая описывает интенсивность в плоскости изображения, создаваемую точкой в ​​плоскости объекта, называется функцией импульсной характеристики.Этот импульсный отклик обычно обозначается как h (x, y; x ₁ , y ₁ ). Шаблон интенсивности входного объекта, f (x ₁ , yx ₁ ), и шаблон интенсивности выходного изображения, g (x, y) связаны простым уравнением свертки:

Это более формально записывается как:

Однако свертки могут потребовать очень больших вычислительных ресурсов. Ответ на решение этого математического уравнения лежит в теории преобразования Фурье.Преобразование Фурье преобразует информацию в пространственной области в частотную информацию, где ее можно описать как линейную комбинацию соответственно взвешенных синусов и косинусов.

Свертки в пространственной области коррелируют с умножениями в частотной области.

Следовательно, если

, затем

, где G (f _x , f _y ), F (f _x , f _y ) и H (f _x , f _y ) — это преобразования Фурье для g (x, y ), f (x ₁ , y ₁ ) и h (x, y; x ₁ , y ₁ ).Функция H (f _x , f _y ) называется передаточной функцией, а в случае оптических систем — оптической передаточной функцией или OTF.

OTF — это сложная функция, состоящая из действительной и мнимой частей:

Действительная часть, или | H (f _x , f _y ) | называется функцией передачи модуляции или MTF, а функция Φ (f) называется функцией передачи фазы. MTF нормирована на единицу при нулевой пространственной частоте

Примечание:

Здесь мы хотели бы отметить, что OTF и MTF обеспечивают частотную характеристику входного синусоидального сигнала, а не реакцию прямоугольных полос с острыми краями.Практически все расчеты и измерения MTF основаны на этом методе вычисления передаточной способности оптической системы. Использование целевых столбцов с прямоугольной волной в настоящее время обычно не используется. Полезно знать, что при определенных условиях прямоугольный отклик можно использовать для получения синусоидального отклика.

Как получить передаточную функцию

Поскольку невозможно построить действительно бесконечно малый источник, нельзя напрямую измерить реакцию системы на точечный импульс.Импульсная характеристика (и, следовательно, передаточная функция) должна быть получена, а не создана. Его можно сгенерировать одним из двух способов:

• использование «очевидно бесконечно малого входа», такого как точечное отверстие 2 мкм с системой f / 20 (это «неразрешимый» объект)
• преобразует функцию источника и функцию изображения в функции в частотной области, затем разделите преобразование функции изображения на преобразование функции источника, чтобы получить передаточную функцию. Обратное преобразование Фурье передаточной функции дает импульсную характеристику.

Каскадные MTF

При определенных условиях MTF системы можно рассчитать путем «каскадирования» MTF компонентных систем. Другими словами, можно построить MTF составной системы на любой частоте, умножив вместе MTF каждого из компонентов на той же частоте:

Рисунок 4 — «Каскадирование» MTF объектива и пленки для получения MTF камеры

Каскадирование полезно при расчете эффектов систем камеры — линза + пленка или линза + CCD.В общем, нельзя просто умножить некогерентные MTF всех линз в многоэлементной системе и получить правильную MTF для системы, даже если все линзы хорошо скорректированы и зрачки совпадают. Об этом неоднократно говорилось в литературе (DeVelis, Parrent 1967; Swing 1974). Это также может быть оправдано простым мысленным экспериментом — представьте систему, в которой объект отображается одной линзой. Затем помещают вторую линзу, чтобы повторно отобразить исходное изображение как второе изображение.Линзы идеальные, без аберраций и потерь на отражение или поглощение. MTF системы не должен быть квадратом MTF одиночной линзы — линзы идеальны по определению, а частота среза определяется первой линзой. ФПМ не должна ухудшаться из-за второго объектива, который идентичен первому. Можно представить себе цепочку из любого количества этих линз. Умножение их индивидуальных MTF вместе сузит MTF на любой частоте до желаемого значения (все, что нам нужно сделать, это добавить больше линз).Но истинная MTF системы определяется исходной линзой и не ухудшается ни одной из последующих релейных линз. Как указывает Свинг, это функция зрачка линз, которые каскадированы, и системная MTF определяется из этой каскадной функции зрачка. Не существует простой взаимосвязи между каскадными передаточными функциями и правильной передаточной функцией, рассчитанной из каскадных функций зрачка.

Следствием этой мысли является то, что объектив с наименьшей числовой апертурой будет определять частоту среза, а объектив с наихудшей функцией зрачка будет больше всего влиять на ФПМ системы.

Можно каскадировать MTF различных компонентов системы при условии, что все каскадные системы являются линейными. Другими словами, системы могут быть включены в каскад, если отклик на определенной частоте линейно пропорционален амплитуде входного сигнала. Это будет иметь место с фотопленкой около середины кривой H-D, но не на ее концах, или с ПЗС-матрицей при умеренных уровнях освещения, но не близких к насыщению (Нельсон, Эйзен и Хиггинс, 1968)

Функция передачи фазы

Функция передачи фазы (PTF) описывает относительные фазы синусоид разной частоты, составляющих преобразование.Ненулевая фаза указывает на сдвиг и / или повторение изображения. Например, рассмотрим одномерную систему, в которой ответ на объект дельта-функции представляет собой изображение, состоящее из двух пятен в плоскости изображения, разделенных расстоянием x0. Поскольку входной объект является точкой или импульсом, это изображение является импульсной характеристикой, а его преобразование Фурье представляет собой функцию оптического преобразования (OTF).

Это двухточечное изображение может быть представлено математически следующим образом:

Здесь функция прямоугольника rect (x) определяется как:

Поскольку ввод объекта представляет собой точку, идеальный импульс, передаточная функция — это просто преобразование Фурье функции изображения.Это дает:

Если бы импульсный отклик состоял только из одного пятна (так что f (x) = rect (x)), то передаточная функция состояла бы только из функции «sinc» h (fx) = [sin (πf _x )] / (πfx). Наличие второго пятна приводит к фазовому члену через теорему «сдвига» преобразований Фурье.

Использование определения функции фазового преобразования

, мы можем использовать последнее уравнение выше, чтобы получить Φ (fx) = -πf _x X ₀ , подтверждая, что линейный сдвиг положения приводит к соответствующему линейному сдвигу фазы.

Перепады фаз происходят, когда модуляция (и PTF) меняет знак. В этом случае белые становятся черными, а черные — белыми. Классическим примером обращения фазы является радиальная цель с чередующимися черными и белыми «круговыми» сегментами, рассматриваемая через несколько расфокусированную (но в остальном идеальную) линзу. На определенном радиальном расстоянии от центра контраст исчезает, и цвет становится однородным серым. Внутри этого круга черные и белые сегменты противоположны тому, что они находятся за пределами этого круга.

Рисунок 5 — Классический пример переворота фазы

Когерентная передаточная функция

Приведенное выше обсуждение предполагало, что формирование изображения было выполнено с использованием источника некогерентного света. Как правило, это наиболее полезный тип измерения, так как в большинстве приложений для получения изображений используется некогерентный свет (естественный солнечный свет, вольфрамовые лампы и т. Д.). В случае некогерентного освещения функция импульсной характеристики связывает интенсивность объекта с интенсивностью изображения.Оптическая передаточная функция — это преобразование Фурье этой импульсной функции.

Визуализация также может выполняться с использованием когерентного света или частично когерентного света. В этих случаях ответ изображения должен быть рассчитан другим способом. Для случая когерентного освещения используется функция импульсного отклика, которая связывает амплитуду освещения объекта с амплитудой освещения изображения. (Интенсивность пропорциональна квадрату модуля амплитуды.Когерентная оптическая передаточная функция представляет собой преобразование Фурье этой функции амплитудно-импульсного отклика и, таким образом, сильно отличается от некогерентной оптической передаточной функции. Они математически связаны (см. Goodman 1968, стр. 115). Частота среза некогерентного OTF в два раза выше, чем у когерентного OTF. Это не означает, что некогерентное изображение передает больше информации, чем когерентное изображение (Goodman 1968, стр. 125-133)

Случай частично когерентного света намного сложнее.Вместо того, чтобы работать либо со сложной амплитудой света, либо с его интенсивностью, мы должны измерить свойство, называемое взаимной интенсивностью, а соответствующая передаточная функция описывает распространение взаимной интенсивности через оптическую систему. Обсуждение этого выходит за рамки данной статьи. Заинтересованный читатель может обратиться к таким источникам, как «Принципы оптики Борна и Вольфа», глава 10.

Коэффициент Штреля

Коэффициент Штреля — это полезное однозначное соотношение между фактической MTF реальной линзы и характеристикой MTF системы, ограниченной дифракцией.Иногда ее называют просто «Штрелом» системы (в честь К. Штреля, который впервые предложил ее в 1902 г.). Он определяется по:

Это просто отношение площади под кривой MTF к площади под кривой MTF, ограниченной дифракцией. По теореме Парсеваля это также отношение освещенности в центре дифракционной картины к центральной интенсивности ограниченного дифракцией диска Эйри.

Наличие аберраций снижает коэффициент Штреля ниже его идеального значения 1.Для небольших аберраций коэффициент Штреля приблизительно равен:

Здесь (Δ OPD) ² — среднеквадратическая ошибка разности оптического пути (от идеальной сферической волны). Не имеет значения, какую именно форму принимают аберрации, если они небольшие.

Коэффициент Штреля

иногда неправильно используется для определения «процента дифракционно ограниченных характеристик» оптической системы, иногда называемого XDL, или «времен (« X ») дифракционного предела».Взаимосвязь между коэффициентом Штреля и значением «XDL» основывается на предположении, что аберрации приводят к увеличению размера дифракционного пятна, не имея другого эффекта. На самом деле это не так. Это приблизительно верно, если аберрации небольшие. В целом, однако, этот термин не компенсирует полные условия испытаний и должен быть ограничен контекстом.

ФПМ круглой линзы с ограничением дифракции

Ограниченная дифракцией некогерентная MTF для линз с круглым зрачком определяется по формуле:

Рисунок 6 — MTF для линзы с ограничением дифракции с круглой апертурой

Это верно для f < f ₀ . За пределами этой области MTF (f) = 0. Для частоты нет индекса x или y, так как это верно для всех радиальных направлений. Частота некогерентной отсечки f ₀ определяется как:

Здесь D — диаметр линзы (на самом деле диаметр входного зрачка), λ — длина волны (обычно используется 0,55 мкм, пик зрительной реакции человека при обычном дневном свете), а efl — фокусное расстояние линзы. Обратите внимание, что (efl) / D = f / # линзы для бесконечно удаленного объекта.

MTF расфокусированной линзы

Расфокусировка — одна из наиболее часто встречающихся аберраций. Его влияние на MTF можно рассчитать математически (см., Например, Goodman 1968, раздел 6-4). MTF на нулевой частоте всегда нормализуется до значения, равного единице, а начальный наклон при нулевой частоте всегда одинаков. MTF равен нулю на частоте среза (и за ее пределами). Эффект любой аберрации заключается в уменьшении значения MTF для частот между нулем и отсечкой.Как показано на следующем графике, OTF сначала падает быстрее всего на средних частотах. OTF может даже стать отрицательным, как на кривой №5. На этом этапе мы увидим «переворот фазы», ​​отмеченный выше, когда черные полосы или сектора кажутся белыми, и наоборот. (MTF, будучи модулем OTF, никогда не бывает отрицательным, но когда OTF становится отрицательным, функция передачи фазы меняет знак.) Обратите внимание, что OTF может снова увеличиваться на определенных частотах по мере увеличения степени расфокусировки.Тем не менее, эффект увеличения аберрации обычно приводит к ухудшению качества изображения. MTF аберрированной системы никогда не бывает таким высоким, как у системы с ограничением дифракции.

Рисунок 7 — OTF линзы с ограничением дифракции при различных величинах расфокусировки

Что такое диаграмма MTF объектива и как ее читать | Технология объектива NIKKOR

Функция передачи модуляции или «MTF» — это измерение потенциала оптических характеристик объектива. Диаграммы MTF могут дать вам лучшее представление об оптическом качестве различных объективов NIKKOR и могут быть полезными справочными материалами при исследовании, сравнении и покупке объективов.Таблицы MTF можно найти на веб-страницах, посвященных каждому объективу NIKKOR, на веб-сайте Nikon.

Диаграмма MTF отображает контраст и разрешение линзы от центра до краев по сравнению с «идеальной» линзой, которая пропускала бы 100% света, проходящего через нее. Контраст объектива важен, поскольку он работает в зависимости от разрешения объектива.

Использование диаграммы MTF является предпочтительным методом для изучения оптических характеристик объектива, поскольку они используют теоретические уравнения для построения графика характеристик и не полагаются на субъективное мнение, предмет, характеристики камеры, программное обеспечение или другие факторы.

Ось Y (вертикальная ось) диаграммы MTF отображает пропускание света через линзу с максимальным значением «1.0», которое указывает на 100% пропускание света, хотя 100% пропускание света невозможно, потому что стекло не на 100% прозрачное.

Ось x (горизонтальная ось) показывает расстояние от центра изображения до его краев. Таким образом, «0» в нижнем левом углу представляет собой центр линзы, а цифры вдоль нижней оси представляют расстояние до края линзы в миллиметрах.

Как читать график MTF

На графике Nikon MTF нанесены две группы данных: сагиттальные и меридониальные линии.

«Сагиттальные линии» (сплошные линии) представляют собой измерения контраста пар линий, идущих параллельно центральной диагональной линии, проходящей через середину линзы от нижнего левого угла к верхнему правому углу.

«Меридониальные линии» (пунктирные линии) представляют пары линий, также расположенных вдоль воображаемой линии от центра линзы до края, но эти пары линий перпендикулярны диагональной линии.

Есть две группы тестовых линий для каждого сагиттального и меридониального значения: одна группа или пары линий из расчета 10 линий на миллиметр и вторая группа из 30 линий на миллиметр. Нижние пары линий (10 линий / мм) обычно отображаются выше на графике, чем более сложное точное разрешение 30 линий / мм.

Определение и пример многосторонней торговой системы (MTF)

Что такое многосторонняя торговая площадка?

Многосторонняя торговая система (MTF) — это европейский термин, обозначающий торговую систему, которая облегчает обмен финансовыми инструментами между несколькими сторонами.Многосторонние торговые механизмы позволяют правомочным участникам контракта собирать и передавать различные ценные бумаги, особенно инструменты, которые могут не иметь официального рынка. Эти объекты часто представляют собой электронные системы, контролируемые утвержденными операторами рынка или более крупными инвестиционными банками. Трейдеры обычно подают заказы в электронном виде, где соответствующий программный механизм связывает покупателей с продавцами.

Основы многосторонней торговой системы (MTF)

Многосторонние торговые площадки (MTF) предоставляют розничным инвесторам и инвестиционным компаниям альтернативу традиционным биржам.До их введения инвесторам приходилось полагаться на национальные биржи ценных бумаг, такие как Euronext или Лондонская фондовая биржа (LSE). Более высокая скорость транзакций, более низкие затраты и торговые стимулы помогли MTF стать все более популярными в Европе, хотя NASDAQ OMX Europe была закрыта в 2010 году, поскольку MTF сталкиваются с острой конкуренцией друг с другом и с установленными биржами. MTF работают в соответствии с нормативной средой Европейского Союза (ЕС) MiFID II — пересмотренной законодательной базой для защиты инвесторов и укрепления доверия к финансовой отрасли.

Продукты, торгуемые на многосторонних торговых площадках

MTF имеют меньше ограничений, связанных с допуском финансовых инструментов к торговле, что позволяет участникам обменивать более экзотические активы и внебиржевые (OTC) продукты. Например, LMAX Exchange предлагает спотовую торговлю иностранной валютой и драгоценными металлами. Введение MTF привело к большей фрагментации финансовых рынков, поскольку отдельные ценные бумаги теперь могут размещаться на нескольких площадках.Брокеры отреагировали, предложив интеллектуальную маршрутизацию заказов и другие стратегии для обеспечения лучшей цены между этими многочисленными площадками.

Многосторонние торговые площадки в США

В Соединенных Штатах альтернативные торговые системы (ATS) работают аналогично MTF. В большинстве случаев ATS регулируются как брокеры-дилеры, а не биржи, но все же должны быть одобрены Комиссией по ценным бумагам и биржам (SEC) и соответствовать определенным ограничениям. В последние годы SEC активизировала свою правоприменительную деятельность в отношении ATS, что может привести к ужесточению регулирования MTF в Европе.Это особенно верно для темных пулов и других САР, которые относительно малоизвестны, их сложно торговать и ценить. Наиболее широко известными в США ATS являются сети электронной связи, или ECN, которые упрощают выполнение заказов.

Ключевые выводы

• MTF предоставляет розничным инвесторам альтернативную платформу для торговли финансовыми ценными бумагами.
• Операторы рынка и инвестиционные банки обычно управляют MTF.
• MTF работают в соответствии с законодательной базой ЕС MiFID II.
• MTF обычно предлагают более экзотические торговые инструменты и внебиржевые продукты.
• MTF известны как альтернативные торговые системы в США.

Пример многосторонней торговли из реальной жизни

Инвестиционные банки и компании, занимающиеся финансовыми данными, могут использовать эффект масштаба, чтобы конкурировать с традиционными биржами ценных бумаг и потенциально реализовать синергию со своими существующими торговыми операциями.

Некоторые инвестиционные банки, которые уже использовали внутренние системы пересечения, также преобразовали свои внутренние системы в MTF.Например, UBS Group AG (UBS) создала собственную MTF, которая работает совместно с ее внутренними системами пересечения, в то время как другие международные инвестиционные банки также планируют запустить свои собственные MTF. Совсем недавно компания Bloomberg, занимающаяся финансовыми данными и СМИ, объявила, что получила разрешение от Управления по финансовым рынкам Нидерландов (AFM) на управление MTF из Амстердама на всей территории ЕС. MTF Bloomberg намеревается предоставить возможность котирования и торговли правомочным участникам продуктов, таких как денежные облигации, операции репо, свопы по кредитному дефолту (CDS), процентные ценные бумаги (IRS), биржевые фонды (ETF), деривативы на акции и форекс (FX). ) производные.

Объективов в аренду | Блог

Этот пост не содержит математики. Объяснять МОГ без математики — все равно, что делать трюк без сети. Это опасно, но по ряду причин может заинтересовать аудиторию.

Почему я делаю это снова?

Несколько лет назад я написал статью о чтении диаграмм MTF. Он был сосредоточен на расшифровке карт MTF, которые публикуют многие производители объективов, когда выпускают объектив, как показано ниже.Но я получаю много писем с вопросами о том, как сравнить графики MTF, которые мы используем при тестировании, с графиками MTF производителя. Или попросить меня показать диаграмму частоты MTF (и если я покажу ее, то будет много писем с вопросами, что это значит). Поэтому я подумал, что напишу небольшой пост о различных типах данных и диаграмм MTF.

Итак, сначала сделаем обзор распространенных типов диаграмм MTF.

Карты MTF

Я использую термин «карта», потому что горизонтальная ось отображает линзу от центра (‘0’ мм) к краю кадра (24 мм).Цветные линии показывают, как изменяются определенные значения MTF при перемещении от центра к краю поля зрения.

График MTF для Nikon 35mm f / 1.4G, Nikon, США.

За исключением карт Zeiss и Leica, эти карты MTF созданы на основе компьютерных моделей. Глядя на карту MTF компьютерной модели, можно сравнить с отретушированной фотографией модели купальника — в реальной жизни изгибы никогда не бывают такими хорошими, как предполагает изображение.

Реальная диаграмма MTF для реального объектива выглядит так, как показано ниже. Обратите внимание, что у него «0» (центр) посередине и он идет по обеим сторонам, показывая один маленький грязный секрет: очень немногие копии любого объектива имеют точно такую ​​же кривую MTF с обеих сторон.

Настоящая диаграмма MTF, измеренная с реальной линзы.

Как насчет тех чисел MTF50 в обзорах объективов?

В наши дни, кажется, все больше людей обращают внимание на таблицы MTF50, созданные с помощью компьютерного целевого анализа, которые появляются на большинстве сайтов для обзоров и тестирования (включая этот).

График, показывающий MTF50 нескольких разных объективов.

График MTF 50 объектива Sigma 50mm f / 1.4, показывающий MTF50 для центра, среднего значения и углов при различных значениях диафрагмы.

Конечно, они полезны, но сейчас мы, наверное, зашли слишком далеко. Люди, которые на самом деле не знают, что означает MTF50, думают, что это означает самый резкий или даже лучший объектив, что не совсем так.Точно так же, как гора Эверест — хорошее, но не идеальное определение «самой высокой горы в мире», самый высокий MTF50 — хорошее, но не идеальное определение «самого резкого объектива». (В зависимости от вашего определения «самый высокий», Мауна-Кеа или Чимбораза на самом деле могут быть самыми высокими.)

Это еще больше сбивает с толку. Карты MTF, представленные производителями камер, например, верхняя, дают результаты MTF в 10 и 30 линий / мм. Некоторые думают, что MTF50 означает MTF при 50 линиях / мм, но это не так. На самом деле он дает вам совершенно другой набор информации.

Графики частот MTF

Наконец, вы иногда видите график MTF частоты для объектива, который выглядит примерно так. Это похоже на карту MTF, которую я показал сначала, но на самом деле у них очень мало общего. График частоты показывает MTF50, но добавляет много дополнительных данных.

Если вы потерпите несколько минут, я объясню, что показывают нам эти различные числа и графики MTF. Если вам нравится лабораторное тестирование, это позволит вам более четко понять тесты.Если вы ненавидите лабораторные испытания, они все равно будут иметь смысл, потому что в онлайн-обсуждениях вы сможете сказать что-то вроде: «Показатели MTF50 в этом сообщении ничего не говорят о возможностях объектива по разрешению мелких деталей».

Так что это за разные номера МОГ, о которых вы говорите?

MTF

На самом деле это не разные MTF, это разные способы использования MTF (функции передачи модуляции) для отображения различной информации. Начнем с простого определения MTF.Мы обойдемся без математики, так будет лучше для всех. (Для 95% людей это будет лучше, потому что они смогут понять, что их интересует. Для остальных 5% это будет лучше, потому что они смогут разбить различные формулы и сделать длинные посты о том, почему это определение является неполным.)

Когда объектив создает изображение, оно никогда не бывает идеальным. Например, давайте начнем с толстых черных и белых полос, например:

.

Если я сфокусирую на них объектив, изображение, которое создает объектив, будет выглядеть почти, но не совсем так, как это:

Если вы присмотритесь, то заметите, что второе изображение немного размыто.Если вы измеряете его очень внимательно, вы обнаружите, что черный не такой черный, как оригинал, а белый — не такой белый. Вы можете не заметить этого на экране компьютера, но разница есть.

Теперь я покажу вам формулу MTF без математических вычислений: MTF = контраст. Мы можем сделать его немного сложнее и точнее, не вдаваясь в математику: MTF = самый черный — самый белый / самый черный + самый белый.

Вы можете справиться с этим даже с некоторыми числами, верно? Допустим, чистый черный цвет равен 1, а чистый белый равен 0.Поскольку исходный объект полностью черно-белый, мы имеем (1-0 / 1 + 0) = 1. Это совершенство.

Изображение, которое создает объектив, не совсем идеальное. В моем примере черный на 98% меньше черного, чем исходное изображение, белый на 98% меньше белого (или, другими словами, белый теперь составляет 2% черного). Если мы подставим это в формулу (это необязательно, просто покажем вам), получится 0,98–0,02 / 0,98 + 0,02 = 0,96. Таким образом, MTF этого объектива для этих толстых черных полос составляет 0,96.

Что, если мы будем использовать более мелкие стержни, расположенные ближе друг к другу, как на изображениях ниже?

У линз больше проблем с уменьшением полос.Довольно скоро сероватое пятно от края одной полосы начинает касаться края следующей полосы. Изображение выглядит так.

Теперь самые черные полосы на изображении на 66% меньше черного, чем оригинал, в то время как белые области фактически на 34% являются черными на изображении. Не буду утомлять вас формулой, но MTF для наших близких линий составляет 0,32. Разница между MTF 0,96 и 0,32 довольно очевидна, просто глядя на изображения, но числа делают вещи более сопоставимыми. Сказать «МОГ выпадает из.От 96 до .32 », говорит кому-то о результатах более точно, чем если бы вы сказали:« От едва размытого до довольно размытого, но я все равно могу сосчитать полосы ».

Что насчет этих линий парных вещей

Если мы хотим быть полностью научными, мы не можем просто использовать произвольные «толстые линии» и «тонкие линии», как я сделал выше. Нам необходимо их количественно определить, и мы используем количество линий или пар линий на мм. По сути, это одно и то же; пара линий — это черная и белая линия, линия будет просто считать черные линии.

Часть «на мм» — это мм в плоскости изображения. (Датчик камеры находится в плоскости изображения). Если бы все было идеально, тестовая мишень показывала бы X линий на каждом миллиметре плоскости изображения. Толстые линии, как в первом примере, могут составлять 10 линий на мм. Более тонкие линии, как во втором примере, могут составлять 40 линий на мм.

Количество линий на миллиметр обычно называют «частотой» или «пространственной частотой». Итак, теперь у нас есть две вещи, на которые мы смотрим: MTF, которая является мерой контраста, и Frequency, которая показывает, насколько маленькими были линии, которые мы использовали для измерения контраста.

В одной точке объектива (например, прямо в центре) я могу измерить MTF на разных частотах (линии / мм) и построить красивый график результатов. Помните, что это не вся передняя часть линзы, как на самом первом графике. Это измерение одной точки на линзе на разных частотах (все меньшие и меньшие линии). Каждый объектив, как и на графике ниже, имеет более низкую MTF, поскольку линии становятся меньше (частота становится выше).

Если вы посмотрите на левую часть графика, измерение MTF (контрастность), то легко найти MTF50 (или MTF 10 или MTF90, если на то пошло).Это просто частота (линий на мм), при которой изображение сохраняет 50% контрастности тестовой мишени. (Или 10% или 90% от исходной контрастности для MTF10 или MTF90).

В этом примере MTF50 составляет около 40 л / мм. Когда я (и большинство нынешних обозревателей) сообщаю о MTF 50, мы показываем вам именно это. Большинство из нас используют высоту LP / изображения, а не мм, поэтому мы просто умножаем LP / мм на 24 (поскольку полнокадровый датчик имеет высоту 24 мм). Так что в одном из моих стандартных отчетов для этого объектива я бы сказал, что MTF50 составляет 960 LP / IH, что неплохо.Но в моих отчетах не сказано, что значение MTF10 составляет около 77 LP / мм, а MTF90 (на котором нет серой линии на изображении выше) — около 22 LP / мм.

Также помните, что график частот предназначен только для одной точки на объективе камеры. Когда мы публикуем набор гистограмм, показывающих центральную, среднюю и угловую MTF50, мы показываем вам MTF50 в разных местах.

Так является ли MTF50 самым важным числом?

Почему мы, тестеры объективов, сообщаем вам значения MTF50? Ну, во-первых, это значение по умолчанию в программном обеспечении Imatest, так что это просто и легко.Существует также тот факт, что большинство тестеров объективов используют его, и людям нравится иметь возможность сравнивать результаты разных тестеров, так что существует своего рода джентльменское соглашение MTF50. Кроме того, 617 различных графиков, показывающих MTF Каждую частоту в местах расположения линз Everywhere, делают статью запутанной и хаотичной.

Но правда в том, что MTF50, вероятно, является наиболее важным общим числом MTF при оценке объектива. В многочисленных исследованиях было показано, что MTF50 является точкой, в которой люди воспринимают изображение как «резкое», а не размытое.В этом есть смысл — в основном это когда контраст больше 50%.

Но MTF50 — не единственное важное число. Эти другие частоты дают нам иную, но важную информацию. Более низкие частоты, такие как MTF от 80 до 90, показывают, насколько «контрастным» является изображение. Если вы фотографируете большие, жирные структуры, эта область частотной кривой может быть для вас более важной, чем MTF50.

Такие числа, как MTF10 или MTF5, являются абсолютным пределом разрешения объектива. Они показывают мельчайшие детали, которые объектив может разрешить.Все, что меньше, просто гладкое серое размытие. Обученные люди-наблюдатели и программы улучшения изображения могут действительно различить некоторые детали в MTF5 на фотографии, но большинству из нас требуется MTF10. Пейзажные и макро-фотографы, пытающиеся получить как можно больше деталей на своих больших отпечатках, могут посчитать MTF10 более важным или, по крайней мере, почти таким же важным, как MTF50.

Например, вот частотный график другого объектива, у которого MTF50 точно такой же, как у указанного выше объектива, 40 LP / мм. Однако MTF10 ниже (около 69 LP / мм по сравнению с 77), а MTF90 выше (30 LP / мм по сравнению с 22).Таким образом, этот объектив должен быть более контрастным, но не разрешать мельчайшие детали так же хорошо, как наш первый объектив.

Некоторые объективы с очень высоким разрешением имеют довольно плохую контрастность. У других объективов очень хороший контраст, но плохое разрешение. Другими словами, у некоторых объективов очень высокий MTF10, но плохой MTF80. У других объективов большие значения MTF50 и MTF30, но низкие значения MTF10.

Одна точка

Очень важно подчеркнуть, что MTF10 на этих частотных диаграммах полностью отличается от MTF на уровне 10 линий / мм на карте MTF объектива, который я показываю в самом начале этого поста.MTF на уровне 10 линий / мм (на карте MTF в верхней части статьи) показывает, насколько контрастны толстые линии в различных положениях при движении от центра объектива к краю. MTF50 на частотном графике показывает, насколько маленькими могут быть линии, сохраняющие 50% своего исходного контраста.

Так почему я поднимаю это сейчас?

Потому что пора совершенствоваться. Как и все остальные, мы показывали результаты MTF50 из Imatest shot на довольно близких графиках.Это дает нам номер для всей системы (камеры и объектива) на карте на передней панели объектива.

Скоро мы добавим результаты оптического стенда к нашим результатам Imatest, когда будем тестировать объективы. Это позволит нам взглянуть на несколько других вещей: производительность только объектива, а не комбинации линза-датчик, производительность на бесконечных дистанциях фокусировки, а не на близком расстоянии, и MTF на разных частотах среди них. Мы даже сможем создать карты MTF передних элементов для тестируемых нами объективов и сравнить их с компьютерной картой MTF производителя.Это должно быть весело и интересно. (Что ж, нам это будет весело и интересно. Думаю, может, некоторые производители не будут так без ума от этого.)

Когда мы будем тестировать объективы, мы продолжим показывать вам те же данные MTF50, которые мы показывали и которые показывают все остальные. Это важные данные, и у нас уже есть огромная база данных результатов MTF50 для большого количества объективов, так что это отлично подходит для сравнения. Мы также добавим графики MTF частоты для центра линзы и, возможно, для одной или двух точек вне центра.У нас пока нет большой базы данных с этой информацией, но я смогу дать вам некоторые сравнения с одним или двумя аналогичными объективами.

Поскольку мы будем показывать не только карту MTF50 переднего элемента, но и показать, что означают эти другие значения и почему это полезная информация. Суть в том, что мы сможем дать более полную оценку линз, чем когда-либо.

Роджер Чикала

Lensrentals.com

Апрель, 2014

Дополнительная литература (с математикой)

http: // www.normankoren.com/Tutorials/MTF.html

http://photo.net/learn/optics/mtf/

https://spie.org/x34298.xml

http://en.wikipedia.org/wiki/Optical_transfer_function

http://diglloyd.com/articles/UnderstandingOptics/understanding-MTF.html

http://www.luminous-landscape.com/tutorials/understanding-series/understanding-mtf.shtml

http://www.imaging.robarts.ca/~icunning/SiteResources/publications/SaulFeb05.pdf

http: // kurtmunger.ru / sitebuildercontent / sitebuilderfiles / zeissmtfcurves2.pdf

Автор: Роджер Чикала

Я Роджер и основатель Lensrentals.com. Меня называют одним из оптических ботаников, и в свободное время я с удовольствием снимаю коллимированный свет через объективы микроскопа с 30-кратным увеличением. Когда я делаю реальные снимки, мне нравится использовать что-то другое: средний формат, или Pentax K1, или Sony RX1R.

Передаточная функция дифракционной модуляции

Diffraction MTF — это расчет волновой оптики, для которого единственными переменными (для данной формы апертуры) являются диаметр апертуры D , длина волны λ и фокусное расстояние f .MTF _{дифракция} — это верхний предел производительности системы; предполагается, что эффекты оптических аберраций незначительны. Аберрации увеличивают размер пятна и, следовательно, способствуют ухудшению MTF. Дифракционная MTF основана на общей ограничивающей апертуре системы (диафрагме). Эффекты дифракции рассчитываются только один раз для каждой системы и не накапливаются мультипликативно для каждого элемента.

Расчет дифракционного MTF

Дифракционный OTF может быть рассчитан как нормализованная автокорреляция выходного зрачка системы.Мы покажем, что это согласуется с определением формул. (1.6), (1.7) и (1.10), которые утверждают, что OTF является преобразованием Фурье импульсной характеристики. Для рассматриваемых нами некогерентных систем импульсная характеристика h ( x, y ) представляет собой квадрат двумерного преобразования Фурье дифрагирующей апертуры p ( x, y ). Квадрат величины дифрагированной амплитуды электрического поля E в В / см дает профиль энергетической освещенности импульсной характеристики в Вт / см ² :

Из уравнения.(1.23), мы должны реализовать замену переменных ξ = x / λ f и η = y / λ f , чтобы выразить импульсную характеристику (которая является преобразованием Фурье функции зрачка) в терминах пространственного положения плоскости изображения. Затем мы вычисляем дифракционную OTF обычным способом, как преобразование Фурье импульсной характеристики h ( x , y ):

Из-за операции возведения в квадрат абсолютного значения две операции преобразования уравнения(1.24) точно не отменяют друг друга — дифракционная OTF — это двумерная автокорреляция дифрагирующей апертуры p ( x, y ). Таким образом, дифракционная MTF представляет собой величину (сложной) дифракционной OTF. В качестве примера этого расчета мы возьмем простой случай квадратной апертуры, показанный на рис. 1.24:

Автокорреляция квадрата представляет собой функцию в форме треугольника,

с частотой отсечки, определенной как

.

Рисунок 1.24 Термины для расчета MTF квадратной апертуры.

Для случая круглой апертуры диаметром D система имеет ту же частоту отсечки, ξ _{отсечка} = 1 / (l F / #), но MTF имеет другую функциональную форму:

для ξ <ξ _{отсечка} и

для ξ> ξ _{отсечка} . Эти кривые MTF с дифракционным ограничением показаны на рис. 1.25. MTF с ограничением дифракции — это простой для расчета верхний предел производительности; нам нужны только λ и F / # для его вычисления.Оптическая система не может работать лучше, чем ее MTF с дифракционным ограничением — любые аберрации приведут к снижению кривой MTF. Полезно сравнить характеристики производительности данной системы с кривой MTF с дифракционным ограничением, чтобы определить выполнимость предложенных спецификаций, решить, какой запас оставлен для производственных допусков, или посмотреть, какие характеристики возможны в контексте заданного выбора λ и F / #.

Рисунок 1.25 Универсальные кривые для дифракционно-ограниченных MTF, для некогерентных систем с круглой или прямоугольной апертурой.

В качестве примера расчетов рассмотрим систему с квадратной апертурой на рис. 1.26 (а) с объектом на конечном расстоянии. Используя пространство объекта или пространство изображения F / # в зависимости от случая, мы можем вычислить отсечение ξ _{либо в плоскости объекта, либо в плоскости изображения:}

или

Потому что p < q , изображение увеличивается по отношению к объекту; следовательно, данная особенность объекта появляется на более низкой пространственной частоте изображения, поэтому две частоты в уравнениях.(1.30) и (1.31) представляют собой одну и ту же особенность. Фильтрация, вызванная дифракцией от конечной апертуры, одинакова, независимо от того, рассматривается ли она в пространстве объекта или пространстве изображения. Имея в руках частоту среза, мы можем ответить на такие вопросы, как для какой пространственной частоты изображения MTF составляет 30%? Мы используем формулу. (1.26), чтобы найти, что 30% MTF соответствует 70% частоты отсечки плоскости изображения, или 223 циклов / мм. Этот расчет предназначен для характеристик с ограничением дифракции. Аберрации сузят полосу пропускания системы, так что частота, на которой MTF составляет 30%, будет ниже 223 циклов / мм.

Рисунок 1.26 (a) Пример ФПМ с конечным сопряжением с прямоугольной апертурой и (b) Пример ФПМ с бесконечным сопряжением с прямоугольной апертурой.

В следующем примере показан расчет для состояния объекта на бесконечности с MTF, полученным в пространстве объектов, а также в пространстве изображений. Мы получаем частоту отсечки в плоскости изображения, используя уравнение. (1.27):

Как и на рис. 1.26 (a), данная характеристика на рис. 1.26 (b) подвергается одинаковой степени фильтрации, независимо от того, выражена ли она в плоскости изображения или в пространстве объекта.В пространстве объектов мы находим, что частота среза равна

. Давайте проверим, что эта угловая пространственная частота соответствует той же характеристике, что и в уравнении. (1.32). Ссылаясь на рис. 1.27, мы используем соотношение между углом объект-пространство θ и расстоянием до плоскости изображения X ,

Инвертируя уравнение. (1.34) для получения угловой пространственной частоты 1 / θ:

Учитывая, что θ выражается в радианах, если X и f имеют одинаковые единицы измерения, мы можем проверить соответствие между частотами в уравнениях.(1.32) и (1.33):

Рисунок 1.27 Зависимость между углом объект-пространство и расстоянием до плоскости изображения (адаптировано из ссылки 1).

Также интересно убедиться, что дифракционные кривые MTF на рис. 1.25 согласуются с результатами простой формулы размера дифракционного пятна для 84% окруженной мощности 2,4 λ ( F / #). На рис. 1.28 мы создаем одномерную пространственную частоту со смежными линиями и пробелами. Мы аппроксимируем дифракционное пятно так, чтобы 84% его потока находилось внутри круга диаметром 2.44 λ ( F / #) и 16% в круге вдвое большего диаметра.

Основная пространственная частота вышеупомянутой диаграммы равна

, а глубина модуляции на этой частоте составляет

, что близко к рисунку 1.25 для круглой апертуры с дифракционным ограничением, на частоте ξ = 0,21 ξ _{отсечка} .

Ссылка

1. E. Dereniak and G. D. Boreman, Infrared Detectors and Systems , Wiley, New York (1996), ссылочные данные перепечатаны с разрешения John Wiley and Sons, Inc.

MTF — объяснение функции передачи модуляции

Введение

Когда дело доходит до качества изображения, объектив стоит на первом месте, и, возможно, самое главное, звено в цепи. Без резкого объектива это не так можно получить четкое изображение. Однако, чтобы определить, резкий ли объектив и как это точно, нам нужен какой-то объективный научный метод проверки, который мы можем одинаково применимы ко всем объективам. Тест на «золотой стандарт» уже много лет определение MTF или функции передачи модуляции.Это звучит сложно но на самом деле это не так. Это просто мера того, сколько модуляции (контраст) в объекте появляется в изображении этого объекта, созданном объектив тестируемый.

Функция передачи модуляции (MTF)

MTF, вероятно, лучше всего объясняется с помощью изображения ниже. В «А» мы видим набор узоров из темных и светлых полос. Есть 4 набора стержней на увеличение малых расстояний. В точке «C» мы видим профиль линии «A», который в основном это график интенсивности через букву «А», где белые области имеют интенсивность 255, а черные области имеют интенсивность 0.(255 — это максимальная интенсивность 8-битного цифрового изображения).

В позиции «B» мы видим, как может выглядеть изображение этих столбиков. когда они отображаются объективом. Темные и светлые области размываются, и чем ближе расстояние между ними становится более размытым. В точке «D» мы видим профиль линии и под графиком показана MTF, которая будет рассчитана на основе этих данных.

MTF определяется как

MTF = (максимальная интенсивность — минимальная интенсивность) / (максимальная интенсивность + минимальная интенсивность)

Здесь важно отметить, что размытие изображение не обязательно связано с дефектом объектива.Даже идеальный объектив делает это из-за дифракции. Дифракция — это тенденция распространения света при проталкивании через отверстие. Это приводит к тому, что часть света от светлые участки переходят в темные участки. Когда светлые и темные участки большой, это не имеет большого эффекта (MTF все еще довольно высок), но когда темные и светлые участки маленькие, даже небольшое распространение света вызывает значительное падение MTF. Результатом этого является снижение MTF как пространственного частота увеличивается даже для идеального объектива.Конечно степень размытости может быть хуже при наличии аберраций линзы. « Пространственная частота » — научный термин, используемый для описания расстояние между элементами в шаблоне.

Получение технической информации

Строго говоря, когда мы говорим о MTF объектива, мы должны определить тип используется тестовый образец. Лучшая модель с точки зрения строгого научного анализа не является пошаговым шаблоном, как показано выше, где элементами являются черные и белые полосы.В предпочтительный образец называется синусоидальным, где оптическая плотность варьируется между черный и белый плавно, а профиль линии выглядит как синусоида. Однако такие узоры сложны в изготовлении, и изображение таких узоров трудно измерить на глаз, поэтому чаще всего используется паттерн бара. Паттерны бара на самом деле дают немного более высокий Измерение MTF, чем у синусоидальных диаграмм, но разница небольшая.

При построении MTF как функции шага паттернов для штрихового паттерна горизонтальная ось находится в единицах пар линий на мм, а для синусоидальной диаграммы горизонтальная ось находится в единицах циклов на мм, но часто это различие не учитывается.Вы можете увидеть такие метки, как «линии на мм» или «пары линий / мм». Обратите внимание, что линии / мм и пары линий / мм обычно одно и то же. В первом случае вы считайте только черные или белые линии. В последнем случае вы считаете черный / белый пары линий.

В дополнение к типу тестовой таблицы, как свет, используемый для ее освещения, так и Тип детектора, используемого для записи изображения, также влияет на MTF. Это потому, что MTF зависит от длины волны используемого света. Использование синего света дает более высокую MTF, чем использование красного свет например.Обычно используется белый свет, но даже в этом случае разница будет между освещением дневным светом и освещением вольфрамовым светом. Вольфрамовый свет имеет более сильная длинноволновая составляющая (составляющая красного света), чем дневной свет, поэтому измерение MTF при вольфрамовом свете ожидается, что он будет ниже, чем MTF, измеренный при дневном свете. В детектор может иметь значение, потому что, если он более чувствителен к синему свету, чем красный свет, он может дают более высокий MTF, чем если бы он более чувствителен к красному свету, чем к синему.

USAF 1951 Испытательный образец

Шаблон, который исторически часто использовался для измерения MTF и разрешения, — это USAF 1951 г. шаблон, показанный выше.Он был разработан ВВС США (в 1951 г.), отсюда и название! Вверху справа сам узор, а слева изображение узора на пленке. Измеряя результаты на пленке, вы можете сравнивать объективы, но вы не можете легко определить MTF объектива, поскольку пленка сама ограничит разрешение и снизит системную MTF. Однако вы можете, имея право оборудования, измеряют характеристики аэрофотоснимка, сформированного линзой, и, таким образом, напрямую измеряют MTF линзы.

[ДАЛЕЕ: Измерение MTF — щелевые функции и преобразования Фурье]

Определение Mtf по Merriam-Webster

\ Em-ˌtē-ˈef \

варианты: или реже MtF

множественные MTF или MTF также MtF или MtF

: трансгендерная женщина Дескрипторы от мужчины к женщине (MTF) и от женщины к мужчине (FTM) часто используются в медицинской и социологической литературе для описания транс-людей, а иногда они используют их, чтобы говорить о себе.Многие трансгендерные люди предпочитают термины «транс-мужчина» (то же, что и FTM) или «транс-женщина» (то же, что и MTF), потому что эти термины подтверждают выбранную ими идентичность. — Лора Эриксон-Шрот, цитируется в The New York Times , 21 апреля 2010 г.

.