Личный бинокль — как выбрать из всего многообразия марок и моделей

Бинокль нужен не только людям по долгу службы, им пользуются охотники, туристы, а также во время проведения различных спортивных мероприятий. Поэтому вопрос «бинокль как выбрать» праздным не назовешь.

В настоящее время существует много разновидностей. И каждая из них отвечает соответствующим критериям. Именно от них нужно идти при выборе модели для личного пользования. К примеру, человеку, желающему понаблюдать за птицами, потребуется учитывать светлость и возможность многократного приближения объекта. А турист будет уделять внимание компактности прибора. Театральный бинокль выбирают, отдавая, в первую очередь, предпочтение цвету и дизайну.

Какие параметры важны для всех пользователей?

Если нужен бинокль, как правильно выбрать его мы подскажем.

1. Возможности увеличения. Чтобы узнать, насколько бинокль увеличивает объекты, обратите внимание на первые цифры. Данный параметр различный. Он может быть фиксированным – 10х, либо переменным – от 8 до 20х (это зуммовые). Чем больше цифра, тем ближе оказывается объект.

Например, если увеличение 10х, то предмет, находящийся на расстоянии в 300 метров, будет смотреться, как с 30 метров. Любителям такого увеличения вполне достаточно.

2. Вам нужен бинокль, как выбрать его и не ошибиться. Немаловажное место отводится диаметру объектива. На эти параметры указывает второе число. Это может быть 10х50, либо 8х21. От диаметра зависит свет. Если придется пользоваться устройством при слабом свете, то останавливайте свой выбор на вариантах с большим диаметром.

Если вам нужен вариант для туристических походов, то наличие больших линз нежелательно, поскольку они утяжеляют его. Лучше воспользоваться устройством, диаметр которого от 46 до 55 мм.

3. Следующий параметр, на который нужно обратить внимание, решая вопрос о выборе, касается поля видимости. Проще говоря, это обзор, который открывается перед наблюдателем. Он имеет конусообразную форму, учитывается удаление на 1000 м.

Немаловажно учитывать отношение к увеличению. Если данный параметр слишком большой, то поле зрения сузится, объект будет ограниченным по ширине. К примеру, если увеличение равняется 8х, ширина будет от 110 до 140 метров. Если же брать вариант с увеличением 10х, то резко снижается. Ширина обозрения от 90 до 120 метров.

4. Что касается относительной яркости, то от нее зависит ясность наблюдаемых предметов. Если вы выбрали бинокль 11х56, то относительная яркость в нем составит 25,9.

Особенности стекол

Решая вопрос о выборе, обратите внимание на то, какой в нем тип стекла.

• В основном в этих устройствах пользуются боросиликатным стеклом — BK 7. С такой оптикой можно спокойно работать днем, даже в том случае, когда на улице пасмурно.
• Для варианта BaK 4 используется бариевое коронное стекло. Оно позволяет четко и ясно видеть объекты на всем поле обозрения. Чаще всего такое стекло комбинируют с антибликовой компоновкой FMC, SMC. Даже ухудшение освещенности не меняет качество наблюдения.

На линзах наносится антибликовый слой, который позволяет отражать часть света. Для каждого слоя имеется своя расшифровка.

Другие параметры выбора

О том, что такое бинокль, как выбрать его, мы вкратце рассказали. Нужно помнить, что бинокли могут различаться стоимостью в зависимости от модели и назначения.

Чаще всего выбирают охотничьи модели. Диаметр обычно от 46 до 63 мм, приближение 8-11. Снаряжение должно обладать устойчивостью, поэтому тело его делают из резины. В таких биноклях хорошие уплотнители, чтобы внутрь не попадала вода. Охотники предпочитают пользоваться изделиями зеленого, черного или камуфляжного цвета.

Для туризма требуются компактные, облегченные модели. Их вес обычно от 200 до 400 граммов, размеры от 120 до 150 миллиметров. Увеличение не более 10х при диаметре объектива от 21 до 42 мм. Устойчивость и водонепроницаемость почти такие, как и у охотничьих.

Особенности выбора морского бинокля

Если требуется бинокль, которым придется пользоваться на воде, то к нему предъявляются особые требования. Кроме оптических возможностей следует уделить внимание водоустойчивости изделия. Лучше всего, если бинокль будет водонепроницаемым. Кроме того, на водоемах световые условия бывают отрицательными из-за тумана или дождя. Подбирайте варианты с диаметром от 50 до 63 мм и увеличением до 10х.

Морские модели могут быть оснащены дополнительными функциями: компасом или дальномером. Цвет предпочтительнее желтый для корпуса и ремня.

Какой лучше бинокль, как правильно выбрать, мы частично рассмотрели. Решать вам.

Популярный, недорогой бинокль из Китая. Вычисляем реальную кратность и другие характеристики.

Здравствуйте. Да, да, знаю что обзоров этого бинокля было уже несколько, что это дешевый бинокль и что от него ожидать? Но тем не менее в этом обзоре я вычислю его реальную кратность и некоторые другие параметры, а так же попробую провести ликбез по основным характеристикам биноклей. Интересно? Тогда читаем далее.

Пробежимся немного по самому биноклю.
Пришел в обычном пакете, без коробки. Сам прибор выглядит вот так

Так же в комплекте чехол, качество отвратительное, но функцию защиты какое то время выполнять будет, выглядит вот так.

Теперь по размерам
Длина 90 мм

Ширина полностью раздвинутого 105 мм

Ширина сложенного 60 мм

Материал пластик, приятный на ощупь.
Длина веревки 60 см.

Заявленные характеристики прибора:
Кратность 30( в маркировке биноклей указывается до знака х), диаметр передней линзы объектива 60 мм( в маркировке биноклей указывается после знака х), ширина поля зрения 7,2 градуса или 126м/1000м. то есть на расстоянии 1000м от наблюдаемого объекта в ваше поле зрения попадет 126 метров.

Ну что же. пройдемся по этим характеристикам измерениями.

Передняя линза объектива.

Начнем с передней линзы объектива. Ее реальный диаметр 23 мм, эта величина нужна нам будет для вычисления кратности бинокля.


Диаметр передней линзы определяет количество света, которое формирует изображение. Чем больше диаметр, тем ярче будет выглядеть объект наблюдения. Особенно эта характеристика важна при наблюдении в мало освещенное время суток, в бинокль при одной и той же кратности, но с большим диаметром в сумерки будет видно лучше чем с меньшим при той же кратности.

Выходной зрачок.

Второй немало важный параметр, это диаметр выходного зрачка.
Диаметр выходного зрачка это диаметр светового пучка из бинокля попадающего в зрачок наблюдателя. Зрачок здорового человека в зависимости от освещения способен расширяться до 7 мм, чем темнее тем шире.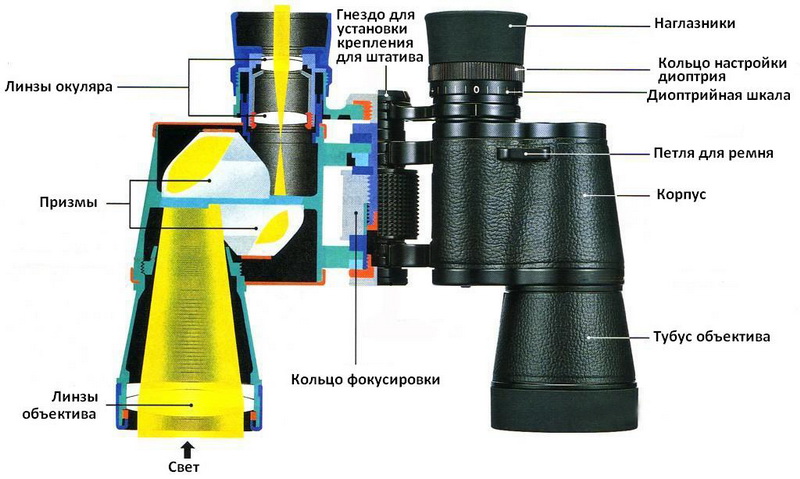

( с возрастом до 4мм). В идеале диаметр выходного зрачка должен быть равен диаметру зрачка человека. Если он меньше, теряется яркость изображения, если больше мы все равно не сможем воспринять избыток света попадающего в наш зрачок.
Диаметр выходного зрачка можно вычислить, для этого надо разделить диаметр передней линзы на кратность, для нашего бинокля он был бы равен 2мм, что не плохо при наблюдении в яркий солнечный день когда наш зрачок сужен. Но так как заявленные характеристики не соответствуют реальным, этот диаметр мы будем измерять штангенциркулем. Делается это так, бинокль наводится на удаленный источник света( Солнце самый лучший вариант), к окуляру прикладывается лист бумаги, на листе бумаги видим четкое белое пятно, это и есть выходной зрачок, измеряем его диаметр.
Выглядит это все вот так, помочь было некому поэтому бумагу на окуляре закрепил резинкой.

Диаметр выходного зрачка данного бинокля 4мм.

Кратность.

Вот мы и подошли к кратности. Кратность означает во сколько раз наблюдаемый объект окажется ближе к вам, то есть если вы в бинокль кратностью 10 будете наблюдать березу находящуюся от вас на расстоянии 1000м, то видеть вы ее будете как будто она в 100м от вас. Кстати кратность и зум (в цифровых камерах )разные характеристики, не путайте их.
Если вы внимательно читали, то по формуле расчета выходного зрачка:
диаметр передней линзы/кратность=диаметр выходного зрачка
можно вычислить кратность данного бинокля.
Итак 23/4=5,75 то есть 6 крат! Вот так вот.
Не много по другим характеристикам

Светопропускание.

Светопропускание характеризует прохождение количества света через линзы бинокля. При прохождении света через линзы происходят потери, и для борьбы с этим увеличивают светопропускную способность стекл линз. Для этого их просветляют. Передние линзы этого бинокля желтого цвета, что как бы намекает на их просветленность, мне кажется что это не так, просветление довольно дорогой процесс, а здесь скорей всего какой то светофильтр.

К стати видимо поэтому в названии бинокля есть словосочетание- ночное видение. Какое в нем ночное видение кроме этих светофильтров я понять не могу.

Система фокусировки.

Этот бинокль снабжен центральной системой фокусировки, сначала настраиваете резкость под левый глаз с помощью барабана центральной фокусировки(правый должен быть закрыт)

на правом окуляре имеется вращающееся кольцо диоптрийной коррекции, вот оно с отметками + 0 —
вращая которое вы адаптируете бинокль к своему правому глазу(левый при этом должен быть закрыт)

в результате наблюдаемое изображение будет более менее резким.

Ширина поля зрения.

Эта величина указана на корпусе бинокля и о ней я писал выше, равна 7,2 градуса или 126м на 1000м.Проверить эти значения я не могу, не хватает знаний геометрии. Можно конечно выехать в поле, отсчитать от какого нибудь одиноко стоящего дерева 1000 метров, посмотреть, засечь крайние точки, измерить между ними расстояние. Но это уже через чур.Если честно, то эта характеристика, по моим наблюдениям примерно соответствует.

Ну вот и все. Я не стал касаться таких характеристик как призма оборачивающей системы, светосила и прочие, думаю в формате этого сайта это ни к чему.
Мои впечатления от использования положительные, при первом наблюдении в него у членов семьи в основном детей. была куча эмоций(я то в армии наблюдал в более качественные бинокли и разнообразные оптические прицелы). Ну и в поход лучше взять такой бинокль чем вообще ни какого.

Котов у меня нет, но зато есть:
Птица Инокентий и пресмыкающееся Степан

Видеоверсия этого обзора и распаковка посылки на моем youtube канале, подписывайтесь кому интересно.

До свидания.

Исследование метода калибровки системы бинокулярного зрения на основе нейронной сети

На этой странице

АннотацияВведениеАнализЗаключениеНаличие данныхКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме

В системе проверки бинокулярного зрения калибровка оборудования обнаружения является основой для обеспечения последующей точности обнаружения. Существующие методы калибровки имеют недостатки, связанные со сложностью расчета, низкой точностью и плохой работоспособностью. Для решения вышеуказанных задач в данной работе исследуются метод калибровки бинокулярной камеры, метод коррекции дисторсии объектива и метод калибровки проектора в системе бинокулярного зрения на основе поверхностного структурированного света. Для коррекции дисторсии объектива на основе анализа традиционных методов коррекции предлагается метод коррекции дисторсии на основе нейронной сети с радиальной базисной функцией. Используя превосходную способность нейронной сети RBF к нелинейному отображению, можно быстро получить модели коррекции искажений для различных объективов. Он устраняет дефект, заключающийся в том, что традиционная модель коррекции не может адаптивно подстраиваться под тип объектива. Экспериментальные результаты показывают, что точность метода может соответствовать требованиям калибровки системы.

1. Введение

С развитием современных электронных технологий применение 3D-детектирования в области механической обработки становится все более и более зрелым. В настоящее время распространенные методы 3D-детектирования в основном включают контактный и бесконтактный методы. В традиционном реверс-инжиниринге распространенным методом обнаружения 3D-объектов является технология контактных измерений, представленная координатно-измерительной машиной (КИМ). Преимущество этого метода в том, что он прост в эксплуатации. Однако он имеет большую погрешность для мягкой измеряемой цели. Кроме того, стоимость специальных крупногабаритных КИМ также очень высока [1]. С развитием компьютерных технологий применение технологий машинного зрения и бесконтактных измерений в системе механического производства постепенно становится предметом исследований.

Обнаружение структурированного света является репрезентативным методом технологии бесконтактных измерений [2]. В процессе обнаружения проектор проецирует структурированный свет по определенным правилам на целевую поверхность. Полоса структурированного света изменяется с глубиной поверхности цели, что приводит к искажению. Из-за разного положения камер по обеим сторонам проектора искаженные изображения, снятые камерами, также различаются. Искаженное структурированное световое изображение содержит информацию о глубине измеренной целевой поверхности и относительном положении проектора и камеры. Анализируя и вычисляя характеристики искажения, можно получить информацию о целевой глубине и получить целевые трехмерные координаты. В процессе расчета для определения связи между трехмерным геометрическим положением точки на поверхности космического объекта и соответствующей ей точкой на изображении необходимо установить геометрическую модель камеры и проектора. Параметрами этих геометрических моделей являются параметры камеры и проектора, включая внутренние параметры, внешние параметры и параметры искажения. В большинстве случаев эти параметры можно получить только экспериментально и расчетно. Этот процесс определения параметров называется калибровкой системы. Точность калибровки системы напрямую определяет точность последующих измерений и расчетов [3–5]. Поэтому очень важно изучить высокоточный и высокоэффективный метод калибровки системы для системы 3D-детектирования.

2. Принцип калибровки бинокулярной структурированной световой системы

Для монокулярной системы технического зрения только с одним проектором и одной камерой эквивалентная камера может быть создана путем жесткого вращения и перемещения проектора и камеры. Однако предпосылка преобразования заключается в том, что внутренние параметры проектора и камеры одинаковы. В инженерной практике вышеуказанные условия, как правило, трудновыполнимы. Поэтому для 3D-реконструкции обычно используют систему бинокулярного зрения, состоящую из одного проектора и двух камер [5, 6]. Вообще говоря, проектор может быть виртуальным как формирователь изображений с точечным отверстием, а камера может быть виртуальной как линейная камера. Когда внутренние параметры двух камер одинаковы и оптический центр находится в одной горизонтальной плоскости, высота изображения одинакова. Соответствующие точки можно определить путем поиска характерных точек на той же высоте. Поэтому при построении системы бинокулярного зрения можно выбрать две камеры одной модели и расположить их с горизонтальным поворотом и наклоном. Проектор расположен между двумя камерами. Две камеры делятся на два угла обзора и одновременно собирают проекционное изображение, проецируемое проектором на 3D-мишень.

Процесс калибровки системы измерения структурированного света — это процесс решения функциональной взаимосвязи между трехмерными координатами измеренной точки в пространстве, информацией об изображении, собранной камерой, и информацией о структурированном свете. Параметры этой функции включают параметры камеры, параметры проектора и взаимосвязь преобразования между системой координат камеры и мировой системой координат. Калибровка бинокулярной системы структурированного света включает в себя калибровку камеры, расчет относительного положения двух камер, коррекцию искажения камеры, калибровку проектора и расчет относительного положения между проектором и камерой [7].

3. Калибровка камеры и проектора

3.1. Принцип работы камеры

В системе обнаружения бинокулярного зрения есть две камеры для получения данных о цели. Эти камеры имеют свои позиции и параметры. Конечный результат реконструкции зависит от соотношения пространственного положения цели и соответствующих точек изображения в камере, то есть от заданной модели и параметров камеры. Поэтому необходимо смоделировать камеру и получить соответствующие параметры для 3D-реконструкции цели. Детектирование бинокулярным зрением заключается в вычислении координат камеры, соответствующих каждой точке, по координатам каждой точки на искаженном структурированном световом плоском изображении, полученном камерой, и последующем получении координат трехмерного мира, соответствующих каждой точке на поверхности цели [8, 9].].

Как показано на рис. 1, пусть левый верхний угол координаты плоского изображения является началом координат , а известная точка на изображении — . и — количество пикселей в горизонтальном и вертикальном направлениях соответственно. Система координат изображения была установлена. Его исходное положение . Если координаты изображения, соответствующие точке, равны , то соответствующая связь между и показана в следующем уравнении:

Его однородная форма показана в следующем уравнении, где d x и d y размер каждого пикселя:

Устанавливаются система координат камеры и мировая система координат. В соответствии с принципом формирования изображения камеры-обскуры взаимосвязь между системой координат изображения и двумя показана на рисунке 2, где O ₂ — оптический центр камеры, а линия O ₁ O ₂ — фокусное расстояние f камеры.

Как видно из рисунка 2, мировая система координат может быть получена вращением и перемещением системы координат камеры. Пусть матрица вращения будет R , а матрица перевода будет t . Связь между мировой системой координат и системой координат камеры может быть получена, как показано в следующем уравнении: система показана в следующем уравнении:

Уравнение (5) представляет собой однородную форму после сортировки.

Из уравнений (1), (3) и (5) можно получить взаимосвязь между координатами плоского изображения и мировыми координатами, как показано в следующем уравнении:

Среди них ; M ₁ относится к , , d x и d y и определяется внутренней структурой камеры и называется внутренним параметром. M ₂ определяется ориентацией камеры относительно мировой системы координат, которая называется внешним параметром. M называется проекционной матрицей.

3.2. Калибровка камеры

Калибровка камеры — это процесс получения внутренних и внешних параметров камеры. Для калибровочной пластины известны 3D-координаты каждой характерной точки. Также известны координаты плоского изображения характерных точек. Следовательно, пока характерных точек достаточно, можно получить матрицу М и тогда М ₁ и М ₂ можно получить. Для каждой характеристической точки на калибровочной пластине зависимость представлена ​​следующим уравнением:

Систему уравнений можно получить, исключив z _ci следующим образом:

Это видно из уравнения (8 ), что каждой характеристической точке могут соответствовать два независимых уравнения. Следовательно, 12 неизвестных в матрице M могут быть получены из 12 уравнений, полученных по 6 характерным точкам. Метод решения – метод наименьших квадратов. Чем больше число характерных точек, тем меньше ошибка. Для n характеристических точек, 2 n уравнений получаются, как показано в следующем уравнении: между и . Следовательно, в уравнении (9) можно указать м ₃₄  = 1. В это время количество неизвестных матрицы M уменьшается до 11. Пусть эти 11 неизвестных будут вектором m , тогда уравнение (9) можно сократить до следующего уравнения: где K — матрица 2 n  × 11, m — 11-мерный неизвестный вектор и 2 n -мерный вектор. При 2 n  > 11 решение уравнения, полученное методом наименьших квадратов, представлено в следующем уравнении:

Чем больше значение 2 n , тем меньше ошибка.

Нахождение вектора m означает получение 11 неизвестных в матрице M . Последнее неизвестное число м ₃₄ решается следующим образом; уравнение (6) можно записать в виде следующего уравнения: где . Так, . Так как это третья строка ортогонального массива единиц, . Отсюда можно получить

После получения 12 неизвестных матрицы M каждый элемент матрицы внутренних и внешних параметров M ₁ и M ₂ можно получить далее.

3.3. Расчет относительного положения между двумя камерами

При калибровке камеры бинокулярного зрения, помимо расчета внутренних и внешних параметров каждой камеры, также необходимо рассчитать относительное положение между двумя камерами. Для двух камер есть где .

После устранения,

Следовательно, относительное положение между двумя камерами может быть представлено R и t следующим образом:

3.4. Калибровка проектора

Проектор можно рассматривать как рабочую камеру заднего вида [10]. Следовательно, математическая модель проектора может быть представлена ​​моделью камеры-обскуры, показанной в уравнении (6). Хотя математическая модель проектора такая же, как у камеры, проектор не может напрямую получить пиксельные координаты каждой характерной точки на плоскости изображения проектора. Решение приведено в ссылке [11]; проектор проецирует горизонтальные и вертикальные полосы кода серого на калибровочную пластину в порядке непрерывного деления. После того, как камера захватила изображение, рассчитываются компоненты прямого и непрямого света и выполняется пороговая сегментация. Затем алгоритм декодирования кода Грея используется для получения координат каждой точки на плоскости изображения проектора.

4. Коррекция дисторсии объектива

4.1. Традиционный метод коррекции дисторсии объектива

Идеальная модель точечного отверстия является лишь приближением к реальной модели объектива. Фактическая камера и проектор отличаются от модели с точечным отверстием из-за другой структуры объектива, а также ошибок обработки и сборки в производственном процессе. Для обычного объектива, особенно для широкоугольного объектива, следует учитывать дисторсию объектива [12]. Наиболее важное влияние на визуализацию оказывает радиальное искажение. Пусть параметры радиальной дисторсии равны к ₁ и к ₂ . Далее идет координата изображения, полученная из модели камеры с одним отверстием, а ( x , y ) — фактическая координата изображения. Формула (17) учитывает только радиальное искажение и игнорирует старший член. В реальном объективе следует учитывать эксцентрическую дисторсию и дисторсию тонкой призмы. Из-за различия оптической модели и погрешности сборки их нельзя выразить одной и той же математической моделью. В ссылке [4] предложен метод коррекции дисторсии объектива на основе нейронной сети BP. Тем не менее, сеть BP медленно вычисляется и легко попадает в локальный оптимум, поэтому она не может соответствовать требованиям в реальном времени и точности трехмерного обнаружения.

4.2. Коррекция искажения объектива на основе сети RBF

Сеть RBF представляет собой эффективную прямую нейронную сеть. Связь между входным слоем и скрытым слоем нелинейна. Существует линейная взвешенная связь между скрытым слоем и выходным слоем [13]. Эта структура позволяет избежать утомительного расчета сети BP. Он обладает не только хорошей нелинейной аппроксимационной способностью, но и быстрой вычислительной способностью. Он особенно подходит для нелинейного прогнозирования из n-мерного пространства в m-мерное пространство.

Структура RBF-сети коррекции дисторсии объектива показана на рисунке 3. Входной сигнал ( x , y ) представляет собой координаты реального снятого изображения. Выходным сигналом являются фактические координаты изображения, которые можно определить как координаты характерных точек на калибровочной доске. Количество узлов в скрытом слое равно количеству выборок n .

Входной вектор системы равен d  = [ x , y ] ^Т . Выходной вектор равен . Весовая матрица представляет собой матрицу 2 ×  n . Элемент представляет собой вес между и -м узлом в скрытом слое и и -м узлом в выходном слое. Радиальная базисная функция φ ( D ^I , D ^P ) -гауссовая функция ядра, где D ^I IS D ^I — D ^I IS — I IS — I . d ^p — вектор центральной точки.

Система предоставляет n характеристических точечных образцов на калибровочной плате. В соответствии со структурой сети выход системы составляет

. Во избежание того, чтобы каждая радиальная базисная функция была слишком резкой или слишком плоской, определение постоянной разложения радиальной базисной функции показано в следующем уравнении: где d _max — максимальное расстояние между образцами и n — количество выборок.

Обучение системы разделено на два этапа. Первый этап – обучение без учителя. Конкретная работа заключается в том, чтобы решить центр и дисперсию в скрытом слое. Второй этап – контролируемое обучение. Конкретная работа заключается в решении весовой матрицы от неявного слоя к выходному слою. Коррекция веса может быть реализована методом наименьшей среднеквадратичной ошибки. Формула корректировки веса:

Среди них j -е ожидаемое значение.

5.

Эксперимент и анализ

5.1. Экспериментальный процесс

В этой статье бинокулярная система обнаружения, показанная на рисунке 4, используется для проверки вышеописанного алгоритма. Пиксель камеры составляет 1,3 миллиона, а формат измерения — 200 мм × 150 мм. Номинальная точность сканирования составляет 0,01 мм. Калибровочная доска, использованная в эксперименте, показана на рисунке 5. На калибровочной доске регулярно расположены 11 × 13 = 169 характерных точек, включая 17 установочных точек.

В калибровочном эксперименте сначала фиксируется положение калибровочной пластины. Проектор проецирует структурированный свет с кодом Грея на калибровочную пластину, как показано на рис. 6. Камера делает снимки. Положение калибровочной доски меняется, и описанная выше работа повторяется. Калибровочная плата размещается в 8 различных положениях в пространстве для измерений, как показано на рис. 7. Каждая камера получает 8 изображений для калибровки системы. При калибровке, во-первых, край изображения извлекается на уровне пикселей, чтобы идентифицировать точки меток и соответствовать центральной точке, а также нумеровать точки меток в соответствии с точками позиционирования. Затем трехмерные координаты точки позиционирования реконструируются с использованием местоположения точки позиционирования на первых двух изображениях. Затем 3D-координаты ориентиров реконструируются с остальными изображениями.

5.2. Анализ данных

После получения 3D-координат точек маркера внутренние и внешние параметры камеры могут быть рассчитаны в соответствии с указанным выше методом, как показано в таблицах 1 и 2.

В эксперименте используется метод перепроекции. используется для проверки точности калибровочных данных. В соответствии с параметрами, полученными в результате калибровки, точки позиционирования перепроецируются на плоскость изображения камеры и сравниваются с реальными точками изображения. Для калибровки используются, соответственно, традиционный метод и метод, предложенный в данной статье. Вычисленная ошибка показана на рисунке 8. Слева результат традиционного метода калибровки. Справа результат калибровки метода.

При использовании двух алгоритмов остаточные данные, соответствующие восьми положениям калибровочной доски, показаны в таблицах 3 и 4.

6. Заключение

Введена структурированная система обнаружения света с бинокулярным зрением. В качестве входной и выходной системы принимается идеальное изображение и фактические координаты изображения, и строится система коррекции искажений изображения на основе нейронной сети RBF. Фактический расчет коррекции искажения камеры выполнен с использованием хорошей способности нейронной сети к нелинейной подгонке. Экспериментальные результаты показывают, что алгоритм может преодолеть недостатки традиционных методов, а результаты обнаружения могут удовлетворить фактические потребности.

Доступность данных

Данные, использованные для поддержки результатов этого исследования, можно получить у соответствующего автора по запросу.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов в связи с публикацией данной статьи.

Благодарности

Эта работа была поддержана проектом Фонда создания Нанкинского технологического института (грант № CXY201933).

Ссылки

1. Л. Ю. Фу, Д. Чжан и К. Л. Е, «Рекуррентная сеть бережливого внимания для распознавания сцен дистанционного зондирования», IEEE Transactions on Geoscience and Remote Sensing , стр. 1–12, 2020.

   Просмотр по адресу:

   Издатель Сайт | Google Scholar

2. С. Ф. Цзян, Л. Беатрис и З. Сонг, «Трехмерное измерение формы с использованием системы структурированного света с двумя проекторами», Applied Optics , vol. 57, нет. 14, с. 3983, 2018.

   Просмотр:

   Сайт издателя | Google Scholar

3. Z. Wang, Z. Wu, X. Zhen, R. Yang, J. Xi и X. Chen, «Двухэтапный метод калибровки бинокулярного датчика стереозрения с большим полем зрения для измерения на месте». Измерение , том. 62, стр. 15–24, 2015 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

4. D. Zhang, G. Zhang и L. Li, «Калибровка шестиосевого параллельного манипулятора на основе нейронной сети BP», Industrial Robot: The International Journal of Robotics Research and Application , том. 46, нет. 5, стр. 692–698, 2019.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

5. В. Г. Ли, Х. Ли и Х. Чжан, «Калибровка световой плоскости и анализ точности для многострочной структурированной системы измерения светового зрения», Optik , vol. 207, ID статьи 163882, 2019.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

6. X. Чен, Ф. Чжоу и Т. Сюэ, «Метод калибровки структурированного света для всенаправленного поля зрения для системы катадиоптрического зрения», Измерение , том. 148, ID статьи 106914, 2019.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

7. Дж. Э. Ха, «Калибровка системы структурированного светового зрения с использованием нескольких вертикальных плоскостей», Journal of Electrical Engineering and Technology , vol. 13, нет. 1, стр. 438–444, 2018 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

8. X. Чен, Р. Фан, Дж. Ву и др., «Метод двухэтапной калибровки камеры на основе преобразования Фурье с простым периодическим шаблоном», Оптика и лазеры в технике , вып. 133, ID статьи 106121, 2020.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

9. J. Jiang, L. Zeng, B. Chen, Y. Lu и W. Xiong, «Точная и гибкая методика калибровки камеры», Computing , vol. 101, нет. 4, стр. 1971–1988, 2019.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

10. С. Ян, М. Лю, Дж. Сонг и др., «Метод калибровки проектора на основе системы стереозрения», Оптическое обозрение , том. 24, нет. 5, стр. 1–7, 2017 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

11. С. К. Найер, Г. Кришнан, М. Д. Гроссберг и Р. Раскар, «Быстрое разделение прямых и глобальных компонентов сцены с использованием высокочастотного освещения», ACM Transactions on Graphics , vol. 25, нет. 3, стр. 935–944, 2006 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

12. M. Zhang, F. L. Wu, L. X. Jin, G. N. Li, S. Han и Y. Zhang, «Коррекция оптимизации радиальной дисторсии объектива с функцией измерения изгиба», Труды Тяньцзиньского университета , том. 22, нет. 98, стр. 94–99, 2016 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

13. Q. Ye, H. Zhao, Z. Li et al., «Быстрый надежный опорный вектор близнецов на основе минимизации расстояния L1-нормы k — кластеризация плоскостей», IEEE Transactions on Neural Networks and Learning Системы , том. 29, нет. 9, стр. 4494–4503, 2018.

    Посмотреть по адресу:

    Сайт издателя | Академия Google

Авторское право

Авторское право © 2021 Hao Zhu et al. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Расшифровка содержимого сознания из префронтальных ансамблей

%PDF-1.5 % 1 0 объект >/Метаданные 3123 0 R/Страницы 2 0 R/StructTreeRoot 3 0 R/Тип/Каталог>> эндообъект 3123 0 объект >поток приложение/pdf

Вишал Капур

Расшифровка содержимого сознания из префронтальных ансамблей

2020-01-28T18:06:47+01:00Microsoft® Word 20162023-04-07T14:54:54-07:002023-04-07T14:54:54-07:00Microsoft® Word 2016uuid:af099595-1dd1-11b2- 0a00-120a276d7200uuid:af099598-1dd1-11b2-0a00-b80000000000 конечный поток эндообъект 2 0 объект > эндообъект 3 0 объект > эндообъект 813 0 объект > эндообъект 814 0 объект > эндообъект 816 0 объект [1229 0 R 1230 0 R 1231 0 R 1232 0 R 1643 0 R 1644 0 R 1645 0 R 1646 0 R 1647 0 R 1234 0 R 1235 0 R 1648 0 R 16490 R 1650 0 R 1237 0 R 1238 0 R 1239 0 R 1240 0 R 1241 0 R] эндообъект 817 0 объект > эндообъект 818 0 объект [1242 0 R 1243 0 R 1244 0 R 1245 0 R 1246 0 R 1247 0 R 1248 0 R 1249 0 R 1250 0 R 1251 0 R 1252 0 R] эндообъект 819 0 объект [1253 0 Р 1657 0 Р 1658 0 Р 1659 0 Р 1660 0 Р 1661 0 Р 1662 0 Р 1663 0 Р 1664 0 Р 1665 0 Р 1666 0 Р 1667 0 Р 1668 0 Р 1669 0 Р 1670 0 Р 11671 0 0 Р 1673 0 Р 1674 0 Р 1675 0 Р 1676 0 Р 1677 0 Р 1678 0 Р 1679 0 Р 1680 0 Р 1681 0 Р 1682 0 Р 1683 0 Р 1684 0 Р 1685 0 Р 1686 0 Р 1687 0 Р 1688 16890 Р] эндообъект 820 0 объект > эндообъект 821 0 объект > эндообъект 822 0 объект > эндообъект 823 0 объект > эндообъект 824 0 объект > эндообъект 825 0 объект > эндообъект 826 0 объект > эндообъект 827 0 объект > эндообъект 828 0 объект > эндообъект 829 0 объект > эндообъект 830 0 объект > эндообъект 831 0 объект > эндообъект 832 0 объект > эндообъект 833 0 объект > эндообъект 834 0 объект > эндообъект 835 0 объект > эндообъект 836 0 объект [1706 0 R 1708 0 R 1707 0 R 1709 0 R 1710 0 R 1711 0 R 1712 0 R 1713 0 R 1714 0 R 1715 0 R 1716 0 R 1717 0 R 1718 0 R 1719 0 R] эндообъект 837 0 объект > эндообъект 838 0 объект > эндообъект 8390 объект > эндообъект 840 0 объект > эндообъект 841 0 объект > эндообъект 842 0 объект > эндообъект 843 0 объект [1257 0 Ч 1258 0 Ч 1259 0 Ч 1726 0 Ч 1727 0 Ч 1728 0 Ч 1729 0 Ч 1730 0 Ч 1731 0 Ч] эндообъект 844 0 объект > эндообъект 845 0 объект > эндообъект 846 0 объект [1734 0 Ч 1736 0 Ч 1735 0 Ч 1737 0 Ч 1738 0 Ч 1739 0 Ч 1264 0 Ч] эндообъект 847 0 объект > эндообъект 848 0 объект > эндообъект 849 0 объект [1265 0 Ч 1742 0 Ч 1743 0 Ч 1744 0 Ч 1745 0 Ч 1746 0 Ч] эндообъект 850 0 объект > эндообъект 851 0 объект > эндообъект 852 0 объект [1267 0 Р 1749 0 Р 1750 0 Р 1751 0 Р 1752 0 Р 1753 0 Р 12690 Р] эндообъект 853 0 объект > эндообъект 854 0 объект > эндообъект 855 0 объект [1270 0 Ч 1756 0 Ч 1757 0 Ч 1758 0 Ч 1759 0 Ч 1760 0 Ч 1761 0 Ч 1762 0 Ч] эндообъект 856 0 объект > эндообъект 857 0 объект > эндообъект 858 0 объект > эндообъект 859 0 объект [1272 0 Ч 1273 0 Ч] эндообъект 860 0 объект [1766 0 Р 1771 0 Р 1767 0 Р 1772 0 Р 1768 0 Р 1773 0 Р 1769 0 Р 1774 0 Р 1770 0 Р 1275 0 Р 1276 0 Р 1775 0 Р 1776 0 Р 1777 0 Р 1778 0 Р 1779 0 0 Р] эндообъект 861 0 объект > эндообъект 862 0 объект > эндообъект 863 0 объект > эндообъект 864 0 объект > эндообъект 865 0 объект > эндообъект 866 0 объект > эндообъект 867 0 объект [1788 0 Р 1797 0 Р 1789 0 Р 1798 0 Р 1790 0 Р 1799 0 Р 1791 0 Р 1800 0 Р 1792 0 Р 1801 0 Р 1793 0 Р 1802 0 Р 1794 0 Р 1803 0 Р 1795 0 Р 1804 0 Р 1780 5 0 Р 1 Р 1806 0 Р 1807 0 Р 1808 0 Р 1809 0 Р] эндообъект 868 0 объект > эндообъект 869 0 объект > эндообъект 870 0 объект > эндообъект 871 0 объект > эндообъект 872 0 объект > эндообъект 873 0 объект > эндообъект 874 0 объект > эндообъект 875 0 объект > эндообъект 876 0 объект > эндообъект 877 0 объект > эндообъект 878 0 объект [1822 0 R 1827 0 R 1823 0 R 1828 0 R 1824 0 R 1829 0 R 1825 0 R 1830 0 R 1826 0 R 1831 0 R 1832 0 R 1833 0 R 1834 0 R 1835 0 R] эндообъект 8790 объект > эндообъект 880 0 объект > эндообъект 881 0 объект > эндообъект 882 0 объект > эндообъект 883 0 объект > эндообъект 884 0 объект > эндообъект 885 0 объект [1842 0 R 1850 0 R 1843 0 R 1851 0 R 1844 0 R 1852 0 R 1845 0 R 1853 0 R 1846 0 R 1854 0 R 1847 0 R 1855 0 R 1848 0 R 1856 0 R 1849 0 R 1128 0 0 Р 1286 0 Р 1857 0 Р 1858 0 Р 1859 0 Р] эндообъект 886 0 объект > эндообъект 887 0 объект > эндообъект 888 0 объект > эндообъект 889 0 объект > эндообъект 890 0 объект > эндообъект 891 0 объект > эндообъект 892 0 объект > эндообъект 893 0 объект > эндообъект 894 0 объект [1288 0 Ч 1289 0 Ч 1290 0 Ч] эндообъект 895 0 объект [1868 0 Ч 1870 0 Ч 1869 0 Ч 1292 0 Ч 1293 0 Ч 1294 0 Ч] эндообъект 896 0 объект > эндообъект 897 0 объект [1872 0 R 1875 0 R 1873 0 R 1876 0 R 1874 0 R 1296 0 R 1297 0 R 1877 0 R 1878 0 R 1879 0 R] эндообъект 898 0 объект > эндообъект 899 0 объект > эндообъект 900 0 объект > эндообъект 901 0 объект [1883 0 Ч 1885 0 Ч 1884 0 Ч 1300 0 Ч 1301 0 Ч 1302 0 Ч 1303 0 Ч] эндообъект 902 0 объект > эндообъект 903 0 объект [1304 0 Р] эндообъект 904 0 объект [1305 0 Ч 1306 0 Ч 1307 0 Ч 1308 0 Ч 1309 0 Ч 1310 0 Ч 1311 0 Ч 1312 0 Ч] эндообъект 905 0 объект [1313 0 Ч 1314 0 Ч 1315 0 Ч 1887 0 Ч 1888 0 Ч 1889 0 Ч] эндообъект 906 0 объект > эндообъект 907 0 объект [1891 0 R 1895 0 R 1892 0 R 1896 0 R 1893 0 R 1897 0 R 1894 0 R 1898 0 R 1899 0 R 1900 0 R] эндообъект 908 0 объект > эндообъект 909 0 объект > эндообъект 910 0 объект > эндообъект 911 0 объект > эндообъект 912 0 объект [1319 0 R 1320 0 R 1321 0 R 1322 0 R 1323 0 R 1324 0 R 1325 0 R 1326 0 R 1327 0 R 1328 0 R 1329 0 R] эндообъект 913 0 объект [1330 0 R 1331 0 R 1332 0 R 1905 0 R 1906 0 R 1907 0 R 1908 0 R 1909 0 R 1910 0 R 1911 0 Р 1912 0 Р 1913 0 Р 1914 0 Р 1915 0 Р 1916 0 Р 1917 0 Р 1918 0 Р 1919 0 Р 1920 0 Р 1921 0 Р 1922 0 Р 1923 0 Р 1924 0 Р 1925 0 Р 1926 0 Р 0 Р 1928 0 Р 1929 0 Р 1930 0 Р 1931 0 Р 1932 0 Р 1933 0 Р 1934 0 Р 1935 0 Р 1936 0 Р 1937 0 Р 1938 0 Р 1939 0 Р 1940 0 Р 1941 0 Р 1942 0 Р 1943 4 0 R 1945 0 R 1946 0 R 1947 0 R 1948 0 R 1949 0 R 1950 0 R 1334 0 R 1335 0 R 1336 0 R 1337 0 R 1338 0 R 1339 0 R] эндообъект 914 0 объект [1340 0 Р 1341 0 Р 1342 0 Р 1992 0 Р 1993 0 Р 1994 0 Р 1995 0 Р 1996 0 Р 1997 0 Р 1998 0 Р 1999 0 Р 2000 0 Р 2001 0 Р 2002 0 Р 2003 0 Р 2004 0 Р 2005 0 Р 2006 0 Р 2007 0 Р 2008 0 Р 2009 0 Р 2010 0 Р 2011 0 Р 2012 30 Р 0 Р 2014 0 Р 2015 0 Р 2016 0 Р 2017 0 Р 2018 0 Р 2019 0 Р 2020 0 Р 2021 0 Р 2022 0 Р 1344 0 Р 1345 0 Р 1346 0 Р 1347 0 Р 1348 0 Р 1349 0 Р 1350] эндообъект 915 0 объект [1351 0 Ч 1352 0 Ч 1353 0 Ч 1355 0 Ч 1356 0 Ч 1357 0 Ч 1358 0 Ч 1354 0 Ч] эндообъект 916 0 объект [1359 0 Ч 1360 0 Ч 1361 0 Ч 1362 0 Ч 1363 0 Ч 1364 0 Ч] эндообъект 917 0 объект [1365 0 Ч 1367 0 Ч 1368 0 Ч 13690 Р 1370 0 Р 1366 0 Р] эндообъект 918 0 объект [1371 0 Ч 1372 0 Ч 1373 0 Ч 1374 0 Ч 1375 0 Ч 1376 0 Ч 1377 0 Ч 1378 0 Ч] эндообъект 919 0 объект [1379 0 Ч 1381 0 Ч 1382 0 Ч 1383 0 Ч 1384 0 Ч 1380 0 Ч] эндообъект 920 0 объект [1385 0 Ч 1386 0 Ч 1387 0 Ч 1388 0 Ч 1389 0 Ч 1390 0 Ч 1391 0 Ч 1392 0 Ч] эндообъект 921 0 объект [1393 0 Ч 1395 0 Ч 1396 0 Ч 1397 0 Ч 1398 0 Ч 1399 0 Ч 1400 0 Ч 1401 0 Ч 1394 0 Ч] эндообъект 922 0 объект [1402 0 Ч 1404 0 Ч 1405 0 Ч 1406 0 Ч 1407 0 Ч 1408 0 Ч 1403 0 Ч] эндообъект 923 0 объект [1409 0 Ч 1410 0 Ч 1412 0 Ч 1413 0 Ч 1414 0 Ч 1415 0 Ч 1411 0 Ч] эндообъект 924 0 объект [1416 0 Ч 1418 0 Ч 1419 0 Ч 1417 0 Ч] эндообъект 925 0 объект [1420 0 Ч 1421 0 Ч 1422 0 Ч 1423 0 Ч 1424 0 Ч 1425 0 Ч 1426 0 Ч 1427 0 Ч] эндообъект 926 0 объект [1428 0 R 1430 0 R 1431 0 R 1432 0 R 1433 0 R 1434 0 R 1435 0 R 1436 0 R 1437 0 R 1429 0 R] эндообъект 927 0 объект [1438 0 R 1440 0 R 1441 0 R 1442 0 R 1443 0 R 1444 0 R 1445 0 R 1446 0 R 1447 0 R 1439 0 R] эндообъект 928 0 объект [1448 0 Ч 1450 0 Ч 1451 0 Ч 1452 0 Ч 1453 0 Ч 1454 0 Ч 1455 0 Ч 1456 0 Ч 1449 0 Ч] эндообъект 929 0 объект [1457 0 Ч 1459 0 Ч 1460 0 Ч 1461 0 Ч 1458 0 Ч] эндообъект 930 0 объект [1462 0 Ч 1463 0 Ч 1464 0 Ч 1465 0 Ч] эндообъект 931 0 объект [1466 0 Ч 1468 0 Ч 1469 0 Ч 1470 0 Ч 1467 0 Ч] эндообъект 932 0 объект [1471 0 Ч 1473 0 Ч 1474 0 Ч 1475 0 Ч 1472 0 Ч] эндообъект 933 0 объект [1476 0 Ч 1478 0 Ч 1479 0 Ч 1480 0 Ч 1481 0 Ч 1482 0 Ч 1483 0 Ч 1477 0 Ч] эндообъект 934 0 объект [1484 0 Ч 1486 0 Ч 1487 0 Ч 1488 0 Ч 1489 0 Ч 1485 0 Ч] эндообъект 935 0 объект [1490 0 Ч 1492 0 Ч 1493 0 Ч 1494 0 Ч 1495 0 Ч 1491 0 Ч] эндообъект 936 0 объект [1496 0 Ч 1498 0 Ч 1499 0 Ч 1497 0 Ч] эндообъект 937 0 объект [1500 0 Ч 1501 0 Ч 1502 0 Ч 1503 0 Ч 1504 0 Ч 1505 0 Ч 1506 0 Ч 1507 0 Ч 1508 0 Ч 15090 Р 1510 0 Р 1511 0 Р] эндообъект 938 0 объект [1512 0 Ч 1514 0 Ч 1515 0 Ч 1513 0 Ч] эндообъект 939 0 объект [1516 0 Ч 1517 0 Ч 1519 0 Ч 1520 0 Ч 1521 0 Ч 1518 0 Ч] эндообъект 940 0 объект [1522 0 Р 1523 0 Р 1524 0 Р 1525 0 Р 1526 0 Р 1527 0 Р 1528 0 Р 1529 0 Р 1530 0 Р 1531 0 Р 1532 0 Р 1533 0 Р 1534 0 Р 1535 0 Р 1536 0 Р 15137 0 0 Р 1539 0 Р] эндообъект 941 0 объект [1540 0 R 1541 0 R 1542 0 R 1543 0 R 1544 0 R 1545 0 R 1546 0 R 1547 0 R 1548 0 R 1549 0 R 1550 0 R 1551 0 R 1552 0 R] эндообъект 942 0 объект > эндообъект 943 0 объект [2054 0 Ч 2052 0 Ч 2055 0 Ч 2056 0 Ч 2057 0 Ч 2058 0 Ч 20590 Р 2060 0 Р 2061 0 Р 2062 0 Р 2063 0 Р 2064 0 Р 2065 0 Р 2066 0 Р 2067 0 Р 2068 0 Р 2069 0 Р 2070 0 Р 2071 0 Р 2072 0 Р 2073 0 Р 2074 5 0 Р 207 2076 0 Р 2077 0 Р 2078 0 Р 2079 0 Р 2080 0 Р 2081 0 Р 2082 0 Р 2083 0 Р 2084 0 Р 2085 0 Р 2086 0 Р 2087 0 Р 2088 0 Р 2089 0 Р 2090 0 Р 2091 0 Р 2093 0 Р 2094 0 Р 2095 0 Р 2096 0 Р 2097 0 Р 2098 0 Р 2099 0 Р 2100 0 Р 2101 0 Р 2102 0 Р 2103 0 Р 2104 0 Р 2105 0 Р 2106 0 Р 2107 0 Р 22108 0 Р 2110 0 Р 2111 0 Р 2112 0 Р 2113 0 Р 2114 0 Р 2115 0 Р 2116 0 Р 2117 0 Р 2118 0 Р 21190 Р 2120 0 Р 2121 0 Р 2122 0 Р 2123 0 Р 2124 0 Р 2125 0 Р 2126 0 Р 2127 0 Р 2128 0 Р 2129 0 Р 2130 0 Р 2131 0 Р 2132 0 Р 2133 0 Р 2134 5 0 Р 2133 2136 0 Р 2137 0 Р 2138 0 Р 2139 0 Р 2140 0 Р 2141 0 Р 2142 0 Р 2143 0 Р 2144 0 Р 2145 0 Р 2146 0 Р 2147 0 Р 2148 0 Р 2149 0 Р 2150 0 Р 2215 0 Р 2153 0 Р 2154 0 Р 2155 0 Р 2156 0 Р 2157 0 Р 2158 0 Р 2159 0 Р 2160 0 Р] эндообъект 944 0 объект > эндообъект 945 0 объект > эндообъект 946 0 объект > эндообъект 947 0 объект > эндообъект 948 0 объект > эндообъект 949 0 объект > эндообъект 950 0 объект > эндообъект 951 0 объект > эндообъект 952 0 объект > эндообъект 953 0 объект > эндообъект 954 0 объект > эндообъект 955 0 объект > эндообъект 956 0 объект > эндообъект 957 0 объект > эндообъект 958 0 объект > эндообъект 959 0 объект > эндообъект 960 0 объект > эндообъект 961 0 объект > эндообъект 962 0 объект > эндообъект 963 0 объект > эндообъект 964 0 объект > эндообъект 965 0 объект > эндообъект 966 0 объект > эндообъект 967 0 объект > эндообъект 968 0 объект > эндообъект 969 0 объект > эндообъект 970 0 объект > эндообъект 971 0 объект > эндообъект 972 0 объект > эндообъект 973 0 объект > эндообъект 974 0 объект > эндообъект 975 0 объект > эндообъект 976 0 объект > эндообъект 977 0 объект > эндообъект 978 0 объект > эндообъект 979 0 объект > эндообъект 980 0 объект > эндообъект 981 0 объект > эндообъект 982 0 объект > эндообъект 983 0 объект > эндообъект 984 0 объект > эндообъект 985 0 объект > эндообъект 986 0 объект > эндообъект 987 0 объект > эндообъект 988 0 объект > эндообъект 989 0 объект > эндообъект 990 0 объект > эндообъект 991 0 объект > эндообъект 992 0 объект > эндообъект 993 0 объект > эндообъект 994 0 объект > эндообъект 995 0 объект > эндообъект 996 0 объект > эндообъект 997 0 объект > эндообъект 998 0 объект > эндообъект 999 0 объект > эндообъект 1000 0 объект [2273 0 Р 2267 0 Р 2274 0 Р 2275 0 Р 2268 0 Р 2276 0 Р 2269 0 Р 2270 0 Р 2277 0 Р 2278 0 Р 2279 0 Р 2280 0 Р 2281 0 Р 2282 0 Р 2283 0 Р 2228 0 5 0 Р 2286 0 Р 2287 0 Р 2288 0 Р 2289 0 Р 2290 0 Р 2291 0 Р 2292 0 Р 2293 0 Р 2294 0 Р 2295 0 Р 2296 0 Р 2297 0 Р 2298 0 Р 2299 0 Р 2300 10 Р 2300 2302 0 Р 2303 0 Р 2304 0 Р 2305 0 Р 2306 0 Р 2307 0 Р 2308 0 Р 2309 0 Р 2310 0 Р 2311 0 Р 2312 0 Р 2313 0 Р 2314 0 Р 2315 0 Р 2316 0 Р 2317 0 2319 р.