Сферические аберрации: Сферическая аберрация в объективах | Перископ
Исправление — сферическая аберрация — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
| Сферическая аберрация и ее исправление в оптической системе, состоящей из двух линз. [1] |
Исправление сферической аберрации в объективах основано на следующем принципе. Лучи краевой зоны после преломления их рассеивающей линзой направляются уже не в точку F4, а в точку FJ, в которой фокусируются лучи центрального пучка. Одновременно несколько уменьшается и аберрация лучей, прошедших сквозь промежуточные зоны линзы. [2]
Для исправления сферической аберрации при наличии пятых порядков обычно добиваются уничтожения сферической аберрации на краю отверстия при некотором заданном угле иг или величине хг. [3]
Для исправления сферической аберрации зеркал ( например, прожекторов) им обычно придают не сферическую форму, а вид параболоида вращения, располагая источник в фокусе; в таких зеркалах при тщательном их выполнении сферическую аберрацию можно сделать очень малой.
Наибольшие трудности представляет исправление меридиональной и сагиттальной сферической аберрации в широких наклонных пучках. Решающим в этом деле является устранение или ослабление роста полевых сферических аберраций, что в большей или меньшей мере может быть обеспечено использованием в силовых элементах концентрических линз. [5]
Очевидно, что при исправлении сферической аберрации значения остальных аберраций существенно меняются, но остаются довольно большими и лишь при значениях d, больших 0 3 и 0 4, становятся достаточно малыми Во второй графе приведены зна — — чения е, при которых сферическая аберрация исправлена.
Простейше оптической системой, удовлетворяющей трем условиям исправления сферической аберрации, комы и хроматической аберрации положения, является двухлинзовый склееи-ный объектив при надлежащей подборе стекол. [7]
Объективы ОМ-16, ОМ-25 имеют коррекционные оправы для исправления сферической аберрации, вызываемой изменением толщины покровного стекла от 0 10 до 0 20 мм. [8]
Апохроматические объективы представляют собой оптические системы, обеспечивающие лучшее исправление сферической аберрации, астигматизма и комы, по сравнению с ахроматами. Кроме того апохроматы отличаются от ахроматов улучшенной хроматической коррекцией, устраняющей вторичный спектр. Однако апохроматы дают более заметную кривизну поля изображения, что приводит к нерезкости последнего по краям. При работе с этими объективами большое значение приобретает центрировка всей оптической системы микроскопа. Изображение поля с помощью апохроматов получается выпуклым, лишенным плоскостности.
В предыдущем параграфе был затронут вопрос о возможности исправления сферической аберрации в воздушных телеанастигматических линзах путем подбора показателей преломления первой и последней среды. [10]
После того как в результате решения системы уравнений для исправления сферической аберрации, комы и астигматизма получены приближенные значения всех конструктивных элементов, целесообразно передать продолжение расчета ЭВМ для доведения системы до оптимального состояния. [11]
Полученные результаты говорят о том, что общепринятый характер исправления сферической аберрации с учетом аберрации пятого порядка не обеспечивает устранения волновой аберрации на краю отверстия; однако при использовании некоторой расфокусировки величины волновой аберрации могут быть существенно уменьшены. [12]
Как уже упоминалось ранее, возможен случай, когда при исправлении сферической аберрации вдоль одной из координатных осей не удастся полностью устранить сферическую аберрацию вдоль другой координатной оси. [13]
[13]
Рассматривая концентрические системы, мы не показали их возможностей в исправлении сферической аберрации; эта задача может быть решена путем использования склеенных концентрических поверхностей нужного радиуса кривизны при выбранных должным образом показателях преломления по обе стороны поверхности склейки. Способы исправления сферической аберрации для концентрических систем будут рассмотрены в гл. [14]
Максутовым компенсаторы не совсем подходят под категорию афокальных компенсаторов, так как исправление сферической аберрации, вызванное ими, осуществляется благодаря отступлению от афокальности и отчасти вследствие сравнительно большой толщины мениска. К тому же следует отметить, что исправление сферической аберрации возможно только при больших крутизнах сферических поверхностей, а это вызывает появление значительных аберраций высших порядков. [15]
Страницы: 1 2 3 4
Аберрации человеческого глаза, способы их измерения и коррекции (обзор литературы)
This article is devoted to the new technology, «new diagnostic tool» –non–invasive wavefront sensing of the human eye, which can provide ophthalmologists with precise measurement of both higher– and lower–order aberrations. It describes most wide–spread types of wavefront systems, which use different principles in there functioning. Many factors, such as age of patient, accommodation, tear film break–up may cause the changes in wavefront map. Also higher order aberrations can be increased, by wearing soft or rigid contact lenses. Refractive and cataract surgery may induce large amount of higher order aberrations, which determine the cause the lower BCVA, than we can expect. This article describes different possible ways of correction higher order aberrations.
It describes most wide–spread types of wavefront systems, which use different principles in there functioning. Many factors, such as age of patient, accommodation, tear film break–up may cause the changes in wavefront map. Also higher order aberrations can be increased, by wearing soft or rigid contact lenses. Refractive and cataract surgery may induce large amount of higher order aberrations, which determine the cause the lower BCVA, than we can expect. This article describes different possible ways of correction higher order aberrations.
Современный мир предъявляет высокие требования к здоровью человека, и в первую очередь к зрению, так как основной объем информации поступает через зрительный анализатор. Для выполнения качественной и быстрой интеллектуальной работы специалист должен не только иметь хорошую остроту зрения, но удовлетворительную зрительную работоспособность, которая зависит от качества поступающего в головной мозг изображения.
Как и любой «неидеальной» оптической системе, человеческому глазу свойственны оптические дефекты – аберрации, которые снижают качество зрения, искажая изображение на сетчатке. Аберрация – это любое угловое отклонение узкого параллельного пучка света от точки идеального пересечения с сетчаткой в центре фовеолы при его прохождении через всю оптическую систему глаза [3].
В технической оптике качество оптической системы определяется аберрациями плоского или сферического фронта световой волны при прохождении через эту систему [5]. Так, глаз без аберраций имеет плоский волновой фронт и дает наиболее полноценное изображение на сетчатке точечного источника (так называемый «диск Эйри», размер которого зависит только от диаметра зрачка) [1]. Но в норме, даже при остроте зрения 100%, оптические дефекты преломляющих свет поверхностей глаза искажают ход лучей и формируют неправильный волновой фронт, в результате чего изображение на сетчатке получается более крупным и асимметричным.
 Такое искажение называется «функцией светорассеяния изображения точки» [1].
Такое искажение называется «функцией светорассеяния изображения точки» [1]. Количественной характеристикой оптического качества изображения является среднеквадратичное значение ошибок отклонения реального волнового фронта от идеального [5]. Zernike ввел математический формализм, использующий серии полиномов для описания аберраций волнового фронта [31]. Полиномы первого и второго, т. е. низших порядков, описывают привычные для офтальмологов оптические аберрации – дефокусировку (аметропии), астигматизм. Менее известны полиномы высших порядков: третий соответствует коме – это сферическая аберрация косых пучков света, падающих под углом к оптической оси глаза. В ее основе лежит асимметрия оптических элементов глаза, в результате которой центр роговицы не совпадает с центром хрусталика и фовеолы. К аберрациям четвертого порядка относится сферическая аберрация, которая в основном обусловлена тем, что периферия хрусталика преломляет падающие на нее параллельные лучи сильнее центра.

Кроме того, сама полихроматическая природа света обусловливает появление аберраций: лучи разной длины волны фокусируются на разном расстоянии от сетчатки (коротковолновые – ближе к роговице, чем длинноволновые). Такие аберрации называют хроматическими [3].
Оптическая система считается хорошей, если коэффициенты Цернике близки к нулю и, следовательно, среднеквадратичное значение ошибок волнового фронта меньше 1/14 длины волны (критерий Марешаля) [20]. При известных волновых аберрациях можно рассчитать коэффициент Штреля (соотношение между пиком интенсивности функции светорассеяния изображения точки определенного глаза и глаза без аберраций), который в определенных условиях хорошо коррелирует с остротой зрения [1]. Исходя из данных этого коэффициента можно прогнозировать остроту зрения, моделируя изображение любых оптотипов на сетчатке.
Вопрос разработки методов качественной и количественной оценки аберраций стоял перед офтальмологами давно.
 Еще в конце 19 века, в 1894 году, Tscherning разработал оригинальный метод, основанный на субъективном определении аберраций [23]. В дальнейшем он был доработан Howland в 1960 году, а в 1989 аберроскопом такого типа пользовался Ю.З. Розенблюм [3]. Но, к сожалению, такая аберрометрия носит только описательный характер, требует активного участия пациента и является весьма трудоемкой процедурой. С приходом в офтальмологию новых технологий появился широкий спектр точных объективных методов как качественного, так (и что особенно важно) количественного способа оценки аберраций глаза.
Еще в конце 19 века, в 1894 году, Tscherning разработал оригинальный метод, основанный на субъективном определении аберраций [23]. В дальнейшем он был доработан Howland в 1960 году, а в 1989 аберроскопом такого типа пользовался Ю.З. Розенблюм [3]. Но, к сожалению, такая аберрометрия носит только описательный характер, требует активного участия пациента и является весьма трудоемкой процедурой. С приходом в офтальмологию новых технологий появился широкий спектр точных объективных методов как качественного, так (и что особенно важно) количественного способа оценки аберраций глаза. Ретинальное изображение этой решетки регистрируется цифровой камерой и обрабатывается на компьютере [23]. При аберрометрии по отслеживанию луча (ray tracing aberrometry) используется прибор, разработанный В.В. и В.С. Молебными совместно с И. Паликарисом. На сетчатку проецируются два параллельных лазерных луча с длиной волны 650 нм и диаметром 0,3 мм, один из которых падает строго по зрительной оси и является опорным, а другой расположен на заданном расстоянии от него. Далее регистрируется степень отклонения второго луча от точки фиксации опорного луча, и таким образом последовательно анализируется каждая точка в пределах зрачка [22].
Ретинальное изображение этой решетки регистрируется цифровой камерой и обрабатывается на компьютере [23]. При аберрометрии по отслеживанию луча (ray tracing aberrometry) используется прибор, разработанный В.В. и В.С. Молебными совместно с И. Паликарисом. На сетчатку проецируются два параллельных лазерных луча с длиной волны 650 нм и диаметром 0,3 мм, один из которых падает строго по зрительной оси и является опорным, а другой расположен на заданном расстоянии от него. Далее регистрируется степень отклонения второго луча от точки фиксации опорного луча, и таким образом последовательно анализируется каждая точка в пределах зрачка [22]. Второй принцип – анализ вышедшего из глаза отраженного луча (outgoing refraction aberrometry) – впервые был описан Hartmann в 1900 году, позднее модифицирован R.V. Shack и B.C. Platt в 1971 году и применялся в астрономии для компенсации аберраций в телескопах при прохождении через атмосферу и космическое пространство. С помощью диодного лазера с длиной волны 850 нм в глаз направляется коллимированный пучок излучения, который, пройдя через все среды глаза, отражается от сетчатки с учетом аберраций и на выходе попадает на матрицу, состоящую из 1089 микролинз.
 Каждая микролинза собирает неаберрированные лучи в своей фокальной точке, а подверженные аберрации лучи фокусируются на некотором расстоянии от нее. Полученная информация обрабатывается компьютером и представляется в виде карты аберраций [28].
Каждая микролинза собирает неаберрированные лучи в своей фокальной точке, а подверженные аберрации лучи фокусируются на некотором расстоянии от нее. Полученная информация обрабатывается компьютером и представляется в виде карты аберраций [28].Третий принцип основан на компенсаторной юстировке падающего на фовеолу светового пучка. Основоположником его был русский физик М.И. Смирнов, который изобрел простейший метод измерения аберраций и опубликовал свою работу в 1961 году. В дальнейшем он был усовершенствован и в настоящее время применяется в качестве субъективного аберрометра, требующего активного участия пациента. В ходе исследования через вращающийся диск с отверстиями 1 мм, расположенный на одной оптической оси со зрачком, в глаз направляется пучок света. При вращении диска узкие параллельные пучки света проходят через каждую точку зрачка и при отсутствии аберраций проецируются на фовеолу, куда направлен другой луч с контрольной меткой в виде крестика. Если у пациента имеется аметропия или другие аберрации более высоких порядков, то он заметит несовпадение этих точек с крестиком и с помощью специального устройства должен будет их сопоставить.
 Угол, на который он смещает точку, отражает степень аберраций [10].
Угол, на который он смещает точку, отражает степень аберраций [10].Принцип классической скиаскопии реализован в виде сканирующего щелевого рефрактометра «OPD Scan», в котором через вращающееся колесо с щелью по оптической оси глаза проецируется инфракрасный пучок. Его отражение воспринимает фотодетектор и оценивает направление и скорость движения отраженного от сетчатки луча [18].
Разнообразие офтальмологических приборов, созданных с учетом новейших технологий и основанных на различных принципах действия, делает реальным не только качественную, но и количественную оценку аберрации низших и высших порядков, а также влияющих на них факторов.
Выявлено, что аберрации оптической системы глаза зависят от формы и прозрачности роговицы и хрусталика; локализации патологических изменений в сетчатке; прозрачности внутриглазной жидкости и стекловидного тела [3,4].
Известно, что увеличение диаметра зрачка вносит изменения в соотношение аберраций высших порядков.
 Если при диаметре зрачка равном 5,0 мм превалируют аберрации 3–го порядка, то при его увеличении до 8,0 мм возрастает доля аберраций 4–го порядка. Рассчитано, что критический размер зрачка, при котором аберрации высших порядков оказывают наименьшее влияние и отвечают критерию Марешаля, составляет 3,22 мм [5].
Если при диаметре зрачка равном 5,0 мм превалируют аберрации 3–го порядка, то при его увеличении до 8,0 мм возрастает доля аберраций 4–го порядка. Рассчитано, что критический размер зрачка, при котором аберрации высших порядков оказывают наименьшее влияние и отвечают критерию Марешаля, составляет 3,22 мм [5].Несомненно воздействие на карту аберраций аккомодации. Отмечено, что с возрастом аберрации увеличиваются, и в период от 30 до 60 лет аберрации высшего порядка удваиваются. Возможно, это связано с тем, что со временем эластичность и прозрачность хрусталика уменьшается, и он перестает компенсировать роговичные аберрации [6].
К факторам, влияющим на аберрации, относится и состояние слезной пленки. Авторами обнаружено, что при разрушении слезной пленки аберрации высших порядков увеличиваются в 1,44 раза [15].
Значительное место в использовании волнового фронта занимают исследования аберраций при кератоконусе. Отмечено значительное увеличение аберраций, особенно кома–подобных, которые превышали в 2,3 раза уровень сферических аберраций [8, 19].
 Метод волнового фронта дает возможность создания «индивидуальной оптики» – контактной линзы (КЛ) для коррекции кератоконуса. «Индивидуальная оптика» предназначена для коррекции аберраций высшего порядка. Алгоритм дизайна КЛ разрабатывается на основе данных волнового фронта и компьютерной топографии роговицы [21].
Метод волнового фронта дает возможность создания «индивидуальной оптики» – контактной линзы (КЛ) для коррекции кератоконуса. «Индивидуальная оптика» предназначена для коррекции аберраций высшего порядка. Алгоритм дизайна КЛ разрабатывается на основе данных волнового фронта и компьютерной топографии роговицы [21].Некоторые исследователи отмечают появление аберраций, индуцированных КЛ. Так, выявлено, что мягкие КЛ могут вызывать волновые монохроматические аберрации высокого порядка, тогда как жесткие КЛ значительно уменьшают аберрации 2–го порядка[14, 17]. Однако асферичность поверхности жестких КЛ может быть причиной сферических аберраций. Асферические КЛ могут вызывать большую нестабильность остроты зрения, чем сферические КЛ при одной и той же подвижности за счет индуцирования аберраций [7]. Мультифокальные КЛ могут индуцировать аберрации по типу комы и 5–го порядка [26].
Использование волнового фронта позволило разработать методы изготовления КЛ с целью максимальной нейтрализации аберраций глаза.
 Однако ротация и изменение положения линзы на роговице ограничивают возможности компенсации аберраций [ 16, 22, 29].
Однако ротация и изменение положения линзы на роговице ограничивают возможности компенсации аберраций [ 16, 22, 29]. Исследования аберраций индуцированных КЛ открыли возможность изготовления линз определенного дизайна, который позволяет снизить уровень суммарных остаточных аберраций глаза и повысить контрастную чувствительность [9, 12].
Несомненным является тот факт, что практически любое хирургические вмешательство индуцирует аберрации высших и низших порядков. Так, фоторефракционные операции увеличивают аберрации роговицы (в основном 3–го и 4–го порядка) и изменяют их соотношение, что может обусловливать низкое зрение после операции и появление жалоб у пациентов на ослепление и двоение изображения [25]. Выявлена строгая корреляция между зрительными симптомами и аберрациями: монокулярная диплопия возникает при горизонтальной коме, а глэр–эффект – при сферических аберрациях [11]. Проведенные исследования показывают, что при диаметре зрачка, превышающем 7,0 мм, Laser in situ keratomileusis (LASIK) индуцирует больше сферических аберраций, чем фоторефрактивная кератэктомия (ФРК).
 Вероятно, этим можно объяснить, что после проведенного LASIK описывается большее количество жалоб пациентов, связанных с ослеплением, чем после ФРК [24].
Вероятно, этим можно объяснить, что после проведенного LASIK описывается большее количество жалоб пациентов, связанных с ослеплением, чем после ФРК [24]. В настоящее время разработана методика проведения индивидуализированной абляции на основе аберрометрии, которая позволяет достичь так называемого «суперзрения», т.е. остроты зрения 1,5 и более. Множество факторов могут ограничивать возможности данной методики. Во–первых, это постоянные динамические изменения параметров глаза, зависящие от тонуса аккомодации, размера зрачка, изменения направления взгляда, которые нельзя полностью учесть при прогнозировании результатов операции. Во–вторых, имеются так называемые рецепторные и нейронные ограничения остроты зрения: плотность фоторецепторов сетчатки определяет минимальные размеры деталей, возможных для их различения. Следовательно, совершенствование оптических свойств глаза, позволяющих получить на сетчатке изображение с более мелкими деталями, не только не улучшит его качества, но может даже исказить реальную картину [1, 2].

После экстракции катаракты даже таким современным методом, как факоэмульсификация с имплантацией ИОЛ, также отмечается значительное увеличение высших аберраций высших (преимущественно 4–го) порядков [30]. Предпринята попытка разработки ИОЛ с отрицательными сферическими аберрациями, которые частично компенсируют положительные сферические аберрации роговицы. Авторами, в предварительных сообщениях, отмечено некоторое повышение контрастной чувствительности при имплантации таких линз [13, 27]. Это направление коррекции аберраций представляется весьма интересным, но требует дальнейшего изучения.
Таким образом, изучение аберраций человеческого глаза позволяет дать дополнительную оценку оптическому аппарату глаза, что расширяет возможности для более углубленной и полноценной диагностики, адекватной коррекции и эффективного лечения большинства офтальмологических заболеваний, сопровождающихся снижением корригированной остроты зрения, появлением астенопических жалоб.
Литература
1. Арталь П. «Суперзрение»: факты и вымыслы.// Вестник оптометрии. – 2002. – №4. – С.34–41.
Арталь П. «Суперзрение»: факты и вымыслы.// Вестник оптометрии. – 2002. – №4. – С.34–41.
2. Балашевич Л.И. Оптические аберрации глаза: диагностика и коррекция.// Окулист. – 2001. – №6(22). – С.12–15.
3. Балашевич Л.И. Рефракционная хирургия. – Санкт–Петербург, 2002. – С.285.
4. Корнюшина Т.А., Розенблюм Ю.З. Аберрации оптической системы глаза человека и их клиническое значение.// Вестник оптометрии. – 2002. – №3. – С.13–20.
5. Семчишен В., Мрохен М., Сайлер Т. Оптические аберрации человеческого глаза и их коррекция.// Рефракционная хирургия и офтальмология. – 2003. – Т.3.– №1. – С. 5–13.
6. Artal P. Understanding Aberrations by using Double–pass techniques.// J. Refract. Surg. – 2000.– Vol. 16. – No 5. – P. 560–562.
7. Atchison D.A. Aberrations associated with rigid contact lenses.// J. Opt. Soc.Am. A. – 1995.– vol.– 12.– №10.– Р. 2267–2273.
8. Barbero S., Marcos S., Merayo–Lloves J., Moreno–Barriuso E. Validation of the estimation of corneal aberration from videokeratography in keratokonus. // J. Refract. Surg. – 2002. – Vol. 18. – No 3. – P. 263–270.
// J. Refract. Surg. – 2002. – Vol. 18. – No 3. – P. 263–270.
9. Brabander J., Chaten N., Bouchard F. et al. Contrast sensivitivity soft contact lenses compensated for spherical aberration in high ametropia.// Optom. Vis. Sci.– 1998.– Vol.75.– №1.– Р.–43.
10. Burns S.A. The Spatially Resolved Refractometer.// J. Refract. Surg. – 2000.– Vol. 16. – No 5 – P. 566–569.
11. Chalita M.R., Waheed S., Xu M., Krueger R.R. Wavefront Analysis in Post–LASIK Eyes and its Correlation with Visual Symptoms, Refraction and Topography.// Invest Ophthalmol Vis Sci. – 2003. – №44(5). – P. 2651.
12. Dietze H.H., Cox VJ. On– and of– eye spherical aberration of soft contact lenses and consequent changes of effective lens power [In Process Citation]. // Optom. Vis. Sci.– 2003.– Vol. 80.– №2.– Р.126–134.
13. Holladay J.T., Piers P.A., Koranyi G., Mooren M., Norrby S. A new intraocular lens design to reduce spherical aberration of pseudopfakic eyes.// J. Refract. Surg. – 2002.– Vol. 18. – No 6. – P. 683–691.
Surg. – 2002.– Vol. 18. – No 6. – P. 683–691.
14. Hong X., Himebaugh N., Thibos LN. On – eye evaluation of optical performance of rigid and soft contact lenses. // Optom. Vis. Sci. –2001.– Vol. 78.–№12.– Р.872–880.
15. Koh S., Maeda N., Kuroda T., Hori Y., Watanabe H., Fujikado T., Tano Y., Hirohara Y., Mihashi T. Effect of tear film break–up on higher–order aberrations measured with wavefront sensor.// Am J Ophthalmol. – 2002. – №134. – P. 115–117.
16. Lopez – Gil N., Castejon – Mochon JF.,Benito A. at al. Aberration generation by contact lenses with aspheric and asymmetric surfaces. // J.Refract. Surg.–2002.– Vol.–18.– №5.– Р. 603–609.
17. Lu F,.Mao X.,Qu J., еt al. Monochromatic wavefront aberration in the human eye with contact lenses.// Optom.Vis. Sci. –2003.– Vol.–80.–№2.– Р.135–141
18. MacRae S., Fujieda M. Slit Skiascopic–guided Ablation Using the Nidek Laser.// J. Refract. Surg. – 2000.– Vol. 16. – No 5. – P. 576–580.
19. Maeda N., Fujikado T., Kuroda T., et al. Wavefront aberrations measured with Hartmann–Shack sensor in patients with keratoconus.// Ophthalmology.– 2002.– Vol.109.– №11.– Р. 1996–2003.
Maeda N., Fujikado T., Kuroda T., et al. Wavefront aberrations measured with Hartmann–Shack sensor in patients with keratoconus.// Ophthalmology.– 2002.– Vol.109.– №11.– Р. 1996–2003.
20. Marechal A. Etude des effect combines de la diffraction et des aberrations geometriques sur L’image d’un point lumineux.// Revue d’optique. – 1947. – P. 257–277.
21. Marsack J., Milner T., Rylander G.,et al. Applying wavefront sensors and corneal topography to keratoconus. // Biomed. Sci. Instrum.– 2002.– Vol.38.– Р. 471–476.
22. Molebny V.V., Panagopoulou S.I., Molebny S.V., Wakil Y.S., Pallikaris I.G. Principles of Ray Tracing Aberrometry.// J. Refract. Surg. – 2000.– Vol. 16. – No 5. – P. 572–575.
23. Mrochen M., Kaemmerer M., Mierdel P., Krinke H.E., Seiler T. Principles of Tscherning Aberrometry.// J. Refract. Surg. – 2000.– Vol. 16. – No 5. – P. 570–571.
24. Oshika T., Klyce S.D., Applegate R.A., Howland H.C., Danasoury M.A. Comparision of corneal wavefront aberrations after photorefractive keratectomy and laser in situ keratomileusis. // Am J Ophthalmol. – Vol. 127. – №1. – P. 1–7.
// Am J Ophthalmol. – Vol. 127. – №1. – P. 1–7.
25. Oshika T., Miyata K., Tokunaga T., Samejima T., Amano S., Tanaka S., Hirohara Y., Mihashi T., Maeda N., Fujikado T. Higher order wavefront aberrations of cornea and magnitude of refractive correction in laser in situ keratomileusis.// Ophthalmology. – 2002. – Vol. 109. – №6. – P. 1154–1158.
26. Patel S., Fakhry M., Alio JL. Objective assessment of aberrations induced by multifocal contact lenses in vivo.// CLAO J.– 2002 – Vol. 28.– №4.– Р. 196–201.
27. Piers P.A., Mester U., Anterist N., Dillinger P., Norrby S. How wavefront–based IOL designs affect pseudophakic visual quality.// Invest Ophthalmol Vis Sci. – 2002. – Vol. 43. – №12.– P. 2022.
28. Thibos L.N. Principles of Hartmann–Shack Aberrometry.// J. Refract. Surg. – 2000.– Vol. 16. – No 5. – P. 563–565.
29. Williams D., Yoon GY., Porter J.,et al. Visual benefit of correcting higher order aberrations of the eye.// J. Refract. Surg.– 2000. – Vol.– 16.– № 5.– Р. 554–559.
– Vol.– 16.– № 5.– Р. 554–559.
30. Xiong Y., Lu Y., Qu X., Xue F., Chu R., He J.C. Investigation of wavefront aberrations for patients with cataract surgery.// Invest Ophthalmol Vis Sci. – 2002. – Vol. 43. – №12.– P. 387.
31. Zernike F. Beugungstheorie des Schneidenverfahrens und seiner verbesserten Form der Phasenkontrastmethode.// Physica I. – 1934. – №2. – Р. 689–704.
Сферическую аберрацию можно исправить. Сферическая аберрация. Устранение сферической абберации
→ Аберрация в астрономииСловом аберрация обозначают множество оптических эффектов связанных с искажением объекта при наблюдении. В этой статье мы расскажет о нескольких видах аберрации, наиболее актуальных для астрономических наблюдений.
Аберрация света в астрономии это кажущееся смещение небесного объекта вследствие конечной скорости распространения света в сочетании с движением наблюдаемого объекта и наблюдателя. Действие аберрации приводит к тому, что видимое направление на объект не совпадает с геометрическим направлением на него в тот же момент времени.
Эффект состоит в том, что вследствие движения Земли вокруг Солнца и времени, необходимого для распространения света, наблюдатель видит звезду не в том месте, где она находится. Если бы Земля была неподвижна, или если бы свет распространялся мгновенно, то световой аберрации не было бы. Поэтому, определяя положение звезды на небе посредством телескопа, мы должны отсчитать не тот угол, под которым наклонена звезда, а несколько увеличив его в сторону движения Земли.
Эффект аберрации не велик. Наибольшая его величина достигается при условии движения земли перпендикулярного направлению луча. При этом отклонение положения звезды составляет всего 20,4 секунды, потому что земля в 1 секунду времени проходит только 30км, а луч света— 300 000км.
Существует также несколько видов геометрической аберрации . Сферическая аберрация — аберрация линзы или объектива, заключающаяся в том, что широкий пучок монохроматического света, исходящий из точки, лежащей на главной оптической оси линзы, при прохождении через линзу пересекается не в одной, а во многих точках, расположенных на оптической оси на разном удалении от линзы, вследствие чего изображение получается нерезким. В результате такой точечный объект как звезду можно видеть как небольшой шарик, принимая размер этого шарика за размеры звезды.
В результате такой точечный объект как звезду можно видеть как небольшой шарик, принимая размер этого шарика за размеры звезды.
Кривизна поля изображения — аберрация, в результате которой изображение плоского объекта, перпендикулярного к оптической оси объектива, лежит на поверхности, вогнутой либо выпуклой к объективу. Эта аберрация вызывает неравномерную резкость по полю изображения. Поэтому, когда центральная часть изображения сфокусирована резко, то его края будут лежать не в фокусе и изображение нерезко. Если установку на резкость производить по краям изображения, то его центральная часть будет нерезкой. Этот вид аберрации не существенен для астрономии.
А вот и еще несколько видов аберрации:
Дифракциoнная аберрация возникает вследствие дифракции света на диафрагме и оправе фотообъектива. Дифракционная аберрация ограничивает разрешающую способность фотообъектива. Из-за этой аберрации минимальное угловое расстояние между точками, разрешаемое объективом, ограничено величиной лямда/D радиан, где ламда — длина волны используемого света (к оптическому диапазону обычно относят электромагнитные волны с длиной от 400 нм до 700 нм), D — диаметр объектива. Глядя на эту формулу становится понятным, на сколько важен диаметр объектива. Именно этот параметр является ключевым для самых больших и самых дорогих телескопов. Также ясно, что телескоп способный видеть в рентгеновских лучах выгодно отличается от обычного оптического телескопа. Дело в том, что длинна волны рентгеновских лучей в 100 раз меньше длинны волны света в оптическом диапазоне. Следовательно для таких телескопов минимально различимое угловое расстояние в 100 раз меньше чем для обычных оптических телескопов с тем же диаметром объектива.
Глядя на эту формулу становится понятным, на сколько важен диаметр объектива. Именно этот параметр является ключевым для самых больших и самых дорогих телескопов. Также ясно, что телескоп способный видеть в рентгеновских лучах выгодно отличается от обычного оптического телескопа. Дело в том, что длинна волны рентгеновских лучей в 100 раз меньше длинны волны света в оптическом диапазоне. Следовательно для таких телескопов минимально различимое угловое расстояние в 100 раз меньше чем для обычных оптических телескопов с тем же диаметром объектива.
Изучение аберрации позволило существенно усовершенствовать астрономические приборы. В современных телескопах эффекты аберрации сведены в минимуму, однако именно аберрация ограничивает возможности оптических приборов.
1. Введение в теорию аберраций
Когда речь идет о характеристиках объектива, очень часто приходится слышать слово аберрации . «Это отличный объектив, в нем практически исправлены все аберрации!», — тезис, который очень часто можно встретить в обсуждениях или обзорах. Гораздо реже можно услышать и диаметрально противоположное мнение, к примеру: «Это замечательный объектив, его остаточные аберрации хорошо выражены и формируют необыкновенно пластичный и красивый рисунок»…
Гораздо реже можно услышать и диаметрально противоположное мнение, к примеру: «Это замечательный объектив, его остаточные аберрации хорошо выражены и формируют необыкновенно пластичный и красивый рисунок»…
Почему же возникают такие разные мнения? Я попробую дать ответ на этот вопрос: насколько это явление действительно хорошо/плохо для объективов и для жанров фотографии в целом. Но для начала, давайте попробуем разобраться, что, же такое аберрации фотографического объектива. Начнем мы с теории и некоторых определений.
В общем применении термин Аберрация (лат. ab- «от» + лат. errare «блуждать, заблуждаться») — это отклонение от нормы, ошибка, некое нарушение нормальной работы системы.
Аберрация объектива — ошибка, или погрешность изображения в оптической системе. Она вызвана тем, что в реальной среде может возникать существенное отклонение лучей от того направления, по которому они идут в расчетной «идеальной» оптической системе.
В итоге страдает общепринятое качество фотографического изображения: недостаточная резкость в центре, потеря контраста, сильная нерезкость по краям, искривление геометрии и пространства, цветные ореолы и т. п.
п.
Основные аберрации, характерные для фотографических объективов, следующие:
- Коматическая аберрация.
- Дисторсия.
- Астигматизм.
- Кривизна поля изображения.
Перед тем как познакомиться поближе с каждой из них, давайте вспомним из статьи , как происходит прохождение через линзу лучей в идеальной оптической системе:
Илл. 1. Прохождение лучей в идеальной оптической системе.
Как мы видим, все лучим при этом собираются в одной точке F — главном фокусе. Но в реальности, все обстоит намного сложнее. Сущность оптических аберраций в том, что лучи, падающие на линзу из одной светящейся точки, не собираются тоже в одной точке. Итак, давайте посмотрим, какие отклонения происходят в оптической системе при воздействии различных аберраций.
Тут еще надо сразу отметить, что и в простой линзе и в сложном объективе все далее описываемые аберрации действуют совместно.
Действие сферической аберрации состоит в том, что лучи, падающие на края линзы, собираются ближе к линзе, чем лучи, падающие на центральную часть линзы. Вследствие этого, изображение точки на плоскости получается в виде размытого кружка или диска.
Вследствие этого, изображение точки на плоскости получается в виде размытого кружка или диска.
Илл. 2. Сферическая аберрация.
В фотографиях действие сферической аберрации проявляется в виде смягченного изображения. Особенно часто эффект заметен на открытых диафрагмах, причем объективы с большей светосилой больше подвержены этой аберрации. Если при этом сохраняется и резкость контуров, такой софт-эффект может быть весьма полезным для некоторых видов съемки, например, портретной.
Илл.3. Софт-эффект на открытой диафрагме обусловленный действием сферической аберрации.
В объективах построенных полностью из сферических линз практически невозможно полностью устранить этот вид аберраций. В сверхсветосильных объективах единственный эффективный способ ее существенной компенсации — использование асферических элементов в оптической схеме.
3. Коматическая аберрация, или «Кома»
Это частный вид сферической аберрации для боковых лучей. Действие ее заключается в том, что лучи, приходящие под углом к оптической оси не собираются в одной точке. При этом изображение светящейся точки на краях кадра получается в виде «летящей кометы», а не в форме точки. Кома также может привести к засвечиванию участков изображения в зоне нерезкости.
Действие ее заключается в том, что лучи, приходящие под углом к оптической оси не собираются в одной точке. При этом изображение светящейся точки на краях кадра получается в виде «летящей кометы», а не в форме точки. Кома также может привести к засвечиванию участков изображения в зоне нерезкости.
Илл. 4. Кома.
Илл. 5. Кома на фотоизображении
Является прямым следствием дисперсии света. Суть ее состоит в том, что луч белого света, проходя через линзу, разлагается на составляющие его цветные лучи. Коротковолновые лучи (синие, фиолетовые) преломляются в линзе сильнее и сходятся ближе к ней, чем длиннофокусные (оранжевые, красные).
Илл. 6. Хроматическая аберрация. Ф — фокус фиолетовых лучей. К — фокус красных лучей.
Здесь, как и в случае сферической аберрации, изображение светящейся точки на плоскости, получается в виде размытого кружка/диска.
На фотографиях хроматическая аберрация проявляется в виде посторонних оттенков и цветных контуров у объектов съемки. Особенно заметно влияние аберрации в контрастных сюжетах. В настоящее время ХА достаточно легко исправляется в RAW-конверторах, если съемка велась в RAW-формате.
Особенно заметно влияние аберрации в контрастных сюжетах. В настоящее время ХА достаточно легко исправляется в RAW-конверторах, если съемка велась в RAW-формате.
Илл. 7. Пример проявления хроматической аберрации.
5. Дисторсия
Дисторсия проявляется в искривлении и искажении геометрии фотоснимка. Т.е. масштаб изображения меняется с удалением от центра поля к краям, вследствие чего прямые линии искривляются к центру или к краям.
Различают бочкообразную или отрицательную (наиболее характерна для широкого угла) и подушкообразную или положительную дисторсию (чаще проявляется на длинном фокусе).
Илл. 8. Подушкообразная и бочкообразная дисторсия
Дисторсия намного сильнее обычно выражена у объективов с переменным фокусным расстоянием (зумы), чем у объективов с постоянным фокусным (фиксы). У некоторых эффектных объективов, например Fish Eye (Рыбий глаз), намеренно не исправляется и даже подчеркивается дисторсия.
Илл. 9. Ярко-выраженная бочкообразная дисторсия объектива Zenitar 16 mm FishEye.
В современных объективах, в том числе с переменным фокусным расстоянием, дисторсия достаточно эффективно корректируется введением в оптическую схему асферической линзы (или нескольких линз).
6. Астигматизм
Астигматизм (от греч. Stigma — точка) характеризуется в невозможности получить на краях поля изображения светящейся точки и в виде точки и даже в виде диска. При этом светящаяся точка, находящаяся на главной оптической оси, передается как точка, но если точка вне этой оси — как затемнение, скрещенные линии и т.д.
Это явление чаще всего наблюдается по краям изображения.
Илл. 10. Проявление астигматизма
7. Кривизна поля изображения
Кривизна поля изображения — это аберрация, в результате которой изображение плоского объекта, перпендикулярного к оптической оси объектива, лежит на поверхности, вогнутой либо выпуклой к объективу.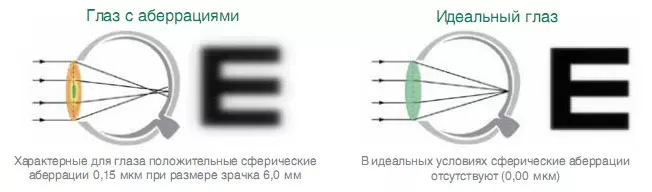 Эта аберрация вызывает неравномерную резкость по полю изображения. Когда центральная часть изображения фокусирована резко, то его края будут лежать не в фокусе, и изобразятся не резко. Если установку на резкость производить по краям изображения, то его центральная часть будет нерезкой.
Эта аберрация вызывает неравномерную резкость по полю изображения. Когда центральная часть изображения фокусирована резко, то его края будут лежать не в фокусе, и изобразятся не резко. Если установку на резкость производить по краям изображения, то его центральная часть будет нерезкой.
Рис.1 Иллюстрация недоисправленных сферической аберрации. Поверхрность на периферии линзы имеет фокусное расстояние короче, чем в центре.
Большинство фотографических объективов состоят из элементов со сферическими поверхностями. Такие элементы относительно легко изготовить, но их форма неидеальна для формирования изображения.
Сферическая аберрация — это один из дефектов при формировании изображения, возникающий из-за сферической формы линзы. Рис. 1 иллюстрирует сферическую аберрацию для положительной линзы.
Лучи, которые проходят сквозь линзу дальше от оптической оси, сфокусированы в позиции с . Лучи, которые проходят ближе к оптической оси, сфокусированы в позиции a , они находятся ближе к поверхности линзы. Таким образом положение фокуса зависит от места, в котором проходят лучи сквозь линзу.
Таким образом положение фокуса зависит от места, в котором проходят лучи сквозь линзу.
Если краевой фокус ближе к линзе, чем осевой фокус, как происходит с положительной линзой Рис. 1, тогда говорят, что сферическая аберрация недоисправленная . И наоборот, если краевой фокус находится за осевым фокусом, то говорят, что сферическая аберрация переисправленная .
Изображение точки, сделанное объективом со сферическими аберрациями обычно получаются точками, окруженными ореолом света. Сферическая аберрация обычно проявляются на фотографиях смягчением контраста и размытием мелких деталей.
Сферическая аберрация однородна по полю, это значит, что продольный фокус между краями линзы и центром не зависит от наклона лучей.
Из Рис.1 кажется, что на линзе со сферической аберрацией невозможно добиться хорошей резкости. В любом положении сзади линзы на светочувствительном элементе (пленка или матрица) вместо четкой точки будет проецироваться диск размытия.
Тем не менее, существует геометрически «лучший» фокус, который соответствует диску наименьшего размытия. Это своеродный ансамбль световых конусов имеет минимальное сечение, в положении b .
Это своеродный ансамбль световых конусов имеет минимальное сечение, в положении b .
Смещение фокуса (Focus shift)
Когда диафрагма находится за линзой, наблюдается интересное явление. Если диафрагма прикрыта таким образом, что срезает лучи на периферии линзы, то фокус сдвигается вправо. При сильно прикрытой диафрагме наилучший фокус будет наблюдаться в положении c , то есть положения дисков наименьшего размытия при прикрытой диафрагме и при открытой диафрагме будут различаться.
Чтобы получить наилучшую резкость на прикрытой диафрагме, матрица (пленка) должна размещаться в положении c . Этот пример четко показывает, что существует вероятность того, что наилучшая резкость не будет достигнута, поскольку большинство фотографических систем рассчитываются на работу с открытой диафрагмой.
Фотограф фокусируется при полностью открытой диафрагме, и проецирует на матрицу диск наименьшего размытия в позиции b , затем при съемке диафрагма автоматически закрывается до установленного значения, и он ничего не подозревает о последующем в этот момент сдвиге фокуса , что не позволяет ему добиться наилучшей резкости.
Конечно, прикрытая диафрагма уменьшает сферические аберрации также и в точке b , но все же в ней будет не наилучшая резкость.
Пользователи зеркальных фотоаппаратов могут закрыть диафрагму для предварительного просмотра , чтобы сфокусироваться при реальной диафрагме.
Автоматическую компенсацию смещения фокуса предложил Норман Гольдберг. Фирма Zeiss запустила линию дальномерных объективов для фотоаппаратов Zeiss Ikon, которые имеют специально разработанную схему для минимизации смещения фокуса с изменением значений диафрагмы. При этом сферические аберрации у объективов для дальномерных фотоаппаратов существенно снижаются. Вы спросите насколько смещение фокуса существенно для объективов дальномерных фотоаппаратов? По заявлению производителя объектива LEICA NOCTILUX-M 50mm f/1, это значение порядка 100 мкм.
Характер размытия вне зоны фокуса
Влияние сферических аберраций на изображение в фокусе трудно различить, но их можно четко увидеть в изображении, которое находится в легком расфокусе. Сферическая аберрация оставляет видимый след в зоне нерезкости.
Сферическая аберрация оставляет видимый след в зоне нерезкости.
Возвращаясь к Рис.1 можно отметить, что распределение интенсивности света в диске размытия при наличии сферической аберрации не является равномерным.
В положении c диск размытия характеризуется яркой сердцевиной, окруженной слабым ореолом. В то время как диск размытия в положении a имеет более темную сердцевину, окруженную ярким кольцом света. Такие аномальные распределения света могут проявляться в зоне нерезкости изображения.
Рис. 2 Изменения размытия перед и за точкой в фокусе
Пример на Рис. 2 показывает точку в центре кадра, снятую в режиме макро 1:1 объективом 85/1.4, установленным на макромех. Когда матрица находится на 5 мм сзади наилучшего фокуса (точка посредине), диск размытия показывает эффект яркого кольца (левое пятно), подобные диски размытия получаются у зеркально-менисковых объективов.
А когда матрица находится на 5 мм впереди наилучшего фокуса, (т. е. ближе к объективу), характер размытия изменился в сторону яркого центра, окуженного слабым ореолом. Как видно, у объектива переисправлена сферическая аберрация, поскольку он ведет себя противоположно примеру на Рис. 1.
е. ближе к объективу), характер размытия изменился в сторону яркого центра, окуженного слабым ореолом. Как видно, у объектива переисправлена сферическая аберрация, поскольку он ведет себя противоположно примеру на Рис. 1.
Следующий пример иллюстрирует действие двух аберраций, на изображениях вне фокуса.
На Рис. 3 изображен крестик, который сфотографирован по центру кадра, тем же объективом 85/1.4. Макромех вытянут примерно на 85 мм, что дает увеличение примерно 1:1. Фотоаппарат (матрица) перемещался с шагом 1 мм в обе стороны от максимального фокуса. Крестик является более сложным изображением чем точка, а показатели цвета дают наглядные иллюстрации его размытий.
Рис. 3 Цифры на иллюстрациях указывают на изменения дистанции от объектива до матрицы, это миллиметры. камера двигается от -4 до +4 мм с шагом 1 мм от положения наилучшего фокуса (0)
Сферическая аберрация отвечает за жесткий характер размытия при отрицательных расстояниях и за переход к мягкому размытию при положительных. Также интерес представляют цветовые эффекты, которые возникают из-за продольной хроматической аберрации (осевой цвет). Если объектив плохо собран, то сферическая аберрация и осевой цвет это единственные аберрации, которые проявляются в центре изображения.
Также интерес представляют цветовые эффекты, которые возникают из-за продольной хроматической аберрации (осевой цвет). Если объектив плохо собран, то сферическая аберрация и осевой цвет это единственные аберрации, которые проявляются в центре изображения.
Чаще всего сила а иногда и характер сферической аберрации зависит от длинны волны света. В таком случае совместное воздействие сферической аберрации и осевого цвета называется . Из этого становится ясно, что явление, проиллюстрированное на Рис. 3 показывает, что данный объектив не предназначен для использовании в качестве макрообъектива. Большинство объективов оптимизированы для использования в ближнем поле фокусировки а также для фокусировки на бесконечность, но не для макро 1:1. При таком приближении обычные объективы будут вести себя хуже чем макрообъективы, которые используются специально на ближних дистанциях.
Тем не менее, даже если объектив используется для стандартного применения, сферохроматизм может проявляться в зоне нерезкости при обыкновенной съемке и влиять на качество .
Выводы
Конечно, иллюстрация на Рис. 1 является преувеличением. В реальности количество остаточных сферических аберраций в фотографических объективах мало. Этот эффект значительно уменьшен благодаря комбинированию элементов объектива в следствии чего компенсируются суммы противоположных сферических аберраций, использованию высококачественного стекла, тщательно продуманной геометрией линз и использованием асферических элементов. Кроме того, могут быть использованы плавающие элементы для уменьшения сферических аберраций в определенном диапазоне рабочих расстояний.
В случае объективов, с недоисправленой сферической аберрацией эффективный способ улучшить качество изображения это прикрыть диафрагму. Для недоисправленного элемента на Рис. 1 диаметр дисков размытия уменьшается пропорционально кубу диаметра диафрагмы.
Эта зависимость может отличаться для остаточных сферических аберраций в сложных схемах объективов, но, как правило закрытие диафрагмы на одну ступень уже дает заметное улучшение изображения.
Альтернативно, вместо того, чтобы бороться со сферической аберрацией, фотограф может намеренно ее использовать. Смягчающие фильтры Zeiss, несмотря на плоскую поверхность добавляют в изображение сферические аберрации. Они популярны среди фотографов-портретистов для получения софт-эффекта и импрессивного характера изображения.
© Paul van Walree 2004–2015
Перевод: Иван Косареков
Из всех видов аберраций сферическая аберрация является наиболее существенной и в большинстве случаев единственной практически значимой для оптической системы глаза. Поскольку нормальный глаз всегда фиксирует взгляд на наиболее важном в данный момент объекте, то аберрации, обусловленные косым падением световых лучей (кома, астигматизм) при этом устраняются. Устранить таким способом сферическую аберрацию невозможно. Если преломляющие поверхности оптической системы глаза имеют сферическую форму, устранить сферическую аберрацию невозможно вообще никаким способом. Ее искажающее влияние уменьшается при уменьшении диаметра зрачка, поэтому при ярком освещении разрешающая способность глаза выше, чем при слабом освещении, когда диаметр зрачка увеличивается и размер пятна, представляющего собой изображение точечного источника света, тоже увеличивается из-за сферической аберрации. Эффективно воздействовать на сферическую аберрацию оптической системы глаза можно лишь одним способом — менять форму преломляющей поверхности. Такая возможность имеется в принципе при хирургической коррекции кривизны роговицы и при замене естественного хрусталика, потерявшего свои оптические свойства, например, из-за катаракты, искусственным. Искусственный хрусталик может иметь преломляющие поверхности любой доступной для современных технологий формы. Исследование влияния формы преломляющих поверхностей на сферическую аберрацию наиболее эффективно и точно может быть выполнено с помощью компьютерного моделирования. Здесь рассматривается достаточно простой алгоритм компьютерного моделирования, позволяющий выполнить такое исследование, а также основные результаты, полученные с помощью этого алгоритма.
Эффективно воздействовать на сферическую аберрацию оптической системы глаза можно лишь одним способом — менять форму преломляющей поверхности. Такая возможность имеется в принципе при хирургической коррекции кривизны роговицы и при замене естественного хрусталика, потерявшего свои оптические свойства, например, из-за катаракты, искусственным. Искусственный хрусталик может иметь преломляющие поверхности любой доступной для современных технологий формы. Исследование влияния формы преломляющих поверхностей на сферическую аберрацию наиболее эффективно и точно может быть выполнено с помощью компьютерного моделирования. Здесь рассматривается достаточно простой алгоритм компьютерного моделирования, позволяющий выполнить такое исследование, а также основные результаты, полученные с помощью этого алгоритма.
Наиболее просто выполняется расчет прохождения светового луча через одиночную сферическую преломляющую поверхность, разделяющую две прозрачные среды с различными показателями преломления. Для демонстрации явления сферической аберрации достаточно выполнить такой расчет в двумерном приближении. Луч света располагается в главной плоскости и направляется на преломляющую поверхность параллельно главной оптической оси. Ход этого луча после преломления может быть описан с помощью уравнения окружности, закона преломления и очевидных геометрических и тригонометрических соотношений. В результате решения соответствующей системы уравнений может быть получено выражение для координаты точки пересечения этого луча с главной оптической осью, т.е. координаты фокуса преломляющей поверхности. Это выражение содержит параметры поверхности (радиус), показатели преломления и расстояние между главной оптической осью и точкой падения луча на поверхность. Зависимость координаты фокуса от расстояния между оптической осью и точкой падения луча и есть сферическая аберрация. Эту зависимость легко рассчитать и изобразить графически. Для одиночной сферической поверхности, отклоняющей лучи по направлению к главной оптической оси, координата фокуса всегда уменьшается при увеличении расстояния между оптической осью и падающим лучом.
Для демонстрации явления сферической аберрации достаточно выполнить такой расчет в двумерном приближении. Луч света располагается в главной плоскости и направляется на преломляющую поверхность параллельно главной оптической оси. Ход этого луча после преломления может быть описан с помощью уравнения окружности, закона преломления и очевидных геометрических и тригонометрических соотношений. В результате решения соответствующей системы уравнений может быть получено выражение для координаты точки пересечения этого луча с главной оптической осью, т.е. координаты фокуса преломляющей поверхности. Это выражение содержит параметры поверхности (радиус), показатели преломления и расстояние между главной оптической осью и точкой падения луча на поверхность. Зависимость координаты фокуса от расстояния между оптической осью и точкой падения луча и есть сферическая аберрация. Эту зависимость легко рассчитать и изобразить графически. Для одиночной сферической поверхности, отклоняющей лучи по направлению к главной оптической оси, координата фокуса всегда уменьшается при увеличении расстояния между оптической осью и падающим лучом.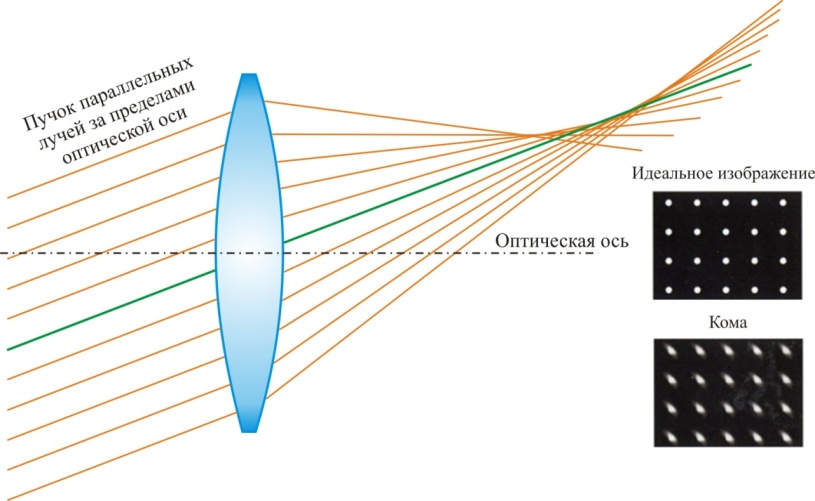 Чем дальше от оси падает луч на преломляющую поверхность, тем ближе к этой поверхности он пересекает ось после преломления. Это положительная сферическая аберрация. В результате лучи, падающие на поверхность параллельно главной оптической оси, не собираются в одной точке в плоскости изображения, а образуют пятно рассеяния конечного диаметра в этой плоскости, что приводит к снижению контраста изображения, т.е. к ухудшению его качества. В одной точке пересекаются только те лучи, которые падают на поверхность очень близко к главной оптической оси (параксиальные лучи).
Чем дальше от оси падает луч на преломляющую поверхность, тем ближе к этой поверхности он пересекает ось после преломления. Это положительная сферическая аберрация. В результате лучи, падающие на поверхность параллельно главной оптической оси, не собираются в одной точке в плоскости изображения, а образуют пятно рассеяния конечного диаметра в этой плоскости, что приводит к снижению контраста изображения, т.е. к ухудшению его качества. В одной точке пересекаются только те лучи, которые падают на поверхность очень близко к главной оптической оси (параксиальные лучи).
Если на пути луча поместить собирательную линзу, образованную двумя сферическими поверхностями, то с помощью расчетов, описанных выше, можно показать, что такая линза также обладает положительной сферической аберрацией, т.е. лучи, падающие параллельно главной оптической оси дальше от нее, пересекают эту ось ближе к линзе, чем лучи, идущие ближе к оси. Сферическая аберрация практически отсутствует также только для параксиальных лучей. Если обе поверхности линзы выпуклые (как у хрусталика), то сферическая аберрация больше, чем в случае, когда вторая преломляющая поверхность линзы является вогнутой (как у роговицы).
Если обе поверхности линзы выпуклые (как у хрусталика), то сферическая аберрация больше, чем в случае, когда вторая преломляющая поверхность линзы является вогнутой (как у роговицы).
Положительная сферическая аберрация обусловлена избыточной кривизной преломляющей поверхности. По мере удаления от оптической оси угол между касательной к поверхности и перпендикуляром к оптической оси увеличивается быстрее, чем это необходимо для того, чтобы направлять преломленный луч в параксиальный фокус. Для уменьшения этого эффекта необходимо замедлить отклонение касательной к поверхности от перпендикуляра к оси по мере удаления от нее. Для этого кривизна поверхности должна уменьшаться по мере удаления от оптической оси, т.е. поверхность не должна быть сферической, у которой кривизна во всех ее точках одинакова. Иными словами, уменьшение сферической аберрации может быть достигнуто только с помощью применения линз с асферическими преломляющими поверхностями. Это могут быть, например, поверхности эллипсоида, параболоида и гиперболоида. В принципе возможно использование и других форм поверхности. Привлекательность эллиптической, параболической и гиперболической форм лишь в том, что они, как и сферическая поверхность, описываются достаточно простыми аналитическими формулами и сферическая аберрация линз с этими поверхностями может быть достаточно легко исследована теоретически с помощью описанного выше приема.
В принципе возможно использование и других форм поверхности. Привлекательность эллиптической, параболической и гиперболической форм лишь в том, что они, как и сферическая поверхность, описываются достаточно простыми аналитическими формулами и сферическая аберрация линз с этими поверхностями может быть достаточно легко исследована теоретически с помощью описанного выше приема.
Всегда имеется возможность подобрать параметры сферической, эллиптической, параболической и гиперболической поверхностей таким образом, чтобы их кривизна в центре линзы была одинаковой. В этом случае для параксиальных лучей такие линзы будут неотличимы друг от друга, положение параксиального фокуса будет одинаковым для этих линз. Но по мере удаления от главной оси поверхности этих линз будут отклоняться от перпендикуляра к оси по-разному. Быстрее всего будет отклоняться сферическая поверхность, медленнее — эллиптическая, еще медленнее — параболическая и медленнее всех (из этих четырех) — гиперболическая. В такой же последовательности будет все заметнее уменьшаться и сферическая аберрация указанных линз. Для гиперболической линзы сферическая аберрация может даже сменить знак — стать отрицательной, т.е. лучи, падающие на линзу дальше от оптической оси, будут пересекать ее дальше от линзы, чем лучи, падающие на линзу ближе к оптической оси. Для гиперболической линзы можно даже подобрать такие параметры преломляющих поверхностей, которые будут обеспечивать полное отсутствие сферической аберрации — все лучи, падающие на линзу параллельно главной оптической оси на любом расстоянии от нее, после преломления будут собираться в одной точке на оси — идеальная линза. Для этого первая преломляющая поверхность должна быть плоской, а вторая — выпуклой гиперболической, параметры которой и показатели преломления должны быть связаны определенными соотношениями.
Для гиперболической линзы сферическая аберрация может даже сменить знак — стать отрицательной, т.е. лучи, падающие на линзу дальше от оптической оси, будут пересекать ее дальше от линзы, чем лучи, падающие на линзу ближе к оптической оси. Для гиперболической линзы можно даже подобрать такие параметры преломляющих поверхностей, которые будут обеспечивать полное отсутствие сферической аберрации — все лучи, падающие на линзу параллельно главной оптической оси на любом расстоянии от нее, после преломления будут собираться в одной точке на оси — идеальная линза. Для этого первая преломляющая поверхность должна быть плоской, а вторая — выпуклой гиперболической, параметры которой и показатели преломления должны быть связаны определенными соотношениями.
Таким образом, применением линз с асферическими поверхностями сферическая аберрация может быть существенно уменьшена и даже полностью устранена. Возможность раздельного воздействия на преломляющую силу (положение параксиального фокуса) и сферическую аберрацию обусловлена наличием у асферических поверхностей вращения двух геометрических параметров, двух полуосей, подбором которых можно обеспечивать уменьшение сферической аберрации без изменения преломляющей силы. У сферической поверхности нет такой возможности, у нее только один параметр — радиус и изменением этого параметра изменить сферическую аберрацию без изменения преломляющей силы невозможно. Для параболоида вращения тоже такой возможности нет, так как у параболоида вращения тоже только один параметр — фокальный параметр. Таким образом, из трех упомянутых асферических поверхностей только две пригодны для управляемого независимого воздействия на сферическую аберрацию — гиперболическая и эллиптическая.
У сферической поверхности нет такой возможности, у нее только один параметр — радиус и изменением этого параметра изменить сферическую аберрацию без изменения преломляющей силы невозможно. Для параболоида вращения тоже такой возможности нет, так как у параболоида вращения тоже только один параметр — фокальный параметр. Таким образом, из трех упомянутых асферических поверхностей только две пригодны для управляемого независимого воздействия на сферическую аберрацию — гиперболическая и эллиптическая.
Подобрать одиночную линзу с параметрами, обеспечивающими приемлемую сферическую аберрацию, несложно. Но будет ли такая линза обеспечивать требуемое уменьшение сферической аберрации в составе оптической системы глаза? Для ответа на этот вопрос необходимо рассчитать прохождение световых лучей через две линзы — роговицу и хрусталик. Результатом такого расчета будет, как и раньше, график зависимости координаты точки пересечения луча с главной оптической осью (координаты фокуса) от расстояния между падающим лучом и этой осью. Варьируя геометрические параметры всех четырех преломляющих поверхностей, можно с помощью этого графика изучать их влияние на сферическую аберрацию всей оптической системы глаза и пытаться минимизировать ее. Можно, например, легко убедиться, что аберрация всей оптической системы глаза с естественным хрусталиком при условии, что все четыре преломляющие поверхности являются сферическими, заметно меньше, чем аберрация одного только хрусталика, и немного больше, чем аберрация одной только роговицы. При диаметре зрачка 5 мм самые далекие от оси лучи пересекают эту ось примерно на 8% ближе, чем параксиальные лучи при преломлении одним только хрусталиком. При преломлении одной только роговицей при таком же диаметре зрачка фокус для дальних лучей ближе примерно на 3%, чем для параксиальных лучей. Вся оптическая система глаза с этим хрусталиком и с этой роговицей собирает дальние лучи примерно на 4% ближе, чем параксиальные лучи. Можно сказать, что роговица частично компенсирует сферическую аберрацию хрусталика.
Варьируя геометрические параметры всех четырех преломляющих поверхностей, можно с помощью этого графика изучать их влияние на сферическую аберрацию всей оптической системы глаза и пытаться минимизировать ее. Можно, например, легко убедиться, что аберрация всей оптической системы глаза с естественным хрусталиком при условии, что все четыре преломляющие поверхности являются сферическими, заметно меньше, чем аберрация одного только хрусталика, и немного больше, чем аберрация одной только роговицы. При диаметре зрачка 5 мм самые далекие от оси лучи пересекают эту ось примерно на 8% ближе, чем параксиальные лучи при преломлении одним только хрусталиком. При преломлении одной только роговицей при таком же диаметре зрачка фокус для дальних лучей ближе примерно на 3%, чем для параксиальных лучей. Вся оптическая система глаза с этим хрусталиком и с этой роговицей собирает дальние лучи примерно на 4% ближе, чем параксиальные лучи. Можно сказать, что роговица частично компенсирует сферическую аберрацию хрусталика.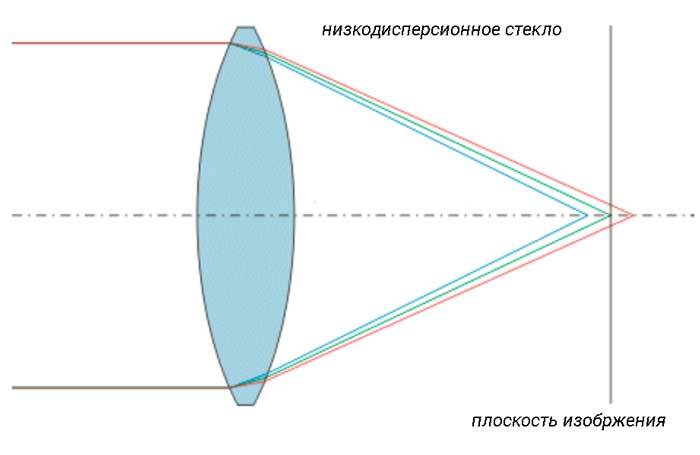
Можно убедиться также, что оптическая система глаза, состоящая из роговицы и идеальной гиперболической линзы с нулевой аберрацией, установленной в качестве хрусталика, дает сферическую аберрацию, примерно такую же, как и одна только роговица, т.е. минимизация сферической аберрации одного только хрусталика недостаточна для минимизации всей оптической системы глаза.
Таким образом, для минимизации сферической аберрации всей оптической системы глаза за счет выбора геометрии одного только хрусталика необходимо подбирать не такую линзу, у которой минимальна сферическая аберрация, а такую, которая минимизирует аберрацию во взаимодействии с роговицей. Если преломляющие поверхности роговицы считать сферическими, то для практически полного устранения сферической аберрации всей оптической системы глаза необходимо подобрать хрусталик с гиперболическими преломляющими поверхностями, который в качестве одиночной линзы дает ощутимую (около 17% в жидкой среде глаза и около 12% в воздухе) отрицательную аберрацию. Сферическая аберрация всей оптической системы глаза при этом не превышает 0.2% ни при каких диаметрах зрачка. Почти такую же нейтрализацию сферической аберрации оптической системы глаза (примерно до 0.3%) можно получить даже с помощью хрусталика, у которого первая преломляющая поверхность является сферической, а вторая — гиперболической.
Сферическая аберрация всей оптической системы глаза при этом не превышает 0.2% ни при каких диаметрах зрачка. Почти такую же нейтрализацию сферической аберрации оптической системы глаза (примерно до 0.3%) можно получить даже с помощью хрусталика, у которого первая преломляющая поверхность является сферической, а вторая — гиперболической.
Итак, применение искусственного хрусталика с асферическими, в частности, с гиперболическими преломляющими поверхностями позволяет практически полностью устранить сферическую аберрацию оптической системы глаза и тем самым значительно улучшить качество изображения, даваемого этой системой на сетчатке. Это показывают результаты компьютерного моделирования прохождения лучей через систему в рамках достаточно простой двумерной модели.
Влияние параметров оптической системы глаза на качество ретинального изображения может быть продемонстрировано также с помощью значительно более сложной трехмерной компьютерной модели, выполняющей трассировку очень большого количества лучей (от нескольких сотен лучей до нескольких сотен тысяч лучей), вышедших их одной точки источника и попадающих в разные точки сетчатки в результате воздействия всех геометрических аберраций и возможной неточной фокусировки системы. Складывая все лучи во всех точках сетчатки, пришедшие туда от всех точек источника, такая модель позволяет получить изображения протяженных источников — различных тест-объектов, как цветных, так и черно-белых. В нашем распоряжении имеется такая трехмерная компьютерная модель и она наглядно демонстрирует значительное улучшение качества ретинального изображения при применении интраокулярных линз с асферическими преломляющими поверхностями за счет значительного уменьшения сферической аберрации и уменьшения тем самым размеров пятна рассеяния на сетчатке. В принципе сферическая аберрация может быть устранена практически полностью и, казалось бы, размер пятна рассеяния можно уменьшить практически до нуля, получив тем самым идеальное изображение.
Складывая все лучи во всех точках сетчатки, пришедшие туда от всех точек источника, такая модель позволяет получить изображения протяженных источников — различных тест-объектов, как цветных, так и черно-белых. В нашем распоряжении имеется такая трехмерная компьютерная модель и она наглядно демонстрирует значительное улучшение качества ретинального изображения при применении интраокулярных линз с асферическими преломляющими поверхностями за счет значительного уменьшения сферической аберрации и уменьшения тем самым размеров пятна рассеяния на сетчатке. В принципе сферическая аберрация может быть устранена практически полностью и, казалось бы, размер пятна рассеяния можно уменьшить практически до нуля, получив тем самым идеальное изображение.
Но не следует упускать из виду то обстоятельство, что идеальное изображение получить невозможно никаким способом, даже если предположить, что все геометрические аберрации устранены полностью. Есть принципиальный предел уменьшения размера пятна рассеяния. Этот предел устанавливает волновая природа света. В соответствии с дифракционной теорией, основывающейся на волновых представлениях, минимальный диаметр светового пятна в плоскости изображения, обусловленный дифракцией света на круглом отверстии, пропорционален (с коэффициентом пропорциональности 2.44) произведению фокусного расстояния на длину волны света и обратно пропорционален диаметру отверстия. Оценка для оптической системы глаза дает диаметр пятна рассеяния около 6.5 мкм при диаметре зрачка 4 мм.
Этот предел устанавливает волновая природа света. В соответствии с дифракционной теорией, основывающейся на волновых представлениях, минимальный диаметр светового пятна в плоскости изображения, обусловленный дифракцией света на круглом отверстии, пропорционален (с коэффициентом пропорциональности 2.44) произведению фокусного расстояния на длину волны света и обратно пропорционален диаметру отверстия. Оценка для оптической системы глаза дает диаметр пятна рассеяния около 6.5 мкм при диаметре зрачка 4 мм.
Уменьшить диаметр светового пятна меньше дифракционного предела невозможно, даже если законы геометрической оптики сводят все лучи в одну точку. Дифракция ограничивает предел улучшения качества изображения, даваемого любой рефракционной оптической системой, даже идеальной. Вместе с тем дифракция света не хуже, чем рефракция, может быть использована для получения изображения, что успешно применяется в дифракционно-рефракционных ИОЛ. Но это уже другая тема.
Библиографическая ссылка
Чередник В. И., Треушников В.М. СФЕРИЧЕСКАЯ АБЕРРАЦИЯ И АСФЕРИЧЕСКИЕ ИНТРАОКУЛЯРНЫЕ ЛИНЗЫ // Фундаментальные исследования. – 2007. – № 8. – С. 38-41;
И., Треушников В.М. СФЕРИЧЕСКАЯ АБЕРРАЦИЯ И АСФЕРИЧЕСКИЕ ИНТРАОКУЛЯРНЫЕ ЛИНЗЫ // Фундаментальные исследования. – 2007. – № 8. – С. 38-41;URL: http://fundamental-research.ru/ru/article/view?id=3359 (дата обращения: 23.03.2020). Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
Рассмотрим даваемое оптической системой изображение Точки, расположенной на оптической оси. Так как оптическая система обладает круговой симметрией относительно оптической оси, то достаточно ограничиться выбором лучей, лежащих в меридиональной плоскости. На рис. 113 показан ход лучей, характерный для положительной одиночной линзы. Положение
Рис. 113. Сферическая аберрация положительной лннзы
Рис. 114. Сферическая аберрация для точки вне оси
идеального изображения предметной точки А определяется параксиальным лучом, пересекающим оптическую ось на расстоянии от последней поверхности. Лучи, образующие с оптической осью конечные углы не приходят в точку идеального изображения. Для одиночной положительной линзы, чем больше абсолютное значение угла тем ближе к линзе луч пересекает оптическую ось. Это объясняется неодинаковой оптической силой линзы в ее различных зонах, которая увеличивается по мере удаления от оптической оси.
Для одиночной положительной линзы, чем больше абсолютное значение угла тем ближе к линзе луч пересекает оптическую ось. Это объясняется неодинаковой оптической силой линзы в ее различных зонах, которая увеличивается по мере удаления от оптической оси.
Указанное нарушение гомоцентричности вышедшего пучка лучей можно характеризовать разностью продольных отрезков для параксиальных лучей и для лучей, проходящих через плоскость входного зрачка на конечных высотах: Эта разность называется продольной сферической аберрацией.
Наличие сферической аберрации в системе приводит к тому, что вместо резкого изображения точки в плоскости идеального изображения получается кружок рассеяния, диаметр которого равен удвоенному значению Последнее связано с продольной сферической аберрацией соотношением
и называется поперечной сферической аберрацией.
Следует отметить, что при сферической аберрации сохраняется симметрия в вышедшем из системы пучке лучей. В отличие от других монохроматических аберраций сферическая аберрация имеет место во всех точках поля оптической системы, причем при отсутствии других аберраций для точек вне оси вышедший из системы пучок лучей будет оставаться симметричным относительно главного луча (рис. 114).
114).
Приближенное значение сферической аберрации можно определить по формулам аберраций третьего порядка через
Для предмета, расположенного на конечном расстоянии, как следует из рис. 113,
В пределах действенности теории аберраций третьего порядка можно принять
Если положить, что то согласно условиям нормировки получим
Тогда по формуле (253) найдем, что поперечная сферическая аберрация третьего порядка для предметной точки, расположенной на конечном расстоянии,
Соответственно для продольной сферической аберраций третьего лорядка при допущении согласно (262) и (263) получим
Формулы (263) и (264) справедливы и для случая предмета, расположенного в бесконечности, если вычислена при условиях нормировки (256), т. е. при реальном фокусном расстоянии.
В практике аберрационного расчета оптических систем при вычислении сферической аберрации третьего порядка удобно пользоваться формулами, содержащими координату луча на входном зрачке. Тогда при согласно (257) и (262) получим:
Тогда при согласно (257) и (262) получим:
если вычислена при условиях нормировки (256).
Для условий нормировки (258), т. е. для приведенной системы, согласно (259) и (262) будем иметь:
Из приведенных выше формул следует, что при данной сферическая аберрация третьего порядка тем больше, чем больше координата луча на входном зрачке.
Так как сферическая аберрация присутствует для всех точек поля, то при аберрационной коррекции оптической системы первостепенное внимание уделяют исправлению сферической аберрации. Наиболее простой оптической системой со сферическими поверхностями, в которой можно уменьшить сферическую аберрацию, является комбинация положительной и отрицательной линз. Как у положительной, так и у отрицательной линз крайние зоны преломляют лучи сильнее, чем зоны, расположенные вблизи оси (рис. 115). Отрицательная линза имеет положительную сферическую аберрацию. Поэтому комбинация положительной линзы, имеющей отрицательную сферическую аберрацию, с отрицательной линзой позволяет получить систему с исправленной сферической аберрацией.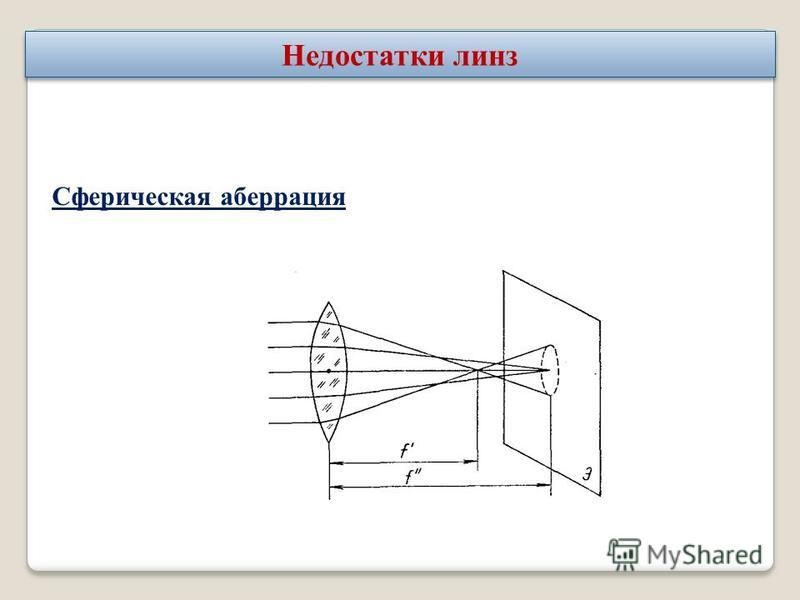 К сожалению, устранить сферическую аберрацию можно только для некоторых лучей, но нельзя ее полностью исправить в пределах всего входного зрачка.
К сожалению, устранить сферическую аберрацию можно только для некоторых лучей, но нельзя ее полностью исправить в пределах всего входного зрачка.
Рис. 115. Сферическая аберрация отрицательной линзы
Таким образом, любая оптическая система всегда имеет остаточную сферическую аберрацию. Остаточные аберрации оптической системы обычно представляют в виде таблиц и иллюстрируют графиками. Для предметной точки, расположенной на оптической оси, приводятся графики продольной и поперечной сферических аберраций, представленные в виде функций координат, или
Кривые продольной и соответствующей ей поперечной сферической аберрации показаны на рис. 116. Графики на рис. 116, а соответствуют оптической системе с недоисправленной сферической аберрацией. Если для такой системы ее сферическая аберрация определяется только аберрациями третьего порядка, то согласно формуле (264) кривая продольной сферической аберрации имеет вид квадратичной параболы, а кривая поперечной аберрации — кубической параболы. Графики на рис. 116, б соответствуют оптической системе, у которой сферическая аберрация исправлена для луча, проходящего через край входного зрачка, а графики на рис. 116, в — оптической системе с перенаправленной сферической аберрацией. Исправление или переисправление сферической аберрации можно получить, например, комбинируя положительную и отрицательную линзы.
Графики на рис. 116, б соответствуют оптической системе, у которой сферическая аберрация исправлена для луча, проходящего через край входного зрачка, а графики на рис. 116, в — оптической системе с перенаправленной сферической аберрацией. Исправление или переисправление сферической аберрации можно получить, например, комбинируя положительную и отрицательную линзы.
Поперечная сферическая аберрация характеризует кружок рассеяния, который получается вместо идеального изображения точки. Диаметр кружка рассеяния для данной оптической системы зависит от выбора плоскости изображения. Если эту плоскость сместить относительно плоскости идеального изображения (плоскости Гаусса) на величину (рис. 117, а), то в смещенной плоскости получим поперечную аберрацию связанную с поперечной аберрацией в плоскости Гаусса зависимостью
В формуле (266) слагаемое на графике поперечной сферической аберрации, построенном в координатах является прямой, проходящей через начало координат. При
Рис. 116. Графическое представление продольной и поперечной сферических аберраций
116. Графическое представление продольной и поперечной сферических аберраций
Аберрации в оптических системах — Основы оптотехники
«Аберрации» — это общая категория, включающая основные факторы которые заставляют оптическую систему работать иначе, чем в идеальном случае. Существует ряд факторов, которые не позволяют объективу достичь своих целей. теоретическая работоспособность.
Физические аберрации
Однородность оптических материалов и поверхностей является первым требование достижения оптимальной фокусировки световых лучей и правильного изображения формирование. Очевидно, что однородность реальных материалов имеет верхний предел определяется различными факторами (например, материальными включениями), некоторые из которых не может быть устранено. Пыль и грязь являются внешними факторами, которые безусловно ухудшают характеристики объектива, поэтому их следует избегать как можно возможный.
Сферические аберрации
Сферические линзы очень распространены, потому что их относительно легко исправить. производство. Однако сферическая форма не идеальна для идеального
изображения — по сути, коллимированные лучи, попадающие в объектив в разные
расстояния от оптической оси будут сходиться в разные точки,
вызывая общую потерю внимания. Как и многие оптические аберрации,
Эффект размытия увеличивается к краю линзы.
производство. Однако сферическая форма не идеальна для идеального
изображения — по сути, коллимированные лучи, попадающие в объектив в разные
расстояния от оптической оси будут сходиться в разные точки,
вызывая общую потерю внимания. Как и многие оптические аберрации,
Эффект размытия увеличивается к краю линзы.
Для уменьшения проблема, часто используются асферические линзы (рис. 16) — их поверхность профиль — это не часть сферы или цилиндра, а более сложный профиль, способный свести к минимуму сферические аберрации. Альтернатива решение работает при высоких значениях F/#, так что лучи, попадающие в объектив, от оптической оси и вызывая сферическую аберрацию, не может достигать датчик.
Хроматическая аберрация
Показатель преломления материала — это число, описывающее
угол рассеяния проходящего через него света – по сути, сколько лучей
изгибаются или преломляются — и это функция длины волны
легкий. Когда белый свет попадает в линзу, каждая длина волны занимает небольшое
другой путь. Это явление называется дисперсией и приводит к
расщепление белого света на его спектральные составляющие, вызывающее хроматические
аберрация. Эффект минимален в центре оптики, нарастает
к краям.
Это явление называется дисперсией и приводит к
расщепление белого света на его спектральные составляющие, вызывающее хроматические
аберрация. Эффект минимален в центре оптики, нарастает
к краям.
Хроматическая аберрация вызывает появление цветных полос на изображении, что приводит к размытым краям, что делает невозможным правильное изображение особенности объекта. В то время как ахроматический дублет может быть использован для уменьшения этого вид аберрации, простое решение, когда нет информации о цвете необходимо использовать монохромный свет. Хроматических аберраций может быть две виды: продольные (рис. 17) и поперечные (рис. 18), в зависимости от направление падающих параллельных лучей.
Астигматизм
Астигматизм — это оптическая аберрация, возникающая, когда лучи, лежащие
две перпендикулярные плоскости на оптической оси имеют разные фокусы. Этот
вызывает размытие в одном направлении, которое отсутствует в другом направлении. Если
мы фокусируем датчик для сагиттальной плоскости, мы видим, что круги становятся
эллипсы в тангенциальном направлении и наоборот.
Кома
Аберрация комы возникает, когда параллельные лучи попадают в линзу под под определенным углом фокусируются в разных положениях, в зависимости от их расстояние от оптической оси. Окружность в плоскости объекта будет появляются на изображении в виде элемента в форме кометы, что и дало название этот конкретный эффект аберрации.
Кривизна поля
Аберрация кривизны поля описывает тот факт, что параллельные лучи
попадающие в объектив с разных сторон фокусируются не на плоскости, а
скорее на криволинейной поверхности.
Это вызывает радиальную расфокусировку, т.е. при заданном положении сенсора в фокусе будет только круглая корона.
Искажение
С идеальным объективом квадратный элемент будет преобразован только в
размера, не влияя на его геометрические свойства. И наоборот, настоящий
объектив всегда вносит некоторую геометрическую дисторсию, в основном радиальную
симметричный (как отражение радиальной симметрии оптики). Этот
Радиальная дисторсия может быть двух видов: бочкообразная и подушкообразная. При бочкообразной дисторсии увеличение изображения уменьшается с расстоянием
от оптической оси, создавая кажущийся эффект изображения
обернутый вокруг сферы. С подушкообразным увеличением изображения искажения
увеличивается с удалением от оптической оси. Линии, которых нет
проходят через центр изображения, загибаются внутрь, как и края
игольница.
При бочкообразной дисторсии увеличение изображения уменьшается с расстоянием
от оптической оси, создавая кажущийся эффект изображения
обернутый вокруг сферы. С подушкообразным увеличением изображения искажения
увеличивается с удалением от оптической оси. Линии, которых нет
проходят через центр изображения, загибаются внутрь, как и края
игольница.
Как насчет исправления искажений?
Поскольку телецентрические линзы являются реальными объектами, они показывают некоторые остаточные искажения, которые могут повлиять на точность измерения. Искажение рассчитывается как процентная разница между реальным и ожидаемым высота изображения и может быть аппроксимирована полиномом второго порядка. Если мы определите радиальные расстояния от центра изображения следующим образом
`R_a = фактический радиус`
`R_e = ожидаемый радиус`
искажение вычисляется как функция Ra: 92 + b * R_a + a`
, где a, b и c — постоянные значения, определяющие кривую искажения
поведение; обратите внимание, что «а» обычно равно нулю, так как искажение обычно
ноль в центре изображения. В некоторых случаях можно использовать многочлен третьего порядка.
требуется, чтобы получить идеальное соответствие кривой.
В некоторых случаях можно использовать многочлен третьего порядка.
требуется, чтобы получить идеальное соответствие кривой.
В дополнение к радиальному перекосу должен быть также трапециевидный перекос принято во внимание. Этот эффект можно рассматривать как перспективу ошибка из-за несоосности между оптическими и механическими компонентами, следствием чего является преобразование параллельных линий в объектном пространстве в сходящиеся (или расходящиеся) линии в пространстве изображения.
Такой эффект, также известный как «трапецеидальное искажение» или «тонкая призма», можно легко исправить с помощью довольно распространенных алгоритмов, вычисляющих точка пересечения сходящихся пучков прямых.
Интересным аспектом является то, что радиальные и трапециевидные искажения
два совершенно разных физических явления, следовательно, их можно
математически корректируется с помощью двух независимых пространственных преобразований
функции, которые также могут быть применены впоследствии.
Альтернативный (или дополнительный) подход заключается в исправлении обоих искажения локально и сразу: изображение сетчатого узора используется для определите величину ошибки искажения и ее ориентацию зона за зоной. конечным результатом является векторное поле, в котором каждый вектор, связанный с конкретная зона изображения определяет, какая коррекция должна быть применена к x, y координатные измерения в пределах диапазона изображения.
Почему для телецентрических линз рекомендуется зеленый свет?
Все линзы, работающие в видимом диапазоне, включая оптические
Телецентрические линзы Engineering® ахроматизированы по всей видимой области.
спектр. Однако параметры, связанные с дисторсией объектива и
телецентричность обычно оптимизированы для длин волн в центре
диапазона VIS, который является зеленым светом. Более того, разрешение стремится
быть лучше в диапазоне зеленого света, где ахроматизация
практически идеально. «Зеленый» также лучше, чем «Красный», потому что более короткий
диапазон длин волн увеличивает дифракционный предел линзы и
максимально достижимое разрешение.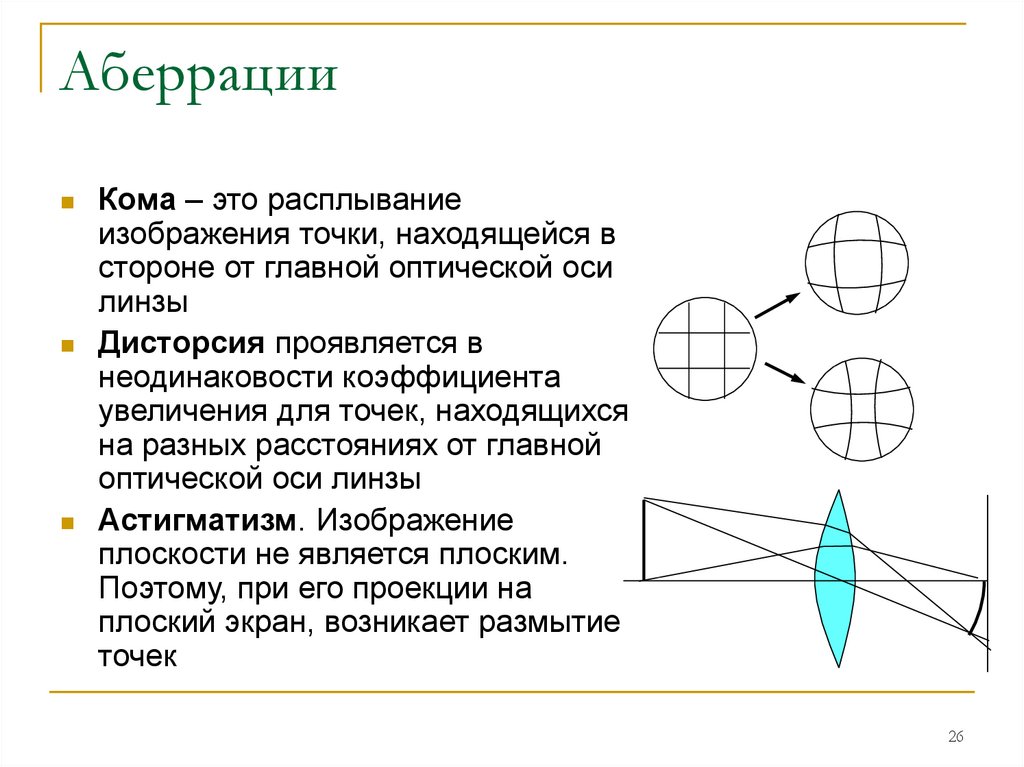
| Оптические аберрацииИнтерактивные учебные пособия Сферическая аберрация Самая серьезная аберрация классической монохроматической линзы Seidel , возникающая при использовании объективов микроскопа, сферическая аберрация приводит к тому, что изображение образца становится нечетким или размытым и немного не в фокусе. Эффект сферической аберрации проявляется двумя способами: центр изображения остается в фокусе больше, чем края, а интенсивность краев падает по сравнению с центром. Этот дефект проявляется как в осевых, так и внеосевых точках изображения. Учебное пособие инициализируется изображением образца (видимого через микроскоп), появляющимся в окне в левой части апплета. Под окном изображения находится раскрывающееся меню с надписью Choose A Specimen , используемое для выбора нового образца. Ползунок Lens Shape предназначен для управления учебным пособием за счет увеличения сферической аберрации в оптической системе. Перемещение ползунка вправо также вызывает изменения, соответствующие введению сферической аберрации в дифракционную картину Эйри, показанную в центре окна апплета. Артефакты сферической аберрации возникают, когда световые волны, проходящие через периферию нескорректированной выпуклой линзы, не фокусируются с волнами, проходящими через центр. Волны, проходящие вблизи центра линзы, лишь незначительно преломляются, тогда как волны, проходящие вблизи периферии, преломляются в большей степени, создавая множество различных фокусных точек вдоль оптической оси. В результате периферийные волны достигают более короткого фокуса (ближе к задней части линзы или объектива), чем лучи, проходящие через центральную или аксиальную область. Это известно как продольная или осевая сферическая аберрация . Осевая аберрация создается несферическими волновыми фронтами, создаваемыми самим объективом или неправильным использованием объектива. В микроскоп видно изображение, полученное путем фокусировки периферийных лучей, окруженных несфокусированным изображением лучей, проходящих через центральную часть линзы (или наоборот). Это один из самых серьезных артефактов разрешения, поскольку изображение образца расплывается, а не находится в резком фокусе. Наилучший фокус в неидеально или не скорректированном объективе будет где-то между фокальными плоскостями периферийного и осевого лучей, в области, известной как диск наименьшей путаницы (показан точкой на оптической оси на учебном рисунке). Световые лучи, преломленные краем хрусталика или зрачка (периферические лучи), имеют наименьшее фокусное расстояние и дают наименьшее изображение, тогда как те, которые пересекаются в параксиальной точке фокуса (аксиальные лучи), начали рассеиваться и не представляют «наилучшего». Оптимальная коррекция сферической аберрации возможна только при точном указании расстояния между образцом и изображением. Этот артефакт может быть легко вызван неправильной длиной трубки, вызванной введением оптических элементов в траекторию сходящегося пучка микроскопов с конечной длиной тубуса. Сферическая аберрация может возникнуть и при использовании неподходящих «окон», таких как покровные стекла нестандартной толщины (отклонения от 0,17 миллиметров) или некачественное иммерсионное масло между передней линзой объектива и покровным стеклом. В учебном пособии показано преувеличенное изображение трех гипотетических монохроматических световых лучей, проходящих через выпуклую линзу и сходящихся в ряде фокальных точек, расположенных вдоль оптической оси (см. Диаграмму трассировки лучей ). Изменения формы объектива с соответствующими регулировками положения(й) фокусной точки можно выполнить с помощью ползунка Lens Shape . Большая часть расхождений в фокусных точках возникает из-за аппроксимаций эквивалентности значений синусов и тангенсов соответствующих углов, сделанных для уравнения линзы Гаусса для сферической преломляющей поверхности : , где n и n’ представляют собой показатель преломления воздуха и стекла, из которых состоит линза, соответственно, s и s’ — расстояние до объекта и изображения, а r — радиус кривизны линзы. По мере увеличения числовой апертуры объектива изменения толщины покровного стекла или показателя преломления становятся критическими, особенно при использовании сухих объективов с большим увеличением, где небольшие изменения длины тубуса быстро приводят к ухудшению качества изображения. Одним из механизмов, используемых для устранения сферической аберрации в масляных иммерсионных объективах, является проектирование оптики вокруг определенных пар сопряженных точек с использованием полусферической и менисковой линзы в передней части объектива. Образцы, помещенные в канадский бальзам или аналогичную среду для заливки, которые имеют показатель преломления, близкий к показателю покровного стекла, не подвержены ошибкам сферической аберрации.
Сферические аберрации очень важны с точки зрения разрешения объектива, поскольку они влияют на совпадающее изображение точек вдоль оптической оси и ухудшают характеристики объектива, что серьезно влияет на резкость и четкость образца. Эти дефекты линзы можно уменьшить, ограничивая внешние края линзы от воздействия света с помощью диафрагм, а также используя асферические поверхности линз внутри системы. Однако следствием уменьшения размера апертуры в оптической системе микроскопа является одновременное уменьшение количества света, попадающего в систему. До недавнего времени ахроматы корректировались сферически только для зеленого света, хотя хроматически корректировались для двух длин волн. Кроме того, апохроматы были скорректированы сферически для двух длин волн, синего и зеленого, но были скорректированы хроматически для трех длин волн. Современные высококачественные объективы для микроскопов устраняют сферические аберрации несколькими способами, включая специальные методы шлифовки линз, улучшенные составы стекла и лучший контроль оптических путей за счет использования элементов с несколькими линзами. В настоящее время объективы самого высокого качества, планохроматы, сферически скорректированы для четырех длин волн, как и планфлюориты (но не с таким точным допуском).
Пользователь также может непреднамеренно внести сферическую аберрацию в хорошо скорректированную систему. Высококачественные масляные иммерсионные объективы работают оптимально только при использовании покровного стекла толщиной 0,17 мм. Чтобы уменьшить вариации покровного стекла, на сухие объективы часто включают корректирующие кольца, позволяющие регулировать промежуточные элементы линзы для компенсации отклонения толщины покровного стекла. Поскольку фокус может сместиться, а изображение может измениться во время настройки корректирующего кольца, использование корректирующих воротников требует, чтобы микроскопист оставался бдительным, чтобы переустановить воротник, используя соответствующие критерии изображения. Соавторы Х. Эрнст Келлер — Carl Zeiss Inc., One Zeiss Dr., Thornwood, NY, 10594. Кеннет Р. Спринг — Научный консультант, Лусби, Мэриленд, 20657. John C. Long и Michael W. Davidson – Национальная лаборатория сильного магнитного поля, 1800 East Paul Dirac Dr., Университет штата Флорида, Таллахасси, Флорида, 32310. НАЗАД К ОПТИЧЕСКИМ АБЕРРАЦИЯМ НАЗАД К ЛИНЗАМ И ГЕОМЕТРИЧЕСКОЙ ОПТИКЕ Вопросы или комментарии? Отправить нам письмо.© 1998-2022 автор Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами.Этот веб-сайт поддерживается нашей командойGraphics & Web Programming Team . в сотрудничестве с Optical Microscopy в Национальной лаборатории сильного магнитного поля. Последнее изменение: вторник, 13 сентября 2016 г., 09:50Число обращений с 30 августа 2000 г.: 86352Для получения дополнительной информации о производителях микроскоповиспользуйте кнопки ниже для перехода на их веб-сайты: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.2: Сферическая аберрация — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7088
- Джереми Татум
- Университет Виктории
Начнем с рассмотрения сферической аберрации, возникающей в результате отражения от сферического зеркала. До сих пор мы предполагали, что параллельный пучок света после отражения от сферического зеркала сходится в точке и что расстояние от точки фокусировки до поверхности зеркала равно половине радиуса кривизны зеркала, как на рисунке IV.1:
До сих пор мы предполагали, что параллельный пучок света после отражения от сферического зеркала сходится в точке и что расстояние от точки фокусировки до поверхности зеркала равно половине радиуса кривизны зеркала, как на рисунке IV.1:
Это примерно верно для зеркала с малой апертурой (отношение диаметра к фокусному расстоянию). Однако это не относится к зеркалу с большой апертурой. На рисунке IV.2 я нарисовал полусферическое зеркало. Я предполагаю, что есть падающий луч света (не нарисованный), идущий горизонтально слева, и я нарисовал лучи после отражения от зеркала. (Некоторые лучи будут отражаться от поверхности во второй раз перед тем, как в конце концов уйти, но я не нарисовал лучи после второго отражения, потому что они только загромождают диаграмму и не подходят для описания того, что я хочу описать. Вы можно видеть, что отраженные лучи ограничены огибающей, известной как каустическая кривая, показанная пунктирной красной кривой на рисунке IV.2.92}}. \label{eq:4. 2.2} \]
2.2} \]
Эти формулы также удобно записывать в терминах угла \(\theta\), который определяется формулой \(h = a\sin \theta\). После небольшой алгебры и применения некоторых тригонометрических тождеств получаем
\[ y = x \tan 2 \theta — \frac{a\sin\theta}{\cos2\theta}\label{eq:4.2.3} \]
для уравнения отраженного луча и
\[ OC = \frac{1}{2} a \sec \theta. \label{eq:4.2.4} \]
Мы можем записать уравнение \(\ref{eq:4.2.3}\) как
\[ f(x,y;\theta)= x\tan2\theta-\frac{a\sin\theta}{\cos2\theta}-y=0.\label{eq:4.2.5} \]
Из наших давно забытых, пожелтевших и заплесневелых математических заметок мы помним, что для нахождения уравнения огибающей семейства кривых вида \(f(x,y;\theta)=0\) нужно исключить параметр \(\theta\) из этого уравнения и уравнения \(\frac{\partial f}{\partial \theta}=0\). После еще немного алгебры и применения тригонометрических тождеств мы обнаруживаем, что последнее уравнение сводится к 92\тета).\метка{уравнение:4. 2.6} \]
2.6} \]
Итак, все, что нам нужно сделать, это исключить параметр \(\theta\) из уравнений \(\ref{eq:4.2.3}\) и \(\ref{eq:4.2.6}\), и это дало бы нам уравнение \(x, y\) для кривой каустики. Эти два уравнения фактически являются параметрическими уравнениями для каустической кривой. Теперь я не знаю, насколько легко было бы избавиться от \(\theta\). Поскольку уравнение \(\ref{eq:4.2.6}\) является кубическим уравнением в \(\cos\theta\), я подозреваю, что оно может оказаться не таким простым. Но (как это часто бывает с двумя параметрическими уравнениями для кривой) мы можем успешно построить кривую численно, без необходимости исключать параметр алгебраически. Таким образом, чтобы построить красную кривую на рис. IV.2, я варьировал \(\theta\) от -9от 0° до +90° и рассчитал \(x\) по уравнению \(\ref{eq:4.2.6}\), а затем я рассчитал \(y\) по уравнению \(\ref{eq:4.2. 3}\).
Во избежание сферической аберрации зеркала телескопов могут быть выполнены в форме параболоида. Можно показать, что падающий пучок света, идущий параллельно оси параболоидного зеркала, после отражения попадет в единственную фокальную точку, а именно в фокус параболы.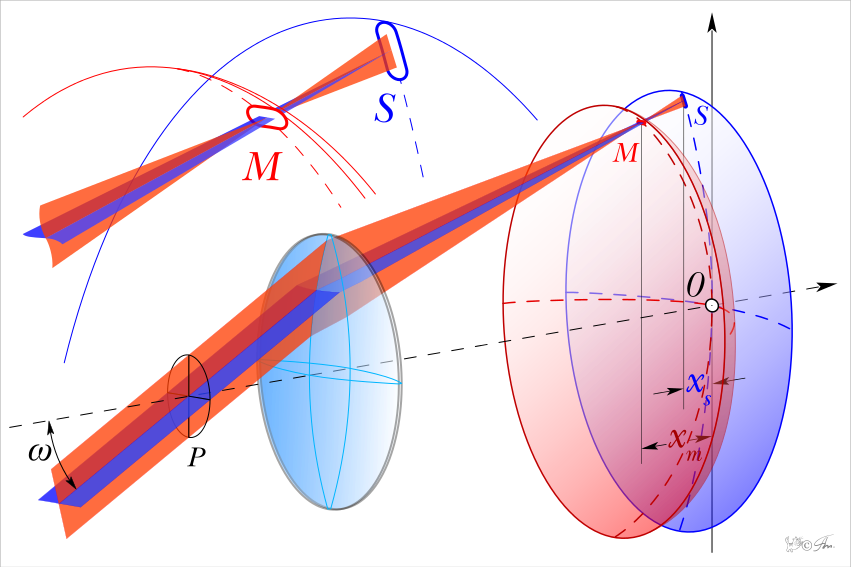 Доказательство этого дано в разделе 2.4 главы 2 моих заметок по небесной механике и там не повторяется. В этой главе также показано, что если ведро с жидкостью вращать вокруг вертикальной оси, поверхность жидкости примет форму параболоида, и там же упоминаются два применения к изготовлению параболоидных зеркал. В одном чан с расплавленным стеклом вращается и постепенно охлаждается до тех пор, пока стекло не затвердеет и не примет форму параболоида. В другом контейнер с ртутью вращается, поверхность ртути принимает форму параболоида, и этот жидкий параболоид затем используется в качестве главного зеркала телескопа-рефлектора. Хотя его можно наблюдать только вблизи зенита, были получены отличные результаты. Я не буду повторять это здесь, но вы, возможно, захотите сослаться на вышеупомянутые примечания, поскольку они здесь уместны.
Доказательство этого дано в разделе 2.4 главы 2 моих заметок по небесной механике и там не повторяется. В этой главе также показано, что если ведро с жидкостью вращать вокруг вертикальной оси, поверхность жидкости примет форму параболоида, и там же упоминаются два применения к изготовлению параболоидных зеркал. В одном чан с расплавленным стеклом вращается и постепенно охлаждается до тех пор, пока стекло не затвердеет и не примет форму параболоида. В другом контейнер с ртутью вращается, поверхность ртути принимает форму параболоида, и этот жидкий параболоид затем используется в качестве главного зеркала телескопа-рефлектора. Хотя его можно наблюдать только вблизи зенита, были получены отличные результаты. Я не буду повторять это здесь, но вы, возможно, захотите сослаться на вышеупомянутые примечания, поскольку они здесь уместны.
Это свойство (свет отражается от поверхности параболы в одну фокусную точку) применимо только к свету, идущему параллельно оси параболоида. Следовательно, зеркала параболоидного телескопа имеют довольно узкое поле зрения. Телескоп Schmidt использует сферическое зеркало (отсюда большое поле зрения) и, чтобы избежать сферической аберрации, перед зеркалом установлена пластина-корректор. Обычно сферическое зеркало находится на «нижнем конце» трубы телескопа, а пластина корректора — на «верхнем конце». Пластина корректора заставляет свет, идущий параллельно трубе телескопа, но на некотором расстоянии от оси трубы, немного отклоняться от оси, прежде чем достигнет сферического зеркала. Таким образом, весь падающий свет после отражения от зеркала фокусируется в одной точке.
Телескоп Schmidt использует сферическое зеркало (отсюда большое поле зрения) и, чтобы избежать сферической аберрации, перед зеркалом установлена пластина-корректор. Обычно сферическое зеркало находится на «нижнем конце» трубы телескопа, а пластина корректора — на «верхнем конце». Пластина корректора заставляет свет, идущий параллельно трубе телескопа, но на некотором расстоянии от оси трубы, немного отклоняться от оси, прежде чем достигнет сферического зеркала. Таким образом, весь падающий свет после отражения от зеркала фокусируется в одной точке.
Объектив, конечно, тоже страдает сферической аберрацией, но он не поддается такому простому анализу, как для сферического зеркала. Чтобы найти точную форму каустической кривой для линзы, необходимо выполнить подробную численную трассировку лучей. Однако в разделе 1.4 главы 1 мы показали, что рефракция даже на плоской поверхности вызывает сферическую аберрацию.
Может возникнуть вопрос, учитывая, что параболоидное зеркало при использовании на оси свободно от сферической аберрации, может ли линза, сделанная с параболоидными поверхностями, также свободна от сферической аберрации. Увы, это не так.
Увы, это не так.
Однако можно сконструировать линзу со сферическими поверхностями, которые сводят к минимуму сферическую аберрацию, за счет соответствующего выбора радиусов или кривизны поверхностей линзы. Это называется «изгиб линзы».
Например, на рис. IV.4 показаны пять линз, в которых я написал рядом с каждой поверхностью ее радиус кривизны в см. Далее я предполагаю, что линза «тонкая» в том смысле, что ее толщина очень мала по сравнению с любыми другими обсуждаемыми расстояниями. Если показатель преломления равен 1,6, каждая из этих линз имеет фокусное расстояние 20 см.
Форму линзы можно охарактеризовать с помощью коэффициента формы .
\[q=\frac{r_1+r_2}{r_1-r_2}\label{eq:4.2.7} \]
На рисунке IV.4 я написал коэффициент формы над каждой линзой.
Для света, падающего горизонтально вблизи оси, фокусное расстояние каждой из этих линз составляет 20 см. Однако свет, идущий горизонтально на некотором расстоянии от оси, после прохождения через линзу падает чуть меньше 20 см. Мы можем охарактеризовать сферическую аберрацию по ее величине. Предполагая, что линзы тонкие (по сравнению с любыми другими рассматриваемыми расстояниями), я вычислил недобор для луча света, падающего слева на высоте 1 см от оси. Это показано на рисунке IV.5, на котором я нарисовал дефицит (обозначенный на рисунке как «Аберрация») в зависимости от коэффициента формы \(q\). Видно, что аберрация минимальна при коэффициенте формы около \(q = -0,38\). Радиусы кривизны линзы должны удовлетворять уравнению \(\ref{eq:4.2.7}\), а также \(q = −0,38\)
Мы можем охарактеризовать сферическую аберрацию по ее величине. Предполагая, что линзы тонкие (по сравнению с любыми другими рассматриваемыми расстояниями), я вычислил недобор для луча света, падающего слева на высоте 1 см от оси. Это показано на рисунке IV.5, на котором я нарисовал дефицит (обозначенный на рисунке как «Аберрация») в зависимости от коэффициента формы \(q\). Видно, что аберрация минимальна при коэффициенте формы около \(q = -0,38\). Радиусы кривизны линзы должны удовлетворять уравнению \(\ref{eq:4.2.7}\), а также \(q = −0,38\)
\[\frac{1}{f}=(n-1)\left(\frac{1}{r_1}-\frac{1}{r_2}\right), \label{eq:4.2.8} \]
, так что для \(f\) = 20 см и \(q\) = -0,38 радиусы кривизны для наименьшей сферической аберрации должны быть \(r_1\) = 17,4 см и \(r_2\) = -38,7 см.
Конечно, линзу нужно использовать правильно! Если вы повернете его или если свет падает справа, коэффициент формы составит +0,38, а сферическая аберрация не будет минимальной. Имейте в виду, что минимум довольно неглубокий, поэтому вы можете значительно варьировать коэффициент формы без значительного увеличения сферической аберрации.

 В идеале объектив без аберраций преобразует плоский волновой фронт в сферический волновой фронт, направляя все световые волны, преломленные объективом, в общую фокусную точку в центре сферы для получения идеального изображения.
В идеале объектив без аберраций преобразует плоский волновой фронт в сферический волновой фронт, направляя все световые волны, преломленные объективом, в общую фокусную точку в центре сферы для получения идеального изображения. Одновременно интенсивность смещается от центрального пика функции рассеяния точки в окружающие кольца, которые становятся гораздо более заметными. Эти изменения также коррелируют с диаграммой трассировки лучей, представленной в правой части апплета.
Одновременно интенсивность смещается от центрального пика функции рассеяния точки в окружающие кольца, которые становятся гораздо более заметными. Эти изменения также коррелируют с диаграммой трассировки лучей, представленной в правой части апплета. Некоторыми из наиболее распространенных причин являются несоблюдение заданной длины тубуса микроскопа или наличие веществ между объективом и фокальной плоскостью, имеющих ложный показатель преломления.
Некоторыми из наиболее распространенных причин являются несоблюдение заданной длины тубуса микроскопа или наличие веществ между объективом и фокальной плоскостью, имеющих ложный показатель преломления. «фокус.
«фокус. Наибольшее преломление периферических лучей у края линзы, за ними следуют лучи посередине и затем лучи в центре. Большее преломление крайними лучами приводит к фокальной точке (фокальная точка 1; см. рис. 1), которая находится перед диск наименьшего смешивания и фокусы, образованные лучами, проходящими ближе к центру линзы (фокусы 2 в центре и 3 в параксиальной фокальной плоскости; рис. 1). На рисунке 1 также показана мера поперечной сферической аберрации , определяемая как расстояние от оптической оси, на котором периферийные лучи пересекают плоскость параксиального фокуса. Как видно из рисунка, поперечная аберрация измеряется в плоскости изображения и полезна в качестве индикатора размытия изображения.
Наибольшее преломление периферических лучей у края линзы, за ними следуют лучи посередине и затем лучи в центре. Большее преломление крайними лучами приводит к фокальной точке (фокальная точка 1; см. рис. 1), которая находится перед диск наименьшего смешивания и фокусы, образованные лучами, проходящими ближе к центру линзы (фокусы 2 в центре и 3 в параксиальной фокальной плоскости; рис. 1). На рисунке 1 также показана мера поперечной сферической аберрации , определяемая как расстояние от оптической оси, на котором периферийные лучи пересекают плоскость параксиального фокуса. Как видно из рисунка, поперечная аберрация измеряется в плоскости изображения и полезна в качестве индикатора размытия изображения.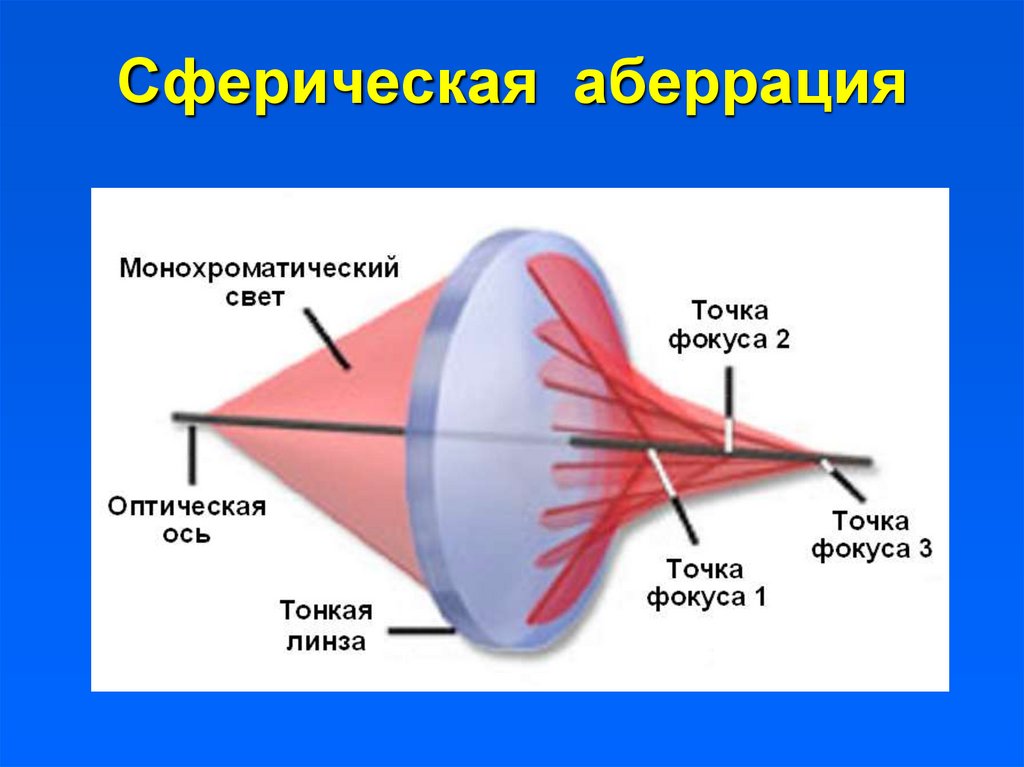 Это выражение определяет взаимное расположение изображений, образованных криволинейной поверхностью линзы радиусом х , зажатой между средами с показателями преломления n и n’ . Уточнение этого уравнения часто называют коррекцией более высокого порядка (первого, второго или третьего) путем включения членов в куб угла апертуры, что приводит к более точному расчету. Отклонение от идеальной сферической волны выражается в долях волны, где одна волна равна средней длине волны освещающего света. Это отклонение называется разность оптического пути , которая должна быть меньше одной четверти длины волны, чтобы объектив с дифракционным ограничением можно было считать свободным от аберраций.
Это выражение определяет взаимное расположение изображений, образованных криволинейной поверхностью линзы радиусом х , зажатой между средами с показателями преломления n и n’ . Уточнение этого уравнения часто называют коррекцией более высокого порядка (первого, второго или третьего) путем включения членов в куб угла апертуры, что приводит к более точному расчету. Отклонение от идеальной сферической волны выражается в долях волны, где одна волна равна средней длине волны освещающего света. Это отклонение называется разность оптического пути , которая должна быть меньше одной четверти длины волны, чтобы объектив с дифракционным ограничением можно было считать свободным от аберраций. Несмотря на то, что сферическую аберрацию можно скорректировать практически до неопределяемых пределов при визуальном наблюдении со всеми типами объективов, должны выполняться оптические характеристики любого данного объектива. Для масляных иммерсионных объективов с высокой числовой апертурой это обычно означает использование покровного стекла толщиной 0,17 мм и иммерсионного масла с показателем преломления 1,5180 (± 0,0004) на длинах волн 546 и 589.нанометры. Усложняет эти условия тот факт, что почти для всех материалов показатель преломления зависит как от длины волны, так и от температуры. В случаях, когда указаны точные свойства покровного стекла и масла, производители микроскопов могут скорректировать сферическую аберрацию для нескольких значений длины волны.
Несмотря на то, что сферическую аберрацию можно скорректировать практически до неопределяемых пределов при визуальном наблюдении со всеми типами объективов, должны выполняться оптические характеристики любого данного объектива. Для масляных иммерсионных объективов с высокой числовой апертурой это обычно означает использование покровного стекла толщиной 0,17 мм и иммерсионного масла с показателем преломления 1,5180 (± 0,0004) на длинах волн 546 и 589.нанометры. Усложняет эти условия тот факт, что почти для всех материалов показатель преломления зависит как от длины волны, так и от температуры. В случаях, когда указаны точные свойства покровного стекла и масла, производители микроскопов могут скорректировать сферическую аберрацию для нескольких значений длины волны. Как показано на рисунке 2, для образца, наблюдаемого в позиции P и окруженный иммерсионным маслом с показателем преломления n , существует сопряженная точка ( P(1) ) для устранения сферической аберрации в первом элементе линзы (полусферической линзе). В этом случае световые лучи, исходящие из точки P , покидают поверхность полусферической передней линзы, как если бы они исходили из точки P(1) . Менисковая линза шлифуется с радиусом поверхности с центром в точке P для образования второй сопряженной пары ( P(1) и P(2) ). Таким образом, свет от образца в точке P в конечном итоге выходит из менисковой линзы, как если бы он исходил из точки P(2) , что устраняет сферическую аберрацию для комбинации линз.
Как показано на рисунке 2, для образца, наблюдаемого в позиции P и окруженный иммерсионным маслом с показателем преломления n , существует сопряженная точка ( P(1) ) для устранения сферической аберрации в первом элементе линзы (полусферической линзе). В этом случае световые лучи, исходящие из точки P , покидают поверхность полусферической передней линзы, как если бы они исходили из точки P(1) . Менисковая линза шлифуется с радиусом поверхности с центром в точке P для образования второй сопряженной пары ( P(1) и P(2) ). Таким образом, свет от образца в точке P в конечном итоге выходит из менисковой линзы, как если бы он исходил из точки P(2) , что устраняет сферическую аберрацию для комбинации линз. Однако это неверно для образцов, помещенных в физиологический раствор или другие водные среды с показателями преломления, значительно отличающимися от покровного стекла. Даже при фокусировке через тонкие слои воды толщиной всего в несколько микрон возникают значительные аберрации, которые могут вызвать существенную асимметрию в функции рассеяния точки, вызывая неравномерное распределение выше и ниже фокальной плоскости. Эта концепция рассматривается в интерактивном руководстве по ссылке ниже.
Однако это неверно для образцов, помещенных в физиологический раствор или другие водные среды с показателями преломления, значительно отличающимися от покровного стекла. Даже при фокусировке через тонкие слои воды толщиной всего в несколько микрон возникают значительные аберрации, которые могут вызвать существенную асимметрию в функции рассеяния точки, вызывая неравномерное распределение выше и ниже фокальной плоскости. Эта концепция рассматривается в интерактивном руководстве по ссылке ниже.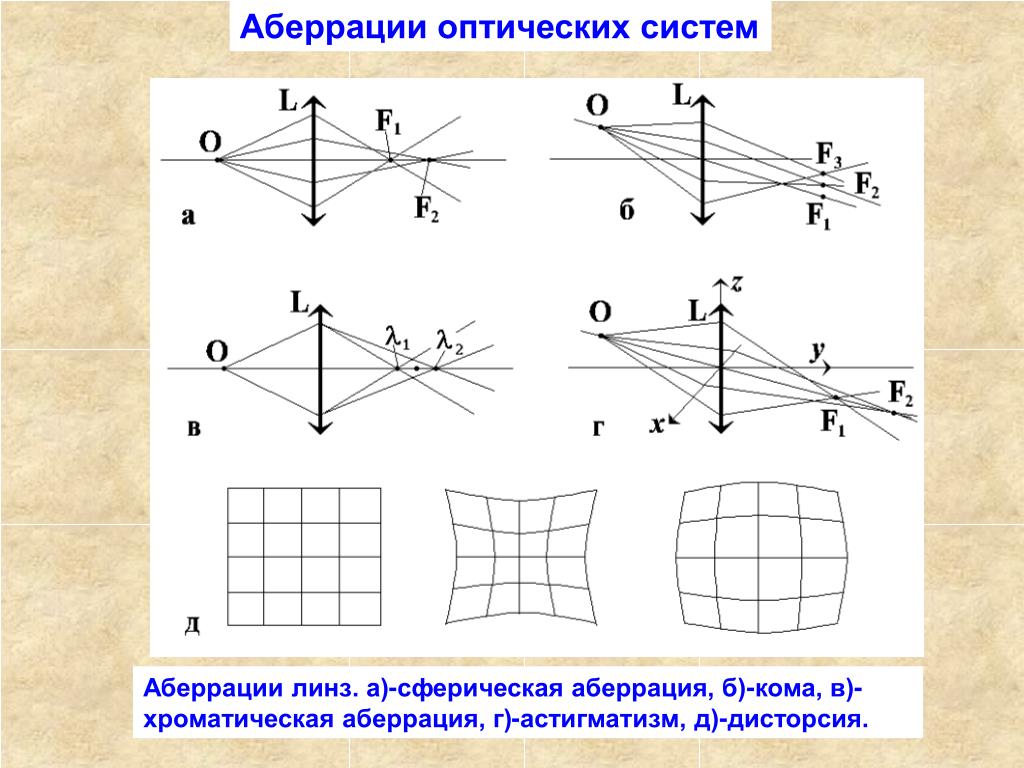 Сферическую аберрацию обычно исправляют с помощью стеклянных элементов (линзы дуплеты или тройки ), склеенные вместе. Стеклянные элементы спроектированы с различными формами выпуклости и/или вогнутости, чтобы гарантировать, что периферийные лучи и осевые лучи, особенно во внешней области поля зрения, будут сведены в общий фокус.
Сферическую аберрацию обычно исправляют с помощью стеклянных элементов (линзы дуплеты или тройки ), склеенные вместе. Стеклянные элементы спроектированы с различными формами выпуклости и/или вогнутости, чтобы гарантировать, что периферийные лучи и осевые лучи, особенно во внешней области поля зрения, будут сведены в общий фокус.
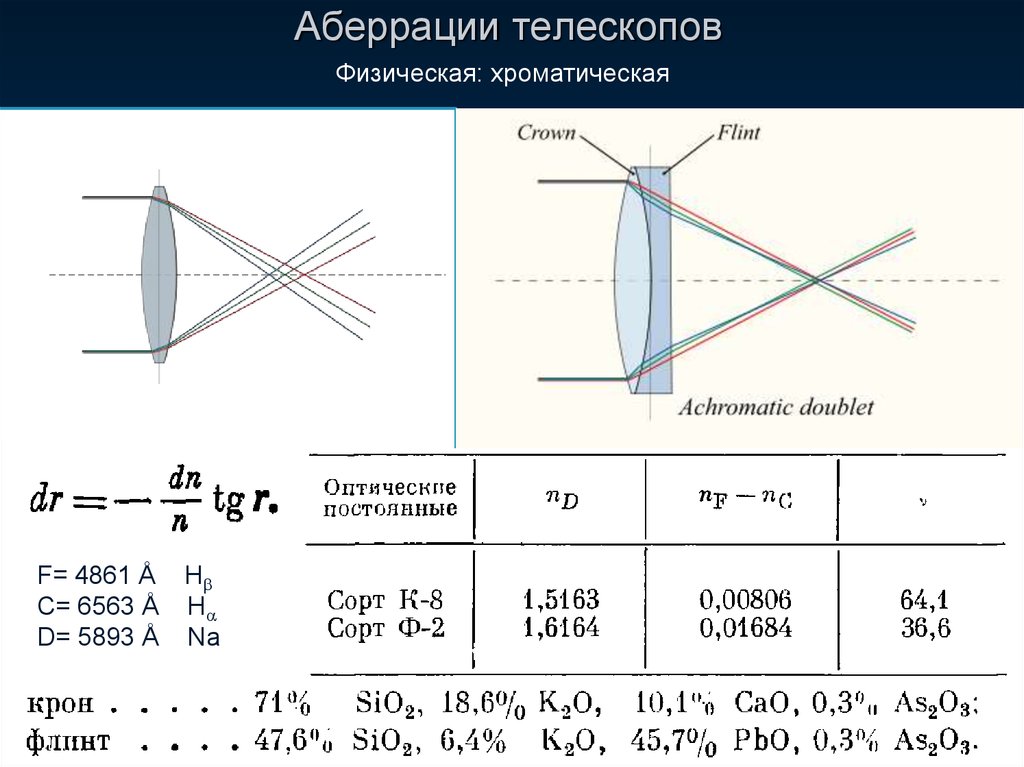 Например, при использовании сухих объективов с большим увеличением и высокой числовой апертурой правильная толщина покровного стекла (рекомендуется 0,17 мм) имеет решающее значение. На рис. 3 показано изменение полуширины кривой распределения интенсивности при изменении толщины покровного стекла. Даже при использовании высококачественных покровных стекол с допуском ±10 мкм полуширина изменяется более чем в два раза. Поскольку числовая апертура объектива увеличивается (выше значения 0,5), особенно с сухими и иммерсионными линзами, выбор покровных стекол правильной толщины становится особенно важным.
Например, при использовании сухих объективов с большим увеличением и высокой числовой апертурой правильная толщина покровного стекла (рекомендуется 0,17 мм) имеет решающее значение. На рис. 3 показано изменение полуширины кривой распределения интенсивности при изменении толщины покровного стекла. Даже при использовании высококачественных покровных стекол с допуском ±10 мкм полуширина изменяется более чем в два раза. Поскольку числовая апертура объектива увеличивается (выше значения 0,5), особенно с сухими и иммерсионными линзами, выбор покровных стекол правильной толщины становится особенно важным.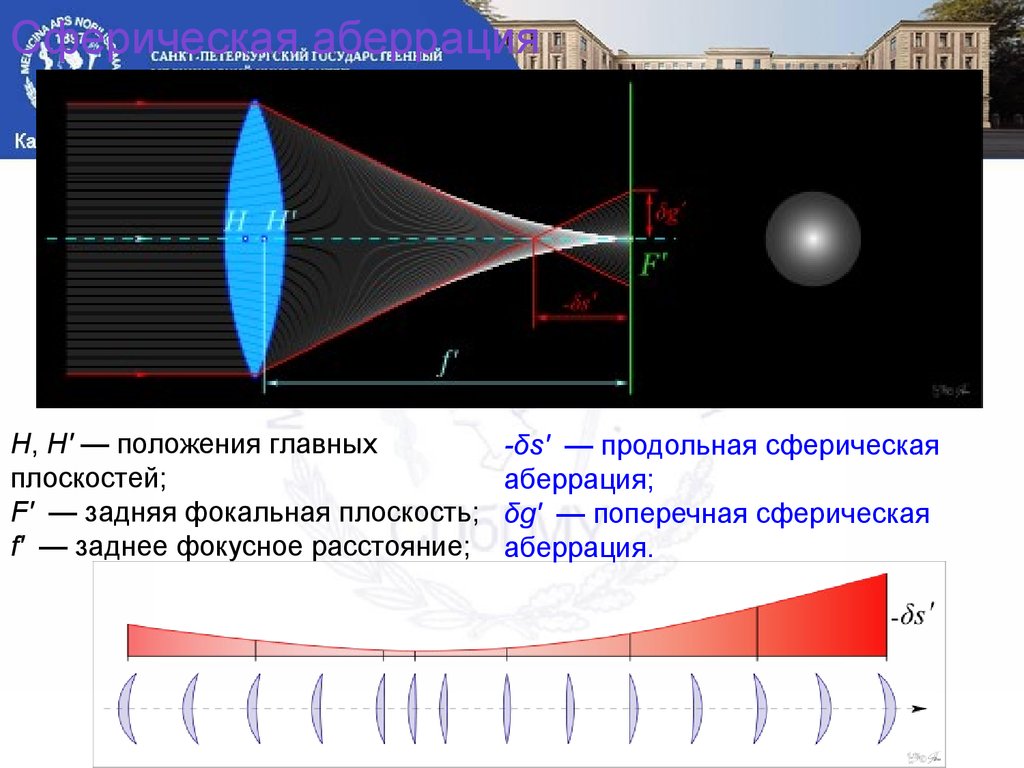 Кроме того, вставка аксессуаров в световой путь объективов с конечной длиной тубуса может привести к аберрациям при перефокусировке образца, если только эти аксессуары не были должным образом разработаны с дополнительной оптикой.
Кроме того, вставка аксессуаров в световой путь объективов с конечной длиной тубуса может привести к аберрациям при перефокусировке образца, если только эти аксессуары не были должным образом разработаны с дополнительной оптикой.