Какие Есть Виды Шумов и Про Отношение Сигнал/Шум

Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием. Насколько сильно значение случайного процесса могут отличаться от мат. ожидания описывает параметр дисперсия — мера разброса случайной величины. Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением, значение его квадратный корень из дисперсии.

• μ – математическое ожидание, вокруг какого значения колеблется.
• σ – дисперсия, насколько отклоняется

На рисунке представлены нормальные распределения четырех случайных процессов с разными значениями математического ожидания и дисперсии. В случае большего значения дисперсии, колокол Гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений и меньшей вероятности значений близких к мат. ожиданию.

В качестве меры скорости изменения случайного процесса может использоваться автокорреляционная функция, или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.

В случае нулевого сдвига, сигналы полностью совпадают и значение автокорреляционной функции максимально. При увеличении расхождения это значение уменьшается. Причем для слабо изменяющихся во времени сигналов спад функции происходит медленнее чем для быстро изменяющихся.

Математическое ожидание, дисперсия, автокорреляционная функция это примеры численных характеристик, которыми можно описать случайный процесс. Законы изменения реальных физических величин весьма сложны, и для того чтобы мы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определенные допущения.

При описании сигналов случайными процессами, мы часто оговариваем свойства стационарности и эргодичности.  Стационарным называется процесс в том случае, когда его плотность вероятности не зависит от временного сечения, то есть его статистические характеристики, мат ожидания, дисперсия, корреляционная функция не будут зависеть от времени. Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализации, мы можем использовать усреднение по времени одной реализации, на практике нам обычно доступна только одна реализация случайного процесса.

Спектральная плотность мощности

Спектральная плотность мощности по определению это распределение мощности сигнала в зависимости от частоты, то есть мощность приходящаяся на единичный интервал частоты. Мы можем рассматривать спектральную плотность мощности как еще одну меру скорости изменения случайного процесса, она связана с корреляционной функции случайного процесса, теоремы Винера — Хинчина — Колмагорова.

Рассмотрим два синусоидальных сигнала разной частоты. Частотные области этих сигналов будут представлены двумя линиями. Положение линии на оси x говорит о величине частоты синусоиды, а длина линии, о ее мощности или амплитуде. Случайные процессы мы также можем рассматривать, как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющейся быстро или медленно.

Спектр медленно изменяющегося случайного процесса содержит больше синусоид или спектральных компонент в левой части оси f, то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент, большей амплитуды в правой части частотной оси.

Белый шум

Случайный процесс у которого область частот заполнено равномерно называется белым шумом.

Белый шум это стационарный случайный процесс, с равномерно распределенной спектральной плотностью мощности.

В таком процессе присутствуют компоненты изменяющиеся быстро, медленно, средне и ни одна из них не преобладает над другими.

Белый шум получил свое название по аналогии со спектром белого света. Известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона.

Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определенным цветом можно обозначить преобладание в спектре сигнала определенных компонент.

Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты.

Если наложим синий фильтр, получим сигнал с относительно высокими частотами в спектре.

Цветовое обозначение частотного состава используется для описания так называемых цветных шумов, они никак не привязаны к какому-либо конкретному частотному диапазону и различаются только видом их спектральной плотности мощности. Цветные шумы, в том числе и белый шум это модели шумов, приближающие некоторые физические явления.

К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к фликкер-шуму, который достаточно успешно описывается моделью розового шума.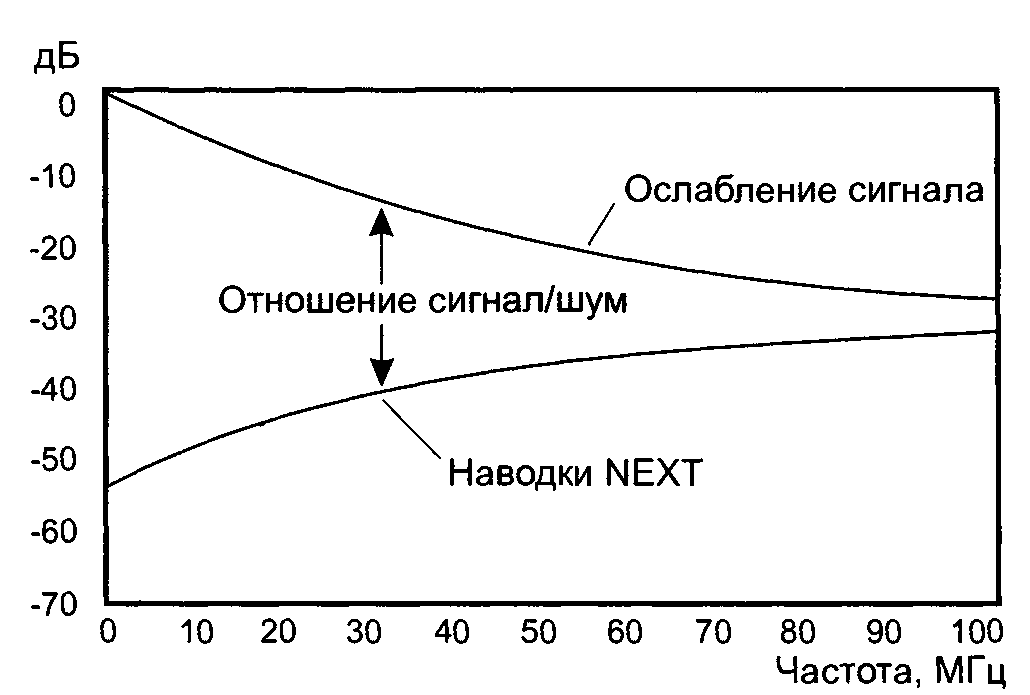 Красный шум описывает броуновское движение, модель серого шума используется в псих акустике и так далее.

Аддитивный белый гауссовский шум

Аддитивный белый гауссовский шум чаще всего используется в цифровой обработке сигналов .

Аддитивный белый гауссовский шум:

• у него равномерная спектральная плотность мощности, поэтому он белый;
• нормальное распределение, поэтому он гауссовский;
• с полезным сигналом он суммируется, поэтому он аддитивный;
• статистически он от сигнала независим.

На системы беспроводной связи и обработки сигналов воздействует множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме, распределение их суммарного воздействия будет близко к нормальному, именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных.

 Отношение сигнал/шум

Шум в подобных системах конечно же является нежелательным явлением. Одной из мер качества системы является отношение сигнал-шум. Это безразмерная величина равная отношению мощности полезного сигнала к мощности шума.

Отношение сигнал-шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться, но в любом случае, чем выше этот показатель, тем лучше. Одна из задач цифровой обработки сигналов повышение отношения сигнал-шум, существуют разные способы повышения это фильтрация и усреднение.

Усреднение или когерентное накопление

Если мы сложим два одинаковых сигнала по фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные с отрицательными.

Но сложить две реализации случайного процесса в фазе не получится, в каких-то точках произойдет усиление, каких-то ослабление шума. Проще говоря, при усреднении амплитуда шума не растет.

Накопление сигнала с шумом в matlab

Динамический диапазон и чувствительность

Динамический диапазон это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу так называемым шумовым дном, или чувствительностью.

Чувствительность это численный параметр равный уровню сигнала различимого системы над шумами, если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счет этого способны различать сигналы малой энергетики.

Виды шумов, отношение сигнал/шум, Статистическая обработка сигнала, Корреляционная функция

Рассмотрены 3 темы по основам цифровой обработки сигналов: виды шумов, отношение сигнал/шум, статистическая обработка сигнала, корреляционная функция.

В данном посте освещены 3 темы по основам цифровой обработки сигналов:

• Виды шумов, отношение сигнал/шум,
• Статистическая обработка сигнала,
• Корреляционная функция.

 

Виды шумов, отношение сигнал/шум.

В данной публикации мы поговорим о характеристиках случайных процессов, познакомимся с разными видами шумов, и узнаем о важном определении – отношение сигнал/шум. Начнём с характеристик.

Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием.

Насколько сильно значения случайного процесса могут отличаться от матожидания описывает параметр дисперсия, мера разброса случайной величины.

Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением. Значение его — квадратный корень из дисперсии.

На рисунке представлены нормальные распределения 4-х случайных процессов с разными значениями матожидания и дисперсии. В случае большего значения дисперсии колокол гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений, и меньшей вероятности значений, близких к матожиданию.

В качестве меры скорости изменения случайного процесса может использоваться авто-корреляционная функция или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.

В случае нулевого сдвига сигналы полностью совпадают, и значение авто-корреляционной функции максимально. При увеличении расхождения это значение уменьшается, причём для слабо изменяющихся во времени сигналов спад функции происходит медленнее, чем для быстро изменяющихся.

Математическое ожидание, дисперсия, авто-корреляционная функция – это примеры численных характеристик, которыми можно описать случайный процесс.

Законы изменения реальных физических величин весьма сложны, и для того, чтобы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определённые допущения.  При описании сигналов случайными процессами мы часто оговариваем свойства стационарности и эргодичности.

Стационарым процесс называется в том случае, когда его плотность вероятности не зависит от временного сечения. То есть его статистические характеристики – матожидание, дисперсия, коореляционная функция – не будут зависеть от времени.

Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализаций мы можем использовать усреднение по времени одной реализации. На практике нам обычна доступна только одна реализация случайного процесса.

Ещё одна важная характеристика случайного процесса – спектральная плотность мощности. По определению, это распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты.

Мы можем рассматривать спектральную плотность мощности как ещё одну меру скорости изменения случайного процесса. Она связана с корреляционной функцией случайного процесса теоремой Винера-Хинчина-Колмогорова, и с ней я советую познакомиться самостоятельно.

А мы пока что рассмотрим два синусоидальных сигнала разной частоты. В частотной области эти сигналы будут представлены двумя линиями. Положение линии на оси Х говорит о величине частоты синусоиды, а длина линии – о её мощности или амплитуде.

Случайные процессы мы также можем рассматривать как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющихся быстро или медленно. Спектр медленно изменяющегося случайного процесса содержит больше синусоид, или спектральных компонент, в левой части оси f – то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент большей амплитуды в левой части частотной оси.

Слуйчайный процесс, у которого область частот заполнена равномерно, называется белым шумом.

Белый шум – это стационарный слуйчайный процесс с равномерно распределённой спектральной плотностью мощности.

В таком процессе присутствуют компоненты, изменяющиеся быстро, медленно, средне, и ни одна из них не преобладает над другими.

Белый шум получил свой название по аналогии со спектром белого света. Нам известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона. Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определённым цветом можно обозначить преобладание в спектре сигнала определённых компонент. Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты. Если наложим синий фильтр – получим сигнал с относительно высокими частотами в спектре.

Цветовое обозначение частотного состава используется для описания так называемых цветных шумов. Они никак не привязаны к какому-либо конкретному частотному диапазону, и различаются только видом их спектральной плотностью мощности. Сразу оговорюсь, что цветные шумы, в том числе и белый шум – это модели шумов, приближающие некоторые физические явления.

 К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к так называемому фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в психоакустике и так далее.

Какая же модель шума чаще всего используется в цифровой обработке сигналов? Это аддитивный белый гауссовский шум.

• У него равномерная спектральная плотность мощности, поэтому он белый.
• Нормальное распределение, поэтому он Гауссовский.
• С полезным сигналом он суммируется, поэтому он аддитивный.
• И  статистически он от сигнала независим.

На системы беспроводной связи и обработки сигналов воздействуют множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме распределение их суммарного воздействия будет близко к нормальному.

Именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных.  Шум в подобных системах, конечно же, является нежелательным явлением.

Одной из мер качества системы является отношение сигнал/шум. Это безразмерная величина, равная отношению мощности полезного сигнала к мощности шума. Отношение сигнал/шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться. Но в любом случае, чес выше этот показатель, тем лучше.

Одна из задач цифровой обработки сигналов – повышение отношения сигнал/шум. Существуют разные способы повышения. О фильтрации мы поговорим в дальнейших публикациях, а сейчас давайте познакомимся с усреднением, или когерентным накоплением.

Если мы сложим два одинаковых сигнала в фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные – с отрицательными. Но сложить две реализации случайного процесса в фазе не получится. В каких-то точках произойдёт усиление, в каких-то – ослабление шума. Проще говоря, при усреднении амплитуда шума не растёт.

Давайте рассмотрим пример накопления сигнала с шумом в MATLAB.

Мы генерируем синусоиду, и добавляем к ней аддитивный белый Гауссовский шум при помощи функции awgn. Функция эта содержится в расширении MATLAB Communications Toolbox. На её вход мы подаём исходный незашумлённый сигнал, и параметр отношения сигнал/шум в децибелах. Строим на графике сигнал с шумом и без шума.

Затем мы выделим только шумовую компоненту, вычитаем из смеcи сигнал/шум исходный сигнал. Визуализируем его отсчёты командой stem. Функция периодограм позволит нам оценить спектральную плотность мощности нашего шума. Мы видим, то что распределение действительно равномерное, это белый шум.

Гистрограмма показывает нам, что распределение значений вектора noise близко к нормальному. 

Теперь мы генерируем большое число зашумлённых сигналов.  Несмотря на то, что мы вызываем одну и ту же команду, реализации шума в каждом из векторов будут отличаться. Можем убедиться в этом, отразив четыре первых вектора на графике.

Если мы будем складывать эти вектора между собой, то их синусоидальная компонента будет всегда складываться в фазе, в то время как шумовые компоненты будут складываться случайным образом. Убедимся в том, что амплитуда шума в результирующей сумме заметно ниже.

В завершении давайте поговорим о ещё двух хар-ках системы, которые непосредственно связаны с шумом.

Динамический диапазон – это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу – так называемым шумовым дном, или чувствительностью.

Чувствительность – это численный параметр, равный уровню сигнала, различимого системой над шумами. Если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счёт этого способна различать сигналы малой энергетики.

В следующей публикации мы подробнее поговорим о статистических параметрах сигнала.

 

 

 

Наверх

 

Статистическая обработка сигнала.

В этой публикации мы под робнее поговорим о статистической обработке сигналов. Давайте вспомним, какие статистические параметры мы рассматривали, когда говорили о случайных процессах. Когда мы рассматривали случайный процесс с нормальным распределением мы оперировали понятиями математического ожидания  и дисперсии. Когда мы рассматриваем сигналы в общем виде, то у них так же есть статистические показатели со схожим смыслом.

У любого сигнала, непрерывного и дискретного, можно определить среднее значение. Оно может вычисляться по-разному.

Если мы ищем среднее арифметическое, то для этого мы складываем все отсчёты сигнала и делим сумму на количество отсчётов.

Но также в качестве среднего значения для дискретной последовательности может применяться медианное значение. При его вычислении все элементы дискретного сигнала выстраиваются по возрастанию, и находится центральный элемент упорядоченной последовательности.

То, что мы называли дисперсией случайного процесса, у произвольного сигнала может именоваться отклонением от среднего значения. Для колебательных процессов отклонение по сути – это амплитуда колебаний.

Для любого сигнала мы можем определить минимальное и максимальное значение на отрезке наблюдения. Минимум и максимум сигнала определяют его размах, или динамический диапазон.

Ну и скорость изменения сигнала может характеризоваться корреляционной функцией. Её мы подробно рассмотрим в следующей публикации.

Статистические показатели реальных сигналов часто изменяются во времени. К примеру, при относительной стабильности амплитуды колебаний во времени, среднее значение, вокруг которого изменяется сигнал, может «плавать».

При обработке зачастую выбирают некоторые временные рамки относительной стабильности статистических характеристик, и подсчитывают эти характеристики для коротких отрезков исходного сигнала. Временной интервал, на котором рассматривается сигнал, называется окном. И окно это обычно перемещается или скользит по исходному сигналу.

Подобным образом мы можем находить локальные статистические характеристики, такие как, например, локальные средние значения, или локальные минимумы и максимумы. Подобная обработка позволяет отслеживать постоянную составляющую сигнала, которую мы также называем трендом, и находить пики или спады на графике сигнала.

Рассмотрим пример нахождения тренда или меняющейся во времени постоянной составляющей сигнала методом скользящего среднего. Как вы поняли из названия, этот метод подразумевает нахождение локального среднего арифметического. Окно перемещается по сигналу, и в результате обработки формируется выходной вектор, в отсчёты которого записываются значения среднего арифметического для каждого шага.

Результирующий вектор становится сглаженным, по сравнению с исходным. И чем больше размер окна – тем больше степень сглаживания. Можно использовать небольшие окна для сглаживания формы сигнала и избавления от нежелательных высокочастотных колебаний, либо можно взять большое окно для выделения постоянной составляющей.

Если рассматривать процесс вычисления среднего значения, как набор арифметических операций над каждым из отсчётов, попавших в окно, то в случае со скользящим средним каждый отсчёт умножается на величину, обратную размеру окна, и затем все результаты произведения складываются.

Если мы берём окно не из трёх, а из пяти элементов, то и коэффициент становится равным одной пятой. Но коэффициенты не обязательно должны быть одинаковыми. В общем случае мы рассматриваем операцию нахождения взвешенного среднего. Окна с разнообразными коэффициентами могут усиливать или ослаблять различные частотные компоненты сигнала. Процесс взвешенного усреднения – одна из форм цифровой фильтрации. О цифровых фильтрах мы будем подробно говорить в других публикациях. А пока что давайте осуществим статистическую обработку сигнала в MATLAB.

 

Мы вновь проанализируем сигнал ЭКГ, но в этот раз мы попробуем выделить из него так называемый Q-R-S комплекс, то есть определить положение Q-, R-, S-зубцов в наших данных. Но наши данные зашумлены и постоянная составляющая у сигнала изменяется во времени, что может помешать нам выделить искомое зубцы. Поэтому нам необходимо отфильтровать наши данные, избавиться от постоянной составляющей и выделить локальные экстремумы. Для фильтрации и удаления тренда мы можем воспользоваться одной и той же функцией movmean из состава Signal Processing Toolbox. Она у нас выполняет операцию скользящего среднего. Если мы возьмём маленькое кошка из 10 отсчётов, то мы сгладим форму нашего сигнала. А если мы возьмём большое окно из 300 отсчётов, то мы выделим постоянную составляющую. Отразим её на том же графике.

Для выделения пиков наших Q-, R-, S-зубцов воспользуемся встроенной функцией findpeaks. Выделение R-, S-зубцов происходит достаточно просто, мы просто берём выбросы величины, которые больше чем 0,5 или меньше чем –0,5 и отображаем их на том же графике.

А вот для выделения Q-зубцов нам придется воспользоваться логической индексацией. Мы знаем то, что Q-выброс лежит в пределах от –0,2 мВ до –0,5 мВ, поэтому мы выделяем только те минимальные, скажем так экстремумы, минимальные значение сигнала, которые лежат в этих пределах.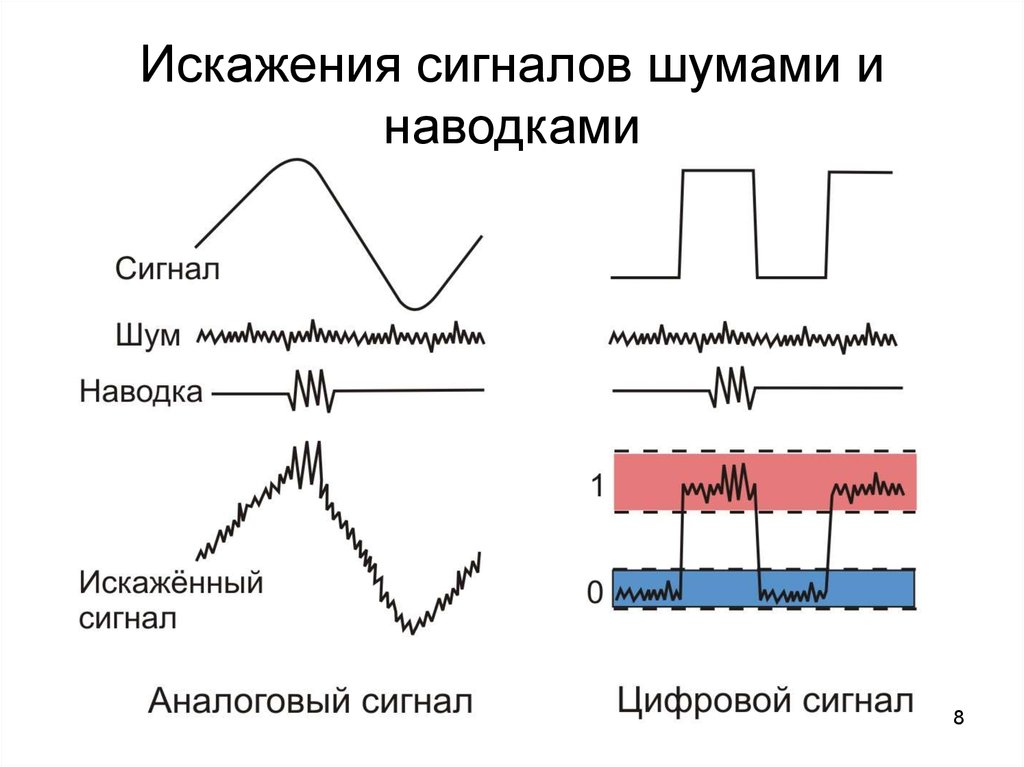 Также можно построить Q-зубцы на том же самом графике.

Как видите воспользовавшись двумя встроенными функциями мы успешно выделили Q-R-S комплекс из наших зашумленных и нестабильных по времени данных ЭКГ. В следующей публикации мы поговорим о корреляционной функции и корреляционной обработке.

 

 

Наверх

 

Корреляционная функция.

Когда мы рассматривали случайные процессы, мы упоминали корреляционную функцию, как меру изменения скорости процесса. КФ измерялась для одного сигнала, а значит происходило сравнение сигнала с самим собой, сдвинутым во времени. По факту мы рассматривали так называемую автокорреляционную функцию. Но в предыдущих видео мы не рассказали, как эта функция вычисляется. Для того, чтобы понять, как мы находим корреляционную функцию сигнала, надо вспомнить понятие корреляции.

Корреляция – это мера зависимости двух величин. Для численной оценки используется коэффициент корреляции. Он не может быть больше единицы, и меньше минус единицы. Когда коэффициент корреляции +1, говорят, что две величины идеально коррелированы друг с другом, а значит что при изменении первой величины на какой-то значение вторая изменяется на такое-же значение. Если коэффициент –1 , то росту первой величины соответствует уменьшение второй величины на такое же значение.

Проиллюстрируем зависимость коэффициента корреляции от временного сдвига двух идентичных сигналов.

В начальный момент времени сигналы выровнены, и коэффициент корреляции равен +1. При равном приращении первая и вторая функции изменяются одинаково. Теперь сдвинем вторую зависимость по времени.

При равном приращении она изменяется на меньшую величину. А значит, коэффициент корреляции между двумя зависимостями становится меньше. Увеличивая временной сдвиг мы доходим до момента, когда умен ьшение значения первой величины соответствует увеличению значения второй, а значит коэффициент корреляции становится отрицательным.

Зависимость коэффициента корреляции от временного сдвига между сигналами – по сути есть корреляционная функция. Но давайте рассмотрим формулу.

В общем случае мы рассматриваем взаимно-корреляционную функцию и оцениваем зависимость между двумя сигналами. Частным случаем взаимно-корреляционной функции является автокорреляционная функция, когда мы сравниваем сигнал с его задержанной во времени копией. 

Рассмотрим формулу. Я тут привёл формулу для непрерывных функций, но если мы берём дискретные величины, то операция интегрирования будет заменена на простое суммирование. Здесь есть две функции. Первая функция f (не обращайте пока что внимания на знак звёздочки, это комплексное сопряжение, но для действительных сигналов оно не важно), так вот, первая функция f умножается на вторую функцию g, при этом вторая функция сдвигается во времени на величину τ. От величины сдвига τ мы и строим зависимость коэффициента корреляции.

Рассмотрим графическое представление. Первую функцию f мы фиксируем на временной оси, а вторая g по этой оси будет перемещаться. Она перемещается из значений отрицательного сдвига между функциями в область положительных значений сдвига. Величина корреляции соответствует площади перекрытия двух графиков, и максимума она достигает, когда две фигуры максимально накладываются друг на друга. Стоит отметить, что если мы поменяем функции местами, то есть зафиксируем g и будем скользить функцией f, то вид корреляционной функции изменится на зеркальный. В случае автокорреляционной функции форма зависимости всегда симметрична, и имеет максимум в точке, равной нулевому сдвигу сигнала относительно самого себя.

Давайте посмотрим на несколько примеров подсчёта корреляционной функции для дискретных сигналов в MATLAB.

Автокорреляционная функция прямоугольного импульса имеет форму треугольника.

Взаимнокорреляционная функция пилообразного импульса и прямоугольного импульса несимметрична.

Автокорреляционная функция отрезка синусоиды симметрична, и имеет вид нарастающего и затухающего колебательного процесса с выраженным максимумом в моменте совпадения импульсов

А автокорреляционная функция бесконечной синусоиды – это такая же синусоида, с той же частотой.

Особо важно отметить автокорреляционную функцию случайного процесса, или шума. Она имеет один выраженный максимум, и при малейшем сдвиге значения её падают почти до нуля. Это говорит о том, что шум – слабо коррелированный процесс, и этим свойством мы будем пользоваться при обработке.

А обработка корреляционными методами – это важная часть ЦОС. При помощи вычисления взаимнокорреляционной функции  мы можем обнаруживать интересующие нас отрезки сигнала в эфире, в том числе на фоне шумов, находить сигналы, похожие на некий выбранный эталон, и оценивать степень схожести, или мы можем точно определять задержу распространения сигнала. К примеру, радиолокационная станция отправляет импульс известной формы в сторону цели и ждёт отражённый сигнал. Максимум корреляционной функции даст нам величину задержки между переданным и принятым импульсами, которую мы затем можем использовать для определения расстояния до цели.

Выполним корреляционную обработку сигнала в MATLAB. В данном случае мы будем пытаться найти фрагмент аудиосигнала в полном сигнале, в том числе на фоне шумов. Загружаемый аудиосигнал – эта запись звука кольца, крутящегося на столе. Давайте загрузим его и послушаем командой Sound. Так вот звучит фрагмент аудиосигнала, который мы попробуем найти. 

Область, которую мы выделили, обозначена на графике двумя пунктирными линиями. Давайте также построим график взаимной корреляционной функции исходного сигнала и выделенного фрагмента. Для этого воспользуемся функцией xcorr и передадим ей исходный сигнал и выделенный фрагмент.

В первую выходной переменной записываются отчёты функции, а во вторую – величины временного сдвига. На графике взаимной корреляционной функции мы видим явно выраженный максимум, в тот момент времени когда наш фрагмент совпадает с самим собой на исходном сигнале. Используем максимум вектора lags для того, чтобы отразить фрагмент на сигнале. 

Теперь давайте добавим шум к исходному сигналу и к фрагментам.

Причем, обратите внимание, что мы добавляем разный шум к полному сигналу и к нашему фрагменту. Послушаем как звучит фрагмент на фоне шума. Уровень шума достаточно велик, и мы совершенно не слышим звука кольца.

Но даже в этом случае корреляционная обработка позволяет нам точно определить момент начала фрагмента, и мы также сможем показать где наш искомый фрагмент на всём сигнале. Пока что закончим с корреляционной функцией и обработкой. Тема следующей публикации – моделирование сигнала, то есть приближение его аналитической функцией.

Уменьшение шума сигнала на практике

Шум сигнала в промышленной среде может вызвать сбои в работе систем управления технологическими процессами. Этот электрический шум может внедряться в аналоговые или цифровые сигналы и обманывать управляющее оборудование, заставляя думать, что переменная процесса отличается от того, чем она является на самом деле. Это недопонимание между оборудованием управления технологическим процессом, как и все виды недопонимания, может привести к любому количеству непредвиденных, непредвиденных последствий. Как скажет вам любой инженер-электрик, ни одна система не может продолжать нормально функционировать без надлежащей связи.

Ни одно промышленное предприятие никогда не будет на 100 % свободным от электрических помех. Низкий уровень шума, присутствующий на большинстве заводов, как правило, недостаточен, чтобы вызвать проблему. Когда отношение сигнал/шум становится неуправляемым, это становится проблемой. Имеются аппаратные и программные решения, помогающие бороться с сигнальным шумом в особо шумных средах, включая настройки шумоподавления, которые могут быть

доступны в уже установленном, но недостаточно используемом оборудовании. Покупка дорогостоящего нового оборудования для фильтрации шума или изоляции сигналов в большинстве случаев не требуется, если в первую очередь соблюдаются надлежащие методы планирования и установки. Знание того, что такое сигнальный шум, что его вызывает и как предотвратить его влияние на сигнальные сети, должно предоставить правильный арсенал инструментов, необходимых для поддержания связи.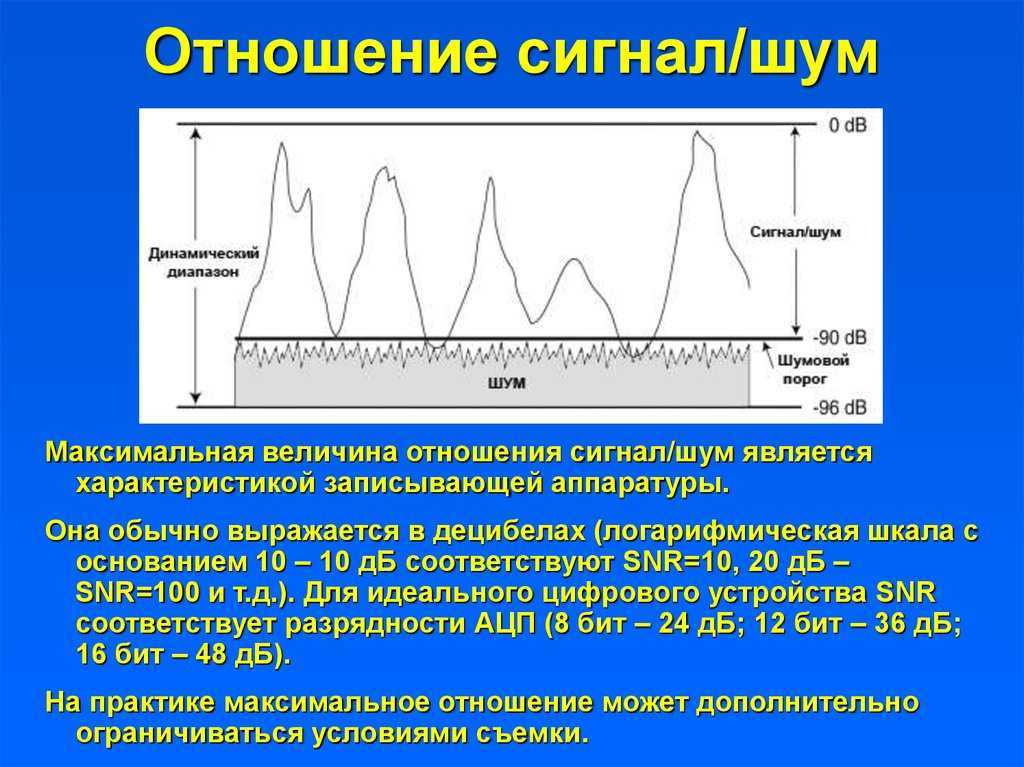

Шум сигнала, в самом общем смысле, — это любые нежелательные помехи, ухудшающие сигнал связи. Шум сигнала может мешать как аналоговым, так и цифровым сигналам; однако количество шума, необходимого для воздействия на цифровой сигнал, намного выше. Это связано с тем, что цифровые сигналы передаются с использованием набора дискретных электрических импульсов для передачи цифровых «битов». Как видно на рисунке 1, эти электрические импульсы требуют большого количества шума, чтобы их можно было спутать друг с другом.

И наоборот, аналоговые сигналы представляют собой бесконечный диапазон возможных значений с использованием установленного диапазона, например, 4-20 мА или 0-10 В. В этом случае любые нежелательные скачки напряжения или тока вызовут колебания в передаваемом сообщении. Незначительные вариации аналоговых сигналов, порядка милливольт или микроампер, обычно не приводят к значительному (или даже заметному) расхождению. Однако высокие уровни электрических помех могут привести к большим колебаниям и, следовательно, к существенным расхождениям, делающим связь между устройствами управления технологическим процессом совершенно невозможной.

Как видно на рис. 2, шум сигнала, введенный в электрическую связь, увеличивает или уменьшает ожидаемое значение сигнала. В производственной ситуации, когда жизненно важные процессы автоматически контролируются на основе измерения этого сигнала, любое изменение может привести к непредсказуемым и потенциально опасным результатам.

Шумовая инъекция может происходить в любом месте системы и в любом физическом месте, где сеть подвергается воздействию. Это может быть результатом действия различных факторов в любом месте сети. Устранение шумов сигнала может показаться сложной задачей; тем не менее, есть некоторые причины, которые встречаются чаще, чем другие. Эти распространенные причины составляют подавляющее большинство шумов сигналов, мешающих работе сетей управления технологическими процессами.

КОНТУРЫ ЗАЗЕМЛЕНИЯ И НЕПРАВИЛЬНОЕ ЗАЗЕМЛЕНИЕ

Как обсуждалось в предыдущем выпуске The Current Quandary, контуры заземления создают дополнительный ток в сигнальном контуре из-за перепада напряжения между двумя точками заземления в системе с несколькими заземлениями. Эта и другие проблемы с заземлением могут привести к притоку сигнального шума в функционирующую в остальном сеть.

НЕПРАВИЛЬНАЯ ПРОВОДКА

Плохо проложенные сети, например, не использующие экранированную витую пару и кабелепровод, более чувствительны к окружающим электрическим помехам.

ПЛОХАЯ КОНСТРУКЦИЯ ЦЕПИ ИЗДЕЛИЯ

Плохо спроектированная электронная схема в устройствах, которая не обеспечивает надлежащей защиты от внутренних и внешних источников шума, также с большей вероятностью будет иметь проблемы с сигналом.

БЛИЖАЙШАЯ БЛИЗОСТЬ К ДРУГОМУ ЭЛЕКТРИЧЕСКОМУ ОБОРУДОВАНИЮ

Устройства или провода, расположенные в непосредственной близости от электрического оборудования, генерирующего сильные магнитные поля, такого как генераторы, двигатели или линии электропередач, могут улавливать некоторые из этих помех, что может способствовать колебаниям в сигналах связи

ДЛИННЫЕ ПРОВОДА, ПОДНИМАЮЩИЕ РАДИОЧАСТОТЫ

Длинные отрезки провода (особенно неэкранированного провода) в основном действуют как антенны; они улавливают радиоволны и преобразуют их в электрические сигналы, создавая дополнительный шум в системе.

ИСКАЖЕНИЕ ТЕХНОЛОГИЧЕСКОГО СИГНАЛА

Наиболее распространенной и очевидной проблемой, вызванной сигнальным шумом, является искажение технологического сигнала, вызывающее неправильную интерпретацию или отображение состояния процесса оборудованием. Добавление и/или вычитание из сигнала процесса преобразуется в неправильную переменную процесса. Чтобы представить это в контексте, см. пример на рис. 3 ниже.

ПОЯВЛЯЕМАЯ ПОТЕРЯ СИГНАЛА

Чрезвычайный шум сигнала может привести к явной потере сигнала, хотя и редко. Большинство современных электронных устройств имеют встроенную фильтрацию шума. Однако в очень шумных условиях этого фильтра будет недостаточно, что может привести к тому, что оборудование не будет принимать сигнал и вообще не будет осуществляться связь.

НЕПРАВИЛЬНОЕ УПРАВЛЕНИЕ ПРОЦЕССОМ

В примере, показанном на рис. 3, каждое устройство в сети работает точно так, как задумано; однако шум сигнала вызвал недопонимание между устройствами. Следовательно, бак остался пустым. Система, испытывающая флуктуации шумового сигнала, может непреднамеренно включать и выключать реле и аварийные сигналы через нерегулярные промежутки времени из-за неправильного понимания шумовых сигналов. Подобная ситуация приводит к неправильному управлению производственным процессом.

ПРИЛОЖЕНИЕ

Радарный уровнемер измеряет уровень жидкости в баке. Он выдает сигнал 4–20 мА (4 мА при пустом баке и 20 мА при полном) на механическое реле, которое при срабатывании 4,5 мА активирует насос, чтобы начать заполнение бака.

ПРОБЛЕМА

Резервуар опорожняется, и датчик выдает сигнал 4 мА, но из-за сильного шума реле получает сигнал 5 мА и никогда не запускает и не активирует насос. Резервуар остается пустым, и процесс останавливается.

Как и в случае всех проблем с подключением к системе управления производственным процессом, гораздо проще следовать некоторым простым рекомендациям при планировании, проектировании и установке устройств управления технологическим процессом, чем пытаться устранять проблемы с системой после того, как она введена в эксплуатацию. Успешное планирование может сэкономить сотни человеко-часов и неисчислимое разочарование, когда речь идет о предотвращении помех от сигнального шума в системе.

Когда речь идет о предотвращении шума сигнала, чем слабее сигнал, тем больше он подвержен шуму. Сигналы низкого уровня, такие как импульсный сигнал расходомера с магнитным датчиком или милливольтовый выход термопары, очень чувствительны к окружающему шуму. Любое количество шума, введенного в эти типы систем, обязательно окажет некоторое влияние на передаваемый сигнал.

Хотя может возникнуть соблазн просто удлинить провода от этих устройств, чтобы подключить их к устройствам отображения или управления, настоятельно рекомендуется использовать передатчик или кондиционер для усиления сигнала перед его передачей по проводу любой длины. Этот усиленный сигнал сможет выдержать большее количество шума, прежде чем его предполагаемое значение начнет искажаться. Однако более эффективным способом избежать шума является преобразование аналогового сигнала в цифровой вместо его усиления. Как показано на рисунке 4, цифровые сигналы с их набором дискретных битов гораздо более устойчивы к шуму, чем аналоговые.

Если систему необходимо установить в зоне, подверженной воздействию электрических помех, установщик должен предусмотреть использование программных или аппаратных фильтров помех, которые часто входят в состав современных устройств управления технологическими процессами. Обратитесь к инструкции по эксплуатации устройства

, чтобы убедиться в наличии шумоподавляющих фильтров. Глубокое понимание среды установки и устройств может сэкономить время и нервы.

Как говорится, ни один план не выдерживает первого контакта с противником. Тем не менее, установщики должны следить за тем, чтобы непредвиденные ограничения окружающей среды или устройств не мешали процессу установки и не создавали проблем с устранением неполадок в будущем. Использование ярлыков для преодоления проблем с установкой может быть заманчивым в краткосрочной перспективе, но в будущем это решение будет стоить дорого.

Монтажники всегда должны использовать экранированную витую пару для соединения компонентов системы. Синфазный шум, или шум, общий для двух проводов витой пары, легче отфильтровать, чем шум, присутствующий только в одном проводе. Кроме того, хотя может показаться удобным прокладывать сигнальные линии через тот же кабелепровод, что и линии электропередач, этого всегда следует избегать. Шум от этих линий 120 или 240 В может легко попасть на сигнальные линии.

Провода также следует держать подальше от любого оборудования, создающего магнитные поля, такого как двигатели, трансформаторы или большие реле с индуктивными нагрузками. Провода, соединяющие разные цепи, должны быть установлены перпендикулярно друг другу, так как параллельные линии с большей вероятностью будут обмениваться помехами. Провода также должны быть как можно короче, чтобы они не действовали как антенны.

Проводка всегда должна прокладываться так, чтобы не было контуров заземления. Для этого используется только одна точка заземления для всех устройств, присутствующих в сети. Если для нескольких устройств в сети требуется заземление, убедитесь, что один и тот же источник заземления используется во всей системе с помощью экранированного кабеля.

Помня об этих простых рекомендациях на протяжении всего процесса установки, вы сможете убедиться, что ваша реализация учитывает шум сигнала так же, как и на первоначальных этапах планирования. Если бы установщик установки, показанной на рис. 3, следовал рекомендациям во время планирования и установки, он бы знал, что линии питания переменного тока всегда должны быть изолированы от сигнальных линий 4–20 мА, прокладывая их вдоль экранированных кабелей внутри независимого кабелепровода.

Шум сигнала — это проблема, с которой сталкиваются все промышленные предприятия из-за работающего электрического оборудования. Шум сигнала становится проблемой для этих объектов, когда он мешает сигналам процесса, передаваемым между устройствами. Это может привести к неточной передаче данных о критических переменных процесса, что может помешать работе систем управления технологическим процессом или даже привести к его остановке.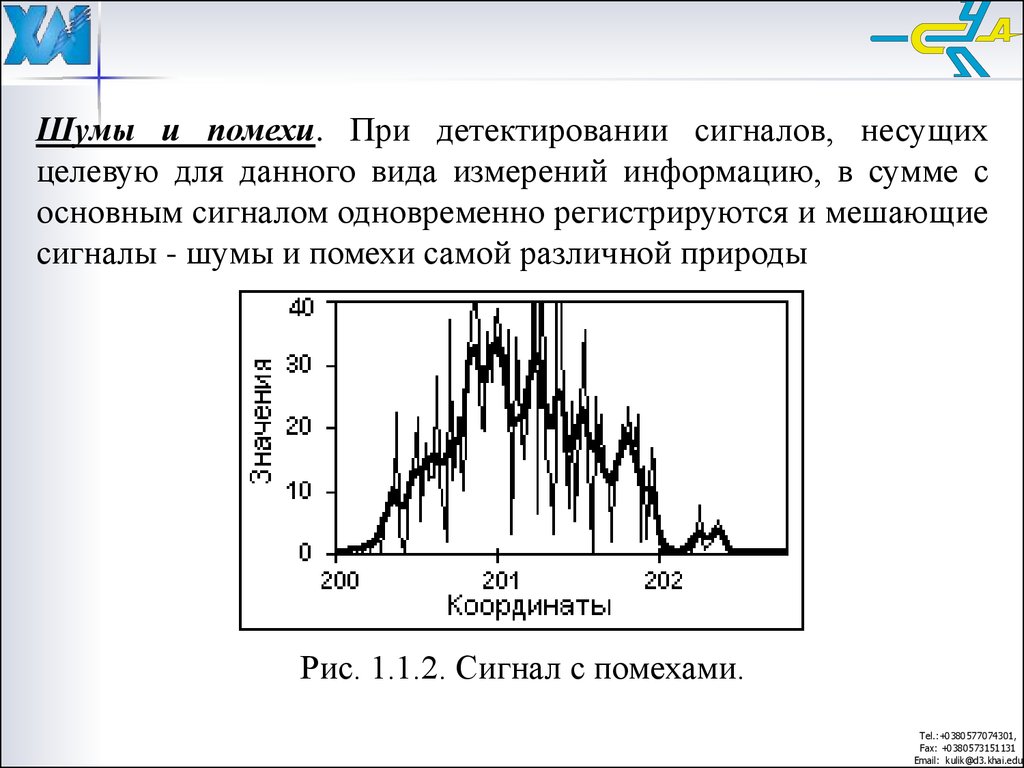 Следование некоторым простым передовым методам при планировании и установке решения для управления технологическим процессом может помочь обеспечить бесперебойную связь и устранить текущие затруднения.

Если у вас есть идея для будущей темы, которая будет представлена ​​в The Current Quandary, свяжитесь с Precision Digital по телефону [email protected]

---

Саймон Паонесса, технический писатель, Precision Digital Corporation

Загрузите это приложение заметка в формате PDF.

Что такое отношение сигнал/шум и как его рассчитать? | Блог Advanced PCB Design

 

Будучи подростком, изучая все тонкости автомобильной аудиосистемы, я часто наслаждался мельчайшими подробностями каждой ноты. Для меня музыка опьяняла почти так же сильно, как науки и электроника. Однако в это время на первый план выходит появление компакт-дисков и, конечно же, автомобильного сабвуфера.

До появления компакт-дисков винил был очевидным выбором для воспроизведения звука с точки зрения удовольствия от прослушивания. Тем не менее, многие утверждают, что это все еще так, при определенных условиях. Более того, компакт-диск в то время изменил правила игры, и его четкость по сравнению с кассетной лентой была неоспоримой. Точно так же, как существовал спрос на устройства для воспроизведения нового видеостандарта 4K, то же самое было и с компакт-дисками.

Что, конечно же, положило начало автомобильному аудио CD-ресиверу. Благодаря превосходной четкости и простоте использования CD-ресивер был полным. Однако там, где есть капитализм, вы обязательно найдете прямую конкуренцию. Это, безусловно, имело место в случае с CD-ресивером, и самым высмеивающим отличием, которое высококачественные автомобильные аудиокомпоненты могли использовать, чтобы повлиять на своих клиентов, была превосходная четкость. Четкость, о которой они говорили, была достижима только благодаря их превосходным характеристикам отношения сигнал/шум.

Единственной характеристикой, которая всегда была лучше, чем у младших брендов, было их отношение сигнал/шум (SNR). Кроме того, даже для нетренированного уха разница в чистоте и музыкальном присутствии была неоспоримой. Таким образом, если SNR может иметь такое большое значение в чистоте музыкального звука, то его важность в приложениях для передачи сигналов экспоненциально более критична. Поэтому в следующих нескольких абзацах я расскажу об отношении SNR и о том, как его рассчитать для обеспечения проектной точности.

Что такое отношение сигнал/шум?

С точки зрения определения, SNR или отношение сигнал/шум – это соотношение между полезной информацией или мощностью сигнала и нежелательным сигналом или мощностью фонового шума.

Кроме того, SNR — это параметр измерения, используемый в областях науки и техники, который сравнивает уровень полезного сигнала с уровнем фонового шума. Другими словами, SNR представляет собой отношение мощности сигнала к мощности шума, и его единицей выражения обычно являются децибелы (дБ). Кроме того, отношение больше 0 дБ или больше 1:1 означает больше сигнала, чем шума.

Помимо технического определения SNR, я определяю его в других терминах с помощью сравнительного анализа. Например, скажите, что вы и еще один человек находитесь в большой комнате и разговариваете. Однако в комнате полно других людей, которые тоже разговаривают. Кроме того, некоторые из других людей также имеют схожие с вами и другим человеком, участвующими в вашем обсуждении, голосовые паттерны. Как вы понимаете, было бы трудно разобрать, кто что говорит.

Почему важно соотношение сигнал/шум?

В предыдущем сравнении вы можете лучше понять, что подразумевается под нежелательным сигналом или шумом. Как вы также можете себе представить, было бы почти невозможно понять другую сторону, участвующую в вашем разговоре. Кроме того, в подобном сценарии мы бы считали это проблемой отношения сигнал-шум или эквивалентом отношения сигнал-шум, которое ниже допустимых параметров.

Теперь предположим, что полезный сигнал представляет собой важные данные со строгим или узким допуском на ошибки, и есть другие сигналы, нарушающие ваш желаемый сигнал. Опять же, это сделало бы задачу приемника экспоненциально более сложной по расшифровке полезного сигнала. Таким образом, именно это делает столь важным высокое отношение сигнал/шум. Кроме того, в некоторых случаях это также может означать разницу в функционировании устройства, и во всех случаях это влияет на производительность между передатчиком и приемником.

В беспроводной технологии ключом к производительности устройства является способность устройства отличать применяемые сигналы как достоверную информацию от любого фонового шума или сигналов в спектре. Это олицетворяет определение стандартов, для установления которых используются спецификации SNR. Кроме того, стандарты, о которых я говорю, также обеспечивают надлежащую работу беспроводной сети.

Основы расчета отношения сигнал/шум

Говоря простыми словами, ОСШ представляет собой разницу между полезным сигналом и минимальным шумом. Кроме того, с точки зрения определения, минимальный уровень шума — это кажущиеся фоновые передачи, создаваемые другими устройствами или устройствами, которые непреднамеренно создают помехи на аналогичной частоте. Следовательно, чтобы установить отношение сигнал/шум, необходимо найти измеримую разницу между уровнем полезного сигнала и нежелательным шумом, вычитая значение шума из значения уровня сигнала.

Достижение желаемой целостности сигнала может быть затруднено на любом этапе проектирования.

 

Гипотетически, если радиоустройство вашего устройства принимает сигнал -65 дБм (децибел на милливатт), а минимальный уровень шума составляет -80 дБм, то результирующее отношение сигнал/шум составляет 15 дБ. Тогда это будет отражаться как мощность сигнала 15 дБ для этого беспроводного соединения. Как я уверен, вы знаете, что с точки зрения подключения к беспроводным сетям, эксперты заявляют о требовании отношения сигнал-шум не менее 20 дБ, чтобы, скажем, просматривать веб-страницы. Однако ниже приведены требования к SNR в сравнении со значениями SNR:

• от 5 дБ до 10 дБ : ниже минимального уровня для установления соединения из-за того, что уровень шума почти неотличим от полезного сигнала (полезная информация).

• от 10 дБ до 15 дБ : принятый минимум для установления ненадежного соединения.

• от 15 дБ до 25 дБ : обычно считается минимально приемлемым уровнем для установления плохой связи.

• от 25 дБ до 40 дБ : считается хорошим.

• 41 дБ или выше : считается отличным.

Хотя SNR обычно используется для количественной оценки четкости или силы электрических сигналов, его также можно применять к любой форме сигнала (передачи). Например, он используется для описания уровней изотопов в ледяных ядрах, биохимических сигналов между клетками или чистоты звука для автомобильных усилителей и источников (DVD, CD или цифровых). Однако для аудиокомпонентов значение SNR всегда положительное. Например, ОСШ 95 дБ означает, что уровень звукового сигнала на 95 дБ выше уровня шума. Что, в свою очередь, означает, что SNR 95 дБ лучше, чем 80 дБ.

Как рассчитать отношение сигнал-шум

Вычисления SNR могут быть простыми или сложными, в зависимости от рассматриваемых устройств и имеющихся у вас данных. Итак, если ваши измерения ОСШ уже представлены в децибелах, вы можете вычесть количество шума из желаемого сигнала: ОСШ = S — N. Это потому, что вычитание логарифмов эквивалентно делению нормальных чисел. Кроме того, разница в числах равна SNR. Например, вы измеряете радиосигнал мощностью -10 дБ и шумовой сигнал -50 дБ. -10 — (-50) = 40 дБ.

Как я уже говорил ранее, вычисление SNR также может быть задействовано. Итак, для сложных вычислений вы делите значение полезного сигнала на количество шума, а затем берете десятичный логарифм результата, то есть log (S ÷ N). После этого, если измерения уровня сигнала выражены в ваттах (мощность), вы умножаете на 20. Однако, если они являются единицами напряжения, вы умножаете на 10.

Кроме того, для мощности SNR = 20 log ( S ÷ N), а для напряжения SNR = 10 log (S ÷ N). Кроме того, результирующий расчет представляет собой SNR в децибелах. Например, ваше измеренное значение шума (N) составляет 2 мкВ, а ваш сигнал (S) — 300 мВ. SNR составляет 10 log (0,3 ÷ 0,000002) или приблизительно 62 дБ.

Формула соотношения сигнал-шум и пропускная способность канала

Соотношение сигнал-шум влияет на все беспроводные сети, включая Bluetooth, Wi-Fi, 4G, 4G LTE и 5G, поскольку их работа зависит от радиосигналов. Кроме того, поскольку они функционируют за счет использования радиосигналов, каждый из упомянутых способов связи имеет максимальную пропускную способность канала. Более того, с увеличением SNR увеличивается и пропускная способность канала.

В целом пропускная способность канала, полоса пропускания и отношение сигнал/шум влияют на максимальную пропускную способность каналов связи. Причем это открытие принадлежит Клоду Шеннону, и он делает эту корреляцию во время Второй мировой войны. В современных областях электроники и науки инженеры и ученые называют его законом Шеннона или теоремой Шеннона-Хартли.

В соответствии с законом Шеннона следующая формула изображает эту корреляцию, которая формирует отношение, зависящее от пропускной способности:

C = W log2(1 + S/N)

В рамках этой формулы:

/s)

S равно средней мощности принимаемого сигнала

N равно средней мощности шума

Вт равно ширине полосы частот (Гц)

Теорема Шеннона-Хартли показывает, что значения S (средняя мощность сигнала), N ( средняя мощность шума), а W (полоса пропускания) устанавливает предел скорости передачи.

Достижение технических решений с учетом сложных требований к сигналу является полезным в современной развивающейся отрасли.

 

Важность точного расчета отношения сигнал/шум является обязательным условием эффективной и точной разработки. Кроме того, вычисление отношения сигнал-шум также позволит получить представление о функциональных возможностях и характеристиках конструкции. Время, чтобы осознать, что дизайн неосуществим, наступает до этапа производства. Поэтому важно оценивать параметры конструкции с помощью расчетов, а также моделирования.

К счастью, благодаря набору инструментов для проектирования и анализа Cadence ваши дизайнеры и производственные группы будут работать вместе над внедрением надлежащих методов расчета отношения сигнал/шум во всех ваших проектах печатных плат. Allegro PCB Designer — это решение для компоновки, которое вы искали, и оно, несомненно, может облегчить реализацию эффективных стратегий соотношения сигнал/шум в ваших текущих и будущих проектах печатных плат.

Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.