Сложные ракурсы: Человек за полгода — 5. Ракурс
как нарисовать куб с любого ракурса — Gamedev на DTF
Советуем приготовить планшет или лист бумаги и ручку, чтобы все сразу попробовать. Читать эту статью просто так не имеет смысла — тут все про практику.
39 563 просмотров
Зачем художнику уметь рисовать куб с любого ракурса?
Освоив кубы, вы сможете рисовать любые объекты: машин, людей, архитектуру. Тоже с любого ракурса, быстро и понятно. Например, вот так можно свести к кубам фигуру человека:
Известный художник Скотт Робертсон рисует технику, отталкиваясь от геометрических примитивов.
Этому методу следует и Moderndayjames:
Дальше будет много примеров. Советуем попробовать нарисовать основные моменты, чтобы лучше понять, о чем речь. Получится своеобразный конспект.
Статья написана по материалам ресурса How to sketch.
Что такое перспектива?
Рисовать куб с любого ракурса — это рисовать его в перспективе.
Расположение объектов.
Стекло здесь — так называемая картинная плоскость. Проведем от камеры сквозь стекло линию — получится то, что называется лучом зрения (ЛЗ). Луч зрения всегда перпендикулярен картинной плоскости. Эти обозначения понадобятся нам дальше.
Нам нужно знать, как линии нашего объекта расположены в пространстве относительно чего-либо. Положение камеры — наша путеводная звезда. Рисовать в перспективе — значит представлять изображение с определенной точки зрения. Не бывает изображения без зрителя.
Дальше мы будем рассматривать сцену с двух точек зрения: то, как ее видит камера, и то, как она расположена относительно объекта. Это нужно, чтобы проще ориентироваться в пространстве.
Куб начинается с квадрата
Куб состоит из шести квадратных плоскостей, соединенных вместе.
Шесть квадратных плоскостей в пространстве.
Здесь мы добавим в наш словарь новое слово — нормальная линия или просто нормаль. Нормаль — это линия, перпендикулярная какой-либо поверхности. Если вы поставите карандаш вертикально на стол, он будет совпадать с направлением нормальной линии. Вы можете встретить этот термин в 3D, но в 2D его тоже используют.
У каждой плоскости есть бесконечное количество этих нормальных линий. Для простоты мы нарисуем только одну по центру.
Возьмем квадрат и расположим его перед камерой. Если нормаль перпендикулярна картинной плоскости и тем самым совпадает с лучом зрения, значит, мы видим поверхность без каких-либо искажений. В данном случае — обычный квадрат.
Слева — расположение объектов, справа — что видит камера.
Если мы наклоним нашу фигуру в каком-либо направлении, то нормаль больше не будет смотреть прямо на картинную плоскость. Поверхность прямоугольника сожмётся в том направлении, куда смотрит нормаль. Этот принцип называется сжатие по нормали. Каждая плоскость всегда сжимается только по своей нормальной линии.
Слева — расположение объектов, по центру — что видит камера, справа — реальный размер плоскости.
На приведенном примере боковые стороны прямоугольника сужаются кверху (с точки зрения камеры). Так получается потому, что это параллельные линии, которые уходят вдаль (относительно картинной плоскости). А вот линии, параллельные картинной плоскости, никогда не сходятся.
Слева — расположение объектов, справа — что видит камера.
Что такое линия горизонта?
Параллельные линии, которые уходят вдаль, сходятся на линии горизонта. Эта истина так широко известна и непреложна, что авторы никогда не пересматривают ее обоснование. А мы пересмотрим — чтобы лучше понять, о чем речь.
А мы пересмотрим — чтобы лучше понять, о чем речь.
Наша камера стоит строго вертикально, то есть ее нижняя плоскость параллельна плоскости земли. Представим себе не один, а несколько горизонтальных прямоугольников перед камерой. По мере того, как эти плоскости всё выше поднимаются над землёй, они всё сильнее сжимаются. В какой-то момент плоскость визуально сожмется в плоскую линию — это будет линия горизонта.
Слева — расположение объектов, справа — что видит камера.
Находим линию горизонта.
Слева — расположение объектов, справа — что видит камера.
Параллельные линии, расположенные на горизонтальных плоскостях (на любой из них) сходятся на линии горизонта. Точки, в которых они сходятся, называются точками схода (ТС).
Слева — расположение объектов, справа — что видит камера.
Как видите, у каждого набора параллельных линий есть своя собственная точка схода. Для перспективы типично наличие центральной (ЦТС), левой (ЛТС) и правой (ПТС) точек схода.
Для перспективы типично наличие центральной (ЦТС), левой (ЛТС) и правой (ПТС) точек схода.
Ориентируемся в пространстве
Теперь попробуем разобраться в том, как прямоугольники изменяются по мере увеличения расстояния от зрителя.
Возьмем несколько прямоугольников и выстроим их в ряд. Все они имеют одинаковый размер и расположены впритык друг к другу. И хотя в действительности все они имеют одинаковый физический размер, каждый последующий прямоугольник в перспективе становится меньше. Благодаря этому явлению параллельные линии «сходятся на линии горизонта».
Прямоугольники в пространстве.
Благодаря изменению размера наш мозг воспринимает глубину. Но оно происходит не линейно: каждый прямоугольник сжимается по своей нормали, когда его наклоняют относительно зрителя. Плоскость сжимается тем сильнее, чем она ближе к линии горизонта.
Разница в размере между парами прямоугольников, лежащих ближе к зрителю, ярче выражена, чем между теми, которые ближе к горизонту.
Измеряем глубину
Проведём три горизонтальные линии в перспективе аналогично прямоугольникам выше. Изменяем только одно требование: интервалы между ними должны быть одинаковыми. Что мы увидим? Отрезок B в два раза короче, чем A, но C в шесть раз короче, чем B.
Каждый следующий сантиметр на бумаге вмещает в себя все больше и больше пространства по мере приближения к горизонту.
Это важно понимать при рисовании не только механизмов, но и природных форм. Даже фигуры человека. Как и любой другой объект, тело существует в пространстве. Важно точно знать, где именно расположены ключевые точки тела. А для этого нужно освоить измерения в перспективе. Набравшись опыта, вы сможете делать обоснованные догадки, уже не рисуя вспомогательные конструкции.
Для правильного куба придется узнать кое-что об эллипсах
Теперь нам нужно нарисовать эллипсы. Тут нам пригодятся те же знания, что мы получили, изучая квадратные плоскости: потому, что плоскость может быть любой формы, в том числе овальной или круглой.
Нормальная линия плоского эллипса всегда совпадает по направлению с его малой осью.
Принцип тот же, что и в случае с прямоугольниками. Слева — вид сверху, справа — что видит камера.
Важно помнить, что у круга всегда одинаковый диаметр, в каком бы направлении мы его не провели. После сжатия круг превращается в овал, и у него появляется самый длинный (большая ось эллипса) и самый короткий (малая ось эллипса) диаметры.
Большая ось не меняет свою длину, как бы сильно мы ни наклоняли плоскость. Малая ось перпендикулярна большой, а ее направление совпадает с нормальной линией. Длина малой оси меняется сильнее всего, когда мы наклоняем плоскость по отношению к камере.
Большая ось сейчас расположена горизонтально, а малая — вертикально. По ней и происходит сжатие. Размеры большой оси не меняются.
Зачем в тексте про кубы информация про эллипсы?
Эллипсы помогают определить направление нормальной линии поверхности, поэтому их удобно использовать, даже если на рисунке нет видимых круглых плоскостей. Они подсказывают, в каком направлении сжимать плоскость, когда она наклонена по отношению к зрителю.
Слева плоскость расположена прямо относительно камеры, справа — наклонена относительно камеры.
Еще эллипс может пригодится, чтобы определить угол наклона плоскости относительно зрителя. Сильнее наклон, сильнее сжатие.
Нет наклона = нет сжатия. В центре и справа плоскости наклонены относительно зрителя.
И, последний, самый важный пункт. Эллипс помогает найти пропорции идеального квадрата: круг, вписанный в квадрат, касается каждой из четырех сторон точно посередине.
Круг всегда касается сторон квадрата посередине.
Первый угол — 90 градусов
Помимо пропорций квадрата, нам нужно убедиться, что у нашей фигуры есть четыре прямых угла (по 90 градусов). Для этого необходимо правильно построить хотя бы один угол — три остальных встанут на свои места.
Эллипс поможет найти правильный угол между двумя линиями на одной плоскости.
Исходное расположение объектов. Смотрите ниже, как мы превращаем круг в квадрат.
Определяем пропорции квадрата с заданного ракурса, используя эллипс.
Слева — что видит камера, справа — расположение камеры относительно фигуры, вид сверху.
Проведем нормальную линию (она здесь вертикальная, потому что плоскость горизонтальная). Её можно проводить в разных местах — в зависимости от того, как мы хотим развернуть к себе угол будущего квадрата.
Как далеко нормаль должна выходить за пределы эллипса до той точки, где она пересекается с касательными? Это зависит от угла наклона эллипса.
Вид из камеры. Нормаль выходит из центра эллипса. Чем меньше его наклон по отношению к камере, тем длиннее линия.
Чем ближе линия горизонта к эллипсу (с учётом его размера), тем сильнее перспективное искажение, и тем быстрее сходятся линии. Это также значит, что объект или находится близко к зрителю, или он большой. Изображение выглядит так, как будто снято через широкоугольный объектив.
Если линия горизонта находится далеко от эллипса, перспективное искажение будет слабым. Линии будут сходиться медленно, объект покажется маленьким или будет расположен далеко от зрителя. Это эффект длиннофокусного объектива.
Слева горизонт очень близко и линии сходятся быстрее, справа горизонт далеко и линии сходятся медленнее.
Здесь видно, что вертикальная линия в обоих случаях выходит за пределы эллипса на одно и то же расстояние. Нижний угол квадрата одинаковый. Разница только в силе перспективы.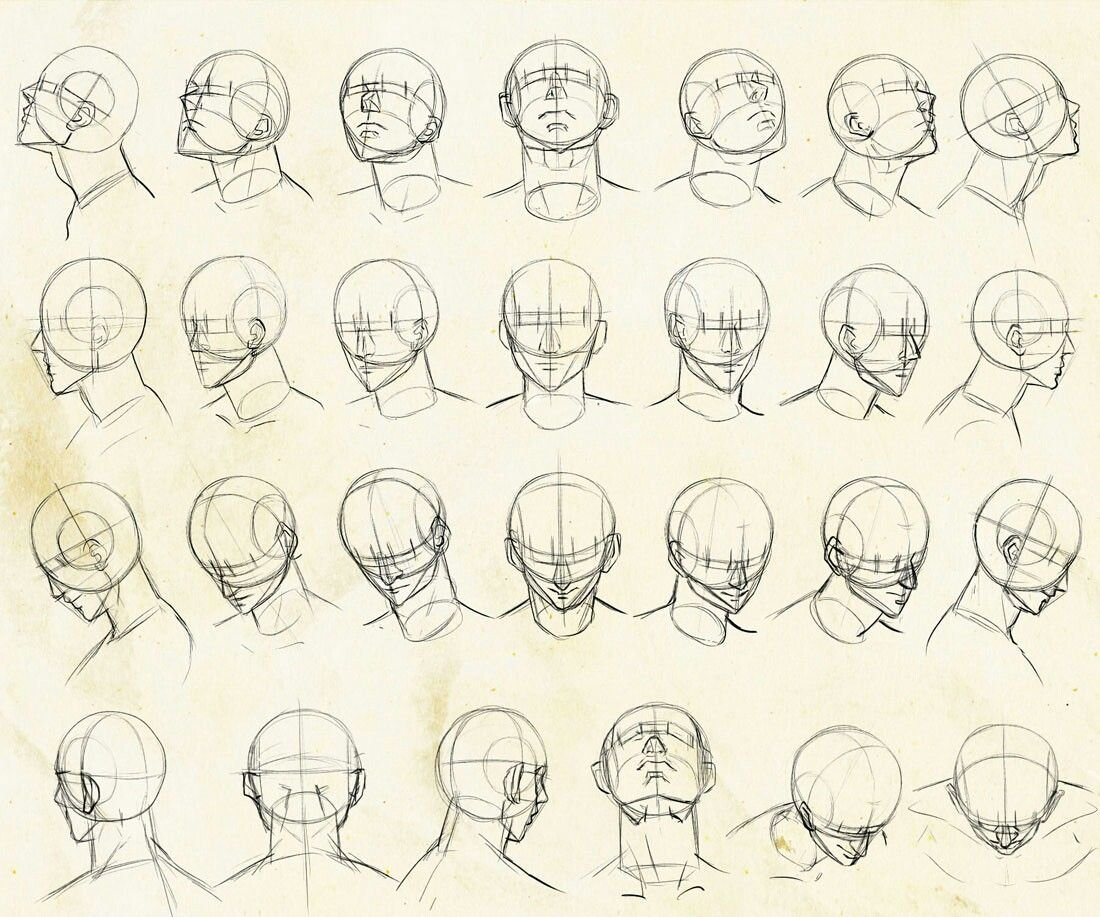 И ещё раз напоминаем: линия горизонта перпендикулярна нормали эллипса (малой оси).
И ещё раз напоминаем: линия горизонта перпендикулярна нормали эллипса (малой оси).
Горизонт — это по сути ещё одна плоскость, параллельная нашему эллипсу. Просто она полностью наклонена по отношению к зрителю.
Итак, наш эллипс готов.
Превращаем эллипс в куб
У куба шесть граней, но одновременно мы можем увидеть лишь три из них. Так что, простоты ради, мы сосредоточимся только на видимых сторонах (пока). Начнем с верхней грани. Вы уже знаете, как изобразить горизонтальный квадрат в любом возможном положении, так что сделайте это — нарисуйте квадрат вокруг эллипса.
Теперь нужно дорисовать две боковые грани. Чтобы найти их, используйте вертикально расположенные рёбра куба — нормали к верхней плоскости.
Осталось еще узнать длину вертикального ребра. Оно параллельно картинной плоскости и становится длиннее, когда перемещается ближе к нам в пространстве (как и любой другой объект), в соответствии с конвергенцией (сближением) линий.
Мы предполагаем, что ребро немного длиннее, чем большая ось нашего верхнего эллипса, на которую тоже не действует перспективное сокращение.
Есть одна хитрость, которая помогает проверить, правильно ли мы построили боковые грани. Это можно сделать с помощью эллипса. Нарисуйте эллипс, малая ось которого направлена в правую точку схода. Эллипс должен касаться рёбер куба посередине. Затем просто закройте снизу левую грань с помощью линии, идущей к левой точке схода. А потом правую грань — линией, идущей к правой точке схода:
Наш куб готов:
Как клонировать наши кубы
Для этого вернемся к рисованию прямоугольников. У каждого прямоугольника есть диагонали, они пересекаются в его центре. Диагонали помогают нам рисовать одинаковые прямоугольники.
Диагонали прямоугольника пересекаются в его центре.
Давайте потренируемся. Найдите центр прямоугольника, используя диагонали.
Нарисуйте среднюю линию прямоугольника и продолжите ее в том направлении, куда собираетесь клонировать прямоугольник. Средняя линия пересечёт сторону прямоугольника в точке А.

Продолжите стороны прямоугольника в том же направлении.
Найдите центр прямоугольника. Продлите линии в ту сторону, куда будете его клонировать.
Проведите через точку A линию из дальнего угла прямоугольника. Она пересечет его продлённую сторону в точке B. Точка B отмеряет ширину нового, точно такого же прямоугольника.
Теперь проведите вертикальную линию. Она станет дальней стороной нового прямоугольника.
Удвоение прямоугольника
Вы можете удваивать прямоугольники с помощью диагонали не только на плоскости, но и в перспективе. Сначала найдите центр прямоугольника, затем размножьте его во всех направлениях. Заполните всю страницу такими конструкциями.
Клонирование прямоугольника во всех направлениях.
Следует помнить, что в перспективе центр прямоугольника смещается по отношению к зрителю. Это происходит из-за схождения линий. Когда перспективное искажение небольшое (горизонт далеко по сравнению с размерами объектов), линии сходятся медленно, и центр прямоугольника смещается незначительно. И наоборот, смещение центра очень ярко выражено в случае сильного перспективного искажения.
Это происходит из-за схождения линий. Когда перспективное искажение небольшое (горизонт далеко по сравнению с размерами объектов), линии сходятся медленно, и центр прямоугольника смещается незначительно. И наоборот, смещение центра очень ярко выражено в случае сильного перспективного искажения.
Смещение центра.
Время активной практики. Клонируем кубы.
Постройте куб. Нижняя грань параллельна земле, никаких причудливых наклонов. Затем клонируйте любую грань куба с помощью метода диагоналей. Наметьте линии, которые будут направлены в точки схода.
Нарисуйте куб в перспективе.
Помните, квадраты сжимаются сильнее по мере удаления от зрителя. Если сравнивать первый и второй квадраты, этот эффект выражен ярко. Для каждого последующего квадрата он менее очевиден, но присутствует всегда.
Постройте новые кубы, клонируя квадратные плоскости.
Нарисуйте кубы один за другим. Заполните ими всю страницу.
Заполните ими всю страницу.
Рисуйте «насквозь»
Сквозное построение означает, что вы рисуете твердые тела так, будто они прозрачные. Так вы всегда будете знать, где именно в пространстве находятся те участки поверхности тела, которые недоступны глазу. Это поможет правильно располагать тела по отношению друг к другу.
Переходим к практике:
Рисуем куб «насквозь», со всеми с невидимыми гранями.
Клонируем куб в сторону ПТС. Не забываем оставить между ними пространство величиной с такой же куб.
Повторяем упражнение к ЛТС.
Интересная деталь. Как вы могли заметить, уходя вдаль, некоторые плоскости сильнее сжимаются (мы уже знаем почему), а другие — наоборот, больше открываются зрителю.
Это происходит потому, что угол между лучом зрения и поверхностью этих плоскостей приближается к прямому (90 градусов).
Как нарисовать куб с любого ракурса за пять шагов?
Теперь переходим к самому интересному!
Шаг 1. Нарисуйте эллипс. Он может располагаться на любой грани куба. Здесь вас должны волновать только сжатие и направление нормали.
Шаг 2. Проведите нормальную линию исходя из того, как вы хотите развернуть ближайшее к зрителю ребро куба. Линия горизонта для этого куба фактически не будет горизонтальной. Да, получился немного каламбур.
Какой она тогда должна быть? Просто перпендикулярной нормали нашей плоскости. Это единственное требование.
Шаг 3. Определитесь с силой перспективного искажения. В нашем случае линия горизонта находится за пределами холста, поэтому оно выражено слабо.
Шаг 4. Определите правильную длину «вертикального» ребра куба, используя эллипс или просто на глаз. Проведите линию к правой точке схода, чтобы закрыть грань снизу.
Шаг 5. Последняя грань сама станет на место. Просто постройте правильные параллельные линии к тем, которые уже есть.
Просто постройте правильные параллельные линии к тем, которые уже есть.
Еще один способ: построение с помощью масс
Масса — это простое сферическое или колбасоподобное тело, используемое в качестве основы для построения сложных форм. Думайте о ней как о комке глины, существующем в трехмерном пространстве.
Это не плоская фигура на бумаге, у нее есть реальный физический объем.
Используя массы, легче воссоздать чувство размера в рисунке. Они же помогут решить проблемы перспективного искажения и наложения объектов друг на друга. Как видите, метод масс работает со всеми тремя ключевыми компонентами глубины в вашем рисунке.
Давайте теперь создадим куб из сферической массы. Независимо от того, как он развернут, куб идеально вписывается в сферу.
Куб, вписанный в сферу.
- Нарисуйте круг.
Постройте куб, используя знания, усвоенные из предыдущих блоков.
 Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.
Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.Прямо сейчас нарисуйте целую страницу кубов, вписанных в сферы. Меняйте размер и ракурс.
Основная идея: каждая масса имеет центр. Центр сферической (или яйцеобразной) массы всегда совпадает с ее геометрическим центром. Давайте построим несколько одинаковых по размеру масс с равными промежутками между ними.
Постройте квадраты в перспективе.
- Нарисуйте сферу вокруг каждой точки. Контур каждой сферы должен касаться линий, которые направлены в центральную точку схода, — если вы хотите, чтобы сферы были одинакового размера.
Нарисуйте сферическую массу вокруг обозначенной точки.
Встройте кубы внутрь сферических масс. Разворачивайте их, как хотите, они всё равно будут одного размера, и расстояния между их центрами будут одинаковыми.

Нарисуйте куб внутри каждой сферы.
Поднимем кубы над землей
- Нарисуйте на земле квадрат, затем проведите внутри него прямую линию. Эта линия представляет собой расстояние между двумя кубами. Обозначьте точку схода, в которую направлена линия.
Проведите прямую линию внутри квадрата.
Постройте вертикальную плоскость.
Нарисуйте массы одинакового размера с центрами в верхних углах плоскости.
Впишите куб в каждую массу.
Рисуем кубы в пространстве по произвольной траектории
Для начала вспомним про диагонали и построим с помощью них кривую в перспективе. Вот, как это сделать.
Шаг 1. Кривая в ортогональном виде, то есть без перспективных искажений, прямо перед зрителем.
Шаг 2 выглядит так. Помните, чем ближе линия горизонта к эллипсу, тем сильнее перспективное искажение.
Нарисуйте квадрат в одноточечной перспективе, где линии параллельны либо картинной плоскости (тогда они вообще не сходятся), либо лучу зрения. Те, которые параллельны лучу зрения, сходятся в центре линии горизонта. Эта точка называется центральной точкой схода, как вы, возможно, помните. Это самый простой способ нарисовать прямоугольник.
Шаг 3. Постройте квадрат вокруг вашего круга.
Затем проведите диагонали и средние линии. Они будут служить вашим ориентиром.
Перенесите точки пересечения кривой с этими линиями из вашего ортографического рисунка. Например, если кривая касается верхней стороны квадрата по центру, она будет делать то же самое и в перспективе.
Шаг 4. Перенесите кривую из вида сверху в перспективный вид, опираясь на опорные точки.
Перенесите кривую из вида сверху в перспективный вид, опираясь на опорные точки.
Объединяем два упражнения
Наша цель — построить кубы одинакового размера с одинаковым расстоянием между ними, но расположенные на неправильной траектории.
Шаг 1. Постройте кривую в перспективе.
Отметьте на кривой точки, соблюдая равные интервалы между ними. Каждая точка соответствует центру массы. Определите размеры масс, которые находятся далеко от зрителя. Тогда вам будет легче определить на глаз размеры масс, расположенных в промежутках.
- Вот как это можно сделать: проведите прямую, проходящую через две точки, и продолжайте её, пока она не пересечётся с горизонтом в точке схода. Линии, по которым мы будем выравнивать размер масс (они касаются контуров обеих сфер), тоже должны быть направлены в эту точку схода.
Шаг 2. Отметьте на теле кривой точки с равными интервалами.
Шаг 3. Нарисуйте массы одинакового размера. Точки на кривой — это их центры.
Впишите куб в каждую массу.
А теперь пора нарисовать пару десятков кубов!
С разных ракурсов, в разных местах, с перекрытиями. Попробуйте разную силу перспективного искажения. Обязательно нарисуйте, даже если считаете, что все поняли. Это ОЧЕНЬ поможет рисовать потом любые другие предметы. Верьте в практику!
Что можно сделать:
Пример домашнего задания.
Дополнительные материалы
Здесь можно посмотреть еще видео по теме.
Когда разберетесь с этими упражнениями, можно попробовать порисовать технику, как в этом плейлисте ModernDayJames. Стартовать можно отсюда:
А тут рассказывают, как понимание геометрических примитивов поможет в рисовании динамичных поз:
Текст переведен авторами Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.
Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.
Внутренняя скульптура — ГМП «Исаакиевский собор»
Значительную роль в убранстве интерьера Исаакиевского собора играет скульптура. Здесь представлены апостолы, пророки, ангелы на сводах, в барабане купола и иконостасах. Особое место занимают работы И.П.Витали. В 1845-1850 годах он с помощниками Р.К.Залеманом и В.В.Беляевым оформлял своды храма.
Пример синтеза скульптуры, архитектуры и живописи – барабан главного купола, выполненный в традициях Возрождения. Его украшают живописные изображения апостолов, между которыми располагаются 12 статуй ангелов. Над ангелами – пилястры, образующие со скульптурой единую вертикаль. Такое решение подчеркивает легкость и цельность архитектурной композиции.
Пророки на сводах в западной части храма, и ангелы в восточной части представлены в сложных динамических позах. Их пропорции учитывают восприятие снизу, в трактовке образов чувствуется влияние итальянского барокко XVIII века.
Их пропорции учитывают восприятие снизу, в трактовке образов чувствуется влияние итальянского барокко XVIII века.
Исключительный интерес представляет убранство иконостасов, гармонично сочетающее живопись, мозаику и скульптуру.
Малые иконостасы венчают скульптурные группы Н.С.Пименова «Воскресение» в приделе св. Екатерины и «Преображение» в приделе св. Александра Невского. Они прекрасно сочетаются с архитектоникой иконостасов, удачно дополняют и завершают их.
«Воскресение» состоит из пяти фигур. Логический и композиционный центр группы – Иисус Христос. Его правая рука поднята вверх, голова запрокинута, всей фигуре придана динамика. Мотив устремленности Господа ввысь поддержан удачным решением позы ангела слева, создающей впечатление необыкновенной легкости. Предлагая динамичное решение этой группы, Пименов все же остался верен традициям классицизма: у скульптуры устойчивая, четкая композиция. Ниже располагаются фигуры воинов, присутствовавших при воскресении Христа. Они зрительно уравновешивают группу, сложные ракурсы которой свидетельствуют о влиянии барочной итальянской скульптуры.
Они зрительно уравновешивают группу, сложные ракурсы которой свидетельствуют о влиянии барочной итальянской скульптуры.
«Преображение» по решению композиционно близко «Воскресению». В центре фигура преображенного Иисуса Христа, слева и справа от Него – пророки, ниже – апостолы Иоанн и Петр. Фигура раскинувшего руки Господа кажется необыкновенно легкой и динамичной, пророки как бы парят в воздухе. Композиция носит остро эмоциональный характер: в образах апостолов Пименову удалось передать удивление, восторг и страх.
В целом убранство малых иконостасов отличается красочностью, богатством отделочных материалов и совершенством исполнения.
Очень важную роль в пластическом убранстве интерьера играют три дубовые двери, украшенные многофигурными рельефами работы И.П.Витали. Северные врата посвящены свв. Исаакию Далматскому и Николаю Мирликийскому, на южных – сюжеты житий свв. Владимира Киевского и Александра Невского, на западных – апостолов Петра и Павла.
Над каждой дверью помещен рельеф, сюжет которого раскрывает смысл находящейся выше надписи. Надпись над северной дверью: «Кесарева Кесареви Божия Богови», под ней рельеф «Христос объясняет поданную Ему монету». Надпись над южной дверью гласит: «Исполни Слава Господня Храм», рельеф – «Торжество освящения Иерусалимского храма». Над западными вратами начертано: «Кресту Твоему поклоняемся», рельеф – «Воздвижение Честного Животворящего Креста».
Надпись над северной дверью: «Кесарева Кесареви Божия Богови», под ней рельеф «Христос объясняет поданную Ему монету». Надпись над южной дверью гласит: «Исполни Слава Господня Храм», рельеф – «Торжество освящения Иерусалимского храма». Над западными вратами начертано: «Кресту Твоему поклоняемся», рельеф – «Воздвижение Честного Животворящего Креста».
Каждая створка двери разделена на четыре кессона с многофигурными композициями. Особое мастерство отличает исполнение рельефов западной двери: слева (сверху вниз) – «Призвание апостола Павла на пути в Дамаск», «Проповедь апостола Павла в Афинском ареопаге», «Апостол Павел перед царем Агриппой» и «Кончина апостола Павла». Очень динамична сцена проповеди: энергично спорящий человек в широком плаще и спокойно внимающий ему философ; напряженная фигура пожилого афинянина, полного раздумья, и в центре – фигура самого Павла, объединяющая композицию. Противопоставление мужества духовного грубой силе отражено в сцене казни апостола. В центре – опустившийся на колено Павел, в облике которого чувствуется спокойствие и смелость человека, верящего в свою правоту. Над ним палач занес секиру, еще мгновенье – и апостолу отсекут голову. Лица палача не видно, но вся его приземистая фигура выглядит зловеще. Равнодушно с трона взирает на казнь римский наместник. В углу рельефа – сочувствующие Павлу люди. Лепка персонажей предполагает руку опытного ваятеля, чувствуется, что это работа самого Витали.
Над ним палач занес секиру, еще мгновенье – и апостолу отсекут голову. Лица палача не видно, но вся его приземистая фигура выглядит зловеще. Равнодушно с трона взирает на казнь римский наместник. В углу рельефа – сочувствующие Павлу люди. Лепка персонажей предполагает руку опытного ваятеля, чувствуется, что это работа самого Витали.
Рельефы южных дверей исполнены неровно. Наиболее удачны композиции правой створки: «Победа Александра Невского над шведами», «Александр Невский отвергает предложение папского нунция о принятии католицизма», «Умирающий Александр Невский принимает монашеский сан» и «Петр I перевозит мощи Александра Невского в Петербург».
На левой створке – фрагменты жития святого равноапостольного князя Владимира Киевского: «Философ проповедует князю Владимиру христианскую веру», «Князь Владимир принимает вернувшихся послов», «Крещение князя Владимира в Херсонесе» и «Крещение киевлян в Днепре».
Интересны рельефы северной двери: «Св. Исаакий Далматский и император Валент», «Спасение св.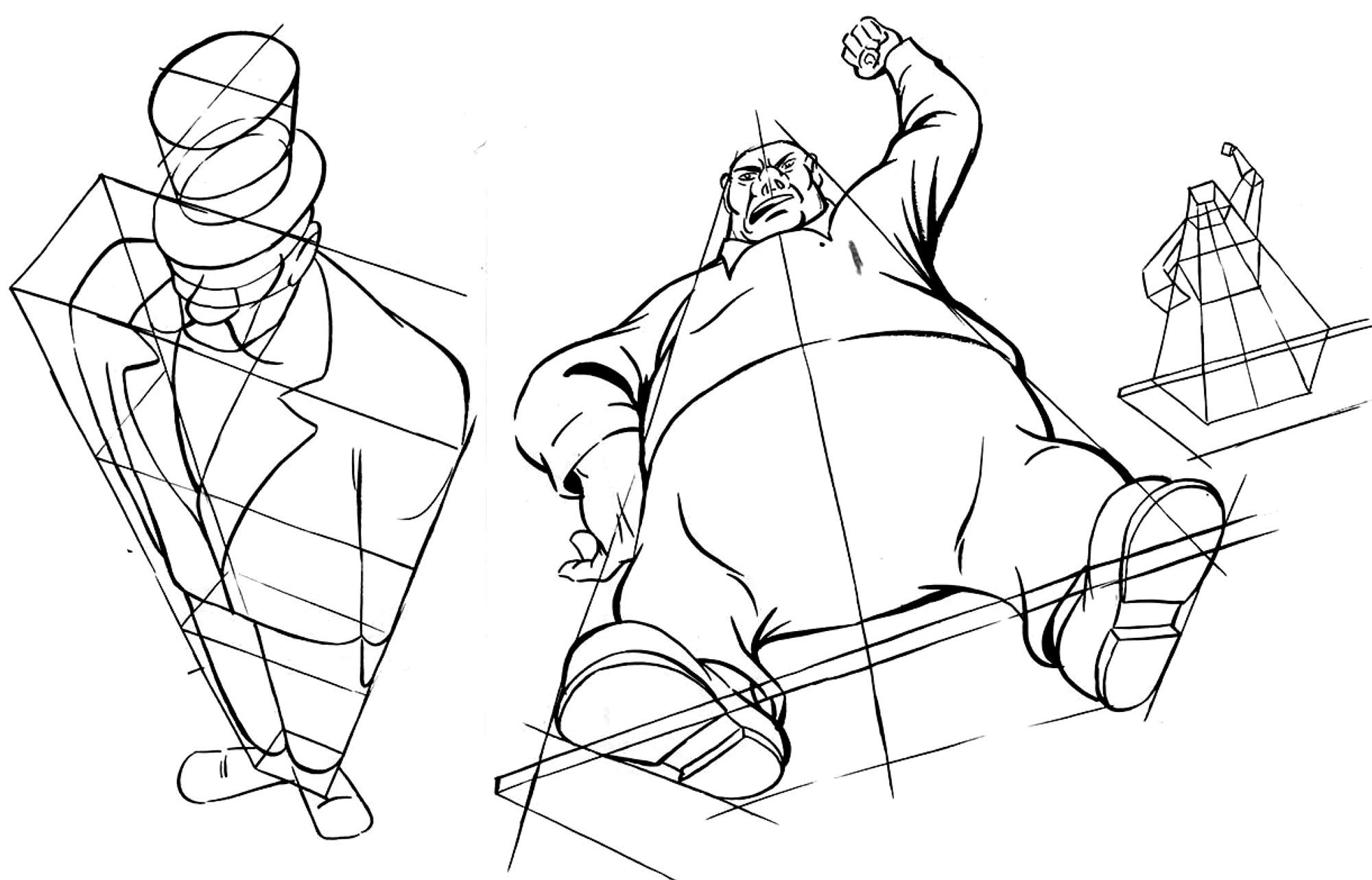 Исаакия Далматского ангелами», «Освобождение св. Исаакия из темницы» и «Св. Исаакий благословляет императора Феодосия»; «Посвящение св. Николая в иеродиаконы», «Св. Николай, открытый в тайном благодеянии», «Избрание св. Николая на архиепископский престол», «Николай Мирликийский изгоняет Ария с Первого Вселенского собора».
Исаакия Далматского ангелами», «Освобождение св. Исаакия из темницы» и «Св. Исаакий благословляет императора Феодосия»; «Посвящение св. Николая в иеродиаконы», «Св. Николай, открытый в тайном благодеянии», «Избрание св. Николая на архиепископский престол», «Николай Мирликийский изгоняет Ария с Первого Вселенского собора».
Кроме того, на всех внутренних дверях храма помещены многочисленные фигуры в нишах и бюсты в круглых медальонах. Витали с помощниками создали ряд образов, резко отличающихся от традиционных идеализированных изображений. Многие бюсты воспроизводят чьи-то конкретные черты. Скорее всего, их лепили с людей, встречавшихся в мастерских, на строительстве собора, на улицах Петербурга. Так, в облике великомученика Федора (северные двери) воплощен тип русского крестьянина: задумчивое скорбное лицо изрезано глубокими морщинами, борода всклочена, волосы резкими прядями ниспадают на лоб. У лиц великомучеников Дамиана и святой Нонны (северные двери) – типично славянские черты. Житейские горести исказили черты Нонны, но не смогли уничтожить выражение гордости и благородства.
Житейские горести исказили черты Нонны, но не смогли уничтожить выражение гордости и благородства.
Скульптура на сводах, барабане купола и иконостасах выполнена из меди методом гальванопластики, впервые использованной в таком масштабе при строительстве Исаакиевского собора. Разработал метод русский профессор Б.С.Якоби. В емкость с
раствором медного купороса помещается покрытая графитом форма будущей скульптуры. К ней подключается анод, а к опущенной в купорос медной пластине — катод электробатареи. При прохождении электрического тока медь тонким слоем оседает на графите скульптурной формы.
За счет сравнительно тонкого слоя меди гальванопластическая скульптура была достаточно легкой. Это позволило Монферрану уменьшить массу собора и ослабить неравномерность его осадки. Гальванопластические работы выполнялись на заводе герцога Лейхтенбергского в Петербурге. По предложению Монферрана скульптура сводов крепилась не к кирпичной кладке, а к специальным металлическим конструкциям, образующим декоративный внутренний свод. Это было новшеством в строительной практике того времени.
Это было новшеством в строительной практике того времени.
Скульптура на дверях храма была отлита из бронзы и покрыта декоративной патиной. Более 350 произведений, созданных русскими скульпторами в Исаакиевском соборе, представляют собой уникальную коллекцию монументально-декоративной пластики XIX века.
Подготовлено И.А.Сидневой.
тригонометрия — Существуют ли «мнимые» и «сложные» углы?
Вот более буквальное толкование.
Да , вы действительно можете создавать геометрические пространства, в которых углы могут быть мнимыми и даже сложными.
Хитрость заключается в том, чтобы отметить, что наиболее общее определение угла проводится в рамках пространств внутреннего произведения : векторных пространств, которые имеют операцию, называемую «внутренним произведением», которая фактически определяет, как «точечный продукт» работает для этого типа вектора. Это определение основано на том, что для векторов в евклидовом $n$-мерном пространстве мы можем определить 9{-1}\left(\frac{\mathbf{v} \cdot \mathbf{w}}{|\mathbf{v}| |\mathbf{w}|}\right)$$
, что, в свою очередь, , получается из «геометрического скалярного произведения»
$$\mathbf{v} \cdot \mathbf{w} = |\mathbf{v}| |\mathbf{ш}| \cos \theta$$
, где $\theta$ — это угол между векторами, но теперь мы пойдем другим путем и возьмем скалярное произведение как примитивную операцию, а не длину и угол, и мы используем это для определить длины и угла, которые являются понятиями, не существующими в обычном векторном пространстве.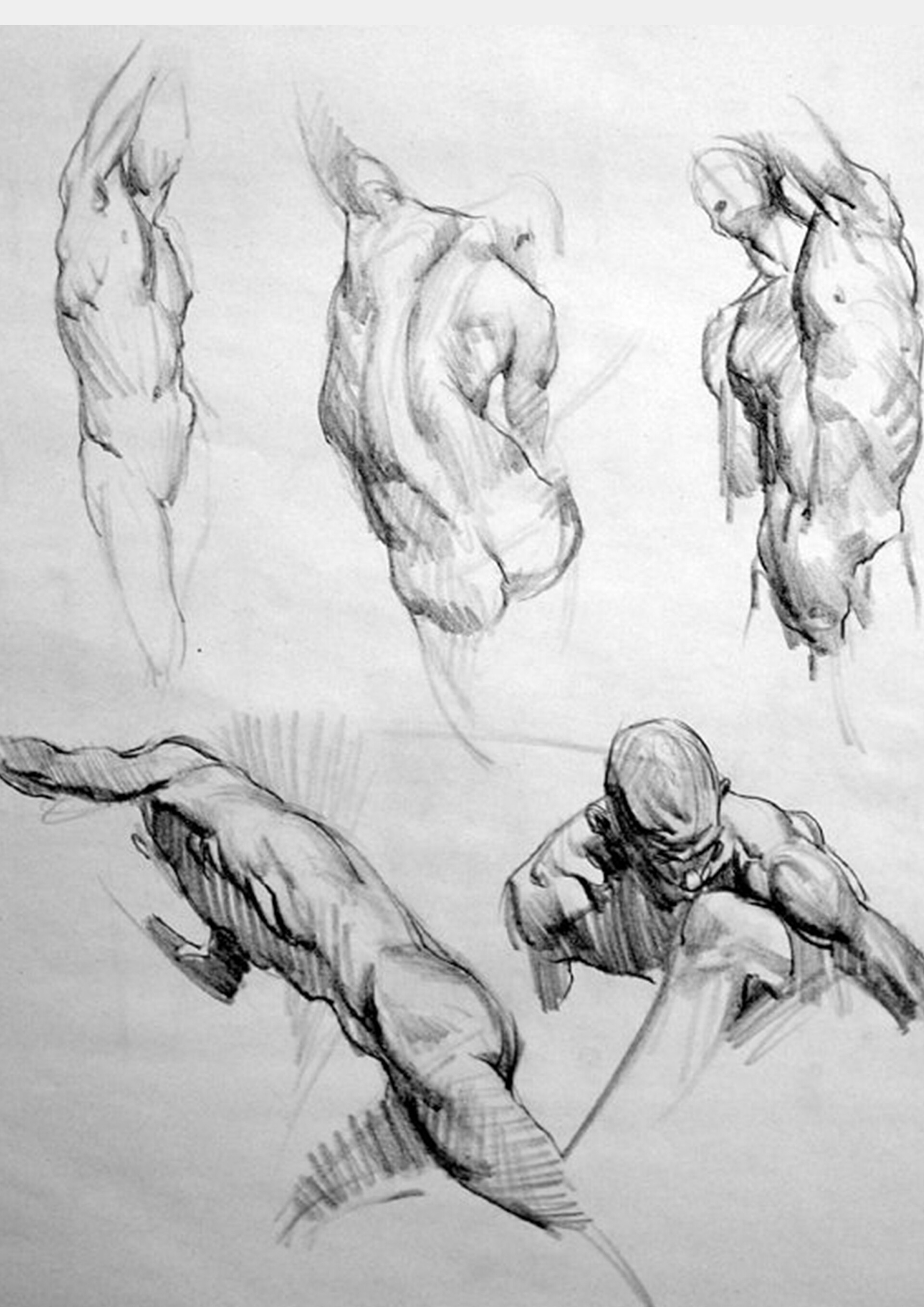 (Таким образом, мы должны также отметить, что длина $|\mathbf{v}|$ тогда определяется, как можно подумать, $|\mathbf{v}| := \sqrt{\mathbf{v} \cdot \mathbf{v}}$.)
(Таким образом, мы должны также отметить, что длина $|\mathbf{v}|$ тогда определяется, как можно подумать, $|\mathbf{v}| := \sqrt{\mathbf{v} \cdot \mathbf{v}}$.)
Чтобы увидеть, как работает эта структура, обратите внимание, что для реального , скажем, двумерного евклидова векторного пространства, мы имеем, что векторы выглядят как
$$\mathbf{v} = \langle v_x, v_y \rangle$$
, так что
$$\mathbf{v} \cdot \mathbf{w} = v_x w_x + v_y w_y$$
и из которого мы получаем обычный угол между двумя точками в двумерном пространстве.
Однако, поскольку мы говорим о более общих векторных пространствах, нет необходимости, чтобы скалярные компоненты вектора были только действительными числами: мы можем — и делаем! — так же хорошо взять их как комплексные числа . Конечно, если у нас есть векторы из двух комплексных чисел, это фактически равнозначно четырем измерениям с действительными числами, но мы определяем новый вид геометрии. В частности, если теперь у нас есть двумерные векторы $\mathbf{v}$ той же формы, что и заданная, только компоненты $v_x$ и $v_y$ являются комплексными , так что пространство имеет двух комплексных измерений ( и, таким образом, четыре действительных измерения), мы можем определить скалярный продукт, например
$$\mathbf{v} \cdot \mathbf{w} := v_x \bar{w}_x + v_y \bar{w}_y$$
, где вы заметили, что мы берем сопряжение: это делается для того, чтобы скалярное произведение по-разному «хорошо» соответствовало структуре комплексных чисел. {- 1}$ — это просто длины, поэтому они будут реальными, 9Числитель 0009 , который является голым скалярным произведением, вообще не должен быть вещественным, и поэтому мы можем в общем случае получить арккосинус комплексного числа и, таким образом, найти векторы с комплексным углом.
{- 1}$ — это просто длины, поэтому они будут реальными, 9Числитель 0009 , который является голым скалярным произведением, вообще не должен быть вещественным, и поэтому мы можем в общем случае получить арккосинус комплексного числа и, таким образом, найти векторы с комплексным углом.
геометрия — Трудности с направленными углами
На мой взгляд, лучшее определение прямого (или ориентированного ) угла векторных полулиний состоит в том, чтобы установить биекцию с поворотом плоскости, следуя комментариям @Jean Marie и @ Дэвид Г. Аист. 9\клинья$ евклидова пространства $E$ равны тогда и только тогда, когда по определению существует поворот $E$, т.е. элемента $\varrho$ группы $\mathbb{SO}(E)$, такой, что
$$ \varrho(\Delta_1)=\Delta’_1\qquad\text{and}\qquad \varrho(\Delta_2)=\Delta’_2. $$
Множество $\;\cal U\;$ классов эквивалентности равных углов находится в биекции с группой $\mathbb{SO}(E)$, поэтому само является группой, называемой группой углы E .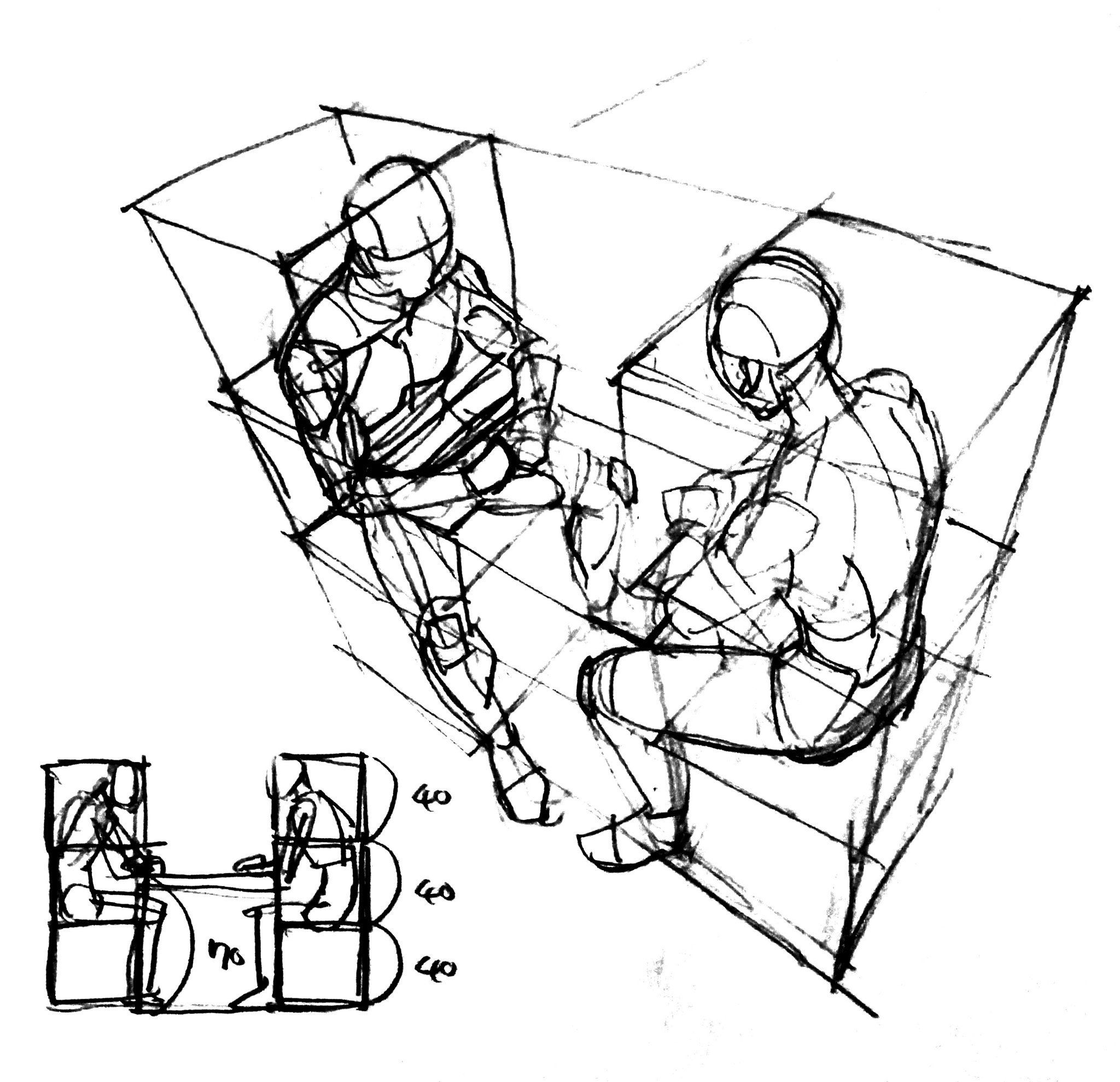 \wedge$, «идя» от $\Delta_1$ к $\Delta_2$ в одном или противоположном направлении, получая таким образом дополнительные углы. Мы можем поступить следующим образом.
\wedge$, «идя» от $\Delta_1$ к $\Delta_2$ в одном или противоположном направлении, получая таким образом дополнительные углы. Мы можем поступить следующим образом.
$\tt Определение\; 2\quad$ Ориентация над векторным пространством $\,E\;$ есть ненулевая альтернированная билинейная форма
$$ \Psi\;:\;E\times E \;\longrightarrow\; \mathbb R. $$
Эта форма ориентации различает положительно и отрицательно ориентированные базисы $\,E\;$ в зависимости от знака, который она принимает на данных базисах. Пространство $\,E\;$, снабженное формой ориентации $\Psi$, называется ориентированным векторным пространством .
$\tt Определение\;3\quad$ Пусть $\Delta_1=\mathbb R_+v_1,\;\; \Delta_2=\mathbb R_+v_2, \;$ с $v_1, v_2\neq0$. 9°(\Delta_1, \Delta_2) := \left\{v\in E\raise.3ex\smallsetminus\{0\}\;:\;\rm{pos}\Big(\Psi(v_1, v), \Psi(v, v_2), \Psi(v_2, v_1)\Big)\geq2\right\}, $$
где $\;\rm{pos}(\alpha, \beta, \gamma)\; $ обозначают количество строго положительных элементов, содержащихся в круглых скобках.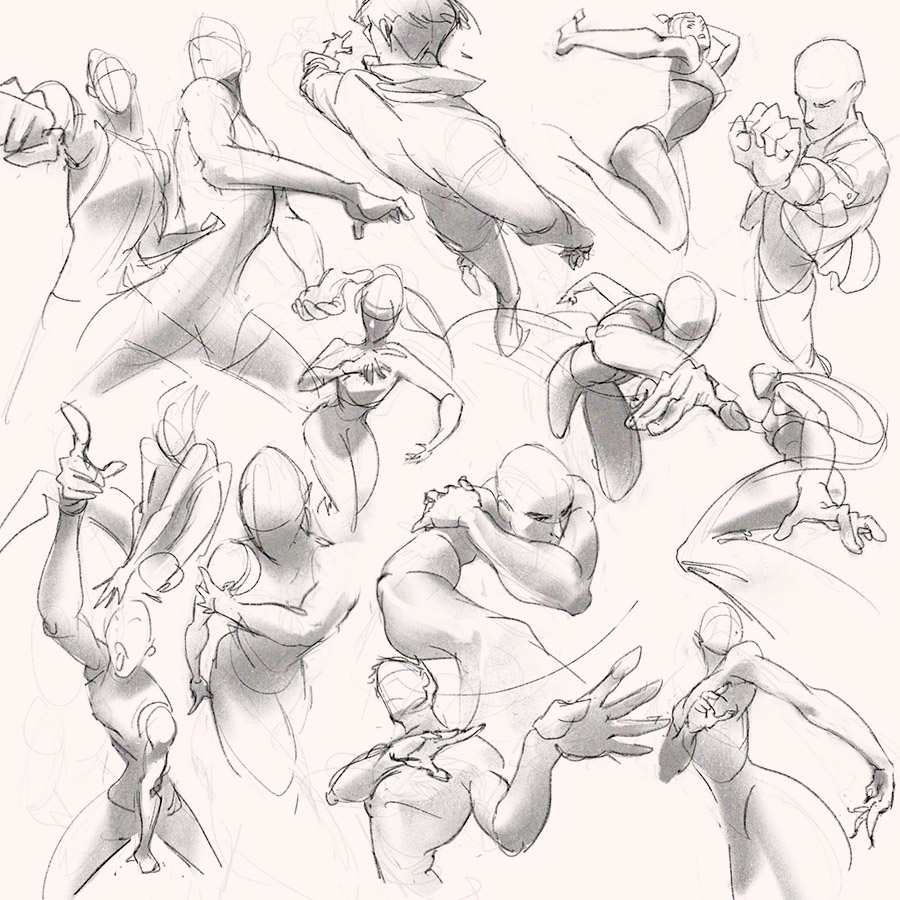


 Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.
Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.