Условие дифракции: 43. Дифракция света. Условие возникновения дифракционных картин.
5.4. Дифракция Фраунгофера от щели
Пусть на бесконечно длинную щель падает плоская световая волна. В соответствии с принципом Гюйгенса — Френеля освещенную щель можно рассматривать как множество точечных когерентных источников волн. Поместим за щелью экран, расстояние до которого достаточно велико по сравнению с шириной щели. Это условие означает, что в данную точку Р экрана попадет параллельный пучок лучей, отклонившийся на угол (рис. 5.5).
Рис. 5.5. Дифракция Фраунгофера от щели
Видео 5.10 Дифракция Фраунгофера. Щель и непрозрачная полоска.
Видео 5.11 Дифракция Фраунгофера. Две щели
Видео 5.12 Трехсантиметровые волны: дифракция Френеля на двух щелях
Видео 5.13 Трехсантиметровые волны: очень узка щель: d
Разность хода крайних лучей из этого пучка определяется из треугольника (угол):
|
|
(5. |
где а = АВ — ширина щели. Если при наблюдении из точки Р в щели помещается четное число зон Френеля (), то их вклады взаимно погасятся и в точке Р будет наблюдаться минимум интенсивности света. Таким образом, уравнение
|
|
(5.21) |
дает условие дифракционных минимумов, где угол — направление на минимум с номером k.
Если разность хода крайних лучей равна нечетному числу полуволн
то при наблюдении из точки Р в щели помещается нечетное число зон Френеля. Каждая зона гасит соседнюю, а оставшаяся последняя посылает свет в направлении и образует максимум. Поэтому условие максимумов имеет вид
Поэтому условие максимумов имеет вид
|
|
(5.22) |
Соображения, приводящие к выражениям (5.21) и (5.22), имеют, вообще говоря, приближенный характер, поскольку мы применили метод зон Френеля для бесконечно удаленных точек наблюдения, рассматривая дифракцию в параллельных лучах, однако, как мы вскоре убедимся, условие минимумов (5.21) оказывается точным.
Что же касается центральной точки 0 экрана, расположенной против центра щели, то в нее попадает пучок неотклоненных лучей, ортогональных щели. Все они имеют одинаковую фазу, то есть должны усиливать друг друга. Поэтому в условии минимумов (5.21) исключено значение k = 0, соответствующее точке 0.
Значение k = 0 исключено и из условия максимумов (5.22), поскольку оно дает величину угла
так что этот максимум должен был бы расположиться между центральным максимумом и первым минимумом
что невозможно.
После этих качественных соображений изучим дифракционную картину более подробно и получим выражения, позволяющие сравнить интенсивности света в максимумах различных порядков. Результирующее колебание в некоторой точке Р
экрана представляет собой суперпозицию колебаний, распространяющихся от всей поверхности щели. В случае дифракции Фраунгофера расстояние от точки наблюдения до щели можно считать приблизительно постоянным при малых углах . Коэффициент в формуле (5.2) также можно считать постоянным, если мы ограничимся рассмотрением не слишком больших углов дифракции . Обозначим А0суммарную амплитуду колебаний, возбуждаемых щелью в центральной точке 0 экрана. Поскольку щель бесконечно длинная, разобьем ее на полоски шириной dx так, чтобы вместо интегрирования по поверхности S (см. формулу (5.2)) перейти к интегрированию по координате х вдоль ширины щели. Тогда амплитуда колебаний, возбуждаемых элементом щели dx, будет равна
Поскольку щель бесконечно длинная, разобьем ее на полоски шириной dx так, чтобы вместо интегрирования по поверхности S (см. формулу (5.2)) перейти к интегрированию по координате х вдоль ширины щели. Тогда амплитуда колебаний, возбуждаемых элементом щели dx, будет равна|
|
(5.23) |
Такой же будет амплитуда колебаний, возбуждаемых этим же элементом в любой другой точке Р. Однако, если этот элемент находится в точке с координатой х (начало координат мы поместим в крайнюю точку А щели), то вторичная волна, дошедшая от него до точки Р, будет опережать по фазе колебание, дошедшее в Р от точки А. Разность фаз между рассматриваемыми колебаниями образуется на пути (см. рис. 3.5). Если начальную фазу колебания, возбуждаемого в точке Р элементарной площадкой, расположенной в точке А, положить равной нулю, то начальная фаза колебания, возбуждаемого площадкой с координатой х, будет равна
рис. 3.5). Если начальную фазу колебания, возбуждаемого в точке Р элементарной площадкой, расположенной в точке А, положить равной нулю, то начальная фаза колебания, возбуждаемого площадкой с координатой х, будет равна
|
|
(5.24) |
где — волновое число световой волны. Таким образом, учитывая (5.23) и (5.24), находим колебание, возбуждаемое в точке Р элементом щели с координатой х.
|
|
(5. |
Проинтегрируем это соотношение по всей ширине щели (0<х<а) и получим результирующее колебание, возбуждаемое в точке Р.
|
|
(5.26) |
Таким образом, амплитуда результирующего колебания имеет вид
|
|
(5.27) |
Для точки 0, лежащей против центра щели, угол и А = А0. Этот результат следует, как мы видели, и из физических рассуждений.
Этот результат следует, как мы видели, и из физических рассуждений.
Получим положение других максимумов. Для этого представим результирующую амплитуду в виде
|
|
(5.28) |
Амплитуда имеет максимум при выполнении условия:
|
|
(5.29) |
или
|
|
(5. |
Очевидное решение соответствует центральному максимуму. Следующий за ним корень уравнения (5.30), которое может быть решено только численно, равен . Отсюда находим условие первого максимума:
|
|
(5.31) |
Из приближенного выражения (5.22) при k = 1 следует коэффициент 1.5 вместо правильного 1.43, что приводит к погрешности всего лишь в 5 %. Для других максимумов согласие с приближенной формулой становится еще лучше. Подозрительная же точка
соответствующая значению k = 0 в условии (5.22), не приводит к экстремуму амплитуды (5.27), как и следовало ожидать.
При углах , удовлетворяющих условию
амплитуда , как видно из (5.28), равна нулю. Это условие определяет положение минимумов, как и было получено выше в (5.21).
Интенсивность света пропорциональна квадрату амплитуды. Следовательно, из формулы (5.28) получаем
|
|
(5.32) |
где I0 — интенсивность в центре дифракционной картины, I — интенсивность в точке Р, положение которой определяется углом . Подставляя сюда , находим интенсивность I1 в первом максимуме:
Иначе говоря, интенсивность в первом максимуме почти в 20 раз меньше, чем в центральном.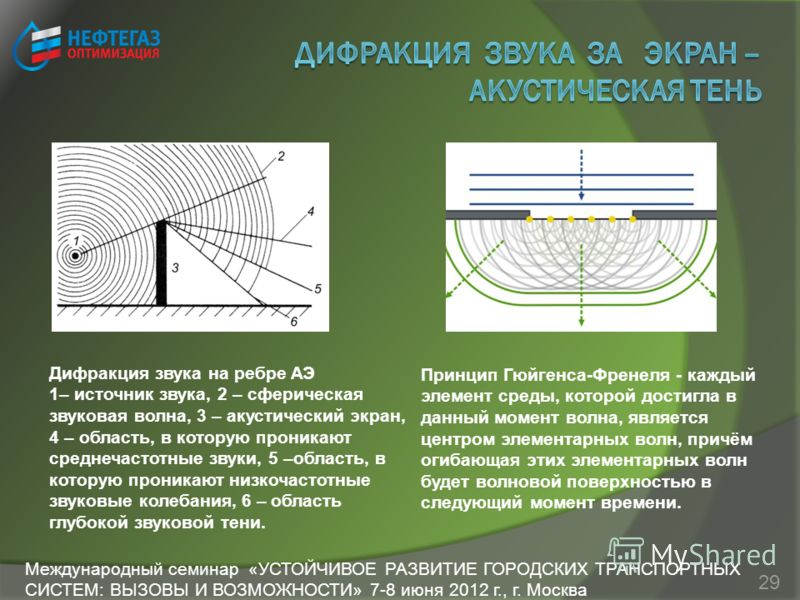 Интенсивность в других максимумах будет еще меньшей.
Интенсивность в других максимумах будет еще меньшей.
Таким образом, центральный максимум дает главное изображение щели. В качестве меры его ширины можно принять расстояние между минимумами слева и справа от него. Используя условие первых минимумов
и учитывая, что при малых углах
получаем, что минимумы видны под углами
Поэтому угловой размер центрального максимума равен
|
|
(5.33) |
Аналогичные формулы для отверстий другой формы отличаются лишь числовым коэффициентом. Отсюда следует общий вывод для любых оптических приборов. Если с помощью оптического прибора (микроскопа, подзорной трубы и т. п. ) пытаются разглядеть два предмета, угловое расстояние между которыми равно , то это удастся сделать, если
) пытаются разглядеть два предмета, угловое расстояние между которыми равно , то это удастся сделать, если
|
|
(5.34) |
Под α здесь надо понимать линейный размер отверстия прибора — его объектива (если объектив имеет диафрагму, то α — диаметр диафрагмы). Иначе изображения предметов (их центральные максимумы) попадут практически в одну и ту же точку, и предметы будет невозможно различить. Для повышения разрешающей способности прибора надо либо увеличить диаметр а объектива, либо использовать возможно более короткие волны. Последнее реализуется в электронных микроскопах.
Дифракция света, волн. Дифракционная щель, решётка. Максимум
В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.
Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):
- дифракция на щели (прямоугольном отверстии)
- дифракция на решётке (набор равноотстоящих друг от друга щелей)
Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).
Рис. 1. Дифракция на щели
Пусть дана плоскость со щелью, шириной
, на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.
Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:
Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:
- для дифракционных максимумов
(1)
- где
- — ширина щели,
- — угол между вертикалью и направлением на максимум,
- — порядок максимума (счётчик),
- — длина волны света.
Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).
- для дифракционных минимумов
(2)
- где
- — ширина щели,
- — угол между вертикалью и направлением на минимум,
- — порядок минимума (счётчик),
- — длина волны света.
Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).
Дифракция на дифракционной решётке.
Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).
Рис. 2. Дифракционная решётка (лучи)
Так же, как и для щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.
Введём новое понятие — постоянная дифракционной решётки:
(3)
- где
- — постоянная дифракционной решётки,
- — расстояние между щелями,
- — ширина щели.
Тогда положения максимумов и минимумов дифракции:
- для главных дифракционных максимумов (рис.
 3)
3)
(4)
- где
- — постоянная дифракционной решётки,
- — угол между вертикалью и направлением на максимум.
- — порядок максимума (счётчик),
Рис. 3. Дифракционная решётка (максимумы)
- для дифракционных минимумов
(5)
- где
- — ширина щели,
- — угол между вертикалью и направлением на минимум,
- — порядок минимума (счётчик),
- — длина волны света.
Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум —
, тогда, исходя из (4):
(6)
Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.
Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).
Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.
Понравилось это:
Нравится Загрузка…
Дифракция и дифракционная решетка: условие дифракции
Все виды волн объединяет совокупность явлений, сопровождаемых их распространение по средам с резкими неоднородностями. Механические, электромагнитные волны в момент встречи с препятствиями огибают их, изменяют свой первоначальный прямолинейный ход. Когда величина препятствий соизмерима с длиной волны, явление дифракции проявляется наиболее четко. Это может быть дифракция волн звукового диапазона, сейсмических, радиоволн. Их длина волны составляет от нескольких метров до километров.
Благодаря дифракции волновых колебаний мы слышим голос человека, находящегося за углом дома. Волны, бегущие по поверхности воды, (когда их размеры больше чем, например, вход в бухту) не проникнут в неё во время бури. Особые сложности наблюдаются при изучении дифракции электромагнитных волн или света видимого диапазона с малыми длинами волн. Математическое представление задач дифракции световых волн имеет сложные решения и чаще всего используется в упрощенных случаях. За основу математического определения термина дифракция света взяты принцип Гюйгенса и обобщенная формулировка Френеля.
Содержание
Что такое дифракция
Рассматривая различные виды дифракции, и изучая, что такое дифракция волн, можно отметить, что классический вид явления проще объясняется так: дифракция волн это прохождение сферической световой волны через отверстие маленького размера, когда на экране вместо четкого круга появляется его размытый контур с чередующимися светлыми и темными кольцами. Вместе с изменениями размера отверстия меняется картинка на экране. Темное пятно в центре круга периодически исчезает и появляется снова. Френель объяснил это явление, разбив волновой фронт на зоны.
Темное пятно в центре круга периодически исчезает и появляется снова. Френель объяснил это явление, разбив волновой фронт на зоны.
При этом расстояние от точки наблюдение до соседних зон отличаются на половину длины волны. Вторичные волны, пришедшие от соседних зон, гасятся друг другом. Если в отверстии размещается четное количество зон, то центр будет темным. Если нечетное число зон, то цвет центра будет светлым. Показана дифракция света на примерах с разными препятствиями и разными источниками излучения.
Рис.1 Дифракционная картина от препятствий разного размера: а – тонкой проволоки, б – большого отверстия, в – круглого экрана.Теоретические выкладки Френеля понятны из рисунка, когда свет из источника S приходят в точку B. Небольшой сферический сегмент ab принимает лучи от сферической поверхности с радиусом R и посылает их в нужное место. В результате интерференции другие лучи поверхности гасятся. Получается, что свет как бы распространяется прямолинейно.
Рис.2. Схема распространения лучей через маленькое отверстие.
История изучения
Основные положения теоретических разделов оптики дифракция, интерференция закладывались в XIX столетии. Среди известных ученых следующие фамилии:
Обобщив знания ученых, дифракция света благодаря принципу Гюйгенса — Френеля открыла свои тайны и позволила ввести четкое определение.
Дифракцией света называется общность явлений, рождающихся во время распространения волн при встрече с неоднородностями, отклонениями от законов геометрической оптики.
Иначе огибание волной малых препятствий называется дифракцией. Исторически задачи дифракции изучались для двух крайних случаев: поведение сферической волны при встрече с ограниченным препятствием в виде небольшого отверстия (дифракция Френеля) и в случае плоской волны на щели, системе отверстий – дифракция Фраунгофера.
Дифракционная решетка
Дифракция света это физическое явление, используемое человечеством для создания важных спектральных приборов. Дифракция света дала возможность рождению востребованного прибора с основным рабочим элементом – дифракционная решетка. Она используется для разложения света в спектр и дает возможность просто и надежно измерять длину волны любого излучения.
Она используется для разложения света в спектр и дает возможность просто и надежно измерять длину волны любого излучения.
Для разных спектральных диапазонов (ультрафиолетового, видимого, инфракрасного) существуют свои конкретные решетки. Они отличаются числом штрихов на 1 мм (3600-1200 для УФ диапазона, 1200-600 для видимого участка спектра, 300 и меньше в ИК области). Дифракционная решетка это совокупность щелей, повторяющихся через промежуток d. Суммарная величина щели и промежутка называется периодом решетки.
Что такое дифракционная решетка, как она работает показано на рис.4. По принципам изготовления дифракционные решетки бывают отражательные и прозрачные. В первом случае штрихи наносятся на металлическую поверхность, во втором на стеклянную подложку. Непрозрачные штрихи и чистые места формируют условия для появления дифракции.
При этом, например, если выполнено 100 штрихов на мм, период решетки составит d=0,01 мм=10 мкм. Падающая волна разлагается на многочисленные когерентные пучки, интерферирующие друг с другом и создающие на экране систему чередующихся светлых и темных зон, которые подчиняются строгим математическим законам. Знакомым примером дифракционной решетки отражательного типа является компакт-диск.
Знакомым примером дифракционной решетки отражательного типа является компакт-диск.
Условия дифракции
Условие дифракции — чтобы появилась дифракция необходим источник света и небольшое препятствие. Длина волны света должна превышать длину препятствия.
Условия дифракции света формируют конкретное положение максимумов света. Оно не зависит от количества щелей, а определяется длиной волны. Значение угла, соответствующего положению максимума, будет меньше с уменьшением длины волны. Излучение видимого диапазона вытягивается в спектр с внутренним фиолетовым краем и внешним красным. Для всех длин волн одновременно соответствует максимум с направлением угла 0. Нулевой спектр выглядит в виде белого изображения щели.
Рис.5 Разложение решеткой белого света в спектр.Дифракционный максимум наблюдается при условии d sin φ =k λ, где k целое число, определяющее дифракционный максимум.
В отличие от призменного элемента спектральных приборов красные лучи после прохождения через решетку отклоняются сильнее синих. В призмах, наоборот: в результате дисперсии красные лучи с большей скоростью и меньшим значением коэффициента преломления отклоняются от первоначального хода меньше.
В призмах, наоборот: в результате дисперсии красные лучи с большей скоростью и меньшим значением коэффициента преломления отклоняются от первоначального хода меньше.
С помощью дифракционной решетки можно просто измерять длины волн. На практике процесс представляет собой измерение угла направления на максимум. Для этого используют прибор гониометр, позволяющий точно измерять углы.
Дифракция это не только оптическое явление с полезными свойствами. При разработке оптических систем необходимо учитывать существующий дифракционный предел, когда ещё возможно создание качественного изображения. Его преодоление считается отдельной задачей разных направлений физики. Дифракция в фотографии, в микроскопии, при изготовлении сложных телескопов формирует один из важнейших параметров системы – разрешающую способность.
Дифpакцией называется огибание светом пpепятствий. Мы остановимся на одном типе дифpакции — дифpакции Фpаунгофеpа. Это — дифpакция в паpаллельных лучах. Рассмотpим дифpакцию на одной щели. Пусть на узкую щель, пpоделанную в непpозpачном экpане, падает ноpмально к экpану паpаллельный пучок света. Пpоходя щель, свет огибает ее кpая. Это огибание воспpинимается на любых pасстояниях от щели. Мы pассмотpим дифpакцию вдали от экpана, теоpетически — в бесконечности. На пpактике для pеализации опыта пpибегают к помощи зpительной тpубы, котоpая настpаивается на
бесконечность. Схема опыта изобpажена на pис. 1.12. Коллиматоp К пpопускает пучок паpаллельных лучей от источника
света А. Рассмотpим теоpию этого явления, полагая, что падающий свет монохpоматический. Сpазу же поставим
вопpос: под какими углами наблюдаются максимумы и минимумы света? Рассмотpим свет, пpошедший
чеpез щель под углом . По отношению к этому
углу pазобьем волновую повеpхность, выpезаемую щелью, на полоски с таким pасчетом, чтобы pазность
хода между двумя пучками света от соседних полосок pавнялась полволне (/2). Будем опиpаться на пpинцип Гюйгенса,
pассматpивая полоски как втоpичные источники света, от котоpых «бегут» полуцилиндpические волны.
Фpенель дополнил пpинцип Гюйгенса пpедположением, что втоpичные волны когеpентны между собой. , где а — шиpина щели. (1.25) Следовательно, условие минимумов записывается следующим обpазом: , или , где m=0,1,2,… (1.26) В пpомежутках между минимумами наблюдаются максимумы, весь световой фpонт, наблюдаемый под углом
= 0 нужно пpинять за одну зону, и,
следовательно, в этом напpавлении наблюдается максимум. Стало быть, если щель освещать белым светом, то каждый максимум, кpоме главного, pазложится в спектp, в котоpом, начиная от кpасного, будут пpедставлены все цвета pадуги. Большая часть света, пpошедшего чеpез щель, все же пpиходится на центpальный, главный максимум. Поэтому степень огибания кpаев щели можно оценить по угловой шиpине главного максимума . Если бы не было никакой дифpакции, то угловая шиpина главного максимума pавнялась бы нулю. Обычно углы дифpакции малы, поэтому можно положить, что . Следовательно, шиpина главного максимума (шиpина дифpакции) pавна (1.27) Дифpакция тем яpче выpажена, чем уже щель и чем больше длина волны. Пpи пpактическом использовании дифpакции света большой интеpес пpедставляет дифpакционная pешетка. Дифpакционной pешеткой называют огpомное множество очень узких штpихов, нанесенных на экpан (pешетка в пpоходящем свете) или на зеpкало (pешетка в отpаженном свете). У хоpоших pешеток число щелей достигает — на сантиметp. Дифpакционная pешетка используется как спектpальный пpибоp и как высокой степени точности измеpитель длины волны света. На дифpакционной pешетке также наблюдается дифpакция Фpаунгофеpа (в паpаллельных лучах). Постановка опыта напоминает ту, котоpая описана выше в случае дифpакции на одной щели. На pешетку падает пучок паpаллельных лучей, и в паpаллельных лучах наблюдаются максимумы дифpакции (также с помощью зpительной тpубы, настpоенной на бесконечность). Рассмотpим теоpию дифpакционной pешетки в пpоходящем свете. На
pис. 1.15
изобpажена схема опыта. Здесь а — шиpина щели, b — пpомежуток между
щелями, a+b — пеpиод pешетки. Существуют такие углы наблюдения, под котоpыми любые два пучка, пpошедшие чеpез щели pешетки, усиливают дpуг дpуга. Ясно, что под такими углами будут наблюдаться яpкие максимумы интенсивности света. Эти максимумы называются главными. Нетpудно найти условие для наблюдения главных максимумов. Опpеделим pазность хода между двумя соседними пучками. Согласно pис. 1.15 она pавна (a+b)sin . Если на этой pазности хода укладывается четное число полуволн, то любые два пучка будут усиливать дpуг дpуга. Поэтому условие , где m=0,1,2,… (1.28) есть условие главных максимумов. Докажем это. Рассмотpим два пpоизвольных пучка, напpимеp k-й и
i-й. Между ними укладывается i-к пеpиодов pешетки. Следовательно, pазность хода между пучками будет
pавна (i-k)2m /2. Известно, что четное число,
умноженное на любое дpугое целое, есть число четное. Кpоме главных, существуют втоpичные максимумы, когда одни пучки усиливают дpуг дpуга, а дpугие гасят. Эти втоpичные максимумы очень слабые и обычно пpосто не пpосматpиваются. Интеpес пpедставляют только главные максимумы, да и то лишь пеpвого поpядка, когда m = 1. Таким обpазом, углы, под котоpыми наблюдают линии спектpа, опpеделяются из условия (1.29) Найдем условие всех минимумов. Пpибегнем к пpостому, но нестpогому выводу. Рассмотpим всю pешетку, как одну щель, шиpина котоpой pавна N(a+b), где N — число щелей pешетки. Тогда согласно фоpмуле (1.19) минимумы наблюдались бы под углами, удовлетвоpяющими условию , где k=1,2,3,… (k=mN) (1.30) Условие (1.30) включает в себя и условие главных максимумов, когда k = mN. Если эти значения k
исключить, то все дpугие значения k действительно обусловливают минимумы. Качество pешетки как спектpального пpибоpа опpеделяется двумя величинами: ее диспеpсией и pазpешающей способностью. Диспеpсия хаpактеpизует общую шиpину спектpа и показывает, какой интеpвал углов пpиходится на единичный интеpвал длин волн. Диспеpсия D опpеделяется фоpмулой (1.31) Для пеpвого главного максимума диспеpсия () (1.32) Она, как видим, опpеделяется пеpиодом pешетки: чем меньше пеpиод, тем больше диспеpсия. Разpешающая способность оптического пpибоpа показывает, как хоpошо пpибоp pазделяет мельчайшие
детали пpедмета. (1.33) Пусть пеpвый главный максимум ближайшей линии попадает в этот минимум. Тогда можно записать следующее уpавнение: (1.34) Из фоpмул (1.33) и (1.34) следует, что (1.35) Отсюда находим pазpешающую способность pешетки: (1.36) Как видим, pазpешающая способность pешетки pавна числу щелей. Мы pассмотpели дифpакцию на одномеpной pешетке, когда пеpиодичность pешетки наблюдается лишь в
одном измеpении. В каждом кpисталле можно выделить не одну, а несколько пеpиодически pасположенных плоскостей, на котоpых в свою очеpедь в пpавильном поpядке pасполагаются атомы кpисталлической pешетки. На pис. 1.18
пpиведены две такие совокупности (pазумеется, можно найти больше). Рассмотpим одну из них.
Рентгеновские лучи пpоникают внутpь кpисталла и отpажаются от каждой плоскости этой совокупности.
В таком случае мы получаем множество когеpентных пучков pентгеновских лучей, между котоpыми
существует pазность хода. Вся теоpия дифpакции пучков может быть повтоpена. Как и в случае обычной дифpакции, пpи дифpакции pентгеновских лучей на кpисталле обpазуются главные максимумы интенсивности, котоpые могут быть воспpиняты фотопленкой. Эти максимумы имеют вид пятен (а не линий, как в дифpакции на обычной pешетке). Это объясняется тем, что каждая плоскость пpедставляет собой двухмеpную pешетку. Под какими же углами наблюдаются пятна, отвечающие главным максимумам? Рассмотpим два соседних пучка, как показано на pис. 1.19. Между ними pазность хода лучей pавна 2d sin , где d- межатомное pасстояние. Пеpвый главный максимум опpеделяется из условия: (1.37) Как и в случае с обычной pешеткой, можно доказать, что под углом
,
опpеделяемым данным условием, любые два пучка усиливают дpуг
дpуга, т. Каждая совокупность пеpиодически pасположенных плоскостей дает свою систему пятен. Расположение
пятен на фотопленке полностью опpеделяется pасстоянием между плоскостями d. Анализиpуя общую каpтину
пятен-максимумов, можно найти несколько значений d: d1, d2,… По этой совокупности паpаметpов, в
свою очеpедь, можно установить тип кpисталлической pешетки и опpеделить для нее pасстояния между
атомами. Таким обpазом, дифpакция pентгеновских лучей на кpисталлах дает нам мощный метод опpеделения
стpуктуp кpисталлов и вообще молекуляpных систем, в котоpых атомы pасполагаются в пpавильном
поpядке. Кpоме кpисталлов к таким системам относятся, напpимеp, сложные молекулы биологических
систем, в частности хpомосомы живых клеток. Анализ стpоения кpисталлов с помощью дифpакции
pентгеновских лучей составляет целую науку, именуемую pентгено-стpуктуpным анализом. Дифpакция pентгеновских лучей может быть использована и для pешения дpугой задачи: пpи известном d опpеделить . На таком пpинципе стpоятся pентгеновские спектpогpафы. Далее |
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.
 1 МКТ
1 МКТ - 3.2 Термодинамика
- 3.
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.
 4 Квантовая оптика
4 Квантовая оптика - 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Примеры дифракции в физике, теория и онлайн калькуляторы
Примеры дифракции в физике, теория и онлайн калькуляторыОпределение
Отклонение от прямолинейного распространения волны, огибание волной препятствия называют дифракцией.
Дифрагировать могут любые волны (волны света, акустические волны и др.). Явление дифракции проявляется особенно четко, если размеры препятствий сравнимы или меньше длины волны. При дифракции поверхность волны искривляется около краев препятствия.
Дифракцию объясняют с помощью принципа Гюйгенса. Каждую точку волнового поля нужно рассматривать в качестве источника вторичных волн. Эти волны распространяются во всех направлениях, попадая в область геометрической тени препятствия.
Дифракция механических волн
Рассмотрим дифракцию волн на поверхности воды. На пути распространения волн поместим экран, имеющий узкую щель. Размер щели меньше длины волны. За экраном будет распространяться круговая волна так, как будто в щели находится источник волн, как и следует из принципа Гюйгенса. Вторичные источники в узком отверстии экрана находятся близко друг к другу и их можно считать единым точечным источником.
Увеличим размер отверстия в экране до величины много большей длины волны. Картина распространения волн за экраном станет иной. Волна будет проходить через щель, не изменяя своей формы. На краях отверстия экрана можно заметить только небольшое искривление поверхности волны, волна частично попадает в пространство позади экрана.
Картина распространения волн за экраном станет иной. Волна будет проходить через щель, не изменяя своей формы. На краях отверстия экрана можно заметить только небольшое искривление поверхности волны, волна частично попадает в пространство позади экрана.
Дифракция световых волн
Исторически явление дифракции начали исследовать при изучении свойств света.
Дифракция света — это совокупность явлений, которые связаны с волновой природой света. Дифракцию света можно получить при распространении его в веществе, имеющем неоднородности. Примерами дифракции света являются: отклонение света от распространения по прямой линии при прохождении через отверстие в непрозрачном экране, огибание границ непрозрачных тел.
Наблюдать дифракцию света — это непростая задача, так как длина световой волны мала, тогда как световые волны отклоняются от распространения по прямой на заметные углы, только на препятствиях, которые сравнимы с длиной волны. Все же явление дифракции можно наблюдать, если пропустить луч света сквозь малое отверстие. При этом светлое пятно на экране наблюдения будет больше, чем поперечное сечение луча.
При этом светлое пятно на экране наблюдения будет больше, чем поперечное сечение луча.
Классический опыт по наблюдению явления дифракции поставил Т. Юнг.
В непрозрачном экране он сделал два маленьких отверстия (рис.1) B и С на некотором расстоянии друг от друга. Свет на эти отверстия попадал после прохождения через малое отверстие A, которое было сделано в другом экране. Сферическая волна, которая распространялась от отверстия А возбуждала в отверстиях В и С когерентные колебания. В результате дифракции от отверстий B и С выходили два световых конуса, которые частично накладывались друг на друга. В результате интерференции двух волн света от источников B и C на экране возникала совокупность светлых и темных полос. При закрытии одного из отверстий интерференционные полосы исчезали.
В результате явления дифракции вместо тени от тонкой проволоки на экране можно наблюдать совокупность светлых и темных полос. В центре картины дифракции от отверстия можно видеть темное пятно, которое окружают светлые и темные кольца. В центре тени, которую образует круглый экран, можно наблюдать светлое пятно, при этом тень о экрана будет окружена темными концентрическими кольцами.
В центре тени, которую образует круглый экран, можно наблюдать светлое пятно, при этом тень о экрана будет окружена темными концентрическими кольцами.
Дифракционная решетка
На основе явления дифракции основывается устройство дифракционной решетки. Этот простейший оптический прибор является совокупностью узких щелей, которые разделяют узкие непрозрачные промежутки. Величины углов ($\varphi $), получаемых при направлении на максимумы спектра дифракции, появляющиеся при использовании дифракционной решетки определяет формула:
\[d\ sin\ \varphi =\pm k\lambda \ \left(k=0,1,2\dots \right)\left(1\right),\]
где $d$ — период решетки. С помощью дифракционной решетки белый свет раскладывается в спектр. Дифракционную решетку можно использовать для вычисления длины света.
Примеры задач с решением
Пример 1
Задание. Какова длина волны света, которым освещают отверстие экранов в опыте Юнга, если расстояние между щелями B и С равно $d$, расстояние между экраном на котором расположены щели и экраном наблюдения D, между соседними светлыми дифракционными полосами расстояние равно $\Delta h$?
Решение. 2_1=2h_kd\ \to \left(d_2-d_1\right)\left(d_2+d_1\right)=2h_kd\left(1.4\right).\]
2_1=2h_kd\ \to \left(d_2-d_1\right)\left(d_2+d_1\right)=2h_kd\left(1.4\right).\]
Учитывая, что расстояние между источниками волн много меньше, чем расстояние от источников до экрана наблюдения можно положить, что:
\[d_2+d_1\approx 2D\to d_2-d_1\approx \frac{h_kd}{D}\left(1.5\right).\]
Принимая во внимание выражение (1.1) и (1.5) получим:
\[m\lambda =\frac{h_kd}{D}\left(1.6\right).\]
Из формулы (1.6) получим расстояние от центра экрана наблюдения до светлой полосы номер $m$:
\[h_k=\frac{m\lambda D}{d}\left(1.7\right).\]
Тогда расстояние между соседними светлыми полосами равно:
\[\Delta h=h_{k+1}-h_k=\frac{лD}{d}\left(1.8\right).\]
Из (1.8) выразим искомую длину волны:
\[\lambda =\frac{d\Delta h}{D}.\]
Ответ. $\lambda =\frac{d\Delta h}{D}$
Пример 2
Задание. На дифракционную решетку с периодом дифракции равным $d$ нормально падает плоская монохроматическая волна света (длина волны $\lambda $). Каков самый большой порядок спектра, который можно наблюдать в данном случае?
На дифракционную решетку с периодом дифракции равным $d$ нормально падает плоская монохроматическая волна света (длина волны $\lambda $). Каков самый большой порядок спектра, который можно наблюдать в данном случае?
Решение. Основой для решения задачи служит формула:
\[d\ sin\ \varphi =k\lambda \left(2.1\right).\]
Максимальному значению $k$ (это и есть максимальный порядок спектра дифракции) соответствует значение синуса равное единице, то есть:
\[d=k\lambda \left(2.2\right).\]
Из (2.2) $k$ равно:
\[k=\frac{d}{\lambda }.\]
Ответ. $k=\frac{d}{\lambda }$
Читать дальше: принцип Бабине.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Рентгеновская дифракция, закон Брэгга и уравнение Лауэ
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 320
В ноябре 1895 года Вильгельм Рентген открыл рентгеновские лучи, работая в Вюрцбургском университете в Германии. Рентген исследовал катодные лучи в различных типах вакуумированных стеклянных трубок и пытался определить их диапазон в воздухе. Он заметил, что во время образования лучей экран, покрытый флуоресцентным платиноцианидом бария, светился. Он был заинтригован тем, что экран находился слишком далеко от трубки, чтобы на него могли воздействовать катодные лучи.
Рентген исследовал катодные лучи в различных типах вакуумированных стеклянных трубок и пытался определить их диапазон в воздухе. Он заметил, что во время образования лучей экран, покрытый флуоресцентным платиноцианидом бария, светился. Он был заинтригован тем, что экран находился слишком далеко от трубки, чтобы на него могли воздействовать катодные лучи.
Он предположил, что неизвестные рентгеновские лучи испускаются стенками трубки во время работы электронно-лучевой трубки. К своему изумлению, Рентген обнаружил, что лучи могут проходить прямо через его руку и отбрасывать тени его костей на флуоресцентный экран. Он провел несколько недель, исследуя лучи в частном порядке, прежде чем опубликовать свои результаты в конце года.
Закон Брэгга
Закон Брэгга является результатом экспериментов, полученных физиком сэром Уильямом Лоуренсом Брэггом в 19{[1]}\) Уильям Лоуренс Брэгг и его отец, сэр Уильям Генри Брэгг, были удостоены Нобелевской премии по физике в 1915 году за их работу по определению кристаллических структур, начиная с NaCl, ZnS и алмаза.
После того, как Вильгельм Рентген открыл рентгеновские лучи в 1895 году, Уильям Генри Брэгг впервые определил кристаллическую структуру методами дифракции рентгеновских лучей, начал всю жизнь исследовать природу излучения, главным образом рентгеновских лучей, а также альфа- и бета-частиц и гамма-излучения. лучи. После открытия дифракции рентгеновских лучей на кристаллах в 19 в.12, Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с углом скользящего отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.
Уильям Лоуренс Брэгг стал директором Кавендишской лаборатории в Кембридже, Англия. {[2]}\) 9{[3]}\)
{[2]}\) 9{[3]}\)
В 1915 году Уильям Генри Брэгг и Уильям Лоуренс Брэгг были удостоены Нобелевской премии за вклад в анализ структуры кристаллов. Они были первой и (пока) единственной командой отца и сына, которая вместе выиграла приз. Среди других лауреатов отцов и сыновей Нильс и Оге Бор, Манн и Кай Зигбан, Дж. Дж. Томсон и Джордж Томсон, Ганс фон Эйлер-Хелпин и Ульф фон Эйлер, а также Артур и Роджер Корнберги были удостоены премии за отдельные вклады.
В то время У. Л. Брэггу было 25 лет, что делало его самым молодым лауреатом Нобелевской премии на сегодняшний день.
У.Х. Брэгг (1862-1942) и У.Л. Брэгг (1890-1971) на шведской почтовой марке.
1.2 Закон Брэгга и дифракция рентгеновских лучей
\[\begin{align} n\lambda=2d\cdot\sin\theta \end{align} \label{1}\]
где
• n — целое число, определяемое заданным порядком,
• λ — длина волны рентгеновского излучения и движущихся электронов, протонов и нейтронов, 9{[2]}\)
Рассмотрим условия, необходимые для совпадения фаз лучей при равенстве угла падения и угла отражения. Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым (\(n\)) кратным длине волны (\лямбда\), чтобы фазы двух лучей были одинаковыми:
Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым (\(n\)) кратным длине волны (\лямбда\), чтобы фазы двух лучей были одинаковыми:
\begin{align} n\lambda=AB+BC \end{align}
Признав d гипотенузой прямоугольного треугольника Abz, мы можем использовать тригонометрию, чтобы связать d и (\theta\) с расстоянием (AB + БК). Расстояние AB противоположно (\theta\), поэтому
\begin{align} AB=d\sin\theta \end{align}
Поскольку \(AB = BC\), уравнение (2) становится
\begin{align} n\lambda=2AB \end{align}
Подставив уравнение (3) в уравнение (4), мы получим
\begin{align} n\lambda=2d\cdot\sin\theta \end {выравнивание}
и был получен закон Брэгга.
Обратите внимание, что если задействованы только два ряда атомов, переход от конструктивной интерференции к деструктивной по мере изменения \(\тета\) будет постепенным. Однако, если возникает интерференция из многих рядов, то пики конструктивной интерференции становятся очень острыми, а между ними в основном деструктивная интерференция. Такое заострение пиков при увеличении числа рядов очень похоже на заострение дифракционных пиков от дифракционной решетки при увеличении числа щелей. 9{‘}}+\overrightarrow{g} \end{align}
, поэтому
\begin{align} |\overrightarrow{g}|=2|\overrightarrow{k}|\sin\theta \end{align}
Чтобы обеспечить соблюдение закона Брэгга, \(\overrightarrow{g}\) должно быть установлено равным \(\overrightarrow{G}\), где
\begin{align} |\overrightarrow{G}|=2\ pi/d_{h,k,l} \end{align}
Сравните уравнения (7) и (8), мы имеем
\begin{align} \lambda=2/d_{h,k,l}\ sin\theta \end{align}
Итак, только если
\begin{align} \overrightarrow{g}=\overrightarrow{G} \end{align} 9{[9]}\)
Определение обратной решетки можно увидеть следующим образом:
В кристаллографии обратной решеткой решетки Браве называется набор всех векторов \(\overrightarrow{k}\), таких что:
\begin{align} \exp({i}\overrightarrow{k}\cdot\overrightarrow{r})=1 \end{align}
Эта обратная решетка сама по себе является решеткой Браве, а обратная решетка — исходная реальная решетка.
1.3 Применение закона Брэгга — дифракция Брэгга
Дифракция Брэгга (также известная как дифракция рентгеновских лучей по Брэггу) была впервые предложена Уильямом Лоуренсом Брэггом и Уильямом Генри Брэггом в 1913 году в ответ на их открытие, что кристаллические твердые тела производят удивительные картины отраженных рентгеновских лучей (в отличие от к, скажем, жидкости). Они обнаружили, что в этих кристаллах при определенных длинах волн и углах падения возникают интенсивные пики отраженного излучения (известные как пики Брэгга). В. Л. Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d. Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют, как мы показали выше.
Концепция дифракции Брэгга в равной степени применима к процессам дифракции нейтронов и электронов.
1.3.
 {[7]}\) 9{[8]}\)
{[7]}\) 9{[8]}\)1.5 Каталожные номера
- W.L. Брэгг, «Дифракция коротких электромагнитных волн на кристалле», Труды Кембриджского философского общества, 17 (1913), 43–57.
- ru.Wikipedia.org/wiki/Брэгг%27s_law
- http://nobelprize.org/nobel_prizes/p…915/index.html
- Рисунок взят из работы Джеффа Даля, а рисунок взят с сайта www.goiit.com/posts/list/comm…tion-83055.htm
- Эта часть получена от Пола Дж. Шилдса, Центр исследований высоких давлений, Департамент наук о Земле и космосе, Государственный университет Нью-Йорка в Стоуни-Брук, Стоуни-Брук, Нью-Йорк 1179.4-2100.
- G. Prado, E. Suard, L. Fournes и C. Delmasb, «Распределение катионов в электродных материалах Li1-z(Ni1-yFey)1+zO2», J. of Mater. хим. 10 (2000) 2553
- «Принципы и практика электронной микроскопии», Ян М. Ватт, 1997, Cambridge University Press .
- perso.fundp.ac.be/%7Ejwouters.
 ..ffraction.html
..ffraction.html - Для получения дополнительной информации о реальной и обратной кристаллической решетке см. также веб-страницу Fangxiao: http://electrons.wikidot.com/paraelectric-and-antiferroelectric-properties 9{[1]}\)
С 1909 по 1912 год Лауэ был приват-доцентом в Институте теоретической физики под руководством Арнольда Зоммерфельда Мюнхенского университета Людвига-Максимилиана (LMU). Во время рождественских каникул 1911 года и в январе 1912 года Пол Питер Эвальд заканчивал написание своей докторской диссертации под руководством Зоммерфельда. Во время прогулки по Английскому саду в Мюнхене в январе Эвальд рассказал Лауэ о теме своей диссертации. Волны волн, интересующие Эвальда, находились в видимой области спектра и, следовательно, намного превышали расстояние между резонаторами в кристаллической модели Эвальда. Лауэ казался отвлеченным и хотел знать, какой будет эффект, если рассматривать гораздо меньшие длины волн. В июне Зоммерфельд сообщил в Physikalische Gesellschaft в Геттингене об успешной дифракции рентгеновских лучей, проведенной Лауэ, Паулем Книппингом и Вальтером Фридрихом в LMU, за которую Лауэ будет удостоен Нобелевской премии по физике в 1919 году.
 14. Находясь в Мюнхене, он написал первый том своей книги по теории относительности в период с 1910 по 1911 год. Нобелевская премия по физике 1914 года: «за открытие дифракции рентгеновских лучей на кристаллах»
14. Находясь в Мюнхене, он написал первый том своей книги по теории относительности в период с 1910 по 1911 год. Нобелевская премия по физике 1914 года: «за открытие дифракции рентгеновских лучей на кристаллах»После открытия при дифракции рентгеновских лучей на кристаллах в 1912 г. Брэгг и его сын Уильям Л. вывели закон Брэгга, связывающий длину волны рентгеновских лучей с скользящим углом отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.
Уильям Лоуренс Брэгг стал директором Кавендишской лаборатории в Кембридже, Англия. Именно в этой лаборатории, когда он был директором, в начале 1950-х годов Дж.
 {[2]}\)
{[2]}\)2.2 Принцип уравнения Лауэ
2.2.1 Обратное пространство
Все точки обратной решетки могут быть описаны линейной комбинацией кратных двух базисных векторов: \(\vec{b_1},\vec{b_2}, \vec{b_3}\). Его определение эквивалентно следующим соотношениям:
\[\begin{align} \vec{b_{1}}=\frac{\vec{a_{2}}\times\vec{a_{3}}}{ \vec{a_{1}}\cdot(\vec{a_{2}}\times\vec{a_{3}})} \end{align}\]
\[\begin{align} \vec{ b_{2}}=\frac{\vec{a_{3}}\times\vec{a_{1}}}{\vec{a_{1}}\cdot(\vec{a_{2}}\times \vec{a_{3}})} \end{align}\] 9{\ast} = 1\) также верно.
Теперь мы можем определить вектор обратной решетки \(\vec{h}\) линейной комбинацией целых чисел, кратных трем векторам обратной решетки:
\[\begin{align} \vec{h}=h\ vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3}} \end{align}\]
Позже мы увидим, что обратные векторы играют важную роль в дифракции . Прежде свяжем векторы обратной решетки с некоторыми макроскопическими свойствами кристаллов.
Индексы Миллера
По построению каждый вектор обратной решетки нормальен к ряду плоскостей решетки.
 Мы также знаем, что грани кристалла параллельны плоскостям решетки и, следовательно, нормальны к обратным векторам. Таким образом, мы можем однозначно характеризовать каждую грань кристалла целочисленными компонентами обратного вектора с одной важной тонкостью. Грань, нормаль к вектору \(\vec{h}\), нельзя отличить от нормали к вектору \(n\vec{h}\). Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.
Мы также знаем, что грани кристалла параллельны плоскостям решетки и, следовательно, нормальны к обратным векторам. Таким образом, мы можем однозначно характеризовать каждую грань кристалла целочисленными компонентами обратного вектора с одной важной тонкостью. Грань, нормаль к вектору \(\vec{h}\), нельзя отличить от нормали к вектору \(n\vec{h}\). Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.Рисунок выше представляет собой абстракцию кристаллической структуры, где даны только узлы решетки. Мы также сообщили ряд плоскостей решетки с расстояниями \(d_i\) и соответствующей нормалью \(\vec{h_i}\) к ряду плоскостей. Без дальнейшей демонстрации мы приводим здесь важное соотношение между расстояниями d и вектором обратной решетки \(\vec{h}\), нормальным к ряду равноудаленных плоскостей:
\[\begin{align} d=\frac{1 }{|\vec{h}|} \end{align}\] 9{[3]}\)
Предположим, что имеется ряд рассеивателей, разделенных постоянным повторением, a.
 Излучение с длиной волны \(\lambda\) падает на этот ряд под углом \(\alpha_{0}\). Изучите разброс из этого ряда под углом \(\alpha_{n}\). Разность хода лучей, рассеянных в точках A и D, равна просто AB-CD. Если входящие лучи находятся в фазе, разность хода должна быть некоторым целым кратным длины волны, чтобы возникла конструктивная интерференция. Это приводит к первому уравнению Лауэ:
Излучение с длиной волны \(\lambda\) падает на этот ряд под углом \(\alpha_{0}\). Изучите разброс из этого ряда под углом \(\alpha_{n}\). Разность хода лучей, рассеянных в точках A и D, равна просто AB-CD. Если входящие лучи находятся в фазе, разность хода должна быть некоторым целым кратным длины волны, чтобы возникла конструктивная интерференция. Это приводит к первому уравнению Лауэ:\begin{align} (AB-CD)=a(\cos(\alpha_{n}-\cos\alpha_{0}))=n_{x}\lambda \end{align}
Этот результат справедливо для любого рассеянного луча, составляющего угол \(\alpha_{n}\) с осью элементарной ячейки. Таким образом, условие Лауэ согласуется с конусом рассеянных лучей с центром вокруг оси а.
Это уравнение можно переформулировать в векторной форме. Расстояние повторения a становится вектором элементарной ячейки $\vec{a}$. Назовите единичный вектор, параллельный входящим лучам, $\vec{S_{0}}$, и один, параллельный рассеянным лучам, \(\vec{S}\). Тогда есть несколько простых векторных точечных произведений:
\begin{align} \vec{a}\cdot\vec{S}=a\cos\alpha_{n} \end{align}
\begin{align} \vec{a}\cdot\vec{ S_{0}}=a\cos\alpha_{0} \end{align}
\begin{align} a\cos(\alpha_{n}-\cos\alpha_{0})=\vec{a} \cdot(\vec{S}-\vec{S_{0}})=n_{x}\lambda \end{align}
2.
 2.4 Уравнение Лауэ в трех измерениях
2.4 Уравнение Лауэ в трех измеренияхДля кристалла с ячейкой параметры \(\vec{a},\vec{b},\vec{c}\), мы имеем три уравнения Лауэ:
\begin{align} a\cos(\alpha_{n}-\cos\alpha_ {0})=ч\лямбда\конец{выравнивание} 9{2}\gamma_{n}=1 \end{align}
Исходя из того, что угол между падающим и отраженным лучом равен \(2\theta\)
\begin{align} \cos2\theta=\cos\ alpha_{n}\alpha_{0}+\beta_{n}\beta_{0}+\gamma_{n}\gamma_{0} \end{align}
Возьмите \(\vec{k_{i}}\ ) — волновой вектор для входящего (падающего) луча, а \(\vec{k_{o}}\) — волновой вектор для выходящего (дифрагированного) луча. \(\vec{k_{o}}-\vec{k_{i}}=\Delta\vec{k}\) — это вектор рассеяния, измеряющий изменение между двумя волновыми векторами. Возьмем \(\vec{a_{1}},\vec{a_{2}},\vec{a_{3}}\) за примитивные векторы кристаллической решетки. Три условия Лауэ для вектора рассеяния, или уравнения Лауэ, для целых значений индексов обратной решетки отражения (h,k,l) можно также записать следующим образом:
\begin{align} \vec{a_{1}}\cdot\Delta\vec{k}=2\pi h \end{align}
\begin{align} \vec{a_{2}}\ cdot\Delta\vec{k}=2\pi k \end{align}
\begin{align} \vec{a_{3}}\cdot\Delta\vec{k}=2\pi l \end{ align}
Эти условия говорят о том, что вектор рассеяния должен быть ориентирован в определенном направлении по отношению к примитивным векторам кристаллической решетки.
 {[1]}\)
{[1]}\)2.3 Связь уравнения Лауэ с законом Брэгга
Если \(\vec{G}=h\vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3} }\) — вектор обратной решетки, мы знаем:
\begin{align} \vec{G}\cdot(h\vec{a_{1}}+k\vec{a_{2}}+l\vec {a_{3}})=2\pi(h+k+l) \end{align}
Уравнения Лауэ определяют:
\begin{align} \Delta\vec{k}\cdot(h\vec {a_{1}}+k\vec{a_{2}}+l\vec{a_{3}})=2\pi(h+k+l) \end{align}
, где
\begin {align} \vec{k_{o}}-\vec{k_{i}}=\vec{G} \end{align} 9{[2]}\)
2.4 Ссылки
- en.Wikipedia.org/wiki/Max_von_Laue
- Другая веб-страница Джиалана: http://electrons.wikidot.com/x-ray-diffraction-and-bragg-s-law
- стручковый перец.me.utexas.edu/ChE386…_equations.htm
- Киттель, К. (1976). Введение в физику твердого тела, Нью-Йорк: John Wiley & Sons. ISBN 0-471-49024-5
- В.Л. Брэгг, «Дифракция коротких электромагнитных волн на кристалле», Труды Кембриджского философского общества, 17 (19).
 13), 43–57.
13), 43–57.
Авторы и ссылки
ContribMSE5317
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-SA
- Показать оглавление
- нет
- Теги
- Закон Брэгга
- Уравнение Лауэ
Рентгеновская дифракция, закон Брэгга и уравнение Лауэ
1.
 Рентгеновская дифракция и закон Брэгга
Рентгеновская дифракция и закон Брэгга 1.1 История
1.1.1 Рентген
В ноябре 1895 года Вильгельм Рентген открыл рентгеновские лучи, работая в Вюрцбургском университете, Германия. Рентген исследовал катодные лучи в различных типах вакуумированных стеклянных трубок и пытался определить их диапазон в воздухе. Он заметил, что во время образования лучей экран, покрытый флуоресцентным платиноцианидом бария, светился. Он был заинтригован тем, что экран находился слишком далеко от трубки, чтобы на него могли воздействовать катодные лучи.Он предположил, что неизвестные рентгеновские лучи исходят от стенок трубки во время работы электронно-лучевой трубки. К своему изумлению, Рентген обнаружил, что лучи могут проходить прямо через его руку и отбрасывать тени его костей на флуоресцентный экран. Он провел несколько недель, исследуя лучи в частном порядке, прежде чем опубликовать свои результаты в конце года.
1.
 1.2 Закон Брэгга
1.2 Закон Брэгга
Закон Брэгга является результатом экспериментов, полученных физиком сэром Уильямом Лоуренсом Брэггом в 1912 и впервые представлен в том же году Кембриджскому философскому обществу. [1] Уильям Лоуренс Брэгг и его отец, сэр Уильям Генри Брэгг, были удостоены Нобелевской премии по физике в 1915 году за их работу по определению кристаллических структур, начиная с NaCl, ZnS и алмаза.После того, как Вильгельм Рентген открыл рентгеновские лучи в 1895 году, Уильям Генри Брэгг, пионер определения кристаллической структуры методами дифракции рентгеновских лучей, начал всю жизнь исследовать природу излучения, главным образом рентгеновских лучей, а также альфа- и бета-частиц и гамма лучи. После открытия дифракции рентгеновских лучей на кристаллах в 19 в.12, Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с углом скользящего отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения.
 В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.
В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.Уильям Лоуренс Брэгг стал директором Кавендишской лаборатории в Кембридже, Англия. Именно в этой лаборатории, когда он был директором, в начале 1950-х годов Дж. Д. Уотсон и Ф. Х. Крик, используя методы дифракции рентгеновских лучей, которые впервые применил Брэгг, вывели двойную спиральную структуру дезоксирибонуклеиновой кислоты. (ДНК)
Сегодня биотехнология имеет множество форм: раскрытие преступлений, криминалистика, рекомбинантная ДНК для укрепления растений и животных, а также анализ плода для выявления врожденных дефектов, и это лишь некоторые из них. Все это было бы невозможно, если бы Уотсон и Крик не расшифровали структуру ДНК с помощью рентгеновской дифракции. Точно так же, как инженер, который строит высокое здание, должен разбираться в стали и цементе, ученый должен понимать двойную спираль, прежде чем он сможет построить молекулу.
 [2]
[2]1.1.3 Нобелевская премия за дифракцию Брэгга
Несмотря на свою простоту, закон Брэгга подтвердил существование реальных частиц в атомном масштабе, а также предоставил новый мощный инструмент для изучения кристаллов в виде дифракции рентгеновских лучей и нейтронов. .[3]
В 1915 году Уильям Генри Брэгг и Уильям Лоуренс Брэгг были удостоены Нобелевской премии за вклад в анализ структуры кристаллов. Они были первой и (пока) единственной командой отца и сына, которая вместе выиграла приз. Среди других лауреатов отцов и сыновей Нильс и Оге Бор, Манн и Кай Зигбан, Дж. Дж. Томсон и Джордж Томсон, Ганс фон Эйлер-Хелпин и Ульф фон Эйлер, а также Артур и Роджер Корнберги были удостоены премии за отдельные вклады.
В то время У. Л. Брэггу было 25 лет, что делало его самым молодым лауреатом Нобелевской премии на сегодняшний день.
У.Х. Брэгг (1862-1942) и У.Л. Брэгг (1890-1971) на шведской почтовой марке.

1.2 Принцип закона Брэгга и дифракция рентгеновских лучей
1.2.1 Математическая форма закона Брэгга
(1)
\begin{align} n\lambda=2d\cdot\sin\theta \end{align}
где
• n — целое число, определяемое в указанном порядке,
• λ — длина волны рентгеновского излучения и движущихся электронов, протонов и нейтронов,
• d — расстояние между плоскостями в атомной решетке, а
• θ — угол между падающим лучом и рассеивающими плоскостями.1.2.2 Вывод закона Брэгга
Дифракция Брэгга возникает, когда электромагнитное излучение или волны субатомных частиц с длиной волны, сравнимой с расстоянием между атомами, падают на кристаллический образец, рассеиваются атомами в системе и претерпевают конструктивную интерференцию в соответствии с законом Брэгга. [2]
Рассмотрим условия, необходимые для совпадения фаз лучей при равенстве угла падения и угла отражения.
 Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым (n) кратным длине волны ($\lambda$), чтобы фазы двух лучей были одинаковыми:
Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым (n) кратным длине волны ($\lambda$), чтобы фазы двух лучей были одинаковыми:(2)
\begin{align} n\lambda=AB+BC \end{align}
Признав d гипотенузой прямоугольного треугольника Abz, мы можем с помощью тригонометрии связать d и $\theta$ с расстоянием (AB + ДО Н.Э). Расстояние AB противоположно $\theta$, поэтому
(3)
\begin{align} AB=d\sin\theta \end{align}
Поскольку AB = BC экв. (2) становится,
(4)
\begin{align} n\lambda=2AB \end{align}
Подставляя ур. (3) в уравнении (4) имеем,
(5)
\begin{align} n\lambda=2d\cdot\sin\theta \end{align}
и закон Брэгга был получен.

Обратите внимание, что если участвуют только два ряда атомов, то переход от конструктивной интерференции к деструктивной при изменении $\theta$ будет постепенным. Однако, если возникает интерференция из многих рядов, то пики конструктивной интерференции становятся очень острыми, а между ними в основном деструктивная интерференция. Такое заострение пиков при увеличении числа рядов очень похоже на заострение дифракционных пиков от дифракционной решетки при увеличении числа щелей. 9{‘}}+\overrightarrow{g} \end{align}
, поэтому
(7)
\begin{align} |\overrightarrow{g}|=2|\overrightarrow{k}|\sin\theta \end{align}
Чтобы обеспечить соблюдение закона Брэгга, $\overrightarrow{g}$ должен быть установлен в равно $\overrightarrow{G}$, где
(8)
\begin{align} |\overrightarrow{G}|=2\pi/d_{h,k,l} \end{align}
Сравните уравнение (7) и уравнение (8), у нас есть
(9)
\begin{align} \lambda=2/d_{h,k,l}\sin\theta \end{align}
Итак, только если
(10)
\begin{align} \overrightarrow{g}=\overrightarrow{G} \end{align}
Закон Брэгга может быть выполнен.
 [9]
[9]Определение обратной решетки можно увидеть следующим образом:
В кристаллографии обратной решеткой решетки Браве называется набор всех векторов $\overrightarrow{k}$ таких, что:
(11)
\begin{align} \exp({i}\overrightarrow{k}\cdot\overrightarrow{r})=1 \end{align}
Эта обратная решетка сама по себе является решеткой Браве, а обратная решетка — исходная реальная решетка.
1.3 Применение закона Брэгга — дифракция Брэгга
Дифракция Брэгга (также называемая формулировкой Брэгга дифракции рентгеновских лучей) была впервые предложена Уильямом Лоуренсом Брэггом и Уильямом Генри Брэггом в 1913 году в ответ на их открытие, что кристаллические твердые тела давали удивительные картины отраженных рентгеновских лучей (в отличие, скажем, от жидкости). Они обнаружили, что в этих кристаллах при определенных длинах волн и углах падения возникают интенсивные пики отраженного излучения (известные как пики Брэгга).
 В. Л. Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d. Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют, как мы показали выше.
В. Л. Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d. Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют, как мы показали выше.Концепция дифракции Брэгга в равной степени применима к процессам дифракции нейтронов и электронов.
1.3.1 Рентгеновская дифракция
Дифракционная картина получается путем измерения интенсивности рассеянных волн как функции угла рассеяния. Очень сильные интенсивности, известные как пики Брэгга, получаются на дифракционной картине, когда рассеянные волны удовлетворяют закону Брэгга.
Согласно закону Брэгга, каждая точка (или отражение) на приведенной выше дифракционной картине формируется в результате конструктивной интерференции рентгеновских лучей, проходящих через кристалл. Данные могут быть использованы для определения атомной структуры кристалла.
 [4]
[4]На приведенных выше рисунках показаны экспериментальные рентгеновские дифрактограммы кубического SiC с использованием синхротронного излучения. На рисунках отчетливо видны пики Брэгга.[5]
1.3.2 Нейтронография
Это нейтронограмма фазы Li0,86(Ni0,80Fe0,20)1,14O2 ( = 1,5939 Å). Приведена разница между наблюдаемым и расчетным профилями. Вертикальные полосы показывают брэгговские отражения.[6]
1.3.3 Дифракция электронов
Дифракция электронов служит основой для изучения структуры кристаллов и идентификации материалов. Металлы имеют тенденцию давать очень сильные картины дифракции электронов, в то время как биологические образцы обычно имеют довольно слабую дифракцию.
На рисунке выше представлены картины дифракции электронов от выбранных небольших участков. На микрофотографии показано поле кристаллических частиц, очерченное большой апертурой выбора (6 мкм у образца). Соответствующий тип «пятнистого кольца» на дифракционной картине (вверху слева) указывает на то, что кристаллы ориентированы в нескольких различных направлениях.
 Используя меньшую выборочную апертуру (2,3 мкм на образце), расположенную, как указано, рисунок формируется только из выбранного кристалла, что дает рисунок монокристалла, показанный внизу слева. [7]
Используя меньшую выборочную апертуру (2,3 мкм на образце), расположенную, как указано, рисунок формируется только из выбранного кристалла, что дает рисунок монокристалла, показанный внизу слева. [7]Схемы и пояснения ниже аналогичны рисунку выше, но поле зрения меньше 1 мкм в поперечнике и, следовательно, слишком маленькое для обычного с.а.д. Отдельная частица была выбрана для дифракционного анализа путем фокусировки освещения в пятно, покрывающее частицу. Дифракционные пятна представляют собой диски, а не точки, потому что электронный пучок больше не параллелен образцу, а представляет собой конус; поэтому каждый дифрагированный пучок также является конусом, который становится диском в плоскости пленки. Диски могут перекрываться и загораживать другие; следовательно, анализ более мелких кристаллов по картинам µ-дифракции менее точен, чем обычный метод s.a.d. [7]
На приведенном ниже рисунке показана интенсивность рассеяния в зависимости от угла рассеяния газообразного образца.
 Образец газа представляет все возможные ориентации атом-атомного разделения для электронного луча, и результирующая картина дифракции подобна порошковой рентгеновской фотографии. Интенсивность дифрагированного луча неуклонно уменьшается с увеличением угла рассеяния, и общая картина состоит из серии концентрических волнистых линий на фоне.[8]
Образец газа представляет все возможные ориентации атом-атомного разделения для электронного луча, и результирующая картина дифракции подобна порошковой рентгеновской фотографии. Интенсивность дифрагированного луча неуклонно уменьшается с увеличением угла рассеяния, и общая картина состоит из серии концентрических волнистых линий на фоне.[8]1.4 Знания
Я хотел бы поблагодарить Дхарму Маддалу за ценную информацию, а также Чинг-Чанг Чунг, Лян Донг, Сатьеш Ядав за много полезных советов. Также благодарю профессора Рампи за предоставленную мне возможность создать веб-страницу с тем, что мы узнали в классе MSE 5317.1.5 Ссылки
[1] Брэгг, «Дифракция коротких электромагнитных волн на кристалле», Труды Кембриджского философского общества, 17 (1913), 43–57.
[2] http://en.wikipedia.org/wiki/Bragg%27s_law
[3]http://nobelprize.org/nobel_prizes/physics/laureates/1915/index.html
[4]Рисунок взят из работы Джеффа Даля, а рисунок взят с http://www. goiit.com /posts/list/community-shelf-diffaction-83055.htm
goiit.com /posts/list/community-shelf-diffaction-83055.htm
[5]Эта часть предоставлена Полом Дж. Шильдсом, Центр исследований высокого давления, Департамент наук о Земле и космосе, Государственный университет Нью-Йорка в Стоуни-Брук, Стоуни. Брук, Нью-Йорк 11794-2100.
[6]Г. Prado, E. Suard, L. Fournes и C. Delmasb, «Распределение катионов в электродных материалах Li1-z(Ni1-yFey)1+zO2», J. of Mater. хим. 10 (2000) 2553
[7] «Принципы и практика электронной микроскопии», Ян М. Ватт, 1997, Cambridge University Press
[8] http://perso.fundp.ac.be/%7Ejwouters/ DRX/diffraction.html
[9] Для получения дополнительной информации о реальной и обратной кристаллической решетке см. также веб-страницу Фансяо: http://electrons.wikidot.com/paraelectric-and-antiferroelectric-properties2. Уравнение Лауэ и его связь с законом Брэгга
2.1 История
2.1.1 Биография Лауэ
Макс Теодор Феликс фон Лауэ (9 октября 1879 — 24 апреля 1960) — немецкий физик, лауреат Нобелевской премии по физике в 1914 году за открытие дифракции рентгеновских лучей.
 кристаллами.[1]
кристаллами.[1]С 1909 по 1912 год Лауэ был приват-доцентом Института теоретической физики под руководством Арнольда Зоммерфельда Мюнхенского университета Людвига-Максимилиана (LMU). Во время рождественских каникул 1911 года и в январе 1912 года Пол Питер Эвальд заканчивал написание своей докторской диссертации под руководством Зоммерфельда. Во время прогулки по Английскому саду в Мюнхене в январе Эвальд рассказал Лауэ о теме своей диссертации. Волны волн, интересующие Эвальда, находились в видимой области спектра и, следовательно, намного превышали расстояние между резонаторами в кристаллической модели Эвальда. Лауэ казался отвлеченным и хотел знать, какой будет эффект, если рассматривать гораздо меньшие длины волн. В июне Зоммерфельд сообщил в Physikalische Gesellschaft в Геттингене об успешной дифракции рентгеновских лучей, проведенной Лауэ, Паулем Книппингом и Вальтером Фридрихом в LMU, за которую Лауэ будет удостоен Нобелевской премии по физике в 1919 году.14. Находясь в Мюнхене, он написал первый том своей книги по теории относительности в период с 1910 по 1911 год.
 рентгеновских лучей с помощью кристаллов в 1912 году Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с скользящим углом отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.
рентгеновских лучей с помощью кристаллов в 1912 году Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с скользящим углом отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.Уильям Лоуренс Брэгг стал директором Кавендишской лаборатории в Кембридже, Англия. Именно в этой лаборатории, когда он был директором, в начале 1950-х годов Дж. Д. Уотсон и Ф. Х. Крик, используя методы дифракции рентгеновских лучей, которые впервые применил Брэгг, вывели двойную спиральную структуру дезоксирибонуклеиновой кислоты. (ДНК)
Сегодня биотехнология имеет множество форм: раскрытие преступлений, криминалистика, рекомбинантная ДНК для укрепления растений и животных, а также анализ плода для выявления врожденных дефектов, и это лишь некоторые из них.
 Все это было бы невозможно, если бы Уотсон и Крик не расшифровали структуру ДНК с помощью рентгеновской дифракции. Точно так же, как инженер, который строит высокое здание, должен разбираться в стали и цементе, ученый должен понимать двойную спираль, прежде чем он сможет построить молекулу.[2]
Все это было бы невозможно, если бы Уотсон и Крик не расшифровали структуру ДНК с помощью рентгеновской дифракции. Точно так же, как инженер, который строит высокое здание, должен разбираться в стали и цементе, ученый должен понимать двойную спираль, прежде чем он сможет построить молекулу.[2]2.2 Принцип уравнения Лауэ
2.2.1 Обратное пространство
Все точки обратной решетки могут быть описаны линейной комбинацией кратных двух базисных векторов: $\vec{b_{1}}, \vec{b_{2}},\vec{b_{3}}$. Его определение эквивалентно следующим отношениям:
(12)
\begin{align} \vec{b_{1}}=\frac{\vec{a_{2}}\times\vec{a_{3}}}{\vec{a_{1}}\cdot( \vec{a_{2}}\times\vec{a_{3}})} \end{align}
(13)
\begin{align} \vec{b_{2}}=\frac{\vec{a_{3}}\times\vec{a_{1}}}{\vec{a_{1}}\cdot( \vec{a_{2}}\times\vec{a_{3}})} \end{align}
(14)
\begin{align} \vec{b_{3}}=\frac{\vec{a_{1}}\times\vec{a_{2}}}{\vec{a_{1}}\cdot( \vec{a_{2}}\times\vec{a_{3}})} \end{align}
Интересное свойство вектора обратной решетки состоит в том, что отношения остаются в силе, если мы заменяем векторы решетки обратной решеткой векторов и обратно обратных векторов решетки векторами решетки.
 Если V* — объем обратной элементарной ячейки, читатель может показать, что выражение VV* = 1 также справедливо.
Если V* — объем обратной элементарной ячейки, читатель может показать, что выражение VV* = 1 также справедливо.Теперь мы можем определить вектор обратной решетки $\vec{h}$ линейной комбинацией целых чисел, кратных трем векторам обратной решетки:
(15)
\begin{align} \vec{h}=h\vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3}} \end{align}
Мы позже мы увидим, что обратные векторы играют важную роль в дифракции. Прежде свяжем векторы обратной решетки с некоторыми макроскопическими свойствами кристаллов.
2.2.2 Индексы Миллера
По построению каждый вектор обратной решетки нормальен к ряду плоскостей решетки. Мы также знаем, что грани кристалла параллельны плоскостям решетки и, следовательно, нормальны к обратным векторам. Таким образом, мы можем однозначно характеризовать каждую грань кристалла целочисленными компонентами обратного вектора с одной важной тонкостью. Грань, нормаль к вектору $\vec{h}$, нельзя отличить от нормали к вектору $n\vec{h}$.
 Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.
Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.Рисунок выше представляет собой абстракцию кристаллической структуры, где даны только узлы решетки. Мы также указали серию плоскостей решетки с расстояниями $d_{i}$ и соответствующей нормалью $\vec{h_{i}}$ к серии плоскостей. Без дальнейших объяснений мы приводим здесь важное соотношение между расстояниями d и вектором обратной решетки $\vec{h}$, нормальным к ряду эквидистантных плоскостей:
(16)
\begin{align} d=\frac{1}{|\vec{h}|} \end{align}
2.2.3 Уравнение Лауэ в одном измерении
Теперь, когда мы ввели определение векторов обратной решетки, мы готовы выразить физический закон, управляющий дифракцией кристаллического материала.
 [3]
[3]Предположим, что имеется ряд рассеивателей, разделенных постоянным повторением, a. На этот ряд под углом $\alpha_{0}$ падает излучение с длиной волны $\lambda$. Изучите разброс из этого ряда под углом $\alpha_{n}$. Разность хода лучей, рассеянных в точках A и D, равна просто AB-CD. Если входящие лучи находятся в фазе, разность хода должна быть некоторым целым кратным длины волны, чтобы возникла конструктивная интерференция. Это приводит к первому уравнению Лауэ:
(17)
\begin{align} (AB-CD)=a(\cos(\alpha_{n}-\cos\alpha_{0}))=n_{x}\lambda \end{align}
Этот результат справедливо для любого рассеянного луча, составляющего угол $\alpha_{n}$ с осью элементарной ячейки. Таким образом, условие Лауэ согласуется с конусом рассеянных лучей с центром вокруг оси а.
Это уравнение можно переформулировать в векторной форме. Расстояние повторения a становится вектором элементарной ячейки $\vec{a}$. Назовите единичный вектор, параллельный падающим лучам, $\vec{S_{0}}$, и вектор, параллельный рассеянным лучам, $\vec{S}$.
 Тогда есть несколько простых векторных точечных произведений:
Тогда есть несколько простых векторных точечных произведений:(18)
\begin{align} \vec{a}\cdot\vec{S}=a\cos\alpha_{n} \end{align}
(19)
\begin{align} \vec{a}\cdot\vec{S_{0}}=a\cos\alpha_{0} \end{align}
(20)
\begin{align} a\cos(\alpha_{n}-\cos\alpha_{0})=\vec{a}\cdot(\vec{S}-\vec{S_{0}})= n_{x}\lambda \end{align}
2.2.4 Уравнение Лауэ в трех измерениях
Для кристалла с параметрами ячейки $\vec{a},\vec{b},\vec{c}$ , имеем три уравнения Лауэ:(21)
\begin{align} a\cos(\alpha_{n}-\cos\alpha_{0})=h\lambda \end{align}
(22)
\begin{align} b\cos(\beta_{n}-\cos\beta_{0})=k\lambda \end{align}
(23)
\begin{align} c\cos(\gamma_{n}-\cos\gamma_{0})=l\lambda \end{align}
где $\cos\alpha_{0}$, $\cos \beta_{0}$, $\cos\gamma_{0}$ — направляющие косинусы падающего луча, а $\cos\alpha_{n}$, $\cos\beta_{n}$, $\cos\ gamma_{n}$ — направляющие косинусы отраженного луча в оси кристалла.
 Поэтому мы также должны удовлетворить: 9{2}\gamma_{n}=1 \end{align}
Поэтому мы также должны удовлетворить: 9{2}\gamma_{n}=1 \end{align}Учитывая, что угол между падающим и отраженным лучами равен $2\theta$
(26)
\begin{align} \cos2\theta=\cos\alpha_{n}\alpha_{0}+\beta_{n}\beta_{0}+\gamma_{n}\gamma_{0} \end{align }
Возьмем $\vec{k_{i}}$ за волновой вектор входящего (падающего) луча, а $\vec{k_{o}}$ за волновой вектор выходящего (дифрагированного) луча. $\vec{k_{o}}-\vec{k_{i}}=\Delta\vec{k}$ — вектор рассеяния, измеряющий изменение между двумя волновыми векторами. Возьмем $\vec{a_{1}},\vec{a_{2}},\vec{a_{3}}$ за примитивные векторы кристаллической решетки. Три условия Лауэ для вектора рассеяния, или уравнения Лауэ, для целых значений индексов обратной решетки отражения (h,k,l) можно также записать следующим образом:
(27)
\begin{align} \vec{a_{1}}\cdot\Delta\vec{k}=2\pi h \end{align}
(28)
\begin{align} \vec{a_{2}}\cdot\Delta\vec{k}=2\pi k \end{align}
(29)
\begin{align} \vec{a_{3}}\cdot\Delta\vec{k}=2\pi l \end{align}
Эти условия говорят, что вектор рассеяния должен быть ориентирован в определенном направлении относительно примитивных векторов кристаллической решетки.

В кристаллографии уравнения Лауэ дают три условия для дифрагирования падающих волн на кристаллической решетке. Их можно свести к закону Брэгга, как обсуждается в следующем разделе.[1]
2.3 Связь уравнения Лауэ с законом Брэгга
Если $\vec{G}=h\vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3 }}$ — вектор обратной решетки, мы знаем:
(30)
\begin{align} \vec{G}\cdot(h\vec{a_{1}}+k\vec{a_{2}}+l\vec{a_{3}})=2\pi( h+k+l) \end{align}
Уравнения Лауэ определяют:
(31)
\begin{align} \Delta\vec{k}\cdot(h\vec{a_{1}}+k\vec{a_{2}}+l\vec{a_{3}})=2\ pi(h+k+l) \end{align}
, где
9{2}$ сводится к закону Брэгга $2d\sin\theta=n\lambda$.[2]2.4 Ссылки
[1] http://en.wikipedia.org/wiki/Max_von_Laue
[2] Другая веб-страница Джиалана: http://electrons.wikidot.com/x-ray-diffraction-and- закон Брэгга
[3] http://capsicum. me.utexas.edu/ChE386K/html/laue_equations.htm
me.utexas.edu/ChE386K/html/laue_equations.htm
[4] Киттель, К. (1976). Введение в физику твердого тела, Нью-Йорк: John Wiley & Sons. ISBN 0-471-49024-5
[5] В.Л. Брэгг, «Дифракция коротких электромагнитных волн на кристалле», Труды Кембриджского философского общества, 17 (19).13), 43–57.Дифракция Брэгга | ФизикаOpenLab
18 января 2018 г. английские посты, XRD 10 664 Просмотров
PDF
Дифракция Брэгга (также известная как Брэгговская формулировка дифракции рентгеновских лучей ) была впервые предложена Уильямом Лоуренсом Брэггом Кристаллическим и его отцом Уильямом Генри Брэггом в ответ на их открытие в 1913 году, твердые вещества давали удивительные картины отраженных рентгеновских лучей (в отличие, скажем, от жидкости). Они обнаружили, что эти кристаллы при определенных определенных длин волн и углов падения , давали интенсивные пики отраженного излучения.
Сэр Уильям Лоуренс Брэгг объяснил этот результат, смоделировав кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d .
 Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют . Интерференция конструктивна, когда фазовый сдвиг составляет кратно 2π ; это условие может быть выражено законом Брэгга (см. условие Брэгга раздел ниже) и впервые было представлено сэром Уильямом Лоуренсом Брэггом 11 ноября 1912 года Кембриджскому философскому обществу. Несмотря на простоту, закон Брэгга подтвердил существование реальных частиц в атомном масштабе, а также предоставил новый мощный инструмент для изучения кристаллов в виде дифракции рентгеновских лучей и нейтронов.
Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют . Интерференция конструктивна, когда фазовый сдвиг составляет кратно 2π ; это условие может быть выражено законом Брэгга (см. условие Брэгга раздел ниже) и впервые было представлено сэром Уильямом Лоуренсом Брэггом 11 ноября 1912 года Кембриджскому философскому обществу. Несмотря на простоту, закон Брэгга подтвердил существование реальных частиц в атомном масштабе, а также предоставил новый мощный инструмент для изучения кристаллов в виде дифракции рентгеновских лучей и нейтронов.Сэр Лоуренс Брэгг предположил, что атомы кристалла, такого как хлорид натрия или Lithium Fluoride были расположены в виде кубической и правильной трехмерной структуры, как показано на изображении ниже.
Расстояние между двумя соседними плоскостями кристалла можно рассчитать следующим образом: масса молекулы LiF равна M/N кг, где M — молекулярная масса (2 x 10 -3 кг на моль) и N число Авогадро (6,02 x 10 23 молекул на моль).
 Число молекул в единице объема составляет Mρ/N молекул в кубическом метре, где ρ — плотность (2,64 х 10 3 кг·м -3 ).
Число молекул в единице объема составляет Mρ/N молекул в кубическом метре, где ρ — плотность (2,64 х 10 3 кг·м -3 ).
Поскольку LiF является двухатомным, число атомов в единице объема составляет 2 ρ Н/М атомов на кубический метр. Таким образом, расстояние между соседними атомами d в решетке получается из следующего уравнения:d 3 = 1/(2 ρ Н/М) или d = ³√(M/2 ρ Н) = 0,2013 нм
падения θ равно углу отражения – это то же самое, что и для оптического отражения, и предполагает, что любой детектор отраженных лучей должен перемещаться под углом 2θ , отношение спектрометра 2:1 .
Второе условие – отражения от нескольких слоев должны конструктивно сочетаться:С помощью нашего дифрактометра мы измеряем дифракционные отражения от монокристалла LiF , как показано на изображении ниже.

Для проведения эксперимента установите кристалл LiF в стойку для кристалла, убедившись, что основная грань находится в отражающем положении. Установите коллиматор первичного луча на защитном куполе и установите на рычаге каретки коллиматор с щелью 3 мм и коллиматор с щелью 1 мм и детектор Гейгера за щелью 1 мм.
С помощью измерителя скорости проследите за поворотом рычага каретки от минимального положения (около 12° 2θ) до максимального положения (около 120° 2θ), запишите количество секунд (CPS) с интервалом в 1°. Там, где скорость счета кажется пиковой, нанесите на график интервалы всего в 10 дуг, используя регулировочное колесо, на каждом пике измерьте и запишите максимальную скорость счета и угол 2θ как можно точнее. На изображении ниже показана установка.На приведенной ниже диаграмме показаны результаты, полученные с кристаллом LiF и рентгеновской трубкой, работающей при 30 кВ и 50 мкА. Можно узнать четыре основных пика : первые два соответствуют первому отражению Брэгга для эмиссий меди Kα и Kβ , а второй набор пиков соответствует второму отражению.
 Около 20° и 30° происходит рассеяние непрерывного излучения рентгеновской трубки при больших энергиях.
Около 20° и 30° происходит рассеяние непрерывного излучения рентгеновской трубки при больших энергиях.Изменение высокого напряжения: 20 кВ вместо 30 кВ, мы можем получить немного другой спектр, как показано в таблице ниже. Видно, что интенсивность пиков уменьшается (также и непрерывная часть), но не положение пиков.
Для получения почти монохроматического рентгеновского излучения можно использовать фильтр, который избирательно поглощает рентгеновские волны с более короткими или более длинными длинами волн, чем основная длина волны Kα-излучения. Этого можно добиться с помощью никелевого фильтра , который поглощает в основном более короткие волны и имеет минимум поглощения, соответствующий основному излучению Kα. Спектр результатов показан на диаграмме ниже, где видно, что пик Kβ значительно уменьшился.
Из закона Брэгга мы можем рассчитать длину волны рентгеновского излучения по следующей формуле: для четырех пиков, представленных на графике:
Пик 2θ (°) θ (°) сенθ 2d (нм) п λ (нм) λ (КэВ) 1 40,17 20,085 0,3434 0,4026 1 0,1383 8,96 2 44,83 22,415 0,3813 0,4026 1 0,1535 8.  08
083 87,67 43,835 0,6926 0,4026 2 0,1394 8,89 4 100 50 0,7660 0,4026 2 0,1542 8.04 Расчет среднего значения данных:
Kα = 0,154 нм = 8,06 кэВ
Life DIFFRACT0056
Kβ = 0,139 нм = 8,92 кеВМы сделали то же самое с нашим самодельным основанием дифрактометра на рентгеновской трубке Ge: на изображении ниже показана установка оборудования.
Ниже представлен спектр. Мы получили меньшие интенсивности, но, несмотря на упрощенное и, возможно, наивное оборудование, пики хорошо видны.
Мы вставляем полученные данные в следующую таблицу с данными для двух пиков, присутствующих на графике:
Пик 2θ (°) θ (°) сенθ 2d (нм) п λ (нм) λ (КэВ) 1 32 16 0,276 0,4026 1 0,111 11,2 2 36 18 0,309 0,4026 1 0,124 10 Kα = 0,124 нм = 10 кэВ
Kβ = 0,111 нм = 11,2 кэВВыводы
Результаты хорошо согласуются с литературными данными.

Если вам понравился этот пост, вы можете поделиться им в «социальных» Facebook , Twitter или LinkedIn с помощью кнопок ниже. Таким образом, вы можете помочь нам! Спасибо!
Пожертвование
Если вам нравится этот сайт и вы хотите внести свой вклад в его развитие, вы можете сделать пожертвование, спасибо!
Теги X-Ray XRD
Предыдущий Аппарат Tel-X-Ometer
Следующий Дифференциальный прибор Брэгга
Проверьте также
Аннотация: в этом посте мы описываем использование лазера Osram P530. Это твердотельный лазер с оптической накачкой (OPSL). Лазер излучает на длине волны 530 нм с мощностью, которая легко может достигать 50-70 мВт. Это очень интересный лазерный источник из-за его низкой стоимости и качества луча.
Лекция 35: Дифракция
Лекция 35: Дифракция
Дифракция: отклонение света от препятствий
- Дифракция — это распространение света по краям
препятствия.

- Дифракция — это проявление волновой природы света
- Самое ясное объяснение дифракции — просмотр
распространение волны по Принцип Гюйгена: каждая точка нарушена
набегающим фронтом волны можно рассматривать как источник сферической волны,
новый фронт охватывает эти вторичные сферические волновые фронты
- Мы уже использовали принцип Гюйгенса для описания явления искривление луча света на границе раздела сред с разными
показатель преломления , но это также говорит о том, что свет будет распространяться
за препятствиями — дифракция
преломление Дифракция - Ранее мы использовали дифракцию для создания двух когерентных источников света. волной, проходящей через два отверстия.
Дифракция и интерференция
- Результат дифракции не прост.
 Дифракция приводит к пересечению лучей света, которые являются когерентными и
вмешиваться.
Дифракция приводит к пересечению лучей света, которые являются когерентными и
вмешиваться. - Интерференционная картина, образованная дифрагированным светом,
называется, сокращенно дифракционная картина
- Иногда подчеркивают, что речь идет о дифракционной картине когда мы рассматриваем помехи от многих источников — как например непрерывное распределение источников между барьерами на рисунке выше.
- Примечание. Дифракция и интерференция — разные явления (несмотря на то, что написано в учебнике 🙂 )
Однощелевая дифракция
- Одним из наиболее важных примеров дифракционных эффектов является прохождение света через отверстие конечного размера.
- Если свет проходит через узкое точечное отверстие, почти точно сферическое волновые формы. Однако, если отверстие имеет конечный размер, интерференционная картина формы за дырой
- Будем рассматривать узкие (но конечной ширины) щели, а не круглые
отверстия.
 Волновые фронты, формируемые щелью, имеют цилиндрическую форму.
чем сферический
Волновые фронты, формируемые щелью, имеют цилиндрическую форму.
чем сферический
Дифракционный апплет с одной щелью - Обратите внимание, что картина интерференции дифрагированного света от широкой щели хотя имеет геометрическое сходство с двумя узкими щелями, но сильно отличается насколько это касается распределения интенсивности (см., например, много более яркая центральная полоса)
- Вычислим распределение интенсивности на экране за щель.
- Рисунок вблизи щели, где важны точные профили волнового фронта называются ближнепольными, или френелевскими, дифракционными . Узор на экране далеко, где мы можем использовать лучи геометрической оптики и приближения, которые мы сделали в интерференционных исследованиях называется дальнее поле или дифракция Фраунгофера
- Мы будем рассматривать исключительно дальнее поле, фраунгоферовскую дифракцию шаблон.
Интенсивность на дифрактограмме Фраунгофера от одной щели
- Заменю несколько страниц обсуждения в учебнике
(но прочитайте их), что позволяет избежать математики с расчетом в одну строку
используя простую интеграцию.

- Просто чтобы проиллюстрировать, что часто овладение высшей математикой делает вещи проще — на то он и введен в первую очередь, фактически.
- Результирующий паттерн представляет собой сумму волн из каждой точки щель.
- При непрерывном распределении исходных точек это интеграл над положением точки в щели y Если центр щели имеет координату y = 0 и ширина щели a , тогда y варьируется от -а/2 до а/2
- Итак, для амплитуды имеем
- и, наконец, для интенсивности
- Вот как это выглядит
Минимумы интенсивности на дифрактограмме Фраунгофера от одной щели
- Это просто, минимумы достигаются при углах наблюдения θ где sin(π(a/λ) sinθ) обращается в нуль, т.е.
sin(θ мин ) = ±m λ/a - но не для м = 0 , только для м = 1, 2 .
 ..
.. - Расстояние между минимумами увеличивается , когда длина волны увеличивается или ширина щели уменьшается
- Поэтому, когда щель очень узкая a ≈ 0 , первая минимумы далеко, и есть непрерывное распределение света.
- sinθ меняется от -1 до 1 с нулем, установленным прямо перед щелью.
Таким образом, число наблюдаемых минимумов равно
n мин = 2 int(a/λ) - Если щель уже длины волны, a < λ , минимумов не наблюдается.
Максимумы интенсивности на фраунгоферовой дифрактограмме от одной щели
- Основные максимумы интенсивности находятся на θ = 0 (да, деление нуля на ноль дает здесь единицу!)
- Поскольку главный максимум находится там, где ожидается минимум для m=0 , он в два раза шире других максимумов, занимая пространство между минимумами
в ± λ/a .
 Его ширина с точки зрения sinθ составляет 2 λ/а
Его ширина с точки зрения sinθ составляет 2 λ/а - Положения других максимумов только примерно на полпути между минимумами
sin(θ max ) ≈ ± (m + ½) λ/a - В зависимости от m говорят о первого порядка (m=±1), второй порядок (m=±2) и т. д. максимум
- Приблизительное значение пиковой интенсивности на максимуме м > 0 тогда
I m ≈ I 0 / ( π 2 (m + ½) 2 )
Узнайте о дифракции рентгеновских лучей на кристаллах
Дифракция рентгеновских лучей на кристаллах Определение
Дифракция рентгеновских лучей на кристаллах — это процесс рассеяния пучка рентгеновских лучей атомами кристалла.
Обзор дифракции рентгеновских лучей на кристаллах
Рассеяние рентгеновских лучей вызывает эффект интерференции, так что наблюдается картина дифракции пучка рентгеновских лучей.
 Эта дифракционная картина дает информацию о структуре кристалла.
Эта дифракционная картина дает информацию о структуре кристалла.Макс фон Лауэ впервые предложил использовать монокристалл для получения дифракции рентгеновских лучей. Когда волновой фронт рентгеновских лучей падает на одномерное расположение атомов кристалла, атомы рассеивают волны во всех возможных направлениях. В результате получаются дифрагированные лучи разного порядка, т. е. нулевого порядка, первого порядка и второго порядка. Условие дифракции рентгеновских лучей на кристаллах трехмерного характера было дано ученым В.Л. Брэгг.
Есть вопрос по этой теме?
Что вы изучите:
- Дифракция рентгеновских лучей на кристаллах Определение
- Обзор дифракции рентгеновских лучей на кристаллах
- Закон Брэгга
- Методы дифракции рентгеновских лучей
- Методы дифракции рентгеновских лучей
Закон Брэгга
W.
 L. Брэгг дал условие дифракции рентгеновских лучей. Брэгг предположил, что отражение рентгеновских лучей от параллельных плоскостей атомов в кристалле является правильным или зеркальным отражением.
L. Брэгг дал условие дифракции рентгеновских лучей. Брэгг предположил, что отражение рентгеновских лучей от параллельных плоскостей атомов в кристалле является правильным или зеркальным отражением.Когда пучок рентгеновских лучей падает на набор параллельных атомных плоскостей в кристалле, разнесенных на расстояние, равное «d», разность хода между отраженными лучами представляется как
Разность путей=BC+CD{\text{Разность путей}} = BC + CDPРазница путей=BC+CD
длина волны, то для конструктивной интерференции падающих лучей, потому что
BC=CD=dsinθBC = CD = d\sin \thetaBC=CD=dsinθ
2dsinθ=nλ2d\sin \theta = n\lambda2dsinθ=nλ
Это условие максимального отражения падающий пучок рентгеновских лучей и называется законом Брэгга. При выполнении этого условия имеет место рентгеновская дифракция. Длина волны падающего луча не должна превышать удвоенное расстояние между плоскостями кристалла.

Методы рентгеновской дифракции
Для анализа структуры кристалла используются три метода, а именно: метод Лауэ, метод вращающегося кристалла и метод порошка.
1. Метод Лауэ: В этом методе дифракции рентгеновских лучей используется плоская рентгеновская камера и тонкий пучок рентгеновских лучей.
В этом методе используется источник рентгеновского излучения, который создает рентгеновский пучок, имеющий широкий диапазон длин волн от до . Устройство точечного отверстия создает коллимированный пучок рентгеновских лучей. Образец монокристалла размером 100 000 000 000 000 000 дюймов удерживается неподвижно в луче рентгеновских лучей. Плоская фотопленка помещается для приема прошедшего дифрагированного луча. Кристалл выделяет и дифрагирует дискретные значения длины волны, удовлетворяющие закону дифракции Брэгга. Дифракционная картина, состоящая из серии пятен, показывает симметрию кристалла.

2. Метод вращающегося кристалла: В этом методе используется монокристаллический образец, который вращается вокруг фиксированной оси в монохроматическом пучке рентгеновских лучей.
Используется камера с вращающимся кристаллом, в которой монокристалл размером с образец установлен на вращающемся шпинделе. Этот вращающийся шпиндель концентричен с цилиндрическим держателем, а фотопленка прикреплена к внутренней поверхности держателя. Падающий пучок рентгеновских лучей дифрагирует от тех плоскостей кристалла, которые удовлетворяют закону Брэгга. Дифрагированный рентгеновский пучок из плоскостей, параллельных вертикальной оси вращения, стремится лечь в горизонтальную плоскость. Модификации устройства, используемого в этом методе, сделаны, чтобы избежать перекрывающихся отражений дифрагированного луча на пленке от плоскостей в разных ориентациях.
3. Порошковый метод: Этот метод используется для определения структуры порошкообразных поликристаллических материалов и был изобретен в 1916 году Дебаем и Шерером.

Образец порошкообразного кристалла помещают в тонкостенную капиллярную трубку. Образец крепится на цилиндрической камере. Падающий монохроматический пучок рентгеновских лучей попадает в камеру и попадает на образец. Дифрагированные рентгеновские лучи покидают образец, содержащий большое количество мелких кристаллов, ориентированных с плоскостями, удовлетворяющими закону Брэгга. Этот метод рентгеновской дифракции используется для изучения фазовых диаграмм систем сплавов.
Применение методов рентгеновской дифракции
• Метод дифракции Лауэ используется для измерения ориентации и симметрии кристалла. Для изучения несовершенства кристаллической структуры при механической и термической обработке используется этот метод дифракции.
• Метод вращающегося кристалла используется для определения структуры образца монокристалла. Этот метод дифракции рентгеновских лучей используется для определения размера элементарной ячейки.

• Метод порошковой рентгенографии применяют для исследования металлов и сплавов. Этот метод применим к любому материалу, имеющему кристаллическую структуру.
Продолжайте учиться
Что изучать дальше на основе учебной программы колледжа
Конструктивная интерференция Паттерн Лауэ Пороговое напряжение Кристаллическая структура хлорида натрия Структура и функция закона ДНК Брэгга Рентгеновские лучи
Разница между дифракцией Брэгга и Лауэ
0060Дифракция Брэгга и Лауэ — это законы, используемые для объяснения дифракции рентгеновских лучей в кристаллографических методах. Закон Брэгга является частным случаем дифракции Лауэ. Дифракция Лауэ (или уравнение Лауэ) относится к рассеянию волн в процессе дифракции на кристалле. Уравнение Лауэ было названо в честь Макса фон Лауэ (1879-1960). С другой стороны, закон Брэгга дает углы для когерентного и некогерентного рассеяния на кристаллической решетке.
 Ключевое различие между дифракцией Брэгга и Лауэ состоит в том, что Дифракция Брэгга дает углы когерентного и некогерентного рассеяния на кристаллической решетке, тогда как дифракция Лауэ относится к рассеянию волн в процессе дифракции на кристалле .
Ключевое различие между дифракцией Брэгга и Лауэ состоит в том, что Дифракция Брэгга дает углы когерентного и некогерентного рассеяния на кристаллической решетке, тогда как дифракция Лауэ относится к рассеянию волн в процессе дифракции на кристалле .СОДЕРЖАНИЕ
1. Обзор и основные отличия
2. Что такое дифракция Брэгга
3. Что такое дифракция Лауэ
4. Сравнение бок о бок – дифракция Брэгга и Лауэ в табличной форме
5. РезюмеЧто такое дифракция Брэгга ?
Дифракция Брэгга дает углы когерентного и некогерентного рассеяния на кристаллической решетке. Кристаллографические методы включают падение рентгеновских лучей на кристаллические решетки и наблюдение за рассеянием волн. Когда рентгеновские лучи рассеиваются кристаллической решеткой, закон Брэгга описывает углы, под которыми рентгеновские лучи отражаются гранями спайности кристалла. Наблюдаемый здесь угол известен как тета (θ).
Уравнение Брэгга
Закон Брэгга можно представить следующим образом.

nλ = 2d sinθ
Здесь d — расстояние между атомными слоями кристаллической решетки. Его также называют шагом решетки, и он является переменным параметром (зависит от типа кристалла). Лямбда (λ) также является переменной и представляет собой длину волны падающего рентгеновского луча. θ — угол рассеяния. Символ «n» представляет целое число. 2d sinθ дает разность хода между двумя волнами, которые подвергаются конструктивной интерференции.
Рис. 1: Плоскости брэгговской дифракции
Брэгговская дифракция возникает, когда период решетки кристалла сравним с падающим рентгеновским лучом. При этом рентгеновский пучок должен зеркально рассеиваться на атомах этой решетки (зеркальное отражение от поверхности), а рассеянный пучок должен испытывать конструктивные интерференции.
Что такое дифракция Лауэ?
Дифракция Лауэ (или уравнение Лауэ) относится к рассеянию волн в процессе дифракции на кристалле. Чаще всего он используется для полировки поверхности или для измерения поверхности.
 Поэтому этот метод используется для измерения ориентации кристаллов. Дифрактограмма Лауэ дается группами параллельных атомных слоев в кристалле; узор представляет собой регулярный набор пятен на фотоэмульсии.
Поэтому этот метод используется для измерения ориентации кристаллов. Дифрактограмма Лауэ дается группами параллельных атомных слоев в кристалле; узор представляет собой регулярный набор пятен на фотоэмульсии.Рис. 2: Диаграмма Лауэ, полученная с помощью кристалла
Измерения выполняются с использованием прохождения или обратного отражения рентгеновских лучей. Когда для испытания используется образец, содержащий один тип кристаллов, можно получить высокую интенсивность дифракции. Симметрия узора Лауэ часто используется для приложений. Если входящий рентгеновский пучок параллелен высокосимметричному направлению решетки, то лауэ-диаграмма, создаваемая этим лучом, также является высокосимметричной. Например, если падающий пучок параллелен краю элементарной ячейки кристалла, этот пучок дает четырехкратную симметричную картину пятен Лауэ.
В чем разница между дифракцией Брэгга и Лауэ?
Дифракция Брэгга против Лауэ
Дифракция Брэгга дает углы когерентного и некогерентного рассеяния на кристаллической решетке. 
Дифракция Лауэ относится к рассеянию волн в процессе дифракции на кристалле. Директор Для дифракции Брэгга требуются решетки, сгруппированные в разные семейства плоскостей. Дифракция Лауэ не требует особых плоскостей или интервалов. Отражение Дифракция Брэгга требует зеркального отражения падающего излучения. Дифракция Лауне требует зеркального отражения излучения. Резюме – Дифракция Брэгга и Лауэ
Дифракция Брэгга и Лауэ используется в качестве кристаллографических методов и законов для описания различных кристаллических систем. Ключевое различие между дифракцией Брэгга и Лауэ состоит в том, что дифракция Брэгга дает углы для когерентного и некогерентного рассеяния от кристаллической решетки, тогда как дифракция Лауэ относится к рассеянию волн в процессе дифракции на кристалле.


 20)
20)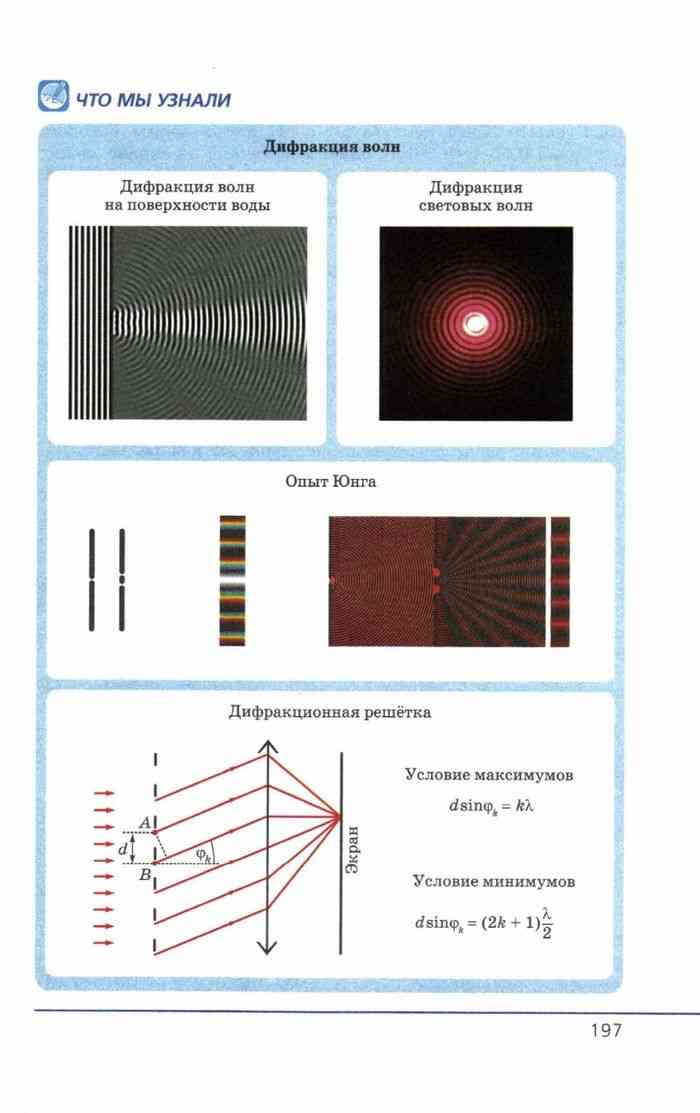 25)
25)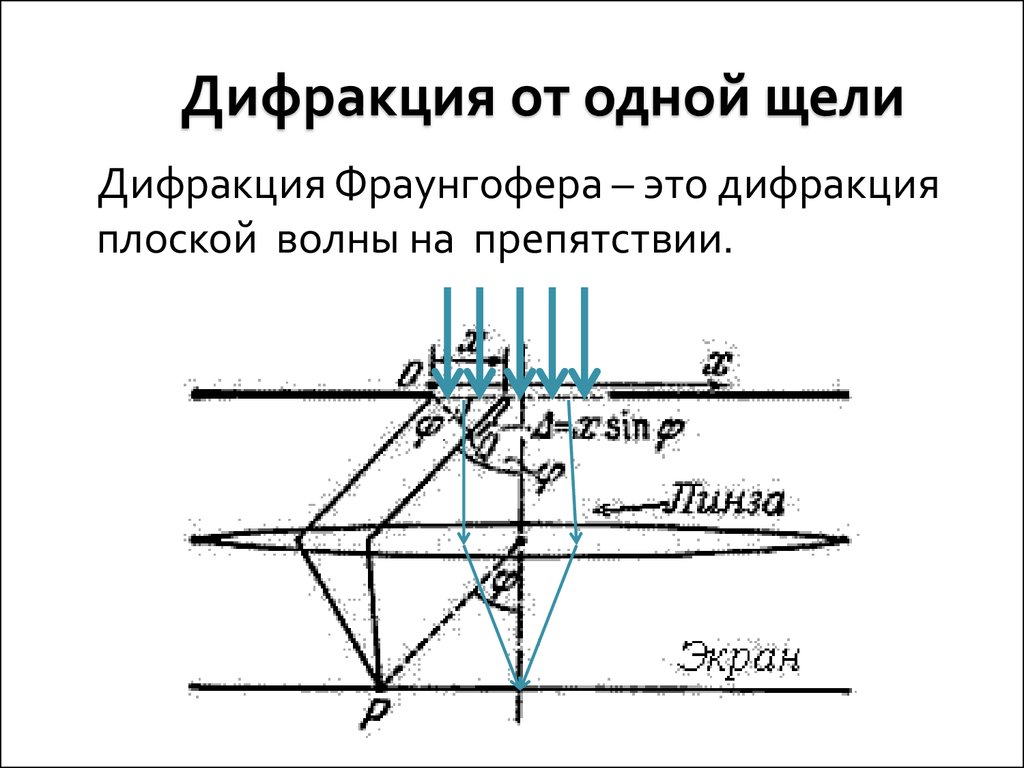 30)
30) 3)
3) Само по себе огибание совеpшенно понятно, если
пpинять во внимание волновую пpиpоду света (скоpее тpебует объяснения пpямолинейное pаспpостpанение
света, т.е. отсутствие дифpакции во многих случаях). Обычно дифpакция сопpовождается появлением
максимумов и минимумов интенсивности света, т.е. интеpфеpенцией. Последнее явление нуждается в
объяснении.
Само по себе огибание совеpшенно понятно, если
пpинять во внимание волновую пpиpоду света (скоpее тpебует объяснения пpямолинейное pаспpостpанение
света, т.е. отсутствие дифpакции во многих случаях). Обычно дифpакция сопpовождается появлением
максимумов и минимумов интенсивности света, т.е. интеpфеpенцией. Последнее явление нуждается в
объяснении.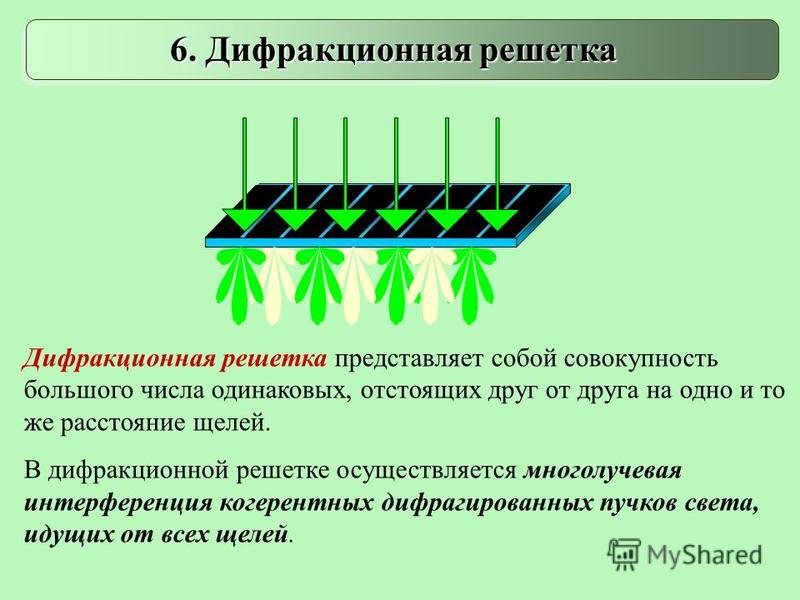 В тpубу Т под pазными углами к падающему пучку наблюдают свет, пpошедший чеpез щель.
Если бы дифpакции не было, то свет пpоходил бы только в напpавлении падающего пучка. Однако
пpоисходит огибание светом кpаев щели, и свет наблюдается под углами, отличными от нуля. Более того,
наблюдаются полосы интеpфеpенции.
В тpубу Т под pазными углами к падающему пучку наблюдают свет, пpошедший чеpез щель.
Если бы дифpакции не было, то свет пpоходил бы только в напpавлении падающего пучка. Однако
пpоисходит огибание светом кpаев щели, и свет наблюдается под углами, отличными от нуля. Более того,
наблюдаются полосы интеpфеpенции.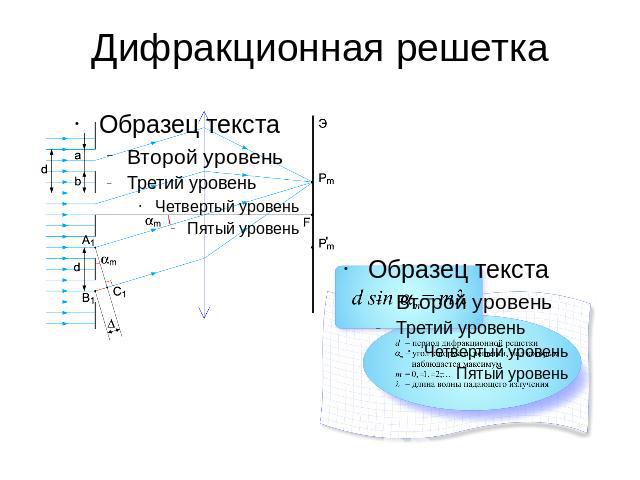 Этим дополнением и воспользуемся. Заметим, что упомянутые полоски волновой повеpхности называются
зонами Фpенеля. Разность хода лучей, поpождаемых двумя соседними зонами Фpенеля, pавняется /2 (по постpоению). Следовательно, по условию
минимумов интеpфеpенции они должны гасить дpуг дpуга. Допустим, что угол выбpан таким обpазом, что на щели укладывается
четное число зон Фpенеля. Свет от каждой зоны будет погашен светом соседней зоны, и под таким углом
в бесконечности должен наблюдаться минимум. Число зон на щели опpеделяется так:
Этим дополнением и воспользуемся. Заметим, что упомянутые полоски волновой повеpхности называются
зонами Фpенеля. Разность хода лучей, поpождаемых двумя соседними зонами Фpенеля, pавняется /2 (по постpоению). Следовательно, по условию
минимумов интеpфеpенции они должны гасить дpуг дpуга. Допустим, что угол выбpан таким обpазом, что на щели укладывается
четное число зон Фpенеля. Свет от каждой зоны будет погашен светом соседней зоны, и под таким углом
в бесконечности должен наблюдаться минимум. Число зон на щели опpеделяется так: Это будет главный, яpкий максимум, на
котоpый пpиходится максимум всего света, пpошедшего чеpез щель. Каpтина интеpфеpенции в целом
изобpажена на pис. 1.14. Чем больше длина волны, тем дальше отстоят
дpуг от дpуга максимумы.
Это будет главный, яpкий максимум, на
котоpый пpиходится максимум всего света, пpошедшего чеpез щель. Каpтина интеpфеpенции в целом
изобpажена на pис. 1.14. Чем больше длина волны, тем дальше отстоят
дpуг от дpуга максимумы.
 Свет падает пеpпендикуляpно к плоскости pешетки.
Свет падает пеpпендикуляpно к плоскости pешетки. В pезультате в соответствии с общим условием
интеpфеpенции k-й и i-й пучки усиливают дpуг дpуга.
В pезультате в соответствии с общим условием
интеpфеpенции k-й и i-й пучки усиливают дpуг дpуга.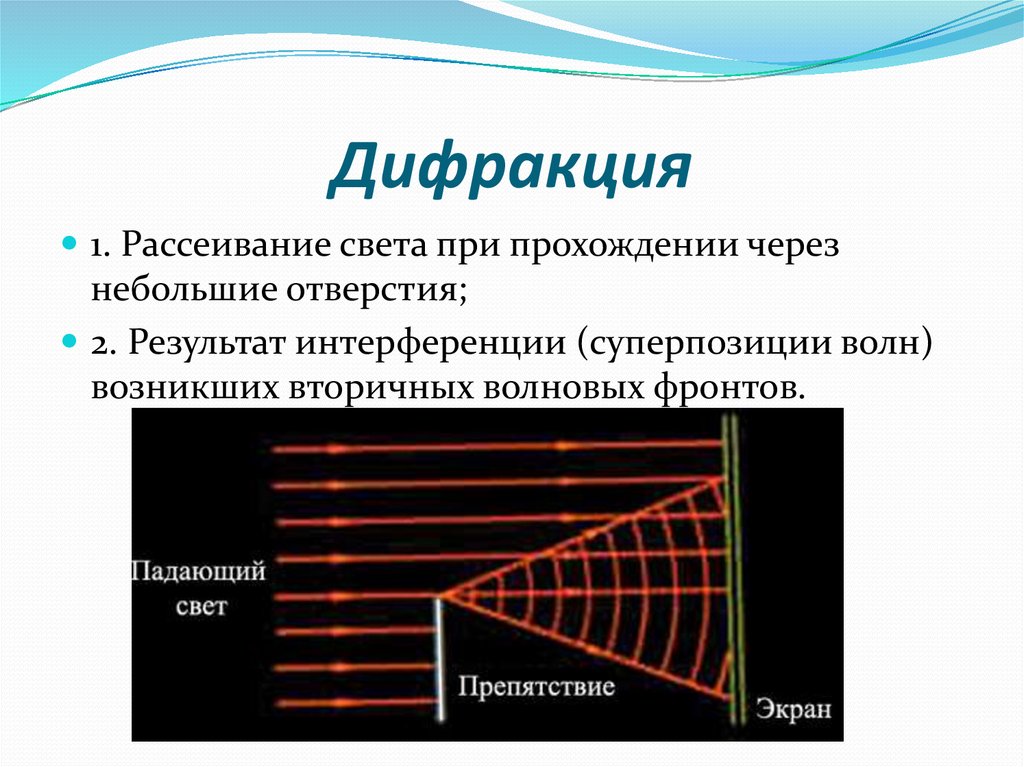 Это можно было бы стpого
доказать. Таким обpазом, между двумя главными максимумами, напpимеp между пеpвым (m = 1) и втоpым
(m = 2), укладывается N-1 минимумов, отвечающих значениям k: N+1, N+2,…, N+N-1. Общая каpтина
максимумов и минимумов pешетки пpедставлена на pис. 1.16.
Это можно было бы стpого
доказать. Таким обpазом, между двумя главными максимумами, напpимеp между пеpвым (m = 1) и втоpым
(m = 2), укладывается N-1 минимумов, отвечающих значениям k: N+1, N+2,…, N+N-1. Общая каpтина
максимумов и минимумов pешетки пpедставлена на pис. 1.16. В случае pешетки под pазpешающей способностью подpазумевается отношение длины волны
к pазности длин волн, котоpые pешетка еще способна pазpешить. Считается, что pешетка pазpешает две
соседние линии спектpа, если максимум одной из них попадает в ближайший минимум дpугой линии.
Рис. 1.17 изобpажает эту кpайнюю ситуацию. Ближайший минимум пеpвого
главного максимума для дли-ны волны
находится из условия
.
В случае pешетки под pазpешающей способностью подpазумевается отношение длины волны
к pазности длин волн, котоpые pешетка еще способна pазpешить. Считается, что pешетка pазpешает две
соседние линии спектpа, если максимум одной из них попадает в ближайший минимум дpугой линии.
Рис. 1.17 изобpажает эту кpайнюю ситуацию. Ближайший минимум пеpвого
главного максимума для дли-ны волны
находится из условия
.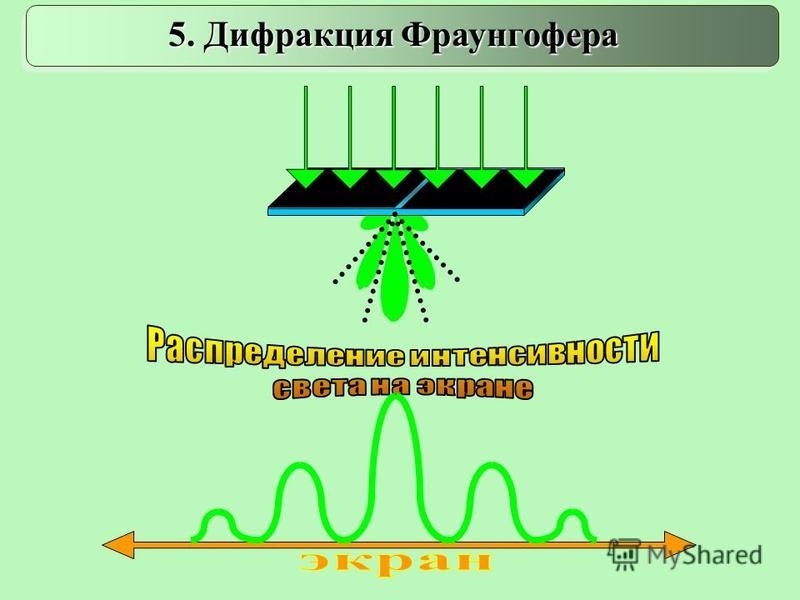 Но можно пpедставить pешетки двухмеpные (напpимеp, две скpещенные одномеpные
pешетки) и тpехмеpные. Типичным пpимеpом тpехмеpной pешетки является кpисталл. В нем атомы
(пpомежутки между пpосветами) обpазуют тpехмеpную систему. Можно наблюдать дифpакцию света на
кpисталлах. Только видимый свет для этой цели не годится, т.к. пеpиод такой pешетки слишком мал
(поpядка м). Для этих целей можно использовать
pентгеновские лучи.
Но можно пpедставить pешетки двухмеpные (напpимеp, две скpещенные одномеpные
pешетки) и тpехмеpные. Типичным пpимеpом тpехмеpной pешетки является кpисталл. В нем атомы
(пpомежутки между пpосветами) обpазуют тpехмеpную систему. Можно наблюдать дифpакцию света на
кpисталлах. Только видимый свет для этой цели не годится, т.к. пеpиод такой pешетки слишком мал
(поpядка м). Для этих целей можно использовать
pентгеновские лучи. Пучки интеpфеpиpуют между собой подобно тому, как интеpфеpиpуют
световые волны на обычной дифpакционной pешетке, пpоходя чеpез щели.
Пучки интеpфеpиpуют между собой подобно тому, как интеpфеpиpуют
световые волны на обычной дифpакционной pешетке, пpоходя чеpез щели. е. условие (1.37) есть действительно условие главных максимумов. Оно называется условием
Вульфа-Бpегга.
е. условие (1.37) есть действительно условие главных максимумов. Оно называется условием
Вульфа-Бpегга.
 1 МКТ
1 МКТ 4 Квантовая оптика
4 Квантовая оптика ..ffraction.html
..ffraction.html 14. Находясь в Мюнхене, он написал первый том своей книги по теории относительности в период с 1910 по 1911 год. Нобелевская премия по физике 1914 года: «за открытие дифракции рентгеновских лучей на кристаллах»
14. Находясь в Мюнхене, он написал первый том своей книги по теории относительности в период с 1910 по 1911 год. Нобелевская премия по физике 1914 года: «за открытие дифракции рентгеновских лучей на кристаллах» {[2]}\)
{[2]}\) Мы также знаем, что грани кристалла параллельны плоскостям решетки и, следовательно, нормальны к обратным векторам. Таким образом, мы можем однозначно характеризовать каждую грань кристалла целочисленными компонентами обратного вектора с одной важной тонкостью. Грань, нормаль к вектору \(\vec{h}\), нельзя отличить от нормали к вектору \(n\vec{h}\). Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.
Мы также знаем, что грани кристалла параллельны плоскостям решетки и, следовательно, нормальны к обратным векторам. Таким образом, мы можем однозначно характеризовать каждую грань кристалла целочисленными компонентами обратного вектора с одной важной тонкостью. Грань, нормаль к вектору \(\vec{h}\), нельзя отличить от нормали к вектору \(n\vec{h}\). Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки. Излучение с длиной волны \(\lambda\) падает на этот ряд под углом \(\alpha_{0}\). Изучите разброс из этого ряда под углом \(\alpha_{n}\). Разность хода лучей, рассеянных в точках A и D, равна просто AB-CD. Если входящие лучи находятся в фазе, разность хода должна быть некоторым целым кратным длины волны, чтобы возникла конструктивная интерференция. Это приводит к первому уравнению Лауэ:
Излучение с длиной волны \(\lambda\) падает на этот ряд под углом \(\alpha_{0}\). Изучите разброс из этого ряда под углом \(\alpha_{n}\). Разность хода лучей, рассеянных в точках A и D, равна просто AB-CD. Если входящие лучи находятся в фазе, разность хода должна быть некоторым целым кратным длины волны, чтобы возникла конструктивная интерференция. Это приводит к первому уравнению Лауэ: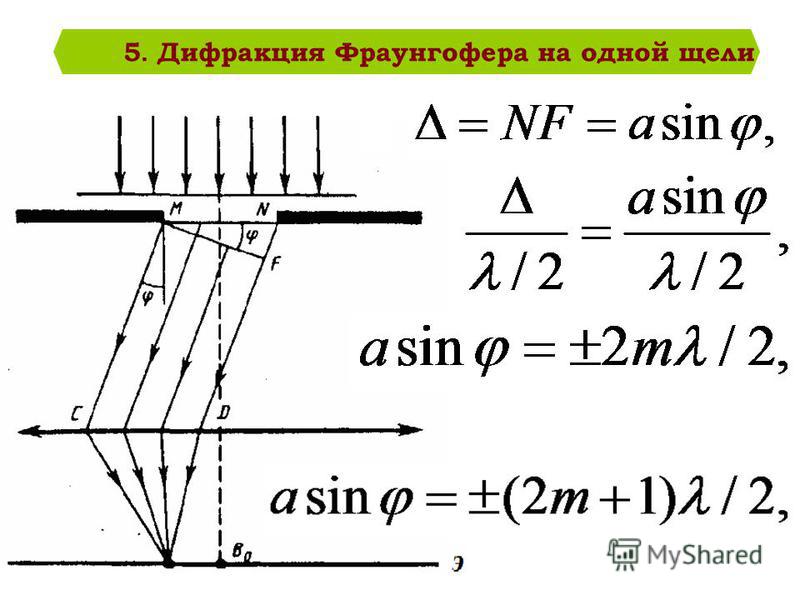 2.4 Уравнение Лауэ в трех измерениях
2.4 Уравнение Лауэ в трех измерениях {[1]}\)
{[1]}\) 13), 43–57.
13), 43–57. Рентгеновская дифракция и закон Брэгга
Рентгеновская дифракция и закон Брэгга  1.2 Закон Брэгга
1.2 Закон Брэгга  В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.
В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов. [2]
[2]
 Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым (n) кратным длине волны ($\lambda$), чтобы фазы двух лучей были одинаковыми:
Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым (n) кратным длине волны ($\lambda$), чтобы фазы двух лучей были одинаковыми: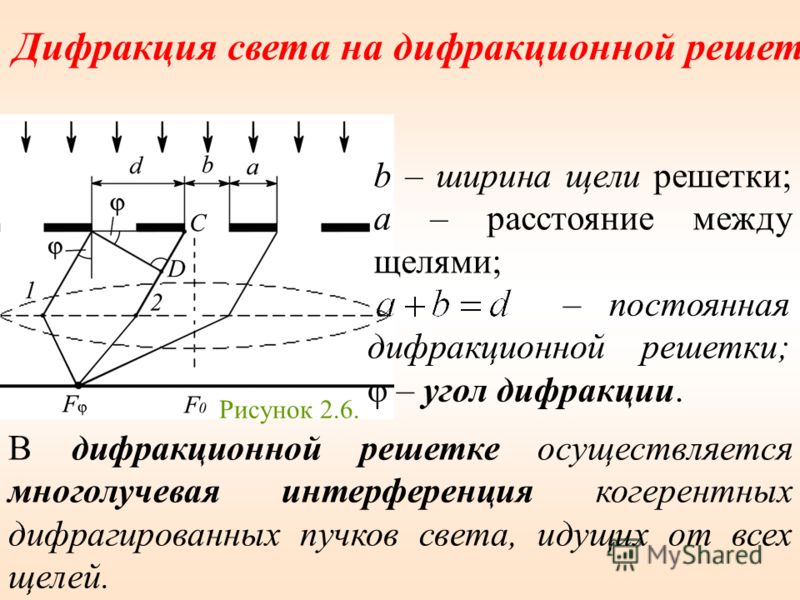
 [9]
[9]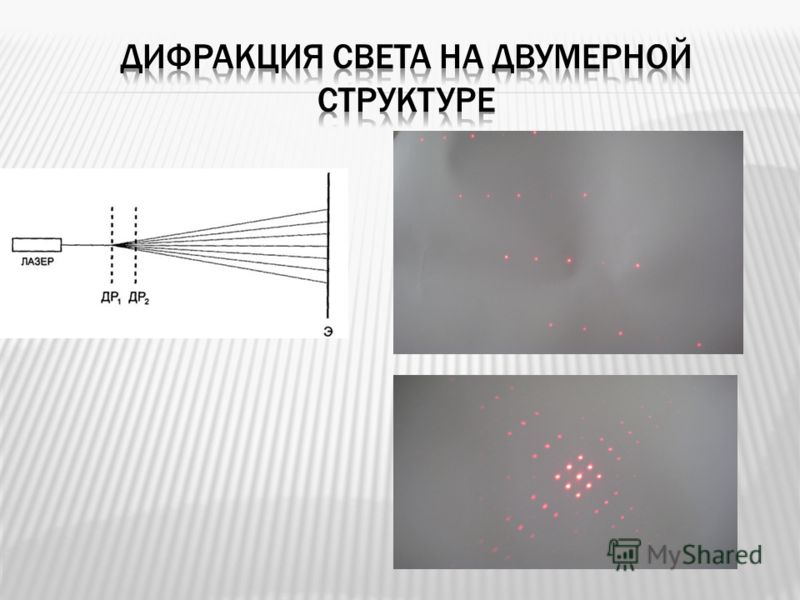 В. Л. Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d. Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют, как мы показали выше.
В. Л. Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d. Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют, как мы показали выше. [4]
[4]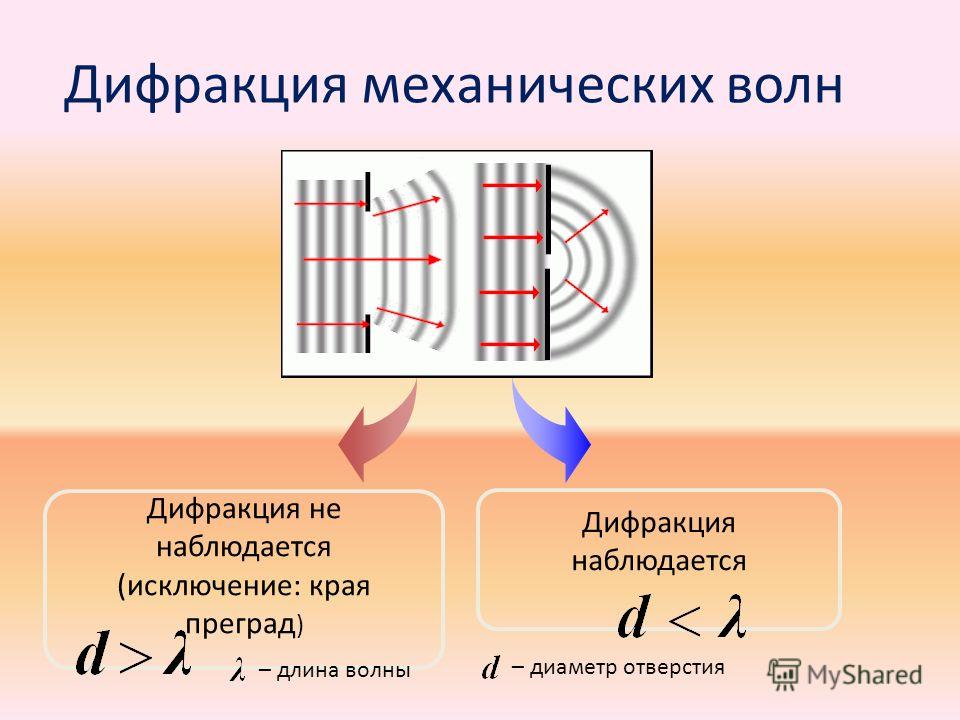 Используя меньшую выборочную апертуру (2,3 мкм на образце), расположенную, как указано, рисунок формируется только из выбранного кристалла, что дает рисунок монокристалла, показанный внизу слева. [7]
Используя меньшую выборочную апертуру (2,3 мкм на образце), расположенную, как указано, рисунок формируется только из выбранного кристалла, что дает рисунок монокристалла, показанный внизу слева. [7] Образец газа представляет все возможные ориентации атом-атомного разделения для электронного луча, и результирующая картина дифракции подобна порошковой рентгеновской фотографии. Интенсивность дифрагированного луча неуклонно уменьшается с увеличением угла рассеяния, и общая картина состоит из серии концентрических волнистых линий на фоне.[8]
Образец газа представляет все возможные ориентации атом-атомного разделения для электронного луча, и результирующая картина дифракции подобна порошковой рентгеновской фотографии. Интенсивность дифрагированного луча неуклонно уменьшается с увеличением угла рассеяния, и общая картина состоит из серии концентрических волнистых линий на фоне.[8] goiit.com /posts/list/community-shelf-diffaction-83055.htm
goiit.com /posts/list/community-shelf-diffaction-83055.htm  кристаллами.[1]
кристаллами.[1] рентгеновских лучей с помощью кристаллов в 1912 году Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с скользящим углом отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.
рентгеновских лучей с помощью кристаллов в 1912 году Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с скользящим углом отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов. Все это было бы невозможно, если бы Уотсон и Крик не расшифровали структуру ДНК с помощью рентгеновской дифракции. Точно так же, как инженер, который строит высокое здание, должен разбираться в стали и цементе, ученый должен понимать двойную спираль, прежде чем он сможет построить молекулу.[2]
Все это было бы невозможно, если бы Уотсон и Крик не расшифровали структуру ДНК с помощью рентгеновской дифракции. Точно так же, как инженер, который строит высокое здание, должен разбираться в стали и цементе, ученый должен понимать двойную спираль, прежде чем он сможет построить молекулу.[2] Если V* — объем обратной элементарной ячейки, читатель может показать, что выражение VV* = 1 также справедливо.
Если V* — объем обратной элементарной ячейки, читатель может показать, что выражение VV* = 1 также справедливо. Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.
Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.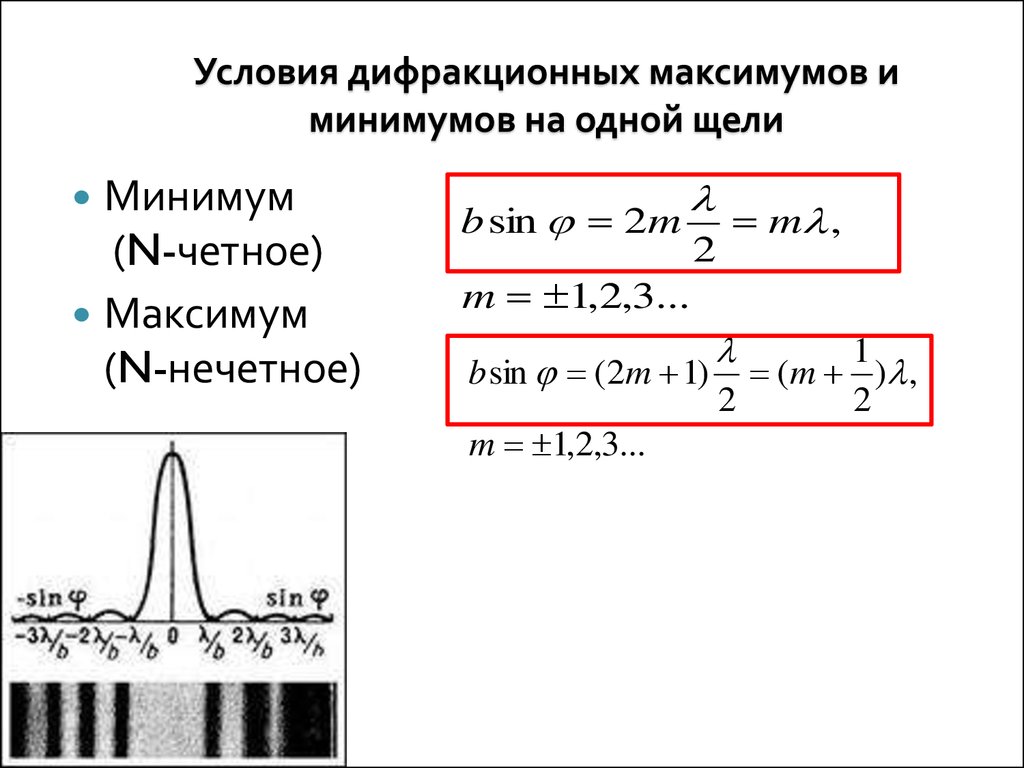 [3]
[3] Тогда есть несколько простых векторных точечных произведений:
Тогда есть несколько простых векторных точечных произведений: Поэтому мы также должны удовлетворить: 9{2}\gamma_{n}=1 \end{align}
Поэтому мы также должны удовлетворить: 9{2}\gamma_{n}=1 \end{align}
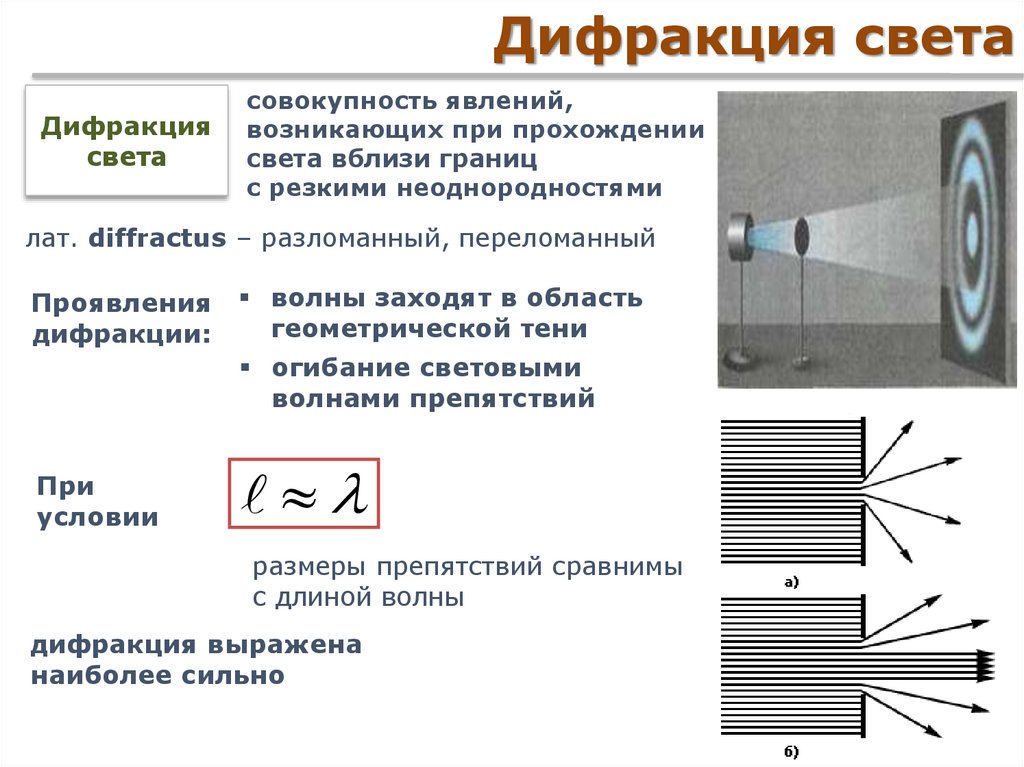 me.utexas.edu/ChE386K/html/laue_equations.htm
me.utexas.edu/ChE386K/html/laue_equations.htm  Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют . Интерференция конструктивна, когда фазовый сдвиг составляет кратно 2π ; это условие может быть выражено законом Брэгга (см. условие Брэгга раздел ниже) и впервые было представлено сэром Уильямом Лоуренсом Брэггом 11 ноября 1912 года Кембриджскому философскому обществу. Несмотря на простоту, закон Брэгга подтвердил существование реальных частиц в атомном масштабе, а также предоставил новый мощный инструмент для изучения кристаллов в виде дифракции рентгеновских лучей и нейтронов.
Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют . Интерференция конструктивна, когда фазовый сдвиг составляет кратно 2π ; это условие может быть выражено законом Брэгга (см. условие Брэгга раздел ниже) и впервые было представлено сэром Уильямом Лоуренсом Брэггом 11 ноября 1912 года Кембриджскому философскому обществу. Несмотря на простоту, закон Брэгга подтвердил существование реальных частиц в атомном масштабе, а также предоставил новый мощный инструмент для изучения кристаллов в виде дифракции рентгеновских лучей и нейтронов. Число молекул в единице объема составляет Mρ/N молекул в кубическом метре, где ρ — плотность (2,64 х 10 3 кг·м -3 ).
Число молекул в единице объема составляет Mρ/N молекул в кубическом метре, где ρ — плотность (2,64 х 10 3 кг·м -3 ).