Восстановить оригинал по изображению: Преобразования Лапласа онлайн
2. Восстановление оригинала по изображению Лапласа
Пример 8. Найти оригинал для изображения
Решение. Используя формулы 2 и 6, получим
Пример 9. Найти оригинал для изображения
Решение. Выделим полный квадрат:
Тогда
Пример 10. Найти оригинал для изображения
Решение. Выделим полный квадрат:
Теперь преобразуем числитель дроби.
Пример11. Найти оригинал для изображения .
Решение. Разложим эту дробь на элементарные дроби методом неопределенных коэффициентов.
. Следовательно,
.
Пример 12. Найти оригинал для изображения
Решение. Разложим дробь на сумму элементарных дробей.
Приравняем числители полученных дробей и применим метод подстановки. Т.е. приравняем корням знаменателя и какому-нибудь небольшому целому числу.
Подставляем значения коэффициентов в разложение и находим оригинал функции.
Пример 13. Найти оригинал для функции
Решение. По формуле 3 . Применяя теорему запаздывания, получим
3. Применение преобразования Лапласа к решению дифференциальных уравнений
Пример 14. Решить задачу Коши с помощью преобразования Лапласа
Решение. Обозначим .
Тогда по формулам 19 и 20 получим
Обозначим .
Тогда по формулам 19 и 20 получим
Применим преобразование Лапласа к обеим частям уравнения, используя аддитивность и однородность этого преобразования.
Подставим начальные условия и найдем
Можно составить систему уравнений, приравнивая коэффициенты при
одинаковых степенях переменной, но т.к. корни знаменателя простые и действительные, то можно использовать метод подстановки. В обе части последнего равенства подставляем значения этих корней.
. Подставим найденные значения в разложение и найдем оригинал. Итак,
Пример 15. Решить, используя преобразование Лапласа, задачу Коши для системы уравнений
Решение. Обозначим и применим преобразование Лапласа к
обоим уравнениям системы. Получим
операторную систему
Получим
операторную систему
Подставив начальные значения, получим:
Решая систему, найдем
,
Разложим каждую из дробей на сумму элементарных дробей, используя метод неопределенных коэффициентов, и найдем оригиналы.
Итак,
Дискретное преобразование Лапласа ( преобразование)
Наряду с функциями,
определенными на всей вещественной
прямой ,
можно рассматривать функции, которые
определены только в некоторых точках .
Такие функции называют решетчатыми.
Обычно рассматривают функции, определенные
в равноотстоящих точках где —
целое число, а —
постоянная, называемая периодом
дискретности. Эти функции обозначают ,
а если ,
то
Эти функции обозначают ,
а если ,
то
Всякая функция , являющаяся оригиналом для обычного преобразования Лапласа, порождает решетчатую функцию , для
которой определено дискретное преобразование Лапласа.
Решетчатая функция называется дискретным оригиналом, если
1) при ,
2)существуют такие числа , что для всех натуральных значений .
Функция называется изображением функции при дискретном преобразовании Лапласа. Это обозначается следующим образом
или
Обычно рассматривают — преобразование для случая , т.е.
Таблица оригиналов и изображений дискретного
Методы приближенного преобразования Фурье и обращения преобразования Лапласа (справочная книга)
Методы приближенного преобразования Фурье и обращения преобразования Лапласа (справочная книга)
ОглавлениеПРЕДИСЛОВИЕЧАСТЬ ПЕРВАЯ. ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА § 1.2. Комплексный интеграл, осуществляющий обращение преобразования Лапласа § 1.3. Представление функций интегралом Лапласа § 1.4. Некорректность задачи обращения преобразования Лапласа ГЛАВА 2.  НЕКОТОРЫЕ АНАЛИТИЧЕСКИЕ МЕТОДЫ ОБРАЩЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА НЕКОТОРЫЕ АНАЛИТИЧЕСКИЕ МЕТОДЫ ОБРАЩЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА§ 2.3. Разложение оригинала в обобщенные степенные ряды ГЛАВА 3. МЕТОДЫ ЧИСЛЕННОГО ОБРАЩЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ СПЕЦИАЛЬНЫХ РАЗЛОЖЕНИЙ § 3.1. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке 3.1.2. Обращение преобразования Лапласа с помощью многочленов Якоби. 3.1.3. Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра. 3.1.4. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода. 3.1.5. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева второго рода. 3.1.6. Другой способ вычисления коэффициентов ak. 3.1.7. Замечание о приведении полуплоскости регулярности изображения к виду … § 3.2. Обращение преобразования Лапласа с помощью ряда Фурье по синусам § 3.3. Обращение преобразования Лапласа с помощью рядов по обобщенным многочленам Чебышева — Лагерра ГЛАВА 4.  МЕТОДЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛА МЕЛЛИНА ПРИ ПОМОЩИ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУРНЫХ ФОРМУЛ МЕТОДЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛА МЕЛЛИНА ПРИ ПОМОЩИ ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУРНЫХ ФОРМУЛ§ 4.2. Интерполяционный метод с равноотстоящими узлами § 4.3. Интерполяционный метод с неравноотстоящими узлами § 4.4. Замечания о других интерполяционных методах. Применение отрезка ряда Тейлора § 4.5. Некоторые теоремы о сходимости интерполирования 4.5.2. Сходимость интерполяционного процесса вида (4.3.4). 4.5.3. Сходимость интерполяционного процесса вида (4.1.4). § 4.6. Теоремы о сходимости интерполяционных методов обращения ГЛАВА 5. МЕТОДЫ ЧИСЛЕННОГО ОБРАЩЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА ПРИ ПОМОЩИ КВАДРАТУРНЫХ ФОРМУЛ, ИМЕЮЩИХ НАИВЫСШУЮ СТЕПЕНЬ ТОЧНОСТИ § 5.1. Теория квадратурных формул § 5.2. Ортогональные многочлены, связанные с квадратурной формулой наивысшей степени точности 5.2.2. Рекуррентное соотношение для многочленов … 5.2.4. Интегральное представление многочленов … 5.  2.5. Производящая функция для многочленов … 2.5. Производящая функция для многочленов …5.2.6. Распределение корней многочленов … § 5.3. Методы вычисления коэффициентов и узлов квадратурной формулы ГЛАВА 6. МЕТОДЫ ОБРАЩЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА С ПОМОЩЬЮ КВАДРАТУРНЫХ ФОРМУЛ С РАВНЫМИ КОЭФФИЦИЕНТАМИ § 6.2. Замечание о расположении узлов ЧАСТЬ ВТОРАЯ. ПРЕОБРАЗОВАНИЯ ФУРЬЕ И ИХ ПРИМЕНЕНИЕ К ОБРАЩЕНИЮ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА § 7.1. Преобразования Фурье § 7.2. Приведение интеграла типа Меллина к преобразованию Фурье ГЛАВА 8. ОБРАЩЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА С ПОМОЩЬЮ РЯДА ФУРЬЕ § 8.2. Случай быстрого убывания модуля изображения F(p) ГЛАВА 9. ИНТЕРПОЛЯЦИОННЫЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ФУРЬЕ § 9.2. Вычислительные формулы, основанные на алгебраическом интерполировании функции f(x) § 9.3. Вычислительные формулы, основанные на интерполировании рациональными функциями 9.3.2. Общее интерполяционное квадратурное правило. 9.3.3. Случай равноотстоящих узлов. 9.3.4. Интерполяционные правила вычислений, связанные с корнями ортогональных многочленов.  9.3.5. О вычислении интегралов … ГЛАВА 10. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЙ, ИМЕЮЩИЕ НАИВЫСШУЮ СТЕПЕНЬ ТОЧНОСТИ § 10.2. Построение формулы наивысшей степени точности ЧАСТЬ ТРЕТЬЯ. ВЫДЕЛЕНИЕ ОСОБЕННОСТЕЙ ФУНКЦИИ ПРИ ВЫЧИСЛЕНИЯХ ГЛАВА 11. ВЫДЕЛЕНИЕ ОСОБЕННОСТЕЙ ИЗОБРАЖЕНИЯ F(p) § 11.2. Устранение и ослабление особенностей изображения F(p) § 11.3. Замечание об увеличении скорости стремления к нулю изображения F(p) ГЛАВА 12. ВЫДЕЛЕНИЕ ОСОБЕННОСТЕЙ ФУНКЦИИ ПРИ ПРЕОБРАЗОВАНИИ ФУРЬЕ § 12.1. Устранение разрывов первого рода ЛИТЕРАТУРА |
Как восстановить фотографии в PaintShop Pro
- Обучение
- Практические руководства
- Восстановить фотографии
Иногда фотографии не выдерживают разрушительного действия времени. Независимо от того, являются ли они старыми, поврежденными или частично поврежденными, восстановление фотографий — это процесс цифрового исправления повреждений, артефактов и других дефектов, который поможет вам сохранить и сохранить приятные воспоминания о прошлом.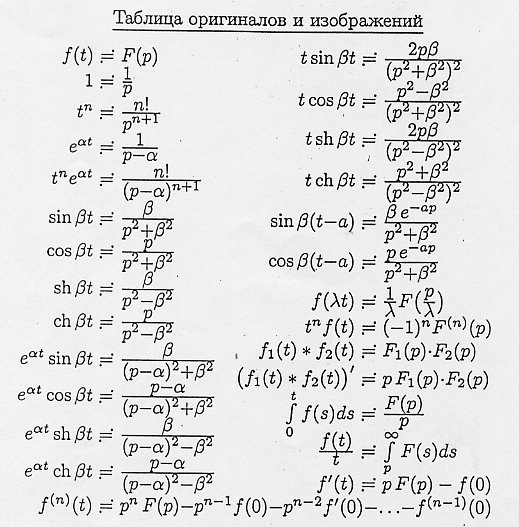 Используя программное обеспечение для обработки изображений, вы можете обрезать, выпрямлять, исправлять повреждения и фильтровать изображения, чтобы улучшить их. Продолжайте читать, чтобы узнать, как восстанавливать фотографии с помощью PaintShop Pro.
Используя программное обеспечение для обработки изображений, вы можете обрезать, выпрямлять, исправлять повреждения и фильтровать изображения, чтобы улучшить их. Продолжайте читать, чтобы узнать, как восстанавливать фотографии с помощью PaintShop Pro.
Попробуйте бесплатно
1. Установите PaintShop Pro
Чтобы установить программное обеспечение для редактирования фотографий PaintShop Pro на свой компьютер, загрузите и запустите установочный файл, указанный выше. Продолжайте следовать инструкциям на экране, чтобы завершить процесс установки.
2. Цифровое увеличение изображения
Идеальный шаг для старых фотографий, которые были отсканированы для создания цифровой копии.
Открыть образ. Выберите Image > Resize > Нажмите Advanced and AI Powered Setting . Нажмите на Повторная выборка с использованием : В раскрывающемся списке выберите AI-Powered .
3. Выберите Коррекция выцветания
Выберите Настройка > Цвет > Коррекция выцветания . Перетащите на панели «До», чтобы отцентрировать важную часть изображения (например, лицо).
Перетащите на панели «До», чтобы отцентрировать важную часть изображения (например, лицо).
4. Отрегулируйте Величину коррекции
Отрегулируйте значение в элементе управления Величина коррекции , пока изображение не станет максимально естественным.
Значение по умолчанию: 45.
Примечание: Используйте минимальное значение, обеспечивающее хорошую коррекцию. Если вы применяете слишком сильную коррекцию, светлые и темные области могут потерять детализацию, а объекты могут сливаться друг с другом.
Нажмите OK .
5. Выберите Удаление артефактов
Выберите > Настройка > Добавить/удалить шум > Удаление артефактов ИИ , чтобы удалить любые нежелательные артефакты, вызванные восстановлением.
Загрузите бесплатную пробную версию и начните восстанавливать изображения уже сегодня
Инструменты редактирования изображений PaintShop Pro позволяют быстро и легко восстанавливать изображения, чтобы вернуть их к жизни.
НАЧНИТЕ СЕЙЧАС
PaintShop Pro не просто восстанавливает изображения
Ознакомьтесь с некоторыми другими функциями редактирования фотографий в Paintshop Pro, такими как изменить цвет изображения, удалить шум изображения, исправить недоэкспонированные изображения, и более! Создавайте высококачественные фотографии в забавном и простом в использовании фоторедакторе и сделайте свои фотографии более заметными, чем когда-либо.
Изменить цвет изображения
Удалить людей с фотографий
Правильная перспектива изображения
Исправить искажение перспективы
Загрузите лучшее решение для восстановления изображений, которое есть
У вас есть старые изображения, которым вы хотите восстановить их первоначальный вид? Мы обещаем, что вам понравятся простые в использовании функции восстановления изображений в PaintShop Pro. Нажмите ниже, чтобы загрузить бесплатную 30-дневную пробную версию и бесплатно восстановить старые фотографии перед покупкой!
Нажмите ниже, чтобы загрузить бесплатную 30-дневную пробную версию и бесплатно восстановить старые фотографии перед покупкой!
Попробуйте бесплатно
Отмена изменений в PDF-файлах и изображениях в режиме предварительного просмотра на Mac
macOS Ventura 13
macOS Монтерей 12
Выберите версию:macOS Вентура 13 macOS Монтерей 12
Изменение этого элемента управления приведет к автоматическому обновлению этой страницы
Искать в этом руководстве
Предварительный просмотр руководства пользователя
- Добро пожаловать
- Открывайте PDF-файлы и изображения
- Просмотр PDF-файлов и изображений
- Поиск текста в PDF-файлах
- Взаимодействие с текстом на фотографии
- Добавляйте PDF-страницы в закладки
- Просмотр информации о файлах PDF и изображениях
- Импорт изображений с камеры
- Посмотрите, где было сделано фото
- Отображение PDF в виде слайд-шоу
- Просмотр анимированных GIF-кадров
- Заполнять и подписывать PDF-формы
- Выделить и скопировать текст в PDF
- Выделение, подчеркивание и зачеркивание текста
- Добавление заметок и речевых пузырей в PDF
- Аннотировать PDF
- Объединить PDF-файлы
- Добавляйте, удаляйте или перемещайте страницы PDF
- Обрезать или повернуть PDF
- Добавление эффектов в PDF
- Изменение размера, поворот или отражение изображения
- Преобразование типов файлов изображений
- Извлечь изображение или удалить фон
- Аннотировать изображение
- Посмотрите, как изображение выглядит на другом устройстве
- Применение цветового профиля к изображению
- Сохраняйте PDF-файлы и изображения
- Отменить изменения в PDF-файлах и изображениях
- Копировать PDF-файлы и изображения
- Блокировка PDF-файлов и изображений
- Экспорт PDF-файлов и изображений
- Защитите PDF паролем
- Сжать PDF-файл
- Печать PDF-файлов и изображений
- Если вы не можете выделить или скопировать текст в PDF
- Если изображения или PDF-файлы имеют неправильный размер
- Если при переходе на страницу отображается неправильная страница PDF-файла
- Изменить настройки предварительного просмотра
- Горячие клавиши
- Авторские права
Preview периодически сохраняет «моментальные снимки» (называемые версиями ) вашего PDF-файла или изображения. Вы можете просмотреть файл, как он выглядел в прошлом, и вернуться к предыдущей версии.
Вы можете просмотреть файл, как он выглядел в прошлом, и вернуться к предыдущей версии.
Открыть предварительный просмотр для меня
Вернуться к последней сохраненной или открытой версии
В приложении «Просмотр» на Mac откройте файл PDF или изображение.
В зависимости от ваших предыдущих действий с файлом выполните одно из следующих действий:
Выберите «Файл» > «Вернуться к» > «Предыдущее сохранение» [дата, время].
Выберите «Файл» > «Вернуться к» > «Последнее сохранение» [дата, время].
Выберите «Файл» > «Вернуться к» > «Последнее открытие» [дата, время].
Просмотр, восстановление или дублирование предыдущих версий
В приложении «Просмотр» на Mac откройте файл PDF или изображение.
Выберите «Файл» > «Вернуться к» > «Просмотреть все версии».


 В. И. Крылов, Н. С. Скобля. Главная редакция физико-математической литературы издательства «Наука», М., 1974.
В. И. Крылов, Н. С. Скобля. Главная редакция физико-математической литературы издательства «Наука», М., 1974.
