Закон квадратов: Эффект Серла. (Джон Серл)
Эффект Серла. (Джон Серл)
Эффект Серла. (Джон Серл)«Утопические социальные теории ни к чему не ведут, они в самих себе изначально уже содержат тупик. Безнадежность мы ощущаем тогда, когда начинаем считать человека чем-то «конечным», законченным, не видим ничего дальше человека. В таком виде вопрос на самом деле безнадежен. От всех социальных теорий, обещающих нам неисчислимые блага на земле, веет холодом, и остается чувство неудовлетворенности и неприятный привкус.
Зачем? К чему все это? Ну, все будут сыты. Прекрасно. А дальше?
Конечно, пока человечество не освободится от голода и нужды, пока рядом с роскошными дворцами и комфортабельными домами будут вонючие и грязные трущобы, пока рядом с нами люди будут топиться и вешаться от голода и от отчаяния, мы не имеем права говорить ни о культуре, ни о цивилизации.
Но допустим, что ничего этого больше нет. На земле настоящая, неподдельная цивилизация и культура. Никто больше не душит никого.
Можно говорить о любых невероятных технических достижениях, «утилизация вращения Земли вокруг Солнца», «сыворотки от всех болезней», «искусственное выращивание людей», но, в самом деле, это по большому счету ничего не значит и никуда не ведет.
Людям нужно разрешение вопроса о судьбе настоящего, современного человечества в таком виде, как оно есть сейчас. Они не хотят признать того, что само человечество может и должно измениться, что «человек» в настоящем виде это только куколка, из которой со временем разовьется бабочка, совсем непохожая на куколку.
Это собственно и есть ключ к пониманию нашей жизни. И ключ этот давно уже найден.
Загадка давно разгадана. Но разные мыслители разных эпох, находя ее решения, называли их разными именами и часто, не зная друг друга, с огромным трудом проходили по одной и той же дороге, не подозревая о своих предшественниках и современниках, шедших и идущих по одному и тому же пути с ними.
Мы приближаемся к эпохе, в которой традиционные роли ученого, философа, шамана и художника объединятся в одной личности нового типа, готовой погрузиться в великое таинство жизни, лежащей за фасадом мира».
«Раса».
Эффект Серла. (Джон Серл)
Четыре года подряд (с 1968 по 1972) каждое первое воскресенье месяца соседи Джона Сёрла и случайные прохожие наблюдали не поддающиеся объяснению явления. В руках профессора оживали, вращались и вырабатывали энергию необычные генераторы; диски диаметром от полуметра до 10 метров поднимались в воздух и совершали управляемые полеты из Лондона в Корнуолл и обратно.
Тележурналисты Би-Би-Си начали снимать документальный фильм о необыкновенных устройствах. Его показали по телевидению. Результат оказался неожиданным: местный комитет по электричеству обвинил Джона Сёрла в воровстве электроэнергии. Электрики не поверили, что его лаборатория питалась от собственного источника. Ученого посадили в тюрьму на 10 месяцев.
Детство
Джон Сёрл родился в 1932 году в Великобритании в графстве Беркшир. Его детство сложно назвать счастливым, по крайней мере, в традиционном смысле. В этом детстве не было любящих родителей; их, по сути, вообще не было. За шесть лет официальной супружеской жизни его отец семь раз уходил из семьи и вообще не уделял внимания сыну. Мама страдала психическими расстройствами, пыталась свести концы с концами и больше заботилась об устройстве собственной жизни, чем о воспитании детей.
В четыре года по решению суда Джона передали под опеку государства, и он переехал в пансион доктора Барнардо. Уже с детства он стал частым гостем в госпиталях, поскольку страдал редким нарушением вестибулярного аппарата и слуха, которое так и не смогли вылечить. Из-за этого в пожилом возрасте Сёрл начал испытывать сильнейшие головные боли.
Из-за этого в пожилом возрасте Сёрл начал испытывать сильнейшие головные боли.
В его детстве было много религиозных догматов и мало друзей. Никто из его приятелей, к большому сожалению Джона, не мог позволить себе презреть запреты и, связав все имеющиеся под рукой простыни, спуститься с третьего этажа запертого пансиона, чтобы почувствовать вкус свободы.
Зато в его детстве были сны. Очень непонятные сны. Ему снились числа, они объединялись в квадраты, причем строго определенным способом: так, что суммы чисел по горизонталям, вертикалям и диагоналям оказывались равными. В математике такие квадраты называются магическими. А еще в его снах было Электричество. Сны возвращались снова и снова, но для мальчика это были всего лишь красивые картинки: он не мог понять образы, которые видел. Но зато понял, что должен связать с электричеством свою жизнь. Со временем такие сновидения стали приходить реже, но они очень влияли на его изобретательскую деятельность. Например, в 1993 году, после многолетних неудачных попыток теоретически объяснить экспериментальные данные, именно во сне Сёрл увидел Пифагора, который дал простое и красивое решение его задачи.
Закон квадратов
В 1946 году Джон Сёрл начал сам зарабатывать себе на жизнь: он устроился на работу инженером по ремонту электродвигателей. Именно тогда он сделал фундаментальное открытие природы магнетизма. Он обнаружил, что добавление небольшой компоненты переменного тока (~100 ma) радиочастоты (~10 MHz) в процессе изготовления постоянных ферритовых магнитов придает им новые неожиданные свойства. После ряда экспериментов с плоскими магнитами Сёрл сделал кольцевой магнит и несколько цилиндрических. Намагнитив их открытым способом, он помещал цилиндрические магниты на внешнюю сторону кольцевого. В этом случае легкий толчок одного из цилиндров приводил к тому, что все цилиндры начинали двигаться по кругу. И это движение не прекращалось.
Сёрл обнаружил, что если количество роликов, расположенных вокруг, равно некоторому конкретному минимальному числу, то они начинают вращаться самостоятельно, увеличивая скорость до тех пор, пока не придут в динамическое равновесие.
Его изобретение открывало доступ к новому, доселе неизвестному способу получения энергии. Без материальных затрат на сам процесс. Но Сёрла интересовало другое: от чего зависят параметры установки? Почему при разных размерах, разном количестве роликов, разных материалах и разной намагниченности далеко не всегда воспроизводим сам эффект? Он понимал, что существуют некоторые «удачные сочетания» параметров установки, но не мог найти ключа, который бы помог понять и рассчитать эти сочетания. До открытия закона квадратов оставался один шаг.
Схема первых опытов Сёрла с намагниченными брусками и роликами
Замена прямоугольного бруска на кольцевой магнит делает движение роликов более естественным
Классическая схема современного трехуровневого генератора на Сёрл-эффекте
Российский вариант генератора Джона Сёрла — установка С. М. Година и В. В. Рощина
В ходе эксперимента было получено до 7 кВт электроэнергии без внешнего источника питания и наблюдалась потеря до 40% веса установки
Первые решения и понимания приходили ночью. Напряженные дневные размышления разрешались во сне, причем неожиданно: Сёрл видел искомые параметры своей установки, их численные значения объединенными в таблицы наподобие этой.
Напряженные дневные размышления разрешались во сне, причем неожиданно: Сёрл видел искомые параметры своей установки, их численные значения объединенными в таблицы наподобие этой.
31 37 28 38
40 26 35 33
34 32 41 27
29 39 30 36
На первый взгляд это обыкновенный магический квадрат: суммы чисел по горизонталям, вертикалям и диагоналям равны. Но Джон Сёрл обнаружил, что его «обыкновенные» магические квадраты обладают необыкновенными свойствами. Для пытливого взора изобретателя и естествоиспытателя они стали, как говорит он сам, «окном в природу». Все в природе построено на строжайших закономерностях, убежден профессор, но мы их не видим. Мы не можем их увидеть, потому что получили стандартное образование, из-за чего просто ослепли. Или надели шоры. Заполнив свое сознание стереотипами, мы утратили саму способность удивляться, искать непредвзято, перестали видеть. И воспринимаем реальность не такой, какая она есть, а такой, какой нас научили ее воспринимать.
Сёрл убежден, что его закон квадратов не открытие. Наоборот, это возрождение принципов древней математики, которым, по его словам, больше 5000 лет. Закон квадратов, подробно описанный в книге Джона Сёрла, является наглядной формой выражения существующих в природе закономерностей. Он открывается непредвзятому исследователю и требует прежде всего решительного расставания с устоявшимися концепциями, взглядами, подходами. Многие пытались воспроизвести установки Сёрла, но получилось это у единиц: у тех, кому хватило терпения разобраться в принципах работы этих установок, кто готов был сказать: «Я знаю, что ничего не знаю» — и не побоялся расстаться со стереотипами.
Закон квадратов не объяснишь в одной статье. Но Джон Сёрл готов выслать свою книгу тому, кто пожелает в нем разобраться.
SEG и IGV
Всю свою жизнь Сёрл мечтал воплотить те образы и идеи, которые посещали его в детстве. Вначале это был пылкий юношеский интерес, замешанный на тяге к неведомому.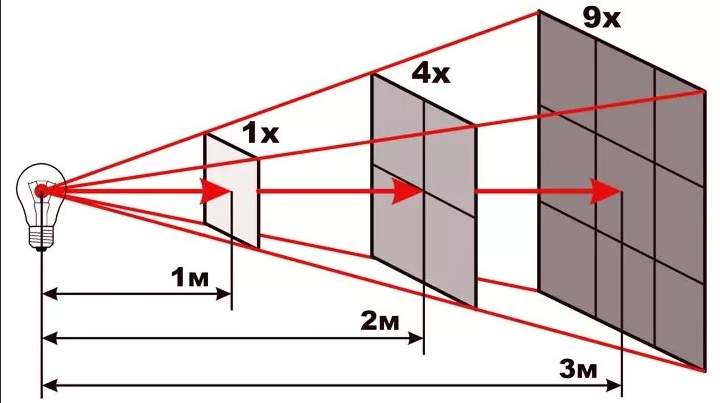 Со временем он перерос в творческий огонь зрелого исследователя. По мере того как совершенствовались прототипы и осмыслялся закон квадратов, все четче обрисовывались и контуры той Мечты, что вела его с детства. Джон Сёрл понял, что он может быть полезен, что его талант принадлежит не столько ему, сколько нуждающимся в его работе.
Со временем он перерос в творческий огонь зрелого исследователя. По мере того как совершенствовались прототипы и осмыслялся закон квадратов, все четче обрисовывались и контуры той Мечты, что вела его с детства. Джон Сёрл понял, что он может быть полезен, что его талант принадлежит не столько ему, сколько нуждающимся в его работе.
Человек сегодня слишком сосредоточен на потреблении, слишком жаден до всевозможных благ, считает профессор. И слишком зависим от источников энергии, которой все равно не хватает. Растущая жажда потребления приводит к загрязнению планеты, в том числе в результате сжигания нефтепродуктов. И если инстинкт потребления не так просто победить, то дать человечеству экологически абсолютно чистый источник энергии вполне реально. Так родилась идея SEG (Searl Effect Generator) — генератора на Сёрл-эффекте.
Джон Сёрл
По сути, Джон Сёрл просто снабдил свою систему самодвижущихся магнитов преобразователем энергии их движения в электрическую энергию. Вращающиеся магнитные цилиндры генерировали в установленных по периметру катушках электрический ток — все было предельно просто. Но для того, чтобы генератор работал максимально эффективно, нужно было строго выдерживать вычисленные по закону квадратов параметры. А это, в свою очередь, требовало все более точного оборудования. В лаборатории стали появляться станки, прессы, оборудование для намагничивания элементов генератора, вакуумная камера для работы с неодимовым порошком, основой магнитных колец. Скромное жилище ученого постепенно превратилось в нечто среднее между лабораторией и мастерской. Зато эта мастерская была абсолютно автономной: ее питали чудо-генераторы Сёрла.
Вращающиеся магнитные цилиндры генерировали в установленных по периметру катушках электрический ток — все было предельно просто. Но для того, чтобы генератор работал максимально эффективно, нужно было строго выдерживать вычисленные по закону квадратов параметры. А это, в свою очередь, требовало все более точного оборудования. В лаборатории стали появляться станки, прессы, оборудование для намагничивания элементов генератора, вакуумная камера для работы с неодимовым порошком, основой магнитных колец. Скромное жилище ученого постепенно превратилось в нечто среднее между лабораторией и мастерской. Зато эта мастерская была абсолютно автономной: ее питали чудо-генераторы Сёрла.
Одновременно с экспериментами продолжались исследования. Ученый обнаружил, что, когда повышается скорость вращения магнитных цилиндров, генератор… теряет в весе. Чтобы исследовать этот эффект, Сёрл сделал отдельный генератор в виде диска и принудительно (с помощью внешнего двигателя) раскрутил его до большой скорости. Испытания происходили на открытом воздухе. Ко всеобщему удивлению, диск, продолжая раскручиваться, отделился от генератора и быстро поднялся вверх метров на 15. От него исходило розовое свечение; чувствовался запах озона. Неожиданно включились находившиеся вокруг радиоприемники. Генератор тем временем разогнался до еще большей скорости и резко взмыл в небо, пропав из виду. Сёрлу потребовалось время, чтобы научиться управлять тем, что потом было названо IGV (Inverse Gravity Vehicle) — антигравитационным транспортным средством. Несмотря на потерю нескольких экспериментальных дисков, которые было непонятно, как останавливать, позже Джон Сёрл научился управлять ими в полете; максимальная дальность управляемого полета — 600 километров!
Испытания происходили на открытом воздухе. Ко всеобщему удивлению, диск, продолжая раскручиваться, отделился от генератора и быстро поднялся вверх метров на 15. От него исходило розовое свечение; чувствовался запах озона. Неожиданно включились находившиеся вокруг радиоприемники. Генератор тем временем разогнался до еще большей скорости и резко взмыл в небо, пропав из виду. Сёрлу потребовалось время, чтобы научиться управлять тем, что потом было названо IGV (Inverse Gravity Vehicle) — антигравитационным транспортным средством. Несмотря на потерю нескольких экспериментальных дисков, которые было непонятно, как останавливать, позже Джон Сёрл научился управлять ими в полете; максимальная дальность управляемого полета — 600 километров!
Эксперименты профессора повторили в России, США и на Тайване. В России, например, в 1999 году под № 99122275/09 была зарегистрирована заявка на патент «устройства для выработки механической энергии». Владимир Витальевич Рощин и Сергей Михайлович Годин, по сути, воспроизвели SEG и провели ряд исследований с ним. Итогом стала констатация: можно получить без затрат 7 КВт электроэнергии; вращающийся генератор терял в весе до 40%. Казалось бы, мы стоим на пороге новой энергетики и уже почти переступили этот порог…
Итогом стала констатация: можно получить без затрат 7 КВт электроэнергии; вращающийся генератор терял в весе до 40%. Казалось бы, мы стоим на пороге новой энергетики и уже почти переступили этот порог…
Но не все так просто.
Фильм о SEG и IGV, снятый Би-Би-Си и показанный по британскому телевидению, сейчас невозможно найти ни в одном архиве. Оборудование первой лаборатории Сёрла было вывезено в неизвестном направлении, пока сам он был в тюрьме. Установка Година и Рощина просто пропала; все публикации о ней, за исключением заявки на изобретение, исчезли. Конечно, можно обвинить во всем энергетические монополии, не желающие терять доход от нефти, и спецслужбы, стремящиеся все инновации превратить в оружие, но это, наверное, лишь вершина айсберга. Айсберга человеческого сознания, которое не меняется в один момент. В этом смысле все новое должно не просто родиться, но и пройти испытание временем, заслужить свое право на существование. Должны появиться те, кто будет готов понять и принять, а не только использовать. И потому единомышленники всегда стократ важнее, чем материальная поддержка или общественное признание.
И потому единомышленники всегда стократ важнее, чем материальная поддержка или общественное признание.
Соратники
Говорят, что подобное притягивает подобное. Несмотря на то что в случае магнетизма этот принцип работает с точностью до наоборот, в жизни самого Джона Сёрла было именно так: каким-то непостижимым образом он притянул на свою орбиту удивительных людей.
Надо сказать, что сам профессор незаслуженно имеет репутацию необщительного человека. Журналисты не упускают случая упрекнуть его в нежелании делиться секретами. Джон Сёрл всегда смеется в ответ: «За свою жизнь я рассказал свои секреты более чем миллиону человек. Интересно, почему они не хотят слышать?» Действительно, последние десятилетия этот немолодой уже человек провел в поездках по миру, посетив все континенты и прочитав огромное количество лекций. Эти лекции не приносили денег, это была попытка достучаться, попытка найти единомышленников.
То, что рассказывал и показывал на своих лекциях Джон Сёрл, не оставляло сомнений в реальности и перспективности его изобретений. И вокруг него постоянно вились предприимчивые люди, готовые найти средства и возможности для организации производства чудо-генераторов. Но, увы, подобных людей совершенно не интересовало, как и почему эти генераторы работают. Их глаза загорались, когда в уме они подсчитывали возможную прибыль, и сразу же гасли, когда профессор говорил, что намерен не зарабатывать деньги, а работать ради общего блага всех людей. Хорошо, что так было не всегда.
И вокруг него постоянно вились предприимчивые люди, готовые найти средства и возможности для организации производства чудо-генераторов. Но, увы, подобных людей совершенно не интересовало, как и почему эти генераторы работают. Их глаза загорались, когда в уме они подсчитывали возможную прибыль, и сразу же гасли, когда профессор говорил, что намерен не зарабатывать деньги, а работать ради общего блага всех людей. Хорошо, что так было не всегда.
Однажды, традиционно отвечая на вопросы после лекции, Джон Сёрл обратил внимание на человека, который буквально замер и лишь глазами внимательно следил за лектором. Они долго говорили наедине, когда все ушли. Брэдли, «человек в черном», стал одним из ближайших соратников Сёрла. Работая в BKL Films, одной из голливудских компаний, он сейчас снимает фильм о Джоне Сёрле и его изобретениях. А также фиксирует на видео все детали текущих экспериментов. На всякий случай. Мало ли что.
Были и другие трогательные истории. Как-то раз после лекции профессора долго дожидалась пожилая пара. Сильно смущаясь, они подарили изобретателю… пару новых туфель. Не сильно разобравшись в теме лекции, они были поражены тем, что старая обувь такого обаятельного лектора вот-вот расстанется с подошвами. Дело в том, что для Сёрла давно стало нормой предельно экономить на еде и одежде, до последнего пенни тратить все имеющиеся средства на исследования. Билл Шервуд и его супруга стали с тех пор заботиться о профессоре и по мере сил помогать ему вести дела.
Сильно смущаясь, они подарили изобретателю… пару новых туфель. Не сильно разобравшись в теме лекции, они были поражены тем, что старая обувь такого обаятельного лектора вот-вот расстанется с подошвами. Дело в том, что для Сёрла давно стало нормой предельно экономить на еде и одежде, до последнего пенни тратить все имеющиеся средства на исследования. Билл Шервуд и его супруга стали с тех пор заботиться о профессоре и по мере сил помогать ему вести дела.
***
Сегодня у Джона Сёрла большая и дружная команда соратников в Великобритании. Он активно сотрудничает с лабораториями в США и на Тайване, ведущими параллельные исследования и разработки SEG. Несколько частных инвесторов помогли ему не только восстановить разграбленную лабораторию, но и оборудовать ее по последнему слову техники. Сам Сёрл постоянно читает лекции, дает интервью. И конечно же продолжает работать. Казалось бы, что еще нужно для счастья?
Но ему все чего-то не хватает. Он не может успокоиться. И сейчас мечтает открыть собственную среднюю школу, чтобы с детства учить детей смотреть на мир шире. Мечтает о таком образовании, которое не будет надевать на детские глаза шоры устаревших догматов, подавляя в детях исследовательский дух, а будет готовить их воспринять мир таким, какой он есть, в его бесконечной гармонии и красоте.
Мечтает о таком образовании, которое не будет надевать на детские глаза шоры устаревших догматов, подавляя в детях исследовательский дух, а будет готовить их воспринять мир таким, какой он есть, в его бесконечной гармонии и красоте.
Джон Сёрл мечтает остановить загрязнение нашей планеты, причину которого видит в неуемной жадности человека, приводящей к нехватке энергии и материальных ресурсов. Он верит, что чистый источник бесплатной электроэнергии позволит решить проблему людей, живущих за чертой бедности.
Возможно, это наивно. Возможно, не всем его мечтам суждено сбыться. Зато точно можно сказать, почему несмотря ни на какие трудности он добился и продолжает добиваться успеха. В одной из газетных публикаций его назвали «человеком, который продолжает мечтать». Лучше, наверное, и не скажешь. Живя в XXI веке, он на самом деле живет не здесь. Он живет в красивом, справедливом, совершенном мире мечты, который всеми силами пытается вернуть людям. И дело даже не в его техническом гении. Он верит и знает, что мир может быть лучше; и своей верой зажигает других.
Он верит и знает, что мир может быть лучше; и своей верой зажигает других.
Интернет-проекты о Джоне Серле, его изобретениях и его команде:
www.swallowcommand.com, www.searleffect.com, www.searlsolution.com, www.johnsearlstory.com, www.johnsearlglastonbury.co.uk, www.sisrc.com
Популярная Механика Newsland – комментарии, дискуссии и обсуждения новости.
Джон Сёрл — это английский учёный с нелёгкой судьбой и чудесными изобретениями, которые до сих пор не признаны широко, хотя и являются революционными.
Он родился в 1932 году в неблагополучной семье, а когда Джону исполнилось 4 года, он был отдан под опеку государства. В детстве Сёрл много болел и находился наедине с собой, что, как он считает, и послужило возникновению у него неординарного типа мышления, позволившего не попасть под догмы образовательной системы.
Кроме того, с детства Сёрл видел вещие сны, которые в будущем послужили необходимыми ключами для создания его изобретений.
Изобретения Сёрла
Не имея классического образования уже в конце 40х — начале 50х годов Джон Сёрл создал то, что называют «вечный двигатель» или источник экологически чистой и бесконечной энергии, который функционировал на основе уравновешенной магнитной системы. Это устройство было названо позже SEG (Searl Effect Generator), генератор эффекта Сёрла.
Эффект Сёрла базируется на магнитных полях, бесконечно вращяющих магнитные роллики вокруг намагниченных колец, за счёт чего и производится электрическая энергия (подробнее о принципах его работы, можно прочитать, например тут)
Фрагмент фильма «История Джона Сёрла» об эффекте Сёрла (англ., www.johnsearlstory.com, полностью на русском языке вы можете посмотреть фильм здесь)
Кроме того, генератор создавал вокруг себя гравитационное поле из-за чего вся конструкция теряла в весе. Так было создано второе изобретение Джона Сёрла, летательный аппарат совершенного нового вида, не требующий дозаправки и независимый от гравитации. Это устройство было названо IGV (Inverse Gravity Vehicle). Это изобретение послужило прообразом «инопланетных» летающих тарелок, а возможно и легло в основу секретных разработок по созданию таких летательных аппаратов.
Это устройство было названо IGV (Inverse Gravity Vehicle). Это изобретение послужило прообразом «инопланетных» летающих тарелок, а возможно и легло в основу секретных разработок по созданию таких летательных аппаратов.
Создание этих устройств было бы невозможным без открытия Джоном Сёрлом «Закона квадратов». Эта математическая модель, положенная в основу эффекта Сёрла, пришла к изобретателю в его снах (также как и устройство генератора), где он ещё с детства видел, так называемые магические квадраты. Магический квадрат — это таблица, заполненная числами так, что их суммы по вертикали, горизонтали и по всем диагоналям равны (самый известный сейчас из таких квадратов — это китайская схема Ло Шу, используемая при рассчётах Фен Шуй).
Джон Сёрл считает, что он далеко не является первооткрывателем этой системы. Он уверен, что описанные им законы природы, были досконально известны древним. По его словам, этим знаниям более 5000 лет.
Левитирующий диск
Эксперименты Сёрла с левитирующим диском (IGV) длились с 1963 по 1978 год, пока не закончилось финансирование этой программы. За это время левитирующий диск облетел Землю 500 раз. Полёт из Англии в Австралию длился около 30 минут.
За это время левитирующий диск облетел Землю 500 раз. Полёт из Англии в Австралию длился около 30 минут.
Фрагмент фильма «История Джона Сёрла» о левитирующем диске (англ.) (полностью на русском языке вы можете посмотреть фильм здесь)
Поскольку многие опыты с левитирующим диском освящались в прессе, последовали предложения от правительств разных стран о покупке технологии, однако Холодная война между США и СССР была в самом разгаре, и логично было предположить, что эта технология будет использована для создания вооружений. Джон Сёрл никогда не потентовал её и уничтожил все рабочие образцы в 1978 году. В 1982 году его нежиданно обвинили в краже электроэнергии и посадили в тюрьму на 10 месяцев, хотя его лаборатория питалась от собственного генератора. Лаборатория Сёрла за время его заключения была уничтожена и всё оборудование исчезло.
Выйдя из тюрьмы, Джон Сёрл оказался полным банкротом, расстался с женой, удалился от публичной жизни и был забыт прессой. Но через 4 года, в 1986, у него вновь появились единомышленники.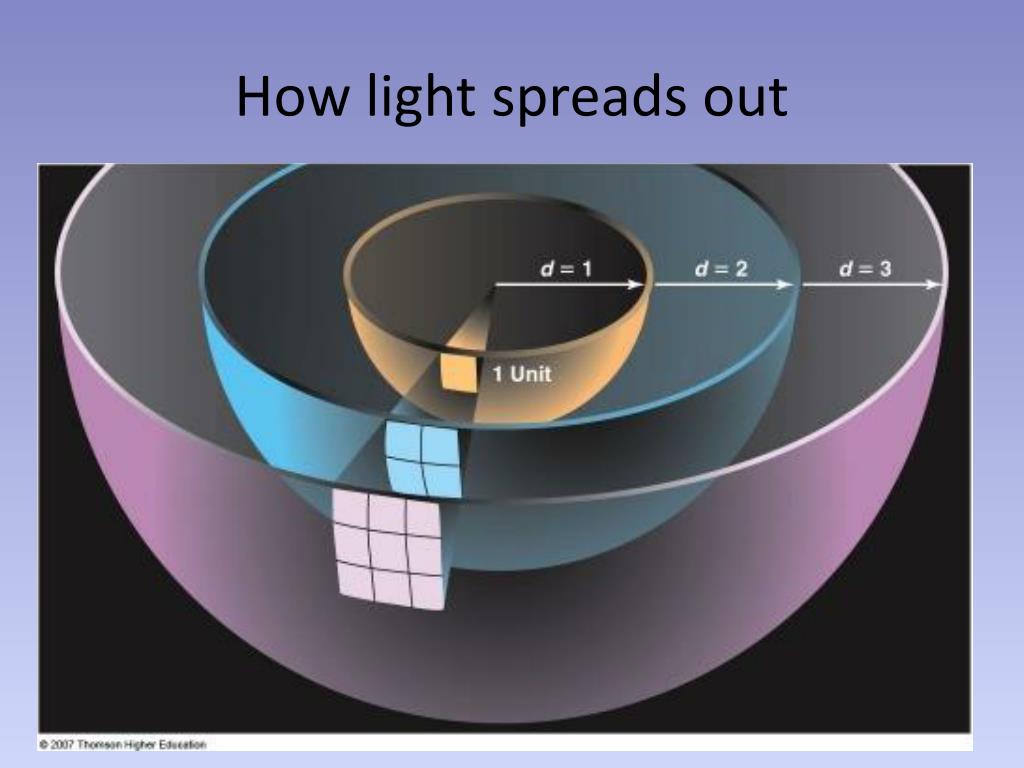 В следующие 15 Сёрл постепенно начал возобновлять свои исследования, обосновывая их теперь не только экспериментально, но и научными выкладками. Также он начал путешествовать с лекциями по миру, что делает до сих пор.
В следующие 15 Сёрл постепенно начал возобновлять свои исследования, обосновывая их теперь не только экспериментально, но и научными выкладками. Также он начал путешествовать с лекциями по миру, что делает до сих пор.
Однако он, к сожалению, заявляет, что боится публично демонстрировать свои изобретения в связи с тем, что есть угроза со стороны спецслужб. Поэтому на данный момент не существует ни одного действующего образца генератора и Джон Сёрл является единственным в мире хранителем этого секрета.
Есть учёные и в России, которые воспроизвели эффект Сёрла — Владимир Рощин и Сергей Годин (см. подробнее описание их опытов). Однако их разработки загадочным образом пропали, осталась лишь заявка на патент.
Несмотря на множество написанных Сёрлом книг с научным обоснованием эффекта, с математическими выкладками, объяснением Закона квадратов, до сих пор в мире не прекращаются споры по поводу его изобретений, и финансирование в нужном ему объёме не поступает изобретателю. Возможно это результат влияния сырьевого бизнеса или тех мировых сил, которые владеют этими технологиями.
Возможно это результат влияния сырьевого бизнеса или тех мировых сил, которые владеют этими технологиями.
В любом случае очевидно (как и в примере с Теслой, который уничтожил свои изобретения), что до сих пор человечество ещё не вышло на тот уровень духовного развития, на котором бесконечная энергия может быть благом и не послужит уничтожению нашего вида.
Это ссылки на проекты команды Джона Сёрла:
www.swallowcommand.com
www.searleffect.com
www.searlsolution.com
www.johnsearlglastonbury.co.uk
Четыре года подряд (с 1968 по 1972) каждое первое воскресенье месяца соседи Джона Сёрла и случайные прохожие наблюдали не поддающиеся объяснению явления. В руках профессора оживали, вращались и вырабатывали энергию необычные генераторы; диски диаметром от полуметра до 10 метров поднимались в воздух и совершали управляемые полеты из Лондона в Корнуолл и обратно.
Тележурналисты Би-Би-Си начали снимать документальный фильм о необыкновенных устройствах. Его показали по телевидению. Результат оказался неожиданным: местный комитет по электричеству обвинил Джона Сёрла в воровстве электроэнергии. Электрики не поверили, что его лаборатория питалась от собственного источника. Ученого посадили в тюрьму на 10 месяцев. За это время в лаборатории произошел странный пожар, но еще до него все оборудование, чертежи и таинственные изобретения исчезли. От ученого ушла жена. В 1983 году 51-летний Джон Сёрл вышел из тюрьмы полным банкротом. Что бы вы стали делать на его месте? Сёрл все начал сначала. Возможно, сказалась закалка, полученная в детстве.
| Магическим квадратом называется квадратная таблица, заполненная целыми числами таким образом, что сумма чисел в каждой строке, в каждом столбце и по каждой диагонали оказывается одинаковой. Магические квадраты были известны в Древнем Египте и Китае, один из самых древних — квадрат Ло Шу — был изображен на черепаховом панцире в 2200 году до н. |
| Джон Сёрл применил математические законы, управляющие магическими квадратами, к своим изобретениям. Он понял, что различные параметры его установок не могут быть определены произвольно, так как подчинены строгим законам древней математики. Только следование этим законам делает его установки рабочими. Прочитать о «законе квадратов» подробнее |
Джон Сёрл родился в 1932 году в Великобритании в графстве Беркшир. Его детство сложно назвать счастливым, по крайней мере, в традиционном смысле. В этом детстве не было любящих родителей; их, по сути, вообще не было. За шесть лет официальной супружеской жизни его отец семь раз уходил из семьи и вообще не уделял внимания сыну. Мама страдала психическими расстройствами, пыталась свести концы с концами и больше заботилась об устройстве собственной жизни, чем о воспитании детей.
В четыре года по решению суда Джона передали под опеку государства, и он переехал в пансион доктора Барнардо. Уже с детства он стал частым гостем в госпиталях, поскольку страдал редким нарушением вестибулярного аппарата и слуха, которое так и не смогли вылечить. Из-за этого в пожилом возрасте Сёрл начал испытывать сильнейшие головные боли.
В его детстве было много религиозных догматов и мало друзей. Никто из его приятелей, к большому сожалению Джона, не мог позволить себе презреть запреты и, связав все имеющиеся под рукой простыни, спуститься с третьего этажа запертого пансиона, чтобы почувствовать вкус свободы.
Зато в его детстве были сны. Очень непонятные сны. Ему снились числа, они объединялись в квадраты, причем строго определенным способом: так, что суммы чисел по горизонталям, вертикалям и диагоналям оказывались равными. В математике такие квадраты называются магическими.
А еще в его снах было Электричество. Сны возвращались снова и снова, но для мальчика это были всего лишь красивые картинки: он не мог понять образы, которые видел. Но зато понял, что должен связать с электричеством свою жизнь. Со временем такие сновидения стали приходить реже, но они очень влияли на его изобретательскую деятельность.
Но зато понял, что должен связать с электричеством свою жизнь. Со временем такие сновидения стали приходить реже, но они очень влияли на его изобретательскую деятельность.
Например, в 1993 году, после многолетних неудачных попыток теоретически объяснить экспериментальные данные, именно во сне Сёрл увидел Пифагора, который дал простое и красивое решение его задачи. Так родился знаменитый закон квадратов.
В 1946 году Джон Сёрл начал сам зарабатывать себе на жизнь: он устроился на работу инженером по ремонту электродвигателей. Именно тогда он сделал фундаментальное открытие природы магнетизма. Он обнаружил, что добавление небольшой компоненты переменного тока (~100 ma) радиочастоты (~10 MHz) в процессе изготовления постоянных ферритовых магнитов придает им новые неожиданные свойства. После ряда экспериментов с плоскими магнитами Сёрл сделал кольцевой магнит и несколько цилиндрических. Намагнитив их открытым способом, он помещал цилиндрические магниты на внешнюю сторону кольцевого. В этом случае легкий толчок одного из цилиндров приводил к тому, что все цилиндры начинали двигаться по кругу. И это движение не прекращалось.
В этом случае легкий толчок одного из цилиндров приводил к тому, что все цилиндры начинали двигаться по кругу. И это движение не прекращалось.
Сёрл обнаружил, что если количество роликов, расположенных вокруг, равно некоторому конкретному минимальному числу, то они начинают вращаться самостоятельно, увеличивая скорость до тех пор, пока не придут в динамическое равновесие.
Его изобретение открывало доступ к новому, доселе неизвестному способу получения энергии. Без материальных затрат на сам процесс. Но Сёрла интересовало другое: от чего зависят параметры установки? Почему при разных размерах, разном количестве роликов, разных материалах и разной намагниченности далеко не всегда воспроизводим сам эффект? Он понимал, что существуют некоторые «удачные сочетания» параметров установки, но не мог найти ключа, который бы помог понять и рассчитать эти сочетания. До открытия закона квадратов оставался один шаг.
| Схема первых опытов Сёрла с намагниченными брусками и роликами |
| Замена прямоугольного бруска на кольцевой магнит делает движение роликов более естественным |
| Классическая схема современного трехуровневого генератора на Сёрл-эффекте |
Российский вариант генератора Джона Сёрла — установка С.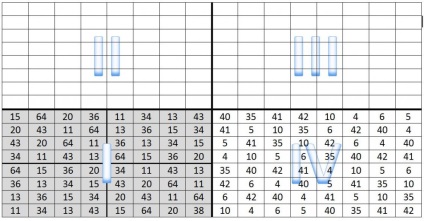 М. Година и В. В. Рощина М. Година и В. В. РощинаВ ходе эксперимента было получено до 7 кВт электроэнергии без внешнего источника питания и наблюдалась потеря до 40% веса установки |
Первые решения и понимания приходили ночью. Напряженные дневные размышления разрешались во сне, причем неожиданно: Сёрл видел искомые параметры своей установки, их численные значения объединенными в таблицы наподобие этой.
| 31 | 37 | 28 | 38 |
| 40 | 26 | 35 | 33 |
| 34 | 32 | 41 | 27 |
| 29 | 39 | 30 | 36 |
На первый взгляд это обыкновенный магический квадрат: суммы чисел по горизонталям, вертикалям и диагоналям равны. Но Джон Сёрл обнаружил, что его «обыкновенные» магические квадраты обладают необыкновенными свойствами. Для пытливого взора изобретателя и естествоиспытателя они стали, как говорит он сам, «окном в природу».
Все в природе построено на строжайших закономерностях, убежден профессор, но мы их не видим. Мы не можем их увидеть, потому что получили стандартное образование, из-за чего просто ослепли. Или надели шоры. Заполнив свое сознание стереотипами, мы утратили саму способность удивляться, искать непредвзято, перестали видеть. И воспринимаем реальность не такой, какая она есть, а такой, какой нас научили ее воспринимать.
Сёрл убежден, что его закон квадратов не открытие. Наоборот, это возрождение принципов древней математики, которым, по его словам, больше 5000 лет. Закон квадратов, подробно описанный в книге Джона Сёрла, является наглядной формой выражения существующих в природе закономерностей.
Он открывается непредвзятому исследователю и требует прежде всего решительного расставания с устоявшимися концепциями, взглядами, подходами. Многие пытались воспроизвести установки Сёрла, но получилось это у единиц: у тех, кому хватило терпения разобраться в принципах работы этих установок, кто готов был сказать: «Я знаю, что ничего не знаю» — и не побоялся расстаться со стереотипами.
Закон квадратов не объяснишь в одной статье. Но Джон Сёрл готов выслать свою книгу тому, кто пожелает в нем разобраться.
Всю свою жизнь Сёрл мечтал воплотить те образы и идеи, которые посещали его в детстве. Вначале это был пылкий юношеский интерес, замешанный на тяге к неведомому. Со временем он перерос в творческий огонь зрелого исследователя. По мере того как совершенствовались прототипы и осмыслялся закон квадратов, все четче обрисовывались и контуры той Мечты, что вела его с детства. Джон Сёрл понял, что он может быть полезен, что его талант принадлежит не столько ему, сколько нуждающимся в его работе.
Человек сегодня слишком сосредоточен на потреблении, слишком жаден до всевозможных благ, считает профессор. И слишком зависим от источников энергии, которой все равно не хватает. Растущая жажда потребления приводит к загрязнению планеты, в том числе в результате сжигания нефтепродуктов. И если инстинкт потребления не так просто победить, то дать человечеству экологически абсолютно чистый источник энергии вполне реально. Так родилась идея SEG (Searl Effect Generator) — генератора на Сёрл-эффекте.
Так родилась идея SEG (Searl Effect Generator) — генератора на Сёрл-эффекте.
| «Нет невозможного. За исключением того, что состояние вашего сознания сделает таковым». Джон Сёрл |
По сути, Джон Сёрл просто снабдил свою систему самодвижущихся магнитов преобразователем энергии их движения в электрическую энергию. Вращающиеся магнитные цилиндры генерировали в установленных по периметру катушках электрический ток — все было предельно просто.
Но для того, чтобы генератор работал максимально эффективно, нужно было строго выдерживать вычисленные по закону квадратов параметры. А это, в свою очередь, требовало все более точного оборудования.
В лаборатории стали появляться станки, прессы, оборудование для намагничивания элементов генератора, вакуумная камера для работы с неодимовым порошком, основой магнитных колец. Скромное жилище ученого постепенно превратилось в нечто среднее между лабораторией и мастерской. Зато эта мастерская была абсолютно автономной: ее питали чудо-генераторы Сёрла.
Зато эта мастерская была абсолютно автономной: ее питали чудо-генераторы Сёрла.
Одновременно с экспериментами продолжались исследования. Ученый обнаружил, что, когда повышается скорость вращения магнитных цилиндров, генератор… теряет в весе. Чтобы исследовать этот эффект, Сёрл сделал отдельный генератор в виде диска и принудительно (с помощью внешнего двигателя) раскрутил его до большой скорости. Испытания происходили на открытом воздухе. Ко всеобщему удивлению, диск, продолжая раскручиваться, отделился от генератора и быстро поднялся вверх метров на 15. От него исходило розовое свечение; чувствовался запах озона.
Неожиданно включились находившиеся вокруг радиоприемники. Генератор тем временем разогнался до еще большей скорости и резко взмыл в небо, пропав из виду. Сёрлу потребовалось время, чтобы научиться управлять тем, что потом было названо IGV (Inverse Gravity Vehicle) — антигравитационным транспортным средством. Несмотря на потерю нескольких экспериментальных дисков, которые было непонятно, как останавливать, позже Джон Сёрл научился управлять ими в полете; максимальная дальность управляемого полета — 600 километров!
Эксперименты профессора повторили в России, США и на Тайване. В России, например, в 1999 году под № 99122275/09 была зарегистрирована заявка на патент «устройства для выработки механической энергии». Владимир Витальевич Рощин и Сергей Михайлович Годин, по сути, воспроизвели SEG и провели ряд исследований с ним. Итогом стала констатация: можно получить без затрат 7 КВт электроэнергии; вращающийся генератор терял в весе до 40%. Казалось бы, мы стоим на пороге новой энергетики и уже почти переступили этот порог…
Но не все так просто.
| Создание и испытание IGV — «летающей тарелки Сёрла» |
Фильм о SEG и IGV, снятый Би-Би-Си и показанный по британскому телевидению, сейчас невозможно найти ни в одном архиве. Оборудование первой лаборатории Сёрла было вывезено в неизвестном направлении, пока сам он был в тюрьме. Установка Година и Рощина просто пропала; все публикации о ней, за исключением заявки на изобретение, исчезли.
Конечно, можно обвинить во всем энергетические монополии, не желающие терять доход от нефти, и спецслужбы, стремящиеся все инновации превратить в оружие, но это, наверное, лишь вершина айсберга. Айсберга человеческого сознания, которое не меняется в один момент. В этом смысле все новое должно не просто родиться, но и пройти испытание временем, заслужить свое право на существование.
Должны появиться те, кто будет готов понять и принять, а не только использовать. И потому единомышленники всегда стократ важнее, чем материальная поддержка или общественное признание.
Говорят, что подобное притягивает подобное. Несмотря на то что в случае магнетизма этот принцип работает с точностью до наоборот, в жизни самого Джона Сёрла было именно так: каким-то непостижимым образом он притянул на свою орбиту удивительных людей.
Надо сказать, что сам профессор незаслуженно имеет репутацию необщительного человека. Журналисты не упускают случая упрекнуть его в нежелании делиться секретами. Джон Сёрл всегда смеется в ответ: «За свою жизнь я рассказал свои секреты более чем миллиону человек. Интересно, почему они не хотят слышать?» Действительно, последние десятилетия этот немолодой уже человек провел в поездках по миру, посетив все континенты и прочитав огромное количество лекций. Эти лекции не приносили денег, это была попытка достучаться, попытка найти единомышленников.
То, что рассказывал и показывал на своих лекциях Джон Сёрл, не оставляло сомнений в реальности и перспективности его изобретений. И вокруг него постоянно вились предприимчивые люди, готовые найти средства и возможности для организации производства чудо-генераторов. Но, увы, подобных людей совершенно не интересовало, как и почему эти генераторы работают. Их глаза загорались, когда в уме они подсчитывали возможную прибыль, и сразу же гасли, когда профессор говорил, что намерен не зарабатывать деньги, а работать ради общего блага всех людей. Хорошо, что так было не всегда.
Однажды, традиционно отвечая на вопросы после лекции, Джон Сёрл обратил внимание на человека, который буквально замер и лишь глазами внимательно следил за лектором. Они долго говорили наедине, когда все ушли. Брэдли, «человек в черном», стал одним из ближайших соратников Сёрла. Работая в BKL Films, одной из голливудских компаний, он сейчас снимает фильм о Джоне Сёрле и его изобретениях. А также фиксирует на видео все детали текущих экспериментов. На всякий случай. Мало ли что.
Были и другие трогательные истории. Как-то раз после лекции профессора долго дожидалась пожилая пара. Сильно смущаясь, они подарили изобретателю… пару новых туфель. Не сильно разобравшись в теме лекции, они были поражены тем, что старая обувь такого обаятельного лектора вот-вот расстанется с подошвами. Дело в том, что для Сёрла давно стало нормой предельно экономить на еде и одежде, до последнего пенни тратить все имеющиеся средства на исследования. Билл Шервуд и его супруга стали с тех пор заботиться о профессоре и по мере сил помогать ему вести дела.
***
Сегодня у Джона Сёрла большая и дружная команда соратников в Великобритании. Он активно сотрудничает с лабораториями в США и на Тайване, ведущими параллельные исследования и разработки SEG. Несколько частных инвесторов помогли ему не только восстановить разграбленную лабораторию, но и оборудовать ее по последнему слову техники. Сам Сёрл постоянно читает лекции, дает интервью. И конечно же продолжает работать. Казалось бы, что еще нужно для счастья?
Но ему все чего-то не хватает. Он не может успокоиться. И сейчас мечтает открыть собственную среднюю школу, чтобы с детства учить детей смотреть на мир шире. Мечтает о таком образовании, которое не будет надевать на детские глаза шоры устаревших догматов, подавляя в детях исследовательский дух, а будет готовить их воспринять мир таким, какой он есть, в его бесконечной гармонии и красоте.
Джон Сёрл мечтает остановить загрязнение нашей планеты, причину которого видит в неуемной жадности человека, приводящей к нехватке энергии и материальных ресурсов. Он верит, что чистый источник бесплатной электроэнергии позволит решить проблему людей, живущих за чертой бедности.
Возможно, это наивно. Возможно, не всем его мечтам суждено сбыться. Зато точно можно сказать, почему несмотря ни на какие трудности он добился и продолжает добиваться успеха. В одной из газетных публикаций его назвали «человеком, который продолжает мечтать». Лучше, наверное, и не скажешь. Живя в XXI веке, он на самом деле живет не здесь. Он живет в красивом, справедливом, совершенном мире мечты, который всеми силами пытается вернуть людям. И дело даже не в его техническом гении. Он верит и знает, что мир может быть лучше; и своей верой зажигает других.
Интернет-проекты о Джоне Серле, его изобретениях и его команде:
www.swallowcommand.com, www.searleffect.com, www.searlsolution.com, www.johnsearlstory.com,www.johnsearlglastonbury.co.uk, www.sisrc.com
Видео с рассказом Джона Сёрла о SEG:
Закон обратных квадратов Википедия
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле.{2}}) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.Проявления
Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном не точечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данные массивные тела, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу [1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы[2], а также отдал дань уважения Буллиальду.
Электростатика
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения
Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — 2,6-кратное увеличение расстояния влечёт 6,7-кратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:
- Ea,Ba∝1r{\displaystyle E_{a},B_{a}\propto {1 \over r}}
Закон обратных квадратов может быть применён только в случае точечных источников света (например, фонарях): весьма распространённые в помещениях цилиндрические лампы дневного света, тем более помещённые в ряд, не являются точечными источниками (пока их характерный размер не является пренебрежимо малым), и поэтому к ним нельзя применять закон обратных квадратов (пока их характерный размер велик, к ним применим закон обратного расстояния), а равномерно светящаяся плоская поверхность даёт постоянную освещённость на расстояниях, малых по сравнению с её размером.
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Приложения в теории поля
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
Примечания
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.
ⓘ Закон обратных квадратов. В физике закон обратных квадратов
2.1. Проявления Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.Если распределение масс в некотором материальном не точечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса материальная точка.
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данные массивные тела, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо Булиальдом. Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы, а также отдал дань уважения Буллиальду.
ⓘ Закон квадрата — куба представляет собой принцип, применяемы
1. Техника
Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится пропорционально коэффициенту увеличения в третьей степени, в то время как площадь его поверхности — квадрату масштабного множителя. Это должно означать, что в том случае, если сегменту поверхности увеличенного в размерах объекта сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление
Рассмотрим простой пример — тело массой m {\displaystyle m} имеет ускорение a {\displaystyle a} и площадь поверхности S {\displaystyle S}, на которую действует ускоряющая сила.{2}\cdot S}}\\&=x{\frac {ma}{S}}\\&=x\cdot T\end{aligned}}}
Таким образом, при простом увеличении размеров объекта с сохранением того же самого материала конструкции плотности, и при том же самом ускорении, давление, производимое им на поверхность, увеличится во столько же раз. Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.
Это и есть объяснение тому, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях, и почему есть пределы высоты строительства высотных зданий. Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление.
Закон квадратов
«В одном пространстве не может быть разной материи,
но можно и другое дело в в разных помещениях одновременно,
или иметь разную материю в одном и том же пространстве в разное время ».
Проф. Джон Р. Р. Серл
Закон Площадей
История магических или латинских квадратов насчитывает тысячи лет, начиная с пирамид. Древнего Египта, и, возможно, даже раньше первых китайских династий.Фактически, сегодня китайцы все еще используют магические квадраты для обрезки деревьев бонсай в соответствии с правильными математическими соотношениями природы. Понимая эти законы природы, можно утверждать, что Вселенная существует согласно точным математическим законам.
Закон квадратов (LOS) или магические квадраты — это не новая технология, а старая технология, которая возродилась после того, как Джон Серл в молодом возрасте разработал ее независимо и обнаружил, что его пронумерованная матрица имеет трехмерные свойства, которые могут моделировать квантовые энергетические состояния массы во времени и пространстве.
Есть три группы квадратов — первая, вторая и третья, других быть не может. Квадраты первой группы состоят из нечетных чисел. Все четные числа, которые делятся на четыре, входят во вторую группу. Все остальные четные числа, не делящиеся на четыре, находятся в третьей группе.Когда правильная матрица случайных чисел в сумме дает одно и то же значение линии поперек, вниз и по диагонали, тогда это так же верно, как и физика в отношении известных законов сохранения, где энергия не создается и не уничтожается, но может быть преобразована из одного форма к другому.
Матрица LOS точно демонстрирует эти консервативные законы путем правильного преобразования случайных чисел квадратов в значения строк, которые в сумме дают одно и то же значение в любом направлении, что приводит к неслучайному или однородному состоянию суммирования без создания большего или меньшего значения, чем общая сумма куба.
ТехнологияLOS вместе с соответствующей стимуляцией представляет собой трансформационное решение для преобразования случайного квантового энергетического состояния в полезное неслучайное (однородное) состояние резонанса и когерентного движения электронов в атомной решетке или, проще говоря, может формировать электрические токи из хаоса.
Примечание: Первый закон термодинамики гласит, что и работа, и тепло являются формами энергии, и что полная энергия сохраняется, как показывает матрица LOS с ее точным суммированием; SEG функционирует в полном соответствии с этим законом.
Также обратите внимание: Где, как Второй закон термодинамики гласит, что в «закрытой системе» беспорядок растет и для работы доступно меньше энергии. SEG функционирует на основе «открытой системы», как и жизнь, ветряные мельницы, гидроэлектростанции, солнечные батареи и т. Д.
Дело в том, что 2 -й закон НЕ распространяется на «открытые системы»; это типичная ошибка самопровозглашенных экспертов, которые говорят об энергетическом цикле SEG иначе.
Квадрат четыре графически проиллюстрирован в трехмерном виде; добавлено по любому направлению сумм 34.
Ядро квадрата — это куб 2×2, который представляет собой ядро квадрата.
Щелкните изображение или здесь, чтобы просмотреть преобразование случайных результатов в однородные.
Для эффективной работы SEG различные материалы или элементы должны иметь определенную природу, вес и размеры. Кроме того, он должен быть настроен таким образом, чтобы он отвечал требованиям LOS с высоким уровнем точности материала на основе строгих математических критериев проектирования.
Профессор Джон Серл написал много книг на тему «Закон квадратов» и использует эти квадратные матрицы и их законы для построения генератора эффекта Серла.Он объяснил уникальные свойства Закона Площади и много ездил с лекциями о нем в школах, конгрессах и университетах многих стран.
Ниже приведены примеры таблиц истинности для квадратов с 4 по 25;
это отрывки из одной из его книг серии .
Щелкните здесь, чтобы посмотреть видео, где профессор Серл работает с квадратами на конференции Tesla 2010 года.
> Далее
Формула закона обратных квадратов
Формула закона обратных квадратовЗакон обратных квадратов описывает интенсивность света на разном расстоянии от источника света.Все источники света разные, но интенсивность меняется одинаково. Интенсивность света обратно пропорциональна квадрату расстояния. Это означает, что по мере увеличения расстояния от источника света интенсивность света равна значению, умноженному на 1 / d 2 ,. Символ пропорциональности используется, чтобы показать, как они соотносятся. Связь между интенсивностью света на разных расстояниях от одного и того же источника света можно найти, разделив один от другого.Формула для этого показана ниже. Видимый свет является частью электромагнитного спектра, и закон обратных квадратов верен для любых других волн или лучей в этом спектре, например радиоволн, микроволн, инфракрасного и ультрафиолетового света, рентгеновских лучей и гамма-лучей. Интенсивность видимого света измеряется в единицах кандел, , а интенсивность других волн измеряется в ваттах на квадратный метр (Вт / м 2 ).
Пропорционально:
I = сила света ( кандела , Вт / м 2 )
означает «пропорционально»
d = расстояние от источника света ( м )
Интенсивность на разных дистанциях:
I 1 = сила света на расстоянии 1
I 2 = сила света на расстоянии 2
d 1 = расстояние 1 от источника света ( м )
d 2 = расстояние 2 от источника света ( м )
Формула закона обратных квадратов Вопросы:
1) Если яркий фонарик имеет силу света 15.0 кандела на расстоянии 1,00 м от объектива, какая сила фонарика 100,0 м от объектива?
Ответ: Интенсивность на дальней дистанции можно найти по формуле:
Если d 1 = 1,00 м от линзы и d 2 = 100,0 м от линзы, то I 1 = 15,0 кандела , и нам нужно найти Я 2 .Для этого необходимо переформулировать уравнение:
Теперь подставьте известные значения в уравнение:
I 2 = (0,0001) (15,0 кандела )
I 2 = 0,0015 кандела
Сила света фонарика на расстоянии 100,0 м составляет 0,0015 кандела .
2) Интенсивность радиосигнала составляет 0,120 Вт / м 2 на расстоянии 16,0 м от небольшого передатчика. Какая интенсивность сигнала 4,00 м от передатчика?
Ответ: Интенсивность на ближнем расстоянии можно найти по формуле:
Если d 1 = 4,00 м от преобразователя и d 2 = 16,0 м от преобразователя, то
I 2 = 0.120 Вт / м 2 , и нам нужно найти I 1 . Для этого необходимо переформулировать уравнение:
Теперь подставьте известные значения в уравнение:
I 1 = (16,0) (0,120 Вт / м 2 )
I 1 = 1,92 / м 2
Интенсивность радиосигнала 4.00 м от передатчика 1,92 Вт / м 2 .
Формула закона обратных квадратов
Закон Кулона и закон обратных квадратов
Откуда берется заряд?
Хотя на самом деле нет точного ответа на вопрос, откуда берется заряд — мы определили, что заряд — это то, что производит электрическое поле.Статические электроны заряжены, и их заряд квантуется, что означает целое число. Мы говорим, что заряд электрона равен -e.
Из предыдущего раздела об электрических зарядах и электрических полях мы знаем, что два разных заряда будут притягиваться каждый. Сила притяжения и электрическое поле будут увеличиваться по мере приближения двух зарядов друг к другу. В случае двух одинаковых зарядов будет сила отталкивания, когда заряды сближаются, и сила будет уменьшаться, когда заряды разойдутся дальше друг от друга.Это потому, что электрические заряды создают электрическое поле. Если два поля существуют в одном и том же пространстве одновременно, то эти два поля действуют друг на друга. Сила, которую они оказывают друг на друга, называется силой Кулона или электростатической силой (электростатика означает электрические заряды без какого-либо движения).
Закон Кулона объясняет, насколько большой будет сила.
Закон Кулона объясняет, что Сила F зависит от отношения q 1 , q 2 , 1 / r 2 .
q 1 и q 2 — это масштабы каждого заряда, а r — расстояние между двумя электрическими зарядами. K c — постоянная величина, которая не меняется. K c называется постоянной силы Кулона или постоянной электростатической силы.
Почему закон Кулона связан с законом обратных квадратов?
Соотношение между силой толчка или притяжения (F) и расстоянием между частицами (r) следует закону обратных квадратов аналогично тому, как это показано для силы тяжести, магнетизма и силы света.Закон обратных квадратов означает, что по мере увеличения расстояния сила (F) будет уменьшаться в соотношении 1 / r 2 . Для получения дополнительной информации о законе обратных квадратов см. Лабораторные работы по математическим отношениям в науке.
Почему эта Сила обратно пропорциональна квадрату расстояния между ними?
Все эти законы обратных квадратов связаны с площадью поверхности сферы. Например, возьмем луч света от источника S (показанного выше)
Примечание: Площадь поверхности сферы — A = 4 * pi * r 2 .
Предположим, что центр источника света (S) излучает свет. Окружите это сферой. По мере роста сферы количество света, падающего на ее поверхность, уменьшается на r 2 .
Проверьте свой Понимание:
square-law — перевод — англо-испанский словарь
en Я не знал о законе обратных квадратов распространения света.
OpenSubtitles2018.v3 es Se aplicarán los siguientes coeficientes de atribución a las cantidades indicadas en los Certificados de exportación solicitados para el período comprendido entre el # de julio de # y el # de junio de # en relaciónos en el productos apartado # del Reglamento (CE) №и расстояние измерения таково, что применяется закон обратных квадратов расстояния;
EurLex-2 es Es mejor que vaya adentroen Прежде всего, свет следует знаменитому закону обратных квадратов.
Common crawl es ¿Por qué? Porque no confiamos en los extrañosen Вы были правы насчет закона обратных квадратов.
OpenSubtitles2018.v3 es Su cama no install hechaen Я не знал о законе обратных квадратов распространения света
opensubtitles2 es ¿Estás bien?en Закон обратных квадратов.
OpenSubtitles2018.v3 es BIBLIOGRAFÍAen Его идеи о гравитации и его притязания на приоритет закона обратных квадратов изложены ниже.
WikiMatrix es Bueno, eso es lo que tú tienes en mente. En serio?ru Из-за закона обратных квадратов излучение в перигелии составляет примерно 106,9% энергии в афелии.
WikiMatrix es Es la primera vez que ve este tipo de cosas?ru Это закон обратных квадратов.
OpenSubtitles2018.v3 es No es un buen momentoen Проблема Кеплера важна в небесной механике, поскольку ньютоновская гравитация подчиняется закону обратных квадратов.
WikiMatrix es Pero el que no arriesga, no ganaru Он показал, что закон обратных квадратов для гравитации объясняет эллиптические орбиты планет и продвигает закон всемирного тяготения.
WikiMatrix es No me importaru После того, как эти объяснения были отброшены, некоторые физики пришли к более радикальной гипотезе о том, что закон обратных квадратов Ньютона неверен.
WikiMatrix es Tal vez juegue con ellaen Проблема Кеплера также важна для движения двух заряженных частиц, поскольку закон электростатики Кулона также подчиняется закону обратных квадратов.
WikiMatrix es No looraremos guerrillerosru Эффект красного X затем увеличивается по закону квадратного корня из суммы квадратов, тем самым изолируя основную причину.
WikiMatrix es ¿Por qué no me sorprende?ru Поскольку звук издается в воздухе вдоль этой колонны, он не подчиняется закону обратных квадратов, согласно которому он падает примерно на две трети каждый раз, когда вы удваиваете расстояние:
QED es Capsaicinaen Аналоговые методы создания плоскости преобразования Хартли сначала с помощью света, а затем с помощью микроволн были продемонстрированы в лаборатории и позволили определить электромагнитную фазу с помощью квадратичных детекторов.
WikiMatrix es Llámame locoru Энергия, которую солнечные батареи могут извлекать из солнечного света, уменьшается в соответствии с законом обратных квадратов: по мере увеличения расстояния от Солнца мощность, доступная космическому кораблю, использующему солнечную энергию, уменьшается.
UN-2 es ¿sacó algo del homicidio?ru Как мы можем согласовать законы физики с нашим повседневным опытом?
OpenSubtitles2018.v3 es Necesitamos que García расследует множество сайтов с видеоru Это закон квадратного куба.
OpenSubtitles2018.v3 es No te preocupes por las cobras, que Chris está pendienteru Вы игнорируете закон квадратных кубов.
OpenSubtitles2018.v3 es Ni siquiera estoy en el último cursoen Закон о квадрате куба Галилея гласит, что его вес будет 27
QED es Voy a metérsela a Michelleen Расчет выполняется как квадрат корень из суммы квадратов («Гауссов закон распространения ошибок»).
eurlex-diff-2018-06-20 es ¡sólo sal de mi vida!Закон косинусов
Для любого треугольника:
a , b и c — боковые стороны. C — угол противоположной стороны c |
Закон косинусов (также называемый правилом косинусов ) гласит:
c 2 = a 2 + b 2 — 2ab cos (C)
Это помогает нам решать некоторые треугольники.Посмотрим, как им пользоваться.
Пример: Какова длина стороны «c» …?
Мы знаем угол C = 37º, а стороны a = 8 и b = 11
Закон косинусов говорит: c 2 = a 2 + b 2 — 2ab cos (C)
Введите известные нам значения: c 2 = 8 2 + 11 2 — 2 × 8 × 11 × cos (37º)
Выполните некоторые вычисления: c 2 = 64 + 121 — 176 × 0,798…
Дополнительные вычисления: c 2 = 44.44 …
Извлеките квадратный корень: c = √44,44 = 6,67 с точностью до 2 знаков после запятой
Ответ: c = 6,67
Как помнить
Как можно запомнить формулу?
Что ж, полезно знать, что это теорема Пифагора с кое-чем дополнительным, чтобы она работала для всех треугольников:
Теорема Пифагора:
(только для прямоугольных треугольников) a 2 + b 2 = c 2
Закон косинусов:
(для всех треугольников) a 2 + b 2 — 2ab cos (C) = c 2
Итак, чтобы запомнить:
- думаю « abc »: a 2 + b 2 = c 2 ,
- , затем 2 nd « abc «: 2ab cos ( C ),
- и сложите их вместе: a 2 + b 2 — 2ab cos (C) = c 2
Когда использовать
Закон косинусов полезно найти:
- третья сторона треугольника, когда мы знаем две стороны и угол между ними (как в примере выше)
- углы треугольника, когда мы знаем все три стороны (как в следующем примере)
Пример: что такое угол «C»…?
Сторона длины «8» противоположна углу C , поэтому это сторона c . Две другие стороны: a и b .
Теперь давайте поместим то, что мы знаем, в Закон косинусов :
Начнем с: c 2 = a 2 + b 2 — 2ab cos (C)
Вставьте a, b и c: 8 2 = 9 2 + 5 2 — 2 × 9 × 5 × cos (C)
Вычислить: 64 = 81 + 25 — 90 × cos (C)
Теперь мы используем наши навыки алгебры, чтобы переставить и решить:
Вычтем 25 с обеих сторон: 39 = 81 -90 × cos (C)
Вычтем 81 из обеих частей: −42 = −90 × cos (C)
Поменять местами стороны: −90 × cos (C) = −42
Разделим обе части на −90: cos (C) = 42/90
Обратный косинус: C = cos −1 (42/90)
Калькулятор: C = 62.2 ° (с точностью до 1 знака после запятой)
В других формах
Более простая версия для углов
Мы только что видели, как найти угол, когда мы знаем три стороны. Это заняло довольно много шагов, поэтому проще использовать «прямую» формулу (которая представляет собой просто перестановку формулы c 2 = a 2 + b 2 — 2ab cos (C) формулы). Может быть в любой из этих форм:
cos (Кл) = а 2 + б 2 — в 2 2ab
cos (А) = б 2 + в 2 — а 2 2bc
cos (В) = с 2 + а 2 — б 2 2ca
Пример: найти угол «C» по закону косинусов (угловая версия)
В этом треугольнике мы знаем три стороны:
Используйте Закон косинусов (угловая версия), чтобы найти угол C :
cos C = (a 2 + b 2 — c 2 ) / 2ab
= (8 2 + 6 2 -7 2 ) / 2 × 8 × 6
= (64 + 36 — 49) / 96
= 51/96
= 0.53125
C = cos −1 (0,53125)
= 57,9 ° с точностью до одного десятичного знака
Версии для a, b и c
Кроме того, мы можем переписать формулу c 2 = a 2 + b 2 — 2ab cos (C) в форму 2 = и b 2 =.
Вот все три:
a 2 = b 2 + c 2 — 2bc cos (A)
b 2 = a 2 + c 2 — 2ac cos (B)
c 2 = a 2 + b 2 — 2ab cos (C)
Но проще запомнить форму « c 2 =» и изменить буквы по мере необходимости!
Как в этом примере:
Пример: найти расстояние «z»
Буквы разные! Но это не имеет значения.Мы можем легко заменить x на a, y на b и z на c
Начнем с: c 2 = a 2 + b 2 — 2ab cos (C)
x для a, y для b и z для cz 2 = x 2 + y 2 — 2xy cos (Z)
Введите известные нам значения: z 2 = 9,4 2 + 6,5 2 — 2 × 9,4 × 6,5 × cos (131º)
Вычислить: z 2 = 88,36 + 42,25 — 122,2 × (-0,656 …)
z 2 = 130,61 + 80.17 …
z 2 = 210,78 …
z = √210,78 … = 14,5 с точностью до 1 десятичного знака.
Ответ: z = 14,5
Вы заметили, что cos (131º) отрицателен, и это меняет последний знак в вычислении на + (плюс)? Косинус тупого угла всегда отрицателен (см. Единичный круг).
Условия использования для разработчиков
Последнее обновление: 12 ноября 2019 г.
Мы добавили аннотации в серые поля ниже, чтобы выделить определенные части наших условий и помочь вам при их чтении.Аннотации — не резюме, поэтому, пожалуйста, найдите время, чтобы прочитать все!
Настоящие Условия использования Square Developer («Условия для разработчиков») являются юридическим соглашением между вами («вы», «ваш») и Square, Inc. («Square», «мы», «наш» или «нас») управление использованием вами файлов комплекта разработки программного обеспечения (SDK) Square, инструментов, программ и служебных программ, а также любых подключаемых модулей или других программных интерфейсов приложений («API»), примеров кода (включая среды выполнения и библиотеки) и связанной документации (вместе «Инструменты разработчика»).Используя Инструменты разработчика и связанные с ними материалы, предоставленные вам, вы соглашаетесь соблюдать настоящие Условия для разработчиков, а также любую документацию и инструкции, сопровождающие Инструменты разработчика, Общие условия обслуживания, Уведомление о конфиденциальности и все другие условия и политики, и руководящие принципы, применимые к вашему использованию, включая, помимо прочего, Условия оплаты, если вы принимаете платежи через Square.
1. Ваш доступ и использование Square Developer Tools и Content
Используйте наши инструменты и услуги для разработчиков только в соответствии с настоящими условиями и в нашей документации.Вы несете ответственность за использование наших услуг. Мы можем изменить или прекратить предоставление этих услуг в любое время.
Вы можете использовать Инструменты разработчика для доступа к информации, созданной или хранимой в учетной записи Square («Контент»), и использовать сервисы обработки платежей Square в связи с приложениями, веб-сайтами, продуктами или услугами, которые вы используете и которые предлагаете и которые взаимодействуют с Инструментами разработчика (« Ваша служба »). Любая обработка платежей, разрешенная вами через Square API, требует наличия учетной записи Square и регулируется Общими условиями.Вы несете исключительную ответственность, и Square снимает с себя всякую ответственность за Ваш Сервис.
Использование вами Инструментов разработчика и Содержимого подлежит определенным ограничениям на доступ, вызовы и использование, как указано в настоящих Условиях для разработчиков, в документации Square, прилагаемой к таким Инструментам разработчика, или иным образом, предоставленным вам Square. Если Square назначает вам учетные данные разработчика или идентификаторы клиентов, вы должны использовать их с соответствующими инструментами разработчика. Вы не будете искажать или маскировать свою личность или личность своей службы при использовании инструментов разработчика или учетных записей разработчиков.Если Square считает, что вы пытались превысить или обойти эти ограничения, ваша возможность использовать Инструменты и Контент разработчика может быть временно или навсегда заблокирована.
Square может обновить Инструменты разработчика в любое время и может прекратить поддержку предыдущих версий Инструментов разработчика по собственному усмотрению Square. Square приложит разумные усилия, чтобы уведомить вас о прекращении поддержки той или иной версии Инструментов разработчика.
Если Ваш Сервис позволяет владельцам учетных записей Square («Продавцы Square») получать доступ к их Контенту, Продавцам Square необходимо предоставить возможность входа в Square через протокол OAuth.Продавцам без учетной записи Square должна быть предоставлена возможность создать новую учетную запись Square, как это предусмотрено Square. Вы не будете запрашивать или хранить пароли Square.
Вы будете использовать Инструменты разработчика и управлять своими Сервисами, которые получают доступ к Инструментам разработчика только в соответствии с законом (включая, помимо прочего, законы, касающиеся импорта или экспорта данных или программного обеспечения, конфиденциальности или безопасности данных, если применимо). Вы не будете использовать Инструменты разработчика для поощрения или продвижения незаконной деятельности.Вы получите доступ к применимым Инструментам разработчика только в соответствии с инструкциями по реализации и другими требованиями, указанными в документации к таким Инструментам разработчика или иным образом, время от времени предоставляемым Square.
Вы несете полную ответственность за безопасность данных на вашем сайте и обрабатываемых с помощью ваших Сервисов. Вы соглашаетесь с тем, что вы и ваши Сервисы в любое время, за счет ваших усилий и средств, будете соответствовать Стандарту безопасности данных индустрии платежных карт (PCI DSS), Стандарту безопасности данных платежных приложений (PA-DSS), если применимо, и всем применимые законы, касающиеся конфиденциальности данных и кибербезопасности.По запросу Square вы незамедлительно предоставите нам документацию, подтверждающую ваше соответствие требованиям PCI DSS, PA-DSS и / или применимого законодательства. Вы будете использовать Инструменты разработчика и получать к ним доступ в соответствии с документацией и инструкциями, предоставленными Square, и ни при каких обстоятельствах вы не будете хранить, обрабатывать или передавать номер счета держателя карты, дату истечения срока действия или CVV2, за исключением случаев, описанных в этой документации. Кроме того, вы не можете раскрывать информацию о карте третьим лицам, кроме как в связи с обработкой транзакции по карте, запрошенной вашим клиентом в рамках Сервиса, и в соответствии с PCI DSS и применимым законодательством.
Вы предоставляете Square платную, бесплатную, отзывную, всемирную, неисключительную, не подлежащую передаче лицензию на использование ваших Сервисов для тестирования, проверки или других связанных целей, чтобы гарантировать соответствие ваших Сервисов настоящим Условиям для разработчиков. Вы можете отозвать эту лицензию в любое время, направив нам письменное уведомление. Если вы отзовете эту лицензию, ваш доступ к Инструментам разработчика и Контенту будет немедленно прекращен.
Если ваша Услуга предоставляется вашим клиентам за плату, взимаемая вами плата будет указана отдельно от платы, взимаемой Square за ее услуги.
Если вы используете Инструменты разработчика для доступа и использования Apple Pay Web API и Apple Pay Platform, вы должны сначала принять Условия и положения для интернет-торговцев платформы Apple Pay.
Если вы используете Инструменты разработчика для доступа и использования Google Pay API, вы должны сначала принять Условия использования Google Pay API.
Вы можете использовать определенные API Square для облегчения сбора платежей Square от Square Sellers.Там, где это возможно, API Square могут использоваться для облегчения взимания сборов с Square Sellers. Вы несете ответственность за четкое и точное описание сборов, которые вы собираете с Square Sellers, и получение всех необходимых разрешений в связи с этими сборами, и вы должны уведомить Square Sellers до внесения каких-либо изменений в эти сборы. Если вы используете Square API, чтобы взимать комиссию с Square Sellers за каждую транзакцию, вы разрешаете Square действовать в качестве вашего агента для ограниченных целей удержания, получения и выплаты платежей, состоящих из и / или полученных от обработка платежей такими продавцами Square Sellers продолжается.Вы признаете и соглашаетесь с тем, что Square не действует от вашего имени или от имени Продавцов Square в качестве службы денежных переводов или бизнеса по оказанию денежных услуг (как эти условия обычно толкуются в соответствии с применимым законодательством) или в любом другом подобном качестве, за исключением случаев, прямо предусмотренных в настоящих Условиях. Условия для разработчиков. Вы признаете и соглашаетесь с тем, что будете нести единоличную ответственность за сбор и перечисление любым налоговым органам любых налогов с продаж, добавленной стоимости или аналогичных налогов для ваших Услуг, а также разрешение любых споров, которые могут возникнуть между вами и любым Продавцом Square, который использует ваши услуги. .
2. Запрет на доступ к инструментам разработчика
Запрещается перепродавать или сублицензировать наши инструменты или контент для разработчиков, а также не создавать сервис, который делает то же самое, что и мы.
Вы не будете и не разрешите другой стороне:
продавать, сдавать в аренду, сдавать в аренду, сублицензировать, распространять или синдицировать доступ к Инструментам разработчика или к Контенту, кроме вашего собственного; или
создать Сервис, который функционирует практически так же, как Инструменты разработчика или любой сервис Square.
3. Запреты на контент.
Не открывайте и не храните информацию о продавце Square, если этот продавец не разрешает это. Если разрешено, не злоупотребляйте своим доступом и объясните продавцу, почему и как вы будете использовать его контент. Удалите и прекратите доступ к контенту, если продавец больше не хочет, чтобы ваше приложение получало доступ к его информации.
Вы не будете и не разрешите другой стороне без явного согласия Продавца Square:
очищать, получать доступ, загружать, хранить, создавать базы данных или иным образом создавать постоянные копии любого Контента Square Seller, включая Контент, связанный или предоставленный любым клиентом любого Square Продавца;
копировать, переводить, изменять, создавать производные работы, продавать, сдавать в аренду, сублицензировать, распространять или публично демонстрировать любой такой Контент Square Seller; или
делать заявления или представлять себя или свою Службу в качестве агента Square.
Кроме того, вы и ваша Служба должны четко обозначать ее цель Продавцу Square и не вводить в заблуждение или обманывать Продавцов Square в отношении функций, которые ваш Сервис выполняет от имени Продавца Square, или того Контента, к которому ваша Служба может получить доступ, хранить и манипулировать.
Если Продавец, который использует ваше Приложение, отменяет ваше разрешение на доступ к своему Контенту («Отзыв Продавца»), вы соглашаетесь: а) немедленно прекратить доступ к Отзывному Содержимому Продавцу, и б) удалить любой и весь Отзыв Продавца Контент из ваших систем.Вы также соглашаетесь с тем, что Square имеет право в любое время проверить ваше удаление Контента, отозванного Продавцом, в том числе после закрытия вашей учетной записи Square.
4. Подача материалов
У нас есть широкие лицензионные права на контент, который вы отправляете или показываете через нашу службу. Мы будем использовать ваш контент только для предоставления наших услуг и в соответствии с нашим уведомлением о конфиденциальности. Вы соглашаетесь с тем, что у вас есть права, необходимые для лицензирования контента, который вы отправляете через наши службы.
Определенные Инструменты разработчика позволяют отправлять Контент, и, за исключением случаев, прямо предусмотренных в настоящих условиях, Square не приобретает никаких прав на интеллектуальную собственность, которые вы или Продавцы Square имеете на Контент, который вы отправляете с помощью Инструментов разработчика. Отправляя, размещая или отображая контент в Инструменты разработчика или из них через Ваш Сервис, вы даете Square бессрочную, безотзывную, всемирную, бесплатную и неисключительную лицензию на воспроизведение, адаптацию, изменение, перевод, публикацию, публичное исполнение, публично отображать и распространять такой Контент.Однако Square будет использовать такой Контент только для того, чтобы позволить Square предоставлять свои услуги, Инструменты разработчика и только в соответствии с Уведомлением о конфиденциальности и другими применимыми политиками. Вы заявляете, что перед отправкой контента через Инструменты разработчика и Ваш Сервис у вас есть необходимые права (включая любые необходимые права от Square Sellers) для предоставления нам лицензии.
5. Использование квадратных знаков
Нам принадлежат логотипы и товарные знаки Square, которые мы предоставляем через наши службы, и вы можете использовать их на наших условиях.Мы можем изменить наши знаки в любое время, и вы должны использовать текущие версии.
Мы также можем периодически предоставлять вам определенные логотипы, товарные знаки или другие идентификаторы Square для вашего использования, как указано в документе Built with Square («Квадратные знаки»). В этом случае вы будете использовать их в соответствии с текущими Условиями использования торговых марок Square и Square и в соответствии с ними. Square может ограничить или отозвать вашу возможность использовать Square Marks в любое время. Все права, не указанные в Условиях использования товарных знаков Square, прямо принадлежат Square.Мы можем время от времени менять квадратные знаки. В случае изменения Условий использования квадратных знаков или товарных знаков Square вы будете (а) использовать текущую версию квадратных знаков и (б) использовать квадратные знаки в соответствии с текущими Условиями использования товарных знаков Square.
6. Право собственности. Отзыв
Нам принадлежат все права на наши инструменты, товарные знаки, контент и услуги. Продавцы Square сохраняют права на свой контент. Вы сохраняете права на свои приложения, веб-сайты, продукты или услуги, которые взаимодействуют с нашими услугами.
Мы можем бесплатно использовать любые ваши отзывы.
Вы прямо подтверждаете, что Square или Square Seller сохраняет за собой все всемирные права, титулы и интересы в отношении Содержимого, включая все права интеллектуальной собственности на него.
Вы также признаете, что в отношениях между вами и Square Square владеет всеми правами, правами собственности и интересами в отношении Инструментов разработчика, Square Marks и услуг Square (и любых производных работ или их усовершенствований), включая, помимо прочего, всю интеллектуальную собственность права в нем.Вы соглашаетесь не делать ничего несовместимого с таким правом собственности. Любые права, прямо не предоставленные здесь, удерживаются.
В соответствии с разделом 1 выше и этим разделом 6 в отношениях между вами и Square вы сохраняете все всемирные права, титулы и интересы в отношении вашей Услуги, включая, помимо прочего, все права интеллектуальной собственности в ней.
Вы можете предоставить Square комментарии относительно Контента или Инструментов разработчика или вашей оценки и их использования.Вы соглашаетесь с тем, что Square и ее представители будут иметь право копировать, изменять, создавать производные работы, публично демонстрировать, раскрывать, распространять, лицензировать и сублицензировать, включать и иным образом использовать отзывы, включая производные работы к ним, для любых и всех коммерческих и не -коммерческие цели без каких-либо обязательств перед вами.
7. Прекращение действия
Мы можем прекратить или отказать вам в доступе к инструментам в любое время по любой причине. Мы также можем изменить или прекратить поддержку определенного инструмента или функции в любое время.Вы можете прекратить действие этих условий для разработчиков, отключив свою учетную запись Square в любое время.
Мы можем прекратить действие настоящих Условий для разработчиков, приостановить или закрыть вашу учетную запись Square в любое время по любой причине. Мы можем добавлять или удалять, приостанавливать, останавливать, удалять, прекращать или налагать условия на Инструменты разработчика или любую функцию или аспект Инструментов разработчика. Мы предпримем разумные меры, чтобы уведомить вас о прекращении действия по электронной почте или при следующей попытке доступа к своей учетной записи Square или Инструментам разработчика.Вы также можете прекратить действие настоящих Условий для разработчиков, деактивировав свою учетную запись Square в любое время.
Если эти Условия разработчика или ваша учетная запись Square прекращена или приостановлена по любой причине или без причины: (а) действие лицензии и любых других прав, предоставленных в соответствии с настоящими Условиями разработчика и любыми другими применимыми условиями, прекратится, (б) мы можем (но имеем нет обязательств) удалять вашу информацию и данные учетной записи, хранящиеся на наших серверах, и (c) Square не несет ответственности перед вами или любой третьей стороной за компенсацию, возмещение или ущерб за любое прекращение или приостановку использования ваших инструментов разработчика или за удаление вашей информации или данных учетной записи.
Если действие вашей учетной записи Square прекращено или приостановлено, вы соглашаетесь: а) продолжать соблюдать настоящие Условия разработчика, б) немедленно прекратить использование Инструментов разработчика; c) немедленно прекратить доступ ко всему Контенту продавца Square; и г) удалить весь Контент Square Seller из ваших систем. Вы также соглашаетесь с тем, что Square имеет право проверять удаление вами всего Контента Square Seller, в том числе после закрытия вашей учетной записи Square.
8. Отсутствие гарантий
Хотя мы делаем все возможное, чтобы предлагать нашим клиентам отличные продукты и услуги, мы предоставляем их «как есть», без каких-либо гарантий.Мы не несем ответственности за какие-либо товары и услуги, которые вы можете купить или продать с помощью услуг Square.
ИНСТРУМЕНТЫ ДЛЯ РАЗРАБОТЧИКАПРЕДОСТАВЛЯЮТСЯ «КАК ЕСТЬ», БЕЗ ЗАЯВЛЕНИЙ ИЛИ ГАРАНТИЙ, ЯВНЫХ, ПОДРАЗУМЕВАЕМЫХ ИЛИ ЗАКОНОДАТЕЛЬНЫХ УСЛОВИЙ. БЕЗ ОГРАНИЧЕНИЙ ВЫШЕИЗЛОЖЕННОГО, SQUARE ОТКАЗЫВАЕТСЯ ОТ ЛЮБЫХ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ КОММЕРЧЕСКОЙ ЦЕННОСТИ, ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ ИЛИ НЕ НАРУШЕНИЯ.
SQUARE НЕ ГАРАНТИРУЕТ И НЕ ГАРАНТИРУЕТ ТОЧНОСТЬ, НАДЕЖНОСТЬ ИЛИ ПРАВИЛЬНОСТЬ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА; ЧТО ИНСТРУМЕНТЫ РАЗРАБОТЧИКА СООТВЕТСТВУЮТ ВАШИМ ТРЕБОВАНИЯМ; ЧТО ИНСТРУМЕНТЫ РАЗРАБОТЧИКА БУДУТ ДОСТУПНЫ В ЛЮБОЕ ОПРЕДЕЛЕННОЕ ВРЕМЯ ИЛИ МЕСТОПОЛОЖЕНИЕ, БЕСПЕРЕБОЙНО, БЕЗ ОШИБОК, БЕЗ ДЕФЕКТОВ ИЛИ БЕЗОПАСНОСТИ; ЧТО ЛЮБЫЕ ДЕФЕКТЫ ИЛИ ОШИБКИ БУДУТ ИСПРАВЛЕНЫ; ИЛИ ЧТО ИНСТРУМЕНТЫ РАЗРАБОТЧИКА СВОБОДНЫ ОТ ВИРУСОВ ИЛИ ДРУГИХ ВРЕДНЫХ КОМПОНЕНТОВ.ЛЮБОЙ СОДЕРЖАНИЕ ИЛИ ДАННЫЕ, ЗАГРУЖЕННЫЕ ИЛИ Иным образом ПОЛУЧЕННЫЕ ПРИ ИСПОЛЬЗОВАНИИ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА, ЗАГРУЖАЮТСЯ НА ВАШ СОБСТВЕННЫЙ РИСК, И ВЫ НЕСЕТЕ ИСКЛЮЧИТЕЛЬНУЮ ОТВЕТСТВЕННОСТЬ ЗА ЛЮБОЙ ПОВРЕЖДЕНИЕ ВАШЕЙ СОБСТВЕННОСТИ ИЛИ ПОТЕРЮ ДАННЫХ, ВЫЗВАННЫХ ТАКИМИ РЕЗУЛЬТАТАМИ ДАННЫХ.
Square не гарантирует, не подтверждает, не гарантирует и не принимает на себя ответственность за любой продукт или услуги, рекламируемые или предлагаемые третьей стороной. Square не контролирует и не несет ответственности за товары или услуги, оплачиваемые с помощью Инструментов разработчика.
9. Ограничение ответственности
Как описано ниже, если что-то случится из-за использования вами наших услуг, наша ответственность ограничена.
В МАКСИМАЛЬНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ДЕЙСТВУЮЩИМ ЗАКОНОДАТЕЛЬСТВОМ, НИ ПРИ КАКИХ ОБСТОЯТЕЛЬСТВАХ SQUAR НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБЫЕ ПРЯМЫЕ, КОСВЕННЫЕ, КАРАТЕЛЬНЫЕ, СЛУЧАЙНЫЕ, ОСОБЫЕ, КОСВЕННЫЕ ИЛИ ПРИМЕРНЫЕ УБЫТКИ, ВКЛЮЧАЯ БЕЗ ОГРАНИЧЕНИЯ УБЫТКОВ, УБЫТКИ ИЛИ УБЫТКОВ НАС ИЛИ ДРУГИЕ НЕМАТЕРИАЛЬНЫЕ УБЫТКИ, ПРИЧИНЕННЫЕ В РЕЗУЛЬТАТЕ ИСПОЛЬЗОВАНИЯ, НЕВОЗМОЖНОСТИ ИЛИ НЕДОСТУПНОСТИ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА.ВО ВСЕХ СЛУЧАЯХ, SQUARE НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБЫЕ УБЫТКИ ИЛИ УЩЕРБ, КОТОРЫЕ НЕОБХОДИМЫЕ.
НИ ПРИ КАКИХ ОБСТОЯТЕЛЬСТВАХ SQUARE SQUARE НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБЫЕ УБЫТКИ, ПОТЕРЯ ИЛИ ТРАВМЫ, ВЫЗВАННЫЕ В результате взлома, взлома ИЛИ ДРУГОГО НЕСАНКЦИОНИРОВАННОГО ДОСТУПА ИЛИ ИСПОЛЬЗОВАНИЯ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА ИЛИ ВАШЕГО АККАУНТА SQUARE ИЛИ ИНФОРМАЦИИ.
В МАКСИМАЛЬНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ДЕЙСТВУЮЩИМ ЗАКОНОДАТЕЛЬСТВОМ, SQUARE НЕ НЕСЕТ НИКАКОЙ ОТВЕТСТВЕННОСТИ ЗА ЛЮБЫЕ (I) ОШИБКИ, ОШИБКИ ИЛИ НЕТОЧНОСТИ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА ИЛИ СОДЕРЖАНИЯ; (II) ЛИЧНЫЕ ТРАВМЫ ИЛИ ПОВРЕЖДЕНИЕ ИМУЩЕСТВА ЛЮБОГО ХАРАКТЕРА, В РЕЗУЛЬТАТЕ ВАШЕГО ДОСТУПА ИЛИ ИСПОЛЬЗОВАНИЯ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА; (III) ЛЮБОЙ НЕСАНКЦИОНИРОВАННЫЙ ДОСТУП К НАШИМ БЕЗОПАСНЫМ СЕРВЕРАМ ИЛИ ИСПОЛЬЗОВАНИЕ ЛЮБОЙ И ВСЕЙ ЛИЧНОЙ ИНФОРМАЦИИ, СОХРАНЕННОЙ НА них; (IV) ЛЮБОЕ ПРЕРЫВАНИЕ ИЛИ ПРЕКРАЩЕНИЕ ПЕРЕДАЧИ НА ИЛИ ОТ ИНСТРУМЕНТОВ РАЗРАБОТЧИКА; (V) ЛЮБЫЕ ОШИБКИ, ВИРУСЫ, ТРОЯНСКИЕ ЛОШАДИ ИЛИ ИХ ТОМ, КОТОРЫЕ МОГУТ БЫТЬ ПЕРЕДАНЫ НА ИНСТРУМЕНТЫ РАЗРАБОТЧИКА ЛЮБОЙ ТРЕТЬЕЙ СТОРОНОЙ; (VI) ЛЮБЫЕ ОШИБКИ ИЛИ УПУЩЕНИЯ В ЛЮБОМ СОДЕРЖАНИИ ИЛИ ДАННЫХ, ИЛИ ЗА ЛЮБЫЕ УБЫТКИ ИЛИ УЩЕРБ, ВЫЯВЛЕННЫЕ В РЕЗУЛЬТАТЕ ИСПОЛЬЗОВАНИЯ ЛЮБОГО СОДЕРЖАНИЯ ИЛИ ДАННЫХ, РАЗМЕЩЕННЫХ, ОТПРАВЛЕННЫХ ПО ЭЛЕКТРОННОЙ ПОЧТЕ, ПЕРЕДАННЫХ ИЛИ Иным образом, ДОСТУПНЫМИ ЧЕРЕЗ ИНСТРУМЕНТЫ РАЗРАБОТЧИКА; И / ИЛИ (VII) ВАШИ УСЛУГИ.
В МАКСИМАЛЬНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ДЕЙСТВУЮЩИМ ЗАКОНОДАТЕЛЬСТВОМ, ОБЩАЯ ОТВЕТСТВЕННОСТЬ SQUARE ОГРАНИЧИВАЕТСЯ В БОЛЬШОМ размере (А) СУММЫ ПЛАТЕЖЕЙ, ЗАРАБОТАЕМЫХ НАМИ В СВЯЗИ С ИСПОЛЬЗОВАНИЕМ ВАМИ УСЛУГ В ТЕЧЕНИЕ ТРИ (3) МЕСЯЦЕВ ПРЕДПОЛАГАЕМЫЙ ПЕРИОД СОБЫТИЕ, ПОЛУЧАЮЩЕЕ ПРЕТЕНЗИЮ ОБ ОТВЕТСТВЕННОСТИ ИЛИ (B) 500 долларов США.
НАСТОЯЩИЙ РАЗДЕЛ ОГРАНИЧЕНИЯ ОТВЕТСТВЕННОСТИ ПРИМЕНЯЕТСЯ, ЕСЛИ УКАЗАННАЯ ОТВЕТСТВЕННОСТЬ ОСНОВАНА НА КОНТРАКТЕ, НЕБРЕЖНОСТИ, СТРОГОЙ ОТВЕТСТВЕННОСТИ ИЛИ ЛЮБОМ ДРУГИМ ОСНОВАНИИ, ДАЖЕ ЕСЛИ SQUARE ПРЕДНАЗНАЧЕНА О ВОЗМОЖНОСТИ ТАКОГО УЩЕРБА.ВЫШЕУКАЗАННОЕ ОГРАНИЧЕНИЕ ОТВЕТСТВЕННОСТИ ПРИМЕНЯЕТСЯ В САМОЙ ПОЛНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ЗАКОНОМ ПРИМЕНИМОЙ ЮРИСДИКЦИИ.
10. Возмещение
Если вы сделаете что-то, что приведет к судебному преследованию нас или оштрафовано, вы соглашаетесь покрыть наши убытки и ущерб.
Вы будете возмещать, защищать и защищать нас и наших процессоров (и наших соответствующих сотрудников, директоров, агентов, аффилированных лиц и представителей) от любых претензий, затрат, убытков, убытков, судебных решений, налоговых начислений, штрафов, процентов. , а также расходы (включая, помимо прочего, разумные гонорары адвокатам), возникающие в связи с любым иском, действием, аудитом, расследованием, расследованием или другим судебным разбирательством, инициированным физическим или юридическим лицом, которое возникает из или связано с: (a) любым фактическим или предполагаемым нарушение ваших заявлений, гарантий или обязательств, изложенных в настоящих Условиях для разработчиков, включая, помимо прочего, любое нарушение наших политик; (б) ваше неправомерное или ненадлежащее использование Инструментов разработчика или Содержимого; (c) нарушение вами любых прав третьих лиц, включая, помимо прочего, право на неприкосновенность частной жизни, права на гласность или права интеллектуальной собственности; (d) нарушение вами любого закона, правила или постановления США или любой другой страны; или (e) доступ любой другой стороны и / или использование Инструментов разработчика с вашим уникальным именем, паролем или другим подходящим кодом безопасности.
11. Изменение условий
Мы можем обновлять наши условия или услуги в любое время. Продолжая пользоваться нашими услугами после этих обновлений, вы соглашаетесь с пересмотренными условиями.
Мы можем вносить поправки в настоящие Условия для разработчиков, а также документацию и инструкции, сопровождающие соответствующие Инструменты разработчика, в любое время с уведомлением, которое мы считаем разумным в данных обстоятельствах, путем публикации пересмотренной версии на нашем веб-сайте или сообщения ее вам через вашу учетную запись Square (каждая — «Исправленная версия»).Пересмотренная версия вступает в силу с момента ее публикации, но не имеет обратной силы. Ваше дальнейшее использование и доступ к Инструментам разработчика после публикации пересмотренной версии означает ваше согласие с такой пересмотренной версией. Любой спор (как определено в Разделе 12), возникший до внесения изменений, будет регулироваться условиями обслуживания, действовавшими на момент возникновения Спора.
12. Обязательный индивидуальный арбитраж
В этом разделе представлена подробная информация о том, как мы будем разрешать споры в арбитражном процессе.
«Споры» определяются как любые претензии, разногласия или споры между вами и Square, ее обработчиками, поставщиками или лицензиарами (или их соответствующими аффилированными лицами, агентами, директорами или сотрудниками), включая любые претензии, связанные каким-либо образом с настоящими Условиями для разработчиков или Инструменты разработчика или любой другой аспект наших отношений.
Вы и Square соглашаетесь разрешать любые споры нейтральным арбитром, который имеет право присуждать такие же индивидуальные убытки и индивидуальную компенсацию, что и суд.ЛЮБОЙ АРБИТРАЖ ПО НАСТОЯЩЕМУ СОГЛАШЕНИЮ БУДЕТ ТОЛЬКО НА ИНДИВИДУАЛЬНОЙ ОСНОВЕ; КЛАССОВЫЕ АРБИТРАЖЫ, КЛАССОВЫЕ ИСКИ, ПРЕДСТАВИТЕЛЬСКИЕ ИСКИ И КОНСОЛИДАЦИЯ С ДРУГИМИ АРБИТРАЖАМИ НЕ РАЗРЕШЕНЫ. ВЫ ОТКАЗЫВАЕТЕСЬ ОТ ЛЮБОГО ПРАВА НА РЕШЕНИЕ ВАШЕГО ДЕЛА ЖЮРИ И ОТКАЗЫВАЕТЕСЬ ОТ ЛЮБОГО ПРАВА НА УЧАСТИЕ В КЛАССНЫХ ДЕЙСТВИЯХ ПРОТИВ SQUARE. Если какое-либо положение этого арбитражного соглашения будет признано не имеющим исковой силы, неисполнимое положение должно быть исключено, а оставшиеся условия арбитража должны быть исполнены (но ни в коем случае не должно быть классового арбитража).Все споры должны решаться окончательно и исключительно путем обязательного индивидуального арбитража с участием одного арбитра («Арбитр») под управлением Американской арбитражной ассоциации (www.adr.org) в соответствии с этим положением и применимыми правилами арбитража для этого форума. Арбитр несет ответственность за определение всех пороговых вопросов арбитрабильности, включая вопросы, касающиеся того, являются ли Общие условия и / или Дополнительные условия (или любой их аспект) исполнимыми, недобросовестными или иллюзорными, а также любые возражения против арбитража, включая отказ, отсрочки, отсрочки, или эстоппель.В соответствии с применимыми юрисдикционными требованиями вы можете выбрать рассмотрение своих исков в местном суде мелких тяжб, а не через арбитраж, если ваше дело остается в суде мелких тяжб и рассматривается только на индивидуальной (неклассовой или непредставительной) основе. . Федеральный закон об арбитраже, 9 U.S.C. §§ 1-16, применяется полностью. Если вы являетесь потребителем, подающим иск, касающийся использования в личных, домашних или семейных целях, любое арбитражное слушание будет проводиться в округе, в котором вы проживаете.В противном случае любое арбитражное слушание будет проводиться в Сан-Франциско, Калифорния, или другом взаимоприемлемом месте. Решение арбитра является обязательным для сторон и может быть принято как решение в любом суде компетентной юрисдикции. Хотя арбитр может присудить декларативное средство правовой защиты или судебный запрет, арбитр может сделать это только в отношении отдельной стороны, требующей судебной защиты, и только в той мере, в какой это необходимо для предоставления судебной защиты, обоснованной иском отдельной стороны. Решение и постановление арбитра по ним не будет иметь прецедентного или побочного действия эстоппеля.Square возместит арбитражные сборы, причитающиеся Американской арбитражной ассоциации за индивидуальные арбитражные разбирательства, возбужденные в соответствии с этим разделом, для всех претензий на общую сумму менее 10 000 долларов США, если только Арбитр не определит, что ваши претензии были необоснованными. Если вы выиграете какой-либо иск, по которому вы имеете законное право на гонорар адвоката, вы можете потребовать взыскать эти гонорары с арбитра. По любым претензиям, по которым вы обращаетесь за помощью, Square не будет требовать от вас оплаты гонорара ее адвоката, даже если в противном случае могут быть присуждены гонорары, если только арбитр не определит, что ваше требование было необоснованным.Для целей данного положения об арбитраже ссылки на вас и Square также включают соответствующих аффилированных лиц, агентов, сотрудников, предшественников, правопреемников и правопреемников, а также авторизованных пользователей или бенефициаров услуг Square. С учетом и без отказа от положений об арбитраже, приведенных выше, вы соглашаетесь с тем, что любое судебное разбирательство (кроме исков о мелких претензиях в делах потребителей, как описано выше) будет инициировано, и настоящим вы соглашаетесь с исключительной юрисдикцией и местом проведения в государственных судах в Город и округ Сан-Франциско, Калифорния, или федеральный суд Северного округа Калифорнии.
13. Применимый закон
Наши отношения регулируются законами Калифорнии, федеральным законом или и тем, и другим.
Настоящие Условия для разработчиков и любые Споры будут регулироваться законодательством штата Калифорния и / или применимым федеральным законом (включая Федеральный закон об арбитраже) без учета выбора закона или принципов коллизионного права.
14. Ограничение времени для возбуждения спора
Если иное не требуется по закону, действие или судебное разбирательство с вашей стороны в отношении любого Спора должно начаться в течение одного года после возникновения причины иска.
15. Переуступка
Вы не можете передавать какие-либо права, которые у вас есть в соответствии с нашими условиями обслуживания, кому-либо еще.
Настоящие Условия для разработчиков и любые права и лицензии, предоставленные в соответствии с ними, не могут быть переданы или назначены вами, и любая попытка передачи или уступки будет недействительной.
16. Прочие условия
Настоящие Условия для разработчиков и любые другие применимые условия или политики являются полным изложением соглашения между вами и Square относительно Инструментов разработчика.Если какое-либо положение настоящих Условий для разработчиков является недействительным или не имеющим исковой силы в соответствии с действующим законодательством, оно будет изменено и истолковано для достижения целей такого положения в максимально возможной степени в соответствии с применимым законодательством, а остальные положения сохранят полную силу. Эти Условия для разработчиков не ограничивают никаких прав, которые Square может иметь в соответствии с законами о коммерческой тайне, авторском праве, патентах или другими законами. Никакой отказ от какого-либо положения настоящих Условий для разработчиков не считается дальнейшим или продолжающимся отказом от такого или любого другого условия.
17. Выживание
Некоторые условия нашего соглашения будут действовать даже после прекращения наших отношений.

 э. Магический квадрат 4*4, изображенный на гравюре Альбрехта Дюрера «Мелонхолия», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).
э. Магический квадрат 4*4, изображенный на гравюре Альбрехта Дюрера «Мелонхолия», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).