Закон обратных квадратов в физике: Закон обратных квадратов | это… Что такое Закон обратных квадратов?
Закон обратных квадратов | это… Что такое Закон обратных квадратов?
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
Содержание
|
Обоснование
Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Проявления
Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними.
 Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данное массивное тело, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу
Электростатика
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.
Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения
Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:
Фотографы и театральные мастера по свету используют закон обратных квадратов для выбора оптимального места положения осветительных приборов.
Закон обратных квадратов может быть применён только для точечных источников света; наиболее распространённые в помещениях цилиндрические лампы дневного света не являются точечными источниками, и поэтому к ним нельзя применять закон обратных квадратов, в отличие от большинства других источников искусственного излучения.
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Формулы закона обратных квадратов в рентгенографии имеют вид:
где
- I — интенсивность,
- r — расстояние (радиус).
Приложения в теории поля
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
Примечания
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.
Закон обратных квадратов | это… Что такое Закон обратных квадратов?
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
Содержание
|
Обоснование
Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Проявления
Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данное массивное тело, и результирующее взаимодействие может не подчиняться закону обратных квадратов.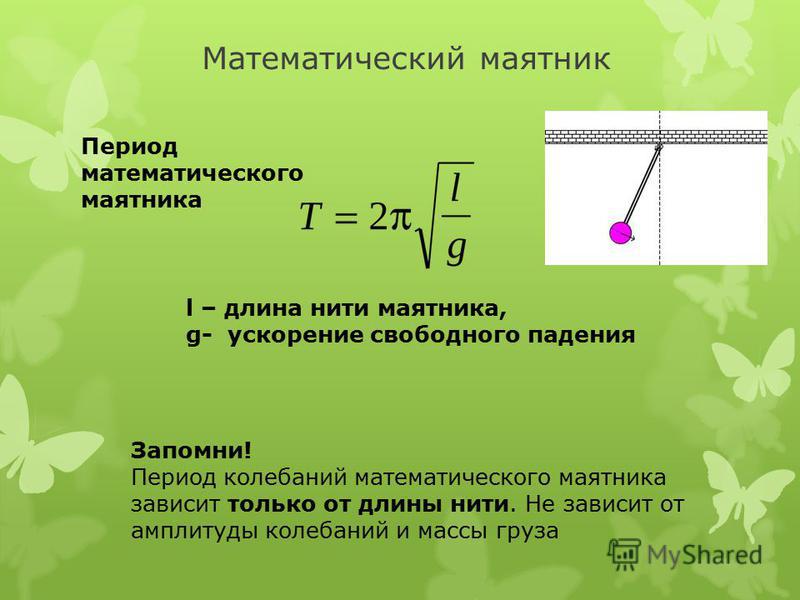 В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу [1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы[2], также как отдал дань уважения Буллиальду.
Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы[2], также как отдал дань уважения Буллиальду.
Электростатика
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения
Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:
Фотографы и театральные мастера по свету используют закон обратных квадратов для выбора оптимального места положения осветительных приборов.
Закон обратных квадратов может быть применён только для точечных источников света; наиболее распространённые в помещениях цилиндрические лампы дневного света не являются точечными источниками, и поэтому к ним нельзя применять закон обратных квадратов, в отличие от большинства других источников искусственного излучения.
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Формулы закона обратных квадратов в рентгенографии имеют вид:
где
- I — интенсивность,
- r — расстояние (радиус).
Приложения в теории поля
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
Примечания
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.

- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.
Закон обратных квадратов | это… Что такое Закон обратных квадратов?
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
Содержание
|
Обоснование
Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Проявления
Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данное массивное тело, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу [1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы[2], также как отдал дань уважения Буллиальду.
Электростатика
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения
Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:
Фотографы и театральные мастера по свету используют закон обратных квадратов для выбора оптимального места положения осветительных приборов.
Закон обратных квадратов может быть применён только для точечных источников света; наиболее распространённые в помещениях цилиндрические лампы дневного света не являются точечными источниками, и поэтому к ним нельзя применять закон обратных квадратов, в отличие от большинства других источников искусственного излучения.
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Формулы закона обратных квадратов в рентгенографии имеют вид:
где
- I — интенсивность,
- r — расстояние (радиус).
Приложения в теории поля
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
Примечания
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.
Все страницы — Юнионпедия
Все страницы — ЮнионпедияНовый! Скачать Юнионпедия на вашем Android™ устройстве!
Свободно
Более быстрый доступ, чем браузер!
Все страницы · Предыдущая (Закон Хольцмана) · Следующий (Законы Великой династии Мин)
Из:
| Закон обратных квадратов | Закон обратного отношения между содержанием и объёмом понятия | Закон обратного отношения между содержанием и объемом понятия |
| Закон ограничивающего фактора | Закон оптимума | Закон прямолинейного распространения света |
| Закон притяжения | Закон природы | Закон природы (значения) |
| Закон прибавочной стоимости | Закон привычных сумм | Закон против интернета |
| Закон против опасных рецидивистов | Закон против пропаганды гомосексуализма в Санкт-Петербурге | Закон противоречия |
| Закон противодействия | Закон предложения | Закон предложения (экономика) |
| Закон преломления | Закон преломления света | Закон преломления световых волн |
| Закон падающей кошки | Закон площадей | Закон постоянства состава |
| Закон повторного логарифма | Закон подлости | Закон подлецов |
| Закон перехода количества в качество | Закон перехода количественных изменений в качественные | Закон Мэрфи |
| Закон Мура | Закон Мёрфи | Закон Мёрфи (сериал) |
| Закон Мёрфи (телесериал) | Закон Мёрфи (мультсериал) | Закон Маттарелла |
| Закон Магнитского | Закон Майло Мёрфи | Закон Майло Мерфи |
| Закон Малюса | Закон Мамми | Закон Манилия |
| Закон Миллера | Закон Мояно | Закон Мореля о четырёх поколениях |
| Закон Мореля о четырех поколениях | Закон Мозли | Закон Моисея |
| Закон Мойано | Закон Меткалфа | Закон Мефри |
| Закон Мерсенна | Закон Мерфи | Закон Мерфи (сериал) |
| Закон Меган | Закон Мейе | Закон Менделеева — Клапейрона |
| Закон Менделеева-Клапейрона | Закон Иллич-Свитыча | Закон Иллича-Свитыча |
| Закон есть закон | Закон есть закон (фильм) | Закон единства и борьбы противоположностей |
| Закон единой цены | Закон единообразия гибридов | Закон единообразия гибридов первого поколения |
| Закон Зибса | Закон Зиверса | Закон Зипфа |
| Закон Бэра | Закон Бутана о местном самоуправлении 2009 года | Закон Бутана о местном управлении 2009 года |
| Закон Бугера | Закон Бугера — Ламберта — Бера | Закон Бугера — Ламберта |
| Закон Бугера — Ламберта — Бера | Закон Бугера-Ламберта-Бера | Закон Брюстера |
| Закон Брэгга | Закон Брукса | Закон Барлоу |
| Закон Базальи | Закон Био — Савара | Закон Био — Савара — Лапласа |
| Закон Био — Савара | Закон Био — Савара — Лапласа | Закон Био-Савара |
| Закон Био-Савара-Лапласа | Закон Блоха | Закон Боски |
| Закон Богуславского — Ленгмюра | Закон Боде | Закон Божий |
| Закон Божий (дисциплина) | Закон Бойля — Мариотта | Закон Бойля-Мариотта |
| Закон Беца | Закон Бера | Закон Бернулли |
| Закон Бенфорда | Закон Вагнера | Закон Ваккернагеля |
| Закон Ваккернагеля в древнерусском языке | Закон Вакернагеля | Закон Вакернагеля в древнерусском языке |
| Закон Вальраса | Закон Вирта | Закон Вигнера |
| Закон Видемана — Франца | Закон Видемана-Франца | Закон Виллия |
| Закон Винтера | Закон Вина | Закон Вольта |
| Закон Вольффа | Закон Вольфа | Закон Вердоорна |
| Закон Вернера | Закон Вебера — Фёхнера | Закон Вебера — Фехнера |
| Закон Вебера-Фехнера | Закон Вегарда | Закон Гэрри |
| Закон Густафсона-Барсиса | Закон Густавсона — Барсиса | Закон Гутеберга — Рихтера |
| Закон Гутенберга — Рихтера | Закон Гутенберга-Рихтера | Закон Гудхарта |
| Закон Гука | Закон Грэхема | Закон Грэма |
| Закон Грэмма — Рудмана — Холлингса | Закон Грэмма — Лича — Блайли | Закон Грэмма-Рудмана-Холлингса |
| Закон Грузии «Об устранении всех форм дискриминации» | Закон Грузии «об оккупированных территориях» | Закон Грузии об оккупированных территориях |
| Закон Грассмана | Закон Грассмана (оптика) | Закон Гримма |
| Закон Гроша | Закон Грешема | Закон Гаюи |
| Закон Гаусса | Закон Гарроу | Закон Гавлика |
| Закон Гласса — Стиголла | Закон Гласса-Стиголла | Закон Гласа-Стиголла |
| Закон Готланда | Закон Гортензия | Закон Гортензия 287 года до н. э. э. |
| Закон Гортензия 287 года до н.э. | Закон Годвина | Закон Голдуотера — Николса |
| Закон Голдуотера-Николса | Закон Гомпгерца | Закон Гомпертца |
| Закон Гопкинсона | Закон Гесса | Закон Гей-Люссака |
| Закон Гей-Люссака — Джоуля | Закон Гейтса | Закон Гейгера — Нэттола |
| Закон Гейгера — Неттола | Закон Гейгера-Нэттола | Закон Гейгера-Неттола |
| Закон Геккеля | Закон Геккеля-Мюллера | Закон Генри |
| Закон Генри — Дальтона | Закон Дюверже | Закон Дюлонга — Пти |
| Закон Дюлонга и Пти | Закон Дюлонга-Пти | Закон Дыбо |
| Закон Дарси | Закон Дальтона | Закон Дании об именах |
| Закон Джоя | Закон Джоуля | Закон Джоуля — Ленца |
| Закон Джоуля — Коппа | Закон Джоуля — Ленца | Закон Джоуля-Коппа |
| Закон Джоуля-Ленца | Закон Джерси | Закон Димы Яковлева |
| Закон Додда — Франка | Закон Долло | Закон Дебая |
| Закон Деметры | Закон Деметра | Закон Еркса-Додсона |
| Закон Лугового | Закон Лахмана | Закон Ламберта |
| Закон Лапласа | Закон Литтла | Закон Литвы о защите несовершеннолетних от воздействия отрицательной публичной информации |
| Закон Литвы о защите несовершеннолетних от негативного влияния публичной информации | Закон Либби Зайон | Закон Либби Зион |
| Закон Либиха | Закон Линуса | Закон Липпса-Мейера |
| Закон Лос-Анджелеса | Закон Лос-Анджелеса (сериал) | Закон Лос-Анджелеса (телесериал) |
| Закон Лос-Анжелеса | Закон Лос-Анжелеса (телесериал) | Закон Лоренца |
| Закон Ле Шапелье | Закон Лескина | Закон Лердо |
| Закон Ленца | Закон Йеркса — Додсона | Закон Йеркса-Додсона |
| Закон-ТВ | Законъ соудный людемъ | Законцовка |
| Законцовка крыла | Законы | Законы (Платон) |
| Законы 12 таблиц | Законы 16 января | Законы сынов Ноевых |
| Законы сохранения | Законы электролиза Фарадея | Законы термодинамики |
| Законы физики | Законы философии | Законы рукопашного боя 2: Тайное задание |
| Законы рукопашного боя 2: Тайное задание (фильм) | Законы развития языка | Законы риторики |
| Законы XII таблиц | Законы Канулея | Законы Канады о пропаганде ненависти |
| Законы Кирхгофа | Законы Коновалова | Законы Кеплера |
| Законы Паркинсона | Законы Осипова — Ланчестера | Законы Осипова-Ланчестера |
| Законы Азимова | Законы Альфреда Великого | Законы Ньютона |
| Законы Рауля | Законы Ур-Намму | Законы Фарадея |
| Законы Фарадея (электролиз) | Законы Фика | Законы Хамураппи |
| Законы Хаммурапи | Законы Хивела Доброго | Законы Эшнунны |
| Законы Этельберта | Законы богов и людей | Законы войны |
| Законы гор | Законы дракона | Законы двенадцати таблиц |
| Законы диалектики | Законы де Моргана | Законы деления |
| Законы деление | Законы денежного обращения | Законы и обычаи войны |
| Законы истории | Законы истории (книга) | Законы из Эшнунны |
| Законы инков | Законы короля Альфреда | Законы логики |
| Законы мафии | Законы моргана | Законы механики Ньютона |
| Законы о времени работы магазинов | Законы о гражданстве Литвы | Законы о диктатуре |
| Законы о клевете на еду | Законы о конфискации наделов | Законы природы |
| Законы привлекательности | Законы привлекательности (фильм) | Законы против содомии |
| Законы Максвелла | Законы Ману | Законы Моргана |
| Законы Моисея | Законы Мерфи | Законы Менделя |
| Законы Бэра | Законы Бутана | Законы Бруклина |
| Законы Билаламы | Законы Вревского | Законы Вольта |
Геометрия пространства или закон обратных квадратов — Студопедия
Поделись
«на пальцах»
Эти две декартовых сущности отличаются свойством протяженности в пространстве: для материи это свойство является существенным, для сознания – нет. Под пространством понимается трехмерное декартово пространство, определяемое тремя (пространственными) координатами. Важно, таким образом, что представляет собой пространство, в котором разворачиваются процессы материальной природы, изучаемые физикой. Рассмотрим один сравнительно простой случай, пользуясь для его анализа минимальным набором инструментов, к каковым отнесем органы чувств (зрение) и способность логически рассуждать, пользуясь минимальными знаниями школьного курса физики.
Под пространством понимается трехмерное декартово пространство, определяемое тремя (пространственными) координатами. Важно, таким образом, что представляет собой пространство, в котором разворачиваются процессы материальной природы, изучаемые физикой. Рассмотрим один сравнительно простой случай, пользуясь для его анализа минимальным набором инструментов, к каковым отнесем органы чувств (зрение) и способность логически рассуждать, пользуясь минимальными знаниями школьного курса физики.
Для этого проведем мысленный или натурный эксперимент. В качестве объекта расположим перед собой кисти рук на разном расстоянии от глаз. Нетрудно согласиться с утверждением о том, что ближайшая к глазам кисть руки кажется нам больше. Так как мы знаем, что кисти у нас одинаковые, в чем мы можем убедиться, совмещая ладони рук, небезынтересно проанализировать причину этого факта. Она лежит в области оптических явлений и касается т.н. геометрической оптики. Из школьного курса физики известно, что при определенных условиях (здесь выполняемых) величина изображения предмета обратно пропорциональна его расстоянию от наблюдателя. В данном случае расстояние отсчитывается от хрусталика глаза, представляющего собой с точки зрения оптики двояковыпуклую линзу.
В данном случае расстояние отсчитывается от хрусталика глаза, представляющего собой с точки зрения оптики двояковыпуклую линзу.
Ход световых лучей показан на рис. 1.3.
В D
А С F O F1A1 D1
R1 B2 B1
R2 D2 C1
Рис. 1.3. Рисунок, иллюстрирующий обратную пропорциональность размера изображения расстоянию до объекта
Дано: два одинаковой высоты R предмета AB и CD расположены на разном расстоянии R2 и R1 от линзы (выпуклой) c оптическим центром O.
Требуется доказать: Размеры их изображенийA1B1=ОB2 и C1D1=OD2 обратно пропорциональны расстояниям AF (R2) и CF (R1) исходных предметов до линзы (до фокуса линзы F).
Доказательство: запишем тангенс <AFB=R/R2 =A1B1/F и
Тангенс <AFD=R/R1=C1D1/F.
Выражая теперь F из обоих равенств и приравнивая полученные выражения, получим F=A1B1*R2/R=C1D1*R1/R, откуда A1B1/C1D1=R1/R2, то есть величины изображений обратно пропорциональны расстояниям предметов до линзы.
Если мы имеем дело с двухмерным предметом, то его площадь (и сила воздействия на глаз – психологический термин) обратно пропорциональна квадрату расстояния до линзы.
Поскольку правила построения изображения в линзе основаны на Евклидовой геометрии, то получаем, что для этой геометрии закон обратных квадратов является «свойством пространства».
Анализ рис. 1.3 подтверждает известный факт, упомянутый выше, о том, что величина изображения объекта обратно пропорциональна его расстоянию от линзы. Поскольку наш объект двумерный, т.е. мы воспринимаем его площадь, то можем, исходя из тех же рассуждений, сказать, что площадь изображения объекта обратно пропорциональна квадрату расстояния от линзы. В самом деле, площадь равна произведению ширины объекта на его высоту, причем каждый из сомножителей по величине обратно пропорционален расстоянию. Получаем «на пальцах» популярный в физике закон обратных квадратов, гласящий, что сила взаимодействия между телами обратно пропорциональна квадрату расстояния между ними.
Поскольку наш объект двумерный, т.е. мы воспринимаем его площадь, то можем, исходя из тех же рассуждений, сказать, что площадь изображения объекта обратно пропорциональна квадрату расстояния от линзы. В самом деле, площадь равна произведению ширины объекта на его высоту, причем каждый из сомножителей по величине обратно пропорционален расстоянию. Получаем «на пальцах» популярный в физике закон обратных квадратов, гласящий, что сила взаимодействия между телами обратно пропорциональна квадрату расстояния между ними.
Какие же тела взаимодействуют в нашем случае? Это (освещенная) ладонь и глаз наблюдателя. Поскольку информацию мы получаем от глаза, имеет смысл оценить воздействие объекта на глаз наблюдателя. Как мы только что установили, сила такого воздействия обратно пропорциональна квадрату расстояния. Напрашивается аналогия с фотометрическим законом, по которому освещенность экрана обратно пропорциональна квадрату расстояния от источника света. Фотометрический закон был известен еще Кеплеру. А Ньютон, живший позднее, наверняка был в курсе этого открытия. Известно, что ранние труды гения механики были посвящены оптике. Закон всемирного тяготения, которым мы успешно пользуемся до сих пор, был сформулирован не без влияния трудов Кеплера, в том числе и его оптических трудов. Открытый значительно позже закон Кулона, описывающий взаимодействие точечных электрических зарядов, тоже дает выражение для силы взаимодействия через квадрат расстояния между взаимодействующими объектами (зарядами). Что же общего между этими физическими законами, установленными в различных областях нашей науки?
А Ньютон, живший позднее, наверняка был в курсе этого открытия. Известно, что ранние труды гения механики были посвящены оптике. Закон всемирного тяготения, которым мы успешно пользуемся до сих пор, был сформулирован не без влияния трудов Кеплера, в том числе и его оптических трудов. Открытый значительно позже закон Кулона, описывающий взаимодействие точечных электрических зарядов, тоже дает выражение для силы взаимодействия через квадрат расстояния между взаимодействующими объектами (зарядами). Что же общего между этими физическими законами, установленными в различных областях нашей науки?
Можно надеяться, что одинаковая математическая форма названных соотношений имеет глубокую физическую природу. И эта природа связана со свойствами самого пространства, в котором и разворачиваются описанные взаимодействия. И эти свойства породили соответствующее математическое описание. Как, по-видимому, догадался читатель, речь идет о евклидовом пространстве, о котором его автор, великий греческий математик говорил: все, что видно, видно по прямой. Перечисленные физические законы имеют место в пространстве, в котором свет распространяется прямолинейно. Эти законы и образуют каркас классической физики.
Перечисленные физические законы имеют место в пространстве, в котором свет распространяется прямолинейно. Эти законы и образуют каркас классической физики.
Закон обратных квадратов, если говорить о его математической стороне, может иметь особенности в области малых расстояний, где сила взаимодействия быстро растет. Такие условия реализуются при взаимодействии света с веществом, в котором характеристические расстояния сравнимы с длиной световой волны (или меньше ее). Можно ожидать, что вблизи вещества или внутри него свет имеет другие законы распространения, а, следовательно, там существует другое пространство, в котором реализуются и другие взаимодействия. В дальнейшем мы увидим, что это интуитивное ожидание оправдывается в физике микромира, проявляющейся в атомных и ядерных процессах, и в тесно связанной с ней физике мегамира, к услугам которой вся вселенная.
Colory.
 Ru
RuЗакон обратных квадратов |
|
| Закон, на основании которого определяются условия фотографического экспонирования, утверждает, что освещенность от точечного или сравнительно малых размеров источника света изменяется обратно пропорционально квадрату расстояния от источника до объекта. Например, увеличение расстояния между вспышкой и объектом в 2 раза приводит к уменьшению освещенности объекта в 4 раза. Если указанные расстояния увеличить в 3 раза, то освещенность уменьшится в 9 раз и т. д. При уменьшении расстояний наблюдается обратная зависимость. |
photoreporter.ru
Закон обратных квадратов.
В
физике, закон обратных квадратов — это
закон, утверждающий, что значение
некоторой физической величины в данной
точке пространства обратно пропорционально
квадрату расстояния от источника поля,
которое характеризует эта физическая
величина.
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
СПЕКТР
электромагнитного излучения, упорядоченная
по длинам совокупность монохроматических
волн, на которую разлагается свет или
иное электромагнитное излучение.
Типичный пример спектра – хорошо
известная всем радуга. Возможность
разложения солнечного света на непрерывную
последовательность лучей разных цветов
впервые экспериментально показал
И.Ньютон в 1666. Направив на трехгранную
призму узкий пучок света, проникавший
в затемненную комнату через маленькое
отверстие в ставне окна, он получил на
противоположной стене изображение
окрашенной полоски с радужным чередованием
цветов, которая была названа им латинским
словом spectrum. Проводя опыты с призмами,
Ньютон пришел к следующим важным выводам:
1) обычный «белый» свет является смесью
лучей, каждый из которых имеет свой
собственный цвет; 2) лучи разных цветов,
преломляясь в призме, отклоняются на
различные углы, вследствие чего «белый»
свет разлагается на цветные составляющие.
Со временем ньютоновская интерпретация
природы света завоевала всеобщее
признание, поскольку хорошо согласовалась
с экспериментальными данными, а сам
эксперимент был принят учеными за основу
научного подхода к изучению явлений
природы.
Проводя опыты с призмами,
Ньютон пришел к следующим важным выводам:
1) обычный «белый» свет является смесью
лучей, каждый из которых имеет свой
собственный цвет; 2) лучи разных цветов,
преломляясь в призме, отклоняются на
различные углы, вследствие чего «белый»
свет разлагается на цветные составляющие.
Со временем ньютоновская интерпретация
природы света завоевала всеобщее
признание, поскольку хорошо согласовалась
с экспериментальными данными, а сам
эксперимент был принят учеными за основу
научного подхода к изучению явлений
природы.
Видимый
свет – это лишь малая часть широкого
спектра электромагнитного излучения,
включающего радиоволновое, микроволновое,
инфракрасное, видимое, ультрафиолетовое,
рентгеновское и гамма-излучения. Каждый
вид излучения представляет собой волну
из взаимно перпендикулярных электрической
и магнитной компонент, периодически
меняющихся с определенными частотами
(иначе говоря, волна имеет определенную
длину). Волны, которые воспринимаются
глазом человека, принадлежат видимой
области; именно к ней в свое время
относился введенный Ньютоном термин
«спектр». В современной науке этот
термин распространен на весь диапазон
электромагнитного излучения.
В современной науке этот
термин распространен на весь диапазон
электромагнитного излучения.
Спектральные исследования сыграли ключевую роль в познании Вселенной. С их помощью удалось понять строение не только атомов и молекул, но и таких астрофизических объектов, как Солнце, звезды, планеты, и получить подробную информацию об их движении. Разработанная теория спектров и накопленные эмпирические данные позволили создать метод спектрального анализа для качественного и количественного определения состава химических веществ. См. также ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ; РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ; СВЕТ.
Классификация спектров.
Все
спектры делятся на два основных класса:
спектры испускания (или эмиссионные) и
спектры поглощения. Каждый класс, в свою
очередь, подразделяется на непрерывные
(сплошные), полосатые и линейчатые
спектры. Поясним эту классификацию на
примере видоизмененной схемы опыта
Ньютона (которая, заметим, была применена
лишь столетие спустя). Основное
нововведение в этой схеме состояло в
том, что круглое отверстие в ставне было
заменено коллиматором – узкой щелью и
линзой перед призмой. Вторая линза
помещалась за призмой и предназначалась
для проецирования спектра на экран, как
это делал сам Ньютон в своих более
поздних опытах. Если на щель простого
спектроскопа (как теперь называется
устройство, состоящее из щели, линз и
призмы) направить свет от лампы
накаливания, то на экране возникает
непрерывный спектр со следующим порядком
чередования цветов: фиолетовый, синий,
голубой, зеленый, желтый, оранжевый и
красный. Если же щель осветить пламенем,
в которое внесена крупинка поваренной
соли (хлорида натрия NaCl), то спектр будет
фактически состоять из двух близко
расположенных ярких желтых линий.
Аналогично, если щель осветить красным
светом неоновой рекламной трубки, то
на экране появится ряд ярких красных
линий. Здесь каждая линия – это изображение
щели спектроскопа, образованное светом
определенной длины волны, а полученный
спектр называется линейчатым спектром
испускания. Существуют спектры, состоящие
из групп линий, расположенных настолько
тесно, что каждая группа выглядит как
узкий участок непрерывного спектра.
Вторая линза
помещалась за призмой и предназначалась
для проецирования спектра на экран, как
это делал сам Ньютон в своих более
поздних опытах. Если на щель простого
спектроскопа (как теперь называется
устройство, состоящее из щели, линз и
призмы) направить свет от лампы
накаливания, то на экране возникает
непрерывный спектр со следующим порядком
чередования цветов: фиолетовый, синий,
голубой, зеленый, желтый, оранжевый и
красный. Если же щель осветить пламенем,
в которое внесена крупинка поваренной
соли (хлорида натрия NaCl), то спектр будет
фактически состоять из двух близко
расположенных ярких желтых линий.
Аналогично, если щель осветить красным
светом неоновой рекламной трубки, то
на экране появится ряд ярких красных
линий. Здесь каждая линия – это изображение
щели спектроскопа, образованное светом
определенной длины волны, а полученный
спектр называется линейчатым спектром
испускания. Существуют спектры, состоящие
из групп линий, расположенных настолько
тесно, что каждая группа выглядит как
узкий участок непрерывного спектра. Такие спектры называются полосатыми.
Такие спектры называются полосатыми.
krugosvet.ru
Спектр.
Спектр — , спектра, м. (латин. spectrum — призрак) (физ.). 1. Разноцветная полоса, получающаяся при прохождении светового луча через стеклянную призму или диффракционную решетку. Солнечный спектр или спектр солнца. Спектр Сириуса. Спектр водорода. 2. распределение лучистой энергии, испускаемой каким-н. источником света, по длине волн. Спектр магнитный (физ.) — распределение сил магнита по разным направлениям, обнаруживаемое в рисунке железных опилок, к-рыми покрывают поверхность магнита.
Проверка гравитационного закона обратных квадратов – Physics World
Если Вселенная содержит более трех пространственных измерений, как считают многие физики, наши современные законы гравитации должны нарушаться на малых расстояниях
Торсионный маятник Нет ничего более достоверного, чем «факт», что пространство имеет три измерения. Но можем ли мы быть уверены, что существует только три измерения? Представьте себе канатоходца, балансирующего на канате высоко над землей. Для канатоходца трос фактически является одномерным объектом, потому что ему нужна только одна координата, чтобы указать свое положение, когда он ходит туда-сюда. Но муравей, например, видит кабель как двумерный объект, потому что он может ползать по кабелю, а также вокруг него.
Для канатоходца трос фактически является одномерным объектом, потому что ему нужна только одна координата, чтобы указать свое положение, когда он ходит туда-сюда. Но муравей, например, видит кабель как двумерный объект, потому что он может ползать по кабелю, а также вокруг него.
Сегодня все больше физиков серьезно задаются вопросом, подобны ли мы канатоходцам, не знающим истинного количества измерений в пространстве. Новые идеи теоретической физики предполагают, что лучший способ обнаружить реальную размерность пространства — это изучить, как гравитационное притяжение между двумя объектами зависит от расстояния между ними.
Когда Исаак Ньютон понял, что ускорение Луны при ее обращении вокруг Земли может быть связано с ускорением яблока при падении на землю, это был первый случай, когда два, казалось бы, не связанных между собой физических явления были «объединены». . Стремление объединить все силы природы до сих пор занимает физиков. Ньютон показал, что гравитационное притяжение между двумя точечными телами пропорционально произведению их масс и обратно пропорционально квадрату расстояния между ними: F = GMm/r 2 , где F — сила, G — гравитационная постоянная Ньютона, M и m — массы тел, r — расстояние между ними. . Закон Гаусса и дополнительные измерения15. Радикально новая теория Эйнштейна привела гравитацию в соответствие с двумя основными идеями относительности: мир четырехмерен — три направления пространства объединены со временем — и никакое физическое воздействие не может двигаться быстрее света. Общая теория относительности утверждает, что гравитация — это не сила в обычном смысле, а следствие искривления этого пространства-времени, создаваемого массой или энергией. Однако в пределе низких скоростей и слабых гравитационных полей теория Эйнштейна по-прежнему предсказывает, что гравитационная сила между двумя точечными объектами подчиняется закону обратных квадратов.
. Закон Гаусса и дополнительные измерения15. Радикально новая теория Эйнштейна привела гравитацию в соответствие с двумя основными идеями относительности: мир четырехмерен — три направления пространства объединены со временем — и никакое физическое воздействие не может двигаться быстрее света. Общая теория относительности утверждает, что гравитация — это не сила в обычном смысле, а следствие искривления этого пространства-времени, создаваемого массой или энергией. Однако в пределе низких скоростей и слабых гравитационных полей теория Эйнштейна по-прежнему предсказывает, что гравитационная сила между двумя точечными объектами подчиняется закону обратных квадратов.
Дополнительные измерения, жирные гравитоны и новые частицы
Общая теория относительности была проверена с исключительной точностью с помощью астрономических наблюдений, лабораторных экспериментов и различных космических аппаратов (см. «Relativity at the centenary» Клиффорда М. Уилла в Physics World January pp27-32 ).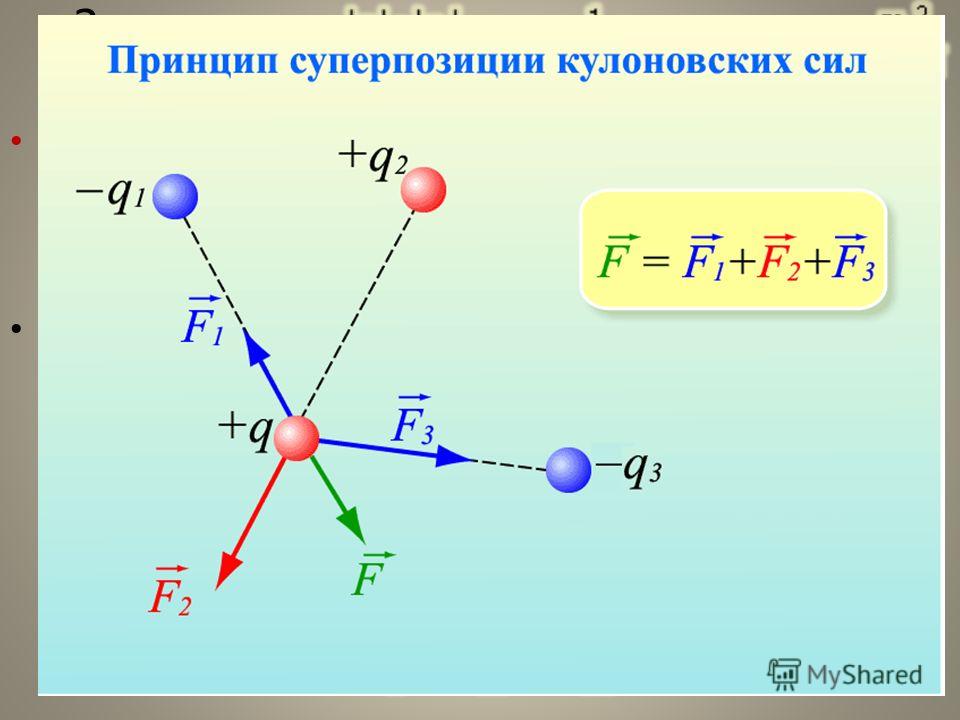 Хотя теория Эйнштейна уже прошла все эти проверки, ясно, что квантовые эффекты приведут к нарушению общей теории относительности на расстояниях, сравнимых с планковской длиной, которая определяется как L P = √( ч бар G/c 3 )≃ 1,6 x 10 -35 м, где ч бар – постоянная Планка, деленная на 2π, а 90 – скорость света 900 c , а 90 . Однако планковская длина настолько мала, что не оказывает заметного влияния ни в одном практическом гравитационном эксперименте.
Хотя теория Эйнштейна уже прошла все эти проверки, ясно, что квантовые эффекты приведут к нарушению общей теории относительности на расстояниях, сравнимых с планковской длиной, которая определяется как L P = √( ч бар G/c 3 )≃ 1,6 x 10 -35 м, где ч бар – постоянная Планка, деленная на 2π, а 90 – скорость света 900 c , а 90 . Однако планковская длина настолько мала, что не оказывает заметного влияния ни в одном практическом гравитационном эксперименте.
Одной из нерешенных задач в физике является завершение того, что начал Ньютон, и достижение окончательного «великого объединения» — объединение гравитации с тремя другими фундаментальными силами (электромагнитным взаимодействием, сильным и слабым ядерными взаимодействиями) в один квант. теория. В теории струн — одном из главных кандидатов на окончательную теорию — фундаментальными сущностями природы являются одномерные струны и многомерные объекты, называемые «бранами», а не знакомые нам точечные частицы.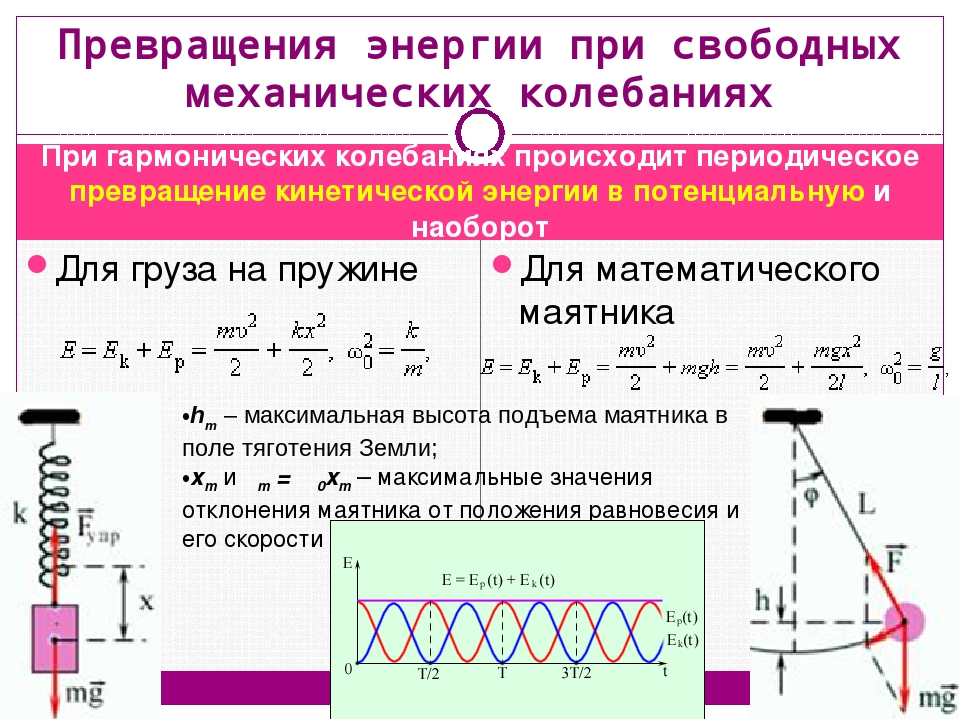 Струнные теоретики серьезно относятся к идее, что на самом деле существует шесть или семь дополнительных пространственных измерений; эти дополнительные измерения необходимы, чтобы сделать теорию математически последовательной и способной описывать гравитацию.
Струнные теоретики серьезно относятся к идее, что на самом деле существует шесть или семь дополнительных пространственных измерений; эти дополнительные измерения необходимы, чтобы сделать теорию математически последовательной и способной описывать гравитацию.
Торсионный маятник Эёта-Ваша
Конечно, эти «дополнительные» измерения должны отличаться от трех бесконечных измерений, с которыми мы знакомы, иначе мы бы заметили их раньше. До недавнего времени предполагалось, что они не бесконечны, а закручены с радиусом, сравнимым с планковской длиной. Хотя это означает, что дополнительные измерения практически невидимы, их присутствие предотвращает неприятные бесконечности, которые досаждают традиционным квантово-полевым теориям гравитации.
Одна из больших загадок гравитации заключается в том, что она намного слабее других взаимодействий: она примерно в 10 40 раз слабее электростатических и магнитных сил. В 1998 году три теоретика — Нима Аркани-Хамед, Савас Димопулос и Гия Двали — предложили смелое объяснение этой слабости (см. дополнительную литературу). По их словам, гравитация кажется слабой, потому что некоторые из дополнительных измерений, предсказанных теорией струн, удивительно велики по сравнению с длиной Планка.
дополнительную литературу). По их словам, гравитация кажется слабой, потому что некоторые из дополнительных измерений, предсказанных теорией струн, удивительно велики по сравнению с длиной Планка.
Аркани-Хамед и его коллеги утверждали, что мы живем на бране с тремя пространственными измерениями, которая встроена во вселенную, содержащую в общей сложности девять пространственных измерений. Все частицы в Стандартной модели (включая фотон) представляют собой струны, концы которых прочно приклеены к бране. Однако гравитон, частица, которая, как считается, несет гравитационную силу, представляет собой замкнутую петлю струны и поэтому может свободно перемещаться во всех девяти пространственных измерениях. Гравитация кажется, что слабее других сил, потому что действует в девяти измерениях, а не в трех, и это «разбавляет» его силу.
2 Проверка новых теорий
Эта картина «мира бран» подразумевает, что мы должны использовать гравитацию, если хотим открыть истинное число пространственных измерений нашей вселенной. Одно большое дополнительное измерение можно исключить, потому что оно должно иметь размер 3 x 10 12 м, чтобы объяснить, почему гравитация такая слабая. Однако Аркани-Хамед и его коллеги показали, что если бы два дополнительных измерения были большими, они должны были бы иметь размер около 0,3 мм, чтобы учесть слабость гравитации. Если исследователи правы, закон Гаусса означает, что гравитационная сила будет изменяться как 1/ r 4 , а не 1/ r 2 , на расстоянии менее 0,3 мм (см. рис. 1). Другими словами, гравитация будет усиливаться на коротких расстояниях.
Одно большое дополнительное измерение можно исключить, потому что оно должно иметь размер 3 x 10 12 м, чтобы объяснить, почему гравитация такая слабая. Однако Аркани-Хамед и его коллеги показали, что если бы два дополнительных измерения были большими, они должны были бы иметь размер около 0,3 мм, чтобы учесть слабость гравитации. Если исследователи правы, закон Гаусса означает, что гравитационная сила будет изменяться как 1/ r 4 , а не 1/ r 2 , на расстоянии менее 0,3 мм (см. рис. 1). Другими словами, гравитация будет усиливаться на коротких расстояниях.
Однако в прошлом году Раман Сандрам из Университета Джона Хопкинса в Балтиморе сделал совершенно иной прогноз. Сандрам пытался понять «темную энергию», загадочную субстанцию, которая противостоит гравитации и, как считается, вызывает ускорение расширения Вселенной. Сначала считалось, что квантово-механическая энергия вакуума — из-за создания короткоживущих пар частица-античастица, что разрешено принципом неопределенности Гейзенберга — ответственна за темную энергию. Единственная проблема заключалась в том, что теоретики предсказывают значение этой вакуумной энергии как минимум 10 60 раз больше, чем наблюдаемое значение темной энергии, которая имеет плотность около 4 кэВ в каждом кубическом сантиметре пространства.
Единственная проблема заключалась в том, что теоретики предсказывают значение этой вакуумной энергии как минимум 10 60 раз больше, чем наблюдаемое значение темной энергии, которая имеет плотность около 4 кэВ в каждом кубическом сантиметре пространства.
Сундрум показал, что это значение, постоянная Планка и скорость света могут быть объединены для определения масштаба длины около 0,1 мм, и далее предположил, что коэффициент 10 60 можно было бы объяснить, если бы гравитация была намного слабее на расстояния короче этого. Он предположил, что гравитон в теории струн может быть «толстым» объектом, который не может «видеть» большинство процессов на коротких расстояниях, ответственных за обычную вакуумную энергию. Это также привело бы к тому, что гравитационное взаимодействие стало бы очень слабым для масс, разделенных меньшим размером, чем размер «толстого» гравитона (см. дальнейшее чтение).
3 Стэнфордский микрокантилевер
Даже без больших дополнительных измерений и толстых гравитонов теории струн содержат много новых и пока не наблюдаемых частиц. К ним относятся дилатон (который является партнером гравитона в теории струн), радион (стабилизирующий размер дополнительных измерений) и различные «модули» (частицы, задающие значения сил связи, масс частиц и других параметров в Стандартная модель). Квантово-механический обмен этими частицами привел бы к очень сильным силам ближнего действия, которые могли бы проявиться при проверке закона обратных квадратов.
К ним относятся дилатон (который является партнером гравитона в теории струн), радион (стабилизирующий размер дополнительных измерений) и различные «модули» (частицы, задающие значения сил связи, масс частиц и других параметров в Стандартная модель). Квантово-механический обмен этими частицами привел бы к очень сильным силам ближнего действия, которые могли бы проявиться при проверке закона обратных квадратов.
Проверка закона обратных квадратов
Удивительно, но еще несколько лет назад даже не было доказано существование гравитации для объектов, расстояние между которыми меньше 1 мм. Для этого было две причины: во-первых, гравитация сама по себе очень слаба по сравнению с электростатическими и магнитными силами; во-вторых, сейсмические, тепловые и другие фоновые воздействия сильно затрудняют проведение экспериментов. К счастью, электростатические силы, в отличие от силы тяжести, можно экранировать с помощью проводящего экрана, и в недавних экспериментах с крутильным маятником была измерена гравитационная сила между объектами, расстояние между которыми составляет менее 65 мкм.
4 Астрономические тесты
Торсионные маятники уже более 200 лет используются для измерения слабых взаимодействий между макроскопическими объектами, и они до сих пор являются наиболее чувствительными инструментами для проведения таких измерений. Ранние версии прибора использовались для измерения плотности Земли (Джон Митчелл в 1750 г.), электростатической силы (Чарль Огюстен де Кулон, 1785 г.) и G (Генри Кавендиш, 1798 г.). Позже, в 1890 году, барон фон Этвос использовал торсионный маятник для проверки эквивалентности гравитационной массы (т.е. м в F = GMm/r 2 ) и инерционная масса ( м в F = ma ). И сегодня современные версии торсионного маятника используются в различных экспериментах, включая высокоточные измерения G и проверки симметрии Лоренца (см. «Нарушение симметрии Лоренца» Роберта Блюма в Physics World , март 2004 г., стр. 41). -46). Торсионный маятник также использовался для проверки того, что «темная материя» подчиняется принципу эквивалентности.
Хотя современные торсионные маятники принимают множество различных форм, которые физик 200-летней давности не распознал бы, основные принципы остались практически неизменными (см. вставку). В традиционном крутильном маятнике гравитационная сила между двумя пробными массами, подвешенными на волокне (маятник), и двумя неподвижными массами (аттрактор) заставляет волокно скручиваться на величину, зависящую от силы. Этот поворот обычно измеряется путем отражения луча света от зеркала на маятнике.
Как ни странно, этот прибор подходит для гравитационных измерений, потому что вращательное движение маятника вокруг оси торсионного волокна не чувствительно к гравитации Земли. Кроме того, он нечувствителен к суммарным силам, действующим на его центр масс, а это означает, что он может быть существенно отделен от внешних колебаний, большинство из которых намного больше, чем интересующие эффекты.
Современные крутильные маятники чувствительны к крутящим моментам до 10 -18 Н·м. Поскольку крутящий момент определяется как произведение силы на длину, а типичная длина маятника составляет около 1 см, это эквивалентно чувствительности к силе около 10 -16 Н. Эта удивительно малая сила примерно эквивалентна 1/100 веса одной части почтовой марки, которая была разделена на триллион равных частей! На сегодняшний день торсионный маятник является единственным инструментом, способным точно измерять свойства гравитационного взаимодействия на масштабах длины менее 1 мм.
Поскольку крутящий момент определяется как произведение силы на длину, а типичная длина маятника составляет около 1 см, это эквивалентно чувствительности к силе около 10 -16 Н. Эта удивительно малая сила примерно эквивалентна 1/100 веса одной части почтовой марки, которая была разделена на триллион равных частей! На сегодняшний день торсионный маятник является единственным инструментом, способным точно измерять свойства гравитационного взаимодействия на масштабах длины менее 1 мм.
С середины 1980-х годов группы Калифорнийского университета в Ирвине, Московского государственного университета, а также авторы и коллеги из группы Эёт-Ваша в Вашингтонском университете в Сиэтле используют торсионные маятники для выполнения все более сложных задач. чувствительные тесты закона обратных квадратов на коротких расстояниях. Если выполняется закон обратных квадратов, гравитационная потенциальная энергия пары точечных масс может быть записана как: В = -GMm/r . Исследователи обычно ищут новую силу, которая нарушает закон обратных квадратов Ньютона с характерным масштабом длины: это включает в себя поиск потенциала формы V = -(GMm/r) (1 + αe -r/λ ) , где α — мера силы новой силы, а λ — ее диапазон. Этот новый «потенциал Юкавы» обычно описывает короткодействующую силу, которую будет нести частица с массой ч бар/сλ , и это хорошее приближение к эффектам дополнительных измерений, пока расстояния не станут меньше, чем размер тех размеров.
Этот новый «потенциал Юкавы» обычно описывает короткодействующую силу, которую будет нести частица с массой ч бар/сλ , и это хорошее приближение к эффектам дополнительных измерений, пока расстояния не станут меньше, чем размер тех размеров.
Измерения при расстоянии всего 0,14 мм, проведенные нашей группой в Сиэтле, уже исключили первоначальный сценарий Аркани-Хамеда и его сотрудников для двух больших дополнительных измерений, а недавние предварительные результаты показывают, что любое дополнительное измерение должно быть меньше примерно 60 мкм (см. рисунок 2).
Минимальное расстояние между маятником и аттрактором в этом эксперименте — самый важный экспериментальный параметр — было ограничено сейсмическими колебаниями, случайными частицами пыли и неопределенностями выравнивания. Будущие усилия будут исследовать гравитацию с расстоянием менее 50 мкм — расстояние, соответствующее примерно половине диаметра человеческого волоса!
Все меньше и меньше
Многообещающие новые методы с использованием небольших осцилляторов и микрокантилеверов также внедряются для поиска новой физики, скрытой в поведении гравитации на коротких расстояниях. Хотя эти устройства еще не достигли чувствительности крутильных маятников, современные технологии изготовления позволяют сделать их намного меньше и жестче. Это устраняет проблемы, связанные с сейсмическим шумом и выравниванием, и позволяет исследовать гораздо меньшие расстояния между тестовыми массами.
Хотя эти устройства еще не достигли чувствительности крутильных маятников, современные технологии изготовления позволяют сделать их намного меньше и жестче. Это устраняет проблемы, связанные с сейсмическим шумом и выравниванием, и позволяет исследовать гораздо меньшие расстояния между тестовыми массами.
В 2003 году Джон Прайс и его коллеги из Университета Колорадо в Боулдере сообщили о первых результатах эксперимента с торсионным генератором, в котором тестовая масса представляет собой вольфрамовую пластину толщиной примерно 0,2 мм, которая вращается вокруг горизонтальной оси и исходная масса представляет собой вольфрамовый кантилевер размерами 35 х 7 х 0,3 мм. Консоль находится под пластиной с одной стороны от оси закручивания, а расстояние между двумя массами составляет около 0,1 мм. Устройство управляется на резонансной частоте одной из крутильных мод пластины, которая составляет около 1 кГц (по сравнению с примерно 1 мГц для крутильного маятника), и отклике пластины тестовой массы на другой стороне ось закручивания наблюдается с использованием емкостных методов (см. Long и др. в дальнейшем чтении).
Long и др. в дальнейшем чтении).
Использование плоских листов для тестовых и исходных масс делает ньютоновский фон в этом эксперименте очень малым, поэтому обнаружение ложного возбуждения на резонансной частоте может означать существование нового короткодействующего эффекта. Хотя это устройство еще недостаточно чувствительно, чтобы обнаруживать гравитацию, оно может обнаруживать новые силы, более сильные, чем гравитация, на небольших расстояниях, и в ближайшем будущем чувствительность должна повыситься до уровня, необходимого для непосредственного исследования гравитации на очень малых расстояниях.
Тем временем Штефан Шиллер и его коллеги из Университета Дюссельдорфа в Германии построили аттракторную массу с вращающимся колесом, которая напоминает ту, что использовалась в торсионном маятнике Эота-Уоша, а их детектор напоминает пластину, использовавшуюся в эксперименте в Колорадо. Новые результаты по этой группе будут сообщены в ближайшем будущем.
В другом месте Аарон Капитульник и его коллеги из Стэнфордского университета использовали методы изготовления полупроводников для изготовления микроконсольных устройств, которые непосредственно воспринимают силу между массами, а не измеряют крутящий момент (см. Chiaverini 9).0009 и др. в дальнейшем чтении и рис. 3). Их первые результаты, полученные при расстоянии всего 25 мкм, обеспечивают наиболее чувствительные ограничения любых таких сил в диапазоне расстояний менее 10 мкм. Стэнфордская группа в настоящее время разрабатывает модифицированный аппарат, который будет иметь значительно повышенную чувствительность.
Chiaverini 9).0009 и др. в дальнейшем чтении и рис. 3). Их первые результаты, полученные при расстоянии всего 25 мкм, обеспечивают наиболее чувствительные ограничения любых таких сил в диапазоне расстояний менее 10 мкм. Стэнфордская группа в настоящее время разрабатывает модифицированный аппарат, который будет иметь значительно повышенную чувствительность.
Проверка гравитации с помощью нейтронов
Торсионные маятники и другие механические осцилляторы достигли наибольшей чувствительности к гравитации на коротких расстояниях, поскольку они содержат огромное количество атомов, а гравитационный сигнал растет примерно пропорционально квадрату числа атомов. Однако в принципе также возможно исследовать поведение гравитации на коротких расстояниях с помощью отдельных частиц или небольших групп частиц. Большинство этих экспериментов было проведено с нейтронами, потому что, будучи нейтральными, они не испытывают значительных электрических сил, вызванных фоновыми полями или поверхностями.
В 2001 году Валерий Несвижевский и его коллеги из нейтронного источника Института Лауэ-Ланжевена в Гренобле, Франция, направили сильно коллимированный пучок ультрахолодных нейтронов на поверхность горизонтальной полированной стеклянной пластины под скользящим углом. Нейтроны двигались так медленно (менее 5 м с -1 ), что они отражались барьером потенциальной энергии, связанным с сильным ядерным взаимодействием на поверхности. Совместное воздействие гравитации (действующей вниз) и поверхности (действующей вверх) создало одномерную потенциальную яму — качественно знакомую всем физикам по их первым лекциям по квантовой механике — в вертикальном направлении.
Несвижевский и его коллеги поместили поглотитель нейтронов над пластиной и подсчитали количество нейтронов, которые отразились от поверхности и достигли детектора на дальней стороне, когда они перемещали поглотитель вверх и вниз. Они обнаружили, что количество нейтронов значительно увеличилось, когда расстояние между пластиной и поглотителем стало больше, чем высота квантового основного состояния гравитационной потенциальной ямы, и что оно снова увеличилось, когда поглотитель был поднят выше высоты первого возбужденное состояние. Это был первый случай наблюдения квантовых состояний в гравитационном поле Земли.
Это был первый случай наблюдения квантовых состояний в гравитационном поле Земли.
Хотя этот и последующие эксперименты не были достаточно чувствительными, чтобы обнаружить отклонения от закона обратных квадратов, Несвижевский и его коллеги смогли установить верхние пределы для новых сил, которые очень намного сильнее гравитации для расстояний между 1 нм и 1 мкм (см. дальнейшее чтение). Такая сила изменила бы потенциальную яму и, следовательно, изменила бы вертикальное распределение нейтронов.
Испытания на астрономических расстояниях
Хотя основное внимание уделяется поведению гравитации на коротких расстояниях, вполне возможно, что крошечные отклонения от закона обратных квадратов возникают на гораздо больших расстояниях. В 2003 году Двали, который сейчас работает в Нью-Йоркском университете, и двое его коллег, Андрей Грузинов и Маттиас Залдарриага, исследовали возможность того, что некомпактные дополнительные измерения могут вызывать такие отклонения на астрономических расстояниях (см. дополнительную литературу).
дополнительную литературу).
Безусловно, самые строгие ограничения на проверку закона обратных квадратов на сегодняшний день связаны с удивительно точными измерениями орбиты Луны вокруг Земли. Однако эта изумительная чувствительность достигается для величин порядка расстояния между Землей и Луной. Эти эксперименты включают отражение лазерных лучей от ретрорефлекторных решеток, размещенных на Луне астронавтами Аполлона и беспилотным советским спускаемым аппаратом. Несмотря на то, что орбита Луны имеет средний радиус 384 000 км, модели согласуются с данными на уровне 4 мм!
Наблюдаемая величина, которая лучше всего подходит для проверки закона обратных квадратов в этой системе, — это прецессия большой оси орбиты Луны (см. рис. 4). Согласно классической механике, большая ось вообще не должна прецессировать при наличии 1/ r 2 гравитационного взаимодействия. Действительно, это был большой триумф общей теории относительности, когда Эйнштейн смог объяснить ранее загадочную прецессию большой оси орбиты Меркурия на 420 миллисекунд дуги в год.
Если учесть эффекты общей теории относительности и влияние Солнца и других планет, прогнозируемое значение прецессии лунной орбиты (19 миллисекунд дуги в год) очень хорошо согласуется с измерениями, и любые вызванные расхождения при возможном нарушении закона обратных квадратов должно быть менее 270 угловых микросекунд в год. Однако, если бы мы могли измерить орбиту Луны еще точнее, мы могли бы обнаружить небольшие отклонения от закона обратных квадратов на больших расстояниях, как и предсказывали некоторые теоретики.
Том Мерфи из Калифорнийского университета в Сан-Диего и его коллеги из Гарвардского и Вашингтонского университетов недавно запустили новую программу лунного лазерного определения дальности под названием APOLLO, в которой будет использоваться более крупный телескоп в лучшем месте (на вершине горы около Уайта). Sands в Нью-Мексико) и более сложный детектор фотонов, чтобы повысить точность этих измерений в 10 раз. Вместо того, чтобы получать примерно один отраженный фотон на каждые 100 лазерных выстрелов, APOLLO должен подсчитывать несколько фотонов за выстрел (см. 9).0009 Мир физики июнь 2004 г. стр. 9).
9).0009 Мир физики июнь 2004 г. стр. 9).
Что, если закон обратных квадратов не работает?
Предположим, что следующее поколение экспериментов обнаружит силу между двумя тестовыми объектами, которая отличается от того, что можно было бы ожидать от обычной гравитации. Несоответствие может быть новым свойством самой гравитации, таким как дополнительное пространственное измерение или большой гравитон, или оно может быть связано с новым взаимодействием, которое действует в дополнение к гравитации. Как можно различить эти возможности?
Первым шагом было бы выяснить, зависит ли размер несоответствия от состава тестовых объектов. Гравитация обладает тем уникальным свойством, что она одинаково взаимодействует со всеми материалами, так что все объекты, независимо от их состава, падают с одинаковой скоростью в однородном гравитационном поле. Это следствие эквивалентности между гравитацией и ускорением, которая является фундаментальным принципом, на котором Эйнштейн основал общую теорию относительности. Любая новая негравитационная сила будет по-разному воздействовать на разные материалы, поэтому, если мы обнаружим, что отклонение от закона обратных квадратов зависит от состава, мы можем исключить дополнительные измерения как источник эффекта. Также было бы важно измерить, как любые отклонения изменялись с расстоянием.
Любая новая негравитационная сила будет по-разному воздействовать на разные материалы, поэтому, если мы обнаружим, что отклонение от закона обратных квадратов зависит от состава, мы можем исключить дополнительные измерения как источник эффекта. Также было бы важно измерить, как любые отклонения изменялись с расстоянием.
Взрыв идей последних лет о новых частицах и новых измерениях изменил наши представления о Вселенной. Открытие темной энергии также подтвердило, что мы многого не понимаем. Если бы Эйнштейн был еще жив, ему наверняка было бы любопытно узнать, не идем ли мы по канату.
Закон обратных квадратов: математика и физика Научная деятельность
Все мы знаем, что чем дальше мы уходим, тем тусклее кажется свет. На вопрос, насколько тусклее он выглядит, был дан ответ давно. Вот простой способ повторить это открытие.
Тема:
Данные
Сбор и анализ данных
Математика
Nature of Science
Измерение
Физика
Light
Ключевые слова:
Sun
График
. EP&C:
EP&C:
PS
PS3
CCC
Образцы
Масштаб, доля и количество
Энергия и материя
Инструменты и материалы
- Фонарик Mini Maglite (или другой небольшой яркий источник света)
- Правитель
- Каталожная карточка 3 x 5
- X-Acto нож или ножницы
- Скрепка среднего размера
- Миллиметровая бумага с квадратами 1/2 дюйма или 1/4 дюйма (если используется метрическая система, используйте миллиметровку с квадратами размером 1 см).
- Картонная коробка или кусок пенопласта (не показан)
- Лента
Сборка
- Используйте линейку и нож X-Acto, чтобы измерить и вырезать квадрат 1/2 × 1/2 дюйма в центре каталожной карточки.
- Прикрепите зажим для переплета к нижней части карты, чтобы сделать подставку.
- Прикрепите миллиметровку к картонной коробке или куску пенопласта, чтобы получился экран.

- Затем отвинтите узел переднего отражателя Mini Maglite, чтобы получить доступ к лампе. Лампа загорится и останется гореть после снятия узла отражателя (см. изображение ниже).
- Подоприте фонарь так, чтобы он был на той же высоте, что и квадратное отверстие, которое вы вырезали в открытке.
- Расположите карту на расстоянии одного дюйма от источника света.
- Выровняйте Mini Maglight, квадратное отверстие и миллиметровку так, чтобы, когда свет проходит через отверстие, вы видели светящийся квадрат на миллиметровке.
Если вы используете метрические единицы:
- Следуйте приведенным выше инструкциям, но вместо отверстия размером 1/2 x 1/2 дюйма вырежьте квадратное отверстие размером 1 x 1 см в центре каталожной карточки.
- Расположите карту на расстоянии 2 см от источника света.
- Используйте миллиметровую бумагу с напечатанными на ней квадратами размером 1 см.

Действия и уведомления
Держите расстояние между лампочкой и картой с квадратным отверстием постоянным и равным одному дюйму. (Если вы используете метрическую миллиметровую бумагу, мы рекомендуем расстояние 2 см.) Поместите миллиметровую бумагу на разное расстояние от лампочки и подсчитайте, сколько квадратов на миллиметровой бумаге освещено на каждом расстоянии (щелкните, чтобы увеличить диаграмму ниже). . Результаты будет легче понять, если вы составите таблицу «количество освещенных квадратов» по сравнению с «расстоянием». Обязательно каждый раз измеряйте расстояние от миллиметровой бумаги до лампочки.
Что происходит?
Когда вы перемещаете миллиметровую бумагу, свет от Mini Maglite равномерно распространяется во всех направлениях. По мере увеличения расстояния от лампочки до миллиметровой бумаги одно и то же количество света распространяется на все большую и большую площадь, и свет, достигающий каждого квадрата, становится соответственно менее интенсивным. Например, отрегулируйте расстояние от лампочки до миллиметровки на 1 дюйм. На этом расстоянии миллиметровка касается карты. Один квадрат (размером 1/2 дюйма) будет освещен. Когда миллиметровка перемещается на 2 дюйма от карты, на миллиметровке загораются четыре квадрата. Когда миллиметровка переместится на 3 дюйма от карты, будут освещены девять квадратов. При 4 дюймах будет освещено шестнадцать квадратов и так далее. Освещенная площадь будет увеличиваться пропорционально квадрату расстояния. (Если вы используете метрическую миллиметровую бумагу, попробуйте перемещать миллиметровую бумагу с шагом 2 см.)
Например, отрегулируйте расстояние от лампочки до миллиметровки на 1 дюйм. На этом расстоянии миллиметровка касается карты. Один квадрат (размером 1/2 дюйма) будет освещен. Когда миллиметровка перемещается на 2 дюйма от карты, на миллиметровке загораются четыре квадрата. Когда миллиметровка переместится на 3 дюйма от карты, будут освещены девять квадратов. При 4 дюймах будет освещено шестнадцать квадратов и так далее. Освещенная площадь будет увеличиваться пропорционально квадрату расстояния. (Если вы используете метрическую миллиметровую бумагу, попробуйте перемещать миллиметровую бумагу с шагом 2 см.)
Интенсивность света – это мощность на единицу площади. Поскольку энергия, проходящая через прорезанное вами отверстие, распространяется на большую площадь, интенсивность света уменьшается. Поскольку площадь увеличивается пропорционально квадрату расстояния, интенсивность света должна уменьшаться пропорционально квадрату расстояния. Таким образом, интенсивность подчиняется закону обратных квадратов.
Идем дальше
Закон обратных квадратов применим не только к интенсивности света, но также к гравитационным и электрическим силам. Сила притяжения Земли падает на 1/9.0289 r 2 , где r — расстояние от центра земли. Притяжение или отталкивание между двумя электрическими зарядами также уменьшается с расстоянием на 1/ r 2 , где r — расстояние между двумя зарядами.
Сопутствующие закуски
Фотометр масляных пятен
Сравните яркость двух источников света с масляным пятном на белой карточке.
Похожие экспонаты
Закон обратных квадратов
Свет становится тем тусклее, чем дальше он распространяется, и простая математика объясняет, как это сделать.
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Атрибуция: Педагогический институт Exploratorium
Определение закона обратных квадратов
Теперь, не волнуйтесь! Для некоторых из вас слова «Закон обратных квадратов» могут вызвать болезненные воспоминания о том уроке математики в старшей школе, который, как вы думали, наконец-то позади, но мы обещаем, что это не так сложно. Мы объясним эту концепцию, используя термины непрофессионала или, как я их называю; «Условия Пиемана».
Мы объясним эту концепцию, используя термины непрофессионала или, как я их называю; «Условия Пиемана».
Закон обратных квадратов можно легко понять, если помнить об этих двух вещах.
- Ваш свет теряет мощность по мере увеличения расстояния от источника до объекта.
- Вы потеряете этот свет быстрее, чем вы думаете.
Например, если вы установили источник света на расстоянии 1 метра от объекта, и вы получаете 100% мощность вспышки, которая попадает на объект. Вы перемещаете свет на 1 метр назад, и теперь вы находитесь на расстоянии 2 метров. Означает ли это, что вы потеряли половину своего света, около 50%? Вроде бы логично, но это не так. Вы фактически теряете 75% своего света. Мы можем сказать это по-другому. У вас есть только 25% интенсивности вашего света, попадающего на объект, или ¼ вашего света. Ниже диаграмма увеличена, чтобы помочь визуализировать это.
Прежде чем мы двинемся дальше, давайте быстро взглянем на реальную формулу.
Интенсивность=1/Расстояние²
Почему он называется законом обратных квадратов? Давайте разберем это дальше шаг за шагом:
Проще говоря, инверсия означает противоположность самой себе. Вы переворачиваете его. Например, 2 будет ½, а 4 будет ¼.
Проще говоря, квадрат означает число, умноженное само на себя. Например, 2х2 или 10х10.
Когда мы объединяем их, мы получаем обратный квадрат.
2 обратное равно ½
½ в квадрате равно ½ X ½
А что такое ½ X ½? Это ¼.
Таким образом, 2 обратного квадрата равно ¼. Другой способ сказать это с точки зрения фотографии: на расстоянии 2 метров вы получаете ¼ мощности. Это закон обратных квадратов. Вот как вы это понимаете. Если вы знаете расстояние, на котором вы собираетесь находиться от объекта, все, что вам нужно сделать, это подставить это число в формулу, чтобы узнать, сколько света вы потеряете.
Глядя на наш график, вы также замечаете кое-что очень интересное. От 1 метра до 6 метров процент потери света драматичен. А вот от 6 до 7 метров не так драматично, всего 0,6%. Также от 7 метров до 8 метров, это всего около 0,5%.
Зная эти основы, закон обратных квадратов чаще всего используется при съемке больших групповых фотографий. Он имеет практический смысл. Если вы разместите свой источник света впереди и в центре своей группы на расстоянии около 3 метров, основываясь на нашей таблице и формуле, вы можете подумать, что группа будет получать 11,11% вашего света, и вы соответствующим образом отрегулируете (увеличив мощность). Но только человек в центре будет получать 11,11%.
Люди в дальних углах группы будут дальше, чем в центре. Они могут находиться на расстоянии 6 метров от источника света, что дает им только 2,78% мощности. Это создает очень нелестный и неравномерный свет для групповых портретов. Поскольку мы знаем, что интенсивность света имеет менее резкое падение на большем расстоянии, мы должны отодвинуть источник света еще дальше, чтобы обеспечить равномерное освещение всех людей.
Равномерное освещение семьи Закон обратных квадратов не так сложен, как кажется, и знание этих основ принесет вам большую пользу.
Закон обратных квадратов на практике | Транскрипция
Ниже приведена полная транскрипция видео выше
Это мой любимый слайд. Перевернутый Квадрат Пай-мэн, что-то вроде Пакмана, но я Пай. Ты понял? Хорошо, вы получите это всего за секунду. Эта прекрасная демонстрация в реальном мире, или действительно моя демонстрация в реальном мире, дает вам пример закона обратных квадратов на практике. Это не очень хорошая практика, но она показывает вам пример. У нас есть свет, размещенный здесь, с левой стороны. Это все разные кадры, и в основном здесь мы находимся в одном футе, двух футах, трех футах, четырех футах, пяти футах, шести футах от света.
Допустим, одним футом мы получаем сто процентов желаемого света. Когда мы отойдем на два фута, вы заметите, что я намного темнее, чем на этом снимке. Этот кадр практически на грани провала. Этот выстрел составляет одну четверть интенсивности этого выстрела. Когда мы отходим, ты видишь, как я становлюсь все темнее и темнее.
Этот выстрел составляет одну четверть интенсивности этого выстрела. Когда мы отходим, ты видишь, как я становлюсь все темнее и темнее.
Интересно отметить, что разница между одним футом и, скажем, тремя футами, чрезвычайно драматична в яркости. Это огромная разница, но разница между пятью и даже семью футами очень мала. Это намного меньше, чем та начальная разница. По сути, мы узнаем, что чем дальше мы удаляемся от источника света, тем свет падает гораздо медленнее, чем вблизи этого источника света.
Мы видели это в мире Пай. Давайте посмотрим еще одну демонстрацию в реальном мире с участием жуткого Джозефа. Что мы здесь сделали? Ну, обратная квадратная линия, и практика, и пусть он не сделает такую дерьмовую фотографию на практике. Это просто потому, что я хочу показать вам жуткую, дерьмовую фотографию, но на этом снимке мы сделали то, что в основном поместили вспышку прямо на левую сторону лица Оливии. Джо находится на расстоянии примерно одного фута от Оливии. Расстояние до Оливии составляет примерно один фут от вспышки, и это делает расстояние Джо от вспышки вдвое больше, чем расстояние Оливии.
Если вы посмотрите на Оливию, она красивая, яркая и с правильной экспозицией, а если вы посмотрите на Джо, то увидите, что он недоэкспонирован примерно на три-четыре шага. Особенно, когда вы начинаете переходить к другой стороне его лица, он становится еще темнее. Теперь Джо немного подкрался к ней, чтобы приблизиться к этому, но здесь вспышка находится в основном в четырех футах от модели. Теперь, что мы сделали здесь, все, что мы делаем, это регулируем мощность вспышки.
Каждый раз, когда мы делаем шаг в сторону, нам приходится увеличивать мощность вспышки, чтобы компенсировать это, потому что теперь расстояние вспышки до объектов становится намного больше. Смотри, в этом Джо был в два раза дальше Оливии от той вспышки. Где, как и на этой стороне, Джо теперь всего на один фут дальше, чем Оливия. Оливия в четырех футах от вспышки, а Джо в пяти футах. Вы заметите, что падение гораздо менее драматично. Джо на самом деле гораздо больше похож на Оливию.
Здесь мы перемещаем вспышку на восемь футов. Мы включили вспышку еще немного выше, и снова Джо оказался в жутких шести дюймах от лица Оливии, и она наслаждается этим. Между прочим, ей все это нравится, но здесь Джо примерно в девяти футах от вспышки, а Оливия примерно в восьми футах. Вы можете видеть, что экспозиции равны. Нам нужно увеличить мощность вспышки, но чем дальше мы удаляемся от источника света, в основном, чем дальше находится группа, тем более похоже относительное расстояние. Сейчас у Оливии всего восемь футов, у Джо девять футов, и мы получаем примерно такое же освещение.
Мы включили вспышку еще немного выше, и снова Джо оказался в жутких шести дюймах от лица Оливии, и она наслаждается этим. Между прочим, ей все это нравится, но здесь Джо примерно в девяти футах от вспышки, а Оливия примерно в восьми футах. Вы можете видеть, что экспозиции равны. Нам нужно увеличить мощность вспышки, но чем дальше мы удаляемся от источника света, в основном, чем дальше находится группа, тем более похоже относительное расстояние. Сейчас у Оливии всего восемь футов, у Джо девять футов, и мы получаем примерно такое же освещение.
Когда мы высаживаем большую группу, предположим, что группа имеет ширину десять футов. Мне может понадобиться вспышка, может быть, в двадцати или тридцати футах от меня. Опять же, в зависимости от угла этого света от группы, чтобы иметь возможность получить примерно одинаковую яркость для всех, и для этого есть и другие методы, которые мы рассмотрим в Lightning 201 и 301, где мы берем камеру, я хочу снять вспышку с камеры. Теперь, прежде чем мы закончим этот сумасшедший дерьмовый тест, многое было усложнено, закон обратных квадратов. Позвольте мне дать вам четыре простых вывода.
Позвольте мне дать вам четыре простых вывода.
Номер один. Закон обратных квадратов по-прежнему применяется к физическим лицам. То есть снимаю ли я прекрасную модель, будь то парень или девушка. Предположим, что в данном случае это Оливия. В этом кадре я поместил источник света так близко к голове Оливии, что если я снимаю Оливию в полный рост, ее голова будет намного ярче, чем остальная часть ее тела, и вы действительно можете это увидеть.
Вспышка прямо здесь, и вы даже можете видеть, когда она достигает ее груди, я получаю только двадцать, тридцать процентов света, как я был на ее лице. Если я помещу модификатор света очень близко к кому-то, он все равно будет иметь тот же эффект, даже если я просто снимаю их по отдельности, а не в группе. Помните, если я хочу равномерно освещать все части тела, то этот свет должен быть примерно на одинаковом расстоянии от всего тела, от головы до пяток.
Номер два. Чем больше людей в кадре, тем больше расстояние вы хотите снять. Чем больше группа, просто отодвиньте свет немного дальше, чтобы равномерно осветить всех, а это значит, что вам нужно будет включить свет. Помните, что вы теряете больше света, чем думаете. Каждый раз, когда вы удваиваете расстояние, вы увеличиваете оставшуюся мощность вспышки в четыре раза. Удвоение расстояния означает увеличение мощности на двадцать пять процентов.
Чем больше группа, просто отодвиньте свет немного дальше, чтобы равномерно осветить всех, а это значит, что вам нужно будет включить свет. Помните, что вы теряете больше света, чем думаете. Каждый раз, когда вы удваиваете расстояние, вы увеличиваете оставшуюся мощность вспышки в четыре раза. Удвоение расстояния означает увеличение мощности на двадцать пять процентов.
Номер три. Основное эмпирическое правило. Когда вы пытаетесь осветить группу людей, скажем, группу из десяти человек, каждый человек в этой группе из десяти человек находится примерно на одинаковом расстоянии от моего источника света. Мой источник света находится на расстоянии пятнадцати футов, двадцати футов, тогда разница в один или два фута между этим относительным расстоянием на самом деле не будет иметь большого значения, но если мы говорим о двадцати футах от источника света с одной стороны. по сравнению с десятью футами от света на другой стороне, да, вы получите двадцать пять процентов вашего света на той стороне, и вы получите сто процентов вашего света на другой стороне. Просто помните, все ли примерно на одинаковом расстоянии от источника света?
Просто помните, все ли примерно на одинаковом расстоянии от источника света?
Число четыре более драматично, угол вспышки, тем больше расстояние, которое вам нужно, чтобы иметь одинаковое относительное расстояние для всех в группе, и вот что это значит. Все это означает, что моя вспышка находится прямо над моей камерой, что опять же зависит от того, какие у вас есть инструменты и что у вас есть, но давайте просто скажем, что я использую прямую вспышку для группы из пятнадцати человек. Если я стою на расстоянии десяти футов, то мое расстояние до всех пятнадцати человек примерно одинаковое.
Это может отличаться от шести дюймов до фута или около того, так как эта прямая вспышка находится на моей камере, и она направлена на каждого человека в группе. Очень небольшая разница, я получу примерно одинаковую яркость для каждого человека под этим углом, но как только я сниму вспышку с камеры, и, скажем, мне даже не нужно снимать вспышку с камеры. Я могу отражаться от отражателя или чего-то еще. Как только я удаляю основной источник света от камеры, картина становится более драматичной. Мы получаем больше теней.
Как только я удаляю основной источник света от камеры, картина становится более драматичной. Мы получаем больше теней.
Теперь этот свет будет благоприятствовать одной стороне группы гораздо сильнее, чем другой стороне. Как только этот свет окажется под углом, группа, которая находится на этой стороне, теперь, вероятно, будет намного ближе, может быть, в десяти футах от вспышки. Где группа на этой стороне будет в двадцати футах от вспышки. Чем драматичнее угол вспышки по отношению к группе, тем большее расстояние вам нужно. Чем больше расстояние, тем больше нужно отступить, чтобы получить равномерный свет справа налево.
Вот почему при групповом снимке они часто размещают свет с обеих сторон. Они будут перекрестно освещать его, чтобы у всех был одинаковый свет, или просто делают групповые снимки с отдельным светом в каждой части группы, и это то, что мы можем сделать в Lightning 201 и Lightning 301. Мы покажем вам продвинутые методы. для съемки больших групп с выносной вспышкой.
На данный момент я знаю, что все вы полностью освоили Закон обратных квадратов, и вы понимаете. Вы можете объяснить это любому, кто спросит, и это будет выглядеть так: «Послушай, чувак, это было намного проще, чем все остальные объясняют, вот оно». Я хочу, чтобы вы сказали это точно таким же тоном, и акцентом, и всем подобным.0003
Формулы — Закон обратных квадратов
Формулы — Закон обратных квадратов
|
Поиск | Карта сайта | Приложение |
Узнайте о законе обратных квадратов
Определение закона обратных квадратов
Закон обратных квадратов гласит, что «энергия источника при попадании в объект вдоль его сферическое ограждение обратно пропорционально квадрату расстояния между источником и объектом».
Обзор закона обратных квадратов
Закон обратных квадратов дает соотношение между энергией источника и расстоянием объекта от источника. 2}}}\;{\rm{or}}\;\frac{1}{4}221or41 дает интенсивность I4\frac{I}{4}4I .
2}}}\;{\rm{or}}\;\frac{1}{4}221or41 дает интенсивность I4\frac{I}{4}4I .
Есть вопрос по этой теме?
Что вы узнаете:
- Определение закона обратных квадратов
- Обзор закона обратных квадратов
- Закон обратных квадратов света
- Закон обратных квадратов излучения
- Закон обратных квадратов гравитации
- Обратный закон электричества поле
Закон обратных квадратов света
Источник света, проецируемый на объект, создает интенсивность, зависящую от расстояния до объекта от источника. Источник света (видимый свет) — это часть электромагнитного спектра, подчиняющаяся закону обратных квадратов, как и другие его компоненты — гамма-лучи, рентгеновские лучи, ультрафиолетовое излучение, инфракрасное излучение, радиоволны. {\rm{ 2}}}} \справа)(Вт/м2). 92}}I2I1=d12d22
{\rm{ 2}}}} \справа)(Вт/м2). 92}}I2I1=d12d22
Закон обратных квадратов излучения
Рассмотрим излучение источника гамма-излучения, распространяющееся наружу от точечного источника. интенсивность излучения распространяется на большую площадь по мере распространения лучей. Это показано на изображении.
Таким образом, интенсивность излучения подчиняется закону обратных квадратов Ньютона. То есть интенсивность обратно пропорциональна расстоянию от источника излучения (здесь источник гамма-излучения).
92}}}Intensity=d21Интенсивность испускаемого гамма-излучения ослабевает по мере его распространения от источника. На самом деле это происходит потому, что одно и то же излучение распространяется на большую площадь, как показано на изображении выше.
Если мы знаем, что интенсивность на расстоянии известна, то интенсивность на другом расстоянии может быть легко вычислена. 2}}I2I1=d12d22
2}}I2I1=d12d22
Закон обратных квадратов всемирного тяготения
Гравитационный эффект больше всего ощущается на поверхности земли и продолжает уменьшаться по мере удаления от земли. Закон обратных квадратов гравитационной силы в основном выводится из свойства планет двигаться вокруг Солнца. Эта информация полезна для изучения гравитационной силы спутников и астрономических объектов вокруг Земли.
Поверхность земли рассматривается как точка источника в этом сценарии. Источник помещен в сферический корпус прочностью 4πGM4\pi GM4πGM. Интенсивность g гравитационной силы на поверхности сферы радиусом 92}}} = \frac{g}{9}(3r)2GM=9×r2GM=9g
Закон обратных квадратов электрического поля
Электрическое поле состоит из зарядов и определяется как сила, приходящаяся на единичный заряд. Электричество — еще один параметр, который подчиняется закону обратных квадратов. Точно так же его противоположное магнитное поле, вместе образующее электромагнитное поле, также подчиняется закону. Электрическое поле может быть создано любым объектом, содержащим заряды.
Точно так же его противоположное магнитное поле, вместе образующее электромагнитное поле, также подчиняется закону. Электрическое поле может быть создано любым объектом, содержащим заряды.
Рассмотрим материал, создающий электрическое поле с напряженностью Q/ε0Q/{\varepsilon _0}Q/ε0с центром в сфере радиусом 92}}}= \frac{E}{9}4πε0(3r)2Q=9×4πε0r2Q=9E
Продолжайте учиться
Что изучать дальше на основе учебной программы колледжа
Работа, выполненная Gravitational ForceMerry-Go-RoundВымышленные силыГравитация РаботаНьютоновское тяготениеСкорость убеганияSi Единица гравитационного потенциала Потенциальная энергияСкорость убегания Марса
Создание чистых портретов с помощью физики
Статьи о свете и о том, как использовать его в фотографии, часто не вдохновляют. Они заполнены техническими диаграммами, диаграммами и уравнениями. И если вы увлекаетесь наукой и математикой, они очень полезны!
Но это не я (может быть, я чуть не завалил математику в средней школе!)… и это не эта статья. Тем не менее, я считаю, что даже такой не слишком увлеченный математик, как я, может понять сложные концепции освещения и понять, почему они работают. Более того, я считаю, что мы можем вдохновиться тем, что свет может сделать с нашими фотографиями, и в результате создать новые захватывающие работы!
Тем не менее, я считаю, что даже такой не слишком увлеченный математик, как я, может понять сложные концепции освещения и понять, почему они работают. Более того, я считаю, что мы можем вдохновиться тем, что свет может сделать с нашими фотографиями, и в результате создать новые захватывающие работы!
На первый взгляд закон обратных квадратов (ISL) звучит довольно пугающе. Все, что содержит в названии теорему, закон или уравнение, обычно вызывает у меня желание бежать куда глаза глядят! Но я обещаю, что урок науки будет коротким, потому что ISL — это круто. Эта волшебная маленькая концепция позволит вам создать чистую сцену даже в самом захламленном доме!
Немного науки и математики
Закон обратных квадратов гласит: «Интенсивность света обратно пропорциональна квадрату расстояния от источника света». Для любителей математики эта формула выглядит так: Интенсивность = 1/Расстояние2
Я чувствую, как вы закатываете глаза. Я рядом с тобой!
Не оставляй меня пока! Эта безумно звучащая концепция на самом деле довольно проста. Все это означает, что чем дальше ваш объект от источника света, тем мягче будет падать на него свет.
Все это означает, что чем дальше ваш объект от источника света, тем мягче будет падать на него свет.
Это также говорит нам о том, что интенсивность света падает экспоненциально, поэтому чем дальше вы темнеете, тем быстрее, чем вы могли бы ожидать. Это потому, что, когда свет проходит через расстояние, он распространяется. Таким образом, все меньше и меньше исходной концентрированной силы света попадает на объект.
Итак, объект, который находится в два раза дальше от источника света, чем другой, не получает половину количества света, как подсказывает нам логика. Физика ни в коем случае не интуитивна — спасибо науке! Вместо этого он получает четверть количества света (отсюда и «квадрат» в законе обратных квадратов).
ОК. На этом я обещаю остановиться на научных объяснениях. Давайте рассмотрим, как мы можем ИСПОЛЬЗОВАТЬ эти концепции!
Посмотрите, как это работает
Вам нужно помнить, что чем ближе ваш объект к источнику света, тем глубже будут тени и тем ближе они будут казаться к вашему объекту. Это драматическое взаимодействие света и тени называется светотенью (возможно, я не фанат науки, но я люблю историю искусства!). Позвольте мне показать вам, что я имею в виду:
Это драматическое взаимодействие света и тени называется светотенью (возможно, я не фанат науки, но я люблю историю искусства!). Позвольте мне показать вам, что я имею в виду:
Здесь мы видим изменение света и тени по мере того, как источник света удаляется от объекта на один фут за раз. Обратите внимание, как в каждом последующем изображении свет рассеивается, становясь мягче. В результате тени становятся менее драматичными, а свет освещает больше волос и ушей.
Применение физики на практике
Мое любимое применение ISL — позволить ему действовать как моя личная служанка. Это позволяет мне стереть беспорядок в моем обжитом доме (заваленном лего, мелками и машинами) и заставить его исчезнуть в сочной и бархатистой пустоте.
Все, что мне нужно сделать, это приблизить объект к свету!
Связано: 5 мест в вашем доме с хорошим освещением
Этот принцип часто применяется в студии, чтобы сделать белый фон серым или даже черным. Это достигается за счет того, что объект находится близко к источнику света, но при этом увеличивается расстояние от фона. По мере того, как объект в нескольких дюймах от фона и к свету, белый фон может двигаться по градиенту серого до черного.
Это достигается за счет того, что объект находится близко к источнику света, но при этом увеличивается расстояние от фона. По мере того, как объект в нескольких дюймах от фона и к свету, белый фон может двигаться по градиенту серого до черного.
Та же идея превращает занятый фон в «фальшиво-черный» фон!
Я сделал следующие снимки с разницей в несколько секунд. Расстояние до камеры и источник естественного света оставались неизменными. Все, что изменилось, это мое расстояние (как объекта) от источника света. Результатом является значительное изменение темноты фоновой области.
Вы можете поверить, что их забрали сюда?!
Когда я нахожусь близко к окну, фон кажется очень темным, а мое лицо выглядит ярко освещенным и контрастным. (Должен любить эти резкие световые морщины!) Чем дальше я отхожу от окна, тем свет рассеивается более равномерно, но некоторое различие все же есть. Когда я возвращаюсь в глубину комнаты, разница между светом, падающим на меня, и светом, падающим на фоновую сцену, становится меньше. В результате вы можете видеть весь беспорядок.
В результате вы можете видеть весь беспорядок.
Чтобы применить закон обратных квадратов и позволить ему стереть беспорядок, вы хотите, чтобы ваш фон был далеко от источника света, а ваш объект находился рядом с источником света. Вы также хотите, чтобы другие источники света не просачивались в фоновое пространство.
Пошаговое руководство
Ваш гараж или коридор — отличное место для практики этой техники. Вот мой пошаговый процесс:
1.) Найдите область с ярким источником света (окном или дверным проемом) и не пропускайте свет на задний план. Возможно, вам придется закрыть окна в задней части помещения.
2.) Переместите объект как можно ближе к источнику света и как можно дальше от фона.
3.) Если вы пытаетесь сделать это в своем гараже с открытой дверью, ищите линию на полу, где встречаются свет и тень. Вы хотите разместить свой объект прямо внутри этой линии тени (не на солнечной стороне).
4.) Грязный фон получит лишь небольшую часть света, который получает ваш объект. Поэтому, когда вы экспонируете свой объект, весь этот фоновый беспорядок растворяется в густых тенях.
Поэтому, когда вы экспонируете свой объект, весь этот фоновый беспорядок растворяется в густых тенях.
5.) Точечный замер для экспонирования самой яркой части кожи объекта.
6.) Сфотографируйтесь и поразитесь своему величию.
7.) Осветляйте, сжигайте и клонируйте по мере необходимости в программе редактирования по вашему выбору.
Связанный: Использование закона обратных квадратов для портретов с естественным освещением
Этот пример стоял в нашем грязном гараже. В нашем гараже есть окна сзади, поэтому мне пришлось их прикрыть. Мне также пришлось немного дополнительно прожечь фон, чтобы сделать его совершенно темным. Но поверите ли вы, что наша сушильная машина действительно находится там, в той темноте?
Я сделал этот портрет в нашей гостиной рядом со стеклянными двойными дверями. Чтобы свет не проникал в заднюю часть комнаты, я задернул шторы.
Этот пример я снял на своей кухне с темной мебелью, белой плиткой и скамейками.

 3 Свет и другие виды электромагнитного излучения
3 Свет и другие виды электромагнитного излучения Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.


 Электромагнитный спектр
Электромагнитный спектр  Дополнительные темы
Дополнительные темы