Закон обратных квадратов

Говоря техническими терминами, закон обратных квадратов в физике утверждает, что «значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина». Вам, должно быть, интересно, что закон с подобным определением может иметь общего с фотографией (и никто вас не осудит). Закон обратных квадратов применим для множества вещей в этом мире. Сегодня, однако, мы рассмотрим лишь одну из них: свет.

Объяснение концепции

Для тех из нас, кто не слишком близко знаком с высшей математикой (или даже с основами математики, если уж на то пошло), нечто вроде закона обратных квадратов может показаться невероятно сложным. Там есть уравнения с числами и переменными, ссылки на физику и множество других вещей, которые, откровенно говоря, кажутся очень скучными. По этой причине мы постараемся охватить данную тему с практической стороны, а не с технической.

Сам закон в фотографии используется в вопросах освещения. Вообще-то, он применим по отношению к любому виду освещения, но наиболее важные области его применения касаются вне-камерного освещения. В общем, закон обратных квадратов учит нас, как работает свет на расстоянии и почему расстояние между источником света и объектом так важно.

Допустим, у нас есть источник света, включенный на полную мощность, и наша модель находится в 1 метре от него. Если мы переместим модель на удвоенное расстояние от источника (2 метра), какова будет мощность света, достигающего ее? Естественная мысль «половина мощности», — но, к сожалению, это не так, а свет работает в соответствии с законом обратных квадратов.

Согласно закону, мощность света будет обратно пропорциональна квадрату расстояния. Таким образом, если мы возьмем расстояние 2 и возведем это число в квадрат, мы получим 4, обратное значение составит ¼, то есть четверть первоначальной мощности — не половину.

Перемещение объекта на три метра от источника (3 * 3 = 9, т.е. 1/9) приведет к тому, что мощность достигающего его света составит 1/9 от первоначального значения.

На рисунке ниже показано, как уменьшается мощность света от 1 до 10 метров, помните, что каждый показатель – просто обратный квадрат расстояния свыше 1.

Закон обратных квадратов объясняет существенное снижение мощности света на расстоянии. Мы можем использовать эту информацию, чтобы лучше понимать, как наше освещение влияет на модель, и в соответствии с этим лучше контролировать его.

Практическое применение

Итак, знание о снижении мощности света забавно и все такое прочее…но как мы можем найти ему достойное применение в нашей фотографической работе? Это касается, в первую очередь, экспозиции и относительного расположения объектов. Когда свет направлен в определенном направлении, первоначально уменьшение мощности происходит очень быстро, а затем замедляется, чем дальше, тем больше.

Помните, что с законом квадратов числа увеличиваются все быстрее и быстрее, но с законом обратных квадратов они уменьшаются все медленнее и медленнее. 

Если мы взглянем на уменьшение мощности света от 1 м до 10 м в процентах с точностью до целого числа, это будет выглядеть так:

Здесь мы видим падение на 75% от 1 до 2 метров, но всего 5%-ное снижение освещенности от 4 метров до 10 метров.

Экспозиция

Таким образом, мы понимаем, что близко к источнику света мощность большая, но далеко от него мы располагаем лишь очень небольшим количеством света. Исходя из этого, для получения правильной экспозиции (предполагается, что мы используем постоянную выдержку), если объект очень близко к свету, то мы должны установить нашу диафрагму примерно на F16, чтобы блокировать все излишки света.

Если, с другой стороны, объект расположен очень далеко от источника, тогда нам следует выбрать значение диафрагмы примерно F4, чтобы захватить больше света. Оба кадра должны выглядеть идентично, потому что мы настроили камеру таким образом, чтобы пропустить одинаковое количество света для каждого из них.

Исходя из этого, мы можем приблизительно оценить, какие значения диафрагмы нужно использовать на том или ином расстоянии, чтобы получить корректную экспозицию. Помните, что мощность света поначалу снижается очень быстро, а затем медленнее. По тому же принципу, мы поначалу открываем диафрагму очень резко, а потом тем медленнее, чем дальше мы от источника света.

Освещение одного объекта

Давайте переместим шкалу с диафрагменными числами на вершину диаграммы в качестве удобной точки отсчета. Теперь следующий момент: некоторые объекты не двигаются, и это означает, что как только вы поместите объект на определенном расстоянии от источника света, вы установите экспозицию, и на этом всё.

Однако если вы снимаете человека (особенно стоящего человека), он имеют тенденцию перемещаться. Если ваша модель очень близко к источнику света, и она (или он) переместится на полшага в любом направлении, то она сразу же окажется недо- или переэкспонирована.

Однако если модель находится дальше от источника, тогда она может перемещаться на несколько шагов в любом направлении, и вам вообще не нужно будет изменять настройки камеры.

Освещение группы объектов

Предыдущее правило работает очень схоже и для группы объектов. Если все ваши объекты находятся очень близко к источнику, тогда тот, что дальше от источника, окажется сильно недоэкспонированным по сравнению с тем, что ближе к свету – в диапазоне от F22 до F11.

Но если вы переместите все объекты дальше от источника, они все будут освещены достаточно хорошо на диафрагме около F4.

Освещение фона

Конечно, порой вы действительно хотите сделать так, чтобы какой-то элемент фотографии был ярким, а другой темным, как в случае с фоном. Так, если вы помещаете модель очень близко к источнику света, а фон на определенном расстоянии, тогда (предполагается, что модель экспонирована корректно) фон будет сильно недоэкспонирован.

Если вы хотите ярко осветить и модель, и фон, переместите их дальше от источника света, но близко друг к другу.

Заключение

Это было лишь небольшое введение в закон обратных квадратов и способы его применения в освещении в фотографии. Есть множество, множество переменных, которые могут быть скорректированы для получения различных эффектов, такие как выдержка, яркость источника света и использование нескольких источников.

Однако надеюсь, что теперь вы понимаете основы закона обратных квадратов и можете начать применять их в вашей фотографической работе для получения лучшего, более подходящего вам освещения.

Если у вас есть какие-то полезные советы, которые помогут людям в понимании данной темы, или что-то еще, чем вы хотите поделиться, вы можете сделать это в комментариях ниже!

Автор статьи: John O’Nolan

photo-monster.ru

Закон обратных квадратов

Говоря техническими терминами, закон обратных квадратов в физике утверждает, что «значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина». Вам, должно быть, интересно, что закон с подобным определением может иметь общего с фотографией (и никто вас не осудит). Закон обратных квадратов применим для множества вещей в этом мире. Сегодня, однако, мы рассмотрим лишь одну из них: свет.

Объяснение концепции

Для тех из нас, кто не слишком близко знаком с высшей математикой (или даже с основами математики, если уж на то пошло), нечто вроде закона обратных квадратов может показаться невероятно сложным. Там есть уравнения с числами и переменными, ссылки на физику и множество других вещей, которые, откровенно говоря, кажутся очень скучными. По этой причине мы постараемся охватить данную тему с практической стороны, а не с технической.

Сам закон в фотографии используется в вопросах освещения. Вообще-то, он применим по отношению к любому виду освещения, но наиболее важные области его применения касаются вне-камерного освещения. В общем, закон обратных квадратов учит нас, как работает свет на расстоянии и почему расстояние между источником света и объектом так важно.

Допустим, у нас есть источник света, включенный на полную мощность, и наша модель находится в 1 метре от него. Если мы переместим модель на удвоенное расстояние от источника (2 метра), какова будет мощность света, достигающего ее? Естественная мысль «половина мощности», — но, к сожалению, это не так, а свет работает в соответствии с законом обратных квадратов.

Согласно закону, мощность света будет обратно пропорциональна квадрату расстояния. Таким образом, если мы возьмем расстояние 2 и возведем это число в квадрат, мы получим 4, обратное значение составит ¼, то есть четверть первоначальной мощности — не половину.

Перемещение объекта на три метра от источника (3 * 3 = 9, т.е. 1/9) приведет к тому, что мощность достигающего его света составит 1/9 от первоначального значения.

На рисунке ниже показано, как уменьшается мощность света от 1 до 10 метров, помните, что каждый показатель – просто обратный квадрат расстояния свыше 1.

Закон обратных квадратов объясняет существенное снижение мощности света на расстоянии. Мы можем использовать эту информацию, чтобы лучше понимать, как наше освещение влияет на модель, и в соответствии с этим лучше контролировать его.

Практическое применение

Итак, знание о снижении мощности света забавно и все такое прочее…но как мы можем найти ему достойное применение в нашей фотографической работе? Это касается, в первую очередь, экспозиции и относительного расположения объектов. Когда свет направлен в определенном направлении, первоначально уменьшение мощности происходит очень быстро, а затем замедляется, чем дальше, тем больше.

Помните, что с законом квадратов числа увеличиваются все быстрее и быстрее, но с законом обратных квадратов они уменьшаются все медленнее и медленнее. 

Если мы взглянем на уменьшение мощности света от 1 м до 10 м в процентах с точностью до целого числа, это будет выглядеть так:

Здесь мы видим падение на 75% от 1 до 2 метров, но всего 5%-ное снижение освещенности от 4 метров до 10 метров.

Экспозиция

Таким образом, мы понимаем, что близко к источнику света мощность большая, но далеко от него мы располагаем лишь очень небольшим количеством света. Исходя из этого, для получения правильной экспозиции (предполагается, что мы используем постоянную выдержку), если объект очень близко к свету, то мы должны установить нашу диафрагму примерно на F16, чтобы блокировать все излишки света.

Если, с другой стороны, объект расположен очень далеко от источника, тогда нам следует выбрать значение диафрагмы примерно F4, чтобы захватить больше света. Оба кадра должны выглядеть идентично, потому что мы настроили камеру таким образом, чтобы пропустить одинаковое количество света для каждого из них.

Исходя из этого, мы можем приблизительно оценить, какие значения диафрагмы нужно использовать на том или ином расстоянии, чтобы получить корректную экспозицию. Помните, что мощность света поначалу снижается очень быстро, а затем медленнее. По тому же принципу, мы поначалу открываем диафрагму очень резко, а потом тем медленнее, чем дальше мы от источника света.

Освещение одного объекта

Давайте переместим шкалу с диафрагменными числами на вершину диаграммы в качестве удобной точки отсчета. Теперь следующий момент: некоторые объекты не двигаются, и это означает, что как только вы поместите объект на определенном расстоянии от источника света, вы установите экспозицию, и на этом всё.

Однако если вы снимаете человека (особенно стоящего человека), он имеют тенденцию перемещаться. Если ваша модель очень близко к источнику света, и она (или он) переместится на полшага в любом направлении, то она сразу же окажется недо- или переэкспонирована.

Однако если модель находится дальше от источника, тогда она может перемещаться на несколько шагов в любом направлении, и вам вообще не нужно будет изменять настройки камеры.

Освещение группы объектов

Предыдущее правило работает очень схоже и для группы объектов. Если все ваши объекты находятся очень близко к источнику, тогда тот, что дальше от источника, окажется сильно недоэкспонированным по сравнению с тем, что ближе к свету – в диапазоне от F22 до F11.

Но если вы переместите все объекты дальше от источника, они все будут освещены достаточно хорошо на диафрагме около F4.

Освещение фона

Конечно, порой вы действительно хотите сделать так, чтобы какой-то элемент фотографии был ярким, а другой темным, как в случае с фоном. Так, если вы помещаете модель очень близко к источнику света, а фон на определенном расстоянии, тогда (предполагается, что модель экспонирована корректно) фон будет сильно недоэкспонирован.

Если вы хотите ярко осветить и модель, и фон, переместите их дальше от источника света, но близко друг к другу.

Заключение

Это было лишь небольшое введение в закон обратных квадратов и способы его применения в освещении в фотографии. Есть множество, множество переменных, которые могут быть скорректированы для получения различных эффектов, такие как выдержка, яркость источника света и использование нескольких источников.

Однако надеюсь, что теперь вы понимаете основы закона обратных квадратов и можете начать применять их в вашей фотографической работе для получения лучшего, более подходящего вам освещения.

Если у вас есть какие-то полезные советы, которые помогут людям в понимании данной темы, или что-то еще, чем вы хотите поделиться, вы можете сделать это в комментариях ниже!

Автор статьи: John O’Nolan

photo-monster.ru

Закон обратных квадратов — это… Что такое Закон обратных квадратов?

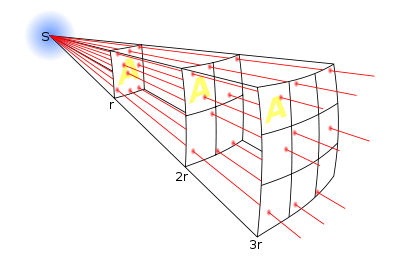Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.

В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.

Обоснование

Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.

Проявления

Гравитация

Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:

Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.

Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).

Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данное массивное тело, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.

Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.

Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу ^[1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы^[2], также как отдал дань уважения Буллиальду.

Электростатика

Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.

Свет и другие виды электромагнитного излучения

Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.

Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.

Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:

Фотографы и театральные мастера по свету используют закон обратных квадратов для выбора оптимального места положения осветительных приборов.

Закон обратных квадратов может быть применён только для точечных источников света; наиболее распространённые в помещениях цилиндрические лампы дневного света не являются точечными источниками, и поэтому к ним нельзя применять закон обратных квадратов, в отличие от большинства других источников искусственного излучения.

Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.

Формулы закона обратных квадратов в рентгенографии имеют вид:

где

I — интенсивность,

r — расстояние (радиус).

Приложения в теории поля

Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.

Примечания

1. ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
2. ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.

dic.academic.ru

Свет фотографии: понимание закона обратных квадратов: cdyu — LiveJournal

С технической точки зрения закон обратных квадратов подразумевает, что некоторая физическая величина или сила обратно пропорциональна квадрату, расстояния от своего источника. Прочитав это грозное определение вы спросите, какое отношение эта тумба-юмба имеет к фотографии, но этот закон распространим на многие вещи в мире. Например, на свет и сегодня мы вместе с John O’Nolan поговорим как раз о нём.

Очень теоритическая теория

Для многих из нас уже давно и напрочь забывших курс школьной математики закон обратных квадратов может показаться сложным. Да, есть уравнения и ссылки на физику, которые откровенно говоря, довольно скучны, поэтому мы рассмотрим вопрос с прикладной точки зрения.

В фотографии этот закон актуален для использования искусственного света, накамерных или синхронизированных вспышек. Закон обратных квадратов учит нас тому, как света работает с расстоянием и почему расстояние между объектом съёмки и источником света так важно.
Допустим у нас есть вспышка и есть объект съёмки в метре о неё. Если мы отодвинем объект съемки на расстояние два метра от вспышки, сколько света его достигнет? В два раза меньше, скажете вы и будете чертовски неправы.

Согласно закону, сила света будет обратно пропорциональная квадрату расстояния. Если наши два метра мы возведём в квадрат, то получим 4 метра. Сила света будет 1\4 от изначальной мощности, а не половина. Половина была ещё на расстоянии метра.

Отодвинем объект на три метра и получим (3 * 3 = 9, так что 1 / 9) от силы источника света.
Падение мощности с расстоянием вы можете рассмотреть на схеме ниже. Нижняя шкала, от 0 до 10 метров:

Закон обратных квадратов объясняет резкое падение мощности света на расстоянии. Мы можем использовать эту информацию, чтобы лучше понять как наш свет влияет на нашу сцену и тем самым добиться лучшего понимания в управлении светом.

От теории к практике

Знать о падении мощности конечно интересно, на нафига козе баян спросите вы!? Как этим пользоваться в фотографии? Конечно в экспонировании сцены и позиционировании объектов.
Давайте обратим внимание, что согласно закону обратных квадратов, чем дальше от источника света, тем более плавным становится падение силы освещения.

Если мы посмотрим на мощность света в процентах, на расстоянии с 1 метра до 10 это будет выглядеть так:

75% падения мощности происходи в промежутке от 1 метра до двух и только 5% в диапазоне от 4 метров до 10.

Экспозиция

Таким образом, мы понимаем, что есть много света в непосредственной близости от от источника света и небольшое количество света вдалеке от него. Исходя из этого для получения правильной экспозиции (держим, в уме, что выдержка у нас правильная и одинаковая) находясь близко к объекту нам нужно установить диафрагму F16:

Напротив если мы поставим объект далеко от источника света, мы сможем использовать диафрагму F4. При этом в обоих случаях объект будет экспонирован правильно:

Если делать это только с одной

Давайте посмотрим на инфографику. Мы разместили значения диафрагмы на панели вверху. Как вы уже заметили, если модель находится близко к источнику света, то даже небольшое её перемещение может серьёзно повлиять на экспозицию:

Напротив если модель находится дальше от источника света, у неё появляется пространство, где она может двигаться без необходимости менять экспопару или настройки света:

Если делать это сразу с тремя

Всё изложенное правило также работает и с группами объектов. Если все они находятся близко к источнику света, но не на одной плоскости то дальний объект будет сильно недодержан по отношению к ближнему. Диапазон на графике от F22 до F11:

Если поместить нашу группу дальше от света, то вся она будет освещена намного более равномерно:

Если делать это на фоне ковра!

Бывает и так, что нужен ярко освещённый объект на переднем плане и тёмный фон. Поместите фон на расстоянии от модели и если модель, экспонированная правильно фон, будет недосвечен:

Чтобы получить яркий объект и яркий фон разместите их дальше от источника света но ближе друг к другу:

Заключение

Конечно, есть много переменных, которые мы не упомянули, например выдержка, или глубина резкости, ну и конечно мощностью самой вспышки и боже их количество. Чтобы сложить полноценное представление о вопросе, нужно ориентироваться в этих переменных хотя бы немного.

Однако используя понимание закона обратных квадратов вы можете начать применять их в фотографии, чтобы достичь лучшего более продуманного и последовательного освещения.

cdyu.livejournal.com

Закон обратных квадратов — Википедия

Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.

В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.

Обоснование

Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле 4πr2{\displaystyle 4\pi r^{2}}) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.

Видео по теме

Проявления

Гравитация

Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:

Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.

Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).

Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данные массивные тела, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, при существенном различии масс гравитирующих тел (если мала разность приведённой массы и массы более тяжёлого тела), изотропное распределение масс тяжёлого тела позволяет аппроксимировать его притяжение его массой, помещённой в центре его сферы.

Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.

Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу ^[1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы^[2], а также отдал дань уважения Буллиальду.

Электростатика

Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.

Свет и другие виды электромагнитного излучения

Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.

Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.

Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:

Ea,Ba∝1r{\displaystyle E_{a},B_{a}\propto {1 \over r}}

Закон обратных квадратов может быть применён только в случае точечных источников света: весьма распространённые в помещениях цилиндрические лампы дневного света, тем более помещённые в ряд, не являются точечными источниками (пока их характерный размер не является пренебрежимо малым), и поэтому к ним нельзя применять закон обратных квадратов (пока их характерный размер велик, к ним применим закон обратного расстояния), а равномерно светящаяся плоская поверхность даёт постоянную освещённость на расстояниях, малых по сравнению с её размером.

Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.

Приложения в теории поля

Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.

Примечания

1. ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
2. ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.

wiki2.red

ГРАВИТАЦИЯ » Законы обратных квадратов

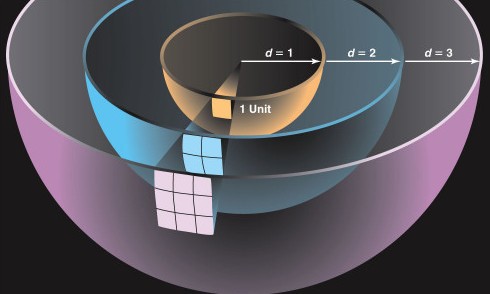
Закон обратных квадратов – закон, согласно которому некая физическая величина в определенной точке, обратно пропорциональна квадрату расстояния до этой точки.

Суть таких законов в том, что некая физическая величина распространяется из центра равномерно во все стороны.

Закону обратных квадратов подчиняются следующие физические явления:

• Звуковые волны от точечного (шарового) источника звуков

I = N/4πr²

• Напряженность электрического поля Е на расстоянии r от точечного заряда Q в вакууме (Закон Кулона)

 E = Q/4πr²

• Напряженность магнитного поля (Закон Био-Савара-Лапласа)

H = I/4πr²

• Освещенность Е_п плоской поверхности, создаваемая точечным источником

Е_п = Icos·α/r²

• Напряженность гравитационного поля (Закон Ньютона)

F = GM/r²

Вот основной набор уравнений волнового излучения, подчиняющихся закону обратных квадратов.

Правда,  есть еще один закон обратных квадратов, некий закон Лотки, который гласит: число научных работников N написавших n статей, пропорционально 1/n². Интересный закон, но его точность сомнительна, поскольку в его основе положены статистические данные. Поэтому сразу оставим его за рамками обсуждения.

Проведем анализ этих законов и попробуем их отождествить с гравитационным взаимодействием.

1) Звуковые волны хороши, но они явно не подходят, так как звук распространяется только в атмосфере, а она, как известно, имеется далеко не у всех небесных тел, не говоря уже о межзвездном пространстве.

2) Законы Кулона и Био-Савара-Лапласа также хороши, но также не подходят под тождество с гравитационным взаимодействием. Электрические и магнитные силы во много раз превосходят гравитационные. Радиус действия этих сил также не сопоставим – электромагнитные силы действуют на более коротких расстояниях. Оставим пока в покое и эти законы.

3) Остается что? Остается – свет?!

Чтобы не забыть, так и запишем: гравитация – это свет!

На квантовом уровне свет у нас представляет фотон, а гравитацию – гипотетический гравитон.

Приравняем кванты фотона и гравитона.

γ = g

На такое скоропалительное заключение кто-то интеллигентно скажет: не корректное отождествление, а кто-то резко: чушь! Но не будем так категоричны и продолжим построение логической цепочки.

Свет, безусловно, хорош, и о нем мы знаем практически все. Оптическое излучение (свет) представляет собой электромагнитное излучение с длиной волны от 0.01 нм до 0,1 мм. Свет подчиняется законам оптики, а оптика, по накопленным наблюдениям и опыту, еще более древняя наука,  чем механика.

Давайте посмотрим на это физическое явление оптическим глазом еще раз и более внимательно. Что может роднить свет с гравитацией?

1. 1/r² – общий знаменатель? И это все? Хотя, просматривая глубже, находим еще несколько соответствий.
2.  Скорость распространения электромагнитной световой волны и скорость распространения гравитационной волны равны: с = 2.998 · 10⁸ м/с (скорость света в вакууме).
3. Свет и гравитация распространяются волнообразно. А, как известно, волны являются переносчиками энергии. Без энергии нет движения, без движения нет энергии.
4. Гравитоны, идентичны фотонам, их  массы связаны только с движением – масса покоя, как таковая, у данных частиц  отсутствует.
5. Фотон – квант электромагнитного поля, гравитон – гипотетический квант гравитационного поля. Квант – это некая минимальная частичка энергии.
6. Фотоны и гравитоны не избирательны к воспринимающим их объектам. Они не поляризованы и не заряжены, им безразлично внутреннее состояние вещества, тела или предмета, они равнозначно взаимодействуют со всеми.

Шесть соответствий – это уже не то что серьезно, а вполне достаточно, чтобы отождествить фотоны с гравитонами.

Вот этим и займемся в ближайшем постраничном пространстве. А для этого заглянем еще глубже, а точнее дальше, где мы должны увидеть свет не только в конце тоннеля, но и в далеком Космосе. Гравитация, похоже, действует таким же образом. Разница только в одном, свет мы видим всегда, а гравитацию – никогда!

Вот написал последнюю фразу и усомнился в ее правильности. Сами фотоны, как переносчики света, мы тоже не видим. Посудите сами, как можно увидеть фотоны, проскакивающие мимо нас со скоростью, чего? Того самого света! Мы видим реакцию этого света с окружающими нас предметами, поэтому нас ни на секунду не покидает ощущение их присутствия. Свет либо отражается от них, тогда мы видим блестящую или зеркальную поверхность, либо поглощается ими, тогда видим оттенки серого и черного. По сути, мы не видим отдельные фотоны, а только их интегральное действие на сетчатку глаза. Чтобы увидеть свет, необходимо интегральное действие 200 фотонов. Итак, седьмое соответствие.

7. Одиночные фотоны света и гравитоны не видимы зрением!

Что касается источников света, например, скептики сразу мне возразят: «Ты что слепой, и Солнце не видишь?». На что я спокойно отвечу: Я вижу Солнце, оно испускает световые волны, я также отчетливо вижу, что оно испускает и гравитационные волны, а вы что их не видите? Тогда, вы невесомы!

Так кто из нас прав?

Гравитационную энергию переносят все волны, а мы видим только в узком промежутке 780–380 нм (3·10¹⁴ — 4·10¹⁴ Гц) из всей шкалы широкого диапазона электромагнитных волн.

Получается – свет загораживает нам гравитационную картину.

Пока не поздно, можно отмахнуться от гравитации известным выражением: «То, что не вижу, для меня не существует!», но не будем спешить, не для того затеян разбор гравитационных полетов.

Здесь, следует напомнить, что солнечный свет или свет от обычной лампы накаливания содержит полный спектр длин волн, который распадается на составляющие при прохождении его через стеклянную призму. «Каждый охотник желает знать…», радуга, которую первым, в искусственных условиях, исследовал тот самый Ньютон.

Далее продолжим об электромагнитных волнах

 

Назад  Вперед

gennady-ershov.ru

Закон обратных квадратов — Википедия. Что такое Закон обратных квадратов

Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.

В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.

Обоснование

Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле 4πr2{\displaystyle 4\pi r^{2}}) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.

Проявления

Гравитация

Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:

Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.

Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).

Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данные массивные тела, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, при существенном различии масс гравитирующих тел (если мала разность приведённой массы и массы более тяжёлого тела), изотропное распределение масс тяжёлого тела позволяет аппроксимировать его притяжение его массой, помещённой в центре его сферы.

Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.

Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу ^[1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы^[2], а также отдал дань уважения Буллиальду.

Электростатика

Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.

Свет и другие виды электромагнитного излучения

Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.

Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.

Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:

Ea,Ba∝1r{\displaystyle E_{a},B_{a}\propto {1 \over r}}

Закон обратных квадратов может быть применён только в случае точечных источников света: весьма распространённые в помещениях цилиндрические лампы дневного света, тем более помещённые в ряд, не являются точечными источниками (пока их характерный размер не является пренебрежимо малым), и поэтому к ним нельзя применять закон обратных квадратов (пока их характерный размер велик, к ним применим закон обратного расстояния), а равномерно светящаяся плоская поверхность даёт постоянную освещённость на расстояниях, малых по сравнению с её размером.

Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.

Приложения в теории поля

Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.

Примечания

1. ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
2. ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.

wiki.sc