Зависимость освещенности от расстояния до источника света

Краткие теоретические сведения

Раздел физики, занимающийся измерением характеристик оптического излучения, называется фотометрией. Для прикладной светотехники важна как объективная энергетическая характеристика света, так и мера воздействия света на глаз наблюдателя. Поэтому в фотометрии приходится вводить двойные единицы измерения: энергетические (оцениваемые по объективным энергетическим характеристикам) и фотометрические (оцениваемые по воздействию на глаз). Энергетические и фотометрические величины взаимосвязаны. Основной фотометрической величиной является единица силы света – кандела. Кандела (Кд) – это сила света, излучаемого перпендикулярно поверхности черного излучателя с площади 1/6´10 -5 м 2 при температуре затвердения платины, находящейся под давлением 101 325 Па.

Рассмотрим точечный источник, сила света которого равна I, и выделим телесный угол aW с вершиной в точке нахождения источника (рис.

1).

Величина

( 1 )

называется элементарным световым потоком, излучаемым в пространство, ограниченным углом aW. Единицей светового потока является люмен (1 Лм = 1 Кд ´ 1 стер.).

Если сила света источника не зависит от направления наблюдения (такой источник называется изотропным), то полный световой поток, излучаемый источником по всем направлениям, равен

( 2 )

На пути светового потока расположим элементарную площадку dS , образующую угол с направлением распространения света. Отношение светового потока к площади освещаемой поверхности

( 3 )

называется освещенностью, которая измеряется в люксах (1 Лк = 1 Лм / м 2 ).

Построим также площадку dS , перпендикулярную к направлению наблюдения и находящуюся на том же расстоянии r от источника света, что и площадка dS . Учитывая, что

( 4 )

и используя соотношение ( 1 ), из формулы ( 3 ) получаем

( 5 )

Таким образом, освещенность поверхности обратно пропорциональна квадрату расстояния от источника света (закон обратных квадратов) и прямо пропорциональна силе света и косинусу угла падения света на поверхность (закон косинусов).

Если источник света – некоторая поверхность, то для ее характеристики вводятся такие величины, как светимость и яркость.

Пусть площадка dS излучает свет. Тогда светимость можно определить как световой поток, испускаемый с единицы площади:

( 6 )

В свою очередь яркостью называют силу света, испускаемого с единицы видимой поверхности в данном направлении:

( 7 )

Из формулы ( 7 ) следует, что яркость источника В может зависеть от угла a. Однако существуют источники света, для которых яркость не зависит от направления наблюдения, то есть

В (a) = const . Такие источники подчиняются закону Ламберта:

( 8 )

и для них справедливо соотношение

( 9 )

Если свечение поверхности обусловлено освещением её внешним источником, то светимость связана с освещенностью соотношением:

( 10 )

где r – коэффициент рассеяния (отражения) света.

Описание установки

Фотометрический прибор состоит из камеры и разъемного корпуса прямоугольной формы. Внутри камеры вмонтирован селеновый фотоэлемент, провода которого выведены на торцевую часть прибора. Фотоэлемент закреплен в специальной оправе, которая может поворачиваться вокруг горизонтальной оси в пределах угла ¦ = 90 0 . Отсчет угла поворота осуществляется по угловой шкале, расположенной на лицевой стороне камеры. Селеновый фотоэлемент состоит из металлической подложки, на одной стороне которой нанесен слой селена толщиной около 0,1 мм. Сверху этот слой покрыт прозрачным электродом. Согласно первому закону фотоэффекта, сила фототока насыщения пропорциональна падающему потоку:

( 11 )

где γ – интегральная чувствительность фотоэлемента.

Селеновый фотоэлемент имеет спектральную характеристику чувствительности, близкую к кривой видимости человеческого глаза. Это позволяет использовать фотоэлемент для фотометрирования дневного света.

Внутри прямоугольного корпуса помещается осветитель с электролампочкой, который может перемещаться вдоль продольной оси прибора. Величина перемещения отсчитывается по линейке, закрепленной на лицевой стороне прибора. В набор также входят линзы в оправе, матовое стекло, набор диафрагм, исследуемая электрическая лампочка, реостат. Питание электролампочек осуществляется от выпрямителя типа ВС-24. Величина фототока измеряется с помощью универсального цифрового прибора типа 4323А.

Выполнение работы

1. Подключить микроамперметр к зажимам фотоэлемента. Установить предел измерений – 10 мкА.

2. Лампочку осветителя соединить последовательно с реостатом и выпрямителем.

3. Установить фотоэлемент перпендикулярно оси прибора (ручку – на нулевую отметку угловой шкалы).

Упражнение 1. Исследование зависимости освещенности

от расстояния до источника света.

1. Установить осветитель на десятом делении шкалы.

2. Для получения параллельного пучка света между источником и фотоэлементом установить линзу в оправе.

3.С помощью реостата подать на лампу такое напряжение, при котором микроамперметр покажет максимальное значение силы тока (i=10 мкА).

4. Снять отсчет i₁₀по шкале микроамперметра.

5. Не меняя напряжения, установить лампу на 20 и 30 делениях шкалы и снять отсчеты i₂₀иi₃₀.

6. Используя полученные данные, проверить справедливость закона обратных квадратов:

Упражнение 2. Исследование зависимости освещенности

От угла падения света.

1. Установить осветитель на десятом делении шкалы прибора.

2. Для получения параллельного пучка света между источником и фотоэлементом установить линзу в оправе.

3. С помощью реостата добиться максимального значения фототока (i=10 мкА) и снять отсчет i.

4. Не меняя напряжения на лампе и расстояние r, повернуть фотоэлемент на 30 0 и 45 0 , и снять отсчеты i₃₀иi₄₅.

по шкале микроамперметра.

5. Используя полученные данные, проверить справедливость закона косинусов:

Упражнение 3. Исследование зависимости светового потока

от площади освещенной поверхности.

1. Убрать линзу и повернуть фотоэлемент перпендикулярно падающему свету (ручку на нулевую отметку угловой шкалы).

2. Установить осветитель на десятом делении шкалы.

3. С помощью реостата подать на лампу такое напряжение, при котором микроамперметр покажет максимальное значение силы тока (i=10 мкА).

4. Поместить между фотоэлементом и световым источником матовое стекло в оправе (при этом площадь открытой поверхности фотоэлемента равна 9 см 2 ). Снять величину фототока i₉по шкале микроамперметра.

5. Установить перед фотоэлементом последовательно диафрагмы с площадью 6 см 2 и 3 см 2 и снять соответственно показания микроамперметра

i₆иi₃.

6. Построить график функции i = f ( S ) и убедиться в линейной зависимости светового потока от площади поверхности при постоянной освещенности.

1. В чем разница между энергетическим и фотометрическими величинами?

2. Основные фотометрические величины и единицы их измерения.

3. Закон обратных квадратов. Закон косинусов.

4. Какие источники света называются ламбертовскими?

ЭЛЕМЕНТЫ ФОТОМЕТРИИ. СВЕТОВЫЕ ВЕЛИЧИНЫ.

ЗАКОН ОСВЕЩЕННОСТИ

Цель работы:Изучить фотометрические световые величины, законы освещенности. Освоить работу с люксметром. Экспериментально и расчетным путем определить зависимость освещенности поверхности от расстояния до источника света.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

СВЕТОВЫЕ ФОТОМЕТРИЧЕСКИЕ ВЕЛИЧИНЫ

Раздел оптики, занимающийся рассмотрением световых и энергетических характеристик излучения в процессах его испускания, распространения и взаимодействия с веществом, называется фотометрией.

Для количественного описания самого излучения, источника излучения и освещенной поверхности применяются энергетические и световые фотометрические величины.

Световые величины используются в видимой области (l = 0,38 … 0,76 мкм) оптического излучения, а энергетические – в ультрафиолетовой и инфракрасной областях.

Рассмотрим световые фотометрические величины и их единицы.

Световое излучение характеризуется световым потоком Ф и силой света I.

Световой поток dФ излучения определяют по формуле

, (1)

где к (l) – световая активность человеческого глаза, лм/Вт,

Ф_е – поток излучения, равный отношению энергии, переносимой излучением в данном телесном угле, ко времени переноса, то есть мощность излучения в заданном телесном угле, Вт.

Световой поток Ф измеряется в люменах (лм, от лат. lumen – свет).

Формула (1) имеет смысл для видимого диапазона оптического излучения. Вне этого диапазона к (l) = 0 и Ф = 0. Внутри видимого диапазона к(l) = f(l). Максимальное значение к_max = 680 лм/Вт соответствует в дневное время зеленому цвету (l = 0,55 мкм).

Силой света I называют световой поток, приходящийся на единицу телесного угла W

. (2)

Единицей силы света является – 1 кандела (от лат. свеча), 1 кд = 1 лм/ср (ср –

стерадиан – единица телесного угла).

В общем случае сила света I зависит от направления. Если сила света источника во всех направлениях одинаковая, то такой источник света называется изотропным. Для изотропного источника, излучающего во все стороны

. (3)

Поверхность, облучаемая потоком света, характеризуется величиной, называемой освещенностью.

Освещенность Е поверхности равна отношению светового потока dФ к площади dS освещаемой поверхности

. (4)

Единицей Е является 1 лк – один люкс (от лат., lux– свет).

По существующим нормативам место для чтения должно иметь Е = 75 … 100 лк.

Для связи светового потока Ф источника света с потребляемой источником мощностью Р вводится величина, называемая световой отдачей.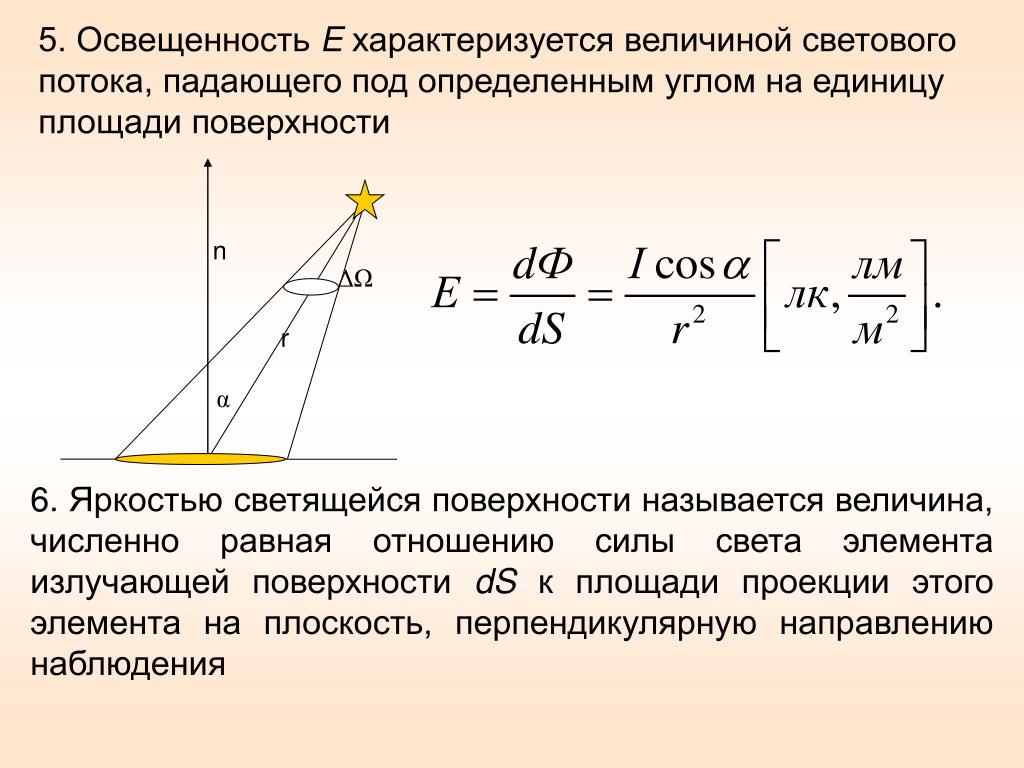

Световая отдача

, лм/Вт. (5)

Лампы накаливания общего назначения имеют к_от= 8 … 20 лм/Вт. Например, аргоновая лампа накаливания напряжением 220 В и мощностью 100 Вт дает световой поток в 1350 лм и, следовательно, к_от = 13,5 лм/Вт. Люминесцентные лампы имеют к_от до 90 лм/Вт, металлогалогенные – 130 лм/Вт.

Как следует из опыта, освещенность поверхности зависит от силы света источника, расстояния между источником света и освещаемой поверхностью и от положения освещаемой поверхности относительно падающих лучей.

1-й закон освещенности: Освещенность поверхности, на которую перпендикулярно падает свет, пропорциональна силе света I источника и

обратно пропорциональна квадрату расстояния R от источника света до освещаемой поверхности

. (6)

2-ой закон освещенности: Освещенность поверхности, создаваемая наклонными параллельными лучами, прямо пропорциональна косинусу угла падения лучей

. (7)

ПРАКТИЧЕСКАЯ ЧАСТЬ

С помощью люксметра измерить освещенность Е_изм на различных расстояниях R от лампы накаливания (5 точек). Построить график Е_изм = f(R).

Для этих же точек рассчитать значения освещенностей Е_изм , используя формулы (6), (3), (5). На том же графике нанести расчетную зависимость Е_расч = f(R).

Рассчитать максимальную относительную разность расчетных и измеренных значений Е. Указать возможные причины расхождения результатов.

Отчет о лабораторной работе должен содержать краткую теоретическую часть, схему эксперимента, таблицу измерений и рассчитанных значений Е, графики Е_изм = f(R) и Е_расч = f(R), выводы.

Дата добавления: 2016-12-06 ; просмотров: 854 | Нарушение авторских прав

Освещённость — световая величина, равная отношению светового потока, падающего на малый участок поверхности, к его площади [1] .

Содержание

Определение и свойства [ править | править код ]

Освещённость численно равна световому потоку, падающему на участок поверхности единичной площади:

E v = d Φ v d σ . <displaystyle E_=<frac>>.>

Единицей измерения освещённости в Международной системе единиц (СИ) служит люкс (1 люкс = 1 люмену на квадратный метр), в СГС — фот (один фот равен 10 000 люксов). В отличие от освещённости, выражение количества света, отражённого поверхностью, называется светимостью.

Освещённость прямо пропорциональна силе света источника света. При удалении его от освещаемой поверхности её освещённость уменьшается обратно пропорционально квадрату расстояния (Закон обратных квадратов). <2>>cos i,>

где I v <displaystyle I_> — сила света в канделах; r <displaystyle r> — расстояние до источника света; i <displaystyle i> — угол падения лучей света относительно нормали к поверхности.

Освещённость в фототехнике определяют с помощью экспонометров и экспозиметров, в фотометрии — с помощью люксметров.

Освещённость
E v <displaystyle E_>
Размерность	J . L −2
Единицы измерения
СИ	лк
СГС	фот
Примечания

Определение зависимости освещенности поверхности от расстояния до источника света.

Суть эксперимента состоит в освоении методики замера освещенности при помощи люксметра и анализе точности его показаний на основе закона обратных квадратов.

Теоретические основы эксперимента

Закон обратных квадратов.

Доказали, что освещенность при изменении расстояния от точечного источника света в 2 раза, меняется в 4 раза.

Например: при увеличении расстояния в два раза освещенность уменьшается в четыре раза,

Это объясняется 4-кратным увеличением площади поверхности, на которую падает свет в 1 кд, если расстояние увеличивается в 2 раза. Это правило распространяется только для точечных источников света.

За точечный источник света приняли источники, у которых диаметр площади излучения превышает расстояние до освещаемого объекта в 7 раз и более. Идеально точечного источника света не существует, поэтому погрешности неизбежны.

Ход работы:

1) На эталонный источник света подавалось напряжение Uэт: 184 в.

2) По табличным расстояниям распологался светоприемник люкстера и измерились значение освещенности. (E.изм)

3) По формуле вычислялись значение и записали в такую же таблицу.

Е_выч= I_эт/L²

Последовательно мы построили графики зависимости Е_выч= f(L) и E_изм= f(L)

4) Далее мы стали вычислять погрешности измерений и перевести значения освещенности из люкс в фут-канделы по формуле

Е (фт-кд)= Е(лк)/ 10. 76

Таблица 1-2

Эталонный источник : тип лампы – КГМ 220V / 650W, U_эт= 188 В, I_эт = 1000 кд.

L, м	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,2	1,4	1,6	1,8	2,0	2,2	2,4
L2,м2	0,09	0,16	0,25	0,36	0,49	0,64	0,81	1,0	1,44	1,96	2,56	3,24	4,00	4,84	5,76
Евыч= Iэт/L2, лк	11111	6250	4000	2778	2040	1562	1234	1000	694	510	390	309	250	207	174
Eизм, лк	14640	7138	4382	2939	2110	1604	1238	990	678	495	383	299	242	201	169
Абсолютная погрешность Δабс , лк	3529	888	382	162	70	42	4	-10	-16	-15	-7	-10	-8	-6	-5
Относительная погрешность Δотн , %	31,7%	14%	9,5%	5,8%	3,4%	2,6%	0,3%	0	-2,3%	-2,9%	-1,7%	-3,2%	-3,2%	-2,8%	-2,8%
Eизм(фут-кд)= Eизм(лк)/10,76	1344	682	418	280	201	153	118	94	64	47	36	28	23	19	16

Δабс= Еизм–Евыч , лк; .

Δабс Δотн = ————-— 100 % Евыч

Вывод:

Эксперимент показал, что закон обратных квадратов действует. Это очень хорошо видно почти во всех измерениях, где погрешность получилось — 7, это допустимая инструментальная погрешность прибора «Minolta», только при маленьких расстоянии (0,3 / 0,4 / 0,5) получается не допустимая погрешность (31,7% / 14% / 9,5%)

Можно сделать вывод, что допущена методическая и инструментальная погрешности. По таблице и графику видно, что в разделе с 0,3 по 1 метр относительная погрешность примерно равномерно уменьшалась. Причин её возникновения ошибки в измерении может быть много, но самая важная из них – на люксметр попадал свет, отраженный от кожуха лампы накаливания. Даже допустив такую ошибку можно сказать, что полученные данные достаточно точны.

Понимание закона обратных квадратов света

В этом сообщении в блоге я хотел бы поделиться с вами некоторыми соображениями относительно связи между апертурой и законом обратных квадратов света, а также их влиянием на падение света. выключенный.

Содержание

Шкала диафрагмы (диафрагма)

Позвольте мне облегчить ваше знакомство с этой темой, объяснив сначала диафрагму.

Переключение с максимальной диафрагмы на следующую меньшую уменьшает количество света, попадающего на объектив. Кроме того, диаметр диафрагмы каждый раз уменьшается в 1/√2 раза, что также сокращает поверхность линзы и, следовательно, количество света в 9 раз.0014 половина .

Благодаря этой градации мы просто адаптируем выдержку и диафрагму к существующему освещению: каждое число f (f-stop) является результатом предыдущего, умноженного на √2 (что равно 1,414). Мы округляем результат до 1,4, чтобы, например, апертура 4 — согласно расчету 4 x 1,4 — превратилась в следующее большее значение апертуры 5,6.

Вот отрывок из этой известной последовательности, которая выглядит следующим образом:

f/1 f/1,4 f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22 f /32

В редких случаях существуют также макрообъективы с максимальным числом f 45. Поскольку макрообъективы часто располагаются очень близко к объекту, огромное число f позволяет достичь хорошей глубины резкости (несмотря на близость).

Закон обратных квадратов света

Мы создаем идеальное освещение для каждого сценария с помощью закона обратных квадратов. Закон обратных квадратов работает следующим образом: если вы удвоите расстояние между объектом и источником света, он освещает площадь поверхности, в четыре раза большую, чем предыдущая.

Обычно мы умножаем расстояние на себя, чтобы рассчитать увеличение площади этой поверхности. Однако большая площадь поверхности приводит к интенсивности света, которая обратно пропорциональна квадрату расстояния, поскольку такое же количество света должно быть распределено на большую площадь поверхности соответственно.

Таким образом, мы видим ослабление света, что означает уменьшение интенсивности света.

С технической точки зрения закон обратных квадратов выглядит следующим образом: Энергия (в нашем случае: интенсивность света) в месте А (области объекта) уменьшается обратно пропорционально квадрату расстояния А до источника энергии (например, нашей вспышки). глава).

Чтобы записать закон обратных квадратов (его формулу), потребуются лишь базовые математические знания. Однако физика, стоящая за этим, как правило, очень сложна. По этой причине мы собираемся подойти к этому закону только иллюстративно и с точки зрения фотографии. По этой причине мы имеем в виду экспозицию датчика изображения или пленки и освещение объекта. При использовании вспышки и прожектора закон обратных квадратов особенно удобен.

Интенсивность света, например, увеличивается в четыре раза (4) при уменьшении вдвое (1/2) расстояния до источника света и объекта. Соответственно, интенсивность света уменьшится до четверти, если мы удвоим расстояние. В соответствии с этим эти примерные пары цифр действительны (расстояние: 3-кратное; интенсивность: 1/9) и (4; 1/16), если мы умножим расстояние соответственно.

В общем, закон обратных квадратов объясняет непропорциональное падение света с увеличением расстояния от объекта до источника света. Эти знания помогают нам лучше понять, как соотнести свет и освещение с расстоянием до объекта и его яркостью.

Практическое применение

Из-за обратно-квадратичной зависимости описанного закона интенсивность света довольно сильно падает, когда объект сначала удаляется от источника света. После этого она непрерывно снижается на более слабом уровне. Например: если мы увеличим расстояние между источником света и объектом с 1 метра до 2 метров, 75 процентов интенсивности света будет потеряно на объекте. Но когда мы увеличиваем дистанцию ​​с 4 до 10 метров, мы теряем всего 5 процентов.

Таким образом, интенсивность света вблизи источника света имеет особенно высокие значения. Но на расстоянии эта интенсивность достигает лишь крошечного значения. Вот как мы создаем соответствующее освещение: при постоянной выдержке значение f увеличивается, чем ближе объект находится к источнику света — чем меньше диафрагма, тем меньше света попадает в камеру.

И наоборот: значение f уменьшается по мере увеличения расстояния от объекта до источника света. В обоих случаях соответствующие снимки выглядят почти одинаково: просто потому, что через объектив проходит одинаковое количество света.

Так мы теоретически создаем правильное значение f для каждой комбинации расстояния, интенсивности света и скорости затвора.

Освещение только одного объекта

Для статических объектов достаточно одного фиксированного значения f. Однако для движущихся объектов требуются гибкие значения f, особенно когда они находятся очень близко к источнику света: из-за закона обратных квадратов небольшое изменение расстояния до источника света приводит к резкому изменению освещения. В свою очередь, одного фиксированного значения f достаточно для объекта, находящегося на большом расстоянии, даже если он перемещается в большем масштабе.

Освещение нескольких объектов

Иногда все объекты располагаются довольно близко к источнику света в виде прожектора или т.п. В таких случаях передний объект может быть переэкспонирован, тогда как тот, что сзади, останется недоэкспонированным.

Например, три объекта, расположенные друг за другом, пересекают значения f в диапазоне от f/22 до f/11. У этой проблемы есть простое решение, позволяющее равномерно осветить все объекты: просто расположите все объекты подальше от источника света. Таким образом, их относительные размеры по отношению друг к другу остаются одинаковыми, и всем им требуется только одно и то же значение f для хорошей экспозиции, например, f/4.

Вы можете очень хорошо увидеть различия в нашем примере ниже. Если освещение расположено на расстоянии 8 метров от первой модели, падение света до 4-й модели составляет всего около 2/3 ступеней. Однако, если бы вы разместили источник света всего в 2 метрах, разница в яркости между 1-й и 4-й моделями составила бы всего 2 1/3 ступени (например, f-stop 8 -> 3,5)!

Специальная задача: Правильное освещение фона

В наших изображениях мы, конечно, часто также хотим видеть контрасты вместо равномерной яркости: Мы хотим, чтобы части изображения были светлее и темнее. Например, нам нужен достаточно темный фон, на котором наша привлекательная модель будет правильно и ярко освещена – близко к источнику света! Квадратичный спад света к более дальнему фону приводит к недоэкспонированному и, следовательно, темному фону. Вот как сильный контраст работает в нашу пользу благодаря закону обратных квадратов.

В свою очередь, мы также используем этот «закон обратных квадратов», когда хотим получить равномерное и хорошее освещение модели и фона: Затем мы размещаем источник света на значительном расстоянии как от модели, так и от фона — таким образом мы достигаем очень ровное освещение.

Как видно на примере ниже, уже достаточно разместить источник света на расстоянии 4 метров от модели, чтобы равномерно осветить и модель, и фон. Разница между моделью и фоном теперь составляет всего 2/2 стопа. Если бы модель была еще ближе к фону, падение света можно было бы уменьшить еще больше.

Кстати, если источник света расположить слишком близко к модели (всего 1 метр здесь), как видно на верхнем примере, падение света на корпусе модели уже настолько велико, что – в случае снимка в полный рост — ноги будут недоэкспонированы. Поэтому такое позиционирование стоит рассматривать только для портретного снимка.

Связь между головкой вспышки, мощностью, ISO и диафрагмой

Чтобы еще лучше увидеть зависимости, мы установили как можно больше значений относительно друг друга, как показано на графической иллюстрации ниже.

Мы предполагаем головку вспышки мощностью 1000 Вт с гигантским диапазоном регулирования от 1 до 10. Значения диафрагмы и ISO были выбраны для отображения зависимости между этими цифрами. Значение ISO или диафрагмы (имеется в виду только одно из этих двух значений) необходимо установить в соответствии с таблицей, чтобы всегда получать одинаковое освещение (яркость) объекта при регулировке выходного контроллера головки вспышки.

Что сразу бросается в глаза, так это то, что выходная мощность головки вспышки (ватт/секунды) должна быть удвоена на каждую диафрагму. Таким образом, выход в верхнем диапазоне между 9и 10 увеличивается в общей сложности на 500 Вт, тогда как выходная мощность в нижнем диапазоне между 1 и 2 изменяется только прибл. 0,2 Вт. Теперь, взглянув на эти довольно экстремальные различия в мощности, вы поймете, какая большая работа по разработке потребовалась производителям головок вспышки, чтобы сделать все возможное с такой исключительно высокой точностью.

Заключение

Так что же вам обязательно следует помнить?

Относительно диафрагмы : Разница от одного диафрагменного числа к другому всегда приводит либо к удвоению, либо к уменьшению вдвое яркости. Для вспышки это также всегда означает удвоение или уменьшение вдвое мощности (Ws). Например, если мощность вспышки изменить с 5 на 6, то это в точности равно одному диафрагменному числу.

Относительно расстояния : Если объект расположен близко к источнику света, падение света на указанном объекте будет очень большим по сравнению с фоном. Легкий спад на площадь! При удвоении расстояния до объекта требуется в 4 раза больше световой энергии, чтобы сбалансировать разницу в яркости.

Удвоение/Уменьшение вдвое расстояния всегда равно 2 ступеням диафрагмы относительно разницы яркости!

Большее расстояние между источником света и объектом приводит к более равномерному освещению как объекта, так и фона, потому что с увеличением расстояния уменьшается ослабление света. Поэтому этот эффект оказывает огромное влияние на дизайн освещения.

---

P.S. Вы можете экспериментировать с расстояниями, апертурой и светоотдачей в set. a.light 3D, который был показан здесь еще в 2013 году. Оно того стоит! Как только вы полностью поймете взаимосвязь между расстоянием, апертурой и ослаблением света, вы сможете легко использовать эти эффекты, чтобы улучшить дизайн освещения и выборочно управлять им.

---

Об авторе : Йоханнес Даунер является основателем и генеральным директором Elixxier, компании-разработчика программного обеспечения set.a.light 3D, которое позволяет фотографам планировать технические детали фотосессии в виртуальной среде. Эта статья также была опубликована здесь.

Формула обратных квадратов

Главная > Формулы > Формулы по физике > Формула обратных квадратов

Формула закона обратных квадратов

Закон обратных квадратов описывает интенсивность света на разных расстояниях от источника света. Все источники света разные, но интенсивность меняется одинаково. Интенсивность света обратно пропорциональна квадрату расстояния.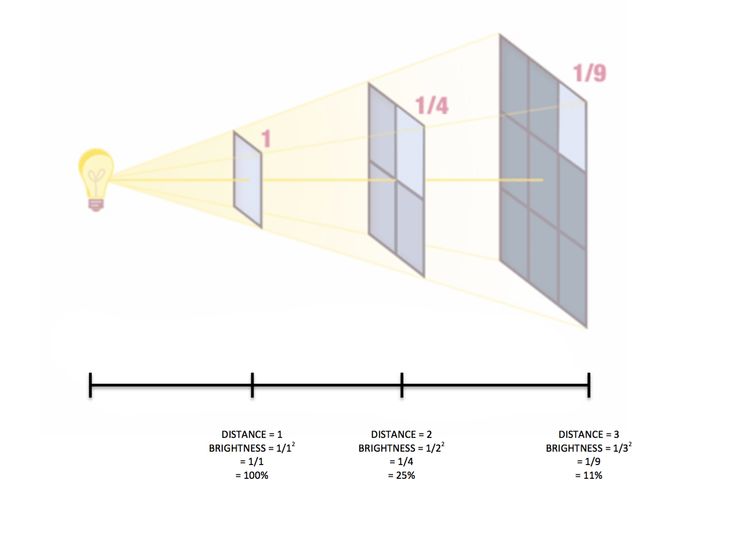 Это означает, что по мере увеличения расстояния от источника света интенсивность света равна значению, умноженному на 1/d ² ,. Пропорциональный символ используется, чтобы показать, как они соотносятся. Зависимость между интенсивностью света на разных расстояниях от одного и того же источника света можно найти, разделив одно на другое. Формула для этого показана ниже. Видимый свет является частью электромагнитного спектра, и закон обратных квадратов верен для любых других волн или лучей в этом спектре, например, радиоволн, микроволн, инфракрасного и ультрафиолетового света, рентгеновских лучей и гамма-лучей. Интенсивность видимого света измеряется в канделы единиц, в то время как интенсивность других волн измеряется в ваттах на квадратный метр (Вт/м ² ).

пропорционально:

I = Интенсивность света ( Candela , W/M ² )

означает «пропорционально»

D = расстояние от источника света M ).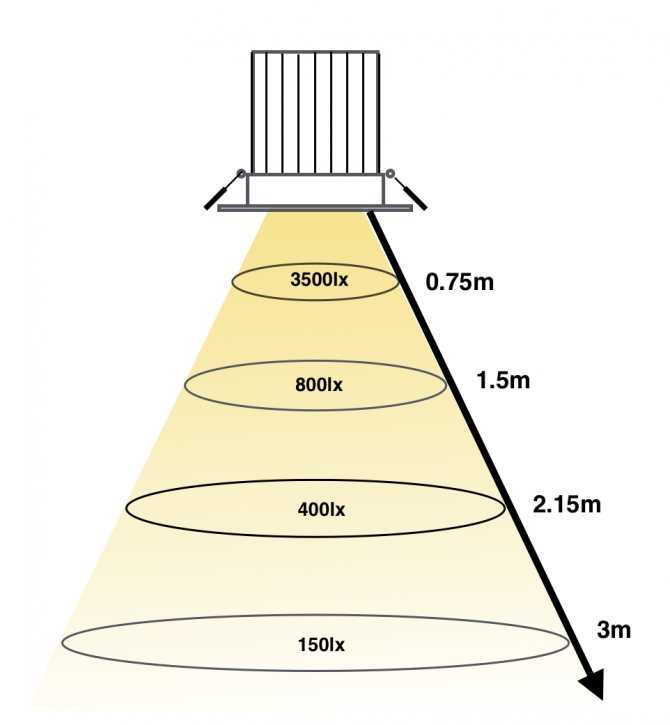

Интенсивность на разных расстояниях:

I ₁ = сила света на расстоянии 1

I ₂ = Интенсивность света на расстоянии 2

D ₁ = расстояние 1 от источника света ( M )

D ₂ )

D ₂ )

D ₂ ). )

Формула обратных квадратов Вопросы:

1) Если яркий фонарик имеет силу света 15,0 кандел на расстоянии 1,00 м от линзы, какова сила света фонарика 100,0 м с объектива?

Ответ : Интенсивность на дальнем расстоянии можно найти по формуле:

Если d ₁ = 1,00 м от линзы, а d ₂

м от линзы 903,5 = 1,00 м. , тогда I ₁ = 15,0 кандела , и нам нужно найти I ₂ . Для этого необходимо изменить уравнение:

Now, substitute the values ​​that are known in to the equation:

I ₂ = (0. 0001)(15.0 candela )

I ₂ = 0.0015 кандела

Сила света фонарика на расстоянии 100,0 м составляет 0,0015 кандела .

2) Интенсивность радиосигнала 0,120 Вт/м ² на расстоянии 16,0 м от маленького передатчика. Какова интенсивность сигнала 4,00 м от передатчика?

Ответ: Интенсивность на ближнем расстоянии можно найти по формуле:

Если d ₁ = 4,00 м от передатчика, а d ₂ = 16,0 м от передатчика, то

I ₂ = 0,120 Вт/м ² , и нам нужно найти I ₁ . Это требует перестановки уравнения:

Now, substitute the values ​​that are known in to the equation:

I ₁ = (16.0)(0.120 W/m ² )

I ₁ = 1,92 /M ²

Интенсивность радиосигнала 4.

No related posts.