Золотое сечение в фотографии это: Золотое сечение — Википедия
Золотое сечение — Википедия
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика» [9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года. {2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении.
 На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны
 {2}}{18}}}[источник не указан 1010 дней]
{2}}{18}}}[источник не указан 1010 дней]Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н
 Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты.
 Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»
Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми» - Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 603 дня].

Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В.
 Лаврус, Золотое сечение
Лаврус, Золотое сечение - ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know.
 — Phantom Press. — 209 с. — ISBN 9785864716700.
— Phantom Press. — 209 с. — ISBN 9785864716700. - ↑
Золотое сечение в дизайне: принципы сбалансированного интерьера
Золотая пропорция – это соотношение, когда отношение большей части к меньшей равно отношению суммы этих частей к большей части. В числовом выражении отношение равно 1 к 1,618, или округляют до 1,62. В процентах отношение будет выражено как 62 и 38 %.
Это проще понять на графическом примере
Этот принцип разделения упоминался у древних греков, и использовался ими для построения правильного пятиугольника. Также под принцип идеального соотношения подходит ряд чисел Фибоначчи, где каждое следующее число – это сумма двух предыдущих:
Ряд чисел Фибоначчи
Большинство гармоничных природных творений соответствуют форме спирали Фибоначчи:
- раковины улиток и моллюсков;
- расположение лепестков и цветков у растений;
- соотношение фаланг пальцев человека.
Семена подсолнечника растут из центра к внешней стороне, заполняя головку семени.
 Обычно они спиралевидные и имеют сходство с золотой спиралью
Обычно они спиралевидные и имеют сходство с золотой спиральюНаиболее показательным примером «золотого сечения» является прямоугольник, все стороны которого находятся в «золотом» соотношении
Изображенная сетка показывает единство между последовательностью Фибоначчи и «золотым» прямоугольником
Древние греки применяли золотой прямоугольник при постройке храма Парфенона. Леонардо да Винчи одним из первых стал применять метод при создании своих полотен, в том числе и знаменитой Моны Лизы.
Леонардо да Винчи руководствовался правилом золотого сечения при создании знаменитой Моны Лизы
За ним тенденцию поддержали другие деятели искусства, которые нашли применение идеальным пропорциям в живописи, портретах, архитектуре, витражах и мозаике. За тысячелетия использования оно не устарело, и сейчас активно используется в современном дизайне и архитектуре.
Золотое сечение было известно строителям Акрополя в Афинах
Принцип золотой пропорции в дизайне
Правило золотого сечения в дизайне применяется часто.
 Оно помогает достичь гармонии между частями. Многие логотипы известных брендов были выполнены с его применением:
Оно помогает достичь гармонии между частями. Многие логотипы известных брендов были выполнены с его применением:- Pepsi;
- Apple;
- Toyota;
- Twitter;
- iCloud;
- и многие другие.
Примеры использования золотого сечения в дизайне логотипов
Гармоничное разделение можно применять в дизайне при создании логотипов, визиток, плакатов, баннеров, сайтов. Применяется оно при выборе размеров элементов, размеров шрифтов и даже соотношения основного и дополнительных цветов. Так если основной текст будет шрифтом в 11 пунктов, то для подзаголовков по правилу нужно брать шрифт 18 пунктов. У National Geographic золотой прямоугольник используется для разделения сайта на основную и боковую колонку.
Совет. При использовании метода не стоит фанатично придерживаться точности соотношения. Иногда небольшое отклонение может выглядеть более эстетично.
В пространстве, оформленном согласно правилу золотого сечения, комфортно жить и отдыхать
Итак, золотое сечение используется в различных сферах:
Направление Пример использования Шрифт Определение размеров шрифтов для текста, заголовков и подзаголовков. 
Сайты Разделение структуры страницы. Расположение элементов согласно кривой Фибоначчи. Печатная продукция Использование правила золотых прямоугольников для деления площади и расчета места для акцентов декора. Дизайн квартиры Расчет размеров, расстановка мебели, определение гаммы. Золотое сечение также используется при определении размеров мебельных дверок. Считается, что именно такое соотношение воспринимается людьми как наиболее эстетичное
Смотрите такжеБильярдная комнатаЗолотое сечение в дизайне интерьера
Метод идеального сечения используется в интерьере для большей гармонии. При выборе места для мебели это правило поможет добиться гармоничного и эстетического положения. При выборе красок, обоев и мебели также его используют.
Идеальная форма помещения имеет соотношение ширины к длине как 5 к 8
Расстановка мебели должна быть сбалансированной
Если считать округленно, то можно пользоваться отношением 2 к 3.
Смотрите такжеДизайн парикмахерской, фото. При этом разделять можно больше чем на 2 части – каждое деление тогда должно выполняться таким же образом и делить следует меньшую часть. При делении на три фрагмента в процентах сначала делим на две, получаем 62 и 38 %, 38 % при делении дадут 24 и 14 %. Получается 62 % будет основным, 24 % – вторым и 14 % – третьим по важности.
При этом разделять можно больше чем на 2 части – каждое деление тогда должно выполняться таким же образом и делить следует меньшую часть. При делении на три фрагмента в процентах сначала делим на две, получаем 62 и 38 %, 38 % при делении дадут 24 и 14 %. Получается 62 % будет основным, 24 % – вторым и 14 % – третьим по важности.Соотношение размеров
Создание размеров, соответствующих идеальному разделению, при перепланировке комнаты, позволит улучшить эстетическое восприятие дизайна. При зонировании комнаты, секция с большей площадью не должна превышать 5/8 от всего пространства. То же относится и к расположению мебели.
Следуя правилу, большую часть гостиной можно отдать диванной группе, а меньшую – столовой зоне
Правилу 62 % должны соответствовать:
- зона отдыха с диваном по отношению к комнате;
- журнальный столик по отношению к длине дивана;
- расстояние от потолка до нижней границы декора и настенного освещения.

Размеры мебели исчисляются от самого большого объекта
Пропорции подойдут для высоты мелкогабаритной мебели. Она не должна быть больше 3/8 от высоты комнаты. Это касается:
- тумбочек;
- высоты спинки кресла или дивана;
- высоты напольных элементов декора.
Размеры прикроватных тумбочек и устанавливаемых на них светильников подбирают так, чтобы их общая высота не превышала 2/3 стены
Общее количество и габариты мебели рассчитывают исходя из самых крупных предметов
Присмотревшись, можно заметить, что метод учитывается и в архитектуре мебели:
- соотношение основной части стенки и шкафа;
- высота нижних тумбочек;
- расположение ключевых элементов.
Правило стоит применять при выборе дивана и стола к нему. У сбалансированного углового дивана меньшая сторона обязана быть не более и не менее 1/3. Журнальный столик также должен соответствовать пропорциям, чтоб удачно вписаться в интерьер.
Желательно, чтобы диван не занимал больше двух третей стены, около которой он стоит
Журнальный столик должен быть не больше, чем две трети размера дивана
Для высоких квартир подходит сегментирование на 2 участка, а для невысоких, дополнительное разделение стены поможет визуально увеличить ее размер.
Смотрите такжеПочему газ горит оранжевым пламенем на плите?
Соотношение цветов
Золотое сечение при цветовом оформлении комнаты применяется для выбора основного цвета интерьера, а также дополнительного и акцентного: 62, 33 и 5 % соответственно.
Большие и темные предметы размещают внизу, маленькие и более светлые – выше
Основная часть интерьерной композиции должна быть самой освещенной и насыщенной
Выбор трех цветов для оформления комнаты наиболее предпочтительный. Основной используется для стен и потолка. Дополнительный цвет подходит для мебели в комнате. И оставшиеся 5 % оформления используется для выделения акцентов.
Можно поделить палитру на 4:
- основная окраска для комнаты – 62 %;
- дополнительная расцветка для мебели – 24 %;
- тона для различного декора – 9 %;
- оформление акцента – 5 %.
Цветовая палитра интерьера разделяется на три части – основную, активную и акцентную
Такое деление больше подходит для интерьеров, которые насыщены декором и позволяют широкий набор палитры.
Смотрите такжеЭргономика пространства в дизайне интерьера.
Золотое сечение в декоре
С применением правила гораздо проще разместить элементы декора, особенно подвесного и настенного.
Прежде чем разместить элементы декора, нужно определить их идеальное месторасположение
Каждая декорирующая деталь меньшего размера должна относится к большей, как та относится к самой крупной
Картина в качестве акцентного элемента, расположенная по этому правилу будет смотреться гармоничнее. Для портретного варианта нижняя граница произведения искусства должна отступать от пола на 38 % высоты стены. Высота такой картины не должна превышать 2/3 оставшегося участка стены. Для горизонтальной картины пропорции применяются немного по-другому. Низ картины должен проходить на границе 5/8 от пола, а короткая сторона составлять 62 % от остатка.
Особенно тщательно необходимо подбирать картины разного размера
Метод можно применить также к расстановке декораций. Мысленно расположив идеальную спираль, нужно вписать декор соответственно его размеру.
 Таким путем получим идеальное расположение. Конечно же, не стоит злоупотреблять правилом и всегда оценивать эстетику получившегося интерьера, полагаясь на чувство прекрасного.
Таким путем получим идеальное расположение. Конечно же, не стоит злоупотреблять правилом и всегда оценивать эстетику получившегося интерьера, полагаясь на чувство прекрасного.К такому небольшому элементу как ваза с цветами тоже подойдет идеальное деление. Подогнав длину стеблей под пропорции можно получить гармоничный вид.
Так выглядит идеальная ваза с цветами
Смотрите такжеПодключение духового шкафа к электросетиНеобходимо помнить, что метод золотого сечения всего лишь еще один инструмент для упрощения создания гармоничного дизайна. Поэтому не обязательно дотошно придерживаться математической точности. Дизайн интерьера – это всегда творческое решение. Главное, чтоб результат соответствовал эстетическим требованиям.
Видео о том, как работать с размерами в интерьере
Смотрите такжеСоздаем оригинальный дизайн детской комнаты для девочкиГалерея
Смотрите такжеСовременные шторы на кухню в 2020 году: идеи и варианты дизайна шторДизайн квартиры с правильными пропорциями в интерьере
Смотрите такжеДизайн детской комнаты для двух девочек разного возрастаКвартира для молодой семьи
Смотрите такжеКухня бежевого цвета: советы по оформлениюСбалансированные интерьеры
Примеры золотого сечения в архитектуре, его применение
Примеры золотого сечения в архитектуре найти можно везде, когда умеешь его видеть.
 Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.
Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.7+ примеров золотого сечения в архитектуре России
Санкт-Петербург
Здания исторического центра Санкт-Петербурга построены в разных архитектурных стилях, таких как барокко, классицизм, ампир, эклектика, необарокко, неоготика. Подчиняются ли они золотому правилу?
Исаакиевский собор
Придворный архитектор Александра I Огюст Монферран строил этот собор с 1819 по 1858 гг. Стиль позднего классицизма, в котором уже проявлены черты неоренессанса и эклектики. Елена задалась вопросом: «В чём же причина гармонии довольно громоздкого здания?»
Свой поиск она начала, как рекомендуется в методике профессора Московского архитектурного института Ю.
 Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.
Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.Первый ряд определён шириной здания, которая принята за 400 ед. и представляет такие цифры 400, 247, 153, 94, 58…
Если 400 разделим на число ≈1,618, то получим приблизительно 247; повторяем действие со следующим числом: 247: 1.618≈153.
И так находим все числа. Теперь смотрим на рисунок. Основная часть с колоннами вписывается в прямоугольник со сторонами 400 и 247. Поскольку стороны находятся в соотношении Ф≈1.618, то они образуют Золотой прямоугольник.
Следующий ряд представлен высотой здания: 370, 228, 140, 87, 53, 33, 20, 12. Эти размеры заложены в более мелкие детали. По вертикали Исаакиевский собор делится Золотым сечением у основания купола, что делает соотношение основной части и купола гармоничным.
Третий ряд размеров начинается со 113, и являет ширину основания главного купола: 113, 69, 42, 26, 16. Числа этого ряда встречаются в размерах окон, в высотах колонн и других деталей собора.

Золотые прямоугольный и равнобедренный треугольники имеют место в здании Исаакиевского собора, как видно из рисунка.
Кунсткамера
На Университетской набережной Васильевского острова стоит здание Кунсткамеры, заложенное в 1718 году под руководством немецкого архитектора Георга Маттарнови: Петровское барокко, два 3-этажных корпуса и сложная многоярусная купольная башня.
Исследование начинается с главных величин: высоты и длины здания, от которых строится золотой ряд. Длина — 450 ед., далее 277, 170, 105, 65, 40, 24. Такие размеры можно видеть в высоте и широте разных уровней башни, длине корпусов. Сама башенная часть вписана в золотой равнобедренный треугольник от основания до вершины. Золотое сечение просматривается в большей степени именно в этом главном элементе, что правильно с точки зрения архитектуры. Вывод: основа Кунсткамеры подчиняется золотому правилу и сохраняет композиционную гармоничность.
Новый золотой ряд начинает высота здания: 211, 130, 80, 49, 30.
 Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.
Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.Торговый дом «Эсдерс и Схейфальс» на пересечении Мойки и Гороховой
Построено в 1907 году по проекту Владимира Александровича Липского и Константина Николаевича де Рошефора (Рошфора). В 1905 г. бельгиец С. Эсдерс и нидерландец Н. Схейфальс подали прошение о разрешении построить пятиэтажное здание с куполом и шпилем на угловой башне для их торгового дома вместо старого.
С длины здания в 671 ед. начинается ряд Золотого сечения, наблюдаемого в размерах: 671, 414, 256, 158, 98, 60, 37, 23. Обращаем внимание на основной элемент — шпиль. Убеждаемся, что композиционное решение завершено гармоничным сочетанием высотных величин.
Дом Советов на Московской площади
Построен в 1941г по проекту Ноя Абрамовича Троцкого. Здание советского периода рассматривают как творческую интерпретацию классики. Центральный портик с четырнадцатью колоннами завершает скульптурный ансамбль на тему строительства социализма и гербом Российской Советской Федеративной Социалистической Республики.

По бокам симметрично расположены пятиэтажные корпуса. Длина Дома достигает 1472 ед., из которого методом деления на число Ф получается ряд размеров элементов здания: 1472, 909, 562, 34, 214, 132, 81, 50 (Приложение 21): высоты сооружения, высоты входа и др.
Вершина Золотого равнобедренного треугольника совпадает с вершиной здания, а его стороны проходят через вехние точки главного входа. Прямоугольный золотой треугольник образован вершинами в верхушке здания и в конце внутренней части бокового крыла. Пропорциональность очевидна, хотя и не имеет большой композиционной значимости.
Москва
Московский Государственный Университет на Воробьёвых горах
Над его проектом работал коллектив под управлением Б.М.Иофана, которого позже сместили с должности главного архитектора. Образец послевоенной советской архитектуры выстроен с 1949 по 1953 годы.
Б.М.Иофан предложил композицию из пяти составляющих с центральной башней. В годы строительства это было самое высокое здание в Европе.

Длина здания равна 1472 ед. и начинает ряд: 909, 562, 347, 214, 132, 81, 50. Золотому сечению подчиняются, в основном высотные размеры. Из ширины башни проистекает другой ряд: 538, 332, 205, 126, который видим в широтных размерах.
Золотой прямоугольный треугольник гипотенузой проходит через угол здания и захватывает пристройки.
Таким образом, во всех исследуемых зданиях ученица обнаружила Золотое сечение, сохраняющее гармонию.
5 примеров дополнительно
Чтобы упростить задачу поиска ЗС, можно брать рациональные дроби 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; и так дальше. Закономерность ясна: 3+2 =5; 5+3=8; 8+5=13… Или ещё проще. Сделайте себе циркуль для определения пропорции по инструкции в видео. Времени уйдет минут 10. Как пользоваться этим циркулем для определения пропорциональности элементов тоже расскажут и покажут.
Применяя этот способ, находим золотую пропорцию русского зодчего Матвея Казакова в кремлёвском здании сената, да и во всех остальных работах: Пречистенском дворце в Москве, Благородном собрании, Голицынской больнице (им.
 Пирогова)…
Пирогова)…Созданный другим великим архитектором Василием Ивановичем Баженовым дом Пашкова в Москве (Российская государственная библиотека) причисляют к образцам совершенных архитектурных памятников, в котором легко определить ЗС.
Ужасный символ Парижа и золотое сечение
Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?
Она же наблюдается и самом знаменитом французском соборе Нотр-Дам-Де-Пари.
Вся правда о древних строителях
Интуитивно или сознательно великие архитекторы строили здания с учётом этих пропорций? Античные математики знали о золотом сечении со времён Пифагора. Находятся всё новые подтверждения его применения в архитектурных пропорциях.
 Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?
Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?Может все выше приведённые исследования являются подгонкой под известный результат? Не так сложно выбрать из множества архитектурных элементов те, которые подтверждают гипотезу, т. к. абсолютной точности никто не требует. Логично задуматься над вопросом: «Что если греки НЕ применяли золотое сечение?»
Собственно говоря, и для Луки Пачоли, написавшего в 1509 году труд «Божественная пропорция», не столь важно было его прикладное значение. Важно было обосновать её мистическую природу. А применять его осознанно стали только с момента издания книги.
Тайна архитектуры Древней Греции
Красивые и гармоничные объекты всегда отвечают правилу ЗС, а при анализе величин определяется эта пропорциональность.
 Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?
Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?Мифы и диковинные факты о пирамиде
Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?
Но тогда возникает вопрос об уровне древнеегипетской математики.
 Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?
Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.
Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.
Как же всё-таки построить «Золотой» дом для себя?
Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия Золотого сечения.
 Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.
В природе подобная соразмерность встречается везде. Тот, кто чувствует гармонию пространства, создаст пропорциональное здание без специальных для этого усилий.
Например, наши предки строили хоромы соразмерные человеку. Мерили высоту и длину в саженях, локтях, аршинах, пядях. Никто не возражает, что в человеческом теле соблюдена золотая пропорция? Длина руки от кончиков пальцев до подмышки относится к расстоянию от той же точки до локтя как эта величина к размеру ладони.
Известный французский архитектор Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.
5 способов соблюдать правило в интерьере
- В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.

- Иногда достаточно переставить мебель или сделать дополнительную перегородку.
- Аналогичным образом меняется высота и длина окон и дверей.
- В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
- Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
О золотом сечении простыми словами
Что же это такое? Отрезки золотой пропорции выражаются бесконечной иррациональной дробью, десятичное значение которой равно приближённо числу Ф≈1,618 или Ф≈1,62. Другими словами: если берём целое и делим его на две части так, что одна из них составляет 62%, а другая — 38%, получаем Золотую пропорцию.
Золотой прямоугольник: когда длину большей стороны делим на длину меньшей и получаем число Ф.
 При делении меньшей на большую получается обратное значение φ ≈ 0,618.
При делении меньшей на большую получается обратное значение φ ≈ 0,618.Золотой равнобедренный треугольник: если отношение размера одной боковой стороны и размера основания составляет золотое число Ф; угол между равными сторонами равен 36°.
Золотой прямоугольный треугольник Кеплера объединяет в себе теорему Пифагора и ЗС: соотношение квадратов его сторон составляет 1,618.
Оцените полезность статьи, поделитесь с друзьями и добавьте в закладки, чтобы было легко найти.
Смотрите познавательное видео по теме
Золотое сечение
Золотое сечение
Бабенко П.Д. 11КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ И.Т. ТРУБИЛИНА
Мамась Н.Н. 11КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ И.
 Т. ТРУБИЛИНА
Т. ТРУБИЛИНАТекст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDFВведение: «Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением…»
«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».
Иоганн Кеплер
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому.
 Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.Цели:
1. Измерить гармонию алгеброй.
2. Изучить разнообразие применения золотого сечения и связанные с ним соотношения в реальной жизни;
2. Разобраться в пропорциях человека как гармонии и красоты.
Задачи:
1. Познакомиться с понятием золотого сечения и с историей его развития;
2. Получить представление о практическом применении золотого сечения в реальной жизни;
3. Выяснить, почему с этим понятием связана гармония и красота.
Предметом исследования является золотое сечение, объектом – гармоническая пропорция.
Актуальность работы – гармония и красота в жизни всегда актуальны
Гипотеза: в окружающем мире “золотое сечение” является основополагающим принципом красоты, прочности, надежности и позволяет осознать связь мира искусства и мира чисел.

1. Понятие «золотое сечение».
«Золотым сечением» и даже «божественной пропорцией» называли математики древности и средневековья такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
а :b = b : c или с : b = b : а
Итак, золотая пропорция = 1 :1,618. Это отношение приближенно равно 0,618 ≈ 5/8.В алгебре это число обозначается греческой буквой фи (φ). Полученное значение есть знаменитое число «фи», названное так американским математиком Марком Баром по первой букве имени великого скульптора Фидия, который, по преданию, использовал «золотое сечение» в своих работах.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник — выпуклый и звездчатый.

Из подобия треугольников АСD и ABE можем вывести уже известную пропорцию:
AB/AC=AC/BC
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
1.1. Задачи на построение.
В геометрии есть понятия: «деление отрезка в золотом отношении», «золотой треугольник», «золотой прямоугольник», «золотая логарифмическая спираль». Мне Dзахотелось научиться строить эти фигуры. Я разобрала три задачи.
Задача №1. «Деление отрезка в золотом отношении»
Дано : Отрезок АВ. E
A CB Построить: золотое сечение отрезка АВ, то есть точку С так, чтобы Построим прямоугольный треугольник, у которого один катет в два раза больше другого.
 Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.
Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.Задача №2. Построение «золотого треугольника».
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции «золотого сечения». Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника
2.
 История развития «золотого сечения».
История развития «золотого сечения».Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети 1 в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответсвуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Также о золотом делении знал Платон. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
 В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во второй книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипеикл (2 в. до н.э.), Папп (3 в. н.э.) и др.
В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж.Кампано из Наварры (3 в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.
 В 1509 г. В Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства Бог сын, Бог отец и Бог дух святой (подразумевалась, что малый отрезок есть олицетворение Бога сына, большой отрезок – Бога отца, а весь отрезок – Бога духа святого).
В 1509 г. В Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства Бог сын, Бог отец и Бог дух святой (подразумевалась, что малый отрезок есть олицетворение Бога сына, большой отрезок – Бога отца, а весь отрезок – Бога духа святого).Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название Золотое Сечение. Так оно и держится до сих пор как самое популярное.
В 1855 г. Немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».
 Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.
Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.В конце 19 – начале 20 вв. появилось немало чисто формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры.
3. «Золотое сечение» в разных сферах
3.1.«Золотое сечение» в скульптуре.
Скульптурное сооружение, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Ещё в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Они утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения».

Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самая знаменитая статуя Зевса Олимпийского и Афины Парфенос (которые считались одним из чудес света). Было проведено большое число измерений на помещённых в журналах крупных портретах мужчин и женщин, на многих их низ указанные отношения представляют «золотое сечение».
3.2.«Золотое сечение» в архитектуре.
Парфенон.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (5 в. До н. э.).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон(синий и красный) для скульптуры.
 Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.Дом Пашкова.
Одним из шедевров архитектуры в Москве – дом Пашкова- является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.
Баженов говорил: «Архитектура – главнейшее имеет три предмета; красоту, спокойность и прочность здания… К достижению сего служит руководством здание пропорций, перспектива, механика или вообще физика, а всем им общим является рассудок».
3.
 3. «Золотое сечение» в живописи.
3. «Золотое сечение» в живописи.«Золотое сечение» в живописи, проглядывалось в работах и творчесте великого Леонардо да Винчи. Он говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Одним из таких портретов является Монны Лизы (Джоконды), долгие годы привлекают внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует много версий об истории этого портрета. Одна из них:
Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекало простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.
3.
 4. «Золотое сечение» в природе.
4. «Золотое сечение» в природе.«Золотое сечение» — один из основополагающих принципов природы. Красота природных форм во взаимодействии двух физических сил – тяготения и инерции. Золотое сечение – символ этого взаимодействия, поскольку диктуемое ею отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный рост побега до зрелости и замедленный рост до момента цветения, когда достигшее полной силы растение готовится дать жизнь новому побегу.
Одним из первых проявления золотого сечения в природе подметил немецкий математик и астроном Иоганн Кеплер (1570-1630 гг.). С ХVII в. наблюдение математических закономерностей в ботанике и зоологии стали быстро накапливаться.
В 1850 г. немецкий ученый А. Цейзинг открыл так называемый закон углов, согласно которому средняя величина углового отклонения ветки растения равно примерно 138 градусов.
Допустим, что две соседние ветки растения исходят из одной точки (на самом деле это не так: в реальности ветви располагаются выше или ниже друг друга).
 Обозначим одну из них через ОА, другую через ОВ. Угол между лучами – ветками обозначим через а, а угол, дополняющий его до 360 , — через Р.
Обозначим одну из них через ОА, другую через ОВ. Угол между лучами – ветками обозначим через а, а угол, дополняющий его до 360 , — через Р.Составим золотую пропорцию деления полного угла, считая, что угол К – большая часть этой величины.
360/Р=Р/360-Р.
Получаем квадратное уравнение: Р² + 360 – Р360² =0. Положительный корень Р= -180+√180²+360²= 180·±√5= 180·1,236= 222,48.
а=360°-222,48°=137,52°≈138°.
Таким образом, величина среднего углового отклонения ветки соответствует меньшей из двух частей, на которые делится полный угол при золотом сечении.
5. Экспериментальная часть
Изучив теорию вопроса, я решила провести исследование и найти пропорции золотого сечения в живой природе (на примере комнатных растений).
Эксперимент №1
Цель: проверить есть ли «золотое сечение» в растительном мире, у комнатных растений.

В первую очередь я заинтересовалась, как проявляется принцип формообразования в живой природе. Выяснилось, что комнатные растения растут и занимают место в пространстве в основном в двух вариантах — рост вверх или расстилание по поверхности, либо закручивание по спирали (вьющиеся растения). Меня заинтересовал первый вариант. Для этого было изучено 6 комнатных растений (среди них бегония клубневая, диффенбахия, традесканция, глоксиния белоцветковая, каланхое, роициссус).
Приглядимся внимательно к схематично изображённому фрагменту комнатного растения. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.
Если измерить расстояние АС и расстояние ВС, и найти отношение
ВС.
 : АС, то оно приближённо равно 0,618, т.е. подчиняется золотой пропорции.
: АС, то оно приближённо равно 0,618, т.е. подчиняется золотой пропорции.Вывод: результаты измерений показывают, что в росте, завоевании пространства, растение сохраняет определенные пропорции. Импульсы его роста постепенно уменьшаются в пропорции «золотого сечения».
Заключение.
В своей работе я хотел продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведенные исследования доказали, что многое в окружающем мире подчиняется правилу золотого сечения.
Физика исследует реальный мир. Биология – живой мир органической природы. Предмет исследования математики нематериальны, в природе нет логарифмов, синус не рассмотришь под микроскопом и при этом математика – самое могущественное орудие познания, созданное человеком, и любая наука достигает совершенства, когда начинает говорить на языке математики.
Значение золотого сечения в современной науке очень велико.
 Эта пропорция используется практически во всех областях знаний.
Эта пропорция используется практически во всех областях знаний.Я говорила только об его эстетическом значении, но существуют примеры его чисто практического применения. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью и т.д.
Список литературы:
Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014.
Пидоу Д. Геометрия и искусство. – М.: Мир, 1989.
Виленкин Н. и др. «Математика», 5, «Мнемозина», 2001
«Энциклопедический словарь юного математика», Москва, «Педагогика», 1985
Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988.
Интернет сайты:
http://www.
 abc-people.com/idea/zolotsech/
abc-people.com/idea/zolotsech/http://n-t.ru/tp/iz/zs.htm
http://tmn.fio.ru/works/04x/304/p3_4.htm
Просмотров работы: 821
Золотое сечение
Любому человеку, которому хотя бы косвенно приходилось сталкиваться с геометрией пространственных объектов в интерьерном дизайне и архитектуре, наверняка хорошо известен принцип золотого сечения. Еще недавно, несколько десятков лет назад, популярность золотого сечения была настолько высокой, что многочисленные сторонники мистических теорий и устройства мира его называют универсальным гармоническим правилом.
Сущность универсальной пропорции
Удивительно другое. Причиной предвзятого, почти мистического отношения к столь простой числовой зависимости послужило несколько необычных свойств:
- Большое количество объектов живого мира, от вируса до человека, имеют основные пропорции тела или конечностей, очень близкие к значению золотого сечения;
- Зависимость 0,63 или 1,62 характерна только для биологических существ и некоторых разновидностей кристаллов, неживые объекты, от минералов до элементов ландшафта, обладают геометрией золотого сечения крайне редко;
- Золотые пропорции в строении тела оказались наиболее оптимальными для выживания реальных биологических объектов.

Сегодня золотое сечение находят в строении тела животных, панцирей и раковин моллюсков, пропорций листьев, веток, стволов и корневых систем у достаточно большого числа кустарников и трав.
Многими последователями теории универсальности золотого сечения неоднократно предпринимались попытки доказать тот факт, что его пропорции являются наиболее оптимальными для биологических организмов в условиях их существования.
Обычно в качестве примера приводится устройство раковины Astreae Heliotropium, одного из морских моллюсков. Панцирь представляет собой свернутую спиралью кальцитовую оболочку с геометрией, практически совпадающей с пропорциями золотого сечения.
Более понятным и очевидным примером является обычное куриное яйцо.
Соотношение основных параметров, а именно, большого и малого фокуса, или расстояний от равноудаленных точек поверхности до центра тяжести, будет также соответствовать золотому сечению. При этом форма скорлупы птичьего яйца является наиболее оптимальной для выживания птицы, как биологического вида.
 При этом прочность скорлупы играет далеко не главную роль.
При этом прочность скорлупы играет далеко не главную роль.Происхождение универсальной пропорции
О золотой пропорции сечения знали древнегреческие математики Евклид и Пифагор. В одном из памятников древней архитектуры — пирамиде Хеопса соотношение сторон и основания, отдельные элементы и настенные барельефы выполнены в соответствии с универсальной пропорцией.
Методика золотого сечения широко использовалась в средние века художниками и архитекторами, при этом суть универсальной пропорции считалась одной из тайн вселенной и тщательно скрывалась от простого обывателя. Композиция многих картин, скульптур и зданий выстраивалась строго в соответствии с пропорциями золотого сечения.
Впервые суть универсальной пропорции документально была сформулирована в 1509 г монахом-францисканцем Лукой Пачоли, обладавшим блестящими математическими способностями. Но настоящее признание состоялось после проведения немецким ученым Цейзингом всестороннего изучения пропорций и геометрии человеческого тела, древних скульптур, произведений искусства, животных и растений.

У большинства живых объектов некоторые размеры тела подчиняются одним и тем же пропорциям. В 1855 г ученым был сделан вывод о том, что пропорции золотого сечения являются своеобразным стандартом гармонии тела и формы. Речь идет, прежде всего, о живых существах, для мертвой природы золотое сечение встречается значительно реже.
Как получили золотое сечение
Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.
Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.
На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.

Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:
- Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению; - Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
- В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде.
 В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.
В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.
Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, к
Что такое золотое сечение в фотографии и как его использовать?
Если хотите узнать все о золотом сечении в фотографии , вы попали в нужное место.
Представьте, что вы стоите на краю скалы. У вас под ногами невероятная сцена. Даже свет идеален. Тем не менее, вы смотрите в видоискатель и чувствуете себя потерянным. Как его запечатлеть?
В такой ситуации характеристики фотоаппарата не дадут вам хорошей фотографии.Вам нужно что-то, что ограничит ваш выбор и поможет вам принять творческое решение. Это композиция.
О композиции мы уже говорили в предыдущем посте. Мы также объяснили основы правила третей — одного из самых полезных инструментов композиции в фотографии.

Теперь мы сделаем шаг вперед и представим золотое сечение . Это более продвинутая версия правила третей, которая поможет вам воспроизвести баланс и порядок природы на ваших фотографиях.
Посмотрим как.
Происхождение золотого сечения
Возможно, вы слышали о золотом сечении в искусстве или архитектуре. Это композиционный принцип упорядочивания элементов в произведении таким образом, чтобы конечный результат эстетически нравился зрителю.
Однако происхождение этого правила математическое. В математике две величины, такие как a и b, находятся в золотом сечении, если их соотношение совпадает с отношением их суммы (a + b) к большей из величин.
Звучит непонятно? Это изображение должно помочь.
Выровненные таким образом a и b выглядят приятными для глаз, поскольку находятся в золотом сечении. A примерно в 1,618 раза больше, чем b.
Не уверены, что вы найдете красоту в этих двух строках? Затем взгляните на два четырехугольника ниже.
 Первый в 1,618 раза больше, чем соседний.
Первый в 1,618 раза больше, чем соседний.Если вы начнете заполнять меньший четырехугольник большим количеством четырехугольников, каждый по 1.В 618 раз меньше, чем предыдущий, в конечном итоге вы получите это:
А теперь начните рисовать кривую, начиная с нижнего угла слева. Проведите кривую через противоположный угол вправо. Продолжайте рисовать, пока он не пройдет через два противоположных угла каждого четырехугольника. И у вас будет это:
Спираль. Образец, который мы находим в природе везде. Представьте себе раковину наутилуса , океанскую волну или глаз урагана .
Этот хорошо известный рисунок объясняет, почему золотое сечение часто называют золотой спиралью . Помните об этом, потому что он понадобится вам в вашей фотографии.
Почему работает золотое сечение?
Как вы видели выше, применение золотого сечения к четырехугольникам привело к красивому гармоничному узору.

Вот и ключ. Золотое сечение помогает нам создавать композиции, которые кажутся естественными, органичными и приятными для глаз.
Когда мы смотрим на фотографию, основанную на золотом сечении, она, естественно, привлекает внимание к интересующей нас вещи.Намеченное сообщение попадает прямо в цель.
Как использовать золотое сечение в вашей фотографии
Теперь, когда вы знаете, почему работает золотое сечение, пора научиться применять его к вашим фотографиям.
Есть два способа его использования. Вы можете использовать Golden Spiral или так называемую Phi Grid .
Давайте подробнее рассмотрим оба.
Сетка Фи
Сетка Фи — это более простой способ использовать золотое сечение в вашей фотографии.Это шаг вперед от использования правила третей, которое добавит вашим изображениям большей силы и смысла.
По правилу третей мы делим рамку на две горизонтальные линии, пересекающиеся с двумя вертикальными линиями.
 Конечным результатом является сетка, образованная девятью прямоугольниками одинакового размера. Идея состоит в том, чтобы расположить интересующие вас объекты рядом с любой из линий или на их пересечении.
Конечным результатом является сетка, образованная девятью прямоугольниками одинакового размера. Идея состоит в том, чтобы расположить интересующие вас объекты рядом с любой из линий или на их пересечении.Расположение линий немного отличается от Phi Grid. Полученные прямоугольники не совпадают по размеру.Верхний и нижний горизонтальные ряды одинаковые по ширине, средний уже. То же верно и для правой и левой вертикальных линий.
Это выравнивание ставит интересующий объект больше в центр, чем принцип правила третей.
На фотографии ниже видно, что маяк расположен немного не по центру. Вторая вертикальная линия следует за ее самой высокой частью. Небо и земля почти в золотом сечении, что делает фотографию более сбалансированной и приятной для глаз.
Если бы я применил здесь Правило третей, у меня было бы больше неба и меньше земли, а маяк был бы расположен не по центру. Это была бы хорошая композиция, но не такая естественная, как эта.
В пейзажной фотографии вы очень часто работаете с естественными линиями, такими как горизонт.
 Вот почему Сетка Фи имеет больше смысла, чем Золотая Спираль. Просто попробуйте расположить горизонт вдоль любой из двух горизонтальных линий, и ваше изображение естественно понравится зрителю.
Вот почему Сетка Фи имеет больше смысла, чем Золотая Спираль. Просто попробуйте расположить горизонт вдоль любой из двух горизонтальных линий, и ваше изображение естественно понравится зрителю.Золотая спираль
Взгляните еще раз на изображение спирали. Его основание — самый маленький четырехугольник — должно быть частью кадра с наибольшей детализацией. В идеале остальная часть объекта должна быть помещена внутри спирали.
Учтите, что центр спирали не обязательно должен находиться в правом нижнем углу. Это может быть где угодно в кадре, в зависимости от вашего объекта.
Теперь представить себе спираль, перекрывающую ваш кадр, может быть очень сложно. Я предлагаю зарезервировать эту технику только для объектов, которые напоминают спираль или имеют кривые.
Пример использования золотой спирали для компоновки пейзажной фотографииЕсли можете, снимайте объект так, чтобы его кривые повторяли кривые воображаемой золотой спирали. Таким образом, взгляд зрителя будет направлен прямо на интересующий объект и проследить его естественное расширение в кадре.

Как наложить на кадр спираль или сетку
Некоторые камеры с цифровым видоискателем позволяют наложить на кадр сетку Фи или спираль. Но, как правило, редактировать композицию во время пост-обработки намного проще.
И Photoshop, и Lightroom позволяют размещать спираль или сетку над вашими изображениями. Чем больше фотографий вы отредактируете таким образом, тем лучше вы натренируете глаз. Постепенно вы начнете применять золотое сечение во время съемки, даже не задумываясь об этом.
Начни с самого простого
Мастеринг композиции — задача, на которую может уйти вся жизнь. Мой личный совет — начать с самого простого метода — правила третей. Затем перейдите к Phi Grid .Тогда ищите возможности использовать Golden Spiral .
Иногда для вашего изображения подойдет только один из приемов. В других случаях у вас может быть больше вариантов с другими результатами. Освоение различных приемов композиции дает возможность сделать правильный выбор для любой ситуации.

Все еще не понимаете, что такое золотое сечение? Спросите меня о чем угодно или поделитесь своим опытом в разделе комментариев ниже.
Статьи, связанные с «золотым сечением в фотографии»
Золотое сечение и правило третей
Золотое сечение и Правило третей , возможно, самые сильные и важные правила композиции.Они, как правило, обеспечивают общую основу изображения, создавая «баланс» и позволяя другим композиционным элементам работать с вашей фотографией. По крайней мере, они являются хорошей отправной точкой при создании кадра.
Золотое сечение или соотношение
Когда две вещи пропорциональны друг другу в соотношении 1: 1,618, они находятся в Золотом сечении.Линия, разделенная на это соотношение, будет выглядеть так:
Прямоугольник с пропорциями золотого сечения.
Так что же такого захватывающего в этом соотношении? В природе золотая середина встречается повсюду .
 .. от классического примера оболочки Наутилуса до образования галактик, от относительного размера и расположения костей в ваших руках и руках до роста и формы деревьев и лесов, она также используется в сложные экономические уравнения, и утверждается, что это даже можно найти в самой структуре вашей ДНК.
.. от классического примера оболочки Наутилуса до образования галактик, от относительного размера и расположения костей в ваших руках и руках до роста и формы деревьев и лесов, она также используется в сложные экономические уравнения, и утверждается, что это даже можно найти в самой структуре вашей ДНК.
По какой бы то ни было причине, по которой это происходит в природе, наш разум кажется запрограммированным на распознавание этого паттерна, даже если даже подсознательно, и в результате изображения, соответствующие этому паттерну, воспринимаются как приятные для глаза.Итак, как это применить? В изобразительном искусстве это применяется путем разделения изображения по этому соотношению. Полученное изображение может выглядеть так.
Обратите внимание, что даже без объекта изображение четко фокусирует взгляд на правую нижнюю часть изображения, создавая интересную точку.В этом случае вы бы разместили важную тему вокруг этой области.
Баланс здесь тоже играет важную роль.
 Большее количество меньших прямоугольников справа уравновешивает общую большую, но пустую левую часть изображения. Составьте композицию вокруг этих линий, чтобы придать изображению лучший баланс.
Большее количество меньших прямоугольников справа уравновешивает общую большую, но пустую левую часть изображения. Составьте композицию вокруг этих линий, чтобы придать изображению лучший баланс.Хотя это отлично подходит для рисования или рисования, это довольно сложно и трудно представить в видоискателе вашей камеры, пока вы пытаетесь скомпоновать свой снимок и справиться с любыми другими отвлекающими факторами, с которыми вы можете столкнуться в поле …
Вот где приходит на помощь правило третей.
Правило третей — это, по сути, упрощение Золотого правила. Хотя его соотношение не соответствует соотношению 1: 1,618, его правильная реализация в композиции даст вам примерно такой же желаемый эффект, но его очень легко представить и реализовать по сравнению с золотым сечением.
Вот как это работает:
1. Разделите изображение на 9 равных частей, три по вертикали и три по горизонтали (по сути, доска X и O).
2.
 Используя эти линии в качестве направляющих, размещайте интересующие вас объекты на пересечениях линий, чтобы удерживать взгляд в пределах изображения. Обратите внимание, как эти местоположения более или менее совпадают с интересными точками в примере с золотым сечением.
Используя эти линии в качестве направляющих, размещайте интересующие вас объекты на пересечениях линий, чтобы удерживать взгляд в пределах изображения. Обратите внимание, как эти местоположения более или менее совпадают с интересными точками в примере с золотым сечением.
(Примечание. Обычно вы не можете физически переупорядочить элементы фотографии, если только вы не делаете студийную или натюрмортную фотосъемку, поэтому под «размещением элементов» подразумевается изменение положения камеры, чтобы расположить элементы внутри рама)
3.Вы часто слышите, как фотографы говорят о весе или балансе изображения.
Это намного легче увидеть, если вставить эти линии. Если вы разместите элементы фотографии на две трети вправо или влево, она снова станет более приятной для глаз. Если вы снимаете вертикально, попробуйте расположить горизонт на две трети вверх или вниз.Правило третей очень простое, но может оказаться довольно сложным при его реализации… Не задумывайтесь.
 Элементы на вашей фотографии часто конфликтуют.Помещая одну вещь на две трети влево, я заставляю другой элемент находиться в месте, которое не соответствует правилу третей … так оно и есть, обычно вы сможете найти хороший баланс между конфликтующими элементами или просто нужно решить, какая из них самая сильная и важная, и сделать на ней акцент.
Элементы на вашей фотографии часто конфликтуют.Помещая одну вещь на две трети влево, я заставляю другой элемент находиться в месте, которое не соответствует правилу третей … так оно и есть, обычно вы сможете найти хороший баланс между конфликтующими элементами или просто нужно решить, какая из них самая сильная и важная, и сделать на ней акцент.Вы редко будете центрировать объекты или линии горизонта на изображении, но бывают случаи, когда вы можете захотеть передать сильную симметрию или, возможно, портрет или снимок головы.Помните, что эти правила должны быть гибкими и никоим образом не будут применяться всегда. На любой фотографии всегда будут элементы, которые будут противоречить самим себе или другим правилам композиции, просто вопрос поиска правильной комбинации и баланса этих элементов, которые лучше всего подходят для каждой фотографии.
Заключительные советы:
— Попробуйте обрезать изображения в программе для редактирования фотографий, чтобы увидеть разные результаты для одного и того же изображения.

— Разделите экран телевизора или компьютера на три части и смотрите что угодно.Рекомендую хорошие документальные фильмы или анимацию. Вы сразу увидите, как фотографы расставляют элементы в своих кадрах в соответствии с правилом третей.
Клейкая лента и шнурок сделают свое дело … Раньше это было очень просто на старых телевизорах, которые собирали пыль на экране, вы могли просто нарисовать в пыли доску X и O, и это работало отлично … не так много с плоским экраном экраны, так как они не так много пыли)— В течение дня оглядывайтесь вокруг и пытайтесь составлять кадры на основе того, что вы видите.Представьте себе границы фотографии и подумайте, как вы разместите линии и объекты внутри этой рамки. По прошествии некоторого времени вы можете со временем обнаружить, что делаете это автоматически.
— Многие камеры теперь накладывают график третей на свои видоискатели. Это отличный инструмент для изучения этой концепции. Постарайтесь не становиться слишком зависимым от него, поскольку это может привести к слишком жесткой интерпретации правила третей.

Расположение элементов в этом кадре четко демонстрирует правило третей.Дерево на переднем плане выровнено по левой трети фотографии, а сарай — по правой и верхней двум третям.
На всю фотографию нанесены трети. Чайка и столбы находятся в нижней правой трети фото. Горизонт находится примерно на верхней трети, а парусная лодка на заднем плане на фоне корабля находится примерно на пересечении линий двух третей.
Этот снимок Ванкувера показывает, как применяется правило третей. Горизонт, разделяющий линию горизонта и квартиру на переднем плане, находится примерно на верхней трети фотографии.
Угол жилого комплекса делится на левую.Это пример нарушения действующего правила третей. Обычно горизонт пополам не разделяют, но в этом случае симметрия работает.
Золотое сечение, Правило третей, Золотое сечение, Золотое сечение.
Основы пейзажной композиции Дайан Джонсон
Эта статья посвящена живописи, но она применима и к фотографии.
Фототехника Джеймса Джентлза
Хорошее описание золотых правил.Правило третей Эдвина Леонга
Электронная книга по фотографии, глава 15. Несколько советов.Золотое сечение Эдвина Леонга
Электронная книга по фотографии, глава 16. Интересное описание.Уроки композиции для фотографа-любителя Дейла Коттона
Эта часть посвящена «Правилу третей».Пропорции: теория и построение Фолькера Мюллера
Объяснил математические правила золотого сечения, модулятора и квадратного корня из двух.Композиция Майкла Миннера
Портретная фотография и правило третей.В поисках подходящего формата для квадратного холста. Джон Хаган.
Примеры живописи.Фотография, золотая середина и вызывающая крутизна Лори Нивин
Несколько коротких примеров.Золотое сечение и фотография Евгения Ильченко
Несколько примеров и инструмент для настройки фото, которые помогут скорректировать композицию.
Творчество и правило третей Джима Альтенгартена
Хорошая статья с описанием и примерами.Правило третей Джона Лонгенекера
Описание правила третей, а также множество связанных ссылок.Золотая середина, Стюарт Лоу
Естественные и математические правила и их применение в дизайне.Урок «Пространство, фигура и земля» Петтери Сулонен
Цель этого урока — познакомить с тремя фундаментальными элементами композиционного мышления.Урок по основам композиции от Майкла Фодора
Общие принципы правила третей и золотого сечения, а также несколько советов по композиции.Урок «Правило третей» Майкла Фодора
Примеры правила третей.1-20
Золотое сечение в дизайне макета
Первоначально опубликовано Момчило Дакич 13 мая 2018 г. 2241 прочитано@dakic Момчило Дакич
Владелец продукта в Symphony.
 есть |
http://momcilodakic.com | Автор книги Treasure Roadmap.
есть |
http://momcilodakic.com | Автор книги Treasure Roadmap.Как создать приятную для глаз пользователя верстку программы? Используйте последовательность Фибоначчи и комбинируйте математику и искусство для получения идеального результата.
Существует общепринятое математическое соотношение, которое можно использовать для создания приятных, естественно выглядящих композиций в ваших дизайнерских работах. Это называется золотым сечением, золотым сечением, спиралью Фибоначчи или последовательностью Фибоначчи.
Золотое сечение или спираль ФибоначчиТакой вид композиции широко используется в искусстве и фотографии.Но в первую очередь это соотношение — обычная закономерность, встречающаяся в природе. Например. форма сосновой шишки, семечки, погодные условия и т. д.
Золотой рацион в композиции фотографииПри разработке программного обеспечения необходимо учитывать множество аспектов. Существует множество книг и статей, посвященных передовым методам создания потрясающего пользовательского опыта.
 Один аспект посвящен исключительно визуальной композиции. Программное обеспечение должно иметь приятную визуальную привлекательность. Если он приятен для глаз, скорее всего, он понравится пользователям подсознательно.Что еще более важно, если композиция будет правильной, взгляд естественным образом остановится на важных вещах.
Один аспект посвящен исключительно визуальной композиции. Программное обеспечение должно иметь приятную визуальную привлекательность. Если он приятен для глаз, скорее всего, он понравится пользователям подсознательно.Что еще более важно, если композиция будет правильной, взгляд естественным образом остановится на важных вещах.Если композиция правильная, взгляд, естественно, будет упираться в важные вещи.
Мы можем многое сделать, чтобы подсознательно привлечь внимание к нашему призыву к действию или любой другой части программы. Мне нравится использовать золотой рацион в композиции макета, потому что он естественным образом подчеркивает все остальные техники UX. Поместите спираль Фибоначчи в верхнюю часть экрана и запустите план разметки.Поместите самую важную информацию в центр спирали. Эти компоненты в центре сразу привлекают внимание пользователей. Этот принцип отлично работает с диаграммой Гутенберга, представленной ниже.
Диаграмма Гутенберга описывает общую закономерность, которой следят наши глаза при взаимодействии с нашим приложением или контентом.
Диаграмма Гутенберга в сочетании со спиралью Фибоначчи Шаблон предполагает, что наши глаза будут скользить по странице в серии горизонтальных движений. Каждая развертка начинается немного дальше от левого края и приближается к правому краю.Общее движение заключается в перемещении глаза от основной области к конечной области. Этот путь называется «Чтение гравитации».
Шаблон предполагает, что наши глаза будут скользить по странице в серии горизонтальных движений. Каждая развертка начинается немного дальше от левого края и приближается к правому краю.Общее движение заключается в перемещении глаза от основной области к конечной области. Этот путь называется «Чтение гравитации».Важные элементы должны быть размещены вдоль пути гравитации чтения. Наиболее важная информация должна быть размещена в основной оптической области. Как видите, основная оптическая область расположена прямо в центре спирали Фибоначчи, что делает ее идеальным местом, чтобы пользователь мог заметить эту область.Область Strong Follow должна также содержать полезные данные, чтобы пользователь мог сосредоточиться. Терминальная зона обычно зарезервирована для CTA — там сосредоточено внимание.
Если вы воспользуетесь этим подходом, он улучшит ваш дизайн на процент или даже меньше. Но детали важны. Этот процент может просто повысить ценность вашего продукта, чтобы он понравился пользователю.
 Между реакцией meh и wow есть тонкая грань, поэтому вы захотите использовать как можно больше уловок, включая этот крошечный.Ура!
Между реакцией meh и wow есть тонкая грань, поэтому вы захотите использовать как можно больше уловок, включая этот крошечный.Ура!Хотите узнать больше?
Узнайте, как превратить свою идею в успешный бизнес уже сегодня.
Эта книга предлагает вам исчерпывающее руководство по всему процессу создания успешного бизнеса. Он разработан, чтобы облегчить вам начало работы, так как в нем представлен весь бизнес-план. Весь процесс сводится к основам, поэтому шаги просты и понятны.
Если вы будете следовать формуле, которую я раскрываю в этой книге, вполне возможно, что вы сможете зарабатывать себе на жизнь, превратив идею в успешный бизнес.
Получите бесплатное краткое содержание книги, нажав на изображение ниже:
Связанные
Теги
Присоединяйтесь к хакеру ПолденьСоздайте бесплатную учетную запись, чтобы разблокировать свой собственный опыт чтения.
Золотое сечение — RationalWiki
Прямоугольник с соотношением сторон, равным золотому сечению. Это вроде бы особенно приятно визуально.
Золотое сечение: Золотое сечение, применяемое к делению линии.
Это вроде бы особенно приятно визуально.
Золотое сечение: Золотое сечение, применяемое к делению линии.Золотое сечение , золотая середина , золотое число или золотое сечение — математическая константа
Что еще более важно, это соотношение двух величин A и B, такое, что отношение от A к B (где A — меньшее) такое же, как отношение от B к A + B; это происходит из-за того, что это положительный реальный корень.
Считается, что он приятен и гармоничен для человеческого восприятия, и является основой многих классических архитектур. Использование греческой буквы phi (φ) для обозначения золотого сечения было предложено математиком Марком Барром из первой буквы Фидия (древнегреческий, Φειδίας), скульптора, который якобы использовал ее в создание статуй Парфенона.
Золотое сечение тесно связано с последовательностью Фибоначчи. Среди прочего, отношения последовательных чисел Фибоначчи сходятся к фи:
1/1 = 1.  000000
0000002/1 = 2.000000 3/2 = 1 500 000 5/3 = 1,666666 8/5 = 1,600000 13/8 = 1,625000 21/13 = 1,615385 34/21 = 1.619048 55/34 = 1,617647 89/55 = 1,618182 144/89 = 1,617978 233/144 = 1.618056 377/233 = 1.618026 610/377 = 1.  618037
618037987/610 = 1.618033 Phi woo [править]
Фи и числа Фибоначчи наделяют множеством очень увлекательных математических свойств, но некоторые чудаки готовы продвинуть их дальше, добавив хорошую дозу парейдолии. [1] [2] Классический пример — раковины наутилуса: часто говорят, что это золотые спирали, хотя на самом деле это просто логарифмические спирали с отношениями обычно около 1,3 или около того. Другие утверждают, что нашли золотое сечение или числа Фибоначчи в красоте человеческого лица, исторической архитектуре (иногда законной), продуктах Apple, планетах, музыкальных инструментах, идеальных корпусах для громкоговорителей … список можно продолжать и продолжать.Во многих случаях они действительно находили золотое сечение в объекте X, но это не особый результат; при достаточной настойчивости вы можете найти золотое сечение примерно в чертовом и в чем угодно .
Aloe polyphylla демонстрирует филлотаксис, подобный спирали Фибоначчи
Разница между реальным случаем «магии» золотого сечения и простым наблюдением кривошипа заключается в том, что наличие золотого сечения может быть фактически объяснено. То есть золотое сечение должно присутствовать как в теоретических моделях, описывающих X, так и в измеренных результатах в X.Изучая филлотаксис, ботаники не только наблюдали рост семян подсолнечника по спирали, пронумерованной Фибоначчи, но и предоставили научное объяснение того, почему это происходит: пример золотого сечения, законно появляющийся в природе.
Нумерологическое ухаживание, окружающее фи и Фибоначчи, является примером строгого закона малых чисел; то есть не так много маленьких чисел (или визуально различимых соотношений между 1 и 2), и они будут появляться во многих несвязанных местах.См. Также теорию Рамсея.
Между тем, в стране креационистов… Годдидит. [3]
Библиография [править]
- Золотое сечение: История Фи, самое удивительное число в мире Марио Ливио (2002) Broadway Books.


 На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }. {2}}{18}}}[источник не указан 1010 дней]
{2}}{18}}}[источник не указан 1010 дней]
 Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23]. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»
Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»
 Лаврус, Золотое сечение
Лаврус, Золотое сечение — Phantom Press. — 209 с. — ISBN 9785864716700.
— Phantom Press. — 209 с. — ISBN 9785864716700. Обычно они спиралевидные и имеют сходство с золотой спиралью
Обычно они спиралевидные и имеют сходство с золотой спиралью Оно помогает достичь гармонии между частями. Многие логотипы известных брендов были выполнены с его применением:
Оно помогает достичь гармонии между частями. Многие логотипы известных брендов были выполнены с его применением:
 При этом разделять можно больше чем на 2 части – каждое деление тогда должно выполняться таким же образом и делить следует меньшую часть. При делении на три фрагмента в процентах сначала делим на две, получаем 62 и 38 %, 38 % при делении дадут 24 и 14 %. Получается 62 % будет основным, 24 % – вторым и 14 % – третьим по важности.
При этом разделять можно больше чем на 2 части – каждое деление тогда должно выполняться таким же образом и делить следует меньшую часть. При делении на три фрагмента в процентах сначала делим на две, получаем 62 и 38 %, 38 % при делении дадут 24 и 14 %. Получается 62 % будет основным, 24 % – вторым и 14 % – третьим по важности.


 Таким путем получим идеальное расположение. Конечно же, не стоит злоупотреблять правилом и всегда оценивать эстетику получившегося интерьера, полагаясь на чувство прекрасного.
Таким путем получим идеальное расположение. Конечно же, не стоит злоупотреблять правилом и всегда оценивать эстетику получившегося интерьера, полагаясь на чувство прекрасного. Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.
Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни. Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.
Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.
 Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.
Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.

 Пирогова)…
Пирогова)… Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?
Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли? Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?
Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект? Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?
Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему? Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
 При делении меньшей на большую получается обратное значение φ ≈ 0,618.
При делении меньшей на большую получается обратное значение φ ≈ 0,618. Т. ТРУБИЛИНА
Т. ТРУБИЛИНА Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

 Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.
Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.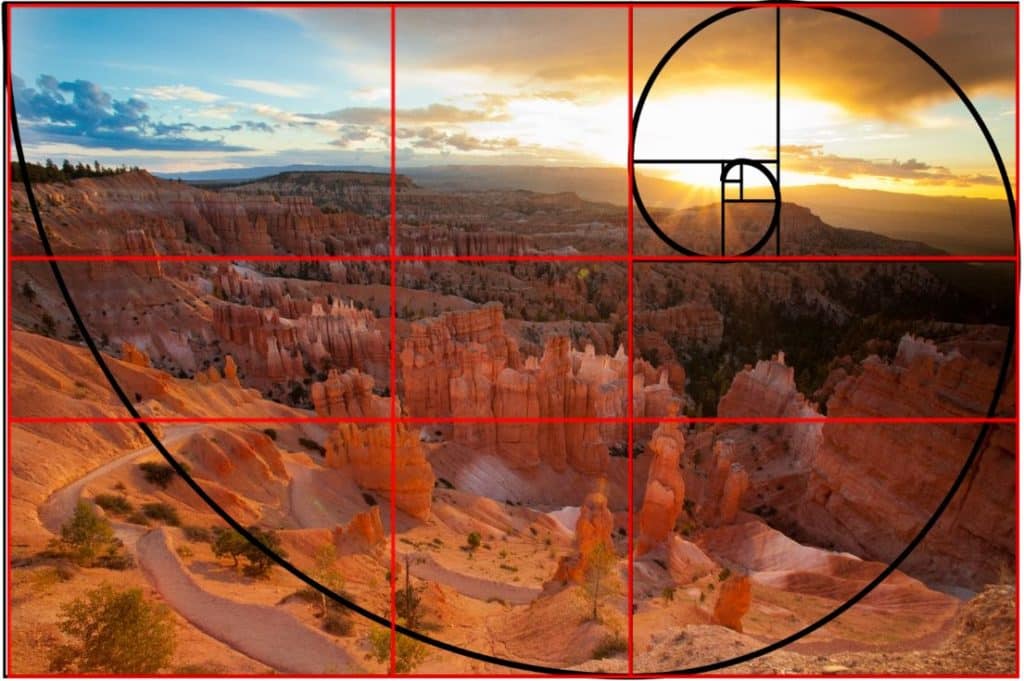 История развития «золотого сечения».
История развития «золотого сечения». В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления. В 1509 г. В Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства Бог сын, Бог отец и Бог дух святой (подразумевалась, что малый отрезок есть олицетворение Бога сына, большой отрезок – Бога отца, а весь отрезок – Бога духа святого).
В 1509 г. В Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства Бог сын, Бог отец и Бог дух святой (подразумевалась, что малый отрезок есть олицетворение Бога сына, большой отрезок – Бога отца, а весь отрезок – Бога духа святого). Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.
Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.
 Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. 3. «Золотое сечение» в живописи.
3. «Золотое сечение» в живописи. 4. «Золотое сечение» в природе.
4. «Золотое сечение» в природе. Обозначим одну из них через ОА, другую через ОВ. Угол между лучами – ветками обозначим через а, а угол, дополняющий его до 360 , — через Р.
Обозначим одну из них через ОА, другую через ОВ. Угол между лучами – ветками обозначим через а, а угол, дополняющий его до 360 , — через Р.
 : АС, то оно приближённо равно 0,618, т.е. подчиняется золотой пропорции.
: АС, то оно приближённо равно 0,618, т.е. подчиняется золотой пропорции. Эта пропорция используется практически во всех областях знаний.
Эта пропорция используется практически во всех областях знаний. abc-people.com/idea/zolotsech/
abc-people.com/idea/zolotsech/
 При этом прочность скорлупы играет далеко не главную роль.
При этом прочность скорлупы играет далеко не главную роль.


 Первый в 1,618 раза больше, чем соседний.
Первый в 1,618 раза больше, чем соседний.
 Конечным результатом является сетка, образованная девятью прямоугольниками одинакового размера. Идея состоит в том, чтобы расположить интересующие вас объекты рядом с любой из линий или на их пересечении.
Конечным результатом является сетка, образованная девятью прямоугольниками одинакового размера. Идея состоит в том, чтобы расположить интересующие вас объекты рядом с любой из линий или на их пересечении. Вот почему Сетка Фи имеет больше смысла, чем Золотая Спираль. Просто попробуйте расположить горизонт вдоль любой из двух горизонтальных линий, и ваше изображение естественно понравится зрителю.
Вот почему Сетка Фи имеет больше смысла, чем Золотая Спираль. Просто попробуйте расположить горизонт вдоль любой из двух горизонтальных линий, и ваше изображение естественно понравится зрителю.
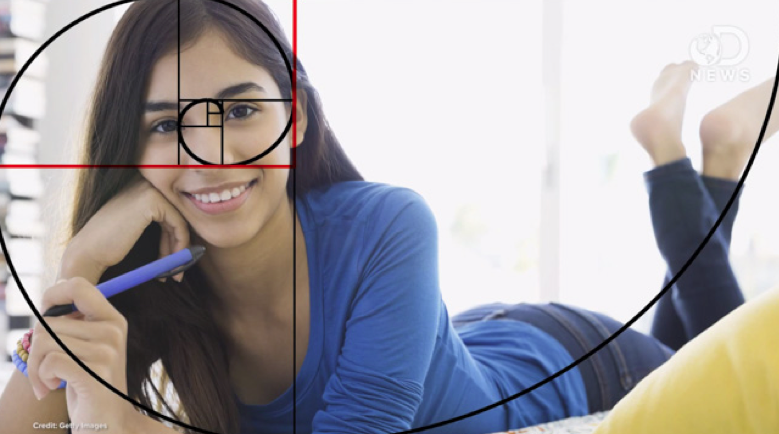
 .. от классического примера оболочки Наутилуса до образования галактик, от относительного размера и расположения костей в ваших руках и руках до роста и формы деревьев и лесов, она также используется в сложные экономические уравнения, и утверждается, что это даже можно найти в самой структуре вашей ДНК.
.. от классического примера оболочки Наутилуса до образования галактик, от относительного размера и расположения костей в ваших руках и руках до роста и формы деревьев и лесов, она также используется в сложные экономические уравнения, и утверждается, что это даже можно найти в самой структуре вашей ДНК. Большее количество меньших прямоугольников справа уравновешивает общую большую, но пустую левую часть изображения. Составьте композицию вокруг этих линий, чтобы придать изображению лучший баланс.
Большее количество меньших прямоугольников справа уравновешивает общую большую, но пустую левую часть изображения. Составьте композицию вокруг этих линий, чтобы придать изображению лучший баланс. Используя эти линии в качестве направляющих, размещайте интересующие вас объекты на пересечениях линий, чтобы удерживать взгляд в пределах изображения. Обратите внимание, как эти местоположения более или менее совпадают с интересными точками в примере с золотым сечением.
Используя эти линии в качестве направляющих, размещайте интересующие вас объекты на пересечениях линий, чтобы удерживать взгляд в пределах изображения. Обратите внимание, как эти местоположения более или менее совпадают с интересными точками в примере с золотым сечением.  Элементы на вашей фотографии часто конфликтуют.Помещая одну вещь на две трети влево, я заставляю другой элемент находиться в месте, которое не соответствует правилу третей … так оно и есть, обычно вы сможете найти хороший баланс между конфликтующими элементами или просто нужно решить, какая из них самая сильная и важная, и сделать на ней акцент.
Элементы на вашей фотографии часто конфликтуют.Помещая одну вещь на две трети влево, я заставляю другой элемент находиться в месте, которое не соответствует правилу третей … так оно и есть, обычно вы сможете найти хороший баланс между конфликтующими элементами или просто нужно решить, какая из них самая сильная и важная, и сделать на ней акцент.



 есть |
http://momcilodakic.com | Автор книги Treasure Roadmap.
есть |
http://momcilodakic.com | Автор книги Treasure Roadmap. Один аспект посвящен исключительно визуальной композиции. Программное обеспечение должно иметь приятную визуальную привлекательность. Если он приятен для глаз, скорее всего, он понравится пользователям подсознательно.Что еще более важно, если композиция будет правильной, взгляд естественным образом остановится на важных вещах.
Один аспект посвящен исключительно визуальной композиции. Программное обеспечение должно иметь приятную визуальную привлекательность. Если он приятен для глаз, скорее всего, он понравится пользователям подсознательно.Что еще более важно, если композиция будет правильной, взгляд естественным образом остановится на важных вещах. Шаблон предполагает, что наши глаза будут скользить по странице в серии горизонтальных движений. Каждая развертка начинается немного дальше от левого края и приближается к правому краю.Общее движение заключается в перемещении глаза от основной области к конечной области. Этот путь называется «Чтение гравитации».
Шаблон предполагает, что наши глаза будут скользить по странице в серии горизонтальных движений. Каждая развертка начинается немного дальше от левого края и приближается к правому краю.Общее движение заключается в перемещении глаза от основной области к конечной области. Этот путь называется «Чтение гравитации». Между реакцией meh и wow есть тонкая грань, поэтому вы захотите использовать как можно больше уловок, включая этот крошечный.Ура!
Между реакцией meh и wow есть тонкая грань, поэтому вы захотите использовать как можно больше уловок, включая этот крошечный.Ура! Это вроде бы особенно приятно визуально.
Золотое сечение: Золотое сечение, применяемое к делению линии.
Это вроде бы особенно приятно визуально.
Золотое сечение: Золотое сечение, применяемое к делению линии. 000000
000000 618037
618037
