Астигматизм в оптике: Оптические аберрации — Кома и Астигматизм
Оптические аберрации — Кома и Астигматизм
к содержанию ↑
к содержанию ↑
Почему возникает оптическая Кома
Кома возникает из-за того, что лучи приходящие под углом к оптической оси собираются не в одной точке.
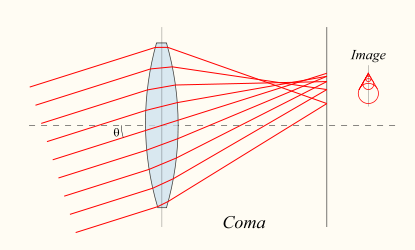
Каждая такая «точка» имеет более яркий и центр и будучи наложенными друг на друга образуют объект с ярким центром и хвостом, напоминающим хвост кометы. Отсюда и название «Coma».
к содержанию ↑
Как выглядит оптическая Кома

как выглядит идеальная точка (без аберраций)
Все аберрационные эффекты Комы повернуты яркими центрами к оптической оси и напоминают раскрытый веер.

чистая Кома
Сложнее визуально определить кому, когда она сложена с другими аберрациями, например, с астигматизмом.

пример Кома + Астигматизм
Хуже всего при пользовании объективами с Комой приходится астрофотографам. Дело в том, что Кома исправляется с диафрагмированием объектива, но астрофотографы часто снимают на открытой диафрагме для того, чтобы уменьшить выдержку (ISO итак бывает очень высоким) и звезды не превратились бы в шлейф.



Слева, на Canon 24/1.4 II видна сильная Кома.
к содержанию ↑
Как исправляется оптическая Кома
Оптическая Кома исправляется диафрагмированием т.к. связана с лучами, попадающими под углом на линзу объектива. Объективы с исправленной Комой называются Апланаты.
к содержанию ↑
к содержанию ↑
Почему возникает
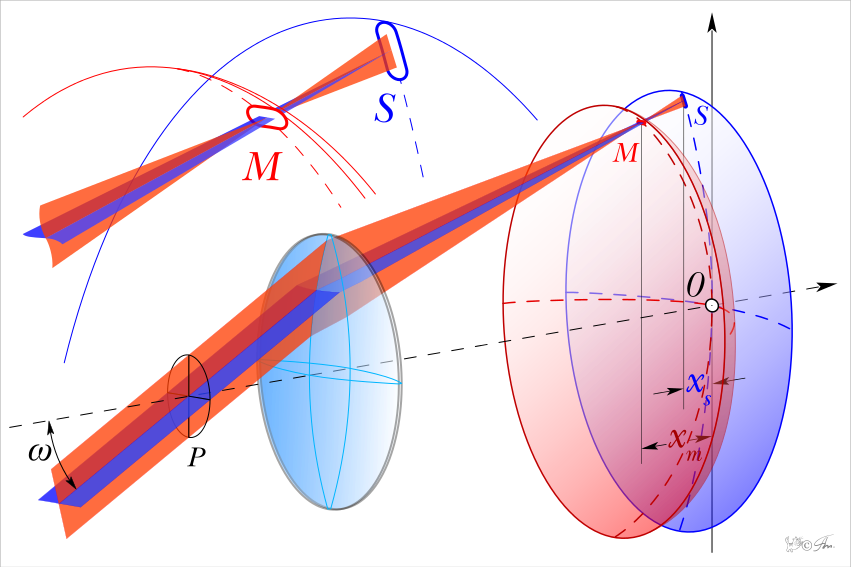
Астигматизмом называется явление при котором преломляющая поверхность имеет форму не сфеты, а, например, овала. Таким образом саггитальные и тангенциальные лучи имеют различные фокусы, образуя овалы вместо кружков/точек.
к содержанию ↑
Как выглядит

точка в случае астигматизма
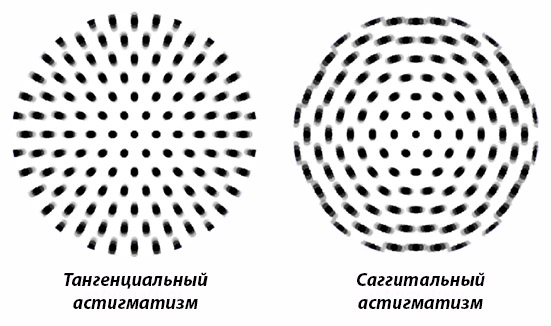
к содержанию ↑
Как исправляется
Астигматизм исправляется сложно т.к. влияет не только на края изображения, но по сути почти на всё изображение, кроме самого центра (маленького пятна в центре линз). Чтобы исправить астигматизм нужны дополнительные линзы и потому простым диафрагмированием это явление не «лечится».
Сильным астигматизмом славились старые объективы и тогда же появилось название «Анастигмат», т.е. объектив с исправленным астигматизмом.
Оптическая система с астигматизмом один , где лучи , распространяющиеся в двух перпендикулярных плоскостях имеют разные фокусы . Если оптическая система с астигматизмом используются для формирования изображения в кресте , вертикальные и горизонтальные линии будут в резком фокусе на два разных расстояниях. Термин происходит от греческого альфа- ( а- ) , означающего «без» и στίγμα ( стигмы ), «отметки, место, прокол».
Формы астигматизма
 Визуальный астигматизм (не оптический)
Визуальный астигматизм (не оптический)Есть две различные формы астигматизма. Первым является третьим порядком аберрацией , которая имеет место для объектов (или частей объектов) от оптической оси . Эта форма аберраций происходит даже тогда , когда оптическая система является совершенно симметричной. Это часто упоминаются как «монохроматическая аберрация», потому что это имеет место даже для света одной длиной волны . Эта терминология может ввести в заблуждение, однако, поскольку количество аберрации могут сильно изменяться в зависимости от длины волны в оптической системе.
Вторая форма астигматизма возникает , когда оптическая система не является симметричной относительно оптической оси. Это может быть конструкцией (как в случае цилиндрической линзой), или из — за ошибки в производстве поверхностей компонентов или несоосность компонентов. В этом случае, астигматизм наблюдается даже для лучей от по оси точек объекта. Эта форма астигматизма является чрезвычайно важной в видении науки и уход за глазами, так как человеческий глаз часто проявляет эту аберрацию из — за несовершенство формы роговицы или хрусталика .
Визуальный астигматизм (не оптический)Третий порядок астигматизм
 Страница объяснения и астигматизм, иллюстрирующая
Страница объяснения и астигматизм, иллюстрирующаяПри анализе этой формы астигматизма, оно является наиболее распространенным рассматривать лучи от заданной точки на объекте, которые распространяются в двух специальных самолетах. Первая плоскостью является касательной плоскостью . Это представляет собой плоскость , которая включает в себя как точку рассматриваемого объекта и ось симметрии. Лучи, распространяющиеся в этой плоскости называются тангенциальными лучи . Самолеты , которые включают оптическую ось меридиональной плоскости. Оно является общим для упрощения проблем в радиально-симметричных оптических системах путем выбора точек объекта по вертикали ( « у ») плоскости только. Эта плоскость затем иногда называют в меридиональной плоскости.
Второй специальный самолет является сагиттальной плоскости . Это определяется как плоскости, ортогональной к касательной плоскости, содержащей точку объекта считается и пересекает оптическую ось на входном зрачке оптической системы. Эта плоскость содержит главный луч , но не содержит оптическую ось. Таким образом , это перекос плоскости, другими словами , не меридиональной плоскости. Лучи , распространяющиеся в этой плоскости называются сагиттальными лучи .
В третьем порядке астигматизме, сагиттальные и поперечные лучи образуют очаги на разные расстояниях вдоль оптической оси. Эти очаги называются сагиттальный фокус и поперечной фокусировки , соответственно. При наличии астигматизма, точка внеосевой на объекте не резко визуализировали с помощью оптической системы. Вместо этого, резкие линии образуются в сагиттальных и поперечных фокусах. Изображение в поперечном фокусе является короткой линией, ориентирован в направлении сагиттальной плоскости; образы окружностей с центром на оптической оси, или линий тангенциальных к таким кругам, будет резким в этой плоскости. Изображение в сагиттальной фокусе короткая линия, ориентированы в тангенциальном направлении; изображения спиц , расходящихся от центра остры в этом фокусе. В промежутке между этими двумя фокусами, круглыми , но «размытое» изображение формируются. Это называется медиальной фокус
или круг наименьшего путанице . Этот самолет часто представляет собой наилучшее место компромисса изображения в системе с астигматизмом.Количество аберрации из — за астигматизма пропорциональна квадрату угла между лучами от объекта и оптической оси системы. С осторожностью, оптическая система может быть разработана , чтобы уменьшить или устранить астигматизм. Такие системы называются anastigmats .
Астигматизм в системах, которые не являются осесимметричными
 Размытие от астигматизма линзы на разных расстояниях.
Размытие от астигматизма линзы на разных расстояниях.Если оптическая система не является осесимметричной, либо из — за ошибки в форме оптических поверхностей или из — за несоосность компонентов, астигматизм может произойти даже для по оси точек объекта. Этот эффект часто используется преднамеренно в сложных оптических системах, особенно некоторых типов телескопа . Некоторые телескопы намеренно используют несферических оптику для преодоления этого явления.
При анализе этих систем, обычно рассматривать тангенциальные лучи (как определено выше), и лучи в меридиональной плоскости (плоскости , содержащей ось оптического) перпендикулярно к касательной плоскости. Эта плоскость называется либо сагиттальной меридиональной плоскости или, смутно, только в сагиттальной плоскости .
офтальмологический астигматизм
В оптометрии и офтальмологии , вертикальные и горизонтальные плоскости обозначены как тангенциальные и сагиттальные меридианы, соответственно. Офтальмологический астигматизм является ошибкой рефракции в глазах , в которой существует разница в степени преломления в различных меридианах. Это , как правило , характеризуется асферической, не-фигурой вращения роговицы , в котором роговичный профиле склон и преломляющая оптическая сила в одном меридиане меньше , чем в перпендикулярной оси.
Астигматизм вызывает трудности в наблюдении мелких деталей. Астигматизм может быть часто исправлены очки с линзой , которая имеет различные радиусы кривизны в разных плоскостях (а цилиндрическая линза), контактные линзы , или рефракционной хирургии .
Астигматизм является довольно распространенным явлением. Исследования показали , что около одного из трех людей страдают от него. Распространенность астигматизма увеличивается с возрастом. Хотя человек может не заметить мягкий астигматизм, большее количество астигматизм может привести к нечеткое зрение, щурясь , вялость , усталость , или головные боли .
Есть целый ряд тестов, которые используются офтальмологов и оптиков в ходе глазных экзаменов , чтобы определить наличие астигматизма и количественной оценки количества и оси астигматизма. Диаграмма оптотипа или другая диаграмма глаз может сначала выявить пониженную остроту зрения . Кератометр может быть использован для измерения кривизны самых крутых и плоских меридианов в передней поверхности роговицы. Топография роговицы также может быть использована для получения более точного представления формы роговицы в. Autorefractor или Ретиноскопия может обеспечить объективную оценка рефракции глаза и использование поперечных цилиндров Джексона в фороптере могут быть использовано для более точных субъективно этих измерений. Альтернативный метод с фороптером требует использования «циферблат» или «Санберст» график для определения астигматизма оси и мощности.
Астигматизм может быть исправлено с помощью очков , контактных линз или рефракционной хирургии . Различные соображения , связанные с глазным здоровьем, рефракцией и образом жизни часто определяют , может ли один вариант лучше другого. В тех с кератоконуса , торические контактные линзы часто позволяют пациентам для достижения лучшего остроты зрения , чем очки. Если астигматизм вызван проблемой , такие как деформации глазного яблока вследствие халязиона , обработки основной причины разрешит астигматизм.
Неровные или деформированные линзы и зеркала
Шлифование и полирование прецизионных оптических деталей, либо вручную, или машиной, как правило, использует значительное понижающее давление, которое в свою очередь, создает значительные трения боковые давления во время полировки штрихов, которые можно комбинировать, чтобы локально гибкость и искажают части. Эти искажения, как правило, не обладают фигурными из-революцией симметрии и, таким образом, астигматизм, и постепенно становятся постоянно отполированы на поверхность, если проблемы, вызывающие искажения не корректируется. Астигматические, искаженные поверхности потенциально внести серьезные ухудшений в производительности оптической системы.
Искажения поверхности за счет шлифования или полирования увеличивается с соотношением сторон детали (диаметр к толщине). Для первого порядка, прочность стекла увеличивается как куб толщины. Толстые линзы в 4: 1 до 6: 1 соотношения сторон будут сгибается гораздо меньше , чем высокие части пропорции, такие как оптические окна, которые могут иметь форматное соотношение 15: 1 или выше. Сочетание поверхности или волновых фронт требований точности ошибки и соотношения сторон части управляет степенью однородности задней опоры , необходимой, особенно при более высоких давлениях и вниз боковых сил во время полировки. Оптические рабочее , как правило , включает в себя степень случайности , что существенно помогает в сохранении фигуры из-вращения поверхностей, при условии , что часть не изгибать во время процесса полировки / молотилки.
Умышленное астигматизм в оптических системах
Компактные дисковые игроки используют астигматизм линзу для фокусировки. Когда одна ось больше в фокусе , чем другие, точечно-подобные функции по проекту диска до овальной формы. Ориентация овала указывает , какая ось больше в фокусе, и , таким образом , в каком направлении объектива должна двигаться. Квадратная расположение только четыре датчика может наблюдать это смещение и использовать его , чтобы принести читать объектив лучшего фокуса, не будучи обмануты продолговатыми углублениями или других признаками на поверхности диска.
В 3D PALM / ШТОРМЕ , тип оптической сверхвысокого разрешения микроскопии , цилиндрическая линза может быть введена в систему формирования изображения для создания астигматизма, который позволяет измерять Z положение источника света дифракционного.
Уровни лазерной линии использовать цилиндрическую линзу для распространения лазерного луча от точки в линию.
Смотрите также
Рекомендации
- Greivenkamp, Джон Е. (2004). Поле Руководство геометрической оптики . SPIE поле Руководства об. FG01 . SPIE. ISBN 978-0-8194-5294-8 .
- Hecht, Евгений (1987). Оптика (2 — е изд.). Addison Wesley. ISBN 978-0-201-11609-0 .
внешняя ссылка
 Астигматизм наклонного пучка лучей.
Астигматизм наклонного пучка лучей.М — меридиональная фокальная поверхность.
S — сагиттальная фокальная поверхность.
Астигмати́зм — аберрация, при которой изображение точки, находящейся вне оси, и образуемое узким пучком лучей, представляет собой два отрезка прямой, расположенных перпендикулярно друг другу на разных расстояниях от плоскости безаберрационного фокуса (плоскости Гаусса). Астигматизм возникает вследствие того, что лучи наклонного пучка имеют различные точки сходимости — точки меридионального или сагиттального фокусов бесконечно тонкого наклонного пучка.
Астигматизм объясняется зависимостью углов преломления лучей пучка от углов их падения.[1] Так как отдельные лучи наклонного пучка падают на преломляющую поверхность под разными углами, то и преломляются на разные углы, пересекаясь на разном же расстоянии от преломляющей поверхности. Причём, можно найти такое положение для поверхности изображения, когда все лучи пучка расположенные в одной из плоскостей (меридиональной или сагиттальной)[2] пересекутся на этой поверхности. Таким образом, астигматический пучок формирует изображение точки в виде двух астигматических фокальных линий, на соответствующих фокальных поверхностях, которые имеют форму поверхностей вращения кривых с различными параметрами, и касаются одна другой в точке оси системы.
Если положения этих поверхностей, для некоторой точки поля, не совпадают, то говорят о наличии астигматизма, понимая под этим астигматическую разность меридионального и сагиттального фокусов.
При этом, если меридиональные фокусы располагаются ближе к поверхности преломления, нежели сагиттальные, то говорят о положительном астигматизме, а если дальше, то об отрицательном. В случае совпадения фокальных поверхностей астигматическая разность равна нулю, астигматический пучок вырождается в гомоцентрический, фигура рассеяния переходит в точку, а кривизна результатирующей поверхности будет определять кривизну поля изображения.
В теории аберраций третьего порядка астигматизм характеризуется третьей суммой (коэффициентом) Зейделя (SIII) и рассматривается совместно с кривизной поверхности изображения, характеризуемой четвёртой суммой Зейделя (SIV). Такое совместное рассмотрение обусловлено зависимостью проявлений этих аберраций.
Причём, формулы, с помощью которых определяются астигматические фокусы, включают оба этих коэффициента. Так, например, меридиональная составляющая для некоторой точки изображения расположенной на высоте может быть определена как
,
где — фокусное расстояние системы.
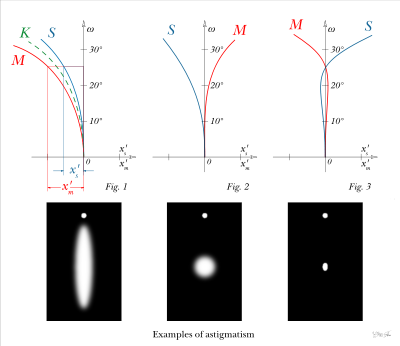
Графическое представление астигматизма
Астигматизм оптической системы часто описывают графически — на основании расчёта положений астигматических фокусов элементарных пучков, откладывая по оси ординат углы наклона главных лучей, а по оси абсцисс расстояния астигматических фокусов от плоскости Гаусса.
Полученные кривые позволяют судить о форме астигматических фокальных поверхностей, и на основании этого о некоторых особенностях исследуемой системы.
Так, например, астигматизм положительного знака, как правило, соответствует случаю, когда система, так же, имеет и кривизну поверхности изображения (понимая под последней поверхность, расположенную между обеими поверхностями астигматических фокусов). В этом случае фигура рассеяния для периферийной точки плоского объекта будет представлять собой размытый овал. Одновременная же фокусировка на все точки плоского объекта для такой системы будет невозможна.
Значительный отрицательный астигматизм позволяет «совместить» поверхность изображения с плоскостью Гаусса. Однако, по причине того, что периферийные точки плоского объекта изображаются недостаточно сфокусированным лучами, резкое изображение точек такого объекта будет возможно только в центре поля.
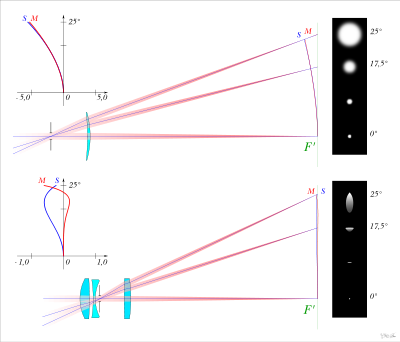 Исправленный астигматизм для объективов разных типов (условного монокля и триплета)
Исправленный астигматизм для объективов разных типов (условного монокля и триплета)Исправление астигматизма
Так как астигматизм присущ не только широким, но и тонким (элементарным) пучкам лучей, то диафрагмирование никак не влияет на его величину. Поэтому, как и другие аберрации, астигматизм коррегируется подбором кривизны поверхностей и толщин оптических компонентов, а также воздушных промежутков между ними.
Одним из примеров простейшего объектива, с исправленным астигматизмом, будет объектив монокль конструкции Уоллостона, где, направляемые апертурной диафрагмой, наклонные пучки лучей встречаются поверхностями менискообразной линзы под небольшими углами к нормалям. При этом, положительный астигматизм задней (выпуклой) поверхности мениска оказывается настолько невелик, что может быть скомпенсирован отрицательным астигматизмом передней (вогнутой) поверхности.
Однако, в этом случае, даже при полном устранении астигматизма, кривизна поверхности изображения велика. Таким образом, скорректированный астигматизм ещё не гарантирует резкости по всему полю изображения.
Поэтому, при расчёте, так называемых, анастигматов используются более сложные решения, позволяющие исправить, в пределах некоторого угла, обе эти аберрации. Причём, как правило, даже исправленный астигматизм имеет небольшую отрицательную величину, тем меньшую, чем шире угол зрения объектива.
Астигматизм системы, не обладающей центральной симметрией
Для оптических систем, не имеющих центральной симметрии, астигматизм может быть обусловлен неодинаковостью кривизны преломляющей поверхности в меридиональном и сагиттальном сечениях.
Частным случаем астигматического пучка, образованного такой системой, является пучок, образованный положительной цилиндрической линзой, одно изображение которой находится на отрезке прямой, а другое — в бесконечности.
Примечания
- ↑ Согласно четвёртому закону геометрической оптики, отношение синуса угла падения к синусу угла преломления — величина постоянная и равна обратному отношению показателей преломления сред.
- ↑ В оптических системах с центральной симметрией меридиональной плоскостью, будет любая плоскость, к которой принадлежит оптическая ось системы. Так, например, практически все изображения оптических схем фотографических объективов являются именно меридиональными сечениями. В европейской и американской оптической литературе эта плоскость чаще именуется тангенциальной.
Сагиттальной плоскостью, для любого пучка лучей лежащего в меридиональной плоскости, будет плоскость, включающая главный луч этого пучка, и перпендикулярная меридиональной плоскости.
В центрально-симметричных оптических системах, такое деление, очень важно для оценки свойств внеосевых и/или наклонных лучей, хотя может и не иметь смысла для лучей расположенных непосредственно на оптической оси.
Литература
- Бегунов Б. Н. Геометрическая оптика. — М.: Изд-во МГУ, 1966.
- Волосов Д. С. Фотографическая оптика. — М.: Искусство, 1971.
- Русинов М. М. Техническая оптика. — Л.: Машиностроение, 1979.
- Слюсарёв Г. Г. Расчёт оптических систем. — Л.: Машиностроение, 1975.
Астигматизм
Что такое астигматизм? Причины, симптомы и способы лечения астигматизма
Более 90% информации человек получает при помощи органов зрения. Глаза нам позволяют видеть близких нам людей, важные жизненные моменты и воспринимать мир во всей его красочности и разнообразии. Различные болезни глаз лишают нас такой возможности, значительно снижая качество нашей жизни. В современном мире заболевания глаз — это довольно частые явления. В окружающей среде, существует множество раздражителей, которые вызывают нежелательные нарушения зрения. Одной из самых распространенных болезней глаз является астигматизм. Но, к счастью, современная медицина способна предложить различные формы лечения и предотвращения такого рода заболевания. Данная статья поможет разобраться в причинах болезней, в способах лечения и профилактики астигматизма, чтобы сохранить здоровое зрение.
Астигматизм — это дефект зрения, вследствие которого, из-за искажения формы хрусталика или роговицы глаза, человек теряет способность видеть четкое изображение различных предметов и явлений окружающего мира. Как известно, для хорошего зрения световые лучи должны фокусироваться в единой точке, находящейся в самом центре сетчатки. При астигматизме эти лучи фокусируются не в одной, а в нескольких точках, находишься перед или за сетчаткой, вследствие чего человек получает размытое или искаженное изображение. Отсюда и название “астигматизм”, которое, переводя с греческого, означает “без точки”.
Правильная форма роговицы напоминает половину футбольного мяча. В такой сферической форме во всех её меридианах лучи преломляются в одной точке с одинаковой силой. Астигматизм нарушает эту сферичность, поэтому в разных сечениях такой роговицы лучи преломляются по-разному, что приводит к неправильной фокусировки изображения на сетчатку. Чтобы лучше понять каким видят мир люди, страдающие астигматизмом, представьте картинку расфокусированного фотоаппарата.
Виды астигматизма
Очень часто астигматизм может проявляться вместе с миопией (близорукостью) и гипермитропией (дальнозоркость).
Поэтому офтальмологи выделяют несколько видов:
- Миопический астигматизм. При такой болезни часть лучей фокусируется перед сетчаткой, а другая часть — на сетчатке. Поэтому в одном меридиане глаза наблюдается нормальное зрение, а в другой — миопия. Данное заболевание разделяют на простое и сложное.
- Гиперметропический астигматизм. Глаза с такого рода заболеванием сочетают в себе в одной части эмметропию, а в другой — дальнозоркость. Также бывает простым и сложным.
- Смешанный астигматизм — сочетает проявления миопии и гиперметропии в разных меридианах глаза.
Также данное заболевание разделяют на хрусталиковый и роговичный астигматизм. Роговичный возникает вследствие искривления формы роговицы, и оказывает большее влияние на зрение. Хрусталиковый — в результате изменения формы хрусталика, и является более редким явлением.
В зависимости от природы зарождения болезни принято различать:
- Врожденный астигматизм — проявляется после рождения ребенка или в дошкольном возрасте.
- Приобретенный — возникает, как результат травм, воспалительных болезней, или после неудачных хирургических вмешательств.
Степени и выявление астигматизма
Степень определяется измерением разницы между сильным меридианом глаза и слабым. Общепринятой считается такая классификация:
- Слабая степень — до 3 Дптр. Наиболее распространенная степень, которая легко поддается лечению любым известным способом.
- Средняя степень — 3-6 Дптр. Очки не смогут корригировать зрение. Контактные линзы, лазерное лечение или хирургическое вмешательство — возможные способы лечения.
- Высокая степень — свыше 6 Дптр. Исправить такое нарушение только под силу жестким контактным линзам и хирургической операции.
Причины астигматизма глаз
Данное нарушения рефракции глаза может поражать и детей и взрослых. В большинстве случаев оно является врожденным, то есть передается генетическим путем и проявляется или сразу после рождения ребенка, или уже в дошкольном и более взрослом возрасте. В иных случаях возможные причины возникновения — рубцовые повреждения роговицы после травмы или операции на глазах.
Симптомы болезни
Астигматизм нарушает процесс фокусировки изображения, вследствие чего зрение ухудшается. Но кроме дискомфорта эта болезнь глаз сопровождается рядом других неприятных симптомов. Астигматизм глаз может стать причиной:
- Головокружений и головных болей.
- Размытости или искажения изображения.
- Раздражение глаз.
- Обильного слезотечения.
- Раннего появления мимических морщин, из-за частого прищуривания.
- Быстрой усталости глаз.
Выявить заболевание можно только путем тщательного компьютерного обследования системы зрения. Чтобы правильно определить степень и вид заболевания необходимо обратиться к врачу для полного офтальмологического обследования.
Способы коррекции
Любое лечение астигматизма направлено на нормализацию фокусировки изображения. В современной медицине коррекция этого заболевания осуществляется тремя возможными способами.
- Корекция астигматизма при помощи очков. Самый легкий и распространенный способ лечения болезни. Это безболезненный метод, не требующий хирургических вмешательств, но действует он только оптика. При астигматизме выписывают цилиндрические очки. В рецепте на астигматические очки встречаются обозначения Cyl и Ax. Cyl — цилиндр — это оптическая сила очковых линз, а Ax — это расположение оси цилиндра, которое обозначается в градусах. Данный способ коррекции не идеальный может исправить до 2 дтпр астигматизма. Больший цилиндр очков воспринимается хуже, вызывая головокружения и головные боли. К тому же очки только корректируют зрение, избавится от проблемы они не помогут. Но все же цилиндрические очки остаются самым простым, популярным и недорогим способом лечения астигматизма.
- Контактные линзы — не менее популярный, но более практичный метод лечения. При астигматизме назначают ношение жестких линз, мягких или торических контактных линз. Контактные линзы обеспечивают лучшую коррекцию зрения, так как линза с роговицей образуют одну оптическую систему, не ограничивая зрение. Торические линзы в отличии от обычных сферических, надежно фиксируются на глазном яблоке, соблюдая правильное положение, при котором главные меридианы линзы совпадаю с глазными. Жесткие линзы хороши тем, что имеют длительный срок службы, и надежно держат форму на роговице, улучшая корректировку зрения. Но им свойственен достаточно длительный срок привыкания. Меньший срок адаптации имеют мягкие линзы. Такая оптика обволакивает роговицу и точно повторяет ее форму, что обеспечивает лучшую коррекцию и комфорт при ношении. Контактные линзы также являются методом корректировки зрительных способностей, действующим только при применении данного рода оптики.
- Лазерная коррекция астигматизма является наиболее современным, эффективным и прогрессивным способом лечения. Это безопасная и безболезненная процедура, способная лишить проблем со зрением на длительный срок.
Зрение имеет огромное влияние на качество нашей жизни, поэтому всегда нужно заботиться о его сохранении. Избегайте вредных привычек, вредящих Вашему зрению, и проходите регулярные обследования, чтобы обезопасить себя от заболеваний и их последствий. Полноценно видеть — значит полноценно жить. Выбор всегда за Вами!
Так же Вы можете узнать, что такое детские силиконовые оправы Fisher Price.
Современная статистика удручает. Более половины населения планеты страдает нарушением зрения, наиболее распространенными проблемами являются близорукость и дальнозоркость. Но офтальмологи часто диагностируют еще одно заболевание, название которого многим незнакомо. Астигматизм – дефект оптической системы глаза, когда резкость изображения ассиметрична по вертикали и горизонтали. И параллельные лучи света, проходящие через глаз, фокусируются не в точку, а в «восьмерку». Для человека это означает, что видимость изображения становится нерезкой, причем часто это касается как дальних, так и близких предметов. В результате вместо нормального изображения человек видит искаженное, в котором одни линии четкие, другие — размытые. Представление об этом можно получить, если посмотреть на свое искаженное отражение в овальной чайной ложке. Аналогичное искаженное изображение формируется при астигматизме на сетчатке глаза.
Окулисты утверждают, что с такой проблемой сталкиваются практически две трети жителей планеты. Но так как степень астигматизма может быть небольшой, то многие практически не ощущают какого-либо дискомфорта. Медикам сложно выделить четкий перечень общих симптомов, указывающих на наличие у пациента астигматизма. В каждом отдельном случае они будут различаться. На самых ранних стадиях его часто путают с усталостью глаз.
Однако, достаточно много людей нуждаются в специальном лечении или коррекции этого нарушения с помощью очков, контактных линз или даже операции.
Общее
Астигматизм – это дефект оптической системы глаза. При этом преломление (или отражение) лучей в различных сечениях проходящего светового пучка неодинаково.
Вследствие этого изображение предметов становится нерезким, каждая точка предмета отображается размытым эллипсом. А вся картинка как в «кривом зеркале» превращается в так называемую фигуру «коноид Штурма». На практике основная жалоба – ухудшение зрения вдаль, нередко расплывчатость вблизи, нечеткость и раздвоенность предметов.
Ход лучей в глазу с астигматизмом выглядит так.
— Я таким родился или жизнь меня испортила?
Это первый вопрос, который задают пациенты, когда слышат этот диагноз впервые.
Астигматизм может быть врождённым или приобретенным, может быть стабильным и прогрессировать.
Довольно часто астигматизм является особенностью строения роговицы при рождении, он даже может передаваться по наследству от родителей. Если его величина оказывает влияние на остроту зрения (как правило, речь идет об астигматизме больше 1 диоптрии), то он обязательно требует коррекции уже с раннего детского возраста. В противном случае глаз плохо видит и развивается амблиопия – «ленивый» глаз, который уже не способен на высокое зрение во взрослом возрасте. Ребенок с астигматизмом, кстати, никогда вам не пожалуется на плохое зрение – он же не знает, как это можно хорошо видеть. Поэтому так важны ранние осмотры у окулиста и ношение очков, «как доктор прописал».
Часто бывает, что уже взрослый человек с удивлением узнает, что у него, оказывается, астигматизм, это в случае необследованных в детстве.
Астигматизм может появиться уже во взрослом возрасте как результат заболеваний роговицы, например, кератоконуса, воспалений, травм и операций.
В любом случае он появляется не от работы за компьютером.
— Что повреждается при астигматизме?
Прежде всего причиной астигматизма могут быть две оптические системы глаза – роговица и хрусталик. Когда подбирают очки или линзы, то учитывают результирующую оптических сил этих двух систем. Обратите внимание, обычно пациенты знают про часто встречающийся роговичный астигматизм, но забывают про хрусталиковый — это может иметь значение, например, при катаракте, когда нерегулярность появляется в хрусталике. «Роговица ровная, но есть астигматизм» — это оно. Часто пациент и оптометрист вообще не заморачиваются тем, что является причиной. При подборе очков важно с помощью коррекции сфокусировать лучи света на сетчатку. А при хирургической коррекции – это важно.
Для упрощенного понимания сути проблемы я часто объясняю пациентам, что оптика глаза с астигматизмом похожа не на сферу (футбольный мяч), а на овал (мяч для рэгби).
— Как отличается астигматизм по величине, форме и содержанию?
Во-первых, имеет значение величина астигматизма – условно до 1 диоптрии астигматизм считается физиологическим, слабым. То есть, как правило, он не требует коррекции. Но в случае, если он даже такой небольшой величины снижает зрение, увы, его нужно корректировать. Средняя степень – до 2 диоптрий, высокая – 2-3 диоптрии и более 3 диоптрий – это очень высокий астигматизм. Есть другие классификации, но эта лучше всего отражает влияние на дефокус.
Во-вторых, есть два вида астигматизма роговицы: регулярный и нерегулярный.
При регулярном астигматизме есть две основные преломляющие перпендикулярные плоскости сечения, в пределах которых оптическая сила не меняется – слабая и сильная. В такой оптике есть хоть какая-то закономерность, даже если оси косые или большая разница в их оптической силе.
Регулярный астигматизм – в этом случае можно выделить две части, где роговица имеет различную степень преломления. Этот тип астигматизма можно исправить с помощью очков с цилиндрическими стекла или мягкими контактными линзами.
Нерегулярный астигматизм – в данном случае две части не могут быть выделены, поскольку существует много оптических осей. Этот тип обычно развивается в результате повреждение роговицы, например, во время аварии (образуется рубцовая ткань), либо обусловлено неравномерными выпуклостями роговицы (кератоконус). Нерегулярный астигматизм как правило плохо корректируется, иногда могут быть полезны жесткие контактные линз или лазерные воздействия на роговицу.
В-третьих, тип астигматизма зависит от расположения сильной оси. Если сильная ось вертикальна или не более, чем на 30 градусов отклоняется от вертикали – астигматизм прямой. Если сильная ось горизонтальна ±30 градусов – астигматизм обратный. Если в промежутке между – астигматизм с косыми осями. Прямой астигматизм чуть увеличивает глубину фокуса, обратный – больше ухудшает видимость, но эти оба варианта неплохо корректируются. А вот коррекция астигматизма с косыми осями очками и линзами хуже выполняется.
В астигматических глазах есть две перпендикулярные плоскости сечения с наибольшей и наименьшей преломляющей силой.
В-четвертых, в зависимости от того, как соотносится фокусировка по отношению к сетчатке, астигматизм делится на близорукий (миопический), дальнозоркий (гиперметропический) и смешанный – это когда в одном глазу часть изображения попадает перед сетчаткой, а часть позади сетчатки. Например, минус два и минус четыре – тогда это сложный близорукий астигматизм, плюс два и плюс четыре – сложный дальнозоркий астигматизм, плюс два и минус четыре – смешанный.
Близорукий астигматизм обозначают знаком «-», дальнозоркий – знаком «+», при смешанном в глазу есть «+» и «-».
— Как я могу заподозрить астигматизм?
Симптомами астигматизма является понижение зрения, иногда видение предметов искривлёнными, их раздвоение, быстрое утомление глаз при работе, головная боль. Часто вы можете даже не подозревать о том, что есть такая проблема, настолько типичными бывают жалобы – плохое зрение для дали или близи, или на всех расстояниях.
— Какая диагностика нужна при астигматизме.
Поскольку астигматизм является дефектом оптики, то, во-первых, тщательно исследуется оптика глаза. И правильное заключение даст только офтальмолог. Для этого у нас есть ряд тестов: исследование на авторефрактокератометре, аберрометре, фороптере с подбором пробных линз для определения остроты зрения с максимальной коррекцией. Очень интересная лучистая фигура дает представление о том, насколько присутствует астигматизм – если вы будете смотреть в центр фигуры снизу, то часть линий будет более четкими, а часть «расплывется» у тех, у кого есть астигматизм.
В тестах фороптера у офтальмолога в арсенале также есть ряд приемов для уточнения наличия астигматизма, его оси и величины. И этот процесс всегда довольно затратный по времени — это смогут подтвердить те пациенты, которые делали у нас, например, СМАЙЛ. Проверка тестов с «затуманиванием, кросс-цилиндрами с силовой и осевой пробами» по времени 20-30 минут.
Итак, когда определили, что астигматизм все же есть, нужно определить «кто виноват» — роговица или хрусталик.
Обследование роговицы должно включать кератотопографию – исследование рельефа и оптической силы роговицы по всей ее площади, оптическую когерентную томографию, которая определяет толщину, морфологию и геометрию роговицы также по всей площади, исследование задней поверхности роговицы с помощью Шаймфлюг камеры для определения нерегулярностей передних и задних поверхностей роговицы, конфокальную микроскопию – исследование заднего слоя роговицы (эндотелия). По результатам этого обследования мы уже можем делать заключение, насколько роговица здорова.
Так выглядит обследование на диагностической системе Шаймфлюг-камера + кольца Плацидо.
Иногда астигматизм связан с хрусталиком – его формой, наличием в нем различных помутнений или изменением его положения в пространстве, такой астигматизм называют хрусталиковым. А бывает, что и роговица неправильная и хрусталик с искажениями, тогда результирующая будет влиять на конечную оптику в целом.
Еще передний отрезок глаза мы можем изучать, проводя ультразвуковую биомикроскопию, чтобы рассмотреть недоступные для других методов отделы глаза и их измерить.
Как это происходит я подробно описывала в предыдущем посте: Мы добрались до побочных эффектов лазерной коррекции зрения — и ещё до диагностики (пост) и еще здесь: «Аугментация» глаза: что мы встраиваем в него сегодня, и под что ещё останется место (пост).Расчёт интраокулярных факичных линз (встраиваемых в глаз) – продолжаем про глаз и его биомеханику (пост).
Да, кстати, для детей есть такой педиатрический авторефрактометр, которым можно измерить оптику глаза у ребенка, бесконтактно, когда не нужно ничего прижимать к его лбу и все происходит на расстоянии 1,5-2 м. Это важно, так как дети вообще капризничают и плохо смотрят (или вообще отказываются смотреть) туда, куда просит офтальмолог. Есть далеко не во всех клиниках, так как дорого стоит. У нас, конечно, он есть, называется PlusOptix. А поздно диагностированный астигматизм приводит к серьезным последствиям.
Это обследование с PlusOptix
А, еще не назвала старый допотопный метод скиаскопии – слежения за движением тени рефлекса с глазного дна при свечении обратным офтальмоскопом и перемещением линейки с линзами. Так диагностировали наши бабушки, кстати, довольно успешно, если умеешь это делать.
Метод скиаскопии.
— Как связан астигматизм с кератоконусом
Одним из основных симптомов, появляющимся при кератоконусе, является как раз астигматизм. Когда мы диагностируем пациента с астигматизмом, то всегда должны исключить скрытую (forme fruste) или начальную форму кератоконуса. Об этом серьезном заболевании я писала в посте:
→ Кератоэктазия (кератоконус, «выпуклая роговица»): что это и что с этим делать
В начале заболевания вы вообще даже о нем можете не подозревать, даже астигматизм может быть совсем небольшим – 0,5 – 0,75 диоптрий, однако изменения в роговице уже есть и доступны только специальными методами обследования. Поэтому, если вам предлагают пообследовать роговицу на предмет ее здоровья, это не коммерческая «накрутка», это стоит сделать, так как лечение в начальных стадиях гораздо эффективнее, чем в развитых и далекозашедших.
При кератоконусе речь идет как раз о нерегулярном астигматизме, который плохо в развитых стадиях поддается коррекции.
Так выглядит кератотопограмма при начальном кератоконусе.
А в следующем посте я расскажу о способах коррекции астигматизма как хирургических, так и нехирургических, а также о том, что самое главное при астигматизме в детском и взрослом возрасте.
ПЕРЕЙТИ К МЕТОДАМ КОРРЕКЦИИ АСТИГМАТИЗМА >>>
Астигматизм: как правильно подобрать очки?
Астигматизм — нарушение зрения, при котором окружающий мир видится не очень четким и контрастным, размытым, словно в тумане. Эта патология обычно сочетается с миопией или дальнозоркостью. Для ее коррекции используют линзы особого дизайна. Расскажем, как подобрать очки при астигматизме и какие процедуры для этого потребуются.
Характерно, что у многих людей существует врожденный физиологический астигматизм до 0,5 диоптрий, он не доставляет заметного дискомфорта. Однако при более высоких значениях качество зрения начинает страдать. Вот каковы основные признаки астигматизма:
- предметы теряют четкие очертания;
- зуд и жжение в глазах, особенно при длительном зрительном напряжении;
- быстрое утомление от работы, головные боли.
Дело в том, что подобные симптомы многие списывают на обычную усталость и не спешат обращаться к офтальмологу. А ведь многих проблем со зрением можно было бы избежать при своевременном лечении.
Для правильного подбора астигматических очков понадобится пройти комплекс исследований, который состоит из нескольких процедур. После того как офтальмолог закончит диагностику, по результатам он выпишет рецепт с необходимыми характеристиками для изготовления оптики.
Рассмотрим, какие бывают виды и степени астигматизма, и какие процедуры необходимо пройти для получения рецепта.
Определение астигматизма и его степени
Название заболевания произошло от греческого «стигма» — точка, «а» — частица отрицания. При этой патологии световые лучи фокусируются на сетчатке не в виде точки, как при нормальном зрении, а в виде круга, овала или линии. Причина этому — искривленная форма роговицы или хрусталика, из-за чего происходит неправильное преломление лучей при прохождении через эти оптические среды глаза.
При роговичном астигматизме один из меридианов роговицы имеет короткий радиус и бОльшую преломляющую силу, другой, наоборот, длинный радиус и слабую силу преломления. Если они взаимно перпендикулярны и рефракция в пределах каждого постоянна, то такой астигматизм поддается коррекции цилиндрическими линзами.
Второй тип этого нарушения зрения — хрусталиковый астигматизм, обусловленный неправильной формой поверхности хрусталика. Данная разновидность патологии встречается гораздо реже и корректировать его сложнее. Как правило, прибегают к операции по замене хрусталика.
Степень астигматизма — это показатель, характеризующий разницу между преломлением главных меридианов. Сложность диагностики состоит в том, что нужно отдельно определить две рефракции глаза, и в соответствии с этим правильно изготовить линзы.
Вот какие степени астигматизма выделяют в офтальмологии.
- Слабая до 0,5D. Это физиологическое нарушение, и специальное лечение в таком случае не требуется.
- Низкая степень от 1,5 до 3D. Хорошо поддается исправлению при ношении очков или контактных линз, а также устраняется посредством лазерной коррекции.
- Средняя от 3 до 6D. В этом случае очками скорректировать астигматизм сложно, поэтому прибегают к использованию торических контактных линз, назначают лазерную или хирургическую операцию.
- Высокая от 6D и выше. Такая сильная степень патологии (роговичный астигматизм) исправляется с помощью жестких ортокератологических линз или же сочетанием хирургической и лазерной коррекции.
Таким образом, чем выше степень заболевания, тем сложнее методы для ее исправления.
Виды астигматизма
В астигматическом глазу расположены фокальные линии в соответствии с меридианами. В зависимости от их нахождения выделяют несколько видов астигматизма:
- простой гиперметропический — дальнозоркость в одном главном меридиане сочетается с эмметропией в другом;
- простой миопический — близорукость в одном главном меридиане сочетается с эмметропией в другом;
- сложный гиперметропический — сочетание дальнозоркости разной степени в двух главных меридианах;
- сложный миопический — близорукость разной степени в двух главных меридианах;
- смешанный — сочетание дальнозоркости в одном главном меридиане и близорукости в другом.
Ни один, даже здоровый глаз, не имеет абсолютно ровной поверхности роговицы в виде полусферы. Однако астигматизм слабой степени до 0,5D считается физиологическим и не влияет на качество зрения, а вот при значениях от 0,75 D и выше уже мешает четкому восприятию окружающего мира.
Комплекс процедур, необходимых для подбора астигматических очков
Для того, чтобы получить рецепт, в соответствии с которым нужно изготовить астигматические очки, необходимо пройти несколько процедур.
В современной офтальмологии такая диагностика осуществляется с помощью высокотехнологичных приборов, позволяющих получить достоверные сведения о состоянии глазных структур и качестве зрения пациента. Обследование проводится отдельно для левого и правого глаза.
Вот какие методы применяются на сегодняшний день для выявления астигматизма.
Компьютерная кератометрия, или офтальмометрия. Этот способ используется для определения кривизны передней поверхности роговицы и степени выраженности ее рельефа. Процедура совершенно безболезненна, и ее результаты помогают затем тщательно подобрать средства контактной коррекции, рассчитать силу интраокулярной линзы для имплантации, оценить состояние роговицы перед операцией, а также определить наличие неправильного астигматизма, его силу в диоптриях. Кератометрия является основной процедурой для диагностики заболевания. Последовательность ее проведения выглядит следующим образом:
- пациент садится на стул перед прибором и фиксирует взгляд в одной точке;
- врач включает кератометр и с его помощью сканирует роговицу несколько секунд;
- аппарат обрабатывает информацию, используя специальную формулу для расчета кривизны роговицы;
- прибор выдает кератотопограмму, которую расшифровывает врач.
Биомикроскопия с помощью щелевой лампы. Врач направляет в глаз пациента световой пучок и с помощью микроскопа исследует передний отрезок глазного яблока, а также хрусталик и роговицу. Использование щелевой лампы позволяет обнаружить различные воспаления, сосудистые нарушения, новообразования во внутренних тканях даже на ранних стадиях, а также имеющиеся рубцы, инородные тела, микротравмы, патологии роговицы, хрусталика и прочие аномалии. Осмотр на щелевой лампе — наилучший способ увидеть ткани органов зрения в увеличенном размере. Биомикроскопия совершенно безопасна и практически не имеет противопоказаний.
Величину рефракции каждого глаза определяют с помощью разных исследований: авторефрактометрии, визометрии, скиаскопии и некоторых других. Другие виды диагностики — прямую и обратную офтальмоскопию, УЗИ глаза и прочие процедуры может назначить врач в зависимости от ситуации.
Что написано в рецепте на очки для астигматизма?
После сбора всей необходимой информации офтальмолог выписывает рецепт на астигматические очки. Вот какие данные будут указаны в нем:
- Sph (сфера) — значение в диоптриях для правого (OD) и левого (OS) глаз;
- DP — расстояние между центрами зрачков;
- Cyl — оптическая сила цилиндра;
- Ax — ось наклона цилиндра.
Именно на эти параметры будет ориентироваться мастер-оптик, изготавливающий астигматические цилиндрические стекла по индивидуальному заказу. Что же они из себя представляют? Их отличие от простых сферических линз заключается в том, что лучи света, попадающие в плоскость, параллельную оси стекла, не преломляются, а лучи в перпендикулярной плоскости, наоборот, имеют свойство преломляться. Для этого в рецепте указывается Ax — ось наклона цилиндра в градусах до 180°.
Очки для астигматизма — доступный и простой способ коррекции этого нарушения зрения. Однако очковую оптику целесообразно использовать только при слабой патологии до –3 диоптрий. При средней и сильной степенях подходят торические контактные линзы или же назначается операция. Дело в том, что астигматические очки заметно ограничивают периферическое зрение, при этом искажая размеры и пропорции изображения, особенно при сильной степени сложного миопического или смешанного астигматизма. Не все пользователи могут адаптироваться к очкам, выбирая для себя контактную оптику.
Как подобрать очки для коррекции астигматизма?
Итак, первое, что нужно будет сделать — посетить офтальмолога, который проведет грамотную диагностику и выпишет рецепт. Кроме того, он посоветует, следует ли в конкретном случае пользоваться именно очковой оптикой или предпочесть средства контактной коррекции зрения.
Если астигматизм сочетается с другими патологиями, например, миопией или дальнозоркостью (а так бывает чаще всего), то в этом случае диагностируется смешанный или сложный вид астигматизма. В таких ситуациях очки становится подобрать еще сложнее, а период адаптации более длительный. На первом этапе изготавливаются очки с менее сильными стеклами, и пациент должен носить их в течение некоторого времени, чтобы привыкнуть. На следующем этапе уже нужны астигматические очки с истинными значениями.
Врачи напоминают: при первых признаках дискомфорта в глазах нужно обращаться за квалифицированной помощью, чтобы вовремя начать лечение заболеваний. Болезнь в запущенной стадии может привести к потере зрительных функций.
Астигматизм
О строении человеческого глаза, основных понятиях и клинических нарушениях его оптической системы – рекомендуем более подробный материал «Глаз. Зрение. Рефракция. Аметропия».
Нарушения рефракции, т.е. преломления света внутриглазными оптическими средами с последующей проекцией наблюдаемого образа на сетчатку, носят собирательное название аметропия. Некоторые разновидности аметропии, – такие, например, как анизометропия или анизейкония, – известны, в основном, узким специалистам. Другие распространены настолько широко, что с детства и до глубокой старости вокруг нас (а со временем и в наш персональный адрес) слышны слова «близорукость» и/или «дальнозоркость».
Если усреднить все эпидемиологические оценки, публикуемые в мировой специальной литературе по отдельным видам аметропии, а потом эти оценки сложить, – то вполне вероятно, что суммарная доля намного превысит 100% населения земного шара (в математике такое, конечно, невозможно, однако в реальной жизни, мы понимаем, случается всякое, особенно на выборах). Причина в том, что множество людей страдает комбинированными формами аметропии, а заболеваемость в значительной степени зависит от региона проживания, возраста, профессии, генетики, этнической принадлежности и множества других факторов, к тому же нередко взаимосвязанных. Соответственно, все эти факторы влияют на результаты медико-статистических исследований, сами исследования очень затруднены, а в глобальном масштабе едва ли осуществимы, – по крайней мере, сегодня трудно представить себе всемирный скрининг с достаточной репрезентативностью и достоверностью результатов.
Астигматизм – один из видов аметропии. Более того, это самый распространенный ее вариант, который, как полагают, встречается гораздо чаще близорукости и дальнозоркости, вместе взятых. Однако суть этого нарушения внутриглазной рефракции нельзя сформулировать так же просто, как при гиперметропии («Плохо вижу вблизи») или миопии («Плохо вижу вдаль»). Астигматизм – это «Плохо вижу вообще».
В древнегреческом языке слово «стигма» было многозначным и употреблялось в зависимости от контекста: так могли назвать клеймо, точку, пятно и т.д. Многозначен этот корень и в современной науке. В социальной психиатрии, скажем, термин «стигматизация» означает коллективно-бессознательное предрассудочное отвержение человека на том лишь основании, что он несет на себе «ярлык» психиатрического диагноза; в промышленной оптике под астигматизмом понимают один из искажающих эффектов объектива, и т.д.
Астигматизм в офтальмологическом значении – это принципиальная неспособность оптической системы глаза четко сфокусировать наблюдаемую картину на сетчатке, причем объекты видятся расплывчатыми независимо от того, на каком расстоянии до глаз они находятся. Таким образом, в данном случае «астигматизм» может быть переведен как «отсутствие (фокусной) точки».
Четкость зрительного восприятия – это, прежде всего, четкость границ. Если представить себе, например, черный квадрат на белоснежном листе, то при здоровом зрении граница между фоном и каждой стороной квадрата выглядит как тонкая прямая линия, и чем эта линия тоньше, тем, как говорят фотографы, «резче» изображение. При аметропии граница в нашем примере перестает быть линией и воспринимается как градиент, плавный переход между черным и белым. Но при астигматизме ситуация еще сложней: какие-то участки видятся более-менее отчетливо, а другие расплывчато. Например, горизонтальные стороны квадрата резки, вертикальные размыты; или, скажем, размыты верхний левый и нижний правый углы.
Астигматизм обычно описывается как «несовпадение силы рефракции в различных поперечно-перпендикулярных плоскостях». Но что это означает и почему так происходит? Вспомним: на схемах глазного яблока роговица и хрусталик в разрезе изображаются идеальными, под циркуль, дугами со строго постоянным радиусом. Однако в действительности радиус где-то может отклониться, т.е. в одном участке поверхность оказывается несколько толще, чем в остальных. Упрощенно говоря, астигматизм – это взгляд на мир сквозь линзу с волнистой поверхностью: мало того, что преломляет, так еще и преломляет неравномерно, в разных осях и меридианах по-разному, и вместо одной фокальной плоскости на сетчатку проецируются несколько – отсюда и нечеткость конечного зрительного образа.
Большинство исследований, проводимых в различных странах, свидетельствуют о распространенности астигматизма в пределах от 30% до 60% взрослого населения (речь только о клинически значимом астигматизме, поскольку те или иные колебания формы внутриглазных оптических структур, не сказывающиеся на остроте зрения, встречаются практически у всех людей). Имеет место прямая зависимость частоты встречаемости от среднего возраста исследуемой выборки (чем старше, тем астигматизма больше), однако эта тенденция не абсолютна: астигматизм, в том числе тяжелый и осложненный, может быть выявлен в любом возрасте.
Причины
Из всех предположительных причин астигматической деформации не вызывает сомнений, пожалуй, только определенное (но, опять же, далеко не абсолютное) влияние наследственного фактора. Прочие этиопатогенетические факторы остаются объектом интенсивного изучения, обсуждения и дискуссии. В частности, большинство локализованных на разных языках страниц Википедии называют причины астигматизма «неясными» или «неизвестными».
Приобретенный астигматизм чаще всего связывают с травмами (в т.ч. офтальмохирургическими, где астигматизм может оказаться послеоперационным осложнением), рубцовыми изменениями роговицы вследствие ожогов, инфекционно-воспалительных и дегенеративно-дистрофических процессов, а также с кератоконусом и другими заболеваниями подобного рода.
Симптоматика
Существует несколько классификаций астигматизма, построенных на различных критериях. Так, различают хрусталиковую, корнеальную (роговичную) и сочетанную формы, прямой и обратный астигматизм, врожденный и приобретенный; по степени тяжести выделяют слабую степень (до 3 диоптрий), среднюю (от 3 до 6) и сильную (свыше 6 диоптрий). Во многих случаях астигматизм сочетается с миопией или гиперметропией.
Как показано выше, ощутимых и субъективно дискомфортных нарушений зрения при легком астигматизме может и не быть. Однако подобная ситуация остается достаточно опасной, особенно в раннем детском и школьном возрасте: косвенными проявлениями астигматизма становятся головные боли, астенопия («слабость глаза», т.е. утомляемость, болезненная реакция на зрительные нагрузки и т.д.), тяжесть или «песчаная» резь в глазах. В некоторых случаях отмечается диплопия (двоение), в других нарушается способность к точной оценке расстояния до объектов, отмечается тенденция к никталопии («куриной слепоте»), та или иная степень светобоязни, привычка прищуриваться или наклонять голову под определенным углом, чтобы лучше видеть.
Выраженный астигматизм, особенно комбинированные его формы, в отсутствие коррекции чреват столь же тяжелыми последствиями, как и другие разновидности аметропии: в силу постоянного перенапряжения развиваются амблиопия, косоглазие, снижение прозрачности оптических сред, нарушения в дренажной системе по глаукоматозному типу, дегенерация и отслоение сетчатки вследствие дефицита кровоснабжения, – в конечном счете, любое из перечисленных осложнений может привести к тотальной слепоте.
Диагностика
Астигматизм требует тщательного офтальмоскопического и офтальмометрического обследования. Проводится визометрия (точная оценка остроты зрения с помощью наборов сменных линз, таблиц Сивцева-Головина и др.), рефрактометрия, скиаскопия; по мере необходимости назначаются компьютерная кератотопография (картирование поверхности роговицы), ультразвуковые и другие исследования, необходимые и целесообразные в данном конкретном случае.
Лечение
Оптической коррекции астигматизма (в просторечье – «очки с цилиндрами»), как и офтальмохирургическому его лечению, следует посвятить отдельные статьи, – поскольку это область, в силу сложности самой патологии, в настоящее время активно разрабатывается научно-исследовательским сектором мировой медицины и лидерами индустрии по производству товаров медицинского назначения.
Основными направлениями коррекции астигматизма (что почти всегда исключительно важно и должно делаться как можно раньше) остаются очки и контактные линзы с цилиндрическим компонентом кривизны поверхности. Такая оптика должна изготавливаться строго по индивидуальным показаниям, полученным в ходе самой тщательной диагностики, и нередко обладает очень сложной топологией, – которая, тем не менее, не всегда компенсирует нарушения рефракции полностью. Во избежание неоправданных ожиданий и претензий к врачам следует понимать: в случае выраженной комбинированной рефракционной аномалии, включающей астигматический компонент, обеспечить этим способом четкое и ясное зрение на любой дистанции подчас невозможно физически. Кроме того, пассивная коррекция не способна ни устранить причины астигматизма, ни замедлить его прогрессирование.
Этиопатогенетическим лечением является исправление радиусов кривизны и общей формы поверхности роговицы и/или хрусталика – в тех случаях, когда это возможно, показано и прогностически оправдано. С этой целью производится либо «традиционная» микрохирургическая операция (например, астигматомия, склеропластика и т.д.), либо имплантируется интраокулярная линза, либо осуществляется лазерная коррекция зрения, получившая широкое распространение и признание во всем мире.
Однако и подбор очков, и выбор оптимальной модели контактных линз (которые значительно различаются качеством, назначением, исходной теоретической базой их разработки, материалом изготовления, стратегией и тактикой применения, правилами ухода и гигиены, стоимостью, долговечностью и многими другими параметрами), и планирование радикального вмешательства, – если именно такое решение принято совместно с пациентом, – все это является, повторим и подчеркнем, исключительно индивидуальным лечебно-диагностическим процессом. Ни один метод, ни один способ коррекции в принципе не может стоять «на потоке» и рекомендоваться всем поголовно.
Поэтому первая и главная задача пациента, если возникают проблемы с остротой зрения (или косвенные признаки латентной патологии в этой сфере), – как можно быстрее обратиться к офтальмологу, не растрачивая время и не рискуя потерять зрение при тестировании купленных наугад очков, при самолечении с помощью каких-то брошюр или «советов из интернета», при закапывании или втирании в глаза неизвестно каких субстанций. Астигматизм лечится, но лечится врачами.
90000 Symptoms, Causes, Types, Treatments, Definition 90001 90002 90003 Causes 90004 90003 Types 90004 90003 Correction options 90004 90009 90010 Astigmatism is a type of refractive error caused by the irregularities in the shape of a person’s cornea. The condition is not an eye disease or eye health issue. In this condition, the eye fails to focus the light equally on the retina leading to blurred or distorted vision.It can be present at the time of birth, or can develop gradually in life. 90011 90010 Put simply, Astigmatism is a problem with how the eye focuses light. 90011 90010 Astigmatism is a common eye condition which usually occurs with myopia (nearsightedness) or hyperopia (farsightedness) and can be easily diagnosed with a simple eye exam. 90011 90010 Symptoms of astigmatism include blurred vision or some degree of vision distortion at all distances. Astigmatism can also cause dizziness, eye strain, headaches, squinting and eye irritation.90011 90010 90019 90020 90011 90022 What causes astigmatism? 90023 90010 Astigmatism is usually caused by an irregularly shaped cornea. Instead of the cornea having a symmetrically rounded ball shape, it is shaped more like an egg, with one side (meridians) being significantly more curved than the side perpendicular to it. 90011 90010 (To understand what meridians are, think of the front of the eye like the face of a clock. A line connecting the 12 and 6 is one meridian; a line connecting the 3 and 9 is another.) 90011 90010 The steepest and flattest meridians of an eye with astigmatism are called the principal meridians. 90011 90010 In some cases, the problem is caused by the distortion of shape of the lens inside the eye. This is called lenticular astigmatism, to differentiate it from the more common corneal astigmatism. 90011 90010 Advertisement 90011 90010 FramesDirect.com boasts the largest online selection of top-brand eyewear, selling over 1 million frames since 1996. We use only premium Essilor prescription lenses, and our trained opticians can help you choose the best lens options.Shop online with confidence-find your favorite designer eyewear, and enjoy free shipping and the FramesDirect Price Match Guarantee. 90011 Shop Designer Eyewear 90022 3 types of astigmatism 90023 90010 There are three primary types of astigmatism: 90011 90040 90003 90010 90043 Myopic astigmatism. 90044 90011 90010 One or both principal meridians of the eye are nearsighted. (If both meridians are nearsighted, they are myopic in differing degree.) 90011 90004 90003 90010 90043 Hyperopic astigmatism.90044 90011 90010 One or both principal meridians are farsighted. (If both are farsighted, they are hyperopic in differing degree.) 90011 90004 90003 90010 90043 Mixed astigmatism. 90044 90011 90010 One prinicipal meridian is nearsighted, and the other is farsighted. 90011 90004 90065 90010 Astigmatism is also classified as regular or irregular. In regular astigmatism, the principal meridians are 90 degrees apart (perpendicular to each other). In irregular astigmatism, the principal meridians are not perpendicular.90011 90010 For most, the condition is regular corneal astigmatism, which gives the front surface of the eye an oval shape. 90011 90010 Irregular astigmatism can result from an eye injury that has caused scarring on the cornea, from certain types of eye surgery or from keratoconus, a disease that causes a gradual thinning of the cornea. 90011 90022 Astigmatism in children 90023 90010 It is common for babies to be born with astigmatism, but it usually clears up in the first year or so of the child’s life.The percentage of children with astigmatism decreases significantly as they reach 5 to 9 years of age. 90011 90010 While most children outgrow eye astigmatism, it is more likely to occur in kids who also struggle with either myopia or hyperopia. Like with adults, mild to severe astigmatism in children can be treated with glasses (or contact lenses if they’re old enough). 90011 90010 Babies do not need to wear glasses to treat their astigmatism as they’re likely to outgrow it before it becomes an issue.90011 90010 It’s important to schedule an eye exam for your child to avoid vision problems in school from uncorrected astigmatism. 90011 90010 90043 SEE RELATED: 90044 Vision problems of preschool children 90011 90022 Astigmatism tests 90023 90010 Astigmatism is detected during a routine eye exam with the same instruments and techniques used for the detection of nearsightedness and farsightedness. 90011 90010 Your eye doctor can estimate the amount of the condition you have by shining a light into your eye while manually introducing a series of lenses between the light and your eye.This test is called retinoscopy. 90011 90022 How to correct astigmatism 90023 90010 Options to correct astigmatism can usually be corrected with eyeglasses, contact lenses or refractive surgery. 90011 90010 Refractive surgery is one of the less common astigmatism treatment options, however, since it is a laser procedure that changes the shape of your eyes, it comes with risks associated with most laser surgeries. 90011 90010 Astigmatism should be treated as soon as possible. Once diagnosed, regular visits to an eye doctor are required as astigmatism can fluctuate over time, making it necessary for prescriptions to be modified.90011 90010 90043 WORRIED YOUR CHILD MAY HAVE ASTIGMATISM? 90044 Book an appointment with a children’s eye doctor near you. 90011 90010 Page updated August 20, 2018 90011 .90000 Astigmatism — Optics, Physiology and Management 90001 \ n \ t \ t \ t \ t 90002 2.1. Preparation of dataset for meta-analysis 90003 \ n \ t \ t \ t \ t 90004 The studies used in this meta-analysis were searched on the ScienceDirect in English, the DBpia database, and the KISS (Koreanstudies Information Service System) in Korean . The search keywords used were CLA, weight, health, or fat and the research was limited to the experimental rat studies. About 50 studies were collected and 12 studies were finally selected after omitting some studies with insufficient information, such as no sample variance or no sample size (5, 8-18).90005 \ n \ t \ t \ t \ t 90004 The factors used to investigate the effect of CLA were collected from target studies, if it was studied in at least 2 studies. The selected factors were body fat (%), epididymal fat (g / 100g), fat cell size (μm), final body weight (g), food intake (g / d), leptin (pg / ml), liver-TC (mg / g), liver-TG (mg / g), plasma-TC (mg / dl), plasma-TG (mg / dl), and weight gain (g / d). The unit of each factor was uniformly changed. 90005 \ n \ t \ t \ t \ t 90004 In each study, there were two groups. One group of rats was treated with fat source such as beef tallow, coconut oil, corn oil, fish oil, safflower oil or soybean oil (FR), and the other group of rats was treated with fat source supplemented with CLA (FRC).Because the size of studies after grouping by treated fat source was not enough large, the each fat source has similar effect on obesity. 90005 \ n \ t \ t \ t \ n \ t \ t \ t \ t 90002 2.2. Measure and models for combining 90003 \ n \ t \ t \ t \ t 90004 Since the mean difference between FR and FRC was used for test on anti-obesity effect of CLA, the association measure was decided as the mean difference (MD) of each factor; mean of FRC minus mean of FR. The combined MD of each factor was calculated by the inverse variance method and the mean weighted by inverse variance in the primary studies.If the homogeneity was accepted by Cochran’s Q test, it is assumed that the effect measured in the study population has a single value. The association measure is estimated by using a variation within the studies in the fixed effect model. To reduce the bias caused by heterogeneity, meta-regression models are used to analyze association between treatment effects and study characteristics. The period and amount of CLA supplementation were considered as covariates, and the estimated coefficients of covariates were investigated for possible sources of heterogeneity.If the homogeneity was rejected, the combined MDs of studies were calculated in random effect model in which total variation defined the variation within studies with estimated variation between studies. 90005 \ n \ t \ t \ t \ n \ t \ t \ t \ t 90002 2.3. Identification the publication bias 90003 \ n \ t \ t \ t \ t 90004 The existence of publication bias was checked by using a funnel plot or Egger’s linear regression test. The funnel plot was a scatter plot of the association measure against a inverse of standard error of measure.If the shape of funnel plot about any factor is not funnel or cone around the combined MD, the publication bias was doubtable. Egger’s linear regression test was used to test the null hypothesis that the funnel plot was not asymmetry. Egger’s linear regression is a linear regression of standard normal deviate (defined as association measure over SE) against the inverse of SE, and there may be publication bias if the estimated intercept is significantly different from 0. A positive intercept indicates that more studies are associated with a bigger effect (19).90005 \ n \ t \ t \ t.90000 90001 Telescope astigmatism 90002 90003 90004 90005 telescope 90006 Ѳ 90005 ptics.net 90006 ▪ 90005 90006 90005 90006 ▪ ▪ 90005 90006 ▪ ▪▪▪▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ 90005 90006 CONTENTS 90017 90018 90019 ◄ 4.2. Coma ▐ 4.4. Defocus ► 90017 90021 90022 Similarly to coma, 90023 astigmatism 90024 is an off-axis point wavefront aberration, caused by obliquity of the incident wavefront relative to the optical surface.Astigmatism results simply from the projectional asymmetry arising from wavefront’s inclination to the optical surface. The diameter of wavefront’s projection onto the surface varies from the minimum in the plane of wavefront tilt — determined by the chief (Central) ray and optical axis, hence coinciding with the 90023 tangential plane 90024 — to the maximum in the direction orthogonal to it (90023 sagittal plane 90024), where it equals aperture diameter.90018 90022 As illustration below shows, vertical diameter of the reflected wavefront is smaller than the horizontal due to the effective (projected) diameter in that plane being reduced by a cos 90005 α 90006 factor, 90005 α 90006 being the mirror-to-wavefront axis inclination i.e. field angle in degrees). Since wavefront depth (sagitta) is constant, the shortest diameter (90005 1 90006) will generate the strongest radius, while the longest one (90005 2 90006) generates the weakest radius (profile for 90005 2 90006 is rotated 90 at right).Consequently, the corresponding wavefront sections will focus at two different points, with all other sections focusing in between. Since focal length (I.e. radius of curvature of the wavefront) changes with the square of the diameter for given sagitta depth, wavefront along these two orthogonal diameters focus at the longitudinal separation of (1-cos2α) i, which constitutes longitudinal astigmatism (90041 90005 i 90006 is the image-to-pupil separation, equal to focal length for distant objects).90018 90022 This applies to a lens with the stop at the surface as well, since the basic principle of wavefront transformation by an optical surface applies to both. Convex mirror (or negative lens) would induce astigmatism of opposite sign, with the stronger, shorter vertical line on the surface focusing farther away than the weaker horizontal line. 90018 90022 Another peculiarity of astigmatism is that a cross-section along any wavefront diameter is still spherical, but with the radius of curvature varying with the pupil angle.Thus the wavefront form as a whole deviates from spherical. 90018 90022 For displaced stop — either first optical surface significantly separated from the aperture stop, or secondary and tertiary surfaces (whose stop is formed by a preceding surface) — other surface properties, such as shape, position and conic, also can influence the size of astigmatism. This is due to the displaced stop for these surfaces changing the surface radial asymmetry profile.As illustrated at left, the only configuration that completely corrects for astigmatism is a sphere with the stop at the center of curvature (90005 1 90006). It is apparent from the two axes — that of the wavefront and that of the section of the sphere — coinciding, thus positioning the wavefront symmetrically vs. surface. Any other stop distance will not be fulfilling this condition, reintroducing off-axis aberrations (90005 2 90006). For conic forms other than the sphere, primary astigmatism can be either corrected with appropriate stop position (closer to mirror with smaller — i.e. negative — conics), or only minimized (with conics larger than zero). However, secondary astigmatism, even if low, remains. For a given stop location other than sphere’s center of curvature, the negative conics will generate less astigmatism than the sphere if their shape results in less of a surface vs. wavefront positional asymmetry. On the illustration, that is the case with the stop position 90005 2 90006, as conics toward parabola and hyperbola open wider than the sphere for given radius of curvature (however, as the surface section outlined by the wavefront is not symmetrical about its axis, coma will be generated even if primary astigmatism is cancelled, with one half of the wavefront flatter than the other one).90018 90022 90005 FIG. 43 90006 illustrates the form of astigmatic wavefront deformation for 90005 primary astigmatism 90006, and the resulting geometric (ray) aberration. 90018 90004 90005 90006 90018 90067 FIGURE 43A: 90023 90024 RIGHT: Primary astigmatism on mirror surface, as a result of the projected diameter of the incoming wavefront (90005 W 90006 90005 i 90006) varying with the radial orientation.For the inclination angle shown, the width of vertical, or tangential (with the tangential plane determined by the axis and chief ray) wavefront projection onto the surface, given by cosαD, is at its minimum, gradually increasing with the radial angle around the chief ray to the maximum projection width 90005 D 90006 in the orthogonal (Horizontal, or sagittal) orientation. With the wavefront sagitta (depth) constant, its radius (the focal length) varies with the square of diameter.Being of the smallest diameter, the wavefront section in the tangential (vertical) plane focuses closest, and the wavefront section in 90023 90024 the 90023 90024 sagittal plane farthest away from the mirror 90023. 90024 LEFT: The actual wavefront deviation from the corresponding reference sphere (red dots): for the reference sphere centered at the mid point of defocus 90005 M 90006, and those centered at either sagittal or tangential focus (90005 S 90006 and 90005 T, 90006 respectively; the deviation for the former has cylindrical form oriented vertically, for the latter horizontally).All three spheres coincide at the red dotted line. The P-V error is identical at all three focus locations; however, the deviation averaged over the wavefront (RMS error) is lower at the mid-focus by a factor 0.82, making it the best (diffraction) focus. Solid blue line in the best focus wavefront deviation 90005 (M) 90006 represents the deviation along the central cross-section of the actual wavefront vs. perfect reference sphere centered at the mid-focus point.The dashed blue line is a projection of the deviation along the wavefront edge, indicating saddle-like shape of the wavefront deformation. 90004 90091 43B: Ray geometry of astigmatism is not immediately obvious. It is determined by the inequality of the two perpendicular radii, so that all sections of the wavefront parallel to the shorter radius — the vertical one in this illustration — focus in a horizontal line closer to the objective, and all sections of the wavefront parallel to the perpendicular to the former, longer radius, focus into a vertical line farther away from the objective.This ray geometry produces a round ray spot plot midway between the two line foci. Below are the corresponding wavefront deformations for the three axial focal points. Since the reference sphere for F1 is with the corresponding, shorter radius, wavefront deformation in the vertical direction is zero (since the wavefront maps are for the Zernike aberration form, their color code shows zero deviation for the intersection with zero mean, while in the classical form zero deviation is what is coded red for the two cylindrical deviation forms; for the saddle-like, it is identical to the Zernike form, light blue).90018 90018 90022 Gaussian focus for astigmatic wavefront lies on the Petzval surface of an optical surface, or a system. Balancing defocus aberration for this point — located on the opposite direction from the sagittal focus, and at identical distance from it as the best focus — is zero, and the wavefront error is largest. Between the sagittal and tangential focus, ray disturbance resulting from the astigmatic wavefront deformation takes on rather peculiar form (90005 FIG.44 90006). 90018 90004 90018 90005 90004 FIGURE 44: Geometry of the astigmatic defocus produced by a mirror with the stop at the surface: the wavefront radius at the pupil gradually increases from the minimum in the tangential (vertical) plane to the maximum in the orthogonal to it sagittal plane. Consequently, all wavefront meridians focus at a different length, producing longitudinal defocus, as an axial separation between tangential and sagittal focus.At the sagittal plane focus 90005 S 90006 it forms sagittal line, contained in the tangential plane. And at the tangential plane focus 90005 T 90006 it forms tangential line, laying in the sagittal plane. The lines transform into ellipses of decreasing eccentricity toward the inside of defocus zone. Midway between the two lines is the circle of least confusion (90005 BF 90006), which is the location of best astigmatic focus.90018 90006 90067 Aberration function for primary astigmatism given in Table 4 is for tangential focus, which is identical to that for the sagittal focus, except for the orientation. Neither coincides with the best (diffraction) focus, which is located midway between the two, hence requires correction by defocus. Since for given longitudinal aberration the P-V wavefront error for primary astigmatism equals that for defocus, the defocus added to it equals half the P-V wavefront error of astigmatism.Aberration function for the 90005 wavefront error 90006 of primary (Lower-order) astigmatism at the best focus is given by: 90018 90004 W 90005 a 90006 = A 90005 ρ 90006 90005 2 90006 (cos 90005 2 90006 θ 90005 90006 — 0.5) 90005 90006 (18) 90018 90022 with 90005 A 90006 being the astigmatism peak aberration coefficient, 90005 ρ 90006 the normalized (to 1) height in the pupil, and 90005 θ 90006 the pupil angle.It shows that the wavefront error peaks for ρ = 1 and cos2θ = 1 and 0 (that is, for θ = 0, π / 2, π, 3π / 2 and 2π), which is, every 90 degrees (with the successive peaks being of opposite sign), and orthogonally to the orientations of the minimum wavefront deviation, occurring for cosθ = 90005 √ 90006 0.5 (For θ = π / 4, 3π / 4, 5π / 4 and 7π / 4). It clearly outlines saddle-shaped wavefront deviation, as illustrated on 90005 FIG.43 90006 left. 90018 90022 Note that the maximum wavefront error given by 90005 Eq. 18 90006 — which gives wavefront deviations, not the peak-to-valley error — is one half of the peak aberration coefficient, which equals the P-V error. Numerically, it is identical to the P-V error at either sagittal or tangential focus, W 90005 a 90006 = Aρ2cos2θ, but its RMS value is smaller by a factor of 1/90005 √ 90006 1.5. 90018 90022 When the point of maximum deviation in the tangential (Vertical) plane is closer to the center of reference sphere than its reference sphere point — i.e. when the tangential focus is precedes sagittal in the direction of light travel (or, simply put, is closer to the objective) — the wavefront error of astigmatism is negative. That is the sign of astigmatism in a concave mirror, illustrated on 90005 FIG. 28 90006. There is no difference in appearance between positive and negative Seidel astigmatism, since the pattern is merely rotated by 90, and has an inherent 180-degree rotational symmetry at the best focus location (90005 FIG.30 90006). 90018 90067 The 90005 peak 90006 90005 aberration coefficient 90006 90005 A 90006, which equals the peak-to-valley wavefront error, is given by: 90018 90004 A = aα 90005 2 90006 d 90005 2 90006 = ah 90005 2 90006 / 4F 90005 2 90006 (18.1) 90022 with 90018 a being the astigmatism aberration coefficient (simplified notation for 2 90005 w 90006 22 in Table 4), 90005 h 90006 the point height in image plane, 90005 α 90006 the field angle in radians (with α = h / for object at infinity, 90041 being the focal length) and 90005 d 90006 the pupil (aperture) radius.The 90005 aberration coefficient 90006 90005 a 90006 is, in general form for a single optical surface, given by 90018 90004 a = -0.5n2 [(1 / n’I) — (1 / nO)], 90018 90022 where 90005 I 90006, 90005 O 90006 are the image and object distance, and 90005 n 90006, 90005 n ‘90006 are the refractive index of incidence and refraction or reflection, respectively. 90018 90022 For a concave mirror and stop at the surface, n ‘= — n, I = O / (O-), = R / 2, and the coefficient is given by: 90018 90004 aM 90005 90006 = N / R (18.2) 90022 with 90005 R 90006 being the mirror radius of curvature. For mirror in air oriented to the left, n = 1 and the aberration coefficient is 90005 a 90006 M 90005 = 1 / R 90006. The sign of aberration coefficient indicates the tangential wavefront radius shorter than sagittal, and the sagittal line farther away from the mirror, as shown on 90005 FIG. 43-44 90006. Positive astigmatism has this order reversed. From another perspective, the astigmatism wavefront error is negative when the optical path difference from the point of peak deviation in the tangential plane is smaller than the radius of a perfect reference sphere (the one centered at the mid point between tangential and sagittal focus).90018 90022 So, the direct relation for the P-V wavefront error of the primary astigmatism of a concave mirror can be written as: 90018 90018 90004 W 90005 a 90006 = 90005 α2 90006 d 90005 2 90006 / R = 90005 α2 90006 D / 8F = h 90005 2 90006 / 8fF 90005 2 90006 (18.3) 90022 90005 Shift to the best focus location 90006 is half the longitudinal aberration from either of the two line foci.In terms of the peak aberration coefficient 90005 A 90006, the needed wavefront error of defocus from either tangential or sagittal focus to best focus location is (A / 2). While the P-V error remains unchanged for all three focus locations — sagittal, tangential and midway between these two — the latter has the RMS wavefront error smaller by a factor of 2/90005 √ 90006 6. As a result, this focus location has has the highest peak diffraction intensity, making it the best focus location.90018 90022 The best focus RMS wavefront error in terms of the peak aberration coefficient — or P-V wavefront error — is given by: 90018 90004 90005 ωa 90006 90018 = A / 24 90005 1/2 90006 (19) 90022 Thus the P-V wavefront error of astigmatism corresponding to the diffraction limited RMS of ω = 1/1801/2 is W 90005 a 90006 = (24/180) 1/2 = 0.365, in units of the wavelength. 90018 90022 It should be noted that for astigmatism, and aberrations in general, the point of minimum wavefront deviation does not coincide with the point of PSF maximum, i.e. diffraction focus, when the aberration exceeds certain level. For aberrations in general, significantly over 1/2 wave P-V. Specifically for astigmatism, the PSF peak at the mid focus becomes slightly lower than those at the tangential and sagittal foci — despite the former still retaining lower RMS wavefront error — at 1 wave P-V (Left). With further P-V error increase, the mid focus PSF peak sinks lower vs. tangential / sagittal, down to six times lower intensity at 2 waves P-V (The overall pattern is similar to the longitudinal PSF peak shift with spherical aberration, only with significantly larger maximum-to-mid-focus PSF peak differential).Minimum wavefront error is always for defocus P-V error half that of astigmatism, i.e. at the mid focus, but for errors larger than 1 wave P-V PSF peaks in the proximity of tangential and sagittal focus. PSF peak at the mid focus at 2 waves P-V is identical to that at 3 waves, despite the P-V / RMS error being 50% larger for the latter. Presence of a larger central obstruction alters longitudinal intensity distribution in a way that the shift occurs at somewhat less than 1 wave P-V, with the peak-to-mid-focus differential greater at 1 wave P-V, but smaller at 2 waves.90018 90022 Note that plots are for negative astigmatism, with the tangential focus closer to the objective than sagittal. 90018 90022 The form of the aberration coefficient shows that the astigmatism wavefront error, unlike coma and spherical aberration, does not change with object distance. This is expected consequence of astigmatism of a mirror — as well as that of a lens (contact) objective — being a result of the asymmetry of wavefront projection onto the surface, rather than a product of the wavefront / surface interaction.90018 90022 Astigmatism 90005 ray aberrations 90006 can also be expressed in terms of the peak aberration coefficient 90005 A 90006 as: 90018 L = 8AF 90005 2 90006, 90005 90006 T = 4FA 90005 90006 and 90005 90006 T 90005 a 90006 = 4A / D 90005 90006 (20) 90022 for the 90023 longitudinal 90024, 90023 transverse 90024 and 90023 angular 90024 astigmatism, respectively (the last two as the circle of least confusion diameter).After substituting for 90005 A 90006 and mirror aberration coefficient 90005 a 90006, the mirror transverse aberration — as the circle of least confusion diameter — can be also expressed as T = -Dα2 / 2 = -H3 / 2DF2 for object at infinity, with 90005 h 90006 being the point height in the image plane (Note that aperture 90005 D 90006 needs to be in the metric used for the coefficient calculation, which also becomes the metric of transverse aberration).Since focal lengths of the astigmatic wavefront do not change with the height in the pupil (i.e. the zonal height), transverse astigmatism changes in proportion to the normalized pupil ray height 90005 ρ 90006. With h = α, 90041 being the focal length, angular astigmatism 90005 T 90006 90005 a = T / = 90006 α 90005 2 / 2F 90006, where 90005 F 90006 is the focal ratio number F = / D. Longitudinal astigmatism 90005 L = — 90006 α 90005 2 90006. 90018 90022 There are simple geometric relationships between the 90023 circle of least confusion 90024 diameter and the 90023 sagittal 90024 and 90023 tangential line length 90024, as well as between the three and the 90023 longitudinal aberration 90024.The line length is double the circle diameter, and the longitudinal aberration is numerically greater than either line by a factor of 90005 F 90006 (The focal ratio), as illustrated in 90005 FIG. 44 90006. 90018 90022 The transverse aberration in terms of the RMS wavefront error is 90005 T 90006 90005 a = ω√384 / 2.44 90006, and in terms of the peak-to-valley error 90005 T 90006 90005 a = 4A / 2.44 90006 (for 90005 ω 90006 and 90005 A 90006 in units of the wavelength), both expressed in units of the Airy disc diameter.That makes the astigmatic geometric blur significantly smaller for given amount of wavefront aberration than geometric blur for either spherical aberration or coma (90005 FIG. 45 90006). It is a stark remainder that optical criteria can not be reduced to geometrical considerations; it is the underlying realm of electromagnetic field that determines the properties of the point object image. 90018 90004 90005 FIGURE 45 90006: The ray spot size (top) and actual diffraction patterns for 0.37 wave P-V wavefront error of primary astigmatism (resulting in 0.80 Strehl, thus comparable to 1/4 wave P-V of primary spherical aberration). Perfect diffraction pattern is to the left. Geometric blur diameter at the best focus location (balanced primary astigmatism) is only 0.6 Airy disc diameters. There is no rays outside the Airy disc, yet considerable amount of energy has spread out from the spurious disc — result of the complex wave interference around best focus point (not unexpected, considering that rays focused to a point still produce a pattern).Compared to spherical aberration and coma, the energy spread is concentrated closer to the disc. 90018 90022 As expected due to its uniformly dense geometric blur, the smallest RMS blur radius for astigmatism is at the location of the circle of least confusion. It is given by rRMS = FA 90005 √ 90006 2, or smaller by a factor of 90005 √ 90006 0.5 than the radius of the circle of least confusion. In units of the Airy disc diameter, the RMS blur diameter is RRMS = A 90005 √ 90006 2/1.22, for the peak aberration coefficient 90005 A 90006 in units of the wavelength. 90018 90022 In terms of the RMS wavefront error of astigmatism 90005 ωa 90006, the RMS blur diameter in units of Airy disc diameter is RRMS = 4 90005 √ 90006 3ω 90005 a 90006 /1.22. 90017 90018 90022 90005 EXAMPLE 90006: A 200mm / 5 concave mirror, d = 100, R = -2000, F = 5. Setting θ = 0 and ρ = 1, the 90005 peak wavefront error 90006 at h = 1.4mm off-axis, giving the field angle α = 1.4 / 1000 = 0.0014, is 90005 W 90006 = A / 2 = α2d2 / 2R = -0.0000049mm. The 90005 P-V wavefront error 90006 is twice greater — equal to the peak aberration coefficient — or -0.0000098mm. In units of 550nm (0.00055mm) wavelength, it is 0.0178, or 1/56 wave. Consequently, the 90005 RMS wavefront error 90006 90005 ω 90006 = A / 90005 √ 90006 24 = 0.000002mm or, in units of 550nm wavelength, 1/275 wave. The 90005 transverse astigmatism 90006 (circle of least confusion diameter) is 90005 T 90006 = 4FA = 20α2d2 / R = = 0.000196mm, or 0.03 Airy disc diameters, and 90005 angular astigmatism 90006 90005 Ta 90006 = T / is 0.000000196 radians, or 206.265×0.000000196 = 0.04 arc seconds. 90018 90022 Since both, wavefront error and geometric (ray) aberrations are directly proportional to the aberration coefficient, it implies that they are in a constant proportion themselves. In other words, doubling the wavefront error also doubles the geometric aberration.90018 90022 The RMS blur radius rRMS = FA 90005 √ 90006 2 = 0.0000098mm, and the RMS blur diameter in units of the Airy disc diameter is RRMS = A 90005 √ 90006 2 / 1.22 = 0.0207, for 90005 A 90006 in units of the wavelength. 90018 90022 Aberration coefficient of astigmatism does not change with 90005 object distance 90006. For relatively close objects, transverse astigmatism increases as i /, 90041 90005 i 90006 being the image-to-pupil separation.However, it does not affect the wavefront error: since the wavefront radius is also longer by the same ratio, identical nominal wavefront error results in proportionally greater longitudinal and transverse aberration. 90018 90022 For the 90005 aperture 90006 90005 stop displaced 90006 from mirror surface, the aberration coefficient of astigmatism changes in proportion to Kσ2 + (1-σ) 2, with 90005 σ 90006 being the mirror-to-stop separation (positive in sign) in units of the mirror radius of curvature.The astigmatism aberration coefficient is: 90018 90004 90018 90022 Needed stop separation for zero astigmatism is given by σ = [1 90005 √ 90006 | K |] / (K + 1). Thus, astigmatism is canceled for σ = 0.5 with a paraboloid and σ = 1 with a sphere. The relation is not defined for K = -1 (parabola), but implicates σ = 0.5 limit for 90005 K 90006 approaching -1. For positive values of the conic 90005 K 90006, the aberration coefficient can not be zero regardless of the stop position, since both Kσ2 and (1-σ) 2 are positive.90018 90022 Unlike coma, change in astigmatism caused by displaced aperture stop is independent of object distance. 90018 90022 Aberration coefficient of primary astigmatism for a 90005 lens 90006 with the aperture stop at the surface is identical to the one given for concave mirror (90005 Eq. 19.1 90006), with the radius of curvature 90005 R 90006 replaced by 2 (Eq. 99), 90005 90006 being the lens ‘focal length. For a contact doublet, it gives the peak aberration coefficient as a sum of the aberration coefficients at the first and second lens, respectively, as: 90018 90004 90018 90022 with 90005 α 90006 being the field angle, and 90005 90006 90005 1 90006, 90041 90005 2 90006 the respective lens focal lengths (keep in mind that focal length of a negative lens is numerically negative in the left-to-right Cartesian coordinate system).Change of the stop position results in change of the aberration coefficient only with systems not corrected for spherical aberration, or coma, or both. Since modern refractor objectives commonly are aplanats, their astigmatism is not affected by the stop position. As already mentioned, wavefront error of astigmatism of the contact doublet does not change with object distance. 90018 90022 Strongly curved surfaces give rise to higher order aberrations, and astigmatism is no exception.Although relatively rare in amateur telescopes, 90005 secondary (higher-order) astigmatism 90006 can be significant in systems with sub-aperture correctors, as well as in eyepieces. Unlike the P-V wavefront error of primary astigmatism, which is at either sagittal or tangential focus described with quadratic function (parabola, blue plot on 90005 FIG. 46 90006 left), that of secondary astigmatism, given as W 90005 a 90006 = Aρ4cos2θ, is quartic (4th power) function with a single turning point (red plot on 90005 FIG.46 90006 left). The shape of wavefront deviation is generally similar to that of primary astigmatism, but its near-cylindrical form has larger near-flat middle area and more strongly curved edges. The wavefront shape implies that secondary astigmatism forms longer sagittal / tangential focus lines when unbalanced, or balanced with defocus. 90018 90004 90005 FIGURE 46 90006: The form of wavefront deviation of secondary (higher-order) astigmatism (red) vs.that of primary astigmatism (blue). For given P-V wavefront error, the secondary astigmatism deviation, in its pure form (left), is flatter for central zones, and steeper toward the edges. Balanced with defocus alone, it takes a form similar to balanced primary astigmatism (shaded gray), only the saddle is flatter. It is minimized when balanced w / primary astigmatism 90018 90022 Similarly to that of the primary, the error of secondary astigmatism at either sagittal or tangential focus (left; tangential focus has the same shape simply rotated by 90 about vertex) is reduced by refocusing to the best focus midway between them (right).In either case, the P-V error remains the same, but the RMS error is reduced, and smaller for given P-V error for secondary astigmatism at both focus location. 90018 90022 The more efficient way of minimizing secondary astigmatism is, however, balancing it with the lower-order form of opposite sign. The error is minimized with adding the primary astigmatism with the peak coefficient smaller by 25%, with W 90005 as 90006 = A (ρ4-0.75ρ2) cos2θ, implying that the P-V error of of secondary astigmatism balanced with the lower-order form is smaller by a factor of 0.25 (fourfold) than at either sagittal or tangential focus. The RMS error is smaller than that of balanced primary astigmatism of identical P-V error by a factor 90005 √ 90006 0.6. 90018 90022 However, due to the different rates of aberration increase for the two astigmatism forms (2nd vs. 4th power of field angle for the primary and secondary form, respectively) this optimized balancing is only possible at a narrow field zone.Usually, primary astigmatism is left to be larger initially, with the two forms balancing farther off axis and secondary astigmatism quickly becoming dominant after that. 90018 90004 90017 ◄ 4.2. Coma ▐ 4.4.Defocus ► 90018 90004 Home | Comments 90017 90018 90018 90473 90474.90000 Astigmatism 90001 90002 90003 Astigmatism 90004 is a common vision condition that causes blurred vision. It occurs when the cornea (the clear front cover of the eye) is irregularly shaped or sometimes because of the curvature of the lens inside the eye. 90005 90002 An irregularly shaped cornea or lens prevents light from focusing properly on the retina, the light-sensitive surface at the back of the eye.As a result, vision becomes blurred at any distance. This can lead to eye discomfort and headaches. 90005 90002 Astigmatism frequently occurs with other vision conditions like myopia (nearsightedness) and hyperopia (farsightedness). Together these vision conditions are referred to as refractive errors because they affect how the eyes bend or «refract» light. 90005 90002 There are many causes to astigmatism. It can be hereditary and is usually present from birth. It can decrease or increase over time.90005 90002 A comprehensive optometric examination will include testing for astigmatism. If necessary, your optometrist can provide eyeglasses or contact lenses that correct the astigmatism by altering the way light enters the eyes. 90005 90002 Another option for treating astigmatism is a corneal procedure called orthokeratology (ortho-k). In this painless, noninvasive procedure, the patient wears a series of specially designed rigid contact lenses to gradually reshape the curvature of the cornea.90005 90002 Laser surgery can also treat some types of astigmatism. The laser changes the shape of the cornea by removing a small amount of eye tissue. 90005 90002 90019 90005 90021 What causes astigmatism? 90022 90023 90002 The curvature of the cornea and lens bends the light entering the eye in order to focus it precisely on the retina at the back of the eye. In astigmatism, the surface of the cornea or lens has a somewhat different curvature. 90005 90002 the surface of the cornea is shaped more like a football instead of round like a basketball, the eye is unable to focus light rays to a single point.Vision becomes out of focus at any distance. 90005 90002 In addition, the curvature of the lens inside the eye can change, resulting in an increase or decrease in astigmatism. This change frequently occurs in adulthood and can precede the development of naturally occurring cataracts. 90005 90002 Sometimes astigmatism may develop following an eye injury or eye surgery. 90005 90002 Astigmatism also occurs due to a relatively rare condition called keratoconus in which the cornea becomes progressively thinner and cone-shaped.This results in a large amount of astigmatism, which causes poor vision that can not be clearly corrected with eyeglasses. People with keratoconus usually need contact lenses for clear vision and eventually may need a corneal transplant. 90005 90021 How is astigmatism diagnosed? 90022 90036 90002 An optometrist can diagnose an astigmatism through a comprehensive eye examination. Testing for astigmatism measures how the eyes focus light and determines the power of any optical lenses needed to improve vision.This examination may include: 90005 90039 90040 90003 Visual acuity 90004 -When you read letters on a distance chart, you are measuring your visual acuity. Visual acuity is given as a fraction (for example, 20/40). The top number is the standardized testing distance (20 feet) and the bottom number is the smallest letter size read. A person with 20/40 visual acuity would have to get within 20 feet to read a letter that should be seen clearly at 40 feet. Normal distance visual acuity is 20/20.90043 90040 90003 Keratometry / Topography 90004 -A keratometer is the primary instrument used to measure the curvature of the cornea. By focusing a circle of light on the cornea and measuring its reflection, it is possible to determine the exact curvature of that area of the cornea’s surface. This measurement is particularly critical in determining the proper fit for contact lenses. A corneal topographer, which is gaining use, generates a contour map of the cornea and provides even more detail of the cornea’s shape.90043 90040 90003 Refraction 90004 -Using an instrument called a phoropter, your optometrist places a series of lenses in front of your eyes and measures how they focus light. This is performed using a handheld lighted instrument called a retinoscope or an automated instrument that evaluates the approximate focusing power of the eye. Based on your responses, the power is then refined to determine the lenses that allow the clearest vision. Despite improved technology, patient input remains integral in determining vision needs.90043 90052 90002 With the information from these tests, your optometrist can determine if you have astigmatism. Your optometrist will use these findings, combined with those of other tests performed, to determine the power of any lens correction you need to provide clear, comfortable vision. Once testing is complete, your optometrist can discuss treatment options. 90005 90021 How is astigmatism treated? 90022 90057 90002 People with astigmatism have several options to regain clear vision.They include: 90005 90039 90040 90003 Eyeglasses. 90004 People with astigmatism primarily choose eyeglasses to improve their vision. The eyeglasses contain a special cylindrical lens prescription that compensates for the astigmatism. This provides additional power in specific parts of the lens. 90002 Generally, a single-vision lens is prescribed to provide clear vision at all distances. However, patients over age 40 who have presbyopia may need a bifocal or progressive addition lens.90005 90043 90040 90003 Contact lenses. 90004 Some people will have better vision with contact lenses rather than eyeglasses. Contact lenses may provide clearer vision and a wider field of view. However, since contact lenses are worn directly on the eyes, they require regular cleaning and care to safeguard eye health. 90002 Standard soft lenses may not be effective in correcting astigmatism. However, special toric soft contact lenses can correct for many types of astigmatism. Because rigid gas-permeable contact lenses maintain their regular shape while on the cornea, they can compensate for the cornea’s irregular shape and improve vision for people with astigmatism.90005 90043 90040 90003 Orthokeratology. 90004 Orthokeratology (ortho-k) involves the fitting of a series of rigid contact lenses to reshape the cornea. The patient wears contact lenses for limited periods, such as overnight, and then removes them. People with moderate astigmatism may be able to temporarily obtain clear vision without lenses for most of their daily activities. Orthokeratology does not permanently improve vision. If patients stop wearing the retainer lenses, their vision may return to its original condition.90043 90040 90003 Laser and other refractive surgery procedures. 90004 Astigmatism can also be corrected by reshaping the cornea through LASIK (laser in situ keratomileusis) or PRK (photorefractive keratectomy). PRK removes tissue from the superficial and inner layers of the cornea. LASIK removes tissue only from the inner layer of the cornea. 90043 90052 90002 If you have an astigmatism, you have a wide range of options to correct your vision problem. In consultation with your optometrist, you can select the treatment that best meets your visual and lifestyle needs.90005 .