Что такое DX, DY? — Русские Блоги

Начнем с дифференциации кривой.

1 Дифференциал кривой

Например, есть кривые :

приКривая секция:

Чтобы найти отрезок прямой линии для аппроксимации этого отрезка кривой, то есть найти дифференциал этого отрезка кривой:

Характерной чертой этой дифференциации является то, что когдаПо мере приближения к сегментам кривой:

2 Касательная

Эта дифференциация на самом деле является касательной.

2.1 Первые впечатления

При изучении геометрии касательные определяются следующим образом:

Например, это тангенс круга и эллипса:

Но это определение не действительно для всех кривых:

2.2 Предел секущей

Нам нужно определить касательные с пределами. Например, кривая требованийвТочка касательная:

вИщите что-то поблизостиПроведите прямую линию после двух точекЭта прямая линия также называется секущей линией:

Тогда ищииТочка междуСделать секущу ：

И так далее, чтобы найти точкуСделать секущу:

Сгруппируйте эти секущиеся строки в ряд:

Его пределыЭто касается:

3 производных

Определение касательной было только что дано, но касательная не может быть получена. Давайте посмотрим, как его найти.

3.1 Склон

притязаниеТочка касательная, понялКоординаты точкиИ наклон касательной:

Из которыхВ соответствии с формулой уклона прямой линии, функция тангенса может быть получена. ：

Вы можете получить функцию тангенса.

3.2 Производные

Легко сделать следующие выводы:

Итак, давайте посмотрим, как найти наклон секущей. Гипотетические требованияНаклон касательной в точке, просто посмотрите вокругСделать секущу:

Вы можете увидеть, когдаВ то же время (это также показывает, что касательная линия является пределом секущей линии), склоны этих двух объектов постоянно приближаются:

Сначала отрежьте наклон секущейРассчитано, предположим ：

Поэтому:

По данным анализа только сейчас:

Этот предел называется 。

Если не толькоТочки могут касаться, то есть не толькоТочки дифференцируемы, но в определенном открытом интервалеМожно ориентироваться внутри, это ：

Многие учебники и документы будут содержать следующие символы, которые также представлены здесь:

ОпределенияназываемыйПроизводная функция может быть выражена как:

Иногда пишуIndicating, указывая, что для независимых переменныхИщите руководство.

Оператор, «оператор» на английском языке, означает операцию.

Операторы и функции все еще очень близки со следующими различиями:

Здесь,Оператор завершает сопоставление между следующими функциями:

4 Касательные и дифференциальные функции

Хорошо, теперь, когда у нас есть производная, мы можем найти касательную функцию и дифференциальную функцию.

4.1 Касательные функции

Что касается касательных,Я также знаю, что наклон является производнойКасательная функция прямой

4.2 Дифференциальные функции

Хотя было сказано, что касательные являются дифференциалами, дифференциальные функции и функции касательных различны, поскольку они находятся в разных системах координат. Давайте шаг за шагом и проясним этот ключевой момент.

Первый заказКасательная функция становится:

Тогда вУстановите прямоугольную систему координат для начала координат (назовем ее дифференциальной системой координат):

сВ дифференциальной системе координат, где точка является началом координат,, Это делает уравнение касательной в дифференциальной системе координат простым:

После ряда операций мы наконец получили дифференциальную функцию:

Математически использовать символ для ряда операцийПредставлять, также известный как ：

дифференцированныйОператор выполняет следующие сопоставления функций:

Таким образом, дифференциальная функция также записывается:

Оригинальная функцияпоОперация стала дифференциальной функциейЭто также различает дифференциальные функции иСистема координат другая.

потому чтоПеременная, такНа самом деле представляет собой целоеОсь:

потому чтоОт имениПрямая линия оси и дифференциация прямой, согласно идее прямой музыки, сама по себе, так что:

Итак, это алгебраическая форма дифференцирования:

Разница между касательной функцией и дифференциальной функцией заключается в том, что первая находится вВ системе координат последнийВ системе координат:

Поскольку алгебраическая форма дифференцирования является такой же, как выше, производная также может быть записана как:

Таким образом, производная также называется «дифференциальный фактор», который является частным дифференцирования и дифференциации.

4.3 Дифференциально-независимые и зависимые переменные

В этом разделе всегда говорилось, что дифференцирование является функцией:

Так каковы его независимые переменные и каковы зависимые переменные?

Дифференциальная функция вВ системе координат пустьПосле возвращенияСистема координат:

Видно, что независимые переменныеЗависимая переменная 。

Если не толькоДифференцирование точек аналогично производной функции.

Чтобы найти дифференциал открытого интервала, дифференциальная функция является бинарной функцией:

4.4 Дифференциал является линейной функцией

Хотя обе являются прямыми линиями, из-за разных систем координат, существует большая разница между функцией тангенса и дифференциальной функцией:

Эта разница иллюстрирует:

В соответствии с тем, что дифференцирование является линейной функцией, мы можем легко использовать знание линейной алгебры для решения нормальной функции.

4.5 Нормальная функция

Линия, перпендикулярная касательной в точке касания, является нормальной:

НадетьВ системе координат два вектора направления касательного и нормального направления находятся случайным образом:

То есть (t обозначает касательную, n обозначает нормальную, то есть касательную и нормальную для английского соответственно):

Согласно знанию линейной алгебры, мы знаем, что скалярное произведение двух ортогональных векторов равно 0, поэтому:

Итак:

Знай нормальный уклон и знайВы можете найтиНормальная функция в системе координат:

Последнюю версию можно найти по адресу:Что такое DX, DY?

Что такое dx в интегралах

Здравствуйте, дорогие студенты вуза Аргемоны!

Мы с вами закончили подкурс, посвящённый непосредственно функциям, а теперь переходим к интегралам. И оставшиеся два модуля будут посвящены именно им.
Для начала нам, конечно, необходимо будет ознакомиться с самим заклинанием «Интеграл». Постараюсь вам рассказать про него как можно проще. Мы не будем вдаваться глубоко в механизм действия этого заклинания. Нам достаточно научиться им пользоваться в не самых сложных случаях.

Это заклинание по действию обратно заклинанию «производная», однако есть небольшие ньюансы. При действии заклинания «интеграл» получается не одна функция, а целое семейство (они ещё называются первообразными), которые отличаются друг от друга лишь наличием константы, обеспечивающей параллельный перенос функции по вертикали.

Если мы применим ко всему семейству таких функций F(x)+C (где C=const) заклинание «производная», то результатом будет функция f(x), потому что производная от константы равна 0 (C’=0).

Давайте рассмотрим более пристально заклинание «интеграл». Оно состоит из трёх частей:
– значка интеграла (∫),
– подынтегральной функции (f(x))
– и так называемого дифференциала dx, который нам будет очень хорошо помогать при выполнении заклинания.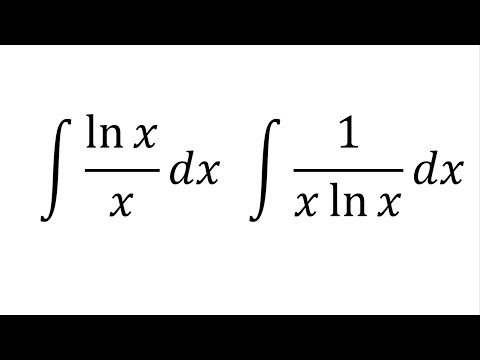

Действие дифференциала чем-то похоже на действие заклинание «производная», потому что

Ну и, соответственно, чтобы занести какую-то функцию под дифференциал, надо вычислить её первоообразную

g(x)*dx=d(G(x)), где G(x) – одна из первоообразных функции g(x).

Понятно, что dx=d(x+2)=d(x-7), то есть добавлять константу в качестве слагаемого под дифференциал (если это нужно) можно безболезненно.

d(k*f(x))=k*d(f(x)), где k=const, то есть из-под дифференциала можно выносить множитель-константу. Или заносить, если это надо.

Не пугайтесь, если на данный момент вы смутно поняли объяснение. Дальше мы разберём всё подробнее, а пока представляю вам табличку интегралов основных элементарных функций (ТИОЭФ)

и основные правила вычисления интегралов (ОПВИ)

А теперь давайте на примерах изучим, как пользоваться этим заклинанием.

Видно, что интеграл подходит под формулу 6 ТИОЭФ, но, к сожалению, степень 2 и то, что под дифференциалом, не совпадает, а совпадать должно в обязательном порядке. Только тогда заклинание придёт в действие. Значит, нам сейчас надо сделать некие преобразования, чтобы достичь такого равновесия.

1-й способ. Пригоден для более опытных в таких преобразованиях магов.
Ставим под дифференциал 3х-1, но чтобы уравновесить всю конструкцию, нам надо всё поделить на 3

Если мы выполним заклинание «дифференциал», то получим наше исходное выражение

Значит, преобразование сделано верно.

Если не видно сразу, на что надо поделить или умножить, то просто делаем замену переменных. Вместо х введём другую переменную

Подставляем всё, применяем 1-е правило ОПВИ и получаем табличный интеграл. Вычислив его, необходимо сделать обратную замену

Замену полезно делать, чтобы избавиться от сложных выражений. Например, вот тут

В 7-ю степень возводить очень хлопотливо (чтобы всё привести к многочлену), поэтому делаем вот такую замену

Таким образом, степень 7 оказалась около простой переменной.

Очень интересный метод интегрирования по частям.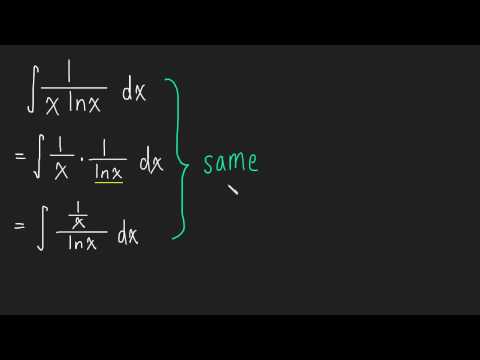 x, а какая-либо тригонометрическая функция совместно со степенным выражением.

Иногда в результате применения такого заклинания мы возвращаемся вроде как к началу, но с некоторым довеском. Например,

При работе с тригонометрическими функциями полезно применять небольшие заклинания, позволяющие понизить степень:

А также не забывать об основном тригонометрическом тождестве, которое позволяет при необходимости выразить одну функцию через другую

Ну, думаю, нам этих сведений вполне хватит для того, чтобы применять заклинание «интеграл» к несложным функциям.

А теперь домашнее задание.
Выберите, на свой вкус, 10 функций из предложенных и примените к ним заклинание «интеграл».

Отправляйте работы через ЛИЧНЫЙ КАБИНЕТ
Свои вопросы смело можете передать с Персефоной

Таблица интегралов представляет собой набор интегралов от различных функций, таких как:

Эти интегралы в основном от элементарных функций и эта таблица приведена ниже:

В колонках этой таблицы:

• В этой таблице в первой колонке приведен интеграл и чему он равен
• Во второй колонке таблицы находится описание этого интеграла в словах
• В третье колонке приведены примеры, как же пользоваться калькулятором интегралов

Получается, что ваша задача здесь научиться не только пользоваться таблицей интегралов, но и научиться вычислять интегралы с помощью калькулятора онлайн на этом сайте kontrolnaya-rabota.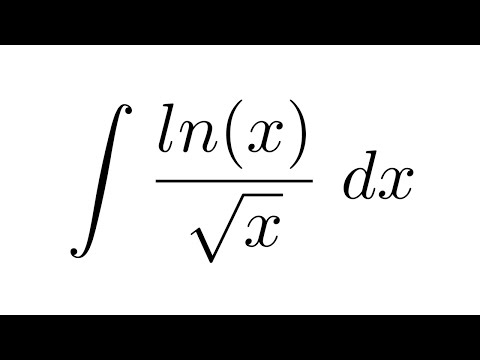 ru. Сам калькулятор интегралов находится по ссылке решение интегралов онлайн. Самое интересное, он умеет выдавать не только ответ, но и подробное решение бесплатно!

Пожалуйста, пишите, что вам не понятно будет на почту [email protected] о недостатках данной таблицы, чтобы вы хотели видеть еще здесь.

Видео примеры по использованию таблицы

Определение. Функция F(x) называется первообразной от функции f(x) на отрезке [a;b] , если во всех точках этого отрезка выполняется равенство F`(x) = f(x) .

(1 – cos x)` = sin x

Функция f(x) непрерывная функция на отрезке [a;b] .

Теорема . Если функция F 1 (x) b F 2 (x) – две первообразные от функции f(x) на отрезке [a;b] , то разность между ними равна постоянному числу.

F 2 `(x) = f(x) , то F 1 `(x) – F 2 `(x) = Const .

φ ` ( x ) = F 1 ` – F 2 ` = 0

F 1 (x) – F 2 (x) = φ( x ) (2)

Тогда на основании равенств (1) будет:

F 1 `(x) – F 2 ` ( x ) = f(x) – f(x) = 0 или φ ` ( x ) = [F 1 (x) – F 2 (x)]` = 0 при любом значении x на отрезке [a;b] . Но из равенства φ ` ( x ) = 0 следует, что φ( x ) есть постоянная.

Действительно , применим теорему Лагранжа к функции φ( x ), которая, очевидно, непрерывна и дифференцируема на отрезке [a;b] . Какова ни была точка x на отрезке [a;b] , мы имеем в силу теоремы Лагранжа.

φ ( x ) – φ ( a ) = φ ` ( x ) (x-a) , где a x x .

Так как φ ` ( x ) = 0, то φ ( x ) – φ ( a ) = 0 или φ ( x ) = φ ( a ) (3)

Таким образом, функция φ( x ) в любой точке x отрезка [a;b] сохраняет значения φ( a ) , а это значит, что функция φ( x ) является постоянной на отрезке [a;b] . Обозначая постоянную φ( a ) через С, из равенств (2) , (3) полу ч аем :

Определение. Если функция F (x) является первообразной для f (x) , то выражение F (x) + С называется неопределённым интегралом от функции f (x) и обозначается символом ∫ f (x) dx. Таким образом, по определению,

∫ f (x) dx = F (x) + С, если F (x) = f (x) .

При этом функцию f (x) называют подынтегральной функцией, f (x) dx – подынтегральным выражением, знак ∫ – знаком интеграла.

Из этого определения следуют свойства:
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е. если F`(x) = f (x) , то и

( ∫ f (x) dx )` = (F (x) + C)` = f (x) (4)

Последнее равенство нужно принимать в том смысле, что производная от любой первообразной равна подынтегральной функции.

2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

d ( ∫ f (x) dx ) = f (x) dx (5)

Это получается на основании формулы (4)

3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Справедливость последнего равенства легко проверить дифференцированием (дифференциала от обоих частей равенства равны dFx) )

Таблица неопределённых интегралов.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

Интегрирование – есть линейная операция.

1. ∫ [f 1 (x) + f 2 (x)] dx = ∫ f 1 (x) dx + ∫ f 2 (x) dx

∫ a f (x) dx = a ∫ f (x) dx

2. ∫ f (x+c) dx = F (x+c) + C

3. Подстановка. 1-ый способ вычисления неопределённых интегралов.

x = φ (t), тогда ∫ f ( φ (t)) φ ` (t) dt = F (x) + C = ∫ f (x) dx

x = φ (t) dx dt = φ `

Интегрирование по частям.

Пусть u и v – две дифференцируемые функции от x . Тогда, как известно, дифференциал произведения uv вычисляется по следующей формуле:

Отсюда, интегрируя, получаем:

Последняя формула называется формулой интегрирования по частям. Эта формула чаще всего применяется к интегрированию выражений, которые можно так представить в виде произведения двух сомножителей u и dv , чтобы отыскание функции v по её дифференциалу dv и вычисление интеграла ∫ v du составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла ∫ u dv .

Пример. ∫ x sin x dx = ∫ – x cos x + ∫ cos x dx = -x cos x + sin x + C

код | это… Что такое DX-код?

DX-код на кассете. ISO 125, 24 кадра, регулировка экспозиции +3 -1

Штрих-код на краю плёнки

Считыватель DX-кода в камере.

DX-код (от англ. Digital indeX — цифровое обозначение) — стандарт ANSI для маркировки плёнок и кассет типа 135 или APS. Стандартная маркировка состоит из 3 частей, описываемых ниже.

Содержание 1 Штрих-код на кассете 2 Штрих-код на краю плёнки 3 Код на кассете 4 Примечания 5 Ссылки

Штрих-код на кассете

Находится рядом с щелью для выхода плёнки.

Представляет собой штрих-код (кодирование 2/5) и читаемый номер, в котором зашифрованы следующие данные:

• DX-номер
• количество кадров
• код производителя

DX-номер, присваиваемый организацией I3A, обозначает конкретного производителя и тип плёнки.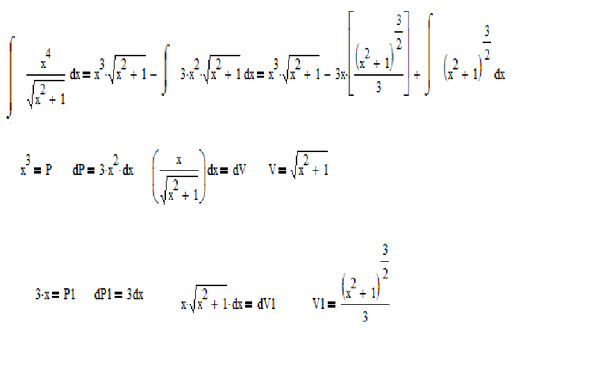 Исходя из этих данных, фотолабы выясняют необходимые условия процесса проявки отснятой плёнки ^[1].

Штрих-код на краю плёнки

Находится на краю каждого кадра ниже уровня перфорации.

Штрих-код невидим до процесса проявки, он оптически запечатлён как скрытое изображение на этапе производства. Используется фотолабами для определения границ кадра и правильной ориентации перед печатью.

Состоит из двух параллельных линейных штрих-кодов

• синхронизация
• кодирование типа плёнки, кода производителя, номера кадра

Код на кассете

Находится на кассете, выглядит как таблица 6×2, составленная из черных и белых прямоугольников.

Белые прямоугольники представляют собой открытый металл кассеты и проводят электрический ток. Чёрные прямоугольники являются закрашенными областями и не проводят ток. Таким образом возможно организовать двоичное кодирование некоторой информации, которая передаётся в фотоаппарат посредством электрического считывающего устройства.

Из этой таблицы фотоаппарат может получить данные о чувствительности плёнки, количестве кадров и фотографической широте. Первым фотоаппаратом с технологией распознавания DX-кода был Konica TC-X, выпущенный в 1985 году.

Общий вид таблицы:

З	Ч1	Ч2	Ч3	Ч4	Ч5
З	Д1	Д2	Д3	К1	К2

• З — земля, два самых левых контакта в каждом ряду
• Ч — чувствительность, поле длиной 5 бит, кодирующее 32 варианта чувствительности плёнки, из которых используются только 24 (в единицах ISO от 25 до 5000), при этом порядок двоичного исчисления не соблюдается
• Д — длина плёнки в кадрах, поле длиной 3 бита, кодирует 8 вариантов длины плёнки, из которых обычно используются 4 (от 12 до 36)
• К — фотографическая широта, поле длиной 2 бита, кодирует 4 диапазона фотографической широты

Скорость

Чувствительность ISO	1-й ряд контактов DX
25/15°
32/16°
40/17°
50/18°
64/19°
80/20°
100/21°
125/22°
160/23°
200/24°
250/25°
320/26°
400/27°
500/28°
640/29°
800/30°
1000/31°
1250/32°
1600/33°
2000/34°
2500/35°
3200/36°
4000/37°
5000/38°
custom 1
custom 2
custom 3
custom 4
custom 5
custom 6
custom 7
custom 8

Длина плёнки

Кадров	2-й ряд контактов DX
нестандартная
12
20
24
36
48
60
72

Регулировка чувствительности

Значение регулировки (в f-стопах)	2-й ряд контактов DX
±½
±1
+2 -1
+3 -1

Примечания

Ссылки

•  (рус. ) DX-код. Научно-технический центр Красногорского завода имени С. А. Зверева.
•  (англ.) Java-апплет для создания и расшифровки DX-кодов

Расчет

— Что такое $dx$ в интеграции?

Интеграл дает площадь между горизонтальной осью и кривая. В большинстве случаев это ось x.

 г
                         | |
                       --|-- ----|---- f(x)
                     / | \ / |
                    / | -------- |
          | / | |
     -----|------- | |
          | | |
          | | |
----------|---------------+--------------------|--- -- Икс
        а б
 9b_a f(x) dx$ 
 
 Но скажем, вы не хотите использовать интеграл для измерения
область между осью x и кривой. Вместо этого вы просто
вычислить среднее значение графика между a и b
и нарисуйте прямую плоскую линию y = avg(x) (среднее
значение x в этом диапазоне). 
 
 Теперь у вас есть такой график: 
 
 y
                         | |
                       - | - - - | - - f(x)
          | / | \ / |
     -----|--------------------------------------------------|---- среднее(х)
          | / | |
     - - -|- - - - | |
          | | |
          | | |
----------|---------------+--------------------|--- -- Икс
        а б
 
 Заключенная область представляет собой прямоугольник:
 Площадь = avg(x) w, где w — ширина i секции
 Высота avg(x), а ширина w = b-a или по-английски,
«ширина среза оси x, идущей от a к b».
 Но скажем, вам нужна более точная площадь. Вы могли бы сломать
разбить график на более мелкие части и сделать из них прямоугольники.
Скажем, вы делаете 4 равные части:
 
 y
 | |
 |----|---| |-------|---- f(x)
 | | | | |
 | | |--------| |
 | | | | | |
 -----|---------| | | | |
 | | | | | |
 | | | | | |
 ----------|---------|----+---|--------|-------|--- -- Икс
 а б
 94_{n=1}avg(x,n) w$
 Но это все еще недостаточно точно. Давайте использовать
бесконечное количество разделов. Теперь наш район
становится суммой бесконечного числа разделов.
Поскольку это бесконечная сумма, мы будем использовать
знак интеграла вместо знака суммы:
 Площадь = $\int avg(x) w$
 где avg(x) для бесконечно тонкого сечения будет
равна f(x) в этом разделе, а w будет «шириной
бесконечно тонкое сечение оси x."
 Таким образом, вместо avg(x) мы можем написать f(x), потому что они
то же самое, если усреднение берется по бесконечно малой ширине.
 И мы можем переименовать переменную w во что угодно.
Ширина сечения – это разница между
правая сторона и левая сторона. Разница между
две точки часто называют дельтой этих значений.
Таким образом, разница двух значений x (например, a и b) будет
называться дельта-х. Но это слишком долго, чтобы использовать в
уравнение, поэтому, когда у нас есть бесконечно малая дельта,
это сокращено до dx.
 Если мы заменим avg(x) и w этими эквивалентными вещами:
 Площадь = $\int f(x) dx$
 Итак, что говорит уравнение:
 Площадь равна сумме бесконечного числа прямоугольников
которые имеют высоту f(x) и ширину dx (где dx — бесконечно
небольшое расстояние).
 Итак, вам нужен dx, потому что иначе вы не суммируете
прямоугольники, и ваш ответ не будет общей площадью.
 dx буквально означает «бесконечно малая ширина x».
 Это даже означает это в производных. производная от
функция представляет собой наклон графика в этой точке.
Наклон обычно измеряется как разница по оси Y двух
очки, деленные на x разность этих очков:
 Наклон = (y2 - y1) / (x2 - x1)
 Но чем ближе эти точки, тем меньше эти
получаются отличия. Давайте начнем называть их дельтами,
потому что разница между двумя точками часто
называется дельтой этих значений.
 Наклон = дельта-y / дельта-x
 Дельты становятся все меньше и меньше, как эти два x,y
точки все ближе и ближе. Когда они
бесконечно маленькое расстояние друг от друга, то дельта-y
а delta-x сокращается до dy и dx:
 Slope = dy / dx
 Наклон по-прежнему Наклон = (y2 - y1) / (x2 - x1)
но эти точки бесконечно близки друг к другу, поэтому
мы используем dy и dx, чтобы сказать себе, что они
бесконечно близкие или «дифференциальные расстояния».
 исчисление - Что означает dx в интеграле? 
 Спросил  7 лет, 3 месяца назад 
 Изменено
 7 лет, 3 месяца назад
 Просмотрено
 44k раз
 $\begingroup$
 Я знаю, что dy/dx, например, означает "производное  y  по отношению к  x ", но меня смущает другой контекст. Обычно вы просто видите термин  dx  в конце интегрального уравнения, и я просто не знаю точно, что он означает и почему он там.
 Например, если я введу в Wolfram Alpha «интеграл от 2x», он выпишет:
 Этот  dx  там! Я предполагаю, что он говорит «интеграл 2x по отношению к x»? Но зачем это вообще нужно? Разве это не подразумевается? Это раздражает, потому что это похоже на умножение, как будто это означает «2 * x * dx», и это просто вводящая в заблуждение запись. 92 ?
$$
Является ли $s$ переменной или $t$ переменной? Конечно, иногда "очевидно", что это за переменная, но это не всегда так.
 Если вы хотите узнать, что на самом деле означает $dx$, этот вопрос задавался здесь много раз. См., например, Что означает $dx$?
 $\endgroup$
 1
 $\begingroup$
 Это потому, что интеграл означает, что вы суммируете множество очень тонких прямоугольников под кривой. Высота прямоугольника равна f(x), а ширина называется $\delta x$ (эти два символа следует читать как один символ, это не означает $\delta \times x$). Таким образом, вы бы написали это так:
 $\sum f(x) \delta x$
 Знак $\Sigma$ означает сигму и означает "сумма". В интеграле вы берете предел, когда $\delta x$ стремится к нулю. Поэтому мы заменяем сигму другим типом s: $\int$. И $\delta$ меняется на d. Итак, теперь написано:
 $\int f(x) dx $
 и это «интеграл от f(x) по x». Но dx сам по себе ничего не значит.
 $\endgroup$
 $\begingroup$
 Мне лично нравится думать о знаке $\int$ и "d" в $dx$ как о левой и правой скобках: они ограничивают размер подынтегральной функции. «x» в $dx$ указывает вам переменную интегрирования.
 Существует также интуитивное понятие, заключающееся в том, что вы суммируете значения подынтегральной функции при изменении $x$ и умножаете каждое значение на маленькую «ширину», чтобы получить площадь прямоугольника, а суммируя эти площади, получаете интеграл . .. если вы берете предел, поскольку «крошечная ширина $\Delta x$ становится все меньше и меньше». «$dx$» позволяет людям неформально думать, что вы умножаете высоту $f(x)$ на «бесконечно малую ширину» $dx$, а затем получаете бесконечную сумму.
 $\endgroup$
 9n f(x_k)\Delta x_k$$
 Что имеет смысл, если вы знакомы с аппроксимацией площади под кривой фигурой, похожей на прямоугольник (суммы Римана). Вы находите сумму площадей прямоугольников, длина которых уменьшается. Когда вы берете предел, когда количество прямоугольников увеличивается до бесконечности, вы получаете площадь под кривой. Вот полезная анимация, показывающая процесс перехода $\Delta x_k$ к 0,
.
 $\endgroup$
 $\begingroup$
 9{k-1}$", "$2x$" означает то же, что и "$\left(2\frac{i}{k}\right)$", а $dx$ означает то же, что и "$\ left(\frac{i+1}{k}-\frac{i}{k}\right)$".
 Этот ход мыслей, конечно, не совсем верен, поскольку $\lim\limits_{k\rightarrow\ infty}\left(\frac{i+1}{k}-\frac{i}{k}\right)=0$, но передает идею о том, что $dx$ просто относится к произвольно малому изменению $x $
 $\endgroup$
 $\begingroup$
 Предположим, что $x$ является константой, тогда
 92+1)у+С$$. {b} f(x)\,dx$ вводится как предел сумм Римана (т.е.  определенный интеграл .) Эти подобные обозначения используются для обозначения, казалось бы, несопоставимых идей в исчислении, которые действительно согласованы только с помощью Фундаментальной теоремы (теорем) исчисления. При этом я не удивлен, что вы немного запутались. Позвольте мне попытаться прояснить ситуацию еще немного...
 Производные: 
 Прежде всего, давайте начнем с производной. Это обычно называют «мгновенной скоростью изменения», что является полным оксюмороном. На самом деле это предел средней скорости изменения, взятой за постоянно сокращающиеся интервалы «времени» (или положения и т. д.). Формально мы говорим, что  производная функции $f$ при значении $a$  является пределом
$$
f'(a):= \lim_{x\to a}\frac{f(x)-f(a)}{x-a},
$$
и обозначается как $f'(a)$ для удобства. Поскольку функция $f$ зависит от переменной (здесь мы называем эту переменную $x$), то запись Лейбница для производной при $x=a$ записывается
$$
\frac{df}{dx}(а). $$
Часть "$df$" должна сообщить читателю, что полученная функция есть $f$; в то время как часть "$dx$" должна напоминать нам, относительно какой переменной берется производная - в данном случае $x$. Часть «$(a)$» говорит вам, что производная берется по вещественному числу $a$ в домене $f$.
 Поскольку производная может (обычно) браться при многих различных значениях области, мы естественным образом расширяем идею производной  в точке  до понятия производной  как функции  . Это приводит к обозначению
$$
f'(x) \quad \text{or} \quad \frac{df}{dx}
$$
который используется для представления новой функции, значение которой  в точке  $x$ определяется производной от $f$  в точке  $x$; таким образом мы получаем (в английском смысле этого слова) совершенно новую функцию из старой.
 Вы также можете иногда встретить понятие "оператор", которое обычно выглядит как $\frac{d}{dx}(f)$. Опять же, "$d$" и "$dx$" не следует рассматривать как отдельные части дроби, а скорее как операцию $\frac{d}{dx}$ (во многом похожую на возведение в квадрат или извлечение квадратного корня). ) для выполнения функции. Таким образом, вы увидите уравнения, написанные как
$$
\frac{d}{dx}(\sin x) = \cos x.
$$
  Примечание:  В общепринятом обозначении $\frac{dy}{dx}$ также нет ничего особенного. Это означает то же самое, что и $\frac{df}{dx}$, но с дополнительной путаницей, связанной с отождествлением переменной $y$ координатной плоскости с функцией $f(x)$ через график $y = f (х)$. Я предпочитаю не учитывать $y$, если только мы не рисуем что-то явно.
 Первичные производные: 
 Обозначение
$$
\целое f(x)\,dx
$$
это немного неудобно, особенно если у вас еще нет связей между  определенными  и  неопределенными  интегралами. Вы должны интерпретировать эти символы как замену новой функции (во многом аналогично тому, как это делает $\frac{df}{dx}$), определенной в терминах $x$ со следующим свойством:
$$
F(x) = \int f(x)\,dx \iff F'(x) = f(x).
$$
То есть, если вы возьмете производную от $F(x)$  как функцию  , вы получите исходную функцию $f(x)$. Отсюда и более подходящее название «антипроизводная».
 Одно любопытное свойство первообразных производных состоит в том, что они  не  уникальны, в отличие от производных. Это связано с тем, что если $F'(x) = f(x)$, то также $\frac{d}{dx}(F(x)+C) = f(x)$ для любой константы $C$ .
 Опять же, часть "$dx$" первообразной на самом деле вовсе не "часть". Это просто для того, чтобы сообщить читателю, какая переменная является «антидифференцируемой». Удлиненная часть «S» не имеет места в нашем обсуждении, пока мы не рассмотрим связь между определенными интегралами (также известными как области под графиками функций) и неопределенными интегралами (также известными как первообразные). К сожалению, это общепринятый символ, и поэтому нам придется иметь с ним дело, хотим мы того или нет.
 Цепное правило: 
 Когда у вас есть  композиция  функций (одна функция помещена внутрь другой), вам нужно  цепное правило  для оценки производных. Условно мы говорим писать
$$
h(x) = (f\circ g)(x), \quad \text{if}\, h(x) = f(g(x)).
$$
Затем это цепное правило говорит нам
\начать{выравнивать}
h'(x) &= (f'\circ g)(x) \cdot g'(x) \\
&= f'(g(x))\cdot g'(x).
\end{выравнивание}
Другими словами: если $h$ — это композиция $f$ и $g$, то производная от $h$ — это производная от $f$, составленная из $g$ и затем умноженная на производную от $g$. . 95.
\end{align}
 В нотации Лейбница это будет записано как
$$
\frac{dh}{dx} = \frac{d(f\circ g)}{dx} = \frac{df}{dx}(g(x))\cdot \frac{dg}{dx}(x ),
$$
где нужно быть осторожным, чтобы указать, что производная от $f$ оценивается по числу $g(x)$ и  НЕ  по числу $x$. Запомнить,
$$
\frac{df}{dx}(g(x))\cdot \frac{dg}{dx}(x) \neq \frac{df}{dx} \cdot \frac{dg}{dx}.
$$
 Поскольку в композиции функций вся функция $g$ заменяет каждый экземпляр переменной $x$ в функции $f$, нередко «злоупотреблять обозначениями» и писать просто $f( g)$, где неявно подразумевается, что поскольку $g$ является функцией $x$, то и композиция должна быть функцией $x$. Таким образом, обозначениями Лейбница также можно злоупотреблять, написав
$$
\frac{d(f\circ g)}{dx} = \frac{df}{dg}\cdot \frac{dg}{dx},
$$
где $\frac{df}{dg}$ означает "взять производную от $f$, как если бы она была функцией переменной с именем $g$". Теперь должно быть ясно, почему эта наводящая на размышления «дробная» запись преобладала так долго: как будто $dg$ «отменяется» посредством умножения, оставляя только желаемое $\frac{df}{dx}$. Опять же, это не то, что на самом деле происходит, но это причина того, что нотация такая, какая она есть.
 $u$-подстановка: 
 $u$-подстановка — это просто обратная сторона цепного правила, как первообразные обратные производным. Используя обычное «интегральное» обозначение для первообразных, мы просто обратимся к предыдущему разделу, чтобы увидеть, как обратить цепное правило:
$$
\int (f\circ g)'(x) \,dx = (f\circ g)(x) + C.
$$
 Ключевая идея использования $u$-подстановки для интегрирования (т. е. антидифференцирования) состоит в том, чтобы изолировать часть функции (часть «$u$»), которая:
 находится "внутри" отдельной функции (например, $f(u(x))$)
 производная которого умножается на "внешнюю" функцию ($\cdot u'(x)$)
 Это не что иное, как простой вызов $g$ из цепного правила под другим именем, $u$:
$$
\int \big( f'(u(x))\cdot u'(x) \big) \,dx = f(u(x)) + C. $$
Идея заменить "$dx$" на "$du$" - это снова  злоупотребление нотацией  .
 Думая о композиции $f(u(x))$ просто как о $f(u)$, т. е. рассматривая $f$ как функцию переменной с именем $u$, а не переменной с именем $x$ -- мы можем злоупотреблять обозначениями Лейбница, чтобы записать приведенное выше уравнение в виде
$$
\int \frac{df}{du} \cdot \frac{du}{dx} \,dx = f(u(x)) + C,\tag{*}
$$
где снова $\frac{df}{du}$ интерпретируется как производная от $f$, обработанная  как функция  $u$. Но заметьте, что если бы $f$ была просто функцией переменной с именем $u$ (и не было никакого упоминания о $x$), то мы бы имели
$$
\int \frac{df}{du} \,du = f(u) + C.
$$
Итак, у нас снова возникает искушение еще больше злоупотребить обозначениями в (*), «отменив» «$dx$» в производной (думая об этом как дробь) с «$dx$» в интеграле. (что бы это ни значило), чтобы «оставить позади» часть «$du$».
 На первый взгляд это откровенно абсурдно: мы разделяем вещи, которые никогда не были разделены на части, и отбрасываем нечетные символы, как если бы они были обычными числами.
No related posts.