Дифракция света примеры: Дифракция света — материалы для подготовки к ЕГЭ по Физике
Явления, связанные с интерференцией и дифракцией света
- Подробности
- Категория: Оптические явления в природе
ТОНКИЕ ПЛЕНКИ
После дождя, когда мокрый асфальт кажется черным, в местах автомобильных стоянок, где на воду в лужах пролито масло и бензин, особенно отчетливо видны блестящие пятна, отливающие всеми цветами радуги. Больше всего заметны цвета зеленый и желтый, но местами видны голубой, синий и пурпурный.
Такие же пятна можно видеть на поверхности воды в реках, озерах и лужах, если они загрязнены нефтью или ее продуктами.
Кто из нас в детстве не выдувал мыльные пузыри. Тонкая пленка мыльного пузыря, так же как и тонкая пленка нефти на поверхности воды, приобретает цветную окраску, тонкий целлофан отсвечивает цветами радуги. Эти красивые явления имеют одну природу, они являются следствием интерференции света в тонких пленках масла, мыльной пены, целлофана.
ИНТЕРФЕРЕНЦИЯ СВЕТА В ТОНКИХ ПЛЕНКАХ
В тонких пленках нефти или мыльной воды происходит разделение, а затем соединение световых волн.
На рисунке 46 представлен ход лучей в пленке. Здесь h — толщина пленки (в сильно увеличенном масштабе), S — источник света. Пусть на пленку из точки S падают два монохроматических пучка лучей 1 и 2. Если источник света расположен далеко (а в случае освещения нефтяных пятен на лужах источником является небосвод, т. е. свет, рассеянный воздухом), его можно считать исходящим из бесконечности. Тогда лучи 1 и 2 будут практически параллельны, а фронт световой волны АВ перпендикулярен им.
Обозначим абсолютный показатель преломления света среды n1, а пленки n2.
Пучок лучей света, встретив пленку в точке А, частично преломляется, а частично отражается. Луч, отраженный в данном случае, нас не интересует, так как он не попадает в глаз. Пучок же преломленных лучей, дойдя до второй поверхности пленки (до точки D), опять частично отражается и частично преломляется. Нас интересует отраженный пучок лучей DC, который в точке С претерпевает частичное преломление и частичное отражение. Пучок лучей 2, преломленный в точке С, попадает в глаз, пучок лучей 2, выходящих из того же источника и падающих на пленку в точке С, также частично преломляется, а частично отражается. Отраженный пучок лучей 2 и пучок лучей 2 интерферируют. Оба пучка лучей могут быть сфокусированы при помощи линзы на экране, где и наблюдается результат интерференции, или на сетчатке глаза, где она воспринимается.

Что же получается на экране? Как видно из рисунка, пучки лучей 2, 2 прошли разные пути до встречи в точке С: первый прошел расстояние AD + DC = 2AD в среде с показателем преломления n2, второй — расстояние ВС в среде с показателем преломления n1
Геометрическая разность хода лучей равна 2AD — ВС; оптическая же разность 1 составляет:
где λ/2 — поправка на потерю полуволны при отражении света от среды, обладающей большим показателем преломления.
Если разность хода равна целому числу волн (Δ = Nλ), то точка С будет наблюдаться ярко светящейся определенным цветом, соответствующим длине волны, для нее будут выполняться условия максимума освещенности. Если же разность хода равна нечетному числу полуволн, то для данной волны выполняется условие минимума освещенности в точке С.
Разность хода Δ можно выразить как функцию толщины пленки h, угла падения (и наблюдения) a и длины волны λ или как функцию толщины пленки и угла преломления ϒ.
Эта зависимость выглядит следующим образом:
На поверхности пленки всегда найдется много точек, для которых соблюдены одинаковые условия интерференции для данной длины волны. Эти точки расположены цепочками. Их геометрические места представляют полосы светлые или темные в зависимости от длины волны и условий интерференции.
Для светлых полос при данной длине волны выполняется условие:
для темных:
Если пленка освещена полихроматическим (сложным, многоцветным) светом, например белым, то для каждой длины волны (для каждого цвета) найдутся полосы максимума освещенности, вне которых для данной длины волны имеет место минимум освещенности. В месте минимума данной волны может оказаться максимум другой волны (другого цвета). Таким образом, максимумы раз личных длин волн расположены друг за другом рядом. В результате образуется спектр.
Спектров может образоваться несколько порядков в зависимости от толщины пленки и угла наблюдения. Может случиться, что соседние спектры накладываются друг на друга своими крайними цветами. Красный накладывается на фиолетовый, в результате чего получается темно-пурпурный, а иногда коричневый цвет.
Цвета, составляющие середину спектра — желтый, зеленый, голубой, всегда видны хорошо.
Если за освещенной пленкой наблюдать несколько минут, то можно заметить изменение очертаний цветных полос. Это происходит вследствие растекания масла, а следовательно, и изменения толщины пленки.
Если на полированную стеклянную пластинку положить плоско-выпуклую линзу, то между линзой и пластинкой возникнет тонкая воздушная прослойка, в которой при определенном освещении (рис. 47) можно наблюдать светлые и темные кольца, соответствующие одинаковой толщине пленки. Увеличенная картина этих колец, рассматриваемых в зеленом и красном свете.

Явление интерференции применяется для многих практически полезных целей.
Так, при помощи интерференции можно проверить качество полировки поверхности деталей машины. На явлении интерференции света основано устройство приборов-интерферометров, служащих для измерения длин с точностью до 0,1 длины волны света, определения показателей преломления и др.
ЯВЛЕНИЕ ДИФРАКЦИИ СВЕТА. НАБЛЮДЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ
Дифракцию света можно наблюдать, например, посмотрев на свет далекого яркого фонаря через капроновый платок, держа его на расстоянии вытянутой руки.
Дифракционные спектры хорошо видны и при рассматривании источника света, например лампы сквозь ресницы.

Если сложить два пальца так, чтобы между ними образовалась узкая щель, и сквозь эту щель смотреть на источник рассеянного света (небо, абажур лампы и т. д.), то можно подобрать такую ширину щели, что в ней явно будет видно несколько темных и светлых полосок. Подобную картину можно видеть в узкой щели открытой двери, если за ней находится лампа или окно. Можно приклеить (парафином или маслом) к картону два лезвия безопасной бритвы и в щели между ними увидеть дифракционную картину.
Дифракционная картина хорошо видна, если в алюминиевой фольге концом иголки (не протыкая насквозь) проколоть маленькое отверстие и смотреть сквозь него на яркий источник света.
Царапины на оконном стекле тоже дают возможность наблюдать дифракцию света. На стекле окон автобусов, троллейбусов имеются царапины. Они возникают при протирании окон, при обдувании их кристалликами песка. Естественно, что большая часть царапин направлена горизонтально или несколько наискось. Стекло с царапинами — это своеобразная дифракционная решетка, на которой дифрагирует свет фонарей, отклоняясь перпендикулярно им. В результате можно видеть два пучка света, исходящих от источника света. Но почему же у них нет спектральной окраски? Это объясняется тем, что период рассматриваемой решетки непостоянен, в результате чего получается сложение спектральных цветов, дающее, как известно, белый свет.
Иногда, когда вы едете в автобусе, на замерзшем оконном стекле можно наблюдать красивую картину. Ледяной покров на окнах при попадании на них света Солнца или фонаря вдруг начинает сиять удивительно прозрачными и чистыми цветами спектра. Явление это несколько минут длится, а затем исчезает вследствие увеличения толщины слоя льда на стекле.
Это видение происходит вследствие дифракции света на иглах кристаллов льда. Возможно, что при некоторой толщине пластинок льда 1 мкм) и расстояниях между ними около 0,1 мм часть света проходит через пластинки, часть — мимо них. Ввиду различия скоростей света в пластинке и в воздухе происходит сдвиг колебаний по фазе. Это приводит к гашению некоторых длин волн вследствие интерференции, а в результате к «окрашиванию» поверхности замерзшего стекла в дополнительный цвет.
ВЕНЦЫ
Полупрозрачные белые облака медленно скользят перед Луной. И каждый раз, когда новое облако закрывает Луну, мы видим вокруг Луны чудесные разноцветные кольца, диаметр которых лишь в несколько раз больше диаметра Луны. Это венцы.
Аналогичные явления можно видеть и вокруг фонарей и Солнца (только при этом нужно позаботиться о том, чтобы Солнце не ослепляло нас, например надеть темные очки). Венцы не следует путать с гало. Диаметр гало 22 или 46°, в то время как диаметр венцов значительно меньше: 1 — 6°.
Объяснение этому явлению природы надо искать в дифракции света. Облака состоят из капелек воды. Проходя через капли, свет претерпевает дифракцию. Расхождение лучей при этом зависит от величины капли. Множество капель не изменяет картину, а только усиливает ее. Ширина ореола зависит от величины капель: чем меньше капельки, тем шире ореол. Возможно, что венцы могут возникнуть и на облаке, состоящем из ледяных игл.
В некоторых случаях световые венцы («глазные») возникают вследствие дифракции света на зернах неоднородностей, имеющихся в роговице глаза. «Глазной» венец по размеру равен «облачному», и их трудно различить. Однако «облачный» венец можно отличить от «глазного». Если перед глазом поместить непрозрачный предмет, то «облачные» венцы остаются, а «глазные» немедленно исчезают.
Дифракция света: явление, наблюдение, примеры
Шесть важных явлений описывают поведение световой волны, если она встречает на своем пути какое-либо препятствие. К этим явлениям относятся отражение, преломление, поляризация, дисперсия, интерференция и дифракция света. В данной статье речь пойдет о последнем из них.
Споры о природе света и опыты Томаса Юнга
В середине XVII века на равных правах существовали две теории, касающиеся природы световых лучей. Основоположником одной из них был Исаак Ньютон, который полагал, что свет — это совокупность быстро движущихся частичек материи. Вторую теорию выдвинул голландский ученый Кристиан Гюйгенс. Он считал, что свет — это особый тип волн, распространяющийся в среде подобно тому, как звук движется в воздухе. Средой для света, согласно Гюйгенсу, был эфир.

Поскольку эфира никто не обнаружил, а авторитет Ньютона был огромным на то время, теорию Гюйгенса отклонили. Однако в 1801 году англичанин Томас Юнг провел следующий эксперимент: он пропускал монохроматический свет через две узкие щели, расположенные близко друг от друга. Проходящий свет он проецировал на стену.
Каков был результат этого опыта? Если бы свет представлял собой частицы (корпускулы), как полагал Ньютон, то изображение на стене соответствовало бы четким двум ярким полосам, происходящим от каждой из щелей. Однако Юнг наблюдал совершенно иную картину. На стене появлялась череда темных и светлых полос, причем светлые линии появлялись даже за пределами обеих щелей. Схематическое изображение описанной световой картины представлено на рисунке ниже.
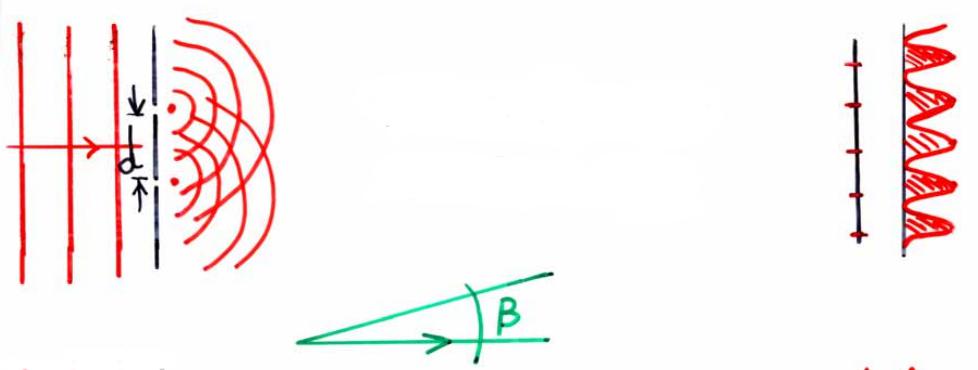
Эта картина говорила об одном: свет является волной.
Явление дифракции
Световая картина в опытах Юнга связана с явлениями интерференции и дифракции света. Оба явления трудно отделить друг от друга, поскольку в ряде экспериментов можно наблюдать их совокупный результат.
Дифракция света заключается в изменении волнового фронта, когда он встречает на своем пути препятствие, размеры которого сравнимы или меньше длины волны. Из этого определения понятно, что дифракция характерна не только для света, но и для любых других волн, например звуковых или волн на поверхности моря.

Также понятно, почему в природе не удается наблюдать это явление (длина световой волны составляет несколько сотен нанометров, поэтому любые макроскопические объекты отбрасывают четкие тени).
Принцип Гюйгенса — Френеля
Явление дифракции света объясняется благодаря названному принципу. Его суть заключается в следующем: распространяющийся прямолинейный плоский волновой фронт приводит к возбуждению вторичных волн. Эти волны являются сферическими, однако если среда однородная, то, налагаясь друг на друга, они приведут к первоначальному плоскому фронту.
Как только возникает какое-либо препятствие (например, две щели в опыте Юнга), то оно становится источником вторичных волн. Поскольку количество этих источников ограничено и определяется геометрическими особенностями препятствия (в случае двух тонких щелей вторичных источников всего два), то результирующая волна уже не даст первоначальный плоский фронт. Последний изменит свою геометрию (например, приобретет сферическую форму), более того, появятся максимумы и минимумы интенсивности света в разных его частях.
Принцип Гюйгенса — Френеля демонстрирует, что явления интерференции и дифракции света являются неразделимыми.
Какие условия необходимы, чтобы можно было наблюдать дифракцию?
Одно из них уже было озвучено выше: это наличие небольших (порядка длины волны) препятствий. Если же препятствие будет относительно больших геометрических размеров, то дифракционная картина будет наблюдаться только вблизи его краев.
Вторым важным условием дифракции света является когерентность волн от разных источников. Это означает, что они должны иметь постоянную разность фаз. Только в этом случае благодаря интерференции можно будет наблюдать устойчивую картину.
Когерентность источников достигается простым способом, достаточно любой световой фронт от одного источника пропустить через одно или несколько препятствий. Вторичные источники от этих препятствий уже будут действовать, как когерентные.
Заметим, что для наблюдения интерференции и дифракции света совершенно не обязательно, чтобы первичный источник был монохроматическим. Об этом будет сказано ниже при рассмотрении дифракционной решетки.
Дифракция Френеля и Фраунгофера
Говоря простым языком, дифракция Френеля заключается в рассмотрении картины на экране, расположенном близко к щели. Дифракция же Фраунгофера рассматривает картину, которая получается на расстоянии гораздо большем ширины щели, кроме того, она предполагает, что падающий на щель волновой фронт является плоским.
Выделяют эти два вида дифракции потому, что картины в них получаются разными. Связано это со сложностью рассматриваемого явления. Дело в том, что для получения точного решения дифракционной задачи необходимо использовать теорию электромагнитных волн Максвелла. Принцип же Гюйгенса — Френеля, упомянутый ранее, является хорошим приближением для получения практически пригодных результатов.
Ниже на рисунке показано, как изменяется изображение на дифракционной картине, когда экран удаляют от щели.
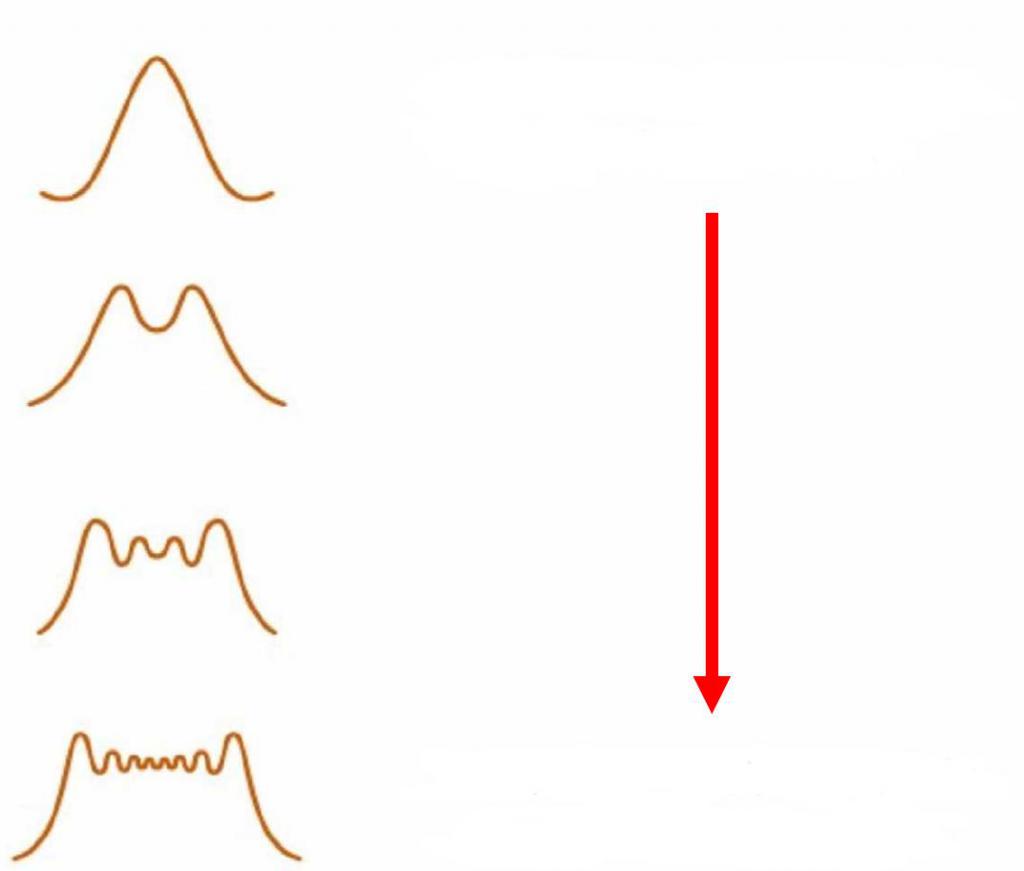
На рисунке красная стрелка показывает направление приближения экрана к щели, то есть верхний рисунок соответствует дифракции Фраунгофера и нижний — Френеля. Как видно, при приближении экрана к щели картина становится более сложной.
Далее в статье будем рассматривать только дифракцию Фраунгофера.
Дифракция на тонкой щели (формулы)
Как выше отмечалось, дифракционная картина зависит от геометрии препятствия. В случае тонкой щели, имеющей ширину a, которую освещают монохроматическим светом с длиной волны λ, положение минимумов (тени) можно наблюдать для углов, соответствующих равенству
sin(θ) = m × λ/a, где m = ±1, 2, 3…
Угол тета здесь отсчитывается от перпендикуляра, соединяющего центр щели и экран. Благодаря этой формуле можно рассчитать, при каких углах будет происходить полное гашение волн на экране. Более того, можно рассчитать порядок дифракции, то есть число m.
Поскольку речь идет о дифракции Фраунгофера, то L>>a, где L — расстояние до экрана от щели. Последнее неравенство позволяет заменить синус угла простым отношением координаты y к расстоянию L, что приводит к следующей формуле:
ym = m×λ×L/a.
Здесь ym — это координата положения минимума порядка m на экране.
Дифракция на тонкой щели (анализ)
Приведенные в предыдущем пункте формулы позволяют проанализировать изменения дифракционной картины при изменении длины волны λ или ширины щели a. Так, увеличение величины a приведет к уменьшению координаты минимума первого порядка y1, то есть свет будет концентрироваться в узком центральном максимуме. Уменьшение же ширины щели приведет к растяжению центрального максимума, то есть он становится расплывчатым. Эта ситуация продемонстрирована на рисунке ниже.
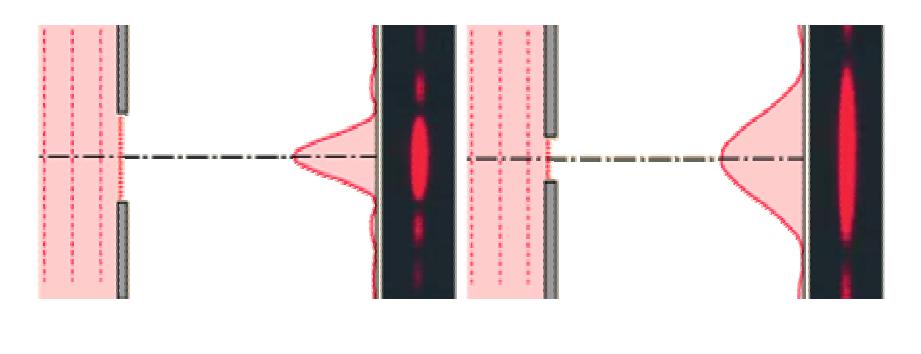
Изменение длины волны действует наоборот. Большие значения λ приводят к размыванию картины. Это означает, что длинные волны лучше дифрагируют, чем короткие. Последнее имеет принципиальное значение при определении разрешающей способности оптических приборов.
Дифракция и разрешающая способность оптических приборов
Наблюдение дифракции света является ограничителем разрешающей способности любых оптических приборов, например телескопа, микроскопа и даже человеческого глаза. Когда речь идет об этих приборах, то рассматривают дифракцию не на щели, а на круглом отверстии. Тем не менее все выводы, сделанные ранее, остаются верными.
Для примера будем рассматривать две светящиеся звезды, которые находятся на огромном расстоянии от нашей планеты. Отверстие, через которое свет попадает в наш глаз, называется зрачком. От двух звезд на сетчатке глаза формируются две дифракционные картины, каждая из которых имеет центральный максимум. Если в зрачок свет от звезд падает под некоторым критическим углом, то оба максимума будут сливаться в один. В этом случае человек будет видеть одну-единственную звезду.
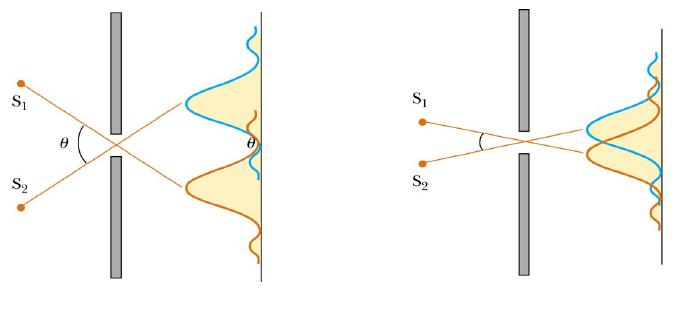
Критерий разрешающей способности был установлен лордом Дж. У. Рэлеем, поэтому в настоящее время он носит его фамилию. Соответствующая математическая формула выглядит так:
sin(θc) = 1,22×λ/D.
Здесь D — диаметр круглого отверстия (объектив, зрачок и так далее).
Таким образом, разрешающую способность можно увеличить (уменьшить θc), если увеличить диаметр объектива или уменьшить длину волны. Первый вариант реализуется в телескопах, позволяющих в несколько раз уменьшать θc по сравнению с глазом человека. Второй вариант, то есть уменьшение λ, находит применение в электронных микроскопах, которые обладают в 100 тысяч раз лучшей разрешающей способностью, чем аналогичные световые приборы.
Дифракционная решетка
Она представляет собой совокупность тонких щелей, находящихся на расстоянии d друг от друга. Если фронт волны является плоским и падает параллельно на эту решетку, тогда положение максимумов на экране описывается выражением
sin(θ) = m×λ/d, где m = 0, ±1, 2, 3…
Формула показывает, что максимум нулевого порядка возникает по центру, остальные расположены под некоторыми углами θ.
Поскольку в формуле стоит зависимость θ от длины волны λ, то это означает, что дифракционная решетка может разлагать свет на цвета подобно призме. Этот факт применяют в спектроскопии для анализа спектров различных светящихся объектов.

Пожалуй, самым известным примером дифракции света является наблюдение цветных оттенков на DVD-диске. Бороздки на нем представляют собой дифракционную решетку, которая, отражая свет, разлагает его на ряд цветов.
Дифракция — Всё для чайников
Дифракция
- Подробности
- Категория: Оптика
ДИФРАКЦИЯ
Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.

Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
Явление дифракции волн на поверхности воды можно наблюдать, если поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны (рис. 128). Хорошо будет видно, что за экраном распространяется круговая волна, как если бы в отверстии экрана располагалось колеблющееся тело -источник волн. Согласно принципу Гюйгенса так и должно быть. Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.
Если размеры щели велики по сравнению с длиной волны, то картина распространения волн за экраном совершенно иная (рис. 129). Волна проходит сквозь щель, почти не меняя своей формы. Только по краям можно заметить небольшие искривления волновой поверхности, благодаря которым волна частично проникает и в пространство за экраном. Принцип Гюйгенса позволяет понять, почему происходит дифракция. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.
ДИФРАКЦИЯ СВЕТА
Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.
Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.

Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).

Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.
Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.
Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.
Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.
На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.

Зоны Френеля для трехсантиметровой волны
Зонная пластинка для трехсантиметровых волн
Трёхсантиметровые волны: пятно Пуассона
Трёхсантиметровые волны: фазовая зонная пластинка
Круглое отверстие. Геометрическая оптика — дифракция Френеля
Круглое отверстие. Дифракция Френеля — дифракция Фраунгофера
Сравнение картин дифракции: ирисовая диафрагма и круглое отверстие
Пятно Пуассона
Дифракция Френеля на краю полуплоскости
Трехсантиметровые волны: дифракция Френеля на двух щелях
Дифракция Фраунгофера. Щель и полоска
Дифракция Фраунгофера. Две щели
Дифракционные решетки с разными периодами
Двумерные дифракционные решетки
Трёхсантиметровые волны и очень узкая щель
Модель спирали Корню
Дифракция света
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т.Юнгом. Независимо от него в 1818 г. французский ученый О.Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающих вторичных волнах Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.
|
Рисунок 3.8.1. Принцип Гюйгенса–Френеля. ΔS1 и ΔS2 – элементы волнового фронта, |
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.
Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.
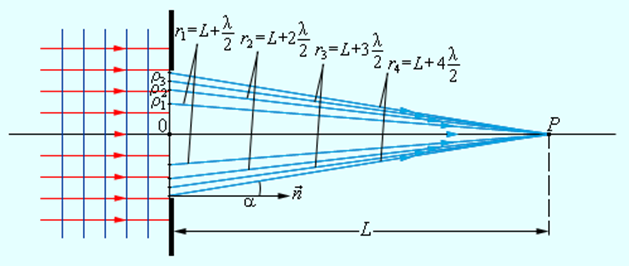
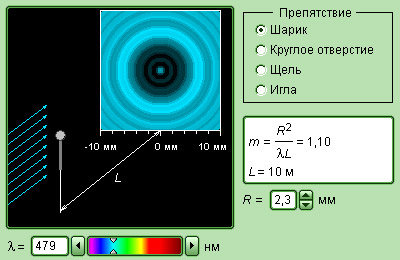
Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).
|
Рисунок 3.8.2. Дифракция плоской волны на экране с круглым отверстием |
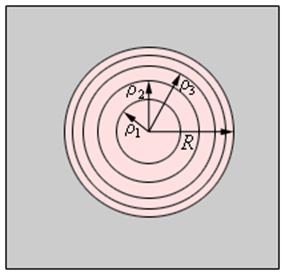
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A0 падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.
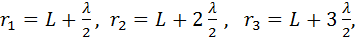 …
…
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).
|
Рисунок 3.8.3. Границы зон Френеля в плоскости отверстия |
Из рис. 3.8.2 легко найти радиусы ρm зон Френеля:
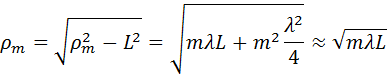
Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R:
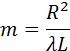
Здесь m – не обязательно целое число. Результат интерференции вторичных волн в точке P зависит от числа m открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:
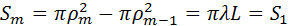
Одинаковые по площади зоны должны были бы возбуждать в точке наблюдения колебания с одинаковой амплитудой. Однако у каждой последующей зоны угол α между лучом, проведенным в точку наблюдения, и нормалью к волновой поверхности возрастает. Френель высказал предположение (подтвержденное экспериментом), что с увеличением угла α амплитуда колебаний уменьшается, хотя и незначительно:
A1 > A2 > A3 > … > A1, |
где Am – амплитуда колебаний, вызванных m-й зоной.
С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.
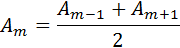
Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть
A = A1 – A2 + A3 – A4 + … = A1 – (A2 – A3) – (A4 – A5) – … < A1. |
Таким образом, суммарная амплитуда колебаний в точке P всегда меньше амплитуды колебаний, которые вызвала бы одна первая зона Френеля. В частности, если бы были открыты все зоны Френеля, то до точки наблюдения дошла бы невозмущенная препятствием волна с амплитудой A0. В этом случае можно записать:
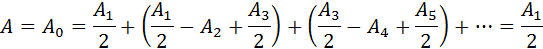
так как выражения, стоящие в скобках, равны нулю. Следовательно, действие (амплитуда), вызванное всем волновым фронтом, равно половине действия одной первой зоны.
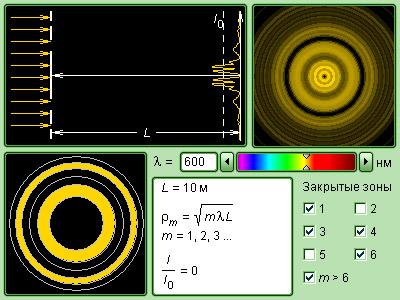
Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность – в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастет. Например, если открыты 1, 3 и 5 зоны, то
Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластинками.
При дифракции света на круглом диске закрытыми оказываются зоны Френеля первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна
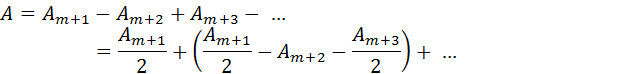
или A = Am + 1 / 2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то Am + 1 ≈ 2A0 и A ≈ A0, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.
Оценим размеры зон Френеля. Пусть, например, дифракционная картина наблюдается на экране, расположенном на расстоянии L = 1 м от препятствия. Длина волны света λ = 600 нм (красный свет). Тогда радиус первой зоны Френеля есть
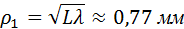
Таким образом, в оптическом диапазоне вследствие малости длины волны размер зон Френеля оказывается достаточно малым. Дифракционные явления проявляются наиболее отчетливо, когда на препятствии укладывается лишь небольшое число зон:
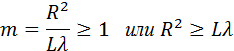
Это соотношение можно рассматривать как критерий наблюдения дифракции. Если число зон Френеля, укладывающихся на препятствии, становится очень большим, дифракционные явления практически незаметны:
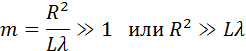
Это сильное неравенство определяет границу применимости геометрической оптики. Узкий пучок света, который в геометрической оптике называется лучом, может быть сформирован только при выполнении этого условия. Таким образом, геометрическая оптика является предельным случаем волновой оптики.
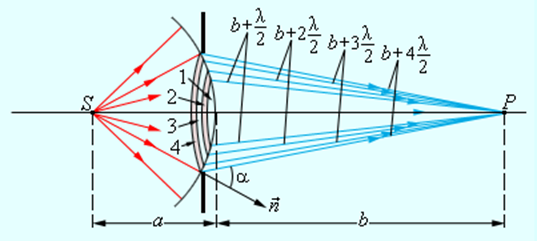
Выше был рассмотрен случай дифракции света от удаленного источника на препятствиях круглой формы. Если точечный источник света находится на конечном расстоянии, то на препятствие падает сферически расходящаяся волна. В этом случае геометрия задачи несколько усложняется, так как теперь зоны Френеля нужно строить не на плоской, а на сферической поверхности (рис. 3.8.4).
|
Рисунок 3.8.4. Зоны Френеля на сферическом фронте волны |
Расчет приводит к следующему выражению для радиусов ρm зон Френеля на сферическом фронте волны:
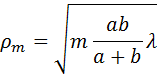
Все выводы изложенной выше теории Френеля остаются справедливыми и в этом случае.
Следует отметить, что теория дифракции (и интерференции) световых волн применима к волнам любой физической природы. В этом проявляется общность волновых закономерностей. Физическая природа света в начале XIX века, когда Т.Юнг, О.Френель и другие ученые развивали волновые представления, еще не была известна.
 |
Модель. Дифракция света |
 |
Модель. Зоны Френеля |
Дифракция света — Класс!ная физика
Дифракция света
- Подробности
- Просмотров: 332
«Физика — 11 класс»
Если свет представляет собой волновой процесс, то наряду с интерференцией должна наблюдаться и дифракция света.
Ведь дифракция — огибание волнами краев препятствий — присуща любому волновому движению.
Но наблюдать дифракцию света нелегко, так как волны отклоняются от прямолинейного распространения на заметные углы только на препятствиях, размеры которых сравнимы с длиной волны, а длина световой волны, как мы с вами знаем, очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света: светлое пятно на экране против отверстия будет иметь бо́льшие размеры, чем размеры пучка.
Опыт Юнга
В 1802 г. Т. Юнг, открывший интерференцию света, поставил классический опыт по дифракции.
В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.
Эти отверстия освещались узким световым пучком, прошедшим через малое отверстие А в другой ширме.
Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта.
Интерферируют ведь только когерентные волны.
Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия Л возбуждала в отверстиях В и С когерентные колебания.
Вследствие дифракции от отверстий В и С выходили два световых конуса, которые частично перекрывались.
В результате интерференции этих двух световых волн на экране появлялись чередующиеся светлые и темные полосы.
Закрывая одно из отверстий, Юнг обнаружил, что интерференционные полосы исчезали.
Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля
Исследование дифракции было завершено в работах О. Френеля.
Френель не только более детально исследовал различные случаи дифракции на опыте, но и разработал количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий.
Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн.
Согласно идее Френеля каждая точка волнового фронта является источником вторичных волн, причем все вторичные источники когерентны (принцип Гюйгенса — Френеля).
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью.
Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
Такие расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки В пространства.
Если рассмотреть вторичные источники на сферической волновой поверхности радиусом R, то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В.
Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в результате интерференции.
Поэтому все происходит так, как если бы свет распространялся вдоль прямой SB, т. е. прямолинейно.
На основе этой теории Френель доказал прямолинейность распространения света и рассмотрел количественно дифракцию на различного рода препятствиях.
Дифракционные картины от различных препятствий
Расчеты, сделанные Френелем, полностью были подтверждены экспериментом.
Из-за того что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик.
Поэтому для отчетливого наблюдения дифракции нужно либо использовать очень маленькие препятствия, либо не располагать экран далеко от препятствий.
При расстоянии между препятствием и экраном порядка метра размеры препятствия не должны превышать сотых долей миллиметра.
Если же расстояние до экрана достигает сотен метров или нескольких километров, то дифракцию можно наблюдать на препятствиях размерами в несколько сантиметров и даже метров.
На рисунке схематично показаны дифракционные картины от различных препятствий: а — от тонкой проволочки; б — от круглого отверстия; в — от круглого экрана.
Вместо тени от проволочки видны светлые и темные полосы; в центре дифракционной картины от отверстия появляется темное пятно, окруженное светлыми и темными кольцами; в центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными концентрическими кольцами.
Изменяя диаметр отверстия, можно в центре дифракционной картины получить и светлое пятно, окруженное темными и светлыми кольцами.
Любопытный случай произошел на заседании Французской академии наук в 1818 г.
Один из ученых, присутствовавших на заседании, обратил внимание на то, что из теории Френеля вытекают факты, явно противоречащие здравому смыслу.
Так, при определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко.
А за маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени.
Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле!
Границы применимости геометрической оптики
Все физические теории отражают происходящие в природе процессы лишь приближенно.
Для любой теории могут быть указаны определенные границы ее применимости.
Можно ли применять в конкретном случае данную теорию или нет, зависит не только от той точности, которую обеспечивает эта теория, но и от того, какая точность требуется при решении той или иной практической задачи.
Границы применимости теории можно установить лишь после того, как разработана более общая теория, охватывающая те же явления.
Все эти общие положения относятся и к геометрической оптике.
Эта теория является приближенной.
Она неспособна объяснить, например, явления интерференции и дифракции света.
Более общей и более точной теорией является волновая оптика.
Согласно ей, закон прямолинейного распространения света и другие законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны.
Но совершенно точно они не выполняются никогда.
Действие оптических приборов описывается законами геометрической оптики.
Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними.
Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.
Разрешающая способность микроскопа и телескопа
Волновая природа света налагает предел на возможность различать детали предмета или очень мелкие предметы при их наблюдении с помощью микроскопа.
Дифракция не позволяет получить отчетливые изображения мелких предметов, так как свет распространяется не строго прямолинейно, а огибает предметы.
Из-за этого изображения получаются размытыми.
Это происходит, когда линейные размеры предметов меньше длины световой волны.
Дифракция также налагает предел на разрешающую способность телескопа.
Вследствие дифракции волн у края оправы объектива изображением звезды будет не точка, а система светлых и темных колец.
Если две звезды находятся на малом угловом расстоянии друг от друга, то эти кольца налагаются друг на друга, и глаз не может различить, имеются ли две светящиеся точки или одна.
Предельное угловое расстояние между светящимися точками, при котором их можно различать, определяется отношением длины волны к диаметру объектива.
Этот пример показывает, что с дифракцией приходится считаться всегда, при любых препятствиях.
Ею при очень тщательных наблюдениях нельзя пренебрегать и в случае препятствий, размеры которых значительно больше, чем длина волны.
Дифракция света определяет границы применимости геометрической оптики.
Огибание светом препятствий налагает предел на разрешающую способность важнейших оптических инструментов — телескопа и микроскопа.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Световые волны. Физика, учебник для 11 класса — Класс!ная физика
Оптика — Скорость света — Принцип Гюйгенса. Закон отражения света — Закон преломления света — Полное отражение — Линза — Построение изображения в линзе — Формула тонкой линзы. Увеличение линзы — Примеры решения задач. Геометрическая оптика — Дисперсия света — Интерференция механических волн — Интерференция света — Некоторые применения интерференции — Дифракция механических волн — Дифракция света — Дифракционная решетка — Поперечность световых волн. Поляризация света — Поперечность световых волн и электромагнитная теория света — Примеры решения задач. Волновая оптика — Краткие итоги главы
Зоны Френеля
Принцип Гюйгенса — Френеля: волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.
Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света А в произвольной точке О изотропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке О, т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно r0. Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны: 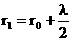 , где λ — длина световой волны. Вторая зона
, где λ — длина световой волны. Вторая зона 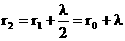 .
.
Аналогично определяются границы других зон. Если разность хода от двух соседних зон равна половине длины волны, то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум, если разность хода равна длине волны, то наблюдается интерференционный максимум.
Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно).
Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает произвольной точки О пространства.
Дифракция света: явление, наблюдение, примеры
Шесть важных явлений описывают поведение световой волны, если она встречает на своем пути какое-либо препятствие. К этим явлениям относятся отражение, преломление, поляризация, дисперсия, интерференция и дифракция света. В данной статье речь пойдет о последнем из них.
Споры о природе света и опыты Томаса Юнга
В середине XVII века на равных правах существовали две теории, касающиеся природы световых лучей. Основоположником одной из них был Исаак Ньютон, который полагал, что свет — это совокупность быстро движущихся частичек материи. Вторую теорию выдвинул голландский ученый Кристиан Гюйгенс. Он считал, что свет — это особый тип волн, распространяющийся в среде подобно тому, как звук движется в воздухе. Средой для света, согласно Гюйгенсу, был эфир.

Поскольку эфира никто не обнаружил, а авторитет Ньютона был огромным на то время, теорию Гюйгенса отклонили. Однако в 1801 году англичанин Томас Юнг провел следующий эксперимент: он пропускал монохроматический свет через две узкие щели, расположенные близко друг от друга. Проходящий свет он проецировал на стену.
Каков был результат этого опыта? Если бы свет представлял собой частицы (корпускулы), как полагал Ньютон, то изображение на стене соответствовало бы четким двум ярким полосам, происходящим от каждой из щелей. Однако Юнг наблюдал совершенно иную картину. На стене появлялась череда темных и светлых полос, причем светлые линии появлялись даже за пределами обеих щелей. Схематическое изображение описанной световой картины представлено на рисунке ниже.

Эта картина говорила об одном: свет является волной.
Явление дифракции
Световая картина в опытах Юнга связана с явлениями интерференции и дифракции света. Оба явления трудно отделить друг от друга, поскольку в ряде экспериментов можно наблюдать их совокупный результат.
Дифракция света заключается в изменении волнового фронта, когда он встречает на своем пути препятствие, размеры которого сравнимы или меньше длины волны. Из этого определения понятно, что дифракция характерна не только для света, но и для любых других волн, например звуковых или волн на поверхности моря.

Также понятно, почему в природе не удается наблюдать это явление (длина световой волны составляет несколько сотен нанометров, поэтому любые макроскопические объекты отбрасывают четкие тени).
Принцип Гюйгенса — Френеля
Явление дифракции света объясняется благодаря названному принципу. Его суть заключается в следующем: распространяющийся прямолинейный плоский волновой фронт приводит к возбуждению вторичных волн. Эти волны являются сферическими, однако если среда однородная, то, налагаясь друг на друга, они приведут к первоначальному плоскому фронту.
Как только возникает какое-либо препятствие (например, две щели в опыте Юнга), то оно становится источником вторичных волн. Поскольку количество этих источников ограничено и определяется геометрическими особенностями препятствия (в случае двух тонких щелей вторичных источников всего два), то результирующая волна уже не даст первоначальный плоский фронт. Последний изменит свою геометрию (например, приобретет сферическую форму), более того, появятся максимумы и минимумы интенсивности света в разных его частях.
Принцип Гюйгенса — Френеля демонстрирует, что явления интерференции и дифракции света являются неразделимыми.
Какие условия необходимы, чтобы можно было наблюдать дифракцию?
Одно из них уже было озвучено выше: это наличие небольших (порядка длины волны) препятствий. Если же препятствие будет относительно больших геометрических размеров, то дифракционная картина будет наблюдаться только вблизи его краев.
Вторым важным условием дифракции света является когерентность волн от разных источников. Это означает, что они должны иметь постоянную разность фаз. Только в этом случае благодаря интерференции можно будет наблюдать устойчивую картину.
Когерентность источников достигается простым способом, достаточно любой световой фронт от одного источника пропустить через одно или несколько препятствий. Вторичные источники от этих препятствий уже будут действовать, как когерентные.
Заметим, что для наблюдения интерференции и дифракции света совершенно не обязательно, чтобы первичный источник был монохроматическим. Об этом будет сказано ниже при рассмотрении дифракционной решетки.
Дифракция Френеля и Фраунгофера
Говоря простым языком, дифракция Френеля заключается в рассмотрении картины на экране, расположенном близко к щели. Дифракция же Фраунгофера рассматривает картину, которая получается на расстоянии гораздо большем ширины щели, кроме того, она предполагает, что падающий на щель волновой фронт является плоским.
Выделяют эти два вида дифракции потому, что картины в них получаются разными. Связано это со сложностью рассматриваемого явления. Дело в том, что для получения точного решения дифракционной задачи необходимо использовать теорию электромагнитных волн Максвелла. Принцип же Гюйгенса — Френеля, упомянутый ранее, является хорошим приближением для получения практически пригодных результатов.
Ниже на рисунке показано, как изменяется изображение на дифракционной картине, когда экран удаляют от щели.

На рисунке красная стрелка показывает направление приближения экрана к щели, то есть верхний рисунок соответствует дифракции Фраунгофера и нижний — Френеля. Как видно, при приближении экрана к щели картина становится более сложной.
Далее в статье будем рассматривать только дифракцию Фраунгофера.
Дифракция на тонкой щели (формулы)
Как выше отмечалось, дифракционная картина зависит от геометрии препятствия. В случае тонкой щели, имеющей ширину a, которую освещают монохроматическим светом с длиной волны λ, положение минимумов (тени) можно наблюдать для углов, соответствующих равенству
sin(θ) = m × λ/a, где m = ±1, 2, 3…
Угол тета здесь отсчитывается от перпендикуляра, соединяющего центр щели и экран. Благодаря этой формуле можно рассчитать, при каких углах будет происходить полное гашение волн на экране. Более того, можно рассчитать порядок дифракции, то есть число m.
Поскольку речь идет о дифракции Фраунгофера, то L>>a, где L — расстояние до экрана от щели. Последнее неравенство позволяет заменить синус угла простым отношением координаты y к расстоянию L, что приводит к следующей формуле:
ym = m×λ×L/a.
Здесь ym — это координата положения минимума порядка m на экране.
Дифракция на тонкой щели (анализ)
Приведенные в предыдущем пункте формулы позволяют проанализировать изменения дифракционной картины при изменении длины волны λ или ширины щели a. Так, увеличение величины a приведет к уменьшению координаты минимума первого порядка y1, то есть свет будет концентрироваться в узком центральном максимуме. Уменьшение же ширины щели приведет к растяжению центрального максимума, то есть он становится расплывчатым. Эта ситуация продемонстрирована на рисунке ниже.

Изменение длины волны действует наоборот. Большие значения λ приводят к размыванию картины. Это означает, что длинные волны лучше дифрагируют, чем короткие. Последнее имеет принципиальное значение при определении разрешающей способности оптических приборов.
Дифракция и разрешающая способность оптических приборов
Наблюдение дифракции света является ограничителем разрешающей способности любых оптических приборов, например телескопа, микроскопа и даже человеческого глаза. Когда речь идет об этих приборах, то рассматривают дифракцию не на щели, а на круглом отверстии. Тем не менее все выводы, сделанные ранее, остаются верными.
Для примера будем рассматривать две светящиеся звезды, которые находятся на огромном расстоянии от нашей планеты. Отверстие, через которое свет попадает в наш глаз, называется зрачком. От двух звезд на сетчатке глаза формируются две дифракционные картины, каждая из которых имеет центральный максимум. Если в зрачок свет от звезд падает под некоторым критическим углом, то оба максимума будут сливаться в один. В этом случае человек будет видеть одну-единственную звезду.

Критерий разрешающей способности был установлен лордом Дж. У. Рэлеем, поэтому в настоящее время он носит его фамилию. Соответствующая математическая формула выглядит так:
sin(θc) = 1,22×λ/D.
Здесь D — диаметр круглого отверстия (объектив, зрачок и так далее).
Таким образом, разрешающую способность можно увеличить (уменьшить θc), если увеличить диаметр объектива или уменьшить длину волны. Первый вариант реализуется в телескопах, позволяющих в несколько раз уменьшать θc по сравнению с глазом человека. Второй вариант, то есть уменьшение λ, находит применение в электронных микроскопах, которые обладают в 100 тысяч раз лучшей разрешающей способностью, чем аналогичные световые приборы.
Дифракционная решетка
Она представляет собой совокупность тонких щелей, находящихся на расстоянии d друг от друга. Если фронт волны является плоским и падает параллельно на эту решетку, тогда положение максимумов на экране описывается выражением
sin(θ) = m×λ/d, где m = 0, ±1, 2, 3…
Формула показывает, что максимум нулевого порядка возникает по центру, остальные расположены под некоторыми углами θ.
Поскольку в формуле стоит зависимость θ от длины волны λ, то это означает, что дифракционная решетка может разлагать свет на цвета подобно призме. Этот факт применяют в спектроскопии для анализа спектров различных светящихся объектов.

Пожалуй, самым известным примером дифракции света является наблюдение цветных оттенков на DVD-диске. Бороздки на нем представляют собой дифракционную решетку, которая, отражая свет, разлагает его на ряд цветов.
90000 Molecular Expressions Microscopy Primer: Light and Color 90001 90002 90003 Diffraction of Light 90004 90005 In his 1704 treatise on the theory of optical phenomena (90006 90007 Opticks 90008 90009), Sir Isaac Newton wrote that «light is never known to follow crooked passages nor to bend into the shadow». He explained this observation by describing how particles of light always travel in straight lines, and how objects positioned within the path of light particles would cast a shadow because the particles could not spread out behind the object.90010 90005 On a large scale, this hypothesis is supported by the seemingly sharp edges of shadows cast by rays from the sun. However, on a much smaller scale, when light waves pass near a barrier, they tend to bend around that barrier and spread at oblique angles. This phenomenon is known as 90006 diffraction 90009 of the light, and occurs when a light wave passes very close to the edge of an object or through a tiny opening, such as a slit or aperture. The light that passes through the opening is partially redirected due to an interaction with the edges.An example of light diffraction is presented in Figure 1 for coherent red laser light passing through a very tiny line grating composed of a series of bars on a glass microscope slide. The bars diffract the laser light into widely spaced periodic beams of bright light that can be observed in the figure. Diffraction is a phenomenon similar to dispersion, but is not related to a variation in the wavelength of light. 90010 90005 Bright bands that are often seen inside the edges of geometric shadows are the result of diffraction.When light waves originating from a distant point of light strike an opaque object, they tend to bend around the edges, curving both into the shadow and back through the path of other light waves from the same source. The waves that bend around behind the object create a bright line where the shadow would ordinarily begin, but waves that bounce back into the path of the light overlap waves from the source, creating an 90006 interference 90009 pattern of light and dark bands around the edge of the object (see Figure 2).Diffraction is often explained in terms of the 90006 Huygens principle 90009, which states that each point on a wavefront can be considered as a source of a new wave. 90010 90005 Depending on the circumstances that give rise to the phenomenon, diffraction can be perceived in a variety of different ways. Scientists have cleverly utilized diffraction of neutrons and X-rays to elucidate the arrangement of atoms in small ionic crystals, molecules, and even such large macromolecular assemblies as proteins and nucleic acids.Electron diffraction is often employed to examine periodic features of viruses, membranes, and other biological organisms, as well as synthetic and naturally occurring materials. No lens exists that will focus neutrons and X-rays into an image, so investigators must reconstruct images of molecules and proteins from the diffraction patterns using sophisticated mathematical analysis. Fortunately, magnetic lenses can focus diffracted electrons in the electron microscope, and glass lenses are very useful for focusing diffracted light to form an optical image that can easily be viewed.90010 90005 A very simple demonstration of light diffraction can be conducted by holding one hand in front of a strong light source and slowly bringing two fingers close together while observing the light transmitted between them. As the fingers approach one another and come very close together (almost touching), one can begin to see a series of dark lines parallel to the fingers. The parallel dark lines together with the bright areas between them are actually 90006 diffraction patterns 90009.This effect is clearly demonstrated in Figure 2, for diffraction rings that appear surrounding the sharp edges of a razor blade when it is illuminated with intense blue light from a laser source. 90010 90005 Another simple, but very common, example of diffraction occurs when light is scattered or bent by small particles having physical dimensions in the same order of magnitude as the wavelength of light. A good illustration is the spreading of automobile headlight beams by fog or fine dust particles.The amount of scattering and the angles taken by the redirected light beams are dependent upon the size and density of the particles causing the diffraction. Light scattering, a form of diffraction, also underlies the blue color of the sky and the often beautifully colored sunrises and sunsets that can be observed on the horizon. If the Earth were devoid of an atmosphere (lacking air, water, dust, and debris), the sky would appear black, even during the daytime. When light from the sun passes through the Earth’s atmosphere, localized volumes of gas molecules having varying densities, due to temperature fluctuations and the amount of water vapor present, will scatter the light.The shortest wavelengths (violet and blue) are scattered to the greatest extent, rendering the sky a rich, deep blue color. When there is a considerable amount of dust or moisture in the air, longer (primarily red) wavelengths also become scattered along with the blue wavelengths, causing the blue sky to become whiter in color. 90010 90005 When the sun is high (around noon) in a clear dry atmosphere, most of the visible light passing through the atmosphere is not scattered to a significant degree, and the sun appears almost white on a deep blue background.As the sun begins to set, the light waves must pass through increasing amounts of atmosphere, usually containing larger quantities of suspended dust and moisture. Under these circumstances, longer wavelengths of light become scattered and other colors start to dominate the color of the sun, which ranges from yellow to orange, finally turning red just before it drops below the horizon. 90010 90005 We can often observe pastel shades of blue, pink, purple, and green in clouds, which are generated by a combination of effects when light is refracted and diffracted from water droplets in the clouds.The amount of diffraction depends on the wavelength of light, with shorter wavelengths being diffracted at a greater angle than longer ones (in effect, blue and violet light are diffracted at a larger angle than is red light). The terms 90006 diffraction 90009 and 90006 scattering 90009 are often used interchangeably and are considered to be almost synonymous in many cases. Diffraction describes a specialized case of light scattering in which an object with regularly repeating features (such as a periodic object or a diffraction grating) produces an orderly diffraction pattern.In the real world, most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light. 90010 90037 90038 90039 90040 90041 90006 Interactive Java Tutorial 90009 90040 90045 90040 90047 90038 90049 90047 90051 90005 In the microscope, scattering or diffraction of light can occur at the specimen plane due to interaction of the light with small particles or features, and again at the margins of the objective front lens or at the edges of a circular aperture within or near the rear of the objective.It is this diffraction, or spreading of light, that makes it possible to observe magnified images of specimens in the microscope, however it is also diffraction that limits the size of objects that can be resolved. If light passes through a specimen and is not absorbed or diffracted, the specimen will not be visible when viewed through the eyepieces. The manner in which an image is formed in the microscope depends on the diffraction of light into divergent waves, followed by their subsequent recombination into a magnified image through constructive and destructive interference.90010 90005 When we view a specimen, whether directly or with a microscope, telescope, or other optical instrument, the image we see is composed of a myriad of overlapping points of light emanating from the plane of the specimen. Therefore, the appearance and integrity of the image from a single point of light holds a significant amount of importance with regards to formation of the overall image. Because the image-forming light rays are diffracted, a single point of light is never really seen as a point in the microscope, but rather as a diffraction pattern containing a central disk or spot of light having a finite diameter and encircled by a fading series of rings.As a result, the image of a specimen is never an exact representation of the specimen, and a lower limit is imposed on the smallest detail in the specimen that can be resolved. The resolving power is the ability of an optical instrument to produce clearly separated images of two adjacent points. Up to the point at which diffraction causes the resolution to be limited, the quality of the lenses and mirrors in the instrument, as well as the properties of the surrounding medium (usually air), determine the final resolution.90010 90005 Several of the classical and most fundamental experiments that help explain diffraction of light were first conducted between the late seventeenth and early nineteenth centuries by Italian scientist Francesco Grimaldi, French scientist Augustin Fresnel, English physicist Thomas Young, and several other investigators. These experiments involve propagation of light waves though a very small slit (aperture), and demonstrate that when light passes through the slit, the physical size of the slit determines how the slit interacts with the light.If the wavelength of light is much smaller than the aperture or slit width, a light wave simply travels onward in a straight line after passing through, as it would if no aperture were present (as presented in Figure 3). However, when the wavelength exceeds the size of the slit, diffraction of the light occurs, causing the formation of a diffraction pattern consisting of a bright central portion (the 90006 primary maximum 90009), bounded on either side by a series of secondary maxima separated by dark regions (90006 minima 90009; see Figure 4).The maxima and minima are created by interference of diffracted light waves. Each successive bright band becomes less intense proceeding outward, away from the central maximum. The width of the central bright portion, and the spacing of the accompanying sidebands, depends on the size of the aperture (slit) and the wavelength of the light. This relationship can be described mathematically and demonstrates that the width of the central maximum decreases with decreasing wavelength and increasing aperture width, but can never be reduced to the size of a point light source.90010 90005 The intensity distribution of light diffracted by the single slit experiment is presented in Figures 3 and 4. It is assumed that both light beams in Figure 3 are composed of coherent, monochromatic waves emitted from a point source that is far enough away from the slit for the wavefronts to be considered linear and parallel. Light passing through aperture 90006 d 90009 on the right-hand side of the figure has a wavelength larger than the aperture and is diffracted, with the primary incident light beam landing at point 90006 P 90009 and the first secondary maximum occurring at point 90006 Q 90009 .As shown on the left-hand side of Figure 3, when the wavelength is much smaller than the aperture width (90006 d 90009), the wave simply travels through in a straight line, just as it would if it were a particle or no aperture were present. However, when the wavelength exceeds the size of the aperture, it is diffracted to produce a central peak containing most of the light intensity accompanied by secondary higher-order maxima and intensity minima governed according to the equation: 90010 90006 sin (q) = ml / d 90009 90005 where 90006 q 90009 is the angle between the central incident propagation direction and the first minimum of the diffraction pattern, and 90006 m 90009 indicates the sequential number of the higher-order maxima.The light intensity is maximum at 90006 q 90009 = zero degrees, and decreases to a minimum (where the intensity is zero) at angles dictated by the equation above. The experiment produces a bright central maximum, which is bounded on both sides by secondary maxima, with the intensity of each succeeding secondary maximum decreasing as the distance from the center increases. Figure 4 illustrates this principle with a plot of beam intensity versus diffraction radius. Note that the minima occurring between secondary maxima are positioned in multiples of pi (90006 p 90009).90010 90005 Both the experiment described above, and the demonstration of diffraction using light passing between the fingers, utilize a narrow slit as an aperture to produce a diffraction pattern. All optical instruments, including microscopes, utilize circular lenses and apertures, as does the human eye itself. Circular apertures produce similar diffraction phenomena, although with circular symmetry (instead of linear geometry, as in the case of slits). Therefore the diffraction pattern of a point source of light, if highly magnified, is seen to consist of a central bright disk surrounded by a series of diffraction rings (the secondary maxima and minima).When a lens, such as a microscope objective lens, is properly focused, the light intensity at the minima between the bright rings in the pattern is zero. No matter how perfect the lens is, the secondary diffraction maxima can not be eliminated nor can the central spot be reduced to a single point of light (unless the lens could be made with an infinite diameter). 90010 90037 90038 90039 90040 90041 90006 Interactive Java Tutorial 90009 90040 90045 90040 90047 90038 90049 90047 90051 90005 The central diffraction spot or disk is called an Airy disk, named after Sir George Airy, who described many aspects of the concept in the nineteenth century.The Airy disk pattern (illustrated in Figure 5) is a direct result of diffraction, and demonstrates the alteration of points of light that make up an image using an optical instrument such as a microscope. In a manner that is similar to diffraction by a slit, the size of the central disk produced by circular lenses is related to the wavelength of the light and the diameter or aperture angle of the lens. In the case of a camera or telescope lens receiving light from an object at great (infinite) distance, the aperture angle depends on the focal ratio 90006 90007 f 90008 / D 90009, where 90006 D 90009 is the lens diameter and 90006 90007 f 90008 90009 is the focal length.The focal ratio is usually referred to in photography as the 90006 90007 f 90008 90009 -number of the lens. The aperture angle can be considered to be the angular diameter of the lens, measured from a reference point at the lens aperture to a point in the image plane positioned at the focal length (90006 90007 f 90008 90009) away from the lens. The radius of the diffraction disk (90006 d 90009) is given by the relationship 90006: 90009 90010 90006 d = 1.22 l (90007 f 90008 / D) 90009 90005 With objective lenses employed by the microscope, the concept of numerical aperture (90006 NA 90009) is used instead of the angular aperture. The definition of numerical aperture includes the refractive index of the medium positioned between the front of the lens and the microscope specimen slide, and the half angle over which the lens can collect light from a nearby specimen placed at the focal distance. Using the variable 90006 n 90009 to designate the refractive index, and 90006 q 90009 for the half angle aperture, the numerical aperture of a microscope objective is defined as: 90010 90006 NA (Numerical Aperture) = n sin (q) 90009 90005 The radius of the diffraction spot (90006 r 90009) for a point of light in the image plane (see Figure 4) is given by the related expression 90006: 90009 90010 90006 r = 1.22 l / (2NA) 90009 90005 The Airy disk patterns, along with 90006 point spread functions 90009, at three hypothetical resolutions are presented in Figure 5. The point spread function is a three-dimensional representation of the diffraction pattern occurring along the optical axis of the microscope. As the lateral resolution increases, Airy disk size decreases and the corresponding point spread function narrows. This can be demonstrated while observing the figure by comparing the Airy disk and point spread function in (a), which display the lowest resolution, with the corresponding set in (c) that have the highest resolution of the group.Experimentally, resolution can be increased by decreasing the wavelength of light utilized to image the specimen (from white light to blue, for example) or by increasing the numerical aperture of the objective and condenser combination. Under most circumstances, it is easier and far more practical to select an objective having a higher numerical aperture in order to increase the resolution of the images produced by the microscope. 90010 90005 Regardless of whether an image is formed in the microscope or another optical instrument, the size of a diffracted point of light becomes smaller with decreasing wavelength or increasing numerical aperture, but always remains a disk that is larger than the point of light originating from the specimen (or other object) being imaged.In evaluating the resolution that is possible with a microscope, if the size of the individual diffraction spot is the limiting factor (rather than lens aberrations or other variables), the image achieved is said to be 90006 diffraction limited 90009. For any optical instrument, therefore, the light gathering ability is fixed by the aperture angle or numerical aperture, and the resolution obtained is controlled by varying these values and the wavelength of light utilized to capture the image in order to obtain the smallest diffraction disk size that is possible with the instrument.Only when specimen details seen in the image are larger than this limiting disk size, can conclusions be made about the size, shape, and arrangement of the features. 90010 90005 90006 Contributing Authors 90009 90010 90005 90006 Thomas J. Fellers 90009 and 90006 Michael W. Davidson 90009 — National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310. 90010 90165 90005 90006 BACK TO DIFFRACTION OF LIGHT 90009 90010 90005 90006 BACK TO LIGHT AND COLOR 90009 90010 90003 Questions or comments? Send us an email.90004 90176 © 1998-2019 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners. 90177 90176 This website is maintained by our 90002 Graphics & Web Programming Team 90002 in collaboration with Optical Microscopy at the 90002 National High Magnetic Field Laboratory.90177 90176 Last modification: Friday, Nov 13, 2015 at 2:18 PM 90177 90176 Access Count Since June 8, 1998: Додати 133699 90177 90176 For more information on microscope manufacturers, 90002 use the buttons below to navigate to their websites: 90177 .90000 Molecular Expressions: Science, Optics, and You: Light and Color 90001 90002 90003 Diffraction of Light 90004 90005 Classically, light is thought of as always traveling in straight lines, but in reality, light waves tend to bend around nearby barriers, spreading out in the process. This phenomenon is known as 90006 diffraction 90007 and occurs when a light wave passes by a corner or through an opening or slit that is the approximate size of, or even smaller than, that light’s wavelength.90008 90005 A very simple demonstration of diffraction can be conducted by holding one’s hand in front of a light source and slowly closing two fingers while observing the light transmitted between them. As the fingers approach each other and come very close together, a series of dark lines parallel to the fingers begins to appear. The parallel lines are an example of 90006 diffraction patterns 90007. This phenomenon can also occur when light is bent around particles that are on the same order of magnitude as the wavelength of the light.An example of such a situation is illustrated above in Figure 1, which exhibits the diffraction of sunlight by clouds during sunset, resulting in what is often referred to as their 90006 silver lining 90007. Pastel shades of blue, pink, purple, and green are also observed at times in cloud cover and are generated when light is diffracted from water droplets within the clouds. The amount of diffraction that occurs depends on the wavelength of the light, and shorter wavelengths are diffracted at a greater angle than longer ones.90008 90005 The image below further illustrates what happens when a light wave traveling through the atmosphere encounters a droplet of water. As demonstrated, the light is first refracted at the interface between air and water, and then it is reflected as it again encounters the interface. The beam, still traveling inside the water droplet, is then refracted once more as it strikes the interface for a third time. This last interaction with the interface refracts the light back into the atmosphere, but it also diffracts a portion of the light as illustrated below.This diffraction element leads to a phenomenon known as 90006 Cellini’s halo 90007, or the 90006 Heiligenschein effect 90007, in which a bright ring of light surrounds the shadow of the observer’s head. 90008 90005 The terms diffraction and 90006 scattering 90007 are often used interchangeably and are considered to be almost synonymous. However, diffraction describes a specialized case of light scattering in which an object with regularly repeating features, such as a diffraction grating, produces an orderly diffraction of light in a diffraction pattern.In the real world, most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light. 90008 90005 One of the most classic and fundamental concepts of diffraction can be demonstrated by the single-slit optical diffraction experiment, first conducted in the early nineteenth century. That is, when a light wave propagates through a slit, the physical size of the aperture with respect to the wavelength of the incident beam determines how the light reacts.This same concept is illustrated below in Figure 2. As demonstrated on the left side of the figure, when the wavelength (90006 l 90007) is much smaller than the aperture width (90006 d 90007), the wave simply travels onward in a straight line , just as it would if it were a particle or no aperture were present. 90008 90005 The right side of Figure 2, however, illustrates a different situation. In this case, the wavelength of light transmitted by a point source exceeds the size of the aperture and light is diffracted, with the primary incident light beam landing at point 90006 P 90007 and the first secondary maxima occurring at point 90006 Q 90007.Such a situation results in a diffraction pattern that consists of a bright central portion called the 90006 primary maximum 90007 flanked on both sides by 90006 secondary maxima 90007, which are separated by dark sections known as 90006 minima 90007. The secondary maxima decrease in intensity as their distance from the center, the area of highest intensity, increases. The relationship between the size of an aperture and the diffraction that occurs can be demonstrated through the equation: 90008 90006 sinq 90007 = 90006 l / d 90007 90005 where 90006 q 90007 is the angle between the incident central propagation direction and the first minimum of the diffraction pattern.Below, Figure 3 further illustrates this point through a plot of beam intensity versus diffraction radius. Note that the minima occurring between secondary maxima are located in multiples of 90006 p 90007. 90008 90005 The single-slit diffraction experiment was first explained by Augustin Fresnel who, along with Thomas Young, produced important evidence confirming that light travels in waves. Based on his findings, Fresnel assumed that the amplitude of the first order maxima at point 90006 Q 90007 (defined as 90006 e 90007 90058 90006 Q 90007 90061) would be given by the equation: 90008 90006 90064 d 90065 e 90058 Q 90061 = a (A / r) 90064 f 90065 (c) d 90007 90005 where 90006 A 90007 is the amplitude of the incident wave, 90006 r 90007 is the distance between 90006 d 90007 and 90006 Q 90007, and 90006 90064 f 90065 90007 (90006 c 90007) is a function of 90006 c 90007, an inclination factor introduced by Fresnel.It is important to note that both this Fresnel equation and the one related previously are only meant to describe the behavior of diffraction through an aperture in the shape of a slit. 90008 90089 90090 90091 90092 90093 90006 Interactive Java Tutorial 90007 90092 90097 90092 90099 90090 90101 90099 90103 90005 Nevertheless, circular apertures are extremely important to consider because all optical instruments have circular apertures.The pupil of an eye and the circular diaphragm and lenses of a microscope are testaments to this fact. Circular apertures produce diffraction patterns similar to those described previously, but the patterns naturally exhibit a circular symmetry. Mathematical analysis of the diffraction patterns produced by a circular aperture provides the equation: 90008 90006 sinq (1) = 1.22 (l / d) 90007 90005 where 90006 q (1) 90007 is the angular position of the first order diffraction minima (the first dark ring), 90006 l 90007 is the wavelength of the incident light, 90006 d 90007 is the diameter of the aperture, and 1.22 is a constant. Under most circumstances, the angle 90006 q (1) 90007 is very small, so the approximation that the sin and tan of the angle are almost equal yields: 90008 90006 q (1) @ 1.22 (l / d) 90007 90005 From these equations it becomes apparent that the central maximum is directly proportional to 90006 l / d 90007, making this maximum more diffuse for longer wavelengths and for smaller apertures. 90008 90005 Diffraction plays a paramount role in limiting the 90006 resolving power 90007 of any optical instrument.The resolving power is the optical instrument’s ability to produce separate images of two adjacent points. No matter how perfect a lens may be, the image of a point source of light produced by the lens is accompanied by secondary and higher order maxima. This phenomenon could be eliminated only if the lens had an infinite diameter. Two objects separated by a distance less than 90006 q (1) 90007 can not be resolved, no matter how high the power of magnification. 90008 90005 Therefore, it is important to realize that although the previous equations were derived for the image of a point source of light an infinite distance from the aperture, a reasonable approximation of the resolving power of a microscope may be obtained when 90006 d 90007 is substituted for the diameter of the objective lens.Consequently, if two objects reside a distance 90006 D 90007 apart from each other and are at a distance 90006 L 90007 from an observer, the angle (expressed in radians) between them is: 90008 90006 q = D / L 90007 90005 The previous two equations can then be condensed to yield: 90008 90006 D (0) = 1.22 (lL / d) 90007 90005 where 90006 D (0) 90007 is the minimum separation distance between the objects that will allow them to be resolved.According to this equation, the human eye should be able to resolve objects separated by a distance of 0.056 millimeters. However, the photoreceptors in the retina are not quite close enough together to permit this degree of resolution and 0.1 millimeters is a more realistic number under normal circumstances. 90008 90005 The resolving power of optical microscopes is determined by a number of factors, such as optical alignment of the microscope, quality of the lenses, and the predominant wavelengths of light used to image the specimen.In the most ideal circumstances, the resolving power is about 0.2 micrometers. However, it is often not necessary to calculate the exact resolving power of each objective used, but it is important to understand the capabilities of microscope lenses as they apply to the real world. 90008 90005 90006 Contributing Authors 90007 90008 90005 90006 Mortimer Abramowitz 90007 — Olympus America, Inc., Two Corporate Center Drive., Melville, New York, 11747. 90008 90005 90006 Shannon H.Neaves 90007 and 90006 Michael W. Davidson 90007 — National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310. 90008 90164 90005 90006 BACK TO LIGHT AND COLOR 90007 90008 90003 Questions or comments? Send us an email. 90004 90171 © 1998-2019 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders.Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners. 90172 90171 This website is maintained by our 90002 Graphics & Web Programming Team 90002 in collaboration with Optical Microscopy at the 90002 National High Magnetic Field Laboratory. 90172 90171 Last modification: Friday, Nov 13, 2015 at 2:18 PM 90172 90171 Access Count Since March 10, 2003: Додати 68406 90172 90171 Visit the websites of our partners in education: 90172 .90000 90001 Diffraction, shadows, beams, Huygens ‘construction: Physclips 90002 90003 90004 90005 90006 90007 Why does sound go around corners, but not light? 90008 It’s a fair question: I put my hand in front of my mouth and you can still hear me, even if you can not see my lips. But does sound always ‘go around corners’? 90004 90005 90011 90012 90005 90006 90015 90016 Sound waves 90017 sometimes 90018 go around corners 90019 90020 90021 90012 90023 90024 You can try this wherever you have a broad band source of sound, such as waves, the wind in the trees, or a busy road.Obviously, light does not (noticeably) bend around the corner. For sound, low frequencies diffract more than high. With a friend, you can probably notice the effect when with your voice. Roughly speaking, vowels have mainly low frequency and consonants high frequency. 90020 90021 90012 90005 90006 90007 The ripple tank 90008 90004 90005 90006 90021 90012 90005 90006 90015 90016 The ripple tank, viewed from above.90019 90020 90021 90012 90023 90015 This clip is just to show the ripple tank. An electromechanical oscillator (like a loudspeaker but with a shaft instead of a cone) drives the horizontal bar (220 mm long) up and down, making a set of parallel wavefronts. A rubber (50 mm long) casts a shadow. This arrangement is unsuitable for filming because we can only see the waves clearly from some angles. 90020 90021 90012 90005 90003 90052 Projecting the waves on a screen 90008 90004 90005 90006 90057 90021 90012 90005 90006 90015 90016 The geometry for projecting images of water waves on a screen 90019 90020 90021 90012 90023 90015 The ripple tank is suspended over an overhead project.The refraction of light at the air-water surface produces dark and bright bands on the screen. 90020 90052 Water wave shadows and beams 90008 90073 90004 90005 90011 90006 90021 90012 90005 90006 90016 Shadow, short wavelength 90019 90021 90006 90016 Shadow, longer wavelength 90019 90021 90012 90005 90006 90021 90006 90021 90012 90005 90006 90016 Beam, short wavelength 90019 90021 90006 90016 Beam, longer wavelength 90019 90021 90012 90023 90015 Two different geometries times two different wavelengths.In the top row, the parallel wavefronts from the source strike an object. When the wavelength is several times smaller than the object (at left), we see a reasonably clear shadow. When the wavelength is longer (roughly half the length of the object), the shadows are rather less clear. 90020 90015 In the bottom row, an aperture in a barrier creates a beam of waves. For the shorter wavelength (left) the beam is reasonably clearly defined, and its edges are reasonably distinct. With the larger wavelength, we see stronger effects of diffraction at the edges of the beam.90020 90111 90021 90012 90023 90115 90005 90006 90052 Diffraction examples 90008 90004 90005 90006 90021 90012 90005 90006 90016 ‘Photo 51’, an X-ray image by Raymond Gosling and Rosalind Franklin in 1952; A neutron diffraction image from the ISIS neutron source 90019 90129; Electron diffraction in the UNSW 2nd year lab; Water waves in a ripple tank from 90017 Diffraction 90018 90132 90021 90012 90023 90015 Four examples of the patterns formed by waves of different sorts: X-rays, like visible light, are electromagnetic waves, neutrons and electrons are matter waves.The wavelengths of the X-rays, neutrons and electrons here are all measured in picometres, which is why they can form interference patterns when interacting with matter. The water waves have a wavelength of about a centimetre. 90020 90015 So, what about the the diffraction of (visible) light? We’ll see this most clearly when the objects or apertures have wavelengths comparable with the wavelength of visible light, 90129 i.e 90132. sizes of microns. However, effects are also visible with larger objects.Go to 90017 Diffraction 90018. 90020 90021 90012 90023 90021 90023.90000 Diffraction Through A Single Slit | 2D And 3D Wavefronts 90001 90002 6.5 Diffraction through a single slit (ESBNJ) 90003 90004 Waves diffract when they encounter obstacles. Why does this happen? If we apply Huygens principle it becomes clear. Think about a wavefront impinging on a barrier with a slit in it, only the points on the wavefront that move into the slit can continue emitting forward moving waves — but because a lot of the wavefront has been blocked by the barrier, the points on the edges of the hole emit waves that bend round the edges.How to use this approach to understand what happens is sketched below: 90005 90004 Before the the wavefront strikes the barrier the wavefront generates another forward moving wavefront (applying Huygens ‘principle). Once the barrier blocks most of the wavefront you can see that the forward moving wavefront bends around the slit because the secondary waves they would need to interfere with to create a straight wavefront have been blocked by the barrier. 90005 90004 If you employ Huygens ‘principle you can see the effect is that the wavefronts are no longer straight lines.90005 90010 Diffraction patterns (ESBNK) 90011 90004 We can learn even more about what happens after the wavefront strikes the barrier by applying Huygens ‘principle further. 90005 90004 Each point on the wavefront moving through the slit acts like a point source. We can think about some of the effects of this if we analyse what happens when two point sources are close together and emit wavefronts with the same wavelength and frequency. These two point sources represent the point sources on the two edges of the slit and we can call the source A and source B.90005 90004 Each point source emits wavefronts from the edge of the slit. In the diagram we show a series of wavefronts emitted from each point source. The black lines show peaks in the waves emitted by the point sources and the gray lines represent troughs. We label the places where constructive interference (peak meets a peak or trough meets a trough) takes place with a solid diamond and places where destructive interference (trough meets a peak) takes place with a hollow diamond. When the wavefronts hit a barrier there will be places on the barrier where constructive interference takes place and places where destructive interference happens.90005 90004 The measurable effect of the constructive or destructive interference at a barrier depends on what type of waves we are dealing with. If we were dealing with sound waves, then it would be very noisy at points along the barrier where the constructive interference is taking place and quiet where the destructive interference is taking place. 90005 90004 The pattern of constructive then destructive interference measured some distance away from a single slit is caused because of two properties of waves, diffraction 90021 and 90022 interference.Sometimes this pattern is called an interference pattern and sometimes it is called a diffraction pattern. Both names are correct and both properties are required for the pattern to be observed. For consistency we will call it a 90023 diffraction pattern 90024 in for the rest of this book. 90005 90004 The intensity of the diffraction pattern for a single narrow slit looks like this: 90005 90004 The picture above sketches how the wavefronts interfere to form the diffraction pattern. The peaks correspond to places where the waves are adding constructively and the minima are places where destructive interference is taking place.If you look at the picture you can see that if the wavelength (the distance between two consecutive peaks / troughs) of the waves were different the pattern would be different. For example, if the wavelength were halved the sketch would be: 90005 90004 The amount that the waves diffract depends on the wavelength. We can compare the spread in the points of constructive and destructive interference by plotting the highlighted points together for the two cases. We have to line up the central maximum from the two cases to see the difference.The case where the wavelength is smaller results in smaller angles between the lines of constructive and destructive interference. 90005 90004 It also depends on the width of the slit, changing the width of the slit would change the distance between the points labelled A and B in the sketch. For example, if we repeat the sketch halving the distance between the points A and B we would get: 90005 90004 We can compare the spread in the points of constructive and destructive interference by plotting the highlighted points together for the two cases.We have to line up the central maximum from the two cases to see the difference. The case where the two points are closer together, in purple, results in bigger angles between the lines of constructive and destructive interference. 90005 90010 Effect of slit width and wavelength on diffraction patterns (ESBNM) 90011 90004 Using our sketches we see that the extent to which the diffracted wave passing through the slit spreads out depends on the width of the slit and the wavelength of the waves.The narrower the slit, the more diffraction there is and the shorter the wavelength the less diffraction there is. The degree to which diffraction occurs is: \ [\ text {diffraction} \ propto \ frac {\ lambda} {w} \] where \ (\ lambda \) is the wavelength of the wave and \ (w \) is the width of the slit. 90005 90004 We can do a sanity check on the relationship by considering some special cases, very big and very small values for each of the numerator and denominator to see what sort of behaviour we expect (this is not a calculation, just a check to see what sort outcomes we expect when we change wavelength or slit width): 90005 90042 90043 Set \ (\ lambda = 1 \) and \ (w \) very large, the result will be \ (\ frac {1} {\ text {very big number}} \) which is a very small number.So for a very big slit there is very little diffraction. 90044 90043 Set \ (\ lambda = 1 \) and \ (w \) very small, the result will be \ (\ frac {1} {\ text {very small number}} \) which is a very big number. So for a very small slit there is large diffraction (this makes sense because eventually you are dealing with a point source which emits circular wavefronts). 90044 90043 Set \ (\ lambda \) very large and \ (w = 1 \), the result will be \ (\ frac {\ text {very big number}} {1} \) which is a very big number. So for a very big wavelength there is large diffraction.90044 90043 Set \ (\ lambda \) very small and \ (w = 1 \), the result will be \ (\ frac {\ text {very small number}} {1} \) which is a very small number. So for a very small wavelength there is little diffraction. 90044 90051 90010 Wave nature of light (ESBNN) 90011 90004 In Grade 10 we learnt about electromagnetic radiation and that visible light is a small part of the EM spectrum. EM radiation is a wave so we should see diffraction for visible light when it strikes a barrier or passes through a slit.In everyday life you do not notice diffraction of light around objects or when light passes through an open door or window. This is because the wavelength of light is very small and the «slits» like doors and windows are quite large. 90005 90004 We can put some everyday numbers into \ [\ text {diffraction} \ propto \ frac {\ lambda} {w} \] to see how much diffraction we expect. White light is combination of light of many different colours and each colour has a different frequency or wavelength. To make things simpler lets just think about one colour, green light has a wavelength of \ (\ text {532} \ times \ text {10} ^ {- \ text {9}} \) \ (\ text {m} \ ).{- \ text {9}} \ End {align *} 90005 Figure 6.3: A diffraction grating reflecting green light. 90004 The result is a very small number so we expect to see very little diffraction. In fact, the effect is so small that we can not see it with the human eye. We can observe diffraction of green light but for us to get \ (\ text {diffraction} \ propto 1 \) we need the wavelength and slit width to be the same number. So we know the effects of diffraction should become noticeable when the wavelength and slit width are similar.We can not change the wavelength of green light but there are objects called diffraction gratings that have very narrow slits that we can use to study the diffraction of light. We let wavefronts of green light strike a diffraction grating and then put a screen on the other side. We can see where the intensity of the the light on the screen is large and where it is small. For green light on a particular diffraction grating the pattern of green light on the screen looks like: 90005 90004 Blue light with a wavelength of \ (\ text {450} \ times \ text {10} ^ {- \ text {9}} \) \ (\ text {m} \) and the same diffraction grating will produce: 90005 90002 Worked example 2: Diffraction 90003 90004 Two diffraction patterns are presented, determine which one has the longer wavelength based on the features of the diffraction pattern.The first pattern is for green light: 90005 90004 The second pattern is for red light: 90005 90004 The same diffraction grating is used in to generate both diffraction patterns. 90005 90010 Determine what is required 90011 90004 We need to compare the diffraction patterns to extract information about the relative wavelengths so we can decide which one is longer. We know that the diffraction pattern depends on wavelength and slit width through: \ [\ text {diffraction} \ propto \ frac {\ lambda} {w} \] 90005 90004 The diffraction grating is the same in both cases so we know that the slit width is fixed.90005 90010 Analyse patterns 90011 90004 By eye we can see that the red pattern is wider than the green pattern. There is more diffraction for the red light, this means that: \ Begin {align *} \ Text {diffraction} _ {red} &> \ text {diffraction} _ {green} \\ \ Frac {\ lambda_ {red}} {w} &> \ frac {\ lambda_ {green}} {w} \\ \ Lambda_ {red} &> \ lambda_ {green} \ End {align *} 90005 90010 Final answer 90011 90004 The wavelength of the red light is longer than that of the green light. 90005 90004 Join thousands of learners improving their science marks online with Siyavula Practice.90005 Sign up here 90002 90003 Exercise 6.1 90004 As the width of the slit producing a single-slit diffraction pattern is reduced, how will the diffraction pattern produced change? 90005 90004 More diffraction is observed as the slit width is reduced. 90005 90004 A water break at the entrance to a harbour consists of a rock barrier with a \ (\ text {50} \) \ (\ text {m} \) wide opening. Ocean waves of \ (\ text {20} \) \ (\ text {m} \) wavelength approach the opening straight on. Light with a wavelength of \ (\ text {500} \ times \ text {10} ^ {- \ text {9}} \) \ (\ text {m} \) strikes a single slit of width \ (\ text { 30} \ times \ text {10} ^ {- \ text {9}} \) \ (\ text {m} \).Which waves are diffracted to a greater extent? 90005 90004 We need to calculate the diffraction for each type of wave. We start by calculating the diffraction of the water waves: 90005 \ Begin {align *} \ Text {diffraction} & \ propto \ frac {\ lambda} {w} \\ & \ Propto \ frac {\ text {20} \ text {m}} {\ text {50} \ text {m}} \\ & \ Propto \ text {0,4} \ End {align *} 90004 The diffraction of the light waves is: 90005 \ Begin {align *} \ Text {diffraction} & \ propto \ frac {\ lambda} {w} \\ & \ Propto \ frac {\ text {500} \ times \ text {10} ^ {- \ text {9}} \ text {m}} {\ text {30} \ times \ text {10} ^ {- \ text {9}} \ text {m}} \\ & \ Propto \ text {16,67} \ End {align *} 90004 The light waves are diffracted more.90005 90004 the wavelength gets larger 90005 90004 More diffraction would occur. The resulting diffraction pattern is wider: 90005 90004 the wavelength gets smaller 90005 90004 Less diffraction would occur. The resulting diffraction pattern is narrower: 90005 90004 the slit width gets larger 90005 90004 Less diffraction would occur. The resulting diffraction pattern is narrower: 90005 90004 the slit width gets smaller 90005 90004 More diffraction would occur.The resulting diffraction pattern is wider: 90005 90004 the frequency of the wave gets smaller 90005 90004 Frequency is inversely related to wavelength. So the wavelength gets longer and more diffraction would occur. The resulting diffraction pattern is wider: 90005 90004 the frequency of the wave gets larger 90005 90004 Frequency is inversely related to wavelength. The wavelength gets shorter and less diffraction would occur. The resulting diffraction pattern is narrower: 90005 90010 Extension: Calculating maxima and minima [NOT IN CAPS] (ESBNP) 90011 90004 There is a formula we can use to determine where the peaks and minima are in the interference spectrum.There will be more than one minimum. There are the same number of minima on either side of the central peak and the distances from the first one on each side are the same to the peak. The distances to the peak from the second minimum on each side is also the same, in fact the two sides are mirror images of each other. We label the first minimum that corresponds to a positive angle from the centre as \ (m = 1 \) and the first on the other side (a negative angle from the centre) as \ (m = -1 \), the second set of minima are labelled \ (m = 2 \) and \ (m = -2 \) etc.90005 90004 The equation for the angle at which the minima occur is given in the definition below: 90005 90132 90133 Interference Minima 90134 90135 90004 The angle at which the minima in the interference spectrum occur is: 90005 \ (\ Sin \ theta = \ frac {m \ lambda} {w} \) 90004 where 90005 90004 θ is the angle to the minimum 90005 90004 w is the width of the slit 90005 90004 λ is the wavelength of the impinging wavefronts 90005 90004 m is the order of the minimum, \ (m = ± 1, ± 2, ± 3 ,… \) 90005 90148 90149 90002 Worked example 3: Diffraction minimum 90003 90004 A slit with a width of \ (\ text {2 511} \) \ (\ text {nm} \) has red light of wavelength \ (\ text {650} \) \ (\ text {nm} \) impinge on it. The diffracted light interferes on a surface. At which angle will the first minimum be? 90005 90010 Check what you are given 90011 90004 We know that we are dealing with diffraction patterns from the diffraction of light passing through a slit.{- \ text {9}} \) \ (\ text {m} \). We are looking to determine the angle to first minimum so we know that \ (m = 1 \). 90005 90010 Applicable principles 90011 90004 We know that there is a relationship between the slit width, wavelength and interference minimum angles: 90005 \ (\ Sin \ theta = \ frac {m \ lambda} {w} \) 90004 We can use this relationship to find the angle to the minimum by substituting what we know and solving for the angle. 90005 90010 Substitution 90011 \ Begin {align *} \ Sin \ theta & = \ dfrac {\ text {650} \ times \ text {10} ^ {- \ text {9}} \ text {m}} {\ text {2 511} \ times \ text {10} ^ {- \ text {9}} \ text {m}} \\ \ Sin \ theta & = \ dfrac {\ text {650}} {\ text {2 511}} \\ \ Sin \ theta & = \ text {0,258861012} \\ \ Theta & = \ sin ^ {- 1} \ text {0,258861012} \\ \ Theta & = 15 ° \ End {align *} 90004 The first minimum is at \ (\ text {15} \) \ (\ text {°} \) from the centre maximum.90005 90002 Worked example 4: Diffraction minimum 90003 90004 A slit with a width of \ (\ text {2 511} \) \ (\ text {nm} \) has green light of wavelength \ (\ text {532} \) \ (\ text {nm} \) impinge on it. The diffracted light interferes on a surface, at what angle will the first minimum be? 90005 90010 Check what you are given 90011 90004 We know that we are dealing with diffraction patterns from the diffraction of light passing through a slit. The slit has a width of \ (\ text {2 511} \) \ (\ text {nm} \) which is \ (\ text {2 511} \ times \ text {10} ^ {- \ text {9} } \) \ (\ text {m} \) and we know that the wavelength of the light is \ (\ text {532} \) \ (\ text {nm} \) which is \ (\ text {532} \ times \ text {10} ^ {- \ text {9}} \) \ (\ text {m} \).We are looking to determine the angle to first minimum so we know that \ (m = 1 \). 90005 90010 Applicable principles 90011 90004 We know that there is a relationship between the slit width, wavelength and interference minimum angles: 90005 \ (\ Sin \ theta = \ frac {m \ lambda} {w} \) 90004 We can use this relationship to find the angle to the minimum by substituting what we know and solving for the angle. 90005 90010 Substitution 90011 \ Begin {align *} \ Sin \ theta & = \ dfrac {\ text {532} \ times \ text {10} ^ {- \ text {9}} \ text {m}} {\ text {2 511} \ times \ text {10} ^ {- \ text {9}} \ text {m}} \\ \ Sin \ theta & = \ dfrac {\ text {532}} {\ text {2 511}} \\ \ Sin \ theta & = \ text {0,211867782} \\ \ Theta & = \ sin ^ {- 1} \ text {0,211867782} \\ \ Theta & = 12.2 ° \ End {align *} 90004 The first minimum is at \ (\ text {12,2} \) \ (\ text {°} \) from the centre peak. 90005 90004 From the formula \ (\ sin \ theta = \ frac {m \ lambda} {w} \) you can see that a smaller wavelength for the same slit results in a smaller angle to the interference minimum. This is something you just saw in the two worked examples. Do a sanity check, go back and see if the answer makes sense. Ask yourself which light had the longer wavelength, which light had the larger angle and what do you expect for longer wavelengths from the formula.90005 90002 Worked example 5: Diffraction minimum 90003 90004 A slit has a width which is unknown and has green light of wavelength 532 nm impinge on it. The diffracted light interferes on a surface, and the first minimum is measure at an angle of \ (\ text {20,77} \) \ (\ text {°} \)? 90005 90010 Check what you are given 90011 90004 We know that we are dealing with diffraction patterns from the diffraction of light passing through a slit. We know that the wavelength of the light is \ (\ text {532} \) \ (\ text {nm} \) which is \ (\ text {532} \ times \ text {10} ^ {- \ text {9 }} \) \ (\ text {m} \).We know the angle to first minimum so we know that \ (m = 1 \) and \ (\ theta = 20.77 ° \). 90005 90010 Applicable principles 90011 90004 We know that there is a relationship between the slit width, wavelength and interference minimum angles: 90005 \ (\ Sin \ theta = \ frac {m \ lambda} {w} \) 90004 We can use this relationship to find the width by substituting what we know and solving for the width. 90005 90010 Substitution 90011 \ Begin {align *} \ Sin \ theta & = \ dfrac {\ text {532} \ times \ text {10} ^ {- \ text {9}} \ text {m}} {w} \\ \ Sin \ text {20,77} ° & = \ dfrac {\ text {532} \ times \ text {10} ^ {- \ text {9}}} {w} \\ w & = \ dfrac {\ text {532} \ times \ text {10} ^ {- \ text {9}}} {\ text {+0,3546666667}} \\ w & = \ text {1 500} \ times \ text {10} ^ {- \ text {9}} \\ w & = \ text {1 500} \ text {nm} \ End {align *} 90004 The slit width is \ (\ text {1 500} \) \ (\ text {nm} \).90005 .
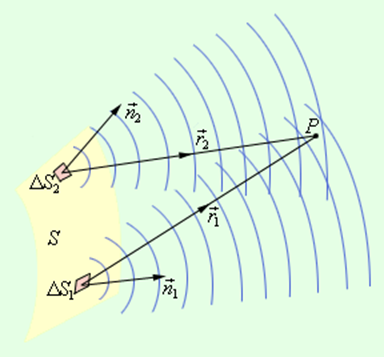
 и
и 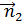 – нормали
– нормали