Дифракция | это… Что такое Дифракция?

Дифракция первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных максимумов

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны.

Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн.^[1]

Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.

Дифракция волн может проявляться:

• в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;
• в разложении волн по их частотному спектру;
• в преобразовании поляризации волн;
• в изменении фазовой структуры волн.

Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).

Содержание 1 Тонкости в толковании термина «дифракция» 2 Частные случаи дифракции 2.1 Дифракция на щели 2.2 Дифракция на отверстии 2.3 Дифракция звука и ультразвуковая локация 2.4 Дифракция радиоволн и радиолокация 2.5 Дифракционная решётка 2.6 Дифракция рентгеновских лучей в кристаллах и рентгеноструктурный анализ 2.7 Дифракция света на ультразвуке 2. 8 Дифракция электронов 2.9 Брегговская дифракция 2.10 Дифракция частиц (нейтронов, атомов, молекул) 3 История исследований 4 Дифракция в фотографии 5 См. также 6 Примечания 7 Литература 8 Ссылки

Тонкости в толковании термина «дифракция»

В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.

Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).

Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.

Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.

Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.

Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.

При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.

Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.

Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).

Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)

Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.

Частные случаи дифракции

Исторически в проблеме дифракции сначала рассматривались два крайних случая, связанных с ограничением препятствием (экраном с дыркой) сферической волны и это была дифракция Френеля, либо плоской волны на щели или системе отверстий — дифракция Фраунгофера

Дифракция на щели

Распределение интенсивности света при дифракции на щели

В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Для написания исходного уравнения используем принцип Гюйгенса.

Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.

Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать

пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).

Расстояние r от щели определяется как:

Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:

Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.

Здесь мы введём некую константу ‘C’, которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.

В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:

Используя формулу Эйлера и её производную: и .

где ненормированная синкус функция определена как .

Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:

См. также Дифракция на N-щелях

Дифракция на отверстии

Дифракция лазерного луча с длиной волны 650 нм, прошедшего через отверстие диаметром 0,2 мм

Дифракция звука и ультразвуковая локация

Дифракция радиоволн и радиолокация

Исследованием дифракции радиоволн занимается геометрическая теория дифракции^[2]

Дифракционная решётка

Основная статья: Дифракционная решётка

Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.

Дифракция рентгеновских лучей в кристаллах и рентгеноструктурный анализ

Дифракция света на ультразвуке

Основная статья: Акустооптика

Одним из наглядных примеров дифракции света на ультразвуке является дифракция света на ультразвуке в жидкости. В одной из постановок такого эксперимента в оптически-прозрачной ванночке в форме прямоугольного параллелепипеда с оптически-прозрачной жидкостью с помощью пластинки из пьезоматериала на частоте ультразвука возбуждается стоячая волна. В её узлах плотность воды ниже, и как следствие ниже её оптическая плотность, в пучностях — выше. Таким образом, при этих условиях ванночка с водой становится для световой волны фазовой дифракционной решёткой, на которой осуществляется дифракция в виде изменения фазовой структуры волн, что можно наблюдать в оптический микроскоп методом фазового контраста или методом тёмного поля.

Дифракция электронов

Основная статья: Дифракция электронов

Дифракция электронов — процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет свойства, аналогичные свойствам волны. При выполнении некоторых условий, пропуская пучок электронов через материал можно зафиксировать дифракционную картину, соответствующую структуре материала. Процесс дифракции электронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов.

Брегговская дифракция

Основная статья: Дифракция Брэгга

Согласно Закону Брэгга каждая точка (или отражение) в этой дифракционной картине формируется конструктивной интерференцией рентгеновских лучей, проходящих через кристалл. Эти данные могут быть использованы для определения атомной структуры кристаллов.

Дифракция от трехмерной периодической структуры, такой как атомы в кристалле называется дифракцией Брегга. Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решётке. Брегговская дифракция является следствием интерференции между волнами, отражёнными от кристаллических плоскостей.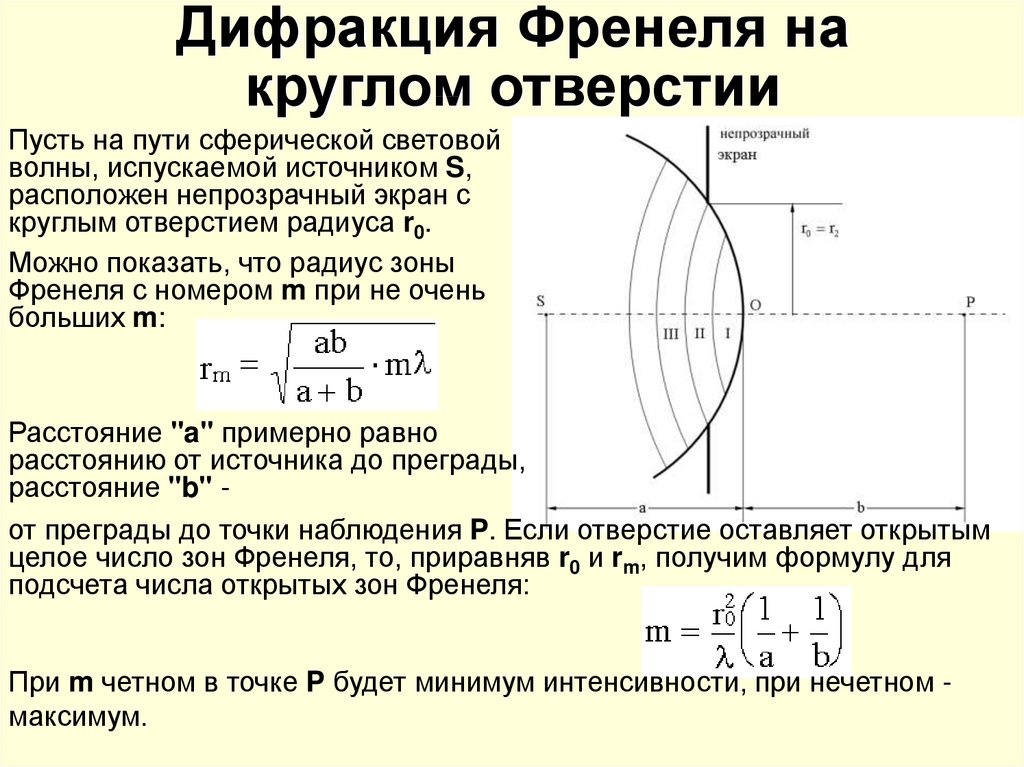

Условие возникновения интерференции определяется законом Вульфа-Брегга:

,

где

d — расстояние между кристаллическими плоскостями,

θ угол скольжения — дополнительный угол к углу падения,

λ — длина волны,

n (n = 1,2…) — целое число называемое порядком дифракции.

Брегговская дифракция может осуществляться при использовании света с очень маленькой длиной волны, такого как рентгеновское излучение, либо волны материи, такие как нейтроны и электроны, длины волн которых сравнимы или много меньше, чем межатомное расстояние.^[3] Получаемые данные дают информацию о межплоскостных расстояния, что позволяет вывести кристаллическую структуру. Дифракционный контраст, в электронных микроскопах и рентгеновских топографических устройствах, в частности, также является мощным инструментом для изучения отдельных дефектов и локальных полей деформации в кристаллах.

Дифракция частиц (нейтронов, атомов, молекул)

История исследований

Основы теории дифракции были заложены при изучении дифракции света в первой половине XIX века в трудах Юнга и Френеля. Среди других учёных, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики).

Обнаружение дифракции частиц (электронов) в 1927 году (опыт Дэвиссона и Джермера) сыграло большую роль в подтверждении существования волн де Бройля и в подтверждении концепции корпускулярно-волнового дуализма (идеи двойственной природы волн и частиц). В XX и XXI веках продолжились исследования дифракции волн на сложных структурах.

Дифракция в фотографии

Дифракцию можно наблюдать в фотографии: чрезмерное закрытие диафрагмы (относительного отверстия) приводит к падению резкости. Поэтому для сохранения оптимально резкого изображения на фотографии не рекомендуется полностью закрывать диафрагму. Нужно отметить, что для каждого объектива существует свои границы до которых стоит закрывать диафрагму, в большинстве случаев они равны f/11. ^[4]

См. также

• Интерференция
• Рефракция
• Рассеяние волн
• Оптика
• Физическая оптика
• Волновая оптика
• Акустооптика
• Электронная оптика
• История оптики
• Волна

Примечания

1. ↑ В явлении рассеяния на мелких неоднородностях среды сказывается не только экранирование фронта волны, но и свойства самой неоднородности (скажем, водяной капли), определяющие индикатрису рассеяния, что рассматривается, например, в научной дисциплине «Оптика атмосферы» в разделе, связанном с аэрозолем.
2. ↑ Боровиков В. А., Кинбер Б. Е. Геометрическая теория дифракции. М.: Связь, 1978, 247 с.
3. ↑ John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6
4. ↑ Что такое дифракция в фотографии. «Про Фото»

Литература

• Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное.  — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
• Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
• И. Г. Кондратьев, Г. Д. Малюжинец Дифракция волн // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.

Ссылки

• Дифракция: тематические медиа-файлы на Викискладе

Решена задача о дифракции на открытом конце волновода с диэлектриком

Дифракция в простом понимании — это отклонение направления распространения волны от прямолинейного при прохождении мимо какого-либо объекта. Теория дифракции, которая рассматривает это явление более широко и с помощью математических методов, обычно имеет дело с так называемыми каноническими задачами, то есть задачами взаимодействия относительно простых волн со сравнительно простыми геометрическими объектами, такими как, например, бесконечно тонкое ребро, клин, шар, цилиндр и тому подобное.

Отдельный класс канонических задач связан с дифракцией волн в резонаторах и на открытом конце волноводов.

Волноводные и резонаторные структуры — одни из ключевых элементов современных ускорителей частиц. В классических ускорителях эти структуры являются чисто вакуумными. Однако в последние годы большое внимание уделяется волноводам и резонаторам с различным диэлектрическим заполнением, так как это открывает перспективы для использования в ускорительной физике эффекта Вавилова-Черенкова. Он возникает при движении заряженной частицы со скоростью, превышающей фазовую скорость распространения волн в среде (в данном случае — в диэлектрике). Излучение расходится конусом от траектории движения частицы, и, поскольку угол при вершине конуса зависит от скорости частицы и скорости света в среде, физики могут определять скорость заряженной частицы и обнаруживать ее в экспериментах.

В интернете можно найти многочисленные фотографии излучения Вавилова-Черенкова в виде голубого свечения. Однако это лишь то, что мы можем видеть глазом. На самом деле эффект Вавилова-Черенкова проявляется в очень широком диапазоне частот электромагнитного спектра, лишь малая часть которого доступна человеческому глазу. В частности, этот эффект имеет место и в диапазонах гига- и терагерцовых частот, которые наиболее интересны для данной работы. В этой связи следует отметить значительные успехи, достигнутые в последнее время в методе кильватерного ускорения заряженных частиц. В этом методе используется излучение Вавилова-Черенкова на гига- или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны. Она подобна той, что возникает за идущими по воде кораблями — правда, в данном случае она имеет электромагнитную природу, а роль «корабля» выполняет движущийся сгусток электронов. Так как частота этой волны может попадать в терагерцовый диапазон, физики обсуждают возможность создания на базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют целый ряд перспективных применений — как сугубо прикладных, например в системах безопасности, так и чисто научных, связанных с исследованиями структуры материи.

Для развития описанных выше технологий крайне полезно иметь математический метод для строгого решения задачи дифракции электромагнитных волн и задачи дифракции поля движущегося сгустка заряженных частиц на открытом конце круглого волновода со слоем диэлектрика. Другими словами, желательно иметь решение соответствующей канонической задачи. Однако до настоящего момента оно отсутствовало, что, вероятно, связано с математическими сложностями, к которым приводит наличие диэлектрического слоя в волноводе: решение не строится в замкнутом виде, возникают бесконечные линейные или нелинейные системы уравнений.

Ученые кафедры радиофизики Санкт-Петербургского государственного университета (СПбГУ) посвятили свою работу строгому аналитическому решению такой канонической задачи. Свой подход они продемонстрировали на примере сплошного заполнения волновода диэлектриком и возбуждения в виде набегающей волноводной моды. Формально задача состояла в решении одного известного уравнения математической физики, но нужно было наиболее удобным образом выбрать представление для электромагнитного поля в каждой области пространства (волноводные стенки и их продолжения, а также торец волновода являются естественными границами, которые разбивают все пространство на ряд таких областей) и удовлетворить граничным условиям на всех отмеченных границах.

«Мы, конечно, не изобрели этот метод с нуля. В теории дифракции на таких структурах известно достаточно подходов и решено много канонических задач, но как раз нужная в данный момент оказалась нерешенной. Наиболее близко к нашей стоит работа московских физиков Воскресенского и Журава конца 1970-х годов. По большому счету нам просто удалось понять, как обобщить их подход на случай цилиндрической геометрии, а также мы апробировали полученные результаты современными численными средствами. Разработанный в итоге метод может применяться для решения более сложных и практически значимых задач со слоистым заполнением, при этом возбуждение может быть и в виде свободной волны, и в виде движущегося заряженного сгустка,— говорит Сергей Галямин, руководитель гранта РНФ, кандидат физико-математических наук, доцент кафедры радиофизики СПбГУ.— Кроме того, полученные нами результаты могут применяться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что особенно важно в случаях, когда моделирование оказывается ресурсозатратным. К решению этих задач мы и планируем приступить в ближайшем будущем».

Теги

Президентская программа, Физика и космос, Спецпроект, Молодежные группы

Дифракция света

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшое отверстие в экранах и т.д.

Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн. Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн.

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.

Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения P по линзе так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы (рис. ).

Принципиально дифракция Фраунгофера не отличается от дифракции Френеля. Количественный критерий, позволяющий установить, какой вид дифракции имеет место, определяется величиной безразмерного параметра , где b – характерный размер препятствия, l – расстояние между препятствием и экраном, на котором наблюдается дифракционная картина,  – длина волны. Если

Явление дифракции качественно объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Для монохроматической волны волновая поверхность есть поверхность, на которой колебания совершаются в одинаковой фазе.

Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис.). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. огибает края отверстия.

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности на фронте волны. Из повседневного опыта известно, что в большом числе случаев лучи света не отклоняются от их прямолинейного распространения. Так, предметы, освещенные точечным источником света, дают резкую тень. Таким образом, принцип Гюйгенса нуждается в дополнении, позволяющем определять интенсивность волны.

Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых малыми элементами некоторой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому источники вторичных волн действуют синфазно. В аналитическом виде для точечного источника этот принцип записывается в виде

, (1) где E – световой вектор, включающий в себя временную зависимость , k – волновое число, r – расстояние от точки P на поверхности S до точки P, K – коэффициент, зависящий от ориентации площадки по отношению к источнику и точке P. Правомерность формулы (1) и вид функции K устанавливается в рамках электромагнитной теории света (в оптическом приближении).

В том случае, когда между источником S и точкой наблюдения P имеются непрозрачные экраны с отверстиями, действие этих экранов может быть учтено следующим образом. На поверхности непрозрачных экранов амплитуды вторичных источников считаются равными нулю; в области отверстий амплитуды источников такие же, как при отсутствии экрана (так называемое приближение Кирхгофа).

Метод зон Френеля. Учет амплитуд и фаз вторичных волн позволяет в принципе найти амплитуду результирующей волны в любой точке пространства и решить задачу о распространении света. В общем случае расчет интерференции вторичных волн по формуле (1) довольно сложный и громоздкий. Однако ряд задач можно решить, применив чрезвычайно наглядный прием, заменяющий сложные вычисления. Метод этот получил название метода зон Френеля.

Суть метода разберем на примере точечного источника света S. Волновые поверхности представляют собой в этом случае концентрические сферы с центром в S. Разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки P отличаются на . Обладающие таким свойством зоны называются зонами Френеля. Из рис. видно, что расстояние от внешнего края – m-й зоны до точки P равно

, где b – расстояние от вершины волновой поверхности O до точки P.

Колебания, приходящие в точку P от аналогичных точек двух соседних зон (например, точек, лежащих в середине зон или у внешних краев зон), находятся в противофазе. Поэтому колебания от соседних зон будут взаимно ослаблять друг друга и амплитуда результирующего светового колебания в точке P

, (2) где , , … – амплитуды колебаний, возбуждаемых 1-й, 2-й, … зонами.

Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты . Обозначив площадь этого сегмента через , найдем, что, площадь m-й зоны Френеля равна . Из рисунка видно, что . После несложных преобразований, учитывая и , получим

. Площадь сферического сегмента и площадь m-й зоны Френеля соответственно равны

, . (3) Таким образом, при не слишком больших m площади зон Френеля одинаковы. Согласно предположению Френеля, действие отдельных зон в точке P тем меньше, чем больше угол между нормалью n к поверхности зоны и направлением на P, т.е. действие зон постепенно убывает от центральной к периферийным. Кроме того, интенсивность излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки P. Таким образом, амплитуды колебаний образуют монотонно убывающую последовательность

.

Общее число зон Френеля, умещающихся на полусфере, очень велико; например, при и число зон достигает ~10⁶. Это означает, что амплитуда убывает очень медленно и поэтому можно приближенно считать

. (4) Тогда выражение (2) после перегруппировки суммируется

, (5) так как выражения в скобках, согласно (4), равны нулю, а вклад последнего слагаемого ничтожно мал. Таким образом, амплитуда результирующих колебаний в произвольной точке P определяется как бы половинным действием центральной зоны Френеля.

При не слишком больших m высота сегмента , поэтому можно считать, что . Подставив значение для , получим для радиуса внешней границы m-й зоны

. (6) При и радиус первой (центральной) зоны . Следовательно, распространение света от S к P происходит так, как если бы световой поток шел внутри очень узкого канала вдоль SP, т.е. прямолинейно.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонная пластинка – в простейшем случае стеклянная пластинка, состоящая из системы чередующихся прозрачных и непрозрачных концентрических колец, с радиусами зон Френеля заданной конфигурации. Если поместить зонную пластинку в строго определенном месте (на расстоянии a от точечного источника и на расстоянии b от точки наблюдения), то результирующая амплитуда будет больше, чем при полностью открытом волновом фронте.

Дифракция Френеля на круглом отверстии. Дифракция Френеля наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, в данном случае экрана с отверстием. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути экран с отверстием. Дифракционная картина наблюдается на экране, параллельном экрану с отверстием. Ее вид зависит от расстояния между отверстием и экраном (для данного диаметра отверстия). Проще определить амплитуду световых колебаний в центре картины. Для этого разобьем открытую часть волновой поверхности на зоны Френеля. Амплитуда колебания, возбуждаемая всеми зонами равна

, (7) где знак плюс отвечает нечетным m и минус – четным m.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в центральной точке будет больше, чем при свободном распространении волны; если четное то амплитуда (интенсивность) будет равна нулю. Например, если отверстие открывает одну зону Френеля, амплитуда , то интенсивность ( ) больше в четыре раза.

Расчет амплитуды колебания на внеосевых участках экрана более сложен, так как соответствующие зоны Френеля частично перекрываются непрозрачным экраном. Качественно ясно, что дифракционная картина будет иметь вид чередующихся темных и светлых колец с общим центром (если m четное, то в центре будет темное кольцо, если m нечетное – то светлое пятно), причем интенсивность в максимумах убывает с расстоянием от центра картины. Если отверстие освещается не монохроматическим светом, а белым светом, то кольца окрашены.

Рассмотрим предельные случаи. Если отверстие открывает лишь часть централь­ной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает. Если отверстие открывает большое число зон, то и амплитуда в центре , т.е. такая же, как и при полностью открытом волновом фронте; чередование светлых и темных колец происходит лишь в очень узкой области на границе геометрической тени. Фактически дифракционная картина не наблюдается, и распространение света, по сути, является прямолинейным.

Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.). Дифракционная картина, наблюдаемая на экране, является центрально симметричной. Определим амплитуду световых колебаний в центре. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда колебаний равна

или , (8) так как выражения, стоящие в скобках, равны нулю. Следовательно, в центре всегда наблюдается дифракционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами. При небольшом числе закрытых зон амплитуда мало отличается от . Поэтому интенсивность в центре будет почти такая же, как при отсутствии диска. Изменение освещенности экрана с расстоянием от центра картины изображено на рис.

Рассмотрим предельные случаи. Если диск закрывает лишь небольшую часть центральной зоны Френеля, он совсем не отбрасывает тени – освещенность экрана всюду остается такой же, как при отсутствии диска. Если диск закрывает много зон Френеля, чередование светлых и темных колец наблюдается только в узкой области на границе геометрической тени. В этом случае , так что светлое пятно в центре отсутствует, и освещенность в области геометрической тени практически всюду равна нулю. Фактически дифракционная картина не наблюдается, и распространение света является прямолинейным.

Дифракция Фраунгофера на одной щели. Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной a. Оптическая разность хода между крайними лучами, идущими от щели в некотором направлении 

.

Разобьем открытую часть волновой поверхности в плоскости щели на зоны Френеля, имеющие вид равновеликих полос, параллельных щели. Так как ширина каждой зоны выбирается такой, чтобы разность хода от краев этих зон была равна , то на ширине щели уместится зон. Амплитуды вторичных волн в плоскости щели будут равны, так как зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Фазы колебаний от пары соседних зон Френеля отличаются на , поэтому, суммарная амплитуда этих колебаний равна нулю.

Если число зон Френеля четное, то

, (9а) и в точке B наблюдается минимум освещенности (темный участок), если же число зон Френеля нечетное, то

(9б) и наблюдается близкая к максимуму освещенность, соответствующей действию одной нескомпенсированной зоны Френеля. В направлении щель действует, как одна зона Френеля, и в этом направлении наблюдается наибольшая освещенность, точке соответствует центральный или главный максимум освещенности.

Расчет освещенности в зависимости от направления дает

, (10) где – освещенность в середине дифракционной картины (против центра линзы), – освещенность в точке, положение которой определяется направлением . График функции (10) изображен на рис. Максимумы освещенности соответствуют значениям , удовлетворяющие условиям

, , и т.д. Вместо этих условий для максимумов приближенно можно пользоваться соотношением (9б), дающим близкие значения углов. Величина вторичных максимумов быстро убывает. Численные значения интенсивностей главного и следующих максимумов относятся как

и т.д., т.е. основная часть световой энергии, прошедшей через щель, сосредоточена в главном максимуме.

Сужение щели приводит к тому, что центральный максимум расплывается, а его освещенность уменьшается. Наоборот, чем щель шире, тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При в центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.

Дифракция Фраунгофера на дифракционной решетке. Дифракционная решетка представляет собой систему одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционную картину от решетки можно рассматривать как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция.

Рассмотрим дифракционную решетку. Если ширина каждой щели равна a, а ширина непрозрачных участков между щелями b, то величина называется периодом дифракционной решетки.

Согласно формуле для многолучевой интерференции (Л3-3-5) освещенность в условиях интерференции световых лучей от N щелей равна

. (1) Из рис. видно, что разность хода от соседних щелей равна . Следовательно разность фаз

, (2) где  – длина волны в данной среде. Подставив в формулу (1) выражение для (освещенность от одной щели) и (2) для , получим

(3) ( – освещенность, создаваемая одной щелью на оси линзы).

Первый множитель обращается в нуль в точках, для которых

. (4) В этих точках освещенность, создаваемая каждой из щелей в отдельности, равна нулю. Будут наблюдаться главные минимумы освещенности.

Второй множитель в правой части (3) принимает экстремальное, а все выражение близкое к экстремальному, значение (локальный максимум) в точках, удовлетворяющих условию

. (5) Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга. Условие (5) с достаточной точностью определяет положения главных максимумов. Число m дает порядок главного максимума.

Кроме главных минимумов в промежутке между соседними главными максимумами имеется дополнительный минимум. Эти минимумы соответствуют направлениям, при которых второй множитель обращается в нуль. В данных направлениях колебания от отдельных щелей взаимно погашают друг друга. В соответствии с (3) направления дополнительных минимумов определяются условием

. (6) В формуле (6) m принимает все целочисленные значения кроме , т.е. кроме тех, при которых условие (6) переходит в (5).

Между дополнительными минимумами располагаются слабых вторичных максимумов. Интенсивность вторичных максимумов не превышает интенсивности ближайшего главного максимума (см. Л3-3). На рис. качественно представлена дифракционная картина от четырех щелей.

Так как , то из (4) следует, что наибольший порядок главного максимума

, т.е. определяется отношением периода решетки к длине волны. Положение главных максимумов зависит от длины волны . Поэтому при пропускании через решетку белого света все максимумы, кроме центрального ( ), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная – наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т. е. дифракционная решетка может быть использована как спектральный прибор.

Основными характеристиками всякого спектрального прибора является его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейной расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на 1 Å). Разрешающая сила определяет минимальную разность длин волн , при которой две линии воспринимаются в спектре раздельно.

Угловой дисперсией называется величина

, где  – угловое расстояние между спектральными линиями, отличающимися по длине волны на . С помощью (4), опуская знаки, получим

. Отсюда, в пределах небольших углов ( ),

. (7)

Разрешающей силой спектрального прибора называют безразмерную величину

, где  – минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.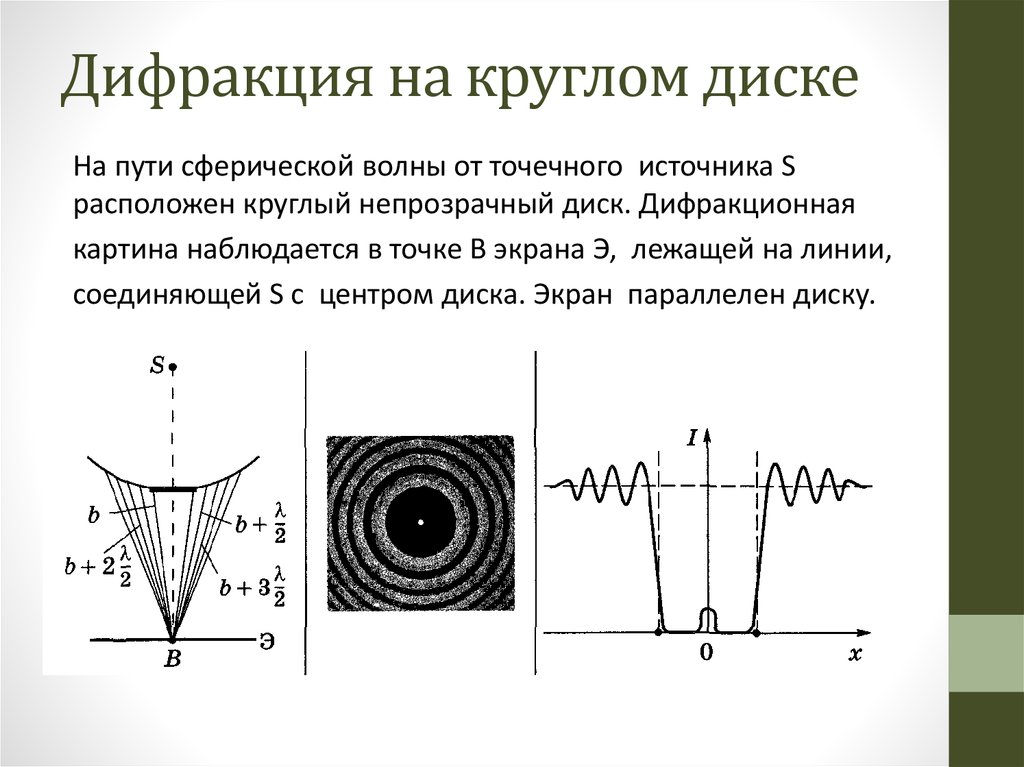

Согласно критерию Рэлея, изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями разрешимы (разделены для восприятия), если центральный максимум от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого (рис.). При выполнении критерия Рэлея интенсивность “провала” между максимумами составляет 80 % интенсивности в максимуме, что является достаточным для разрешения источников (линий).

Положение m-го максимума для длины волны и минимума, следующего за m-м максимумом для длины волны , определяется соответственно условиями

. Согласно критерию Рэлея две эти линии разрешаются спектральным прибором, если правые части этих соотношений равны между собой или

. Отсюда, для разрешающей силы получим выражение

. (8) Современные дифракционные решетки обладают довольно высокой разрешающей способностью (до ).

Разрешающая сила объектива. Используя даже идеальную оптическую систему невозможно получить стигматическое изображение точечного источника, что объясняется волновой природой света. Если на объектив падает свет от удаленного точечного источника, то вследствие дифракции световых волн, в фокальной плоскости объектива вместо точки наблюдается дифракционная картина. В результате точечный источник отображается в виде светлого пятна, окруженного чередующимися темными и светлыми кольцами. Соответствующий расчет (дифракции Фраунгофера на круглом отверстии) дает, что первый минимум отстоит от центра дифракционной картины на угловое расстояние

, где D – диаметр объектива (или диафрагмы). Полезно сравнить этот результат с подобным результатом для дифракции на щели. В последнем случае , где a – ширина щели. Если , можно положить

.

Если на объектив падает свет от двух удаленных точечных источников и с некоторым угловым расстоянием , то имеет место наложение их дифракционных картин (рис. ). Согласно критерию Рэлея, который в данном случае гласит что, две близкие точки будут еще разрешены, если середина центрального максимума для одной точки совпадает с первым минимумом для второй точки. Таким образом, наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются объективом

. (9) Величина, обратная , называется разрешающей силой объектива

. (10)

Диаметр зрачка глаза при нормальном освещении равен примерно 2 мм. Подставив это значение в формулу (9) и взяв , получим

. Примечательно, что расстояние между соседними светочувствительными элементами сетчатки глаза соответствует этому угловому расстоянию.

Дифракция рентгеновских лучей. Дифракция наблюдается не только на одномерной дифракционной решетке, но также трехмерных периодичных структурах. Подобными структурами являются все кристаллические тела. Однако их период () слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете.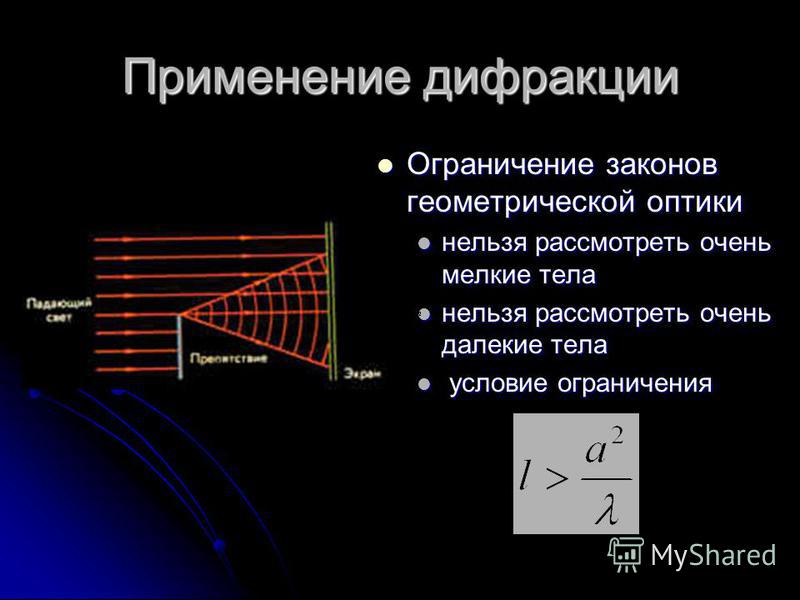 В случае кристаллов соотношение выполняется только для рентгеновских лучей.

В случае света лучи сводятся при помощи линзы. Для рентгеновских лучей осуществить линзу невозможно, так как показатель преломления этих лучей во всех веществах практически равен единице. Поэтому интерференция вторичных волн достигается путем использования весьма узких пучков лучей, которые и без линзы дают на экране (или фотопластинке) пятна очень малых размеров.

Рассматриваем кристалл как совокупность параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы кристаллической решетки), отстоящих друг от друга на расстояние d. Полагаем, что при падении рентгеновского излучения на кристалл происходит частичное отражение излучения от этих плоскостей. Вторичные волны, отразившиеся от разных плоскостей, когерентны и будут интерферировать между собой. Из рис. видно, что разность хода двух волн, отразившихся от соседних плоскостей, равна , где  – угол, называемый углом скольжения падающих лучей. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления определяются условием

. (11) Это соотношение называется Вульфа-Брегга.

Кристаллографические плоскости можно провести в кристалле множеством способов (рис.). Каждая система плоскостей может дать дифракционный максимум, если для нее окажется выполненным условие (11). Однако заметную интенсивность имеет лишь те максимумы, которые дают плоскости с густо расположенными узлами.

Дифракция рентгеновских лучей от кристаллов находит два основных применения. Она используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия) и для изучения структуры кристаллов (рентгеноструктурный анализ). Определяя направления максимумов, получающихся при дифракции исследуемого рентгеновского излучения от кристаллов с известной структурой, можно вычислить длины волн. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристалле неизвестного строения можно найти межплоскостные расстояния и расшифровать структуру кристалла.

Голография. Голография есть особый способ записи и последующего восстановления изображения предмета, основанный на регистрации интерференционной картины. При освещении фотопластинки (голограммы) пучком света изображение предмета восстанавливается в почти первоначальном виде, так что создается ощущение его реальности.

Для записи предмета на светочувствительной пластинке кроме волны, отраженной от предмета (так называемой предметной волны), используется когерентная с ней волна от источника света (так называемая опорная волна). На фотопластинке фиксируется распределение интенсивности в интерференционной картине, возникающей при наложении предметной и опорной волн. При освещении проявленной фотопластинки происходит дифракция света в фотослое. В результате дифракции восстанавливается изображения предмета.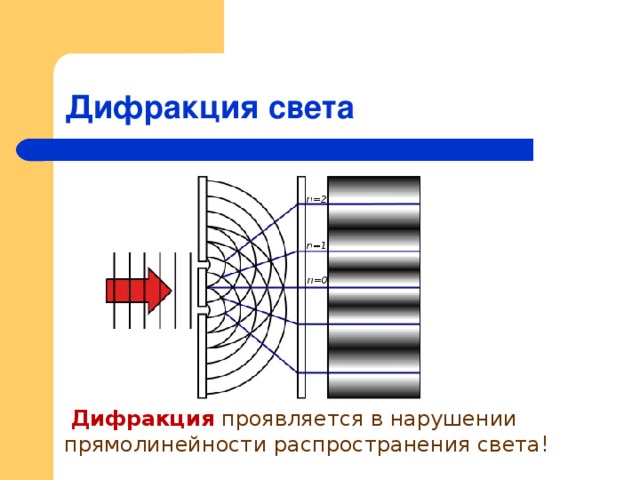

Практически идея голографии осуществляется с помощью схемы, изображенной на рис. Лазерный пучок делится на две части, причем одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предметная волны, являясь когерентными, при наложении интерферируют. Интерференционная картина фиксируется на фотопластинке, после ее проявления получается голограмма – изображение интерференции.

Для восстановления изображения голограмма помещается в то же самое положение, где она находилась до регистрации. Ее освещают опорным пучком того же лазера (вторая часть лазерного пучка перекрывается диафрагмой). В результате дифракции опорной волны возникает несколько волн. Одна волна дает мнимое изображение, которое точно воспроизводит предмет. Другая волна образует действительное изображение предмета. Действительное изображение псевдоскопично – оно имеет рельеф, обратный рельефу предмета (выпуклые места заменены вогнутыми и наоборот). Третья волна является продолжением падающей с меньшей интенсивностью.

Рассмотрим принцип голографии на простом примере. Пусть на фотопластинку падают две когерентные волны, идущих под углом друг к другу. Волна 1 является опорной, волна 2 – предметной (предмет в данном случае представляет бесконечно удаленную точку). Для простоты, предположим, что волна 1 падает на пластинку нормально.

Вследствие интерференции волн на пластинке образуется (и фиксируется) система прямолинейных полос – максимумов и минимумов интенсивности. Пусть точки a и b соответствуют серединам соседних максимумов. Тогда разность хода соответствующих лучей предметной волны до этих точек равна . Из рис. видно, что разность хода и, следовательно,

. (12)

Направим свет опорной волны на проявленную фотопластинку. Пластинка является дифракционной решеткой, период которой определяется формулой (12). Особенность этой решетки состоит в том, что ее прозрачность изменяется плавно (у обычных решеток она изменялась скачком). Эта особенность приводит к тому, что интенсивность дифракционных максимумов выше 1-го практически равна нулю и результирующая дифракционная картина определяется условием

. (13) Максимум m  0 лежит на продолжении опорного пучка. Максимум m  +1 имеет такое же направление, какое имела предметная волна. Кроме того, возникает максимум m  1.

Сходная ситуация возникает и при освещении голограммы, полученной от реального предмета. При этом будет восстановлена световая волна, отраженная предметом (ей отвечает m  +1). Кроме нее, возникают еще две волны (отвечающие m  0 и m  1). Последние распространяются в других направлениях и не мешают восприятию мнимого изображения предмета (которое и представляет главный интерес).

Рассмотренный способ дает одноцветные изображения (цвета лазера). Цветное зрение связано с тремя типами светочувствительных элементов сетчатки глаза, реагирующих на красное, зеленое и синее. Зрительное восприятие, поэтому, складывается из трех одноцветных изображений, соответственно красного, зеленого и синего. Это свойство зрения используется в цветной голографии.

Цветная голография основана на записи объемной интерференционной картины. Восстановление изображения происходит при отражении света от голограммы. Схема записи и восстановления цветного изображения приведена на рис. При записи предмет (последовательно или одновременно) освещается излучением трех цветов: красным, зеленым и синим. В толще фотоэмульсии образуется (и фиксируются) три пространственные интерференционные картины. При освещении белым цветом каждая из систем формирует свое одноцветное изображение предмета. В результате, при наложении трех одноцветных, получаются цветное изображение предмета.

Определение, уравнения, типы и примеры

Дифракция — это явление, которое влияет на волны, когда они сталкиваются с объектом или отверстием на пути своего распространения. То, как на их распространение влияет объект или отверстие, зависит от размеров препятствия.

Явление дифракции

Когда волна распространяется по объекту, между ними возникает взаимодействие. Примером может служить спокойный бриз, двигающий воду вокруг скалы, прорезающей поверхность озера. В этих условиях образуются параллельные волны там, где их ничто не блокирует, а сразу за скалой форма волн становится неправильной. Чем больше камень, тем больше неровность.

Продолжая тот же пример, но заменив камень на открытые ворота, мы испытаем то же самое поведение. Волна образует параллельные линии перед препятствием, но неправильные при прохождении через проем ворот и за его пределами. Неровности вызваны краями ворот.

Рис. 1. Волна распространяется к отверстию. Стрелки указывают направление распространения, а пунктирные линии — фронты волн до и после препятствия. Обратите внимание, как фронт волны ненадолго становится круглым, но возвращается к своей первоначальной линейной форме, когда препятствия остаются позади. Источник: Даниэле Тома, StudySmarter.

Однощелевая апертура

Размер апертуры влияет на ее взаимодействие с волной. В центре апертуры, когда ее длина d больше длины волны λ, часть волны проходит неизмененной, создавая за ней максимум.

Рис. 2. Волна, проходящая через апертуру, длина апертуры которой d больше длины волны λ. Источник: Даниэле Тома, StudySmarter.

Если мы увеличим длину волны, разница между максимумами и минимумами перестанет быть очевидной. Происходит то, что волны деструктивно интерферируют друг с другом в зависимости от ширины щели d и длины волны λ. Мы используем следующую формулу, чтобы определить, где происходит деструктивная интерференция:

n λ = d sin θ

Здесь n = 0, 1, 2 используется для обозначения целых кратных длин волн. Мы можем прочесть его как n, умноженное на длину волны, и эта величина равна длине апертуры, умноженной на синус угла падения θ, в данном случае π/2. Таким образом, мы имеем конструктивную интерференцию, которая дает максимум (более яркие участки изображения) в тех точках, которые кратны половине длины волны. Мы выражаем это следующим уравнением:

n (λ / 2) = d sin θ

Рис. 3. Здесь энергия распределяется на более широкой длине волны, что обозначено расстоянием между синими линиями. Перед открытием диафрагмы происходит более медленный переход между максимумом (синий) и минимумом (черный). Источник: Даниэле Тома, StudySmarter.

Наконец, n в формуле указывает не только на то, что мы имеем дело с кратными длинам волн, но и с порядком минимума или максимума. При n = 1 результирующий угол падения является углом первого минимума или максимума, а n = 2 — вторым, и так далее, пока мы не получим невозможное утверждение, например, что sin θ должен быть больше 1,9. 0003

Дифракция, вызванная препятствием

Первым примером дифракции был камень в воде, т. е. объект на пути волны. Это обратная сторона апертуры, но поскольку существуют границы, вызывающие дифракцию, давайте рассмотрим и это. В то время как в случае апертуры волна может распространяться, создавая максимум сразу после апертуры, объект «разбивает» фронт волны, вызывая минимум сразу после препятствия.

Рис. 4. Под препятствием генерируется волна, гребни которой показаны цветом, а впадины — черным. Источник: Даниэле Тома, StudySmarter.

На рисунке показан сценарий, в котором волна всегда одна и та же, а препятствия становятся все шире.

Волна прерывается мельчайшим препятствием, но не настолько, чтобы разбить фронт волны. Это связано с тем, что ширина препятствия мала по сравнению с длиной волны.

Препятствие большего размера, ширина которого равна длине волны, вызывает одиночный минимум сразу после него (красный кружок, 2-е изображение слева), что свидетельствует о нарушении фронта волны.

Третий случай представляет собой сложную закономерность. Здесь фронт волны, соответствующий первому гребню (красная линия), разделен на три части и имеет два минимума. Фронт следующей волны (синяя линия) имеет один минимум, после чего мы снова видим разницу между гребнями и впадинами, даже если они изогнуты.

Очевидно, что препятствие вызывает смещение фронта волны. Над желтой линией есть два неожиданных небольших гребня, вызванных изгибом волны. Это рассогласование наблюдается во внезапных максимумах после фазового сдвига препятствия.

Дифракция — основные выводы

• Дифракция — это результат влияния границы на распространение волны, когда она встречает препятствие или отверстие.
• Размер препятствия имеет важное значение в дифракции. Его размеры по сравнению с длиной волны определяют форму гребней и впадин после того, как волна пройдет препятствие.
• Фаза изменяется из-за достаточно большого препятствия, из-за чего фронт волны изгибается.

Объяснение урока: Дифракция световых волн

В этом объяснении мы научимся описывать интерференционные картины, создаваемые волнами, которые дифрагируют, проходя через щели и преодолевая различные расстояния.

Световые волны от источника света распространяются от источника во всех направлениях. Барьер с небольшим зазором можно разместить рядом с источником света. Зазор иногда называют отверстием или щелью. Только световые волны, проходящие через зазор, переходят на другую сторону зазора, как показано на следующем рисунке.

Однако рисунок, на котором показаны волны, проходящие через щель, на самом деле не совсем точен. Более правильное представление волновых фронтов эти волны показаны на рисунке ниже.

На этом рисунке видно, что эти волновые фронты удлиняются по мере удаления от зазора. Поэтому волны, проходящие через зазор, меняют направление.

Важно понимать, что изменение направления световых волн не связано ни с отражением волн от границы, ни с преломлением световых волн.

Световые волны могут менять направление из-за отражения, а также из-за преломления. Однако явление, описываемое в этом объяснителе, является явлением, отдельным от отражения и преломления.

Как при отражении, так и при преломлении световые волны должны падать на границу между областями, содержащими вещества с разными показателями преломления. Однако в этом случае одно и то же вещество занимает пространство по обе стороны от зазора, а также внутри зазора. Изменение показателя преломления не происходит.

Процесс изменения направления световых волн без падения волн на границу между областями с разными показателями преломления называется дифракцией.

Дифракция происходит не только в промежутках. Дифракция также происходит, когда световые волны распространяются параллельно поверхности и достигают конца поверхности. Это показано на следующем рисунке.

Величина изменения направления волн может варьироваться при дифрагировании световых волн. Величина изменения направления называется углом дифракции.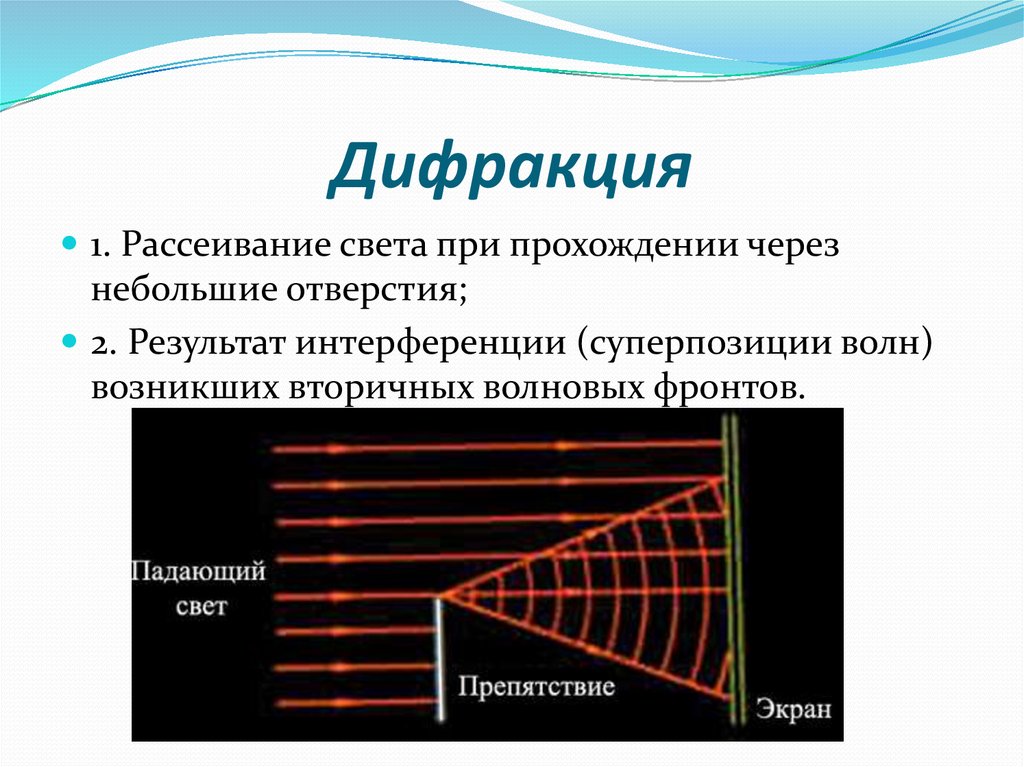 Угол дифракции световых волн, проходящих через зазор, показан на следующем рисунке как угол 𝜃.

Для световых волн, дифрагированных при прохождении через щель в барьере, угол дифракции зависит от ширины щели и длины волны света. Угол дифракции должен быть меньше 90 градусов.

Давайте теперь рассмотрим пример, касающийся дифракции.

Пример 1: Определение дифракции

Какое из следующих определений является правильным определением дифракции?

1. Дифракция – это изменение направления волны, которая проходит вблизи объекта и меняет свое направление на угол, меньший 90 градусов.
2. Дифракция – изменение направления волны, проходящей из одной среды в другую с другой плотностью.
3. Дифракция — это изменение длины волны волны, проходящей через отверстие.
4. Дифракция — это изменение направления волны, которая проходит вблизи объекта и меняет свое направление на угол, превышающий 90 градусов.
5. Дифракция — это изменение скорости волны, проходящей через отверстие.

Ответ

Изменение направления световых волн при прохождении через отверстие является примером дифракции.

Дифракция произойдет, если среда, в которой распространяется волна, по обе стороны от апертуры и внутри апертуры одинакова. Это означает, что плотность среды, в которой движется волна, не является частью правильного определения дифракции.

Скорость, с которой движется световая волна, зависит от показателя преломления среды, в которой распространяется свет. Свет может дифрагировать, путешествуя в среде с постоянным показателем преломления. Это означает, что изменение скорости световой волны не является частью правильного определения дифракции.

Длина волны световой волны данной частоты зависит от показателя преломления среды, в которой распространяется свет. Свет может дифрагировать, путешествуя в среде с постоянным показателем преломления. Это означает, что изменение длины волны световой волны не является частью правильного определения дифракции.

Не исключены только варианты, что дифракция — это изменение направления волны, проходящей вблизи объекта. Угол изменения направления волны менее 90 градусов в одном варианте и более 90 градусов в другом варианте.

Дифракция световых волн не может изменить направление распространения волн. Угол преломления дифрагированного света не может быть больше 90 градусов, а фактически должен быть меньше 90 градусов.

Существует зависимость между углом дифракции для дифрагированного света, проходящего через зазор, длиной волны света и шириной зазора.

Зависимость: длина волны света, дифрагированного под углом, и ширина зазора, через который проходит свет

Чем меньше ширина щели, тем больше угол дифракции проходящего через нее света.

На следующем рисунке показана дифракция световых волн через три щели разной ширины. Через каждую щель проходит свет с одинаковой длиной волны 𝜆.

Мы видим, что наибольший угол дифракции приходится на самую узкую щель. Однако важно понимать, что, когда свет проходит через зазор уже, чем длина волны света, хотя свет и дифрагирует, это не приводит к созданию наблюдаемой дифракционной картины того типа, который будет описан позже в этом документе. объяснитель.

На диаграмме видно, что волновые фронты волны, проходящей через самую широкую щель, имеют заметно отличающуюся форму от света, проходящего через другие щели.

Мы также можем видеть, что волновые фронты света, проходящего через самую широкую щель, сразу после прохождения шире, чем волновые фронты света, проходящего через другие щели.

Свет, проходящий через зазор шириной 𝜆, однако, преломляется под большим углом, чем свет, проходящий через самый широкий зазор.

На следующем рисунке показано, что произойдет с волновыми фронтами волн, проходящих через самый широкий зазор и через зазор шириной 𝜆 после того, как они оба пройдут некоторое расстояние от зазоров.

Мы видим, что распространение волновых фронтов от зазора шириной 𝜆 больше, чем от более широкого зазора за пределами определенного расстояния от зазоров, показанных зеленой линией на следующем рисунке.

Мы видим, что, поскольку наклон белой линии больше, чем наклон черной линии, для горизонтальных расстояний от щели до зеленой линии больше, чем это, расхождение волновых фронтов больше для щели шириной 𝜆 .

Мы видим также, что вблизи щели формы волновых фронтов совсем другие, но по мере удаления от щели волновые фронты волн от обеих щелей все больше приближаются к фронтам плоских волн.

Когда свет проходит расстояние от зазора, намного превышающее ширину зазора, ширина зазора пренебрежимо мала по сравнению с расстоянием, пройденным светом от зазора. В этом случае угол дифракции можно приблизительно определить как измеренный от центра зазора, как показано на следующем рисунке.

При рассмотрении дифракции в этом объяснении мы будем рассматривать свет только на горизонтальном расстоянии от промежутка, превышающем расстояние, соответствующее расстоянию до зеленой линии на предыдущих рисунках.

Давайте теперь рассмотрим пример с углами дифракции для света, проходящего через разные промежутки.

Пример 2. Сравнение дифракции световых волн, проходящих через разные зазоры

Свет проходит через зазоры в экране A, B и C, как показано на схеме. Свет, проходящий через каждую щель, падает на экран перпендикулярно. Длина волны света через каждую из щелей одинакова, но щели имеют разную ширину. Свет, проходящий через каждую щель, дифрагирует. После перемещения на расстояние 𝑑 мимо промежутков показаны волновые фронты волн, отстоящих на одну длину волны; 𝑑 намного больше, чем длина волны 𝜆. Длины передних волновых фронтов 𝐿, 𝐿 и 𝐿 варьируются в зависимости от размера зазора, через который прошел свет.

1. Какая из щелей ближе всего по ширине к длине волны проходящего через нее света?
2. Ширина какой из щелей дальше всего от длины волны проходящего через нее света?

Ответ

Часть 1

Величины длин 𝐿, 𝐿 и 𝐿 показывают величину растекания волновых фронтов света, прошедшего через зазоры A, B, и C.

В вопросе говорится, что расстояние 𝑑 намного больше, чем длина волны 𝜆, поэтому углы дифракции можно принять от центра зазора.

Наибольшее распространение волновых фронтов происходит при наибольшем угле дифракции, как показано на следующем рисунке.

Наибольший угол дифракции возникает для щели шириной, равной длине волны проходящего через нее света. Величина 𝐿 наибольшая, поэтому зазор A должен быть ближе всего по ширине к длине волны света.

Часть 2

Значения 𝐿 и 𝐿 меньше, чем у 𝐿, поэтому ширина промежутков B и C должна быть менее близкой к ширине длины волны света. Наименьший угол дифракции имеет место для зазора B. Зазор B должен быть дальше всего по ширине от длины волны света.

Свет от одного источника света может дифрагировать от двух промежутков, расположенных так близко друг к другу, что дифрагированный свет от каждого промежутка проходит через одно и то же пространство. Волновые фронты света от каждого зазора перекрывают друг друга, когда это происходит. Это показано на следующем рисунке.

Там, где фронты волн от каждого зазора перекрываются, световые волны интерферируют. Световые волны, прошедшие равные расстояния, конструктивно интерферируют. Это показано на следующем рисунке.

Синие и красные линии начинаются от источника света. Мы видим, что общая длина двух синих линий равна общей длине двух красных линий. Это означает, что в точке на перекрывающихся волновых фронтах, где встречаются синяя и красная линии, световые волны от источника света прошли одинаковое расстояние от источника.

Когда световые волны прошли равные расстояния от источника света, разница между расстоянием, которое прошли волны, равна нулю.

Волны не должны проходить равные расстояния, чтобы интерферировать конструктивно, они также интерферируют конструктивно, если расстояние, которое они прошли от своего источника, отличается на целое число их длин волн.

Любое целое число длин волн приводит к конструктивной интерференции, поэтому интерференция является конструктивной, когда разница в числе длин волн между расстоянием, пройденным волнами, имеет значение 0,1,2,3,…,𝑛, где 𝑛 — целое число.

Световые волны из щелей также могут разрушать интерференцию. Это происходит, когда разница в числе длин волн между расстоянием, пройденным волнами, имеет значение 12,32,52,…,𝑛2, где 𝑛 — целое число.

Рассмотрим теперь пример интерференции дифрагированных световых волн.

Пример 3: Идентификация конструктивной и деструктивной интерференции в дифрагированных световых волнах

На диаграмме показаны волновые фронты двух волн, которые преломились через одинаково узкие промежутки. Обе волны имеют одинаковую скорость, длину волны, частоту и начальное смещение.

1. Сколько длин волн этого света составляет промежуток слева от точки А?
2. Сколько длин волн этого света составляет правый зазор от точки А?
3. Является ли интерференция двух световых волн в точке А конструктивной или деструктивной?
4. Сколько длин волн этого света составляет левый зазор от точки B?
5. Сколько длин волн этого света составляет правый зазор от точки B?
6. Является ли интерференция двух световых волн в точке B конструктивной или деструктивной?
7. Сколько длин волн этого света составляет левый зазор от точки C?
8. Сколько длин волн этого света составляет правый зазор от точки C?
9. Является ли интерференция двух световых волн в точке C конструктивной или деструктивной?
10. Сколько длин волн этого света составляет левый зазор от точки D?
11. Сколько длин волн этого света составляет правый зазор от точки D?
12. Является ли интерференция двух световых волн в точке D конструктивной или деструктивной?

Ответ

Этот вопрос состоит из трех частей для каждого из пунктов A, B, C и D. Для каждого пункта три вопроса одинаковы. Вопросы следующие: сколько длин волн прошел свет из левой щели? Сколько длин волн прошел свет из правого зазора? Является ли вмешательство конструктивным или деструктивным?

Рассмотрим приведенную схему.

Все точки, пересекающие фронт оранжевой волны, прошли целое число длин волн от левого зазора. Ближайший к зазору фронт волны находится на расстоянии 1 фронта от зазора, фронт следующей волны — на расстоянии 2 волновых фронтов от зазора и так далее.

То же самое относится к синим волновым фронтам, за исключением того, что для этих волновых фронтов расстояния составляют несколько длин волн от правого зазора.

Интерференция в точке является конструктивной, если количество длин волн на расстоянии как от левого, так и от правого зазора является целым числом.

Если расстояния от двух щелей в точке отличаются на половину длины волны, то интерференция в этой точке разрушительна.

Теперь мы можем ответить на вопросы по каждой точке.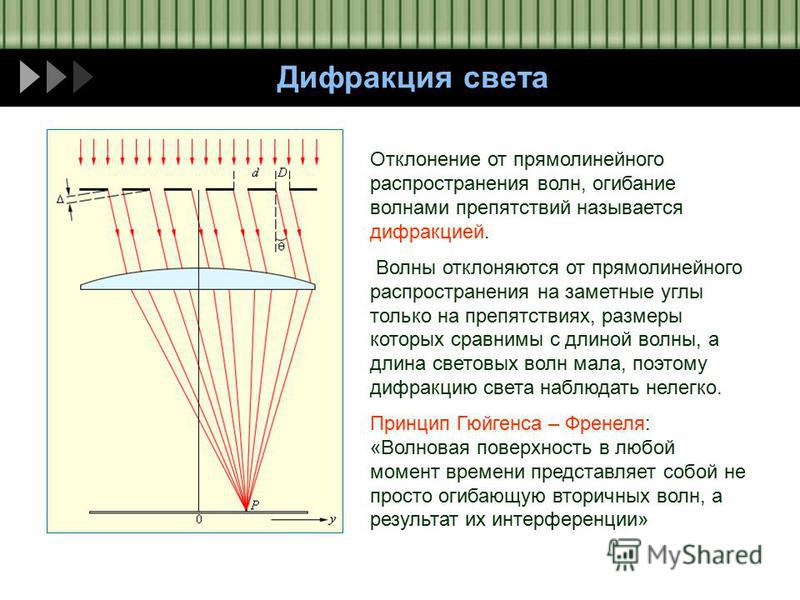

Части с 1 по 3

Точка А находится на расстоянии 2 длин волн от любого зазора. Расстояния, пройденные волнами, равны. Таким образом, интерференция в точке А является конструктивной.

Детали с 4 по 6

Точка B находится на расстоянии 4 длин волн от любого зазора. Расстояния, пройденные волнами, равны. Таким образом, интерференция в точке B является конструктивной. Точка C находится на полпути между третьим и четвертым фронтами волны от правого зазора. Тогда точка C находится на расстоянии 3,5 длины волны от правого зазора. Разница длин волн, пройденных волнами из двух зазоров в точке C, равна 3,5−3=0,5=12.

Таким образом, вмешательство в точке C является разрушительным.

Детали с 10 по 12

Точка D находится на расстоянии 3 длин волн от левого зазора и 2 длин волны от правого зазора. Разница длин волн, пройденных волнами из двух зазоров в точке D, равна 4−3=1.

Таким образом, интерференция в точке D является конструктивной.

В точке, где две световые волны конструктивно интерферируют, амплитуда световых волн равна сумме амплитуд двух световых волн. Там, где световые волны деструктивно интерферируют, амплитуда равна нулю.

Рассмотрим волновые фронты света, дифрагированного от двух близких щелей. Это показано на следующем рисунке.

Мы видим, что для одних углов дифракции интерференция конструктивна, а для других интерференция деструктивна.

Мы видим, что параллельно промежуткам, в точке посередине между ними интерференция носит конструктивный характер.

Мы также видим, что углы конструктивной и деструктивной интерференции чередуются симметрично по обе стороны от зазора.

Если свет, дифрагированный от двух близлежащих промежутков, падает на экран перпендикулярно промежуткам, он создает узор из чередующихся светлых и темных областей. Это показано на следующем рисунке.

Мы видим, что самая яркая часть паттерна находится в центре. По обеим сторонам от центра симметрично чередуются светлые и темные области, называемые бахромой. Яркость середины яркой каймы уменьшается по мере удаления от центра узора.

Ранее в этом объяснении упоминалось, что свет, проходящий через зазор уже, чем длина волны света, не будет давать дифракционную картину.

Напомним, что угол дифракции для света, дифрагированного на зазоре, более узком, чем длина волны света, был очень велик. На самом деле угол дифракции был бы достаточно велик, чтобы вся картина состояла из одной яркой области. Только когда наблюдаются несколько ярких областей, разделенных темными областями, это считается дифракционной картиной.

Давайте теперь рассмотрим пример с дифракционной картиной.

Пример 4. Идентификация узора, создаваемого светом, дифрагированным через близлежащие зазоры

Источник света излучает свет, который проходит через две узкие щели и затем падает на экран, как показано на схеме. Какой из четырех рисунков на экранах A, B, C и D наиболее точно отображает рисунок, который будет создаваться на экране светом, дифрагированным через щели?

Ответить

Свет, проходящий через щели, образует узор из чередующихся светлых и темных полос. Этого нет в паттерне B, поэтому мы можем его исключить.

Самая яркая часть полученного рисунка будет в центре рисунка. В узоре С центр узора представляет собой темную бахрому. Мы можем исключить паттерн C.

Неясно, светлый центр паттерна D или темный. Узор D очень асимметричен. Полученный узор будет симметричным. Мы можем устранить паттерн D.

Образец A имеет яркую бахрому в центре. По бокам от центра симметрично чередуются светлые и темные полосы. Паттерн А — это паттерн, который будет создан.

Нет ничего особенного в том, что количество промежутков, через которые преломляется свет, равно двум. Подобные узоры создаются при большем количестве пробелов, чем два. Также подобный узор получается всего за один разрыв.

Давайте рассмотрим пример, включающий узоры, создаваемые дифрагированием света через разное количество промежутков.

Пример 5: Связь картины, создаваемой дифракцией света, проходящего через промежутки, с количеством промежутков

Какое из следующих утверждений наиболее правильно описывает взаимосвязь между количеством соседних промежутков, через которые проходят волны, и дифракционной картиной, создаваемой волны?

1. Дифракционная картина получается при любом количестве зазоров.
2. Дифракционная картина создается только при наличии одного зазора.
3. Дифракционная картина создается только при наличии двух зазоров.
4. Дифракционная картина образуется только за счет количества зазоров, равного длине волны.

Ответ

Из многих примеров известно, что свет, дифрагированный через два соседних промежутка, образует узор. Рисунок создается интерференцией света, проходящего через зазоры. Если добавить больше промежутков, свет, дифрагированный через добавленные промежутки, будет мешать свету, дифрагировавшему через изначально существующие промежутки. Это означает, что шаблон будет создан, если количество промежутков больше двух.

Единственный вариант, который согласуется с этим фактом, состоит в том, что паттерн будет создаваться любым количеством пробелов. Важно признать, что это включает в себя номер один. Дифракционная картина будет создаваться светом, проходящим через одиночный зазор.

Давайте теперь обобщим то, что было изучено в этом объяснителе.

Ключевые моменты

• Процесс изменения направления световых волн без падения волн на границу между областями с разными показателями преломления называется дифракцией.
• Дифракция возникает, когда световые волны проходят через зазор или распространяются параллельно поверхности и достигают конца поверхности.
• Угол дифракции световых волн максимален для щели шириной, равной длине волны световых волн.
• Дифракция световых волн вызывает как конструктивную, так и деструктивную интерференцию.
• Дифрагированный свет, падающий на экран перпендикулярно щелям, преломляющим свет, создает узор из ярких и темных полос.

Явления оптической дифракции вокруг краев фотодетекторов: упрощенный метод для метрологических приложений

Abstract

В этой статье сообщается об оптическом методе одновременной генерации и обнаружения дифракции света вокруг краев фотодетекторов, а также о его применении для измерения вибрации. . В методе используется инновационное освещение световым пучком, при котором лазерный луч падает на границу раздела между активной и непрозрачной областями фотодетектора. Дифракция и индуцированная интерференция возникают вместе в чувствительной области фотодетектора. Тот же фотодетектор реагирует на динамические изменения интенсивности, соответствующие интерференционной картине, вызванной дифракцией, и одновременно генерирует динамический электрический выходной сигнал. По сравнению с известными методами дифракции, использующими ребра, предлагаемый метод прост в реализации и расширяет область применения измерений. Полученные здесь экспериментальные результаты подтверждают эффективность предложенного метода, указывая на его пригодность для применения в практических условиях для нового класса датчиков.

Введение

Лазеры в основном используются в качестве диагностических инструментов или источников энергии в научных исследованиях. Управление профилем лазерного луча в пространстве и времени является важной исследовательской задачей в области оптических технологий. Когда лазерный луч используется для измерительных приложений, гораздо важнее пространственный профиль лазерного луча, демонстрирующий определенные схемы распределения и свойства распространения в пространстве и времени. Наиболее яркими примерами являются интерференционные и дифракционные картины, часто наблюдаемые каждый день в экспериментах со светом. В действительности разницы между интерференционной и дифракционной картиной нет. Дифракционная картина, видимая на любом экране наблюдения, на самом деле является еще одной интерференционной картиной. Однако эти два явления настолько различны и так адекватно объясняются во многих учебниках. Даниэль Малакара ¹ в своей книге подробно описал эти явления, их отличия, преимущества и недостатки и различные приборы, которые изготавливаются для физических измерений. Измерения смещения и вибрации представляют интерес для многих инженерных задач, использующих эти два явления.

Разработано несколько методов, использующих оптическую интерференцию для измерения перемещений и вибраций ² . Многочисленные традиционные интерферометры ¹ в настоящее время используются для миссии обычного человека от исследовательских лабораторий до летающих спутников. Эти оптические методы в сочетании с передовыми компьютерами, захватчиками кадров и алгоритмами обработки изображений делают их удобными для большинства промышленных применений. Среди классических интерферометрических методов ¹ муаровая интерферометрия ^3,4 , голографическая интерферометрия ^5,6 , лазерная доплеровская виброметрия ⁷ , спекл-интерферометрия ^8,9 ученых и инженеров. Считается, что эти интерферометрические методы обладают высокой эффективностью и в целом хорошо подходят и надежны для метрологических приложений. Однако с их практическим использованием связаны серьезные недостатки, особенно когда рассматривается несколько точек измерения или установка должна выполняться на открытых пространствах. Действительно, сенсорные системы, использующие интерферометрию, являются громоздкими, поскольку они связаны с рядом оптических элементов, а их сложность существенно возрастает и предъявляет строгие механические требования, поскольку выравнивание имеет решающее значение. Поэтому они очень дорогие.

Аналогичным образом, в качестве альтернативы оптической интерферометрии было разработано несколько методов, использующих оптическую дифракцию ^11,12 . Различные понятия используются для описания явления дифракции как интерференции ^13,14 , но его использование, особенно для измерения вибрации, до сих пор не используется в полной мере. Несколько исследователей внесли свой вклад в изучение явления краевой дифракции. Разработанные теории были применены ко многим проблемам, представляющим научный и инженерный интерес ^{15,16,17,18,19,20} . Однако проблема краевой дифракции не получила значительной идентичности в метрологических приложениях, как ее аналог традиционной интерферометрии, в основном из-за ее геометрических ограничений. Сложность введения непрозрачного края на пути света является ключевым геометрическим ограничением с точки зрения системы. В этой статье представлен относительно простой и эффективный метод, в котором отсутствует необходимость во внешнем непрозрачном крае. В качестве внешнего непрозрачного края в предлагаемой методике рассматривается внешний край чувствительной области самого фотоприемника. Таким образом, одновременная генерация и регистрация оптической дифракционной картины реализуются с помощью одного фотодетектора. Этот упрощенный метод достаточно оптически стабилен и может расширить область применения оптической дифракции до нового уровня. Продемонстрировано эффективное использование предложенного метода на оптическом микрофоне, а полученные результаты проверены на стандартном микрофоне.

Методы

Понятие краевой дифракции

Оптическая дифракция очень часто относится к огибанию световых волн вокруг препятствия. На рисунке 1 схематично показана концепция создания оптической дифракционной картины из монохроматического света. Световая волна частично блокируется непрозрачным предметом, прежде чем попасть на экран, как показано на рис. 1. Согласно сложившимся геометрическим теориям оптики, острая кромка непрозрачного предмета отбрасывает тень, имеющую достаточно резкие очертания той же формы.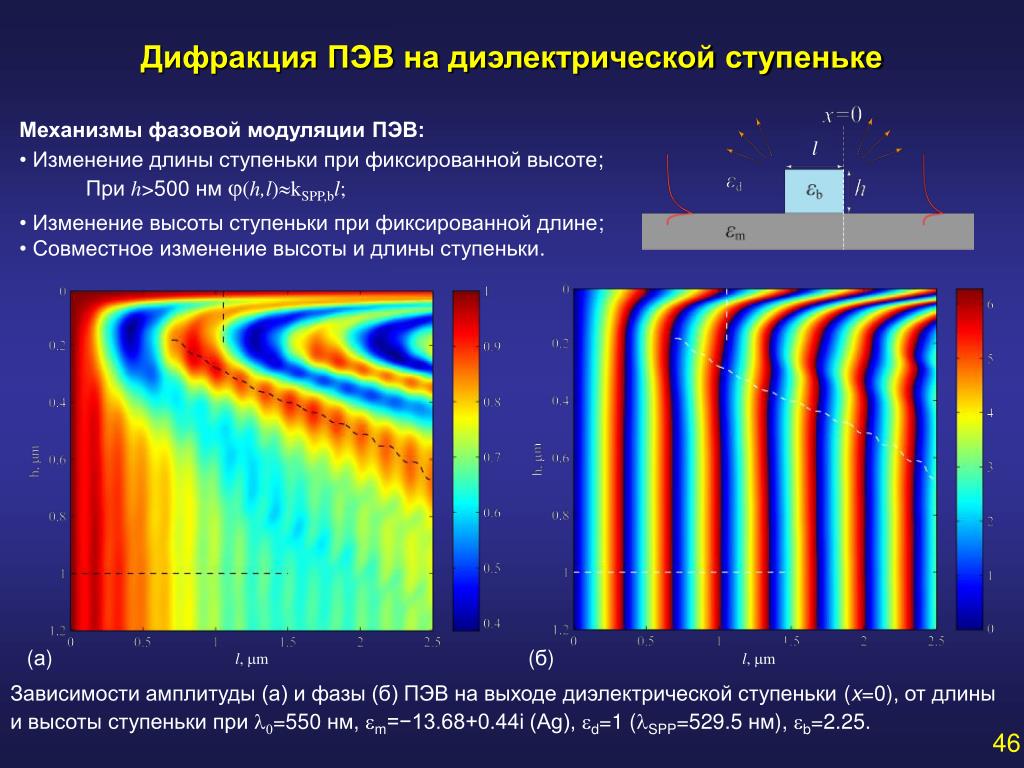 как непрозрачный объект в точке P. Однако при более внимательном рассмотрении оказывается, что край этой тени не является абсолютно резким, а показывает систему темных и светлых полос в непосредственной близости от края в точке P. Эти темные и яркие полосы называются картиной дифракции, как показано на рис. 1. Эта картина возникает из-за дифракции света вокруг нижнего края непрозрачного объекта и в результате интерференции прямых и дифрагированных световых лучей. Если освещенность в какой-либо точке равна нулю или минимальна, это называется деструктивной интерференцией, которая представляет собой темную полосу, а если она максимальна, это называется конструктивной интерференцией, которая представляет собой яркую полосу. Дальнейшее рассмотрение этого традиционного метода дифракции доступно в учебнике по физике Serway и Jewett 9.0353 21 . Традиционная краевая дифракционная картина и распределение интенсивности, показанные на рис. 1, используются далее в этой статье для сравнения предложенной нами концепции.

Рисунок 1

Схематическая диаграмма, иллюстрирующая явление дифракции на линейке.

Изображение полного размера

Явление дифракции изучается в рамках двух классов, а именно теорий дифракции Френеля и Фраунгофера ^22,23,24 . Дифракция Френеля представляет собой плохое приближение — случаи, когда один или оба источника и экрана наблюдения находятся достаточно близко к апертуре, поэтому необходимо учитывать кривизну волнового фронта. Работа, представленная в этой статье, посвящена дифракции Френеля. Дифракционная картина Френеля имеет математически сложный характер ^13,25 .

Среди них хорошо известен подход Френеля, основанный на принципе Гюйгенса ^26,27 . Он описывает дифракционное поле в терминах суперпозиции двух волн: одна волна распространяется через дифрагирующий объект без каких-либо возмущений (называется геометрической волной), а вторая волна исходит из каждой точки освещенной границы объекта или края (называется границей). дифрагированная волна). Распределение интенсивности на экране наблюдения можно записать как 9{2}\), он касается первого, когда cos( kδ ) = +1, и позже, когда cos( kδ ) = −1. Это показывает, что в плоскости наблюдения интерференционные полосы генерируются в области прямого освещения, где U ^(ж) интерферирует с U ^(г) , однако в области геометрической тени только U ^{( г)} присутствует и, следовательно, помех не наблюдается. Контраст этих полос продолжает уменьшаться по мере удаления от границы тени. Это связано с тем, что амплитуда геометрической волны почти постоянна в области прямого освещения, в то время как амплитуда граничной дифракционной волны быстро падает по мере удаления от граничной тени. Ширина бахромы 9{1/2}]\,n=1,\,2,\,3,\ldots ,$$

(2)

где r — расстояние между источником и непрозрачным краем, а b — расстояние между непрозрачным краем и экраном наблюдения. Уравнение (2) показывает, что ширина полосы β продолжает уменьшаться с увеличением порядка полосы n .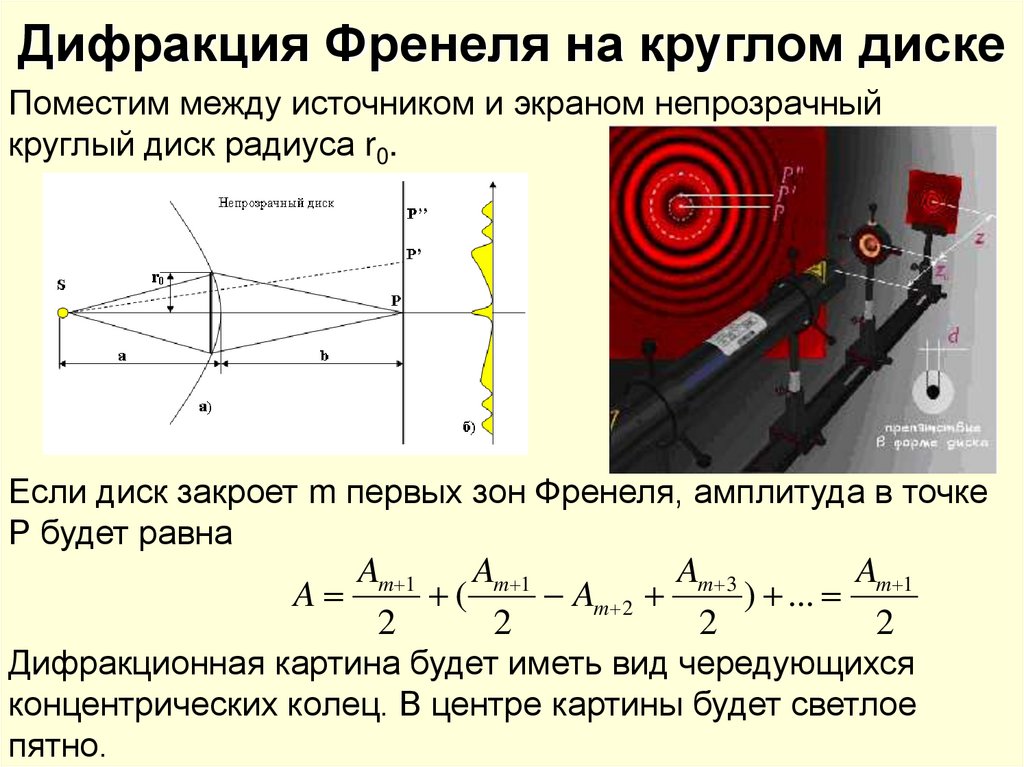 Кроме того, для конкретного порядка интерференционных полос n , β можно увеличить, уменьшив r . Уравнение (2) также показывает, что его можно использовать для описания явления на основе освещения точечным источником, а не на основе коллимированного источника света. Позже в разделе обсуждений мы расскажем, что в качестве источника света использовался диодный лазер. Он имеет микролинзу, прикрепленную к его излучающей головке, чтобы изменить форму луча от эллиптической до круглой, и имеет расходимость около 0,8 мрад. Мы не использовали никакую внешнюю оптику для коллимации лазерного луча в наших экспериментах. Следовательно, уравнение (2) по-прежнему можно использовать для описания явления, поскольку лазерный источник с расходимостью 0,8 мрад можно приблизить к точечному источнику. С другой стороны, расходимость играет решающую роль в дифракционных экспериментах, и поэтому ею нельзя пренебрегать, в отличие от интерференционных экспериментов. Однако достижимое изменение ширины полосы за счет изменения r не будет существенным, если расстояние между непрозрачной кромкой и экраном наблюдения b будет очень меньше по сравнению с r . В предлагаемом методе краевой дифракции b очень меньше по сравнению с r .

Концепция дифракции вокруг края фотодетектора: одновременная генерация и детектирование

В этой работе оптическая дифракция устанавливается без поддержки какого-либо внешнего непрозрачного объекта. С другой стороны, в качестве непрозрачного объекта использовался край чувствительной области фотодетектора, который используется для регистрации дифракционной картины. Экспериментальная установка, используемая для одновременной генерации и обнаружения такой дифракционной картины, показана на рис. 2 (а). Дифракционная картина создается на фотодетекторе путем освещения фотодетектора таким образом, что световой луч падает на границу раздела между активной чувствительной и непрозрачной областями фотодетектора, как показано на рис. 2(b). Дифракционная картина, сформированная на фотодетекторе, показана на рис. 2(в), а соответствующее распределение интенсивности, полученное вдоль центральной горизонтальной оси, показано на рис. 2(г). Одновременно фотодетектор генерирует электрический сигнал, соответствующий картине интерференционных полос в реальном времени. Поэтому этот метод называется одновременным.

Рисунок 2

Дифракция вокруг края фотоприемника: ( a ) Экспериментальная схема для одновременной генерации и регистрации; ( b ) Освещение по краям; ( c ) Полученная дифракционная картина и ( d ) Полученное распределение интенсивности.

Полноразмерное изображение

Изображения, представленные на рис. 2(b,c), сняты внешней цифровой зеркальной камерой Nikon D5600. Изображение, представленное на рис. 2(b), не может показать явление дифракции с деталями и диапазоном освещения непосредственно для глаза, но оно может указывать на общий характер эффекта. Изображение, показанное на рис. 2(c), представляет собой увеличенную часть краевой области дифракции на фотодетекторе. Впоследствии изображение, показанное на рис. 2(c), подвергается анализу с использованием программного обеспечения Matlab. Значения интенсивности преобразуются в цифровую информацию путем тщательного считывания координатных точек. Данные, представленные на рис. 2(d), получены путем извлечения значений интенсивности вдоль центральной горизонтальной оси рис. 2(c).

Полученная картина интерференционных полос и распределение интенсивности, показанное на рис. 2(c,d) с помощью предлагаемого метода, сравниваются с таковыми для традиционно установленной прямолинейной дифракции Френеля ²¹ , показанной на рис. 1. Сравнение подтверждает, что существуют сходство и близкое соответствие между традиционным и предлагаемым случаями краевой дифракции. Полосы, полученные предложенным методом, имеют искривленную форму, а чередующиеся полосы проявляют более высокую интенсивность, чем предыдущие. Причина такого изогнутого вида полос и изменения амплитуды чередующихся полос связана с тем, что край фотодетектора, использованного в этом исследовании, представляет собой не совсем один прямой край, а изогнутый край. Кривые ребра можно рассматривать как состоящие из бесконечного числа бесконечно малых прямых ребер, имеющих разную ориентацию. Из-за этого внутри фотодетектора в разных ориентациях формируются разные прямолинейные дифракционные картины, которые интерферируют между собой. Это чаще встречается в задачах дифракции и называется эффектом каустики 9.0353 28,29 . Сравнение качественно показало, что сходства намного больше, чем различий, за исключением очевидной кривизны. Никакого другого прямого сравнения в традиционной литературе и искусстве не существует. Однако исследования, проведенные П. М. Ринаром ³⁰ в 1976 г. на крупномасштабных дифракционных картинах от круглых объектов, также подтверждают данные, представленные на рис. 2(d). Чтобы дополнительно обосновать эти данные, можно рассмотреть эквивалентный муаровый узор, нарисовав различные полосы прямых краев на экране наблюдения по всей ориентации изогнутого края, в результате чего будут получены данные, аналогичные показанным на рис. 2 (c). .

Предложенная система краевой дифракции обладает многочисленными преимуществами по сравнению с другими традиционными методами, такими как интерферометры. Основным преимуществом этого метода является простота его реализации, когда нет необходимости в оптике. Традиционные методы включают использование высококачественных оптических элементов, таких как линза, светоделитель, зеркало, и, следовательно, существуют связанные с этим сложности, такие как оптические проблемы выравнивания, аберрации и астигматизма. Традиционные интерферометры требуют относительно мощных лазерных источников, поскольку свет проходит несколько путей через светоделители и, следовательно, связанные с этим потери интенсивности света неизбежны. Другими важными преимуществами являются (i) экономичность и меньшая чувствительность к экологическим и тепловым проблемам, поскольку не используется дополнительная оптика, (ii) возможность оценить радиус кривизны изогнутой дифракционной кромки, (iii) не зависит от свойства материала дифрагирующей кромки, независимо от того, является ли он проводящим или непроводящим, отражающим или поглощающим, металлическим или неметаллическим и т. д. Наиболее спонтанным неотъемлемым преимуществом является то, что предлагаемая система краевой дифракции имеет сравнимую более высокую интенсивность дифрагированной волны с прямой геометрической волной и следовательно, можно наблюдать четкие полосовые узоры, поскольку дифракционная кромка встроена в экран наблюдения фотодетектора.

Предлагаемый метод имеет дополнительные преимущества по сравнению с системой квадрантного детектора. Квадрантный детектор имеет четыре ячейки, разделенные промежутком. Основным требованием для использования этого детектора является то, что световой луч должен освещаться во всех четырех квадрантах одновременно. Это условие вводит определенные ограничения в чувствительности, точности, динамическом диапазоне и, следовательно, в приложениях.

Метод, рассмотренный выше в этой статье, находит ряд метрологических, гражданских и оборонных применений. Некоторыми из наиболее важных и ярких примеров являются (i) дистанционный мониторинг акустического сигнала, (ii) аппаратура для работы в качестве оптического микрофона, (iii) бесконтактная аппаратура для измерения перемещений объектов, (iv) аппаратура для работы в качестве оптический гидрофон для подводного акустического обнаружения, (v) аппаратура для подслушивания, (vi) аппаратура для обнаружения поверхностных волн, внутренних волн и любых гидродинамических возмущений в океане, (vii) аппаратура для обнаружения гравитационных волн (viii) аппаратура для обнаружения колебаний давления в любой оптически прозрачной среде (ix) аппаратура для обнаружения выживших из труднодоступных завалов, образовавшихся в результате стихийных бедствий и т. д.

Результаты и обсуждение

При обсуждении предложенной краевой дифракционной системы очевидно интересно узнать о влиянии площади экспозиции между непрозрачной краевой областью и активной воспринимающей областью. Эффект зависит от нескольких факторов, таких как размер лазерного луча, угол краевого освещения и, следовательно, угол дифракции и юстировка фотодетектора в дополнение к соотношению площадей экспозиции. Подробное изучение и демонстрация этого эффекта требует большого объема исследований и, следовательно, не предпринимается в данной работе.

Реалистичные условия экспозиции 50:50 соблюдались во всех экспериментах, описанных в этой статье. Тем не менее, мы сделали логический анализ, чтобы разумно устранить этот важный эффект, поскольку это было бы полезно для читателей. Наиболее вероятным и заметным результатом из-за влияния площади экспозиции будет увеличение и уменьшение выходного электрического сигнала фотодетектора. Для объяснения этого эффекта сделаны следующие допущения: (i) если экспонируемая площадь активной чувствительной области больше (т. е. условия экспонирования 25:75), то очевидно ожидание, что дифракционная полоса первого порядка будет иметь большую интенсивность и впредь с другими краями. Однако точно оценить эти изменения интенсивности достаточно сложно, так как площадь экспонирования дифрагированного луча внутри фотоприемника зависит от угла освещения и юстировки фотоприемника. Но несомненно, что чистый электрический сигнал на выходе фотодетектора будет увеличиваться из-за комплексного эффекта объясненных выше фактов. (ii) Обратное имеет место, если экспонируемая площадь активной сенсорной области меньше (т.е. условия экспонирования 75:25).

Также интересно выделить эффект пространственной неоднородности, поскольку большинство фотодетекторов имеют проблемы, связанные с такой неоднородностью. Пространственные неоднородные отклики возникают из-за нескольких факторов, таких как кристаллическая структура, качество изготовления, излучение, теплопроводность и конвекционные потери, неоднородность материала и эффекты поверхностной рекомбинации и т. д. Также установлено, что он зависит от длины волны, поскольку поглощение сильно зависит на длине волны. Поглощение в видимой области становится достаточно умеренным в кремниевых фотодетекторах, чтобы фотоны могли достигать обедненной области, поэтому генерация носителей из обедненной области становится доминирующей и приводит к хорошей однородности ^31,32 . Мы провели качественный анализ этого эффекта и обнаружили, что неравномерная пространственная чувствительность кремниевых фотодетекторов меньше в видимой области при умеренно низкой интенсивности входного лазерного излучения. Однако при более высокой интенсивности лазера неоднородные отклики возникают даже в видимой области. Мы проверили этот эффект на том же фотодетекторе с входной мощностью лазера 4,9  мВт и заметили, что нет значительных изменений отклика на его активной чувствительной поверхности. Следовательно, эффект пространственной неоднородности не внес бы существенной погрешности в наши измерения ^31,32 .

Экспериментальный метод и изготовленный датчик были предварительно охарактеризованы в лаборатории, а затем сравнены с традиционным методом и датчиками. В следующем разделе сообщаются и обсуждаются экспериментальные результаты.

Лабораторная характеристика для измерения вибрации

Чтобы продемонстрировать возможности применения метода, в этой статье для демонстрации выбран соответствующий пример измерения вибрации. Функциональность обнаружения вибрации с помощью дифракции краев фотодетектора реализована на оптическом столе в лаборатории. В частности, динамический отклик был протестирован и сравнен с традиционным методом. Для этой цели используется экспериментальная установка, показанная на рис. 3. Здесь лазерный луч освещается отражающей вибрирующей испытательной поверхностью, а отраженный луч света собирается на краю фотодетектора, как описано в предыдущих параграфах. В этой установке в качестве вибрирующей испытательной поверхности выбрано маленькое отражающее зеркало, закрепленное на центральной диафрагме лабораторного громкоговорителя. Диодный лазер с круговым лучом мощностью 4,9мВт и длина волны 635 нм, который относится к классу VHK ^™ производства M/s. В качестве источника света использовали Coherent Inc., США. Кремниевый фотодетектор с круглой сенсорной областью 100 мм ² с выходным разъемом BNC, полученным из M/s. В эксперименте использовалась компания Edmond Optics. Любые собственные или индуцированные вибрации, проявляющиеся на диафрагме, изменяют путь лазерного луча, который, в свою очередь, проявляется в виде изменяющейся во времени дифракционной картины на фотодетекторе. В этом случае простое изменение длины пути не изменит дифракционную картину. Тот же фотодетектор регистрирует временные изменения интенсивности света благодаря изменяющейся во времени дифракционной картине, которая, в свою очередь, является проявлением вибраций в реальном времени.

Рисунок 3

Экспериментальная установка для измерения вибрации.

Изображение полного размера

Известный эталонный тестовый сигнал с помощью генератора сигналов подается на громкоговоритель, заставляя диафрагму громкоговорителя вибрировать в ответ на эталонный сигнал. Интенсивность дифракционной картины, генерируемой на фотодетекторе, модулируется с той же скоростью (амплитудой и частотой) вибрации. Выход фотодетектора подключается к одному из каналов осциллографа, а опорный тестовый сигнал подключается к другому каналу для целей проверки. В частности, экспериментальная характеристика расширена до частоты 20  кГц, что является спектральным диапазоном, имеющим первостепенное значение для обнаружения акустических колебаний. Два типичных результата этого эксперимента по определению характеристик в виде снимков экрана показаны на рис. 4.

Рис. 4

Экспериментальные результаты, подтверждающие возможности предлагаемого метода измерения вибрации и сравнения опорного сигнала и сигнала наблюдения. ( a ) сигнал 100 Гц и ( b ) сигнал 5 кГц, поступающий на громкоговоритель.

Изображение полного размера

На рис. 4 график желтого цвета соответствует входу генератора сигналов, а график зеленого цвета соответствует выходу предлагаемого метода. Отмечено, что частоты, измеренные осциллографом для опорного сигнала и выходного сигнала фотоприемника по предлагаемому методу, хорошо согласуются и совпадают.

Валидация обнаружения вибрации с несколькими частотами

Для дальнейшей проверки концепции мониторинга вибрации с помощью спектра частот в реальном времени на компьютере воспроизводится звуковой волновой файл, а выход подключается к громкоговорителю. Экспериментальная установка, показанная на рис. 3, использовалась для этого проверочного эксперимента. Выход фотодетектора подключен к одному из каналов платы сбора данных (DAQ) NI PCI 6014 от National Instruments, которая установлена ​​на другом ПК, и сигнал звуковой волны также подается на другой канал платы сбора данных NI PCI 6014. Мгновенно входные данные, поступающие на карту сбора данных NI PCI 6014, собираются и сохраняются с помощью программного обеспечения LabVIEW. Полученные результаты временного ряда представлены на рис. 5.

Рисунок 5

Экспериментальная проверка предложенного метода в качестве датчика вибрации для полосы частот с вводом звукового волнового файла.

Изображение в натуральную величину

Из рис. 5 видно, что выходной сигнал, зарегистрированный предлагаемым методом, хорошо согласуется и согласуется с заданным сигналом. Это подтверждает эффективность предлагаемого метода мониторинга звука и вибрации и его способность одновременно обнаруживать и различать несколько частот.

Валидация в качестве оптического микрофона

Чтобы продемонстрировать функциональность предлагаемого метода в качестве оптического микрофона, был разработан и изготовлен компактный прототип прибора с использованием метода, показанного на рис. 3. Эскиз концептуальной конструкции, использованный для этого прибора, показан на Рис. 6. Лазер и фотоприемник смонтированы внутри цилиндрического корпуса с соответствующим питанием от батареи и выключателем. Передняя поверхность цилиндрического корпуса была зафиксирована акустически чувствительным материалом с внутренней поверхностью с отражающим покрытием и внешним вращающимся ключом для целей выравнивания.

Рисунок 6

Концептуальный эскиз оптического микрофона, использующего краевую дифракцию фотодетектора.

Полноразмерное изображение

Динамический отклик датчика был проверен с помощью человеческого речевого сигнала. Разработанный датчик оптического микрофона и стандартный микрофон (производства M/s Phillips, модель: SBCMD150/01) располагались перед человеком на расстоянии 15 см, а его речевой сигнал записывался и извлекался при поддержке NI. Карта сбора данных PCI 6104 и программное обеспечение LabVIEW. Впоследствии данные этого временного ряда были подвергнуты спектральному анализу с использованием функций PWELCH и BICOHER в Matlab, чтобы получить представление о спектральном отклике и свойствах когерентности между разработанным датчиком оптического микрофона и стандартным микрофоном. На рисунке 7 показаны типичные временные ряды, спектры и характеристики спектральной когерентности оптического и стандартного микрофонов. Из графиков видно, что оптический микрофон демонстрирует сравнимую частотную характеристику, за исключением небольших отклонений в амплитуде. Амплитудные характеристики различаются из-за встроенного предусилителя, присутствующего в стандартном микрофоне. Обнаружено, что когерентность сохраняется в диапазоне частот 600–4000 Гц, что демонстрирует точность метода для работы в качестве оптического микрофона. Остальные колебания, обнаруженные на спектральном графике, можно отнести к малейшим колебаниям, исходящим от посторонних источников в лаборатории.

Рисунок 7

Временные, спектральные и когерентные характеристики оптического микрофона. ( a ) Время отклика; ( b ) Спектральный отклик и ( c ) Спектральная когерентность.

Полноразмерное изображение

Стоит отметить, что существуют специальные приложения, в которых требуется постоянная запись сигналов, обнаруженных прибором, например, показанный на рис. 6. Этого можно добиться, подключив выходные клеммы фотодетектора, показанные на рис. 6, к любому другому стандартному аудиорекордеру, чтобы его можно было воспроизвести для воспроизведения записанного сигнала. С другой стороны, выходные клеммы фотодетектора можно подключить к стандартной акустической системе с подходящим усилителем, а входной сигнал, подаваемый на оптический микрофон, можно отчетливо слышать вживую.

Выводы

Было успешно продемонстрировано новое наблюдение явления оптической дифракции вокруг краев фотодетектора. Дифракционные полосы генерируются и одновременно регистрируются одним и тем же фотодетектором за счет освещения световым лучом границы между чувствительной и непрозрачной областями фотодетектора. Это упрощает решение традиционных задач краевой дифракции и, таким образом, расширяет возможности применения в приложениях для измерения звука и вибрации. Полученные дифракционные полосы и распределение интенсивности были проверены традиционными методами и признаны соответствующими. Чтобы продемонстрировать возможности метода измерения вибрации, сенсорная система была охарактеризована в лаборатории для диапазона частот от 100 Гц до 10 кГц. Полезность этого метода была использована в различных приложениях для измерения вибрации, и был изготовлен и успешно продемонстрирован датчик оптического микрофона. Предполагается, что концепция и методология, предложенные в документе, могут найти потенциальное метрологическое применение в гражданских и оборонных целях, особенно в подводном зондировании в ближайшем будущем.

Доступность данных

Авторы подтверждают, что данные, подтверждающие результаты этого исследования, доступны в статье. Однако любые наборы данных, сгенерированные и/или проанализированные в ходе текущего исследования, доступны у соответствующего автора по разумным запросам.

Ссылки

1. Малакара, Д. Магазин оптики Тестирование . 3-е изд. (Wiley-Interscience, John Wiley & Sons, Нью-Джерси, 2007 г.).

2. Малакара, Д. Интерференция: физическая оптика и световые измерения. Методы экспериментальной физики 26 , 1–48 (1989).

   ОБЪЯВЛЕНИЕ Статья Google ученый

3. «>

   Harding, K.G. & Harris, J.S. Проекционный интерферометр Муара для анализа вибрации. Прикладная оптика 22 , 856–861 (1983).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

4. Forno, C. Измерение деформации с помощью муаровой фотографии высокого разрешения. Оптика и лазеры в технике 8 , 189–212 (1988).

   ОБЪЯВЛЕНИЕ Статья Google ученый

5. Вест, К. М. Голографическая интерферометрия . (Джон Уайли и сыновья, Нью-Йорк, 1979).

6. Кумар, У. П., Кальяни, Ю., Кришна Мохан, Н. и Котиял, М. П. Телевизионная голография со средним временем для анализа вибрационных полос. Прикладная оптика 48 , 3094–3101 (2009 г.).

   ОБЪЯВЛЕНИЕ Статья Google ученый

7. «>

   Halliwell, N.A. Лазерно-доплеровское измерение вибрирующих поверхностей: портативный прибор. Журнал звука и вибрации 62 , 312–315 (1979).

   ОБЪЯВЛЕНИЕ Статья Google ученый

8. Høgmoen, K. & Løkberg, OJ. Обнаружение и измерение малых вибраций с помощью электронной интерферометрии спекл-спектра. Прикладная оптика 16 , 1869–1875 (1977).

   ОБЪЯВЛЕНИЕ Статья Google ученый

9. Сантханакришнан, Т., Паланисами, П.К. и Сирохи, Р.С. Формирование полос в конфигурации измерения смещения в плоскости с двукратным увеличением чувствительности: теория и эксперимент. Прикладная оптика 37 , 4150–4153 (1998).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

10. Пизани, М. Гомодинный интерферометр Майкельсона с субпикометрическим разрешением. Наука и техника измерений 20 , 084008 (6 стр.) (2009).

11. Малакара, Д. Дифракция и рассеяние: физическая оптика и измерения света. Методы экспериментальной физики 26 , 49–105 (1989).

    ОБЪЯВЛЕНИЕ Статья Google ученый

12. Госвик, К. Дж. Оптическая метрология . (Джон Вили и сыновья, Нью-Йорк, 1987).

13. Борн М. и Вольф Э. Основы оптики . 7-е изд. (Издательство Кэм Юниверсити, Эдинбург, 1999).

14. Ван С. О принципах дифракции. Оптик 100 , 107–108 (1995).

    Google ученый

15. Отис Г., Лашамбр Ж.-Л., Лит В.Ю. и Лавин П. Дифрагированные волны в области теневой границы. Журнал Оптического общества Америки 67 , 551–553 (1977).

    ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый

16. «>

    Ганчи, С. Эксперимент по физической реальности дифрагированных волн. Американский журнал физики 57 , 370–373 (1989).

    ОБЪЯВЛЕНИЕ Статья Google ученый

17. Хижняк А. И., Анохов С. П., Лымаренко Р. А., Соскин М. С., Васнецов М. В. Структура краевой дислокационной волны, возникающей при дифракции плоской волны на полуплоскости. Журнал Оптического общества Америки A 17 , 2199–2207 (2002).

    ОБЪЯВЛЕНИЕ Статья Google ученый

18. Lit, JWY & Tremblay, R. Теория граничных волн дифракции с каскадными апертурами. Журнал Оптического общества Америки 59 , 559–567 (1969).

    ОБЪЯВЛЕНИЕ Статья Google ученый

19. Langlois, P. & Lessard, R. A. Одновременное профилирование и масштабирование лазерного луча с использованием краевой волны дифракции (DEW). SPIE Proceedings 661 , 315–321 (1986).

    ОБЪЯВЛЕНИЕ Статья Google ученый

20. Полянский П.В., Полянская Г.В. Голограмма Юнга – голограмма пятого типа. Журнал оптических технологий 64 , 321–330 (1997).

    ОБЪЯВЛЕНИЕ Google ученый

21. Serway, R. A. & Jewett, J. W. Физика для ученых и инженеров . 6-е изд. (Томсон Брукс/Коул, Бостон, 2004 г.).

22. Сирохи, Р. С. Курс экспериментов с гелий-неоновым лазером . (Wiley Eastern Limited, Нью-Дели, 1986 г.).

23. Эрик Удд. Волоконно-оптические датчики: Введение для инженеров и ученых . (John Wiley and Sons Inc., Нью-Йорк, 1991).

24. Педротти, Ф. Л. и Педротти, Л. С. Введение в оптику, второе издание . (Прентис Холл, Нью-Джерси, 1993).

25. Дженкинс, Ф. А. и Уайт, Х. Э. Основы оптики, четвертое издание . (Макгроу-Хилл, Нью-Йорк, 2001 г.).

26. Дженнингс, Дж. К. и Макгрудер, Ч. Х. III. Сравнение дифракционной картины диска с дифракционной картиной прямой ребра в покрытиях. Астрономический журнал 118 , 3061–3067 (1999).

    ОБЪЯВЛЕНИЕ Статья Google ученый

27. Кумар, Р., Каура, С.К., Шарма, А.К., Чхачхия, Д.П. и Аггарвал, А.К. Дифракционная картина на кромке ножа как явление интерференции: экспериментальная реальность. Оптика и лазерные технологии 39 , 256–261 (2007).

    ОБЪЯВЛЕНИЕ Статья Google ученый

28. Берри, М. В. Разрушение изображений: теорема каустического касания. Журнал Оптического общества Америки A 4 , 561–569 (1987).

    ОБЪЯВЛЕНИЕ Статья Google ученый

29. Берри, М. В. и Уилсон, А. Н. Черно-белые полосы и цвета каустик. Прикладная оптика 33 , 4714–4718 (1994).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

30. Ринар, П. М. Крупномасштабные дифракционные картины от круглых объектов. Американский журнал физики 44 , 70–76 (1976).

    ОБЪЯВЛЕНИЕ Статья Google ученый

31. Фишер, Дж. и Фу, Л. Измерение нелинейности фотодиодов с использованием лазера со стабилизацией интенсивности в качестве источника излучения. Прикладная оптика 32 , 4187–4190 (1993).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

32. Кюбарсепп, Т., Хаапалинна, А. , Карха, П. и Иконен, Э. Измерения нелинейности кремниевых фотодетекторов. Прикладная оптика 37 , 2716–2722 (1998).

    ОБЪЯВЛЕНИЕ Статья Google ученый

Ссылки на скачивание

Благодарности

Авторы признательны Shri. С.К. Шеной, ученому «Х», директору NPOL за предоставление всей необходимой поддержки, критические комментарии и разрешение на публикацию статьи. Авторы благодарят Шри. Правин Нареш, ученый F, за помощь в создании распределения интенсивности по изображению дифракционных полос.

Информация о авторе

Авторы и принадлежности

1. Военно -морская физическая и океанографическая лаборатория, Триккакара П.О., Кочи, 682 021, Керала, Индия

   Т. Сантханакришнан, Р. Раджеш, Рам Лочан Айст. Авторы

   1. T. Santhanakrishnan

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

   2. Р. Раджеш

      Просмотр публикаций автора

      Вы также можете искать этого автора в PubMed Google Scholar

   3. Ram Lochan Awasthi

      Посмотреть публикации автора

      Вы также можете искать этого автора в PubMed Google Scholar

   4. C.V. Sreehari

      Просмотреть публикации автора

      Вы также можете искать этого автора в PubMed Google Scholar

   Вклады

   Т.С. и Р. Р. придумали идею исследования. Р.Л.А. проводят характеристики в лаборатории. C.V.S. спроектировал, изготовил датчик оптического микрофона и провел проверочные эксперименты. Т.С. и Р.Р. координировали исследования и разработали приложения. Р.Л.А. и C.V.S. провел анализ данных. Т.С. и Р.Р. написали рукопись с последующим вкладом Р.Л.А. и C.V.S. Все авторы внесли свой вклад в рукопись, рассмотрели и одобрили подачу окончательной версии рукописи.

   Автор, ответственный за переписку

   Переписка с Т. Сантанакришнан.

   Декларации этики

   Конкурирующие интересы

   Авторы не заявляют о конкурирующих интересах.

   Дополнительная информация

   Примечание издателя: Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

   Права и разрешения

   Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете соответствующую ссылку на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя.

   No related posts.