PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Физика для углубленного изучения. 2. Электродинамика. Оптика

Физика для углубленного изучения. 2. Электродинамика. Оптика

Бутиков Е. И., Кондратьев А.С. Физика для углубленного изучения. Электродинамика. Оптика. Том 2. М.: Физматлит. — 336 с. Учебник принципиально нового типа. Последовательность изложения соответствует логической структуре физики как науки и отражает современные тенденции ее преподавания. Материал разделен на обязательный и дополнительный, что позволяет строить процесс обучения с учетом индивидуальных способностей учащихся, включая организацию их самостоятельной работы. Задачи служат как для получения новых знаний, так и для развития навыков исследовательской деятельности. Для учащихся школ, гимназий, лицеев с углубленным изучением физико-математических дисциплин, а также для подготовки к конкурсным экзаменам в вузы. Оглавление Введение I. ЭЛЕКТРОСТАТИКА § 1. Электрический заряд. Закон Кулона § 2. Электрическое поле. Напряженность поля § 3. Теорема Гаусса § 4. Потенциал электростатического поля. Энергия системы зарядов § 5. Расчет электрических полей § 6. Проводники в электрическом поле § 7. Силы в электростатическом поле § 8. Конденсаторы. Электроемкость § 9. Энергия электрического поля II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 10. Характеристики электрического тока. Закон Ома § 11. Соединение проводников в электрические цепи § 12. Закон Ома для неоднородной цепи § 13. Расчет цепей постоянного тока § 14. Работа и мощность постоянного тока § 15. Магнитное поле постоянного тока § 16. Действие магнитного поля на движущиеся заряды III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 17. Явление электромагнитной индукции § 18. Электрические машины постоянного тока § 19. Энергия магнитного поля § 20. Основы теории электромагнитного поля § 21. Квазистационарные явления в электрических цепях IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 22. Цепи переменного тока. Закон Ома § 23. Работа и мощность переменного тока. Передача электроэнергии § 24. Трехфазный ток. Электрические машины переменного тока V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 25. Колебательный контур § 26. Вынужденные колебания в контуре. Резонанс § 27. Незатухающие электромагнитные колебания § 28. Электромагнитные волны § 29. Свойства и применения электромагнитных волн VI. ОПТИКА § 30. Свет как электромагнитные волны. Интерференция § 31. Дифракция света § 32. Спектральные приборы. Дифракционная решетка § 33. Протяженные источники света § 34. Интерференция немонохроматического света § 35. Физические принципы голографии § 36. Геометрическая оптика § 37. Оптические приборы, формирующие изображение

19.2: Дифракционные картины — технические библиотеки LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

7907

• Распространение ИТ для продвижения материаловедения (DoITPoMS)
• Кембриджский университет

Эксперименты по лазерной дифракции можно проводить с помощью оптической скамьи, как показано ниже. Свет от лазера (с длиной волны

λ ) преломляется маской (обычно небольшой апертурой или решеткой) и проецируется на экран, расположенный на большом расстоянии, так что применяется геометрия Фраунгофера. Свет на экране известен как картина дифракции.

Форма дифракционной картины от одной щелевой маски шириной w включает математическую «функции sinc», где 9{2}\влево(\frac{\pi x w}{\лямбда L}\вправо)\]

Обратите внимание, что sinc(0) = 1.

Дифракционные картины можно рассчитать математически. Операция, которая напрямую предсказывает амплитуду дифракционной картины от маски, известна как преобразование Фурье (при условии, что выполняются условия для дифракции Фраунгофера). Вывод некоторых простых шаблонов можно найти здесь.

(а) с = 12 мк м	(б) с = 3 мк м

Дифракционная решетка представляет собой множество равноотстоящих щелей. Дифракционная картина от сложной маски, такой как решетка, может быть построена из более простых картин с помощью теоремы свертки. Наблюдаемая дифракционная картина состоит из повторяющихся функций «sinc-squared». Их положение от центральной точки определяется s (расстояние между щелями), а их относительная интенсивность зависит от w (ширина отдельных щелей).

Расстояние между щелями s и ширина щели w

Дифрактограммы от решеток (а) и (б).

Рассматривая дифракцию на решетке, можно установить взаимный характер картины. Эту взаимосвязь можно увидеть на дифракционных картинах щелей: мелкие детали дифрагирующего объекта дают большие расстояния в дифракционной картине

\[s=\frac{\lambda L}{x}\]

Дифрактограммы от щелей разной ширины.

Более сложные маски, например, периодический ряд отверстий, будут отображать более сложные дифракционные картины, но по-прежнему будут следовать той же базовой обратной зависимости.

Маска, состоящая из периодического ряда отверстий

Дифрактограмма для периодического ряда отверстий

---

Эта страница под названием 19.2: Дифракционные картины распространяется по лицензии CC BY-NC-SA и была создана, изменена и/или курирована организацией Распространение ИТ для продвижения материаловедения (DoITPoMS).

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   ДОИТПОМС

   Лицензия

   CC BY-NC-SA

   Показать оглавление

   нет

2. Теги

   На этой странице нет тегов.

оптика — Дифракционная картина и интерференционная картина

спросил 3 года 11 месяцев назад

Изменено 1 год, 10 месяцев назад

Просмотрено 1к раз

$\begingroup$

Меня не смущает разница между двухщелевым экспериментом Юнга и дифракцией.

В эксперименте Юнга с двумя щелями интерференционная картина представляет собой яркие полосы, равномерно разделенные с расстоянием, определяемым выражением $\Delta y=\frac{D\lambda}{d}$, где $D$ — расстояние от щели до экрана, $ d$ — расстояние между щелями, $\lambda$ — длина волны.

Дифракционная картина имеет центральный максимум, а яркие полосы с каждой стороны разделены неравномерно, т. е. расстояние между 1-м максимумом и 2-м максимумом не равно расстоянию между 2-м максимумом и 3-м максимумом.

Причина, по которой эксперимент Юнга с двумя щелями с равномерным разделением полос заключается в том, что мы считаем ширину щели настолько узкой, что свет, выходящий из каждой щели, можно рассматривать как точечный источник (так что это просто интерференция между двумя источниками). ) ? Однако при дифракции у нас конечная ширина щели, поэтому яркие полосы распределяются неравномерно. Не в этом ли причина неравномерного распределения ярких полос?

Кроме того, для дифракционной решетки должны ли быть также неравномерно распределены яркие полосы с каждой стороны?

• оптика
• двухщелевой эксперимент
• интерференция
• дифракция

$\endgroup$

2

$\begingroup$

Центр ярких полос, которые вы видите при использовании дифракционной решетки, на самом деле находится точно в том же положении, что и полосы, создаваемые двумя щелями с тем же расстоянием, что и между соседними щелями при использовании дифракционной решетки.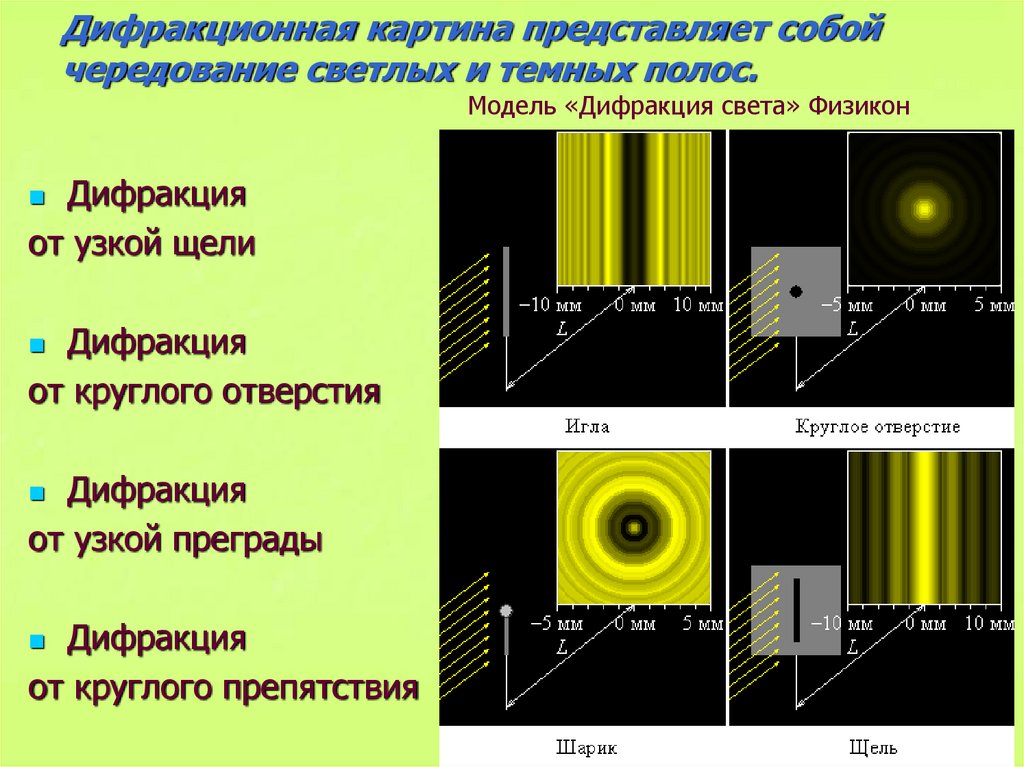 9Максимум {\rm th}$ обычно записывается как $n\lambda = d \sin \theta_{\rm n}$, и то же самое для двойной щели можно сказать, что полосы неравномерно разнесены.

Однако для нормального расположения двух щелей угол $\theta_{\rm n}$ мал, поэтому можно использовать приближение $\sin \theta_{\rm n} \ приблизительно \theta_{\rm n}$.
Итак, $y_{\rm n} \ приблизительно D \,\theta_{\rm n} = \frac{n \lambda\,D}{d} \Rightarrow y_{\rm n+1} -y_{\rm n} = \Delta y = \frac{(n+1) \lambda\,D}{d} — \frac{n\,\lambda\,D}{d} = \frac{\lambda\,D} {г}$

Это приводит к тому, что полосы находятся на одинаковом расстоянии друг от друга.

---

Преимущество использования дифракционной решетки заключается в том, что яркие полосы узкие и намного ярче, чем у двухщелевой решетки, как описано здесь.

Ширина щели регулирует дифракционную огибающую, т.е. модулирует интенсивность интерференционных полос.

$\endgroup$

2

$\begingroup$

Приступая к определениям, интерференция относится к действию волн, встречающихся друг с другом и объединяющихся конструктивно или деструктивно.