Гистограммы: Создание гистограммы
Создание гистограммы
Гистограмма — это столбчатая диаграмма, которая показывает частоту повторяемости значений.
Примечание: В этой статье рассматривается только создание гистограмм. Сведения о диаграммах Парето (отсортированных гистограммах) см. в статье Создание диаграммы Парето.
Какие версии или продукты вы используете?
- Какие версии или продукты вы используете?
- Excel 2016 и более новых версиях
- Excel 2007–2013
- Outlook, PowerPoint, Word 2016
-
Выберите Вставка > Вставить диаграмму статистики > Гистограмма.
Гистограмму также можно создать с помощью вкладки Все диаграммы в разделе Рекомендуемые диаграммы.
Выделите данные.
(Это типичный пример данных для гистограммы.)
Советы:
-
На вкладках Конструктор и Формат
можно настроить внешний вид диаграммы.
-
Если они не отображаются, щелкните в любом месте гистограммы, чтобы добавить на ленту область Работа с диаграммами.
-
Правой кнопкой мыши щелкните горизонтальную ось диаграммы, выберите Формат оси, а затем щелкните Параметры оси.
Руководствуясь приведенной ниже таблицей, вы сможете выбрать параметры, которые нужно задать в области задач Формат оси.

Параметр
Описание
По категориям
Выберите этот вариант, если категории (горизонтальная ось) текстовые, а не числовые.
 На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.
На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.Совет: Чтобы подсчитать количество появлений текстовых строк, добавьте столбец и укажите в нем значение «1», а затем отобразите гистограмму и выберите параметр По категориям.
Автоматическая
Это вариант по умолчанию для гистограмм. Длина интервала вычисляется по формуле Скотта.
Длина интервала
Введите положительное десятичное число, задающее количество точек данных в каждом диапазоне.

Количество интервалов
Введите количество интервалов гистограммы (включая интервалы для значений, выходящих за верхнюю и нижнюю границы).
Выход за верхнюю границу интервала
Установите этот флажок, чтобы создать интервал для всех значений, превышающих значение в поле справа.

Выход за нижнюю границу интервала
Установите этот флажок, чтобы создать интервал для всех значений, не превышающих значение в поле справа. Чтобы изменить его, введите в поле другое десятичное число.
Совет: Дополнительные сведения о гистограммах и их пользе для визуализации статистических данных см. в этой записи о гисторамме, диаграммах Парето и «ящик с усами» блога группы разработчиков Excel.
Вариант «Автоматическая» (формула Скотта)
Формула Скотта минимизирует отклонение вариационного ряда на гистограмме по сравнению с набором данных, исходя из предположения о нормальном распределении данных.
Вариант «Выход за верхнюю границу интервала»
Вариант «Выход за нижнюю границу интервала»
-
Загрузите надстройку «Пакет анализа». Дополнительные сведения см.
 в статье Загрузка надстройки «Пакет анализа» в Excel.
в статье Загрузка надстройки «Пакет анализа» в Excel. -
В один столбец на листе введите исходные данные. При необходимости добавьте в первую ячейку подпись.
Используйте количественные числовые данные, например, количество элементов или результаты тестов. Мастер гистограмм не будет работать с такими количественными числовыми данными, как идентификационные номера, введенные в виде текста.
-
В следующий столбец введите интервалы в возрастающем порядке. При необходимости добавьте в первую ячейку подпись.
Используйте собственные интервалы, поскольку они могут лучше соответствовать целям вашего анализа.
 Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек.
Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек. -
Откройте вкладку Данные и выберите команду Анализ данных.
-
Выберите пункт Гистограмма и нажмите кнопку OK.
-
В разделе Ввод выполните указанные ниже действия:
-
В поле Формировать список по диапазону введите ссылку на ячейку с диапазоном данных, который содержит исходные числа.
-
В поле Интервал карманов введите ссылку на ячейку с диапазоном, который содержит числа интервала.
Если на листе использовались подписи столбцов, можно включать их в ссылки на ячейки.
Совет: Вместо того чтобы вводить ссылки вручную, щелкните , чтобы временно свернуть диалоговое окно, чтобы выбрать диапазоны на этом сайте. При повторном нажатии этой кнопки диалоговое окно опять разворачивается.
Если подписи столбцов были включены в ссылки на ячейки, установите флажок Подписи.
В группе Параметры вывода выберите местоположение выходных данных.
Гистограмму можно расположить на том же листе, новом листе в текущей книге или в новой книге.
Установите один или несколько флажков:
<c0>Парето (отсортированная гистограмма)</c0>. Отображает частоту данных по убыванию.
<c0><c1>Суммарный процент</c1></c0>.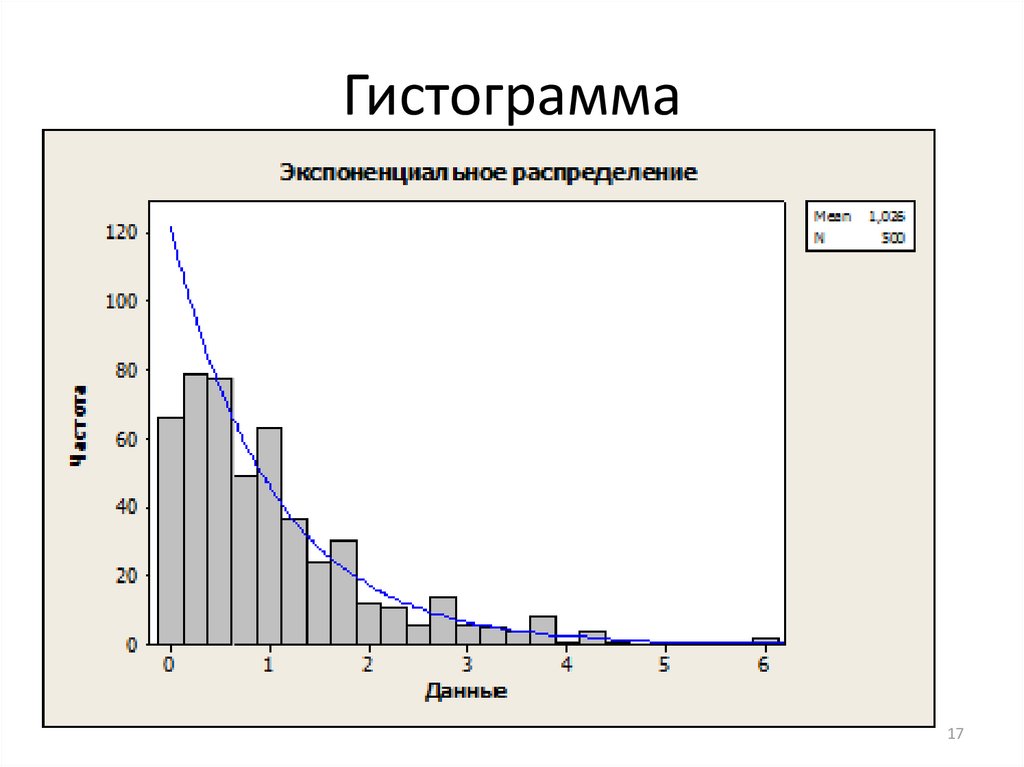 Отображает суммарные проценты и добавляет в гистограмму строку суммарных процентов.
Отображает суммарные проценты и добавляет в гистограмму строку суммарных процентов.
<c0><c1>Вывод диаграммы</c1></c0>. Отображает встроенную гистограмму.
Нажмите кнопку ОК.
Если вы хотите настроить гистограмму, вы можете изменить подписи текста и щелкнуть в любом месте гистограммы, чтобы использовать кнопки Элементы диаграммы, Стили диаграмм и Фильтр диаграммы справа от диаграммы.
Выделите данные.
(Это типичный пример данных для гистограммы.)
На вкладке Вставка нажмите кнопку Диаграмма.
В диалоговом окне Вставка диаграммы в разделе Все диаграммы выберите пункт Гистограмма, а затем нажмите кнопку ОК.
Советы:
- org/ListItem»>
-
Если они не отображаются, щелкните в любом месте гистограммы, чтобы добавить на ленту область Работа с диаграммами.
С помощью параметров на вкладках Конструктор и Формат настройте внешний вид диаграммы.
-
Правой кнопкой мыши щелкните горизонтальную ось диаграммы, выберите Формат оси, а затем щелкните Параметры оси.
org/ListItem»>
Руководствуясь приведенной ниже таблицей, вы сможете выбрать параметры, которые нужно задать в области задач Формат оси.
|
Параметр |
Описание |
|
По категориям |
Выберите этот вариант, если категории (горизонтальная ось) текстовые, а не числовые. Совет: Чтобы подсчитать количество появлений текстовых строк, добавьте столбец и укажите в нем значение «1», а затем отобразите гистограмму и выберите параметр По категориям. |
|
Автоматическая |
Это вариант по умолчанию для гистограмм. |
|
Длина интервала |
Введите положительное десятичное число, задающее количество точек данных в каждом диапазоне. |
|
Количество интервалов |
Введите количество интервалов гистограммы (включая интервалы для значений, выходящих за верхнюю и нижнюю границы). |
|
Выход за верхнюю границу интервала |
Установите этот флажок, чтобы создать интервал для всех значений, превышающих значение в поле справа. |
|
Выход за нижнюю границу интервала |
Установите этот флажок, чтобы создать интервал для всех значений, не превышающих значение в поле справа. Чтобы изменить его, введите в поле другое десятичное число. |
Чтобы создать гистограмму в Excel для Mac, выполните указанные Excel для Mac.
Выделите данные.
(Это типичный пример данных для гистограммы.)
На ленте на вкладке Вставка нажмите кнопку (статистический значок) и в области Гистограммавыберите гистограмма.
Советы:
-
На вкладках Конструктор и Формат можно настроить внешний вид диаграммы.
-
Если они не отображаются, щелкните в любом месте гистограммы, чтобы добавить их на ленту.

Чтобы создать гистограмму в Excel 2011 для Mac, необходимо скачать сторонную надстройку. Дополнительные сведения см. в Excel 2011 для Mac.
В Excel Online вы можете просмотреть гистограмму (гистограмму с частотой), но не можете создать ее, так как для нее требуется надстройка Excel, не поддерживаемая в Excel в Интернете.
Если у вас есть Excel, вы можете нажать кнопку Изменить в Excel, чтобы открыть Excel на компьютере и создать гистограмму.
-
Коснитесь данных, чтобы выделить их.
-
Если вы на телефоне, коснитесь значка редактирования , чтобы отдемонстрировать ленту.
 и нажмите Главная.
и нажмите Главная. -
Выберите элементы Вставка > Диаграммы > Гистограмма.
При необходимости вы можете настроить элементы диаграммы.
Примечание: Эта функция доступна только при наличии подписки на Microsoft 365.. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
Купить или попробовать Microsoft 365
-
Коснитесь данных, чтобы выделить их.
org/ListItem»>
-
Выберите элементы Вставка > Диаграммы > Гистограмма.
Если вы на телефоне, коснитесь значка «Правка» ленты, а затем нажмите Главная .
Чтобы создать гистограмму в Excel, необходимо предоставить данные двух типов: данные, которые нужно проанализировать, и интервалы, которые представляют интервалы для измерения частоты. Данные необходимо расположить в двух столбцах на листе. Ниже приведены типы данных, которые должны содержаться в этих столбцах.
-
Введенные данные. Это данные, которые вы хотите проанализировать с помощью мастера гистограмм.

-
Числовые интервалы. Они представляют диапазоны, на основании которых мастер гистограмм проводит оценку введенных данных во время их анализа.
При использовании инструмента Гистограмма Excel количество точек данных в каждом из них. Точка данных включается в определенный интервал, если соответствующее значение больше нижней границы интервала данных и меньше верхней. Если диапазон диапазонов диапазонов Excel создается набор равномерно распределенных диапазонов между минимальным и максимальным значениями входных данных.
Результат анализа гистограммы отображается на новом листе (или в новой книге) и содержит таблицу и гистограмму, которая отражает данные этой таблицы.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание каскадной диаграммы
Создание диаграммы Парето
Создание диаграммы «солнечные лучи» в Office
Создание диаграммы «ящик с усами»
Создание диаграммы «дерево» в Office
Гистограммы—ArcMap | Документация
Доступно с лицензией Geostatistical Analyst.
- Частотное распределение
- Суммарная статистика
- Примеры
Инструмент Гистограмма (Histogram) предоставляет одномерное (с одной переменной) описание данных. В диалоговом окне инструмента отображается частотное распределение интересующего набора данных и вычисляется суммарная статистика.
Частотное распределение
Частотное распределение представляет собой столбчатую диаграмму для отображения частотности попадания наблюдаемых значений в определенные интервалы или классы. Можно указать ряд классов с одинаковой шириной, которые будут использоваться в гистограмме. Относительная пропорция данных, которая распределяется по каждому классу, выражается высотой каждого столбца. Например, в гистограмме ниже показано частотное распределение (10 классов) для набора данных.
Пример диалогового окна Гистограмма (Histogram)Суммарная статистика
Важные объекты распределения могут быть суммированы с помощью различных статистик, которые характеризуют их местоположение, распределение и форму.
Показатели расположения
Показатели расположения дают представление о том, где находятся центр и другие части распределения.
Показатели разброса
Разброс точек вокруг среднего значения — еще одна характеристика отображаемого частотного распределения.
- Дисперсия данных представляет собой среднеквадратическое отклонение всех значений от среднего.
 Поскольку в нее включаются квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается суммированием квадратических отклонений от среднего и делением суммы на (N-1).
Поскольку в нее включаются квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается суммированием квадратических отклонений от среднего и делением суммы на (N-1). - Стандартное отклонение представляет собой квадратный корень из дисперсии и описывает разброс данных вокруг среднего. Чем меньше дисперсия и стандартное отклонение, тем гуще сконцентрирован кластер измерений вокруг среднего значения.
На диаграмме ниже показаны два распределения с различными стандартными отклонениями. Частотное распределение, представленное черной линией, более переменчиво (с широким разбросом), чем частотное распределение, представленное красной линией. Дисперсия и стандартное отклонение для черного частотного распределения больше, чем для красного.
Показатели диаграммы разбросаПоказатели формы
Частотное распределение также характеризуется формой.
Коэффициент асимметрии — это показатель симметрии распределения. Для симметричных распределений коэффициент асимметрии равен нулю. Если у распределения есть длинный правый хвост больших значений, то у него положительная асимметрия, а если длинный левый хвост малых значений — то отрицательная. Среднее значение для распределений с положительной асимметрией больше, чем медиана, а для распределений с отрицательной асимметрией — наоборот. На рисунке ниже показано распределение с положительной асимметрией.Пример распределения с положительной асимметрией
Для симметричных распределений коэффициент асимметрии равен нулю. Если у распределения есть длинный правый хвост больших значений, то у него положительная асимметрия, а если длинный левый хвост малых значений — то отрицательная. Среднее значение для распределений с положительной асимметрией больше, чем медиана, а для распределений с отрицательной асимметрией — наоборот. На рисунке ниже показано распределение с положительной асимметрией.Пример распределения с положительной асимметрией
Эксцесс основан на размере хвостов распределения и представляет собой показатель вероятности того, что распределение будет создавать выпадающие значения. Эксцесс нормального распределения равен трем. Распределения с относительно толстыми хвостами называются островершинными (лептокуртическими), и у них эксцесс больше трех. Распределения с относительно тонкими хвостами называются плосковершинными (платикуртическими), и у них эксцесс меньше трех. На следующей диаграмме нормальное распределение показано красным цветом, а островершинное (с толстыми хвостом) — черным.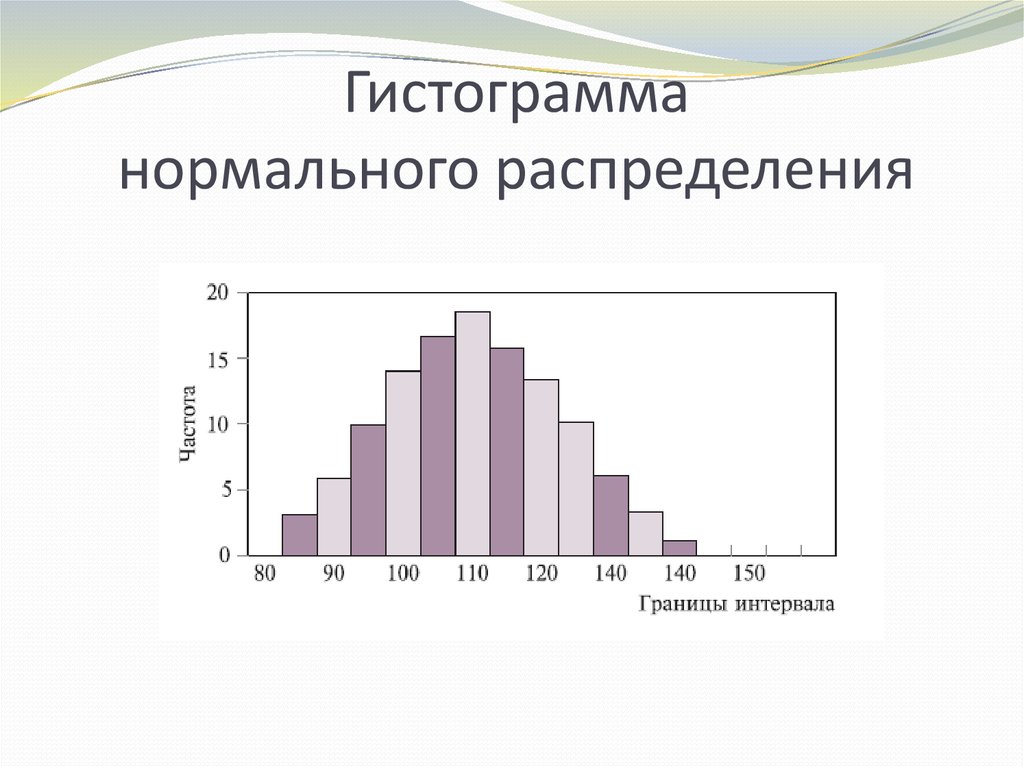
Примеры
С помощью инструмента Гистограмма (Histogram) можно исследовать форму распределения путем прямого наблюдения. Просматривая статистику среднего значения и медианы, можно определить расположение центра распределения. На рисунке внизу обратите внимание на колоколообразное распределение, и так как значения среднего арифметического и медианы близки, это распределение близко к нормальному. Также можно выделить экстремальные значения в хвосте гистограммы и увидеть, как они расположены в пространстве на отображаемой карте.
Пример колоколообразной гистограммы
Если асимметрия данных слишком большая, можно протестировать эффекты трансформации на данных. На этом рисунке показано распределение с асимметрией перед применением преобразования.Пример гистограммы с асимметрией
К асимметричным данным применяется логарифмическое преобразование, и в этом случае преобразование приближает распределение к нормальному.Пример гистограммы логарифмического преобразования
Более подробно о преобразованиях, доступных в инструменте Гистограмма (Histogram), см. в разделе Преобразования по методу Box-Cox, арксинуса- и логарифмические.
в разделе Преобразования по методу Box-Cox, арксинуса- и логарифмические.
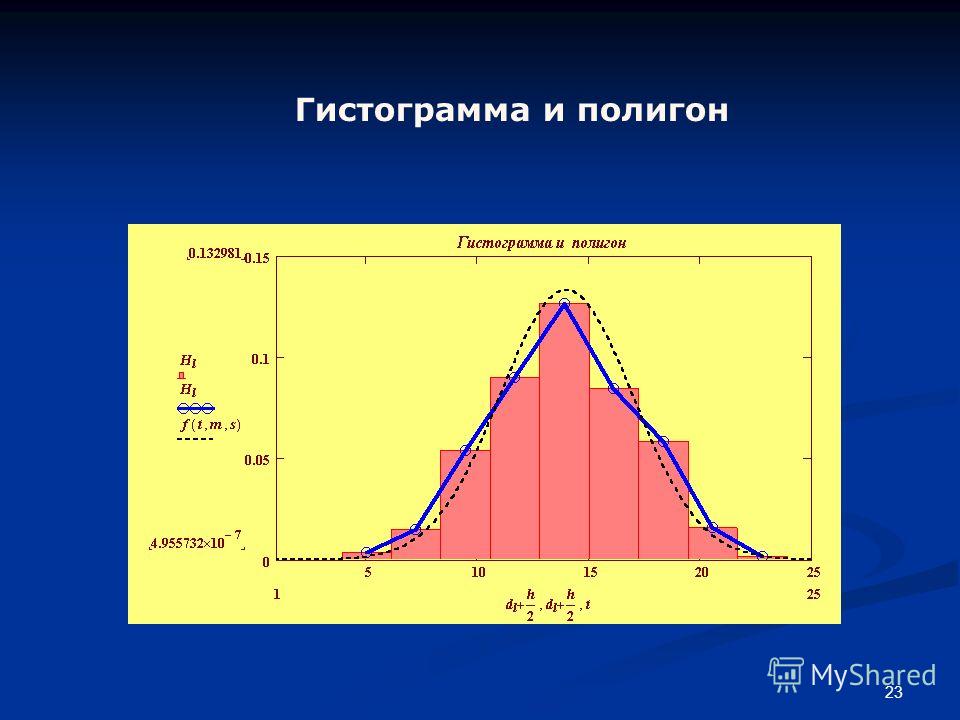
и гистограмма — рассказывание историй с данными
Рассмотрим приведенную выше иллюстрацию двух визуализаций данных.
Слева находится гистограмма, а справа — гистограмма (также называемая гистограммой). Гистограммы и гистограммы выглядят почти одинаково, но при этом существенно различаются. Понимание их различий важно, поэтому вы знаете, когда использовать каждое из них, и точно передать или использовать содержащуюся в них информацию.
Давайте посмотрим поближе.
Гистограммы и гистограммы имеют разные варианты использования
Чтобы понять, когда уместно использовать гистограмму и гистограмму, давайте воспользуемся набором данных о продажах недвижимости для жилых домов, проданных в Большом Манчестере.
Следующая гистограмма визуализирует эти данные и вдохновлена инфографикой Грэма Гурлея (заявка #SWDchallenge за декабрь 2019 г.).
Что вы можете сказать об этих данных?
Я вижу, что самая распространенная цена на недвижимость составляла от 100 до 150 тысяч фунтов стерлингов.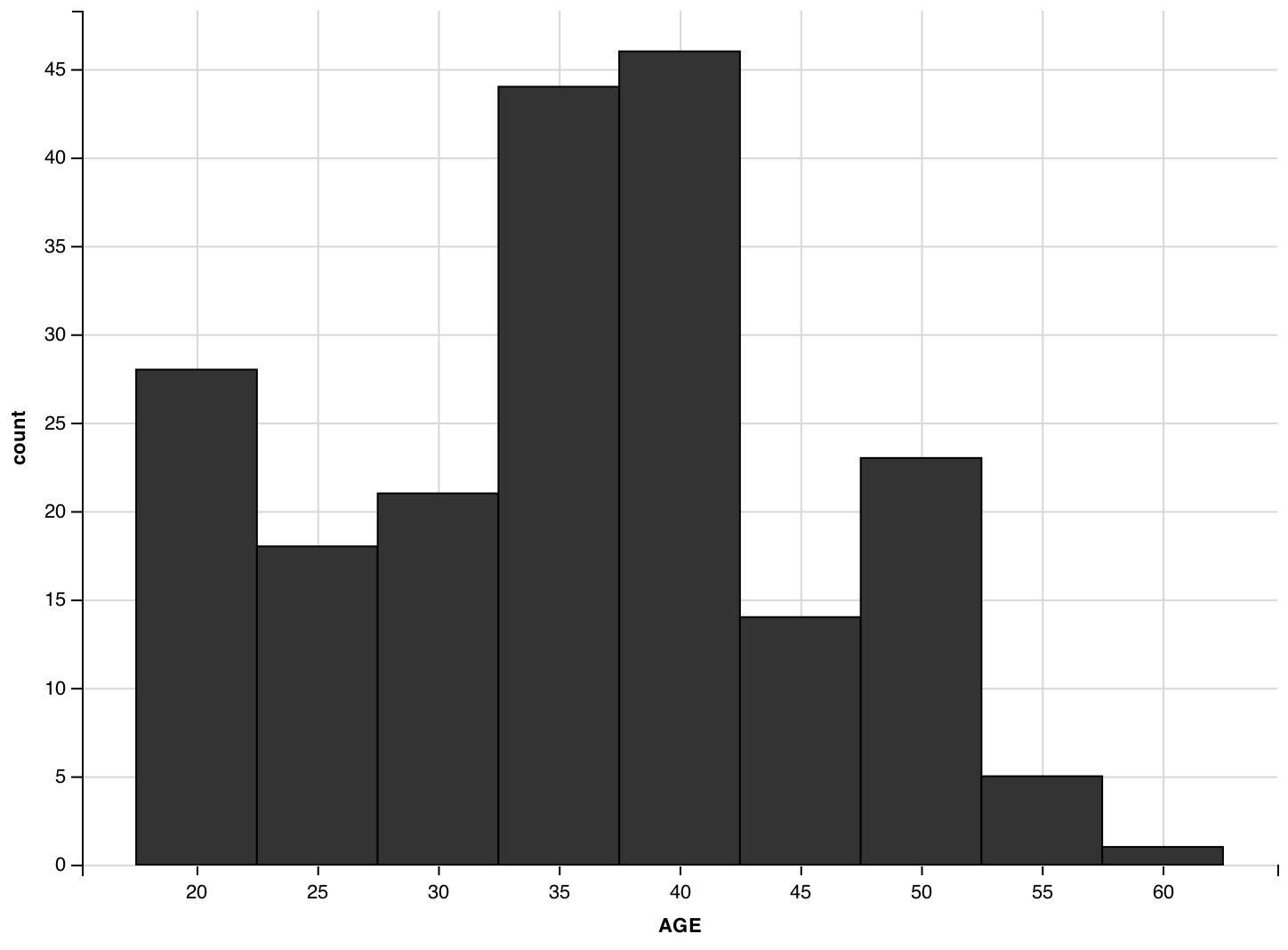 Я также могу определить, что недвижимость редко продается ниже 50 тысяч фунтов стерлингов. Гистограмма позволяет мне лучше понять форму или асимметрию числовой переменной, цены продажи. это Основная причина использования гистограммы — когда вы хотите понять лежащее в основе распределение ряда числовых данных. В статистике преобладают гистограммы, поэтому они чаще используются при исследовательском анализе, чем при объяснительном анализе.
Я также могу определить, что недвижимость редко продается ниже 50 тысяч фунтов стерлингов. Гистограмма позволяет мне лучше понять форму или асимметрию числовой переменной, цены продажи. это Основная причина использования гистограммы — когда вы хотите понять лежащее в основе распределение ряда числовых данных. В статистике преобладают гистограммы, поэтому они чаще используются при исследовательском анализе, чем при объяснительном анализе.
С другой стороны, гистограмма хорошо подходит для сравнения категорий. Наша гистограмма отвечает только на вопросы об общем распределении, но что, если я хочу узнать больше о составе наших данных? Где было продано большинство этих объектов? Какие типы недвижимости продаются: квартиры, таунхаусы, особняки, таунхаусы? Это все вопросы о категоричности, , а не числовые данные. Ниже приведен пример гистограммы с разбивкой по местоположению. (Чтобы узнать больше о гистограммах, ознакомьтесь с нашим полным руководством, что такое гистограмма? . )
)
Гистограммы и гистограммы отображают различные типы данных
Гистограммы визуализируют количественные данные или числовые данные, тогда как гистограммы отображают категориальные переменные .
В большинстве случаев числовые данные в гистограмме будут непрерывными (имеющими бесконечные значения). Попытка отобразить все возможные значения непрерывной переменной вдоль оси была бы глупой. Вместо этого непрерывные данные группируются в диапазоны, называемые бинами. На гистограмме продаж недвижимости диапазон ячеек составляет 50 000 фунтов стерлингов.
В отличие от гистограмм, гистограммы имеют конечный набор категорий — например, десять районов, показанных на гистограмме выше.
Одно предостережение: когда ваши числовые данные являются дискретными, то есть счетными. Для дискретных данных различие между гистограммой и гистограммой менее очевидно. Вы можете использовать любой из них. Выбор будет зависеть от вашей цели и количества дискретных значений, которые у вас есть. Например, цена недвижимости технически является дискретной величиной, но из-за изменчивости и широкого диапазона значений проще рассматривать ее как непрерывную, группируя значения в управляемые ячейки.
Например, цена недвижимости технически является дискретной величиной, но из-за изменчивости и широкого диапазона значений проще рассматривать ее как непрерывную, группируя значения в управляемые ячейки.
Гистограммы и гистограммы имеют разные правила форматирования
Для гистограмм, как и для большинства графиков, существует достаточная гибкость в отношении формата и дизайна. С другой стороны, гистограммы подчиняются жестким правилам. Давайте рассмотрим три основные области, в которых столбцы и гистограммы имеют различные ограничения форматирования.
Вы не можете изменить порядок баров на гистограмме; вы можете сделать это на гистограмме
В гистограмме существует неотъемлемая упорядоченность, поскольку базовые данные непрерывны или, по крайней мере, рассматриваются как таковые. Крайне важно сохранить естественный порядок, как и в случае с временными данными, от меньшего к большему.
Это может быть, а может и не быть для гистограммы. Для любых порядковых категорий — шкал Лайкерта, возрастных диапазонов — имеет смысл сохранять естественный порядок.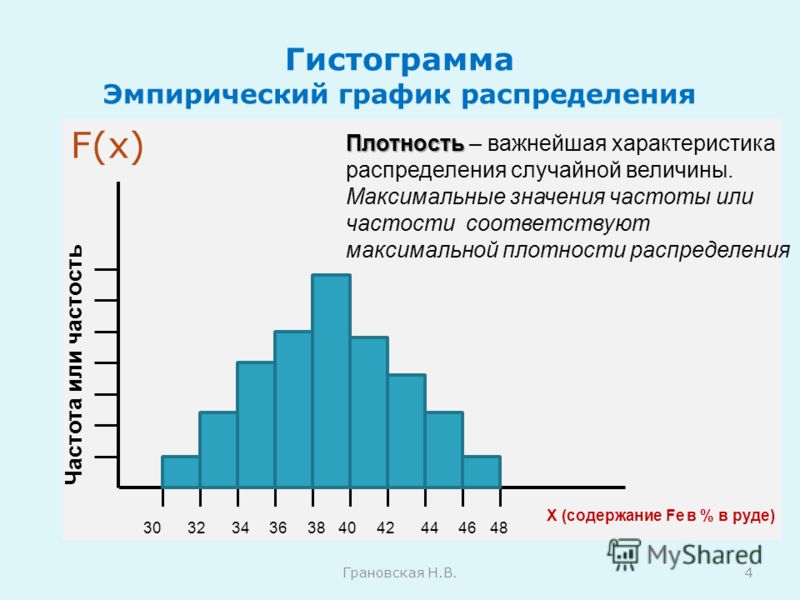 Но в большинстве случаев можно изменить порядок столбцов в соответствии с данными или выводами (от меньшего к большему, от большего к меньшему и т. д.).
Но в большинстве случаев можно изменить порядок столбцов в соответствии с данными или выводами (от меньшего к большему, от большего к меньшему и т. д.).
На гистограмме столбцы должны соприкасаться; на гистограмме есть пробел
На гистограмме столбцы должны соприкасаться, чтобы показать, что данные расположены вдоль числовой оси.
В столбчатой диаграмме между столбцами необходимо оставить промежутки, чтобы различать категории. Не существует конкретного правила о том, сколько места нужно предоставить, но выбор ширины зазора между 30%-40% является хорошей отправной точкой.
Различное расстояние между столбцами является важным соглашением при построении графиков и одним из наиболее заметных визуальных различий между гистограммами и столбчатыми диаграммами.
Гистограммы могут иметь неодинаковую ширину столбцов; столбчатые диаграммы имеют одинаковую ширину Гистограммы могут иметь разную ширину столбцов, если интервалы бинов различаются.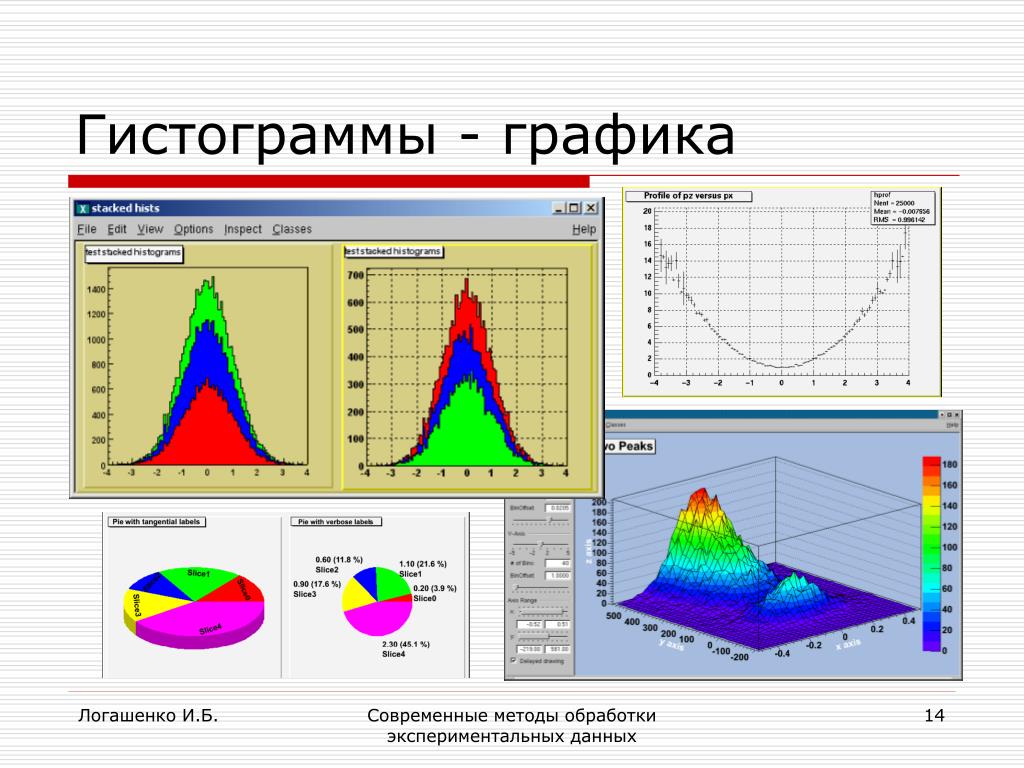
Следует отметить, что гистограммы кодируют числовые данные как по длине, так и по ширине, также известной как площадь. Площадь каждого столбца гистограммы должна быть пропорциональна данным. Это означает, что если вы создадите корзины разных размеров, размеры длины и ширины должны быть изменены соответствующим образом.
Если мы вернемся к гистограмме цен на недвижимость, то увидим, что концы имеют общие столбцы: меньше или равно 50 000 фунтов стерлингов и больше или равно 500 000 фунтов стерлингов.
Это может быть или не быть точным представлением области. Вполне возможно, что все объекты недвижимости, проданные на сумму более 500 000 фунтов стерлингов, попали в диапазон от 500 000 до 550 000 фунтов стерлингов (контейнеры одинакового размера). Но предположим, что несколько домов проданы выше верхней границы в 550 тысяч фунтов стерлингов. В этом случае длина и ширина конечного стержня должны измениться, чтобы пропорционально представить площадь.
Стоит отметить, что я видел много случаев, когда первый или последний столбцы гистограммы масштабировались неправильно. Если вы хотите создать точную гистограмму, подумайте о том, чтобы размеры столбцов пропорционально соответствовали интервалу, или, что еще лучше, не усложняйте задачу, используя интервалы одинакового размера.
В линейчатой диаграмме, независимо от того, выбираете ли вы узкие или более широкие полосы, ширина должна быть одинаковой. Гистограммы отображают категории, а не числовые диапазоны, поэтому ширина не имеет значения.
Подводя итог, можно сказать, что и гистограммы, и гистограммы состоят из столбцов, но на этом перекрытие заканчивается. Они имеют разные варианты использования, отображают разные типы данных и имеют определенные правила форматирования.
Известны ли вам другие различия между гистограммами и столбчатыми диаграммами? Есть ли дополнительные типы диаграмм, которые вы хотели бы, чтобы мы изучили помимо нашего руководства по диаграммам SWD? Дайте нам знать об этом в комментариях.
Гистограммы—ArcMap | Документация
Доступно с лицензией Geostatistical Analyst.
- Распределение частот
- Сводная статистика
- Примеры
Инструмент «Гистограмма» обеспечивает одномерное (с одной переменной) описание ваших данных. Диалоговое окно инструмента отображает частотное распределение интересующего набора данных и вычисляет сводную статистику.
Распределение частот
Распределение частот представляет собой гистограмму, показывающую, как часто наблюдаемые значения попадают в определенные интервалы или классы. Вы можете указать количество классов одинаковой ширины, которые используются в гистограмме. Относительная доля данных, попадающих в каждый класс, представлена высотой каждого столбца. Например, на гистограмме ниже показано частотное распределение (10 классов) для набора данных.
Пример диалогового окна гистограммыСуммарная статистика
Важные особенности распределения могут быть обобщены статистическими данными, описывающими его положение, распространение и форму.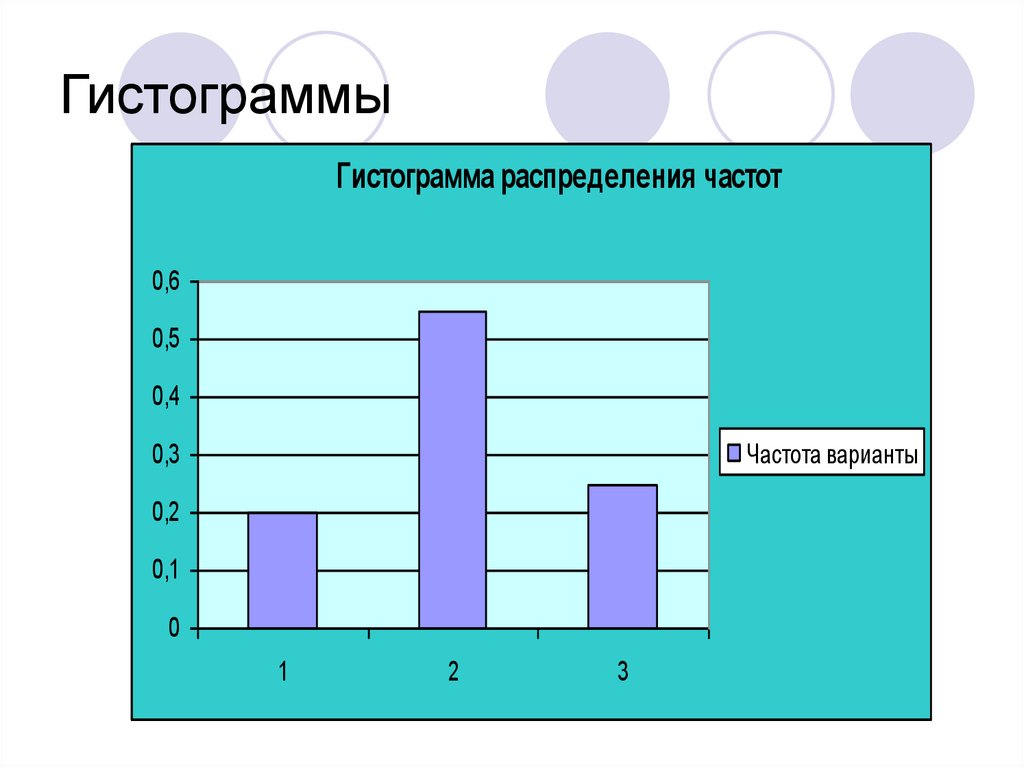
Меры местоположения
Меры местоположения дают вам представление о том, где находится центр и другие части распределения.
Меры разброса
Разброс точек вокруг среднего значения является еще одной характеристикой отображаемого частотного распределения.
- Дисперсия данных представляет собой среднеквадратичное отклонение всех значений от среднего. Поскольку она включает квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается путем суммирования квадратов отклонений от среднего значения и деления суммы на (N-1).
- Стандартное отклонение представляет собой квадратный корень из дисперсии и описывает разброс данных относительно среднего значения. Чем меньше дисперсия и стандартное отклонение, тем теснее кластер измерений относительно среднего значения.
На приведенной ниже диаграмме показаны два распределения с разными стандартными отклонениями. Распределение частот, представленное черной линией, более изменчиво (более широкий разброс), чем распределение частот, представленное красной линией.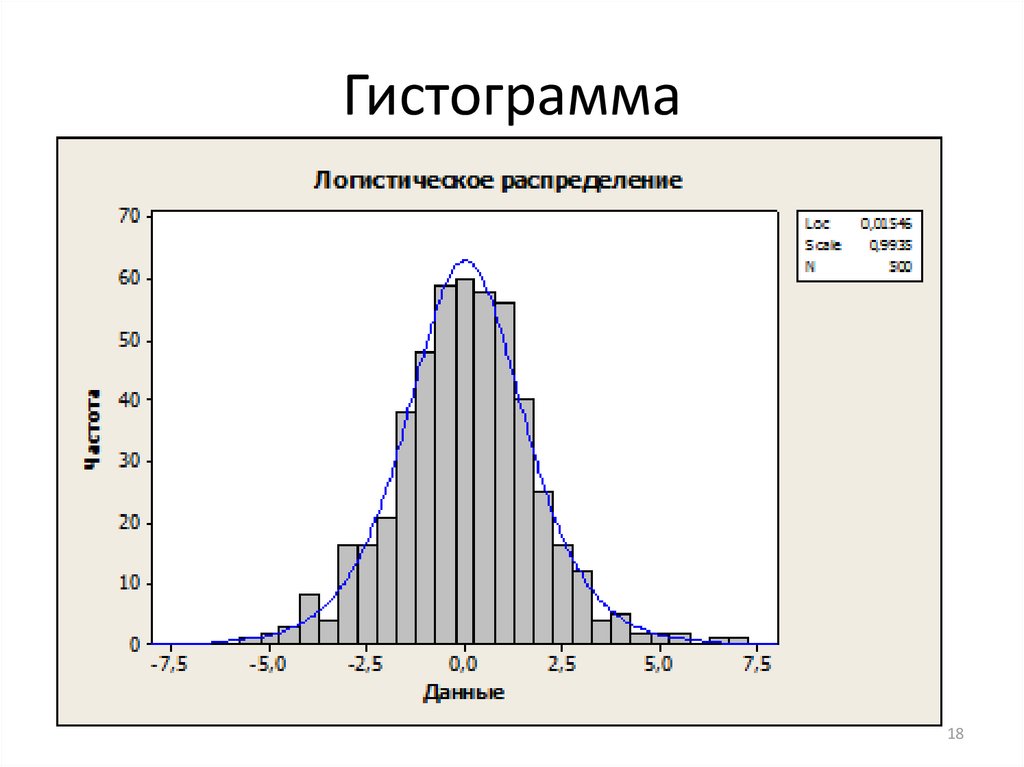 Дисперсия и стандартное отклонение для черного частотного распределения больше, чем для красного частотного распределения.
Дисперсия и стандартное отклонение для черного частотного распределения больше, чем для красного частотного распределения.
Показатели формы
Частотное распределение также характеризуется своей формой.
Коэффициент асимметрии является мерой симметрии распределения. Для симметричных распределений коэффициент асимметрии равен нулю. Если распределение имеет длинный правый хвост больших значений, оно имеет положительную асимметрию, а если оно имеет длинный левый хвост малых значений, оно имеет отрицательную асимметрию. Среднее значение больше, чем медиана для распределений с положительной асимметрией, и наоборот, для распределений с отрицательной асимметрией. На изображении ниже показано распределение с положительной асимметрией. Пример 9 распределения с положительной асимметрией0003
Эксцесс основан на размере хвостов распределения и обеспечивает меру вероятности того, что распределение будет давать выбросы. Эксцесс нормального распределения равен трем.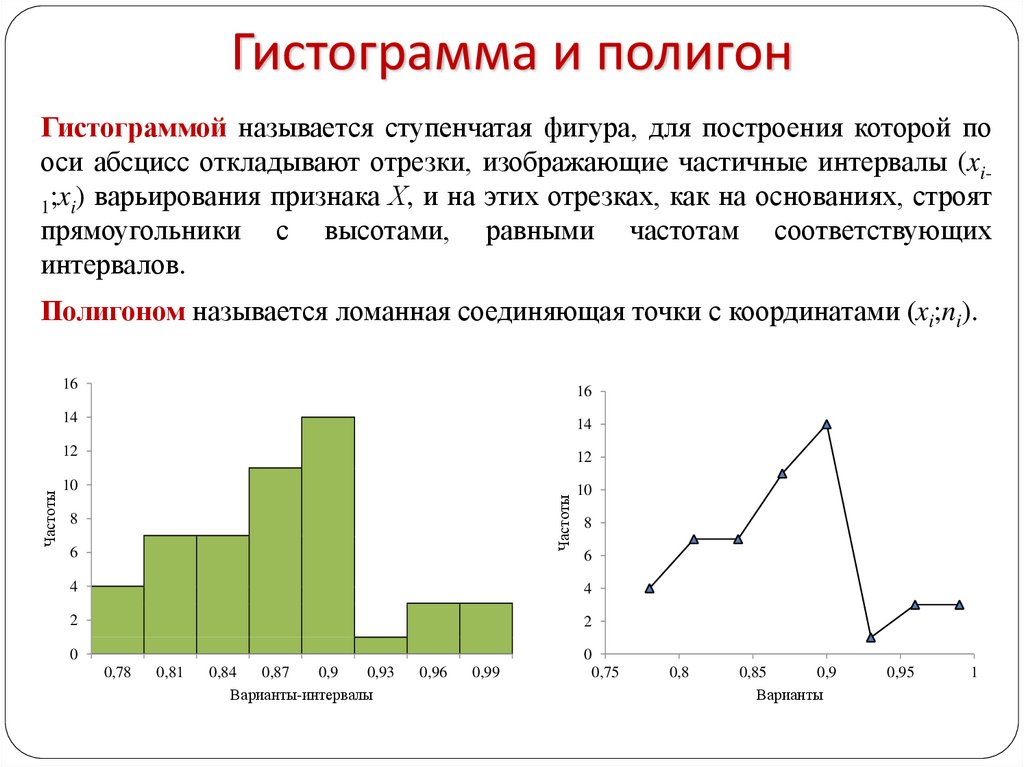 Распределения с относительно толстыми хвостами называются лептокуртическими и имеют эксцесс больше трех. Распределения с относительно тонкими хвостами называются платикуртическими и имеют эксцесс менее трех. На следующей диаграмме нормальное распределение показано красным цветом, а лептокуртическое (толстохвостое) распределение — черным.
Распределения с относительно толстыми хвостами называются лептокуртическими и имеют эксцесс больше трех. Распределения с относительно тонкими хвостами называются платикуртическими и имеют эксцесс менее трех. На следующей диаграмме нормальное распределение показано красным цветом, а лептокуртическое (толстохвостое) распределение — черным.
Примеры
С помощью инструмента «Гистограмма» вы можете исследовать форму распределения путем непосредственного наблюдения. Просмотрев среднюю и медианную статистику, вы можете определить положение центра распределения. Обратите внимание, что на рисунке ниже распределение имеет форму колокола, а поскольку среднее и медиана очень близки, это распределение близко к нормальному. Вы также можете выделить экстремальные значения в хвосте гистограммы и посмотреть, как они пространственно расположены на отображаемой карте.
Пример колоколообразной гистограммы
Если ваши данные сильно искажены, вы можете проверить влияние преобразования на ваши данные.



 На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.
На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.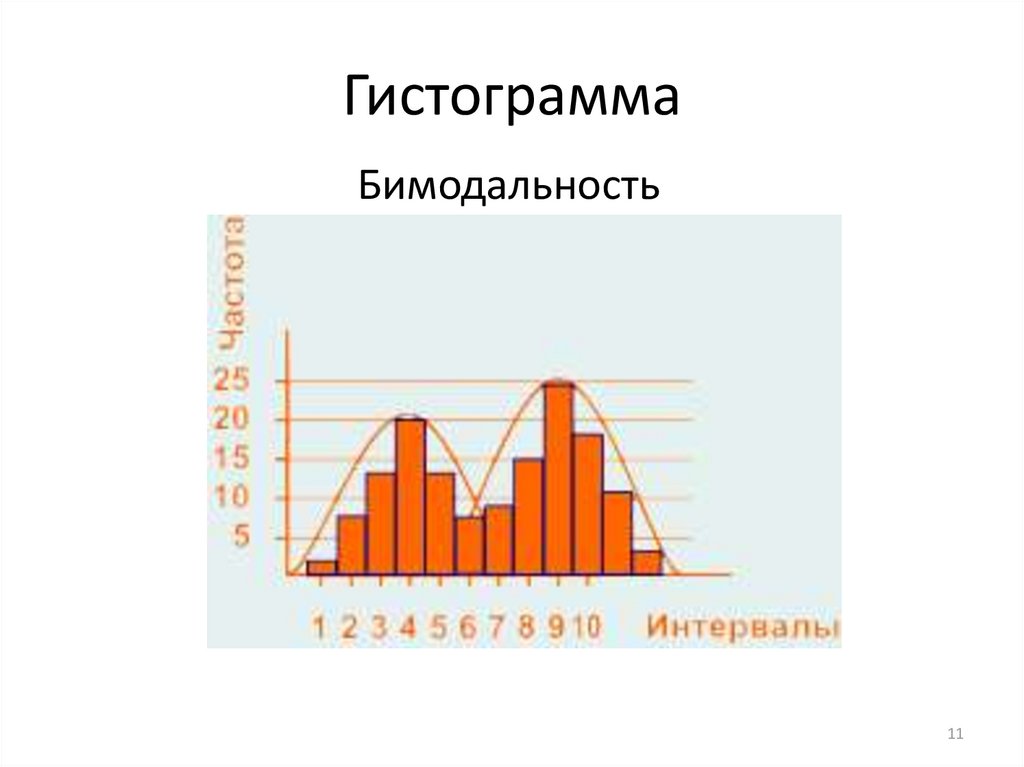

 в статье Загрузка надстройки «Пакет анализа» в Excel.
в статье Загрузка надстройки «Пакет анализа» в Excel. Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек.
Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек.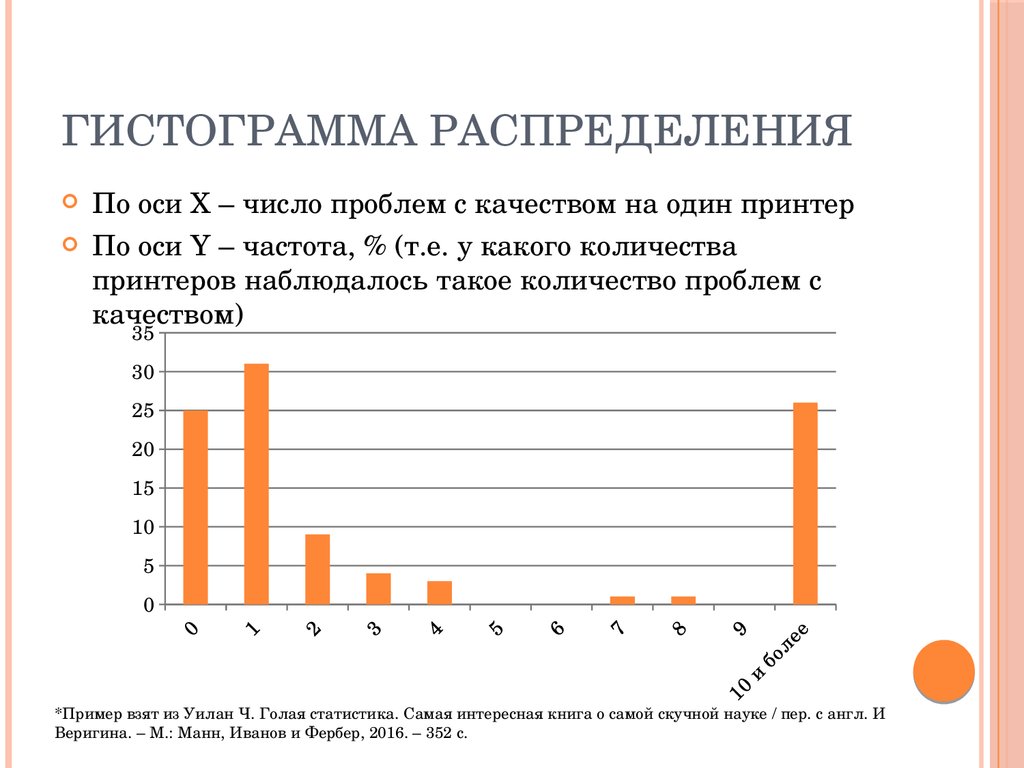 На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.
На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.
 Чтобы изменить его, введите в поле другое десятичное число.
Чтобы изменить его, введите в поле другое десятичное число.
 и нажмите Главная.
и нажмите Главная.
 Поскольку в нее включаются квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается суммированием квадратических отклонений от среднего и делением суммы на (N-1).
Поскольку в нее включаются квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается суммированием квадратических отклонений от среднего и делением суммы на (N-1).