Квадрат расстояния: Найдите квадрат расстояния между вершинами… — Задание 8 ЕГЭ по математике (Стереометрия)
ИЗЛУЧЕНИЕ: Закон обратного квадрата излучения
СВЯЗЬ МЕЖДУ РАССТОЯНИЕМ ОТ ИСТОЧНИКОВ ИЗЛУЧЕНИЯ И БЕЗОПАСНОСТЬЮ — «ЗАКОН ОБРАТНОЙ ПЛОЩАДИ» В ЭМП / РЧ ИЗЛУЧЕНИЯХ
Закон обратных квадратов гласит, что величина его воздействия значительно уменьшается пропорционально квадрату его расстояния от источника.
И наоборот, степень воздействия также резко увеличивается с приближением.
В следующих таблицах указаны приблизительные расстояния, необходимые для достижения Зальцбургского Предела Предосторожности 2001 и 2002 годов. Целью приведенных ниже расчетов является демонстрация того, что закон обратных квадратов (определенный справа) не так полезен, как вы думаете, когда уровень воздействия на здоровье намного ниже мощности передачи устройств (и международных стандартов).
После выполнения расчётов становится понятно, что наличие беспроводной телефонной станции, использующей непрерывное излучение DECT или маршрутизатор Wi-Fi в той же комнате,обеспечивает такую же (или большую) плотность мощности, что и при проживании рядом с вышкой сотовой связи.
Ниже приведены сравнения между:
- Устройства Wi-Fi, Беспроводные телефоны, Мобильные телефоны и Интеллектуальные счётчики, Вышки сотовой связи и Радиовышки.
- Будильник и Линии Питания
Обратите внимание, что измерения ниже предполагают излучение в прямой видимости. Дерево и гипсокартон практически не блокируют беспроводные сигналы. Окна с покрытием с низким E или плёнками с низким E, бетон и кирпич могут обеспечивать более высокий уровень затухания и не учитываются в расчётах ниже
Маршрутизатор Wi-Fi (микроволновое воздействие) с мощностью передачи (30 мВт)
Зависимость удалённости от источников излучения и безопасности — «ЗАКОН ОБРАТНОЙ ПЛОЩАДИ»
| Расстояние | Прибл. Удельная мощность** Удельная мощность** |
Примечания |
|---|---|---|
| 30см | 26.5mW/m2 | Расчёт: 30/4Π(0.3*0.3) =~26.5 |
| 1m | 2.387 mW/m2 | Расчёт: 30/4Π =~2.387 |
| 1,55 m | 1 mW/m2 | Предел Предосторожности Зальцбурга (2001) Биоинициативная Рекомендация — (2007) |
| 3,7 m | 170 microW/m2 | Селетунская Научная Группа (2011) |
| 5m | 100 microW/m2 | STOA (2001) |
| 15,5 m | 10 microW/m2 | Новые Меры Предосторожности на Открытом Воздухе (Salzburg Precautionary Outdoor, 2002) |
Метод Расчёта: Мы можем аппроксимировать среднюю плотность мощности, используя уравнение P * G / 4Πr2, где 4Πr2 — площадь поверхности сферы, а G — коэффициент усиления антенны. Для приблизительных целей приведенные ниже числа предполагают изотропную антенну с постоянной интенсивностью.
Для приблизительных целей приведенные ниже числа предполагают изотропную антенну с постоянной интенсивностью.
** Обратите внимание, что направленное действие антенны здесь не учитывается, что может привести к недооценке мощности в определённых направлениях и переоценке мощности в других направлениях. Для направленного действия антенн, мы должны учитывать коэффициент усиления, чтобы рассчитать максимальное требуемое расстояние. Расстояния в этом сегменте, возможно, потребуется дополнительно отрегулировать, умножив его на квадратный корень коэффициента усиления. Он может варьироваться от 1,3 до 7, в зависимости от усиления антенны.
Следующая презентация Грэма Филипса показывает, что ноутбук с поддержкой Wi-Fi на расстоянии 50 см может источать большее излучение, чем вышка мобильного телефона (вышка сотовой связи) на расстоянии 100 метров (см. слайд 13).
Рекомендуемые расстояния для беспроводных устройств
В следующей таблице показаны минимальные расстояния, необходимые для соблюдения пределов Зальцбурга 2001 и 2002 вне помещений, основанные на предположении об изотропной антенне. Согласно таблице эффектов, упомянутой выше, некоторые эффекты всё ещё наблюдаются на пределе Зальцбурга (2001). Следовательно, предел Зальцбурга (2002) предпочтителен или находится где-то посередине. Чтобы рассчитать эти числа самостоятельно с учётом мощности передачи беспроводного продукта, обратитесь к странице формул.
Согласно таблице эффектов, упомянутой выше, некоторые эффекты всё ещё наблюдаются на пределе Зальцбурга (2001). Следовательно, предел Зальцбурга (2002) предпочтителен или находится где-то посередине. Чтобы рассчитать эти числа самостоятельно с учётом мощности передачи беспроводного продукта, обратитесь к странице формул.
**Запись: Поскольку антенна может быть направленной, а не изотропной, указанные ниже расстояния могут быть выше в зависимости от направления и усиления антенны. В некоторых направлениях
Это только общие рекомендации. Различные беспроводные маршрутизаторы различаются по мощности. Некоторые беспроводные маршрутизаторы позволяют снизить мощность передачи и даже запланировать часы, в которые Wi-Fi будет включён.
| Расстояние | Прибл. Удельная мощность** | Примечания |
|---|---|---|
| 30см | 26. 5mW/m2 5mW/m2 |
Расчёт: 30/4Π(0.3*0.3) =~26.5 |
| 1m | 2.387 mW/m2 | Расчёт: 30/4Π =~2.387 |
| 1,55 m | 1 mW/m2 | Предел Предосторожности Зальцбурга (2001) Биоинициативная Рекомендация — (2007) |
| 3,7 m | 170 microW/m2 | Селетунская Научная Группа (2011) |
| 5m | 100 microW/m2 | STOA (2001) |
| 15,5 m | 10 microW/m2 | Новые Меры Предосторожности на Открытом Воздухе (Salzburg Precautionary Outdoor, 2002) |
| Устройство | Продолжительность Мощность Передачи |
Зальцбург (2001)** |
Зальцбург (2002)** |
Комментарии |
|---|---|---|---|---|
Маршрутизаторы Wi-Fi (пониженное энергопотребление) Маршрутизаторы Wi-Fi (внешняя точка доступа) Маршрутизаторы Wi-Fi (высокой мощности) |
Непрерывно с маршрутизатора или точки доступа, даже когда не используется 30 mW (~ 15 dBm) 63 mW(~ 18 dBm) 500 mW (~ 27dBm) |
1,55 m 2,24 м 6. |
15,5 m 22,4 m 63m |
Обратите внимание, что компьютеры с поддержкой Wi-Fi могут иметь мощность 15 дБмВт. Если возможно, выберите маршрутизатор Wi-Fi с настраиваемой мощностью и возможностью планирования. Например, одна конкретная модель обеспечивает 10 уровней мощности, что позволяет резко снизить ее. Маршрутизаторы Wi-Fi и цифровые беспроводные системы могут иметь мощность передачи до 1 Вт (требуются рекомендации 9 м / 90 м для Зальцбурга (2001 г.) и (2002 г.) соответственно. |
| Беспроводная телефонная система (Более ранний аналог) | Ожидание от базовой станции, когда не используется ~ 1 mW |
0,3m | 3m | Обратите внимание, что очень ранние беспроводные телефоны были, для сравнения, всего ~ 1 мВт, но теперь FCC допускает более высокую мощность передатчика 1 Вт. см. ссылку. |
| Беспроводная телефонная система (Современный цифровой) |
Непрерывно с базовой станции, даже когда не используется Пиковая: ~ 250 mW Среднее: ~ 10 mW |
4,5m | 45m | В то время как средняя выходная мощность составляет ~ 10 мВт, она выражается в виде 100 импульсов в секунду. 250 мВт мощность, каждый в течение ~ 0,4 мс, согласно HPA на беспроводных телефонах. Следовательно, его пиковая выходная мощность сравнима с выходной мощностью мобильного телефона. Пульсирующие сигналы включения / выключения считаются опасными. 250 мВт мощность, каждый в течение ~ 0,4 мс, согласно HPA на беспроводных телефонах. Следовательно, его пиковая выходная мощность сравнима с выходной мощностью мобильного телефона. Пульсирующие сигналы включения / выключения считаются опасными. |
| Мобильный телефон |
Настройки определяют продолжительность воздействия ~ 125 mW (класс мощности 4) ~ 250mW (3 класс мощности) 600mW Адаптивная мощность |
3,2m 4,5m 6,9m |
32m 45m 69m |
Чтобы уменьшить продолжительность воздействия, отключите службы передачи данных, такие как> «Мобильные данные» и «Wi-Fi», за исключением случаев, когда это необходимо, отключите фоновую передачу данных или увеличьте интервалы автоматической синхронизации и избегайте использование при слабом приеме сигнала. Хотя режим динамика или проводная гарнитура на расстоянии 1 метра значительно снижает удельную мощность, этого может быть недостаточно для достижения предупредительного предела. (17/10) = 0,08 * 50 = 4 mW / m2 (17/10) = 0,08 * 50 = 4 mW / m2 |
| 200m | 1 mW/m2 | <== Зальцбургский предел Предосторожности (2001) | ||
| 630 m | 100 mW / m2 | <== EU STOA 2001 | ||
| 2 km | 10 mW / m2 | <== Новые Меры Предосторожности на Открытом Воздухе (New Salzburg Precautionary Outdoor, 2002) |
Метод Расчёта: Плотность мощности можно оценить с помощью уравнения P * G / 4Πr2, где G — коэффициент усиления направленной антенны, а 4Πr2 — площадь поверхности сферы. На практике излучение вышки сотовой связи, обычно, не изотропно, а является направленным к главным и боковыми лепестками. Обратите внимание, что направленная антенна фокусирует мощность в определенных направлениях, что приводит к увеличению требуемых расстояний. Если мы предположим, что направленная антенна с усилением 17 dB= 50, тогда расстояния, необходимые в определённых направлениях, могут потребовать коэффициент умножения sqrt (50) = 7.
Рекомендуемые Расстояния для Беспроводных Вышек
Заметка: Многие исследования обнаруживают рак или другие последствия для здоровья в пределах 300-400 метров.
| Передатчик | Мощность Передачи предполагаемого усиления 17dB |
Зальцбург (2001)* |
Зальцбург (2002)* |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Очень слабый передатчик | 1 W | 63m | 630 m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Слабая сотовая башня | 10 W | 200m | 2 km | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сильная башня сотовой связи | 50 W | 446m | 4.46 km | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сильная башня сотовой связи | 100 W | 630 m | 6. 1,7 = 50), как было предложено профессором Кумаром. Чтобы учесть это, расстояние умножается примерно на sqrt (50) = 7 по сравнению с моделью изотропной антенны. 1,7 = 50), как было предложено профессором Кумаром. Чтобы учесть это, расстояние умножается примерно на sqrt (50) = 7 по сравнению с моделью изотропной антенны.
3. РадиовышкаЗаметка: Исследование радиовышки Ватикана выявило риск рака в радиусе 5,5 миль = 8.85 км. Говорят, что на радиовышке установлен передатчик мощностью 500 кВт для Дальнего Востока и Латинской Америки.
Метод Расчёта: Мы можем аппроксимировать плотность мощности с помощью уравнения P * G / 4Πr2, где 4Πr2 — площадь поверхности сферы, а G — коэффициент усиления антенны. 4. Будильник (Воздействие Линии Электропередачи)Обратите внимание, что магнитные поля линии электропередачи (переменного тока) падают намного быстрее до безопасного уровня.
5. Линии электропередач
Эти приближения взяты из статьи «Покупка собственности с« безопасностью от электромагнитных полей »- 2. Кроме того, обратите внимание, что в идеале целевой уровень должен быть <1 mG, с соблюдением ещё более строгих рекомендаций <0,2 mG для спальных помещений. См. Информационный Бюллетень про линии электропередач и стандартах SBM 2008 для линий электропередач, с рекоммендованным уровнем <1 mG. Закон обратного квадрата расстояния — Энциклопедия по машиностроению XXLВеличина ИНН, обратная произведению двух главных радиусов кривизны, называется гауссовой (или второй) кривизной поверхности. Из (34) следует, что в любой точке прямолинейного луча интенсивность пропорциональна гауссовой кривизне волнового фронта, проходящего через эту точку В частности, если все (прямолинейные) лучи имеют одну общую точку, го волновые фронты имеют вид сферических поверхностей с центром в этой точке, тогда Н1= Ri= R[, и мы получим (опуская индексы) закон обратного квадрата расстояния, т. е,
[c.122] е,
[c.122]
Обратимся теперь к вычислению интенсивности звука, излучаемого резонатором, возбужденным потоком воздуха. Очевидно, что достаточно вычислить энергию, излучаемую через устье резонатора, и для дальнейшего воспользоваться законом обратного квадрата расстояния. Средний поток энергии через устье резонатора согласно общей формуле (1.58) равен [c.167] Пересчетом по закону обратных квадратов определяют мощность дозы на расстоянии / [м] от мишени для тока / [ма] [c.238] По закону обратных квадратов, исходя из планировки помещения, определяют плотность потоков нейтронов на расстоянии R [м] от мишени [c.239] Однако положение не безнадежно, так как мы знаем, что значение любой силы, действующей между двумя телами, должно довольно быстро уменьшаться по мере увеличения расстояния между этими телами. Если бы силы не уменьшались достаточно быстро с увеличением расстояний между взаимодействующими телами, то мы никогда не смогли бы изолировать взаимодействие двух тел от взаимодействий их со всеми другими телами во Вселенной. Если известно, что значение силы обратно пропорционально квадрату расстояния, то какие особые заключения следуют из этого Какие принципиальные свойства Вселенной являются следствиями закона обратных квадратов Займемся теперь этими важными вопросами. Мы будем чаще иметь дело с потенциальной энергией, а не силой. При решении задач на определение потенциальной энергии или силы студенту почти всегда легче [c.269] Из закона обратных квадратов можно вывести важное следствие сила, действующая на материальную точку с массой М (пробную массу), находящуюся на расстоянии г от центра однородного тонкого шарового слоя радиусом R, имеет при r >R (т. е. если эта материальная точка находится вне шара) такую величину и направление, как если бы вся масса слоя была сконцентрирована в его центре. Второе следствие сила, действующая на материальную точку, находящуюся внутри слоя, т. е. при г специальный метод решения, в котором используется геометрическая симметрия условий задачи. Из теоремы о вириале в ее общем виде (112) следует не только то, что материальные точки, связанные между собой силами, действующими по закону обратных квадратов, должны иметь кинетическую энергию, но и то, что кинетическая и потенциальная энергии такой системы всегда сравнимы по величине. Даже если часть материальных точек в начальный момент не движется, силы притяжения, значения которых обратно пропорциональны квадрату расстояния, сближают эти точки друг с другом, увеличивая как потенциальную, так и кинетическую энергии до тех пор, пока средняя кинетическая энергия не станет равной с обратным знаком половине средней потенциальной энергии. В приводимом ниже примере мы воспользуемся теорем ой. о вириале, чтобы оценить температуру внутри Солнца, представляющего собой, как почти все звезды, массу сжатого раскаленного газа. [c.302] Теорема о вириале служит ключом к пониманию строения любого вещества, в котором силы сцепления обусловлены главным образом притяжением частиц по закону обратных квадратов. Любая достаточно большая газовая туманность, соединенная в одно целое собственным взаимным гравитационным притяжением, превратится в ходе эволюции в звезду или в несколько звезд это является необходимым следствием того факта, что зависимость сил притяжения от расстояния подчиняется закону обратных квадратов. [c.305] Полученное выражение показывает, что освещенность, создаваемая точечным источником ), обратно пропорциональна квадрату расстояния от источника до поверхности и прямо пропорциональна косинусу угла, составляемого направлением светового потока (осью узкого конуса, внутри которого распространяется поток) с нормалью к освещаемой поверхности. Для протяженных источников мы можем разбить поверхность источников на элементарные участки (достаточно малые по сравнению с Д) и, определив освещенность, создаваемую каждым из них по закону обратных квадратов, проинтегрировать затем по всей площади источника, приняв, конечно, во внимание зависимость силы света от направления. Зависимость освещенности от R окажется при этом более сложной. Однако при достаточно больших (по отношению к величине источника) расстояниях можно пользоваться и законом обратных квадратов, т. е. считать источник точечным. Этот упрощенный расчет дает практически хорошие результаты, если линейные размеры источника не превышают /ю расстояния от источника до освещаемой поверхности. Так, если источником служит равномерно освещенный диск диаметром 50 см, то в точке, лежащей на нормали к центру диска, ошибка в расчете по упрощенной формуле для расстояния 50 см достигает приблизительно 25%, для расстояния 2 м не превышает 1,5%, а для расстояния 5 м составляет всего лишь 0,25%. Пределы измерения фотоэлектрического калориметра можно, почти не снижая точности, расширять при помощи рассеиваю-щего ослабителя. Яркость лазерного пучка можно уменьшать за счет ослабления по закону обратных квадратов (фиг. 4.18). Излучение, диффузно отраженное от рассеивающей поверхности, падает на фотоэлемент, расположенный на расстоянии R от рассеивателя в направлении, близком к нормали. Перед катодом фотоэлемента помещена диафрагма с отверстием площадью S. Отношение энергии излучения, падающего на фотоэлемент, к энергии лазерного пучка равно [c.181] Поверхность сферической волны, излучаемой баллоном, увеличивается по. мере удаления от баллона соответственно интенсивность звука уменьшается. Каждому увеличению расстояния вдвое соответствует увеличение поверхности звуковой волны в 4 раза, что приводит к снижению интенсивности звука, а следовательно и уровня звукового давления, на 6 дБ. Другими словами, интенсивность звука обратно пропорциональна квадрату расстояния от источника — это так называемый закон обратных квадратов. На распространение звука на открытом воздухе влияют не только градиенты ветра и температуры. На больших расстояниях для высоких частот очень существен другой фактор — вязкость воздуха. Так как частицы воздуха непрерывно совершают колебательные движения, то между соседними частицами возникают силы трения. Тренне всегда приводит к поглощению энергии на высоких частотах, когда соседние частицы колеблются друг относительно друга с большой скоростью, влияние трения -может стать заметным. В результате трения звук частотой 10 кГц на расстоянии в 1 км затухает примерно на 40 дБ, это помимо ослабления, обусловленного законом обратных квадратов. Земля также поглощает звуковую энергию. Об этом мы узнаем в следующей главе. Если местность холмистая, заросшая лесом или покрыта снегом, поглощение может оказаться очень существенным. [c.134] Рассмотрим сферический источник звука с уровнем звуковой мощности 100 дБ. Согласно закону обратных квадратов облучение точечным источником обратно пропорционально квадрату расстояния от источника. Этот закон достаточно точен в случаях, когда расстояния велики по сравнению с размерами источника. [c.183] Изменение фокусного расстояния можно скомпенсировать использованием закона обратных квадратов. [c.306] Опыт. Измерение мощности и световой эффективности электрической лампы. Для этого опыта нам понадобится лампа накаливания (либо с прозрачным, либо с матовым баллоном), свеча, две восковые пластинки ( домашний воск , используемый для запечатывания домашних консервов, желе и джемов) и кусок алюминиевой фольги. Таким образом, освещенность, создаваемая точечным источником в отсутствие поглощения, обратно пропорциональна квадрату расстояния до него и прямо пропорциональна косинусу угла между направлением падающих лучей и нормалью к освещаемой поверхности. Первая часть этого утверждения, а также ( юрмула (22.6) называются законом обратных квадратов. Единица освещенности есть люкс (лк) — освещенность, создаваемая световым потоком в [c.149] Найти освещенность, создаваемую однородным светящимся шаром радиуса а на расстоянии Я от его центра, если освещаемая площадка перпендикулярна к радиусу, а поверхность шара излучает по закону Ламберта с поверхностной яркостью В. Показать, что в этих условиях на любых расстояниях от центра шара строго выполняется закон обратных квадратов, т, е. освещенность площадки меняется обратно пропорционально квадрату Я. [c.153] Из законов Кеплера и из принципов центральной силы следует, что если рассматривать планеты как тела бесконечно малых размеров по сравнению с их расстоянием от Солнца, то они движутся под влиянием сил, направленных к центру Солнца и меняющихся обратно пропорционально квадратам их расстояний от него. Попробуйте качественно понять, как изменились бы траектории движения, если бы сила тяготения изменялась с расстоянием не по закону обратных квадратов. [c.116] В сферических волнах поле убывает по мере удаления от центра волны, причем, как будет показано, начиная с достаточно большого расстояния давление и скорость частиц убывают обратно пропорционально расстоянию от центра, а плотность энергии — обратно пропорционально квадрату этого расстояния. Этот закон обратных квадратов связан с конечностью скорости звука и справедлив в общем случае только при отсутствии дисперсии. Для иллюстрации рассмотрим, например, сферу, которую расширили [c.272] Если сфера не просто расширяется от одного радиуса до другого, а совершает какое-нибудь другое движение, то расстояние, начиная с которого справедлив закон обратных квадратов, следует определять, беря в качестве Т характерное время процесса.  Например, для гармонических пульсаций сферы следует взять в качестве Т период колебаний расстояние в этом случае должно быть много больше длины волны.
[c.273] Например, для гармонических пульсаций сферы следует взять в качестве Т период колебаний расстояние в этом случае должно быть много больше длины волны.
[c.273]Если условие г > сТ не выполнено, то приведенные рассуждения несправедливы и убывание плотности энергии не подчиняется закону обратных квадратов. Например, в несжимаемой среде, где это условие никогда не выполняется, так как любое возмущение охватывает мгновенно все пространство, скорость частиц убывает обратно пропорционально квадрату расстояния, и поэтому плотность энергии убывает обратно пропорционально четвертой степени расстояния. [c.273] В этой главе, в основно.м с помощью примеров, наш метод развивается дальше. Вначале обсуждается эксперимент с освещенностью стульев и показывается, что относительная яркость стульев, определенная с по.мощью субъективных парных сравнений, очень близка к яркости, предсказываемой законом обратного квадрата оптики. Для дальнейшей иллюстрации того, что нашим методом близкая аппроксимация получается при известных фактических данных, представлены результаты элементарного исследования влияния стран в зависимости от их национальных богатств. Иногда утверждают, что отсутствие Г. п. в ОТО обусловлено тем, что в этой теории скорость распространения тяготения конечна (ур-ния ОТО — гиперболич. типа), в отличие от ньютоновской теории (ур-ние Пуассона — эллиптическое). Такое объяснение некорректно. Согласно ОТО, со скоростью света распространяется только изменение гравитац. поля. Сама же ку-лоиовская часть , соответствующая ньютоновскому закону обратных квадратов расстояния, с самого начала простираясь в бесконечность, никуда не распространяется. Математически это выражается в том, что в ОТО нач. данные для решений ур иий поля, задаваемые в иек-рый момент времени (i= onst), должны удовлетворять системе ур-иий, в к-рую входит и ур-ние эллиптич. типа, аналогичное ур-нию Пуассона ньютоновской теории. В действительности причиной отсутствия Г. п. в ОТО является то, что ур-ния пишутся ера-зу для наблюдаемых величин и кол-во ур-ний достаточно для определения всех этих величин. По мере удаления от центра волны различие уменьшается и плотность кинетической энергии стремится к плотности потенциальной энергии, убывая вместе с ней по закону обратных квадратов расстояния от центра волны. Вблизи же центра волны, в неволновой зоне, главную долю кинетической энергии составляет положительный добавочный член он убывает с расстоянием как 1/г . [c.297] На основании очень точных измерений установлено, что показатель степени при г в уравнении (1а) равен 2,000. .. для электростатических сил это проверено вплоть до расстояний порядка 10- см. Имеется большое число результатов измерений, выполненных настолько точно, что они позволили бы обнаружить даже небольшие отклонения от закона обратных квадратов. Основные данные этих измерений излагаются в т. II в связи с обсуждением электростатических сил. В качестве экспериментального подтверждения справедливости закона обратных квадратов для сил тяготения можно прежде всего указать на превос-
[c. Закон обратных квадратов, определяющий центральные силы, может быть также выражен в виде соотношения, согласно-которому потенциальная энергия обратно пропорциональна первой степени расстояния. Как мы видели в гл. 5, абсолютная величина силы F равна —dVIdr. Тогда, согласно уравнению (1а), [c.268] Через несколько лет Эдмунд Г аллей на основе третьего закона Кеплера пришел к выводу, что сила притяжения Солниа тоже должна уменьшаться обратно пропорционально квадрату расстояния планет от него, и пытался определить их пути. Не сумев этого сделать и не получив помощи от Гука и Рена, он поехал к Ньютону, у которого с удивлением обнаружил не только уже гото вое решение, но и еще немало важных материалов. Галлей предложил немедленно опубликовать их, но Ньютон, боясь новых споров и скандалов, только в 1686 г. представил их в Королевское общество. Гук немедленно заявил, что Ньютон использовал его результаты. Ньютон ответил резким письмом Галлею, указав, что Гук сам черпает свои данные у Борелли, а возможно, и у него, поскольку еще в 1673 г. он писал о законе обратных квадратов Гюйгенсу через Королевское общество, секретарем которого был Гук. Наконец конфликт уладили, и в 1687 г. труд Ньютона в трех книгах вышел в свет под названием Математические начала натуральной философии . В нем упоминались имена Гука, Рена и Галлея. Первые две книги посвящены классической механике, в третьей законы механики применяются для описания системы мира — это небесная механика, неизбежно затрагивающая интересы официальной христианской идеологии. Ньютон долга не соглашался на издание третьей книги. 22 мая 1686 г. он писал Третью книгу я намерен теперь устранить, философия — это такая наглая и сутяжная дама, что иметь с ней дело — это все равно, что быть вовлеченным в судебную тяжбу .
[c.85] Ньютон ответил резким письмом Галлею, указав, что Гук сам черпает свои данные у Борелли, а возможно, и у него, поскольку еще в 1673 г. он писал о законе обратных квадратов Гюйгенсу через Королевское общество, секретарем которого был Гук. Наконец конфликт уладили, и в 1687 г. труд Ньютона в трех книгах вышел в свет под названием Математические начала натуральной философии . В нем упоминались имена Гука, Рена и Галлея. Первые две книги посвящены классической механике, в третьей законы механики применяются для описания системы мира — это небесная механика, неизбежно затрагивающая интересы официальной христианской идеологии. Ньютон долга не соглашался на издание третьей книги. 22 мая 1686 г. он писал Третью книгу я намерен теперь устранить, философия — это такая наглая и сутяжная дама, что иметь с ней дело — это все равно, что быть вовлеченным в судебную тяжбу .
[c.85]По мере удаления от пластины, а также с увеличением длинььволны взаимное уничтожение волн по краям пластины становится менее полным. Итак, подведем некоторые итоги. Во-первых, установлено, что звук ведет себя в помещении так же, как и в открытом пространстве, только тогда, когда стенки помещения практически полностью поглощают звук. Во всех других случаях приходится иметь дело с двумя, если даже не с тремя типами шумовых полей. В обычных помещениях мы имеем дело с прямым звуком во всей области, где он является доминирующим. В этол области звуковое поле с точки зрения слушателя имеет направленный характер и подчиняется закону обратных квадратов. ВБрочем, если в помещении с хорошо отражающими стенками находится много источников звука, то суммарное реверберацион-ное поле может превосходить по интенсивности прямой звук вплоть до самых малых расстояний от источника или даже повсюду. И еще одна неприятность. Все, что пока говорилось в этой главе, относится к звуку в воздухе. Мы умолчали о том, что, попав в какую-нибудь кирпичную стену, звук распространяется уже в твердом теле, хотя в дальнейшем он снова может выйти в воздух. А в твердых телах звук может распространяться на большие расстояния с очень малыми потерями энергии. Здесь звук не подчиняется закону обратных квадратов, потому что в стене он не расходится во все стороны в виде сферических волн, а канализируется внутри стены в виде плоских или нагибных волн. При этом возможны крайне нежелательные последствия. Звук в воздухе, падая на стену помещения, превращается в звук в твердом теле. Даже если в результаге несогласования импедансов в стену войдет только 10% энергии воздушного звука, это приведет к уменьшению уровня всего на 10 дБ. Попав в твердую стену, звук не только будет выходить снова в воздух по другую сторону, но и распространится вдоль стены в остальную часть здания. Другие законы тяготения. Пример 2. Еслн бы вместо закона обратных квадратов имел место закои тяготения — ф (р), где р — расстояние, то потенциал тела в произвольной внешней точке S имел бы выражение Р )> в котором ф (р) — производная от фх (р). В этом случае, рассуждая точно таким же образом, как и в п. 513, получим [c.386] В момент, когда приближающийся к Луне космп-ческнй корабль находится на расстоянии Н от ее поверхности и имеет скорость г о, направленную к центру Луны, включается тормозной двигатель. Итак, ускорение планеты, движущейся но законам Кеплера, направлено но радиусу-вектору точки к фшсусу, т. е. к Солнцу, и но величине обратно пропорционально квадрату расстояния до Солнца. [c.353] Покажем, как может быть решена задача динамики, состоящая в том, чтобы, зная закон данного движения (законы Кеплера), определить действующую силу. Из первого закона Кеплера непосредственно вытекает, что действующая на планеты сила есть сила центральная, направление которой проходит через центр Солнца (см. 33, п. 2). Из второго закона легко найти, что сила, действующая на планеты, будет силой, притягивающей их к Солнцу обратно пропорционально квадрату расстояния. Для этого воспользуемся формулой Бинэ. [c.387] Эта формула выражает закон всемирного тяготения два тела пратягаваются с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Единицы измерения расстояний и редактирование—СправкаПри редактировании единицы карты для фрейма данных используются при получении и вводе измерений и расстояний. Единицами карты называются единицы, используемые для отображения пространственных данных во фрейме данных. Единицы карты определяются системой координат фрейма данных. При редактировании все значения, которые вы вводите, по умолчанию будут считаться введенными в единицах карты. Вы можете посмотреть, какие единицы используются системой координат, если зайдёте в диалоговое окно Свойства фрейма данных (Data Frame Properties) на закладку Общие (General). Иногда при создании объектов необходимо ввести значения, которые записаны в других единицах измерения, отличных от единиц карты. Когда вы вводите измерения, в ряде случаев возможен ввод значения в единицах измерения, отличных от единиц карты, с помощью добавления аббревиатур единиц измерения. Например, представьте, что данные имеют систему координат State Plane и линейными единицами измерения являются футы. Когда требуется ввести расстояние в инструменты редактирования, то всегда есть возможность указать единицы измерения и ввести число, которое будет преобразовано в единицы карты. Аббревиатуры единиц измерения работают только при использовании системы координат проекции, а не географической системы координат для фрейма данных. Следующие секции описывают основные сокращения, которые поддерживаются для ввода при редактировании, а также их применение. Метрические единицы
Британские единицы
Геодезические единицы измерений США
Ввод определенных местоположений (DD, DMS, DDM, MGRS, USNG и UTM)В командах редактирования, которые требуют ввода определенных местоположений, вы можете указывать местоположения с помощью пары координат широта/долгота, местоположения в системе грид координат Military Grid Reference System (MGRS), местоположение в системе координат U.S. National Grid (USNG) или с помощью координат в системе координат UTM. Это те же форматы, которые используются в команде Перейти к точке XY (Go To XY). Ниже приведены указания для ввода таких значений. Их можно использовать для команды Абсолютные XY (Absolute XY) и таких команд, как Переместить в, которые позволяют перемещать вершины или элементы топологии в заданную точку.
Примеры корректного ввода координат в виде долгота-широта
Примеры корректного ввода координат в форматах MGRS и USNG
Примеры корректного ввода координат в формате UTM
Коэффициенты конвертацииДля конвертации из одной системы измерений в другую используются специальные коэффициенты пересчёта. Если ссылка не работает, то можно открыть файл conversion_constants.pdf из папки \Documentation в директории установки ArcGIS. Для просмотра этого документа нужна программа Adobe Reader. О геодезических футах СШАВ 1959 году Национальное Бюро стандартов и Служба береговой и геодезической съёмки США решили переопределить отношение дюйм-сантиметр. Решили, что один дюйм равен ровно 2,54 сантиметрам, а один фут — ровно 0,3048 метрам. Однако в данном соглашении оговаривается, что более старое значение 39,37 дюймов в одном метре будет относиться к геодезическим футам США (U.S. survey foot). Одной из причин этой оговорки является то, что государственные системы координат, которые созданы на основе национальной геодезической сети, основываются на отношении метра к дюйму в соотношении 1 к 39,37. Разница между этими двумя значениями одного фута невелика, две миллионных, однако она всё же влияет на точность измерений. Основные объекты геодезической съёмки — роды, чейны, акры, статутные мили, округа и районы — все привязаны к соотношению 39,37 дюймов в одном метре. Таблица геодезических футов США представляет исправленные значения (геодезические значения) с помощью таблицы преобразования с коэффициентом 39,37. Связанные темыОтзыв по этому разделу?Не удается найти страницу | Autodesk Knowledge Network(* {{l10n_strings.REQUIRED_FIELD}}) {{l10n_strings.CREATE_NEW_COLLECTION}}* {{l10n_strings.ADD_COLLECTION_DESCRIPTION}} {{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings. TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}} TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}} {{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}} {{l10n_strings. AUTHOR}} AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}} {{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Squared Distance — обзор7.2.1 Модель линейной регрессииОсновное уравнение прогнозирования выражает линейную зависимость между независимой переменной ( x , предикторная переменная) и зависимой переменной ( y , критериальная переменная или ответ человека) (1)y=mx+b , где м — наклон зависимости, а b — точка пересечения y . Рисунок 7.11.Линейная зависимость между независимой переменной ( x ) и зависимой переменной ( y ). Чтобы построить это уравнение, нам сначала понадобится набор из x-y точек выборки. Хотя подходят любые две переменные шкалы отношений, чаще всего x-y точек сочетают настройку независимой переменной шкалы отношений ( x ) с измеренным значением реакции человека на зависимую переменную ( y ). Поскольку мы имеем дело с людьми, изменчивость неизбежна, поэтому маловероятно, что точки выборки будут лежать на прямой.Они разбегутся. Если модель хороша, точки будут достаточно близки к прямой линии. Насколько близко — ключевой вопрос. Поиск наиболее подходящей прямой линии включает в себя процесс, известный в статистике как линейная регрессия . Цель состоит в том, чтобы найти коэффициенты m и b в уравнении 1 для линии, которые минимизируют квадраты расстояний ( наименьших квадратов ) точек от линии. В рамках эксперимента по изучению ввода текста с помощью стилуса на программных клавиатурах Маккензи и Чжан (2001) также задались вопросом, можно ли предсказать скорость ввода с помощью стилуса на основе скорости пользователя при слепой печати на стандартной клавиатуре.В эксперименте приняли участие 12 человек. Участникам дали предварительный тест, чтобы измерить их скорость слепой печати. Во время эксперимента участники вводили текст с помощью стилуса и мягкой клавиатуры Qwerty, отображаемой на ЖК-планшете и дигитайзере. Предтестовая скорость слепой печати (независимая переменная) и экспериментально измеренная скорость постукивания стилусом (зависимая переменная) приведены на рис. Рисунок 7.12. Взаимосвязь между скоростью постукивания стилусом и скоростью слепой печати: (а) Данные.(б) Диаграмма рассеяния. (Адаптировано из MacKenzie and Zhang, 2001, рис. 4)Часто перед построением прогнозного уравнения задается более простой вопрос: существует ли связь между двумя переменными? Для этого примера вопрос заключается в следующем: быстро ли печатающие с быстрым касанием быстро нажимают стилусом? 8 Визуализация данных в виде диаграммы рассеивания помогает (см. рис. 7.12b). Да, похоже, есть связь. Например, самый медленный наборщик, P12 со скоростью 19 слов в минуту, также был довольно медленным при постукивании стилусом (13.1 сл/мин). Для 12 точек на рисунке коэффициент корреляции равен r = 0,5228. 9 Это скромная положительная корреляция. Следующим шагом является построение уравнения прогнозирования — наиболее точного уравнения прямой линии, предсказывающего скорость постукивания стилусом ( y ) на основе скорости печати вслепую ( x ). (2)y=0.1342 x+15,037 Рисунок 7.13 представляет собой улучшенную версию диаграммы на рисунке 7.12b. Помимо разброса точек, он показывает линию для уравнения прогноза вместе с уравнением и квадратом коэффициента корреляции, R 2 = 0,2733. (По соглашению R 2 задается в верхнем регистре, r в нижнем регистре.) R 2 интерпретируется как величина вариации данных, которая объясняется моделью. Обычно выражается в процентах.Таким образом, модель в уравнении 2 объясняет около 27 процентов вариаций данных на рис. 7.12а. Это не очень много, так что в данном случае модель в лучшем случае является скромным предсказателем скорости нажатия стилуса по скорости слепой печати. 11 Рисунок 7.13. Диаграмма рассеяния на рис. Одним из преимуществ прогностической модели является возможность прогнозировать результат на основе значения предиктора, который фактически никогда не посещался.Обратите внимание на рис. 7.12а, что ни у одного из участников скорость слепой печати не превышала 60 слов в минуту. Тем не менее, мы можем предположить, что пользователь со скоростью слепого набора 60 слов в минуту будет иметь скорость постукивания стилусом: на рис. 7.12а этот прогноз явно связан с некоторой неопределенностью. Стандартная ошибка оценки ( SE ) является полезной статистикой для измерения этой неопределенности. SE устанавливает доверительные интервалы вокруг прогноза.Для данных на рисунке 7.12a SE = 3,39 сл/мин. 12 Значения в пределах -1,96 SE и +1,96 SE прогноза находятся в пределах 95% доверительного интервала. Обычно сообщают о моделях линейной регрессии, дающих уравнение и R 2 .Доверительные интервалы и SE обычно не приводятся, хотя есть и исключения (Chung and Hossain, 2008; Johnsen, Raij, Stevens, Lind, and Lok, 2007; MacKenzie and Buxton, 1994). Иногда стандартная ошибка указывается отдельно для коэффициентов наклона и пересечения в модели линейной регрессии (Accot and Zhai, 2001; Cao et al., 2008; Pastel, 2006). Давайте перейдем к популярной модели прогнозирования в HCI, закону Фиттса. Евклидово расстояние в квадрате — обзорДалее нас интересует матрица расстояний для всех пар Δ формы m×n с использованием квадрата евклидова расстояния в качестве меры сходства: (6. , где i∈{0, …,m−1} и j∈{0,…,n−1}. Мы видим, что временная сложность алгоритма O(m⋅d⋅n) почти на три порядка выше, чем его сложность памяти, равная O(m⋅n), поскольку количество пикселей на изображение d=784 достаточно велико. Следовательно, мы ожидаем, что эта программа будет масштабироваться значительно лучше, чем рассмотренные ранее примеры сложения векторов и матричного умножения векторов. Более того, если мы перепишем уравнение(6.4) путем разложения его в терминах биномиальной теоремы ]⋅Xtrain(j)[k])+∑k=0d−1(Xtrain(j)[k])2. Мы наблюдаем разложение на два члена самодействия (первый и последний), которые зависят только либо от индекса i , либо j , и третий член смешения (средний), зависящий как от i , так и от j , которые на самом деле плотное матричное умножение матриц. Следовательно, обсуждаемые методы распараллеливания могут также применяться к другим постепенно накапливаемым мерам подобия, таким как коэффициент корреляции Пирсона двух z-нормализованных (исчезающее среднее значение и единичная дисперсия) случайных величин x(i) и y(j) ( 6. кросс-энтропия и дивергенция Кульбака – Лейблера векторов вероятностей p(i) и q(j) (6.7)H(p(i),q(j))=−∑k=0d−1p(i)[k]⋅log(q(j )[k]),KLD(p(i)||q(j))=∑k=0d−1p(i)[k]⋅log(p(i)[k]/q(j)[k ]), и расстояние Хэмминга между парами строк s(i) и t(j) фиксированной длины d (6.8)Ham(s(i),t(j))=∑k=0d −1{0if s(i)[k]==t(j)[k]1else. Общим для всех вышеупомянутых парных показателей является то, что они могут быть вычислены независимо для фиксированной комбинации индексов (i,j).Более того, их окончательное значение вычисляется как сумма индивидуальных вкладов для каждого значения k . В результате у нас есть в основном два варианта распараллеливания: либо мы распараллеливаем набор независимых индексов (i,j), либо выполняем параллельную редукцию суммы по внутреннему индексу k . Эффективность распараллеливания зависит от размерности матриц данных m,n,d. Далее мы будем называть распараллеливание внешних циклов «крупнозернистым» распараллеливанием, а внутренних — «мелкозернистым». Формула Евклидова расстояния – вывод, примерыПрежде чем приступить к изучению формулы евклидова расстояния, давайте посмотрим, что такое евклидово расстояние. В координатной геометрии евклидово расстояние – это расстояние между двумя точками. Чтобы найти две точки на плоскости, измеряется длина отрезка, соединяющего две точки. Мы выводим формулу евклидова расстояния, используя теорему Пифагора. Давайте изучим формулу евклидова расстояния вместе с несколькими решенными примерами. Что такое формула евклидова расстояния?Формула Евклидова расстояния, как следует из ее названия, дает расстояние между двумя точками (или) расстояние по прямой линии. Предположим, что \((x_1,y_1)\) и \((x_2,y_2)\) — две точки на двумерной плоскости. Вот формула Евклидова расстояния. Формула Евклидова расстоянияФормула Евклидова расстояния говорит: d = √[ (х\(_2\) – х\(_1\)) 2 + (у\(_2\) – у\(_1\)) 2 ] где,
Вывод формулы евклидова расстоянияЧтобы вывести формулу евклидова расстояния, рассмотрим две точки A (x\(_1\), y\(_1\)) и B (x\(_2\), y\(_2\)) и предположим, что d — расстояние между ними. Соедините A и B отрезком линии. Чтобы вывести формулу, построим прямоугольный треугольник, гипотенуза которого равна АВ.Для этого мы проводим горизонтальные и вертикальные линии от A и B, которые встречаются в C, как показано ниже. Теперь применим теорему Пифагора к треугольнику ABC. Тогда мы получаем, AB 2 = AC 2 + BC 2 d 2 = (х\(_2\) – х\(_1\)) 2 + (у\(_2\) – у\(_1\)) 2 Извлечение квадратного корня с обеих сторон, d = √[ (х\(_2\) – х\(_1\)) 2 + (у\(_2\) – у\(_1\)) 2 ] Отсюда выводится формула Евклидова расстояния. Хотите найти сложные математические решения за считанные секунды? Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами. Забронировать бесплатный пробный урок Мы увидим больше применений формулы Евклидова расстояния в разделе ниже. Примеры использования формулы евклидова расстоянияПример 1: Найдите расстояние между точками P(3, 2) и Q(4, 1). Решение: Дано: P(3, 2) = \((x_1,y_1)\) Q(4, 1) = \((x_2,y_2)\) Используя формулу Евклидова расстояния, d = √[(x\(_2\) – x\(_1\)) 2 + (y\(_2\) – y\(_1\)) 2 ] PQ = √[(4 – 3) 2 + (1 – 2) 2 ] PQ = √[(1) 2 + (-1) 2 ] PQ = √2 единицы. Ответ: Евклидово расстояние между точками A(3, 2) и B(4, 1) составляет √2 единицы. Пример 2: Докажите, что точки A(0, 4), B(6, 2) и C(9, 1) лежат на одной прямой. Решение: Чтобы доказать коллинеарность данных трех точек, достаточно доказать, что сумма расстояний между двумя парами точек равна расстоянию между третьей парой. Мы найдем расстояние между каждой парой точек, используя формулу Евклидова расстояния. AB = √[(6 – 0) 2 + (2 – 4) 2 ] = √[36 + 4] = √40 = 2√10 до н.э. = √[(9 – 6) 2 + (1 – 2) 2 ] = √[9 + 1] = √10 CA = √[(0 – 9) 2 + (4 – 1) 2 ] = √[81 + 9] = √90 = 3√10 Здесь мы видим, что АВ + ВС = СА (это потому, что 2√10 + √10 = 3√10). Ответ: Мы доказали, что A, B и C коллинеарны. Пример 3: Убедитесь, что точки A(√3, 1), B(0, 0) и C(2, 0) являются вершинами равностороннего треугольника. Решение: Три вершины A, B и C являются вершинами равностороннего треугольника тогда и только тогда, когда AB = BC = CA. Дано: А(√3, 1) = \((x_1,y_1)\) Б(0, 0) = \((х_2,у_2)\) С(2, 0) = \((х_3,у_3)\) Используя формулу Евклидова расстояния, AB = √[(x\(_2\) – x\(_1\)) 2 + (y\(_2\) – y\(_1\)) 2 ] = √[(0 – √3) 2 + (0-1) 2 ] = √(3 + 1) = √4 = 2 BC = √[(x\(_3\) – x\(_2\)) 2 + (y\(_3\) – y\(_2\)) 2 ] = √[(2-0) 2 + (0-0) 2 ] = √(4 + 0) = √4 = 2 CA = √[(x\(_3\) – x\(_1\)) 2 + (y\(_3\) – y\(_1\)) 2 ] = √[(2 — √3) 2 + (0 – 1 ) 2 ] = √(9 + 25) = √34 Здесь AB = BC ≠ CA. Ответ: A, B и C НЕ являются вершинами равностороннего треугольника. Часто задаваемые вопросы о формуле евклидова расстоянияЧто такое формула евклидова расстояния?Формула Евклидова расстояния используется для нахождения расстояния между двумя точками на плоскости. Эта формула говорит, что расстояние между двумя точками (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) равно d = √[(x 2 – х 1 ) 2 + (у 2 – у 1 ) 2 ]. Как вывести формулу евклидова расстояния?Чтобы вывести формулу евклидова расстояния, рассмотрим две точки A(x\(_1\), y\(_1\)) и B(x\(_2\), y\(_2\)) и соединим их линией сегмент. Затем проведите горизонтальные и вертикальные линии от A и B до точки C. Тогда ABC — прямоугольный треугольник, и, следовательно, мы можем применить к нему теорему Пифагора. Тогда мы получаем AB 2 = AC 2 + BC 2 d 2 = (x\(_2\) – x\(_1\))2 + (y\(_2\) – y\(_1\)) 2 Извлечение квадратного корня с обеих сторон, d = √[ (х\(_2\) – х\(_1\)) 2 + (у\(_2\) – у\(_1\)) 2 ] Для получения подробной информации нажмите здесь. Каковы применения формулы Евклидова расстояния?Формула Евклидова расстояния используется для нахождения длины отрезка по двум точкам на плоскости. Нахождение расстояния помогает доказать, что заданные вершины образуют квадрат, прямоугольник и т. д. (или) доказать, что заданные вершины образуют равносторонний треугольник, прямоугольный треугольник и т. д. В чем разница между формулой евклидова расстояния и формулой манхэттенского расстояния?Для любых двух точек (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) на плоскости
Расстояние между 2 точкамиКраткое пояснениеКогда мы знаем горизонтальных и вертикальных расстояний между двумя точками, мы можем вычислить расстояние по прямой линии следующим образом: расстояние = √ a 2 + b 2
Представьте, что вы знаете расположение двух точек (А и В), как здесь. Какое расстояние между ними?
Мы можем провести линии вниз от A и вдоль от B, чтобы получился прямоугольный треугольник. И с небольшой помощью Пифагора мы знаем, что: а 2 + б 2 = в 2
Теперь обозначьте координаты точек A и B. x A означает координату x точки A Горизонтальное расстояние a равно (x A − x B ) Вертикальное расстояние b равно (y A − y B )
Теперь мы можем найти c (расстояние между точками): Начните с:c 2 = a 2 + b 2 Поместите в вычисления для a и b:c 2 = (x A − x B ) 2 + (y A − y B ) 2 2 2 Квадратный корень из обеих сторон: c = √(x A − x B ) 2 + (y A − y B ) 2 Сделанный!ПримерыПример 1Заполните значения: с = √(9 − 3) 2 + (7 − 2) 2 Рассчитать:
с = √6 2 + 5 2 Пример 2Неважно, в каком порядке расположены точки, потому что возведение в квадрат удаляет все отрицательные числа: Заполните значения: с = √(3 − 9) 2 + (2 − 7) 2 Рассчитать:
c = √(−6) 2 + (−5) 2 Пример 3А вот еще пример с некоторыми отрицательными координатами… все еще работает:
Заполните значения: c = √(−3 − 7) 2 + (5 − (−1)) 2 Рассчитать:
c = √(−10) 2 + 6 2 (Примечание: √136 можно упростить до 2√34, если хотите) Попробуйте самиПеретащите точки: изображения / dist2pts. Три или более размеровОтлично работает в 3-х (или более!) измерениях. Возведите в квадрат разницу для каждой оси , затем суммируйте их и извлеките квадратный корень: Расстояние = √ (x A — x B ) 2 + (Y A — Y B ) 2 + (Z A — Z B ) 2 Пример: расстояние между двумя точками (8,2,6) и (3,5,7): = √(8−3) 2 + (2−5) 2 + (6−7) 2 Что примерно 5.9 Подробнее о теореме Пифагора в 3D 513, 514, 1148, 1149, 2994, 2995, 2996, 2997, 4034, 4035 Квадратное евклидово расстояние: статистический тест для оценки изменения растительного сообществаКвадрат евклидова расстояния: статистический тест для оценки изменения растительного сообщества | Поиск по дереву Перейти к основному содержанию . Сайт защищен. Первичная(ые) станция(и):Тихоокеанская юго-западная исследовательская станция Источник: Рез. Описание Описаны концепции и процедура оценки изменения растительного сообщества с использованием функции сходства квадрата евклидова расстояния (SED). Анализы основаны на концепции, согласно которой евклидовы расстояния составляют выборку из совокупности расстояний между единицами выборки (СЕ) для определенного количества раз и СЕ.При разных временах расстояния будут внутрикластерными или межкластерными. Межкластерные расстояния представляют собой контрольную обработку. Если сообщества различаются между временами, популяция будет содержать кластеры (области высокой плотности с короткими расстояниями между СЕ), которые разделены областями низкой плотности (большие расстояния между СЕ). Цитата Рэтлифф, Рэймонд Д. ПроцитированоПримечания к публикации
https://www.fs.usda.gov/treesearch/pubs/32547 Как работает инверсная взвешенная интерполяция расстояния — ArcGIS Pro Доступно с лицензией Geostatistical Analyst. Интерполяция, взвешенная по обратному расстоянию (IDW), явно предполагает, что объекты, находящиеся близко друг к другу, более похожи, чем те, которые находятся дальше друг от друга. Чтобы спрогнозировать значение для любого неизмеренного местоположения, IDW использует измеренные значения, окружающие прогнозируемое местоположение.Ближайшие к прогнозируемому местоположению измеренные значения оказывают большее влияние на прогнозируемое значение, чем те, которые находятся дальше. IDW предполагает, что каждая измеренная точка имеет локальное влияние, которое уменьшается с расстоянием. Он дает больший вес точкам, ближайшим к местоположению прогноза, и веса уменьшаются в зависимости от расстояния, отсюда и название «взвешенное обратное расстояние». Веса, присвоенные точкам данных, показаны в следующем примере: Иллюстрация Search Neighborhood Окно Weights содержит список весов, присвоенных каждой точке данных, которая используется для создания прогнозируемого значения в месте, отмеченном перекрестием. Узнайте больше о методах интерполяции, доступных в ArcGIS Geostatistical Analyst. . В результате с увеличением расстояния веса быстро уменьшаются. Скорость уменьшения весов зависит от значения p . Если p = 0, уменьшение с расстоянием не происходит, и поскольку все веса λ i одинаковы, прогноз будет средним значением всех значений данных в окрестности поиска.По мере увеличения p веса удаленных точек быстро уменьшаются. Если значение p очень велико, на прогноз будут влиять только ближайшие окружающие точки. Уменьшение веса с помощью иллюстрации расстояния Geostatistical Analyst использует значения степени, большие или равные 1. Когда p = 2, метод известен как взвешенная интерполяция с обратным квадратом расстояния. Значение по умолчанию — p = 2, хотя нет теоретического обоснования предпочтения этого значения по сравнению с другими, и влияние изменения p следует исследовать путем предварительного просмотра выходных данных и изучения статистики перекрестной проверки. Окрестность поискаПоскольку объекты, расположенные близко друг к другу, больше похожи друг на друга, чем объекты, расположенные дальше, по мере удаления местоположений измеренные значения будут мало связаны со значением прогнозируемого местоположения. Для ускорения расчетов можно исключить более удаленные точки, которые мало повлияют на прогноз. В результате общепринятой практикой является ограничение количества измеренных значений путем указания области поиска. Форма окрестности ограничивает, как далеко и где искать измеренные значения, которые будут использоваться в прогнозе.Другие параметры соседства ограничивают места, которые будут использоваться в этой фигуре. На следующем изображении пять измеренных точек (соседей) будут использоваться при прогнозировании значения для местоположения без измерения, желтая точка. Пример поиска окрестности На форму окрестности влияют входные данные и поверхность, которую вы пытаетесь создать. Если в ваших данных нет направленных влияний, вы захотите рассмотреть точки одинаково во всех направлениях. После указания формы соседства вы можете ограничить, какие местоположения данных внутри формы должны использоваться.Вы можете определить максимальное и минимальное количество локаций для использования, а также разделить район на сектора. Если вы разделите окрестности на сектора, к каждому сектору будут применены максимальное и минимальное ограничения. Точки, выделенные в окне просмотра данных, показывают местоположения и веса, которые будут использоваться для прогнозирования местоположения в центре эллипса (положение перекрестия). Когда использовать IDWПоверхность, рассчитанная с использованием IDW, зависит от выбора значения степени ( p ) и стратегии поиска соседства. IDW — это точный интерполятор, в котором максимальное и минимальное значения (см. диаграмму ниже) на интерполированной поверхности могут встречаться только в точках выборки. Пример профиля, взвешенного по обратному расстоянию Выходная поверхность чувствительна к кластеризации и наличию выбросов. IDW предполагает, что моделируемое явление обусловлено локальными вариациями, которые можно зафиксировать (смоделировать), определив адекватную окрестность поиска. Поскольку IDW не дает стандартных ошибок прогнозирования, обоснование использования этой модели может быть проблематичным. Похожие темыОтзыв по этой теме? 4 измерения расстояния для машинного обученияПоследнее обновление: 19 августа 2020 г. Меры расстояния играют важную роль в машинном обучении. Они обеспечивают основу для многих популярных и эффективных алгоритмов машинного обучения, таких как k-ближайших соседей для обучения с учителем и кластеризация k-средних для обучения без учителя. В зависимости от типов данных необходимо выбирать и использовать различные меры расстояния. Таким образом, важно знать, как реализовать и рассчитать ряд различных популярных мер расстояния и интуицию для полученных результатов. В этом руководстве вы познакомитесь с мерами расстояния в машинном обучении. После прохождения этого урока вы будете знать:
Начните свой проект с моей новой книги «Мастерство машинного обучения с Python», включающей пошаговых руководств и файлов исходного кода Python для всех примеров. Давайте начнем. Измерение расстояния для машинного обучения Обзор учебникаЭто руководство разделено на пять частей. они:
Роль мер расстоянияМеры расстояния играют важную роль в машинном обучении. Мера расстояния — это объективная оценка, которая суммирует относительную разницу между двумя объектами в проблемной области. Чаще всего эти два объекта представляют собой строки данных, которые описывают предмет (например, человека, машину или дом) или событие (например, покупку, претензию или диагноз). Возможно, наиболее вероятно, что вы столкнетесь с мерами расстояния, когда вы используете определенный алгоритм машинного обучения, который использует меры расстояния в своей основе. Наиболее известным алгоритмом этого типа является алгоритм k ближайших соседей, или сокращенно KNN. В алгоритме KNN для новых примеров выполняется классификация или регрессионный прогноз путем вычисления расстояния между новым примером (строкой) и всеми примерами (строками) в обучающем наборе данных. Затем выбираются k примеров в наборе обучающих данных с наименьшим расстоянием, и делается прогноз путем усреднения результата (мода метки класса или среднее значение реального значения для регрессии). KNN принадлежит к более широкой области алгоритмов, называемых обучением на основе конкретных случаев или обучением на основе примеров, большинство из которых аналогичным образом используют меры расстояния.Другим популярным алгоритмом на основе экземпляров, который использует меры расстояния, является алгоритм квантования вектора обучения или LVQ, который также можно рассматривать как тип нейронной сети. алгоритм самоорганизующейся карты, или SOM, также использует меры расстояния и может использоваться для контролируемого или неконтролируемого обучения. Другим алгоритмом обучения без учителя, который в своей основе использует меры расстояния, является алгоритм кластеризации K-средних.
— стр. 135, Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, 4-е издание, 2016 г. Краткий список некоторых из наиболее популярных алгоритмов машинного обучения, использующих в своей основе меры расстояния, выглядит следующим образом:
Существует множество методов на основе ядра, которые также можно считать алгоритмами на основе расстояния. Знаете ли вы другие алгоритмы, использующие меры расстояния? При вычислении расстояния между двумя примерами или строками данных возможно использование разных типов данных для разных столбцов примеров. Пример может иметь действительные значения, логические значения, категориальные значения и порядковые значения. Для каждого из них могут потребоваться разные меры расстояния, которые суммируются в одну оценку расстояния. Числовые значения могут иметь разный масштаб. Это может сильно повлиять на вычисление меры расстояния, и часто рекомендуется нормализовать или стандартизировать числовые значения перед вычислением меры расстояния. Числовая ошибка в задачах регрессии также может считаться расстоянием. Например, ошибка между ожидаемым значением и прогнозируемым значением — это одномерная мера расстояния, которую можно суммировать или усреднить по всем примерам в тестовом наборе, чтобы получить общее расстояние между ожидаемыми и прогнозируемыми результатами в наборе данных. Как мы видим, меры расстояния играют важную роль в машинном обучении. Вот, пожалуй, четыре наиболее часто используемых показателя расстояния в машинном обучении: .
Какие другие меры расстояния вы использовали или слышали? Вам необходимо знать, как вычислять каждую из этих мер расстояния при реализации алгоритмов с нуля, и понимать, что вычисляется при использовании алгоритмов, использующих эти меры расстояния. Давайте рассмотрим каждый по очереди. Расстояние Хэмминга Расстояние Хэмминга вычисляет расстояние между двумя двоичными векторами, также называемыми двоичными строками или битовыми строками для краткости. Скорее всего, вы столкнетесь с битовыми строками при горячем кодировании категориальных столбцов данных. Например, если столбец имеет категории « красный », « зеленый » и « синий », вы можете сразу закодировать каждый пример как битовую строку с одним битом для каждого столбца.
Расстояние между красным и зеленым можно рассчитать как сумму или среднее количество битовых различий между двумя битовыми строками. Это расстояние Хэмминга. Для строк с горячим кодированием может быть более целесообразно суммировать их до суммы битовых различий между строками, которая всегда будет равна 0 или 1.
Для строк битов, которые могут иметь много битов 1, более распространено вычисление среднего количества битовых различий, чтобы получить оценку расстояния Хэмминга от 0 (идентичные) до 1 (все разные).
Мы можем продемонстрировать это на примере вычисления расстояния Хэмминга между двумя битовыми строками, приведенными ниже. # вычисление расстояния Хэмминга между битовыми строками # рассчитать расстояние Хэмминга определение hamming_distance(a, b): возвращаемая сумма (abs (e1 — e2) для e1, e2 в zip (a, b)) / len (a) # определить данные строка1 = [0, 0, 0, 0, 0, 1] строка2 = [0, 0, 0, 0, 1, 0] # рассчитать расстояние расстояние = hamming_distance (строка1, строка2) печать(расстояние)
При выполнении примера сообщается расстояние Хэмминга между двумя битовыми строками. Мы видим, что между строками есть две разницы, или 2 из 6 битовых позиций различаются, что в среднем (2/6) составляет около 1/3 или 0,333. Мы также можем выполнить те же вычисления, используя функцию hamming() из SciPy. Полный пример приведен ниже. # вычисление расстояния Хэмминга между битовыми строками импорт Хэмминга из scipy.spatial.distance # определить данные строка1 = [0, 0, 0, 0, 0, 1] строка2 = [0, 0, 0, 0, 1, 0] # рассчитать расстояние расстояние = Хэмминг (строка1, строка2) печать(расстояние)
Запустив пример, мы видим, что получили тот же результат, что подтверждает нашу ручную реализацию. Евклидово расстояниеЕвклидово расстояние вычисляет расстояние между двумя векторами с действительными значениями. Скорее всего, вы будете использовать евклидово расстояние при вычислении расстояния между двумя строками данных, которые имеют числовые значения, такие как значения с плавающей запятой или целые числа. Если столбцы имеют значения с разным масштабом, перед вычислением евклидова расстояния обычно нормализуют или стандартизируют числовые значения во всех столбцах. В противном случае столбцы с большими значениями будут доминировать в показателе расстояния.
— стр. 135, Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, 4-е издание, 2016 г. Евклидово расстояние рассчитывается как квадратный корень из суммы квадратов разностей между двумя векторами. Этот расчет связан с нормой вектора L2 и эквивалентен сумме квадратов ошибок и сумме квадратов ошибок при добавлении квадратного корня. Мы можем продемонстрировать это на примере вычисления евклидова расстояния между двумя действительными векторами, приведенными ниже. # расчет евклидова расстояния между векторами из математического импорта sqrt # рассчитать евклидово расстояние определение евклидового_расстояния (а, б): вернуть sqrt (сумма ((e1-e2) ** 2 для e1, e2 в zip (a, b))) # определить данные ряд1 = [10, 20, 15, 10, 5] строка2 = [12, 24, 18, 8, 7] # рассчитать расстояние расстояние = евклидово_расстояние (строка1, строка2) печать(расстояние)
При выполнении примера отображается евклидово расстояние между двумя векторами. Мы также можем выполнить те же вычисления, используя функцию euclidean() из SciPy. Полный пример приведен ниже. # расчет евклидова расстояния между векторами из scipy.spatial.distance импорт евклидов # определить данные ряд1 = [10, 20, 15, 10, 5] строка2 = [12, 24, 18, 8, 7] # рассчитать расстояние расстояние = евклидово (строка1, строка2) печать(расстояние)
Запустив пример, мы видим, что получили тот же результат, что подтверждает нашу ручную реализацию. Расстояние до Манхэттена (такси или расстояние до городского квартала) Манхэттенское расстояние, также называемое расстоянием такси или расстоянием городского квартала, вычисляет расстояние между двумя векторами с действительными значениями. Возможно, это более полезно для векторов, описывающих объекты на единой сетке, например, шахматную доску или городские кварталы. Название такси для меры относится к интуитивному пониманию того, что вычисляет мера: кратчайший путь, по которому такси может пройти между городскими кварталами (координаты в сетке). Возможно, имеет смысл вычислять манхэттенское расстояние вместо евклидова расстояния для двух векторов в целочисленном пространстве признаков. Манхэттенское расстояние рассчитывается как сумма абсолютных разностей между двумя векторами.
Манхэттенское расстояние связано с нормой вектора L1 и метрикой абсолютной ошибки суммы и средней абсолютной ошибки. Мы можем продемонстрировать это на примере вычисления манхэттенского расстояния между двумя целочисленными векторами, приведенными ниже. # расчет манхэттенского расстояния между векторами из математического импорта sqrt # рассчитать манхэттенское расстояние определение manhattan_distance(a, b): возвращаемая сумма (abs (e1-e2) для e1, e2 в zip (a, b)) # определить данные ряд1 = [10, 20, 15, 10, 5] строка2 = [12, 24, 18, 8, 7] # рассчитать расстояние расстояние = расстояние_манхэттена (строка1, строка2) печать(расстояние)
При выполнении примера отображается манхэттенское расстояние между двумя векторами. Мы также можем выполнить те же вычисления, используя функцию cityblock() из SciPy. Полный пример приведен ниже. # расчет манхэттенского расстояния между векторами из scipy.spatial.distance импортировать городской квартал # определить данные ряд1 = [10, 20, 15, 10, 5] строка2 = [12, 24, 18, 8, 7] # рассчитать расстояние расстояние = городской квартал (строка1, строка2) печать(расстояние)
Запустив пример, мы видим, что получили тот же результат, что подтверждает нашу ручную реализацию. Расстояние Минковского Расстояние Минковского вычисляет расстояние между двумя векторами с действительными значениями. Где « p » — параметр заказа. Если для p установлено значение 1, вычисление будет таким же, как и для манхэттенского расстояния. Когда p установлено равным 2, оно совпадает с евклидовым расстоянием.
Промежуточные значения обеспечивают контролируемый баланс между двумя показателями. Обычно расстояние Минковского используется при реализации алгоритма машинного обучения, который использует меры расстояния, поскольку он дает контроль над типом меры расстояния, используемой для действительных векторов, с помощью гиперпараметра « p », который можно настроить. Мы можем продемонстрировать это вычисление на примере вычисления расстояния Минковского между двумя действительными векторами, перечисленными ниже. # расчет расстояния Минковского между векторами из математического импорта sqrt # рассчитать расстояние Минковского def minkowski_distance(a, b, p): возвращаемая сумма (abs (e1-e2) ** p для e1, e2 в zip (a, b)) ** (1/p) # определить данные ряд1 = [10, 20, 15, 10, 5] строка2 = [12, 24, 18, 8, 7] # рассчитать расстояние (p=1) расстояние = minkowski_distance (строка1, строка2, 1) печать (расстояние) # рассчитать расстояние (p=2) расстояние = minkowski_distance (строка1, строка2, 2) печать(расстояние)
При выполнении примера сначала вычисляется и печатается расстояние Минковского с p , установленным на 1, чтобы получить манхэттенское расстояние, затем с p , установленным на 2, чтобы получить евклидово расстояние, соответствующее значениям, рассчитанным на тех же данных из предыдущих разделов. Мы также можем выполнить те же вычисления, используя функцию minkowski_distance() из SciPy. Полный пример приведен ниже. # расчет расстояния Минковского между векторами из scipy.spatial импортировать minkowski_distance # определить данные ряд1 = [10, 20, 15, 10, 5] строка2 = [12, 24, 18, 8, 7] # рассчитать расстояние (p=1) расстояние = minkowski_distance (строка1, строка2, 1) печать (расстояние) # рассчитать расстояние (p=2) расстояние = minkowski_distance (строка1, строка2, 2) печать(расстояние)
Запустив пример, мы видим, что получаем те же результаты, что подтверждает нашу ручную реализацию. Дополнительное чтениеВ этом разделе содержится больше ресурсов по теме, если вы хотите углубиться. КнигиAPIАртикулРезюмеВ этом руководстве вы узнали о мерах расстояния в машинном обучении. В частности, вы узнали:
Есть вопросы? Откройте для себя быстрое машинное обучение в Python!Разработка собственных моделей за считанные минуты… всего несколькими строками кода scikit-learn Узнайте, как в моей новой электронной книге: Охватывает учебные пособия для самостоятельного изучения и комплексные проекты , такие как: |

 3m
3m 3 km
3 km
 Линии электропередач и опоры» из Powerwatch UK и PowerWatch Handbook, стр. 43. Однако, следует подчеркнуть, что для уверенности необходимо измерить магнитное поле. Даже при отсутствии линий электропередачи, существуют другие факторы, которые также могут влиять на магнитное поле линии электропередачи.
Линии электропередач и опоры» из Powerwatch UK и PowerWatch Handbook, стр. 43. Однако, следует подчеркнуть, что для уверенности необходимо измерить магнитное поле. Даже при отсутствии линий электропередачи, существуют другие факторы, которые также могут влиять на магнитное поле линии электропередачи. Значение всех известных сил, действующих между частицами, убывает по крайней мере не менее быстро, чем по закону обратных квадратов. Мы, как и всякое другое тело на Земле, испытываем притяжение главным образом к центру Земли и только в ничтожной степени — к ка-какой-либо удаленной части Вселенной. Если бы мы не опирались о пол, то получили бы ускорение 980 см/с по направлению к центру Земли. Менее сильно нас притягивает Солнце согласно уравнению (7) мы движемся с направленным к нему ускорением 0,6 см/с . Если разумно оценивать возможное ускорение, то следует ожидать, что на тело, значительно удаленное от всех других тел, вероятно, не будут действовать силы, и поэтому оно не будет иметь ускорения. Типичная звезда удалена от ближайших соседних небесных тел на расстояние не менее 10 см ), и поэтому следует ожидать, что она имеет лишь маленькое ускорение. Таким образом, мы пришли к утверждению, что с хорошей степенью приближения можно определить связанную с неподвижными звездами систему координат как удобную систему, не имеющую ускорения.
Значение всех известных сил, действующих между частицами, убывает по крайней мере не менее быстро, чем по закону обратных квадратов. Мы, как и всякое другое тело на Земле, испытываем притяжение главным образом к центру Земли и только в ничтожной степени — к ка-какой-либо удаленной части Вселенной. Если бы мы не опирались о пол, то получили бы ускорение 980 см/с по направлению к центру Земли. Менее сильно нас притягивает Солнце согласно уравнению (7) мы движемся с направленным к нему ускорением 0,6 см/с . Если разумно оценивать возможное ускорение, то следует ожидать, что на тело, значительно удаленное от всех других тел, вероятно, не будут действовать силы, и поэтому оно не будет иметь ускорения. Типичная звезда удалена от ближайших соседних небесных тел на расстояние не менее 10 см ), и поэтому следует ожидать, что она имеет лишь маленькое ускорение. Таким образом, мы пришли к утверждению, что с хорошей степенью приближения можно определить связанную с неподвижными звездами систему координат как удобную систему, не имеющую ускорения. [c.80]
[c.80] [c.269]
[c.269] Среднее расстояние между атомами рли атомными ядрами в типичной звезде, по-видимому, всегда больше 10- см, так как плотность такой звезды не превышает 10- г/см . Такие расстояния слишком велики для сильных ядерных взаимодействий, эффективных в пределах около 10 з см поэтому только силы гравитационного притяжения соединяют звезду в единое целое.
[c.302]
Среднее расстояние между атомами рли атомными ядрами в типичной звезде, по-видимому, всегда больше 10- см, так как плотность такой звезды не превышает 10- г/см . Такие расстояния слишком велики для сильных ядерных взаимодействий, эффективных в пределах около 10 з см поэтому только силы гравитационного притяжения соединяют звезду в единое целое.
[c.302] Это есть основной закон освещенности, создаваемой точечным источником (закон обратных квадратов).
[c.46]
Это есть основной закон освещенности, создаваемой точечным источником (закон обратных квадратов).
[c.46] [c.46]
[c.46] [c.128]
[c.128] Согласно закону обратных квадратов, в открытом пространстве уровень интенсивности звука на расстоянии 3 м от такого источника составит 79 дБ. Внесем этот источник в большое помещение размерами, скажем, ЮХ ХЗ м. Допустим, что коэффициент поглощения стен, потолка и пола в этом помещении равен 0,05 (так будет, если помещение построено, например, из оштукатуренного кирпича или бетона). Что мы услышим теперь Во-первых, по-прежнему прямой звук будет приходить непосредственно от источника к уху, и, если мощность источника не изменилась и между ним и ухом не поставили какого-либо препятствия, уровень интенсивности этого звука по-прежнему составит 79 дБ. Однако, после того как мы услышали прямой звук, волна пробежит далее и упадет на стены, пол и потолок. Эти поверхности поглотят 5% звуковой энергии, а 95% отразят обратно к нам. Звуковые волны снова пробегут мимо нас, и этот процесс будет повторяться снова и снова. Чтобы звук потерял 20% своей энергии, то есть чтобы его уровень упал на 1 дБ, он должен испытать более четырех отражений.
Согласно закону обратных квадратов, в открытом пространстве уровень интенсивности звука на расстоянии 3 м от такого источника составит 79 дБ. Внесем этот источник в большое помещение размерами, скажем, ЮХ ХЗ м. Допустим, что коэффициент поглощения стен, потолка и пола в этом помещении равен 0,05 (так будет, если помещение построено, например, из оштукатуренного кирпича или бетона). Что мы услышим теперь Во-первых, по-прежнему прямой звук будет приходить непосредственно от источника к уху, и, если мощность источника не изменилась и между ним и ухом не поставили какого-либо препятствия, уровень интенсивности этого звука по-прежнему составит 79 дБ. Однако, после того как мы услышали прямой звук, волна пробежит далее и упадет на стены, пол и потолок. Эти поверхности поглотят 5% звуковой энергии, а 95% отразят обратно к нам. Звуковые волны снова пробегут мимо нас, и этот процесс будет повторяться снова и снова. Чтобы звук потерял 20% своей энергии, то есть чтобы его уровень упал на 1 дБ, он должен испытать более четырех отражений. В результате добавления всех последовательных отражений, следующих друг за другом, пока они совершенно не затухнут, интенсивность первой отраженной волны окажется увеличенной в 18 раз. Можно показать, что в результате от сложения всех отражений интенсивность звука увеличивается в
[c.181]
В результате добавления всех последовательных отражений, следующих друг за другом, пока они совершенно не затухнут, интенсивность первой отраженной волны окажется увеличенной в 18 раз. Можно показать, что в результате от сложения всех отражений интенсивность звука увеличивается в
[c.181] Эталоном будет служить свеча. Мы предполагаем, что эта свеча близка к стандартной свече, т. е. испускает свет мощностью около 20 мет в видимой области спектра. Параметры лампы неизвестны. Однако полная мощность лампы известна и указана на баллоне. Выходную мощность лампы в видимом диапазоне можно измерить сравнением со свечой. Положите алюминиевую фольгу между двумя пластинками парафина. Поднесите этот бутерброд из алюминия и парафина к свече. Запомните яркость пластинки, обращенной к свече, и темноту второй пластинки, следующей за фольгой. Теперь поднесите этот бутерброд к лампе. Далее (вечером, когда зажжена только свеча и горит лампа) расположите парафиновый детектор между лампой и свечой так, чтобы каждая пластинка освещалась одним источником. Найдите положения источников, при которых две пластинки будут освещены одинаково. Измерьте эти расстояния. Теперь дело за арифметикой (используйте закон обратных квадратов). Ответ для мощности лампы дайте в свечах и ваттах (предполагая, что свеча — это эталон).
Эталоном будет служить свеча. Мы предполагаем, что эта свеча близка к стандартной свече, т. е. испускает свет мощностью около 20 мет в видимой области спектра. Параметры лампы неизвестны. Однако полная мощность лампы известна и указана на баллоне. Выходную мощность лампы в видимом диапазоне можно измерить сравнением со свечой. Положите алюминиевую фольгу между двумя пластинками парафина. Поднесите этот бутерброд из алюминия и парафина к свече. Запомните яркость пластинки, обращенной к свече, и темноту второй пластинки, следующей за фольгой. Теперь поднесите этот бутерброд к лампе. Далее (вечером, когда зажжена только свеча и горит лампа) расположите парафиновый детектор между лампой и свечой так, чтобы каждая пластинка освещалась одним источником. Найдите положения источников, при которых две пластинки будут освещены одинаково. Измерьте эти расстояния. Теперь дело за арифметикой (используйте закон обратных квадратов). Ответ для мощности лампы дайте в свечах и ваттах (предполагая, что свеча — это эталон). Определите эффективность лампы.
[c.207]
Определите эффективность лампы.
[c.207] Это наводит на мысль, что закон обратных квадратов может еще точнее объяснить движения, если рассматривать тела как имеющие конечные размеры, где каждая частица притягивает всякую другую частицу тела. Соответствующее исследование показывает, что это правильно.
[c.97]
Это наводит на мысль, что закон обратных квадратов может еще точнее объяснить движения, если рассматривать тела как имеющие конечные размеры, где каждая частица притягивает всякую другую частицу тела. Соответствующее исследование показывает, что это правильно.
[c.97] Затем следует пример оценки относительного расстояния шести городов от Филадельфии. Далее рассматривается различие между полной и неполной иерархиями.
[c.50]
Затем следует пример оценки относительного расстояния шести городов от Филадельфии. Далее рассматривается различие между полной и неполной иерархиями.
[c.50] [c.532]
[c.532] 267]
267]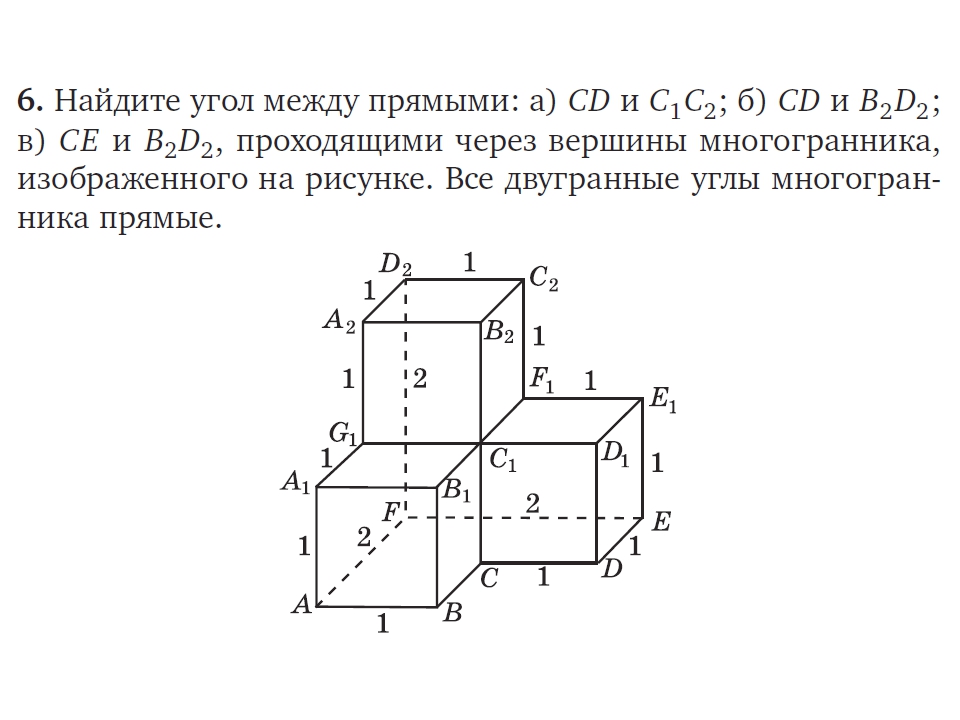 Поэтому на расстоянии нескольких метров от нее, в так называемой дальней зоне, форма волн снова приближается к сферической, а закон обратных квадратов опять входит в силу, однако лишь для каждого направления в отдельности, поскольку в разных направлениях интенсивность звука может быть различной. Зависимость доли излученной интенсивности от направления называют коэффициентом направленности Qв.
[c.130]
Поэтому на расстоянии нескольких метров от нее, в так называемой дальней зоне, форма волн снова приближается к сферической, а закон обратных квадратов опять входит в силу, однако лишь для каждого направления в отдельности, поскольку в разных направлениях интенсивность звука может быть различной. Зависимость доли излученной интенсивности от направления называют коэффициентом направленности Qв.
[c.130] [c.193]
[c.193] В результате, если в здании имеются два или три смежных помещения, звук будет переходить из одного в другое не только прямо сквозь стену, но и путем распространения вдоль стен и перекрытия и дальнейшего переизлу-чения в воздух. На рис. 46 показаны пути, по которым звук может перейти из одного помещения в другие. К сожалению, бетон — один из наилучших твердых проводников звука, так как внутреннее поглощение звука в нем весьма мало звук в жилом доме может гфопутешествовать по бетону от верхнего этажа жилого дома до самого подвала.
[c.195]
В результате, если в здании имеются два или три смежных помещения, звук будет переходить из одного в другое не только прямо сквозь стену, но и путем распространения вдоль стен и перекрытия и дальнейшего переизлу-чения в воздух. На рис. 46 показаны пути, по которым звук может перейти из одного помещения в другие. К сожалению, бетон — один из наилучших твердых проводников звука, так как внутреннее поглощение звука в нем весьма мало звук в жилом доме может гфопутешествовать по бетону от верхнего этажа жилого дома до самого подвала.
[c.195] Учитывая, что сила тяготения обратно пропорциональна квадрату расстояния от корабля до центра Луны и принимая, что масса корабля изменяется по закону т —
[c.337]
Учитывая, что сила тяготения обратно пропорциональна квадрату расстояния от корабля до центра Луны и принимая, что масса корабля изменяется по закону т —
[c.337]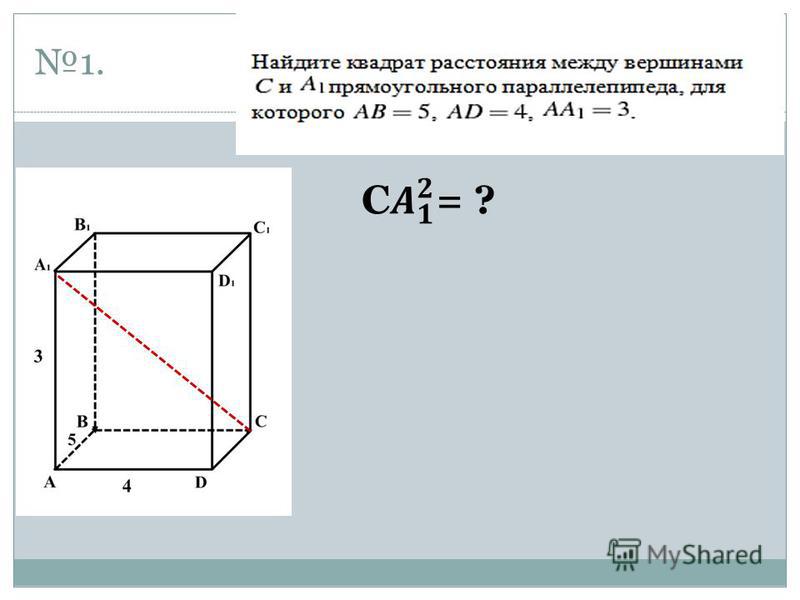 [c.389]
[c.389] Вы получили измерения в метрах. Вместо преобразования измерений в футы, вы можете указать аббревиатуру для метров, m, после значения измерения и инструменты корректно преобразуют это расстояние.
Вы получили измерения в метрах. Вместо преобразования измерений в футы, вы можете указать аббревиатуру для метров, m, после значения измерения и инструменты корректно преобразуют это расстояние. 01
01 344
344 9144
9144 3048006096
3048006096 0292100584
0292100584 По умолчанию единицами измерения являются единицы карты, но вы можете нажать кнопку Единицы чтобы выбрать единицы для ввода координат.
По умолчанию единицами измерения являются единицы карты, но вы можете нажать кнопку Единицы чтобы выбрать единицы для ввода координат.
 50W
50W Для конвертации значений из одной системы единиц измерения в другую следует использовать соответствующие коэффициенты пересчёта. Например, чтобы пересчитать футы в сантиметры, надо умножить футы на число 30,48 (27 футов x 30,48 = 822,96 сантиметров). Их список содержится в PDF файле коэффициентов пересчета.
Для конвертации значений из одной системы единиц измерения в другую следует использовать соответствующие коэффициенты пересчёта. Например, чтобы пересчитать футы в сантиметры, надо умножить футы на число 30,48 (27 футов x 30,48 = 822,96 сантиметров). Их список содержится в PDF файле коэффициентов пересчета.
 (См. Рисунок 7.11.)
(См. Рисунок 7.11.)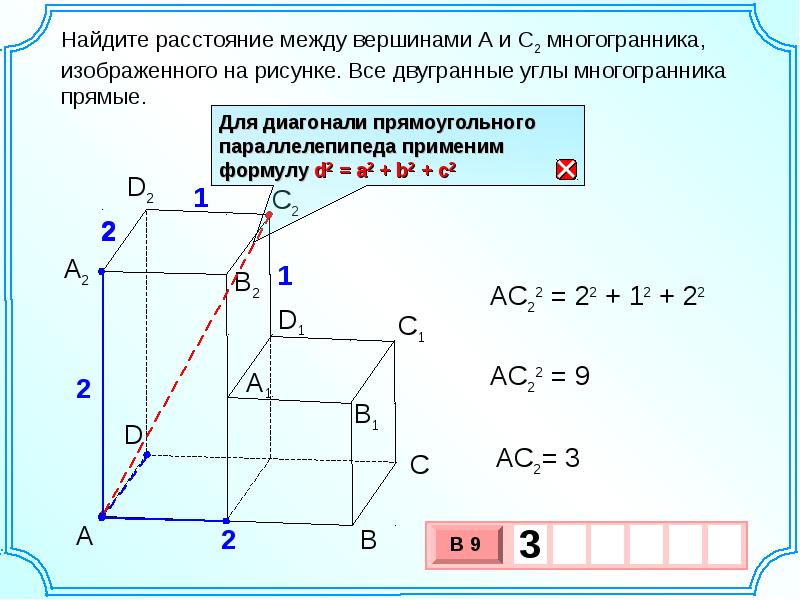 7 Результатом является уравнение предсказания — уравнение, которое дает наилучшую оценку y в терминах x .Конечно, модель основана на точках выборки, используемых при построении уравнения. Если данные хорошие и модель верна, должно появиться хорошее уравнение прогноза. Существует также встроенное предположение о том, что связь является линейной, что не обязательно так. Давайте рассмотрим пример в HCI.
7 Результатом является уравнение предсказания — уравнение, которое дает наилучшую оценку y в терминах x .Конечно, модель основана на точках выборки, используемых при построении уравнения. Если данные хорошие и модель верна, должно появиться хорошее уравнение прогноза. Существует также встроенное предположение о том, что связь является линейной, что не обязательно так. Давайте рассмотрим пример в HCI. 7.12а для каждого участника.
7.12а для каждого участника.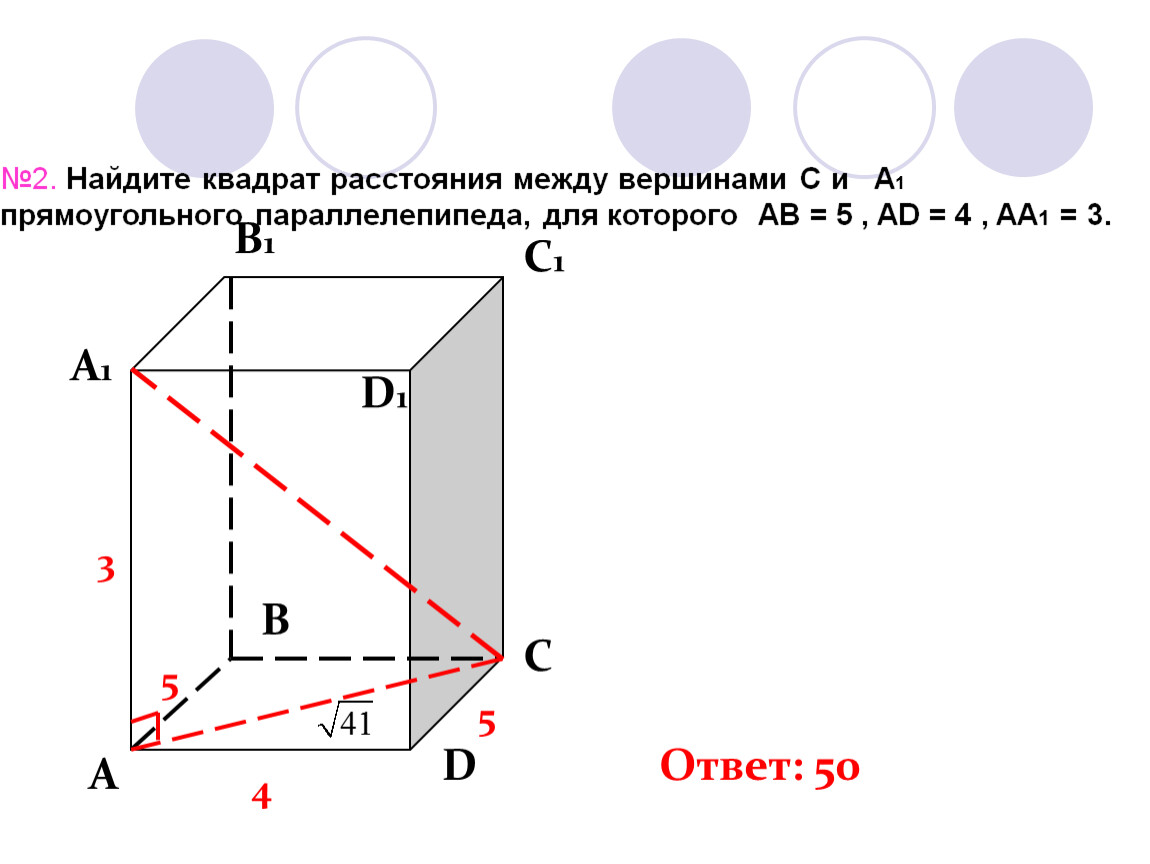 Это легко сделать с помощью приложения для работы с электронными таблицами, такого как Microsoft Excel. 10 Для данных на рис. 7.12а уравнение прогноза выглядит следующим образом:
Это легко сделать с помощью приложения для работы с электронными таблицами, такого как Microsoft Excel. 10 Для данных на рис. 7.12а уравнение прогноза выглядит следующим образом: 7.12b украшена линией линейной регрессии, уравнением прогнозирования, квадратом коэффициента корреляции ( R 2 ) и пунктирными линиями, показывающими 95% доверительный интервал.
7.12b украшена линией линейной регрессии, уравнением прогнозирования, квадратом коэффициента корреляции ( R 2 ) и пунктирными линиями, показывающими 95% доверительный интервал. Таким образом, для разработанной здесь модели с вероятностью 95 % пользователь, чья скорость слепого набора составляет 60 слов в минуту, будет иметь скорость постукивания стилусом от 23,1 – (1,96 × 3,39) = 16,4 слов/мин до 23,1 + (1,96 × 3,39) = 29,7 слов в минуту. Пунктирные линии, показывающие окно достоверности 95%, включены в рисунок 7.13.
Таким образом, для разработанной здесь модели с вероятностью 95 % пользователь, чья скорость слепого набора составляет 60 слов в минуту, будет иметь скорость постукивания стилусом от 23,1 – (1,96 × 3,39) = 16,4 слов/мин до 23,1 + (1,96 × 3,39) = 29,7 слов в минуту. Пунктирные линии, показывающие окно достоверности 95%, включены в рисунок 7.13.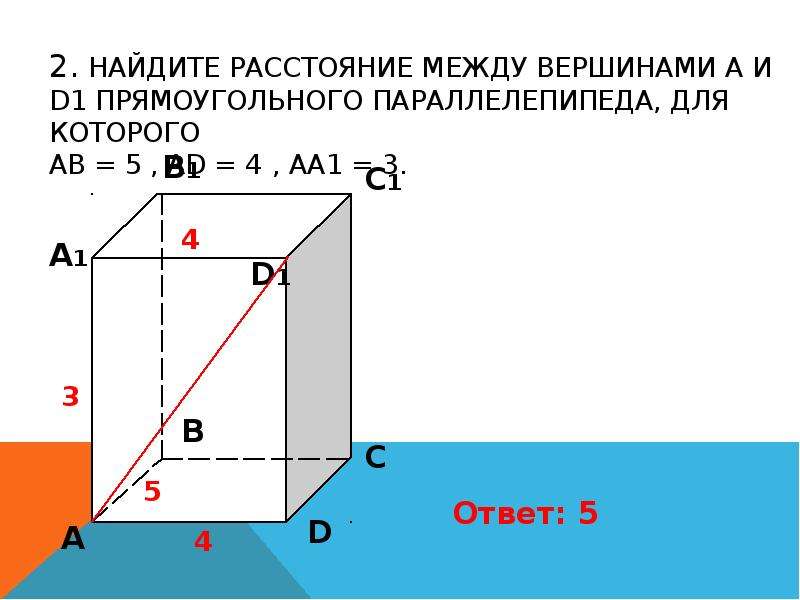 4)Δij=dist(Xtest(i),Xtrain(j))=∑k=0d−1(Xtest(i)[k]−Xtrain(j)[k])2,
4)Δij=dist(Xtest(i),Xtrain(j))=∑k=0d−1(Xtest(i)[k]−Xtrain(j)[k])2, 6)ρ(x(i),y(j))=∑k=0d−1x(i)[k]⋅y(j)[k](средний член),
6)ρ(x(i),y(j))=∑k=0d−1x(i)[k]⋅y(j)[k](средний член), ”
”

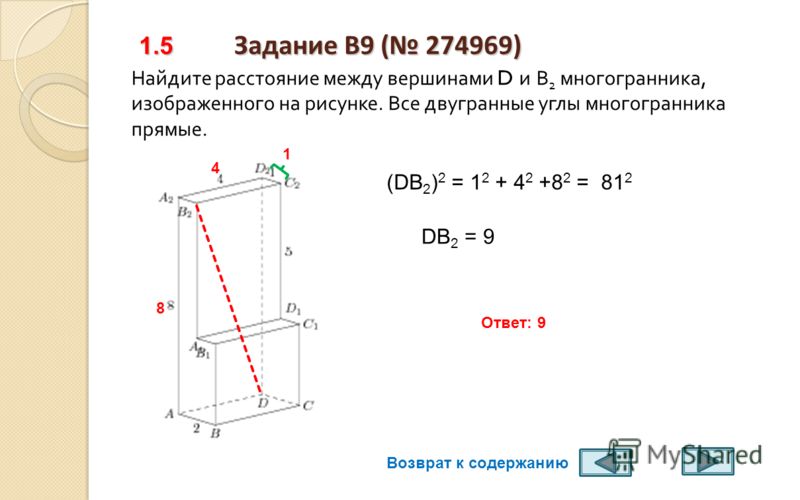




 8102…
8102… js
js gov означает, что это официально.
gov означает, что это официально.  Примечание PSW-RN-416. Олбани, Калифорния: Министерство сельского хозяйства США, Лесная служба, Тихоокеанская юго-западная исследовательская станция. 4 стр
Примечание PSW-RN-416. Олбани, Калифорния: Министерство сельского хозяйства США, Лесная служба, Тихоокеанская юго-западная исследовательская станция. 4 стр Средние квадраты внутри и между годами, полученные в результате анализа дисперсии для каждого вида (sp) в матрице данных, могут использоваться для вычисления средних расстояний внутри кластера и между кластерами.Многомерный ANOV A дает проверку гипотезы о том, что среднее расстояние внутри кластера равно среднему расстоянию между кластерами при общей частоте ошибок, примерно равной ex. Статистическое распределение SED представляет собой распределение линейной комбинации независимых случайных величин хи-квадрат. Знание этого распределения и использование обычных приближений делает возможной и надежной оценку приблизительных доверительных интервалов для средних межкластерных и внутрикластерных расстояний и их разности.Можно изучить доверительные интервалы и принять решение относительно любого указанного изменения в сообществе. Приводится простой пример, позволяющий изучить вычислительные методы.
Средние квадраты внутри и между годами, полученные в результате анализа дисперсии для каждого вида (sp) в матрице данных, могут использоваться для вычисления средних расстояний внутри кластера и между кластерами.Многомерный ANOV A дает проверку гипотезы о том, что среднее расстояние внутри кластера равно среднему расстоянию между кластерами при общей частоте ошибок, примерно равной ex. Статистическое распределение SED представляет собой распределение линейной комбинации независимых случайных величин хи-квадрат. Знание этого распределения и использование обычных приближений делает возможной и надежной оценку приблизительных доверительных интервалов для средних межкластерных и внутрикластерных расстояний и их разности.Можно изучить доверительные интервалы и принять решение относительно любого указанного изменения в сообществе. Приводится простой пример, позволяющий изучить вычислительные методы. ; Мори, Сильвия Р. 1993. Евклидово расстояние в квадрате: статистический тест для оценки изменения растительного сообщества. Рез. Примечание PSW-RN-416. Олбани, Калифорния: Министерство сельского хозяйства США, Лесная служба, Тихоокеанская юго-западная исследовательская станция.4 стр
; Мори, Сильвия Р. 1993. Евклидово расстояние в квадрате: статистический тест для оценки изменения растительного сообщества. Рез. Примечание PSW-RN-416. Олбани, Калифорния: Министерство сельского хозяйства США, Лесная служба, Тихоокеанская юго-западная исследовательская станция.4 стр


 Для этого вы определите область поиска как круг.Однако, если в ваших данных есть влияние направления, например преобладающий ветер, вы можете захотеть скорректировать его, изменив форму окрестности поиска на эллипс с большой осью, параллельной ветру. Поправка на это влияние направления оправдана, поскольку вы знаете, что места с наветренной стороны от прогнозируемого местоположения будут более похожими на удаленных расстояниях, чем местоположения, перпендикулярные ветру, но расположенные ближе к прогнозируемому местоположению.
Для этого вы определите область поиска как круг.Однако, если в ваших данных есть влияние направления, например преобладающий ветер, вы можете захотеть скорректировать его, изменив форму окрестности поиска на эллипс с большой осью, параллельной ветру. Поправка на это влияние направления оправдана, поскольку вы знаете, что места с наветренной стороны от прогнозируемого местоположения будут более похожими на удаленных расстояниях, чем местоположения, перпендикулярные ветру, но расположенные ближе к прогнозируемому местоположению. Окрестность поиска ограничена внутренней частью эллипса. В приведенном ниже примере двум красным точкам будет присвоен вес более 10 процентов.В восточном секторе одной точке (коричневой) будет присвоен вес от 5 до 10 процентов. Остальные точки в окрестности поиска получат меньшие веса.
Окрестность поиска ограничена внутренней частью эллипса. В приведенном ниже примере двум красным точкам будет присвоен вес более 10 процентов.В восточном секторе одной точке (коричневой) будет присвоен вес от 5 до 10 процентов. Остальные точки в окрестности поиска получат меньшие веса.



 Возможно, наиболее широко известным методом ядра является алгоритм опорных векторов, или сокращенно SVM.
Возможно, наиболее широко известным методом ядра является алгоритм опорных векторов, или сокращенно SVM. Расчет ошибки, такой как среднеквадратическая ошибка или средняя абсолютная ошибка, может напоминать стандартную меру расстояния.
Расчет ошибки, такой как среднеквадратическая ошибка или средняя абсолютная ошибка, может напоминать стандартную меру расстояния.



 2
2


 (1 шт.)
(1 шт.) .
.