Квадрат расстояния: Значение, Определение, Предложения . Что такое квадрат расстояния
Значение, Определение, Предложения . Что такое квадрат расстояния
- Онлайн-переводчик
- Грамматика
- Видео уроки
- Учебники
- Лексика
- Специалистам
- Английский для туристов
- Рефераты
- Тесты
- Диалоги
- Английские словари
- Статьи
- Биографии
- Обратная связь
- О проекте
Примеры
Значение слова «КВАДРАТ»
Равносторонний прямоугольник.
Смотреть все значения слова КВАДРАТ
Значение слова «РАССТОЯНИЕ»
Пространство, разделяющее два пункта, промежуток между чем-н..
Смотреть все значения слова РАССТОЯНИЕ
Предложения с «квадрат расстояния»
Оно не становится сильнее, когда квадрат расстояния между излучателем и приемником уменьшается. | |
Радиоволны быстро уменьшаются в интенсивности на обратный квадрат расстояния, когда они распространяются от передающей антенны. | |
| Другие результаты | |
Расстояние между двумя точками по определению равно квадратному корню из суммы квадратов разностей координат точек в трёх пространственных измерениях. | |
Расстояние до квадрата примерно… | |
Переместив квадрат на такое же расстояние под прямым углом к самому себе, мы получим куб. | |
Каждый квадратный член-это нормированное расстояние, отображающее энергию символа. | |
В общем числе наименьших квадратов остаток представляет собой расстояние между точкой данных и подогнанной кривой, измеренное вдоль некоторого направления. | |
В статистике расстояние Кука или D Кука-это обычно используемая оценка влияния точки данных при выполнении регрессионного анализа наименьших квадратов. | |
В этом случае расстояние — это квадратная или абсолютная разница между пикселем и центром кластера. | |
Линия проходила на довольно значительном расстоянии от скопления черных квадратов, обозначавших большие соборы или церкви. | |
| Японские и корейские пенхолдеры часто используют ракетку с квадратной головкой для игры на расстоянии от стола. | |
Беспроводные точки доступа также часто находятся рядом с людьми, но падение мощности на расстоянии происходит быстро, следуя закону обратных квадратов. | |
Выражая формулу Херона с определителем Кэли-Менгера в терминах квадратов расстояний между тремя заданными вершинами,. | |
Глубина резкости изменяется линейно с числом F и кругом путаницы, но изменяется пропорционально квадрату фокусного расстояния и расстоянию до объекта. | |
Да, да, притяжение ослабевает с квадратом расстояния. | |
Но нам всем известен остроумный ответ на вопрос, что есть филантроп: Это человек, чье милосердие увеличивается прямо пропорционально квадрату расстояния. | |
Это говорит нам, что сила притяжения между двумя телами … находится в прямой пропорции к их массам … и в обратной пропорции к квадрату расстояния между ними. | |
Сила пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между ними. | |
И то и другое-законы обратных квадратов, где сила обратно пропорциональна квадрату расстояния между телами. | |
Отношение расстояния между объектами, находящимися в свободном падении, к квадрату времени было недавно подтверждено Гримальди и Риччоли между 1640 и 1650 годами. | |
Интенсивность радиоволн быстро уменьшается на величину, обратную квадрату расстояния, по мере их распространения от передающей антенны. | |
Квадрат евклидова расстояния используется в качестве метрики для декодеров мягких решений. | |
Таким образом, вычисление расстояния в квадрате Евклидовой метрики для вычисления метрики ветви может быть выполнено с помощью простой операции сложения/вычитания. | |
Другими словами, погрешность пропорциональна квадрату расстояния между точками данных. | |
Как правило, алгоритм использует квадратные расстояния для сравнения, чтобы избежать вычисления квадратных корней. | |
Кроме того, он может сэкономить вычисление, удерживая квадрат текущего наилучшего расстояния в переменной для сравнения. | |
Квадратурные правила с равными расстояниями между точками обладают очень удобным свойством вложенности. | |
ГУК, не имея доказательств в пользу этого предположения, мог только предполагать, что закон обратных квадратов приблизительно действителен на больших расстояниях от центра. | |
Это требует чрезвычайно чувствительных экспериментов, которые ищут отклонение от закона обратных квадратов гравитации на различных расстояниях. | |
На данной странице приводится толкование (значение) фразы / выражения «квадрат расстояния», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных. Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «квадрат расстояния», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «квадрат расстояния», просим написать нам в разделе «Обратная связь».
Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «квадрат расстояния», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «квадрат расстояния», просим написать нам в разделе «Обратная связь».
ИЗЛУЧЕНИЕ: Закон обратного квадрата излучения
СВЯЗЬ МЕЖДУ РАССТОЯНИЕМ ОТ ИСТОЧНИКОВ ИЗЛУЧЕНИЯ И БЕЗОПАСНОСТЬЮ — «ЗАКОН ОБРАТНОЙ ПЛОЩАДИ» В ЭМП / РЧ ИЗЛУЧЕНИЯХ
Закон обратных квадратов гласит, что величина его воздействия значительно уменьшается пропорционально квадрату его расстояния от источника.
И наоборот, степень воздействия также резко увеличивается с приближением.
В следующих таблицах указаны приблизительные расстояния, необходимые для достижения Зальцбургского Предела Предосторожности 2001 и 2002 годов. Целью приведенных ниже расчетов является демонстрация того, что закон обратных квадратов (определенный справа) не так полезен, как вы думаете, когда уровень воздействия на здоровье намного ниже мощности передачи устройств (и международных стандартов).
После выполнения расчётов становится понятно, что наличие беспроводной телефонной станции, использующей непрерывное излучение DECT или маршрутизатор Wi-Fi в той же комнате,обеспечивает такую же (или большую) плотность мощности, что и при проживании рядом с вышкой сотовой связи. Сон с будильником в одном футе от головы — все равно что иметь личную электрическую вышку. Есть исследования, показывающие, что как вышки сотовой связи (например, см. Исследования Роберта Сантини), так и беспроводные телефоны (например, см. исследования Леоннарта Харделла) могут представлять потенциальный риск для здоровья. Сообщалось об очень низком уровне воздействия.
Ниже приведены сравнения между:
- Устройства Wi-Fi, Беспроводные телефоны, Мобильные телефоны и Интеллектуальные счётчики, Вышки сотовой связи и Радиовышки.
- Будильник и Линии Питания
Обратите внимание, что измерения ниже предполагают излучение в прямой видимости. Дерево и гипсокартон практически не блокируют беспроводные сигналы. Окна с покрытием с низким E или плёнками с низким E, бетон и кирпич могут обеспечивать более высокий уровень затухания и не учитываются в расчётах ниже
Окна с покрытием с низким E или плёнками с низким E, бетон и кирпич могут обеспечивать более высокий уровень затухания и не учитываются в расчётах ниже
Маршрутизатор Wi-Fi (микроволновое воздействие) с мощностью передачи (30 мВт)
Зависимость удалённости от источников излучения и безопасности — «ЗАКОН ОБРАТНОЙ ПЛОЩАДИ»
| Расстояние | Прибл. Удельная мощность** | Примечания |
|---|---|---|
| 30см | 26.5mW/m2 | Расчёт: 30/4Π(0.3*0.3) =~26.5 |
| 1m | 2.387 mW/m2 | Расчёт: 30/4Π =~2.387 |
| 1,55 m | 1 mW/m2 | Предел Предосторожности Зальцбурга (2001) Биоинициативная Рекомендация — (2007) |
| 3,7 m | 170 microW/m2 | Селетунская Научная Группа (2011) |
| 5m | 100 microW/m2 | STOA (2001) |
| 15,5 m | 10 microW/m2 | Новые Меры Предосторожности на Открытом Воздухе (Salzburg Precautionary Outdoor, 2002) |
Метод Расчёта: Мы можем аппроксимировать среднюю плотность мощности, используя уравнение P * G / 4Πr2, где 4Πr2 — площадь поверхности сферы, а G — коэффициент усиления антенны. Для приблизительных целей приведенные ниже числа предполагают изотропную антенну с постоянной интенсивностью.
Для приблизительных целей приведенные ниже числа предполагают изотропную антенну с постоянной интенсивностью.
** Обратите внимание, что направленное действие антенны здесь не учитывается, что может привести к недооценке мощности в определённых направлениях и переоценке мощности в других направлениях. Для направленного действия антенн, мы должны учитывать коэффициент усиления, чтобы рассчитать максимальное требуемое расстояние. Расстояния в этом сегменте, возможно, потребуется дополнительно отрегулировать, умножив его на квадратный корень коэффициента усиления. Он может варьироваться от 1,3 до 7, в зависимости от усиления антенны.
Следующая презентация Грэма Филипса показывает, что ноутбук с поддержкой Wi-Fi на расстоянии 50 см может источать большее излучение, чем вышка мобильного телефона (вышка сотовой связи) на расстоянии 100 метров (см. слайд 13).
Рекомендуемые расстояния для беспроводных устройств
В следующей таблице показаны минимальные расстояния, необходимые для соблюдения пределов Зальцбурга 2001 и 2002 вне помещений, основанные на предположении об изотропной антенне. Согласно таблице эффектов, упомянутой выше, некоторые эффекты всё ещё наблюдаются на пределе Зальцбурга (2001). Следовательно, предел Зальцбурга (2002) предпочтителен или находится где-то посередине. Чтобы рассчитать эти числа самостоятельно с учётом мощности передачи беспроводного продукта, обратитесь к странице формул.
Согласно таблице эффектов, упомянутой выше, некоторые эффекты всё ещё наблюдаются на пределе Зальцбурга (2001). Следовательно, предел Зальцбурга (2002) предпочтителен или находится где-то посередине. Чтобы рассчитать эти числа самостоятельно с учётом мощности передачи беспроводного продукта, обратитесь к странице формул.
**Запись: Поскольку антенна может быть направленной, а не изотропной, указанные ниже расстояния могут быть выше в зависимости от направления и усиления антенны. В некоторых направлениях
Это только общие рекомендации. Различные беспроводные маршрутизаторы различаются по мощности. Некоторые беспроводные маршрутизаторы позволяют снизить мощность передачи и даже запланировать часы, в которые Wi-Fi будет включён.
| Расстояние | Прибл. Удельная мощность** | Примечания |
|---|---|---|
| 30см | 26. 5mW/m2 5mW/m2 |
Расчёт: 30/4Π(0.3*0.3) =~26.5 |
| 1m | 2.387 mW/m2 | Расчёт: 30/4Π =~2.387 |
| 1,55 m | 1 mW/m2 | Предел Предосторожности Зальцбурга (2001) Биоинициативная Рекомендация — (2007) |
| 3,7 m | 170 microW/m2 | Селетунская Научная Группа (2011) |
| 5m | 100 microW/m2 | STOA (2001) |
| 15,5 m | 10 microW/m2 | Новые Меры Предосторожности на Открытом Воздухе (Salzburg Precautionary Outdoor, 2002) |
| Устройство | Продолжительность Мощность Передачи |
Зальцбург (2001)** |
Зальцбург (2002)** |
Комментарии |
|---|---|---|---|---|
Маршрутизаторы Wi-Fi (пониженное энергопотребление) Маршрутизаторы Wi-Fi (внешняя точка доступа) Маршрутизаторы Wi-Fi (высокой мощности) |
Непрерывно с маршрутизатора или точки доступа, даже когда не используется 30 mW (~ 15 dBm) 63 mW(~ 18 dBm) 500 mW (~ 27dBm) |
1,55 m 2,24 м 6. |
15,5 m 22,4 m 63m |
Обратите внимание, что компьютеры с поддержкой Wi-Fi могут иметь мощность 15 дБмВт. Если возможно, выберите маршрутизатор Wi-Fi с настраиваемой мощностью и возможностью планирования. Например, одна конкретная модель обеспечивает 10 уровней мощности, что позволяет резко снизить ее. Маршрутизаторы Wi-Fi и цифровые беспроводные системы могут иметь мощность передачи до 1 Вт (требуются рекомендации 9 м / 90 м для Зальцбурга (2001 г.) и (2002 г.) соответственно. |
| Беспроводная телефонная система (Более ранний аналог) | Ожидание от базовой станции, когда не используется ~ 1 mW |
0,3m | 3m | Обратите внимание, что очень ранние беспроводные телефоны были, для сравнения, всего ~ 1 мВт, но теперь FCC допускает более высокую мощность передатчика 1 Вт. см. ссылку. |
| Беспроводная телефонная система (Современный цифровой) |
Непрерывно с базовой станции, даже когда не используется Пиковая: ~ 250 mW Среднее: ~ 10 mW |
4,5m | 45m | В то время как средняя выходная мощность составляет ~ 10 мВт, она выражается в виде 100 импульсов в секунду.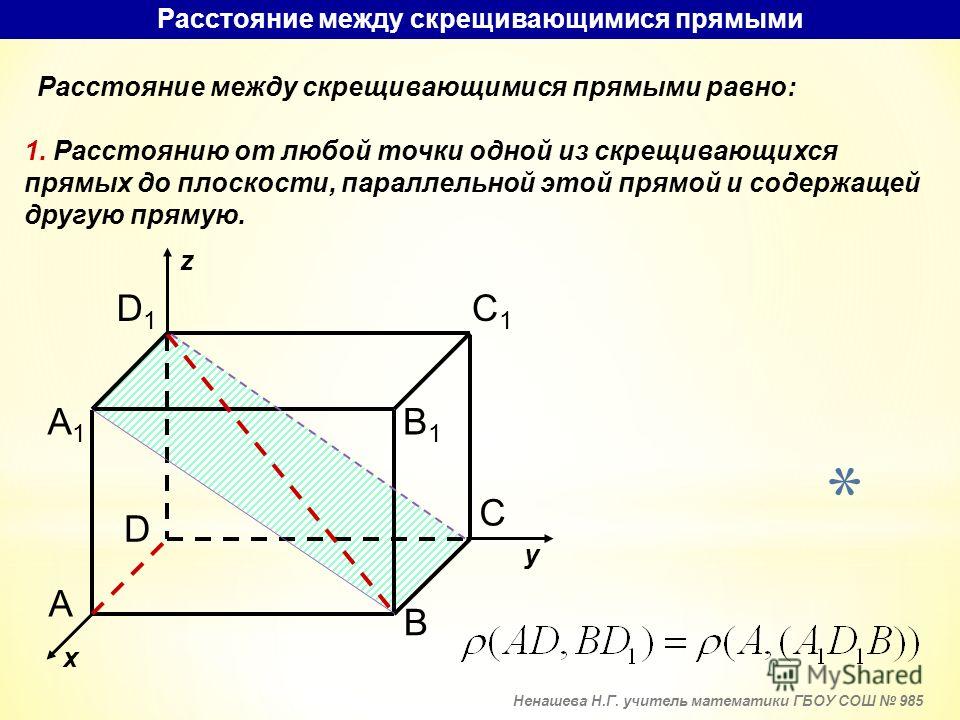 250 мВт мощность, каждый в течение ~ 0,4 мс, согласно HPA на беспроводных телефонах. Следовательно, его пиковая выходная мощность сравнима с выходной мощностью мобильного телефона. Пульсирующие сигналы включения / выключения считаются опасными. 250 мВт мощность, каждый в течение ~ 0,4 мс, согласно HPA на беспроводных телефонах. Следовательно, его пиковая выходная мощность сравнима с выходной мощностью мобильного телефона. Пульсирующие сигналы включения / выключения считаются опасными. |
| Мобильный телефон |
Настройки определяют продолжительность воздействия ~ 125 mW (класс мощности 4) ~ 250mW (3 класс мощности) 600mW Адаптивная мощность |
3,2m 4,5m 6,9m |
32m 45m 69m |
Чтобы уменьшить продолжительность воздействия, отключите службы передачи данных, такие как> «Мобильные данные» и «Wi-Fi», за исключением случаев, когда это необходимо, отключите фоновую передачу данных или увеличьте интервалы автоматической синхронизации и избегайте использование при слабом приеме сигнала. Хотя режим динамика или проводная гарнитура на расстоянии 1 метра значительно снижает удельную мощность, этого может быть недостаточно для достижения предупредительного предела. (17/10) = 0,08 * 50 = 4 mW / m2 (17/10) = 0,08 * 50 = 4 mW / m2 |
| 200m | 1 mW/m2 | <== Зальцбургский предел Предосторожности (2001) | ||
| 630 m | 100 mW / m2 | <== EU STOA 2001 | ||
| 2 km | 10 mW / m2 | <== Новые Меры Предосторожности на Открытом Воздухе (New Salzburg Precautionary Outdoor, 2002) |
Метод Расчёта: Плотность мощности можно оценить с помощью уравнения P * G / 4Πr2, где G — коэффициент усиления направленной антенны, а 4Πr2 — площадь поверхности сферы. На практике излучение вышки сотовой связи, обычно, не изотропно, а является направленным к главным и боковыми лепестками. Обратите внимание, что направленная антенна фокусирует мощность в определенных направлениях, что приводит к увеличению требуемых расстояний. Если мы предположим, что направленная антенна с усилением 17 dB= 50, тогда расстояния, необходимые в определённых направлениях, могут потребовать коэффициент умножения sqrt (50) = 7. Для получения дополнительной информации см. “Отчёт о радиации вышек сотовой связи”, представленный секретарю DOT, Delhi, подготовленный профессором Гиришем Кумаром, IIT.
Для получения дополнительной информации см. “Отчёт о радиации вышек сотовой связи”, представленный секретарю DOT, Delhi, подготовленный профессором Гиришем Кумаром, IIT.
Рекомендуемые Расстояния для Беспроводных Вышек
Заметка: Многие исследования обнаруживают рак или другие последствия для здоровья в пределах 300-400 метров.
| Передатчик | Мощность Передачи предполагаемого усиления 17dB |
Зальцбург (2001)* |
Зальцбург (2002)* |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Очень слабый передатчик | 1 W | 63m | 630 m | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Слабая сотовая башня | 10 W | 200m | 2 km | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сильная башня сотовой связи | 50 W | 446m | 4.46 km | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сильная башня сотовой связи | 100 W | 630 m | 6. 1,7 = 50), как было предложено профессором Кумаром. Чтобы учесть это, расстояние умножается примерно на sqrt (50) = 7 по сравнению с моделью изотропной антенны. 1,7 = 50), как было предложено профессором Кумаром. Чтобы учесть это, расстояние умножается примерно на sqrt (50) = 7 по сравнению с моделью изотропной антенны.
3. РадиовышкаЗаметка: Исследование радиовышки Ватикана выявило риск рака в радиусе 5,5 миль = 8.85 км. Говорят, что на радиовышке установлен передатчик мощностью 500 кВт для Дальнего Востока и Латинской Америки.
Метод Расчёта: Мы можем аппроксимировать плотность мощности с помощью уравнения P * G / 4Πr2, где 4Πr2 — площадь поверхности сферы, а G — коэффициент усиления антенны. 4. Будильник (Воздействие Линии Электропередачи)Обратите внимание, что магнитные поля линии электропередачи (переменного тока) падают намного быстрее до безопасного уровня.
5. Линии электропередач
Эти приближения взяты из статьи «Покупка собственности с« безопасностью от электромагнитных полей »- 2. Кроме того, обратите внимание, что в идеале целевой уровень должен быть <1 mG, с соблюдением ещё более строгих рекомендаций <0,2 mG для спальных помещений. См. Информационный Бюллетень про линии электропередач и стандартах SBM 2008 для линий электропередач, с рекоммендованным уровнем <1 mG. Мы экранируем Здания / Пространства и мы обнаруживаем электромагнитные поля, которые существуют в районах, поселениях и зданиях из-за наличия антенных парков в этом районе … Работа со светом — закон обратных квадратов
В техническом плане, закон обратных квадратов является законом, который утверждает о том, что значение физической величины в определенной точке пространства является обратно пропорциональным квадрату расстояния к источнику поля, непосредственно которое и характеризует эта самая физическая величина. КонцепцияДанный закон позволяет легче понимать важность расстояния от объекта съемки до источника света. По сути, закон обратных квадратов поясняет степень уменьшения яркости света в зависимости от увеличения расстояния. Допустим, что есть источник света, который работает на полную мощность. Объект стоит от него на расстоянии двух метров. А как изменится освещение объекта, если он отойдет на 2 метра от источника света. многим может показаться, что освещение уменьшится в 2 раза, но на самом деле это не так.
Опираясь на закон обратных квадратов, можно сказать, что сила света будет обратно пропорциональна квадрату расстояния. Получается, что если взять расстояние 2 метра, то квадрат этого числа будет равняться 4, а так как нам необходимо обратно пропорциональное значение, то мы получим 1/4. Таким образом, можно построить таблицу, которая будет описывать интенсивность света в зависимости от источника света до объекта.
ПрактикаВ фотографии описанный выше закон влияет на экспозицию. Можно говорить о том, что первоначальное падение освещенности объекта происходит быстро, но чем дальше удаляется объект, тем падение освещенности уменьшается. Для наглядности можно взглянуть на схему, которая демонстрирует процентное отношения падения освещенности на расстоянии 10 метров:
Можно заметить, что с первого по второй метр интенсивность света уменьшается на целых 75%, но затем, с 4 по 20 падает только лишь на 5%. Экспонирование
Мы разобрались с тем, что чем объект съемки находится ближе к источнику света, тем сильнее он освещен, а чем он находится дальше, тем, соответственно, освещен он слабее.
Это позволяет примерно рассчитать, на каком расстоянии от источника света какое значение диафрагмы следует использовать:
Освещение одного объекта
Теперь поместим значения диафрагмы на верхнюю часть схемы и представим, что источником света освещена модель, которая постоянно двигается в кадре.
Расположив модель на расстоянии от 6 до 9 метров, можно позволить ей ходить во все стороны, а вы можете сконцентрироваться на съемке и не перестраивать камеру.
Освещение нескольких объектовПри работе с несколькими объектами или моделями может оказаться, что они окажутся неравномерно освещены. Например, расположив объекты съемки близко к источнику света, они окажутся в диапазоне от F22 до F11. Это значит, что некоторые объекты могут оказаться пересвечены, а некоторые слишком темные:
Если же переместить те же объекты на расстояние 7-9 метров от источника света, все они окажутся в одной световой зоне и будут освещены одинаково:
Освещение фона
Часто в съемке необходимо, чтобы одни предметы были светлее других.
Чтобы получить одинаковое освещение модели и фона, их необходимо расположить подальше от источника света и поставить недалеко друг от друга:
ВыводНа самом деле то, что было описано в статье — это лишь основы закона обратных квадратов. Он на самом деле намного более запутанный. Дело в том, что в нем очень много переменных. К ним относится мощность источника света, несколько источников, скорость затвора камеры, дополнительные линзы и многое другое. Зная основу, всегда можно продолжить изучение. Даже описанная выше информация, при правильном её использовании может помочь делать более качественные снимки. На основе материалов с сайта: http://photomotion.ru Квадрат расстояния между вершинами С и А1 прямоугольного параллелепипедаПохожие презентации: Элементы комбинаторики ( 9-11 классы) Применение производной в науке и в жизни Проект по математике «Математика вокруг нас. Знакомство детей с математическими знаками и монетами Тренажёр по математике «Собираем урожай». Счет в пределах 10 Методы обработки экспериментальных данных Лекция 6. Корреляционный и регрессионный анализ Решение задач обязательной части ОГЭ по геометрии Дифференциальные уравнения Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи 1. Егэ 2014ЗАДАНИЕ В 102. 1. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.1. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ С ИА1 ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ДЛЯ КОТОРОГО АВ = 5 , AD = 4 , AA1 = 3. B1 A1 C1 D1 3 B C 5 5 41 A 4 D Ответ: 50 3. 2. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.2. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ВЕРШИНАМИ А И D1ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ДЛЯ КОТОРОГО АВ = 5 , AD = 4 , AA1 = 3.  B1 C1 4 A1 D1 3 B C 5 A 4 D Ответ: 5 4. 3. Найдите угол ABD1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3. Ответ дайте в градусах.3. НАЙДИТЕ УГОЛ ABD1 ПРЯМОУГОЛЬНОГОПАРАЛЛЕЛЕПИПЕДА, ДЛЯ КОТОРОГО АВ = 5 , AD = 4 , AA1 = 3. ОТВЕТ ДАЙТЕ В ГРАДУСАХ. A1 B1 C1 D1 3 3 5 A 5 B 4 D C Ответ: 45 5. 4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.4. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ A И E1. F 1 1 A 120° 3 1 1 1 3 Ответ: 2 1 E 6. 5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.5. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ B И E. 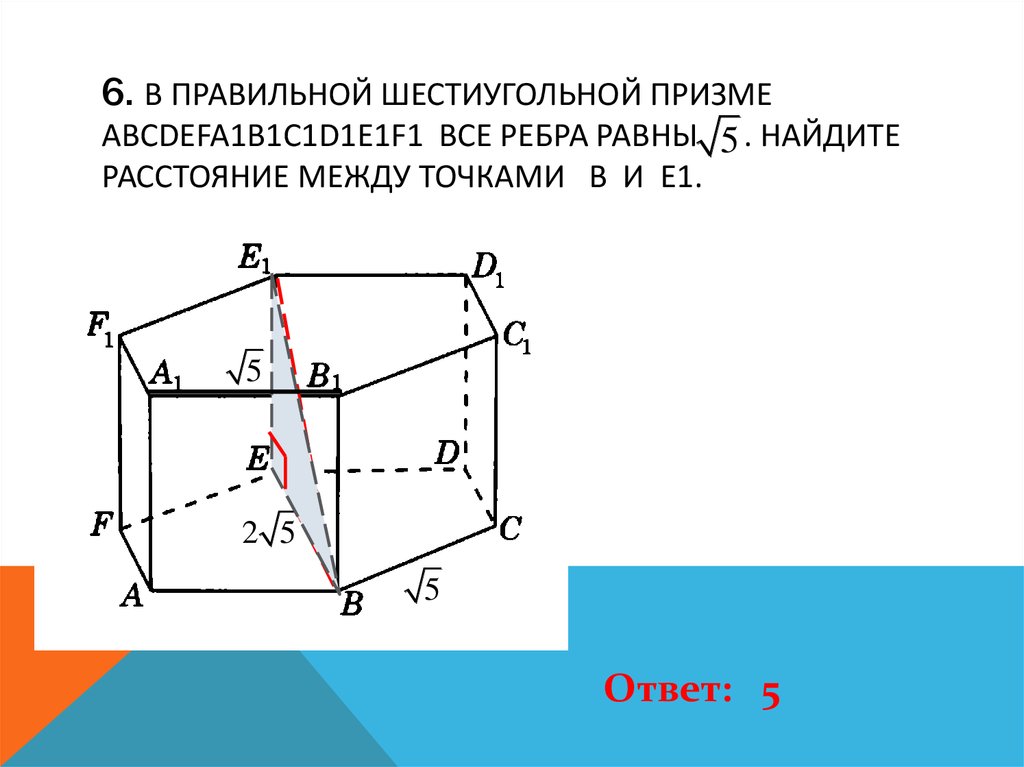 E 1 O 1 B 1 Ответ: 2 1 7. 6. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите расстояние между точками B и E1.6. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 5 . НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ B И E1. 5 2 5 5 Ответ: 5 8. 7. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.7. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ ТАНГЕНС УГЛА AD1D. Найдите угол DAB. Ответ дайте в градусах. 1 2 1 Ответ: 60 2 Ответ: 9. 8. Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.8. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ВЕРШИНАМИ A ИC2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ. Найдите квадрат расстояния между вершинами D и C2.  8 Ответ: Ответ: 53 10. 9. Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника9. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ВЕРШИНАМИ B1 ИD2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ. 1 2 8 Ответ: 3 11. 10. Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы10. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ BИ D2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ. 1 2 1 13 Ответ: 14 12. 11. Найдите тангенс угла CDC3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.11. НАЙДИТЕ ТАНГЕНС УГЛА CDC3 МНОГОГРАННИКА,ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ. 2 tgCDC3 1 2 2 2 Ответ: 1 13. 12. Найдите квадрат расстояния между вершинами C и D2 многогранника, изображенного на рисунке. Все двугранные углы12. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ C Все двугранные углы12. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ CИ D2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ. 2 2 Ответ: 6 14. 13. Найдите угол D2EA многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в13. НАЙДИТЕ УГОЛ D2EA МНОГОГРАННИКА, ИЗОБРАЖЕННОГОНА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ. ОТВЕТ ДАЙТЕ В ГРАДУСАХ. Δ D2EA – равносторонний, значит, <D2EA = 60°. Ответ: 60 15. 14. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен 3. боковое ребро равно 5. Найдите14. РАДИУС ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛООСНОВАНИЯ ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЫ, РАВЕН 3. БОКОВОЕ РЕБРО РАВНО 5. НАЙДИТЕ ВЫСОТУ ПИРАМИДЫ. 5 О 3 Ответ: 4 16. 15. В правильной треугольной пирамиде SABC N — середина ребра BC , S — вершина. Известно, что AB = 1 , а площадь боковой15. В ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЕ SABC N —СЕРЕДИНА РЕБРА BC , S — ВЕРШИНА.  ИЗВЕСТНО, ЧТО AB = 1 , ИЗВЕСТНО, ЧТО AB = 1 ,А ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ РАВНА 3. НАЙДИТЕ ДЛИНУ ОТРЕЗКА NS . Sбок 3 Sбок N 1 Росн SN 2 1 3 3 SN 2 1 Ответ: 2 17. 16. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P . Объем пирамиды равен 1, PS = 1 . Найдите16. В ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЕ SABC МЕДИАНЫОСНОВАНИЯ ПЕРЕСЕКАЮТСЯ В ТОЧКЕ P . ОБЪЕМ ПИРАМИДЫ РАВЕН 1, PS = 1 . НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА ABC . V 1 1 V S ABC PS 3 1 1 1 S ABC 1 3 P Ответ: 3 18. 17. В правильной четырехугольной пирамиде SABCD диагональ основания равна 6, высота равна 4. Найдите боковое ребро пирамиды.17. В ПРАВИЛЬНОЙ ЧЕТЫРЕХУГОЛЬНОЙ ПИРАМИДЕ SABCDДИАГОНАЛЬ ОСНОВАНИЯ РАВНА 6, ВЫСОТА РАВНА 4. НАЙДИТЕ БОКОВОЕ РЕБРО ПИРАМИДЫ. ОС = 3 4 О 6 Ответ: 5 19. 18. Высота правильной шестиугольной пирамиды равна 5. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите18. ВЫСОТА ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПИРАМИДЫ Найдите18. ВЫСОТА ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПИРАМИДЫРАВНА 5. БОКОВОЕ РЕБРО НАКЛОНЕНО К ПЛОСКОСТИ ОСНОВАНИЯ ПОД УГЛОМ 30°. НАЙДИТЕ БОКОВОЕ РЕБРО ПИРАМИДЫ. AS = 2 · SO 5 30° О Ответ: 10 20. 19. Радиус основания цилиндра равен 4, а диагональ осевого сечения равна 10. Найдите образующую цилиндра.19. РАДИУС ОСНОВАНИЯ ЦИЛИНДРА РАВЕН 4, А ДИАГОНАЛЬОСЕВОГО СЕЧЕНИЯ РАВНА 10. НАЙДИТЕ ОБРАЗУЮЩУЮ ЦИЛИНДРА. Р О 4 А 10 С 8 В Ответ: 6 21. 20. Радиус основания цилиндра равен 3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60°.20. РАДИУС ОСНОВАНИЯ ЦИЛИНДРА РАВЕН 3. ДИАГОНАЛЬОСЕВОГО СЕЧЕНИЯ ЦИЛИНДРА НАКЛОНЕНА К ПЛОСКОСТИ ОСНОВАНИЯ ПОД УГЛОМ 60°. НАЙДИТЕ ДИАГОНАЛЬ ОСЕВОГО СЕЧЕНИЯ ЦИЛИНДРА. S 3 В 30° 60° С А 6 Ответ: 12 22. 21. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.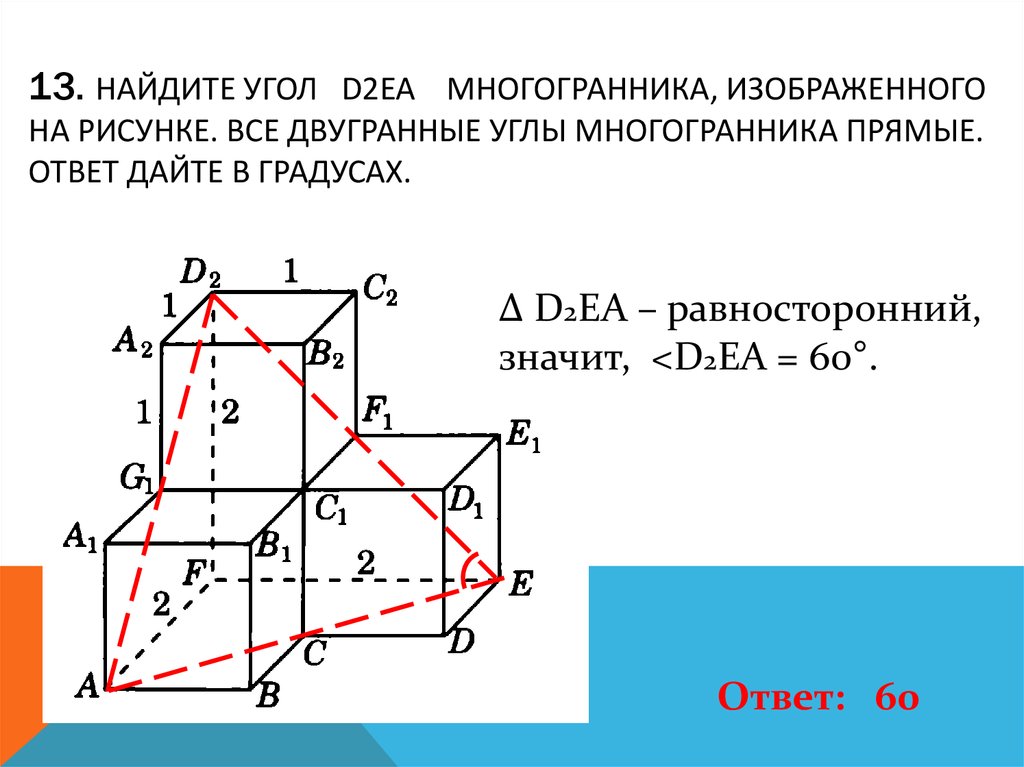 21. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА РАВНА 21. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА РАВНА2Π, А ДИАМЕТР ОСНОВАНИЯ — 1. НАЙДИТЕ ВЫСОТУ ЦИЛИНДРА. Sбок 2 RH S 2 2 0,5 H 1 В H О R 0,5 А Ответ: 2 23. 22. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.22. ВЫСОТА КОНУСА РАВНА 4, А ДЛИНА ОБРАЗУЮЩЕЙ — 5.НАЙДИТЕ ДИАМЕТР ОСНОВАНИЯ КОНУСА. S 5 4 O 3 A Ответ: 6 24. 23. Высота конуса равна 4. Образующая наклонена к плоскости основания под углом 30°. Найдите образующую конуса.23. ВЫСОТА КОНУСА РАВНА 4. ОБРАЗУЮЩАЯ НАКЛОНЕНАК ПЛОСКОСТИ ОСНОВАНИЯ ПОД УГЛОМ 30°. НАЙДИТЕ ОБРАЗУЮЩУЮ КОНУСА. S 4 30° О А Ответ: 8 25. 24. Найдите радиус сферы, вписанной в куб, ребра которого равны 4.24. НАЙДИТЕ РАДИУС СФЕРЫ, ВПИСАННОЙ В КУБ, РЕБРАКОТОРОГО РАВНЫ 4. 4 2 4 4 Ответ: 2 26. 25. Найдите образующую цилиндра, описанного около сферы радиуса 3. 25. НАЙДИТЕ ОБРАЗУЮЩУЮ ЦИЛИНДРА, 25. НАЙДИТЕ ОБРАЗУЮЩУЮ ЦИЛИНДРА,ОПИСАННОГО ОКОЛО СФЕРЫ РАДИУСА 3. 3 6 Ответ: 6 27. 26. Найдите квадрат диаметра сферы, описанной около прямоугольного параллелепипеда, ребра которого равны 3, 4, 5.26. НАЙДИТЕ КВАДРАТ ДИАМЕТРА СФЕРЫ, ОПИСАННОЙОКОЛО ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, РЕБРА КОТОРОГО РАВНЫ 3, 4, 5. 5 5 3 4 Ответ: 50 English Русский Правила Помогите решить / разобраться (М)Сообщения без ответов | Активные темы | Избранное Правила форумаПосмотреть правила форума
Модераторы: Модераторы Математики, Супермодераторы
В кубе найдите квадрат расстояния между прямымиАвтор Сфера закона На чтение 8 мин Просмотров 3 Опубликовано Среди огромного количества стереометрических задач в учебниках геометрии, в различных сборниках задач, пособиях по подготовке в ВУЗы крайне редко встречаются задачи на нахождение расстояния между скрещивающимися прямыми. Практика проведения ЕГЭ показывает, что многие учащиеся вообще не приступают к выполнению заданий по геометрии, входящих в экзаменационную работу. Для обеспечения успешного выполнения геометрических заданий повышенного уровня сложности необходимо развивать гибкость мышления, способность анализировать предполагаемую конфигурацию и вычленять в ней части, рассмотрение которых позволяет найти путь решения задачи. Школьный курс предполагает изучение четырех способов решения задач на нахождение расстояния между скрещивающимися прямыми. Выбор способа обусловлен, в первую очередь, особенностями конкретной задачи, предоставленными ею возможностями для выбора, и, во вторую очередь, способностями и особенностями «пространственного мышления» конкретного учащегося. Каждый из этих способов позволяет решить самую главную часть задачи — построение отрезка, перпендикулярного обеим скрещивающимся прямым (для вычислительной же части задач деление на способы не требуется). Основные способы решения задач на нахождение расстояния между скрещивающимися прямыми Нахождение длины общего перпендикуляра двух скрещивающихся прямых, т.е. отрезка с концами на этих прямых и перпендикулярного каждой из этих прямых. Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую. Нахождение расстояния между двумя параллельными плоскостями, проходящими через заданные скрещивающиеся прямые. Нахождение расстояния от точки, являющейся проекцией одной из скрещивающихся прямых, на перпендикулярную ей плоскость (так называемый «экран») до проекции другой прямой на ту же самую плоскость. Проведем демонстрацию всех четырех способов на следующей простейшей задаче: «В кубе с ребром а найти расстояние между любым ребром и диагональю не пересекающей его грани». Ответ: . hскр перпендикулярна плоскости боковой грани, содержащей диагональ d и перпендикулярна ребру, следовательно, hскр и является расстоянием между ребром а и диагональю d. Плоскость A параллельна ребру и проходит через данную диагональ, следовательно, данная hскр является не только расстоянием от ребра до плоскости A, но и расстоянием от ребра до данной диагонали. Плоскости A и B параллельны и проходят через две данные скрещивающиеся прямые, следовательно, расстояние между этими плоскостями равно расстоянию между двумя скрещивающимися прямыми. Плоскость A перпендикулярна ребру куба. При проекции на A диагонали d данная диагональ обращается в одну из сторон основания куба. Данная hскр является расстоянием между прямой, содержащей ребро, и проекцией диагонали на плоскость C, а значит и между прямой, содержащей ребро, и диагональю. Остановимся подробнее на применении каждого способа для изучаемых в школе многогранников. Применение первого способа достаточно ограничено: он хорошо применяется лишь в некоторых задачах, так как достаточно сложно определить и обосновать в простейших задачах точное, а в сложных — ориентировочное местоположение общего перпендикуляра двух скрещивающихся прямых. Задача 1. В прямоугольном параллелепипеде с размерами a, b, h найти расстояние между боковым ребром и не пересекающейся с ним диагональю основания. Пусть AHBD. Так как А1А перпендикулярна плоскости АВСD , то А1А AH. AH перпендикулярна обеим из двух скрещивающихся прямых, следовательно AH?- расстояние между прямыми А1А и BD. В прямоугольном треугольнике ABD, зная длины катетов AB и AD, находим высоту AH, используя формулы для вычисления площади прямоугольного треугольника. Ответ: Задача 2. В правильной 4-угольной пирамиде с боковым ребром L и стороной основания a найти расстояние между апофемой и стороной основания, пересекающей боковую грань, содержащую эту апофему. SHCD как апофема, ADCD, так как ABCD — квадрат. Следовательно, DH — расстояние между прямыми SH и AD. Применение этого способа также ограничено в связи с тем, что если можно быстро построить (или найти уже готовую) проходящую через одну из скрещивающихся прямых плоскость, параллельную другой прямой, то затем построение перпендикуляра из любой точки второй прямой к этой плоскости (внутри многогранника) вызывает трудности. Однако в несложных задачах, где построение (или отыскивание) указанного перпендикуляра трудностей не вызывает, данный способ является самым быстрым и легким, и поэтому доступен. Задача 2. Решение уже указанной выше задачи данным способом особых трудностей не вызывает. Плоскость EFM параллельна прямой AD, т. к AD || EF. Прямая MF лежит в этой плоскости, следовательно, расстояние между прямой AD и плоскостью EFM равно расстоянию между прямой AD и прямой MF. Проведем OHAD. OHEF, OHMO, следовательно, OH(EFM), следовательно, OH — расстояние между прямой AD и плоскостью EFM, а значит, и расстояние между прямой AD и прямой MF. Задача 3. В прямоугольном параллелепипеде с размерами a,b и h найти расстояние между боковым ребром и не пересекающейся с ним диагональю параллелепипеда. Прямая AA1 параллельна плоскости BB1D1D, B1D принадлежит этой плоскости, следовательно расстояние от AA1 до плоскости BB1D1D равно расстоянию между прямыми AA1 и B1D. Проведем AHBD. Также, AH B1B, следовательно AH(BB1D1D), следовательно AHB1D, т. е. AH — искомое расстояние. Находим AH из прямоугольного треугольника ABD. Задача 4. В правильной шестиугольной призме A:F1 c высотой h и стороной основания a найти расстояние между прямыми: Рассмотрим плоскость E1EDD1. A1E1EE1, A1E1E1D1, следовательно A1E1(E1EDD1). Проведем из точки F прямую FH перпендикулярно BE. EE1FH, FHBE, следовательно FH(BEE1B1), следовательно FH является расстоянием между прямой AF и (BEE1B1), а значит и расстоянием между прямой AF и диагональю BE1. Ответ: Применение этого способа крайне ограничено, так как плоскость, параллельную одной из прямых (способ II) строить легче, чем две параллельные плоскости, однако способ III можно использовать в призмах, если скрещивающиеся прямые принадлежат параллельным граням, а также в тех случаях, когда в многограннике несложно построить параллельные сечения, содержащие заданные прямые. а) Плоскости BAA1B1 и DEE1D1 параллельны, так как AB || ED и AA1 || EE1. ED1DEE1D1, AA1(BAA1B1), следовательно, расстояние между прямыми AA1 и ED1 равно расстоянию между плоскостями BAA1B1 и DEE1D1. A1E1AA1, A1E1A1B1, следовательно, A1E1BAA1B1. Аналогично доказываем, что A1E1(DEE1D1). Т.о., A1E1 является расстоянием между плоскостями BAA1B1 и DEE1D1, а значит, и между прямыми AA1 и ED1. Находим A1E1 из треугольника A1F1E1, который является равнобедренным с углом A1F1E1, равным . б) Расстояние между AF и диагональю BE1 находится аналогично. Задача 5. В кубе с ребром а найти расстояние между двумя непересекающимися диагоналями двух смежных граней. Данная задача рассматривается как классическая в некоторых пособиях, но, как правило, ее решение дается способом IV, однако является вполне доступной для решения с помощью способа III. Некоторую трудность в данной задаче вызывает доказательство перпендикулярности диагонали A1C обеим параллельным плоскостям (AB1D1 || BC1D). B1CBC1 и BC1A1B1, следовательно, прямая BC1 перпендикулярна плоскости A1B1C, и следовательно, BC1A1C. Также, A1CBD. Следовательно, прямая A1C перпендикулярна плоскости BC1D. Вычислительная же часть задачи особых трудностей не вызывает, так как hскр = EF находится как разность между диагональю куба и высотами двух одинаковых правильных пирамид A1AB1D1 и CC1BD. Данный способ имеет достаточно широкое применение. Для задач средней и повышенной трудности его можно считать основным. Нет необходимости применять его только тогда, когда один из трех предыдущих способов работает проще и быстрее, так как в таких случаях способ IV может только усложнить решение задачи, или сделать его труднодоступным. Данный способ очень выгодно использовать в случае перпендикулярности скрещивающихся прямых, так как нет необходимости построения проекции одной из прямых на «экран» Задача 5. Все та же «классическая» задача (с непересекающимися диагоналями двух смежных граней куба) перестает казаться сложной, как только находится «экран» — диагональное сечение куба. Рассмотрим плоскость A1B1CD. C1F (A1B1CD), т. к. C1FB1C и C1FA1B1. Тогда проекцией C1D на «экран» будет являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием между двумя непересекающимися диагоналями двух смежных граней. Задача 6. В правильной треугольной пирамиде найти расстояние и угол между скрещивающимися прямыми: боковым ребром l и стороной основания a. В данной и аналогичных ей задачах способ IV быстрее других способов приводит к решению, так как построив сечение, играющее роль «экрана», перпендикулярно AC (треугольник BDM), видно, что далее нет необходимости строить проекцию другой прямой (BM) на этот экран. DH — искомое расстояние. DH находим из треугольника MDB, используя формулы площади. Ответ: . Источник Формула Евклидова расстояния — Вывод, Примеры Прежде чем приступить к изучению формулы Евклидова расстояния, давайте посмотрим, что такое Евклидово расстояние. В координатной геометрии евклидово расстояние – это расстояние между двумя точками. Чтобы найти две точки на плоскости, измеряется длина отрезка, соединяющего две точки. Мы выводим формулу евклидова расстояния, используя теорему Пифагора. Что такое формула евклидова расстояния?Формула Евклидова расстояния, как следует из ее названия, дает расстояние между двумя точками (или) расстояние по прямой линии. Предположим, что \((x_1,y_1)\) и \((x_2,y_2)\) — две точки на двумерной плоскости. Вот формула Евклидова расстояния. Формула Евклидова расстоянияФормула Евклидова расстояния говорит: (_1\)) 2 ] где,
Вывод формулы евклидова расстояния Чтобы вывести формулу евклидова расстояния, рассмотрим две точки A (x\(_1\), y\(_1\)) и B (x\(_2\), y\(_2\)) и предположим, что d — расстояние между ними. Теперь применим теорему Пифагора к треугольнику ABC. Тогда получим _2\) – y\(_1\)) 2 Извлечение квадратного корня с обеих сторон, d = √[ (x\(_2\) – x\(_1\)) 2 + ( y\(_2\) – y\(_1\)) 2 ] Отсюда выводится формула евклидова расстояния. Хотите найти сложные математические решения за считанные секунды? Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами. Забронируйте бесплатный пробный урок Мы увидим больше применений формулы Евклидова расстояния в следующем разделе. Примеры с использованием формулы евклидова расстояния Пример 1: Найдите расстояние между точками P(3, 2) и Q(4, 1). Решение: Дано: P(3, 2) = \((x_1,y_1)\) Q(4, 1) = \((x_2,y_2)\) Используя формулу Евклидова расстояния, d = √[(x\(_2\) – x\(_1\)) 2 + (y\(_2\) – y\(_1\)) 2 ] PQ = √[(4 – 3) 2 + (1 – 2) 2 ] PQ = √[(1) 2 + (-1) 2 ] PQ = √2 единиц. Ответ: Евклидово расстояние между точками A(3, 2) и B(4, 1) составляет √2 единицы. Пример 2: Докажите, что точки A(0, 4), B(6, 2) и C(9, 1) лежат на одной прямой. Решение: Чтобы доказать коллинеарность данных трех точек, достаточно доказать, что сумма расстояний между двумя парами точек равна расстоянию между третьей парой. Мы найдем расстояние между каждой парой точек, используя формулу Евклидова расстояния. AB = √[(6 – 0) 2 + (2 – 4) 2 ] = √[36 + 4] = √40 = 2√10 BC = √[(9 – 6) 2 + (1 – 2) 2 ] = √[9 + 1] = √10 CA = √[(0 – 9) 2 ( 4 – 1) 2 ] = √[81 + 9] = √90 = 3√10 Здесь мы видим, что AB + BC = CA (Это потому, что 2√10 + √10 = 3√10). Ответ: Мы доказали, что A, B и C коллинеарны. Пример 3: Убедитесь, что точки A(√3, 1), B(0, 0) и C(2, 0) являются вершинами равностороннего треугольника. Решение: Три вершины A, B и C являются вершинами равностороннего треугольника тогда и только тогда, когда AB = BC = CA. Дано: A(√3, 1) = \((x_1,y_1)\) B(0, 0) = \((x_2,y_2)\) C(2, 0) = \((x_3,y_3)\) Используя формулу Евклидова расстояния, AB = √[(x\(_2\) – x\(_1\)) 2 + (y\(_2\) – y \(_1\)) 2 ] = √[(0 – √3) 2 + (0-1) 2 ] = √(3 + 1) = √4 = 2 BC = √[(x\(_3\) – x\(_2\)) 2 + (y\(_3\) – y\(_2\)) 2 ] = √[(2-0) 2 + (0-0) 2 ] = √(4 + 0) = √4 = 3 CA (x\(_3\) – x\(_1\)) 2 + (y\(_3\) – y\(_1\)) 2 ] = √[(2 — √3) 2 + (0 – 1 ) 2 ] = √(9 + 25) = √34 Здесь AB = BC ≠ CA. Ответ: A, B и C НЕ являются вершинами равностороннего треугольника. Часто задаваемые вопросы о формуле евклидова расстоянияЧто такое формула евклидова расстояния?Формула Евклидова расстояния используется для нахождения расстояния между двумя точками на плоскости. Эта формула говорит, что расстояние между двумя точками (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) равно d = √[(x 2 – х 1 ) 2 + (у 2 – у 1 ) 2 ]. Как вывести формулу евклидова расстояния?Чтобы вывести формулу евклидова расстояния, рассмотрим две точки A(x\(_1\), y\(_1\)) и B(x\(_2\), y\(_2\)) и соединим их точкой отрезок. Затем проведите горизонтальные и вертикальные линии от A и B до точки C. Тогда ABC — прямоугольный треугольник, и, следовательно, мы можем применить к нему теорему Пифагора. Тогда получаем AB 2 = AC 2 + BC 2 d 2 = (x\(_2\) – x\(_1\))2 + (y\(_2\) – y\(_1\)) 2 Извлечение квадратного корня с обеих сторон, d = √[ (x\(_2\) – x\(_1\)) 2 + (y\(_2\) – y\(_1\)) 2 ] Подробный вывод кликните сюда. Каковы применения формулы Евклидова расстояния?Формула Евклидова расстояния используется для нахождения длины отрезка прямой по двум точкам на плоскости. Нахождение расстояния помогает доказать, что заданные вершины образуют квадрат, прямоугольник и т. д. (или) доказать, что заданные вершины образуют равносторонний треугольник, прямоугольный треугольник и т. д. В чем разница между формулой евклидова расстояния и формулой манхэттенского расстояния?Для любых двух точек (x\(_1\), y\(_1\)) и (x\(_2\), y\(_2\)) на плоскости
Евклидово расстояние | EngatiЧто такое Евклидово расстояние? Около 300 г. Евклидово пространство — это двух- или трехмерное пространство, к которому применимы аксиомы и постулаты евклидовой геометрии. Евклидово расстояние — это расстояние между двумя точками в евклидовом пространстве. Используя формулу Пифагора для расстояния, евклидово пространство (или даже любое внутреннее произведение) стало бы метрическим пространством. Ранее эта метрика также была известна как метрика Пифагора. Из-за того, что вы можете найти евклидово расстояние, используя координатные точки и теорему Пифагора, его также иногда называют расстоянием Пифагора. Источник: ВикипедияКакие три основных евклидовых члена? 1. Евклидово расстояние — это расстояние от каждой ячейки растра до ближайшего источника. 2. Евклидово распределение помогает определить ячейки, которые должны быть отнесены к источнику в зависимости от близости. 3. Евклидово направление показывает нам направление от каждой клетки к ближайшему источнику. Как применяется евклидово расстояние в машинном обучении?В машинном обучении он чаще всего используется для понимания и измерения того, насколько наблюдения похожи друг на друга. Как работает евклидово расстояние? Расстояние от каждой ячейки до каждой исходной ячейки определяется путем вычисления гипотенузы с x_max и y_max в качестве двух других сторон треугольника. Этот метод помогает нам найти фактическое расстояние, а не расстояние до ячейки. Если кратчайшее расстояние до источника меньше заданного максимального расстояния, мы присваиваем значение местоположению ячейки на выходном растре. 3-кратный доход от чат-ботов и живого чата Запланировать демонстрацию Как рассчитать евклидово расстояние (формула)? Предположим, что (x1, x2) и (y1, y2) существуют в двумерном пространстве. Тогда две другие стороны прямоугольного треугольника будут равны |x1 — y1| и |х2 — у2|. Евклидово расстояние между (x1, x2) и (y1, y2) можно рассматривать как длину гипотенузы прямоугольного треугольника. Поскольку это не что иное, как расстояние по прямой между двумя заданными точками, мы можем воспользоваться теоремой Пифагора. Расстояние между (x1, x2) и (y1, y2) будет равно (x1 — y1)2+(x2 — y2)2. Теперь, если бы точки (x1, x2, x3) и (y1, y2, y3) находились в трехмерном пространстве, евклидово расстояние между ними было бы (x1 — y1)2+(x2 — y2)2 +(х3 — у3)2. Далее, чтобы вычислить евклидово расстояние между (x1, x2,…, xn) и (y1, y2,…, yn) в n-мерном пространстве, формула будет (x1 — y1)2+(x2 — y2)2+…+ (xn — yn)2 Что такое метрика евклидова квадрата расстояния? Метрика евклидова квадрата расстояния использует то же уравнение, что и метрика евклидова расстояния, но не извлекает квадратный корень. Даже если вы замените евклидово расстояние метрикой евклидова квадрата расстояния, результаты кластеризации Джарвиса-Патрика и кластеризации K-средних не пострадают. Но если вы сделаете это, результат иерархической кластеризации, скорее всего, изменится. Поскольку квадрат евклидова расстояния не удовлетворяет неравенству треугольника, он не образует метрическое пространство. Вместо этого это гладкая, строго выпуклая функция двух точек, в отличие от расстояния, которое не является гладким (около пар равных точек) и выпуклым, но не строго выпуклым. Евклидов квадрат расстояния предпочтительнее в теории оптимизации, поскольку он позволяет использовать выпуклый анализ. Из-за того, что возведение в квадрат является монотонной функцией неотрицательных значений, минимизация квадрата расстояния эквивалентна минимизации евклидова расстояния. Совокупность всех квадратов расстояний между парами точек из конечного набора может быть сохранена в евклидовой матрице расстояний и может использоваться в этой форме в геометрии расстояний. Как работает обратная взвешенная интерполяция расстояния—ArcGIS ProДоступно с лицензией Geostatistical Analyst. Интерполяция, взвешенная по обратному расстоянию (IDW), явно предполагает, что объекты, расположенные близко друг к другу, более похожи, чем те, которые находятся дальше друг от друга. Чтобы спрогнозировать значение для любого неизмеренного местоположения, IDW использует измеренные значения, окружающие прогнозируемое местоположение. Ближайшие к прогнозируемому местоположению измеренные значения оказывают большее влияние на прогнозируемое значение, чем те, которые находятся дальше. IDW предполагает, что каждая измеренная точка имеет локальное влияние, которое уменьшается с расстоянием. Окно Weights содержит список весов, присвоенных каждой точке данных, которая используется для создания прогнозируемого значения в месте, отмеченном перекрестием. Узнайте больше о методах интерполяции, доступных в ArcGIS Geostatistical Analyst Степенная функция Как упоминалось выше, веса обратно пропорциональны расстоянию (между точкой данных и прогнозируемым местоположением), возведенному в степень стр . В результате с увеличением расстояния веса быстро уменьшаются. Скорость уменьшения весов зависит от значения p . Если p = 0, уменьшение с расстоянием не происходит, и поскольку все веса λ i одинаковы, прогноз будет средним значением всех значений данных в окрестности поиска. Geostatistical Analyst использует значения степени, большие или равные 1. Когда p = 2, метод известен как взвешенная интерполяция обратного квадрата расстояния. Значение по умолчанию — p = 2, хотя нет теоретического обоснования предпочтения этого значения по сравнению с другими, и влияние изменения p следует исследовать путем предварительного просмотра вывода и изучения статистики перекрестной проверки. Район поиска Поскольку объекты, расположенные близко друг к другу, больше похожи друг на друга, чем объекты, расположенные дальше, по мере удаления местоположений измеренные значения будут мало связаны со значением прогнозируемого местоположения. Для ускорения расчетов можно исключить более удаленные точки, которые мало повлияют на прогноз. На форму окрестности влияют входные данные и поверхность, которую вы пытаетесь создать. Если в ваших данных нет направленных влияний, вы захотите рассмотреть точки одинаково во всех направлениях. Для этого вы определите область поиска как круг. Однако, если в ваших данных есть влияние направления, например преобладающий ветер, вы можете захотеть скорректировать его, изменив форму окрестности поиска на эллипс с большой осью, параллельной ветру. Поправка на это влияние направления оправдана, поскольку вы знаете, что места с наветренной стороны от прогнозируемого местоположения будут более похожими на удаленных расстояниях, чем местоположения, перпендикулярные ветру, но расположенные ближе к прогнозируемому местоположению. После указания формы соседства вы можете ограничить, какие местоположения данных внутри формы должны использоваться. Вы можете определить максимальное и минимальное количество локаций для использования, а также разделить район на сектора. Если вы разделите окрестности на сектора, к каждому сектору будут применены максимальное и минимальное ограничения. Точки, выделенные в окне просмотра данных, показывают местоположения и веса, которые будут использоваться для прогнозирования местоположения в центре эллипса (положение перекрестия). Окрестность поиска ограничена внутренней частью эллипса. В приведенном ниже примере двум красным точкам будет присвоен вес более 10 процентов. В восточном секторе одной точке (коричневой) будет присвоен вес от 5 до 10 процентов. Остальные точки в окрестности поиска получат меньшие веса. Пример весов секторов соседстваКогда использовать IDW Поверхность, рассчитанная с использованием IDW, зависит от выбора значения мощности ( p ) и стратегии поиска соседства. Выходная поверхность чувствительна к кластеризации и наличию выбросов. IDW предполагает, что моделируемое явление обусловлено локальными вариациями, которые можно зафиксировать (смоделировать), определив адекватную окрестность поиска. Поскольку IDW не дает стандартных ошибок прогнозирования, обоснование использования этой модели может быть проблематичным. Похожие темыОтзыв по этой теме? Новый метод расчета квадрата евклидова расстояния (SED) с использованием технологии PTreE и анализ его эффективности — Experts@Minnesota Одним из преимуществ евклидова расстояния является то, что он измеряет обычное расстояние между двумя точками в пространстве. По этой причине он широко используется в приложениях, где необходимо рассчитать расстояние между точками данных для измерения сходства.
Авторское право издателя: Найти в библиотеках U of M
Хоссейн М. Новый метод расчета квадрата евклидова расстояния (SED) с использованием технологии PTreE и анализ его производительности. / Хоссейн Мохаммад К.; Абуфарде, Самир. Материалы 34-й Международной конференции по компьютерам и их приложениям, CATA 2019. Под ред. / Гордон Ли; Ин Джин. Международное общество компьютеров и их приложений (ISCA), 2019. с. 45–54 (Материалы 34-й Международной конференции по компьютерам и их приложениям, CATA 2019). Результат исследования: глава в книге/отчете/материалах конференции › Вклад конференции Хоссейн, М. Хоссейн М.К., Абуфардех С. Новый метод расчета квадрата евклидова расстояния (SED) с использованием технологии PTreE и анализ его производительности. В Ли Г., Джин И, редакторы, Материалы 34-й Международной конференции по компьютерам и их приложениям, CATA 2019. Международное общество компьютеров и их приложений (ISCA). 2019. с. 45-54. (Материалы 34-й Международной конференции по компьютерам и их приложениям, CATA 2019). Хоссейн Мохаммад К. ; Абуфарде, Самир. / Новый метод расчета квадрата евклидова расстояния (SED) с использованием технологии PTreE и анализ его производительности . @inproceedings{59fdb5b5b6fb48bf942f506b6b5d23ba, title = «Новый метод вычисления квадрата евклидова расстояния (SED) с использованием технологии PTreE и анализ его производительности», abstract = «Одним из преимуществ евклидова расстояния является то, что он измеряет обычное расстояние между двумя точками в пространстве. Для по этой причине он широко используется в приложениях, где необходимо рассчитать расстояние между точками данных для измерения сходства.Однако этот метод является дорогостоящим, поскольку включает дорогостоящие операции с квадратным квадратом и квадратным корнем.Одно полезное наблюдение заключается в том, что во многих случаях интеллектуального анализа данных приложения абсолютные измерения расстояния не нужны, если расстояния используются для сравнения близости между различными точками данных. автор = «Хоссейн, {Мохаммад К.} и Самир Абуфарде», примечание = «Авторские права издателя: Copyright {\textcopyright} 2012-2020 easychair.org. Все права защищены.; 34-я Международная конференция по компьютерам и их приложениям , CATA 2019 ; Дата конференции: с 18-03-2019 по 20-03-2019″, year = «2019», month = mar, day = «13», language = «English (US )», series = «Материалы 34-й Международной конференции по компьютерам и их приложениям, CATA 2019», издатель = «Международное общество компьютеров и их приложений (ISCA)», страницы = «45—54», редактор = «Гордон Ли и Ин Джин», booktitle = «Proceedings of the 34-я Международная конференция по компьютерам и их приложениям, CATA 2019», } TY — GEN T1 — Новый метод расчета квадрата евклидова расстояния (SED) с использованием технологии PTreE и анализ ее производительности AU — Hossain, Mohammad К. AU — Abufardeh, Sameer N1 — Авторские права издателя: Copyright © 2012-2020 easychair.org. Все права защищены. PY — 2019/3/13 Y1 — 2019/3/13 N2 — Одним из преимуществ евклидова расстояния является то, что оно измеряет обычное расстояние между двумя точками в пространстве. По этой причине он широко используется в приложениях, где необходимо рассчитать расстояние между точками данных для измерения сходства. Однако этот метод является дорогостоящим, поскольку включает дорогостоящие операции с квадратным корнем и квадратным корнем. Одно полезное наблюдение заключается в том, что во многих приложениях для интеллектуального анализа данных нет необходимости измерять абсолютные расстояния, если расстояния используются для сравнения близости между различными точками данных. Например, при классификации и кластеризации мы часто измеряем расстояния между несколькими точками данных, чтобы сравнить их расстояния от известных классов или от центроидов, чтобы отнести эти точки к классу или кластеру. AB. Одним из преимуществ евклидова расстояния является то, что оно измеряет обычное расстояние между двумя точками в пространстве. По этой причине он широко используется в приложениях, где необходимо рассчитать расстояние между точками данных для измерения сходства. Однако этот метод является дорогостоящим, поскольку включает дорогостоящие операции с квадратным корнем и квадратным корнем. Одно полезное наблюдение заключается в том, что во многих приложениях для интеллектуального анализа данных нет необходимости измерять абсолютные расстояния, если расстояния используются для сравнения близости между различными точками данных. UR – http://www.scopus.com/inward/record.url?scp=85078019592&partnerID=8YFLogxK UR – http://www.scopus.com/inward/citedby.url?scp=85078019592&partnerID=8YFLogxK M3 — Conference contribution AN — SCOPUS:85078019592 T3 — Proceedings of 34th International Conference on Computers and Their Applications, CATA 2019 SP — 45 EP — 54 BT — Proceedings of 34th International Conference on Компьютеры и их приложения, CATA 2019 A2 — Lee, Gordon A2 — Jin, Ying PB — Международное общество компьютеров и их приложений (ISCA) T2 — 34-я Международная конференция по компьютерам и их приложениям, CATA 2019 Y2 — 18 марта с 2019 г. ER —
Эффективная справочная таблица, использующая линейную функцию обратного квадрата расстоянияСохранить цитату в файлФормат: Резюме (текст) PubMedPMIDAbstract (текст) CSV Добавить в коллекции
Назовите свою коллекцию: Имя должно содержать менее 100 символов Выберите коллекцию: Не удалось загрузить вашу коллекцию из-за ошибки Добавить в мою библиографию
Не удалось загрузить делегатов из-за ошибки Ваш сохраненный поискНазвание сохраненного поиска: Условия поиска: Тестовые условия поиска Эл. Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт. Отправить, даже если нет новых результатов Необязательный текст в электронном письме: Создайте файл для внешнего программного обеспечения для управления цитированиемПолнотекстовые ссылкиУайли Полнотекстовые ссылки . doi: 10.1002/jcc.23404. Epub 2013 12 августа. Джэун Юнг 1 , Такахару Мори, Юдзи Сугита принадлежность
Чжэун Юнг и др.
J Comput Chem. . . 2013 30 октября; 34 (28): 2412-20. doi: 10.1002/jcc.23404. Epub 2013 12 августа. АвторыДжэун Юнг 1 , Такахару Мори, Юдзи Сугита принадлежность
Абстрактный Основное узкое место в молекулярно-динамическом (МД) моделировании биомолекул существует при расчете парных несвязанных взаимодействий, таких как Леннард-Джонс, и дальнодействующих электростатических взаимодействий. Ключевые слова: доктор медицинских наук; ПМЭ; Справочная таблица. Авторское право © 2013 Wiley Periodicals, Inc. Похожие статьи
Посмотреть все похожие статьи Цитируется
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





 3m
3m 3 km
3 km
 Линии электропередач и опоры» из Powerwatch UK и PowerWatch Handbook, стр. 43. Однако, следует подчеркнуть, что для уверенности необходимо измерить магнитное поле. Даже при отсутствии линий электропередачи, существуют другие факторы, которые также могут влиять на магнитное поле линии электропередачи.
Линии электропередач и опоры» из Powerwatch UK и PowerWatch Handbook, стр. 43. Однако, следует подчеркнуть, что для уверенности необходимо измерить магнитное поле. Даже при отсутствии линий электропередачи, существуют другие факторы, которые также могут влиять на магнитное поле линии электропередачи. У многих данное определение вызовет недоумение. Казалось бы, как это относится к фотографии, и вообще, что это значит? На самом деле, это напрямую относится к фотографии, а точнее, к работе со светом.
У многих данное определение вызовет недоумение. Казалось бы, как это относится к фотографии, и вообще, что это значит? На самом деле, это напрямую относится к фотографии, а точнее, к работе со светом. Получается, что на расстоянии 2 метра от источника света освещение уменьшится на 1/4. На расстоянии 3 метра интенсивность освещенности уменьшится до значения 1/9, так как квадрат числа 3=9, а обратная пропорциональность дает значение 1/9.
Получается, что на расстоянии 2 метра от источника света освещение уменьшится на 1/4. На расстоянии 3 метра интенсивность освещенности уменьшится до значения 1/9, так как квадрат числа 3=9, а обратная пропорциональность дает значение 1/9. Основываясь на имеющихся данных, можно сказать, что для создания снимка с нормальной экспозицией при близко стоящем к источнику света объекте, следует использовать значение диафрагмы F16. Закрытая диафрагма отсечет часть света, которая в данном случае может дать переэкспонирование. В том случае, если объект расположен достаточно далеко, диафрагму желательно открыть до значения F4. Это позволит большему количеству света пройди сквозь объектив и попасть на матрицу. При одинаковой выдержке обе фотографии должны смотреться примерно одинаково, так как диафрагмой мы уравняли количество света, попадающего на сенсор камеры.
Основываясь на имеющихся данных, можно сказать, что для создания снимка с нормальной экспозицией при близко стоящем к источнику света объекте, следует использовать значение диафрагмы F16. Закрытая диафрагма отсечет часть света, которая в данном случае может дать переэкспонирование. В том случае, если объект расположен достаточно далеко, диафрагму желательно открыть до значения F4. Это позволит большему количеству света пройди сквозь объектив и попасть на матрицу. При одинаковой выдержке обе фотографии должны смотреться примерно одинаково, так как диафрагмой мы уравняли количество света, попадающего на сенсор камеры. Вы наверняка заметил, что чем ближе объект съемки находится к источнику света, тем чаще происходят колебания числа F. Это значит, что если наша модель, находясь близко к источнику света, сделает шаг назад или вперед, нужно перестраивать камеру, иначе снимок получится или пересвеченный или слишком темный.
Вы наверняка заметил, что чем ближе объект съемки находится к источнику света, тем чаще происходят колебания числа F. Это значит, что если наша модель, находясь близко к источнику света, сделает шаг назад или вперед, нужно перестраивать камеру, иначе снимок получится или пересвеченный или слишком темный. Это часто используется при работе с фоном. В таком случае можно поместить модель значительно ближе к источнику света, чем фон. При таком построении кадра фон будет казаться темным, а модель светлой.
Это часто используется при работе с фоном. В таком случае можно поместить модель значительно ближе к источнику света, чем фон. При таком построении кадра фон будет казаться темным, а модель светлой. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»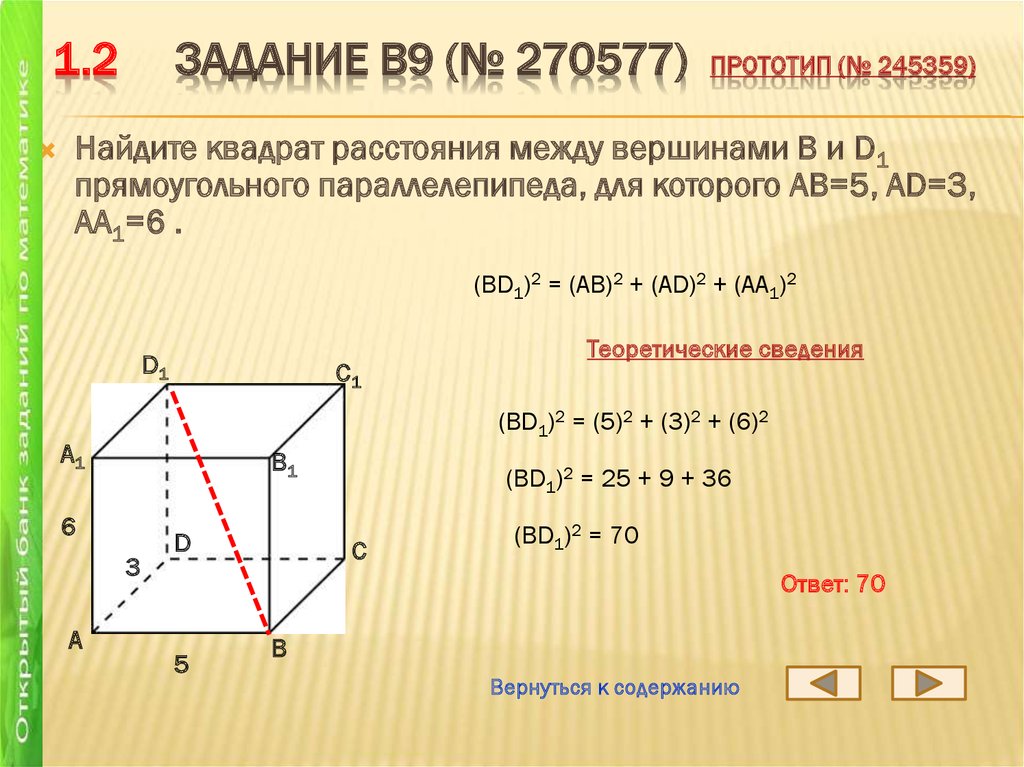 06.2017, 14:32
06.2017, 14:32  06.2017, 16:57
06.2017, 16:57  06.2017, 18:44
06.2017, 18:44  06.2017, 19:03
06.2017, 19:03 
 06.2017, 19:33
06.2017, 19:33  06.2017, 19:39
06.2017, 19:39  06.2017, 20:32
06.2017, 20:32  06.2017, 20:39
06.2017, 20:39  06.2017, 21:02
06.2017, 21:02  06.2017, 22:29
06.2017, 22:29  Там точно нет абсолютной величины? Или Вы просто не искали?
Там точно нет абсолютной величины? Или Вы просто не искали?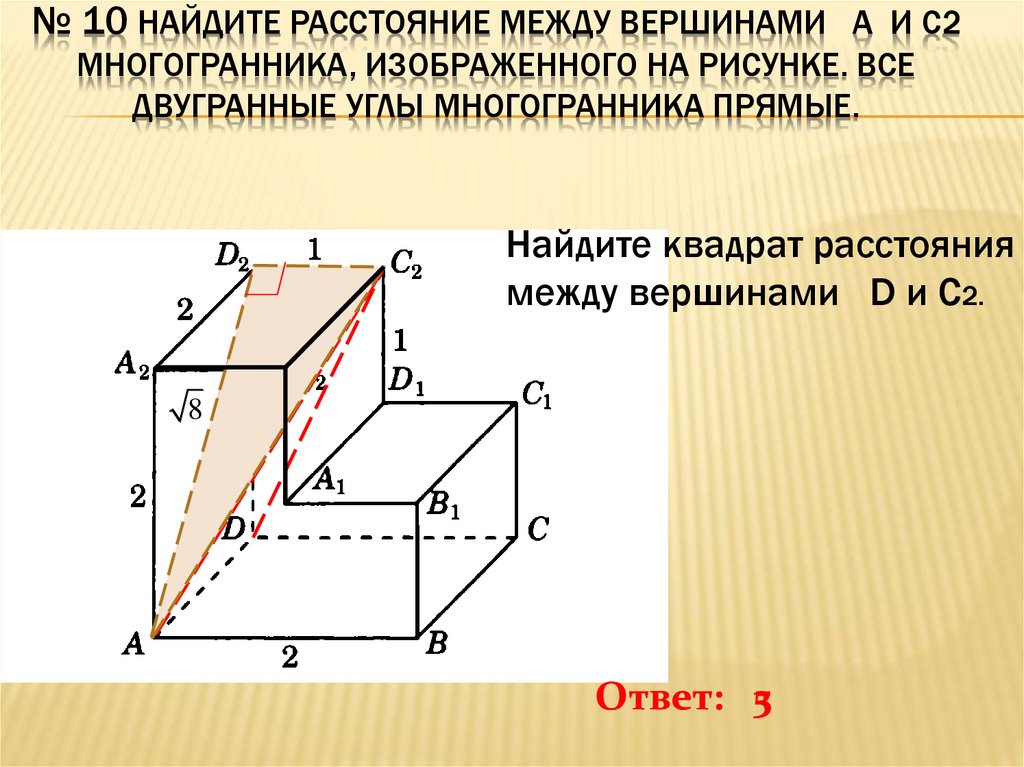
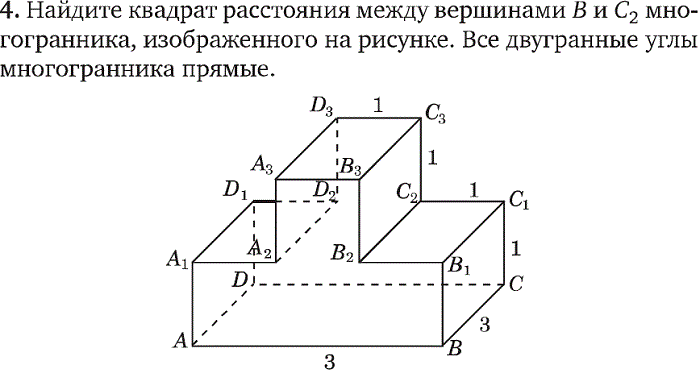 2] is not automatically converted to z.».
2] is not automatically converted to z.».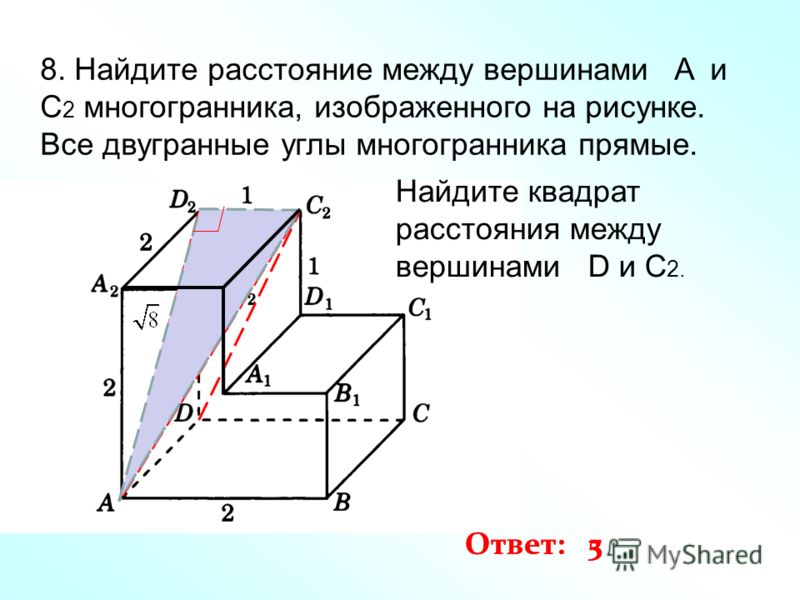 Возможно, это обусловлено как узостью их практического применения (относительно школьной программы, в отличие от «выигрышных» задач на вычисление площадей и объемов), так и сложностью данной темы.
Возможно, это обусловлено как узостью их практического применения (относительно школьной программы, в отличие от «выигрышных» задач на вычисление площадей и объемов), так и сложностью данной темы.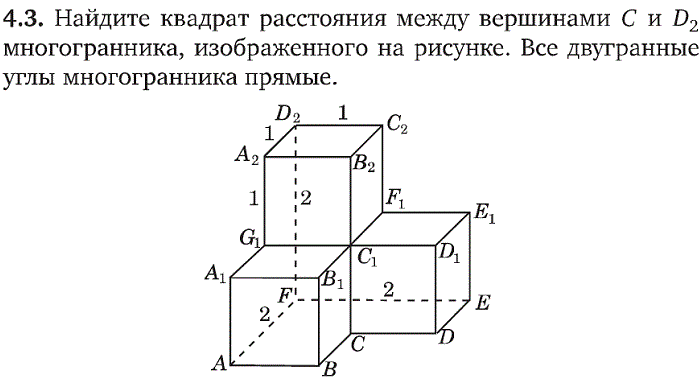

 Кроме того, при нахождении длины этого перпендикуляра в сложных задачах можно столкнуться с непреодолимыми трудностями.
Кроме того, при нахождении длины этого перпендикуляра в сложных задачах можно столкнуться с непреодолимыми трудностями. DH равно половине стороны CD. Ответ:
DH равно половине стороны CD. Ответ: Находим OH из треугольника AOD.
Находим OH из треугольника AOD. Также A1E1AA1. Следовательно, A1E1 является расстоянием от прямой AA1 до плоскости E1EDD1. ED1(E1EDD1)., следовательно AE1 — расстояние от прямой AA1 до прямой ED1. Находим A1E1 из треугольника F1A1E1 по теореме косинусов. Ответ:
Также A1E1AA1. Следовательно, A1E1 является расстоянием от прямой AA1 до плоскости E1EDD1. ED1(E1EDD1)., следовательно AE1 — расстояние от прямой AA1 до прямой ED1. Находим A1E1 из треугольника F1A1E1 по теореме косинусов. Ответ:
 Ответ:
Ответ: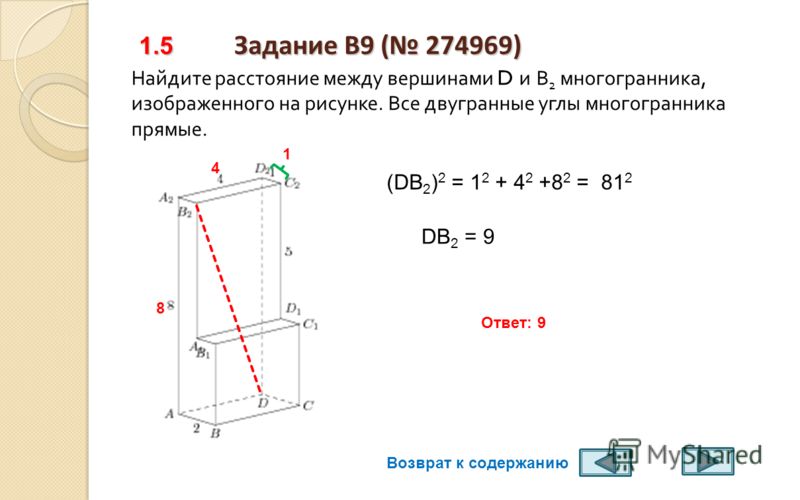
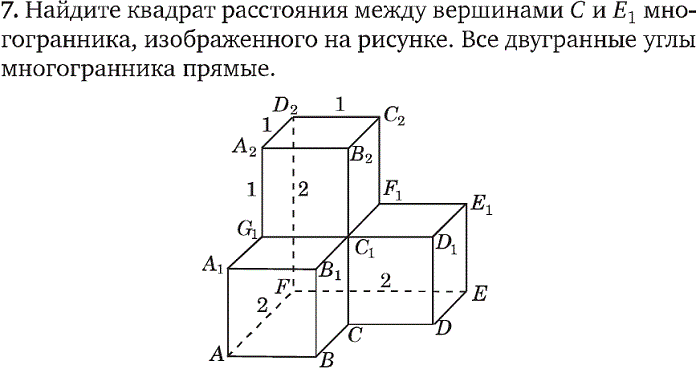 Находим EM из прямоугольного треугольника EDF. Ответ:.
Находим EM из прямоугольного треугольника EDF. Ответ:. Давайте изучим формулу евклидова расстояния вместе с несколькими решенными примерами.
Давайте изучим формулу евклидова расстояния вместе с несколькими решенными примерами. Соедините A и B отрезком линии. Чтобы вывести формулу, построим прямоугольный треугольник, гипотенуза которого равна АВ. Для этого мы проводим горизонтальные и вертикальные линии от A и B, которые встречаются в C, как показано ниже.
Соедините A и B отрезком линии. Чтобы вывести формулу, построим прямоугольный треугольник, гипотенуза которого равна АВ. Для этого мы проводим горизонтальные и вертикальные линии от A и B, которые встречаются в C, как показано ниже.


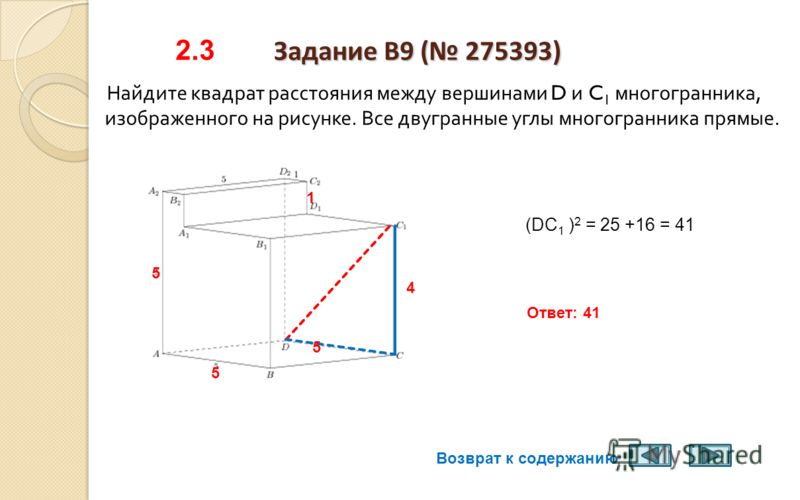
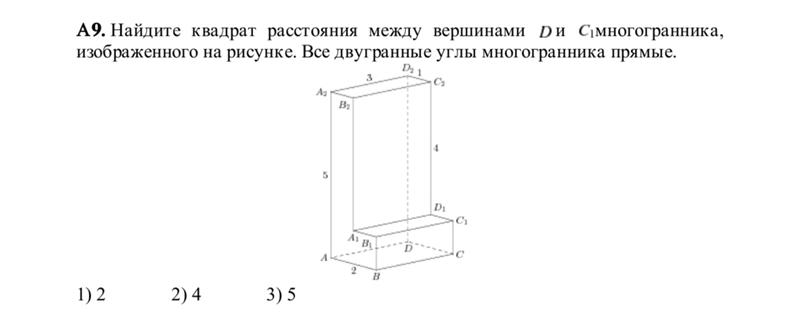
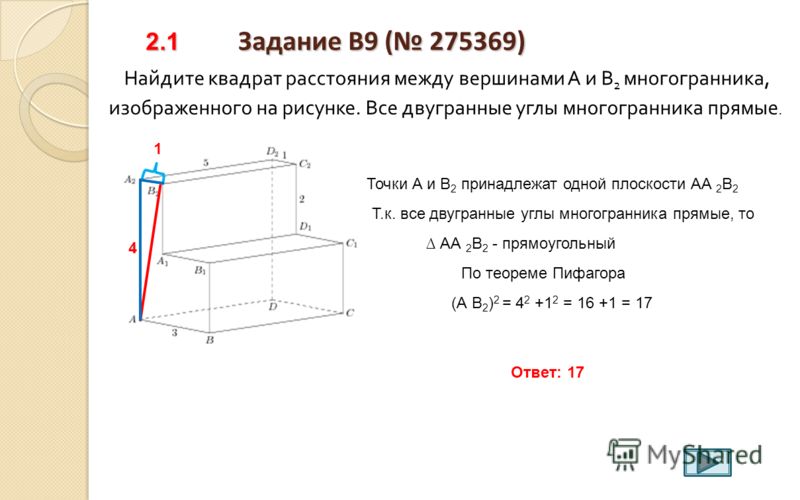 до н. э. греческий математик Евклид исследовал отношения между углами и расстояниями. Евклидова геометрия по-прежнему широко используется и преподается даже сегодня и применима к пространствам с двумя или тремя измерениями, но ее можно обобщить на измерения более высокого порядка. На данный момент евклидово расстояние является наиболее распространенным использованием расстояния. В большинстве ситуаций, когда люди говорят о расстоянии, они имеют в виду евклидово расстояние. Он исследует корень квадратов расстояний между координатами пары объектов. Чтобы получить евклидово расстояние, вам нужно будет вычислить квадратный корень из суммы квадратов разностей между соответствующими значениями.
до н. э. греческий математик Евклид исследовал отношения между углами и расстояниями. Евклидова геометрия по-прежнему широко используется и преподается даже сегодня и применима к пространствам с двумя или тремя измерениями, но ее можно обобщить на измерения более высокого порядка. На данный момент евклидово расстояние является наиболее распространенным использованием расстояния. В большинстве ситуаций, когда люди говорят о расстоянии, они имеют в виду евклидово расстояние. Он исследует корень квадратов расстояний между координатами пары объектов. Чтобы получить евклидово расстояние, вам нужно будет вычислить квадратный корень из суммы квадратов разностей между соответствующими значениями. 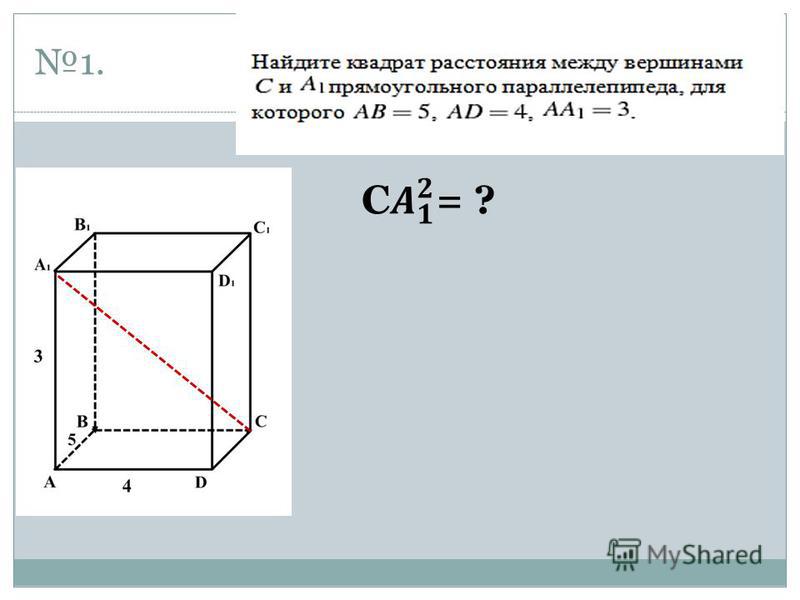 Связанная норма называется евклидовой нормой, которая определяется как расстояние каждого вектора от начала координат. Одним из важных свойств евклидовой нормы по сравнению с другими нормами является то, что она остается неизменной при произвольных поворотах пространства вокруг начала координат. Согласно теореме Дворецкого, каждое конечномерное нормированное векторное пространство имеет многомерное подпространство, на котором норма более или менее евклидова. Евклидова норма — единственная норма, обладающая этим свойством.
Связанная норма называется евклидовой нормой, которая определяется как расстояние каждого вектора от начала координат. Одним из важных свойств евклидовой нормы по сравнению с другими нормами является то, что она остается неизменной при произвольных поворотах пространства вокруг начала координат. Согласно теореме Дворецкого, каждое конечномерное нормированное векторное пространство имеет многомерное подпространство, на котором норма более или менее евклидова. Евклидова норма — единственная норма, обладающая этим свойством. 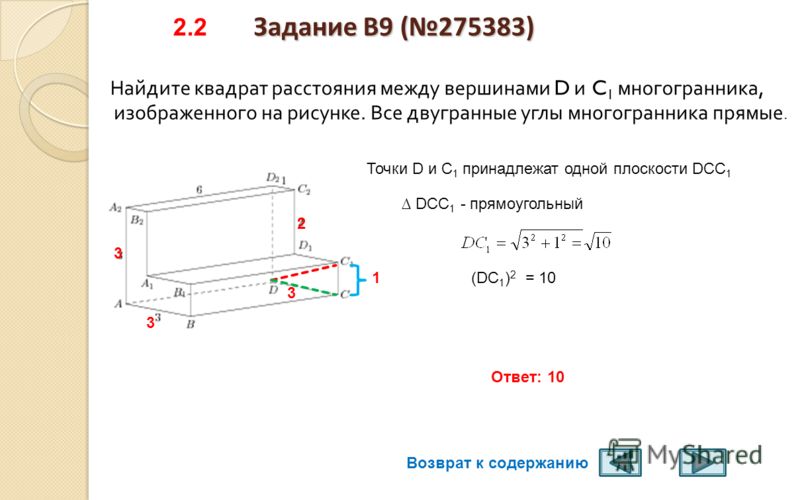
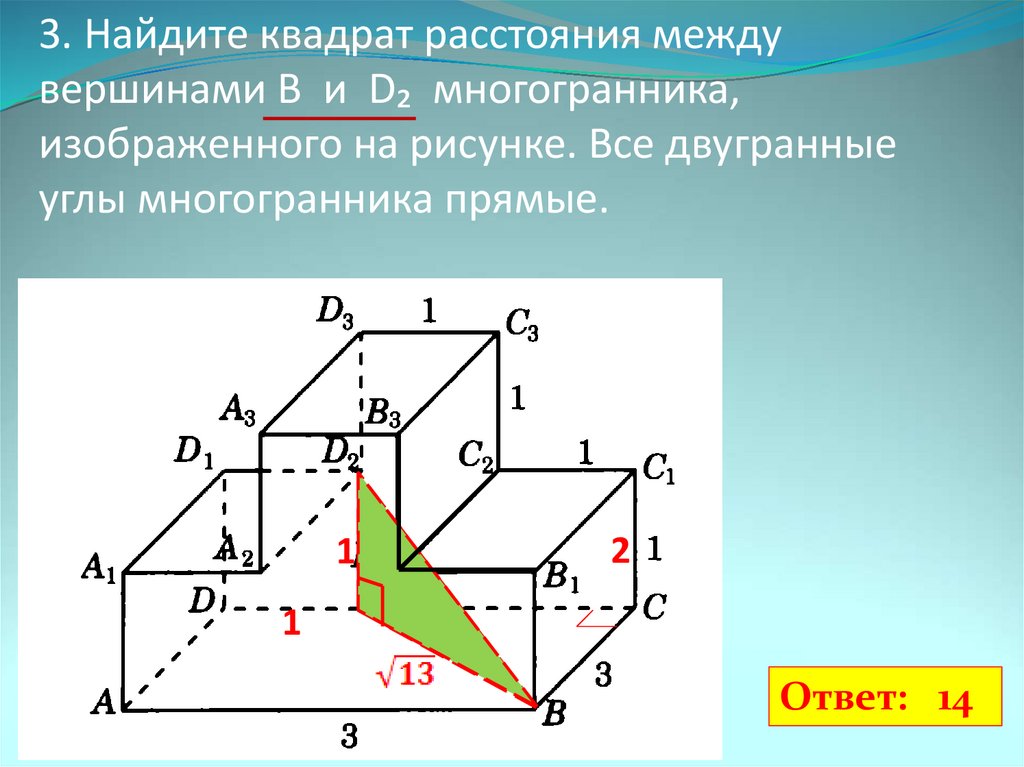 Если бы между этими двумя точками образовался отрезок, он мог бы быть гипотенузой прямоугольного треугольника.
Если бы между этими двумя точками образовался отрезок, он мог бы быть гипотенузой прямоугольного треугольника.  Из-за этого кластеризация может выполняться быстрее с помощью метрики евклидова квадрата расстояния, чем с обычным евклидовым расстоянием.
Из-за этого кластеризация может выполняться быстрее с помощью метрики евклидова квадрата расстояния, чем с обычным евклидовым расстоянием. Следовательно, задача оптимизации эквивалентна в обоих случаях, но ее легче решить, используя квадрат расстояния.
Следовательно, задача оптимизации эквивалентна в обоих случаях, но ее легче решить, используя квадрат расстояния. 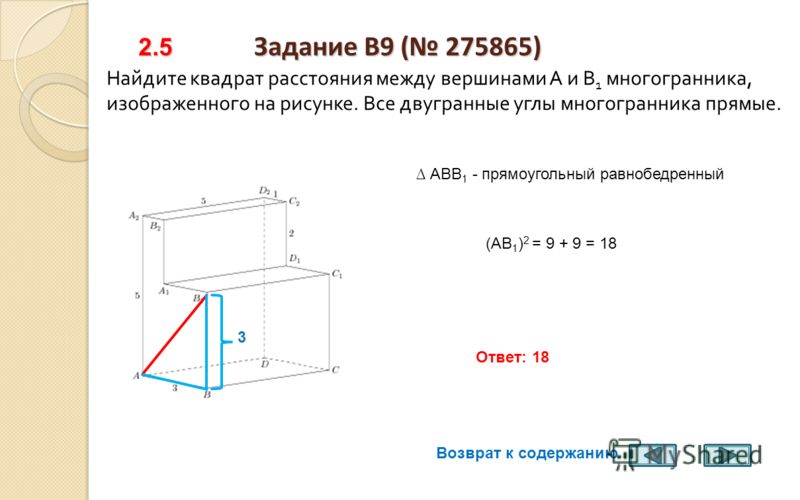 Он дает больший вес точкам, ближайшим к местоположению прогноза, и веса уменьшаются в зависимости от расстояния, отсюда и название «взвешенное обратное расстояние». Веса, присвоенные точкам данных, показаны в следующем примере:
Он дает больший вес точкам, ближайшим к местоположению прогноза, и веса уменьшаются в зависимости от расстояния, отсюда и название «взвешенное обратное расстояние». Веса, присвоенные точкам данных, показаны в следующем примере: По мере увеличения p веса удаленных точек быстро уменьшаются. Если значение p очень велико, на прогноз будут влиять только ближайшие окружающие точки.
По мере увеличения p веса удаленных точек быстро уменьшаются. Если значение p очень велико, на прогноз будут влиять только ближайшие окружающие точки. В результате общепринятой практикой является ограничение количества измеренных значений путем указания области поиска. Форма окрестности ограничивает, как далеко и где искать измеренные значения, которые будут использоваться в прогнозе. Другие параметры соседства ограничивают места, которые будут использоваться в этой фигуре. На следующем изображении пять измеренных точек (соседей) будут использоваться при прогнозировании значения для местоположения без измерения, желтая точка.
В результате общепринятой практикой является ограничение количества измеренных значений путем указания области поиска. Форма окрестности ограничивает, как далеко и где искать измеренные значения, которые будут использоваться в прогнозе. Другие параметры соседства ограничивают места, которые будут использоваться в этой фигуре. На следующем изображении пять измеренных точек (соседей) будут использоваться при прогнозировании значения для местоположения без измерения, желтая точка.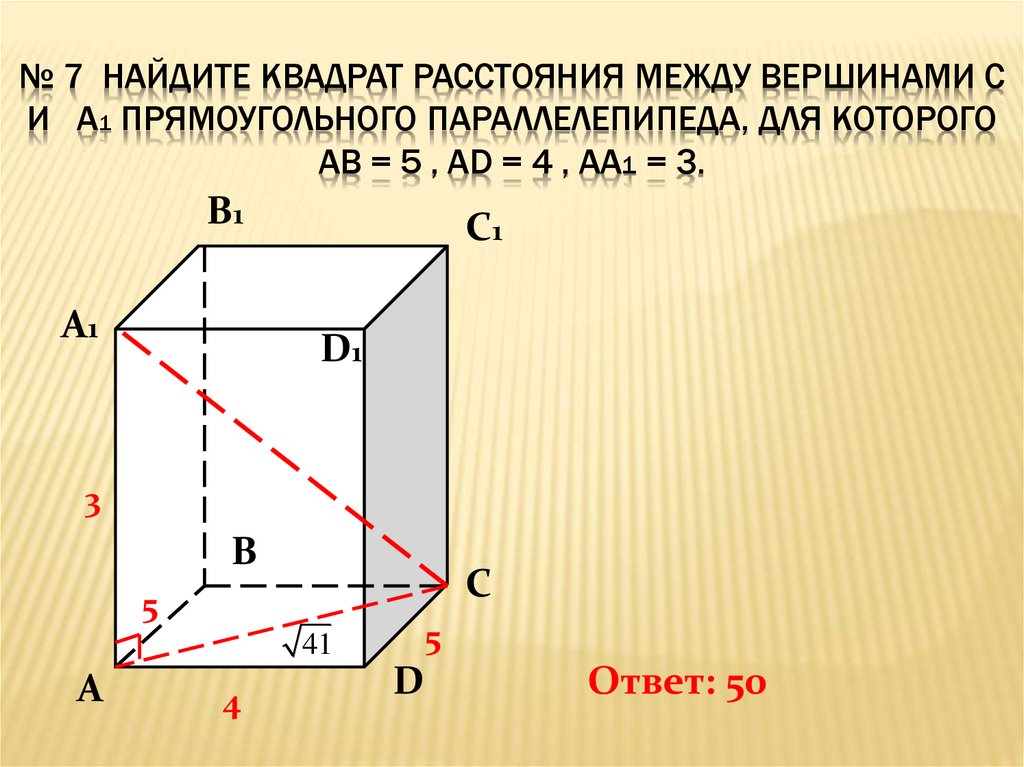
 IDW — это точный интерполятор, в котором максимальное и минимальное значения (см. диаграмму ниже) на интерполированной поверхности могут встречаться только в точках выборки.
IDW — это точный интерполятор, в котором максимальное и минимальное значения (см. диаграмму ниже) на интерполированной поверхности могут встречаться только в точках выборки.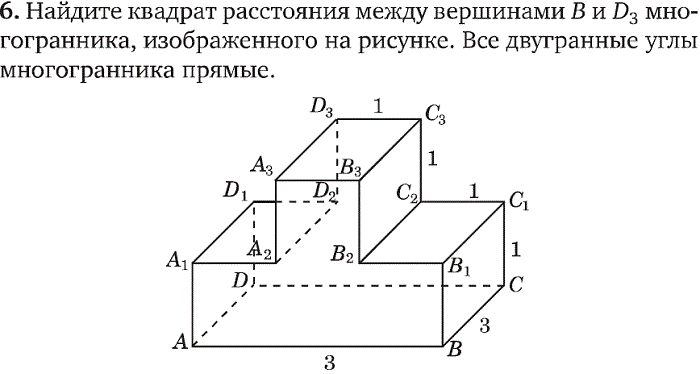 Однако этот метод является дорогостоящим, поскольку включает дорогостоящие операции с квадратным корнем и квадратным корнем. Одно полезное наблюдение заключается в том, что во многих приложениях для интеллектуального анализа данных нет необходимости измерять абсолютные расстояния, если расстояния используются для сравнения близости между различными точками данных. Например, при классификации и кластеризации мы часто измеряем расстояния между несколькими точками данных, чтобы сравнить их расстояния от известных классов или от центроидов, чтобы отнести эти точки к классу или кластеру. В связи с этим можно использовать альтернативный подход, известный как квадратное евклидово расстояние (SED), чтобы избежать вычисления квадратного корня для получения квадрата расстояния между точками данных. SED использовался в классификации, кластеризации, обработке изображений и других областях для экономии вычислительных затрат. В этой статье мы покажем, как можно рассчитать SED для вертикальных данных, представленных в pTree.
Однако этот метод является дорогостоящим, поскольку включает дорогостоящие операции с квадратным корнем и квадратным корнем. Одно полезное наблюдение заключается в том, что во многих приложениях для интеллектуального анализа данных нет необходимости измерять абсолютные расстояния, если расстояния используются для сравнения близости между различными точками данных. Например, при классификации и кластеризации мы часто измеряем расстояния между несколькими точками данных, чтобы сравнить их расстояния от известных классов или от центроидов, чтобы отнести эти точки к классу или кластеру. В связи с этим можно использовать альтернативный подход, известный как квадратное евклидово расстояние (SED), чтобы избежать вычисления квадратного корня для получения квадрата расстояния между точками данных. SED использовался в классификации, кластеризации, обработке изображений и других областях для экономии вычислительных затрат. В этой статье мы покажем, как можно рассчитать SED для вертикальных данных, представленных в pTree.