Линза схема: Построение изображения предмета в тонкой линзе — урок. Физика, 9 класс.
Тонкие линзы. Построение изображений — материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы.
Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению.
Теорема об изображении. Если перед линзой находится светящаяся точка , то после преломления в линзе все лучи (или их продолжения) пересекаются в одной точке .
| Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы. |
Точка называется изображением точки .
Если в точке пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке концентрируется энергия световых лучей.
Если же в точке пересекаются не сами преломлённые лучи, а их продолжения (так бывает, когда преломлённые лучи расходятся после линзы), то изображение называется мнимым. Его нельзя получить на экране, поскольку в точке не сосредоточено никакой энергии. Мнимое изображение, напомним, возникает благодаря особенности нашего мозга — достраивать расходящиеся лучи до их мнимого пересечения и видеть в этом пересечении светящуюся точку.Мнимое изображение существует лишь в нашем сознании.
Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы.
Собирающая линза: действительное изображение точки.
Сперва рассмотрим собирающую линзу. Пусть — расстояние от точки до линзы, — фокусное расстояние линзы.
обсудим свойства изображений точечного источника и протяжённого объекта.
Первый случай: . Точечный источник света расположен дальше от линзы, чем левая фокальная плоскость (рис. 1).
| Рис. 1. Случай a>f: действительное изображение точки S |
Луч , идущий через оптический центр, не преломляется. Мы возьмём произвольный луч , построим точку , в которой преломлённый луч пересекается с лучом , а затем покажем, что положение точки не зависит от выбора луча (иными словами, точка является одной и той же для всевозможных лучей ). Тем самым окажется, что все лучи, исходящие из точки , после преломления в линзе пересекаются в точке и теорема об изображении будет доказана для рассматриваемого случая .
Точку мы найдём, построив дальнейший ход луча . Делать это мы умеем: параллельно лучу проводим побочную оптическую ось до пересечения с фокальной плоскостью в побочном фокусе , после чего проводим преломлённый луч до пересечения с лучом в точке .
Теперь будем искать расстояние от точки до линзы. Мы покажем, что это расстояние выражается только через и , т. е. определяется лишь положением источника и свойствами линзы, и не зависит тем самым от конкретного луча .
Опустим перпендикуляры и на главную оптическую ось. Проведём также параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников:
, (1)
, (2)
. (3)
В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено).
(4)
Но , так что соотношение (4) переписывается в виде:
. (5)
Отсюда находим искомое расстояние от точки до линзы:
. (6)
(6)
Как видим, оно и в самом деле не зависит от выбора луча . Следовательно, любой луч после преломления в линзе пройдёт через построенную нами точку , и эта точка будет действительным изображением источника
Теорема об изображении в данном случае доказана.
Практическая важность теоремы об изображении состоит вот в чём. Коль скоро все лучи источника пересекаются после линзы в одной точке — его изображении — то для построения изображения достаточно взять два наиболее удобных луча. Какие именно?
Если источник не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие:
— луч, идущий через оптический центр линзы — он не преломляется;
— луч, параллельный главной оптической оси — после преломления он идёт через фокус.
Построение изображения с помощью этих лучей показано на рис. 2.
| Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то удобный луч остаётся лишь один — идущий вдоль главной оптической оси. В качестве второго луча приходится брать «неудобный» (рис. 3).
В качестве второго луча приходится брать «неудобный» (рис. 3).
| Рис. 3. Построение изображения точки S, лежащей на главной оптической оси |
Посмотрим ещё раз на выражение ( 5). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево:
Теперь разделим обе части этого равенства на a:
(7)
Соотношение (7) называется формулой тонкой линзы (или просто формулой линзы). Пока что формула линзы получена для случая собирающей линзы и для . В дальнейшем мы выведем модификации этой формулы для остальных случаев.
Теперь вернёмся к соотношению (6). Его важность не исчерпывается тем, что оно доказывает теорему об изображении. Мы видим также, что не зависит от расстояния (рис. 1, 2) между источником и главной оптической осью!
Это означает, что какую бы точку отрезка мы ни взяли, её изображение будет находиться на одном и том же расстоянии от линзы. Оно будет лежать на отрезке — а именно, на пересечении отрезка с лучом , который пойдёт сквозь линзу без преломления. В частности, изображением точки будет точка .
Оно будет лежать на отрезке — а именно, на пересечении отрезка с лучом , который пойдёт сквозь линзу без преломления. В частности, изображением точки будет точка .
Тем самым мы установили важный факт: изображением отрезка лужит отрезок . Отныне исходный отрезок, изображение которого нас интересует, мы называем предметом и обозначаем на рисунках красной стрелочкой. Направление стрелки нам понадобится для того, чтобы следить — прямым или перевёрнутым получается изображение.
Собирающая линза: действительное изображение предмета.
Перейдём к рассмотрению изображений предметов. Напомним, что пока мы находимся в рамках случая . Здесь можно выделить три характерных ситуации.
1. . Изображение предмета является действительным, перевёрнутым, увеличенным (рис. 4; двойной фокус обозначен ). Из формулы линзы следует, что в этом случае будет (почему?).
Рис. 4. : изображение действительное, перевёрнутое, увеличенное 4. : изображение действительное, перевёрнутое, увеличенное |
Такая ситуация реализуется, например, в диапроекторах и киноаппаратах — эти оптические приборы дают на экране увеличенное изображение того, что находится на плёнке. Если вам доводилось показывать слайды, то вы знаете, что слайд нужно вставлять в проектор перевёрнутым — чтобы изображение на экране выглядело правильно, а не получилось вверх ногами.
Отношение размера изображения к размеру предмета называется линейным увеличением линзы и обозначается Г — (это заглавная греческая «гамма»):
.
Из подобия треугольников и получим:
. (8)
Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы.
2. . В этом случае из формулы (6) находим, что и . Линейное увеличение линзы согласно (8) равно единице, т. е. размер изображения равен размеру предмета (рис. 5).
Рис. 5.a=2f: размер изображения равен размеру предмета 5.a=2f: размер изображения равен размеру предмета |
3. . В этом случае из формулы линзы следует, что (почему?). Линейное увеличение линзы будет меньше единицы — изображение действительное, перевёрнутое, уменьшенное (рис. 6).
| Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное |
Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов — словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости.
Рассмотрение первого случая нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.
Собирающая линза: мнимое изображение точки.
Второй случай: . Точечный источник света расположен между линзой и фокальной плоскостью (рис.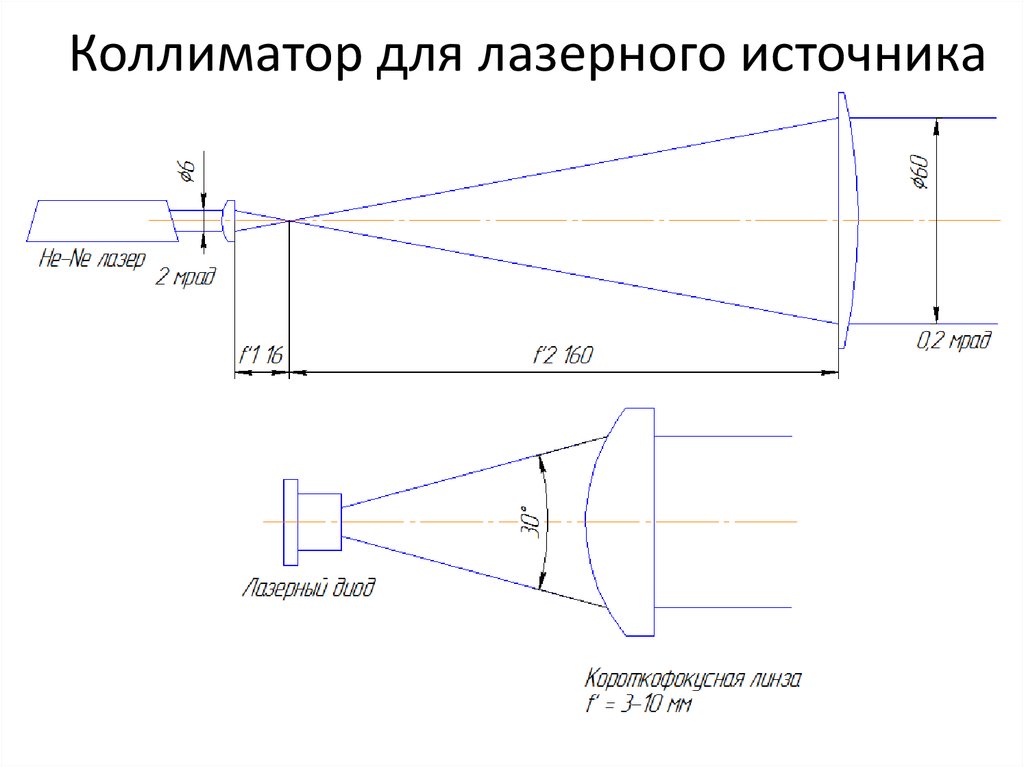 7).
7).
| Рис. 7. Случай a < f: мнимое изображение точки |
Наряду с лучом , идущим без преломления, мы снова рассматриваем произвольный луч . Однако теперь на выходе из линзы получаются два расходящихся луча и . Наш глаз продолжит эти лучи до пересечения в точке .
Теорема об изображении утверждает, что точка будет одной и той же для всех лучей , исходящих из точки . Мы опять докажем это с помощью трёх пар подобных треугольников:
Снова обозначая через расстояние от до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):
. (9)
Отсюда
. (10)
Величина не зависит от луча , что и доказывает теорему об изображении для нашего случая . Итак, — мнимое изображение источника . Если точка не лежит на главной оптической оси, то для построения изображения удобнее всего брать луч, идущий через оптический центр, и луч, параллельный главной оптической оси (рис.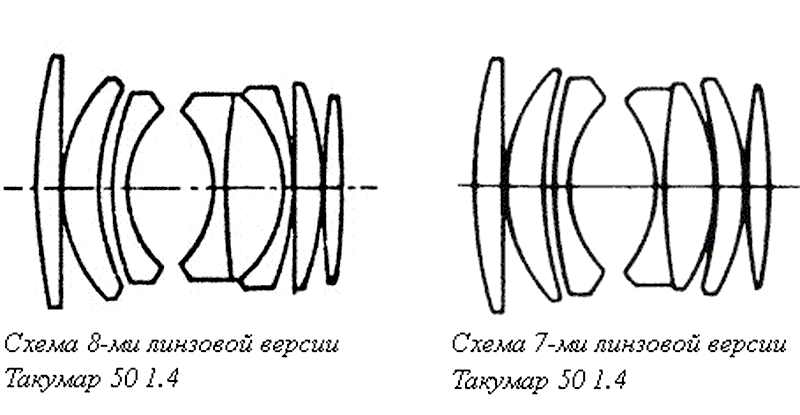 8).
8).
| Рис. 8. Построение изображения точки S, не лежащей на главной оптической оси |
Ну а если точка лежит на главной оптической оси, то деваться некуда — придётся довольствоваться лучом, падающим на линзу наклонно (рис. 9).
| Рис. 9. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (9) приводит нас к варианту формулы линзы для рассматриваемого случая . Сначала переписываем это соотношение в виде:
,
а затем делим обе части полученного равенства на a:
. (11)
Сравнивая (7) и (11), мы видим небольшую разницу: перед слагаемым стоит знак плюс, если изображение действительное, и знак минус, если изображение мнимое.
Величина , вычисляемая по формуле (10), не зависит также от расстояния между точкой и главной оптической осью. Как и выше (вспомните рассуждение с точкой ), это означает, что изображением отрезка на рис. 9 будет отрезок .
Как и выше (вспомните рассуждение с точкой ), это означает, что изображением отрезка на рис. 9 будет отрезок .
Собирающая линза: мнимое изображение предмета.
Учитывая это, мы легко строим изображение предмета, находящегося между линзой и фокальной плоскостью (рис. 10). Оно получается мнимым, прямым и увеличенным.
| Рис. 10. : изображение мнимое, прямое, увеличенное |
Такое изображение вы наблюдаете, когда разглядываете мелкий предмет в увеличительное стекло — лупу. Случай полностью разобран. Как видите, он качественно отличается от нашего первого случая . Это не удивительно — ведь между ними лежит промежуточный «катастрофический» случай .
Собирающая линза: предмет в фокальной плоскости.
Промежуточный случай:. Источник света расположен в фокальной плоскости линзы (рис. 11).
Как мы помним из предыдущего раздела, лучи параллельного пучка после преломления в собирающей линзе пересекутся в фокальной плоскости — а именно, в главном фокусе, если пучок падает перпендикулярно линзе, и в побочном фокусе при наклонном падении пучка. Воспользовавшись обратимостью хода лучей, мы заключаем, что все лучи источника , расположенного в фокальной плоскости, после выхода из линзы пойдут параллельно друг другу.
Воспользовавшись обратимостью хода лучей, мы заключаем, что все лучи источника , расположенного в фокальной плоскости, после выхода из линзы пойдут параллельно друг другу.
| Рис. 11. a=f: изображение отсутствует |
Где же изображение точки ? Изображения нет. Впрочем, никто не запрещает нам считать, что параллельные лучи пересекаются в бесконечно удалённой точке. Тогда теорема об изображении сохраняет свою силу и в данном случае — изображение находится на бесконечности.
Соответственно, если предмет целиком расположен в фокальной плоскости, изображение этого предмета будет находиться на бесконечности (или, что то же самое, будет отсутствовать).
Итак, мы полностью рассмотрели построение изображений в собирающей линзе.
Рассеивающая линза: мнимое изображение точки.
К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.
Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.
Снова берём луч и произвольный луч (рис. 12). На выходе из линзы имеем два расходящихся луча и , которые наш глаз достраивает до пересечения в точке .
| Рис. 12. Мнимое изображение точки S в рассеивающей линзе |
Нам снова предстоит доказать теорему об изображении — о том, что точка будет одной и той же для всех лучей . Действуем с помощью всё тех же трёх пар подобных треугольников:
.
Имеем:
(12)
Отсюда
. (13)
Величина b не зависит от луча span
, поэтому продолжения всех преломлённых лучей span
пересекутся в точке — мнимом изображении точки . Теорема об изображении тем самым полностью доказана.
Вспомним, что для собирающей линзы мы получили аналогичные формулы (6) и (10). В случае их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации и .
В случае их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации и .
А вот у формулы (13) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника — случай тут, как мы и сказали выше, имеется только один.
Если точка не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой — параллельно главной оптической оси (рис. 13).
| Рис. 13. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то второй луч приходится брать произвольным (рис. 14).
Рис. 14. Построение изображения точки S, лежащей на главной оптической оси 14. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (13) даёт нам ещё один вариант формулы линзы. Сначала перепишем:
,
а потом разделим обе части полученного равенства на a:
(14)
Так выглядит формула линзы для рассеивающей линзы.
Три формулы линзы (7), (11) и (14) можно записать единообразно:
если соблюдать следующую договорённость о знаках:
— для мнимого изображения величина считается отрицательной;
— для рассеивающей линзы величина считается отрицательной.
Это очень удобно и охватывает все рассмотренные случаи.
Рассеивающая линза: мнимое изображение предмета.
Величина , вычисляемая по формуле (13), опять-таки не зависит от расстояния между точкой и главной оптической осью. Это снова даёт нам возможность построить изображение предмета , которое на сей раз получается мнимым, прямым и уменьшенным (рис. 15).
Рис. 15. Изображение мнимое, прямое, уменьшенное 15. Изображение мнимое, прямое, уменьшенное |
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Построение изображения в линзе | СПАДИЛО
теория по физике 🧲 оптика
Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
Внимание!Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
Рассеивающая линза всегда дает только мнимые изображения.
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
ОпределениеВторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
Построение изображения в собирающей линзе
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Для этого из этой точки нужно пустить два луча:
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.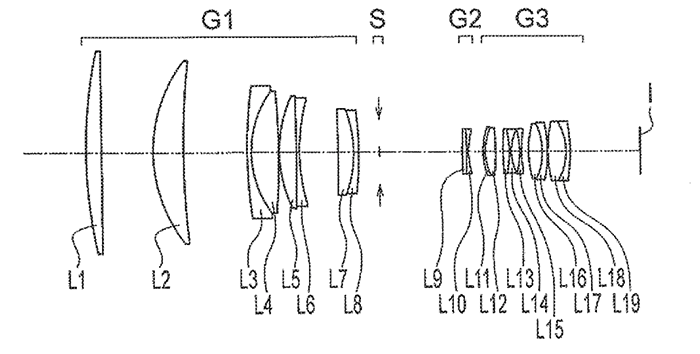
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
Предмет располагается за двойным фокусом.
Изображение:
| |
Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
| |
Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
| |
| Предмет находится в фокальной плоскости. Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. | |
Предмет располагается между линзой и фокусом.
Изображение:
|
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
Частный случай — построение изображения точки
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см.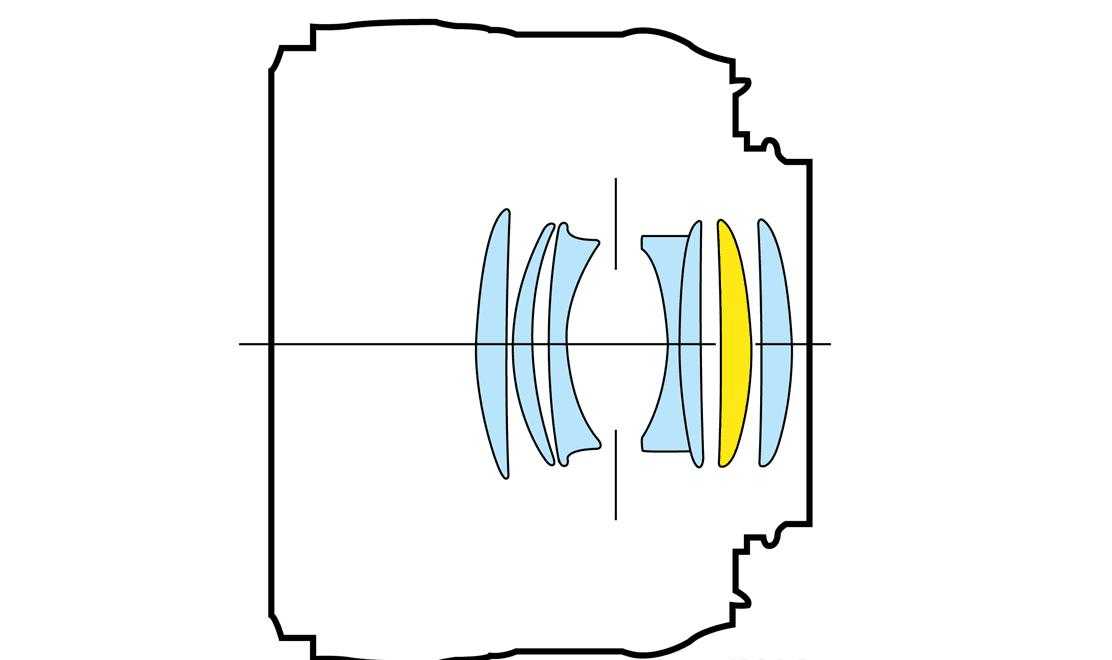 рисунок ниже). Так, изображению точки S соответствует точка S´.
рисунок ниже). Так, изображению точки S соответствует точка S´.
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
Построение изображения в рассеивающей линзе
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
Пример №3. Построить изображение предмета в рассеивающей линзе.
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
ОпределениеПлоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).

- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
Изображение и сам предмет всегда симметричны относительно зеркала.
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.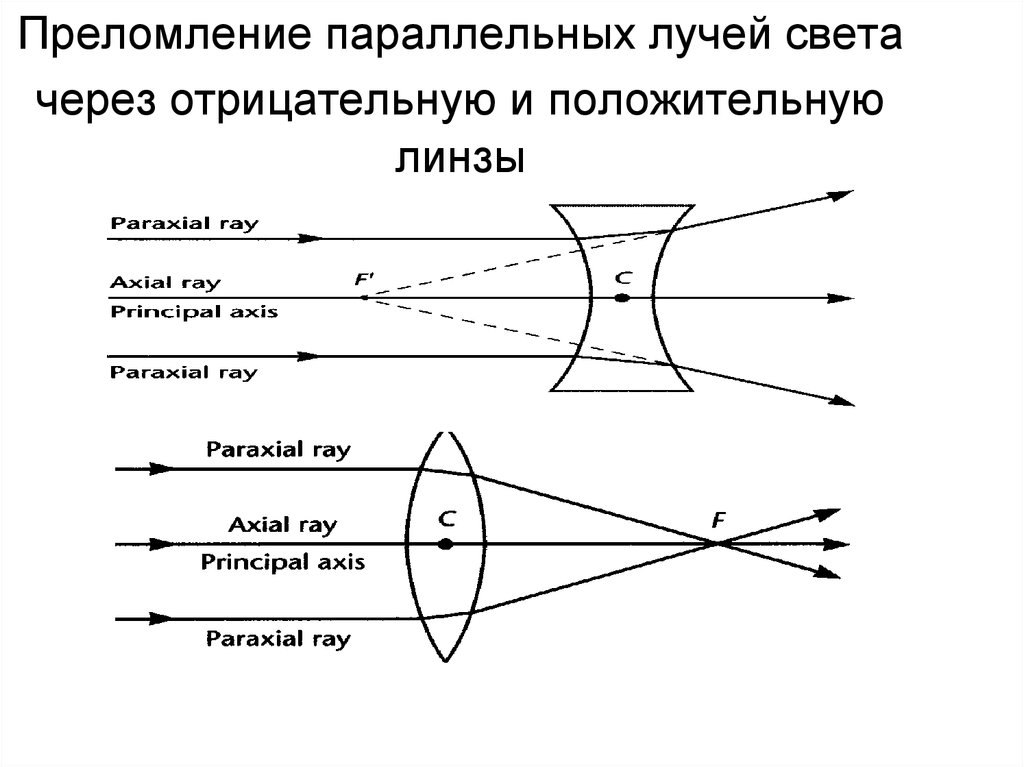
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d..+1f..=1F..
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F..+1f..=1F..
1f..=1F..−12F..=2−12F..=12F..
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2.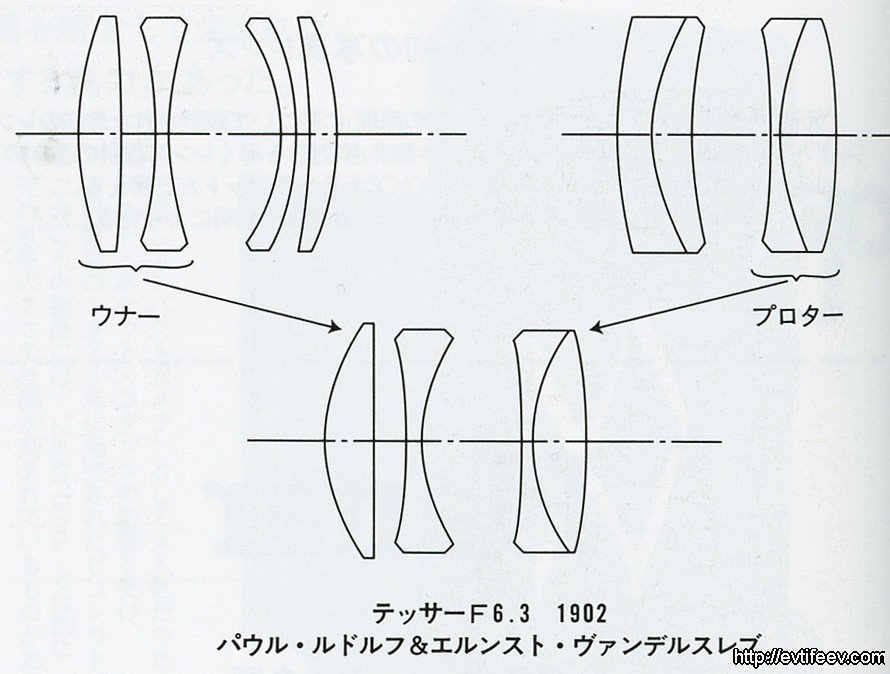 .
.
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D..=12,5..=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76..+1f..=1F..
1fC..=1F..−10,76..=0,76−F0,76F..=0,76−0,40,76·0,4..
fC=0,76·0,40,76−0,4..=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´..=ACA´C´..
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´..=ACA´C´..
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2..=(0,044)22..=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18181Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала.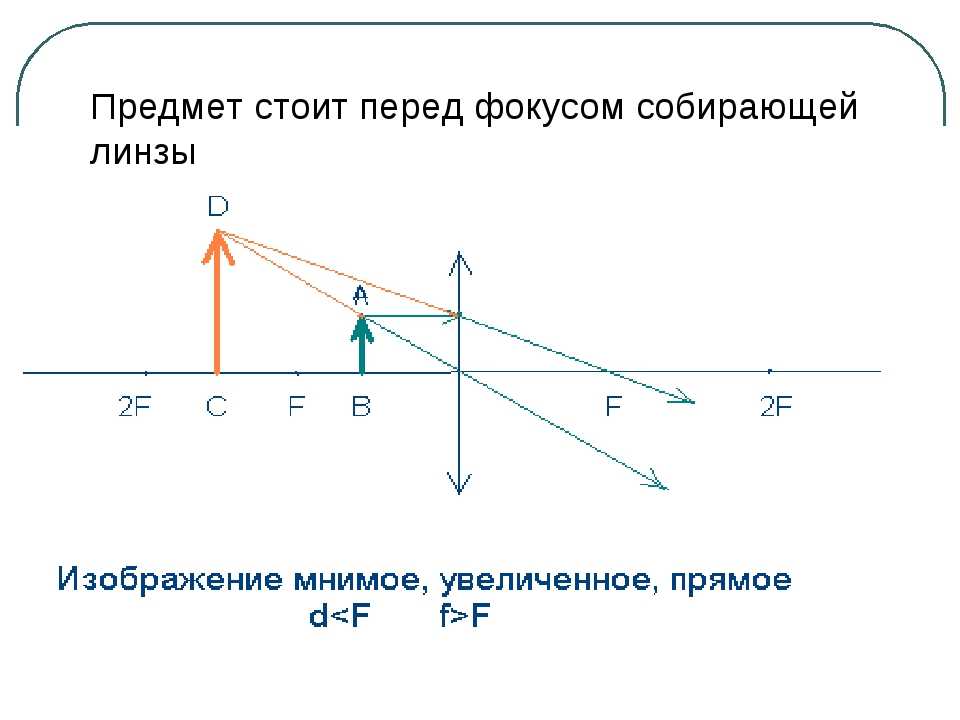 Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Симметричными являются только предмет и его изображение на последнем рисунке — Г.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18876Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?
Алгоритм решения
1.Построить изображение точки.
2.Выбрать верный ответ.
Решение
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
Ответ: 4pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 21. 7k | Оценить:
7k | Оценить:
выпуклые, вогнутые. Где используются линзы? Читайте в блоге lenlasers.ru
Линза — это прозрачный оптический компонент, используемый для фокусировки или дефокусировки излучения, излучаемого периферийным объектом. Световые лучи, прошедшие линзу, формируют действительное или мнимое изображение.
Изображения, формируемые линзами, возникают из-за преломления света. Выпуклая линза еще называется собирающей или положительной. Она фокусирует лучи, исходящие от точечного объекта, в определенной точке; следовательно, сформированное изображение считается действительным.
Двояковыпуклая линза – это линза с двумя выпуклыми поверхностями, оптические центры которых совпадают.
Рисунок 1 – Схема ДВЛ
Когда излучение попадает на края линзы, оптические лучи становятся параллельны друг другу.
Типы линз
По кривизне двух оптических плоскостей линзы бывают двух типов: двояковыпуклые, выпукло-вогнутые
и с одной плоской стороной.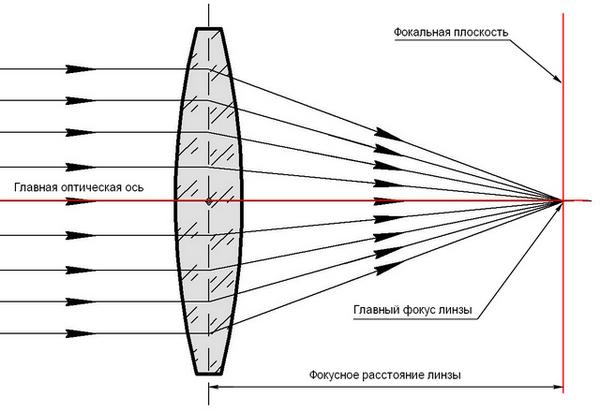 Элемент является двояковыпуклым, если обе плоскости выпуклые.
Элемент является двояковыпуклым, если обе плоскости выпуклые.
Двояковыпуклые линзы (ДВЛ) применяются как увеличительные или конденсирующие компоненты. Они также находят применение во многих системах формирования изображений, таких как телескопы, монокуляры, микроскопы, бинокли, камеры, проекторы и т. д.
ДВЛ представляют собой простые симметричные элементы, которые содержат две выпуклые линзы со сферической формой, каждая из которых имеет одинаковый радиус кривизны (см. рис 1).
Формула ДВЛ
Для расчета фокусного расстояния сферической линзы можно применить уравнение для толстой линзы, приведенное ниже. В этом выражении n — показатель преломления материала, R1 и R2 — радиусы кривизны, а d — толщина.
Для двояковыпуклых линз, у которых передний и задний радиусы кривизны равны по величине и противоположны по знаку, R1 = -R2 = R, имеем
Типовые материалы и параметры линз
BK7, вероятно, представляет собой наиболее распространенное оптическое стекло, из которого производят высококачественные оптические компоненты видимого и ближнего инфракрасного диапазона.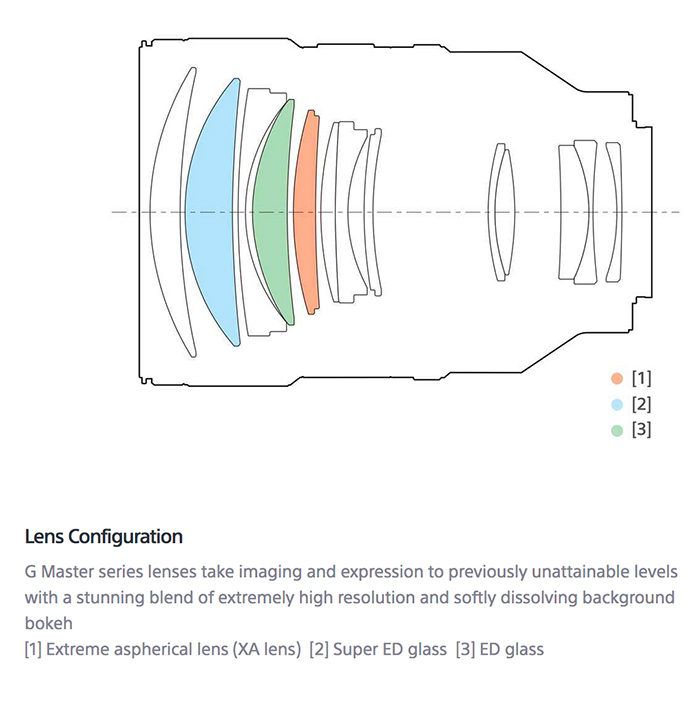 Его обычно выбирают всякий раз, когда дополнительные преимущества УФ плавленого кварца (то есть хорошее пропускание в УФ и более низкий коэффициент теплового расширения) не являются необходимыми. Его высокая однородность, низкое содержание пузырьков и включений, а также простота изготовления делают его хорошим выбором для пропускающей оптики. BK7 также относительно твердый материал, он показывает хорошую устойчивость к царапинам.
Его обычно выбирают всякий раз, когда дополнительные преимущества УФ плавленого кварца (то есть хорошее пропускание в УФ и более низкий коэффициент теплового расширения) не являются необходимыми. Его высокая однородность, низкое содержание пузырьков и включений, а также простота изготовления делают его хорошим выбором для пропускающей оптики. BK7 также относительно твердый материал, он показывает хорошую устойчивость к царапинам.
CaF2 обычно используется для приложений, требующих высокого пропускания в инфракрасном и ультрафиолетовом спектральных диапазонах. Его чрезвычайно высокий порог лазерного повреждения делает CaF2 полезным для использования с эксимерными лазерами. Материал демонстрирует низкий показатель преломления, варьирующийся от 1,35 до 1,51 в диапазоне его использования от 180 нм до 8,0 мкм. Фторид кальция также довольно химически инертен и обладает превосходной твердостью.
Линзы из ZnSe особенно хорошо подходят для использования с мощными CO2-лазерами.
|
Материал |
Диапазон пропускания |
|
BK7 |
350 нм — 2.0 мкм |
|
УФ Плавленый кварц |
185 нм — 2.1 мкм |
|
CaF2 |
0.18 — 8.0 мкм |
|
ZnSe |
0.6 — 21.0 мкм, обычно используется AR покрытие 7 мкм — 12 мкм |
Так как данные оптические элементы применяются в высокоточных оптических установках, необходимо тщательно подбирать изделие под конкретную задачу, ориентируясь на допуски.
- Допуск диаметра: критический механический допуск, который необходимо учитывать при установке оптики. Отклонения от номинального диаметра могут помешать правильной посадке линз в их монтажном приспособлении, что приведет к децентрализации или наклону внутри оптического узла.
- Центрирование: точное выравнивание оптической оси гарантирует, что линзы могут использоваться в сложных приложениях для обработки изображений. В сочетании с упомянутыми выше прецизионными допусками на диаметр, строгие допуски на центровку обеспечивают минимальное биение изображения в оптической сборке.
- Качество поверхности: даже незначительные царапины или ямки на оптической плоскости элемента могут привести к рассеянию лучей, что может быть вредным для лазерных приложений. Данный параметр также влияет на порог лазерного повреждения. Объективы с плохим допуском на данный параметр могут выйти из строя при воздействии излучения даже средней мощности.
 Царапины и углубления на линзе также могут привести к тому, что лазерный свет будет рассеиваться взад и вперед, разрушая покрытие.
Царапины и углубления на линзе также могут привести к тому, что лазерный свет будет рассеиваться взад и вперед, разрушая покрытие.
Пример важности допусков
В расширителях луча ошибки центрирования могут привести к дрейфу луча, в результате чего выходной луч не параллелен входному лучу. Дрейф луча усложняет юстировку лазерных систем, поскольку требует наклона механического корпуса для компенсации несоосности входной и выходной осей.
Рисунок 2 — Влияние ошибок центрирования на расширитель луча
Типичные характеристики линз приведены в таблице ниже.
|
Параметр |
Значение |
|
Неравномерность поверхности |
λ/4 |
|
Качество поверхности |
40-20 S-D |
|
Допуск на толщину |
±0. |
|
Допуск на диаметр |
+0.0 / -0.1 мм |
|
Центровка |
<3 угловых минут |
|
Световой диаметр |
>90% от диаметра линзы |
|
Допуск на фокусное расстояние |
±1% |
Многие линзы имеют антиотражающие покрытия на своих плоскостях, которые существенно уменьшают отражения, вызванные изменением показателя преломления. Обратите внимание, однако, что это работает только в ограниченном диапазоне длин волн. Существует компромисс между сильным подавлением отражений и широкой полосой пропускания.
ДВЛ работают лучше всего, когда объект и изображение находятся на противоположных сторонах линзы, а отношение объекта к расстоянию до изображения (сопряженное соотношение) составляет от 0,2 до 5.
ДВЛ исправляют следующие проблемы, возникающие в оптических системах:
- Кома
- Искажение
- Хроматические и сферические аберрации
Благодаря своим особенностям, ДВЛ применяются для фокусировки лучей в объективах и конденсорах. Они обеспечивают меньший фокус по сравнению с аналогичными плоско-выпуклыми линзами. ДВЛ также применяются как расширители пучка и в комбинациях с другими оптическими элементами в проекционных системах.
Применение
Ниже приведены самые распространенные сферы использования ДВЛ:
- в очках
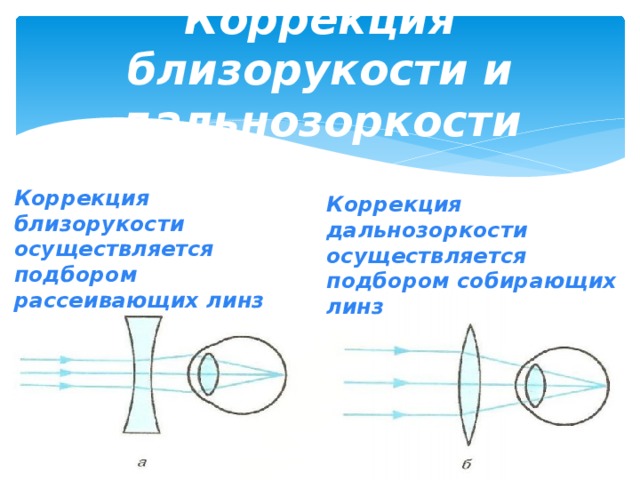
У человека могут быть такие проблемы, как дальнозоркость или близорукость, поскольку хрусталик глаза не может правильно фокусировать лучи на сетчатке.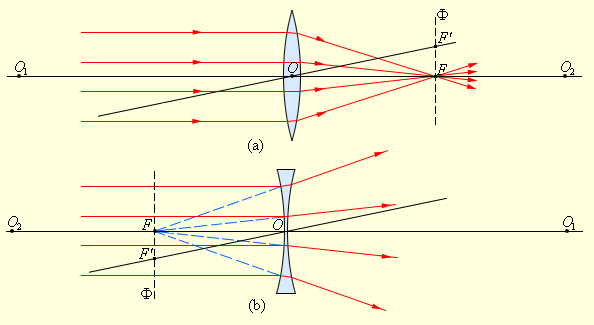 У человека, страдающего дальнозоркостью, изображение, формируемое хрусталиком, находится далеко за сетчаткой. ДВЛ, установленная перед глазом, может скорректировать эту проблему. Она уменьшает длину фокусировки, и излучение должным образом фокусируется на сетчатке.
У человека, страдающего дальнозоркостью, изображение, формируемое хрусталиком, находится далеко за сетчаткой. ДВЛ, установленная перед глазом, может скорректировать эту проблему. Она уменьшает длину фокусировки, и излучение должным образом фокусируется на сетчатке.
- в фотоаппаратах
В фотоаппаратах ДВЛ используется для фокусировки на изображении, а также для увеличения изображения объекта. Кроме того, объектив камеры состоит из комбинации выпуклой и вогнутой линз, за которыми следует вторая выпуклая линза.
- в микроскопах
В микроскопе ДВЛ увеличивают изображения. Микроскопы создают увеличенные изображения очень маленьких объектов, для этого очень полезны выпуклые линзы. Более того, простые микроскопы в большинстве своем состоят из трех линз.
Понравилось?
Обязательно поделитесь статьей в социальных сетях!
План вознаграждений за контактные линзы | Контактные линзы со скидкой
Что входит в бесплатную пробную версию контактных линз?
Испытательный срок состоит из пяти пар однодневных одноразовых линз или месячного запаса выбранных однодневных многоразовых линз. Это испытание не включает ежеквартальную замену, ежегодную замену, жесткие газопроницаемые линзы и цветные контактные линзы. Пробная версия также не распространяется на текущих клиентов плана вознаграждения за контактные линзы Boots Opticians.
Это испытание не включает ежеквартальную замену, ежегодную замену, жесткие газопроницаемые линзы и цветные контактные линзы. Пробная версия также не распространяется на текущих клиентов плана вознаграждения за контактные линзы Boots Opticians.
На чем основана годовая экономия?
Годовая экономия включает в себя экономию, которая может быть сделана на проверку зрения, проверку контактных линз, покупку очков и покупку продукции торговой марки Boots в рамках плана.
• Экономия на очках рассчитана на основе средних расходов клиентов салонов оптики в возрасте от 19 до 60 лет в период с января 2016 г. по декабрь 2016 г.
• Экономия на проверке зрения рассчитана на основе рекомендуемого двухлетнего цикла проверки зрения (исключая клиентов, которые имеют право на бесплатную проверку зрения NHS). )
• Экономия на проверке контактных линз, основанная на годовом цикле проверки контактных линз. 74 % клиентов плана вознаграждения за контактные линзы проходят ежегодный цикл проверки контактных линз
• Скидка 10 % – это средняя экономия, которую клиенты, действующие в рамках программы вознаграждений за контактные линзы, сэкономили на продуктах марки Boots в период с февраля 2016 года по февраль 2017 года. схема оплаты и бесплатная доставка заказов на контактные линзы. Эта экономия является дополнением к вышеуказанной общей экономии.
схема оплаты и бесплатная доставка заказов на контактные линзы. Эта экономия является дополнением к вышеуказанной общей экономии.
Что такое план вознаграждения за контактные линзы Boots Opticians?
Программа вознаграждения за контактные линзы Boots Opticians — это схема прямого дебетования, которая обеспечивает удобный способ распределения стоимости ношения контактных линз. Кроме того, в зависимости от типа ваших контактных линз, в ваш план могут быть включены растворы. План вознаграждений за контактные линзы Boots Opticians — это не кредитное соглашение, это план платежей, который позволяет вам платить заранее за каждый заказ. Вы должны будете внести платежи за первые три месяца вперед, когда присоединитесь к плану вознаграждения за контактные линзы Boots Opticians. С вашего банковского счета будет списываться каждый месяц после регистрации. Ваши контактные линзы будут автоматически заказываться каждые три месяца, и вы будете вносить три платежа за каждый заказ.
Как долго действует мое соглашение?
Boots Opticians План вознаграждений за контактные линзы не имеет минимального срока соглашения и может быть отменен в любое время, все, что мы просим, это уведомить нас о своем желании отменить за 28 дней, и мы отменим ваш план и вернем вам деньги. любые авансовые платежи непосредственно на ваш банковский счет. Мы оставляем за собой право изменить условия вашего соглашения о программе вознаграждения за контактные линзы Boots Opticians, уведомив вас об этом за три месяца.
Сколько я буду платить?
Все платежи, которые вы делаете (включая первоначальный платеж и последующие ежемесячные прямые дебеты), состоят из (i) платы за профессиональные услуги по выдаче, включая осмотры, и (ii) платы за товары, включая почтовые расходы и упаковку. Из вашего общего платежа 50% приходится на услуги по выдаче и 50% на товары.
Все цены подлежат пересмотру, и любые изменения в вашем прямом дебете будут подробно описаны в письме с уведомлением не менее чем за пять недель.
Что произойдет, если при оплате будет допущена ошибка?
Если компания Boots Opticians, ваш банк или строительное общество допустили ошибку при ежемесячном платеже прямым дебетом, можно запросить немедленный возврат средств в соответствии с условиями гарантии прямого дебета, связавшись напрямую с вашим банком или строительным обществом. Также свяжитесь со схемой вознаграждения контактных линз Boots Opticians по телефону 0345 603 2020 (звонки оплачиваются по местному тарифу) или по электронной почте [email protected].
Что произойдет, если я пропущу платеж?
Если по какой-либо причине ваш банк или строительное общество отклонит наш запрос на ваш ежемесячный платеж прямым дебетом, мы попытаемся получить платеж в следующую запланированную дату платежа. Имейте в виду, что мы не можем отправить ваши контактные линзы, пока вы не оплатите полную стоимость доставки, и любые пропущенные платежи могут привести к изменению вашего графика доставки. Мы свяжемся с вами, чтобы договориться о выплате любых непогашенных денежных средств и можем изменить ваш график доставки, если это необходимо. Если мы не сможем получить ваши платежи в течение трех месяцев подряд, ваше участие в программе будет автоматически аннулировано.
Мы свяжемся с вами, чтобы договориться о выплате любых непогашенных денежных средств и можем изменить ваш график доставки, если это необходимо. Если мы не сможем получить ваши платежи в течение трех месяцев подряд, ваше участие в программе будет автоматически аннулировано.
Как я могу сменить оптику Boots, в которую я хожу?
Если вы переезжаете, просто зайдите в свою новую местную клинику Boots Optics и сообщите им, что вы переехали в этот район. Ваша практика Boots Opticians организует передачу вашего плана вознаграждения за контактные линзы Boots Opticians и истории болезни. В большинстве случаев вам не потребуется подписывать новую Инструкцию по прямому дебетованию.
Что произойдет, если я поменяю контактные линзы?
Если вам нужен новый тип линз или ваш рецепт изменился в течение срока действия вашего участия в плане вознаграждений за контактные линзы Boots Opticians, мы можем организовать перенос ваших новых линз на вашу учетную запись.![]() Вы увидите корректировку платежа в следующую дату платежа после смены типа объектива.
Вы увидите корректировку платежа в следующую дату платежа после смены типа объектива.
Что происходит с решениями моего плана?
Если вам нужен раствор для контактных линз для вашего типа линз, ваш офтальмолог может включить его в ваши ежемесячные платежи. Если вы выбрали получение линз из магазина, каждые три месяца вам будет доступен пакет растворов, который вы сможете забрать в магазине. Если вы выбрали доставку на дом, ваши линзы и растворы будут доставлены на ваш домашний адрес.
Как я могу сообщить вам об изменении моих личных данных?
Сообщите об этом в местную клинику Boots Opticians (практику, в которой вы посещаете встречи с контактными линзами), по электронной почте [email protected] или вы можете написать по адресу: Boots Opticians Contact Lens Rewards Plan, Administration Office, 225 Bath Street, Glasgow, G2 4GZ, с указанием вашего членского номера. Если вы хотите изменить данные своего банка или строительного общества или дату платежа прямым дебетом, обратитесь в местную практику Boots Opticians или отправьте электронное письмо по адресу contactlenses@boots-opticians. co.uk.
co.uk.
Могу ли я накапливать баллы Boots Advantage Card?
Вы будете получать по одному баллу за каждый фунт стерлингов, потраченный на линзы и растворы в рамках плана вознаграждения за контактные линзы Boots Opticians. Мы можем начислить баллы на вашу карту Advantage Card, когда вы приходите в клинику, чтобы забрать линзы, или приходите на прием по контактным линзам или на проверку зрения. Если вы выбрали доставку на дом в своем плане, баллы вашей карты Advantage Card будут автоматически загружены на вашу карту Advantage Card через пять дней после доставки ваших линз. Мы не обмениваем баллы Advantage Card на наличные деньги. Баллы Advantage Card нельзя потратить в магазинах оптики Boots, на «сторонних сайтах», включая Boots Hearingcare, bootskitchenappliances.com, рецептурных препаратах, грудном молоке (до 6 месяцев), подарочных ваучерах/картах, почтовых марках, картах пополнения мобильного телефона, туристические услуги и страхование обуви. Применяются положения и условия карты Full Boots Advantage Card.
Программа вознаграждения за контактные линзы Boots Opticians
Будучи участником плана вознаграждения за контактные линзы Boots Opticians, вы также получаете доступ к другим замечательным предложениям. Они не являются частью вашего соглашения, и мы оставляем за собой право изменять или отзывать связанные преимущества без предварительного уведомления.
Проверка контактных линз
Мы хотим убедиться, что ваши глаза здоровы и что ваши линзы максимально удобны, поэтому нам нужно, чтобы вы посещали комплексную проверку контактных линз не реже одного раза в 24 месяца; Ваш окулист сообщит, нужно ли нам видеть Вас чаще. Имейте в виду, что если срок проверки контактных линз просрочен, ваши линзы будут направлены в вашу базовую практику и не будут доступны вам до тех пор, пока вы не пройдете проверку контактных линз. Эти проверки важны, так как ваши глаза и здоровье глаз могут меняться со временем. Мы сообщим вам, когда будет назначена ваша следующая встреча.
Включенная проверка зрения и проверка контактных линз
Как клиент плана вознаграждений за контактные линзы Boots Opticians, вы имеете право на неограниченное количество проверок зрения и проверок контактных линз в рамках ежемесячного прямого дебета. Эти встречи проводятся в зависимости от наличия возможности (если вы имеете право на проверку зрения NHS, вы можете подать заявку через NHS или план вознаграждений за контактные линзы. Наши коллеги в магазине могут объяснить любое влияние, если вы имеете право на ваучер NHS). Денежная альтернатива или возмещение стоимости проверки зрения NHS не предусмотрены.
Сэкономьте 50% на паре полных очков и солнцезащитных очков (включая оправы, линзы и выдачу) и 25% на солнцезащитные очки без рецепта в Boots Opticians
Все наши цены на очки включают сбор за выдачу и сбор за оправа и сапоги стандартные однофокальные линзы. Ваучеры NHS можно использовать в качестве денежного вклада в окончательную стоимость ваших очков. Цены, указанные в магазинах оптики Boots, включают оправу и стандартные однофокальные линзы Boots. Это предложение включает в себя брендовые и дизайнерские оправы Boots с линзами по рецепту. Вы также можете сэкономить 25% на солнцезащитных очках без рецепта в Boots Opticians. Эти предложения не включают только покупку рамы и повторную глазурь и не могут быть использованы в сочетании с любыми другими предложениями или скидками для персонала.
Цены, указанные в магазинах оптики Boots, включают оправу и стандартные однофокальные линзы Boots. Это предложение включает в себя брендовые и дизайнерские оправы Boots с линзами по рецепту. Вы также можете сэкономить 25% на солнцезащитных очках без рецепта в Boots Opticians. Эти предложения не включают только покупку рамы и повторную глазурь и не могут быть использованы в сочетании с любыми другими предложениями или скидками для персонала.
Запасные контактные линзы для экстренных случаев
Мы знаем, что иногда случаются несчастные случаи, поэтому мы будем рады предложить вам время от времени замену линз по запросу, в зависимости от типа вашего плана. Ежемесячные/двухмесячные линзы – не более трех линз в год, однодневные одноразовые линзы – не более 10 пар в год. Ежеквартальные/годовые/заказные линзы — одна линза в год со скидкой 50%, исходя из обычной цены продажи за наличные. Если вам потребуются контактные линзы для экстренной замены, обратитесь в местную практику, и они будут рады помочь.
Скидка 10 % на продукцию бренда Boots в магазинах Boots в Великобритании подать заявку на сайте boots.com).
Скидка 10% будет активирована автоматически, когда вы зарегистрируете свою карту Advantage Card в магазине Boots Opticians. Вы должны предъявлять свою постоянную карту Advantage Card каждый раз, когда совершаете покупки, чтобы получить скидку 10%. Скидка не будет предоставлена задним числом. Предложение 10 % не распространяется на товары марки Boots в магазинах Boots Opticians, покупки на «сторонних сайтах», включая Boots Hearingcare, BootsKitchenAppliances.com, рецептурные товары Boots, детское молоко (до 6 месяцев), подарочные ваучеры/карты, страховку, дорожные деньги и туристические услуги. Это предложение открыто для жителей Великобритании. Недоступно на boots.com. Действуют правила и условия полной карты Advantage Card. Мы оставляем за собой право отменить или изменить это предложение в любое время. Доступен во всех магазинах Boots. Наличной альтернативы нет. Это предложение не может быть использовано в сочетании с любой другой скидкой.
Это предложение не может быть использовано в сочетании с любой другой скидкой.
Запланируйте отпуск
Если вы обнаружите, что не надели все свои линзы до прибытия следующей доставки, свяжитесь с нами по телефону 0345 603 2020, чтобы обсудить план отпуска, поскольку мы можем приостановить ваши платежи и линзы до максимум шесть месяцев в течение 12 месяцев. Звонки оплачиваются по местному тарифу.
Бесплатная пробная проверка контактных линз
Пожалуйста, спросите своего офтальмолога, когда придете на проверку контактных линз, о новых линзах на рынке. Мы рады предложить вам бесплатную пробную версию любых альтернативных объективов.
Доставка на дом контактных линз и растворов
Слишком заняты, чтобы прийти и забрать линзы? Теперь вы можете выбрать доставку на дом для большинства типов линз (за исключением годовых или других контактных линз, сделанных на заказ). Мы будем доставлять ваши линзы и растворы (если применимо) каждые три месяца. За эту услугу не взимается дополнительная плата, и вам не нужно расписываться за доставку. Мы можем доставить на любой адрес Великобритании. Если вы не получили контактные линзы или растворы, сообщите об этом как можно скорее по телефону 0345 603 2020, звонки оплачиваются по местному тарифу. Важно, чтобы мы заботились о здоровье ваших глаз, поэтому, если вы пропустите регулярные встречи для проверки контактных линз, ваши линзы будут автоматически отправлены в вашу местную клинику Boots Opticians, которая свяжется с вами, чтобы договориться о встрече и забрать ваши линзы. Мы можем хранить ваши линзы только в течение ограниченного периода времени, поэтому, пожалуйста, запишитесь на прием для проверки контактных линз как можно скорее. Вы также можете забрать свои контактные линзы и растворы (если применимо) в своей клинике Boots Opticians, которая сообщит вам, когда ваши линзы прибудут.
За эту услугу не взимается дополнительная плата, и вам не нужно расписываться за доставку. Мы можем доставить на любой адрес Великобритании. Если вы не получили контактные линзы или растворы, сообщите об этом как можно скорее по телефону 0345 603 2020, звонки оплачиваются по местному тарифу. Важно, чтобы мы заботились о здоровье ваших глаз, поэтому, если вы пропустите регулярные встречи для проверки контактных линз, ваши линзы будут автоматически отправлены в вашу местную клинику Boots Opticians, которая свяжется с вами, чтобы договориться о встрече и забрать ваши линзы. Мы можем хранить ваши линзы только в течение ограниченного периода времени, поэтому, пожалуйста, запишитесь на прием для проверки контактных линз как можно скорее. Вы также можете забрать свои контактные линзы и растворы (если применимо) в своей клинике Boots Opticians, которая сообщит вам, когда ваши линзы прибудут.
Все преимущества для клиентов распространяются только на клиентов плана вознаграждения за контактные линзы Boots Opticians. Отмена вашей схемы или невыполнение ваших платежей в актуальном состоянии приведет к отмене ваших пособий. Преимущества плана вознаграждения за контактные линзы Boots Opticians могут быть изменены в любое время без предварительного уведомления.
Отмена вашей схемы или невыполнение ваших платежей в актуальном состоянии приведет к отмене ваших пособий. Преимущества плана вознаграждения за контактные линзы Boots Opticians могут быть изменены в любое время без предварительного уведомления.
Упаковка для контактных линз Easycare | Specsavers UK
- Главная
- > Информация
Контактные линзы просты, но почему бы не сделать все возможное и не сделать вашу жизнь супер-простой? С нашей ежемесячной схемой прямого дебетования (мы называем ее пакетом easycare) вы получите все необходимое для беспроблемного ношения контактных линз, а также множество дополнительных услуг. Зарегистрироваться тоже легко — просто спросите в магазине при следующей встрече или позвоните в местный магазин.
Записаться на прием
Уже зарегистрировались и хотите внести изменения в свою подписку? Вы можете сделать это онлайн.
Войдите в систему my Easycare
Что включает в себя пакет easycare?
Помимо ваших линз, вы также получите все эти замечательные преимущества (которые в сумме могут сэкономить вам до 140 фунтов стерлингов*)
Бесплатная проверка состояния контактных линз и бесплатная доставка
Получите бесплатные визиты для проверки контактных линз по мере необходимости, а также линзы с доставкой прямо к вашей двери, бесплатно, каждый квартал. Зарегистрируйтесь в магазине сегодня.
Зарегистрируйтесь в магазине сегодня.
Управляйте своей подпиской онлайн
Просматривайте предстоящие доставки, заказывайте добавки, изменяйте адрес доставки или количество линз или даже пропускайте доставку с помощью нашего нового онлайн-сервиса самообслуживания.
Специализированный контактный центр в Великобритании
Наша команда будет рядом, если у вас есть какие-либо вопросы.
Скидка 50 % на очки с контактными линзами
Вы можете приобрести одну пару очков со скидкой из ассортимента от 69 фунтов стерлингов и выше.
Бесплатная замена линз
Если ваши линзы утеряны или повреждены, вы можете получить до двух бесплатных многоразовых контактных линз или пять пар ежедневных линз в год для их замены.
Бесплатные проверки зрения
Для тех, кто еще не имеет права на бесплатную проверку зрения , финансируемую NHS.
Нужна поддержка или есть вопрос?
Если у вас есть какие-либо вопросы, которые не могут быть решены онлайн, просто заполните нашу онлайн-форму, и один из наших сотрудников свяжется с вами в течение 48 часов после получения вашего сообщения. На выходных может быть небольшая задержка с ответом.
На выходных может быть небольшая задержка с ответом.
Свяжитесь с нами. Просто заполните нашу онлайн-форму ниже, и один из наших представителей свяжется с вами в течение 48 часов после получения вашего запроса. Приносим свои извинения за задержку с ответом в выходные.
Свяжитесь с нами
Готовы зарегистрироваться?
Подключиться к нашей схеме прямого дебетования очень просто — просто спросите в магазине или позвоните нам.
Найти мой магазин
Хотите попробовать перед покупкой?
Если вы хотите опробовать свои линзы перед покупкой, вы можете получить одну пару контактных линз на месяц или пять пар однодневных одноразовых контактных линз на пробу бесплатно
Забронируйте мою бесплатную пробную версию
Есть вопрос о easycare ?
Если вы все еще не нашли то, что ищете, просмотрите наши наиболее часто задаваемые вопросы.
Узнать больше
Положения и условия
Клиент получает право на проверку зрения через 28 дней после подписки на пакет easycare. Первоначальный трехмесячный платеж требуется от новых клиентов пакета easycare, для линз RGP вам необходимо будет приобрести 1 пару линз. Возврат средств за уже оказанную офтальмологическую помощь невозможен. Все преимущества пакета easycare могут быть использованы только лицом, указанным в пакете easycare. Пакет действителен до тех пор, пока ваше членство не прекратится путем отмены ваших платежей по прямому дебету или после того, как рецепт перестанет действовать (обычно два года).
Все преимущества пакета easycare действительны до тех пор, пока ваше членство не прекратится либо в результате отмены ваших платежей прямым дебетом, либо после того, как срок действия вашего рецепта (обычно два года, если не будет обновлено). Все преимущества пакета могут быть использованы только указанным лицом в пакете easycare.
Клиент Easycare получает право на бесплатную проверку зрения через 28 дней с момента подписки на пакет easycare и после внесения первоначального трехмесячного платежа. Проверка зрения не включает ОКТ (оптическую когерентную томографию), за которую взимается дополнительная плата. Возврат средств за уже предоставленную офтальмологическую помощь (или проверку зрения) невозможен. За исключением клиентов, имеющих право на проверку зрения, финансируемую NHS.
В дополнение к бесплатной проверке зрения клиенты easycare получают бесплатную проверку состояния контактных линз. Обычно они проводятся в соответствии с профессиональными рекомендациями не реже одного раза в 2 года.
Клиенты Easycare могут получить 3-месячный запас контактных линз и растворов (при необходимости) с доставкой по адресу по выбору клиента без платы за доставку.
При покупке пары очков из нашего ассортимента стоимостью 69 фунтов стерлингов и выше. Не подлежит возврату или передаче на уже купленные очки. Нельзя использовать с другими предложениями или ваучерами, а также частично или полностью обменять на наличные. Исключая реглазы, защитные очки, любые продукты для контактных линз и безрецептурные очки. Новые очки должны быть только по вашему рецепту. Требуется действующий рецепт. Скидка 50 % распространяется на оправы, линзы и любые дополнительные опции только для указанных клиентов easycare, один раз в год только в одном магазине.
Нельзя использовать с другими предложениями или ваучерами, а также частично или полностью обменять на наличные. Исключая реглазы, защитные очки, любые продукты для контактных линз и безрецептурные очки. Новые очки должны быть только по вашему рецепту. Требуется действующий рецепт. Скидка 50 % распространяется на оправы, линзы и любые дополнительные опции только для указанных клиентов easycare, один раз в год только в одном магазине.
Клиенты Easycare могут бесплатно получить некоторое количество сменных линз. Владельцы однодневных контактных линз могут иметь не более 5 пар бесплатных сменных линз в год. Владельцы многоразовых контактных линз могут иметь максимум 2 линзы для бесплатной замены (или 1 пару линз для бесплатной замены) в год. За дополнительные сменные линзы сверх права на бесплатную замену взимается плата. Линзы можно приобрести в зарегистрированном магазине.
Клиенты Easycare могут приостанавливать свои ежемесячные платежи на срок от 3 до 6 месяцев за любой календарный год.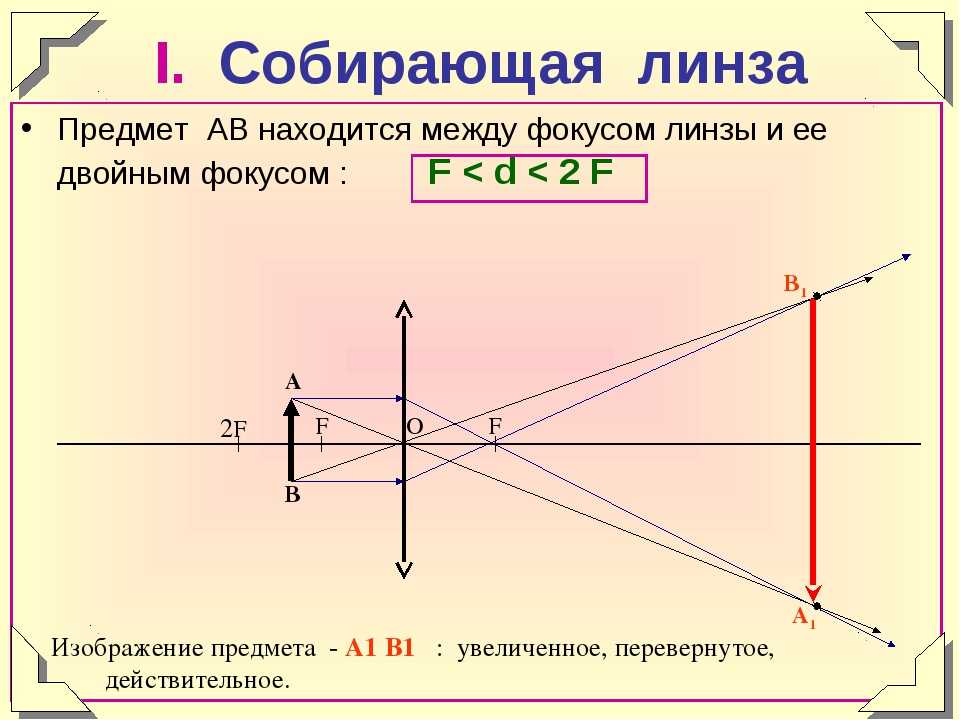 Во время платежных каникул с клиентов не будет взиматься плата и они не будут получать свой ежеквартальный запас контактных линз, но все другие льготы по простому уходу останутся доступными.
Во время платежных каникул с клиентов не будет взиматься плата и они не будут получать свой ежеквартальный запас контактных линз, но все другие льготы по простому уходу останутся доступными.
Палата представителей США, группы потребителей обдумывают федеральный иск против схем продажи контактных линз DTC
Обеспокоенные тем, что регулирующий надзор может быть шагом в развитии схем продаж медицинского оборудования напрямую потребителю (DTC), члены Конгресса требуют федерального расследования продаж практики при поддержке AOA и коалиции организаций потребителей и здравоохранения.
В письме от 6 декабря Генеральному контролеру США 21 ведущий член Палаты представителей США попросили Счетную палату правительства (GAO) провести официальное исследование по изучению федерального регулирования практики DTC в рекламе рецептурных медицинских устройств, особо отметив контактные линзы и сославшись на Статья New York Times с подробным описанием того, как Hubble Contacts воспользовалась федеральными правилами. Обеспокоенность законодателей перекликается со многими опасениями по поводу здоровья и безопасности, которые AOA, средства массовой информации и группы защиты прав потребителей в течение многих лет подчеркивали в связи с рецептурными медицинскими устройствами DTC.
Обеспокоенность законодателей перекликается со многими опасениями по поводу здоровья и безопасности, которые AOA, средства массовой информации и группы защиты прав потребителей в течение многих лет подчеркивали в связи с рецептурными медицинскими устройствами DTC.
«Рост интернет-маркетинга и стремление к модели DTC в оказании медицинских услуг представляет собой серьезное изменение в нашей системе здравоохранения», — говорится в двухпартийном письме. «Мы обеспокоены тем, что из-за быстрого роста рекламы DTC может отставать надлежащий надзор со стороны регулирующих органов».
В частности, члены Палаты представителей упомянули о проблемах в отношениях между врачом и пациентом, связанных с некоторыми продуктами DTC, позволяющими потребителям полностью обойти рутинную оценку или надзор со стороны поставщиков медицинских услуг, а также сообщения о низком качестве и побочных эффектах, связанных с продуктами DTC. В письме описывается онлайн-продавец контактных линз, «обвиняемый в использовании старых материалов и замене предписанных линз на другие бренды», а также группы защиты, утверждающие, что онлайн-компании обходят существующие требования проверки рецептов в соответствии с правилом Федеральной торговой комиссии США (FTC) в отношении контактных линз.
В таком случае члены палаты призвали беспристрастное аудиторское и следственное агентство разработать исследование, которое могло бы помочь оценить и направить потенциальные регулирующие или законодательные действия, в частности, изучив: как контактные линзы, непосредственно потребителям.
Действия, которые в настоящее время предпринимают агентства, такие как FTC или Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США (FDA), для решения выявленных проблем.
Ограничение возможностей этих федеральных агентств по обеспечению соблюдения существующих законов и правил, регулирующих рекламу DTC рецептурных медицинских продуктов.
Примечательно, что среди 20 сторон, подписавших соглашение, 14 членов Комитета Палаты представителей по энергетике и торговле, а также председатели и высокопоставленные члены двух подкомитетов с непосредственной юрисдикцией над федеральными агентствами, которые управляют этими правилами и обеспечивают их соблюдение. Однако растущая поддержка федеральных действий выходит за пределы Капитолийского холма, когда национальная группа потребителей поддерживает озабоченность Конгресса.
Однако растущая поддержка федеральных действий выходит за пределы Капитолийского холма, когда национальная группа потребителей поддерживает озабоченность Конгресса.
В ответ на письмо Палаты представителей Национальная лига потребителей (NCL) отметила, что она «аплодирует и полностью поддерживает» двухпартийный призыв к пересмотру федерального регулирования, касающегося назначения DTC Практика рекламы медицинских изделий.
«Мы наблюдаем все более распространенную практику пропуска опыта медицинских работников в предоставлении определенных медицинских услуг, чтобы предоставлять услуги и лечение непосредственно потребителям с меньшими затратами и более эффективно», — отмечает NCL, добавляя что такие удобства не могут «обеспечиваться за счет здоровья и безопасности потребителей».
В частности, в письме NCL упоминаются поставщики контактных линз DTC с бизнес-моделями, которые, по-видимому, поощряют потребителей обходить оценку или наблюдение своих врачей, и аналогичным образом цитируется статья New York Times о пациентах, пострадавших от продавцов контактных линз DTC. заменили прописанные контактные линзы собственной марки.
заменили прописанные контактные линзы собственной марки.
В обоих случаях — письмо Палаты представителей и поддержка NCL — призыв к федеральным действиям — это то, что AOA, Health Care Alliance for Patient Safety и другие организации здравоохранения решительно поддерживают и отстаивают в течение многих лет.
Защита интересов пациентов с контактными линзами AOAAOA уже давно высказывается против схем продажи контактных линз DTC, которые стремятся нарушить отношения между врачом и пациентом, и других онлайн-продавцов, которые обходят федеральные законы и правила рынка контактных линз, создавая большую упор на удобство, а не на зрение пациентов и здоровье глаз.
В дополнение к статье New York Times 2019 года, на которую ссылаются законодатели, статья Quartz 2018 года и другие последующие сообщения в СМИ независимо подтверждали жалобы, которые AOA впервые подала в правоохранительные органы в 2017 году. В то время AOA разослала письма в FDA, FTC и Министерство юстиции с просьбой провести расследование нарушений розничных продавцов, связанных с проверкой рецептов на контактные линзы.
Кроме того, Quartz опубликовал статью с подробным описанием того, как ее репортер обошел онлайн-процесс заказа контактных линз DTC с помощью ложной информации о рецепте. Кроме того, четыре других человека смогли использовать ложную информацию для размещения заказов, отметила репортер Quartz в своем разоблачении.
Еще совсем недавно, когда FTC проводила обзор правил контактных линз, AOA выступала за необходимость реформирования процесса проверки рецептов на контактные линзы с отчетами врачей о пациентах, получающих контактные линзы без действительных рецептов, или о компаниях, заменяющих линзы, назначенные врачом.
Несмотря на то, что контактные линзы являются безопасным и эффективным средством коррекции зрения, при правильном ношении и уходе за ними плохо подобранные или неправильно используемые контактные линзы могут привести к серьезным нарушениям здоровья глаз и зрению. Эти медицинские устройства, регулируемые FDA, не являются универсальными, как иногда изображают, и требуют рецепта врача и контроля для покупки, как указано в Законе о справедливости для потребителей контактных линз и Правиле контактных линз.



 Царапины и углубления на линзе также могут привести к тому, что лазерный свет будет рассеиваться взад и вперед, разрушая покрытие.
Царапины и углубления на линзе также могут привести к тому, что лазерный свет будет рассеиваться взад и вперед, разрушая покрытие. 1 мм
1 мм