Матрица что означает: Недопустимое название — Викисловарь
Что такое Матрица судьбы и как ее просчитать
Матрица судьбы довольно новый способ поиска своего предназначения. Первую популярность Матрица получила в 2006-м, так что это наиболее современным метод, в отличие от того же Квадрата Пифагора и Дизайна человека. Да и построить свою матрицу довольно просто. Для того чтобы рассчитать ее, необходимо знать свою дату рождения и начертить на листе бумаги квадрат в квадрате. В результате элементарных математических вычислений, по углам квадратов расставляются энергии — индивидуальные программы человека. Эзотерики называют Матрицу судьбы — жемчужиной среди инструментов самопознания.
Чтобы разобраться, что такое на самом деле Матрица судьбы, 5-tv.ru изучил вопрос и обратился за комментарием к мастеру тета-хилинга.
Как появилась Матрица судьбы?Увлеченным эзотерикой известно, что авторский метод чтения судьбы по матрице создала Наталья Ладини. Как утверждает кармический целитель, идея создать Матрицу судьбы пришла к ней в процессе изучения 22 арканов Таро.
Наталья Ладини
Автор методики «Матрица судьбы. Диагностика Предназначения»— Это очень красиво, наложить нумерологию на какой-то красивый сакральный узор. Мне пришла фигура восьмигранной звезды, и я разложила дату рождения, как старший аркан Таро, на эту фигуру.
По философии данного метода, каждый человек — это бессмертная душа, которая из жизни в жизнь приходит на Землю, для того, чтобы самосовершенствоваться. И поэтому жизнь преподносит нам определенные уроки, с помощью которых человек прорабатывает ранее не усовершенствованные части души. И якобы так можно повысить вибрационность.
Вибрация в понятии эзотерики — это энергия, которую человек транслирует в мир из себя и которую притягивает к себе как магнитом. Иными словами, когда человек «вибрирует» на высоком уровне, он счастлив. А когда издает низкие колебания, то несчастлив.
Иными словами, когда человек «вибрирует» на высоком уровне, он счастлив. А когда издает низкие колебания, то несчастлив.
Представьте ситуацию, что вы вроде бы работаете на работе, которая вам нравится и получается, но в глубине души чувствуете, что что-то не то. Как найти направление на это «то», может показать именно метод Матрицы судьбы. И это касается не только работы, а абсолютно всех сфер жизни.
Подсчеты и комбинации Матрицы, дают понять, что возможно, вы еще не изучили в себе.
- Особенности характера;
- Что нужно в себе развить, чтобы начать выполнять жизненное предназначение;
- Правильное использование ресурсов рода;
- Поиск негативного опыта в прошлом, который оказывает на вас воздействие;
- Достижение комфорта в социуме;
- Открытие денежного потока;
- Предназначение души;
- Истинные причины недугов и болезней;
- Вероятность событий в ближайшем будущем;
- Поиск подхода к близким людям.

Юлия Ушланова
Мастер чтения Матрицы судьбы, тета-хилер— Матрица судьбы — это система самопознания, она похожа на астрологию и нумерологию. По ней можно понять, с каким потенциалом, качествами и способностями человек пришел на Землю и какие задачи ему необходимо реализовать. И также можно понять не только свою текущую ситуацию, но и определить путь дальнейшего развития. Проанализировав эту информацию, человеку становится намного проще двигаться по жизни.
К данному методу автор методики советует обращаться для того, чтобы познать свое истинное предназначение, жизненные задачи и их пути воплощение в жизнь. Чаще всего к Матрице судьбы приходят, когда понимают, что делают что-то не так в этой жизни. Но как проработать свои сильные стороны, и на какие ошибки обратить внимание, чтобы начинать выполнять свою жизненную задачу?
Как рассчитать Матрицу судьбы?
Рассчитать Матрицу самостоятельно можно с помощью своей даты рождения, знания 22 Старших аркана Таро и 22 энергий Вселенной. Цифры, которые получаются при расчете, являются основными кодами судьбы или по-эзотерически, арканами.
Цифры, которые получаются при расчете, являются основными кодами судьбы или по-эзотерически, арканами.
Схема Матрицы судьбы. Фото: 22energy.com.ua
Считается, что под влиянием этих чисел протекает вся жизнь человека, формируется личность и судьба. Но для развернутого объяснения лучше всего обратиться к мастеру чтения Матрицы судьбы.
С помощью метода можно увидеть основные энергии, которые присутствуют в вашей Матрице. Каждая полученная энергия в процессе подсчета, является архетипом вашего характера, может выступать как в плюсе, так и в минусе. Но только сам человек поймет, в каком именно ключе идет та или иная энергетика. Всего Матрица судьбы содержит в себе 22 энергии, которые похожи на 22 старших аркана Таро, но без белой карты.
Рано или поздно человек, составляющий Матрицу, задастся вопросом: «У людей, рожденных в один день одинаковые Матрицы судьбы?» Здесь тоже есть свои нюансы.
Юлия Ушланова
Мастер чтения Матрицы судьбы, тета-хилер— У людей, которые рождены в один день, одинаковая Матрица.
Но это не значит, что люди тоже одинаковые. Да, у них будут какие-то схожие черты в характерах и по проявлениям. Благодаря тому, что мы все рождаемся в разных обстоятельствах, в разных семьях, в разное время и в разных странах, то проживаем Матрицу совершенно по-разному. Она ни в коем случае не ограничивает человека, говоря ему о том, какие у него таланты. Метод является дополнительной опорой и позволяет лучше понять себя.
Точного объяснения, почему Матрица судьбы является точным методом познания себя и открытия новых энергий, нет. За последние несколько лет, такие эзотерические «науки», как астрология и нумерология приобрели большую популярность. Если раньше к этому не относились всерьез и смеялись над «Луной в Близнецах» Василисы Володиной, то сейчас все изменилось. Почему? Поиски себя и смысла в жизни были актуальны всегда, но в наше время, когда человек перенасыщен информацией, материальными благами и практически безграничными возможностями, этот вопрос стоит особо остро. Согласитесь, что вы хоть раз задавались вопросом: «А для чего я все это делаю?»
Согласитесь, что вы хоть раз задавались вопросом: «А для чего я все это делаю?»
Эзотерики объясняют это высоким уровнем осознанности поколений Y и Z, которые кардинально отличаются от своих предшественников. Существует множество объяснений повышенного интереса к астрологии и нумерологии, вплоть до связи с несостоявшимся концом света в 2012-м. Но мнения разделяются и не все верят в эти гипотезы, так как многие из них не подкреплены научным объяснением. Тут либо верь, либо будь на стороне скептиков.
Что значит сцена после титров «Матрица 4: Воскрешение». Объяснение концовки
Что значит сцена после титров «Матрица 4: Воскрешение». Объяснение концовки
В прокат вышла новая часть франшизы «Матрица», которая возвращает к своим ролям Киану Ривза и Керри-Энн Мосс, а также закладывает основу для продолжения.
Хотя у фильма есть сцена после титров, она не тизерит сиквел, как это делают другие блокбастеры. Вместо этого, сценка высмеивает современные тренды. Ну, или пытается это сделать.
Вместо этого, сценка высмеивает современные тренды. Ну, или пытается это сделать.
Ниже следуют спойлеры!
В сцене после титров разработчики студии Deus Ex Machina во время обсуждения идей для новый игры франшизы The Matrix (как выясняется, в матрице оригинальная трилогия фильмов существует в видеоиграх) затрагивают тему видео про котиков. Один из сотрудников предлагает сделать «серию видосов названием «Котятница»».
Кино сдохло, игры сдохли, журналистика сдохла. Все скатилось к цепочке стимул-реакции и виральности.
Конечно, тут подразумевается в виду популярность кошек в социальных сетях в настоящем, когда целые аккаунты посвящены исключительно им. Упоминание «стимул-реакции» указывает на то, что люди могут долго «залипать» в такой контент, а «виральности» – что они хотят делиться этим контентом с друзьями и знакомыми.
При этом «Матрица: Воскрешение» оставляет дверь открытой для сиквела, в финале когда оказывается, что Тринити тоже Избранная. В то же время агент Смит все еще пытается захватить матрица, а машины используют людей как «батарейки».
В то же время агент Смит все еще пытается захватить матрица, а машины используют людей как «батарейки».
В концовке Аналитик говорит, что «люди жаждут стабильности», на что Нео и Тринити говорят, что уже «начали перестраивать его мир». Герои также отмечают, что антагонист предоставил им еще один шанс.
Как вам фильм? Напишите свое мнение в комментариях ниже!
Премьера в кинотеатрах состоялась 16 декабря 2021 года.
Комитет 1540 — Матрица Комитета 1540
Матрица Комитета 1540
С момента утверждения в начале 2005 года матрицы по резолюции 1540 (2004) Комитет 1540 использовал ее в качестве основного инструмента организации информации об осуществлении государствами-членами резолюции 1540 (2004) Совета Безопасности. Матрица для каждого государства — члена Организации Объединенных Наций была подготовлена группой экспертов, а затем утверждена Комитетом. Информация, содержащаяся в матрицах, получена главным образом из национальных докладов, представленных государствами Комитету 1540, и дополнена официальной информацией от правительств, включая информацию, представленную межправительственным организациям.
Комитет 1540 использует эти матрицы в качестве справочного инструмента для содействия оказанию технической помощи и дальнейшего укрепления диалога с государствами по вопросу об осуществлении ими резолюции 1540 (2004) Совета Безопасности. Матрицы являются не инструментом оценки степени выполнения государствами их обязанностей в отношении нераспространения, а средством содействия осуществлению резолюций Совета Безопасности 1540 (2004), 1673 (2006), 1810 (2008), 1977 (2011) и 2325 (2016).
Они не отражают итогов каких-либо обсуждений, проходящих за рамками Комитета в Совете Безопасности или в любом из его органов по вопросу о соблюдении тем или иным государством его обязанностей в отношении нераспространения или любых других обязанностей, и не влияют на такие обсуждения. Информация о добровольных обязательствах представляется исключительно для целей отчетности и никоим образом не составляет правового обязательства, вытекающего из резолюции 1540 (2004) или последующих соответствующих резолюций.
Матрица содержит поля данных с указанием предусмотренных в резолюции требований, а также мер, принятых государствами для выполнения этих требований. Комитет 1540 рассматривает и утверждает каждую матрицу. В каждом поле матрицы Комитет 1540 помечает один из трех возможных ответов:
- знак «X», проставленный в любом поле данных, означает лишь, что государство, представившее доклад, подтверждает, что оно приняло соответствующие меры или что Комитет 1540 проверил наличие конкретных указаний на применимые нормативно-правовые основы или решения исполнительной власти в качестве подтверждения принятия таких мер;
- знак «?», проставленный в любом поле данных, свидетельствует о том, что, хотя в национальном докладе или другом источнике данных содержатся указания на принятые законы или приводятся иные подтверждения принятия государством соответствующей меры, детали приведенной справочной информации заставляют усомниться в ее релевантности или же информация свидетельствует о том, что государство приняло требуемое решение, но текст закона пока не получен или не проверен;
- пробел в любом поле данных означает, что государство не представило информацию или что полученная информация не позволяет Комитету 1540 проставить знаки «Х» или «?» в соответствующей позиции.

Анализируя матрицу 1540, все стороны должны понимать, что знак «X» не означает, что принятая мера или меры обеспечивают полное выполнение соответствующей обязанности по резолюции 1540 (2004). Этот знак лишь означает, что Комитет 1540 и его эксперты удостоверились в принятии государством меры или мер, имеющих отношение к той или иной конкретной области.
Пересмотр шаблона матрицы
В 2012 году в свете произошедших событий Комитет принял решение пересмотреть и обновить шаблон матрицы. Пересмотренный шаблон, принятый в 2013 году, был упрощен, а поля данных, относящиеся к мерам в ядерной, химической и биологической областях, были сведены воедино. На тот момент предполагалось, что позднее шаблон матрицы потребуется вновь пересмотреть, чтобы учесть соответствующие изменения, в частности всеобъемлющий обзор, который будет проведен в 2016 году.
В ходе всеобъемлющего обзора, проведенного в 2016 году, с учетом опыта последнего обновления матриц был рассмотрен вопрос о дальнейшем пересмотре и упрощении шаблона матрицы, с тем чтобы он более точно отражал соответствующие обязанности, налагаемые резолюцией 1540 (2004). В ходе этого обзора группа экспертов предложила пересмотренный шаблон матрицы, в котором количество полей данных было сокращено с 389 до 263 и в котором основной упор делается на ключевых обязанностях по резолюции 1540 (2004). Этот новый предлагаемый шаблон обеспечивает возможность для проведения более точного и краткого обзора соответствующих мер, принятых для осуществления резолюции 1540 (2004), с должным учетом конкретных обстоятельств отдельных государств.
В ходе этого обзора группа экспертов предложила пересмотренный шаблон матрицы, в котором количество полей данных было сокращено с 389 до 263 и в котором основной упор делается на ключевых обязанностях по резолюции 1540 (2004). Этот новый предлагаемый шаблон обеспечивает возможность для проведения более точного и краткого обзора соответствующих мер, принятых для осуществления резолюции 1540 (2004), с должным учетом конкретных обстоятельств отдельных государств.
Члены Комитета представили замечания в отношении предлагаемого нового шаблона. В 2017 году после консультаций с членами Комитет рассмотрел и одобрил пересмотренный шаблон матрицы.
В будущем, с учетом постоянных изменений в сферах международного права, науки и техники, вероятнее всего, придется вновь провести пересмотр шаблона матрицы.
Форма матрицы
Матрицы утвержденные Комитетом 1540 (2004)
Матрица классификации (Analysis Services — интеллектуальный анализ данных)
- Статья
- Чтение занимает 3 мин
Оцените свои впечатления
Да Нет
Хотите оставить дополнительный отзыв?
Отзывы будут отправляться в корпорацию Майкрософт. Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.
Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.
Отправить
Спасибо!
В этой статье
Область применения: SQL Server Analysis Services Azure Analysis Services Power BI Premium
Матрица классификации сортирует все варианты из модели по категориям, определяя, соответствовало ли прогнозируемое значение действительному. Затем все варианты в каждой категории пересчитываются, и полученные количества выводятся в виде матрицы. Матрица классификации — это стандартный инструмент для оценки статистических моделей, иногда ее называют матрицей противоречий.
Диаграмма, созданная с выбранным параметром Матрица классификации , сравнивает действительное значение с прогнозируемым для каждого заданного прогнозируемого варианта. Строки в матрице представляют прогнозируемые значения для модели, а в столбцах представлены действительные значения. В анализе используются категории ложный положительный результат, истинный положительный результат, ложный отрицательный результат и истинный отрицательный результат
Строки в матрице представляют прогнозируемые значения для модели, а в столбцах представлены действительные значения. В анализе используются категории ложный положительный результат, истинный положительный результат, ложный отрицательный результат и истинный отрицательный результат
Матрица классификации — это важный инструмент для оценки результатов прогнозирования, так как позволяет легко понять и объяснить последствия неверных прогнозов. Просматривая суммы и проценты в каждой ячейке этой матрицы, можно быстро понять, как часто предсказания модели были верны.
В этом разделе поясняется, как создать матрицу классификации и интерпретировать получаемые результаты.
Основные сведение о матрице классификации
Рассмотрим модель, созданную для учебника по интеллектуальному анализу данных. Модель [TM_DecisionTree] помогает создать целевую рассылку и позволит спрогнозировать, какие клиенты с наибольшей вероятностью купят велосипед. Для проверки эффективности модели используется набор данных, для которого значения атрибута результата [Bike Buyer] уже известны. Обычно используется набор проверочных данных, сохраненный со времени создания структуры интеллектуального анализа данных, которая используется для обучения модели.
Обычно используется набор проверочных данных, сохраненный со времени создания структуры интеллектуального анализа данных, которая используется для обучения модели.
Возможны два результата: «да» (существует вероятность того, что клиент купит велосипед) и «нет» (скорее всего, клиент велосипед не купит). Таким образом, результирующая матрица классификации относительно проста.
Интерпретация результатов
В следующей таблице показана матрица классификации для модели TM_DecisionTree. Помните, что для этого прогнозируемого атрибута значение 0 означает «нет», а значение 1 — «да».
| Прогноз | 0 (фактическое значение) | 1 (фактическое значение) |
|---|---|---|
| 0 | 362 | 144 |
| 1 | 121 | 373 |
Первая ячейка результата, которая содержит значение 362, указывает количество истинных положительных результатов для значения 0. Поскольку 0 означает, что клиент не приобрел велосипед, этот статистический показатель сообщает, что модель спрогнозировала правильное значение для клиентов, не купивших велосипед, в 362 случаях.
Ячейка, которая расположена непосредственно ниже и содержит значение 121, указывает число ложных положительных результатов, то есть количество раз, когда ожидалось, что клиент приобретет велосипед, но в действительности покупка не состоялась.
Ячейка, которая содержит значение 144, указывает количество ложных положительных результатов для значения 1. Поскольку 1 означает, что клиент приобрел велосипед, этот статистический показатель сообщает, что модель в 144 случаях спрогнозировала, что клиент не приобретет велосипед, а в действительности покупка состоялась.
Наконец, ячейка результата, которая содержит значение 373, указывает количество истинных положительных результатов для целевого значения 1. Другими словами, в 373 случаях модель правильно предсказала, что некто приобретет велосипед.
Сложив значения в ячейках, расположенных на одной диагонали, можно определить общую точность модели. Одна диагональ позволяет определить общее число точных прогнозов, а вторая — общее число ошибочных прогнозов.
Использование нескольких прогнозируемых значений
Вариант [Bike Buyer] особенно просто интерпретировать, поскольку для него возможны только два значения. Если прогнозируемый атрибут имеет несколько возможных значений, матрица классификации добавляет новый столбец для каждого возможного фактического значения и затем подсчитывает число совпадений для каждого прогнозируемого значения. В следующей таблице показаны результаты для другой модели, когда возможны три значения (0, 1, 2).
| Прогноз | 0 (фактическое значение) | 1 (фактическое значение) | 2 (действительное значение) |
|---|---|---|---|
| 0 | 111 | 3 | 5 |
| 1 | 2 | 123 | 17 |
| 2 | 19 | 0 | 20 |
Хотя добавление столбцов делает отчет более сложным, дополнительные данные могут оказаться очень полезными, когда необходимо оценить совокупную стоимость неправильных прогнозов. Чтобы вычислить суммы по диагоналям или сравнить результаты для различных сочетаний строк, можно нажать кнопку Копировать на вкладке Матрица классификации и вставить отчет в Excel. Кроме того, можно использовать клиент (например, клиент интеллектуального анализа данных для Excel), который поддерживает SQL Server 2005 (9.x) и более поздние версии, для создания прямо в Excel классификационного отчета, включающего как численные, так и процентные результаты. Дополнительные сведения см. в разделе Интеллектуальный анализ в SQL Server.
Чтобы вычислить суммы по диагоналям или сравнить результаты для различных сочетаний строк, можно нажать кнопку Копировать на вкладке Матрица классификации и вставить отчет в Excel. Кроме того, можно использовать клиент (например, клиент интеллектуального анализа данных для Excel), который поддерживает SQL Server 2005 (9.x) и более поздние версии, для создания прямо в Excel классификационного отчета, включающего как численные, так и процентные результаты. Дополнительные сведения см. в разделе Интеллектуальный анализ в SQL Server.
Ограничения для матрицы классификации
Матрицу классификации можно использовать только с дискретными прогнозируемыми атрибутами.
Хотя при выборе моделей на вкладке Выбор входа конструктора Диаграмма точности интеллектуального анализа можно добавить несколько моделей, на вкладке Матрица классификации будет показана отдельная матрица для каждой модели.
См.
 также
такжеВ следующих разделах содержатся дополнительные сведения о том, как создать и использовать матрицу классификации и другие диаграммы.
См. также:
Тестирование и проверка (интеллектуальный анализ данных)
Новая «Матрица» и «Дюна» уходят в онлайн: означает ли это смерть кинотеатров?
Студия Warner Bros. объявила о том, что в 2021 году выпустит 17 новых фильмов на стриминговом сервисе HBO Max одновременно с кинотеатрами. Компания отказывается от традиционного кинотеатрального окна в 90 дней, которое позволяло эксклюзивно прокатывать новые фильмы в кино, и таким образом окончательно и бесповоротно меняет устоявшуюся модель проката, существовавшую на протяжении десятков лет. Американские СМИ называют это решение не иначе как революционным.
В ноябре Warner Bros. рассказала о том, что их новый фильм «Чудо-женщина: 1984» выпустят одновременно на сервисе компании HBO Max и в кинотеатрах 25 декабря. Релиз картины уже не раз откладывали из-за пандемии, и эта разовая операция всем показалась логичной и понятной в условиях разбушевавшегося коронавируса. Но, видимо, студии окончательно надоело ломать голову над тем, что делать с каждым отдельным крупным проектом, и бесконечно двигать сетку релизов, поэтому она решила просто выпустить все свои картины по модели «Чудо-женщины: 1984».
Но, видимо, студии окончательно надоело ломать голову над тем, что делать с каждым отдельным крупным проектом, и бесконечно двигать сетку релизов, поэтому она решила просто выпустить все свои картины по модели «Чудо-женщины: 1984».
Кадр из фильма «Чудо-женщина: 1984»
© WARNER BROS. ENTERTAINMENT INC.Это означает, что онлайн в 2021 году выйдут «Дюна», «Матрица-4», «Отряд самоубийц — 2», «Смертельная битва» (Mortal Kombat), «Годзилла против Конга», «Том и Джерри», приквел «Клана Сопрано» и другие крупные проекты, которые, несомненно, очень ждут кинотеатры, чтобы восстать из мертвых. Однако их воскрешение, судя по всему, откладывается
На эту тему
По плану Warner Bros. фильмы будут показывать на HBO Max одновременно с кинотеатрами в течение одного месяца, затем их уберут с сервиса, и картины последуют уже привычным путем — постепенно покинут кинотеатры и направятся в iTunes и на DVD, пока снова не вернутся на стриминг. Данное решение позиционируется как «эксклюзивное предложение», действующее только в течение 2021 года.
Студия пытается минимизировать свои риски, распределяя дистрибуцию по двум каналам — стримингу и кинотеатрам. Во многом этому решению способствовало желание развивать ее новый онлайн-сервис HBO Max, который запустился в Америке в мае этого года и пока результатами не впечатляет: к конце сентября число его подписчиков достигло 38 млн человек, однако активировали свои аккаунты только 8,6 млн человек. Для сравнения, у сервиса Disney+, который тоже появился на рынке недавно, уже 73,7 млн подписчиков — этого результата Disney планировали достичь только в течение пяти лет после запуска, а в итоге выполнили пятилетку за 11 месяцев. Обе компании намерены конкурировать с Netflix, который пока лидирует на рынке с 73 млн подписчиков в США и почти 200 млн по всему миру.
Здание Warner Bros в Калифорнии
© EPA-EFE/ETIENNE LAURENTWarner Bros. далеко не первый мейджор, который заигрывает с онлайн-релизами в период пандемии. Еще весной студия Universal решила выпустить «Троллей-2» онлайн, игнорируя закрытые кинотеатры, и не прогадала. Хотя последним это, конечно, совсем не понравилось. В итоге компания пошла на мировую и заключила с американскими сетями договор: кинотеатры смогут показывать ее новые фильмы в течение 17 дней перед тем, как она будет размещать их онлайн. Семнадцать дней — это совсем не привычные 90, но, учитывая суровые условия, в которых оказался кинопрокат, это гораздо лучше, чем ничего. Disney в свою очередь выпустили «Мулан» сразу на своем сервисе, хотя в странах, где его еще нет, все осталось по-прежнему — фильм можно было посмотреть в кино. Это привело в яростное отчаяние не только американские кинотеатры. Пандемия ярко продемонстрировала, что даже страны с крепкой системой поддержки национальной киноиндустрии, например Франция, не выживут без Голливуда. При этом Disney предоставляла возможность посмотреть «Мулан» не просто по подписке, но заплатив дополнительно $29, что как минимум в два раза дороже обычного билета в кино. Warner Bros. не будут брать дополнительную плату за просмотр новых фильмов.
Хотя последним это, конечно, совсем не понравилось. В итоге компания пошла на мировую и заключила с американскими сетями договор: кинотеатры смогут показывать ее новые фильмы в течение 17 дней перед тем, как она будет размещать их онлайн. Семнадцать дней — это совсем не привычные 90, но, учитывая суровые условия, в которых оказался кинопрокат, это гораздо лучше, чем ничего. Disney в свою очередь выпустили «Мулан» сразу на своем сервисе, хотя в странах, где его еще нет, все осталось по-прежнему — фильм можно было посмотреть в кино. Это привело в яростное отчаяние не только американские кинотеатры. Пандемия ярко продемонстрировала, что даже страны с крепкой системой поддержки национальной киноиндустрии, например Франция, не выживут без Голливуда. При этом Disney предоставляла возможность посмотреть «Мулан» не просто по подписке, но заплатив дополнительно $29, что как минимум в два раза дороже обычного билета в кино. Warner Bros. не будут брать дополнительную плату за просмотр новых фильмов. Стандартная подписка на HBO Max стоит $15. Для сравнения — за подписку на Netflix в США придется отдать $8,99, а за Disney+ — $7 в месяц.
Стандартная подписка на HBO Max стоит $15. Для сравнения — за подписку на Netflix в США придется отдать $8,99, а за Disney+ — $7 в месяц.
На эту тему
В отличие от других мейджоров Warner Bros. во время разгара пандемии долгое время надеялась на кинотеатры. Главным их спасителем считался многомиллионный блокбастер для интеллектуалов «Довод» британского режиссера Кристофера Нолана, который является известным защитником «кинотеатрального опыта» и призывал показывать его новый фильм только в кино. По горькой иронии «Довод» в итоге оказался не спасителем, а чуть ли не убийцей кинотеатров. Картина с общим бюджетом приблизительно в $200 млн собрала $307,4 млн: $45,1 млн в США и $262,2 — в остальном мире, что для такого крупного релиза, мягко говоря, недостаточно. Все были настолько подавлены этими результатами, что студии просто-напросто отменили все премьеры и перенесли их на 2021 год. А Warner Bros. посмотрела на ситуацию с коронавирусом в США (там по-прежнему все очень плохо), проконсультировалась с эпидемиологами, послушала их неутешительные прогнозы и решила сделать ставку на свой новый сервис.
Отказываясь от кинотеатрального окна, студия лишает изрядной доли прибыли не только кинотеатры, но и саму себя. Аналитики индустрии уверены, что компании не удастся окупить свои затраты на производство картин (а все они являются главными, высокобюджетными проектами студии) только с помощью HBO Max.
© nikkimeel/Shutterstock/FOTODOMБолее того, в данном случае страдают партнеры Warner Bros., режиссеры и продюсеры. С ними, судя по всему, никто не посоветовался, поэтому после объявления этого решения индустрию изрядно лихорадит. В то же время менеджеры студии сохраняют позитивный настрой и утверждают, что кинотеатры по-прежнему будут жить и большинство людей не откажутся от похода в кино в пользу дивана. Все-таки это уникальный опыт, который можно получить только благодаря большому экрану. Однако Warner Bros. подчеркивает, что даже если ситуация с коронавирусом выправится и будет разрешена в 2021 году, компания не откажется от своих планов.
Пока планируется, что эксперимент продлится всего один год, который пока также непредсказуем, как и 2020-ый, поэтому логика студии понятна. В конце концов, никто точно не может сказать, откроются кинотеатры или нет, и безопасность зрителей должна быть в приоритете. Также остаются под вопросом дальнейшие действия других крупных голливудских студий: последуют ли они примеру Warner Bros., предпочтут принимать решение по каждому фильму отдельно или подождут первых результатов эксперимента?
В конце концов, никто точно не может сказать, откроются кинотеатры или нет, и безопасность зрителей должна быть в приоритете. Также остаются под вопросом дальнейшие действия других крупных голливудских студий: последуют ли они примеру Warner Bros., предпочтут принимать решение по каждому фильму отдельно или подождут первых результатов эксперимента?
Стоит учитывать, что эти действия рассчитаны только на американский рынок, — компания намерена расширять в 2021 году свой стриминг на Латинскую Америку и Европу, однако политика одновременного релиза будет распространяться только на США. Так что «угрозы» российскому рынку пока нет. Скорее всего, у нас фильмы Warner Bros. будут прокатывать по модели «Чудо-женщины: 1984», то есть по старинке, в кино.
Несомненно, данное решение — невероятный прецедент в истории киноиндустрии, который показывает, что прежней она уже никогда не будет. Кинотеатры действительно теряют свою силу и авторитет, но это не означает, что их окончательно предадут забвению. Это не произошло ни в эпоху торжества телевидения, ни после появления видеокассет, а потом и DVD. Зрители по-прежнему заинтересованы в кино — все-таки смотреть новую «Матрицу» на большом экране гораздо приятнее, чем по телевизору. Другое дело, что кинотеатрам точно придется поубавить спесь и амбиции. Вряд ли они теперь смогут диктовать свои условия так же уверенно, как до пандемии. Кажется, что в долгоиграющем споре кинотеатров и Netflix победили последние.
Это не произошло ни в эпоху торжества телевидения, ни после появления видеокассет, а потом и DVD. Зрители по-прежнему заинтересованы в кино — все-таки смотреть новую «Матрицу» на большом экране гораздо приятнее, чем по телевизору. Другое дело, что кинотеатрам точно придется поубавить спесь и амбиции. Вряд ли они теперь смогут диктовать свои условия так же уверенно, как до пандемии. Кажется, что в долгоиграющем споре кинотеатров и Netflix победили последние.
Тома Ходова
Плод фантазии: ученые ищут доказательства нашего нахождения в матрице
Живем ли мы настоящей жизнью или наш мир — всего лишь хорошо проработанная симуляция, а мы лишь строчки в компьютерном коде, нули и единицы? РБК Тренды разобрались, как идеи фантастов стали предметом исследований ученых
⏰ Время на чтение: 12–14 минут
Теория матрицы, или гипотеза симуляции — философская идея о том, что наша действительность не что иное, как хорошо выполненная иллюзия. Кто-то умнее нас, более развитый и технологически превзошедший нашу цивилизацию создал весь этот мир, Вселенную — случайно, в качестве эксперимента, или, может, ради забавы.
Кто-то умнее нас, более развитый и технологически превзошедший нашу цивилизацию создал весь этот мир, Вселенную — случайно, в качестве эксперимента, или, может, ради забавы.
И если раньше вопросом «Насколько реален окружающий нас мир?» задавались в основном философы, то после выхода фильма сестер Вачовски «Матрица» и статьи Ника Бострома «Доказательство симуляции» тема обрела новых последователей с современным подходом.
Возможно, мы живем в симуляции. Возможно, нет. Сегодня наука не может дать однозначный ответ на этот вопрос. Десятки ученых пытаются найти доказательства или опровержения гипотезы симуляции, но пока все, к чему они пришли, сводится к предположениям, аналогиям и допущениям.
О чем этот текст?
Прочитав этот текст, вы узнаете о доказательстве Ника Бострома и что о нем думает Илон Маск; есть ли у Вселенной предустановленные параметры и можно ли ее просчитать; что, по мнению философа Неда Блока, невозможно сымитировать, какая существует связь между теорией моделирования и инопланетянами и кто метит на роль современного Нео. Специально для тех, кто считает, что живет в компьютерной симуляции, — бонус: пять советов от Робина Хансона.
Специально для тех, кто считает, что живет в компьютерной симуляции, — бонус: пять советов от Робина Хансона.
Реальна ли реальность
Человек познает мир с помощью чувств: зрение, осязание, слух… Но можем ли мы быть уверены в том, что чувствуем? Можем ли мы быть уверены, что сон — это действительно сон, и после пробуждения нас ожидает «настоящая» реальность, а не еще одно сновидение?
В 1981 году американский философ Хилари Патнэм провел мысленный эксперимент «мозг в колбе», который показал иллюзорность нашего восприятия. Некий ученый, предполагает Патнэм, мог бы извлечь мозг человека из тела, поместить его в колбу с питательным раствором и подключить нейроны к компьютеру. Электрические импульсы, поступающие в мозг, идентичны тем, что он получает, находясь в теле. Таким образом, компьютер мог бы симулировать виртуальную реальность, и человек, точнее его мозг, продолжал бы осознавать себя существующим, а окружающий мир, создаваемый компьютером, — реальным.
Согласно Патнэму, человек не может достоверно утверждать, что воспринимаемая им реальность является «объективной», потому что это всего лишь его вера в это утверждение.
Патнэм не был первопроходцем, поставившим реальность окружающего мира под сомнение. В 1641 году подобный мысленный эксперимент описал французский философ Рене Декарт в своей книге «Размышления о первой философии»:
«Я допускаю, что все видимое мною ложно. Я предполагаю никогда не существовавшим все, что являет мне обманчивая память. Я полностью лишен чувств. Мои тело, очертания, протяженность, движения и место — химеры. Но что же тогда остается истинным? Быть может, одно лишь то, что не существует ничего достоверного».
До Декарта об этом говорили Платон в мифе о пещере и Чжуан-Цзы в притче о бабочке.
Очень большая The Sims
С тех пор как Ник Бостром, шведский философ-трансгуманист, профессор из Оксфордского университета написал в 2003 году основополагающую статью «Доказательство симуляции», философы, физики и космологи пытаются подтвердить или опровергнуть идею симуляции вселенского масштаба всеми доступными им способами.
Доказательство Бострома того, что наша реальность есть иллюзия, воссозданная компьютерной программой, строится на предположении, что если общества не склонны уничтожить себя до приобретения технологий с высокой вычислительной мощностью, разрешенной законами физики, то вероятность нашей жизни внутри симуляции приближается к 100%.
По мнению сторонников теории, мир вокруг нас может быть ничем иным, как одной большой игрой The Sims с людьми в качестве главных персонажей. Современный уровень игровой компьютерной индустрии давно перешагнул уровень Pac-Man и позволяет создавать достаточно реалистичные симуляции. А если это можем мы при нашем уровне развития технологий, на что были бы способны цивилизации, превосходящие нас?
Все вокруг можно просчитать
Вселенная не хаотична. Она четко упорядочена: относительность, термодинамика, магнетизм, гравитация. Физические законы нашего мира остаются неизменными.
Почему значение параметров нашей Вселенной — масса электрона или космологической константы — именно такие, какие они есть? В современной науке отсутствуют математические уравнения, объясняющие, например, почему масса электрона равна именно 9,1093837015 (28) ×10⁻³¹ кг. Физик-теоретик из Массачусетского технологического института Зора Давуди не исключает, что это лишь исходные данные, предустановленные базовые параметры нашей Вселенной. Вполне возможно в какой-то момент ученые обнаружат одну из констант, имеющую произвольную величину, и найдут в ней закодированное послание на простом языке, говорящее: «Да, вы правильно догадались — это симуляция».
Вполне возможно в какой-то момент ученые обнаружат одну из констант, имеющую произвольную величину, и найдут в ней закодированное послание на простом языке, говорящее: «Да, вы правильно догадались — это симуляция».
Физик Джеймс Гейтс из Мэрилендского университета (США) изучает материю на уровне кварков — субатомных частиц, из которых состоят протоны и нейтроны в атомных ядрах. И он склонен допускать, что за физические законы нашей Вселенной отвечает компьютерная симуляция.
В своих исследованиях Гейтс обнаружил странную вещь: кварки подчиняются правилам, которые напоминают компьютерные корректирующие коды. Последние помогают обнаружить и исправить ошибки, возникающие при передаче данных. Гейт говорит: «Откуда они в уравнениях о кварках или суперсимметрии из моих исследований? Это привело меня к осознанию: я уже не могу говорить о том, что люди поддерживающие теорию симуляции — сумасшедшие».
Вычислить Вселенную до последней единицы
Рич Террил, директор Центра эволюционных вычислений и автоматизированного проектирования НАСА, научный и технический консультант фильма «Когда сталкиваются миры» и телешоу «Сквозь червоточину», предполагает, что в скором времени люди сами смогут создавать обширные симуляции.
Суть теории Террила состоит в том, что программист из будущего спроектировал нашу реальность.
Он подтверждает свои слова тем фактом, что известная нам Вселенная — «пиксельная» во времени, пространстве, объеме и энергии. Существует фундаментальная единица, которую невозможно разделить на что-либо меньшее. Это значит, что Вселенная состоит из конечного числа этих единиц, а значит вычислима. Если она вычислима, то человечество само сможет создавать собственные симуляции с сознательными и разумными существами.
Маск: вероятность, что мы в базовой реальности — один к миллиарду
Теорию о матрице активно продвигают не только ученые, но и публичные личности. В ходе конференции Code Conference-2016 Илон Маск, основатель Tesla и SpaceX, заявил, что человечество находится на пути создания компьютерных игр, неотличимых от реальности. Поэтому «вероятность того, что мы находимся в базовой реальности, составляет один к миллиарду». По словам Маска, у нас два варианта исхода: «Или мы создадим неотличимые от реальности симуляторы, или цивилизация прекратит свое существование».
Илон Маск уверен, что вскоре люди смогут создавать компьютерные игры, неотличимые от реальности.
По мнению Бострома, слова бизнесмена о жизни в матрице нужно воспринимать буквально:
«Важно понимать, что мы сами и весь мир вокруг нас, который мы видим, слышим и чувствуем, существует внутри компьютера, построенного некоторой развитой цивилизацией. Гипотеза моделирования может быть очень хорошей или очень плохой в зависимости от того, какие, по вашему мнению, мотивы создателей симуляций: что произойдет в симуляции, что произойдет после того, как симуляция закончится. Очевидно, для этого есть как оптимистичные, так и пессимистические возможности».
Очевидно, для этого есть как оптимистичные, так и пессимистические возможности».
Симулировать наш мир невозможно даже в теории. Пока
Исследование физиков-теоретиков из Оксфордского университета под руководством Зохара Рингеля и Дмитрия Коврижи, которое было опубликовано в 2017 году в журнале Science Advances, показывает, что жизнь и реальность — не продукты компьютерного моделирования. Ученые пришли к такому выводу, заметив новую связь между гравитационными аномалиями и сложностью квантовых вычислений. Создание симуляции, подобной нашему миру, видится им невозможным даже в теории.
Свою оценку вероятности провели Александр Бибо-Делиль и Жиль Брассар из Монреальского университета (Канада). Они исследовали возможность моделирования наших мыслительных, а также биологических, химических, социальных и физических процессов с помощью квантовых компьютеров и квантовых операций. И пришли к схожим выводам, что и их коллеги из Оксфорда.
Обладая достаточно высокими технологиями, представители некой другой цивилизации теоретически вполне способны смоделировать развитие виртуального мозга человека. Но для создания мира, все физические законы которого соответствовали бы законам реальности, необходимы колоссальные ресурсы. Кроме того, увеличить и так немалые затраты на расчеты виртуального мира может рекурсивное моделирование, то есть когда симуляция находится внутри симуляции, которая, в свою очередь, также находится внутри симуляций. Такая вложенность нагружала бы вычислительные мощности в геометрической прогрессии. На основании этих факторов ученые сделали вывод: вероятность того, что наш мир полностью виртуален, — ниже 50%.
Но для создания мира, все физические законы которого соответствовали бы законам реальности, необходимы колоссальные ресурсы. Кроме того, увеличить и так немалые затраты на расчеты виртуального мира может рекурсивное моделирование, то есть когда симуляция находится внутри симуляции, которая, в свою очередь, также находится внутри симуляций. Такая вложенность нагружала бы вычислительные мощности в геометрической прогрессии. На основании этих факторов ученые сделали вывод: вероятность того, что наш мир полностью виртуален, — ниже 50%.
Но есть «но». И сводится оно к вечному вопросу: «Одни ли мы во вселенной?». По словам Бибо-Делиля и Брассара, тот факт, что мы до сих пор не обнаружили свидетельства существования внеземных цивилизаций, можно рассматривать как наиболее убедительный аргумент в пользу теории моделирования.
Сознание — «козырь» человека
Американский философ Нед Блок считает, что нет причин полагать, будто наша реальность не является базовой. Главный человеческий «козырь» — сознание — сымитировать невозможно, как невозможно сделать мокрыми капли в симуляции дождя. И неважно, какими мощностями обладает «создатель». Ученый уверен:
И неважно, какими мощностями обладает «создатель». Ученый уверен:
«Квантовые компьютеры могут выполнять вычисления быстрее и эффективнее, чем традиционные. Но это все еще компьютеры. Они по-прежнему представляют собой описание того, как мы шифруем, вычисляя, что мы будем делать в данных обстоятельствах. Возможно, однажды мы смоделируем сознание, но у нас нет оснований полагать, что даже квантовые вычисления воспроизведут оригинал».
Гопник, Мандела и сбой в матрице
После выхода знаменитой трилогии «Матрица» тысячи людей начали искать подтверждения того, что мир вокруг нас лишь иллюзия. Мистические, паранормальные и другие явления, которые не способна объяснить наука, автоматически попали под категорию «сбой в матрице».
Футурология Как фильм «Матрица» показал нам наше будущееСреди них — дежавю, или психическое состояние, когда человек ощущает, что уже был в ситуации или в месте, но не может связать это «воспоминание» с конкретным моментом из прошлого.
«Дежавю означает сбой в матрице, когда меняют программу», — так объясняет суть явления Тринити неопытному Нео в сцене с кошкой.
В фильме «Сбой в матрице» режиссер Родни Ашер приводит другой пример — эффект Манделы. Первые упоминания о нем появились в 2009 году, когда в интернете начали обсуждать смерть президента ЮАР Нельсона Манделы. Оказалось, многие были убеждены, что политик скончался в тюрьме еще в 1980 годах (реально он умер в 2013-м). Кроме того, люди «вспоминали» выпуски новостей с сообщениями о смерти Манделы.
Психологи объясняют эффект тем, что иногда человек, вспоминая о событии, трансформирует его в своем сознании, создавая таким образом ложные воспоминания. Однако в сети популярно мнение, что эффект Манделы лишь подтверждает то, что кто-то пытается переписать нашу реальность, своеобразный баг в системе.
Журналист Адам Гопник считает, что в пользу идеи матрицы свидетельствует накладка, произошедшая на 89-й церемонии вручения наград премии «Оскар». Тогда фильм «Ла-Ла Ленд» ошибочно получил статуэтку за лучшую картину вместо «Лунного света».
Тогда фильм «Ла-Ла Ленд» ошибочно получил статуэтку за лучшую картину вместо «Лунного света».
Новая религия
Пока одни ищут доказательства, что все вокруг лишь иллюзия, а другие разрабатывают технологии, чтобы самим создать гиперреалистичную симуляцию, не менее талантливые люди уже готовят план спасения человечества. Среди них хакер, взломавший iPhone и консоль Sony, предприниматель, основавший стартап в области искусственного интеллекта Comma.ai, Джордж Хотц.
Хотц считает, что доказательств того, что мы не находимся в симуляции нет: «Можно легко представить себе сущности гораздо умнее нас, которые способны построить клетку, о существовании которой вы даже не знаете».
О своих планах основать религию, посвященную эмулированной вселенной, он рассказал на фестивале SXSW в 2019 году. Как именно Хотц планирует вырвать человечество из симуляции, пока неизвестно. Его последователям стоит надеяться лишь на богатый хакерский опыт компьютерного эксперта.
Возможно, наш мир виртуален.
 Но имеет ли это значение?
Но имеет ли это значение?Американский астрофизик, писатель и популяризатор науки Нил Деграсс Тайсон в шоу Ларри Кинга сказал:
«Трудно спорить с утверждением, что все мы — просто плод фантазии какого-нибудь парня, который сидит в подвале родительского дома и ради собственной забавы создает мир. И каждый раз, когда происходит что-то странное, может быть, ему просто становится скучно, он вносит какое-то изменение — так, для интереса. Если тебя кто-то программирует, то ты ничего сделать не сможешь. Знаешь ли ты об этом или нет — разницы нет никакой».
Как жить в симуляции
Одновременно с трудом Бострома в журнале Journal of Evolution and Technology вышла статья «Как жить в симуляции». В ней научный сотрудник Института будущего человечества Оксфордского университета Робин Хансон дает несколько советов людям, которые считают, что живут в симуляции:
- жить сегодняшним днем;
- стремиться к благополучию, в том числе и материальному;
- иметь активную жизненную позицию;
- быть интересным окружающим;
- прилагать все усилия, чтобы люди вокруг были счастливы.

Макс Тегмарк, космолог и астрофизик из Массачусетского университета, считает, что если вы не уверены, находитесь ли вы в симуляции или нет, то «разбейте свою скорлупу и проживите по настоящему интересную жизнь, поступайте неожиданно, чтобы программистам нашей вселенной не стало скучно и они вас не отключили».
Понимание матрицы Эйзенхауэра — Dropbox Business
Что такое матрица Эйзенхауэра?
Никто не хочет быть непродуктивным, особенно на работе. Но на протяжении дня появляются срочные запросы, и, по мере того как ваш список задач растет, становится все сложнее поддерживать это стремление к продуктивности. Если вы не успеваете выполнять ключевые задачи в срок, или вам сложно придерживаться графика в долгосрочных проектах, эффективная расстановка приоритетов в выполнении задач может вывести вас из отстающих в лидеры. И здесь на сцену выходит матрица Эйзенхауэра.
Понимание матрицы Эйзенхауэра
Матрица Эйзенхауэра, также известная под названием «коробка Эйзенхауэра» или «матрица срочных/важных задач» — это простая схема определения приоритетности задач и регулирования рабочей нагрузки. Она названа в честь Дуайта Д. Эйзенхауэра, пятизвездочного генерала и 34-го президента США. Эйзенхауэр известен благодаря своей неимоверной продуктивности, поэтому его подход к постановке целей и управлению временем всесторонне изучался многими людьми, одним из которых был Стивен Кови. В своей книге «7 навыков высокоэффективных людей» Кови создал на основе идей Эйзенхауэра простой инструмент расстановки приоритетов в выполнении задач: матрицу Эйзенхауэра.
Она названа в честь Дуайта Д. Эйзенхауэра, пятизвездочного генерала и 34-го президента США. Эйзенхауэр известен благодаря своей неимоверной продуктивности, поэтому его подход к постановке целей и управлению временем всесторонне изучался многими людьми, одним из которых был Стивен Кови. В своей книге «7 навыков высокоэффективных людей» Кови создал на основе идей Эйзенхауэра простой инструмент расстановки приоритетов в выполнении задач: матрицу Эйзенхауэра.
Что же представляет из себя матрица Эйзенхауэра? По сути, это стратегия, которая позволяет вам применить на практике следующую цитату, приписываемую Эйзенхауэру: «У меня есть два типа проблем: срочные и важные. Срочные не важны, а важные никогда не бывают срочными». Вам нужно просто оценить свои задачи по критериям срочности и важности.
Как работает коробка Эйзенхауэра?
Компании и частные лица могут использовать матрицу Эйзенхауэра для планирования, делегирования, определения приоритетности и включения задач в график работы на день или на неделю. Распределив задачи в один из четырех квадрантов ниже, вы сможете определить их срочность и решить, как с ними следует поступить:
Распределив задачи в один из четырех квадрантов ниже, вы сможете определить их срочность и решить, как с ними следует поступить:
- Первый Квадрант. Срочное и важное (задачи, которые необходимо выполнить немедленно). Это очень важные задачи, которые нужно сделать в первую очередь и как можно скорее. Как правило, это запросы, полученные в последний момент по причине непредвиденных обстоятельств. Обычно такие задачи нужно выполнять немедленно или в тот же день. Сюда можно отнести работу в проекте вместо заболевшего коллеги или реагирование на непредвиденную ситуацию, например сбои в цепи поставок.
- Второй квадрант. Важное, но не срочное (задачи, которые можно запланировать на более поздний срок). Это важные долгосрочные цели или задачи, не имеющие жесткого срока выполнения, поэтому их можно запланировать на более поздний срок. Сюда можно отнести получение профессиональной квалификации или планирование долгосрочных бизнес-целей, например сокращение бюджета.
- Третий квадрант.
 Срочное, но не важное (задачи, которые можно кому-то делегировать). Эти задачи нужно выполнить немедленно, но они могут быть не настолько важными, чтобы привлечь ваше внимание, а значит, их можно делегировать другим участникам рабочей группы. Сюда можно отнести повседневную работу, длительные встречи или телефонные звонки без четкой цели.
Срочное, но не важное (задачи, которые можно кому-то делегировать). Эти задачи нужно выполнить немедленно, но они могут быть не настолько важными, чтобы привлечь ваше внимание, а значит, их можно делегировать другим участникам рабочей группы. Сюда можно отнести повседневную работу, длительные встречи или телефонные звонки без четкой цели. - Четвертый квадрант. Несрочное и неважное (задачи, которые можно убрать из плана). Эти задачи только отвлекают вас, поэтому их нужно избегать по возможности. Во многих случаях можно просто игнорировать или отменить такие задачи. Сюда можно отнести общественные мероприятия или излишне длительные перерывы на чай или кофе.
Проще говоря, применение коробки Эйзенхауэра может помочь вам визуализировать ваши задачи с точки зрения важности и срочности. Когда вы начнете рассматривать свой рабочий процесс с такой позиции, вам гораздо проще будет расставить приоритеты для самых важных задач и выполнить их как можно скорее.
Как различить срочность и важность?
Нет универсальной формулы для определения различия между срочностью и важностью при создании матрицы приоритетов, но это очень важно. Чаще всего различие между этими двумя категориями в реальности определить намного труднее, чем при составлении абстрактной коробки Эйзенхауэра. Если вкратце, срочные задачи неизбежны и требуют незамедлительного уделения им внимания, а важные задачи в большей степени требуют планирования и способствуют достижению долгосрочных целей. Например, отвечать на телефонные звонки крупного клиента — это срочная задача, а ознакомиться с последними исследованиями в своей сфере — важная.
Чаще всего различие между этими двумя категориями в реальности определить намного труднее, чем при составлении абстрактной коробки Эйзенхауэра. Если вкратце, срочные задачи неизбежны и требуют незамедлительного уделения им внимания, а важные задачи в большей степени требуют планирования и способствуют достижению долгосрочных целей. Например, отвечать на телефонные звонки крупного клиента — это срочная задача, а ознакомиться с последними исследованиями в своей сфере — важная.
Каковы преимущества матрицы Эйзенхауэра?
Одним из основных преимуществ матрицы Эйзенхауэра является простота ее реализации. Не нужно покупать дорогостоящий пакет программного обеспечения и уделять много времени составлению матрицы. В общем, матрица приоритетов позволяет вам оптимизировать управление временем, установив четкие и однозначные приоритеты. Этот инструмент очень полезен для сотрудников, занимающих руководящие должности, или собственников бизнеса, а также фрилансеров, которым нужно совмещать задачи из нескольких различных проектов или работу с несколькими клиентами одновременно.
Каковы недостатки матрицы Эйзенхауэра?
С матрицей приоритетов связаны некоторые недостатки. Особо следует отметить, что зачастую бывает сложно точно определить важность задачи. Это означает, что в конечном итоге вы можете делегировать задачу не тому человеку, что приведет к снижению качества. Более того, важно помнить, что не всегда есть возможность действовать немедленно, когда вы имеете дело с событиями, требующими мгновенной реакции. Это может быть невозможным по причине недостатка знаний, времени, из-за существующих правил и бюрократических процедур или большого количества срочных/важных задач, что снижает эффективность матрицы приоритетов при принятии решений и управлении временем.
Как использовать коробку Эйзенхауэра для управления задачами и рабочей нагрузкой
Матрица срочных/важных задач может стать отличной отправной точкой для управления рабочими процессами и проектами. После того как вы разместите свои задачи по соответствующим квадрантам, можно приступать к настройке процессов управления временем, что поможет вам своевременно реагировать на важные события. Например, вы можете использовать Dropbox для более эффективного управления своим списком заданий. Можно использовать эти инструменты управления задачами для делегирования срочных, но не важных задач другим участникам вашей рабочей группы, а также установить сроки сдачи и напоминания для срочных, но не важных задач, которые можно запланировать на более поздний срок.
Например, вы можете использовать Dropbox для более эффективного управления своим списком заданий. Можно использовать эти инструменты управления задачами для делегирования срочных, но не важных задач другим участникам вашей рабочей группы, а также установить сроки сдачи и напоминания для срочных, но не важных задач, которые можно запланировать на более поздний срок.
Также стоит подумать о внедрении средств автоматизации на рабочем месте. Автоматизация, где это возможно, является отличным способом работы с задачами, которые необходимо выполнить, но не требующими длительного планирования или анализа до начала их выполнения. С помощью средств автоматизации или интеграции в Dropbox вы можете делегировать задачи из квадранта Q3 (срочное, но не важное) таким образом, чтобы это было эффективно с точки зрения времени для вашего бизнеса. Вы можете назначать задачи участникам рабочей группы в Dropbox Paper с указанием сроков их выполнения или переносить их непосредственно в карточки Trello для участников вашей рабочей группы из файлов Dropbox. Инструменты автоматического создания контента помогут вам избежать трудоемких, не защищенных от ошибок задач, которые могут создавать помехи в работе, обеспечив таким образом более продуктивную работу вашей рабочей группы в будущем.
Инструменты автоматического создания контента помогут вам избежать трудоемких, не защищенных от ошибок задач, которые могут создавать помехи в работе, обеспечив таким образом более продуктивную работу вашей рабочей группы в будущем.
Более того, можно объединить коробку Эйзенхауэра с другими методиками управления временем для достижения лучших результатов. Например, можно использовать метод «Съешь лягушку». В основе этой техники лежит высказывание Марка Твена: «Если с утра первым делом съесть лягушку, остаток дня будет чудесным». В контексте бизнеса это означает, что сначала нужно выполнить самую большую или сложную задачу, а затем перейти к более мелким задачам, приоритетность которых вы можете определить на основании других факторов, например, сроков их выполнения. Также существует метод ABCDE, где вы присваиваете своим задачам буквенное значение в зависимости от их важности, и затем выполняете их в этом порядке.
Заключительные соображения
Коробка Эйзенхауэра — чрезвычайно эффективный инструмент управления временем и задачами. Узнав, как эффективно определять приоритетность задач, вы сможете повысить эффективность своей работы, избежать действий, занимающих много времени, и достичь долгосрочных целей в бизнесе.
Узнав, как эффективно определять приоритетность задач, вы сможете повысить эффективность своей работы, избежать действий, занимающих много времени, и достичь долгосрочных целей в бизнесе.
Норма матрицы — обзор
5.36 Норма бигаммы
Свойство масштабирования, ‖ r ⊗ V ‖ = | р | ⊗ ‖ V ‖, выраженное через матричную спектральную норму, оказывается полезным в геометрии бигировекторных пространств. Таким образом, он демонстрирует, что матричная норма, соответствующая геометрии бигировекторных пространств, является матричной спектральной нормой. В следующей теореме представлены результаты, которые также указывают на то, что матричная норма, удовлетворяющая геометрии бигировекторных пространств, является матричной спектральной нормой.
Теорема 5.106 Бигамма Норма
Для любых m, n∈ℕ и c > 0 пусть V∈ℝcn×m. Тогда
(5,544)ΓVL=ΓVLΓVR=ΓVR.
Доказательство
С помощью (5.115), с. 201 и (5.411), с. 265 имеем
(5.545)ΓVL=In−c−2VVt−1=OnIk−c−2Σk2−10k,n−k0n−k,kIn−kOnt,
k = rank( V ), где Σ k — диагональ, как в (5.402),
(5.546)Σk=diagσ1σ2…σk.
Диагональные элементы Σ k положительны и называются сингулярными числами V . Они удовлетворяют условию
(5,547)0<σi i = 1, 2,…, k , так как V∈ℝcn×m. (5.545) ℝk×k диагональ, (5,549)Sk2=Ik−c−2Σk2−1≕diags12s22…sk2. Диагональные элементы s i , i = 1, 2,…, k , of S k являются k сингулярными значениями Каждое из оставшихся n − k сингулярных значений Γ V L равно 1, как видно из (5.548). Следовательно, диагональные элементы S k связаны с диагональными элементами Σ k уравнениями (5. 0 < σ i < c . Пусть 1 ≤ j ≤ k — целое число, для которого (5,551)σj=maxσii=1,2,…,k. Тогда из (5.550) видно, что (5.552)sj=maxsii=1,2,…,k. Из (5.551) следует, что норма V∈ℝcn×m равна (5.553)V=σj. Аналогично, из (5.552) следует, что норма ΓVL∈ℝn×n равна (5.554)ΓVL=sj. Отсюда по (5.550), (5.553) и (5.554), а также по определению Γ V L в (5.115), с. 201 имеем следующую цепочку уравнений: (5,555)ΓVL=maxsii=1,2,…,k=sj=11−c−2σj2=11−c−2V2=ΓVL. Цепочка уравнений (5.555) завершает доказательство первого тождества в (5.544). Доказательство второго тождества в (5.544) аналогично. Определение 2.1 Набираем матрицы так:
\[A= \begin{pmatrix}
1 & 2 & 3 \\ 0 & -1 & \pi
\end{pmatrix}, B=\begin{pmatrix}
1\2\3
\end{pmatrix}, C=\begin{pmatrix}
0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1
\конец{pmatrix}\]
это матрица 2✕3, вектор-столбец 3✕1 и
3✕3 квадратная матрица соответственно. Определение 2.2 Элемент матрицы i , j представляет собой число в строке i и столбце j . Например, запись 1, 2 матрицы A выше равна 2, запись 2, 1 равна 0,
а запись 2, 3 — это \(\pi\). Очень часто мы пишем \(A=(x_{ij})\), чтобы обозначить, что A является
матрица, чьи i , j записи равны \(x_{ij}\). Если две матрицы A и B имеют одинаковый размер (т. м ✕ н для тех же м и н ) потом их складываем и вычитаем
добавляя и вычитая каждую запись отдельно: \[\begin{align*} \begin{pmatrix}
1 и 2 \\ 3 и 4
\end{pmatrix} + \begin{pmatrix}
0 и 1 \\-1 и -1
\end{pmatrix} &= \begin{pmatrix}
1 и 3 \\ 2 и 3
\end{pматрица} \\
\begin{pматрица}
1&0
\end{pmatrix} — \begin{pmatrix}
9 и 9
\end{pmatrix} &= \begin{pmatrix}
-8 и -9
\end{pматрица}
\конец{выравнивание*}\] Мы также умножаем матрицы на числа по одной записи за раз
(«по входу»):
\[2 \begin{pmatrix}
1&2&3 \\0 & 1 & 0
\end{pmatrix}= \begin{pmatrix}
2&4&6\\0&2&0
\end{pmatrix}\] Это называется скалярным умножением на .Он удовлетворяет некоторым
простые тождества: для любых матриц A и B одинакового размера и
любой номер л и м ,
\[\начать{выравнивать*}
(l + m) A &= lA + m A \\
л(А+В) &= л А + л В \\
l(m A) &= (lm)A. . Определение 2.3. равны нулю. Определение 2.Т = А\). Большинство старшеклассников в США узнают о матрицах и умножении матриц, но их часто не учат почему умножение матриц работает именно так. Добавлять матрицы легко: вы просто добавляете соответствующие записи. Однако умножение матриц так не работает, и для того, кто не понимает теории матриц, этот способ умножения матриц может показаться чрезвычайно надуманным и странным.Чтобы по-настоящему понять матрицы, мы рассматриваем их как представление части более широкой картины. Матрицы представляют функций между пространствами, называемыми векторными пространствами, и не просто любые функции, а линейных функций. Именно поэтому линейная алгебра фокусируется на матрицах. Два фундаментальных факта о матрицах состоят в том, что каждая матрица представляет некоторую линейную функцию , а каждая линейная функция представлена матрицей . Скорее всего, если вы изучали алгебру в средней школе, вы видели что-то вроде следующего: Ваш школьный учитель алгебры, вероятно, сказал вам, что это «матрица». Затем вы узнали, как работать с матрицами. Например, вы можете добавить две матрицы, и операция будет достаточно интуитивной: Вы также можете вычитать матрицы, что работает аналогично.Вы можете умножить матрицу на число: Потом, когда тебя учили перемножать матрицы, все казалось неправильным: То есть, чтобы найти запись в -й строке, -м столбце произведения, вы смотрите на -ю строку первой матрицы, -й столбец второй матрицы, перемножаете их соответствующие числа и затем вы суммируете результаты, чтобы получить запись в этой позиции. Почему умножение матриц работает не так, как сложение и вычитание? И если умножение работает таким образом, как, черт возьми, работает деление? Цель этого поста — ответить на эти вопросы. Чтобы понять, почему умножение матриц работает таким образом, необходимо понять, что такое матрицы на самом деле. Но прежде чем мы перейдем к этому, давайте кратко рассмотрим, почему мы вообще заботимся о матрицах.Самое основное применение матриц — решение систем линейных уравнений. Линейное уравнение — это уравнение, в котором все переменные появляются сами по себе без степеней; они не умножаются ни друг на друга, ни на самих себя, и никаких забавных функций тоже. Примером системы линейных уравнений является Решение этой системы . Такие уравнения кажутся простыми, но они легко возникают в жизни. Например, предположим, что у меня есть два друга Алиса и Боб, которые пошли в магазин за конфетами.Алиса купила 2 плитки шоколада и 1 пакет кеглей и потратила 3 доллара, тогда как Боб купил 4 плитки шоколада и 3 пакета кеглей и потратил 7 долларов. Если мы хотим выяснить, сколько стоят шоколадные батончики и кегли, пусть это будет цена плитки шоколада и цена пакета кеглей, а переменные будут удовлетворять приведенной выше системе линейных уравнений. Следовательно, мы можем сделать вывод, что плитка шоколада стоит 1 доллар, как и пакет кеглей. Эту систему было особенно легко решить, потому что можно угадать и проверить решение, но в целом с переменными и уравнениями вместо 2 это намного сложнее.Вот где на помощь приходят матрицы! Обратите внимание, что путем матричного умножения приведенная выше система линейных уравнений может быть переписана как Если бы мы только могли найти матрицу , обратную матрице , так что если бы мы умножили обе части уравнения (слева) на мы получили бы Применение матриц выходит далеко за рамки этой простой задачи, но пока мы будем использовать это как мотивацию. Самый важный факт о векторных пространствах заключается в том, что они всегда имеют основу. Базис векторного пространства — это набор векторов, такой, что любой вектор в пространстве может быть записан как линейная комбинация этих векторов базиса.Если ваши базисные векторы, то это линейная комбинация, если это действительные числа. Конкретный пример следующий: основой для плоскости x-y являются векторы . Любой вектор имеет вид, который можно записать как , так что у нас действительно есть основа! Это не единственное возможное основание. На самом деле векторы в нашем базисе даже не обязательно должны быть перпендикулярны! Например, векторы образуют основу, так как мы можем написать . Теперь линейное преобразование это просто функция между двумя векторными пространствами, которая оказывается линейной .Быть линейным — чрезвычайно приятное свойство. Например, функция, заданная на вещественной прямой, не является линейной, поскольку . Теперь мы соединяем воедино все идеи, о которых мы говорили до сих пор: матрицы, базис и линейные преобразования. Связь заключается в том, что матрицы являются представлениями линейных преобразований , и вы можете понять, как записать матрицу, увидев, как она действует на основе.Чтобы понять первое утверждение, нам нужно понять, почему верно второе. Идея состоит в том, что любой вектор представляет собой линейную комбинацию базисных векторов, поэтому вам нужно только знать, как линейное преобразование влияет на каждый базисный вектор. Это потому, что, поскольку функция линейна, если у нас есть произвольный вектор, который можно записать в виде линейной комбинации , то Обратите внимание, что значение полностью определяется значениями , поэтому это вся информация, необходимая для полного определения линейного преобразования. Тогда соответствующая матрица будет Причина, по которой это работает, заключается в том, что умножение матриц было разработано таким образом, что если вы умножаете матрицу на вектор со всеми нулями, кроме 1 в -м элементе, то результатом будет только -й столбец матрицы. Теперь, наконец, ответ на поставленный в начале вопрос. Почему умножение матриц работает именно так? Давайте посмотрим на две матрицы, которые у нас были в начале: и . Мы знаем, что они соответствуют линейным функциям на плоскости, обозначим их и соответственно. Умножение матриц соответствует составлению их функций. Поэтому делать то же самое, что и для любого вектора. Чтобы определить, как должна выглядеть матрица, мы можем посмотреть, как она влияет на базисные векторы. , поэтому первый столбец должен быть , а , поэтому второй столбец должен быть . Действительно, это согласуется с ответом, который мы получили в начале путем умножения матриц! Хотя это вовсе не строгое доказательство, поскольку это всего лишь пример, оно улавливает идею о том, почему умножение матриц такое, какое оно есть. Теперь, когда мы понимаем, как и почему работает умножение матриц, как работает деление матриц? Вы, вероятно, знакомы с функциональными инверсиями. обратное функции — это функция, такая, что для всех . Поскольку умножение матриц соответствует композиции функций, имеет смысл только то, что мультипликативная обратная матрица является композиционной обратной соответствующей функции. Вот почему не все матрицы имеют мультипликативные обратные. Некоторые функции не имеют композиционных инверсий! Например, линейная функция, отображаемая на определенную, не имеет обратной, поскольку многие векторы отображаются на одно и то же значение (что будет? ? ?). Нравится Загрузка… 550)si=11−c−2σi2>1,
550)si=11−c−2σi2>1, 2.1 Определения и матричная алгебра
Определения и матричная алгебра


 \конец{выравнивание*}\]
\конец{выравнивание*}\] Линейная алгебра: что такое матрицы на самом деле
 Поэтому на самом деле между матрицами и линейными функциями существует взаимно однозначное соответствие.Мы покажем, что умножение матриц соответствует составлению функций, которые они представляют. Попутно мы рассмотрим, для чего нужны матрицы и почему вообще возникла линейная алгебра.
Поэтому на самом деле между матрицами и линейными функциями существует взаимно однозначное соответствие.Мы покажем, что умножение матриц соответствует составлению функций, которые они представляют. Попутно мы рассмотрим, для чего нужны матрицы и почему вообще возникла линейная алгебра. В приведенном выше примере запись 1-й строки и 2-го столбца равна a, потому что 1-я строка первой матрицы равна , 2-й столбец второй матрицы равен , и у нас есть .Более того, это означает, что умножение матриц даже не является коммутативным! Если мы поменяем порядок умножения выше, мы получим
В приведенном выше примере запись 1-й строки и 2-го столбца равна a, потому что 1-я строка первой матрицы равна , 2-й столбец второй матрицы равен , и у нас есть .Более того, это означает, что умножение матриц даже не является коммутативным! Если мы поменяем порядок умножения выше, мы получим
 Вернемся к пониманию того, что такое матрицы. Чтобы понять матрицы, мы должны знать, что такое векторы.Векторное пространство – это множество с определенной структурой, а вектор – это просто элемент векторного пространства. На данный момент, для технической простоты, мы будем использовать векторные пространства над действительными числами, также известные как вещественных векторных пространств . Реальное векторное пространство — это в основном то, о чем вы думаете, когда думаете о пространстве. Числовая прямая представляет собой одномерное вещественное векторное пространство, плоскость x-y представляет собой двумерное вещественное векторное пространство, трехмерное пространство представляет собой трехмерное вещественное векторное пространство и так далее.Если вы узнали о векторах в школе, то вы, вероятно, привыкли думать о них как о стрелках, которые можно сложить, умножить на действительное число и так далее, но умножение векторов работает по-другому.
Вернемся к пониманию того, что такое матрицы. Чтобы понять матрицы, мы должны знать, что такое векторы.Векторное пространство – это множество с определенной структурой, а вектор – это просто элемент векторного пространства. На данный момент, для технической простоты, мы будем использовать векторные пространства над действительными числами, также известные как вещественных векторных пространств . Реальное векторное пространство — это в основном то, о чем вы думаете, когда думаете о пространстве. Числовая прямая представляет собой одномерное вещественное векторное пространство, плоскость x-y представляет собой двумерное вещественное векторное пространство, трехмерное пространство представляет собой трехмерное вещественное векторное пространство и так далее.Если вы узнали о векторах в школе, то вы, вероятно, привыкли думать о них как о стрелках, которые можно сложить, умножить на действительное число и так далее, но умножение векторов работает по-другому. Это звучит знакомо? Должно. Именно так работают матрицы, и это не случайно.
Это звучит знакомо? Должно. Именно так работают матрицы, и это не случайно. Функция является линейной, если выполняются следующие два свойства:
Функция является линейной, если выполняются следующие два свойства: При чем здесь матрица? Что ж, как только мы выберем основу как для домена, так и для цели линейного преобразования, столбцы матрицы будут представлять изображения базисных векторов под функцией. Например, предположим, что у нас есть линейное преобразование, которое отображается на , что означает, что оно принимает трехмерные векторы и выдает двумерные векторы. Прямо сейчас это просто какая-то абстрактная функция, которую мы не можем записать на бумаге. Давайте выберем основу как для нашей области (3-пространство), так и для нашей цели (2-пространство или плоскость).Хороший выбор будет для первого и для второго. Все, что нам нужно знать, это то, как влияет на , а основой для цели является конкретное запись значений. Матрица для нашей функции будет матрицей 2 на 3, где 3 столбца проиндексированы , а 2 строки проиндексированы . Все, что нам нужно записать, это значения. Для конкретности скажем
При чем здесь матрица? Что ж, как только мы выберем основу как для домена, так и для цели линейного преобразования, столбцы матрицы будут представлять изображения базисных векторов под функцией. Например, предположим, что у нас есть линейное преобразование, которое отображается на , что означает, что оно принимает трехмерные векторы и выдает двумерные векторы. Прямо сейчас это просто какая-то абстрактная функция, которую мы не можем записать на бумаге. Давайте выберем основу как для нашей области (3-пространство), так и для нашей цели (2-пространство или плоскость).Хороший выбор будет для первого и для второго. Все, что нам нужно знать, это то, как влияет на , а основой для цели является конкретное запись значений. Матрица для нашей функции будет матрицей 2 на 3, где 3 столбца проиндексированы , а 2 строки проиндексированы . Все, что нам нужно записать, это значения. Для конкретности скажем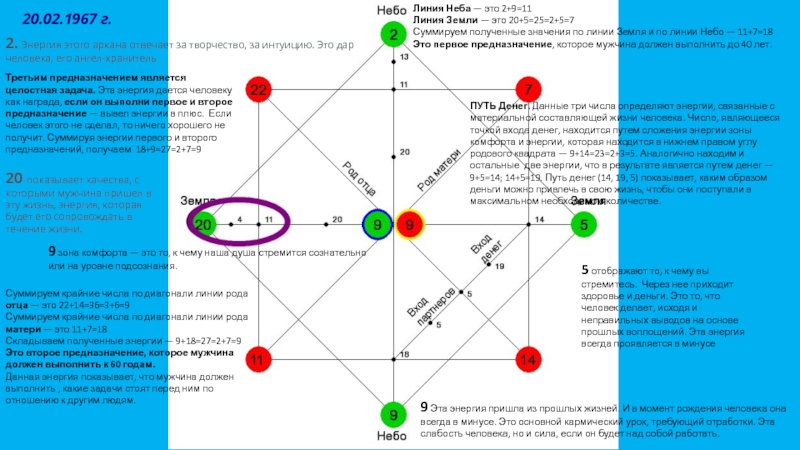 Вы можете проверить это сами. Итак, мы знаем, что матрица работает правильно, когда применяется к базисным векторам (умножается на них). Но также матрицы удовлетворяют тем же свойствам, что и линейные преобразования, а именно и , где — векторы и — действительное число. Поэтому работает для всех векторов, так что это правильное представление . Обратите внимание, что если бы мы выбрали разные векторы для базисных векторов, матрица выглядела бы иначе. Следовательно, матрицы не являются естественными в том смысле, что они зависят от того, какие основания мы выбираем.
Вы можете проверить это сами. Итак, мы знаем, что матрица работает правильно, когда применяется к базисным векторам (умножается на них). Но также матрицы удовлетворяют тем же свойствам, что и линейные преобразования, а именно и , где — векторы и — действительное число. Поэтому работает для всех векторов, так что это правильное представление . Обратите внимание, что если бы мы выбрали разные векторы для базисных векторов, матрица выглядела бы иначе. Следовательно, матрицы не являются естественными в том смысле, что они зависят от того, какие основания мы выбираем. У нас есть
У нас есть Это соответствует тому факту, что матрица 1 × 2 не имеет мультипликативной обратной. Таким образом, деление на матрицу — это просто умножение на , если оно существует. Существуют алгоритмы вычисления обратных матриц, но мы оставим их для другого поста.
Это соответствует тому факту, что матрица 1 × 2 не имеет мультипликативной обратной. Таким образом, деление на матрицу — это просто умножение на , если оно существует. Существуют алгоритмы вычисления обратных матриц, но мы оставим их для другого поста. Нравится:
Объяснение урока: Сила матрицы
В этом объяснении мы узнаем, как использовать умножение матриц для определить квадрат и куб квадратной матрицы.
Существует множество матричных операций, очень похожих на хорошо известную операции из обычной алгебры, такие как сложение, вычитание и масштабирование. Кроме того, хотя умножение матриц принципиально более сложный, чем его обычный аналог, он все же в некоторой степени отражает некоторые алгебраические свойства оригинала.
Одна операция, которая занимает центральное место как в традиционной алгебре, так и в алгебре с использованием
матрицы — это возведение в степень, которое обычно называют взятием степень числа или матрицы. В
обычная алгебра, можно взять почти любое число 𝑥
и возводим в степень 𝑦, что дает 𝑥. За исключением возведения нуля в отрицательную степень, это не имеет значения.
является ли 𝑥 или 𝑦 нулем, отличным от нуля, целым числом,
нецелое, рациональное, иррациональное или сложное, так как вывод всегда может быть
вычислено. То же самое неверно при работе с матрицами, где матрица
𝐴 не всегда можно возводить в степень. Для того, чтобы лучше всего обрисовать
эти потенциальные осложнения, давайте сначала определим простейшую форму
возведение матрицы в степень: возведение матрицы в квадрат.
В
обычная алгебра, можно взять почти любое число 𝑥
и возводим в степень 𝑦, что дает 𝑥. За исключением возведения нуля в отрицательную степень, это не имеет значения.
является ли 𝑥 или 𝑦 нулем, отличным от нуля, целым числом,
нецелое, рациональное, иррациональное или сложное, так как вывод всегда может быть
вычислено. То же самое неверно при работе с матрицами, где матрица
𝐴 не всегда можно возводить в степень. Для того, чтобы лучше всего обрисовать
эти потенциальные осложнения, давайте сначала определим простейшую форму
возведение матрицы в степень: возведение матрицы в квадрат.
Определение: Квадрат матрицы
Если 𝐴 — квадратная матрица, 𝐴 определяется формулой 𝐴=𝐴×𝐴.
Другими словами, так же, как для возведения чисел в степень (т. е. 𝑎=𝑎×𝑎), квадрат получается умножением Матрица сама по себе.
Как можно заметить, основное требование для возведения матрицы в степень:
определено, что 𝐴 должен быть квадратным. Это потому, что на двоих
общие матрицы 𝐴 и 𝐵, матрица
умножение 𝐴𝐵 корректно определено только при одинаковом количестве столбцов
в 𝐴, так как в 𝐵 есть строки.Если
𝐴 имеет порядок 𝑚×𝑛 и
𝐵 имеет порядок 𝑛×𝑝, то
𝐴𝐵 корректно определен и имеет порядок 𝑚×𝑛. Если бы мы только рассмотрели матрицу 𝐴 и попытались завершить
умножение матриц 𝐴=𝐴×𝐴, то мы были бы
пытаясь умножить матрицу порядка 𝑚×𝑛 на
другая матрица порядка 𝑚×𝑛. Это может быть только хорошо
определяется, если 𝑚=𝑛, а это означает, что 𝐴 должно быть
матрица порядка 𝑛×𝑛 (другими словами, квадратная). То
поэтому порядок 𝐴 идентичен исходной матрице
𝐴.
Это потому, что на двоих
общие матрицы 𝐴 и 𝐵, матрица
умножение 𝐴𝐵 корректно определено только при одинаковом количестве столбцов
в 𝐴, так как в 𝐵 есть строки.Если
𝐴 имеет порядок 𝑚×𝑛 и
𝐵 имеет порядок 𝑛×𝑝, то
𝐴𝐵 корректно определен и имеет порядок 𝑚×𝑛. Если бы мы только рассмотрели матрицу 𝐴 и попытались завершить
умножение матриц 𝐴=𝐴×𝐴, то мы были бы
пытаясь умножить матрицу порядка 𝑚×𝑛 на
другая матрица порядка 𝑚×𝑛. Это может быть только хорошо
определяется, если 𝑚=𝑛, а это означает, что 𝐴 должно быть
матрица порядка 𝑛×𝑛 (другими словами, квадратная). То
поэтому порядок 𝐴 идентичен исходной матрице
𝐴.
Существуют и другие ограничения на взятие степеней матриц, которые не
существуют для действительных чисел. Например, в отличие от обычных чисел, у нас нет
способ определения того, что такое 𝐴, и отрицательная сила
матрицу вычислить намного сложнее. Кроме того, обычные законы
возведение в степень не обязательно распространяется на матрицы так же, как
они делают это для чисел, которые мы рассмотрим позже в этом объяснении.
А пока давайте продемонстрируем, как возведение матрицы в квадрат работает на простом, нетривиальном кейс.Определим матрицу 𝐴=1−325.
Чтобы вычислить матрицу 𝐴, мы умножаем матрицу 𝐴 само собой. Другими словами, мы имеем 𝐴=𝐴×𝐴=1−3251−325.
Как и ожидалось, это умножение корректно определено, так как у нас есть Матрица 2×2, умноженная на матрицу 2×2 матрица. Теперь осталось завершить умножение матриц, что мы и можем сделать для каждой записи (𝑖,𝑗) путем умножения элементов в строке 𝑖 левой матрицы элементами столбца 𝑗 правой матрицы и суммируя их.Мы демонстрируем это процесс ниже:
Теперь, когда все записи вычислены, мы можем написать, что 𝐴=−5−181219.
Теперь рассмотрим пример, в котором мы можем применить этот метод возведения в квадрат Матрица для решения проблемы.
Пример 1. Нахождение квадрата матрицы
Для
𝐴=4−54−5,
напишите 𝐴 как кратное 𝐴.
Ответ
Перед попыткой записать 𝐴 как кратное 𝐴, нам нужно вычислить саму 𝐴.Заполнение необходимой матрицы умножение дает 𝐴=𝐴×𝐴=4−54−54−54−5=−45−45.
Выходная матрица 𝐴 совпадает с исходной матрицей 𝐴, за исключением того, что каждая запись была умножена на -1. Мы следовательно, найдите, что 𝐴 может быть записано в терминах самого себя с помощью выражение 𝐴=−𝐴.
Увидев простой пример взятия степени матрицы, отметим, что мы часто приходится иметь дело с выражениями, которые потенциально включают несколько матрицы, а также другие матричные операции.К счастью, у нас не должно быть проблемы, связанные с такими вопросами, пока мы применяем те же принципы мы только что узнали.
Пример 2. Вычисление матричных выражений с участием степеней
Рассмотрим матрицы 𝑋=−3−35−6,𝑌=136−6. Что такое 𝑋−𝑌?
Ответ
Мы должны начать с вычисления как 𝑋, так и 𝑌
обычным способом. Мы вычисляем, что 136−6=19−15−3054.
Мы вычисляем, что 136−6=19−15−3054.
Теперь, когда у нас есть и 𝑋, и 𝑌, просто вычислить это 𝑋−𝑌=−627−4521−19−15−3054=−2542−15−33.
Вероятно, неудивительно, что мы можем легко взять, например, третью мощность матрицы, используя наше понимание того, как мы находим вторую степень матрицы, как мы это сделали выше.
Давайте посмотрим, как работает третья степень матрицы. По определению, третья степень квадратной матрицы 𝐴 определяется выражением 𝐴=𝐴×𝐴×𝐴.
Обратите внимание, что, используя ассоциативное свойство матричного умножения, наряду с определение 𝐴, мы можем написать правую часть это как 𝐴×𝐴×𝐴=(𝐴×𝐴)×𝐴=𝐴×𝐴.
В качестве альтернативы, мы можем использовать ассоциативность двух последних членов, чтобы записать это как 𝐴×𝐴×𝐴=𝐴×(𝐴×𝐴)=𝐴×𝐴.
Итак, мы показали, что 𝐴=𝐴𝐴=𝐴𝐴. В других
словами, как только мы вычислили 𝐴, мы можем найти
𝐴 путем умножения 𝐴 справа (или
слева) от 𝐴.
Увидев, как работает возведение в степень для возведения в квадрат и куба, мы можем себе представить мы можем применить те же принципы к любой степени 𝐴.С Следуя определению, это возможно.
Определение: степень матрицы
Если 𝐴 — квадратная матрица, а 𝑘 — натуральное число, 𝑘-я степень 𝐴 дана от 𝐴=𝐴×𝐴×⋯×𝐴, где имеется 𝑘 копий матрицы 𝐴.
В дополнение к этому определению отметим, что, используя ту же логику, что и выше, можно вычислить 𝐴 (для любого положительного целого числа 𝑘) сначала вычислив 𝐴 и умножив на дополнительный 𝐴 справа или слева.Так, например, 𝐴=𝐴×𝐴=𝐴×𝐴, и так далее.
Давайте теперь рассмотрим пример, где нам нужно вычислить третью степень числа матрица.
Пример 3: вычисление высших степеней матриц
Учитывая матрицу 𝐴=40−37, вычислить 𝐴−3𝐴.
Ответ
Мы должны начать с вычисления 𝐴, а затем использовать этот результат для
рассчитать 𝐴. Мы находим, что
𝐴=40−37,𝐴=160−3349,
что означает, что мы можем вычислить 𝐴 как умножение матриц
между 𝐴 и 𝐴:
𝐴=𝐴×𝐴=40−37160−3349=640−279343.
Мы находим, что
𝐴=40−37,𝐴=160−3349,
что означает, что мы можем вычислить 𝐴 как умножение матриц
между 𝐴 и 𝐴:
𝐴=𝐴×𝐴=40−37160−3349=640−279343.
Теперь у нас есть все необходимое для вычисления требуемого выражения: 𝐴−3𝐴=640−279343−3160−3349=640−279343−480−99147=160−180196.
До сих пор мы видели только расчеты с участием матрицы 2 × 2, но расширение до более высоких порядков квадратные матрицы очень естественны. Давайте теперь посмотрим на пример того, как мы могли бы найти мощность матрицы 3×3.
Пример 4. Возведение в квадрат матрицы 3 × 3
Рассмотрим 𝐴=112101210.
Найти 𝐴.
Ответ
Матрица 𝐴 имеет порядок 3×3, значит,
𝐴 также будет иметь этот порядок. Таким образом, мы ожидаем найти матрицу
вида
где элементы * должны быть вычислены. Мы заполним матрицу
умножение полностью, полностью иллюстрируя каждый шаг.
Сначала вычисляем запись в первой строке и первом столбце самой правой матрицы: 112101210112101210=6∗∗∗∗∗∗∗∗.
Расчет 1×1+1×1+2×2=6. Теперь вычисляем запись в первая строка и второй столбец самой правой матрицы: 112101210112101210=63∗∗∗∗∗∗∗.
Расчет 1×1+1×0+2×1=3. Далее мы сосредоточимся на записи в первая строка и третий столбец самой правой матрицы: 112101210112101210=633∗∗∗∗∗∗.
Расчет 1×2+1×1+2×0=3. Теперь переходим ко второму ряду самая правая матрица, сбрасываемая в первый столбец: 112101210112101210=6333∗∗∗∗∗.
Расчет 1×1+0×1+1×2=3. Затем мы берем запись во втором строка и второй столбец: 112101210112101210=63332∗∗∗∗,
Расчет 1×1+0×0+1×1=2. Последняя запись во второй строке затем вычислено: 112101210112101210=633322∗∗∗.
Расчет
1×2+0×1+1×0=2. Запись в третьем ряду и первом
столбец вычисляется:
112101210112101210=6333223∗∗.
Запись в третьем ряду и первом
столбец вычисляется:
112101210112101210=6333223∗∗.
Расчет 2×1+1×1+0×2=3. Тогда предпоследняя запись завершенный: 112101210112101210=63332232∗.
Расчет 2×1+1×0+0×1=2. Затем обрабатывается окончательная запись: 112101210112101210=633322325.
Расчет 2×2+1×1+0×0=5. Теперь, когда все записи самого правого матрица найдена, ответ можно записать в виде 𝐴=633322325.
Учитывая, что получение степени матрицы включает повторяющуюся матрицу
умножение, мы могли бы разумно ожидать, что алгебраические правила матрицы
умножение в некоторой степени повлияло бы на правила возведения матрицы в степень
Аналогичным образом.Несмотря на то, что это до некоторой степени очевидно, опасно
обращаться к правилам обычной алгебры при ответе на вопросы, связанные с
матрицы в предположении, что они сохранятся. В следующих
Например, мы будем рассматривать каждое утверждение отдельно и представим
соответствующие свойства матричного умножения в тандеме, объясняющие, почему
данные утверждения выполняются или не выполняются в результате.
В следующих
Например, мы будем рассматривать каждое утверждение отдельно и представим
соответствующие свойства матричного умножения в тандеме, объясняющие, почему
данные утверждения выполняются или не выполняются в результате.
Пример 5: Проверка свойств степеней матриц
Какое из следующих утверждений верно для всех 𝑛×𝑛 матрицы 𝐴 и 𝐵?
- 𝐴𝐵 = 𝐴 (𝐴𝐵) 𝐵
- (𝐴-𝐵) = 𝐴-2𝐴𝐵 + 𝐵
- (𝐴𝐵) = 𝐴𝐵
- (𝐴 + 𝐵) = 𝐴 + 2𝐴𝐵 + 𝐵
- (𝐴+𝐵)(𝐴−𝐵)=𝐴−𝐵
Ответ
- Умножение матриц ассоциативно, т. е.
𝐴(𝐵𝐶)=(𝐴𝐵)𝐶.Мы могли бы продолжить эту роль, чтобы получить результаты
например (𝐴𝐵)(𝐶𝐷)=𝐴(𝐵𝐶)𝐷=𝐴𝐵𝐶𝐷 и так далее. В данном
уравнения, левая часть равна 𝐴𝐵, что по определению
можно записать как 𝐴𝐵=𝐴𝐴𝐵𝐵. Учитывая ассоциативность
свойство матричного умножения, мы можем написать, что 𝐴𝐵=𝐴(𝐴𝐵)𝐵 и, следовательно, подтвердить, что данное утверждение верно.

- Обычная алгебра коммутативна относительно умножения. Для двух действительных чисел 𝑎 и 𝑏, это означает, что 𝑎𝑏=𝑏𝑎.Этот результат позволяет нам принять такое выражение, как (𝑎−𝑏)=𝑎−𝑎𝑏−𝑏𝑎+𝑏 и использовать коммутативное свойство собрать два средних члена правой части: (𝑎−𝑏)=𝑎−2𝑎𝑏+𝑏. Однако, умножение матриц, как правило, не является коммутативным, а это означает, что 𝐴𝐵≠𝐵𝐴 за исключением особых обстоятельств (таких как диагональные матрицы или одновременно диагональные матрицы). Следовательно, расширение (𝐴−𝐵)=𝐴−𝐴𝐵−𝐵𝐴+𝐵 не может упростить в предположении, что 𝐴𝐵=𝐵𝐴.Следовательно, данный утверждение ложно.
- Чтобы завершить умножение матриц (𝐴𝐵), мы можем начать с
записи (𝐴𝐵)=(𝐴𝐵)(𝐴𝐵)=𝐴(𝐵𝐴)𝐵, где мы использовали свойство ассоциативности для организации
окончательное выражение. Поскольку умножение матриц не является коммутативным, член в квадратных скобках
(𝐵𝐴) нельзя переставить как (𝐴𝐵), что означает
что мы не можем переписать окончательное выражение как 𝐴𝐴𝐵𝐵, что было бы
допустили упрощение 𝐴𝐵.
 Учитывая, что это не
случае утверждение ложно.
Учитывая, что это не
случае утверждение ложно. - Мы имеем, что (𝐴+𝐵)=𝐴+𝐴𝐵+𝐵𝐴+𝐵. Поскольку в общем случае 𝐴𝐵≠𝐵𝐴, мы не можем получить упрощение, указанное в вопросе.
- Начнем с завершения разложения (𝐴+𝐵)(𝐴−𝐵)=𝐴+𝐵𝐴−𝐴𝐵−𝐵. Мы знаем, что, вообще говоря, 𝐵𝐴≠𝐴𝐵, а это значит, что мы не можем записать правую часть в виде 𝐴−𝐵 и, следовательно, утверждение в вопросе неверно.
Следовательно, правильный ответ — вариант А.
Несмотря на то, что некоторые общепринятые правила алгебры не выполняются для матриц, все еще существуют некоторые правила, определяющие степени матриц, которые мы можем положиться. В частности, законы показателей степени для чисел могут быть распространяется на матрицы следующим образом.
Свойство: сложение и умножение степеней матрицы
Если 𝐴 — квадратная матрица и 𝑟 и 𝑠 — целые положительные числа, то 𝐴𝐴=𝐴,(𝐴)=𝐴.
В последнем примере мы рассмотрим возведение матрицы в гораздо большую степень
и посмотрите, как вышеупомянутые свойства могут быть использованы в сочетании с идентификацией
образец того, как матрица ведет себя при возведении в степень.
Пример 6. Нахождение степени матрицы высшего порядка путем исследования шаблона его полномочий
Заполните пропуск: Если 𝐴=403−4, тогда 𝐴=.
Ответить
Как 𝐴=𝐴×𝐴×⋯×𝐴 (пятьдесят раз), очевидно, нам следует избегать попыток вычислить его напрямую. Вместо этого давайте исследуем эффект от того, что 𝐴 имеет малые степени 𝐴 и см. можем ли мы определить закономерность.
Если мы умножим 𝐴 само на себя, другими словами, если мы найдем 𝐴=𝐴×𝐴, имеем 𝐴=403−4403−4=4004.
Заметим, что, поскольку это диагональная матрица, она может оказаться полезной для матрица, в которой будет находиться. Продолжая далее, если мы вычислим 𝐴=𝐴×𝐴, имеем 𝐴=4004403−4=404⋅3−4.
Интересно, что матрица больше не является диагональной. Чтобы продолжить расследование узор, посчитаем 𝐴=𝐴×𝐴. Это 𝐴=404⋅3−4403−4=4004.
В этот момент можно распознать закономерность. Для четных сил
𝐴 мы предполагаем, что матрица является диагональной и
ненулевые записи равны 4, где 𝑛 —
мощность матрицы.Для нечетных степеней это не так, так как
в левом нижнем углу и в правом нижнем углу есть ненулевой элемент
запись становится отрицательной. Однако, поскольку нам нужно найти только
𝐴 где 50 — четная степень, нам нужно только рассмотреть
первый случай.
Для четных сил
𝐴 мы предполагаем, что матрица является диагональной и
ненулевые записи равны 4, где 𝑛 —
мощность матрицы.Для нечетных степеней это не так, так как
в левом нижнем углу и в правом нижнем углу есть ненулевой элемент
запись становится отрицательной. Однако, поскольку нам нужно найти только
𝐴 где 50 — четная степень, нам нужно только рассмотреть
первый случай.
Теперь покажем, как можно найти 𝐴, используя четное мощность матрицы, 𝐴. Напомним, что 𝐴=4004.
Заметим, что скаляр 4 можно вынести за пределы матрицы, переписав его в виде: 𝐴=41001.
Это единичная матрица 2×2 𝐼 раз постоянная. Теперь мы знаем, что единичная матрица имеет имущество 𝐼𝑋=𝑋𝐼=𝑋, где 𝑋 — любая матрица 2 × 2. В частности, если 𝑋=𝐼, имеем 𝐼=𝐼×𝐼=𝐼.
Мы можем распространить это на любую степень 𝐼, то есть
𝐼=𝐼.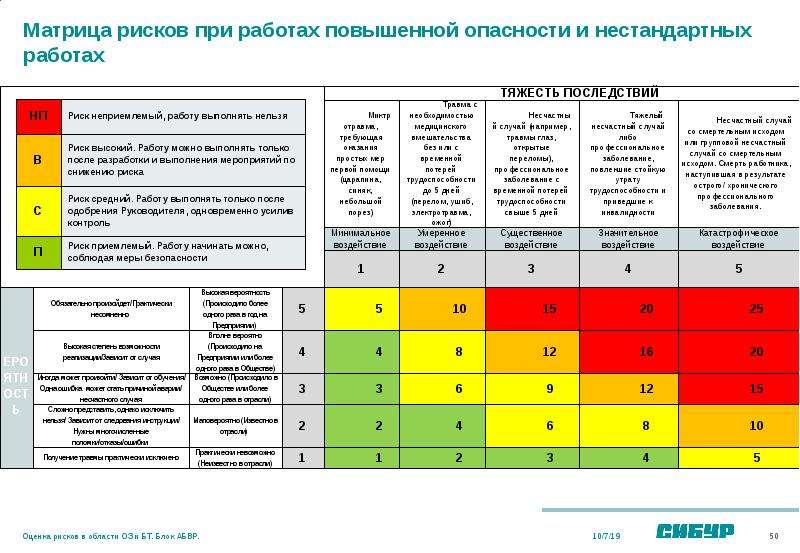
Мы можем использовать это свойство для вычисления 𝐴. Давайте также вспомнить свойство (𝐴)=𝐴, что позволяет нам переписать 𝐴 следующим образом: 𝐴=𝐴.
Поскольку 𝐴=4𝐼, это означает
Так как 4=2 4=2=2.
Есть много связанных тем, которые подтверждают обоснованность изучения возведения матриц в степень. При работе с квадратной матрицей ясно, что многократное умножение такой матрицы само по себе приведет к обычно приводят к результатам, которые последовательно сложнее вычислить, учитывая большие числа участие, как мы видели в нескольких из приведенных выше примеров.Поэтому выгодно иметь возможность максимально уменьшить сложность этих вычислений. При определенных обстоятельств можно диагонализовать матрицу, что значительно уменьшает сложность вычисления его целых степеней.
Давайте закончим рассмотрением основных вещей, которые мы узнали в этом
объяснитель.
Ключевые моменты
- Для квадратной матрицы 𝐴 и положительного целого числа 𝑘 мы определяем мощность матрицы повторяющейся матрицей умножение; Например, 𝐴=𝐴×𝐴×⋯×𝐴, где есть 𝑘 копий матрицы 𝐴 с правой стороны.
- Важно понимать, что мощность матрицы зависит только от определяется, если матрица является квадратной матрицей. Кроме того, если 𝐴 имеет порядок 𝑛×𝑛, то это будет случай для 𝐴, 𝐴 и так далее.
- Высшие степени матрицы могут быть вычислены относительно меньшие степени матрицы. Другими словами, 𝐴=𝐴×𝐴, 𝐴=𝐴×𝐴, и так далее.
- Если 𝐴 — квадратная матрица и 𝑟 и 𝑠 — целые положительные числа, то 𝐴𝐴=𝐴,(𝐴)=𝐴.
Определение и примеры матрицы, ее элементы, строки, столбцы, нотация матрицы. Матрица это просто…
Матрица — это способ организации данных в столбцах и строках. Матрица записывается внутри скобок [ ]. Посмотрите на картинку ниже, чтобы увидеть пример.
Матрица записывается внутри скобок [ ]. Посмотрите на картинку ниже, чтобы увидеть пример.
Каждый элемент матрицы называется записью.
Матрица, изображенная ниже, состоит из двух строк и трех столбцов.
- Размеры 2 × 3
- Элементы приведенной ниже матрицы: 2, -5, 10, -4, 19, 4.
Размер матрицы
Размеры матрицы относятся к количеству строк и столбцов данной матрицы. По соглашению размерность матрицы определяется количеством строк • количеством столбцов
Одним из способов, с помощью которого некоторые люди помнят, что обозначения размеров матрицы представляют собой строки за столбцами (а не столбцы за строками), является воспоминание некогда популярной газировки:
RC Cola -- строки перед столбцами!
Ниже вы видите две картинки одной и той же матрицы с выделенными строками и столбцами.
Размеры данной матрицы
- Размеры: 2 × 3
- 2 ряда × 3 столбца
Матричное обозначение
Чтобы идентифицировать запись в матрице, мы просто пишем нижний индекс строки соответствующей записи, за которой следует столбец.
В матрице A слева мы пишем 23 для обозначения записи во второй строке и третьем столбце.
Один из способов запомнить, что эта нотация ставит строки на первое место, а столбцы — на второе, — думать об этом как о чтении книги. Вы всегда сначала читаете сбоку, точно так же, как вы всегда сначала пишете ряды. Продолжая аналогию, когда вы закончите читать строку в книге, ваши глаза опускаются вниз, как столбцы после строк. 23 сначала указывает номер строки, 2, затем номер столбца 3.
Практика идентификации записей
Практика 1
Шаг 1 Габаритные размеры
Размеры матрицы 3 × 3 (3 строки × 3 столбца)
Шаг 2 Идентифицируйте запись G 23 в матрице G слева.
G 23 — запись во второй строке и третьем столбце: 55.
Шаг 3 Габаритные размерыРазмеры 3 × 5 (3 ряда × 5 столбцов)
Практика 2
Шаг 1 Отвечать
Запись j 34 — запись в третьей строке и четвертом столбце.
J 12 — число в первой строке и втором столбце: -5
Практика 3
Шаг 1 Отвечать
Размеры матрицы 4 × 5 (4 строки × 5 столбцов)
Шаг 2 ОтвечатьЗапись 31 (строка 1 и столбец 4)
Шаг 3 Отвечать v 45 обозначает запись в четвертой строке и пятом столбце, цифра 15 в правом нижнем углу.
Сложение и вычитание матриц
Вы можете складывать или вычитать матрицы, если все матрицы имеют одинаковые размеры (другими словами, каждая из них должна иметь одинаковое количество столбцов и строк).
Чтобы добавить или вычесть матрицы, вы просто добавляете или вычитаете соответствующие записи (элементы или числа, которые находятся в одном и том же месте).
Почему для сложения и вычитания требуются одни и те же размеры?
Подумайте об этом: Так как добавление/вычитание матриц подразумевает добавление/вычитание соответствующих записей. Что бы вы сделали с записями в одной матрице, которым нет соответствующей записи в другой?)
Рассмотрим пример, изображенный выше. . В матрице №1 на один столбец больше, чем в матрице №2. Как бы вы сопоставили, не говоря уже о том, чтобы добавить, записи столбца 3 #1 с соответствующими в #2. Что ж, ответ таков: вы не можете, поскольку вы не можете складывать матрицы, если они не имеют одинаковое количество строк и столбцов.
. В матрице №1 на один столбец больше, чем в матрице №2. Как бы вы сопоставили, не говоря уже о том, чтобы добавить, записи столбца 3 #1 с соответствующими в #2. Что ж, ответ таков: вы не можете, поскольку вы не можете складывать матрицы, если они не имеют одинаковое количество строк и столбцов.
Что означает матрица? определение, значение и звуковое произношение (Бесплатный словарь английского языка)
Детали словарной статьи
• MATRIX (существительное)
Смысл 1
Значение:
(математика) прямоугольный массив величин или выражений, составленный по строкам и столбцам; рассматривается как единый элемент и управляется в соответствии с правилами
Классифицировано под:
Существительные, обозначающие группы людей или предметов
Гиперонимы («матрица» — род…):
массив (упорядоченное расположение)
Категория домена:
математика; математика; математика (наука (или группа родственных наук), занимающаяся логикой количества, формы и расположения)
Гипонимы (каждый из следующих является своего рода «матрицей»):
матрица корреляции (матрица, дающая корреляции между всеми парами наборов данных)
точечная матрица (прямоугольная матрица точек, из которых могут быть сформированы письменные символы)
квадратная матрица (матрица с одинаковым количеством строк и столбцов)
вещественная матрица (матрица, все элементы которой являются действительными числами)
транспонирование (матрица, образованная путем перестановки строк и столбцов данной матрицы)
Смысл 2
Значение:
(геология) Масса мелкозернистой горной породы, в которой заключены окаменелости, кристаллы или драгоценные камни
Классифицировано под:
Существительные, обозначающие вещества
Гиперонимы («матрица» — род. ..):
..):
камень; камень (материал, состоящий из совокупности минералов, подобных тем, которые составляют земную кору)
Категория домена:
геология (наука, изучающая историю Земли, записанную в горных породах)
Смысл 3
Значение:
Оболочка, в которой что-то зарождается или развивается (от латинского «матка»)
Классифицировано под:
Существительные, обозначающие природные объекты (не созданные человеком)
Гиперонимы («матрица» — род…):
корпус; естественный вольер (естественно замкнутое пространство)
Смысл 4
Значение:
Вещество тела, в которое встроены клетки тканей
Классифицировано под:
Существительные, обозначающие части тела
Синонимы:
измельченное вещество; межклеточное вещество; матрица
Гиперонимы («матрица» — разновидность…):
вещество тела (вещество тела)
Холонимы («матрица» является частью. ..):
..):
кость; os (жесткая соединительная ткань, из которой состоит скелет позвоночных)
соединительная ткань (ткань мезодермального происхождения, состоящая, например, из коллагеновых фибробластов и жировых клеток; поддерживает органы и заполняет промежутки между ними и образует сухожилия и связки)
хряща; хрящ (жесткая эластичная ткань; у взрослых в основном превращается в кость)
Смысл 5
Значение:
Формирующая ткань у основания ногтя
Классифицировано под:
Существительные, обозначающие части тела
Гиперонимы («матрица» — род…):
ткани животных (ткани в телах животных)
Холонимы («матрица» является частью…):
гвоздь (роговая пластинка, покрывающая и защищающая часть тыльной поверхности пальцев)
Смысл 6
Значение:
Форма, используемая при производстве грампластинок, литера или другая рельефная поверхность
Классифицировано под:
Существительные, обозначающие искусственные объекты
Гиперонимы («матрица» — род. ..):
..):
литых; плесень; форма (емкость, в которую заливают жидкость для создания заданной формы при ее затвердевании)
Контекстные примеры
Этот аллель, кодирующий акрозин-связывающий белок, играет роль в упаковке проакрозина и конденсации зимогена акрозина в акросомальном матриксе .
(аллель ACRBP wt, тезаурус NCI)
Этот аллель, кодирующий щелочную фосфатазу, тканенеспецифический изоферментный белок, может быть вовлечен в минерализацию матрикса .
(аллель ALPL wt, тезаурус NCI)
Это повышение температуры, в свою очередь, привело к тому, что матрица из полимера с памятью формы размягчилась и стала гибкой.
(Крошечные магнитные частицы позволяют новому материалу изгибаться, скручиваться и захватываться, Национальный научный фонд)
Изучаемые в настоящее время подходы включают ингибирование стимуляторов ангиогенеза (например, VEGF) или их рецепторов, блокаду активации эндотелиальных клеток, ингибирование матриксных металлопротеиназ и ингибирование сосудистой сети опухоли.
(Путь ангиогенеза, Тезаурус NCI/BIOCARTA)
Этот белок может играть роль в минерализации матрикса .
(щелочная фосфатаза, тканевой неспецифический изофермент, тезаурус NCI)
Детектируемая частица, содержащая фосфолипиды, белок и кальций, найденная в митохондриальном матриксе .
(гранулы митохондриальной матрицы, тезаурус NCI)
AKAP95 (белок, заякоривающий A-киназу) представляет собой белок, ассоциированный с ядерным матриксом , который также связывает ДНК и различные белки на разных фазах клеточного цикла.
(AKAP8 в пути митоза, NCI Thesaurus/BIOCARTA)
ADAM (домен дезинтегрина и металлопротеиназы) представляют собой заякоренные в мембране протеазы, которые регулируют поведение клеток путем протеолитической модификации клеточной поверхности и внеклеточного матрикса .
(ген семейства ADAM, тезаурус NCI)
Это ингибитор металлопротеиназы матрицы , принадлежащий к семейству препаратов, называемых ингибиторами ангиогенеза.
(AG3340, словарь NCI)
Этот аллель, кодирующий белок ADAM15, участвует в протеолизе, что способствует реструктуризации мезангиального матрикса .
(аллель ADAM15 wt, тезаурус NCI)
| Изучайте английский язык с… Пословицы |
«Красивый так же красив». (английская пословица)
«В смерти я рождаюсь». (Индейская пословица, хопи)
«Не просите певца спеть, пока он не захочет петь сам». (арабская пословица)
«Страдание любит компанию». (голландская пословица)
| 6 |
| 6 |
Что такое единичная матрица?
Идентификационная матрица
Узнав о нулевой матрице, пришло время изучить другой тип матрицы, содержащий постоянный определенный набор значений каждый раз, нам пора изучить единичные матрицы.
Что такое единичная матрица?
Единичная матрица – это заданная квадратная матрица любого порядка, которая содержит на своей главной диагонали элементы со значением 1, а остальные элементы матрицы равны нулю.
Чтобы объяснить это определение по частям, начнем с того, что напомним вам, что квадратная матрица относится к матрице, содержащей одинаковое количество строк и столбцов. Порядок матрицы зависит от ее размеров, а ее главная диагональ относится к массиву элементов внутри матрицы, которые образуют наклонную линию из верхнего левого угла в нижний правый угол.Учитывая характеристики единичной матрицы, мы также можем заключить, что матрицы этого типа также являются диагональными матрицами.
Диагональная матрица — это матрица, в которой все ее элементы равны нулю, за исключением элементов, находящихся на ее главной диагонали. В этом случае все ненулевые элементы в матрице будут иметь значение, равное единице, и это является одной из причин, по которой единичную матрицу также иногда называют единичной матрицей.
В случае обозначения матричной линейной алгебры единичная матрица служит эквивалентным объектом единице в числовой алгебре (по другой причине она называется единичной матрицей).Другими словами, единичная матрица эквивалентна единице, но в данном случае это алгебраический объект с размерами и организацией массива, который можно использовать в операциях с другими массивами упорядоченных чисел (другими матрицами).
В следующем разделе мы рассмотрим свойства единичной матрицы, и определение единичной матрицы будет иметь гораздо больше смысла, особенно в случае матричных умножений, включающих единичную матрицу (посмотрите на свойство номер 3).Математически единичная матрица представляется как:
Уравнение 1: Общее выражение единичной матрицы Чтобы не путать с идентичностью матрицы, обратите внимание, что единичная матрица имеет столько элементов главной диагонали, сколько ее порядок (обозначается субиндексом n в термине, находящемся в левой части уравнения). Примеры единичных матриц разных размерностей можно увидеть в следующем уравнении: Уравнение 2: Примеры единичных матриц разных размеров Помните, что порядок матрицы относится к количеству содержащихся в ней строк и столбцов, которые также называются размерами mxn.
 Обратите внимание, что, поскольку единичная матрица является квадратной матрицей, она содержит одинаковое количество строк и столбцов, поэтому ее порядок можно обозначить просто как nxn или как одноразрядный субиндекс, как показано в уравнениях 1 и 2, который мы называем « n» (учитывая, что размеры m и n, исходящие из типичной матричной записи, равны для квадратных матриц, только одна из этих букв необходима в качестве субиндекса для описания порядка таких матриц).
Обратите внимание, что, поскольку единичная матрица является квадратной матрицей, она содержит одинаковое количество строк и столбцов, поэтому ее порядок можно обозначить просто как nxn или как одноразрядный субиндекс, как показано в уравнениях 1 и 2, который мы называем « n» (учитывая, что размеры m и n, исходящие из типичной матричной записи, равны для квадратных матриц, только одна из этих букв необходима в качестве субиндекса для описания порядка таких матриц). Итак, в уравнении 2 мы легко можем видеть, что I2 относится к единичной матрице с двумя строками и двумя столбцами, которая в то же время имеет только два элемента на своей главной диагонали; обозначение I3 соответствует единичной матрице порядка 3 или матрице, содержащей три строки и три столбца и 3 элемента на главной диагонали; и система обозначений продолжается таким же образом для любого субиндекса n.
Свойства матрицы идентичности
- Единичная матрица всегда является квадратной матрицей:
Как видно из уравнений 1 и 2, порядок единичной матрицы всегда равен n, что относится к размерам nxn (это означает, что в таблице всегда одинаковое количество строк и столбцов). матрица).
матрица). - Единичная матрица может умножать любую матрицу любого порядка (размерности), если она соответствует следующим правилам:
- Если при умножении единичная матрица является первым фактором, то единичная матрица должна иметь размеры с таким количеством столбцов, сколько строк умножаемой матрицы.Уравнение 3: Умножение единичной матрицы на неединичную матрицу
- Если единичная матрица является вторым фактором умножения, единичная матрица должна иметь такое же количество строк, как и матрица, которая умножает ее столбец Уравнение 4: Умножение неединичной матрицы на единичную матрицу Эти два правила исходят из условий умножения матриц.
- В результате первых двух правил, если единичная матрица умножается на квадратную матрицу тех же размеров, результатом также будет квадратная матрица, которая будет такой же, как неединичная матрица умножения, независимо от порядок перемножения матриц друг с другом.
- Следуя двум уравнениям из второго свойства, объясненного выше, из всех свойств единичной матрицы, основное можно ясно наблюдать в уравнениях 3 и 4: всякий раз, когда единичная матрица умножает другую матрицу, и умножение может быть решено (следуя правилам для умножения матриц), результат равен задействованной неединичной матрице.
 Математически говоря: Уравнение 5: Умножение единичной матрицы на другую матрицу
Если подумать, это эквивалентно умножению обычного действительного числа на единицу (на единицу).Любое число, умноженное на единицу, дает одно и то же исходное число. То же самое касается матрицы, умноженной на единичную матрицу: результатом всегда является одна и та же исходная неединичная (неединичная) матрица, и, таким образом, как объяснялось ранее, единичная матрица получает прозвище «единичная матрица».
Математически говоря: Уравнение 5: Умножение единичной матрицы на другую матрицу
Если подумать, это эквивалентно умножению обычного действительного числа на единицу (на единицу).Любое число, умноженное на единицу, дает одно и то же исходное число. То же самое касается матрицы, умноженной на единичную матрицу: результатом всегда является одна и та же исходная неединичная (неединичная) матрица, и, таким образом, как объяснялось ранее, единичная матрица получает прозвище «единичная матрица». - Умножение матрицы на обратную ей дает единичную матрицу того же порядка, что и перемножаемые матрицы. Математически говоря: Уравнение 6: Умножение матрицы на обратную
Матрицы, участвующие в таком умножении, называются мультипликативными обратными друг другу.Мы оставим объяснение обратных матриц для последующих уроков, начав с темы, обратной матрице 2×2. На данный момент просто важно, чтобы вы знали, что это одно из свойств единичной матрицы, которое мы можем использовать для решения матричных уравнений.

- Определитель единичной матрицы In всегда равен 1, а ее след равен n.
Хотя мы до сих пор не видели, что такое определитель, на данный момент важно знать, что причина, по которой определитель любой единичной матрицы равен единице, заключается в том, что диагональ этих матриц содержит только единицы, а остальные элементы внутри этих матрицы нулевые.Мы представим понятие определителя в более позднем уроке под названием определитель матрицы 2×2, где определитель единичной матрицы будет объяснен более подробно.
С другой стороны, трассировку объяснить гораздо проще. К настоящему времени вы должны знать, что след матрицы относится к сложению элементов, находящихся на ее главной диагонали. Поскольку в единичной матрице все диагональные элементы равны единице, при сложении их всех для получения следа у вас всегда будет столько элементов, сколько порядка единичной матрицы, то есть n.Возьмем следующую единичную матрицу в качестве примера: Уравнение 7: Пример единичной матрицы порядка 3×3 Уравнение 7 показывает единичную матрицу 3×3, таким образом, n=3 для этой матрицы. Таким образом, след представляет собой сложение элементов его диагонали, то есть трех элементов со значением 1, добавленных друг к другу, и поэтому след равен 3. Следовательно, след единичной матрицы равен n .
Таким образом, след представляет собой сложение элементов его диагонали, то есть трех элементов со значением 1, добавленных друг к другу, и поэтому след равен 3. Следовательно, след единичной матрицы равен n . - Для нашего последнего свойства мы начнем с вопроса: обратима ли единичная матрица? Ответ положительный.Мы объясним больше по этой теме в нашем уроке об обратимой матрице 2×2, а пока просто запомните: инверсия единичной матрицы — это она сама. Уравнение 8: единичная матрица как обратная мультипликативная сама по себе. Мы можем доказать, что матрица, обратная единичной, есть сама по себе, перемножив их вместе. Помните из нашего четвертого свойства, что умножение матрицы на ее обратную дает единичную матрицу, и поэтому мы вычислили соответствующее умножение для этого случая (показанное в уравнении 8) и доказали, что обратная единичная матрица 2×2 является ею самой.
Примеры задач матрицы идентичности
Используя свойства, изученные в предыдущем разделе, и определение единичной матрицы, данное в начале этого урока, решите следующие примеры задач:
Пример 1
Учитывая матрицы ниже: Уравнение 9: Матрицы A и B Выполните следующие матричные операции:- I3⋅AI_{3} \cdot AI3⋅A
В этом случае у нас есть пример третьего свойства единичной матрицы: умножение, включающее единичную матрицу и любую другую матрицу, если определяется по правилам матричного умножения, результатом является неединичная матрица (в данном случае матрица A).Итак, это умножение происходит следующим образом: Уравнение 10. Умножение матриц с использованием единичной матрицы - 2A+4I32A + 4I_{3}2A+4I3
Для этой матричной операции мы вычисляем два случая скалярного умножения, второй включает единичную матрицу 3×3. Решение такой операции выглядит так: Уравнение 11: Сложение двух скалярных матричных умножений - −4B+2I2-4B + 2I_{2}−4B+2I2
Еще раз, эта операция состоит в использовании единичной матрицы для сложения двух скалярных умножений, где второе умножение включает единичную матрицу 2×2.Мы решаем их, как показано ниже: Уравнение 12: Сложение двух скалярных матричных умножений - I2⋅BI_{2} \cdot BI2⋅B
По третьему свойству мы знаем, что результатом этого умножения является матрица B: Уравнение 13: Умножение единичной матрицы 2×2 на другую матрицу того же порядка - 0⋅I40 \cdot I_{4}0⋅I4
В этом случае у нас есть скалярное умножение единичной матрицы с числом ноль, таким образом, результатом должна быть нулевая матрица, как показано ниже: Уравнение 14: Скалярное умножение единичной матрицы, дающее нулевую матрицу
Пример 2
Покажите, являются ли следующие матрицы мультипликативными обратными друг другу:- Имея матрицы X и Y, как показано ниже: Уравнение 15: Матрицы X и Y Выполним матричное умножение X ⋅\cdot⋅ Y: Уравнение 16: Перемножение матриц X и Y Учитывая, что результатом является единичная матрица, мы заключаем, что X и Y являются мультипликативными инверсиями друг друга.
- Имея матрицы A и B, как показано ниже: Уравнение 17: Матрицы A и B Выполним матричное умножение A ⋅\cdot⋅ B: Уравнение 18: Умножение матриц A и B Таким образом, A и B мультипликативно обратны друг другу.
- Имея матрицы C и D, как показано ниже: Уравнение 19: Матрицы C и D Выполним матричное умножение C ⋅\cdot⋅ D: Уравнение 20: Перемножение матриц C и D Матрица, полученная в результате описанной выше операции, хотя и очень похожа, не является единичной матрицей.Следовательно, эта операция показывает, что C и D НЕ являются мультипликативными инверсиями друг друга.
- Имея матрицы E и F, как показано ниже: Уравнение 21: Матрицы E и F Выполним матричное умножение E ⋅\cdot⋅ F: Уравнение 22: Перемножение матриц E и F Следовательно, E и F мультипликативно обратны друг другу.
Прежде чем мы начнем, позвольте порекомендовать вам следующую маленькую ссылку, кратко определяющую единичную матрицу, и эту статью, которая касается как темы умножения матриц, так и единичной матрицы, говоря о коммутативном свойстве умножения любой квадратной матрицы на единичная матрица того же порядка (точно так же, как описано в третьем свойстве во втором разделе этого урока), и как это не применяется к другим матричным умножениям.
Итак, на сегодня все, до встречи на следующем уроке! .


 Но это не значит, что люди тоже одинаковые. Да, у них будут какие-то схожие черты в характерах и по проявлениям. Благодаря тому, что мы все рождаемся в разных обстоятельствах, в разных семьях, в разное время и в разных странах, то проживаем Матрицу совершенно по-разному. Она ни в коем случае не ограничивает человека, говоря ему о том, какие у него таланты. Метод является дополнительной опорой и позволяет лучше понять себя.
Но это не значит, что люди тоже одинаковые. Да, у них будут какие-то схожие черты в характерах и по проявлениям. Благодаря тому, что мы все рождаемся в разных обстоятельствах, в разных семьях, в разное время и в разных странах, то проживаем Матрицу совершенно по-разному. Она ни в коем случае не ограничивает человека, говоря ему о том, какие у него таланты. Метод является дополнительной опорой и позволяет лучше понять себя.

 Срочное, но не важное (задачи, которые можно кому-то делегировать). Эти задачи нужно выполнить немедленно, но они могут быть не настолько важными, чтобы привлечь ваше внимание, а значит, их можно делегировать другим участникам рабочей группы. Сюда можно отнести повседневную работу, длительные встречи или телефонные звонки без четкой цели.
Срочное, но не важное (задачи, которые можно кому-то делегировать). Эти задачи нужно выполнить немедленно, но они могут быть не настолько важными, чтобы привлечь ваше внимание, а значит, их можно делегировать другим участникам рабочей группы. Сюда можно отнести повседневную работу, длительные встречи или телефонные звонки без четкой цели.
 Учитывая, что это не
случае утверждение ложно.
Учитывая, что это не
случае утверждение ложно. матрица).
матрица). Математически говоря: Уравнение 5: Умножение единичной матрицы на другую матрицу
Если подумать, это эквивалентно умножению обычного действительного числа на единицу (на единицу).Любое число, умноженное на единицу, дает одно и то же исходное число. То же самое касается матрицы, умноженной на единичную матрицу: результатом всегда является одна и та же исходная неединичная (неединичная) матрица, и, таким образом, как объяснялось ранее, единичная матрица получает прозвище «единичная матрица».
Математически говоря: Уравнение 5: Умножение единичной матрицы на другую матрицу
Если подумать, это эквивалентно умножению обычного действительного числа на единицу (на единицу).Любое число, умноженное на единицу, дает одно и то же исходное число. То же самое касается матрицы, умноженной на единичную матрицу: результатом всегда является одна и та же исходная неединичная (неединичная) матрица, и, таким образом, как объяснялось ранее, единичная матрица получает прозвище «единичная матрица».
 Таким образом, след представляет собой сложение элементов его диагонали, то есть трех элементов со значением 1, добавленных друг к другу, и поэтому след равен 3. Следовательно, след единичной матрицы равен n .
Таким образом, след представляет собой сложение элементов его диагонали, то есть трех элементов со значением 1, добавленных друг к другу, и поэтому след равен 3. Следовательно, след единичной матрицы равен n .