Относительное отверстие объектива это: Относительное отверстие объектива — это… Что такое Относительное отверстие объектива?
 Шкала наводки на резкость (сверху),
Шкала наводки на резкость (сверху),калькулятор ГРИП (в центре),
шкала диафрагм (снизу).
Относительное отверстие объектива — отношение диаметра действующего отверстия (диаметра действующей диафрагмы) объектива 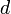 к его главному фокусному расстоянию
к его главному фокусному расстоянию 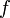 . Его величину выражают в виде дроби:
. Его величину выражают в виде дроби: 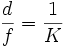 , когда числитель приведён к единице.
, когда числитель приведён к единице.
Для всех объективов с фиксированным фокусным расстоянием справедливо также утверждение, что относительное отверстие приблизительно равно отношению фокусного расстояния к диаметру изображения диафрагмы, образованного передним компонентом и измеренного на главной плоскости объектива. Для неширокоугольных объективов упрощённо можно считать, что относительное отверстие приблизительно равно отношению фокусного расстояния к диаметру передней линзы объектива.
Относительное отверстие объектива уменьшают ирисовой диафрагмой, позволяющей менять её величину (как правило — ступенчато, однако существуют объективы и с плавной регулировкой). На оправу объектива может быть нанесена шкала из знаменателей относительных отверстий (числа ирисовой диафрагмы), соответствующих различному диафрагмированию, на большинстве современных объективов такая шкала (как и кольцо регулировки диафрагмы) отсутствует и установка диафрагмы производится органами управления на теле камеры. Перевод ирисовой диафрагмы на одно деление изменяет относительное отверстие в 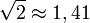
Шкала ирисовой диафрагмы стандартизована, и образует следующий ряд:
1:0,7; 1:1; 1:1,4; 1:2; 1:2,8; 1:4; 1:5,6; 1:8; 1:11; 1:16; 1:22; 1:32; 1:45; 1:64.
Впрочем, первые диафрагменные числа на объективах могут и не совпадать со стандартными (1:2,5; 1:1,7).
Для удобства пользования на шкалу диафрагм обычно наносят только знаменатели относительных отверстий.
В современных автоматических и полуавтоматических фотоаппаратах, число диафрагмы может устанавливаться не только на значения стандартного ряда, но и на промежуточные величины.
Следует отметить, что для некоторых зеркально-линзовых объективов данные рассуждения применимы с оговорками. В них диафрагма может иметь форму не круга, а кольца, и для расчёта радиуса следует использовать другие формулы.
См. также
Литература
Яштолд-Говорко В. А. Фотосъемка и обработка. Съемка, формулы, термины, рецепты. Изд. 4-е, сокр. М., «Искусство», 1977.
Wikimedia Foundation. 2010.
ОТНОСИТЕЛЬНОЕ ОТВЕРСТИЕ (СВЕТОСИЛА) ОБЪЕКТИВА
Светосилой объектива называется его способность давать ту или иную яркость изображения для светочувствительного слоя. Чем выше светосила объектива, тем меньшая выдержка требуется при съемке. Светосила объектива зависит от двух величин: от размера отверстия и от фокусного расстояния. Объектив тем светосильное, чем больше его отверстие и чем короче его фокусное расстояние. Эта взаимосвязь выражается величиной относительного отверстия, которое представляет собой отношение диаметра полного действующего отверстия объектива к его главному фокусному расстоянию. Например, диаметр отверстия объектива 5 см, а фокусное расстояние 20 см. Выполняем арифметический подсчет: 5:20 = 1/4. Это и есть числовое значение относительного отверстия, которое показывает, во сколько раз диаметр полного отверстия данного объектива меньше его фокусного расстояния, обозначаемого буквой F (а данном случае F 1:4). Чем больше второй член отношения, тем меньше само относительное отверстие, тем хуже с потребительской точки зрения объектив. Например, есть два объектива с относительными отверстиями 1/1,6 и 1/5,6. При съемке в конкретных условиях при недостаточном освещении первым объективом выдержка, например, будет 1/30 секунды, тогда как для второго объектива, соответственно, выдержка будет довольно большой — 1/2 секунды, так что возникнут технические трудности во время съемки.

На этом снимке диафрагма была полностью прикрыта, и ее значение составляло 22.
На этом снимке диафрагма была полностью открыта, и ее значение составляло 2.
Поделитесь на страничке Следующая глава >Относительное отверстие объектива — оптическая мера светопропускания объектива. Различают геометрическое и эффективное относительные отверстия. Геометрическим отверстием считается отношение диаметра входного зрачка объектива к его заднему фокусному расстоянию[1]. Эффективное относительное отверстие всегда меньше, чем геометрическое, поскольку учитывает потери света при его прохождении через стекло и рассеянии на границах с воздухом и деталях оправы.
Зависимость светопропускания объектива от относительного отверстия
Энциклопедичный YouTube
1/3
Просмотров:901
1 653
✪ Виды объективов, уроки по фототехнике, оптика, фототехника, оптические оберрации.
✪ Диафрагма (Апертура)
✪ Лекция № 10 по курсу общей физики, раздел «Оптика»
Содержание
Расчёт относительного отверстия
Геометрическое относительное отверстие N {\displaystyle N} выражают в виде дроби[2]:
- N = D f ′ {\displaystyle N={D \over f’}} ,
где D {\displaystyle D} обозначает диаметр входного зрачка, а f ′ {\displaystyle f’} — заднее фокусное расстояние. Относительное отверстие принято обозначать соотношением двух чисел, написанных через двоеточие. При этом первое число всегда принимается за единицу, например 1:5,6. В современной литературе более широкое распространение получило обозначение относительного отверстия в виде дроби с числителем f, например f/5,6. Для зеркально-линзовых объективов площадь входного зрачка рассчитывается по более сложному закону, поскольку его центральная часть экранирована [1]. В этом случае диафрагма может иметь форму не круга, а кольца, и для нахождения диаметра входного зрачка необходимо реальный входной зрачок (кольцо) заменить при расчёте кругом эквивалентной площади. Диаметр найденного круга и будет являться искомым диаметром входного зрачка для применения в дальнейших расчётах.
Квадрат относительного отверстия называется светосилой и определяет соотношение яркости объекта и освещённости его изображения в фокальной плоскости[1]. Эффективное относительное отверстие вычисляется с учётом коэффициента светопропускания τ {\displaystyle \tau } оптической системы, учитывающего общую толщину стекла и количество границ воздух/стекло. Коэффициент, снижающий прозрачность объектива, определяется по формуле:
- τ = ( 1 − P ) n ⋅ ( 1 − α ) m {\displaystyle \tau =(1-P)^{n}\cdot (1-\alpha )^{m}} ,
где P {\displaystyle P} — доля света, теряемая при отражении одной поверхностью раздела сред;
- n {\displaystyle n} — число поверхностей раздела воздух/стекло;
- α {\displaystyle \alpha } — удельное поглощение света в 1 сантиметре стекла;
- m {\displaystyle m} — суммарная толщина линз объектива в сантиметрах.
Для объективов без просветления τ {\displaystyle \tau } не превышает 0,65. Объективы с просветлением теряют не более 10% света при его прохождении и рассеянии.
Приведённые способы расчёта геометрического и эффективного относительного отверстия справедливы только при фокусировке объектива на «бесконечность». Для конечных дистанций знаменатель дроби увеличивается из-за выдвижения объектива, приводя к уменьшению относительного отверстия. Эффект особенно заметен при макросъёмке, когда сопряжённое фокусное расстояние может превосходить расчётное в два и более раз. В этом случае пренебрегать изменением относительного отверстия недопустимо и требуются поправки при расчёте экспозиции[3].
Диафрагменное число

Шкала диафрагмы объектива (нижняя), размеченная в диафрагменных числах. Положение кольца соответствует относительному отверстию f/8
Если принять диаметр входного зрачка равным единице, геометрическое относительное отверстие может быть выражено следующим образом[4]:
- N = D f ′ = 1 k {\displaystyle N={D \over f’}={1 \over k}} .
В этом случае знаменатель относительного отверстия k {\displaystyle k} называют диафрагменное число или «число диафрагмы». Диафрагменное число вычисляется как отношение фокусного расстояния объектива к диаметру его входного зрачка и обозначается цифрой. Диафрагменное число является величиной, обратной относительному отверстию[5][6].
- k = f ′ D = 1 N {\displaystyle k={f’ \over D}={1 \over N}} .
Этот параметр наиболее удобен для разметки шкал диафрагмы, поскольку не содержит дробей[7]. Регулировочная шкала ирисовой диафрагмы киносъёмочных объективов и фотообъективов старых типов (без автофокуса) градуируется в диафрагменных числах эффективного относительного отверстия, учитывающих потери света при его прохождении через стекло.
Каждое деление такой шкалы соответствует изменению светосилы в два раза, а относительного отверстия — в 2 ≈ 1 , 41 {\displaystyle {\sqrt {2}}\approx 1,41} раз[7][2]. Исключение могут составлять самые малые значения диафрагменного числа, соответствующие оптическим возможностям объектива и не укладывающиеся в стандартный ряд[8]. Такое строение шкалы диафрагменных чисел используется с 1950-х годов, когда появилось понятие экспозиционного числа, и позволяет при повороте кольца на одно деление менять экспозицию точно на одну экспозиционную ступень.
На современных фотообъективах такая шкала (как и кольцо регулировки диафрагмы) отсутствует, и установка диафрагмы производится дистанционно органами управления фотоаппарата. Шкала диафрагменных чисел современных цифровых фотоаппаратов имеет промежуточные значения, соответствующие 1/3 экспозиционной ступени:
| 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 |
При автоматическом управлении экспозицией относительное отверстие регулируется бесступенчато, поэтому диафрагменное число может принимать любые дробные значения.
См. также
Источники
- ↑ 1 2 3 Фотокинотехника, 1981, с. 228.
- ↑ 1 2 Гордийчук, 1979, с. 152.
- ↑ Гордийчук, 1979, с. 153.
- ↑ Общий курс фотографии, 1987, с. 17.
- ↑ Фотокинотехника, 1981, с. 78.
- ↑ Фотография: Техника и искусство, 1986, с. 20.
- ↑ 1 2 Краткий справочник фотолюбителя, 1985, с. 34.
- ↑ Общий курс фотографии, 1987, с. 18.
Литература
- Гордийчук, И. Б. Справочник кинооператора / И. Б. Гордийчук, В. Г. Пелль. — М. : Искусство, 1979. — 440 с. — 30 000 экз.
- Е. А. Иофис. Фотокинотехника / И. Ю. Шебалин. — М.,: «Советская энциклопедия», 1981. — С. 228. — 447 с. — 100 000 экз.
- Н. Д. Панфилов, А. А. Фомин. Краткий справочник фотолюбителя / Н. Н. Жердецкая. — М.: «Искусство», 1985. — С. 179—184. — 367 с. — 100 000 экз.
- Фомин А. В. § 4. Фотографические объективы // Общий курс фотографии / Т. П. Булдакова. — 3-е. — М.,: «Легпромбытиздат», 1987. — С. 124—130. — 256 с. — 50 000 экз.
 Эта страница в последний раз была отредактирована 10 мая 2020 в 20:57.
Эта страница в последний раз была отредактирована 10 мая 2020 в 20:57.Относительное отверстие — Википедия
Материал из Википедии — свободной энциклопедии
Относительное отверстие объектива — оптическая мера светопропускания объектива. Различают геометрическое и эффективное относительные отверстия. Геометрическим отверстием считается отношение диаметра входного зрачка объектива к его заднему фокусному расстоянию[1]. Эффективное относительное отверстие всегда меньше, чем геометрическое, поскольку учитывает потери света при его прохождении через стекло и рассеянии на границах с воздухом и деталях оправы.
 Зависимость светопропускания объектива от относительного отверстия
Зависимость светопропускания объектива от относительного отверстияРасчёт относительного отверстия
Геометрическое относительное отверстие N {\displaystyle N} выражают в виде дроби[2]:
- N = D f ′ {\displaystyle N={D \over f’}} ,
где D {\displaystyle D} обозначает диаметр входного зрачка, а f ′ {\displaystyle f’} — заднее фокусное расстояние. Относительное отверстие принято обозначать соотношением двух чисел, написанных через двоеточие. При этом, первое число всегда принимается за единицу, например 1:5,6. В современной литературе более широкое распространение получило обозначение относительного отверстия в виде дроби с числителем f, например f/5,6. Для зеркально-линзовых объективов площадь входного зрачка рассчитывается по более сложному закону, поскольку его центральная часть экранирована[1]. В этом случае диафрагма может иметь форму не круга, а кольца, и для нахождения диаметра входного зрачка необходимо реальный входной зрачок (кольцо) заменить при расчёте кругом эквивалентной площади. Диаметр найденного круга и будет являться искомым диаметром входного зрачка для применения в дальнейших расчётах.
Квадрат относительного отверстия называется светосилой и определяет соотношение яркости объекта и освещённости его изображения в фокальной плоскости[1]. Эффективное относительное отверстие вычисляется с учётом коэффициента светопропускания τ {\displaystyle \tau } оптической системы, учитывающего общую толщину стекла и количество границ воздух/стекло. Коэффициент, снижающий прозрачность объектива, определяется по формуле:
- τ = ( 1 − P ) n ⋅ ( 1 − α ) m {\displaystyle \tau =(1-P)^{n}\cdot (1-\alpha )^{m}} ,
где P {\displaystyle P} — доля света, теряемая при отражении одной поверхностью раздела сред;
- n {\displaystyle n} — число поверхностей раздела воздух/стекло;
- α {\displaystyle \alpha } — удельное поглощение света в 1 сантиметре стекла;
- m {\displaystyle m} — суммарная толщина линз объектива в сантиметрах.
Для непросветлённых объективов τ {\displaystyle \tau } не превышает 0,65. Объективы с просветлением теряют не более 10% света при его прохождении и рассеянии.
Приведённые способы расчёта геометрического и эффективного относительного отверстия справедливы только при фокусировке объектива на «бесконечность». Для конечных дистанций знаменатель дроби увеличивается из-за выдвижения объектива, приводя к уменьшению относительного отверстия. Эффект особенно заметен при макросъёмке, когда сопряжённое фокусное расстояние может превосходить расчётное в два и более раз. В этом случае пренебрегать изменением относительного отверстия недопустимо и требуются поправки при расчёте экспозиции[3].
Диафрагменное число
 Шкала диафрагмы объектива (нижняя), размеченная в диафрагменных числах. Положение кольца соответствует относительному отверстию f/8
Шкала диафрагмы объектива (нижняя), размеченная в диафрагменных числах. Положение кольца соответствует относительному отверстию f/8Если принять диаметр входного зрачка равным единице, геометрическое относительное отверстие может быть выражено следующим образом[4]:
- N = D f ′ = 1 k {\displaystyle N={D \over f’}={1 \over k}} .
В этом случае знаменатель относительного отверстия k {\displaystyle k} называют «диафрагменное число» или «число диафрагмы». Диафрагменное число вычисляется, как отношение фокусного расстояния объектива к диаметру его входного зрачка и обозначается цифрой. Диафрагменное число является величиной, обратной относительному отверстию[5][6].
- k = f ′ D = 1 N {\displaystyle k={f’ \over D}={1 \over N}} .
Этот параметр наиболее удобен для разметки шкал диафрагмы, поскольку не содержит дробей[7]. Регулировочная шкала ирисовой диафрагмы киносъёмочных объективов и фотообъективов старых типов (без автофокуса) градуируется в диафрагменных числах эффективного относительного отверстия, учитывающих потери света при его прохождении через стекло.
Каждое деление такой шкалы соответствует изменению светосилы в два раза, а относительного отверстия в 2 ≈ 1 , 41 {\displaystyle {\sqrt {2}}\approx 1,41} раз[7][2]. Исключение могут составлять самые малые значения диафрагменного числа, соответствующие оптическим возможностям объектива, и не укладывающиеся в стандартный ряд[8]. Такое строение шкалы диафрагменных чисел используется с 1950-х годов, когда появилось понятие экспозиционного числа, и позволяет при повороте кольца на одно деление менять экспозицию точно на одну экспозиционную ступень.
На современных фотообъективах такая шкала (как и кольцо регулировки диафрагмы) отсутствует и установка диафрагмы производится дистанционно органами управления фотоаппарата. Шкала диафрагменных чисел современных цифровых фотоаппаратов имеет промежуточные значения, соответствующие 1/3 экспозиционной ступени:
| 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 |
При автоматическом управлении экспозицией относительное отверстие регулируется бесступенчато и диафрагменное число может принимать любые дробные значения.
См. также
Источники
- ↑ 1 2 3 Фотокинотехника, 1981, с. 228.
- ↑ 1 2 Гордийчук, 1979, с. 152.
- ↑ Гордийчук, 1979, с. 153.
- ↑ Общий курс фотографии, 1987, с. 17.
- ↑ Фотокинотехника, 1981, с. 78.
- ↑ Фотография: Техника и искусство, 1986, с. 20.
- ↑ 1 2 Краткий справочник фотолюбителя, 1985, с. 34.
- ↑ Общий курс фотографии, 1987, с. 18.
Литература
- Гордийчук, И. Б. Справочник кинооператора / И. Б. Гордийчук, В. Г. Пелль. — М. : Искусство, 1979. — 440 с. — 30 000 экз.
- Е. А. Иофис. Фотокинотехника / И. Ю. Шебалин. — М.,: «Советская энциклопедия», 1981. — С. 228. — 447 с. — 100 000 экз.
- Н. Д. Панфилов, А. А. Фомин. Краткий справочник фотолюбителя / Н. Н. Жердецкая. — М.: «Искусство», 1985. — С. 179—184. — 367 с. — 100 000 экз.
- Фомин А. В. § 4. Фотографические объективы // Общий курс фотографии / Т. П. Булдакова. — 3-е. — М.,: «Легпромбытиздат», 1987. — С. 124—130. — 256 с. — 50 000 экз.
 Шкала наводки на резкость (сверху),
Шкала наводки на резкость (сверху),калькулятор ГРИП (в центре),
шкала диафрагм (снизу). Установлена диафрагма 1:8.
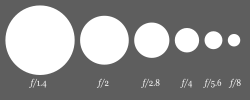 На данной иллюстрации наглядно показано, что чем больше диафрагма (численно меньше), тем больше света попадает через объектив.
На данной иллюстрации наглядно показано, что чем больше диафрагма (численно меньше), тем больше света попадает через объектив.Относительное отверстие объектива — отношение диаметра входного зрачка (изображения апертурной диафрагмы, построенного стоящими перед ней линзами в обратном ходе лучей (обычно совпадающего с первой линзой объектива)) объектива к его заднему фокусному расстоянию . Его величину выражают в виде дроби: , когда числитель приведён к единице. Знаменатель относительного отверстия называют «диафрагменным числом» или «числом диафрагмы».
Следует заметить, что утверждение: «диаметр входного зрачка = диаметру первой линзы объектива» несправедливо, поскольку диаметр входного зрачка приблизительно равен диаметру изображения апертурной диафрагмы, образованного передним компонентом. Сам диаметр передней линзы определяется требуемым углом изображения объектива и допустимым виньетированием.
Теоретический предел относительного отверстия для апланатических систем 1:0,5
Относительное отверстие объектива уменьшают ирисовой диафрагмой, позволяющей менять её величину (как правило — ступенчато, однако существуют объективы и с плавной регулировкой). На оправу объектива может быть нанесена шкала из знаменателей относительных отверстий (числа ирисовой диафрагмы), соответствующих различному диафрагмированию, на большинстве современных объективов такая шкала (как и кольцо регулировки диафрагмы) отсутствует и установка диафрагмы производится органами управления на теле камеры. Перевод ирисовой диафрагмы на одно деление изменяет относительное отверстие в раза, что даёт увеличение или уменьшение освещённости оптического изображения в два раза, за исключением первых двух чисел ирисовой диафрагмы, у которых такого изменения может и не быть.
Шкала ирисовой диафрагмы стандартизована, и образует следующий ряд:
1:0,7; 1:1; 1:1,4; 1:2; 1:2,8; 1:4; 1:5,6; 1:8; 1:11; 1:16; 1:22; 1:32; 1:45; 1:64.
Впрочем, первые диафрагменные числа на объективах могут и не совпадать со стандартными (1:2,5; 1:1,7).
Для удобства пользования на шкалу диафрагм обычно наносят только знаменатели относительных отверстий.
В современных автоматических и полуавтоматических фотоаппаратах число диафрагмы может устанавливаться не только на значения стандартного ряда, но и на промежуточные величины.
Следует отметить, что для некоторых зеркально-линзовых объективов данные рассуждения применимы с оговорками. В них диафрагма может иметь форму не круга, а кольца, и для нахождения диаметра входного зрачка необходимо реальный входной зрачок (кольцо) заменить при расчёте кругом эквивалентной площади. Диаметр найденого круга и будет являться искомым диаметром входного зрачка для применения в дальнейших расчётах.
См. также
Литература
Яштолд-Говорко В. А. Фотосъемка и обработка. Съемка, формулы, термины, рецепты. Изд. 4-е, сокр. М., «Искусство», 1977.
Относительное отверстие — Википедия
Материал из Википедии — свободной энциклопедии
Относительное отверстие объектива — оптическая мера светопропускания объектива. Различают геометрическое и эффективное относительные отверстия. Геометрическим отверстием считается отношение диаметра входного зрачка объектива к его заднему фокусному расстоянию[1]. Эффективное относительное отверстие всегда меньше, чем геометрическое, поскольку учитывает потери света при его прохождении через стекло и рассеянии на границах с воздухом и деталях оправы.
 Зависимость светопропускания объектива от относительного отверстия
Зависимость светопропускания объектива от относительного отверстияРасчёт относительного отверстия
Геометрическое относительное отверстие N {\displaystyle N} выражают в виде дроби[2]:
- N = D f ′ {\displaystyle N={D \over f’}} ,
где
D
{\displaystyle D}
обозначает диаметр входного зрачка, а
f
′
{\displaystyle f’}
— заднее фокусное расстояние. Относительное отверстие принято обозначать соотношением двух чисел, написанных через двоеточие. При этом, первое число всегда принимается за единицу, например 1:5,6. В современной литературе более широкое распространение получило обозначение относительного отверстия в виде дроби с числителем f, например f/5,6. Для зеркально-линзовых объективов площадь входного зрачка рассчитывается по более сложному закону, поскольку его центральная часть экранирована
Квадрат относительного отверстия называется светосилой и определяет соотношение яркости объекта и освещённости его изображения в фокальной плоскости[1]. Эффективное относительное отверстие вычисляется с учётом коэффициента светопропускания τ {\displaystyle \tau } оптической системы, учитывающего общую толщину стекла и количество границ воздух/стекло. Коэффициент, снижающий прозрачность объектива, определяется по формуле:
- τ = ( 1 − P ) n ⋅ ( 1 − α ) m {\displaystyle \tau =(1-P)^{n}\cdot (1-\alpha )^{m}} ,
где P {\displaystyle P} — доля света, теряемая при отражении одной поверхностью раздела сред;
- n {\displaystyle n} — число поверхностей раздела воздух/стекло;
- α {\displaystyle \alpha } — удельное поглощение света в 1 сантиметре стекла;
- m {\displaystyle m} — суммарная толщина линз объектива в сантиметрах.
Для непросветлённых объективов τ {\displaystyle \tau } не превышает 0,65. Объективы с просветлением теряют не более 10% света при его прохождении и рассеянии.
Приведённые способы расчёта геометрического и эффективного относительного отверстия справедливы только при фокусировке объектива на «бесконечность». Для конечных дистанций знаменатель дроби увеличивается из-за выдвижения объектива, приводя к уменьшению относительного отверстия. Эффект особенно заметен при макросъёмке, когда сопряжённое фокусное расстояние может превосходить расчётное в два и более раз. В этом случае пренебрегать изменением относительного отверстия недопустимо и требуются поправки при расчёте экспозиции[3].
Диафрагменное число
 Шкала диафрагмы объектива (нижняя), размеченная в диафрагменных числах. Положение кольца соответствует относительному отверстию f/8
Шкала диафрагмы объектива (нижняя), размеченная в диафрагменных числах. Положение кольца соответствует относительному отверстию f/8Если принять диаметр входного зрачка равным единице, геометрическое относительное отверстие может быть выражено следующим образом[4]:
- N = D f ′ = 1 k {\displaystyle N={D \over f’}={1 \over k}} .
В этом случае знаменатель относительного отверстия k {\displaystyle k} называют «диафрагменное число» или «число диафрагмы». Диафрагменное число вычисляется, как отношение фокусного расстояния объектива к диаметру его входного зрачка и обозначается цифрой. Диафрагменное число является величиной, обратной относительному отверстию[5][6].
- k = f ′ D = 1 N {\displaystyle k={f’ \over D}={1 \over N}} .
Этот параметр наиболее удобен для разметки шкал диафрагмы, поскольку не содержит дробей[7]. Регулировочная шкала ирисовой диафрагмы киносъёмочных объективов и фотообъективов старых типов (без автофокуса) градуируется в диафрагменных числах эффективного относительного отверстия, учитывающих потери света при его прохождении через стекло.
Каждое деление такой шкалы соответствует изменению светосилы в два раза, а относительного отверстия в 2 ≈ 1 , 41 {\displaystyle {\sqrt {2}}\approx 1,41} раз[7][2]. Исключение могут составлять самые малые значения диафрагменного числа, соответствующие оптическим возможностям объектива, и не укладывающиеся в стандартный ряд[8]. Такое строение шкалы диафрагменных чисел используется с 1950-х годов, когда появилось понятие экспозиционного числа, и позволяет при повороте кольца на одно деление менять экспозицию точно на одну экспозиционную ступень.
На современных фотообъективах такая шкала (как и кольцо регулировки диафрагмы) отсутствует и установка диафрагмы производится дистанционно органами управления фотоаппарата. Шкала диафрагменных чисел современных цифровых фотоаппаратов имеет промежуточные значения, соответствующие 1/3 экспозиционной ступени:
| 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 |
При автоматическом управлении экспозицией относительное отверстие регулируется бесступенчато и диафрагменное число может принимать любые дробные значения.
См. также
Источники
- ↑ 1 2 3 Фотокинотехника, 1981, с. 228.
- ↑ 1 2 Гордийчук, 1979, с. 152.
- ↑ Гордийчук, 1979, с. 153.
- ↑ Общий курс фотографии, 1987, с. 17.
- ↑ Фотокинотехника, 1981, с. 78.
- ↑ Фотография: Техника и искусство, 1986, с. 20.
- ↑ 1 2 Краткий справочник фотолюбителя, 1985, с. 34.
- ↑ Общий курс фотографии, 1987, с. 18.
Литература
- Гордийчук, И. Б. Справочник кинооператора / И. Б. Гордийчук, В. Г. Пелль. — М. : Искусство, 1979. — 440 с. — 30 000 экз.
- Е. А. Иофис. Фотокинотехника / И. Ю. Шебалин. — М.,: «Советская энциклопедия», 1981. — С. 228. — 447 с. — 100 000 экз.
- Н. Д. Панфилов, А. А. Фомин. Краткий справочник фотолюбителя / Н. Н. Жердецкая. — М.: «Искусство», 1985. — С. 179—184. — 367 с. — 100 000 экз.
- Фомин А. В. § 4. Фотографические объективы // Общий курс фотографии / Т. П. Булдакова. — 3-е. — М.,: «Легпромбытиздат», 1987. — С. 124—130. — 256 с. — 50 000 экз.
Почему диафрагма не бывает больше 22.
Диафрагма объектива. Назначение.
Диафрагма – механическое устройство с лепестками, устанавливающая диаметр прохождения пучка света.
Размер и положение диафрагмы определяют поле зрения, освещённость и качество изображения, глубину резкости и разрешающую способность оптической системы.
Т.к. выше 22 возникает дифракция. При сильной закрытой диафрагме качество хуже, чем при открытой, т.к. происходит дифракция света. Дифракция света – это явление, при котором мы можем наблюдать расщепление луча света, когда он огибает препятствие. Дифракция света, явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической оптики
Светоси́ла объекти́ва — величина, характеризующая степень ослабления объективом светового потока.
Иногда светосилой неправильно называют величину знаменателя относительного отверстия (диафрагменное число), так как светосила — характеристика самого объектива, а не связана с величиной диафрагмы, насадками в виде бленд, каше, светофильтров и т. п.
Светосила = освещенность объекта/яркость изображения
Относительное отверстие=диаметр линзы/фокусное расстояние
Освещенность объекта в идеале должна совпадать с яркостью изображения. Объектив поглощает 10-20% света. Светосила объектива 1:1,2 1:1 0,5
Относительное отверстие – это сколько пропускает света отверстие.
Яркость кадра ан матрице зависит от диаметра линз (d) и фокусного расстояния (f)
Относительнео отверстие D = d/f. Если d=f=1, то светосила объектива 1:1
Относительное отверстие объектива — отношение диаметра входного зрачка (изображения апертурной диафрагмы, построенного стоящими перед ней линзами в обратном ходе лучей (обычно совпадающего с первой линзой объектива)) объектива 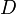 к его заднему фокусному расстоянию
к его заднему фокусному расстоянию 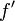 . Его величину выражают в виде дроби:
. Его величину выражают в виде дроби: 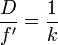 , когда числитель приведён к единице. Знаменатель относительного отверстия
, когда числитель приведён к единице. Знаменатель относительного отверстия 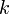 называют «диафрагменным числом» или «числом диафрагмы».
называют «диафрагменным числом» или «числом диафрагмы».
Следует заметить, что утверждение: диаметр входного зрачка = диаметру первой линзы объектива действует только для нормальных и телеобъективов с фиксированным фокусным растоянием. У широкоугольных объективов имеющих удлиненной задний отрезок диаметр входного зрачка = диаметру максимально открытой диафрагмы.
Теоретический предел относительного отверстия для апланатических систем 1:0,5
Относительное отверстие объектива уменьшают ирисовой диафрагмой, позволяющей менять её величину (как правило — ступенчато, однако существуют объективы и с плавной регулировкой). На оправу объектива может быть нанесена шкала из знаменателей относительных отверстий (числа ирисовой диафрагмы), соответствующих различному диафрагмированию, на большинстве современных объективов такая шкала (как и кольцо регулировки диафрагмы) отсутствует и установка диафрагмы производится органами управления на теле камеры. Перевод ирисовой диафрагмы на одно деление изменяет относительное отверстие в 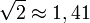 раза, что даёт увеличение или уменьшение освещённости оптического изображения в два раза, за исключением первых двух чисел ирисовой диафрагмы, у которых такого изменения может и не быть.
раза, что даёт увеличение или уменьшение освещённости оптического изображения в два раза, за исключением первых двух чисел ирисовой диафрагмы, у которых такого изменения может и не быть.
Шкала ирисовой диафрагмы стандартизована, и образует следующий ряд:
1:0,7; 1:1; 1:1,4; 1:2; 1:2,8; 1:4; 1:5,6; 1:8; 1:11; 1:16; 1:22; 1:32; 1:45; 1:64.
Впрочем, первые диафрагменные числа на объективах могут и не совпадать со стандартными (1:2,5; 1:1,7).
Для удобства пользования на шкалу диафрагм обычно наносят только знаменатели относительных отверстий.
В современных автоматических и полуавтоматических фотоаппаратах, число диафрагмы может устанавливаться не только на значения стандартного ряда, но и на промежуточные величины.
Следует отметить, что для некоторых зеркально-линзовых объективов данные рассуждения применимы с оговорками. В них диафрагма может иметь форму не круга, а кольца, и для нахождения диаметра входного зрачка необходимо реальный входной зрачок (кольцо) заменить при расчёте кругом эквивалентной площади. Диаметр найденого круга и будет являться искомым диаметром входного зрачка для применения в дальнейших расчётах.
Что такое объектив с постоянной апертурой?
Вы ищете новый объектив? Знание постоянной апертуры поможет вам в принятии решения.
Это особенность бюджетных объективов, особенно телеобъективов и объективов с большим фокусным расстоянием. Читайте дальше, чтобы узнать, что это значит, и если вам нужно этого избежать.

[ Примечание: ExpertPhotography поддерживается читателями. Ссылки на продукты на ExpertPhotography являются реферальными ссылками.Если вы используете один из них и покупаете что-то, мы зарабатываем немного денег. Нужна дополнительная информация? Посмотрите, как все это работает здесь. ]


Что такое апертура?
Апертура — это один элемент, который составляет треугольник экспозиции. Это составляет 1/3 от этого, поэтому очень важно знать об этом.
Ваш объектив и система камеры захватывают свет по-разному. Отверстие в вашем объективе — это отверстие, и вы можете им управлять.
Апертура делает две вещи. Он контролирует, сколько света вы пропускаете, а затем попадает на ваш датчик. Он также контролирует глубину резкости вашей сцены.
Вы управляете диафрагмой через объектив для пленочных камер и на камере для цифровых камер. Это отверстие проходит между двумя числами, самой широкой и самой узкой апертурой.
Открывая или закрывая диафрагму, вы перемещаете перекрывающиеся лопасти. Закрывая диафрагму до минимального значения, вы ограничиваете свет до минимума.Наименьшая диафрагма — самая широкая диафрагма, обеспечивающая наименьшую глубину резкости.
F / 22 — это обычно самый большой f / stop, которого вы можете достичь. Это достигается путем открытия диафрагмы до ее самой большой, которая дает вам самую узкую апертуру и самую широкую глубину резкости.
Это сбивает с толку, поэтому я предоставил небольшой масштаб:
F / 2 — самая широкая диафрагма — наименьшее число диафрагм / стоп — наименьшая глубина резкости
F / 22 — самая узкая диафрагма — самая большая диафрагма / остановка — самая короткая глубина резкости
Портретные фотографы, вероятно, будут использовать самую широкую диафрагму, в то время как пейзажные фотографы будут использовать самую узкую диафрагму.

Что такое объектив с постоянной апертурой?
Когда дело доходит до покупки телеобъективов, есть несколько вещей, о которых вам нужно знать. Оставляя в стороне стабилизацию изображения и другие элементы профессионального уровня, вам нужно подумать о диафрагме объектива.
Посмотрите на следующий пример:
Canon EF 70-200mm f / 2.8L USM Телеобъектив.
Есть несколько вещей, которые мы можем сказать об объективе из приведенных сокращений и цифр.Мы строго смотрим на апертуру.
Это телеобъектив, означающий, что фокусное расстояние может меняться от 70 мм до 200 мм. Апертура f / 2.8, и она не меняется.
При перемещении объектива для изменения фокусного расстояния диафрагма может оставаться на уровне f / 2,8. Это означает, что объектив имеет фиксированное фокусное расстояние или объектив с постоянной апертурой.
Вы можете подумать, что это стандарт для всех объективов, но вы ошибаетесь. Это особенность более дорогих объективов, так как для поддержания диафрагмы в пределах диапазона изменения фокусировки требуется много исследований и разработок.
Давайте посмотрим на другой пример:
Объектив Canon EF 100-400мм f / 4.5-5.6L IS II USM.
Этот объектив, как вы заметили, имеет два отверстия; f / 4.5 и f / 5.6. Это означает, что это не фиксированное фокусное расстояние или объектив с постоянной апертурой.
Что произойдет, при фокусном расстоянии 100 мм вы получите диафрагму f / 4.5. При изменении фокусного расстояния на 400 мм диафрагма изменится на f / 5.6.

Преимущества и недостатки
Наличие объектива с переменным фокусным расстоянием может показаться ужасным объективом по сравнению с объективом с фиксированным фокусным расстоянием.Ну, это так, а это не так.
Объективы с постоянной апертурой очень дороги. Гораздо дороже, чем объективы с переменным фокусным расстоянием. Выгода — это стоимость.
Если вы фотограф-пейзажист или, другими словами, вам не нужна широкая диафрагма, вам не нужен объектив с постоянной диафрагмой. При съемке сцен на f / 11 или выше, не имеет значения, если вы получите f / 4.5 или f / 5.6.
Есть несколько объективов с нужным фокусным расстоянием, но вы можете получить их только с переменным фокусным расстоянием.Тогда у вас нет выбора.
Но если вам действительно нужен зум-объектив с широкой диафрагмой, вам придется раскошелиться на дополнительные деньги, чтобы получить его.
При использовании объективов с датчиком кадрирования можно подумать, что вы можете сохранить широкую диафрагму, увеличивая фокусное расстояние. Проблема в том, что ваша диафрагма также изменится.
Ознакомьтесь с нашими руководствами по аббревиатурам объективов Canon, Nikon, Sigma, Tamron и Tokina далее!
, 
Объективы камеры объяснены: Апертура
Апертура объектива — это отверстие, которое используется для контроля количества света, попадающего в камеру. Это отверстие создается серией лезвий внутри объектива, которые образуют радужную оболочку, которая может двигаться, чтобы открываться или закрываться и изменять размер апертуры.
Величина диафрагмы рассчитывается по следующим формулам:
Величина диафрагмы = фокусное расстояние (f) / Диаметр апертуры в мм
Подробнее: Sigma 60-600mm f / 4.5-6.3 DG OS HSM | Спорт
Несмотря на то, что диаметр диафрагмы двух разных объективов может быть разным, если значение диафрагмы (или число f /) одинаковое, они пропускают одинаковое количество света.
Например, апертура f / 11 на объективе 100 мм обозначает апертуру диаметром 100/11, которая составляет 9,09 мм.
С объективом 50 мм такая же апертура (f / 11) имеет диаметр 4,54 мм.
Несмотря на эту разницу в размерах, две линзы пропускают одинаковое количество света, когда они установлены на f / 11.

Объективы камеры объяснены: Быстрые и медленные объективы
Объективы помечены с максимальной настройкой диафрагмы. Основные объективы с коротким фокусным расстоянием обычно имеют максимальную диафрагму f / 1,4, f / 1,8 или f / 2, в то время как телеобъектив с большей вероятностью имеет максимальные значения диафрагмы f / 2,8, f / 4 или даже f / 5,6.
Высококачественные дорогостоящие зум-объективы способны поддерживать одинаковую настройку максимальной диафрагмы во всем диапазоне фокусных расстояний. Однако менее дорогие зум-объективы имеют переменную настройку максимальной диафрагмы.
Объективы, продающиеся со многими зеркальными фотокамерами и компактными системными камерами, часто имеют максимальную диафрагму f / 3,5-5,6.
Это означает, что при самой широкой установке диафрагма может быть открыта до f / 3.5, тогда как в самой длинной телеобъективной точке максимальная диафрагма составляет f / 5.6.
Если вы установите объектив на f / 3.5 в самой широкой точке и увеличите масштаб, диафрагма изменится на f / 5.6 к тому времени, когда вы достигнете самой длинной точки.
Длинные объективы с максимальной диафрагмой f / 2,8 или более и более короткие линзы с диафрагмой f / 2 или f / 1.8 часто называют «быстрыми» линзами.
Это потому, что они пропускают больше света, чем их более медленные коллеги с меньшими максимальными значениями диафрагмы, и это позволяет использовать более высокие скорости затвора.
Быстрые телеобъективы поэтому очень популярны среди профессиональных спортивных фотографов, потому что длинное фокусное расстояние обеспечивает плотное кадрирование удаленного объекта, а широкая максимальная диафрагма позволяет использовать выдерживающие движение выдержки.

Объективы камеры объяснены: Стабилизация
Внутри некоторых объективов есть элемент, который может перемещаться, чтобы компенсировать те случайные движения, которые возникают, когда мы держим камеру в руках.
В некоторых случаях эта система стабилизации имеет несколько настроек; например, есть такая, которая ограничивает коррекцию вертикальными движениями, что полезно при панорамировании для следования за движущимся объектом.
Некоторые системы стабилизации изображения также можно активировать, только когда спуск затвора полностью нажат, чтобы сделать снимок.
Это означает, что вид через видоискатель не стабилизирован, как это было бы обычно, но диапазон коррекции, доступный во время захвата, больше, что потенциально делает его более эффективным.

Объективы камеры объяснены: ограничитель фокуса
У некоторых более длинных объективов есть ограничители фокуса, которые предназначены для сокращения времени, необходимого объективу для фокусировки на объекте, когда он находится в пределах определенного расстояния от камеры.
Это также уменьшает любые отвлекающие факторы для системы AF, делая ее более точной. В некоторых случаях можно даже настроить диапазон фокусировки для объектива. Это особенно полезно, когда между вами и объектом могут быть какие-либо объекты, поскольку камера их игнорирует и фокусируется только в указанном диапазоне.
,можно рассчитать по известной формуле, введенной Эрнстом Аббе в конце XIX века, и представляет собой меру резкости изображения светового микроскопа:
Разрешение x, y = λ / 2 [η • sin (α)] (2) разрешение z = 2λ / [η • sin (α)] 2 (3)
, где λ — длина волны света, η представляет показатель преломления носителя изображения, как описано выше, и объединенный термин η • sin (α) известен как объективная числовая апертура (NA).Объективы, обычно используемые в микроскопии, имеют числовую апертуру менее 1,5, что ограничивает термин α в уравнениях (2) и (3) до менее 70 градусов (хотя новые высокопроизводительные задачи близко приближаются к этому пределу). Следовательно, предел теоретического разрешения на самой короткой практической длине волны (приблизительно 400 нм) составляет около 150 нм в поперечном измерении и приближается к 400 нм в осевом измерении при использовании объектива с числовой апертурой 1.40. Таким образом, структуры, которые находятся ближе, чем это расстояние, не могут быть разрешены в боковой плоскости с помощью микроскопа. В связи с центральным значением взаимосвязи между показателем преломления среды изображения и угловой апертурой объектива, Аббе ввел понятие числовой апертуры в ходе объяснения разрешения микроскопа.
Дифракционные кольца в диске Эйри вызваны функцией ограничения апертуры объектива, так что объектив действует как отверстие, за которым находятся дифракционные кольца.Чем выше апертура объектива и конденсатора, тем меньше будет d0. Таким образом, чем выше числовая апертура всей системы, тем лучше разрешение. Одно из нескольких уравнений, относящихся к исходной формуле Аббе, которые были получены для выражения взаимосвязи между числовой апертурой, длиной волны и разрешением:
Разрешениеx, у или d0 = 1,22λ / [NAObj + NACon] (4)
Где λ — длина волны светового изображения, NACon — числовая апертура конденсатора, а NAObj — объективная числовая апертура.Коэффициент 1.22 был взят из расчета для случая, показанного на рисунке 4 для близкого сближения двух дисков Эйри, где профили интенсивности были наложены друг на друга. Если две точки изображения находятся далеко друг от друга, их легко распознать как отдельные объекты. Однако, когда расстояние между дисками Эйри все больше уменьшается, предельная точка достигается, когда главный максимум второго диска Эйри совпадает с первым минимумом первого диска Эйри. Наложенные профили отображают два максимума яркости, которые разделены долиной.Интенсивность в долине снижается примерно на 20 процентов по сравнению с двумя максимумами. Этого достаточно для того, чтобы человеческий глаз мог видеть две отдельные точки, предел, который называется критерием Рэлея .
Числовая апертура оптической системы определяется как произведение показателя преломления луча, от которого поступает свет, и синуса максимального угла луча относительно оси, для которого свет может проходить через систему, исходя из чисто геометрических соображений (лучевая оптика ):
Для максимального угла падения требуется, чтобы свет проходил через всю систему и не только через входное отверстие.
Простой случай — это коллиматорная линза:
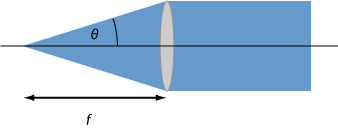 Фигура 1:
Коллимирующая линза теоретически может принимать свет от конуса, угол раскрытия которого ограничен его размером.
Фигура 1:
Коллимирующая линза теоретически может принимать свет от конуса, угол раскрытия которого ограничен его размером.Экстремальные лучи ограничены размером линзы или, в некоторых случаях, несколько меньше, если есть непрозрачная грань.
Часто не рекомендуется использовать объектив или всю его площадь, так как могут быть значительные сферические аберрации. Числовая апертура, однако, является полностью геометрической мерой, которая не учитывает такие аспекты.
Числовая апертура зависит от местоположения плоскости объекта, определенной дизайнером!В приведенном выше примере числовая апертура объектива определяется его диаметром и фокусным расстоянием. Однако обратите внимание, что линза может быть предназначена не для коллимации света, а, например, для визуализации объектов на большем расстоянии. В этом случае можно рассмотреть лучи, идущие от этого расстояния до объекта, и полученная числовая апертура будет соответственно меньше — иногда даже намного меньше.Это показывает, что числовая апертура зависит от местоположения некоторой плоскости объекта, определенной проектировщиком в соответствии с предполагаемым использованием.
Некоторые линзы используются для фокусировки коллимированных лазерных лучей на небольшие пятна. Числовая апертура такой линзы зависит от ее апертуры и фокусного расстояния, как и для коллимационной линзы, рассмотренной выше. Радиус луча Вт Объектив на объективе должен быть достаточно мал, чтобы избежать усечения или чрезмерных сферических аберраций. Как правило, он будет порядка половины радиуса диафрагмы объектива (или, возможно, немного больше), и в этом случае ( Вт, , , объектив = , D /4 = NA · , /2, с угол расходимости луча составляет только половину NA) достижимый радиус луча в фокусе составляет
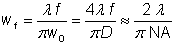
, где D — диаметр апертуры, — — фокусное расстояние и λ — длина оптической волны.Обратите внимание, что расчет основан на параксиальном приближении и поэтому не точен для случаев с очень высоким NA.
Несколько меньший размер пятна может быть возможен при соответственно большем радиусе входного луча, если рабочие характеристики не испорчены аберрациями. В случае сомнений следует спросить производителя, какой максимальный радиус входного луча подходит для определенного объектива.
Линзы High-NA требуются для различных применений:
- В проигрывателях и рекордерах оптических носителей данных, таких как компакт-диски, DVD-диски и диски Blu-ray, важно фокусировать лазерный свет в маленькое пятно (яму) и получать свет от такого пятна.
- Линзы с высоким NA также необходимы для коллимирующих лазерных лучей, которые происходят из небольших отверстий. Например, это относится к маломощным одномодовым лазерным диодам. При использовании линзы со слишком низким NA результирующий коллимированный луч может быть искажен (аберрирован) или даже усечен.
