Пропорция фибоначчи: Золотое сечение и пропорции Фибоначчи

Содержание

Что такое числа Фибоначчи, золотое сечение? ⋆ FutureNow

Твитнуть

Последовательность Фибоначчи – одна из самых известных формул математики. Так, что такое числа Фибоначчи, золотое сечение и какая их интересная стория?

Что такое числа Фибоначчи?

Каждое число в последовательности Фибоначчи – это сумма двух чисел, предшествующих ему.

Итак, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Математическое уравнение, описывающее число Фибоначчи: Xn + 2 = Xn + 1 + Xn

Фибоначчи числа иногда называют “секретным кодом природы” и “общем правилом природы”. Говорят, что данная последовательность руководит размерами всего сущего, в том числе обьясняет Великую пирамиду в Гизе, так и многие вещи, с которыми мы сталкиваемся каждый день.

Числа Фибоначчи: богатая история

Поэтому какова реальная история стоит за этой знаменитой последовательностью?

Многие источники утверждают, что ее впервые обнаружил или “изобрел” Леонардо Фибоначчи.

Итальянский математик, родился около 1170 года нашей эры и первоначально был известен как Леонардо из Пизы. Лишь в 19 веке историки придумали прозвище Фибоначчи, чтобы отличить математика от другого известного Пизарського Леонардо.

Но Леонардо из Пизы на самом деле не изобрел последовательность. Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.

Однако в 1202 Леонардо из Пизы опубликовал большой том “Liber Abaci,” книгу по математике “о том, как производить вычисления”. “Liber Abaci”, написанная для торговцев, где изложена индуистско-арабский арифметика, которая является полезной для отслеживания прибыли, убытков, остатков по кредитам и тому подобное.

ЧТО ТАКОЕ ШАРОВАЯ МОЛНИЯ: СУЩЕСТВУЕТ ЛИ ОНА?

В книге Леонардо из Пизы вводит последовательность с задачей о кроликах. Проблема заключается в следующем: начнем с самца и самки кролика. Через месяц они созревают и дают помет в результате которого мы имеем еще самца и самку кролика.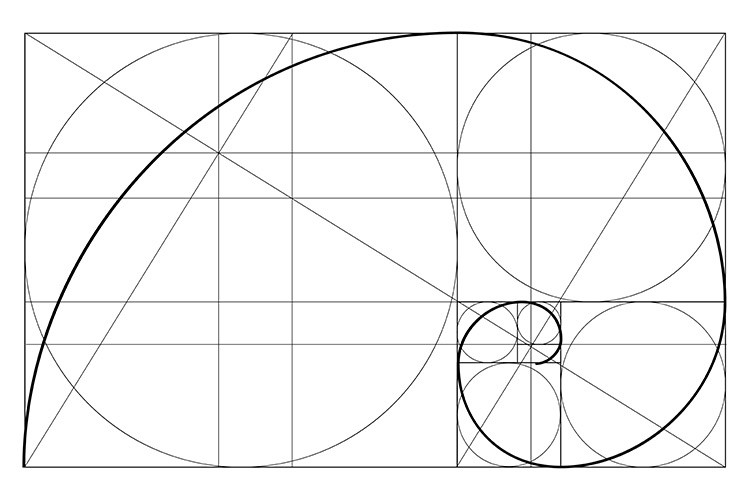 Через месяц эти кролики размножаются и получается – вы догадались – еще один самец и самка, которые также могут спариваться через месяц. Через год сколько бы у вас было кроликов? Ответ, 144, спрятан в формуле, которая сейчас известна как последовательность Фибоначчи.

“Liber Abaci” впервые представила эту последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы больше никогда не вспоминал ее.

На самом деле эти числа Фибоначчи были забыты до 19 века, когда математики подробнее изучили математические свойства последовательности. В 1877 году французский математик Эдуард Лукас официально назвал задачу о кроликах “последовательностью Фибоначчи”.

Числа Фибоначчи и золотое сечение

Мы узнали что такое числа Фибоначчи, но какое же значение имеет последовательность Фибоначчи?

Кроме как учебный инструмент, она проявляется во многих случаях в природе. Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.

Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как “золотое сечение”. Проще говоря, отношение чисел в последовательности, поскольку последовательность идет к бесконечности, приближается к золотому сечению, который составляет +1,6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмической спирали, коэффициент роста которой равен золотому сечению.

Золотое сечение объясняет рост некоторых растений. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Но есть также растения, которые не соблюдают этого правила.

Мистификации и выдумки

Когда люди начинают связывать человеческое тело, искусство и архитектуру, много вымышленных теорий и мистификаций ссылаются на последовательность Фибоначчи.

“Понадобится большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, многие из которой – это просто повторение одних и тех же фантазий разных авторов”, – написал Джордж Марковский, математик из университета Мэн в 1992 году.

Значительная часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Зейзинга. Он утверждал, что пропорции человеческого тела основана на золотом сечении.

Золотое соотношение проросло в “золотые прямоугольники”, “золотые треугольники” и всевозможные теории об этих знаковых размерах.

С тех пор люди говорят, что золотое соотношение или золотое сечение можно найти в размерах Пирамиды в Гизе, Парфеноне, “Витрувийським человеке” Леонардо да Винчи и ренессансных сооружениях.

Под сомнение можно поставить и беспрекословное утверждение о том, что золотое сечение является “однозначно приятным” для человеческого глаза – на чем часто настаивают фотографы.

Часто все эти утверждения, когда их проверяют, являются ошибочными. Люди часто выдают желаемое за действительное.

Источник: www.livescience.com/

Разметчик Фибоначчи

Разметчик Фибоначчи — это устройство, позволяющее вам всегда иметь под рукой соотношениие размеров для ваших изделий, удовлетворяющее принципам Золотого Соотношения. Если вы хотите, чтоб мебель, которую вы делаете, была не только функциональна, но и по-настоящему красива, то начинать нужно с пропорций предмета в целом и его частей. Если эти пропорции правильны, ваше произведение будет радовать глаз, иначе — может быть ужасным. Разметчик Фибоначчи — отличное подручное средство для проектирования красивых изделий.

Разметчик Фибоначчи, специальный инструмент, назван по имени итальянского математика Фибоначчи, жившего в XIII веке.

«Фибоначчи» у этого учёного — это псевдоним, происхождение которого не известно он же — Fibonacci, он же — Леона́рдо Пиза́нский, он же — Leonardo Pisano.

В честь учёного назван и числовой ряд, в котором каждое последующее число равно сумме двух предыдущих. Эта числовая последовательность носит название чисел Фибоначчи:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, …

Хотя этот ряд и был известен ещё в Древней Индии, т. е. задолго до рождения умного Фибоначчи, но, тем не менее, своё нынешнее название числа Фибоначчи получили благодаря исследованию свойств этих чисел, проведённому именно этим учёным в его труде «Книга абака» (Издательство РИМГНИЗ «Римское Государственное Народное Издательство», 1202 г.).

Ряды Фибоначчи, спирали Фибоначчи, уровни Фибоначчи — об этом много можно прочитать.

К чёму всё это? Одна закономерность упомянута, но можно заметить и другую — деление числа в ряду Фибоначчи на предыдущее даёт практически постоянный результат — 1,618 — проверьте, если не лень. С этими последовательностями много чего связано — от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции. Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.

Даже если вы одарены превосходным видением, не так-то просто спроектировать предмет мебели без использования основополагающих принципов для определения размеров этого предмета мебели и, главное, пропорций между его элементами. Будет ли это подход к проектированию, который передаётся от мастера к ученику или ваше врожденное чувство равновесия и гармонии, которым обладают лишь некоторые одарённые люди, в любом случае без такой совокупности знаний и опыта вы не сможете создать совершенное изделие, которое будет радовать ваш глаз и вызывать восхизение окружающих и ваших друзей. Можно создать изделие, которое будет прочно и функционально адекватно, но не будет радовать и вызывать приятные чувства. Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.

Главным среди множества совокупностей фундаментальных установок, сложившихся за сотни лет представлений и понятий, которые разработчики предметов мебели использовали и продолжают использовать для обеспечения баланса и хороших пропорций в дизайне мебели является золотая пропорция или соотношение (также называемое золотой серединой или золотым сечением). Обозначается эта пропорция греческой буквой ∳ (фи). Золотое соотношение может быть выражено уравнением ∳ (фи)= [1 + √ 5] / 2. Для простоты практического применения, мы можем взять лишь результирующее значение ∳ (фи), равное 1,618. Т.е. одно значение к другому должно относится как 1 к 1,618. Одна длина, к другой, например.

Один из многих замечательных принципов золотой пропорции является то, что коротий отрезок прямой линии по отношению к длинному отрезку этой же линии относится так же, как длинный отрезок линии относится к общей длине линии, и это соотношение равно ∳ (фи) = 1,618:

Именно это соотношение заложено в самой конструкции замечательного разметочного инструмента — Разметчика Фибоначчи:

Исходя из описанного принципа, Золотым (или гармоничным) Прямоугольником является такой, стороны в котором соотносятся как 1 : 1,618, т.е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:

Узнаёте? Это же столешница гармоничного стола! Или фасад тумбы и много чего ещё.

Аналогично, Золотым (или гармоничным) Параллелепипедом является тот, стороны в котором тоже соотносятся как 1 : 1,618, т.е. длина большей стороны параллелепипеда равна высоте параллелепипеда, умноженной на ∳ (фи)=1,618, а ширина параллелепипеда равна высоте параллелепипеда, поделённой на ∳ (фи)=1,618:

Узнаёте? Это же мебельная тумба, пристенный стол (консоль) и т.д.

Золотая Пропорция лежит в основе многих (если не всех) естественных соотношений и даже построения нашей Вселенной. Примеры есть в изобилии на каждом уровне, от размножения кроликов, расположения семян в подсолнухе и орешков в шишке, до астрофизики и квантовой механики. Планетарные орбиты и даже структура человеческой фигуры являются ещё одним подвержедния соблюдения этой замечательной пропорции.

Соотношение между соседними фалангами пальцев — это ∳ (фи) = 1,618, Соотношение между локтем и кистью — это ∳ (фи) = 1,618, соотношение расстояния от макушки до глаз и растояния от глаз до подбородка — это ∳ (фи) = 1,618, соотношение расстояния от макушки до пупка и растояния от пупка до пяток — это опять-таки ∳ (фи) = 1,618:

Дистанции между солнцем и первыми пяти планетами в солнечной системе так же соотносятся (примерно) как ∳ (фи) = 1,618, поэтому, как безусловно известно, астронометрия использует золотое соотношение при определении планет на их орбитах:

Будучи столь фундаментальным и столь широко распространённым в природе, это отношение просто призывает нас на подсознательном уровне как абсолютно правильное, которому надо следовать. Как таковое, это соотношение было использовано на протяжении веков дизайнерами и архитекторами, от пирамид до мебельных шедевров.

Большая пирамида в Гиза, как теперь понятно, тоже построена в соответствии с Золотым Сечением: высота стороны пирамиды равна длине основания стороны пирамиды, умноженной на всё ту же величину ∳ (фи) = 1,618:

При строительстве Парфенона (древнегреческий храм, расположенный на афинском Акрополе, главный храм в древних Афинах) использовалось соотношение ∳ (фи) = 1,618 при определении внешних размеров и соотношения его частей:

Достоверно не известно, применялись ли при построении Парфенона калькуляторы или Разметчики Фибоначчи, но соотношение точно применялось. Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:

В вышеприведённом ролике, наконец-то, дело дошло и до предмета мебели, пусть и простого. Главное — соотношение всё то же — ∳ (фи) = 1,618.

В одном из видов комода с множеством ящиков называемом в разных изданиях как Highboy или Popadour («Высокий парень» или «Помпадур»), сделанном в Филадельфии в промежутке между 1762 и 1790 годами, используется Золотая Пропорция в соотношении размеров многих из его элементов. Каркас — это Золотой прямоугольник, положение сужения («талии» шкафа) определяется делением общей высоты шкафа на ∳ (фи) = 1,618. Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:

Золотое Сечение применяется при изготовлении мебели чаще всего в качестве некоего прямоугольника, который строится с помощью ∳ (фи) = 1,618 для двух его измерений, т.е. уже упоминаемого Золотого прямоугольника, где длина в 1,618 раз больше ширины (или наоборот). Эти пропорции могут быть использованы для определения габаритных размеров мебели, а также деталей интерьера, таких как двери и ящики. Можно применять рассчёты, деля и умножая на такое «круглое» и удобное число, как 1,618, но можно просто использовать Разметчик Фибоначчи, просто снимая размеры бОльшего предмета и откладывая после этого размер меньшего предмета.

Или наоборот. Быстро, просто и удобно.

Предметы мебели являются трехмерными и Золотое Соотношение может быть применено ко всем трем измерениям, т.е. предмет мебели становится Золотым Параллелепипедом, если сделать его по правилам Золотого Соотношения. К примеру, в простом случае, глядя на предмет мебели сбоку, его высота может быть наибольшим измерением в Золотом Прямоугольнике. Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.

Необходимо отметить, однако, что форма предмета должна следовать за его функцией. Даже превосходные пропорции мебели могут оказаться быть бессмысленными, если этот предмет не может быть использован, например потому, что он слишком маленький или слишком большой или по другим причинам не может быть использован с комфортом. Следовательно, практические соображения должны быть на первом месте. В самом деле, большинство проектов мебели требуют, чтоб вы начали проектирование с некоторых заданных размеров: стол должен быть определенной высоты, шкаф возможно, придется приноравливать к конкретному пространству, а в книжном шкафу может потребоваться определенное количество полок. Но почти наверняка вы вынуждены будете определять множество других размеров, в отношении которых можно применить правильные пропорции. Но результат будет стоит затраченных усилий, чтоб в результате увидеть, как Золотое Соотношение может работать для всех этих элементов. Принятие решения о размерах «на глаз» или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.

Итак, размеры отдельных частей мебели должны быть пропорциональны в соответствии с Золотым Соотношением. Такие элементы, как ножки стола, относительные размеры элементов каркаса, такие как вертикальные и горизонтальные части фасадов, проноги, царги и т.д., могут быть рассчитаны с применением Золотой Пропорции. Золотое сечение также предлагает один из способов решение проблемы проектирования ящиков в комоде с ступенчатым увеличением высоты ящиков. С помощью Разметчика Фибоначчи легко осуществить такую разметку — надо просто взять размер бОльшего ящика и по разметчику отложить размеры двух соседних ящиков и т. д. После этого, взяв размер ящика, по разметчику отложить расстояние от верха ящика до места расположения его ручки.

Такой метод использования Разметчика Фибоначчи, как инструмента для практического применения Золотого Соотношения будут эффективен для определения и других размеров, таких, как положение полок в шкафу, разделителей между ящиками и т.д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части — дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.

Спроектировать что-то с абсолютно совершенными пропорциями редко удается в реальности. Почти каждый предмет мебели или дерева придётся соотносить с ограничениями, накладываемыми функциональностью, возможностями столярных соединений или экономией средств. Но даже попытка приблизиться к совершенству, которое может быть определено как размеры, в точности соответствующие Золотому Соотношению гарантирет вам получение лучшего результата по сравнению с разработкой без внимания к этим основополагающим принципам. Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.

Наконец, мы часто корректируем вещи на глаз, чтобы сделать предмет легче и лучше сбалансированным, и делаем мы это с помощью методов, которые являются повседневными в деревообработке. Эти методы включают в себя учёт изменения размеров заготовки, исходя из направления волокон древесины, учёт рисунка древесины, с помощью которого можно предмет мебели сделать более привлекательным, отделку краёв и углов, которая создаст впечатление большей или меньшей толщины элемента изделия, использование молдингов для более точного соответствия изделия Золотому Прямоугольнику или Параллелепипеду, использование сужающихся ножек, чтобы сделать ощущение большего приближения предмета мебели к идеальной пропорции, и, в конце концов, смешивание всех этих методов для достижения идеального дизайна. Использование Золотого Сечения и инструмента для его применения — Разметчика Фибоначчи — начало этого стремления к совершенству.

В статье использованы материалы главы «A Guide to Good Design» из книги «Practical Furniture Design», написанной Graham Blackburn — признанным мебельным мастером, популяризатором деревообработки и издателем.

Евгений Фукс

технический консультант
LeighJigs.ru
[email protected]

Уровни Фибоначчи. Что это и как их использовать в трейдинге

Золотое сечение или с чего все начиналось

Те, кого интересует сугубо прикладной аспект данных инструментов, могут пропустить этот раздел — экскурс в историю чисел Фибоначчи, а также их появления в трейдинге.

Последовательность Фибоначчи была хорошо известна еще в древней Индии, где применялась в стихосложении. Но имя свое она получила благодаря европейскому математику XII века Леонардо Пизанскому, более известному по псевдониму Фибоначчи. Фибоначчи, помимо других многочисленных математических задач, подробно исследовал и описал эту последовательность в труде «Liber Abaci» («Книга Абака» или «Книга об Абаке»). Последовательность эта представляет из себя бесконечный ряд чисел, каждый следующий член которого равен сумме двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

У этого ряда есть много замечательных математических особенностей, но главным является то, что отношение члена ряда к предыдущему стремится к знаменитому «Золотому сечению» — числу 1,618. Это число известно с античных времен и впервые встречается в «Началах» Евклида (около 300 лет до н. э.), где применялось для построения правильного пятиугольника.

Золотое сечение считается наиболее гармоничной пропорцией отношения целого к части. Магическим образом число 1,618 очень часто встречается в природных формах, напрямую не имеющих ничего общего между собой. Эту пропорцию можно заметить в раковинах улиток, расстоянии между листьями на ветке, форме спиралей галактик и даже в среднестатистическом соотношении частей тела человека.

Белорусский ученый Эдуард Сороко, который изучал формы золотых сечений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм — это закручивание по спирали.

В музыкальных произведениях, стихотворениях и художественных произведениях также встречается пропорция 1,618. Ученые умы XIX века признали золотое сечение эталоном гармонии пропорций в природе.

Идея искать золотое сечение в графиках биржевых котировок принадлежала американскому инженеру и управленцу Ральфу Hельсону Эллиотту, который увлекся анализом цен после серьезной болезни в начале 1930х гг. Эллиотт изучал годовые, месячные, недельные, дневные, часовые и получасовые графики различных фондовых индексов, охватывающих 75-летнюю историю поведения рынка. В процессе исследования он заметил, что движения индексов подчинены определенным ритмам — волнам, в пропорциях которых прослеживаются те самые 1,618. Эллиот написал на эту тему ряд трудов, самым масштабным из которых стала книга «Закон природы — секрет вселенной» (англ. Nature’s Law — The Secret of the Universe)», в которую он включил все свои наработки, касающиеся теории волн и соотношения Фибоначчи.

После Эллиота многие трейдеры и исследователи рынка искали различные применения числам Фибоначчи в биржевой торговле. Развитие вычислительной техники позволило аналитикам далеко продвинуться в этом направлении. Современные трейдеры активно используют инструменты, основанные на данном математическом.

Уровни Фибоначчи в биржевой торговле

Пожалуй, самый распространенный терминал для торговли на российском фондовом рынке Quik предлагает пользователю четыре инструмента, основанных на последовательности Фибоначчи. Это уровни, веер, дуги и временные зоны Фибоначчи. Начнем с самых популярных — уровней.

Одним из самых старых и надежных инструментов трейдера являются широко распространенные уровни поддержки и сопротивления. Участникам рынка нужны ценовые ориентиры, чтобы понять, выгодно ли покупать сейчас, не пора ли продавать и где цена может сменить свое направление. Однако не всегда удается точно определить, какой уровень отработает, а какой цена даже не заметит. Как раз эту проблему помогают решить уровни Фибоначчи.

Определение уровней коррекции

По правилам, инструмент «Уровни Фибоначчи» растягивается от начала тренда к его окончанию (на самом деле, если вы растянете уровни наоборот от конца к началу, в Quik разницы не будет). Если растянуть его таким образом, то получившиеся уровни станут возможными целям для коррекции. От этих уровней можно входить по тренду, либо использовать в качестве цели в контр-трендовых сделках.

На примере графика акций «Норильского никеля» хорошо видно, как четко были отработаны уровни 23,6 и 38,2. Причем тут есть особенность: если уровень Фибоначчи совпадает с уровнем на графике, как в данном примере, то вероятность, что он будет отработан, становится очень высокой. Еще лучше, если при этом он будет расположен на круглом числе.

Стоит сразу оговорить ограничение применения. Данный инструмент применяется только при наличии явно выраженного тренда. Если применять его на инструменте, который движется внутри боковика, то уровни отрабатываются очень «грязно», и вряд ли их использование принесет вам прибыль в долгосрочной перспективе.

Движение по Русгидро происходило внутри флэта с большим откатом. В этом случае уровень 23,6 отработал очень «грязно», и цена могла много раз зацепить стоп-заявку.

Также, уровни становятся более «грязными», когда фаза коррекции затягивается. Однако и в этом случае уровни коррекции по Фибоначчи могут оставаться актуальными, причем могут работать в том числе и зеркально.

Еще одним способом применения коррекционных уровней может быть торговля откатов. Когда инструмент делает быстрое движение к значимому уровню, от которого высока вероятность отката, коррекционный уровень 38,2 может показать вам потенциал, до которого можно держать позицию.

Что касается таймфреймов, применять инструмент стоит в диапазоне таймфреймов М15 — D1.

Определение волн Эллиота

Часто уровни Фибоначчи используются в связке с волновой теорией Эллиота. Согласно этой теории, любое трендовое движение по финансовому инструменту можно разложить на пять волн: три основных (импульсных) по тренду и две коррекционных против тренда. Импульсные волны нумеруются как первая, третья и пятая, а коррекционные, в свою очередь, вторая и четвертая.

Любое коррекционное движение тоже можно разложить, но только на три волны. Все внутренние волны также раскладываются по принципу фрактала (фрактал — самоподобная структура). Наглядно этот процесс представлен на рисунке ниже.

Понимание, какую волну формирует цена сейчас, дает возможность предположить, куда она пойдет далее. Самой интересной для трейдеров является третья волна. Она считается самой длинной и самой быстрой. Идеальная сделка с использованием теории Эллиота — это войти в сделку в конце второй волны и выйти из неё в конце третьей.

Согласно теории, высота 3-й волны относится к 1-й, как 1,618. Значит, если мы видим уже сформировавшиеся 1-ю и 2-ю волны, то мы можем рассчитать длину 3-й, используя уровни Фибоначчи. Для этого в некоторых терминалах специально предусмотрен инструмент «расширение Фибоначчи». Строится он по трем точкам: начало первой волны, конец первой волны и конец второй волны. (главное соблюсти эти точке на ценовой шкале по вертикали. По горизонтали положение точек не так важно). На экране появятся уровни Фибоначчи, и уровень с отметкой 1,618 будет отмечать расчетный конец третьей волны.

В терминале Quik инструмента «расширение Фибоначчи» нет. Но его можно заменить обычными уровнями Фибоначчи. Для этого нужно растянуть их так, чтобы 0 был на начале первой волны, а 100 на её окончании. А потом просто перетащить всю конструкцию так, чтобы 0 оказался в конце второй волны.

Хочется отметить, что не всегда конец третьей волны приходится на уровень 1,618. Довольно часто цена немного не доходит или немного опережает эту отметку.

Помимо определения длины третьей волны, ряд специалистов предлагали способы определения и других волн. В книге Б. Вильямса «Торговый хаос» предлагается следующая система определения длин волн:

1 волна — определяется по факту формирования

2 волна — чаще всего заканчивается на уровнях коррекции 50,0 и 61,8.

3 волна — составляет от 1 до 1,618 от длины первой волны.

4 волна — чаще всего заканчивается между уровнями коррекции 38,2 и 50,0 и чаще всего выглядит в виде бокового движения.

5 волна — составляет от 61,8% до 100% от диапазона между началом первой волны и концом третьей.

Рассмотрим на примере графика Россетей. Зеленым отмечены импульсные волны, а красным — коррекционные.

Самым сложным в применении волн Эллиота является вопрос: «В какой волне цена находится сейчас?» Консенсуса по поводу того, как определить точку отсчета первой волны у адептов волновой теории нет по сей день и, возможно, так и не будет.

С практической точки зрения наиболее эффективным является подход: «Не уверен — не торгуй». На некоторых инструментах в определенной фазе волны прорисовываются очень четко и легко идентифицируются. На других же, выделить волны практически невозможно. Необходимо путем регулярного наблюдения отыскивать среди всего многообразия инструментов те, которые ходят понятным для вас образом, и торговать только их. А как только волны начинают ломаться, переходить на другой инструмент.

Очень важно не зацикливаться на одной ценной бумаге, пытаясь отыскать волны там, где их нет. Кроме того, торговая система обязательно должна включать в себя план на случай негативного стечения событий. Стоп—лосс должен обеспечивать соотношение риск/прибыль не менее 1/2.

Веер Фибоначчи

Как и уровни, этот инструмент, может использоваться для определения точек, где завершится коррекция. Алгоритм, по которому строятся лучи веера достаточно простой. Если провести вертикальную линию через точку окончания трендового движения, то лучи будут проходить через точки пересечения этой линии с соответствующими уровнями Фибоначчи.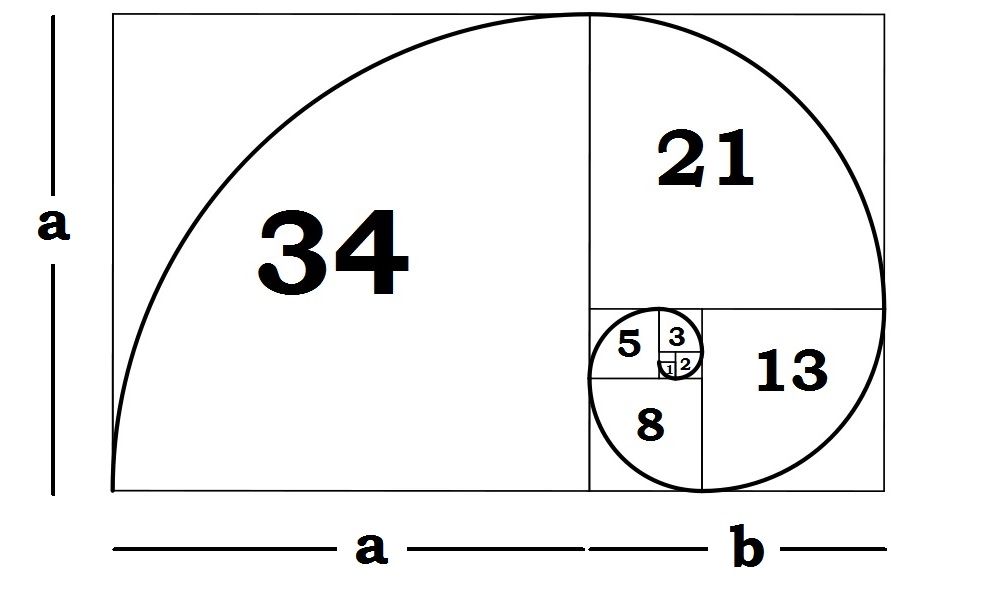 В большинстве терминалов этот алгоритм представлен в виде готового инструмента, который растягивается от начальной точки трендового движения к её концу. Лучи веера, в таком случае, будут показывать возможные окончания коррекции, где можно открывать позицию по тренду.

По умолчанию в инструменте могут быть разные настройки, но наиболее распространенными являются настройки лучей 38,2; 50,0; 61,8. В Quik их можно задать следующим образом: щелчок правой кнопкой мыши по вееру -> редактировать -> в разделе «Уровни Фибоначчи» задаете нужные значения.

Веер рекомендуется использовать в связке с другими методами определения длины коррекции. Построение веера имеет погрешность в зависимости от масштаба и таймфрейма, что может привести к неверной трактовке сигналов.

Дуги Фибоначчи

В отличие от предыдущих инструментов, дуги примечательны тем, что они учитывают еще и временной фактор. Это позволяет трейдеру не только предположить, как поведет себя цена, но и в какой момент это произойдет.

Дуги Фибоначчи строятся следующим образом: сначала между началом и концом тренда строится прямая. Затем строятся три дуги с центром в конце пересекающие прямую на уровнях Фибоначчи 38,2%, 50% и 61,8%. В большинстве терминалом дуги, точно так же реализованы в виде отдельного инструмента.

Дуги Фибоначчи очень сильно зависят от масштаба графика. Наиболее подходящий масштаб можно выбрать проанализировав эффективность инструмента на истории. Так же, как и веер рекомендуется использовать дуги совместно с другими методами технического анализа.

Временные зоны Фибоначчи

В основе временных зон Фибоначчи положена одноименная последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21… Исходной точкой для построения выбирается локальный максимум или минимум. Вторая точка позволит определить длину единичного интервала. На графике появятся вертикальные линии с шагом, соответствующем последовательности чисел Фибоначчи в единичном интервале.

Вертикальные линии помогают идентифицировать моменты времени, когда стоит ожидать разворота.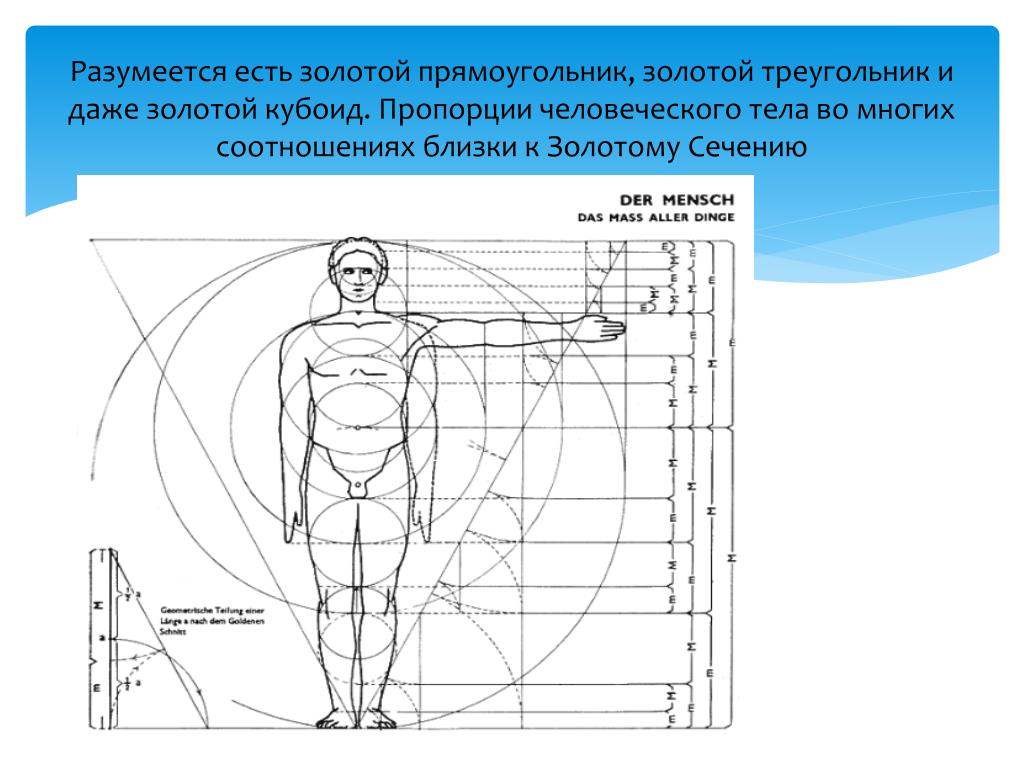 При нахождении цены в районе очередной линии необходимо использовать другие индикаторы и сигналы для поиска точки входа против движения. Можно, например, комбинировать временные зоны с веером или уровнями Фибоначчи.

Другие инструменты

Помимо представленных способов использования чисел Фибоначчи в торговле придумана еще масса вариантов: спираль Фибоначчи, канал Фибоначчи, клин Фибоначчи и т. д. Они немного отличаются по методам построения и внешнему виду, но суть их одна — определение длины коррекции. Вы можете выбрать наиболее подходящие для себя инструменты и пополнить ими свой торговый арсенал.

Книги, которые можно прочитать на эту тему

В книге А. Фроста и Р. Пректера «Волновой принцип Эллиота» можно ознакомиться с основными принципами волновой теории Эллиота в её классическом виде.

В книге Б. Мендельброта и Р. Хадсона «(Не)послушные рынки» можно прочесть о современном взгляде на ритмы финансовых рынков и фрактальной структуре изменения цен.

В книге Б. Вильямса «Торговый хаос» можно подробнее ознакомиться с методом подсчета волн, кратко изложенном в данном материале.

В книге Р. Фишеpа «Последовательность Фибоначчи: приложения и стратегии для трейдеров» изложен еще один взгляд на использование уровней Фибоначчи при подсчете волн.

Открыть счет

БКС Экспресс

Фибоначчи и золотое сечение

Существует уникальное соотношение, которое можно использовать для описания пропорций всего, от мельчайших строительных блоков природы, таких как атомы, до самых сложных структур во Вселенной, таких как невообразимо большие небесные тела. Природа полагается на эту врожденную пропорцию для поддержания баланса, но финансовые рынки, похоже, также подчиняются этому «золотому сечению».

Золотое сечение получено из чисел Фибоначчи, последовательности чисел, где каждая запись является суммой двух предыдущих записей. Хотя эта последовательность связана с Леонардо Пизанским, на самом деле числа Фибоначчи впервые были сформулированы индийским математиком Вираханкой за 600 лет до их представления западному миру.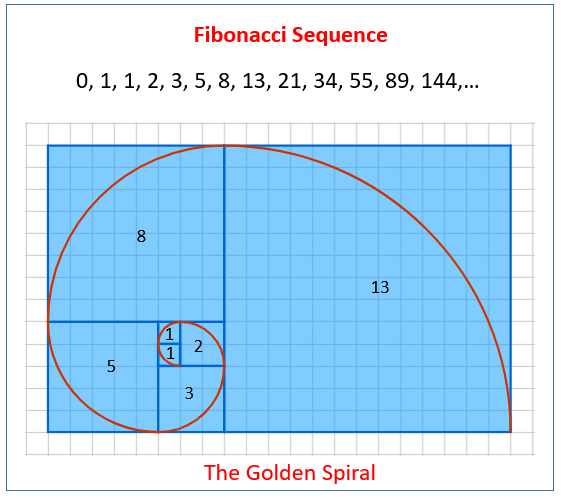

Здесь мы рассмотрим некоторые инструменты технического анализа, которые были разработаны, чтобы воспользоваться преимуществами этой модели.

Key Takeaways

Золотое сечение — это иррациональное число, равное (1+√5)/2, или приблизительно 1,618…
Это соотношение получено из древней индийской математической формулы, которую западное общество назвало в честь Леонардо Фибоначчи. , который представил эту концепцию Европе.
Природа использует это соотношение для поддержания баланса, как и финансовые рынки.
Последовательность Фибоначчи может быть применена к финансам с использованием четырех основных методов: откатов, дуг, вееров и часовых поясов.
Числа Фибоначчи стали известны в популярной культуре, хотя некоторые эксперты говорят, что их важность преувеличена.

История математики

Математики, ученые и естествоиспытатели знали о золотом сечении на протяжении веков. Он получен из последовательности Фибоначчи, названной в честь пизанского математика Леонардо Фибоначчи, который жил примерно с 1175 по 1250 год нашей эры.

Хотя Фибоначчи представил эти числа западному миру, на самом деле они были открыты индийскими математиками за сотни лет до этого. Поэт Пингала использовал их для подсчета слогов в санскритской поэзии около 200 г. до н.э., а метод их подсчета был сформулирован индийским математиком Вираханкой около 800 лет спустя.

В этой последовательности каждое число представляет собой просто сумму двух предыдущих чисел (1, 1, 2, 3, 5, 8, 13 и т. д.).

Фибоначчи в значительной степени заимствовал из индийских и арабских источников. В своей книге Liber Abaci, он описал индийско-арабскую систему счисления, представленную числами от 0 до 9. Он назвал это «Modus Indorum», или методом индийцев.

Но эта последовательность не так уж и важна. Существенной частью является то, что по мере того, как числа становятся больше, частное между каждой последовательной парой чисел Фибоначчи приближается к 1,618 или к обратному 0,618. Эта пропорция известна под многими названиями: золотое сечение, золотая середина, ϕ, божественная пропорция и другие.

Итак, почему это число так важно? Что ж, многие вещи в природе обладают размерными свойствами, которые соответствуют соотношению 1,618, так что, похоже, оно выполняет фундаментальную функцию строительных блоков природы.

Точное значение золотого сечения можно рассчитать по формуле:

ϕ = (1+√5) / 2

Примеры золотого сечения

Не верите? Возьмем, к примеру, медоносных пчел. Если вы разделите пчелиных самок на пчелиных самцов в любом данном улье, вы получите число около 1,618. У подсолнухов, которые имеют противоположные спирали семян, соотношение между диаметрами каждого вращения составляет 1,618. Это же соотношение можно увидеть в отношениях между различными компонентами в природе.

Золотое сечение также появляется в искусстве, потому что оно более эстетично, чем другие пропорции. Парфенон в Афинах, Великая пирамида в Гизе и Мона Лиза да Винчи состоят из прямоугольников, размеры которых основаны на золотом сечении. Это кажется неизбежным.

Но значит ли это, что это работает в сфере финансов? На самом деле финансовые рынки имеют ту же математическую основу, что и эти природные явления. Ниже мы рассмотрим некоторые способы применения золотого сечения в финансах и покажем несколько графиков в качестве доказательства.

Торговля и инвестирование с использованием золотого сечения

Золотое сечение часто используется трейдерами и техническими аналитиками, которые используют его для прогнозирования ценовых движений, обусловленных рынком. Это связано с тем, что числа Фибоначчи и золотое сечение имеют большое психологическое значение в стадном поведении. Трейдеры с большей вероятностью зафиксируют прибыль или покроют убытки в определенных ценовых точках, которые отмечены золотым сечением.

Любопытно, что широкое использование золотого сечения в торговом анализе формирует нечто вроде самосбывающегося пророчества: чем больше трейдеры полагаются на торговые стратегии, основанные на Фибоначчи, тем более эффективными будут эти стратегии.

Благодаря таким книгам, как « Код да Винчи» Дэна Брауна, , золотое сечение было поднято до почти мистического уровня в массовой культуре. Однако некоторые математики заявляют, что важность этого соотношения сильно преувеличена.

Золотое сечение и технический анализ

При использовании в техническом анализе золотое сечение обычно переводится в три процента: 38,2%, 50% и 61,8%. Однако при необходимости можно использовать большее количество множителей, например 23,6 %, 161,8 %, 423 % и т. д. Между тем, есть четыре способа применения последовательности Фибоначчи к графикам: восстановление, дуги, веер и часовые пояса. Однако не все могут быть доступны в зависимости от используемого приложения для построения графиков.

1. Восстановления Фибоначчи

Восстановления Фибоначчи используют горизонтальные линии для обозначения областей поддержки или сопротивления. Уровни рассчитываются с использованием максимальной и минимальной точек графика. Затем проводится пять линий: первая на 100% (максимум на графике), вторая на 61,8%, третья на 50%, четвертая на 38,2% и последняя на 0% (минимум на графике). ). После значительного движения цены вверх или вниз новые уровни поддержки и сопротивления часто находятся на этих линиях или рядом с ними.

Изображение Сабрины Цзян © Investopedia 2020

2. Дуги Фибоначчи

Нахождение максимума и минимума графика — это первый шаг к построению дуг Фибоначчи. Затем движением компаса рисуются три изогнутые линии на 38,2 %, 50 % и 61,8 % от нужной точки. Эти линии предвосхищают уровни поддержки и сопротивления, а также торговые диапазоны.

Изображение Сабрины Цзян © Investopedia 2020

3. Веер Фибоначчи

Веер Фибоначчи состоит из диагональных линий. После определения максимума и минимума графика через крайнюю правую точку проводится невидимая горизонтальная линия. Эта невидимая линия затем делится на 38,2%, 50% и 61,8%, и линии проводятся от крайней левой точки через каждую из этих точек. Эти линии указывают области поддержки и сопротивления.

Изображение Сабрины Цзян © Investopedia 2020

4. Часовые пояса Фибоначчи

В отличие от других методов Фибоначчи, часовые пояса представляют собой серию вертикальных линий. Они состоят из деления диаграммы на сегменты с вертикальными линиями, расположенными друг от друга с шагом, соответствующим последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. д.). Каждая линия указывает время, когда можно ожидать существенного движения цены.

Какая связь между рядом Фибоначчи и золотым сечением?

Золотое сечение получается путем деления каждого числа ряда Фибоначчи на его непосредственное предшествующее число. С математической точки зрения, если F( n ) описывает n число Фибоначчи, частное F( n )/F( n -1) будет приближаться к пределу 1,618… для все более высоких значений н. Этот предел более известен как золотое сечение.

Почему последовательность Фибоначчи так важна?

Последовательность Фибоначчи представляет собой рекурсивный ряд чисел, в котором каждое значение определяется двумя значениями непосредственно перед ним. По этой причине числа Фибоначчи часто появляются в задачах, связанных с ростом населения. При использовании в изобразительном искусстве они также эстетически приятны, хотя их значение в массовой культуре сильно преувеличено.

Почему 1.618 так важен?

Число 1,61803… более известно как золотое сечение и часто встречается в искусстве, архитектуре и естественных науках. Он получен из ряда чисел Фибоначчи, где каждая запись рекурсивно определяется предшествующими ей записями. Золотое сечение также используется в техническом анализе, потому что трейдеры склонны вести себя предсказуемым образом вблизи психологически важных линий Фибоначчи.

Практический результат

Исследования Фибоначчи не предназначены для предоставления первичных указаний для определения времени входа и выхода из позиции; однако числа полезны для оценки областей поддержки и сопротивления. Многие люди используют комбинации исследований Фибоначчи для получения более точного прогноза. Например, трейдер может наблюдать точки пересечения в комбинации дуг Фибоначчи и сопротивлений.

Исследования Фибоначчи часто используются в сочетании с другими формами технического анализа. Например, исследования Фибоначчи в сочетании с волнами Эллиотта можно использовать для прогнозирования степени восстановления после различных волн. Надеюсь, вы сможете найти свою собственную нишу для исследований Фибоначчи и добавить их в свой набор инвестиционных инструментов.

Определение, принцип работы и использование

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи была разработана итальянским математиком Леонардо Фибоначчи в 13 веке. Последовательность чисел, начинающаяся с нуля и единицы, представляет собой постоянно возрастающий ряд, в котором каждое число равно сумме двух предыдущих чисел.

Некоторые трейдеры считают, что числа и соотношения Фибоначчи, созданные последовательностью, играют важную роль в финансах, которые трейдеры могут применять с помощью технического анализа.

Ключевые выводы

Последовательность Фибоначчи представляет собой набор постоянно возрастающих чисел, где каждое число равно сумме двух предыдущих чисел.
Золотое сечение 1,618 получено из последовательности Фибоначчи.
Многие объекты в природе обладают размерными свойствами, соответствующими золотому сечению 1,618.
Последовательность Фибоначчи может быть применена к финансам с использованием четырех методов, включая восстановление, дуги, веер и часовые пояса.

Понимание последовательности Фибоначчи

Числа в последовательности Фибоначчи не приравниваются к определенной формуле, однако числа, как правило, имеют определенные отношения друг с другом. Каждое число равно сумме двух предыдущих чисел. Например, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.

Последовательность Фибоначчи Правило

xn = xn−1 + xn−2

где:

xn номер термина «n»

xn−1 предыдущий термин (n−1)

xn−2 термин до этого (n−2)

Золотое сечение 1,618, важное значение для математиков, ученых и естествоиспытателей на протяжении веков, получено из последовательности Фибоначчи. Частное между каждой последующей парой чисел Фибоначчи в последовательности приблизительно равно 1,618 или обратному ему значению 0,618.

Золотое сечение

Золотое сечение получается путем деления каждого числа ряда Фибоначчи на предшествующее ему число. Где F(n) — n-е число Фибоначчи, частное F(n)/F(n-1) будет приближаться к пределу 1,618, известному как золотое сечение.

Многие объекты в природе обладают размерными свойствами, которые соответствуют соотношению 1,618, например пчела. Если вы разделите пчелиных самок на пчелиных самцов в любом данном улье, вы получите число около 1,618. Золотое сечение также появляется в искусстве, а прямоугольники, размеры которых основаны на золотом сечении, появляются в Парфеноне в Афинах и Великой пирамиде в Гизе.

Как использовать последовательность Фибоначчи

Последовательность Фибоначчи может быть применена к финансам с использованием четырех методов, включая восстановление, дуги, веер и часовые пояса.

Восстановления Фибоначчи требуют двух ценовых точек, выбранных на графике, обычно максимума колебания и минимума колебания. После выбора двух точек числа и линии Фибоначчи рисуются в процентах от этого движения. Если акции растут с 15 до 20 долларов, то уровень 23,6% составляет 18,82 доллара, или 20 долларов — (5 долларов x 0,236) = 18,82 доллара. Уровень 50% составляет 17,50 долларов США, или 15 долларов США — (5 долларов США x 0,5) = 17,50 долларов США.

Восстановления Фибоначчи являются наиболее распространенной формой технического анализа, основанной на последовательности Фибоначчи. Во время тренда уровни Фибоначчи можно использовать для определения глубины отката. В это время трейдеры обычно наблюдают за коэффициентами Фибоначчи между 23,6% и 78,6%. Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться обратно в направлении тренда, инвестор может торговать в направлении тренда.

Дуги, вееры и часовые пояса — похожие понятия, но они применяются к диаграммам по-разному. Каждый из них показывает потенциальные области поддержки или сопротивления на основе чисел Фибоначчи, примененных к предыдущим ценовым движениям. Эти уровни поддержки или сопротивления можно использовать для прогнозирования того, где цены могут упасть или вырасти в будущем.

Что такое спираль Фибоначчи?

Пределы квадратов последовательных чисел Фибоначчи образуют спираль, известную как спираль Фибоначчи. Она следует поворотам на постоянный угол, близкий к золотому сечению, и обычно называется золотой спиралью. Количество спиралей в сосновых шишках — это числа Фибоначчи, как и количество лепестков в каждом слое определенных цветов. У спиралевидных растений каждый лист растет под углом по сравнению с его предшественником, а семена подсолнуха упакованы в виде спирали в центре своего цветка в геометрии, регулируемой золотым сечением.

Где очевидна последовательность Фибоначчи?

Почти у всех цветковых растений число лепестков на цветке равно числу Фибоначчи. Крайне редко число лепестков может быть не таким, и примеры этого явления включают кукурузные календулы, цинерарии и маргаритки с 13 лепестками, астры и цикорий с 21 лепестком.

Как последовательность Фибоначчи может повлиять на торговое поведение?

Люди склонны определять модели, а трейдеры легко сопоставляют модели на графиках с последовательностью Фибоначчи. Не доказано, что числа Фибоначчи связаны с фундаментальными рыночными силами, однако рынки по своей природе реагируют на убеждения своих игроков. Следовательно, если инвесторы покупают или продают на основе анализа Фибоначчи, они склонны создавать самоисполняющиеся пророчества, влияющие на рыночные тенденции.

Итог

Последовательность Фибоначчи представляет собой набор постоянно возрастающих чисел, где каждое число равно сумме двух предыдущих чисел. Многие вещи в природе обладают размерными свойствами, которые соответствуют золотому сечению 1,618, частному, полученному из последовательности Фибоначчи. Применительно к финансам и торговле инвесторы применяют последовательность Фибоначчи с помощью четырех методов, включая восстановление, дуги, веер и часовые пояса.

Что такое последовательность Фибоначчи?

Семена подсолнуха имеют золотую спираль, которая связана с последовательностью Фибоначчи. (Изображение предоставлено: Белтерц/Getty Images)

Последовательность Фибоначчи представляет собой ряд чисел, в котором каждое число является суммой двух предшествующих ему чисел. Начиная с 0 и 1, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее до бесконечности. Последовательность Фибоначчи можно описать с помощью математического уравнения: Xn+2= Xn+1 + Xn

. Люди утверждают, что у числовой последовательности есть много особых свойств, например тот факт, что это «секретный код природы» для построения совершенных структур. , вроде Великая пирамида в Гизе или культовая морская ракушка, которая, вероятно, украшала обложку вашего школьного учебника по математике .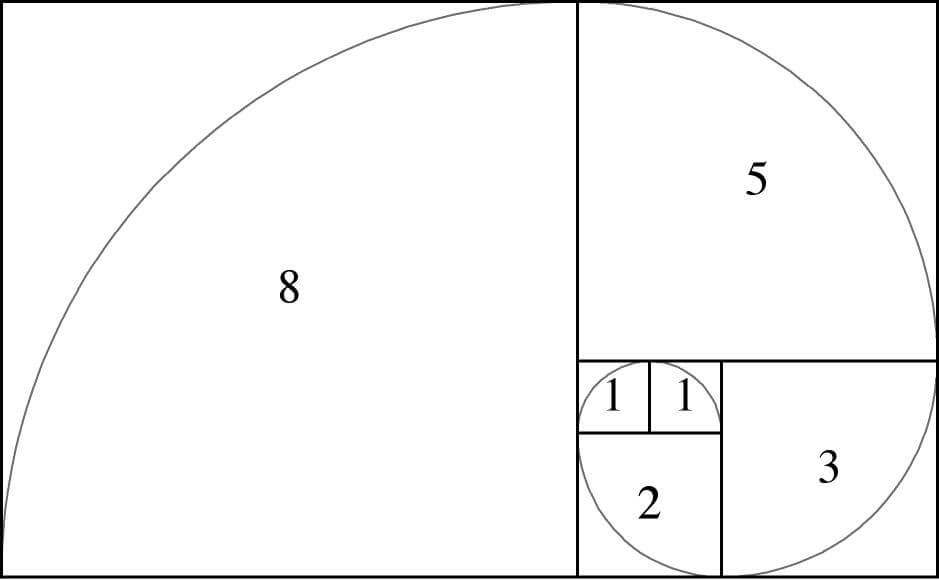 Но многое из этого неверно, и истинная история сериала немного более приземленная.

История последовательности Фибоначчи

Первое, что нужно знать, это то, что эта последовательность изначально не принадлежала Фибоначчи, который на самом деле никогда не носил этого имени. Итальянский математик, которого мы называем Леонардо Фибоначчи, родился около 1170 года и первоначально был известен как Леонардо Пизанский, сказал Кит Девлин, математик из Стэнфордского университета.

Только в 19 веке историки придумали прозвище Фибоначчи (примерно означающее «сын клана Боначчи»), чтобы отличить математика от другого знаменитого Леонардо Пизанского , сказал Девлин.

Подробнее: Большие числа, определяющие Вселенную

Леонардо Пизанский на самом деле не открыл эту последовательность, сказал Девлин, который также является автором книги «В поисках Фибоначчи: поиски нового математического гения». Кто изменил мир» (Princeton University Press, 2017).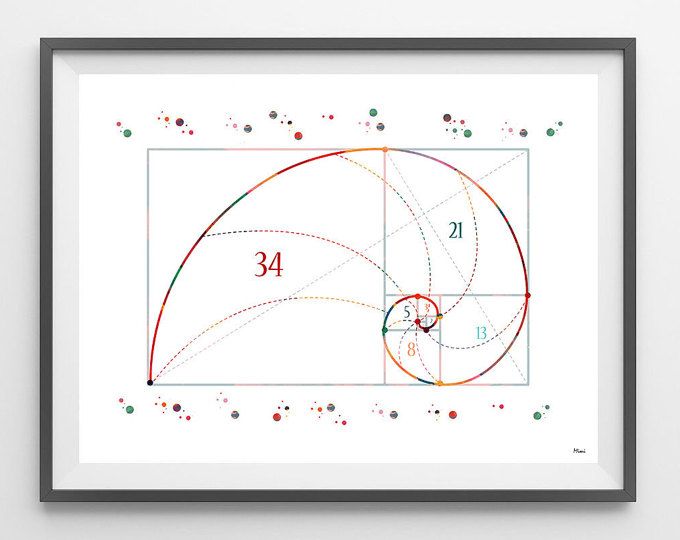 Древние санскритские тексты, в которых использовалось Индо-арабская система счисления впервые упоминается в 200 г. до н.э. на несколько столетий раньше Леонардо Пизанского.

«Это было всегда», — сказал Девлин Live Science.

Портрет Леонардо Фибоначчи, который, как считается, открыл знаменитую последовательность Фибоначчи. Однако в 1202 году в массивном томе он вводит последовательность с проблемой, связанной с кроликами. (Изображение предоставлено: Stefano Bianchetti/Corbis через Getty Images)

(открывается в новой вкладке)

Однако в 1202 году Леонардо Пизанский опубликовал массивный фолиант «Liber Abaci», математическую «поваренную книгу о том, как выполнять вычисления», — сказал Девлин. . «Liber Abaci», написанная для торговцев, изложила индийско-арабскую арифметику, полезную для отслеживания прибылей, убытков, остатков по кредитам и так далее, добавил он.

В одном месте книги Леонардо Пизанский вводит последовательность с задачей, включающей кролика . Задача выглядит следующим образом: начните с самца и самки кролика. Через месяц они созревают и производят помет с еще одним кроликом-самцом и самкой. Месяц спустя эти кролики размножаются, и, как вы уже догадались, появляются еще один самец и самка, которые также могут спариваться через месяц. (Не обращайте внимания на крайне неправдоподобную биологию.) Сколько кроликов у вас будет через год?

Ответ, как оказалось, равен 144, и формула, которая использовалась для получения этого ответа, теперь известна как последовательность Фибоначчи.

Подробнее: 9 уравнений, изменивших мир

«Liber Abaci» впервые представила последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо Пизанский больше никогда не упоминал об этой последовательности. На самом деле, о нем почти забыли до 19 века, когда математики больше проработали математические свойства последовательности. По словам Девлина, в 1877 году французский математик Эдуард Лукас официально назвал задачу о кролике «последовательностью Фибоначчи».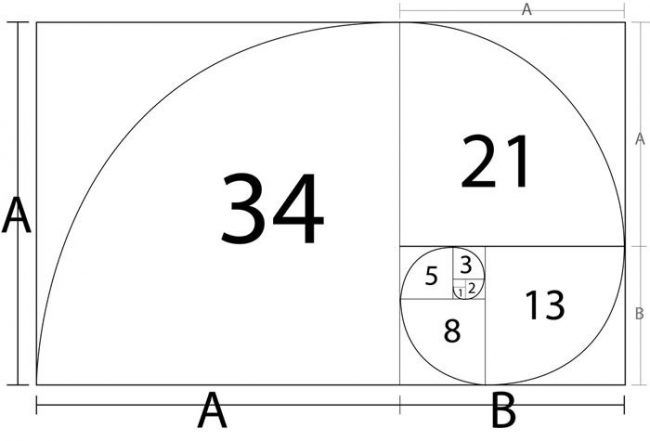

Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но они не такие волшебные, как могут показаться. (Изображение предоставлено Shutterstock)

(открывается в новой вкладке)

Почему важна последовательность Фибоначчи?

Помимо того, что последовательность Фибоначчи является прекрасным учебным пособием, она встречается в нескольких местах в природе. Однако Девлин сказал, что это не какой-то секретный код, управляющий архитектурой вселенной.

Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение, phi , иррациональное число , в котором много собственных сомнительных знаний. Отношение последовательных чисел в последовательности Фибоначчи становится все ближе к золотому сечению, которое равно 1,6180339887498948482…

Подробнее: типы роста растений, сказал Девлин. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Сосновые шишки имеют золотую спираль, как и семена подсолнуха, согласно «9».0194 Phyllotaxis: A Systemic Study in Plant Morphogenesis » (Cambridge University Press, 1994). Но столько же растений не следуют этому правилу.

«Это не единственное правило Бога для выращивание вещей, скажем так, — сказал Девлин. — добавил он. — Когда люди начинают связывать человеческое тело , искусство и архитектура, ссылки на последовательность Фибоначчи из незначительных превратились в совершенно вымышленные.

«Потребуется большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, большая часть которой является просто повторением одних и тех же ошибок разными авторами», — Джордж Марковски, математик, работавший в то время в Университете штата Мэн, . написал в статье 1992 года (открывается в новой вкладке) в College Mathematics Journal.

Большая часть этой дезинформации может быть приписана книге 1855 года немецкого психолога Адольфа Цейзинга под названием «Эстетические исследования». Зейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. В последующие годы золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения.

С тех пор люди говорят, что золотое сечение можно найти в размерах пирамиды в Гизе, Парфенона, Леонардо да Винчи «Витрувианского человека» и множества зданий эпохи Возрождения. По словам Девлина, всеохватывающие утверждения о том, что это соотношение «уникально приятно» для человеческого глаза, были сформулированы некритически. Он добавил, что все эти утверждения при проверке оказываются в значительной степени ложными.

«Мы умеем распознавать образы. Мы можем видеть образы независимо от того, есть они или нет», — сказал Девлин. «Это все просто принятие желаемого за действительное».

Примечание редактора: Адам Манн участвовал в написании этой статьи .

Первоначально опубликовано на Live Science .