Сигма 0 2: Условный предел текучести
Условный предел текучести. Сигма ноль-два ? : Механика и Техника
| Neuter |
| ||
02/01/13 |
| ||
| |||
| angor6 |
| ||
11/03/12 |
| ||
| |||
| Neuter |
| ||
02/01/13 |
| ||
| |||
| angor6 |
| ||
11/03/12 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 4 ] |
Модераторы: photon, profrotter, Парджеттер, Супермодераторы
Сталь 20 конструкционная углеродистая качественная
Сталь 20 конструкционная углеродистая качественная- ГОСТы
- Стали
Сталь 20 относится к разряду обогащенных углеродом конструкционным сталям высокого уровня качества. На производства поставляется в нескольких вариациях – серебрянка, калиброванная, кованная или горячекатаная. Можно выделить пять типов данной разновидности стали по требованиям к ее механическим свойствам.
На производства поставляется в нескольких вариациях – серебрянка, калиброванная, кованная или горячекатаная. Можно выделить пять типов данной разновидности стали по требованиям к ее механическим свойствам.
Типы стали по требованию к механическим свойствам:
- Первый тип представляет собой сталь всех используемых видов обработки, но без проведенных испытаний по растяжению и ударной вязкости.
- Второй тип – это образцы нормализованной стали всех типов обработки размеров в двадцать пять миллиметров, которые подвергаются испытаниям на растяжение и ударную вязкость.
- Третий тип представляет собой все те же образцы, на которых проводятся вышеупомянутые испытания. Единственное отличие – это их размер. В этом типе он составляет от двадцати шести до ста миллиметров.
- Четвертый тип представляет собой образцы из заготовок с размером — до сотни миллиметров, которые были обработаны термическим путем. Они также применяются для проведения испытаний над материалом.

- Пятый тип – это также образцы, которые изготовлены из отожженных или выскоопущенных сталей. Еще одно технологическое решение – это образцы из нагартованной стали.
Сталь 20 может быть при необходимости заменена схожими материалами марок 15 и 25.
Технологические свойства стали 20
Для начала процесса ковки достаточно разогреть сталь до +1280 градусов Цельсия, а завершаться процесс должен при температуре -750 градусов Цельсия, при том что охлаждение поковки производится воздушным способом. Сталь марки 20 относится с типу нефлокеночувствительных, а также она не склонна к отпускной способности. Возможность сваривания данного типа стали ничем не ограничена, за исключением тех деталей, которые подвергались химико-термической обработке.
Сталь 20 зачастую используется в процессе производства тех деталей, которые работают со сравнительно небольшим нагружением. Это могут быть оси, пальцы или шестерни, а также и те детали, которые будут подвергаться цементированию для продления срока службы. Помимо всего, такой тип стали может быть использован в процессе изготовления особо тонких деталей, в большинстве своем работающих на истирание. Без термической обработки этот вид стали используется в производстве крюков подъемных кранов, а также прочих деталей, эксплуатация которых производится под некоторым давлением в диапазоне температур от -40 до +450 градусов Цельсия. Химико-термическая обработка наделяет сталь 20 всеми необходимыми свойствами для использования ее в качестве основы для деталей, главной особенностью которых является высокий уровень прочности поверхности.
Помимо всего, такой тип стали может быть использован в процессе изготовления особо тонких деталей, в большинстве своем работающих на истирание. Без термической обработки этот вид стали используется в производстве крюков подъемных кранов, а также прочих деталей, эксплуатация которых производится под некоторым давлением в диапазоне температур от -40 до +450 градусов Цельсия. Химико-термическая обработка наделяет сталь 20 всеми необходимыми свойствами для использования ее в качестве основы для деталей, главной особенностью которых является высокий уровень прочности поверхности.
Химический состав стали 20
Состав марки стали 20 очень разнообразен, ведь в нем представлен углерод, марганец, кремний, медь, мышьяк, никель, фосфор и сера. По сути своей данный тип стали представляет собой очень интересную смесь, в составе которой имеется феррит и перлит. В процессе термической обработки структуру материала можно изменить до пакетного мартенсита. Стоит отметить, что данные преобразования структуры приведут к тому, что прочность стали увеличиться, а ее пластичность, наоборот, уменьшиться.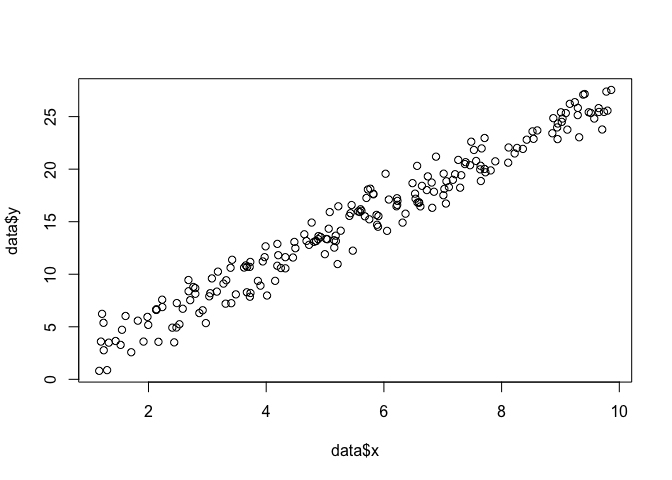
| C | Si | Mn | S | P | Ni | Cr | Cu | As | Fe |
| 0,17 — 0,24 | 0,17 — 0,37 | 0,35 — 0,65 | до 0,04 | до 0,04 | до 0,25 | до 0,25 | до 0,08 | ~98 |
Зарубежные аналоги стали 20
| США | 1020, 1023, 1024, G10200, G10230, h20200, M1020, M1023 |
| Германия | 1. 0402, 1.0405, 1.1151, C22, C22E, C22R, Ck22, Cm22, Cq22, St35, St45-8 0402, 1.0405, 1.1151, C22, C22E, C22R, Ck22, Cm22, Cq22, St35, St45-8 |
| Япония | S20C, S20CK, S22C, STB410, STKM12A, STKM12A-S, STKM13B, STKM13B-W |
| Франция | 1C22, 2C22, AF42, AF42C20, C20, C22, C22E, C25E, XC15, XC18, XC25 |
| Англия | 050A20, 055M15, 070M20, 070M26, 1449-22CS, 1449-22HS, 1C22, 22HS, 430, C22, C22E |
| Евросоюз | 1.1151, 2C22, C20E2C, C22, C22E |
| Италия | C18, C20, C21, C22, C22E, C22R, C25, C25E |
| Бельгия | C25-1, C25-2 |
| Испания | 1C22, C22, C25k, F.112, F.1120 |
| Китай | 20, 20G, 20R, 20Z |
| Швеция | 1450 |
| Болгария | 20, C22, C22E |
| Венгрия | A45.47, C22E |
| Польша | 20, K18 |
| Румыния | OLC20, OLC20X |
| Чехия | 12022, 12024 |
| Австралия | 1020, M1020 |
| Швейцария | Ck22 |
Юж. Корея Корея | SM20C, SM20CK, SM22C |
Физические свойства стали 20
| T | E 10— 5 | a 10 6 | l | r | C | R 10 9 |
| Град | МПа | 1/Град | Вт/(м·град) | кг/м3 | Дж/(кг·град) | Ом·м |
| 20 | 2,13 | 52 | 7859 | |||
| 100 | 2,03 | 11,60 | 50.6 | 7834 | 486 | 219 |
| 200 | 1,99 | 12,60 | 48. 6 6 | 7803 | 498 | 292 |
| 300 | 1,90 | 13,10 | 46.2 | 7770 | 514 | 381 |
| 400 | 1,82 | 13,60 | 42.8 | 7736 | 533 | 487 |
| 500 | 1,72 | 14,10 | 39.1 | 7699 | 555 | 601 |
| 600 | 1,60 | 14,60 | 35.8 | 7659 | 584 | 758 |
| 700 | 14,80 | 32 | 7617 | 636 | 925 | |
| 800 | 12,90 | 7624 | 703 | 1094 | ||
| 900 | 7600 | 703 | 1135 | |||
| 1000 | 695 |
Механические свойства стали 20 при температуре 20
0С| Соответствие по ГОСТ | Вид поставки | σВ (МПа) | δ 5 (%) | ψ (%) | HB (не более) |
| 1050-74 | Сталь калиброванная: | ||||
| горячекатаная, кованая и серебрянка 2-й категории после нормализации | 410 | 25 | 55 | ||
| 5-й категории после нагартовки | 490 | 7 | 40 | ||
| 5-й категории после отжига или высокого отпуска | 390 | 21 | 50 | ||
| 10702-78 | Сталь калиброванная и калиброванная со специальной отделкой: | ||||
| после отпуска или отжига | 390-490 | 50 | 163 | ||
| после сфероидизирующего отжига | 340-440 | 50 | 163 | ||
| нагартованная без термообработки | 490 | 7 | 40 | 207 |
Механические свойства стали 20 при повышенных температурах
0С| Температурные испытания, °С | σ0,2, МПа | σВ, МПа | δ5, % | ψ, % | KCU, Дж/см2 |
| 20 | 280 | 430 | 34 | 67 | 218 |
| 200 | 230 | 405 | 28 | 67 | 186 |
| 300 | 170 | 415 | 29 | 64 | 188 |
| 400 | 150 | 340 | 39 | 81 | 100 |
| 500 | 140 | 245 | 40 | 86 | 88 |
| 700 | 130 | 39 | 94 | ||
| 800 | 89 | 51 | 96 | ||
| 900 | 75 | 55 | 100 | ||
| 1000 | 47 | 63 | 100 | ||
| 1100 | 30 | 59 | 100 | ||
| 1200 | 20 | 64 | 100 |
Пределы выносливости стали 20
| σ-1, МПа | J-1, МПа | n | δ5, МПа | σ0,2,МПа | Термообработка, состояние стали |
| 206 | 1Е+7 | 500 | 320 | ||
| 245 | 520 | 310 | |||
| 225 | 490 | 280 | |||
| 205 | 127 | Нормализация 910 С, отпуск 620 С. | |||
| 193 | 420 | 280 | |||
| 255 | 451 | Цементация 930 С, закалка 810 С, отпуск 190 С. |
Механические свойства стали 20 после ХТО
| Сечение, мм | σ0,2, МПа | σВ, МПа | δ5, % | y , % | KCU, Дж/м 2 | HB | HRC |
| Цементация 920-950 °С, воздух. Закалка 800-820 °С, вода. Отпуск 180-200 °С, воздух. | |||||||
| 50 | 290-340 | 490-590 | 18 | 45 | 54 | 156 | 55-63 |
Технологические свойства стали 20
| Коррозионная стойкость | В среде H2S: скорость общей коррозии ≤ 0,5 мм/год; стойкость к водородному растрескиванию CLR ≤ 3 % CTR ≤ 6 %; стойкость к сульфидному коррозионному растрескиванию под напряжением ≥ 75 % от σ0,2. По ТУ 14-3-1971-97 металл труб должен выдерживать испытания на водородное растрескивание по стандарту NACE ТМ 02 84 (испытательная среда NACE TM 01 77). Предельные значения коэффициентов длины (CLR) и толщины трещин (CTR) не должны превышать соответственно 3 и 6%. Металл труб должен выдерживать испытания на стойкость к сульфидному растрескиванию под напряжением. Пороговое напряжение СКРН должно быть не менее 75% (254 МРа) от минимального гарантируемого предела текучести материала. Скорость общей коррозии металла труб не должна превышать 0,5 мм/год. По ТУ 14-3-1971-97 металл труб должен выдерживать испытания на водородное растрескивание по стандарту NACE ТМ 02 84 (испытательная среда NACE TM 01 77). Предельные значения коэффициентов длины (CLR) и толщины трещин (CTR) не должны превышать соответственно 3 и 6%. Металл труб должен выдерживать испытания на стойкость к сульфидному растрескиванию под напряжением. Пороговое напряжение СКРН должно быть не менее 75% (254 МРа) от минимального гарантируемого предела текучести материала. Скорость общей коррозии металла труб не должна превышать 0,5 мм/год. |
| Наплавка | Наплавка уплотнительных поверхностей деталей трубопроводной арматуры в соответствии с ОСТ 26-07-2028-81 производится ручной электродуговой наплавкой электродами типа Э-20Х13 с обмазкой УОНИ-13НЖ, НИИ-48, НИИ-48Ж-1 или проволокой СВ-12Х13 или СВ-20Х13. Подготовка поверхности под наплавку производится механической обработкой. Наплавка производится с предварительным и сопутствующим нагревом детали до 400-450 °C не менее чем в 3 слоя толщиной не менее 4 мм без учета припуска на механическую обработку. Термообработка после наплавки производится путем отпуска при 550-600 °C (выдержка 2-5 ч) на твердость НВ=301-350, при 600-650 °C (выдержка 2-5 ч) на твердость НВ=240-300, при 400-450 °C (выдержка 2-5 ч) на твердость НВ=351-400. Температура печи при загрузке деталей для отпуска должна быть не более 300 °C. Термообработка после наплавки производится путем отпуска при 550-600 °C (выдержка 2-5 ч) на твердость НВ=301-350, при 600-650 °C (выдержка 2-5 ч) на твердость НВ=240-300, при 400-450 °C (выдержка 2-5 ч) на твердость НВ=351-400. Температура печи при загрузке деталей для отпуска должна быть не более 300 °C. |
| Обрабатываемость резаньем | В горячекатанном состоянии при НВ 126-131 и sВ=450-490 МПа Kn тв.спл.=1,7 Kn б.ст.=1,6. |
| Свариваемость | Сваривается без ограничений, кроме деталей после химико-термической обработки. Способы сварки РДС, АДС под флюсом и газовой защитой, КТС. Для ручной дуговой сварки используются электроды МР-3 или УОНИ13/45А; для автоматической под флюсом — проволока Св-08А, Cв-08ГA или Св-10Г2 с флюсом АН-348А; для сварки в защитных газах Ar и CO2 — сварочная проволока Св-08Г2С. |
| Склонность к отпускной хрупкости | Не склонна. |
| Температура ковки | Начала — 1280 °C, конца — 750 °C. Охлаждение на воздухе. |
| Флокеночувствительность | не чувствительна. |
Ударная вязкость стали 20 KCU (Дж/см3) при низких температурах °С
| Соответствие по ГОСТ | Вид поставки | Сечение, мм | KCU при +20 | KCU при -40 | KCU при -60 |
| 19281-73 | Сортовой и фасонный прокат | от 5 до 10 | 64 | 39 | 34 |
| от 10 до 20 вкл. | 59 | 34 | 29 | ||
| от 20 до 100 вкл. | 59 | 34 | — |
Предел текучести стали 20
| Температура испытания, °C/s0,2 | |||||||
| 150 | 200 | 250 | 300 | 320 | 350 | 400 | 450 |
| ≥215 | ≥210 | ≥196 | ≥180 | ≥160 | ≥137 | ≥127 | |
Химический состав стали 20 по ТУ и ГОСТ
| НТД | C | S | P | Mn | Cr | Zn | V | Sn | Si | Sb | Pb | Ni | N | Mo | Fe | Cu | Bi | As | Al |
| ТУ 14-1-3987-85 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,30 | — | — | — | ≤0,30 | — | — | — |
| ТУ 14-1-5058-91 | 0,18-0,24 | ≤0,012 | ≤0,020 | 0,35-0,65 | ≤0,15 | ≤0,0040 | ≤0,040 | ≤0,005 | 0,17-0,37 | 0,00015-0,00045 | ≤0,0030 | ≤0,10 | ≤0,010 | — | — | ≤0,10 | 0,0002-0,00045 | ≤0,010 | — |
| ГОСТ 11017-80 | 0,17-0,24 | ≤0,035 | ≤0,035 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,30 | ≤0,006 | — | — | ≤0,30 | — | ≤0,080 | — |
| ГОСТ 19277-73, ГОСТ 21729-76 | 0,17-0,24 | ≤0,035 | ≤0,035 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | — | — | ≤0,20 | — | — | — |
| ТУ 14-1-1529-2003 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | — | Ост. | ≤0,30 | — | — | — |
| ТУ 14-3Р-251-2007, ТУ 14-3-251-74, ГОСТ 1050-88 | 0,17-0,24 | ≤0,040 | ≤0,035 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,30 | ≤0,006 | — | — | ≤0,30 | — | ≤0,080 | — |
| ТУ 14-3-808-78 | 0,17-0,24 | ≤0,040 | ≤0,035 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | ≤0,006 | — | — | ≤0,25 | — | ≤0,080 | 0,02-0,08 |
| ТУ 14-3-1971-97 | 0,17-0,21 | ≤0,008 | ≤0,012 | 0,35-0,65 | ≤0,25 | — | ≤0,060 | — | 0,17-0,37 | — | — | ≤0,30 | — | — | — | ≤0,30 | — | — | 0,02-0,05 |
| ТУ 14-3-341-75 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,025 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | — | — | ≤0,30 | — | — | — |
| ТУ 14-162-14-96 | 0,17-0,22 | ≤0,015 | ≤0,015 | 0,50-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | — | — | ≤0,25 | — | — | 0,03-0,05 |
| ТУ 14-1-5185-93 | 0,18-0,24 | 0,002-0,015 | 0,005-0,015 | 0,35-0,65 | ≤0,15 | 0,0005-0,0040 | 0,002-0,100 | 0,0005-0,0040 | 0,17-0,37 | 0,0005-0,0030 | 0,0003-0,0040 | ≤0,15 | 0,002-0,012 | — | — | ≤0,15 | 0,0001-0,0030 | ≤0,010 | 0,002-0,009 |
ТУ 08. 002.0501.5348-92 002.0501.5348-92 | 0,17-0,24 | ≤0,020 | ≤0,035 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,30 | — | — | — | ≤0,30 | — | — | — |
| ТУ 14-159-1128-2008 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,30 | ≤0,006 | — | — | ≤0,30 | — | ≤0,080 | — |
| ТУ 14-161-148-94 | 0,17-0,24 | ≤0,013 | ≤0,018 | 0,35-0,65 | — | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | — | — | ≤0,25 | — | — | — |
TУ 1317-006. 1-593377520-2003 1-593377520-2003 | 0,17-0,24 | ≤0,015 | ≤0,017 | 0,35-0,65 | ≤0,40 | — | ≤0,050 | — | 0,17-0,37 | — | — | ≤0,25 | ≤0,008 | — | — | ≤0,25 | — | — | 0,02-0,05 |
| ТУ 1301-039-00212179-2010 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | ≤0,15 | — | ≤0,30 | — | — | — |
| ТУ 14-3Р-55-2001, ТУ 14-3-460-2003 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,25 | — | — | — | ≤0,30 | — | — | — |
| ТУ 14-3Р-1128-2007 | 0,17-0,24 | ≤0,025 | ≤0,030 | 0,35-0,65 | ≤0,25 | — | — | — | 0,17-0,37 | — | — | ≤0,30 | ≤0,008 | — | — | ≤0,30 | — | — | — |
Обозначения используемые в таблицах
Механические свойства:
- sв — Предел кратковременной прочности, [МПа]
- sТ — Предел текучести, [МПа]
- s0,2 — Предел пропорциональности (допуск на остаточную деформацию — 0,2%), [МПа]
- d5 — Относительное удлинение при разрыве, [ % ]
- y — Относительное сужение, [ % ]
- KCU — Ударная вязкость, [ кДж / м2]
- HB — Твердость по Бринеллю, [МПа]
- HV — Твердость по Виккерсу, [МПа]
- HSh — Твердость по Шору, [МПа]
Физические свойства:
- T — Температура, при которой получены данные свойства, [Град]
- E — Модуль упругости первого рода, [МПа]
- a — Коэффициент температурного (линейного) расширения (диапазон 20o — T ) , [1/Град]
- l — Коэффициент теплопроводности (теплоемкость материала) , [Вт/(м·град)]
- r — Плотность материала , [кг/м3]
- C — Удельная теплоемкость материала (диапазон 20o — T ), [Дж/(кг·град)]
- R — Удельное электросопротивление, [Ом·м]
Имя:
Телефон или email для связи:
даю согласие на обработку персональных данных в соответствии с «Политикой конфиденциальности»
На нашем сайте мы используем cookie для сбора информации технического характера. В частности, для персонифицированной работы сайта мы обрабатываем IP-адрес региона вашего местоположения. | OK |
Ст3сп сталь: характеристики и расшифовка, применение и свойства стали
- Стали
- Стандарты
Всего сталей
| Страна | Стандарт | Описание | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Россия | ГОСТ 380-2005 | Сталь углеродистая обыкновенного качества. Марки Марки | ||||||||||
| Россия | ГОСТ 535-2005 | Прокат сортовой и фасонный из стали углеродистой обыкновенного качества. Общие технические условия | ||||||||||
| Россия | ГОСТ 4781-85 | Профили стальные горячекатаные для шпунтовых свай. Технические условия | ||||||||||
| Россия | ГОСТ 5781-82 | Сталь горячекатаная для армирования железобетонных конструкций. Технические условия Технические условия | ||||||||||
| Россия | ГОСТ 8696-74 | Трубы стальные электросварные со спиральным швом общего назначения. Технические условия | ||||||||||
| Россия | ГОСТ 10705-80 | Трубы стальные электросварные. Технические условия | ||||||||||
| Россия | ГОСТ 10706-76 | Трубы стальные электросварные прямошовные. Технические требования Технические требования | ||||||||||
| Россия | ГОСТ 10707-80 | Трубы стальные электросварные холоднодеформированные. Технические условия | ||||||||||
| Россия | ГОСТ 10884-94 | Сталь арматурная термомеханически упрочненная для железобетонных конструкций. Технические условия | ||||||||||
| Россия | ГОСТ 10885-85 | Сталь листовая горячекатаная двухслойная коррозионно-стойкая. Технические условия Технические условия | ||||||||||
| Россия | ГОСТ 14637-89 | Прокат толстолистовой из углеродистой стали обыкновенного качества. Технические условия | ||||||||||
| Россия | ГОСТ 14918-80 | Сталь тонколистовая оцинкованная с непрерывных линий. Технические условия | ||||||||||
| Россия | ГОСТ 16523-97 | Прокат тонколистовой из углеродистой стали качественной и обыкновенного качества общего назначения.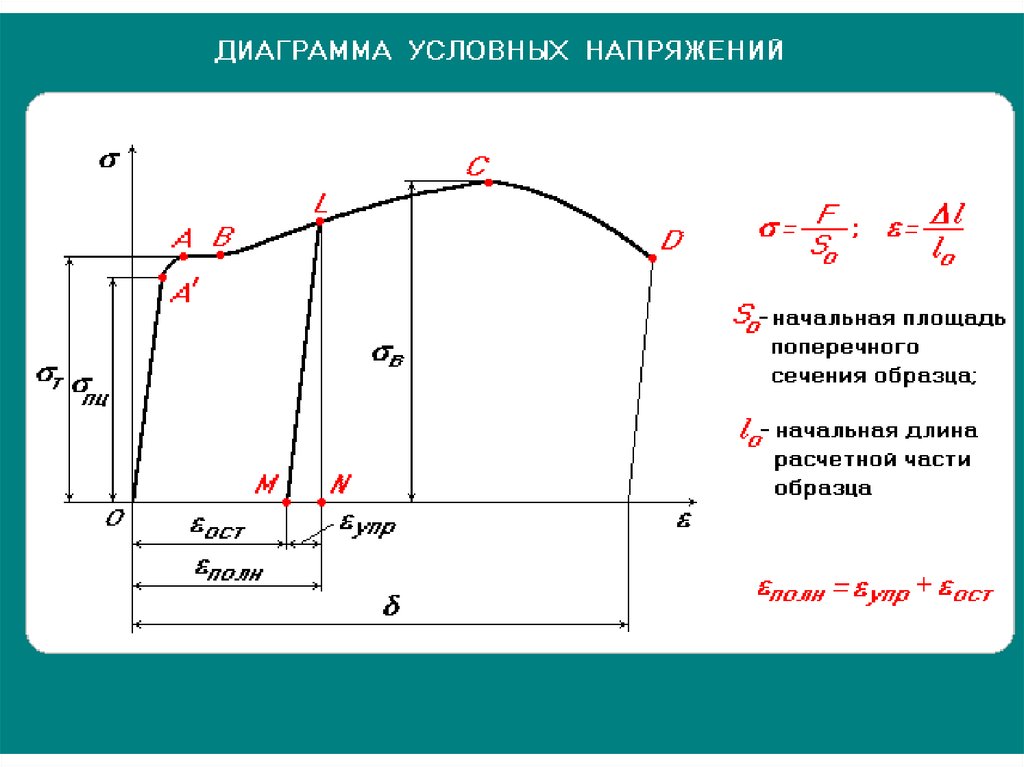 Технические условия Технические условия | ||||||||||
| Россия | ГОСТ 30136-95 | Катанка из углеродистой стали обыкновенного качества. Технические условия | ||||||||||
| Россия | ГОСТ 32678-2014 | Трубы стальные бесшовные и сварные холоднодеформированные общего назначения. Технические условия | ||||||||||
Механические свойства Ст3сп
Механические свойства по стандарту ГОСТ 380-2005
|
Предел текучести, σ0,2, МПа |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ5, % |
| 205 — 255 | 370 — 490 |
23 — 26 |
Механические свойства по стандарту ГОСТ 535-2005
| Толщина, мм |
Предел текучести для остаточной деформации, σт, МПа |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ5, % |
Изгиб до параллельности сторон* |
| до 10 |
> 255 |
380 — 490 |
> 26 |
d=a |
| 11 — 20 | > 245 | 370 — 480 | > 26 | d=a |
| 21 — 40 | > 235 |
370 — 480 |
> 25 |
d=2a |
| 41 — 100 | > 225 |
370 — 480 |
> 23 | d=2a |
| более 100 | > 205 |
370 — 480 |
> 23 | d=2a |
По согласованию с потребителем для фасонного проката толщиной более 20 мм допускается снижение предела текучести на 10 МПа
Допускается снижение относительного удлинения на 1% (по согласованию с потребителем)
Допускается превышение верхнего предела временного сопротивления на 49 МПа, а по согласованию с потребителем — без ограничения верхнего предела временного сопротивления при условии выполнения остальных норм. По требованию потребителя превышение верхнего предела временного сопротивления не допускается.
По требованию потребителя превышение верхнего предела временного сопротивления не допускается.
* a — толщина образца, d — диаметр оправки
Нормы ударной вязкости KCU, Дж/см2
| Толщина, мм |
При температуре +20 °C |
При температуре -20 °C |
После механического старения |
| Категория стали 3 (Ст3сп3)** | |||
| 3 — 9,9 |
> 108 |
- | - |
| 10 — 25 | > 98 | - | - |
| 26 — 40 |
> 88 |
- | - |
| Категория стали 4 (Ст3сп4) | |||
| 3 — 9,9 | - | > 49 | - |
| 10 — 25 | - | > 29 | - |
| Категория стали 5 (Ст3сп5) | |||
| 3 — 9,9 | - | > 49 | > 49 |
| 10 — 25 | - | > 29 | > 29 |
** Категории стали:
3 — сталь с испытанием механических свойств на растяжение на образцах, изготовленных из нормализованных заготовок указанного в заказе размера, но не более 100 мм
4 — сталь с испытанием механических свойств на растяжение и ударную вязкость на образцах, изготовленных из термически обработанных (закалка + отпуск) заготовок указанного в заказе размера, но не более 100мм
5 — сталь с испытанием механических свойств на растяжение на образцах, изготовленных из сталей в нагартованном или термически обработанном состоянии (отожженной или высокоотпущенной)
Механические свойства по стандарту ГОСТ 5781-82
| Сортамент |
Класс прочности |
Диаметр, мм |
Временное сопротивление разрыву, σв, МПа** |
Предел текучести, σ0,2, МПа |
Относительное удлинение при разрыве, δ5, % |
Испытание на изгиб в холодном состоянии* |
| Арматура | А-I (А240) | 6 — 40 |
> 373 |
> 235 |
> 25 |
180 °C; c=d** |
* c — толщина оправки, d — диаметр стержня
** Для арматурной стали диаметром от 20 до 40 мм испытание на изгиб в холодном состоянии при 180 °C: c=2d
Механические свойства по стандарту ГОСТ 8696-74
|
Предел текучести для остаточной деформации, σт, МПа (кгс/мм2) |
Временное сопротивление разрыву, σв, МПа (кгс/мм2) |
Относительное удлинение при разрыве, δ5, % |
| > 245 (25) |
> 372 (38) |
> 23 |
Нормы ударной вязкости KCV, Дж/см2 (кгс⋅м/см2)
| Категория стали* | При температуре +20 °C |
При температуре -20 °C |
После механического старения |
| 3 (Ст3сп3) | > 59 (6) | ||
| 4 (Ст3сп4) | - |
> 29,4 (3) |
- |
|
5 (Ст3сп5) |
- |
> 29,4 (3) |
> 29,4 (3) |
Механические свойства по стандарту ГОСТ 10705-80
| Сортамент |
Диаметр, мм |
Толщина, мм |
Временное сопротивление разрыву, σв, МПа |
Предел текучести, σ0,2, МПа |
Относительное удлинение при разрыве, δ5, % |
| Термически обработанная продукция | |||||
| Трубы | все | все |
> 372 |
> 225 |
> 22 |
| Без термической обработки | |||||
| Трубы | от 10 до 19 | не более 0,06*D |
> 441 |
> 216 |
> 13 |
| Трубы | от 19 до 60 | не более 0,06*D |
> 392 |
> 216 |
> 13 |
| Трубы | от 10 до 19 | более 0,06*D |
> 441 |
> 216 |
> 5 |
| Трубы | от 19 до 60 | более 0,06*D |
> 392 |
> 216 | > 5 |
| Трубы | от 60 до 152 | все |
> 372 |
> 216 |
> 20 |
| Трубы | от 152 до 377 | не более 6 | > 353 |
> 216 |
> 17 |
| Трубы | от 152 до 377 | более 6 |
> 353 |
> 216 |
> 14 |
| Трубы | более 377 | не более 6 |
> 353 |
> 216 |
> 19 |
| Температура испытания, °C |
Ударная вязкость KCU, Дж/см2 (кгс⋅м/см2) |
| +20 | 78,4 (8) |
| -20 | 39,2 (4) |
| +20 (после механического старения) | 39,2 (4) |
Механические свойства по стандарту ГОСТ 10706-76
| Сортамент |
Временное сопротивление разрыву, σв, МПа |
Предел текучести для остаточной деформации, σт, МПа |
Относительное удлинение при разрыве, δ5, % |
| Трубы |
> 372 |
> 245 |
> 20 |
| Толщина, мм |
Температура испытания, °C |
Ударная вязкость KCU, Дж/см2 |
| Категория стали 3 (Ст3сп3)* | ||
| 5 — 9 |
+20 |
> 59 |
| 9 — 25 | +20 |
> 49 |
| более 25 | +20 |
> 29 |
| Категория стали 4 (Ст3сп4)* | ||
|
5 — 9 |
-20 |
> 20 |
|
9 — 25 |
-20 | > 15 |
Для магистральных тепловых сетей
|
Временное сопротивление разрыву, σв, МПа |
Предел текучести для остаточной деформации, σт, МПа |
Относительное удлинение при разрыве, δ5, % |
Условия испытаний |
Ударная вязкость KCU, Дж/см2 |
| Категория стали 4 (Ст3сп4)* | ||||
|
> 372 |
> 245 |
> 23 |
-20 °C |
- |
| Категория стали 5 (Ст3сп5)* | ||||
|
> 372 |
> 245 |
> 23 |
-20 °C |
> 30 |
|
> 372 |
> 245 |
> 23 |
механическое старение |
> 29 |
* Категории стали в зависимости от нормируемых характеристик:
3 — сталь с испытанием механических свойств на растяжение на образцах, изготовленных из нормализованных заготовок указанного в заказе размера, но не более 100 мм
4 — сталь с испытанием механических свойств на растяжение и ударную вязкость на образцах, изготовленных из термически обработанных (закалка + отпуск) заготовок указанного в заказе размера, но не более 100мм
5 — сталь с испытанием механических свойств на растяжение на образцах, изготовленных из сталей в нагартованном или термически обработанном состоянии (отожженной или высокоотпущенной)
Механические свойства по стандарту ГОСТ 10707-80
| Сортамент |
Временное сопротивление разрыву, σв, МПа |
Предел текучести для остаточной деформации, σт, МПа |
Относительное удлинение при разрыве, δ5, % |
|
Термически обработанная продукция |
|||
| Трубы |
> 372 |
> 225 |
> 22 |
|
Без термической обработки |
|||
|
Трубы |
> 314 |
> 216 |
> 5 |
Механические свойства по стандарту ГОСТ 10884-94
| Сортамент | Класс прочности | Диаметр, мм | Диаметр оправки* |
Временное сопротивление разрыву, σв, МПа** |
Предел текучести, σ0,2, МПа |
Относительное удлинение при разрыве, δ5, % |
Испытание на изгиб в холодном состоянии |
| Арматура | Ат400 | 6 — 40 | 3d |
> 550 |
> 440 |
> 16 |
90 °C |
* d — номинальный диаметр стержня
** В стержнях временное сопротивление разрыву не должно превышать 750 МПа
Механические свойства по стандарту ГОСТ 14637-89
| Толщина, мм |
Предел текучести для остаточной деформации, σт, МПа |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ5, % |
Изгиб до параллельности сторон* |
| Категории 1, 2, 3, 4, 5 (Ст3сп, Ст3сп2, Ст3сп3, Ст3сп4, Ст3сп5)** | ||||
| 4 — 20 |
> 245 |
370 — 480 |
> 26 |
d=1,5a |
| 20 — 40 |
> 235 |
360 — 460 |
> 25 |
d=2,5a |
| 40 — 100 |
> 225 |
360 — 460 |
> 23 |
d=2,5a |
| 100 — 160 |
> 205 |
360 — 460 |
> 23 |
d=2,5a |
| Категория 6 (Ст3сп6)** | ||||
| не более 20 |
> 295 |
> 430 |
> 16 |
d=4a |
| более 20 |
> 295 |
> 430 |
> 16 |
d=5a |
Допускается превышение верхнего предела временного сопротивления не более чем на 50 МПа при соблюдении остальных норм; по согласованию с потребителем — без ограничения верхнего предела.
По согласованию с потребителем для проката толщиной более 20 мм допускается значение предела текучести ниже на 10 МПа.
Допускается снижение относительного удлинения на 1% абс. для проката толщиной более 8 мм и на каждый миллиметр уменьшения толщины для проката толщиной 8 мм и менее.
* a — толщина образца, d — диаметр оправки
** Категории стали в зависимости от нормируемых характеристик:
1 — механические свойства при растяжении и изгибе
2 — химический состав и механические свойства при растяжении и изгибе
3 — химический состав, механические свойства при растяжении и изгибе, ударная вязкость при температуре +20°С
4 — химический состав, механические свойства при растяжении и изгибе, ударная вязкость при температуре –20°С
5 — химический состав, механические свойства при растяжении и изгибе, ударная вязкость: при температуре –20°С, после старения и КСV при температуре +20°С
6 — химический состав, механические свойства при растяжении и изгибе, ударная вязкость: при температуре –40°С, после старения и КСV при температуре 0°С
Нормы ударной вязкости KCU, Дж/см2 (кгс⋅м/см2)***
|
Толщина, мм |
При температуре +20 °C |
При температуре -20 °C |
При температуре -40 °C |
После механического старения |
| Категория стали 3,4,5 (Ст3сп3, Ст3сп4, Ст3сп5) | ||||
| 5 — 9 | > 78 (8) | > 39 (4) | - | > 39 (4) |
| 10 — 25 | > 69 (7) | > 29 (3) | - | > 29 (3) |
|
26 — 40 |
> 49 (5) | - | - | - |
| Категория стали 6 (Ст3сп6) | ||||
| все | - | - |
> 39 (4) |
> 29 |
*** Для проката категорий 1 (Ст3сп) и 2 (Ст3сп2) ударную вязкость не нормируют
Нормы ударной вязкости KCV, Дж/см2 (кгс⋅м/см2)
|
Толщина, мм |
При температуре -40 °C |
При температуре 0 °C |
| Категория стали 5 (Ст3сп5) | ||
| 5 — 20 | 34 (3,5) | - |
| более 20 | - | - |
| Категория стали 6 (Ст3сп6) | ||
| 8 — 9 | - |
34 (3,5) |
| 10 — 20 | - | 30 (3,1) |
| более 20 | - | - |
Механические свойства по стандарту ГОСТ 14918-80
Сталь группы ХШ*
| Толщина, мм |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ4, % |
| Категория вытяжки Н** | ||
| до 0,7 | 300 — 490 | > 21 |
| 07 — 1,5 |
300 — 490 |
> 22 |
| 1,5 — 2 |
300 — 490 |
> 23 |
| более 2 |
300 — 490 |
> 24 |
| Категория вытяжки Г | ||
|
до 0,7 |
275 — 430 | > 23 |
|
07 — 1,5 |
275 — 430 | > 24 |
|
1,5 — 2 |
275 — 430 | > 25 |
|
более 2 |
275 — 430 | > 26 |
| Категория вытяжки ВГ | ||
| до 0,7 | 255 — 410 | > 26 |
| 07 — 1,5 | 255 — 410 | > 28 |
| 1,5 — 2 | 255 — 410 | > 29 |
| более 2 | 255 — 410 | > 30 |
Сталь группы ХП, ПК
| Толщина, мм |
Предел текучести для остаточной деформации, σт, МПа |
Относительное удлинение при разрыве, δ5, % |
| до 0,7 |
> 230 |
> 20 |
| 07 — 1,5 |
> 230 |
> 22 |
| 1,5 — 2 |
> 230 |
- |
| более 2 | > 230 | - |
* Группы стали в зависимости от назначения:
ХШ — сталь для холодной штамповки
ХП — сталь для холодного профилирования
ПК — сталь под окраску
** Категории вытяжки (в зависимости от степени к вытяжке):
Н — сталь нормальной вытяжки
Г — сталь глубокой вытяжки
ВГ — весьма высокой вытяжки
Глубина сферической лунки стали группы ХШ
| Толщина, мм | Категория вытяжки Н | Категория вытяжки Г | Категория вытяжки ВГ |
|
0,5 |
> 6,9 | > 8 | > 8,5 |
| 0,6 | > 7,2 |
> 8,5 |
> 8,9 |
| 0,7 | > 7,5 | > 8,9 | > 9,2 |
| 0,8 | > 7,8 | > 9,3 | > 9,5 |
| 0,9 | > 8,2 | > 9,6 | > 9,9 |
| 1 | > 8,6 | > 9,9 | > 10,1 |
| 1,1 | > 8,7 | > 10,1 | > 10,3 |
| 1,2 | > 8,8 | > 10,3 | > 10,5 |
| 1,3 | > 8,9 | > 10,5 | > 10,7 |
| 1,4 | > 9 | > 10,6 | > 10,8 |
| 1,5 | > 9,1 | > 10,8 | > 11 |
| 1,6 | > 9,5 | > 11 | > 11,3 |
| 1,7 | > 9,6 | > 11,1 | > 11,4 |
| 1,8 | > 9,7 | > 11,2 | > 11,5 |
| 1,9 | > 9,8 | > 11,3 | > 11,6 |
| 2 и более | > 9,9 | > 11,4 | > 11,7 |
Механические свойства по стандарту ГОСТ 16523-97
Группа прочности ОК360В
| Сортамент | Толщина, мм |
Временное сопротивление разрыву, σв, МПа* |
Относительное удлинение при разрыве, δ4, %** |
Испытание на изгиб в холодном состоянии*** |
| Категория стали 1 (Ст3сп)*** | ||||
| Труба | до 2 | - | - | d=a |
| Труба | более 2 | - | - | d=2a |
| Категория стали 4 (Ст3сп4) | ||||
| Труба | до 2 | 360 — 530 | > 20 | - |
| Труба | более 2 | 360 — 530 | > 22 | - |
| Категория стали 5 (Ст3сп5) | ||||
| Труба | до 2 | 360 — 530 | > 20 | d=a |
| Труба | более 2 | 360 — 530 | > 22 | d=2a |
Группа прочности ОК370В
| Сортамент | Толщина, мм |
Временное сопротивление разрыву, σв, МПа* |
Относительное удлинение при разрыве, δ5, %** |
Испытание на изгиб в холодном состоянии*** |
| Категория стали 1 (Ст3сп)**** | ||||
| Труба | до 2 | - | - | d=a |
| Труба | более 2 | - | - | d=2a |
| Категория стали 4 (Ст3сп4) | ||||
| Труба | до 2 | 370 — 530 | > 20 | - |
| Труба | более 2 | 370 — 530 | > 22 | - |
| Категория стали 5 (Ст3сп5) | ||||
| Труба | до 2 | 370 — 530 | > 20 | d=a |
| Труба | более 2 | 370 — 530 | > 22 | d=2a |
* Допускается изготовление проката без ограничения верхнего предела временного сопротивления
** Для холоднокатаного проката относительное удлинение при разрыве +2%
*** a — толщина образца, d — диаметр оправки
**** Категории стали в зависимости от нормируемых характеристик:
1 — без испытания механических свойств на растяжение и ударную вязкость
4 — сталь с испытанием механических свойств на растяжение и ударную вязкость на образцах, изготовленных из термически обработанных (закалка + отпуск) заготовок указанного в заказе размера, но не более 100мм
5 — сталь с испытанием механических свойств на растяжение на образцах, изготовленных из сталей в нагартованном или термически обработанном состоянии (отожженной или высокоотпущенной)
Механические свойства по стандарту ГОСТ 30136-95
| Сортамент | Способ охлаждения* | Временное сопротивление разрыву, σв, МПа |
Относительное сужение, ψ, % |
| Катанка | УО1, ВО |
< 490 |
< 60 |
| Катанка | УО2 |
< 540 |
< 60 |
*Способы охлаждения катанки:
УО1 — одностадийное охлаждение
УО2 — двухстадийное охлаждение
ВО — охлаждение на воздухе
Механические свойства по стандарту ГОСТ 32678-2014
| Сортамент |
Временное сопротивление разрыву, σв, МПа |
Предел текучести для остаточной деформации, σт, МПа |
Относительное удлинение при разрыве, δ5, % |
| Термически обработанная продукция | |||
| Трубы |
> 372 |
> 225 |
> 22 |
|
Без термической обработки* |
|||
| Трубы | > 315 |
> 216 |
> 5 |
* Механические свойства труб без термической обработки устанавливают по согласованию между изготовителем и потребителем. В случае отсутствия такого согласования производство сварных холоднодеформированных труб должно соответствовать нормам, указанным в таблице.
В случае отсутствия такого согласования производство сварных холоднодеформированных труб должно соответствовать нормам, указанным в таблице.
Дополнительные свойства Ст3сп
Сварка стали Ст3сп
Ст3сп характеризуется уникальной свариваемостью, что обеспечивает большой диапазон технических характеристик, которые можно улучшить при помощи легирующих добавок. Свойства стали дают возможность применять дуговую сварку – автоматическую и ручную, сварку по контактно-точечной и электрошлаковой технологии.
Важно для проведения всех сварочных работ, что сталь данной марки легко сваривается без подготовительных мероприятий – специальной подготовки, и изделия не требуют обработки после сварки. Хотя это касается только сварки изделий с толщиной менее 3,6 см. Стальные изделия с большей толщиной рекомендовано предварительно разогреть (100 °С) и выполнить термообработку после сварки.
Для сварки изделий из Ст3сп целесообразно использовать проволочные электроды (чаше всего, с большим сечением), плавящимися мундштуками.
Форма поставки стали Ст3сп
Поставляется данная сталь в различных формах — поковки и отливки, сортовая сталь – листы, трубы квадратные и круглые, прокат фасонный (двутавры, тавры, швеллеры, уголки), слитки, слябы и блюмы, сутунки, заготовки, метизы, проволока, ленты, штамповки и пр.
Область применения
Изготовление элементов несущих конструкций, сварных и не сварных деталей и изделий, эксплуатируемых при положительных температурных режимах. А также листовой и фасонный прокат, эксплуатация которого производится при условиях температур -40°С — +425°С, и/или нагрузок с переменными значениями (статических, динамических).
Применение стали Ст3сп с учётом характеристик и свойств
Сталь данного типа является одной из самых востребованных в строительстве и промышленности.
Отсутствие в сплаве кислорода, и однородная структура – это факторы, повышающие стойкость к образованию коррозии в агрессивных средах. Эти качества, а также большая пластичность делают данную сталь незаменимой при производстве конструкций, элементов, к которым предъявляются большие требования по жёсткости.
Эти качества, а также большая пластичность делают данную сталь незаменимой при производстве конструкций, элементов, к которым предъявляются большие требования по жёсткости.
Это прокат – листовой и фасонный (швеллеры, двутавры и тавры, уголки), заготовки для арматуры, элементы трубопроводов (в частности, квадратные трубы), и пр.
Характеристики стали дают возможность возводить из неё опорные несущие конструкции, каркасы, эксплуатация которых ведётся в сложных условиях.
Из стали Ст3сп изготавливают элементы и детали без термообработки, что даёт возможность сохранить все характеристики сплава – фланцы, тройники, переходы.
Сталь используют также в качестве основного слоя при производстве горячекатаных 2-слойных листов, стойких к коррозии.
Аналоги Ст3сп
Марка ст3сп (аналоги — С255, ВСт3сп5-1 и 18сп, Е 235-C по ISO 630:1995)
×
Отмена Удалить
×
Выбрать тариф
×
Подтверждение удаления
Отмена Удалить
×
Выбор региона будет сброшен
Отмена
×
×
Оставить заявку
×
| Название | |||
Отмена
×
К сожалению, данная функция доступна только на платном тарифе
Выбрать тариф
Сигма 0 2 в Комсомольске-на-Амуре: 155-товаров: бесплатная доставка [перейти]
Партнерская программаПомощь
Комсомольск-на-Амуре
Каталог
Каталог Товаров
Одежда и обувь
Одежда и обувь
Стройматериалы
Стройматериалы
Текстиль и кожа
Текстиль и кожа
Здоровье и красота
Здоровье и красота
Детские товары
Детские товары
Продукты и напитки
Продукты и напитки
Электротехника
Электротехника
Дом и сад
Дом и сад
Сельское хозяйство
Сельское хозяйство
Промышленность
Промышленность
Мебель и интерьер
Мебель и интерьер
Все категории
ВходИзбранное
Сигма 0 2
regmarkets.ru/listpreview/idata2/33/e2/33e2a6df45f1a1468a403bcf5ad96d5d.jpg»>96 500
Мотобуксировщик компактный ЛИДЕР-СИГМА—2, 8,0+ л.с., с лыжным модулем, ВАРИАТОР TAV2-40 Видео:
ПОДРОБНЕЕЕще цены и похожие товары
95 880
Мотобуксировщик с лыжным модулем Лидер — Сигма — 2 компактный, 8,0+ л.с. Тип: мотобуксировщик
ПОДРОБНЕЕЕще цены и похожие товары
mds.yandex.net/get-marketpic/5399334/pic51626b64273522a4b5753f2d9a8afd2a/300×300″>96 500
Мотобуксировщик компактный ЛИДЕР-СИГМА—2, 8,0 л.с., с лыжным модулем, ВАРИАТОР TAV2-40 Видео:
ПОДРОБНЕЕЕще цены и похожие товары
ru/listpreview/idata2/4d/0a/4d0af40281535f70f30a12e178f4df54.jpg»>98 600
Мотобуксировщик компактный ЛИДЕР-СИГМА—2, 8,0 л.с., с РЫЧАЖНЫМ лыжным модулем ВАРИАТОР TAV2-40
ПОДРОБНЕЕЕще цены и похожие товары
59 690
Объектив Sigma 20mm f/1.4 DG HSM Art Sony E широкоугольный, АФ, УЗ мотор, 90.7×129.8 мм, 950 г, Sony
ПОДРОБНЕЕЕще цены и похожие товары
99 600
Мотобуксировщик компактный ЛИДЕР-СИГМА—2, 8,0+ л.с., с РЫЧАЖНЫМ лыжным модулем, ВАРИАТОР TAV2-40
ПОДРОБНЕЕЕще цены и похожие товары
0 Фоторамка Interior Office 2 серия 288/ 21х30 карельская берёза пластиковая, цена за 1 шт Цвет:
В МАГАЗИНЕще цены и похожие товары
mds.yandex.net/get-mpic/4262452/img_id2995095488591825526.jpeg/300×300″>2 бокала для красного вина Riedel The O Wine Tumbler 600 мл (0414/0)
В МАГАЗИНЕще цены и похожие товары
mds.yandex.net/get-mpic/5323398/img_id2879263370630942253.jpeg/300×300″>16 282
2 Аккумулятора Metabo, 18 В — 4.0 А·Ч
В МАГАЗИНЕще цены и похожие товары
638
958
2 шт. Цифровой вольтметр DC 5V до 120 В На панель напряжения 0 56 дюйма светодиодный дисплей тестер для лабораторной электрической техники мотоцикл автомобиль B
В МАГАЗИНЕще цены и похожие товары
mds.yandex.net/get-mpic/5315102/img_id4457813533676186227.jpeg/300×300″>73 900
Объектив Sigma 28-70mm f/2.8 DG DN Contemporary SONY E стандартный, Zoom, АФ, 72.2×101.5 мм, 470 г,
ПОДРОБНЕЕЕще цены и похожие товары
2*0,9м. Электрогирлянда »Бахрома с звёздочками» контроллером (теплый) 138LED IP20 Vegas 55134
В МАГАЗИНЕще цены и похожие товары
mds.yandex.net/get-mpic/5521597/img_id1274508074215216563.png/300×300″>1 406
2300
2-шт Покрышка 10 дюймов 10×2.0 ( 54-152 ) НОТА Комплект — 2 ШТ Полукольца для коляски детской детских колясок велосипеда
В МАГАЗИНЕще цены и похожие товары
99 590
Объектив Sigma 12-24mm f/4 DG HSM Art Nikon F широкоугольный, Zoom, АФ, УЗ мотор, асф. линзы, 1134 г
линзы, 1134 г
ПОДРОБНЕЕЕще цены и похожие товары
692
990
2-шт Камера 10 x 2.0 A/V Кривой ниппель Wandersmann — 2 ШТ Комплект для коляски детской велосипеда универсальная бутиловая 10х2 2 штуки
В МАГАЗИНЕще цены и похожие товары
1 182
1890
2-шт Покрышка 10 дюймов 10×2.0 ( 54-152 ) НОТА (А-1022) 2 ШТ — комплект для коляски детской детских колясок велосипеда
В МАГАЗИНЕще цены и похожие товары
mds.yandex.net/get-marketpic/4872461/pic19af008bb72b327fe0488f84c8ad13a8/300×300″>129 519
2-секционный SIGNAL2-L210-RG-0
В МАГАЗИНЕще цены и похожие товары
83 948
2-секционный SIGNAL2-G210-RG-0
В МАГАЗИНЕще цены и похожие товары
jpeg/300×300″>2-сп с европростыней Постельное белье «Ненаглядная 2» ( 2.0 европростыня) сатин Цвет: Фиолетовый,
ПОДРОБНЕЕЕще цены и похожие товары
regmarkets.ru/listpreview/images/34/cf/34cf6fe8d0aaa0c76d729d335239a5ad.jpg»>2-сп с европростыней Постельное белье «Безмятежная даль 2» ( 2,0 европростыня) Перкаль Цвет: Серый,
ПОДРОБНЕЕЕще цены и похожие товары
jpg»>2-спальное Постельное белье «Юлианна 1» ( 2,0) Перкаль Цвет: Красный, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Пальмира 2» ( 2,0 европростыня) Перкаль Цвет: Серый, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
mds.yandex.net/get-mpic/4377400/img_id5493521992173928423.jpeg/300×300″>2-спальное Постельное белье «Ненаглядная 2» ( 2,0 ) сатин Цвет: Фиолетовый, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
jpeg/300×300″>74 190
Объектив Sigma 20mm F2 DG DN Contemporary Sony E широкоугольный, АФ, асф. линзы, 70×74.4 мм, 370 г,
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Джулия 4» ( 2,0) Сатин Цвет: Фиолетовый, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Узоры 5» ( 2,0 европростыня) Сатин Цвет: Коричневый, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
mds.yandex.net/get-marketpic/5866089/pic23f85c595a6cea75f9c49804901bded4/300×300″>2-спальное Постельное белье «Узоры 5» ( 2,0) Сатин Цвет: Коричневый, Размер: КПБ [2. 0], Материал:
0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Пальмира 2» ( 2,0) Перкаль Цвет: Серый, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
89 990
Объектив Sigma AF 24-35mm f/2 DG HSM Nikon F широкоугольный, Zoom, АФ, УЗ мотор, асф. линзы, 88×123
ПОДРОБНЕЕЕще цены и похожие товары
regmarkets.ru/listpreview/images/67/b3/67b3c2a9e157770c1c1ec7395c30388b.jpg»>2-сп с европростыней Постельное белье «Заповедный мир 3» ( 2,0 европростыня) Прекаль Цвет:
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Заповедный мир 3» ( 2,0) Перкаль Цвет: Коричневый, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
jpg»>2-спальное Постельное белье «Дуновение 1» (2.0 простыня на резинке ) Перкаль Цвет: Зеленый, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
2-спальный (172х215) Пододеяльник » Эко 15″ (2,0) Перкаль Размер: Пододеяльник [172×215], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
mds.yandex.net/get-marketpic/5938227/pic68738234f287c85cd1bfdc7a493ba93b/300×300″>2-спальное Постельное белье «Даниэлла 5» ( 2,0) сатин Цвет: Розовый, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Утренняя прохлада» (2,0 европростыня), Перкаль Цвет:
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Затаив дыхание 5», Бязь (2. 0) Цвет: Голубой, Размер: КПБ [2.0],
0) Цвет: Голубой, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
30 524
Сигма-ИС Источники бесперебойного питания до 12В ИБП-12 IP55 исп.2
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Лапландия 1 (2.0 европростыня)» Цвет: Красный, Размер: КПБ
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Дуновение 1», бязь (2. 0), Цвет: Зеленый, Размер: КПБ [2.0],
0), Цвет: Зеленый, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Яркий персик», сатин (2.0) Цвет: Розовый, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Горчица», сатин (2.0) Цвет: Желтый, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
regmarkets.ru/listpreview/images/4b/f6/4bf6a4d25039197b36132db03294db45.jpg»>2-сп с европростыней Постельное белье «Эдуард 1», сатин (2.0 европростыня (4 нав.)) Цвет: Синий,
ПОДРОБНЕЕЕще цены и похожие товары
18 981
Сигма-ИС Прибор приемно-контрольный охранно-пожарный ПИ-04 исп.2
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Божья коровка», бязь (2.0), простыня на резинке Цвет: Зеленый, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Хаски», перкаль (2. 0 европростыня) Цвет: Голубой, Размер:
0 европростыня) Цвет: Голубой, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Парадиз 1», перкаль (2.0 европростыня) Цвет: Бежевый,
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Масаи 3» ( 2,0 европростыня) перкаль Цвет: Серый, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
regmarkets.ru/listpreview/images/1c/8c/1c8c1ca5c3fe71fb9b4584888d2d97a2.jpg»>2-спальное Постельное белье «Таймс-сквер», перкаль (2.0) Цвет: Серый, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Ореховая роща», Бязь (2.0) Цвет: Коричневый, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Золотая осень 2», Бязь (2.0) Размер: КПБ [2.0], Материал: Бязь,
ПОДРОБНЕЕЕще цены и похожие товары
jpg»>2-спальное Постельное белье «Ежевичное варенье», трикотаж (2.0) на резинке Цвет: Фиолетовый,
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Баттерфляй 3», бязь (2.0 европростыня) Цвет: Сиреневый,
ПОДРОБНЕЕЕще цены и похожие товары
2-сп с европростыней Постельное белье «Гравюра 2», Бязь (2.0) Размер: КПБ [2.0], Материал: Бязь,
ПОДРОБНЕЕЕще цены и похожие товары
jpg»>2-сп с европростыней Постельное белье «Сокровищница 3», сатин (2.0) Цвет: Серый, Размер: КПБ [2.0],
ПОДРОБНЕЕЕще цены и похожие товары
2-спальное Постельное белье «Элис 10», перкаль (2.0) Цвет: Фиолетовый, Размер: КПБ [2.0], Материал:
ПОДРОБНЕЕЕще цены и похожие товары
regmarkets.ru/listpreview/images/5f/5a/5f5acbdde3a59777f673c43df55ff108.jpg»>2-сп с европростыней Постельное белье «Легкое дыхание 1» (2.0 европростыня) Цвет: Черный, Размер:
ПОДРОБНЕЕЕще цены и похожие товары
2 страница из 18
Прочность стали на срез таблица
Текучесть расплава металла
Текучестью расплава металла называют его свойство полностью заполнять литейную форму, проникая в малейшие полости и детали рельефа. От этого зависит точность отливки и качество ее поверхности.
Жидкий металл для процессоров
Свойство можно усилить, если поместить расплав под избыточное давление. Это физическое явление используется в установках литья под давлением. Такой метод позволяет существенно повысить производительность процесса литья, улучшить качество поверхности и однородность отливок.
youtube.com/embed/P5RZDuu5Hsk?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Как производится испытание на прочность
Изначально особенных мероприятий не было. Люди брали предмет, использовали его, а как только он ломался, анализировали поломку и снижали нагрузку на аналогичное изделие. Теперь процедура гораздо сложнее, однако, до настоящего времени самый объективный способ узнать ПП — эмпирический путь, то есть опыты и эксперименты.
Все испытания проходят в специальных условиях с большим количеством точной техники, которая фиксирует состояние, характеристики подопытного материала. Обычно он закреплен и испытывает различные воздействия — растяжение, сжатие. Их оказывают инструменты с высокой точностью — отмечается каждая тысячная ньютона из прикладываемой силы. Одновременно с этим фиксируется каждая деформация, когда она происходит. Еще один метод не лабораторный, а вычислительный. Но обычно математический анализ используется вместе с испытаниями.
Но обычно математический анализ используется вместе с испытаниями.
Определение термина
Образец растягивается на испытательной машине. При этом сначала он удлиняется в размере, а поперечное сечение становится уже, а затем образуется шейка — место, где самый тонкий диаметр, именно здесь заготовка разорвется. Это актуально для вязких сплавов, в то время как хрупкие, к ним относится чугун и твердая сталь, растягиваются совсем незначительно без образования шейки. Подробнее посмотрим на видео:
Условный предел текучести
Условный предел текучести
(он же технический предел текучести). Для материалов, не имеющих на диаграмме
площадки текучести
, принимают
условный предел текучести
— напряжение, при котором остаточная деформация образца достигает определённого значения, установленного техническими условиями (большего, чем это установлено для предела упругости). [2] Под условным пределом текучести обычно подразумевают такое напряжение, при котором остаточная деформация составляет 0,2%. Таким образом обычно условный предел текучести при растяжении обозначается σ0,2.
[2] Под условным пределом текучести обычно подразумевают такое напряжение, при котором остаточная деформация составляет 0,2%. Таким образом обычно условный предел текучести при растяжении обозначается σ0,2.
Выделяют также условный предел текучести при изгибе
и
условный предел текучести при кручении
.
Состав стальных сплавов
Свойства металла зависят от сформированной кристаллической решетки, которая, в свою очередь, определяется содержанием углерода. Зависимость типов решетки от количества углерода хорошо прослеживается на структурной диаграмме. Если, например, в решетке стали насчитывается до 0.06% углерода, то это классический феррит, который имеет зернистую структуру. Такой материал непрочный, но текучий и имеет большой предел ударной вязкости.
По структуре стали делятся на:
- ферритную;
- перлитно-ферритовую;
- цементитно-ферритную;
- цементитно-перлитовую;
- перлитную.
Добавки углерода и прочность
Закон аддитивности подтверждается процентными изменениями цементита и феррита в стали. Если количество углеродной добавки составляет около 1,2%, то предел текучести стального материала увеличивается и повышается твердость, прочность и температуростойкость. При последующем увеличении содержания углерода технические параметры ухудшаются. Сталь плохо сваривается и неохотно поддается штамповке. Самым лучшим образом при сварке ведут себя сплавы с небольшим содержанием углерода.
Если количество углеродной добавки составляет около 1,2%, то предел текучести стального материала увеличивается и повышается твердость, прочность и температуростойкость. При последующем увеличении содержания углерода технические параметры ухудшаются. Сталь плохо сваривается и неохотно поддается штамповке. Самым лучшим образом при сварке ведут себя сплавы с небольшим содержанием углерода.
Марганец и кремний
В виде добавки, чтобы увеличить степень раскисления, дополнительно добавляют марганец. Кроме того, этот элемент уменьшает вредное воздействие серы. Содержание марганца обычно не более 0.8% и он не влияет на технологические свойства сплава. Присутствует как твердый компонент.
Кремний тоже особо не влияет на характеристики металла. Он необходим для увеличения качества сварки деталей. Содержание этого элемента не превышает 0.38% и он добавляется во время процесса раскисления.
Читать также: Мойка высокого давления своими руками из компрессора
Сера и фосфор
Сера содержится в виде хрупких сульфитов. Повышенное количество этого элемента влияет на механические показатели сплава. Чем больше серы, тем хуже пластичность, текучесть и вязкость сплава. Если превышен предел в 0.06%, то изделие сильнее подвержено коррозии и становится способным к сильному истиранию.
Повышенное количество этого элемента влияет на механические показатели сплава. Чем больше серы, тем хуже пластичность, текучесть и вязкость сплава. Если превышен предел в 0.06%, то изделие сильнее подвержено коррозии и становится способным к сильному истиранию.
Наличие фосфора увеличивает показатель текучести, но при этом уменьшается пластичность и вязкость. В общем, завышенное содержание фосфора значительно ухудшает качество металла. Особенно вредно сказывается на характеристиках совместное высокое содержание фосфора и углерода. Допустимыми пределами содержания фосфора считаются значения от 0.025 до 0.044%.
Азот и кислород
Это неметаллические примеси, которые понижают механические свойства сплава. Если содержание кислорода больше чем 0.03%, то металл быстрее стареет, падают значения пластичности и вязкости. Азотные добавки увеличивают прочность, но в этом случае предел текучести уменьшается. Увеличенное содержание азота делает сталь ломкой и способствует быстрому старению металлической конструкции.
Поведение легирующих добавок
Для улучшения всех физических показателей стали, в сплав добавляют специальные легирующие элементы. Такими добавками могут быть вольфрам, молибден, никель, хром, титан и ванадий. Совместное добавление в необходимых пропорциях, дает самые приемлемые результаты.
Легирование значительно повышает показатель текучести, ударной вязкости и препятствует деформации и растрескиванию.
Сталь 45
Главная->Справочник->Марочник сталей->Конструкционная сталь
Сталь 45Г Сталь 40ХФА
Конструкционная качественная углеродистая сталь 45
Марка 45 – назначение
Конструкционная качественная углеродистая сталь 45 используется для изготовления улучшаемых, нормализованных, с поверхностной обработкой деталей повышенной прочности – распределительные/ коленчатые валы, кулачки, цилиндры, бандажи, шпиндели, шестерни, вал-шестерни, другие изделия.
Сталь 45 – отечественные аналоги
| Марка металлопроката | Заменитель |
| 45 | 40Х |
| 50 | |
| 50Г2 |
Материал 45 – характеристики
| Марка | Классификация | Вид поставки | ГОСТ | Зарубежные аналоги |
| 45 | Сталь конструкционная углеродистая качественная | Сортовой прокат | 1050–88 | есть |
| 10702–78 | ||||
| Поковки | 8479–70 | |||
| Трубы | 8731–74 | |||
| 8733–74 | ||||
| 13663–86 | ||||
| Лист | 1577–93 | |||
| 16523–97 | ||||
| Лента | 2284–79 | |||
| Полоса | 1577–93 | |||
| Проволока | 5663–79 |
Марка 45 – технологические особенности
Термообработка
| Режим |
| Состояние поставки |
Ковка
| Вид полуфабриката | t, 0С | Охлаждение | |
| Размер сечения | Условия | ||
| мм | |||
| Слиток | 1250–780 | все размеры – поковки ответственного назначения | Нормализация |
| Переохлаждение | |||
| Переохлаждение | |||
| Отпуск | |||
| до 400 | На воздухе | ||
| 401–800 | Низкотемпературный отжиг | ||
| >800 | Низкотемпературный отжиг | ||
| Переохлаждение | |||
| Заготовка | 1250–750 | до 400 | На воздухе |
Сварка
| Свариваемость | Способы сварки | Рекомендации |
| трудно свариваемая | РДС, КТС | Подогрев + термообработка |
Флокеночувствительность
Мало чувствительна.
Резка
| Исходные данные | Обрабатываемость резанием Ku | |||
| Состояние | HB, МПа | sB, МПа | твердый сплав | быстрорежущая сталь |
| горячекатаное | 170–179 | 650 | 1,0 | 1.0 |
Склонность к отпускной хрупкости
Не склонна.
Сталь 45 – химический состав
Массовая доля элементов не более, %:
| Кремний | Марганец | Медь | Мышьяк | Никель | Сера | Углерод | Фосфор | Хром |
| 0,17–0,37 | 0,5–0,8 | 0,3 | 0,08 | 0,3 | 0,04 | 0,42–0,5 | 0,035 | 0,25 |
Материал 45 – механические свойства
| Сортамент | ГОСТ | Размеры – толщина, диаметр | Термообработка | KCU | y | d5 | sT | sв |
| мм | кДж/м2 | % | % | МПа | МПа | |||
| Трубы | 8731–87 | 14 | 323 | 588 | ||||
Пруток калиброван. | 10702–78 | Отжиг | 40 | 590 | ||||
| Прокат | 1050–88 | до 80 | Нормализация | 40 | 16 | 355 | 600 | |
| нагартован. | 30 | 6 | 640 | |||||
| отожжен. | 40 | 13 | 540 | |||||
| Лента отожжен. | 2284–79 | 14 | 440–690 | |||||
| нагартован. | 690–1030 | |||||||
| Полоса | 1577–93 | 6–60 | Нормализация | 40 | 16 | 355 | 600 |
Твердость, Мпа
| Сортамент | ГОСТ | HB 10-1 |
| Трубы | 8731–87 | 207 |
| Прокат горячекатан. | 1050–88 | 229 |
| калиброван. нагартован. | 241 | |
| калиброван. отожжен. | 207 | |
| горячекатан. отожжен. | 197 |
Температура критических точек, 0С
| Критические точки | Ac1 | Ac3 | Ar1 | Ar3 | Mn |
| Температура | 730 | 755 | 780 | 690 | 350 |
Ударная вязкость, Дж/см2
| Режимы термообработки | KCU при температурах | ||||||
| -1000С | -800С | -600С | -400С | -200С | 00С | +200С | |
| Нормализация | 12 | 40 | 6149 | 61 | 90–94 | ||
| Отпуск | |||||||
Предел выносливости, МПа
| Термообработка | t-1 | s-1 | |
| Режим | t, 0С | ||
| Нормализация | 850 | 170 | 280 |
| Отпуск | 550–650 | ||
Марка 45 – физические свойства
| t | r | R 109 | E 10-5 | l | a 106 | C |
| 0С | кг/м3 | Ом·м | МПа | Вт/(м·град) | 1/Град | Дж/ (кг·град) |
| 20 | 7826 | 2 | ||||
| 100 | 7799 | 2. 01 01 | 48 | 11.9 | 473 | |
| 200 | 7769 | 1.93 | 47 | 12.7 | 494 | |
| 300 | 7735 | 1.9 | 44 | 13.4 | 515 | |
| 400 | 7698 | 1.72 | 41 | 14.1 | 536 | |
| 500 | 7662 | 39 | 14.6 | 583 | ||
| 600 | 7625 | 36 | 14.9 | 578 | ||
| 700 | 7587 | 31 | 15.2 | 611 | ||
| 800 | 7595 | 27 | 720 | |||
| 900 | 26 | 708 |
Сталь 45 – точные и ближайшие зарубежные аналоги
| Австрия | Австралия | Англия | Бельгия | Болгария | Венгрия |
| ONORM | AS | BS | NBN | BDS | MSZ |
| C45SW |
| HK1042 |
| K1042 |
| 080M |
| 080M46 |
| 1449-50CS |
| 1449-50HS |
| 50HS |
| C45 |
| C45E |
| C45-2 |
| C46 |
| C45 |
| C45E |
| Германия | Евросоюз | Испания | Италия | Китай | Польша | Румыния |
| DIN, WNr | EN | UNE | UNI | GB | PN | STAS |
1. 0503 0503 | ||||||
| 1.1191 | ||||||
| 1.1193 | ||||||
| C45 | ||||||
| C45E | ||||||
| C45R | ||||||
| Cf45 | ||||||
| Ck45 | ||||||
| Cm45 | ||||||
| Cq45 |
| 1.1191 |
| 1.1192 |
| 2C45 |
| C45 |
| C45E |
| C45EC |
| C46 |
| C45E |
| C45k |
| C48k |
| F.114 |
| F.1140 |
| F.1142 |
| C43 |
| C45 |
| C45E |
| C45R |
| C46 |
| 45H |
| ML45 |
| SM45 |
| ZG310-570 |
| ZGD345-570 |
| OLC45q |
| OLC45X |
| США | Франция | Чехия | Швейцария | Швеция | Юж. Корея Корея | Япония |
| — | AFNOR | CSN | SNV | SS | KS | JIS |
| 1044 | ||||||
| 1045 | ||||||
| 1045H | ||||||
| G10420 | ||||||
| G10430 | ||||||
| G10440 | ||||||
| G10450 | ||||||
| M1044 |
| 2C45 |
| AF65 |
| C40E |
| C45 |
| C45E |
| C45RR |
| CC45 |
| XC42h2 |
| XC42h2TS |
| XC45 |
| XC45h2 |
| XC48 |
| XC48h2 |
| S48C |
| SWRCh55K |
| SWRCh58K |
Материал 45 – область применения
Сталь марки 45 используют в машиностроении для изготовления деталей повышенной прочности.
Условные обозначения
Механические свойства
| HRCэ | HB | KCU | y | d5 | sT | sв |
| МПа | кДж / м2 | % | % | МПа | МПа | |
| Твердость по Роквеллу | Твердость по Бринеллю | Ударная вязкость | Относительное сужение | Относительное удлинение при разрыве | Предел текучести | Предел кратковременной прочности |
| Ku | s0,2 | t-1 | s-1 |
| Коэффициент относительной обрабатываемости | Условный предел текучести с 0,2% допуском при нагружении на значение пластической деформации | Предел выносливости при кручении (симметричный цикл) | Предел выносливости при сжатии-растяжении (симметричный цикл) |
| N | число циклов деформаций/ напряжений, выдержанных объектом под нагрузкой до появления усталостного разрушения/ трещины |
Свариваемость
| Без ограничений | Ограниченная | Трудно свариваемая | |
| Подогрев | нет | до 100–1200С | 200–3000С |
| Термообработка | нет | есть | отжиг |
Физические свойства
| R | Ом·м | Удельное сопротивление |
| r | кг/м3 | Плотность |
| C | Дж/(кг·град) | Удельная теплоемкость |
| l | Вт/(м·град) | Коэффициент теплопроводности |
| a | 1/Град | Коэффициент линейного расширения |
| E | МПа | Модуль упругости |
| t | 0С | Температура |
Купить металлопрокат из конструкционной качественной углеродистой стали 45 в Санкт-Петербурге Вы можете по телефону + 7 (812) 703-43-43. Специалисты оформят заказ, сориентируют по сортаменту, ценам, условиям доставки.
Специалисты оформят заказ, сориентируют по сортаменту, ценам, условиям доставки.
Cталь 30ХГТ Cталь 35ХН1М2ФА Cталь 40 Cталь 40Г Cталь 45ХН Марка А20 Марка А30 Сталь 08 Сталь 08кп Сталь 08пс Сталь 08Ю Сталь 09Г2 Сталь 09Г2С Сталь 10 Сталь 10Г2 Сталь 10Г2БД Сталь 10Г2С1 Сталь 10кп Сталь 10пс Сталь 10Х14Г14Н4Т Сталь 10ХНДП Сталь 10ХСНД Сталь 12ГС Сталь 12К Сталь 12Х18Н10Т Сталь 12Х2Н4А Сталь 12ХН2 Сталь 12ХН2А Сталь 12ХН3А Сталь 14Г2 Сталь 14Г2АФ Сталь 14Х2ГМР Сталь 14ХГС Сталь 15 Сталь 15Г Сталь 15Г2АФДпс Сталь 15Г2СФД Сталь 15К Сталь 15кп Сталь 15пс Сталь 15Х Сталь 15ХСНД Сталь 15ХФ Сталь 16Г2АФ Сталь 16ГС Сталь 16К Сталь 17Г1С Сталь 17ГС Сталь 18Г2АФпс Сталь 18К Сталь 18кп Сталь 18Х2Н4ВА Сталь 18Х2Н4МА Сталь 18ХГТ Сталь 20 Сталь 20Г Сталь 20К Сталь 20кп Сталь 20пс Сталь 20Х Сталь 20Х2Н4А Сталь 20ХГ2Ц Сталь 20ХГНР Сталь 20ХГР Сталь 20ХГСА Сталь 20ХН Сталь 20ХН2М Сталь 20ХН3А Сталь 20ХН4ФА Сталь 20ХНР Сталь 22К Сталь 25 Сталь 25Г2С Сталь 25пс Сталь 25ХГСА Сталь 25ХГТ Сталь 30 Сталь 30X Сталь 30Г Сталь 30ХГС Сталь 30ХГСА Сталь 30ХГСН2А Сталь 30ХН2МА Сталь 30ХН2МФА Сталь 30ХН3М2ФА Сталь 31Х19Н9МВБТ Сталь 33ХС Сталь 34ХН1М Сталь 34ХН3М сталь 35 Сталь 35Г Сталь 35Г2 Сталь 40Г2 Сталь 40Х Сталь 40Х2Н2МА Сталь 40ХС Сталь 40ХФА Сталь 45 Сталь 45Г Сталь 45Г2 Сталь 45Х сталь 60С2А сталь 60С2Н2А сталь 60С2ХА сталь 60С2ХФА сталь 65 сталь 65Г сталь 65С2ВА сталь 70 сталь 70С3А сталь А12 Сталь А40Г Сталь ВСт3кп Сталь обыкновенного качества ВСт2кп Сталь обыкновенного качества ВСт2пс Сталь обыкновенного качества ВСт2сп Сталь обыкновенного качества ВСт3Гпс Сталь обыкновенного качества ВСт3пс Сталь обыкновенного качества ВСт3сп Сталь обыкновенного качества ВСт4кп Сталь обыкновенного качества Вст4пс Сталь обыкновенного качества ВСт5пс Сталь обыкновенного качества ВСт5сп Сталь обыкновенного качества ВСт6сп Сталь обыкновенного качества Ст0 Сталь ОсВ Сталь ШХ15 Сталь ШХ15СГ Сталь ШХ4
Легирующие добавки в составе сплавов
Легирующими добавками называют вещества, намеренно введенные в состав сплав для целенаправленного изменения его свойств до нужных показателей. Такие сплавы называют легированными сталями. Лучших показателей можно добиться, добавляя одновременно несколько присадок в определенных пропорциях.
Такие сплавы называют легированными сталями. Лучших показателей можно добиться, добавляя одновременно несколько присадок в определенных пропорциях.
Влияние легирующих элементов на свойства стали
Распространенными присадками являются никель, ванадий, хром, молибден и другие. С помощью легирующих присадок улучшают значение предела текучести, прочности, вязкости, коррозионной стойкости и многих других физико-механических и химических параметров и свойств.
Предел прочности на растяжение стали
Стальные конструкции давно заменили прочие материалы, так как они обладают отличными эксплуатационными характеристиками — долговечностью, надежностью и безопасностью. В зависимости от применяемой технологии, он подразделяется на марки. От самой обычной с ПП в 300 Мпа, до наиболее твердой с высоким содержанием углерода — 900 Мпа. Это зависит от двух показателей:
- Какие способы термообработки применялись — отжиг, закалка, криообработка.
- Какие примеси содержатся в составе.
 Одни считаются вредными, от них избавляются для чистоты сплава, а вторые добавляют для укрепления.
Одни считаются вредными, от них избавляются для чистоты сплава, а вторые добавляют для укрепления.
Сигма x Masters FA обзор матча 09.06.2022 ✅ azscore.ru
ТОП ТурнирыБундеслига
Германия
Лига Чемпионов УЕФА
Европа
Лига Европы УЕФА
Европа
Премьер-лига
Англия
Ла Лига
Испания
Лига 1
Франция
Серия А
Италия
Чемпионат Мира Квалификация, Европа
Европа
Лига наций УЕФА
Европа
Лига конференций УЕФА
Европа
- Австралия
- Австрия 0 / 6
- Азербайджан
- Албания
- Алжир
- Англия 0 / 57
- Ангола
- Андорра
- Антигуа и Барбуда
- Аргентина 2 / 14
- Армения
- Аруба
- Афганистан
- Бангладеш 0 / 2
- Барбадос
6 Сигма
24 Сигма
34 Сигма
48 Masters FA
55 Сигма
Коэффициенты
1
1. 41
41
X 4.82
2 6.63
Больше коэффициентов
Результат к концу полного времени 1X2
Больше прогнозов
Полная статистика
Сигма
Masters FA
Нет матчей
Это первый матч этих команд, данные появятся позже.
Игра команд Сигма и Masters FA в рамках турнира Чемпионат Канады. Лига 1. Онтарио.
Дата начала матча: 09.06.2022.
Время игры: 03:00.
Статистика команды Сигма:
Футбольный клуб Сигма играет за страну Чехия.
Стадион команды: Стадион « Андрув».
Актуальный тренер: Jilek, Vaclav.
Прошедшие 5 игр с участием Сигма:
- Динамо Ческе-Будеёвице 0:3 Сигма — 17.09.2022
- Уничов 2:4 Сигма — 13.09.2022
- Сигма 2:3 Виктория Пльзень — 10.09.2022
- Пардубице 0:2 Сигма — 04.09.2022
- Сигма 1:1 Слован Либерец — 31.08.2022
Информация о Masters FA:
Команда Masters FA выступает за Канада.
Родной стадион клуба: L’Amoreaux Park.
Последние 5 противостояний с участием Masters FA:
- Masters FA 4:0 Юнионвилл Милликен — 21.08.2022
- Masters FA 1:2 Гамильтон Юнайтед — 14.08.2022
- Оквилл Блю Дэвилз 7:1 Masters FA — 07.
 08.2022
08.2022 - Вудбридж Страйкерз 1:1 Masters FA — 20.06.2022
- Норт Миссисауга 2:3 Masters FA — 16.06.2022
Результаты матчей между командами Сигма и Masters FA. Футбол онлайн на azscore.ru.
Топ букмекеры
1 СайтBetwinner Сайт
2 СайтTipico Сайт
3 СайтBet365 Germany Сайт
4 СайтBwin Сайт
5 СайтMozzartbet Сайт
Все букмекеры
- Дата:
- 9 Июнь 2022, 03:00
Булевы функции (формы SOP, POS)
Схема
Представление булевых функций
Использование переключающих устройств, таких как транзисторы, порождает особый случай булевой алгебры, называемый алгеброй переключения. В алгебре переключения все переменные принимают одно из двух значений: 0 и 1.
В алгебре переключения все переменные принимают одно из двух значений: 0 и 1.
[adsense1]
В булевой алгебре 0 используется для представления «открытого» или «ложного» состояния логического элемента. Точно так же 1 используется для представления «закрытого» состояния или «истинного» состояния логического элемента.
Логическое выражение — это выражение, состоящее из переменных, констант (0 — ложь и 1 — истина) и логических операторов, результатом которых является истина или ложь.
Булева функция — это алгебраическая форма логического выражения. Булева функция n-переменных представлена как f(x1, x2, x3….xn). Используя булевы законы и теоремы, мы можем упростить булевы функции цифровых схем. Краткое примечание о различных способах представления булевой функции показано ниже.
- Сумма продуктов (СОП) Форма
- Суммарное произведение (POS) форма
- Канонические формы
Существует два типа канонических форм:
- Сумма минимальных членов или каноническая СОП
- Product-of-max terms или Canonical POS
Булевы функции могут быть представлены с помощью вентилей И-НЕ, а также с помощью метода K-карты (карты Карно). Мы можем стандартизировать логические выражения, используя две стандартные формы.
Мы можем стандартизировать логические выражения, используя две стандартные формы.
Форма СОП – Сумма произведений, форма
Форма POS – произведение сумм форма
Стандартизация логических уравнений сделает внедрение, развитие и упрощение более простым и систематическим.
Форма суммы произведений (SOP)
Форма суммы произведений (SOP) представляет собой метод (или форму) упрощения логических выражений логических вентилей. В этой SOP-форме представления булевой функции переменные обрабатываются по И (продукт) для формирования термина продукта, и все эти термины продукта объединяются по ИЛИ (суммируются или складываются) вместе, чтобы получить окончательную функцию.
[адсенс2]
Форма суммы произведений может быть сформирована путем сложения (или суммирования) двух или более членов произведения с использованием логической операции сложения. Здесь термины произведения определяются с помощью операции И, а термин суммы определяется с помощью операции ИЛИ.
Форма суммы произведений также называется дизъюнктивной нормальной формой, так как термины произведения объединяются вместе, а операция дизъюнкции является логическим ИЛИ. Форма суммы продуктов также называется стандартной СОП. Представление формы
SOP наиболее подходит для их использования в FPGA (программируемых вентильных матрицах).
Примеры
AB + ABC + CDE
(AB) ̅ + ABC + CD E ̅
Форма SOP может быть получена с помощью
- Запись условия И для каждой входной комбинации, которая дает ВЫСОКИЙ выход.
- Запись входных переменных, если значение равно 1, и запись дополнения переменной, если ее значение равно 0.
- ИЛИ условия И для получения выходной функции.
Пример: логическое выражение для функции большинства F = A’BC + AB’C + ABC ‘ + ABC
Таблица истинности:
Теперь запишите комбинацию входных переменных с высоким выходом. F = АВ + ВС + АС.
Проверка
По закону идемпотентности мы знаем, что
([ABC + ABC)] + ABC) = (ABC + ABC) = ABC
Теперь функция F = A’BC + AB’C + ABC ‘ + ABC
= A’BC + AB’C + ABC’ + ([ABC + ABC)] + ABC)
= (ABC + ABC’) + (ABC + AB’C) + (ABC + A’ ВС)
= АВ (С + С’) + А (В + В’) С + (А + А’) ВС
= АВ + ВС + АС.
Форма произведения сумм (POS)
Форма произведения сумм – это метод (или форма) упрощения логических выражений логических вентилей. В этой форме POS все переменные объединяются по ИЛИ, т. е. записываются как суммы для формирования суммирующих условий.
Все эти составляющие суммы объединяются (умножаются) вместе, чтобы получить форму произведения суммы. Эта форма прямо противоположна форме СОП. Так что это также можно назвать «двойной формой SOP».
Здесь условия суммы определяются с помощью операции ИЛИ, а условия произведения определяются с помощью операции И. Когда два или более членов суммы умножаются с помощью логической операции ИЛИ, результирующее выходное выражение будет иметь форму произведения сумм или форму POS.
Форма произведения сумм также называется конъюнктивной нормальной формой, поскольку члены суммы объединяются вместе, а операция конъюнкции является логическим И. Форма произведения сумм также называется стандартной POS.
Примеры
(A+B) * (A + B + C) * (C +D)
(A+B) ̅ * (C + D + E ̅)
Форма POS может быть получена по телефону
- Запись условия ИЛИ для каждой комбинации входов, которая производит НИЗКИЙ выходной сигнал.

- Запись входных переменных, если значение равно 0, и запись дополнения переменной, если ее значение равно 1.
- И условия ИЛИ для получения выходной функции.
Пример: логическое выражение для функции большинства F = (A + B + C) (A + B + C ‘) (A + B’ + C) (A’ + B + C)
Теперь запишите ввод комбинация переменных с высокой производительностью. F = АВ + ВС + АС.
Проверка
По закону идемпотентности мы знаем, что
[(A + B + C) (A + B + C)] (A + B + C) = [(A + B + C)] ( A + B + C) = (A + B + C)
Теперь функция
F = (А + В) (В + С) (А + С)
= (А + В + С) (А + В + С’) (А + В’ + С) (А’ + В + В)
= [(А + В + С) (А + В + С)] (А + В + С) (А + В + С’) (А + В’ + С) (А’ + В + В)
= [(А + В + С) (А + В + С’)] [(А + В + С) (А’ + В + С)] [(А + В + С) (А + Б’ + В)]
= [(А + В) + (С * С’)] [(В + С) + (А * А’)] [(А + С) + (В * В’)]
= [(A + B) + 0] [(B + C) + 0] [(A + C) + 0] = (A + B) (B + C) (A + C)
Каноническая форма (Стандартная форма SOP и POS)
Любая булева функция, которая выражается как сумма minterms или как произведение maxterms, называется «канонической формой».
Он в основном включает два логических термина: «minterms» и «maxterms».
Когда форма SOP логического выражения находится в канонической форме, каждый из его терминов продукта называется «minterm». Таким образом, каноническая форма функции суммы произведений также известна как «каноническая форма minterm», или «Sum-of-minterms», или стандартная каноническая форма SOP.
Аналогичным образом, когда POS-форма логического выражения находится в канонической форме, каждый из его суммирующих терминов называется «maxterm». Таким образом, каноническая форма функции произведения сумм также известна как «каноническая форма maxterm или произведение суммы или стандартная каноническая форма POS».
Минимальные термины
Минтерм определяется как произведение n переменных, в котором каждая из n переменных появляется один раз либо в своей дополненной, либо в недополняемой форме. Минимальный член обозначается как mi, где i находится в диапазоне 0 ≤ i <2ⁿ.
Переменная находится в дополненной форме, если ее значение присвоено 0, и переменная находится в недополненной форме, если ее значение присвоено 1.
Для логической функции с 2 переменными (x и y) возможные минтермы:
x’y’, x’y, xy’ и xy.
Для булевой функции с 3 переменными (x, y и z) возможные minterms:
x’y’z’, x’y’z, x’yz’, x’yz, xy’z’ , xy’z, xyz’ и xyz.
- 1 – Minterms = minterms, для которых функция F = 1,
- 0 – Minterms = minterms, для которых функция F = 0.
Любая логическая функция может быть выражена как сумма (ИЛИ) ее 1-минутных членов. Представление уравнения будет
- F (список переменных) = Σ (список 1-минутных индексов)
Пример: F (x, y, z) = Σ (3, 5, 6, 7)
Обратная функция может быть выражена как сумма (ИЛИ) ее нулевых членов. Представление уравнения будет
- F (список переменных) = Σ (список индексов 0-минутного члена)
Пример: F’ (x, y, z) = Σ (0,1, 2, 4)
Примеры канонической формы выражения суммы произведений (каноническая форма минимального члена):
i) Z = XY + XZ’
ii) F = XYZ’ + X’YZ + X’YZ’ + XY’Z + XYZ
В стандартной форме СОП максимально возможные условия произведения для n переменных задаются как 2ⁿ. Таким образом, для уравнений с 2 переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8.
Таким образом, для уравнений с 2 переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8.
Максимальное число членов
Максимальный термин определяется как произведение n переменных в диапазоне 0 ≤ i < 2ⁿ. Максимальный член обозначается как Mi. В термине max каждая переменная дополняется, если ее значение равно 1, и каждая переменная не дополняется, если ее значение присваивается 0.
Для булевой функции с двумя переменными (x и y) возможное максимальное термины:
x + y, x + y’, x’ + y и x’ + y’.
Для булевой функции с тремя переменными (x, y и z) возможные maxterms:
x + y + z, x + y + z’, x + y’ + z, x + y’ + z ‘, x’ + y + z, x’ + y + z’, x’ + y’ + z и x’ + y’ + z’.
- 1 – Максимальное число членов = максимальное число членов, для которых функция F = 1.
- 0 – максимальное число членов = максимальное число членов, для которых функция F = 0.
Любая логическая функция может быть выражена произведением (И) ее 0-макс. членов. Представление уравнения будет
членов. Представление уравнения будет
- F (список переменных) = Π (список индексов 0-max)
Пример: F (x, y, z) = Π (0, 1, 2, 4)
Обратная функция может быть выражена как произведение (И) ее 1-макс. членов. Представление уравнения будет
- F(список переменных) = Π(список индексов 1-max)
Пример: F’ (x, y, z) = Π (3, 5, 6, 7)
Примеры канонической формы произведения выражений сумм (каноническая форма максимального члена):
i. Z = (X + Y) (X + Y′)
ii. F = (X′ + Y + Z′) (X′ + Y + Z) (X′ + Y′ + Z′)
В стандартной форме POS максимально возможные члены суммы для n переменных задаются как 2ⁿ . Итак, для уравнений с 2 переменными сумма членов равна 22 = 4. Аналогично, для уравнений с 3 переменными сумма членов равна 23 = 8,9.0003
Таблица для 2n минимальных членов и 2n максимальных членов
Приведенная ниже таблица поможет вам понять представление средних и максимальных членов 3 переменных.
Преобразование канонических форм
Мы можем представить одно каноническое сформированное уравнение в другой канонической форме, т.е. мы можем представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, мы поменяем местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.
Важно помнить о логических функциях, что формы SOP и POS дублируют друг друга. Чтобы преобразовать каноническую форму уравнений, необходимо выполнить 2 шага. Это
Шаг 1: Поменяйте местами рабочие символы Σ и Π в уравнении.
Шаг 2: Используйте принцип двойственности Де Моргана для порядковых номеров булевой функции или записывайте порядковые номера членов, которые не представлены в данной форме уравнения.
Преобразование формы SOP в форму POS
Чтобы преобразовать форму SOP в форму POS, сначала мы должны изменить Σ на Π, а затем записать числовые индексы отсутствующих переменных данной булевой функции.
Пример:
Функция SOP
F = ∑ A, B, C (0, 2, 3, 5, 7) = A’ B’ C’ + A B’ C’ + A B’ C + ABC ‘ + ABC записывается в форме POS как
Шаг 1: изменение операционного знака на Π
Шаг 2: запись недостающих индексов членов, 001, 100 и 110. Теперь напишите форму суммы для этих отмеченных членов.
001 = (A + B + C) 100 = (A + B’ + C’) 110 = (A + B’ + C’)
Запись нового уравнения в форме POS,
F = Π A, B, C (1, 4, 6) = (A + B + C) * (A + B’ + C’) * (A + B’ + C’)
Преобразование формы POS в SOP form
Чтобы преобразовать форму POS в форму SOP, сначала мы должны изменить Π на Σ, а затем написать числовые индексы отсутствующих переменных данной булевой функции.
Пример: Функция POS F = Π A, B, C (2, 3, 5) = A B’ C’ + A B’ C + ABC’ записывается в форме SOP как
Шаг 1: изменение знака операции на Σ
Шаг 2: запись отсутствующих индексов терминов 000, 001, 100, 110 и 111. Теперь напишите форму произведения для этих отмеченных термов.
000 = A’ * B’ * C’ 001 = A’ * B’ * C 100 = A * B’ * C’
110 = A * B* C’ 111 = A * B * C
Запись вниз по новому уравнению в форме СОП,
F = Σ A, B, C (0, 1, 4, 6, 7) = (A’ * B’ * C’) + (A’ * B’ * C) + (A * B’ * C’) + (A * B * C’) + (A * B * C)
Преобразование формы СОП в стандартную форму СОП или форму канонической СОП
Мы можем включить все переменные в каждый член произведения уравнения формы СОП, в котором нет всех переменных, путем преобразования в стандартную форму СОП. Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры (A + A’ = 1) и выполнив следующие шаги.
Шаг 1:
Путем умножения каждого нестандартного термина продукта на сумму его отсутствующей переменной и ее дополнения, что дает 2 термина продукта
Шаг 2:
Повторяя шаг 1 до тех пор, пока все результирующие условия продукта не будут содержать все переменные
С помощью этих двух шагов мы можем преобразовать функцию SOP в стандартную функцию SOP. В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.
В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.
Пример:
Преобразование нестандартной SOP-функции F = x y + x z + y z
Sol:
F = x y + x z + y z
= x y (z + z’) + x (y + y’) г + (х + х’) у г
= x y z + x y z’ + x y z + x y’ z + x y z + x’ y z
= x y z + x y z’ + x y’ z + x’ y z
Стандартная форма СОП: F = x y z + x y z’ + x y’ z + x’ y z
Преобразование формы POS в стандартную форму POS или каноническую форму POS
Мы можем включить все переменные в каждый термин продукта уравнения формы POS, который не имеет всех переменные путем преобразования в стандартную форму POS. Обычную функцию формы POS можно преобразовать в стандартную форму POS, используя закон алгебры логики (A * A’ = 0) и выполнив следующие шаги.
Шаг 1:
Путем добавления каждой нестандартной суммы к произведению ее отсутствующей переменной и ее дополнения, что дает 2 суммы
Шаг 2:
Применяя булев алгебраический закон, A + BC = (A + B) * (A + C)
Шаг 3:
Повторяя шаг 1, пока все результирующие члены суммы не будут содержать все переменные
Этими тремя шагами мы можем преобразовать функцию POS в стандартную функцию POS.
Пример:
F = (A’ + B + C) * (B’ + C + D’) * (A + B’ + C’ + D)
В первом члене отсутствует переменная D или D’, поэтому мы добавляем к ней D*D’ = 1. Тогда
(A’ + B + C + D*D’) = (A’ + B + C + D) * (A’ + B + C + D’)
Аналогично, во втором члене переменная A или A’ отсутствует, поэтому мы добавляем к нему A*A’ = 1. Тогда
(B’ + C + D’ + A*A’) = (A + B’ + C + D’) * (A’ + B’ + C + D’)
Третий член уже в стандартная форма, так как она имеет все переменные. Теперь стандартное уравнение формы POS функции
F = (А’ + В + С + D) * (А’ + В + С + D’) * (А + В’ + С + D’) * (А’ + В’ + С + D’) * (A + B’ + C’ + D)
K Карты | Карты Карно | Решанные примеры
Минимизация логических выражений-Существуют два метода минимизации или снижения логических выражений-
- с использованием законов Boolean Algebra
- с использованием законов Boolean Algebra
- .
 называется K Maps
называется K Maps - Карта K с двумя переменными строится для логического выражения, состоящего из двух переменных.
- Количество ячеек, присутствующих в двух переменных K Map = 2 2 = 4 ячейки.
- Итак, для булевой функции, состоящей из двух переменных, мы рисуем карту 2 x 2 K.
- K-карта с тремя переменными строится для логического выражения, состоящего из трех переменных.
- Количество ячеек, присутствующих в трех переменных K Map = 2 3 = 8 ячеек.
- Итак, для булевой функции, состоящей из трех переменных, мы рисуем карту 2 x 4 K.
- K-карта с четырьмя переменными строится для логического выражения, состоящего из четырех переменных.
- Количество ячеек, присутствующих в четырех переменных K Map = 2 4 = 16 ячеек.
- Итак, для булевой функции, состоящей из четырех переменных, мы рисуем карту 4 x 4 K.
- Мы рисуем K-карту в соответствии с количеством переменных, которые она содержит.
- Мы заполняем K-карту нулями и единицами в соответствии с ее функцией.
- Затем мы минимизируем функцию в соответствии со следующими правилами.
- Мы можем сгруппировать 0 с 0 или 1 с 1, но мы не можем сгруппировать 0 и 1 вместе.
- X, представляющий безразличие, может быть сгруппирован как с 0, так и с 1.
- Группы могут перекрывать друг друга.

- Мы можем создать только группу, количество ячеек которой может быть представлено в степени двойки. т. е. 1, 2, 4, 8, 16 и т. д. количество ячеек.
- Группы могут быть только горизонтальными или вертикальными.
- Мы не можем создавать группы диагональной или любой другой формы.
- Каждая группа должна быть как можно больше.
- Допускается группировка в противоположных направлениях и группировка по углам.
- Пример противоположной группировки показан в Правиле-05.
- Пример группировки углов показан ниже.

- Должны быть как можно меньше.
- Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K.
- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем мы формируем группы в соответствии с вышеуказанными правилами.
- Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K.

- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K.
- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Поскольку данное логическое выражение имеет 3 переменные, мы рисуем карту 2 x 4 K.

- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Можно отметить, что нет необходимости рассматривать четверную группу.
- Это потому, что даже если мы рассмотрим эту группу, нам придется рассмотреть два других дуэта.
- Итак, нет смысла рассматривать эту четверную группу.
- Поскольку данное логическое выражение имеет 3 переменные, мы рисуем карту 2 x 4 K.

- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Поскольку данное логическое выражение имеет 3 переменные, мы рисуем карту 2 x 4K.
- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем мы формируем группы в соответствии с вышеуказанными правилами.
- имеет 4 переменные, поэтому мы рисуем карту 4 x 4K.

- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K.
- Заполняем ячейки K Map в соответствии с заданной булевой функцией.
- Затем формируем группы в соответствии с указанными выше правилами.
- Раствор
- Если на вашем компьютере установлена Windows 8 (64-разрядная), перед установкой SIGMA Photo Pro 6.
 8.2 установите программу обновления Windows (KB2929755) для 64-разрядной системы. Пожалуйста, загрузите программу обновления Windows (KB2929755) в Центре загрузки Microsoft Windows, если вам необходимо вручную загрузить и установить SIGMA Photo Pro 6.8.2 после завершения обновления системы.
8.2 установите программу обновления Windows (KB2929755) для 64-разрядной системы. Пожалуйста, загрузите программу обновления Windows (KB2929755) в Центре загрузки Microsoft Windows, если вам необходимо вручную загрузить и установить SIGMA Photo Pro 6.8.2 после завершения обновления системы. - Прежде чем начать загрузку программы установки, убедитесь, что все приложения на вашем компьютере завершены.
- Нажмите кнопку загрузки или нажмите правую кнопку мыши («правый клик») и начните загрузку.
- Убедитесь, что SPP_6.8.2_setup.exe сохранен в указанном месте назначения.
- Из SIGMA Photo Pro Ver. 6.6.0 возможна работа только с 64-битной версией ОС Windows и предустановленной Windows 8 или Windows 10. Если на вашем компьютере установлена 32-разрядная версия ОС Windows, используйте SIGMA Photo Pro 6.5.4, которую можно загрузить здесь.
- SIGMA Photo Pro 6.7.4 требуется для обработки данных RAW (файлов DNG), снятых с помощью SIGMA fp с прошивкой версии 2.
 0 или более поздней.
0 или более поздней. - Если на вашем компьютере установлено приложение «SIGMA Photo Pro 6.8.1», удалите его. Невозможно правильно установить «SIGMA Photo Pro 6.8.2», если уже установлена «SIGMA Photo Pro 6.8.1». Вам необходимо перезагрузить компьютер вскоре после удаления этого программного обеспечения. После завершения установки перезагрузите компьютер.
- Начните установку программного обеспечения, дважды щелкнув загруженный файл «SPP_6.8.2_setup.exe».
- Во-первых, вы должны выбрать язык устанавливаемой программы. Выберите язык и нажмите кнопку OK.
- Затем выполните установку в соответствии с процедурами, отображаемыми на экране.
- Вам необходимо перезагрузить компьютер вскоре после установки этого программного обеспечения.
- ЦП: Эквивалент процессора Intel® Core2 Duo или выше (рекомендуется процессор Intel® серии Core i или выше)
- ОС: Windows 8.
 1 или Windows 10 (64-разрядная ОС), Windows 11
1 или Windows 10 (64-разрядная ОС), Windows 11 - ОЗУ: 4 ГБ или больше ОЗУ (рекомендуется 8 ГБ или больше)
- Жесткий диск: 5 ГБ свободного места на жестком диске (рекомендуется 10 ГБ или больше)
- GPU: 24-битная (16 770 000 цветов) видеокарта или выше
- Разрешение монитора: 1280×960 пикселей или выше
- Перед началом загрузки программы установки убедитесь, что все приложения на вашем компьютере закрыты.
- Нажмите кнопку загрузки или нажмите кнопку мыши, удерживая нажатой клавишу Control на клавиатуре (Control+щелчок).
- Выберите «загрузить связанный файл» из отображаемого меню. Запустите загрузку файла.
- После завершения загрузки файла «PhotoPro6.8.2.dmg» он будет смонтирован автоматически и отобразится образ диска «PhotoPro.
 6.8.2». Если файл не монтируется автоматически, дважды щелкните файл «PhotoPro6.8.2.dmg». Отобразится образ диска «PhotoPro6.8.2».
6.8.2». Если файл не монтируется автоматически, дважды щелкните файл «PhotoPro6.8.2.dmg». Отобразится образ диска «PhotoPro6.8.2». - После установки программного обеспечения первая загрузка займет пару минут. Пожалуйста, воздержитесь от использования других приложений, пока не завершится процесс запуска.
- SIGMA Photo Pro 6.8.2 требуется для обработки данных RAW (файлов DNG), снятых с помощью SIGMA fp с прошивкой версии 2.0 или более поздней.
- Дважды щелкните образ диска «SIGMA Photo Pro 6.8.2» и откройте диалоговое окно установки.
- Перетащите значок «SIGMA Photo Pro 6» в папку приложения. Затем процесс установки завершится.
- Процессор: Эквивалент процессора Intel® Core2 Duo или выше (рекомендуется процессор Intel® серии Core i или выше), чип Apple серии M1 (работает с Rosetta 2.
 )
) - ОС: macOS Mojave 10.14, macOS Catalina 10.15, macOS Big Sur 11, macOS Monterey 12
- ОЗУ: 4 ГБ или больше (рекомендуется 8 ГБ или больше)
- Жесткий диск: 5 ГБ свободного места на жестком диске (рекомендуется 10 ГБ или больше)
- GPU: 24-битная видеокарта (16,8 млн цветов) или выше
- Разрешение монитора: 1280×960 пикселей или выше
- Математическая нотация
- Греческие буквы
- Superscripts / Подписей
- Chemical
- Chemical Fommulals
- Chemical FormulaLARALS
- . Gas
- Встроенный режим — поместите
$$вокруг вашей разметки LaTeX, и Gradescope отобразит ваши математические выражения в тексте. - Режим отображения (абзац). Ваши математические выражения будут отображаться крупнее и в отдельном абзаце.
В этой статье мы обсудим карты Karnaugh Maps или K Maps.
Карта Карно-
| Карта Карно, также называемая K-картой, представляет собой графическое представление , которое обеспечивает систематический метод упрощения логических выражений. |
Для логического выражения, состоящего из n переменных, количество ячеек, необходимых в K Map = 2 n кл.
Карта K с двумя переменными-
Две переменные K Map могут быть представлены как
Здесь A и B — две переменные данной логической функции.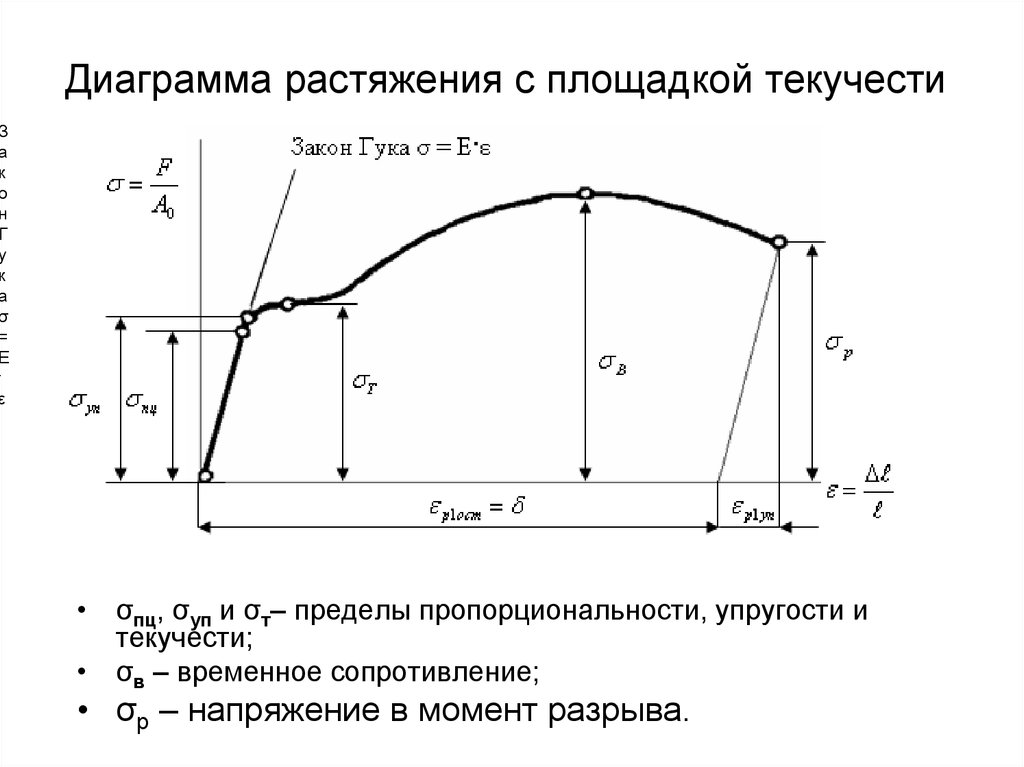
K-карта с тремя переменными-
Карта K с тремя переменными может быть представлена как
Здесь A, B и C — три переменные данной булевой функции.
K-карта с четырьмя переменными-
Карта K с четырьмя переменными может быть представлена как
Здесь A, B, C и D — четыре переменные данной булевой функции.
Правила упрощения карты Карно-
Чтобы минимизировать заданную логическую функцию,
Правило-01:
| ПРИМЕЧАНИЕ Нет необходимости отдельно группировать X, т. е. их можно игнорировать, если все 0 и 1 уже сгруппированы. |
Правило-02:
Правило-03:
Пример —
Правило-04:
Правило-05:
Пример:
Правило-06:
Проблемы, основанные на карту Карно, Проблема-01:
Минимизируйте следующую логическую функцию-
F (A, B, C, D) = σm (0, 1, 2
F (A, B, C, D) = σm (0, 1. , 5, 7, 8, 9, 10, 13, 15)
Решение-
Тогда имеем-
Теперь
F(A, B, C, D) + (CAB’02 = CDAB’02 =
=
(A’B’ + A’B + AB + AB’)C’D + (A’B’ + AB’)(C’D’ + CD’)
= BD + C’D + B’D’
Таким образом, минимизированное логическое выражение равно0078
Минимизация следующей булевой функции:
F(A, B, C, D) = Σm(0, 1, 3, 5, 7, 8, 9, 11, 13, 15) Решение-
Тогда имеем-
Теперь,
F(A, B, C, D)
= (A’B’ + A’B + AB + AB’)(C’D + CD) + (A ‘B’ + AB’)(C’D’ + C’D)
= D + B’C’
Таким образом, минимизированное логическое выражение равно
F(A, B, C, D) = B’C’ + D
Задача-03:
Минимизация следующей булевой функции-
F(A, B, C, D) = Σm(1, 6, 4, 4 , 8, 9, 11, 13, 15) + Σd(0, 2, 14)
Решение-
Тогда имеем-
Теперь
F(A, B, C, D) + ‘DAB’ A’B’ + AB’)(C’D + CD) + (A’B’ + AB’)(C’D’ + C’D) + (A’B’ + A’B)(C’D ‘ + CD’)
= AD + B’D + B’C’ + A’D’
Таким образом, минимизированное логическое выражение равно
F(A, B, C, D) = AD + B’D + B ‘C’ + A’D’
Задача-04:
Минимизируйте следующую логическую функцию-
F(A, B, C) = Σm(0, 7, 1) + Σd(3, 5)
Решение-
Тогда имеем-
Теперь
F(A, B, C)
+ A’C’B’C + A’B’C) + A’B’C BC’)= A’B’ + AB
Таким образом, минимизированное логическое выражение равно0003
ПРИМЕЧАНИЕ.
Задача-05:
Минимизировать следующую булеву функцию-
F(A, B, C) = Σm(1, 2, 5, 7, 7) + Σd )
Решение-
Тогда имеем-
Теперь
F(A, B, C)
‘C +) = (A, B, C)
‘C +) = (A, B, C) А(В’С’ + В’С + ВС + ВС’) + (А + А’)(В’С’ + ВС’)
= B’ + A + C’
Таким образом, минимизированное логическое выражение равно:
Минимизация следующей булевой функции-
F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 4, 5)
Решение-
Тогда имеем-
Теперь
F(A, B, C)
‘C +) = (A, B, C)
‘C +) = (A, B, C) A(B’C’ + B’C + BC + BC’)
= B’ + A
Таким образом, минимизированное логическое выражение равно:
F(A, B, C) = A + B’
Задача-07:
Минимизация следующей логической функции-
F(A, B, C, D) = Σm(0, 2, 8, 10, 14) + Σd(5, 15)
Решение-
Тогда имеем-
Сейчас,
F(A, B, C, D)
= (AB + AB’)CD’ + (A’B’ + AB’)(C’D’ + CD’)
= ACD’ + B’ D ‘
Таким образом, минимизированное логическое выражение составляет
F (A, B, C, D) = ACD’ + B’D ‘
Проблема-08:Минимализификация. следующая логическая функция-
F(A, B, C, D) = Σm(3, 4, 5, 7, 9, 13, 14, 15)
Решение-
- данное логическое выражение имеет 4 переменные, поэтому мы рисуем карту 4 x 4 K.
Тогда имеем-
Теперь
F(A, B, C, D) + (C’D)
‘B’D)= A’B’ + A’B)(CD) + (AB + AB’)(C’D) + AB(CD + CD’)
= A’BC’ + A’CD + AC’D + ABC
Таким образом, минимизированное логическое выражение равно
F(A, B, C, D) = A’BC’ + A’CD + AC’D + ABC
Важно отметить, что мы не рассматриваем четверную группу, потому что мы должны учитывать дуэты во всяком случае.
Задача-09:
Рассмотрим следующую логическую функцию:
F(W, X, Y, Z) = Σm(1, 3, 4, 6, 9, 11, 12 )
Эта функция независима от ________ числа переменных. Заполнить бланк.
Решение-
Тогда имеем-
Теперь
F(W, X, Y, Z)
‘Y’X’X = (W’Y’X’X) ) + (W’X’ + WX’)(Y’Z + YZ)= XZ’ + X’Z
= X ⊕ Z
Таким образом, минимизированное логическое выражение равно данная логическая функция зависит только от двух переменных X и Z.
Следовательно, она не зависит от двух других переменных W и Y.
учебный материал Digital Design .
Смотрите видеолекции, посетив наш канал YouTube LearnVidFun .
Сводка
Разница | Стандартное отклонение
← предыдущее
следующее →
Рассмотрим две случайные величины $X$ и $Y$ со следующими PMF.
$$ \label{eq:X-var}
\номер P_X(x) = \влево\{
\begin{массив}{л л}
0,5 & \quad \text{для} x=-100\\
0,5 & \quad \text{для} x=100\\
0 & \quad \text{иначе}
\end{массив} \right.
\hspace{10pt} (3.3)
$$
$$ \label{eq:Y-var}
\номер P_Y(y) = \влево\{
\begin{массив}{л л}
1 & \quad \text{для} y=0\\
0 & \quad \text{иначе}
\end{массив} \right.
\hspace{20pt} (3.4)
$$
Обратите внимание, что $EX=EY=0$. Хотя обе случайные величины имеют одинаковое среднее значение, их распределение
совершенно другое. $Y$ всегда равно своему среднему значению $0$, а $X$ равно либо $100$, либо $-100$,
довольно далеко от своего среднего значения. Дисперсия является мерой того, насколько рассредоточено распределение
случайная величина есть. Здесь дисперсия $Y$ довольно мала, так как ее распределение сосредоточено в
единственное значение, в то время как дисперсия $X$ будет больше, поскольку его распределение более рассредоточено. 92$
часто велико, поэтому $X$ часто принимает значения, далекие от своего среднего значения. Это означает, что распределение очень
распространяться. С другой стороны, низкая дисперсия означает, что распределение сконцентрировано вокруг своего среднего значения.
Здесь дисперсия $Y$ довольно мала, так как ее распределение сосредоточено в
единственное значение, в то время как дисперсия $X$ будет больше, поскольку его распределение более рассредоточено. 92$
часто велико, поэтому $X$ часто принимает значения, далекие от своего среднего значения. Это означает, что распределение очень
распространяться. С другой стороны, низкая дисперсия означает, что распределение сконцентрировано вокруг своего среднего значения.
Обратите внимание, что если бы мы не возводили в квадрат разницу между $X$ и его средним значением, результат был бы равен $0$. То есть $$E[X-\mu_X]=EX-E[\mu_X]=\mu_X-\mu_X=0.$$ $X$ иногда ниже среднего, а иногда выше среднего. Таким образом, $X-\mu_X$ иногда отрицательный, а иногда и положительный, но в среднем он равен нулю. 92$. Чтобы решить эту проблему, мы определяем другую меру, называемую стандартным отклонением , обычно отображается как $\sigma_X$, что представляет собой просто квадратный корень из дисперсии.
Стандартное отклонение случайной величины $X$ определяется как
$$\textrm{SD}(X)= \sigma_X= \sqrt {\textrm{Var}(X)}. $$
$$
Стандартное отклонение $X$ имеет ту же единицу измерения, что и $X$. Для $X$ и $Y$, определенных в уравнениях 3.3 и 3.4, у нас есть
| $\sigma_X$ | $=\sqrt{10,000}= 100$ 92 \textrm{Var}(X)\\
\end{выравнивание} Из уравнения 3.6 мы заключаем, что для стандартного отклонения $\textrm{SD}(aX+b)=|a|\textrm{SD}(X)$. Мы упомянул, что дисперсия НЕ является линейной операцией. Но есть очень важный случай, когда дисперсия ведет себя как линейная операция, и это когда мы смотрим на сумму независимых случайных величин. Теорема Мы докажем эту теорему в главе 6, а пока посмотрим на пример, чтобы увидеть, как мы можем ее использовать. Пример Если $X \sim Binomial(n,p)$ найти Var$(X)$. ← предыдущая следующая → Печатная версия книги доступна на Amazon здесь. SIGMA Photo Pro | Программное обеспечениеSIGMA Photo Pro 6.8.2 — это эксклюзивный программный пакет для отображения и обработки изображений RAW, снятых всеми цифровыми камерами SIGMA, на вашем компьютере. Можно скачать программу установки SIGMA Photo Pro 6.8.2 для Windows и SIGMA Photo Pro 6.8.2 для Macintosh. Пожалуйста, убедитесь, что вы прочитали системные требования для этого программного обеспечения перед их загрузкой. Цели загрузкиКлиенты, использующие камеры серии SIGMA fp, серии SIGMA dp Quattro, серии SIGMA sd Quattro, серии SIGMA SD и DP. Скачать SIGMA Photo Pro для Windows (146,59 МБ) Ваше устройство не поддерживает эту службу загрузки. История обновленийПредупрежденияИнформацию о клиентах, которые не могут использовать режим ускорения графического процессора, см. на веб-странице. УстановкаУсловия эксплуатации SIGMA Photo Pro для Mac (217,85 МБ) Ваше устройство не поддерживает эту службу загрузки. История обновленийПредупрежденияИнформацию о клиентах, которые не могут использовать режим ускорения графического процессора, см. на веб-странице. УстановкаУсловия эксплуатацииПисьменные формулы и уравнения (латекс) LaTeX можно использовать для математических символов в элементах рубрики, комментариях, текстовых аннотациях, названиях групп ответов, онлайн-заданиях и ответах, а также запросах и ответах на переоценку. Мы не поддерживаем единый доллар Обратите внимание, что в поле для комментариев для конкретного учащегося LaTeX в настоящее время не отображается на странице оценивания. Однако ваши учащиеся смогут увидеть правильно отображаемую нотацию при просмотре комментария. Чтобы еще раз убедиться, что ваш комментарий LaTeX был отрендерен правильно, вы можете перейти на страницу «Просмотр оценок» и щелкнуть имя учащегося, чтобы увидеть его точку зрения на представленную работу. Полный список поддерживаемых функций см. в документации $$\KaTeX$$ и документации mhchem. Математические обозначенияГреческие буквы
Кроншеты
Матрицы
Также ознакомьтесь с нашими таблицами уценки для альтернативного способа отображения табличных данных. Обратите внимание, что в настоящее время наш редактор требует, чтобы начальная функция находилась в отдельной строке для правильного отображения (например, Химические формулы Преподаватели, которые хотят использовать химические уравнения, могут использовать команду Убедитесь, что ваш код $$\LaTeX$$ заключен в
Если вы обнаружите, что ваши уравнения выглядят не совсем правильно, вы всегда можете уточнить их, добавив специальные индикаторы для подстрочных и надстрочных индексов ( 9{227}_{90}Th+ } $$ |
Стрелки реакции
| $$\ce{ A->B }$$ | $$ \ce{A->B} $$ |
| $$\ce{A<-B}$$ | $$ \ce{A<-B} $$ |
| $$\ce{A<-->B}$$ | $$ \ce{A<-->B} $$ |
Чтобы разместить текст над или под стрелкой, каждая стрелка может принимать два необязательных аргумента.
| $$\ce{ A->[h3O]B }$$ | $$ \ce{A->[h3O]B } $$ |
| $$\ce{ A->[{текст выше}][{текст ниже}]B }$$ | $$ \ce{ A->[{текст выше}][{текст ниже}]B } $$ |
| $$\ce{A<-->B}$$ | $$ \ce{A<-->B} $$ |
Облигации
| $$\ce{ C6H5-CHO }$$ | $$ \ce{C6H5-CHO} $$ |
| $$\ce{AB=C#D}$$ | $$ \ce{AB=C#D} $$ |
В зависимости от контекста \ce{-} может быть залогом, залогом или рекламой. Вы можете использовать команду bond \bond , за которой следует число или символ, чтобы быть более точным.
| $$\ce{ A\bond{-}B\bond{=}C\bond{#}D }$$ | $$ \ce{A\bond{-}B\bond{=}C\bond{#}D } $$ |
| $$\ce{A\bond{1}B\bond{2}C\bond{3}D}$$ 9) } $$ |
Есть еще вопросы об использовании $$\LaTeX$$ в Gradescope? Свяжитесь с нами!
Была ли эта статья полезной?
Круто, рада, что полезно! 🙌 Есть идеи, как мы можем улучшить? Жаль это слышать. Дайте нам знать, что мы можем улучшить!
Нужна помощь?
Исчисление II — серия Тейлора
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-16: Серия Taylor
В предыдущем разделе мы начали рассматривать запись функции в виде степенного ряда. Проблема с подходом в этом разделе заключается в том, что все сводилось к необходимости каким-то образом связать функцию с
. \[\frac{1}{{1 - x}}\]
, и хотя есть много функций, которые могут быть связаны с этой функцией, есть еще много других, которые просто не могут быть связаны с этой.
Итак, ничего не отвлекая от процесса, который мы рассмотрели в предыдущем разделе, нам нужно придумать более общий метод записи представления степенного ряда для функции. 94} + \cdots\]
94} + \cdots\]
Далее нам нужно будет предположить, что функция \(f\left( x \right)\) имеет производные любого порядка и что мы можем найти их все.
Теперь, когда мы предположили, что представление в виде степенного ряда существует, нам нужно определить, каковы коэффициенты \({c_n}\). Это проще, чем может показаться на первый взгляд. Давайте сначала просто оценим все в \(x = a\). Это дает,
\[f\влево( а \вправо) = {c_0}\] 92} + \cdots \\ f''\left( a \right) & = 2{c_2}\end{align*}\]
Итак, похоже,
\[{c_2} = \frac{{f''\left( a \right)}}{2}\]
Использование третьей производной дает,
\[\begin{align*}f'''\left( x \right) & = 3\left( 2 \right){c_3} + 4\left( 3 \right)\left( 2 \right){c_4 }\left( {x - a} \right) + \cdots \\ f'''\left( a \right) & = 3\left( 2 \right){c_3}\hspace{0. i}} \]
9п}} \]
i}} \]
9п}} \]
\(n\) -й -й степени многочлена Тейлора является лишь частичной суммой ряда.
Далее, остаток определяется как
\[{R_n}\влево( x \вправо) = f\влево( x \вправо) - {T_n}\влево( x \вправо)\]
Таким образом, остаток на самом деле просто ошибка между функцией \(f\left( x \right)\) и \(n\) полиномом Тейлора -й степени для заданного \(n\).
Обратите внимание, что с этим определением мы можем записать функцию как
\[f\влево( x \вправо) = {T_n}\влево( x \вправо) + {R_n}\влево( x \вправо)\]
Теперь у нас есть следующая Теорема.
Теорема
Предположим, что \(f\left( x \right) = {T_n}\left( x \right) + {R_n}\left( x \right)\). Тогда если,
\[\ mathop {\lim}\limits_{n \to \infty} {R_n}\left( x \right) = 0\] 9п}\]
Хорошо, теперь нам нужно поработать с некоторыми примерами, которые не включают экспоненциальную функцию, так как они, как правило, требуют немного больше работы. {\ left ( 6 \ right)} }\left( 0 \right) = - 1\\ \vdots \,\,\,\,\,\,\,\,\,\, & & \hspace{0.5in} & \,\,\, \,\,\,\, \vdots \end{align*}\]
9{2n}}}}{{\left( {2n} \right)!}}} \]
{\ left ( 6 \ right)} }\left( 0 \right) = - 1\\ \vdots \,\,\,\,\,\,\,\,\,\, & & \hspace{0.5in} & \,\,\, \,\,\,\, \vdots \end{align*}\]
9{2n}}}}{{\left( {2n} \right)!}}} \]
Эта идея перенумерации членов ряда, как мы сделали в предыдущем примере, используется не так часто, но иногда очень полезна. Есть еще одна серия, где нам нужно это сделать, поэтому давайте посмотрим на нее, чтобы мы могли получить еще один пример перенумерации членов серии.
Пример 6. Найдите ряд Тейлора для \(f\left( x \right) = \sin \left( x \right)\) относительно \(x = 0\).
Показать решение 9{2n + 1}}}}{{\left( {2n + 1} \right)!}}} \]
Нам действительно нужно поработать еще один или два примера, в которых \(f\left( x \right)\) не относится к \(x = 0\).
Пример 7. Найдите ряд Тейлора для \(f\left( x \right) = \ln \left( x \right)\) относительно \(x = 2\). 2}}}\) относительно \(x = - 1\).
93}\конец{выравнивание*}\]
2}}}\) относительно \(x = - 1\).
93}\конец{выравнивание*}\]
При нахождении ряда Тейлора многочлена мы не делаем никакого упрощения правой части. Оставляем как есть. На самом деле, если бы мы все перемножили, мы просто вернулись бы к исходному многочлену!
Хотя не очевидно, что запись ряда Тейлора для многочлена полезна, бывают случаи, когда это необходимо сделать. Проблема в том, что они выходят за рамки этого курса и поэтому здесь не рассматриваются. Например, есть одно приложение к рядам в области дифференциальных уравнений, где это нужно делать время от времени.
Итак, к этому моменту мы видели довольно много примеров ряда Тейлора, и во всех из них мы смогли найти общие формулы для ряда. Так будет не всегда. Чтобы увидеть пример того, у которого нет общей формулы, посмотрите последний пример в следующем разделе.
Прежде чем покинуть этот раздел, остановимся на трех важных рядах Тейлора, которые мы получили в этом разделе и которые мы должны обобщить в одном месте.

 Это остаточное удлинение составляет 0,2 … 0,3 %.
Это остаточное удлинение составляет 0,2 … 0,3 %.


 Одни считаются вредными, от них избавляются для чистоты сплава, а вторые добавляют для укрепления.
Одни считаются вредными, от них избавляются для чистоты сплава, а вторые добавляют для укрепления. 08.2022
08.2022
 называется K Maps
называется K Maps



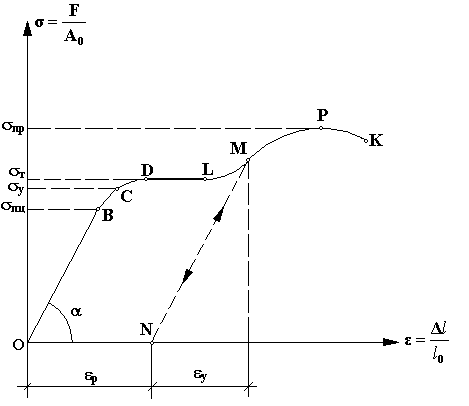


 8.2 установите программу обновления Windows (KB2929755) для 64-разрядной системы. Пожалуйста, загрузите программу обновления Windows (KB2929755) в Центре загрузки Microsoft Windows, если вам необходимо вручную загрузить и установить SIGMA Photo Pro 6.8.2 после завершения обновления системы.
8.2 установите программу обновления Windows (KB2929755) для 64-разрядной системы. Пожалуйста, загрузите программу обновления Windows (KB2929755) в Центре загрузки Microsoft Windows, если вам необходимо вручную загрузить и установить SIGMA Photo Pro 6.8.2 после завершения обновления системы. 0 или более поздней.
0 или более поздней. 1 или Windows 10 (64-разрядная ОС), Windows 11
1 или Windows 10 (64-разрядная ОС), Windows 11 6.8.2». Если файл не монтируется автоматически, дважды щелкните файл «PhotoPro6.8.2.dmg». Отобразится образ диска «PhotoPro6.8.2».
6.8.2». Если файл не монтируется автоматически, дважды щелкните файл «PhotoPro6.8.2.dmg». Отобразится образ диска «PhotoPro6.8.2».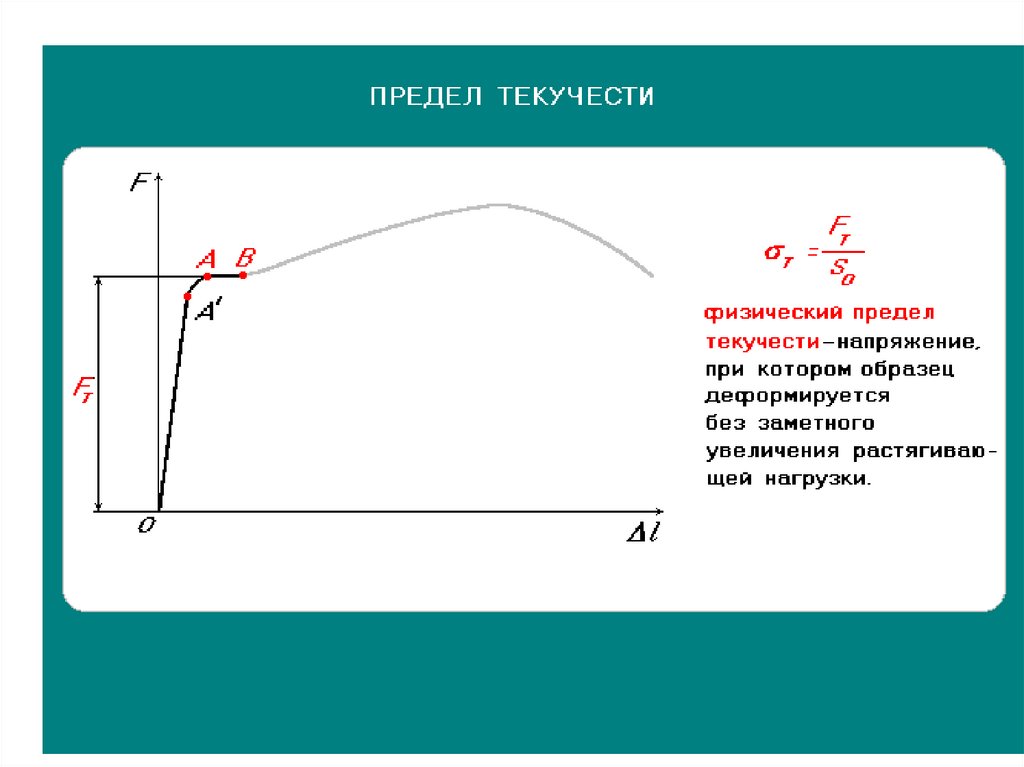 )
)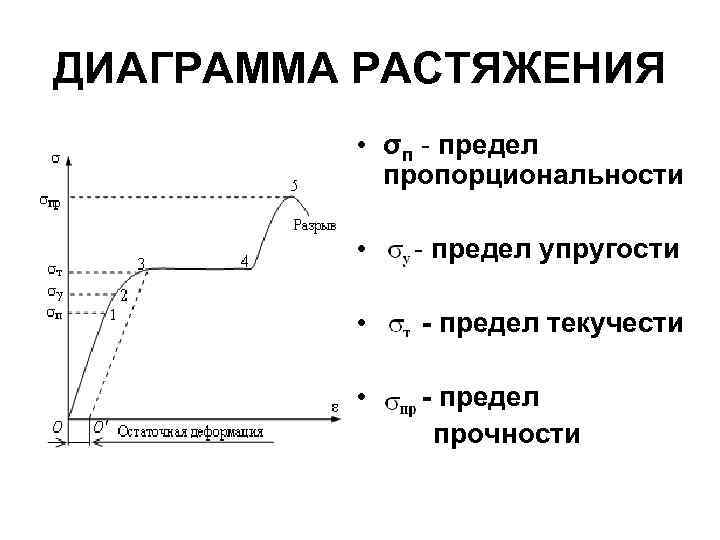 Мы поддерживаем следующие варианты:
Мы поддерживаем следующие варианты: