Расчет фокусного расстояния: Online калькулятор расчета фокусного расстояния
Расчёт угла обзора видеокамеры
Расчёт угла обзора объектива производиться по формуле:
α = 2arctg(d/2F)
α — Угол обзора объектива, (гр)
d — Размер матрицы, (мм)
F — Фокусное расстояние, (мм)
Пояснения к расчёту
При выборе фокусного расстояния объектива следует учитывать, что угол ясного зрения человека по горизонтали составляет примерно 36°, что соответствует фокусному расстоянию ~ 6,9 мм (для видеокамеры с размером матрицы 1/3″). Поэтому видеокамеры с фокусным расстоянием объектива менее 6,9 мм будут визуально отдалять изображение, более 6,9 мм – соответственно приближать.
Расчёт дистанций производится на основе требований европейских норм для CCTV:
— линейное разрешение для обнаружения объекта — 20 пикселей/м;
— линейное разрешение для распознавания — 100 пикселей/м;
— линейное разрешение для идентификации — 250 пикселей/м;
при разрешении матрицы видеокамеры 1920 (2Мп Full HD), 700, 560, 480, и 380 Твл.
ТВЛ (Телевизионные Вертикальные Линии) – параметр, характеризующий чёткость телевизионного изображения. Показывает максимальное количество различимых вертикальных линий на изображении, ограниченном сторонами квадрата (a=b, рис. 1), расположенного в середине экрана, например 240 белых и 240 чёрных полос соответствуют 480 ТВЛ.
Точно определить этот параметр можно с помощью тестовой таблицы ISO 12233 (рис. 2), распечатав её на листе формата А1 (желательно, но можно и А3, А2 с максимальным разрешением и контрастностью), так как реальные цифры часто не соответствуют заявленным производителями видеокамер (в т.ч. и для IP-видеокамер). Соответственно расчёт дистанций нужно производить на основе полученных результатов.
| Рис. 1 | Рис. 2 |
Для получения корректных результатов необходимо, чтобы весь измерительный тракт (Видеокамера – Кабель – Монитор) был, по возможности, минимальной длины и максимального качества. Измерительная таблица должна быть равномерно освещена. Для получения результатов, приближенных к реальным можно провести измерения при различной освещённости, например 1000, 100, 10 и 1 люкс (потребуется люксметр и регулируемый источник света).
Измерительная таблица должна быть равномерно освещена. Для получения результатов, приближенных к реальным можно провести измерения при различной освещённости, например 1000, 100, 10 и 1 люкс (потребуется люксметр и регулируемый источник света).
Желательно для измерений использовать аналоговый кинескопный монитор с разрешением 1000 – 1200 ТВЛ (для аналоговых видеокамер) или с разрешением WQXGA 2560×1440 и выше (для IP-видеокамер), а также стабилизированный трансформаторный источник питания видеокамеры с низким уровнем собственных шумов и пульсаций напряжения.
Для справки в таблице представлены самые распространённые размеры матриц, используемых в видеокамерах для охранного телевидения.
|
Размер матрицы |
Ширина, мм |
Высота, мм |
Диагональ, мм |
Размер матрицы |
Ширина, мм |
Высота, мм |
Диагональ, мм |
|---|---|---|---|---|---|---|---|
Формат матрицы 4:3 |
Формат матрицы 16:9 |
||||||
| 1″ | 13,54 | 10,16 | 16,93 | 1″ | 14. 76 76 |
8.30 | 16,93 |
| 2/3″ | 9,04 | 6,78 | 11,28 | 2/3″ | 9.84 | 5.54 | 11,28 |
| 1/2″ | 6,77 | 5,08 | 8,47 | 1/2″ | 7.38 | 4.15 | 8,47 |
| 1/2,5″ | 5,42 | 4,06 | 6,77 | 1/2,5″ | 5.90 | 3.32 | 6,77 |
| 1/2,7″ | 5,02 | 3,76 | 6,27 | 1/2,7″ | 5.47 | 3.07 | 6,27 |
| 1/2,8″ | 4.84 | 3.63 | 6.05 | 1/2,8″ | 5.27 | 2.96 | 6.05 |
| 1/3″ | 3,39 | 5,64 | 1/3″ | 4. 92 92 |
2.77 | 5,64 | |
| 1/4″ | 3,39 | 2,54 | 4,23 | 1/4″ | 3.69 | 2.08 | 4,23 |
Следует учесть, что из-за наличия сильных искажений в короткофокусных объективах угол обзора может отличаться от расчётного.
|
Пожелания, замечания, рекомендации по улучшению раздела расчётов на нашем сайте просьба присылать по электронной почте [email protected] Разрешается копирование java-скриптов при условии ссылки на источник. |
ВСЕ РАСЧЁТЫ
Программа для расчета фокусного расстояния
Программа для расчета фокусного расстояния
СКАЧАТЬ
Краткие пояснения к работе программы.
Основные термины. Англоязычные и их русский перевод.
CCD-Chip — ПЗС матрица, её размер в дюймах.
focal length — фокусное расстояние объектива
evaluation — определение, оценка (позволяет выбрать между focal length и lens size relative)
lens size relative — относительный размер объектива
perspective — проекция (в нашем случае требования к размеру максимально удаленного видимого объекта относительно поля монитора в %, выбирается исходя из задач системы видеонаблюдения: обнаружение, различение, распознование)
vertical — вертикальная плоскость зоны обзора камеры
horizontal — горизонтальная плоскость зоны обзора камеры
vertical camera mounting bracket — вертикальная линия установки кронштейна камеры (в нашем случае отклонение от линии горизонта в градусах, по другому либо камера параллельна земле, либо наклонена вверх или вниз на указанный угол)
Imax (real) — реальная задаваемая максимальная зона видимости видеокамеры (на рис.
 3 — серая полоса с пометкой 33 соответствует действительному значению 33,5 метра)
3 — серая полоса с пометкой 33 соответствует действительному значению 33,5 метра)Imin (real) — реальная задаваемая минимальная зона видимости видеокамеры (на рис.3 — красная полоса с пометкой 12 соответствует действительному значению 12,5 метра)
Цветовая маркировка и обозначения
Желтая линия — высота установки камеры по вертикали относительно земли.
Красная линия — «мертвая зона» под камерой, зона не видимости.
Зеленая линия — граница рабочей зоны обзора камеры, включает в себя и вертикальную проекцию поля зрения камеры.
Принципы и этапы работы с программой
- Выбрать размер используемой ПЗС матрицы.
- Выбрать режим вычислений программы. Выбирается или режим с постоянным фокусным расстоянием объектива focal length или режим относительного размера удаленного объекта lens size relative иperspective.
 Ввести требуемые значения в поля.
Ввести требуемые значения в поля. - Выбрать высоту установки камеры.
- Задайте высоту объекта наблюдения (человечек с бегунком на голове).
- Задайте максимальную дистанцию до самого удаленного различимого объекта (серая шкала).
- В режиме focal length управляя ползунками добейтесь приемлемого для Вас результата, программа автоматически вычислит углы обзора камеры по вертикали и горизонтали (соотношение сторон кадра 3/4), угол наклона камеры относительно горизонта, расстояние рабочей и «мертвой» зоны, покажет на экране «виртуального» монитора как бы это выглядело.
В режиме lens size relative результат будет зависеть от того каким ползунком Вы будете управлять. Вертикальным изменяется только угол наклона камеры. Управляя горизонтальным ползунком можно изменятьугол наклона камеры относительно горизонта, расстояние рабочей и «мертвой» зоны, параметры focal length,lens size relative и perspective. На экране «виртуального» монитора отобразиться результат. При изменении фокусного расстояния объектива ориентируйтесь не принятый модельный ряд
На экране «виртуального» монитора отобразиться результат. При изменении фокусного расстояния объектива ориентируйтесь не принятый модельный ряд
Принцип расчета фокусного расстояния камеры видеонаблюдения
Фокусное расстояние объектива камеры видеонаблюдения — это параметр, который мы берем за основу при расчете зоны обзора камеры. От его величины и физического размера матрицы зависит угол обзора объектива. Проведя не сложные геометрические расчеты можно довольно точно определить зону, которая будет попадать в кадр камеры видеонаблюдения.
Параметры, влияющие на угол обзора
Как известно, три основных параметра видеокамеры взаимозависимы, это:
- Фокусное расстояние объектива;
- Угол обзора объектива;
- Физический размер матрицы видеокамеры.
Чем больше фокусное расстояние объектива, тем меньше угол обзора. Это значит, что можно наблюдать за объектами, которые находятся на относительно большом удалении от камер видеонаблюдения. И наоборот, чем меньше фокусное расстояние, тем больше угол обзора.
И наоборот, чем меньше фокусное расстояние, тем больше угол обзора.
Угол обзора, также зависит от размера матрицы. Чем больше размер матрицы, тем меньше угол обзора камеры и наоборот.
Угол обзора камеры влияет:
- на качество изображения;
- на обозреваемую площадь;
- на функцию детализации;
- на функцию различия лиц;
- на размеры находящихся под наблюдением объектов.
Расчет фокусного расстояния камеры видеонаблюдения нужен для правильного подбора видеокамеры. Зачастую роизводители указывают в технических характеристиках физический размер матрицы, фокусное расстояние и реже угол обзора. Но для понимания, рассмотрим, что влияет на выбор фокусного расстояния. Это:
- На каком расстоянии находится объект наблюдения;
- Физического размера матрицы;
- Размера объекта.
Итак, имея технические характеристики камеры, можно рассчитать фокусное расстояние объектива камеры видеонаблюдения по следующим формулам:
F= h*S/Н или F= v*S/V,
где h – размер матрицы по горизонту;
S – расстояние до объекта видеонаблюдения;
H – горизонтальный размер объекта;
v – размер матрицы по вертикали;
V – вертикальный размер объекта.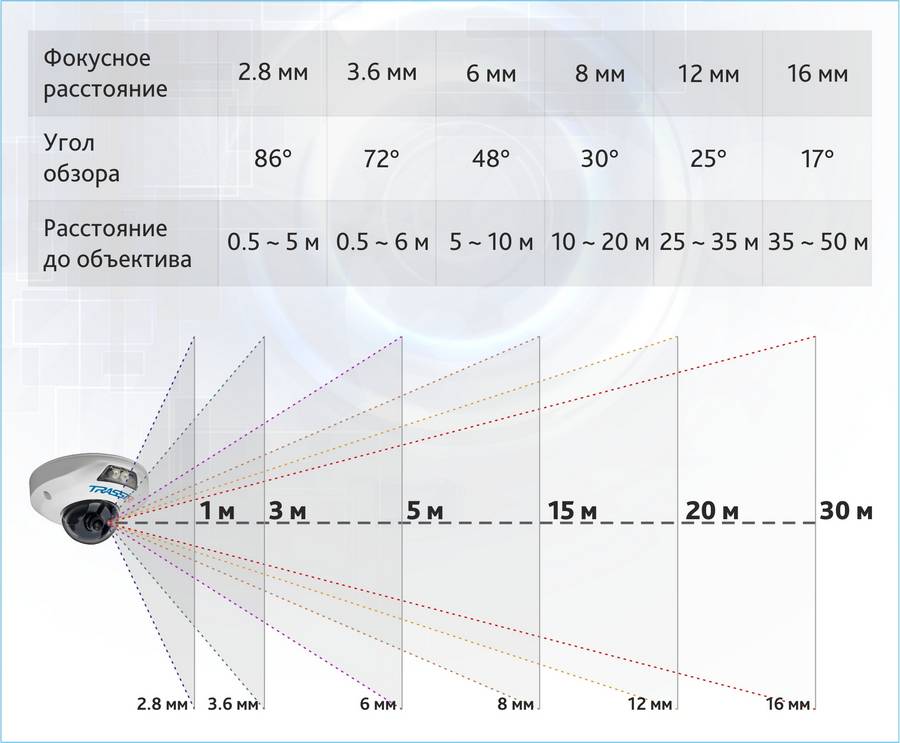
Размеры сторон матрицы камеры видеонаблюдения приведены в таблице:
| Размер матрицы | 1/4” | 1/3” | 1/2” |
| По горизонтали, мм | 3,2 | 4,8 | 6,4 |
| По вертикали, мм | 2,4 | 3,6 | 4,8 |
Приведем пример расчета фокусного расстояния и выбор камеры. Так при необходимости наблюдения за въездом и проходом через ворота на территорию предприятия с целью обнаружение автомобилей и людей при въезде-входе на территорию предприятия;
Ширина прохода и ворот 6 метров;
Расстояние от камеры до прохода 7 метров;
Камера Proto AHD-1W-Eh20F(?)IR, после буквы F должно указываться фокусное расстояние. Его мы рассчитаем по вышеприведенной формуле:
F=3.2*7/6=3,7 мм,
где 3,2 размер матрицы по вертикали, т.к. в камере Proto AHD-1W-Eh20F(?)IR установлена матрица размером 1/4”.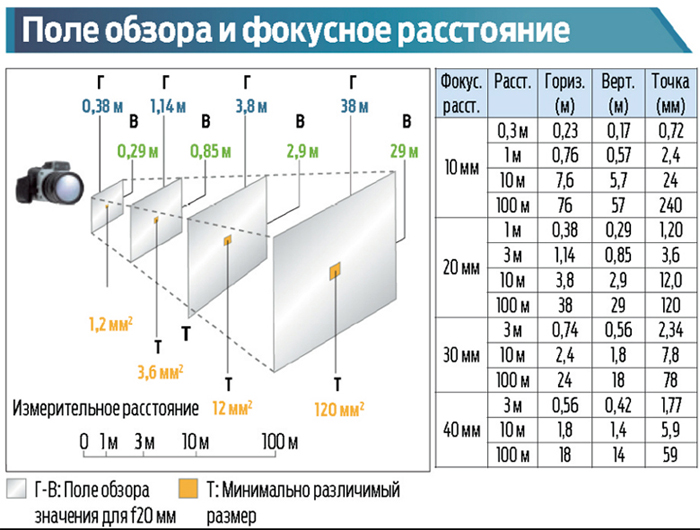
Так как объективы на видеокамере выполнены с фиксированными фокусными расстояниями, то выбираем ближайший меньший т.к. если выбрать ближайший больший, то часть объекта не будет попадать в кадр камеры.
При достаточно простых расчетах видно, что камере Proto AHD-1W-Eh20F36IR по силам не только обнаружение, но и распознавание человека на объекте, не говоря уже о номерах автомобилей.
На самом деле кроме этого необходимо вычислить фокусное расстояние по вертикали, а также высоту и угол установки видеокамеры, но мы эти расчеты намеренно упускаем, т.к.мы не ставим перед собой задачу полного расчета, мы лишь хотели показать на данном примере только методику расчета фокусного расстояния и выбора камеры по этому расчету.
Бывают ситуации, когда невозможно четко определить зону контроля видеокамеры или существует необходимость менять размер этой зоны, с определенной периодичностью периодичностью и наоборот, когда нужно более точно определить зону контроля. В этих случаях поможет камера с вариофокальным объективом, на которых можно менять без особых проблем фокусное расстояние вручную.
Для расчета фокусного расстояния камер видеонаблюдения есть специальные онлайн калькуляторы. Вы можете перейти по ссылкам ниже, чтобы быстро рассчитать нужные параметры.
Ссылка 1, ссылка 2.
Есть одна интересная особенность, которая позволяет определить расстояние уверенного распознавания объекта, и может служить своеобразной шпаргалкой при выборе камеры. Она заключается в примерном равенстве фокусного расстояния, выраженного в миллиметрах с дистанцией уверенного распознавания в метрах.
Например, камера с матрицей 1/3 дюйма и объективом с фокусным расстоянием 12 мм сможет распознать человеческую фигуру на расстоянии 12 метров. На этом расстоянии размер наблюдаемой зоны будет равняться 3 метра в высоту, и 4 в ширину, что позволит достаточно уверенно провести идентификацию человека.
Также на практике можно отталкиваться от следующих правил:
дистанция уверенного распознавания знакомого вам человека, выраженная в метрах, примерно соответствует фокусному расстоянию, выраженному в миллиметрах. | |
| дистанция для идентификации незнакомого человека. Значение фокусного расстояния объектива в миллиметрах примерно равно расстоянию до человека в метрах, деленное на два. | |
| дистанция для обнаружения человека в поле зрения камеры. Значение фокусного расстояния объектива в миллиметрах примерно равно расстоянию до человека в метрах, помноженное на семь. | |
| дистанция для распознавания номера автомобиля. Значение фокусного расстояния объектива в миллиметрах примерно в 1,5 раза меньше расстояния до номера автомобиля в метрах. | |
| для распознавания силуэта человека требуется, чтобы на экране монитора он занял 1/10 часть. | |
| для идентификации знакомого вам человека его фигура должна занимать 1/3 экрана монитора. | |
| для идентификации не известного вам лица на экране монитора необходимо отобразить 2/3 высоты человека | |
| для распознавания номера автомобиля, номер должен занимать не менее 1/2 части экрана |
Также в некоторых случаях, может оказаться полезной информация о максимальных линейных размерах (горизонтальные х вертикальные) видимого объекта в зависимости от дистанции до него и фокусного расстояния объектива. Расчеты сделаны для видеокамер с форматом матрицы 1/3″.
Расчеты сделаны для видеокамер с форматом матрицы 1/3″.
| Дистанция | Фокусное расстояние объектива, мм | ||||||||||||
| 2,45 | 2,8 | 2,96 | 3,6 | 3,7 | 4 | 4,9 | 6 | 8 | 12 | 16 | 36 | 72 | |
| 3 м. | 6х4,5 | 5,1×3,8 | 5×3,75 | 4×3 | 3,95×2,96 | 3,8×2,85 | 3×2,25 | 2,4×1,8 | 1,8×1,35 | 1,2×0,9 | 0,9×0,67 | ||
| 5 м. | 10×7,5 | 8,25×6,2 | 8,4×6,3 | 6,6×4,5 | 6,5×4,9 | 6×4,5 | 4,9×3,7 | 4×3 | 3×2,25 | 2×1,5 | 1,5×1,12 | 0,66×0,5 | |
10 м.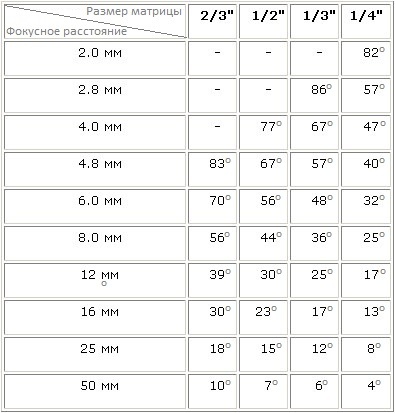 | 20×15 | 13×9,7 | 17×12,8 | 13×10 | 13×9,8 | 12×9 | 10×7,5 | 8×6 | 6×4,5 | 4×3 | 3×2,2 | 1,3×0,97 | 0,66×0,5 |
| 20 м | 40×30 | 34×25,5 | 34×25 | 26×20 | 28×19 | 22×16,5 | 19,5×14,6 | 16×12 | 12×9 | 8×6 | 6×4,5 | 2,7×2 | 1,3×0,97 |
| 30 м. | 60×45 | 51×38 | 50×37 | 40×30 | 39×29 | 36×16,5 | 29,5×22,1 | 24×18 | 18×13,5 | 12×9 | 9×6,7 | 4×3 | 2×1,5 |
| 40 м. | 80×60 | 69×52 | 65×49 | 53×40 | 52×39 | 48×36 | 39,5×29,6 | 34×25 | 24×18 | 16×12 | 12×9 | 5,4×4,1 | 2,7×2 |
50 м.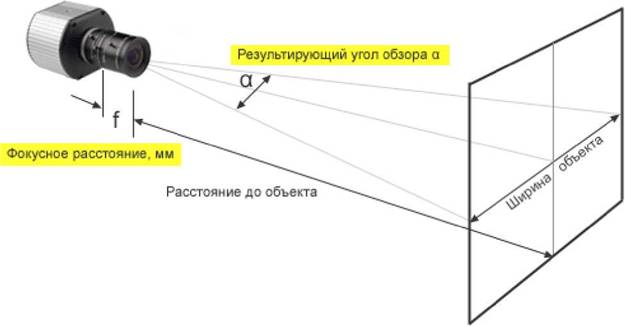 | 65×49 | 95×71 | 49×37 | 40×30 | 30×22 | 20×15 | 15×11,2 | 6,6×4,9 | 3,4×2,5 | ||||
| 80 м. | 79×59 | 64×48 | 48×32 | 32×24 | 24×18 | 11×8,2 | 5,4×4 | ||||||
| 100 м. | 60×45 | 40×30 | 30×22 | 13,5×10 | 6,6×4,9 | ||||||||
| 150 м. | 60×45 | 45×34 | 20×15 | 9,5×7,1 | |||||||||
АйТек ПРО — системы видеонаблюдения
Углы обзора видеокамер, фокусные расстояния объективов Одним из важнейших параметров при выборе камеры видеонаблюдения является угол обзора объектива. Этот параметр характеризует ширину той картины, будет охвачена камерой. Расчет угла обзора, при этом, вовсе не является сложным инженерным вычислением, и может быть выполнен даже начинающим специалистом.
Этот параметр характеризует ширину той картины, будет охвачена камерой. Расчет угла обзора, при этом, вовсе не является сложным инженерным вычислением, и может быть выполнен даже начинающим специалистом.
От чего зависит угол обзора камеры?
— от двух основных параметров:
1. Фокусное расстояние. Оно является величиной, обратно пропорциональной углу обзора: чем больше фокусное расстояние объектива, тем меньше угол обзора. Таким образом, камеры длинным фокусным расстоянием применяются, как правило, для — охраны периметра или идентификации государственных номерных знаков. Существует ещё одна особенность – глубина резкости, чем больше величина f= фокусного расстояния тем выше требования к линзам объектива.
Фокусное расстояние, в свою очередь, зависит от размера матрицы, величины наблюдаемого объекта и расстояния, на которое объект удален объект от камеры (если объектов несколько, то берется расстояние до самого дальнего).
Для расчета оптимального фокусного расстояния применяется следующая формула: f= h*S/Н или F= v*S/V, где h – размер горизонтальной стороны матрицы; S – расстояние до объекта слежения; H – размер объекта наблюдения по горизонтали; v – размер вертикальной стороны матрицы; V – размер объекта наблюдения по вертикали.
Таким образом, для расчетов могут применяться или вертикальные размеры матрицы и наблюдаемого объекта, или горизонтальные параметры.
2. Размер матрицы. Как указано выше, данный параметр влияет и на угол обзора, и на оптимальное фокусное расстояние. Величина сенсора прямо пропорциональна углу обзора – чем больше матрица, тем больше угол обзора. Например, камеры с матрицей 1/2.7 будут иметь больший угол обзора, чем устройства с матрицей 1/3. Широкоугольные камеры применяются для наблюдения за вытянутыми вширь площадями, например, за территорией, прилегающей к предприятию.
Как рассчитать угол обзора?
Для расчета угла обзора используется формула α = 2arctg(d/2F), где α — угол обзора объектива; d — размер матрицы; f — фокусное расстояние.
Соответственно, исходя из того, какие параметры были использованы при расчете фокусного расстояния – вертикальные или горизонтальные – рассчитывается вертикальный или горизонтальный угол обзора. Специалисты по проектированию и монтажу систем видеонаблюдения, однако, не рассчитывают угол обзора вручную, а используют готовые калькуляторы и таблицы. Ниже приведены таблицы, в которых содержатся значения угла обзора для наиболее распространенных размеров матрицы в соотношении с зонами детализации:
Ниже приведены таблицы, в которых содержатся значения угла обзора для наиболее распространенных размеров матрицы в соотношении с зонами детализации:
1. Наблюдение: объект занимает от 25 до 30 % высоты экрана. В этом масштабе различаются характерные детали объекта, например, цвет волос, одежда.
2. Узнавание: объект занимает как минимум 50 % высоты экрана, что позволяет с высокой долей вероятности определить, находился ли этот объект в зоне наблюдения ранее.
3. Идентификация: объект занимает 100 % высоты экрана, качество изображения и уровень детализации достаточны для однозначного установления личности.
Угол обзора камеры | расчет углов обзора камеры видеонаблюдения для различных фокусных расстояний и размеров матриц
При выборе видеокамеры для объекта одной из важных характеристик камеры, на которую необходимо обратить внимание — это угол обзора камеры видеонаблюдения. Что лучше выбрать для того, чтобы охватить наибольшую площадь на объекте?
Угол обзора видеокамеры
Угол обзора зависит от типоразмера (формата) матрицы видеокамеры 1/4″, 1/3″, 2/3″, 1/2 дюйма, а также от фокусного расстояния объектива. Рассмотрим расчет угла обзора для камер видеонаблюдения на основе фокусного расстояния и размера матрицы ниже.
Рассмотрим расчет угла обзора для камер видеонаблюдения на основе фокусного расстояния и размера матрицы ниже.
Для начала, отметим несколько важных моментов:
- Чем больше фокусное расстояние у камеры видеонаблюдения, тем уже угол обзора, или, наоборот, чем меньше фокусное расстояние у камеры, тем шире угол обзора. То есть, выбираем меньшее фокусное расстояние, чтобы снимать обзорное видео (всю парковку, весь двор, большой периметр, и т.п.) и большее фокусное расстояние, если необходимо приблизить объект оптикой и получить наилучшую картинку для идентификации.
- При равном фокусном расстоянии у объективов камеры видеонаблюдения больший угол обзора будет у камеры где матрица большего размера, то есть угол обзора будет больше у камеры 1/3 дюйма, чем у камеры с типоразмером матрицы 1/4 дюйма.
В видеонаблюдении есть несколько негласных правил для выбора фокусного расстояния для идентификации и распознавания человека:
- Распознавание знакомого человека возможно на расстоянии (приблизительно) равное фокусному.
 То есть для камеры видеонаблюдения с фокусным расстоянием 2.8 мм распознавание возможно на расстоянии до 3 м, для камеры с фокусным расстоянием 12 мм на расстоянии до 12 м и т.п.
То есть для камеры видеонаблюдения с фокусным расстоянием 2.8 мм распознавание возможно на расстоянии до 3 м, для камеры с фокусным расстоянием 12 мм на расстоянии до 12 м и т.п.
- Для идентификации незнакомого человека и четкой картинки лица расстояние равное половине фокусного.
Таким образом, можно сделать выводы, что:
- Больший угол обзор в камере дает общую картинку происходящего на объекте. Распознать лицо человека можно на расстоянии не более 3 — 4 метров – все это широкоугольные объективы с фокусным расстоянием 2.8-3.6 мм и углом обзора 70-130°;
- С помощью камер с меньшим углом обзора и с большим фокусным расстоянием можно приблизить объект оптикой и распознать лицо человека на расстоянии от 15 до 50 метров.
Как правило, производители указывают горизонтальный угол обзора видеокамеры и вертикальный угол обзора, но некоторые производители указывают в характеристиках для камеры только горизонтальный угол обзора.
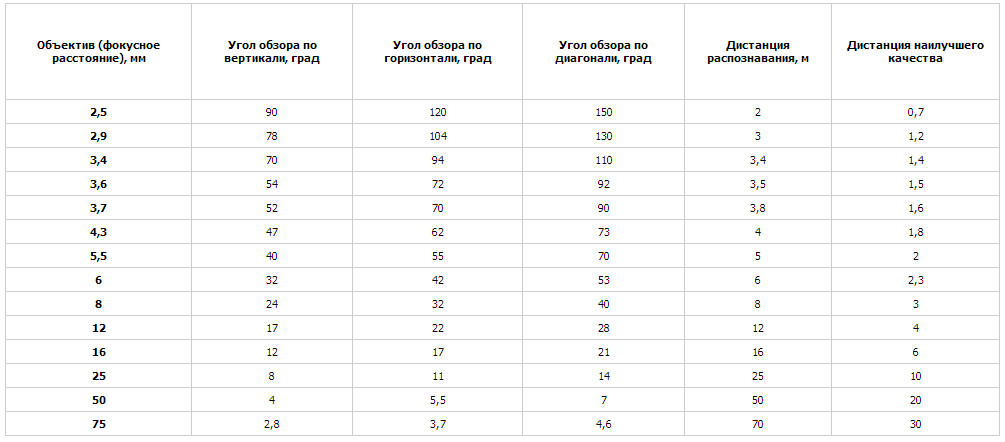
Соответствие угла обзора и фокусного расстояния для матриц 1/3 и 1/4 дюйма (для 1 — 2 Мп матриц) приведены в таблице ниже.
| Формат матрицы 1/4″ | Формат матрицы 1/3″ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для расчета фокусного расстояние и угла обзора можно также использовать бесплатные калькуляторы и программы (например, все тот же CCTV Design Lens Calculator от CCTVCAD Software).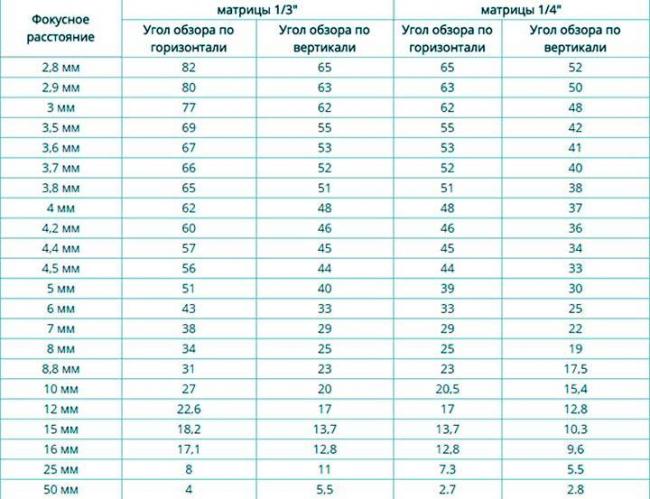
Также, обратите внимание, что кроме объективов с фиксированным фокусным расстоянием еще существуют вариофокальные и моторизированные объективы, а также роботизированные (Speed Dome) камеры видеонаблюдения, где можно менять фокусное расстояние и углы обзора, а в Speed Dome камерах вообще возможно вращение объектива на 360 градусов и многократный оптический zoom.
Расчет углов обзора на основе фокусного расстояния камер
Для видеокамер с матрицей 1/3 дюйма:
| Фокусное расстояние объектива, мм | Угол обзора видеокамеры, ° | Рекомендумая дистанция до объекта наблюдения, м | Горизонтальная зона обзора видеокамеры, м | |||||
|---|---|---|---|---|---|---|---|---|
| По горизонтали | По вертикали | Минимальная | Максимальная | На минимальной дистанции | На максимальной дистанции | |||
2. 8 8 |
81.2 | 65.5 | 1 | 4 | 2 | 7 | ||
| 2.96 | 78.1 | 62.6 | 1 | 4 | 2 | 6 | ||
| 3.6 | 67.4 | 53.1 | 2 | 5 | 2 | 7 | ||
| 3.7 | 65.9 | 51.9 | 2 | 6 | 3 | 7 | ||
3. 8 8 |
64.6 | 50.7 | 2 | 6 | 3 | 7 | ||
| 4 | 61.9 | 48.5 | 2 | 6 | 3 | 7 | ||
| 4.7 | 54.1 | 41.9 | 3 | 7 | 3 | 7 | ||
| 5 | 51.3 | 39.6 | 3 | 7 | 3 | 7 | ||
| 6 | 43. 6 6 |
33.4 | 4 | 9 | 3 | 7 | ||
| 8 | 33.4 | 25.4 | 5 | 12 | 3 | 7 | ||
| 9 | 29.9 | 22.6 | 6 | 13 | 3 | 7 | ||
| 9.5 | 28.4 | 21.5 | 6 | 14 | 3 | 7 | ||
10. 5 5 |
25.8 | 19.5 | 7 | 15 | 3 | 7 | ||
| 11 | 24.6 | 18.6 | 7 | 16 | 3 | 7 | ||
| 12 | 22.6 | 17.1 | 8 | 17 | 3 | 7 | ||
| 16 | 17.1 | 12.8 | 11 | 23 | 3 | 7 | ||
| 50 | 5. 5 5 |
4.1 | 35 | 74 | 3 | 7 | ||
| 84.6 | 3.2 | 2.4 | 59 | 122 | 3 | 7 | ||
Для видеокамер с матрицей 1/4 дюйма:
| Фокусное расстояние объектива, мм | Угол обзора видеокамеры, ° | Рекомендуемая дистанция до объекта наблюдения, м | Горизонтальная зона обзора видеокамеры, м | |||
|---|---|---|---|---|---|---|
| По горизонтали | По вертикали | Минимальная | Максимальная | На минимальной дистанции | На максимальной дистанции | |
3. 6 6 |
53.1 | 41.1 | 2 | 7 | 2 | 7 |
| 3.8 | 50.7 | 39.1 | 2 | 7 | 2 | 7 |
| 3.9 | 49.6 | 38.2 | 2 | 7 | 2 | 7 |
| 85.9 | 2.4 | 1.8 | 80 | 163 | 3 | 7 |
97. 2 2 |
2.1 | 1.6 | 90 | 189 | 3 | 7 |
Просмотров: 3939
Дата: Вторник, 19 Ноября 2013
Зависимость угла обзора от фокусного расстояния камер видеонаблюдения
Фокусное расстояние — это расстояние между оптическим центром линзы объектива и фокальной плоскостью матрицы камеры видеонаблюдения. От фокусного расстояния объектива зависит максимальная дистанция, на которой можно уверенно рассмотреть объект.
Расчёт зоны обзора камера видеонаблюдения
Угол обзора α для объективов (без учёта сферической аберрации) можно рассчитать, зная размер светочувствительного элемента (матрицы) d и эффективное фокусное расстояние объектива F:
α = 2arctg(d/2F)
На сегодняшний день существует три стандартных размера матрицы видеокамеры:
· матрица формата 1/2 по вертикали 4,8мм, по горизонтали 6,4мм
· матрица формата 1/3 по вертикали 3,6мм, по горизонтали 4,8мм
· матрица формата 1/4 по вертикали 2,4мм, по горизонтали 3,2мм
Чем больше размер матрицы, тем больше площадь сенсора и выше качество получаемого изображения. Самое качественное изображение выдает камера видеонаблюдения на матрице CCD 1/2″, но такая матрица встречается редко и имеет большую стоимость. Поэтому на практике как правило применяются матрицы формат 1/3″.
Самое качественное изображение выдает камера видеонаблюдения на матрице CCD 1/2″, но такая матрица встречается редко и имеет большую стоимость. Поэтому на практике как правило применяются матрицы формат 1/3″.
В таблице показана зависимость угла обзора камеры видеонаблюдения от фокусного расстояния объектива с матрицами 1/3″ и 1/4″.
| Фокусное расстояние | матрицы 1/3″ | матрицы 1/4″ | ||
| Угол обзора по горизонтали | Угол обзора по вертикали | Угол обзора по горизонтали | Угол обзора по вертикали | |
| 2,8 мм | 82 | 65 | 65 | 52 |
| 2,9 мм | 80 | 63 | 63 | 50 |
| 3 мм | 77 | 62 | 62 | 48 |
| 3,5 мм | 69 | 55 | 55 | 42 |
| 3,6 мм | 67 | 53 | 53 | 41 |
| 3,7 мм | 66 | 52 | 52 | 40 |
| 3,8 мм | 65 | 51 | 51 | 38 |
| 4 мм | 62 | 48 | 48 | 37 |
| 4,2 мм | 60 | 46 | 46 | 36 |
| 4,4 мм | 57 | 45 | 45 | 34 |
| 4,5 мм | 56 | 44 | 44 | 33 |
| 5 мм | 51 | 40 | 39 | 30 |
| 6 мм | 43 | 33 | 33 | 25 |
| 7 мм | 38 | 29 | 29 | 22 |
| 8 мм | 34 | 25 | 25 | 19 |
| 8,8 мм | 31 | 23 | 23 | 17,5 |
| 10 мм | 27 | 20 | 20,5 | 15,4 |
| 12 мм | 22,6 | 17 | 17 | 12,8 |
| 15 мм | 18,2 | 13,7 | 13,7 | 10,3 |
| 16 мм | 17,1 | 12,8 | 12,8 | 9,6 |
| 25 мм | 8 | 11 | 7.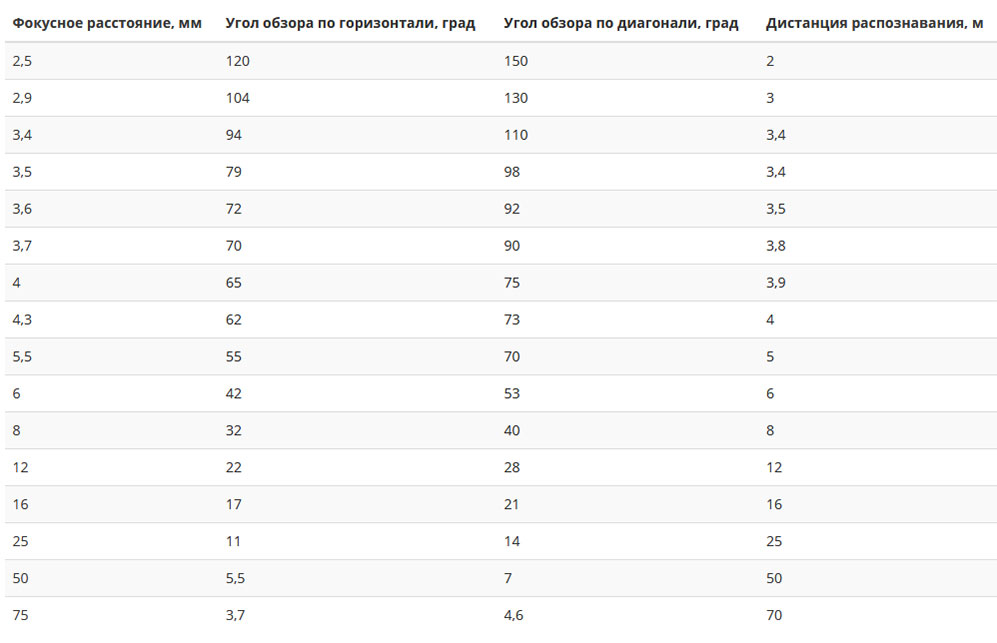 3 3 |
5.5 |
| 50 мм | 4 | 5,5 | 2.7 | 2.8 |
Следует учесть, что из-за наличия сильных искажений в короткофокусных объективах угол обзора может отличаться от расчётного.
Добавить комментарий
Как рассчитать фокусное расстояние линзы
Обновлено 28 декабря 2020 г.
Карен Дж. Блаттлер
До 1590-х годов простые линзы, появившиеся еще у римлян и викингов, допускали ограниченное увеличение и простые очки. Захариас Янсен и его отец объединили линзы из простых увеличительных стекол для создания микроскопов, и с тех пор микроскопы и телескопы изменили мир. Понимание фокусного расстояния линз имело решающее значение для объединения их возможностей.
Типы линз
Есть два основных типа линз: выпуклые и вогнутые. Выпуклые линзы посередине толще, чем по краям, и поэтому световые лучи сходятся в одну точку. Вогнутые линзы по краям толще, чем в середине, и поэтому световые лучи расходятся.
Вогнутые линзы по краям толще, чем в середине, и поэтому световые лучи расходятся.
Выпуклые и вогнутые линзы бывают разных конфигураций. Плоско-выпуклые линзы плоские с одной стороны и выпуклые с другой, в то время как двояковыпуклые (также называемые двояковыпуклыми) линзы выпуклые с обеих сторон.Плоско-вогнутые линзы плоские с одной стороны и вогнутые с другой стороны, в то время как двояковогнутые (или двояковогнутые) линзы вогнуты с обеих сторон.
Комбинированные вогнутые и выпуклые линзы, называемые вогнутыми и выпуклыми линзами, чаще называют линзами с положительным (сходящимся) мениском. Эта линза является выпуклой с одной стороны и вогнутой поверхностью с другой стороны, а радиус на вогнутой стороне больше, чем радиус выпуклой стороны.
Комбинированная выпуклая и вогнутая линза, называемая выпукло-вогнутой линзой, чаще называется линзой с отрицательным (расходящимся) мениском.Эта линза, как и вогнуто-выпуклая линза, имеет вогнутую сторону и выпуклую сторону, но радиус на вогнутой поверхности меньше, чем радиус на выпуклой стороне.
Фокусное расстояние Физика
Фокусное расстояние объектива f — это расстояние от объектива до фокальной точки F . Световые лучи (одной частоты), идущие параллельно оптической оси выпуклой или вогнуто-выпуклой линзы, встретятся в точке фокуса.
Выпуклая линза сводит параллельные лучи к точке фокусировки с положительным фокусным расстоянием.Поскольку свет проходит через линзу, положительные расстояния изображения (и реальные изображения) находятся на противоположной стороне линзы от объекта. Изображение будет перевернуто (вверх ногами) относительно фактического изображения.
Вогнутая линза отклоняет параллельные лучи от точки фокусировки, имеет отрицательное фокусное расстояние и формирует только виртуальные изображения меньшего размера. Отрицательные расстояния между изображениями формируют виртуальные изображения на той же стороне линзы, что и объект. Изображение будет ориентировано в том же направлении (правая сторона вверх), что и исходное изображение, только меньшего размера.
Формула фокусного расстояния
Для определения фокусного расстояния используется формула фокусного расстояния и требуется знание расстояния от исходного объекта до объектива u и расстояния от объектива до изображения v . Формула линзы говорит, что расстояние, обратное расстоянию от объекта плюс расстояние до изображения, равно обратному фокусному расстоянию f . Математически уравнение записывается так:
\ frac {1} {u} + \ frac {1} {v} = \ frac {1} {f}
Иногда уравнение фокусного расстояния записывается как:
\ frac {1} {o} + \ frac {1} {i} = \ frac {1} {f}
, где o обозначает расстояние от объекта до линзы, i обозначает расстоянию от объектива до изображения, а f — фокусное расстояние.
Расстояние измеряется от объекта или изображения до полюса линзы.
Примеры фокусного расстояния
Чтобы найти фокусное расстояние объектива, измерьте расстояния и подставьте числа в формулу фокусного расстояния. Убедитесь, что все измерения используют одну и ту же систему измерения.
Убедитесь, что все измерения используют одну и ту же систему измерения.
Пример 1 : Измеренное расстояние от линзы до объекта составляет 20 сантиметров, а от линзы до изображения — 5 сантиметров. Завершение формулы фокусного расстояния дает:
\ frac {1} {20} + \ frac {1} {5} = \ frac {1} {f} \\ \ text {или} \; \ frac {1} {20} + \ frac {4} {20} = \ frac {5} {20} \\ \ text {Уменьшение суммы дает} \ frac {5} {20} = \ frac {1} {4}
Таким образом, фокусное расстояние 4 сантиметра.
Пример 2 : Измеренное расстояние от линзы до объекта составляет 10 сантиметров, а расстояние от линзы до изображения составляет 5 сантиметров. Уравнение фокусного расстояния показывает:
\ frac {1} {10} + \ frac {1} {5} = \ frac {1} {f} \\ \ text {Then} \; \ frac {1} {10} + \ frac {2} {10} = \ frac {3} {10}
\ frac {3} {10} = \ frac {1} {3.33}
Фокусное расстояние линзы, следовательно, составляет 3,33 сантиметра.
Фокусное расстояние объективов микроскопов
В составных световых микроскопах используется несколько линз для наблюдения за объектами, которые слишком малы, чтобы их можно было увидеть невооруженным глазом. Эти микроскопы содержат как минимум две линзы: линзу объектива, которую держат рядом с наблюдаемым объектом, и линзу окуляра, или окулярную линзу, которая расположена рядом с глазом. Фокусное расстояние — самая важная характеристика объектива, связанная с тем, насколько объектив увеличивает объект.
Эти микроскопы содержат как минимум две линзы: линзу объектива, которую держат рядом с наблюдаемым объектом, и линзу окуляра, или окулярную линзу, которая расположена рядом с глазом. Фокусное расстояние — самая важная характеристика объектива, связанная с тем, насколько объектив увеличивает объект.
Структура линзы
Объективы микроскопа изготовлены из специального оптического стекла, которое по качеству превосходит стекло, которое используется в большинстве окон. Линза имеет форму круглого диска с двумя загнутыми наружу гранями, известными как выпуклые.Когда параллельные лучи света падают на одну сторону линзы объектива, они фокусируются по мере прохождения и встречаются в одной точке, называемой фокусной точкой.
Фокусное расстояние
Расстояние от центра объектива до фокальной точки называется фокусным расстоянием. Поскольку изображение находится на другой стороне линзы, с которой расположен объект, фокусное расстояние для выпуклых линз имеет положительный знак. Вогнутые линзы — где грани линзы изогнуты внутрь — имеют отрицательное фокусное расстояние.
Вогнутые линзы — где грани линзы изогнуты внутрь — имеют отрицательное фокусное расстояние.
Сила линзы
Фокусное расстояние важно, потому что оно определяет силу линзы, которая является показателем того, насколько линза увеличивает изображение. Сила линзы рассчитывается путем деления числа один на фокусное расстояние — получая значение, обратное фокусному расстоянию. Объектив с меньшим фокусным расстоянием будет иметь большую силу линзы и больше увеличит изображение. Объективы микроскопов имеют короткое фокусное расстояние, что позволяет значительно увеличивать изображения.
Линза окуляра
Фокусное расстояние объектива — это расстояние от линзы до точки, где сходятся параллельные лучи света, проходящие через линзу.Созданное здесь изображение становится по существу объектом, наблюдаемым через линзу окуляра или окуляра. Когда большее изображение создается линзой объектива с меньшим фокусным расстоянием, линза окуляра видит это большее изображение.
Формы уравнений увеличения | Sciencing
На самом деле существует два основных уравнения увеличения: уравнение линзы и уравнение увеличения. Оба необходимы для вычисления увеличения объекта выпуклой линзой. Уравнение линзы связывает фокусное расстояние, определяемое формой линзы, с расстояниями между объектом, линзой и проецируемым изображением.Уравнение увеличения связывает высоту и расстояние до объектов и изображений и определяет M, увеличение. Оба уравнения имеют несколько форм.
Уравнение линзы
Уравнение линзы говорит, что 1 / f = 1 / Do + 1 / Di, где f — фокусное расстояние линзы, Do — расстояние от объекта до линзы, а Di — расстояние от объектив на проецируемое изображение в фокусе. Эта форма уравнения линзы дает три более удобных в вычислительном отношении форм с помощью алгебраически простых решений для трех переменных.Эти формы следующие: f = (Do * Di) / (Do + Di), Do = (Di * f) / (Di — f) и Di = (Do * f) / (Do — f). Эти три формы намного проще использовать, если у вас есть две переменные и вам нужно вычислить третью переменную. Уравнение линзы не только говорит вам, как далеко будет изображение от объекта и линзы, но и может сказать вам, какой тип линзы использовать, если вы знаете расстояния.
Эти три формы намного проще использовать, если у вас есть две переменные и вам нужно вычислить третью переменную. Уравнение линзы не только говорит вам, как далеко будет изображение от объекта и линзы, но и может сказать вам, какой тип линзы использовать, если вы знаете расстояния.
Уравнение увеличения
Уравнение увеличения утверждает, что M = Hi / Ho = — Di / Do, где M — увеличение, Hi — высота изображения, Ho — высота объекта, Di — расстояние от линза до изображения, а Do — расстояние от объекта до линзы.Знак минус означает, что изображение будет перевернуто. Два знака равенства означают, что есть три непосредственных формы (и еще четыре, если вы проигнорируете M и решите четыре других переменных), а именно M = Hi / Ho, M = — Di / Do и Hi / Ho = — Di / Do.
Использование уравнений
Уравнение линзы может сказать вам, какой тип линзы использовать, если вы знаете соответствующие расстояния. Например, если камера будет снимать с расстояния 10 футов и проецировать на пленку на расстоянии 6 дюймов, фокусное расстояние объектива должно быть f = (10 * 0.5) / (10 + 0,5) = 5 / 10,5 = 0,476, с округлением до трех разрядов для соответствия точности входных параметров. Используя прямую перестановку одной из форм уравнения увеличения, мы можем вычислить размер изображения объекта на пленке камеры. Хай = — (Ди * Хо) / До = — (0,5 * Хо) / 10 = — (1/20) * Хо. Изображение на пленке будет 1/20 размера снимаемого изображения. Знак минус означает, что изображение будет перевернуто.
Например, если камера будет снимать с расстояния 10 футов и проецировать на пленку на расстоянии 6 дюймов, фокусное расстояние объектива должно быть f = (10 * 0.5) / (10 + 0,5) = 5 / 10,5 = 0,476, с округлением до трех разрядов для соответствия точности входных параметров. Используя прямую перестановку одной из форм уравнения увеличения, мы можем вычислить размер изображения объекта на пленке камеры. Хай = — (Ди * Хо) / До = — (0,5 * Хо) / 10 = — (1/20) * Хо. Изображение на пленке будет 1/20 размера снимаемого изображения. Знак минус означает, что изображение будет перевернуто.
РАССЧИТАТЬ ФОКУСНОЕ РАССТОЯНИЕ l Калькулятор фокусного расстояния
Как найти фокусное расстояние
Фокусное расстояние объектива — это расстояние в миллиметрах между оптическим центром объектива и датчиком камеры.Оптический центр также называют узловой точкой. Узловая точка линзы может рассматриваться как точка, в которой сходятся световые лучи, попадающие в линзу. Имейте в виду, что фокусное расстояние определяется, когда камера сфокусирована на бесконечность. В настоящее время найти фокусное расстояние объектива легко, потому что оно всегда печатается на современных объективах. Однако, как я обнаружил, на винтажных объективах это не всегда так, поэтому вам нужно рассчитать фокусное расстояние.
В настоящее время найти фокусное расстояние объектива легко, потому что оно всегда печатается на современных объективах. Однако, как я обнаружил, на винтажных объективах это не всегда так, поэтому вам нужно рассчитать фокусное расстояние.
Как творчески использовать фокусное расстояние:
На практике фокусное расстояние говорит вам, каков угол обзора с определенным объективом.Основное правило: чем короче фокусное расстояние (или чем меньше число на объективе), тем шире угол обзора. С другой стороны, чем больше фокусное расстояние (или чем больше число на объективе), тем уже угол обзора. Я написал отдельный блог о уравнении фокусного расстояния, где сравниваю разные фокусные расстояния. Вы найдете разные изображения для уравнения линзы. Также я объясню, как можно творчески использовать разные фокусные расстояния и в какой ситуации. Этот блог можно найти здесь: «Сравните фокусные расстояния — что такое фокусное расстояние».
Теперь, когда мы точно понимаем, что такое фокусное расстояние, я расскажу вам о практических шагах по его вычислению!
Как рассчитать фокусное расстояние объектива
Расчет фокусного расстояния объектива — довольно интересный и простой процесс. Вы легко можете измерить это с помощью рулетки! Этот метод можно использовать только с собирающими линзами, но не с расходящимися линзами.
Вы легко можете измерить это с помощью рулетки! Этот метод можно использовать только с собирающими линзами, но не с расходящимися линзами.
Конвергентные линзы в сравнении с расходящимися линзами
Сходящиеся линзы — это линзы, которые собирают световые лучи, идущие к ним, тогда как расходящиеся линзы — это линзы, которые рассеивают световые лучи, идущие к ним.Сводящие линзы формируют реальное изображение, а расходящиеся линзы формируют виртуальное изображение. Сводящая линза также известна как выпуклая линза, а расходящаяся линза также известна как вогнутые линзы. Насколько мне известно, собирающие линзы используются только для фото- и видеосъемок, но поправьте меня в разделе комментариев, если я ошибаюсь!
Необходимость определения фокусного расстояния
Следующие шаги объясняют, как определить фокусное расстояние:
Необходимости:
— Рулетка или линейка
— Темная комната с белой стеной (подойдут и другие цвета
— Сильная лампа для создания некоторой задней подсветки
Преломление и лучевая модель света
Диаграммы лучей могут использоваться для определения местоположения изображения, его размера, ориентации и типа изображения, сформированного из объектов при размещении в заданном месте перед линзой. Использование этих диаграмм было продемонстрировано ранее в Уроке 5 как для собирающих, так и для расходящихся линз. Диаграммы лучей предоставляют полезную информацию об отношениях объект-изображение, но не могут предоставить информацию в количественной форме. Хотя диаграмма лучей может помочь определить приблизительное местоположение и размер изображения, она не предоставит числовую информацию о расстоянии до изображения и размере изображения. Чтобы получить этот тип числовой информации, необходимо использовать уравнение объектива и уравнение увеличения .Уравнение объектива выражает количественную зависимость между расстоянием до объекта (d o ), расстоянием до изображения (d i ) и фокусным расстоянием (f). Уравнение сформулировано следующим образом:
Использование этих диаграмм было продемонстрировано ранее в Уроке 5 как для собирающих, так и для расходящихся линз. Диаграммы лучей предоставляют полезную информацию об отношениях объект-изображение, но не могут предоставить информацию в количественной форме. Хотя диаграмма лучей может помочь определить приблизительное местоположение и размер изображения, она не предоставит числовую информацию о расстоянии до изображения и размере изображения. Чтобы получить этот тип числовой информации, необходимо использовать уравнение объектива и уравнение увеличения .Уравнение объектива выражает количественную зависимость между расстоянием до объекта (d o ), расстоянием до изображения (d i ) и фокусным расстоянием (f). Уравнение сформулировано следующим образом: Уравнение увеличения связывает отношение расстояния до изображения и расстояния до объекта с отношением высоты изображения (h i ) и высоты объекта (h o ).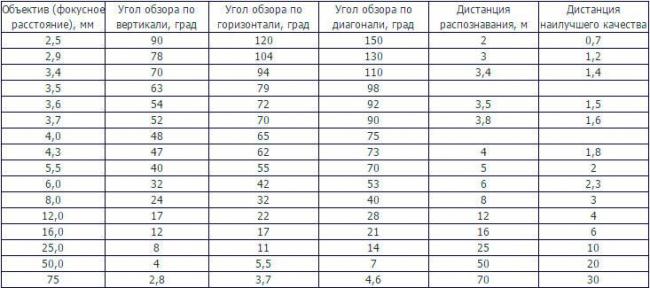 Уравнение увеличения сформулировано следующим образом:
Уравнение увеличения сформулировано следующим образом:
Эти два уравнения можно объединить для получения информации о расстоянии до изображения и высоте изображения, если известны расстояние до объекта, высота объекта и фокусное расстояние.
Практические задачиВ качестве демонстрации эффективности уравнения линзы и уравнения увеличения рассмотрим следующий пример задачи и ее решение.
Пример задачи № 1Лампочка высотой 4,00 см расположена на расстоянии 45,7 см от двойной выпуклой линзы с фокусным расстоянием 15,2 см. Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с выявления известной информации.
| h o = 4,00 см | d o = 45,7 см | f = 15,2 см |
Затем определите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение линзы.Следующие строки представляют решение для расстояния до изображения; показаны замены и алгебраические шаги.
1 / f = 1 / do + 1 / d и1 / (15,2 см) = 1 / (45,7 см) + 1 / d i
0,0658 см -1 = 0,0219 см -1 + 1 / d i
0,0439 см -1 = 1 / d i
Числовые значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа.Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, четвертая величина может быть вычислена. Решение показано ниже.
h i / h o = — d i / d oh i /( 4,00 см) = — (22,8 см) / (45,7 см)
ч i = — (4.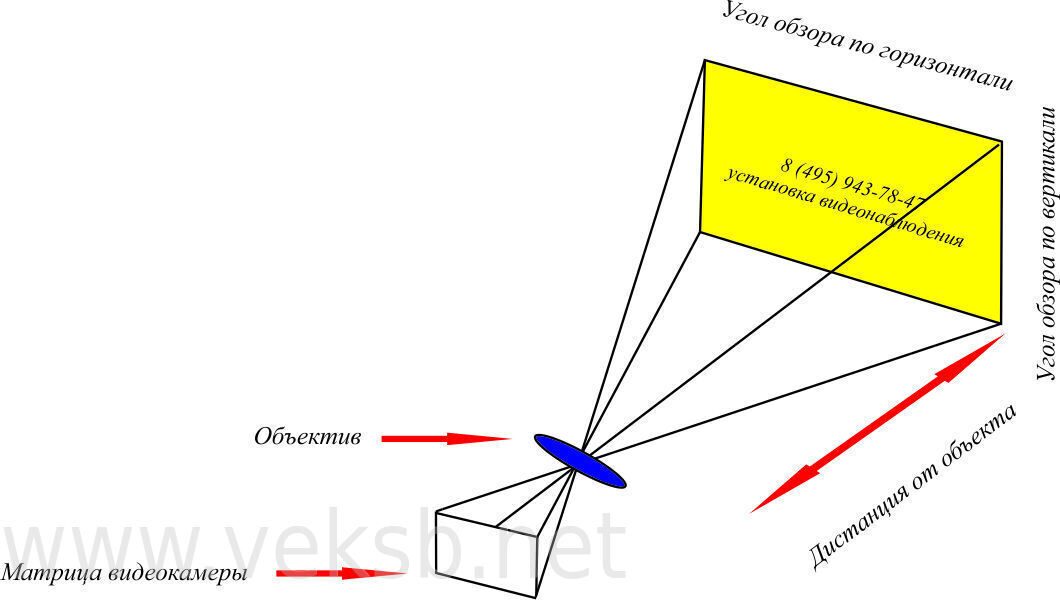 00 см) • (22,8 см) / (45,7 см)
00 см) • (22,8 см) / (45,7 см)
Отрицательные значения высоты изображения указывают на то, что изображение является перевернутым. Как это часто бывает в физике, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае высоты изображения отрицательное значение всегда указывает на перевернутое изображение.
Из расчетов в этой задаче можно сделать вывод, что если поместить объект высотой 4,00 см 45.7 см от двойной выпуклой линзы с фокусным расстоянием 15,2 см, то изображение будет перевернутым, высотой 1,99 см и расположенным на расстоянии 22,8 см от линзы. Результаты этого расчета согласуются с принципами, рассмотренными ранее в этом уроке. В этом случае объект расположен на за пределами точки 2F (что было бы на два фокусных расстояния от объектива), а изображение расположено между точкой 2F и фокусной точкой. Это попадает в категорию случая 1: объект расположен на за 2F для собирающей линзы.
Теперь давайте попробуем второй пример задачи:
Пример задачи № 2Лампочка высотой 4,00 см расположена на расстоянии 8,30 см от двойной выпуклой линзы с фокусным расстоянием 15,2 см. (ПРИМЕЧАНИЕ: это тот же объект и тот же объектив, только на этот раз объект расположен ближе к объективу.) Определите расстояние до изображения и размер изображения.
Опять же, начнем с определения известной информации.
| h o = 4,00 см | d o = 8,3 см | f = 15,2 см |
Затем определите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение линзы. Следующие строки представляют решение для расстояния до изображения; показаны замены и алгебраические шаги.
1 / f = 1 / do + 1 / d и1 / (15,2 см) = 1 / (8,30 см) + 1 / d i
0,0658 см -1 = 0,120 см -1 + 1 / d i
-0,0547 см -1 = 1 / d i
Числовые значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа.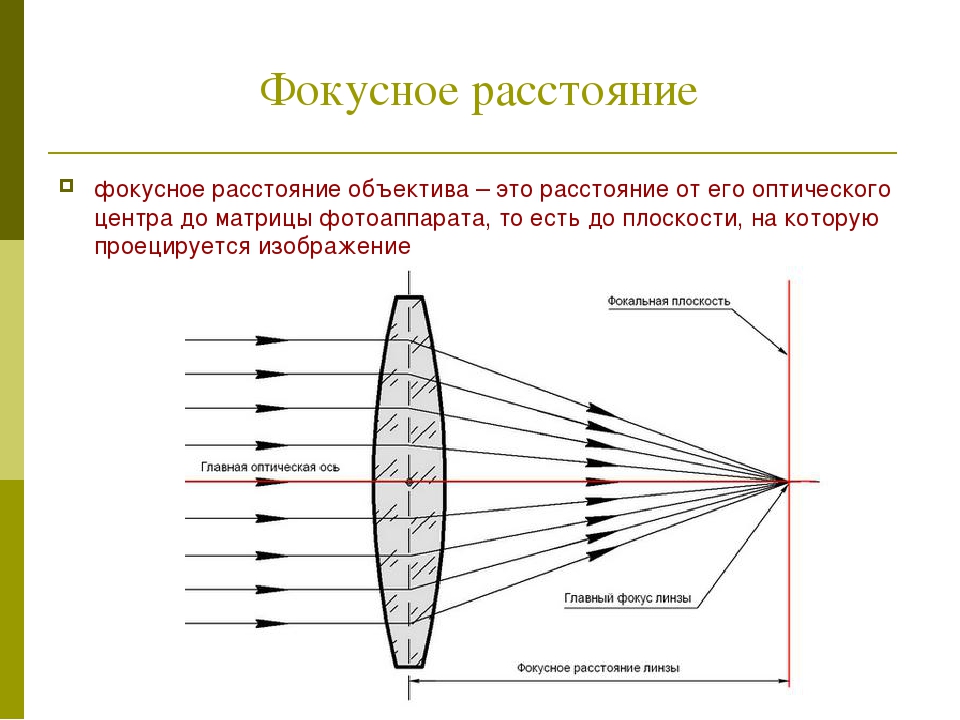 Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, четвертая величина может быть вычислена. Решение показано ниже.
h i / h o = — d i / d oh i /( 4,00 см) = — (-18,3 см) / (8,30 см)
h i = — (4,00 см) • (-18,3 см) / (8,30 см)
Отрицательное значение расстояния до изображения указывает, что изображение является виртуальным изображением, расположенным на стороне объекта линзы.Опять же, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда означает, что изображение находится на стороне объекта линзы. Также обратите внимание, что высота изображения — положительное значение, что означает вертикальное изображение. Любое изображение, расположенное вертикально и расположенное на стороне линзы объекта, считается виртуальным изображением.
Любое изображение, расположенное вертикально и расположенное на стороне линзы объекта, считается виртуальным изображением.
Из вычислений во втором примере задачи можно сделать вывод, что если 4.Объект высотой 00 см помещается на 8,30 см от двойной выпуклой линзы с фокусным расстоянием 15,2 см, затем изображение будет увеличено, вертикально, высотой 8,81 см и расположено на расстоянии 18,3 см от линзы на стороне объекта. Результаты этого расчета согласуются с принципами, рассмотренными ранее в этом уроке. В этом случае объект находится перед фокусной точкой (т.е. расстояние до объекта меньше фокусного расстояния), а изображение располагается за линзой. Это попадает в категорию случая 5: объект расположен перед F (для собирающей линзы).
Третья проблема, связанная с образцом, относится к рассеивающей линзе.
Пример задачи № 3Лампочка высотой 4,00 см помещена на расстоянии 35,5 см от расходящейся линзы с фокусным расстоянием -12,2 см.Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с выявления известной информации.
| h o = 4.00 см | d o = 35,5 см | f = -12,2 см |
Затем определите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение линзы. Следующие строки представляют решение для расстояния до изображения; показаны замены и алгебраические шаги.
1 / f = 1 / do + 1 / d и1 / (- 12.2 см) = 1 / (35,5 см) + 1 / d i
-0,0820 см -1 = 0,0282 см -1 + 1 / d i
-0,110 см -1 = 1 / d i
Числовые значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа.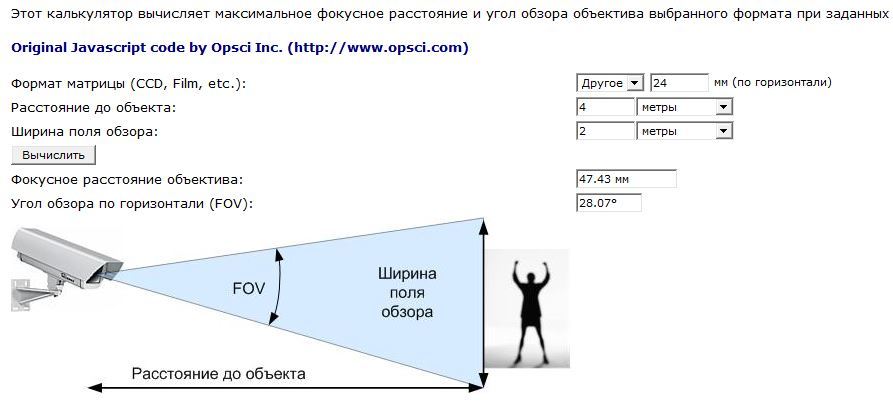 Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения.Поскольку три из четырех величин в уравнении (без учета M) известны, четвертая величина может быть вычислена. Решение показано ниже.
h i / h o = — d i / d oh i /( 4,00 см) = — (-9,08 см) / (35,5 см)
h i = — (4,00 см) * (-9,08 см) / (35,5 см)
Отрицательные значения расстояния до изображения указывают на то, что изображение расположено на стороне объекта линзы.Как уже упоминалось, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда указывает на существование виртуального изображения, расположенного на стороне объекта линзы. В случае высоты изображения положительное значение указывает на вертикальное изображение.
Из вычислений в этой задаче можно сделать вывод, что если поместить объект высотой 4,00 см на расстоянии 35,5 см от расходящейся линзы с фокусным расстоянием 12.2 см, то изображение будет вертикальным, высотой 1,02 см и расположено на расстоянии 9,08 см от линзы на стороне объекта. Результаты этого расчета согласуются с принципами, рассмотренными ранее в этом уроке. Расходящиеся линзы всегда создают вертикальные, виртуальные, уменьшенные изображения, расположенные на стороне линзы объекта.
Практика ведет к совершенству! Используйте виджет Find the Image Distance ниже, чтобы исследовать влияние фокусного расстояния и расстояния до объекта на расстояние до изображения.Просто введите фокусное расстояние и расстояние до объекта. Затем нажмите кнопку Рассчитать расстояние до изображения , чтобы просмотреть результат. Используйте виджет как инструмент практики. Постоянная задача фотографов — создать изображение, на котором сфокусировано как можно больше объекта. Цифровые камеры используют линзы для фокусировки изображения на чувствительной пластине, на том же расстоянии от объектива. Однако на этом уроке мы узнали, что расстояние до изображения зависит от расстояния до объекта.Так как же фотографу сфокусировать объекты в поле зрения, если они находятся на разном расстоянии от камеры? Это постоянная проблема для фотографов (будь то любители-энтузиасты или профессионалы), которые хотят контролировать, насколько сфокусирована часть объекта. Глубина резкости — это термин фотографа для описания расстояния от ближайшего до самого дальнего объекта в поле зрения, которые приемлемо сфокусированы на фотографии. Виджет Photography и Depth of Field позволяет вам исследовать переменные, влияющие на глубину резкости.
Цифровые камеры используют линзы для фокусировки изображения на чувствительной пластине, на том же расстоянии от объектива. Однако на этом уроке мы узнали, что расстояние до изображения зависит от расстояния до объекта.Так как же фотографу сфокусировать объекты в поле зрения, если они находятся на разном расстоянии от камеры? Это постоянная проблема для фотографов (будь то любители-энтузиасты или профессионалы), которые хотят контролировать, насколько сфокусирована часть объекта. Глубина резкости — это термин фотографа для описания расстояния от ближайшего до самого дальнего объекта в поле зрения, которые приемлемо сфокусированы на фотографии. Виджет Photography и Depth of Field позволяет вам исследовать переменные, влияющие на глубину резкости. f-stop или f-number объектива камеры зависит от размера круглого отверстия или апертуры, через которую свет проходит на своем пути к цифровому датчику. Чем больше число f, тем меньше отверстие и тем меньше света попадает на датчик. Круг нечеткости связан с ограничением глаза на разрешение деталей изображения в небольшой области. Для 35-мм камеры, изображения которой увеличены до отпечатка 5 «x7», общепринятое значение кружка нерезкости равно 0.0333 мм.
Круг нечеткости связан с ограничением глаза на разрешение деталей изображения в небольшой области. Для 35-мм камеры, изображения которой увеличены до отпечатка 5 «x7», общепринятое значение кружка нерезкости равно 0.0333 мм.
Условные обозначения для указанных величин в уравнении линзы и увеличении следующие:
- f равно +, если линза представляет собой двойную выпуклую линзу (собирающую линзу)
- f is — если линза двояковогнутая (рассеивающая линза)
- d i равно +, если изображение является реальным и расположено на противоположной стороне объектива.
- d i is — если изображение является виртуальным и расположено на стороне объекта линзы.
- h i равно +, если изображение является вертикальным (и, следовательно, также виртуальным)
- h i is — если изображение перевернутое изображение (а значит, тоже реальное)
Подобно многим математическим задачам в физике, этот навык можно приобрести только через личную практику. Возможно, вы захотите потратить некоторое время на решение следующих задач.
Возможно, вы захотите потратить некоторое время на решение следующих задач.
1. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, помещенного на 45,0 см от двойной выпуклой линзы с фокусным расстоянием 15,0 см.
2. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, помещенного на 30.0 см от двойной выпуклой линзы с фокусным расстоянием 15,0 см.
3. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, помещенного на расстоянии 20,0 см от двойной выпуклой линзы с фокусным расстоянием 15,0 см.
4. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, размещенного на расстоянии 10,0 см от двойной выпуклой линзы с фокусным расстоянием 15.0 см.
5. Увеличенное перевернутое изображение находится на расстоянии 32,0 см от двойной выпуклой линзы с фокусным расстоянием 12,0 см. Определите расстояние до объекта и определите, является ли изображение реальным или виртуальным.
6. ZINGER : перевернутое изображение увеличивается в 2 раза, когда объект помещается на 22 см перед двойной выпуклой линзой. Определите расстояние до изображения и фокусное расстояние объектива.
Определите расстояние до изображения и фокусное расстояние объектива.
7. Двойная вогнутая линза имеет фокусное расстояние -10,8 см. Объект находится на расстоянии 32,7 см от поверхности линзы. Определите расстояние до изображения.
8. Определите фокусное расстояние двойной вогнутой линзы, которая дает изображение на расстоянии 16,0 см позади линзы, когда объект 28.5 см от объектива.
9. Монета диаметром 2,8 см помещается на расстоянии 25,0 см от двойной вогнутой линзы с фокусным расстоянием -12,0 см. Определите расстояние до изображения и диаметр изображения.
10. Точка фокусировки расположена на расстоянии 20,0 см от двойной вогнутой линзы. Объект находится на расстоянии 12 см от линзы. Определите расстояние до изображения.
Калькулятор фокусного расстояния объектива
Калькулятор фокусного расстояния объективаВведение
При фотосъемке или видеосъемке фотоаппаратом, объективом (или системой
линзы) используется для проецирования изображения сцены, которую мы хотим записать на свет
на чувствительной пленке или на цифровом датчике (называемом тепловизором). Тепловизоры бывают разных размеров, но обычно довольно маленькие (от нескольких
от миллиметров до нескольких сантиметров), но сцена, которую мы хотим снять, может
быть любого размера: менее одного миллиметра в случае макросъемки
фотографии до тысяч километров при воспроизведении, например,
Луна.Расстояние до сцены также может варьироваться от нескольких миллиметров до бесконечности.
(или очень-очень далеко).
Вопрос в том, как выбрать наиболее подходящий объектив по фокусному расстоянию.
чтобы соответствовать конкретной потребности.
Тепловизоры бывают разных размеров, но обычно довольно маленькие (от нескольких
от миллиметров до нескольких сантиметров), но сцена, которую мы хотим снять, может
быть любого размера: менее одного миллиметра в случае макросъемки
фотографии до тысяч километров при воспроизведении, например,
Луна.Расстояние до сцены также может варьироваться от нескольких миллиметров до бесконечности.
(или очень-очень далеко).
Вопрос в том, как выбрать наиболее подходящий объектив по фокусному расстоянию.
чтобы соответствовать конкретной потребности.
Эта линза лупы проецирует изображение вида за пределы
окно на экране (щелкните для увеличения).
Определение проблемы
Линза — это интерфейс между пространством объекта (сцена, реальный мир
мы хотим записать) и пространство изображения (проекция излучаемого света
по месту происшествия).На рисунке ниже объектное пространство находится слева от линзы, а
пространство изображения находится справа.
Объект, линза и изображение с расстояниями, размерами и плоскостями.
Свет идет слева (объект) направо (изображение).
Даже если он не нарисован явно, между этими двумя пространствами свет только разрешено проходить через линзу; свет не может идти прямо от объекта пространство в пространство изображения. Физически это достигается за счет помещения тепловизора и объектива в герметичный коробку, оставляя только небольшое отверстие, пропускающее свет через предназначенное дорожка.Этот корпус отсутствует на изображении с лупой выше (или объектив камеры ниже), и получившееся изображение имеет низкую контрастность и выглядит сероватый.
Предположим, мы хотим получить изображение объекта, представленного здесь
красная жирная вертикальная стрелка.
Стрелки используются для обозначения объектов и их изображений, потому что это
немедленно очистить, если изображения вертикальные или перевернутые.
Объект расположен на расстоянии x o от объектива и
имеет высоту y o (суффиксы «o» обозначают
объектное пространство). Изображение формируется на плоскости пленки (тепловизора) на расстоянии x i и имеет высоту y i ( «i» суффиксы обозначают пространство изображения).
Изображение формируется на плоскости пленки (тепловизора) на расстоянии x i и имеет высоту y i ( «i» суффиксы обозначают пространство изображения).
Здесь для наглядности объект представлен лежащим на оптическом ось и занимая только половину возможного пространства; на самом деле объект обычно центрируется на оптической оси и занимает все пространство (и может также быть в любом месте выше, ниже или поперек оптической оси).При использовании здесь приближений первого порядка ничего не меняет пропорции, если объект центрирован или нет, и применяются те же формулы: x o — это размер объекта, а x i — это размер объекта. размер его изображения вне зависимости от вертикального положения относительно оптического ось.
Расстояния x o и x i измеряются от
передняя и задняя главные плоскости объектива соответственно.
Если бы у нас была только одна тонкая линза (то есть они тонкие по сравнению с их
фокусное расстояние и радиусы кривизны их поверхностей), мы могли измерить x o и x i от самого объектива, но
поскольку линзы камеры представляют собой сложные оптические системы, состоящие из нескольких линз. упакованы вместе в тубу, даже если вся система ведет себя как единая
линзу, обычно не представляется возможным рассматривать ее как единую «тонкую
линза »; линза имеет толщину, которой нельзя пренебречь.У толстой линзы есть две основные плоскости: лучи входят в толстую линзу, как если бы
Линза была тонкой и располагалась на переднем торце главной плоскости, выходила из нее, как будто
Линза была тонкой и располагалась в задней главной плоскости.
Сложность в том, что эти два самолета не обязательно совпадают, они могут
находиться в любом месте внутри или снаружи объектива, а передняя плоскость также может быть позади
задний самолет.
Если объект находится далеко, это не проблема, но при выполнении макроса
фотографии трудно понять, откуда следует измерять расстояния.
упакованы вместе в тубу, даже если вся система ведет себя как единая
линзу, обычно не представляется возможным рассматривать ее как единую «тонкую
линза »; линза имеет толщину, которой нельзя пренебречь.У толстой линзы есть две основные плоскости: лучи входят в толстую линзу, как если бы
Линза была тонкой и располагалась на переднем торце главной плоскости, выходила из нее, как будто
Линза была тонкой и располагалась в задней главной плоскости.
Сложность в том, что эти два самолета не обязательно совпадают, они могут
находиться в любом месте внутри или снаружи объектива, а передняя плоскость также может быть позади
задний самолет.
Если объект находится далеко, это не проблема, но при выполнении макроса
фотографии трудно понять, откуда следует измерять расстояния.
Положение этих плоскостей почти никогда не определяется объективом.
производителя и их позицию сложно угадать.
Если вы используете коммерческую камеру с совместимым объективом, расстояние x i уже настроен для обеспечения идеальной фокусировки, а вы
не беспокойтесь (задняя главная точка всегда одно фокусное расстояние
впереди плоскости пленки, когда объектив сфокусирован на бесконечность). Вы также должны учитывать, что обычные фотообъективы состоят из нескольких
группа линз, которые перемещаются относительно друг друга для фокусировки (или масштабирования) и
это также может изменить положение главных плоскостей.
Вы также должны учитывать, что обычные фотообъективы состоят из нескольких
группа линз, которые перемещаются относительно друг друга для фокусировки (или масштабирования) и
это также может изменить положение главных плоскостей.
Положение передней главной плоскости нельзя игнорировать при выполнении макросъемка. Чтобы определить его местонахождение, достаточно сфотографировать объективом, определить увеличение (соотношение размеров изображения и объекта), вычислить x o и x i и измерьте их обратно от объект и изображение соответственно, чтобы увидеть, где расположены плоскости.
Этот фотообъектив SLR проецирует изображение за пределы
окно на экране (щелкните для увеличения).
Бесконечность — это очень большое расстояние, и теоретически световые лучи исходят от
объекты на бесконечности параллельны друг другу, но на практике вы не
нужно зайти так далеко.
Расстояние x o , которое намного больше фокусного расстояния f достаточно близко к бесконечности.
Геометрическая оптика: изображение одной линзы
У нас есть объект, излучающий (отражающий) свет, и линза, формирующая изображение. этого объекта на расстоянии за линзой.Чтобы вычислить размер и положение этого изображения, два уравнения необходимы. В этих уравнениях используется фокусное расстояние объектива f , которое составляет характеристика линзы и обычно выражается в миллиметрах. Первое уравнение определяет условие фокуса и устанавливает соотношение между расстоянием до объекта x o , расстояние до изображения x i и фокусное расстояние f .
Здесь размеры — это просто расстояния, а не координаты: все они положительны. и выложен, как показано на диаграмме выше.Некоторые формулы в учебниках используют знак минуса для перевернутых изображений или пространство изображения; здесь дело обстоит не так.
Второе полезное уравнение устанавливает связь между увеличением, объектом
или расстояние изображения, и фокусное расстояние. Увеличение — это по определению соотношение между размером изображения y i и размер объекта y o .
Из-за схожих треугольников M также является соотношением между изображениями
расстояние x i и расстояние до объекта x o (два
части с f уже являются комбинациями предыдущих уравнений).
Увеличение — это по определению соотношение между размером изображения y i и размер объекта y o .
Из-за схожих треугольников M также является соотношением между изображениями
расстояние x i и расстояние до объекта x o (два
части с f уже являются комбинациями предыдущих уравнений).
С помощью этих двух уравнений можно определить все параметры простая (геометрическая) оптическая система, состоящая из одной линзы. За исключением проблемы главных плоскостей, объясненной ранее, это также допустимо, если линза представляет собой сложную систему, состоящую из множества линз, ведущих себя как один объектив, как в случае с фотообъективами.
С помощью тригонометрии также можно рассчитать угол обзора. ω , которое является функцией фокусного расстояния f ,
увеличение M и размер тепловизора, представленные здесь как y i , которое следует интерпретировать как самое большое изображение, которое
поместится в тепловизор.
Калькулятор фокусного расстояния
Следующий калькулятор выполнит вычисления за вас, просто введите размер объекта. y o , размер изображения y i , расстояние до объекта x o и нажмите кнопку «вычислить»; калькулятор вычислит недостающие значения.
Если вы используете объектив камеры, вам не следует слишком заботиться о x i : объектив уже предназначен для формирования изображения на правильное расстояние, соответствующее креплению камеры.
На самом деле x i il всегда очень близко к f .
Когда объектив сфокусирован на бесконечность ( x o = ∞), x i и f равны.
В обычных условиях фотографии x i просто немного больше
чем f .
По мере того, как расстояние до объекта x o становится меньше, расстояние до изображения x i увеличивается.![]() Фокусировка объектива достигается регулировкой x i .В макросъемке, где x o очень мало, x i может быть довольно большим и для получения резкого изображения,
может потребоваться увеличить расстояние между объективом и тепловизором,
например, с удлинительной трубкой.
Это заставит немакрообъектив работать с близкого расстояния, но качество
изображение может (будет) ухудшиться.
Тем не менее, попробовать стоит.
Фокусировка объектива достигается регулировкой x i .В макросъемке, где x o очень мало, x i может быть довольно большим и для получения резкого изображения,
может потребоваться увеличить расстояние между объективом и тепловизором,
например, с удлинительной трубкой.
Это заставит немакрообъектив работать с близкого расстояния, но качество
изображение может (будет) ухудшиться.
Тем не менее, попробовать стоит.
Обратите внимание, что обычно формирователи изображений или пленки имеют прямоугольную форму, а это означает, что если вы используете калькулятор для определения поля зрения, вы получите три разные значения, если вы рассчитываете высоту, ширину или диагональ.
Стандартные размеры тепловизора
В таблице ниже указаны размеры наиболее распространенных тепловизоров и пленок.
Эти значения полезны при определении максимального размера объекта. y i для данного тепловизора.
| Размер тепловизора | Высота [мм] | Ширина [мм] | Диагональ [мм] |
| 24 × 36 мм 2 | 24.0 | 36,0 | 43,3 |
| APS-C | 14,8 | 22,2 | 26,7 |
| 1 « | 9,6 | 12,8 | 16,0 |
| 2/3 дюйма | 6,6 | 8,8 | 11,0 |
| 1/2 « | 4,8 | 6,4 | 8,0 |
| 1/3 дюйма | 3.6 | 4,8 | 6,0 |
| 1/4 дюйма | 2,7 | 3,6 | 4,5 |
Если вам интересно, что означает размер тепловизора в дюймах и как он связан
на его физическую поверхность, это происходит от старых трубок видеокамеры (вакуумных) и
описывает их внешний диаметр. Диагональ составляет примерно две трети внешнего диаметра.
Трубки камеры исчезли в 1990-х годах, и их заменили ПЗС-сенсоры, но старые
номинал стандартного размера все еще используется.
Диагональ составляет примерно две трети внешнего диаметра.
Трубки камеры исчезли в 1990-х годах, и их заменили ПЗС-сенсоры, но старые
номинал стандартного размера все еще используется.
Заключение
Основные понятия геометрической оптики (первого порядка) применительно к фотографической линзы были ненадолго экспонированы. По этой причине, к сожалению, физические концепции, лежащие в основе этих явлений, были значительно упрощен; для получения более подробной информации я настоятельно рекомендую обратиться к книгам сообщается в разделе библиографии. Тем не менее, я надеюсь, что простой калькулятор поможет выбрать наиболее подходящие линзы для любых условий.
Библиография и дополнительная литература
| [1] | Уоррен Дж.Смит. Современная оптическая инженерия — Дизайн оптических систем. 3 rd Edition, McGraw-Hill, 2000 г., раздел 2.3. |
| [2] | Юджин Хехт. Оптика. 4 th Edition, Addison Wesley, 2002,
Глава 5. Оптика. 4 th Edition, Addison Wesley, 2002,
Глава 5. |
RP Photonics Encyclopedia — фокусное расстояние, фокусное расстояние, диоптрическая сила, изогнутое зеркало, уравнение линзы, микроскоп, фотографический объектив, фокус, радиус луча
Энциклопедия> буква F> фокусное расстояние
Определение: мера того, насколько сильно оптическая система фокусирует или расфокусирует свет
Немецкий: Brennweite
Категория: оптика общая
Обозначение формулы: f
Квартир: m
Как цитировать статью; предложить дополнительную литературу
Автор: Dr.Rüdiger Paschotta
Различные типы оптических систем (например, объективы микроскопов и изогнутые лазерные зеркала) могут фокусировать или расфокусировать свет, а фокусное расстояние используется для количественной оценки таких эффектов.
Самый простой случай — это тонкая фокусирующая линза (рис. 1а).
Если на линзу падает достаточно большой коллимированный луч света, луч будет сфокусирован, а фокусное расстояние — это расстояние от линзы до этого фокуса (при условии, что линза окружена вакуумом или воздухом, а не каким-то плотным веществом. со значительным показателем преломления).Для дефокусирующей линзы (рис. 1b) фокусное расстояние — это расстояние от линзы до виртуального фокуса (обозначено пунктирными линиями), принимаемое как отрицательное значение.
Однако некоторые авторы используют разные условные обозначения, особенно в отношении переднего и заднего фокусного расстояния (см. Ниже).
1а).
Если на линзу падает достаточно большой коллимированный луч света, луч будет сфокусирован, а фокусное расстояние — это расстояние от линзы до этого фокуса (при условии, что линза окружена вакуумом или воздухом, а не каким-то плотным веществом. со значительным показателем преломления).Для дефокусирующей линзы (рис. 1b) фокусное расстояние — это расстояние от линзы до виртуального фокуса (обозначено пунктирными линиями), принимаемое как отрицательное значение.
Однако некоторые авторы используют разные условные обозначения, особенно в отношении переднего и заднего фокусного расстояния (см. Ниже).
Фокусное расстояние тонкой или толстой линзы
Идеальная тонкая линза с заданным фокусным расстоянием f (принимаемое как положительное в случае фокусирующей линзы) создает радиально изменяющуюся фазовую задержку для лазерного луча в соответствии со следующим уравнением:
Эта формула игнорирует постоянную часть оптического изменения фазы, а также оптические аберрации.
Следующее уравнение позволяет рассчитать диоптрическую силу и, следовательно, фокусное расстояние линзы, изготовленной из материала с показателем преломления n и радиусами кривизны R 1 и R 2 на двух поверхностях:
Радиусы кривизны принимаются за положительные значения для выпуклых поверхностей и отрицательные для вогнутых поверхностей. Положительные результаты получаются при фокусировке линз, отрицательные — при расфокусировке линз. Последний термин актуален только для толстых линз со значительной кривизной с обеих сторон.Формула дает фокусное расстояние в параксиальном приближении, например, без учета сферических аберраций.
Уравнение справедливо для параксиальных лучей, не слишком далеко от оси симметрии.
Фокусное расстояние изогнутого зеркала
Изогнутые зеркала часто используются для фокусировки или расфокусировки света.
Например, в лазерных резонаторах чаще используются изогнутые лазерные зеркала с диэлектрическим покрытием, чем линзы, главным образом потому, что они вносят меньшие потери.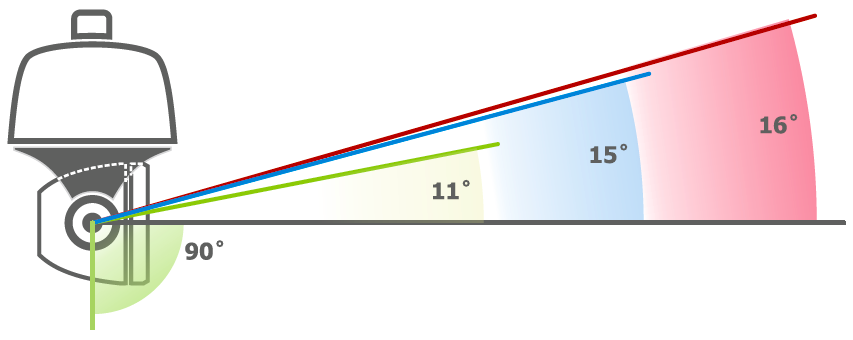
Зеркало с радиусом кривизны R поверхности имеет фокусное расстояние f = R /2, если ось луча перпендикулярна поверхности зеркала. (Принимаем положительные знаки за вогнутые кривизны и фокусирующие зеркала.) Если есть некоторый ненулевой угол θ между осью луча и нормальным направлением, фокусное расстояние будет f tan = ( R /2) · cos θ в тангенциальном направлении (т. Е. В плоскости падения) и f прогиб = ( R /2) / cos θ в сагиттальном направлении.
Изогнутые лазерные зеркала обычно имеют радиус кривизны от 10 мм до 5 м. Изготовление диэлектрических зеркальных покрытий может быть более трудным для очень сильно изогнутых подложек зеркал, но с помощью усовершенствованных технологий можно достичь фокусных расстояний всего в несколько миллиметров, что требуется для некоторых миниатюрных лазеров.
Фокусное расстояние расширенной оптической системы
Не очевидно, как определить фокусное расстояние расширенной системы — есть разные возможности! Для оптической системы, которая может состоять из нескольких линз и других оптических элементов, указанное выше определение фокусного расстояния не может использоваться, поскольку для расширенной системы не ясно априори, где измерять расстояние до фокуса: от вход в оптическую систему, с выхода, из середины или из другого положения?
В принципе, произвольное определение контрольной точки (е.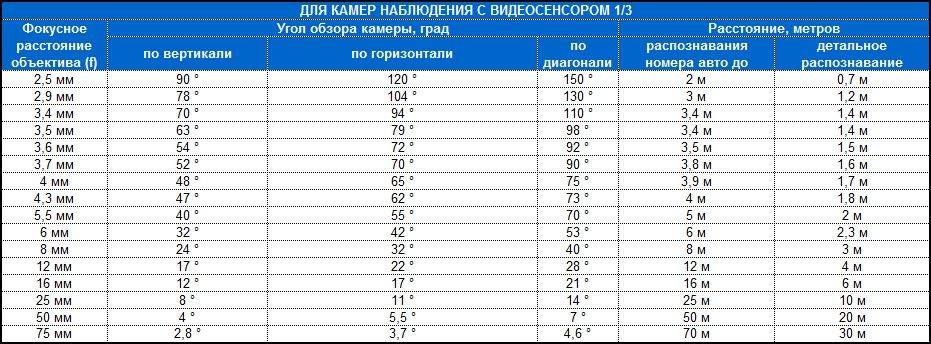 грамм. вход или середина) могут быть использованы, но в целом это будет означать, что некоторые общие правила не могут быть применены, например, удерживайте радиус перетяжки луча в фокусе позади некоторой линзы с заданным фокусным расстоянием (см. ниже) или возможное увеличение телескопа, содержащего эту оптическую систему.
грамм. вход или середина) могут быть использованы, но в целом это будет означать, что некоторые общие правила не могут быть применены, например, удерживайте радиус перетяжки луча в фокусе позади некоторой линзы с заданным фокусным расстоянием (см. ниже) или возможное увеличение телескопа, содержащего эту оптическую систему.
Общий (но не универсальный) подход к определению фокусных расстояний расширенных систем основан на геометрической оптике.
Для нахождения передней фокальной точки вычисляются лучи, которые являются горизонтальными на задней стороне (см. Рисунок 2), используя параксиальное приближение.Оптическая система считается «черным ящиком», в котором фактические траектории лучей не заботятся; вместо этого работают с внутренними лучами, которые экстраполируются из внешних лучей.
Основываясь на этих экстраполированных лучах, можно определить переднюю главную плоскость (или первую главную плоскость ).
Переднее фокусное расстояние — это расстояние между передней фокусной точкой (в передней фокальной плоскости) и передней главной плоскостью (см. Рисунок 2).
Некоторые авторы определяют фокусное расстояние как отрицательное в ситуации на Рисунке 2, потому что точка фокусировки расположена на до передней главной плоскости; другие принимают абсолютное значение.
Рисунок 2).
Некоторые авторы определяют фокусное расстояние как отрицательное в ситуации на Рисунке 2, потому что точка фокусировки расположена на до передней главной плоскости; другие принимают абсолютное значение.
Для системы расфокусировки передняя фокальная плоскость может располагаться на выходной стороне; он содержит виртуальный фокус. Опять же, фокусное расстояние — это расстояние между главной плоскостью и фокальной плоскостью.
Аналогичным образом можно определить заднюю фокальную плоскость (или вторую фокальную плоскость ) и заднюю главную плоскость (или вторую главную плоскость ), где горизонтальные лучи возникают с левой стороны, а с правой стороны. имеет сходящиеся лучи для фокусирующей системы и расходящиеся лучи для дефокусирующей системы. Если показатели преломления на входе и выходе одинаковы (например, & приблизительно; 1 для воздуха), переднее фокусное расстояние и заднее фокусное расстояние идентичны (за исключением возможных различий знаков, используемых некоторыми авторами), и поэтому их можно просто назвать Фокусное расстояние .
Однако две основные плоскости обычно не совпадают для толстых линз, и они могут даже лежать вне линзы.
Если показатели преломления на входе и выходе одинаковы (например, & приблизительно; 1 для воздуха), переднее фокусное расстояние и заднее фокусное расстояние идентичны (за исключением возможных различий знаков, используемых некоторыми авторами), и поэтому их можно просто назвать Фокусное расстояние .
Однако две основные плоскости обычно не совпадают для толстых линз, и они могут даже лежать вне линзы.
Объясненное определение дает фокусное расстояние, которое также может использоваться, например, в уравнениях для размера фокуса (см. Ниже).
Обратите внимание, что расположение левого и правого краев оптической системы (например, положение внешних поверхностей линз, оптических окон и т. Д.) Или ее корпуса не имеют отношения к этим определениям.
В литературе используются разные обозначения фокусных расстояний.
Например, можно иметь отрицательное переднее фокусное расстояние, если передняя фокусная точка находится перед передней главной плоскостью.
Очевидно, что любые уравнения, включающие фокусные расстояния, должны использоваться с принятыми знаковыми соглашениями.
См. Также статью о главных самолетах.
Фокусное расстояние
В отличие от фокусных расстояний, фокусные расстояния , связаны не с главными плоскостями, а скорее с вершинами линз (не заботясь о корпусе, который может быть дополнительно увеличен). Таким образом, переднее фокусное расстояние — это расстояние между передней фокусной точкой и входной поверхностью оптики, а заднее фокусное расстояние — это расстояние между задней поверхностью и задней фокусной точкой.
Фокусные расстояния иногда путают с фокусными расстояниями!К сожалению, эти термины также используются по-разному другими авторами. Например, бывает, что фокусное расстояние считается таким же, как и фокусное расстояние. Поэтому в некоторых каталогах продуктов указываются фокусные расстояния, которые на самом деле следует называть фокусными расстояниями, а также эффективное фокусное расстояние .
Фокусное расстояние также не следует путать с рабочим расстоянием, которое представляет собой расстояние между образцом и корпусом объектива. Обратите внимание, что образец не обязательно помещается в фокальную плоскость, например когда входной свет в объектив не коллимирован.
Обратите внимание, что образец не обязательно помещается в фокальную плоскость, например когда входной свет в объектив не коллимирован.
Эффективное фокусное расстояние фотографического объектива
Значительная путаница возникает из-за того, что в контексте фотоаппаратов термин эффективное фокусное расстояние также используется в совершенно другом значении, как объясняется ниже.
Угол обзора камеры определяется соотношением размера изображения на пленке и фокусного расстояния.В пленочных камерах долгое время в основном использовалась 35-миллиметровая пленка (также называемая пленкой 135 в соответствии со стандартом ISO 1007), где размер изображения на пленке обычно составляет 36 мм × 24 мм.
(Ширина катушки с пленкой составляет 35 мм, что несколько больше 24 мм, так как изображение не доходит до краев катушки.)
Стандартный объектив тогда имеет фокусное расстояние 50 мм.
Однако современные цифровые камеры (особенно более компактные) часто содержат датчики изображения размером менее 36 мм × 24 мм, так что объектив с соответственно меньшим фокусным расстоянием (например. грамм. 32 мм вместо 50 мм) требуется для получения того же поля зрения.
Поскольку многие фотографы все еще привыкли к ранее действовавшему соотношению между фокусным расстоянием и углом зрения, стало обычным определять эффективное фокусное расстояние объектива цифровой камеры как такое фокусное расстояние, которое дает тот же угол обзора. в сочетании с обычной 35-мм пленкой.
Например, тогда можно сказать, что объектив с истинным фокусным расстоянием 32 мм имеет эффективное фокусное расстояние 50 мм и, таким образом, функционирует как стандартный объектив, а не e.грамм. макро- или телеобъектив.
грамм. 32 мм вместо 50 мм) требуется для получения того же поля зрения.
Поскольку многие фотографы все еще привыкли к ранее действовавшему соотношению между фокусным расстоянием и углом зрения, стало обычным определять эффективное фокусное расстояние объектива цифровой камеры как такое фокусное расстояние, которое дает тот же угол обзора. в сочетании с обычной 35-мм пленкой.
Например, тогда можно сказать, что объектив с истинным фокусным расстоянием 32 мм имеет эффективное фокусное расстояние 50 мм и, таким образом, функционирует как стандартный объектив, а не e.грамм. макро- или телеобъектив.
Можно ожидать, что от этого типа преобразования придется отказаться, поскольку 35-мм пленка становится все менее распространенной.
Оптические системы с регулируемым фокусным расстоянием
Для некоторых приложений, в частности для фокусировки систем формирования изображений, важно, чтобы фокусное расстояние оптической системы можно было точно отрегулировать. Могут быть использованы следующие физические принципы:
Могут быть использованы следующие физические принципы:
- Если линза сделана из деформируемого материала, приложение некоторого механического давления может изменить ее форму, а это может изменить фокусное расстояние.Этот принцип используется в хрусталике глаза. Фокусное расстояние несколько уменьшается для фокусировки на близлежащих объектах.
- Когда оптическая система содержит несколько оптических элементов (например, линзы), фокусное расстояние можно настраивать, регулируя относительные расстояния между оптическими элементами. Этот принцип используется, например, в объективах с фотографическим зумом.
Зависимость фокусного расстояния от длины волны; Использование изогнутых зеркал
Обычные линзы, работающие на основе преломления, имеют фокусное расстояние, которое немного зависит от длины волны из-за зависимости показателя преломления от длины волны (-> хроматическая дисперсия).Этот эффект приводит к хроматическим аберрациям, систем формирования изображений и аналогичным проблемам в других приложениях, где оптическая система используется для широкого диапазона оптических длин волн.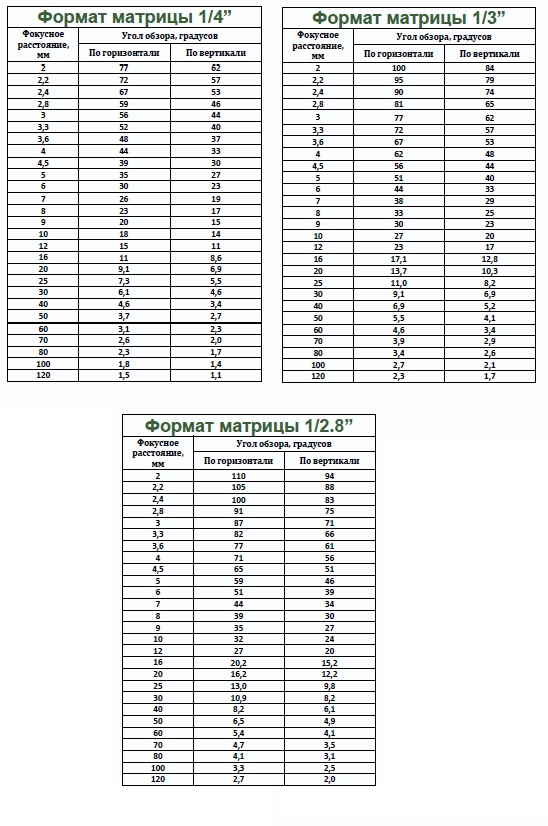 Комбинации линз (например, объективы для фотоаппаратов) могут быть сконструированы таким образом, чтобы минимизировать хроматические аберрации.
Наиболее распространенным является использование ахроматических дублетов , то есть линз, состоящих из двух разных стеклянных материалов, выбранных таким образом, чтобы в значительной степени подавлялись общие хроматические аберрации.
Комбинации линз (например, объективы для фотоаппаратов) могут быть сконструированы таким образом, чтобы минимизировать хроматические аберрации.
Наиболее распространенным является использование ахроматических дублетов , то есть линз, состоящих из двух разных стеклянных материалов, выбранных таким образом, чтобы в значительной степени подавлялись общие хроматические аберрации.
Полностью устранить хроматические аберрации можно, используя только оптические системы с зеркалами. Изогнутое зеркало с радиусом кривизны R имеет фокусное расстояние f = R /2 (для нормального падения), которое определяется только геометрией и, следовательно, не зависит от длины волны. С другой стороны, при ненормальном падении фокусное расстояние в тангенциальном направлении уменьшается на косинус угла падения и увеличивается на обратный косинус этого угла в сагиттальном направлении.Следовательно, такие зеркала могут привносить астигматизм.
Диоптрийная сила
Диоптрическая сила (также называемая фокусирующей силой ) линзы определяется как величина, обратная эффективному фокусному расстоянию (которое равно переднему и заднему фокусному расстоянию, если медиана с обеих сторон оптики равна одно и тоже). Это означает, что сильно фокусирующая линза имеет небольшое фокусное расстояние, но большую диоптрическую силу.
Для очков по рецепту обычно указывается диоптрическая сила, тогда как фокусное расстояние указывается для стандартных линз, объективов микроскопов и фотографических объективов.
Это означает, что сильно фокусирующая линза имеет небольшое фокусное расстояние, но большую диоптрическую силу.
Для очков по рецепту обычно указывается диоптрическая сила, тогда как фокусное расстояние указывается для стандартных линз, объективов микроскопов и фотографических объективов.
Фокусировка расходящихся лучей
Фигура 3: Иллюстрация уравнения линзы.Если расходящийся (а не коллимированный) луч попадает на фокусирующую линзу, расстояние b от линзы до фокуса становится больше, чем f (Рисунок 2). Уравнение линзы утверждает, что
, где a — расстояние от исходного фокуса до линзы. Это показывает, что b ≈ f , если a >> f , но b> f в противном случае.Это соотношение можно интуитивно понять: для коллимации падающего луча (т. Е. Для устранения его расходимости) потребуется фокусирующая сила 1/ a , так что только фокусирующая сила 1/ f — 1/ a оставил для фокусировки.
Если a ≤ f , уравнение не может быть выполнено: линза не может фокусировать луч.
Обратите внимание, что уравнение линзы применяется для лучей, предполагая, что параксиальное приближение действительно, т.е. все углы относительно оси луча остаются малыми.
Достижимый радиус талии луча
Если коллимированный гауссов луч с радиусом луча w 0 попадает в фокусирующую линзу с фокусным расстоянием f , радиус перетяжки луча (фокуса) после линзы может быть рассчитан по уравнению
, где предполагается, что радиус луча в фокусе намного меньше, чем начальный радиус луча w 0 . (Это условие нарушается для лучей со слишком малым радиусом падения; тогда фокус больше, чем согласно данному уравнению.) Также предполагается, что радиус луча значительно больше длины волны λ, так что параксиальное приближение действительно.
Уравнение показывает, что минимально возможный радиус луча определяется не только фокусным расстоянием f , а скорее отношением f к радиусу открытой апертуры линзы, которое устанавливает максимум радиуса входного луча. Вт 0 .
Для фокусирующей или коллимационной линзы это соотношение по существу равно числовой апертуре линзы .
Вт 0 .
Для фокусирующей или коллимационной линзы это соотношение по существу равно числовой апертуре линзы .
Можно ли применить это правило к расширенной оптической системе с фокусным расстоянием f , зависит от применяемого определения f . Полезно указать эффективное фокусное расстояние , которое действительно для таких отношений.
Вопросы и комментарии пользователей
Здесь вы можете оставлять вопросы и комментарии. Если они будут приняты автором, они появятся над этим абзацем вместе с ответом автора. Автор примет решение о приеме на основании определенных критериев.По сути, вопрос должен представлять достаточно широкий интерес.
Пожалуйста, не вводите здесь личные данные; в противном случае мы бы скоро удалили его. (См. Также нашу декларацию о конфиденциальности.) Если вы хотите получить личный отзыв или консультацию от автора, пожалуйста, свяжитесь с ним, например по электронной почте.
Отправляя информацию, вы даете согласие на возможную публикацию ваших материалов на нашем веб-сайте в соответствии с нашими правилами. (Если вы позже отзовете свое согласие, мы удалим эти данные.) Поскольку ваши материалы сначала рассматриваются автором, они могут быть опубликованы с некоторой задержкой.
(Если вы позже отзовете свое согласие, мы удалим эти данные.) Поскольку ваши материалы сначала рассматриваются автором, они могут быть опубликованы с некоторой задержкой.
См. Также: фокусное расстояние, числовая апертура, оптические апертуры, главные точки и главные плоскости, расходимость луча, хроматические аберрации, оптические аберрации, число f, ахроматическая оптика, матрица ABCD, линзы, зеркала
и другие товары в категории общая оптика
Если вам понравилась эта страница, поделитесь ссылкой со своими друзьями и коллегами, e.грамм. через соцсети: Эти кнопки обмена реализованы с учетом конфиденциальности! |
Код для ссылок на других сайтах
Если вы хотите разместить ссылку на эту статью на каком-либо другом ресурсе (например, на своем веб-сайте, в социальных сетях, дискуссионном форуме, Википедии), вы можете получить здесь требуемый код.
HTML-ссылка на эту статью:
rp-photonics.com/focal_length.html">
Статья о фокусном расстоянии
в
Энциклопедия фотоники RP С изображением для предварительного просмотра (см. Рамку чуть выше):
 alt = "article">
alt = "article"> Для Википедии, например в разделе «== Внешние ссылки ==»:
* [https://www.rp-photonics.com/focal_length.html
, статья «Фокусное расстояние» в энциклопедии RP Photonics] .

 Ввести требуемые значения в поля.
Ввести требуемые значения в поля.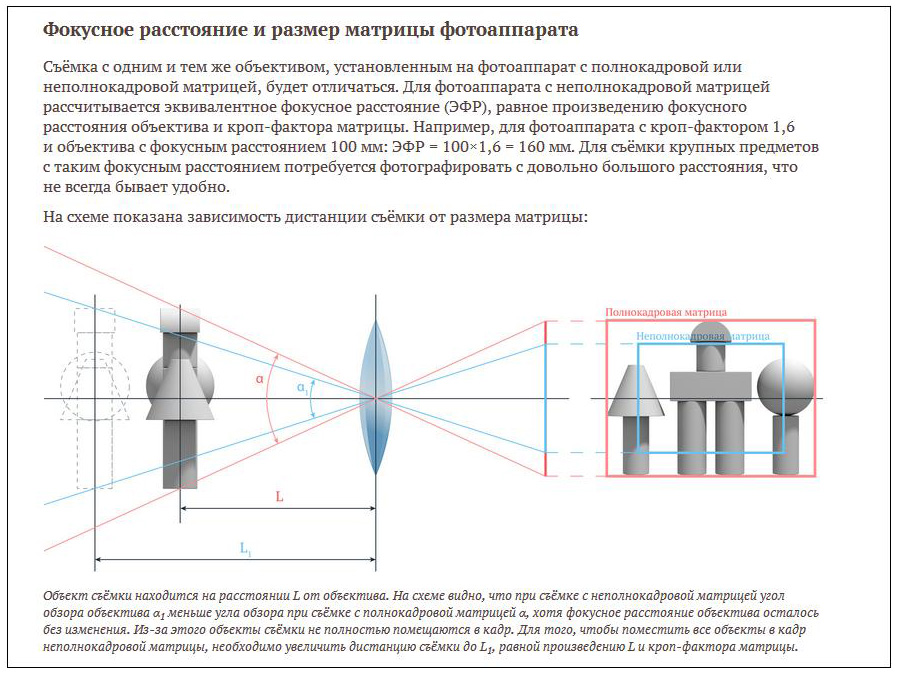 То есть для камеры видеонаблюдения с фокусным расстоянием 2.8 мм распознавание возможно на расстоянии до 3 м, для камеры с фокусным расстоянием 12 мм на расстоянии до 12 м и т.п.
То есть для камеры видеонаблюдения с фокусным расстоянием 2.8 мм распознавание возможно на расстоянии до 3 м, для камеры с фокусным расстоянием 12 мм на расстоянии до 12 м и т.п. Определите расстояние до изображения и размер изображения.
Определите расстояние до изображения и размер изображения.