Линзы и системы линз

Явление преломления света на сферической поверхности раздела двух оптических сред позволяет получать изображения светящихся предметов. Эта возможность осуществляется с помощью линзы — прозрачного тела, ограниченного двумя сферическими поверхностями. Линза является основным оптическим элементом в таких приборах, как фотоаппарат, проекционный фонарь, микроскоп, телескоп и т. д.

На рисунке 1 показан разрез преломляющей сферической поверхности, разделяющей две оптические среды с различными показателями преломления. Очевидно, качественное изображение любого предмета возможно только в том случае, когда пучок лучей, исходящих из любой точки предмета (например, из точки \(P\)), после преломления соберется снова в точку. Вообще говоря, сферическая граница раздела двух сред не обеспечивает этого условия. Так, луч \(NB\) после преломления пересечет ось \(PQ\), строго говоря, в другой точке, нежели луч \(MA\). Однако при некоторых условиях пучок лучей, испущенных точкой, может собраться практически в точку. Это будет в том случае, когда высота \(h\), на которой все лучи этого пучка пересекают преломляющую поверхность, мала по сравнению с радиусом кривизны \(OC\) преломляющей поверхности. Другими словами, когда мал угол \(\alpha\). Лучи, удовлетворяющие этому условию, называются параксиальными. Для удаленных источников требование малости угла \(\alpha\) эквивалентно требованию малости угла \(u\). Но малость угла \(u\) не является достаточным условием параксиальности. Действительно, луч, параллельный оси \(PQ\) (\(u = 0\)), но достаточно удаленный от нее (\(h\) велико), не будет параксиальным.

Рис. 1.

Таким образом, в зависимости от того, сколь хорошо выполняется условие параксиальности, в окрестности точки \(P\) будет более или менее большой кружок размытия. Однако на практике нет необходимости делать его меньше некоторой, вполне определенной, величины. Например, если кружок размытия станет меньше элемента сетчатки глаза (зерна фотоэмульсии на фотопленке, неровностей матового стекла и т.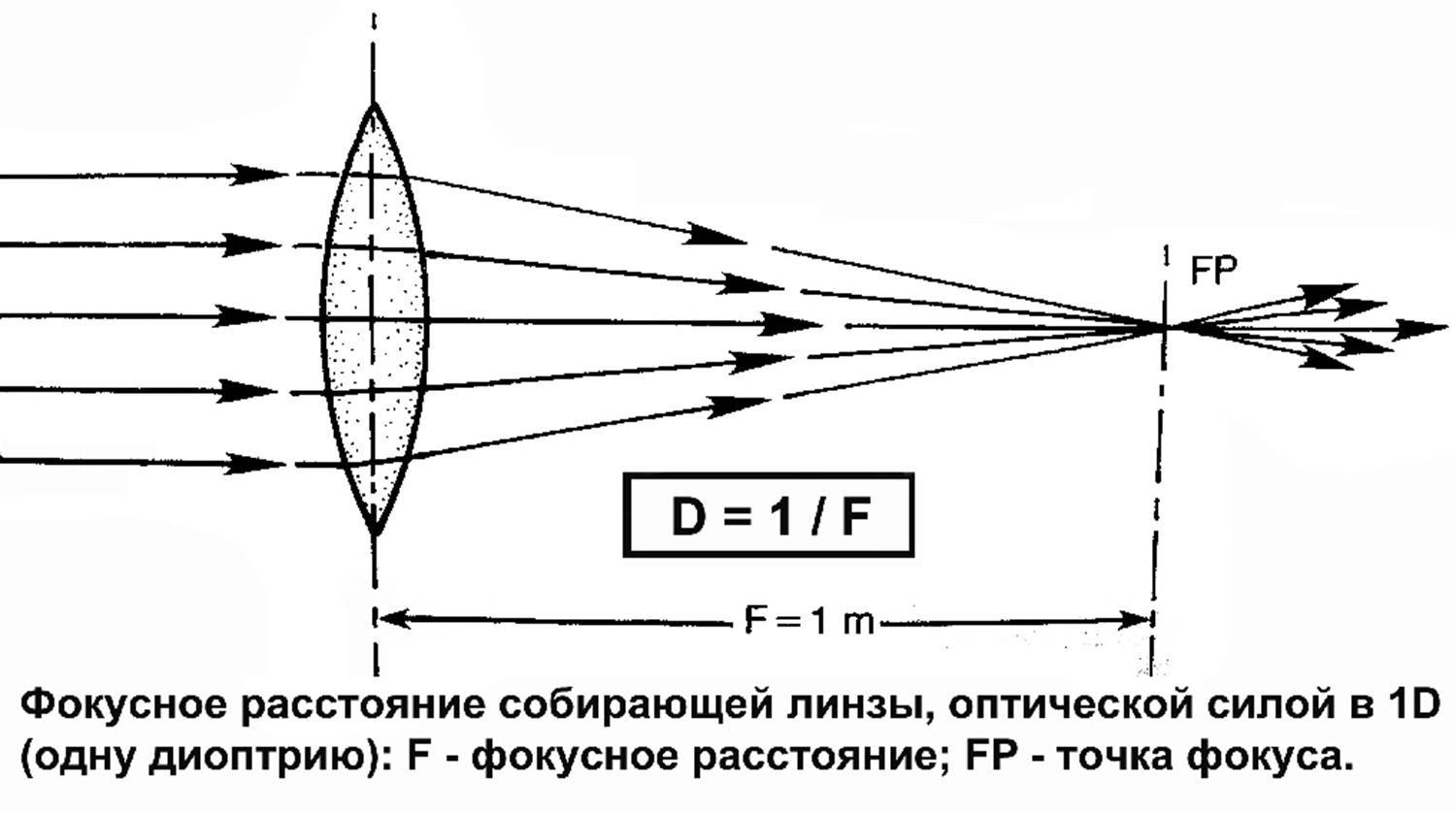 п.), он будет восприниматься нами как точка. Его дальнейшее уменьшение в нашем зрительном ощущении ничего не изменит.

Всюду в дальнейшем мы будем иметь дело только с параксиальными лучами (можно, в принципе, придумать такие преломляющие поверхности, для которых условие параксиальности лучей не является обязательным. Однако наиболее просты в изготовлении именно сферические поверхности). Кроме того, ограничимся рассмотрением только тонких линз, то есть таких линз, фокусные расстояния которых существенно больше их толщины.

Если тонкая линза изготовлена из материала с показателем преломления \(n\), слева от линзы находится среда показателем преломления \(n_1\), а справа — с показателем преломления \(n_2\), то имеют место соотношения:

\(\frac{{{n_2}}}{{{F_2}}} = \frac{{n – {n_1}}}{{{R_1}}} + \frac{{n – {n_2}}}{{{R_2}}}\),    (1)

\(\frac{{{n_1}}}{{{F_1}}} = \frac{{n – {n_1}}}{{{R_1}}} + \frac{{n – {n_2}}}{{{R_2}}}\),    (2)

Здесь \(F_1\) и \(F_2\) — переднее и заднее фокусные расстояния линзы, \(R_1\) и \(R_2\) — радиусы кривизны, соответственно, передней и задней поверхностей линзы. Эти соотношения можно получить (проделайте это самостоятельно!), рассматривая ход лучей, идущих от бесконечно удаленного источника, находящегося в первом случае слева от линзы, а втором случае — справа. В частности, когда с обеих сторон от линзы находится воздух (\(n_1 = n_2 = 1\)),

\(\frac{1}{{{F_1}}} = \frac{1}{{{F_2}}} = \left( {n – 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\).    (3)

Принято считать, что если поверхность своей выпуклой стороной обращена к среде с меньшим показателем преломления, то ее радиус кривизны \(R\) положителен (\(R > 0\)), в противном случае \(R < 0\). Линзы, у которых фокусное расстояние положительно (\(F > 0\)), называются положительными или собирающими, если же \(F < 0\) — отрицательными или рассеивающими. Величина \(D = \frac{1}{F}\) называется оптической силой линзы; она измеряется в диоптриях.

При построении изображений, полученных с помощью тонких линз, используют три основных (или базисных) луча, показанных на рисунке 2. С помощью этого рисунка нетрудно получить формулу тонкой линзы:

\(\frac{1}{d} + \frac{1}{f} = \frac{1}{F}\),

а также выражения для её линейного (поперечного) увеличения:

\(\Gamma = \frac{H}{h} = \frac{f}{d} = \frac{{f – F}}{F} = \frac{F}{{d – F}}\)

и для углового увеличения:

\(\gamma = \frac{{tg\,u’}}{{tg\,u}} = \frac{{h/f}}{{h/d}} = \frac{d}{f} = \frac{1}{\Gamma }\).

Рассмотрим теперь несколько конкретных задач.

Рис. 2.

Задача 1

На поверхности воды \(n_в = 1,3\) лежит двояковыпуклая тонкая стеклянная линза \(n_{ст} = 1,5\) с радиусами кривизны \(R_1 = R_2 = 10\) см. Определите переднее и заднее фокусные расстояния линзы. Чему равно фокусное расстояние этой линзы в воздухе?

Это относительно простая задача. Непосредственное применение формул (1) и (2), где \(n_1 = 1\), \(n_2 = n_в = 1,3\) и \(n = n_{ст} = 1,5\), дает

\({F_1} \approx 14\) см и \({F_2} \approx 18,5\) см.

Для фокусного расстояния линзы в воздухе формула (3) приводит к результату \(F = 10\) см.

Задача 2

На рисунке 3 дан ход луча \(ABC\) через тонкую положительную линзу. Построить ход произвольного луча \(DE\) после преломления в линзе.

Рис. 3.

Проведем \(A’O\), параллельный лучу \(AB\) и проходящий через оптический центр линзы. Он не преломится. Точка \(O\) пересечения этого луча с лучом \(BC\) лежит в фокальной плоскости \(H\). Луч \(D’O\), параллельный \(DE\), пересечет фокальную плоскость в точке \(P\). Через эту же точку пройдет, преломившись, и луч \(DE\).

3адача 3

Какие очки вы пропишите близорукому человеку, который может читать текст, расположенный не далее 20 см?

Очки ни в коей мере не исправляют дефектов человеческого глаза. Их роль сводится к тому, чтобы отобразить объекты окружающего мира на такое расстояние, с которого глаз четко различает предметы. В нашем случае для того чтобы близорукий человек мог видеть удаленные предметы, например, звезду, очки должны создавать изображение звезды не далее 20 см от глаза, а глаз будет рассматривать уже это изображение. Предположим, что линза очков вплотную придвинута к глазу (небольшой зазор между линзой и глазом несущественно исказит приведенные ниже расчеты), и запишем формулу линзы:

\(\frac{1}{d} – \frac{1}{f} = \frac{1}{F}\),

Здесь \(d\) —расстояние до звезды, а \(f\) — максимальное расстояние от изображения звезды до глаза. Член \(\frac{1}{f}\) берется со знаком минус, поскольку изображение мнимое. Так как \(d\) очень велико, можно смело положить \(\frac{1}{d} = 0\). По условию задачи \(f = 20\) см. Отсюда

\(F = – 20\) см, \(D = – 5\) дптр.

Таким образом, близорукому человеку следует прописать очки с рассеивающими линзами оптической силы -5 дптр.

Задача 4

С помощью линзы с фокусным расстоянием \(F\) на экране получают уменьшенное и увеличенное изображения предмета, находящегося на расстоянии \(L\) от экрана. Найти отношение размеров изображений.

Пусть высота предмета равна \(h\). Тогда изображение имеет высоту \(H = \Gamma h\), и отношение размеров изображений есть

\(\frac{{{H_1}}}{{{H_2}}} = \frac{{{\Gamma _1}h}}{{{\Gamma _2}h}} = \frac{{{f_1}/{d_1}}}{{{f_2}/{d_2}}}\). \circ \).

Задача 6

Сложный объектив состоит из двух тонких линз: положительной с фокусным расстоянием \(F_1 = 20\) см и отрицательной с фокусным расстоянием \(F_2 = -10\) см. Линзы расположены на расстоянии \(l = 15\) см друг от друга. С помощью объектива получают на экране изображение Солнца. Какое фокусное расстояние \(f\) должна иметь тонкая линза, чтобы изображение Солнца, полученное с ее помощью, имело такой же размер?

Здесь мы уже имеем дело с системой линз.

Найдем размер изображения Солнца, создаваемого сложным объективом, рассматривая ход лучей последовательно в обеих линзах. Изображение, создаваемое первой линзой, находится, очевидно, в ее фокальной плоскости. Размер этого изображения \({H_1} = {F_1}tg\alpha \), где \(\alpha\) — угловой диаметр Солнца, видимый с Земли (рис.5). Увеличение, даваемое второй линзой, равно \(\frac{{{H_2}}}{{{H_1}}} = \frac{{{f_2}}}{{{d_2}}}\). По формуле линзы имеем

\[ – \frac{1}{{{d_2}}} + \frac{1}{{{f_2}}} = \frac{1}{{{F_2}}},\]

где \(d_2 = F_1 – l\) (изображение Солнца в первой линзе является мнимым источником для второй).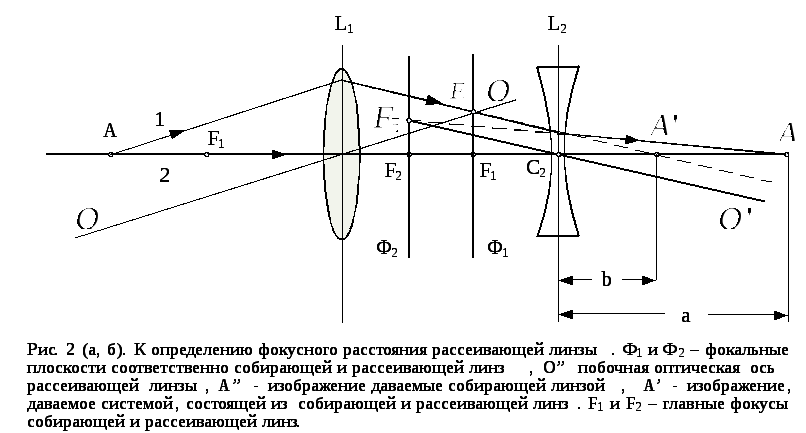 Отсюда

\[{f_2} = \frac{{{F_2}\left( {{F_1} – l} \right)}}{{{F_1} + {F_2} – l}}.\]

Рис. 5.

Таким образом, размер изображения, создаваемого всем объективом,

\[{H_2} = \frac{{{F_1}{F_2}tg\alpha }}{{{F_1} + {F_2} – l}}.\]

Одиночная линза с фокусным расстоянием \(F\) дает изображение, имеющее размер \({H_2} = F\;tg\alpha \). Сопоставляя два последних выражения, получим

\[F = \frac{{{F_1}{F_2}}}{{{F_1} + {F_2} – l}} = \frac{{20\left( { – 10} \right)}}{{20 + \left( { – 10} \right) – 15}} = 40\;см\]

Только что разобранная задача является частным случаем более общей, практически важной задачи: дана система двух (или более) тонких линз с общей оптической осью; необходимо найти одну тонкую линзу, действие которой эквивалентно действию данной системы. Эта задача будет полностью решена, если мы найдем фокусное расстояние эквивалентной линзы и ее местоположение (или, что то же самое, положение ее фокуса). Попробуйте вывести соответствующие формулы самостоятельно. Для ориентировки приведем окончательные результаты: фокусное расстояние искомой эквивалентной линзы равно

\[F = \frac{{{F_1}{F_2}}}{\Delta },\]

а ее фокус находится от второй линзы на расстоянии \(f_2\), равном

\[{f_2} = \frac{{{F_2}\left( {\Delta – {F_2}} \right)}}{\Delta }. \]

Здесь \(F_1\) и \(F_2\) — фокусные расстояния первой и второй линз соответственно, а \(\Delta\) — расстояние между задним фокусом первой линзы и передним фокусом второй (его называют оптическим интервалом). Принято считать \(\Delta > 0\), если передний фокус второй линзы лежит левее заднего фокуса первой линзы, и \(\Delta < 0\) в противном случае.

В заключение предлагаем несколько задач для самостоятельного решения.

Упражнения

1. На рисунке 6 дан ход луча \(ABC\) через тонкую отрицательную линзу. Определить построением фокусное расстояние линзы.

Рис. 6.

1. Какие очки вы пропишите дальнозоркому человеку, который резко видит предметы, расположенные не ближе 50 см?
2. Положительная линза дает действительное изображение с увеличением в 2 раза. Определить фокусное расстояние линзы, если расстояние между линзой и изображением 24 см.
3. Предмет в виде отрезка длиной \(l\) расположен вдоль оптической оси тонкой положительной линзы с фокусным расстоянием \(F\). Середина отрезка находится на расстоянии \(d\) от линзы. Линза дает действительное изображение всех точек предмета. Определить продольное увеличение предмета.
4. Положительная линза с фокусным расстоянием \(F\) и отрицательная с фокусным расстоянием \(-F\) расположены на расстоянии \(a\) друг от друга так, что их оптические оси совпадают. На расстоянии \(a\) перед положительной линзой находится источник света. Изображение этого источника, даваемое системой линз, располагается на таком же расстоянии \(a\) за отрицательной линзой. Определить это расстояние.
5. Оптическая система состоит на двух линз: собирающей с фокусным расстоянием \(F_1 = 30\) см и рассеивающей с фокусным расстоянием \(F_2 = – 30\) см. Оптические оси линз совпадают. Параллельный пучок лучей падает на первую линзу и, пройдя через систему, собирается в некоторой точке, лежащей на оптической оси. На сколько сместится эта точка, если линзы поменять местами?
6. В проекционном аппарате используется сложный объектив, состоящий из двух собирающих линз с фокусными расстояниями \(F_1 = 20\) см и \(F_2 = 15\) см. Линзы расположены на расстоянии \(a=5\) см друг от друга. Определить, с каким увеличением будет проецироваться диапозитив на экран, находящийся на расстоянии \(b=10\) м от объектива проектора. К диапозитиву обращена линза с фокусным расстоянием \(F_2\).

Источник: Журнал “Квант”, №4 1977 г. Автор: Е. Кузнецов.

Что такое главный фокус собирающей линзы

Прочее › Находится › На рисунке показан ход лучей преломленных собирающей линзой в какой точке находится фокус этой линзы

Фокусное расстояние собирающей линзы — это расстояние от плоскости линзы, на котором параллельные лучи собираются в одну точку.

1. Что такое фокус линзы простыми словами
2. Что называется главным фокусным расстоянием
3. Как определить главный фокус линзы
4. Что такое главный фокус и фокусное расстояние линзы
5. Что такое собирающая линза
6. Какой фокус у собирающей линзы
7. Что такое фокусное расстояние простыми словами
8. Какое фокусное расстояние лучше
9. Какой буквой обозначается главный фокус линзы
10. Как найти фокус собирающей линзы
11. Чему равно главное фокусное расстояние собирающей линзы
12. Какое изображение дает собирающая линза
13. Что будет если увеличить фокусное расстояние
14. Для чего используется собирающая линза
15. Что определяет фокусное расстояние
16. Что такое фокус линзы 8 класс
17. Что такое D и F в оптике
18. Что будет если постоянно носить линзы
19. Что влияет на фокусное расстояние
20. На каком расстоянии от линзы с фокусным расстоянием 12 см
21. В чем измеряется фокус линзы
22. Что такое фокус линзы в физике
23. Чему равно фокусное расстояние собирающей линзы 20 см
24. В каком случае собирающая линза дает особенно большое увеличение
25. Что такое линза простыми словами

Что такое фокус линзы простыми словами

Фокус линзы — точка, в которой пересекутся лучи, которые проходят параллельно ГОО. Обратите внимание, что точка фокуса есть и справа, и слева от линзы.

Что называется главным фокусным расстоянием

Расстояние от линзы до главного фокуса есть величина для всякой линзы постоянная и называется главным фокусным расстоянием, или просто фокусным расстоянием линзы. Это расстояние условно обозначается буквой.

Как определить главный фокус линзы

Главный фокус находится на расстоянии f1 от первой ГЛАВНОЙ ПЛОСКОСТИ h2, которая определяется как геометрическое место точек пересечения падающих лучей с их продолжениями за линзой. f1 = f2 = f. Величина D=1/f называется ОПТИЧЕСКОЙ СИЛОЙ линзы.

Что такое главный фокус и фокусное расстояние линзы

Главный оптический фокус — точка, в которой после преломления пересекаются все лучи, падающие на линзу, параллельно главной оптической оси. Фокусное расстояние — расстояние от линзы до ее фокуса.

Что такое собирающая линза

Собирающая линза — это линза которая в средней части толще, чем по краям. Если на собирающую линзу попадает пучок лучей, параллельных главной оптической оси, то после преломления в линзе они собираются в одной точке F, которую обозначают как главный фокус линзы.

Какой фокус у собирающей линзы

У собирающей линзы фокус действительный, потому — положительный. Фокальная плоскость линзы — плоскость, проходящая через главный фокус линзы перпендикулярно главной оптической оси. Точки пересечения побочных оптических плоскостей с фокальными плоскостями называются побочным фокусом (F ‘).

Что такое фокусное расстояние простыми словами

Фокусное расстояние объектива — это оптическое расстояние (обычно измеряемое в миллиметрах) от точки схождения лучей света внутри объектива до матрицы камеры. «Изображение на телефоне можно увеличить, однако фокусное расстояние при этом не изменится.

Какое фокусное расстояние лучше

Получается, чем меньше фокусное расстояние, тем больше объектов помещается в кадр и тем больше искажения этих объектов. А чем больше фокусное расстояние, тем лучше объектив приближает удаленные объекты и задний план.

Какой буквой обозначается главный фокус линзы

Ход лучей в линзе.

Луч, идущий через оптический центр линзы (О), не испытывает преломления. Луч, параллельный главной оптической оси, после преломления проходит через главный фокус (F). Луч, проходящий через главный фокус (F), после преломления идет параллельно главной оптической оси.

Как найти фокус собирающей линзы

Чтобы определить фокусное расстояние собирающей линзы F, воспользуемся формулой тонкой линзы: 1/F = (1/f) + (1/d).

Чему равно главное фокусное расстояние собирающей линзы

D = 1/F. Подставим в данную формулу известное значение фокусного расстояния собирающей линзы и получим: D = 1/F = 1/0,1 м = 10 дптр (диоптрий).

Какое изображение дает собирающая линза

Изображение предмета получается мнимым. Обрати внимание! Изображение, полученное в рассеивающей линзе, всегда мнимое, прямое, уменьшенное. Характер же изображения, даваемого собирающей линзой, зависит от положения предмета относительно линзы.

Что будет если увеличить фокусное расстояние

Фокусное расстояние объектива определяет две важнейших характеристики: коэффициент увеличения и угол обзора. Чем больше фокусное расстояние, тем больше увеличение, и наоборот.

Для чего используется собирающая линза

Собирающие линзы чаще всего используют в фотоаппаратах и лупах, а рассеивающая линза в изготовления коррекционных очков. Электростатические и магнитные линзы.

Что определяет фокусное расстояние

Фокусное расстояние является важным показателем, поскольку оно определяет охват сцены, попадающей в кадр (угол обзора). Как показано на следующих фотографиях, чем меньше фокусное расстояние, тем более широкий угол способна захватить камера, а чем больше фокусное расстояние, тем больше кажутся удаленные объекты.

Что такое фокус линзы 8 класс

Фокус линзы — точка, в которой пересекаются после преломления линзой лучи, падающие на неё параллельно главной оптической оси. Каждая линза имеет два фокуса. В однородной среде они располагаются по обе стороны линзы на одинаковом расстоянии от неё.

Что такое D и F в оптике

Оптическая сила — это физическая величина, характеризующая преломляющую способность линз и оптических систем линз. Оптическая сила линзы обозначается латинской буквой D и измеряется в диоптриях (дптр). D = 1 F, где F — фокусное расстояние линзы.

Что будет если постоянно носить линзы

Если носить их дольше срока, указанного производителем, то начнётся гипоксия роговицы, что может привести к ее зарастанию кровеносными сосудами и отёку.

Что влияет на фокусное расстояние

Для системы линз, как и для простой линзы конечной толщины, фокусное расстояние зависит от радиусов кривизны поверхностей, показателей преломления оптических материалов и толщин элементов системы.

На каком расстоянии от линзы с фокусным расстоянием 12 см

Ответ; линзу надо расположить на расстоянии 14,4 см от предмета.

В чем измеряется фокус линзы

Измеряется в диоптриях (обозначение: дптр): 1 дптр=1 м−1.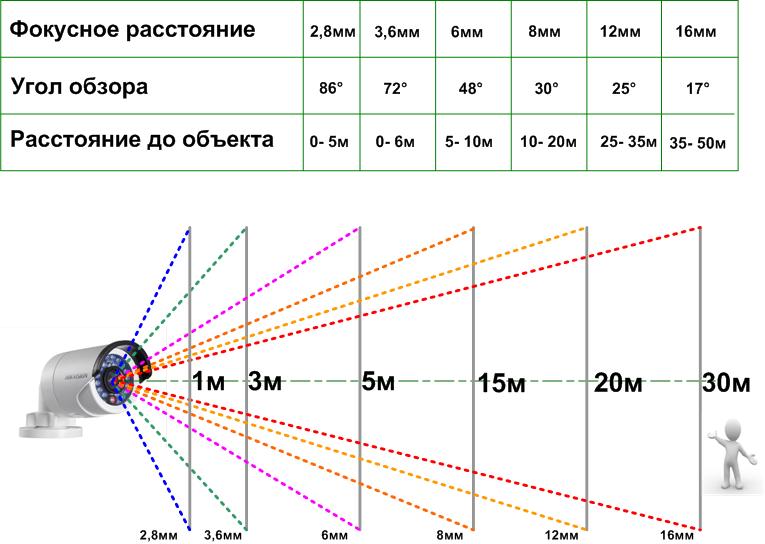 Диоптрия не входит в Международную систему единиц (СИ) и считается внесистемной единицей.

Что такое фокус линзы в физике

Focus — «очаг») оптической системы — точка, в которой пересекаются («фокусируются») первоначально параллельные лучи после прохождения через собирающую систему (либо где пересекаются их продолжения, если система рассеивающая).

Чему равно фокусное расстояние собирающей линзы 20 см

Ответ: Предмет необходимо поместить на расстоянии 0,4 м от заданной собирающей линзы.

В каком случае собирающая линза дает особенно большое увеличение

Собирающая линза дает особенно большое увеличение, когда предмет находится ближе её фокуса, другими словами, если предмет находится между фокусом и центром линзы.

Что такое линза простыми словами

Линза — деталь из прозрачного однородного материала, ограниченная криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями. В зависимости от формы различают два типа линз: собирающие — линзы, у которых середина толще их краёв; рассеивающие — линзы, края которых толще середины.

Оптика

. Будет ли комбинированный объектив иметь симметричное фокусное расстояние с обеих сторон?

спросил 4 года 10 месяцев назад

Изменено 4 месяца назад

Просмотрено 275 раз

$\begingroup$

В этом обсуждении определения фокусного расстояния для комбинированного объектива изображение, описанное в ответе, показывает меру фокусных расстояний.

Описание уравнения Гульстранда также говорит о переднем и заднем фокусных расстояниях.

Объективы цифровых зеркальных фотокамер относятся к ретрофокальным.

Я хочу знать, как найти переднее и заднее фокусное расстояние комбинации линз, если они вообще обладают этим свойством.

• оптика
• видимый свет
• геометрическая оптика
• линзы

$\endgroup$

$\begingroup$

Да, определение эффективного фокусного расстояния для пары линз симметрично независимо от того, направляете ли вы оптический луч спереди или сзади вашей комбинации линз, т.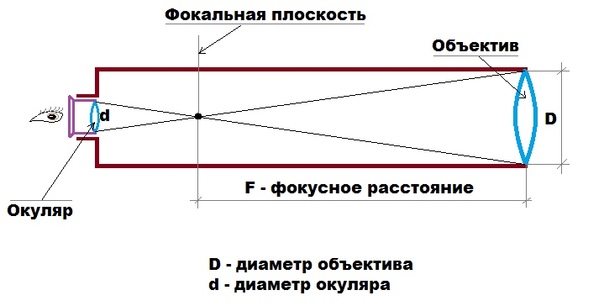

е. симметрично в $f_1 \leftrightarrow f_2$. Симметрия нарушается из-за разных передних и задних рабочих расстояний комбинации линз. В приведенной вами ссылке уравнения Гуллстранда мощности передних и задних вершин — это просто сложный способ выражения обратной величины переднего и заднего рабочих расстояний.

Вообще почти любое оптическое расположение линз можно заменить одной эквивалентной линзой с эффективным фокусным расстоянием, которое зависит от фокусных расстояний линз и их расстояний, независимо от того, смотрите ли вы на нее спереди или сзади.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Фокусное расстояние — Энциклопедия Нового Света

Фокусное расстояние F и фокусное расстояние f положительной (выпуклой) линзы, отрицательной (вогнутой) линзы, вогнутого зеркала и выпуклого зеркала.

Фокусное расстояние оптической системы — это свойство, которое обеспечивает меру того, насколько сильно система сводит (фокусирует) или расходит (рассеивает) свет. Оптическая система может состоять из линзы или зеркала или некоторой комбинации линз и зеркал. Система с более коротким фокусным расстоянием имеет большую оптическую силу, чем система с большим фокусным расстоянием.

Содержимое

• 1 Аппроксимация тонкой линзы
• 2 Общие оптические системы
• 3 В фотографии
• 4 Примечания
• 5 Каталожные номера
• 6 кредитов

Знание этого свойства полезно для создания различных оптических устройств, таких как очки, фотоаппараты, телескопы и микроскопы.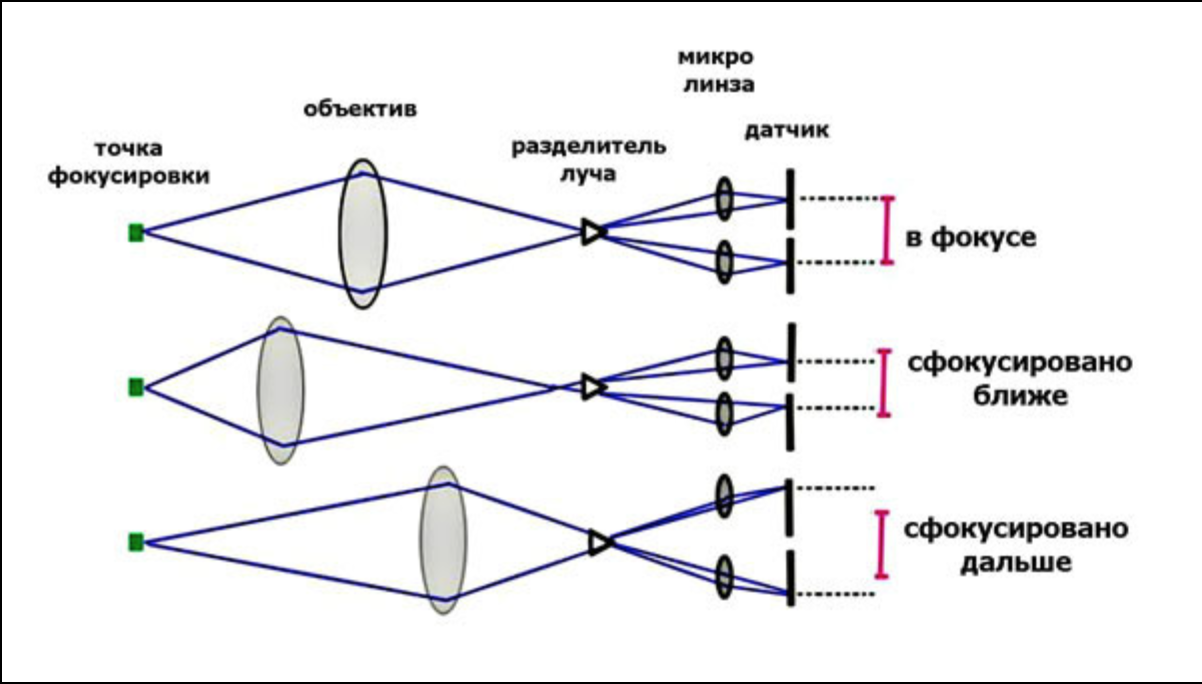

Аппроксимация тонкой линзы

Для тонкой линзы в воздухе фокусное расстояние — это расстояние от центра линзы до главных фокусов (или фокусных точек) линзы. Для собирающей линзы (например, выпуклой линзы) фокусное расстояние положительно и представляет собой расстояние, на котором пучок коллимированного света будет сфокусирован в одном месте. Для рассеивающей линзы (например, вогнутой линзы) фокусное расстояние отрицательно и представляет собой расстояние до точки, из которой коллимированный луч кажется расходящимся после прохождения через линзу.

Общие оптические системы

Для толстой линзы (имеющей незначительную толщину) или системы формирования изображения, состоящей из нескольких линз и/или зеркал (например, фотографического объектива или телескопа), фокусное расстояние часто называют эффективным фокусным расстоянием (EFL), чтобы отличить его от других часто используемых параметров:

• Переднее фокусное расстояние (FFL) или
  Переднее фокусное расстояние (FFD) — это расстояние от переднего фокуса системы до вершины первая оптическая поверхность. ^[1]
• Заднее фокусное расстояние (BFL) или Заднее фокусное расстояние (BFD) — это расстояние от вершины последней оптической поверхности системы до задней фокусной точки. ^[1]

Для оптической системы в воздухе эффективное фокусное расстояние представляет собой расстояние от передней и задней главных плоскостей до соответствующих фокусных точек. Если окружающая среда не воздух, то расстояние умножается на показатель преломления среды. Некоторые авторы называют это расстояние передним (задним) фокусным расстоянием, отличая его от переднего (заднего) фокусного расстояние, \, определенное выше. ^[1]

В общем, фокусное расстояние или EFL — это значение, которое описывает способность оптической системы фокусировать свет, и это значение используется для расчета увеличения системы. Другие параметры используются для определения того, где будет формироваться изображение для данного положения объекта.

Для случая линзы толщиной d в воздухе и поверхностей с радиусами кривизны R ₁ и R ₂ эффективное фокусное расстояние f определяется по формуле:

1f = (n−1) [1R1−1R2 + (n−1) dnR1R2], {\ displaystyle {\ frac {1} {f}} = (n-1) \ left [{\ frac {1} {R_ {1}}} — {\ frac {1} {R_ {2}}} + {\ frac {(n-1) d} {nR_ {1} R_ {2}}} \ right],}

, где n — показатель преломления среды линзы. Величина 1/ f также известна как оптическая сила линзы.

Соответствующее переднее фокусное расстояние:

FFD = f (1+ (n−1) dnR2), {\ displaystyle {\ mbox {FFD}} = f \ left (1 + {\ frac {(n-1) d} {nR_ {2} }}\справа),}

и заднее фокусное расстояние:

BFD = f (1−(n−1)dnR1).{\displaystyle {\mbox{BFD}}=f\left(1-{\frac {(n-1)d}{nR_{1} }}\right).}

В используемом здесь соглашении о знаках значение R ₁ будет положительным, если первая поверхность линзы выпуклая, и отрицательным, если она вогнутая. Значение R ₂ положительно, если вторая поверхность вогнута, и отрицательно, если выпуклая. Обратите внимание, что соглашения о знаках различаются у разных авторов, что приводит к разным формам этих уравнений в зависимости от используемого соглашения.

Для сферически изогнутого зеркала в воздухе величина фокусного расстояния равна радиусу кривизны зеркала, деленному на два. Фокусное расстояние положительно для вогнутого зеркала и отрицательно для выпуклого зеркала. В соглашении о знаках, используемом в оптических схемах, вогнутое зеркало имеет отрицательный радиус кривизны, поэтому

f = −R2{\displaystyle f=-{R \over 2}},

, где R{\displaystyle R} — радиус кривизны поверхности зеркала. ^[2]

В фотографии

Как фокусное расстояние влияет на композицию фотографии: регулируя расстояние камеры от основного объекта при изменении фокусного расстояния, главный объект может оставаться одного размера, а другой на другом расстоянии изменять размер. На этом эффекте основан кукольный зум.

Когда фотообъектив установлен на «бесконечность», его задняя узловая точка отделяется от сенсора или пленки в фокальной плоскости на фокусное расстояние объектива. Объекты, находящиеся далеко от камеры, затем создают четкие изображения на датчике или пленке, которые также находятся в плоскости изображения. Фотографы иногда называют плоскость изображения фокальной плоскостью; эти плоскости совпадают, когда объект находится в бесконечности, но для более близких объектов фокальная плоскость фиксирована относительно линзы, а плоскость изображения перемещается в соответствии со стандартными оптическими определениями.

Фокусное расстояние объектива определяет увеличение, при котором он отображает удаленные объекты. Фокусное расстояние объектива равно расстоянию между плоскостью изображения и точечным отверстием (см. модель камеры-обскуры), которое отображает удаленные небольшие объекты того же размера, что и рассматриваемый объектив. Сочетание этого определения с предположением о прямолинейности изображения (то есть без искажения изображения) приводит к простой геометрической модели, которую фотографы используют для вычисления угла обзора камеры.

Чтобы сделать более близкие объекты в резком фокусе, необходимо отрегулировать объектив, чтобы увеличить расстояние между задней узловой точкой и пленкой, чтобы поместить пленку в плоскость изображения. Фокусное расстояние f {\ displaystyle f}, расстояние от передней узловой точки до фотографируемого объекта S1 {\ displaystyle S_ {1}} и расстояние от задней узловой точки до плоскости изображения S2 {\ displaystyle S_ { 2}} затем связаны:

1S1 + 1S2 = 1f {\ displaystyle {\ frac {1} {S_ {1}}} + {\ frac {1} {S_ {2}}} = {\ frac {1} {f}}} .

При уменьшении S1{\displaystyle S_{1}} необходимо увеличить S2{\displaystyle S_{2}}. Например, рассмотрим обычный объектив для 35-мм камеры с фокусным расстоянием f=50 мм{\displaystyle f=50{\text{мм}}}. Чтобы сфокусироваться на удаленном объекте (S1≈∞{\displaystyle S_{1}\приблизительно \infty}), задняя узловая точка линзы должна находиться на расстоянии S2=50 мм{\displaystyle S_{2}=50{\displaystyle S_{2}=50мм text{ мм}}} из плоскости изображения.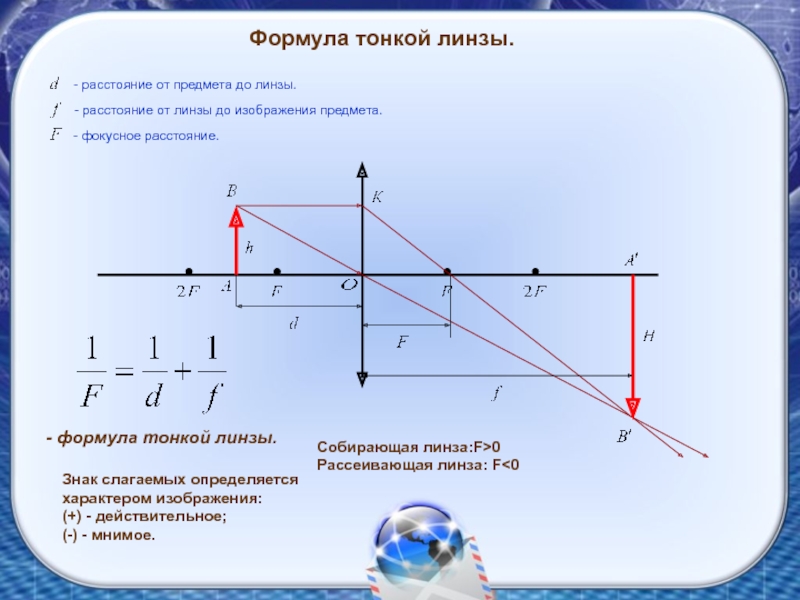 Чтобы сфокусировать объект на расстоянии 1 м (S1 = 1000 мм {\ displaystyle S_ {1} = 1000 {\ text {мм}}}), объектив необходимо переместить на 2,6 мм дальше от плоскости изображения, чтобы S2 = 52,6 мм. {\ displaystyle S_ {2} = 52,6 {\ text {мм}}}.

Обратите внимание, что некоторые простые и обычно недорогие камеры имеют линзы с фиксированным фокусным расстоянием, которые нельзя регулировать.

Фокусное расстояние обычно указывается в миллиметрах (мм), но старые объективы с маркировкой в ​​сантиметрах (см) и дюймах все еще встречаются. Угол зрения зависит от соотношения между фокусным расстоянием и размером пленки.

Объектив с фокусным расстоянием, примерно равным размеру диагонали формата пленки или сенсора, называется нормальным объективом; его угол обзора аналогичен углу, образуемому достаточно большим отпечатком, рассматриваемым с типичного расстояния просмотра по диагонали отпечатка, что, следовательно, дает нормальную перспективу при просмотре отпечатка; ^[3] этот угол обзора составляет около 53 градусов по диагонали. Для полнокадровых камер формата 35 мм диагональ составляет 43 мм, а типичный «обычный» объектив имеет фокусное расстояние 50 мм. Объектив с фокусным расстоянием короче обычного часто называют широкоугольным объективом (обычно 35 мм и меньше для камер формата 35 мм), в то время как объектив значительно длиннее обычного может называться телеобъективом (обычно 85 мм и более для камер формата 35 мм), хотя использование этого термина является неточным, поскольку подразумевает определенные качества оптической конструкции, которые могут применяться или не применяться к данному объективу.

Из-за популярности стандарта 35 мм комбинации камеры и объектива часто описываются с точки зрения их эквивалентного 35-мм фокусного расстояния, то есть фокусного расстояния объектива, который будет иметь такой же угол обзора или поле зрения. вид, если используется на полнокадровой 35-мм камере. Использование фокусного расстояния, эквивалентного 35 мм, особенно распространено в цифровых камерах, в которых часто используются датчики размером менее 35 мм пленки, и поэтому для достижения заданного угла обзора требуются соответственно более короткие фокусные расстояния с помощью фактора, известного как кроп-фактор.

Примечания

1. ↑ ^{1.0 1.1 1.2} John E. Greivenkamp, ​​ SPIE Field Guides, v. FG01 (Bellingham, Вашингтон: SPIE Press, 2004, ISBN 0819452947).
2. ↑ Уравнение, данное здесь, зависит от произвольного соглашения о знаках, как объяснено на странице. В некоторых книгах используется другое соглашение о знаках.
3. ↑ Лесли Д. Стробель, View Camera Technique, 7-е изд. (Бостон: Focal Press, 1999, ISBN 0240803450).

Ссылки

Ссылки ISBN поддерживают NWE за счет реферальных сборов

• Грейвенкамп, Джон Э. Полевое руководство по геометрической оптике. Полевые руководства SPIE, v. FG01. Беллингем, Вашингтон: SPIE Press, 2004. ISBN 0819452947
• Хехт, Юджин. Оптика, 4-е изд. Рединг, Массачусетс: Аддисон-Уэсли, 2002. ISBN 0805385665
• Stroebel, Leslie D. View Camera Technique, 7-е изд. Бостон: Focal Press, 1999. ISBN 0240803450

---

Кредиты

Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia .