Фокусное расстояние системы линз: Линзы и системы линз

Содержание

Линзы и системы линз

Явление преломления света на сферической поверхности раздела двух оптических сред позволяет получать изображения светящихся предметов. Эта возможность осуществляется с помощью линзы — прозрачного тела, ограниченного двумя сферическими поверхностями. Линза является основным оптическим элементом в таких приборах, как фотоаппарат, проекционный фонарь, микроскоп, телескоп и т. д.

На рисунке 1 показан разрез преломляющей сферической поверхности, разделяющей две оптические среды с различными показателями преломления. Очевидно, качественное изображение любого предмета возможно только в том случае, когда пучок лучей, исходящих из любой точки предмета (например, из точки \(P\)), после преломления соберется снова в точку. Вообще говоря, сферическая граница раздела двух сред не обеспечивает этого условия. Так, луч \(NB\) после преломления пересечет ось \(PQ\), строго говоря, в другой точке, нежели луч \(MA\). Однако при некоторых условиях пучок лучей, испущенных точкой, может собраться практически в точку. Это будет в том случае, когда высота \(h\), на которой все лучи этого пучка пересекают преломляющую поверхность, мала по сравнению с радиусом кривизны \(OC\) преломляющей поверхности. Другими словами, когда мал угол \(\alpha\). Лучи, удовлетворяющие этому условию, называются параксиальными. Для удаленных источников требование малости угла \(\alpha\) эквивалентно требованию малости угла \(u\). Но малость угла \(u\) не является достаточным условием параксиальности. Действительно, луч, параллельный оси \(PQ\) (\(u = 0\)), но достаточно удаленный от нее (\(h\) велико), не будет параксиальным.

Рис. 1.

Таким образом, в зависимости от того, сколь хорошо выполняется условие параксиальности, в окрестности точки \(P\) будет более или менее большой кружок размытия. Однако на практике нет необходимости делать его меньше некоторой, вполне определенной, величины. Например, если кружок размытия станет меньше элемента сетчатки глаза (зерна фотоэмульсии на фотопленке, неровностей матового стекла и т. п.), он будет восприниматься нами как точка. Его дальнейшее уменьшение в нашем зрительном ощущении ничего не изменит.

Всюду в дальнейшем мы будем иметь дело только с параксиальными лучами (можно, в принципе, придумать такие преломляющие поверхности, для которых условие параксиальности лучей не является обязательным. Однако наиболее просты в изготовлении именно сферические поверхности). Кроме того, ограничимся рассмотрением только тонких линз, то есть таких линз, фокусные расстояния которых существенно больше их толщины.

Если тонкая линза изготовлена из материала с показателем преломления \(n\), слева от линзы находится среда показателем преломления \(n_1\), а справа — с показателем преломления \(n_2\), то имеют место соотношения:

\(\frac{{{n_2}}}{{{F_2}}} = \frac{{n – {n_1}}}{{{R_1}}} + \frac{{n – {n_2}}}{{{R_2}}}\), (1)

\(\frac{{{n_1}}}{{{F_1}}} = \frac{{n – {n_1}}}{{{R_1}}} + \frac{{n – {n_2}}}{{{R_2}}}\), (2)

Здесь \(F_1\) и \(F_2\) — переднее и заднее фокусные расстояния линзы, \(R_1\) и \(R_2\) — радиусы кривизны, соответственно, передней и задней поверхностей линзы. Эти соотношения можно получить (проделайте это самостоятельно!), рассматривая ход лучей, идущих от бесконечно удаленного источника, находящегося в первом случае слева от линзы, а втором случае — справа. В частности, когда с обеих сторон от линзы находится воздух (\(n_1 = n_2 = 1\)),

\(\frac{1}{{{F_1}}} = \frac{1}{{{F_2}}} = \left( {n – 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\). (3)

Принято считать, что если поверхность своей выпуклой стороной обращена к среде с меньшим показателем преломления, то ее радиус кривизны \(R\) положителен (\(R > 0\)), в противном случае \(R < 0\). Линзы, у которых фокусное расстояние положительно (\(F > 0\)), называются положительными или собирающими, если же \(F < 0\) — отрицательными или рассеивающими. Величина \(D = \frac{1}{F}\) называется оптической силой линзы; она измеряется в диоптриях.

При построении изображений, полученных с помощью тонких линз, используют три основных (или базисных) луча, показанных на рисунке 2.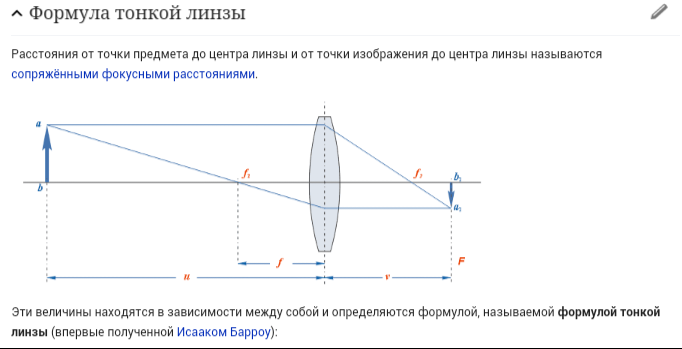 С помощью этого рисунка нетрудно получить формулу тонкой линзы:

\(\frac{1}{d} + \frac{1}{f} = \frac{1}{F}\),

а также выражения для её линейного (поперечного) увеличения:

\(\Gamma = \frac{H}{h} = \frac{f}{d} = \frac{{f – F}}{F} = \frac{F}{{d – F}}\)

и для углового увеличения:

\(\gamma = \frac{{tg\,u’}}{{tg\,u}} = \frac{{h/f}}{{h/d}} = \frac{d}{f} = \frac{1}{\Gamma }\).

Рассмотрим теперь несколько конкретных задач.

Рис. 2.

Задача 1

На поверхности воды \(n_в = 1,3\) лежит двояковыпуклая тонкая стеклянная линза \(n_{ст} = 1,5\) с радиусами кривизны \(R_1 = R_2 = 10\) см. Определите переднее и заднее фокусные расстояния линзы. Чему равно фокусное расстояние этой линзы в воздухе?

Это относительно простая задача. Непосредственное применение формул (1) и (2), где \(n_1 = 1\), \(n_2 = n_в = 1,3\) и \(n = n_{ст} = 1,5\), дает

\({F_1} \approx 14\) см и \({F_2} \approx 18,5\) см.

Для фокусного расстояния линзы в воздухе формула (3) приводит к результату \(F = 10\) см.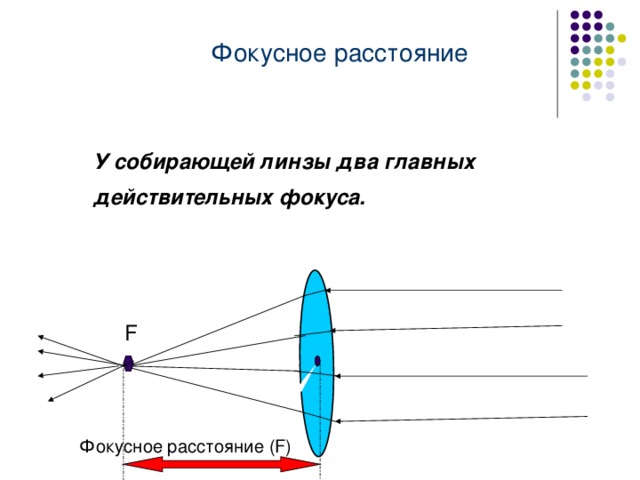

Задача 2

На рисунке 3 дан ход луча \(ABC\) через тонкую положительную линзу. Построить ход произвольного луча \(DE\) после преломления в линзе.

Рис. 3.

Проведем \(A’O\), параллельный лучу \(AB\) и проходящий через оптический центр линзы. Он не преломится. Точка \(O\) пересечения этого луча с лучом \(BC\) лежит в фокальной плоскости \(H\). Луч \(D’O\), параллельный \(DE\), пересечет фокальную плоскость в точке \(P\). Через эту же точку пройдет, преломившись, и луч \(DE\).

3адача 3

Какие очки вы пропишите близорукому человеку, который может читать текст, расположенный не далее 20 см?

Очки ни в коей мере не исправляют дефектов человеческого глаза. Их роль сводится к тому, чтобы отобразить объекты окружающего мира на такое расстояние, с которого глаз четко различает предметы. В нашем случае для того чтобы близорукий человек мог видеть удаленные предметы, например, звезду, очки должны создавать изображение звезды не далее 20 см от глаза, а глаз будет рассматривать уже это изображение. Предположим, что линза очков вплотную придвинута к глазу (небольшой зазор между линзой и глазом несущественно исказит приведенные ниже расчеты), и запишем формулу линзы:

\(\frac{1}{d} – \frac{1}{f} = \frac{1}{F}\),

Здесь \(d\) —расстояние до звезды, а \(f\) — максимальное расстояние от изображения звезды до глаза. Член \(\frac{1}{f}\) берется со знаком минус, поскольку изображение мнимое. Так как \(d\) очень велико, можно смело положить \(\frac{1}{d} = 0\). По условию задачи \(f = 20\) см. Отсюда

\(F = – 20\) см, \(D = – 5\) дптр.

Таким образом, близорукому человеку следует прописать очки с рассеивающими линзами оптической силы -5 дптр.

Задача 4

С помощью линзы с фокусным расстоянием \(F\) на экране получают уменьшенное и увеличенное изображения предмета, находящегося на расстоянии \(L\) от экрана. Найти отношение размеров изображений.

Пусть высота предмета равна \(h\). Тогда изображение имеет высоту \(H = \Gamma h\), и отношение размеров изображений есть

\(\frac{{{H_1}}}{{{H_2}}} = \frac{{{\Gamma _1}h}}{{{\Gamma _2}h}} = \frac{{{f_1}/{d_1}}}{{{f_2}/{d_2}}}\). \circ \).

Задача 6

Сложный объектив состоит из двух тонких линз: положительной с фокусным расстоянием \(F_1 = 20\) см и отрицательной с фокусным расстоянием \(F_2 = -10\) см. Линзы расположены на расстоянии \(l = 15\) см друг от друга. С помощью объектива получают на экране изображение Солнца. Какое фокусное расстояние \(f\) должна иметь тонкая линза, чтобы изображение Солнца, полученное с ее помощью, имело такой же размер?

Здесь мы уже имеем дело с системой линз.

Найдем размер изображения Солнца, создаваемого сложным объективом, рассматривая ход лучей последовательно в обеих линзах. Изображение, создаваемое первой линзой, находится, очевидно, в ее фокальной плоскости. Размер этого изображения \({H_1} = {F_1}tg\alpha \), где \(\alpha\) — угловой диаметр Солнца, видимый с Земли (рис.5). Увеличение, даваемое второй линзой, равно \(\frac{{{H_2}}}{{{H_1}}} = \frac{{{f_2}}}{{{d_2}}}\). По формуле линзы имеем

\[ – \frac{1}{{{d_2}}} + \frac{1}{{{f_2}}} = \frac{1}{{{F_2}}},\]

где \(d_2 = F_1 – l\) (изображение Солнца в первой линзе является мнимым источником для второй). Отсюда

\[{f_2} = \frac{{{F_2}\left( {{F_1} – l} \right)}}{{{F_1} + {F_2} – l}}.\]

Рис. 5.

Таким образом, размер изображения, создаваемого всем объективом,

\[{H_2} = \frac{{{F_1}{F_2}tg\alpha }}{{{F_1} + {F_2} – l}}.\]

Одиночная линза с фокусным расстоянием \(F\) дает изображение, имеющее размер \({H_2} = F\;tg\alpha \). Сопоставляя два последних выражения, получим

\[F = \frac{{{F_1}{F_2}}}{{{F_1} + {F_2} – l}} = \frac{{20\left( { – 10} \right)}}{{20 + \left( { – 10} \right) – 15}} = 40\;см\]

Только что разобранная задача является частным случаем более общей, практически важной задачи: дана система двух (или более) тонких линз с общей оптической осью; необходимо найти одну тонкую линзу, действие которой эквивалентно действию данной системы. Эта задача будет полностью решена, если мы найдем фокусное расстояние эквивалентной линзы и ее местоположение (или, что то же самое, положение ее фокуса). Попробуйте вывести соответствующие формулы самостоятельно. Для ориентировки приведем окончательные результаты: фокусное расстояние искомой эквивалентной линзы равно

\[F = \frac{{{F_1}{F_2}}}{\Delta },\]

а ее фокус находится от второй линзы на расстоянии \(f_2\), равном

\[{f_2} = \frac{{{F_2}\left( {\Delta – {F_2}} \right)}}{\Delta }. \]

Здесь \(F_1\) и \(F_2\) — фокусные расстояния первой и второй линз соответственно, а \(\Delta\) — расстояние между задним фокусом первой линзы и передним фокусом второй (его называют оптическим интервалом). Принято считать \(\Delta > 0\), если передний фокус второй линзы лежит левее заднего фокуса первой линзы, и \(\Delta < 0\) в противном случае.

В заключение предлагаем несколько задач для самостоятельного решения.

Упражнения

На рисунке 6 дан ход луча \(ABC\) через тонкую отрицательную линзу. Определить построением фокусное расстояние линзы.

Рис. 6.

Какие очки вы пропишите дальнозоркому человеку, который резко видит предметы, расположенные не ближе 50 см?
Положительная линза дает действительное изображение с увеличением в 2 раза. Определить фокусное расстояние линзы, если расстояние между линзой и изображением 24 см.
Предмет в виде отрезка длиной \(l\) расположен вдоль оптической оси тонкой положительной линзы с фокусным расстоянием \(F\). Середина отрезка находится на расстоянии \(d\) от линзы. Линза дает действительное изображение всех точек предмета. Определить продольное увеличение предмета.
Положительная линза с фокусным расстоянием \(F\) и отрицательная с фокусным расстоянием \(-F\) расположены на расстоянии \(a\) друг от друга так, что их оптические оси совпадают. На расстоянии \(a\) перед положительной линзой находится источник света. Изображение этого источника, даваемое системой линз, располагается на таком же расстоянии \(a\) за отрицательной линзой. Определить это расстояние.
Оптическая система состоит на двух линз: собирающей с фокусным расстоянием \(F_1 = 30\) см и рассеивающей с фокусным расстоянием \(F_2 = – 30\) см. Оптические оси линз совпадают. Параллельный пучок лучей падает на первую линзу и, пройдя через систему, собирается в некоторой точке, лежащей на оптической оси. На сколько сместится эта точка, если линзы поменять местами?
В проекционном аппарате используется сложный объектив, состоящий из двух собирающих линз с фокусными расстояниями \(F_1 = 20\) см и \(F_2 = 15\) см. Линзы расположены на расстоянии \(a=5\) см друг от друга. Определить, с каким увеличением будет проецироваться диапозитив на экран, находящийся на расстоянии \(b=10\) м от объектива проектора. К диапозитиву обращена линза с фокусным расстоянием \(F_2\).

Источник: Журнал “Квант”, №4 1977 г. Автор: Е. Кузнецов.

Оптическая сила линзы — формулы и примеры

Этим сегодня и займемся:

узнаем, что такое линза в физике и какие бывают линзы;
поговорим о том, что такое оптическая сила линзы, на что она влияет и в каких единицах ее измеряют;
свяжем физику с математикой и посмотрим, как с помощью формул можно рассчитать оптическую силу.

А еще мы немного порисуем: даже самые серьезные физики любят иллюстрировать свои объяснения забавными рисунками. 🙂

Что такое линзы

Вспомните, в каких ситуациях вы сталкивались со словом «линза». Верно, есть линзы для зрения, линзы в объективе фотоаппарата. Теперь пришло время разобраться, что такое линза в мире физики.

Ли́нза — прозрачное тело, ограниченное либо двумя сферическими поверхностями, либо одной сферической и одной плоской.

Действие линз основано на законах преломления света. Параллельные пучки световых лучей, проходя через линзу, преломляются и меняют свое направление: они могут сходиться в одной точке или же рассеиваться в разные стороны.

Виды линз

Линзы делятся на две группы: рассеивающие и собирающие, чье назначение понятно из названия. В свою очередь, и рассеивающие, и собирающие линзы бывают различных видов по своему строению. Давайте внимательно рассмотрим рисунок.

Запомните и еще одно отличие: в собирающих линзах середина толще краев, а в рассеивающих — края толще середины.

Хорошая новость: при решении физических задач мы не будем прописывать строение линзы или определять: это вогнуто-выпуклая или выпукло-вогнутая.

Мы будем использовать схематичное изображение для собирающей и рассеивающей линзы, где сразу будет понятно, с чем мы имеем дело.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Что такое оптическая сила линзы

Тема нашей статьи — «Оптическая сила линзы», но чтобы детально разобраться в этом понятии, нам необходимо вспомнить еще несколько моментов, связанных с основными точками и линиями линзы для построения хода лучей. Эти точки будут одинаковыми и для собирающей, и для рассеивающей линз.

Главная оптическая ось (далее — ГОО) — воображаемая линия, которая проходит через центр линзы и перпендикулярна плоскости линзы. Точка О — оптический центр линзы. Лучи света, которые проходят через эту точку, не будут преломляться.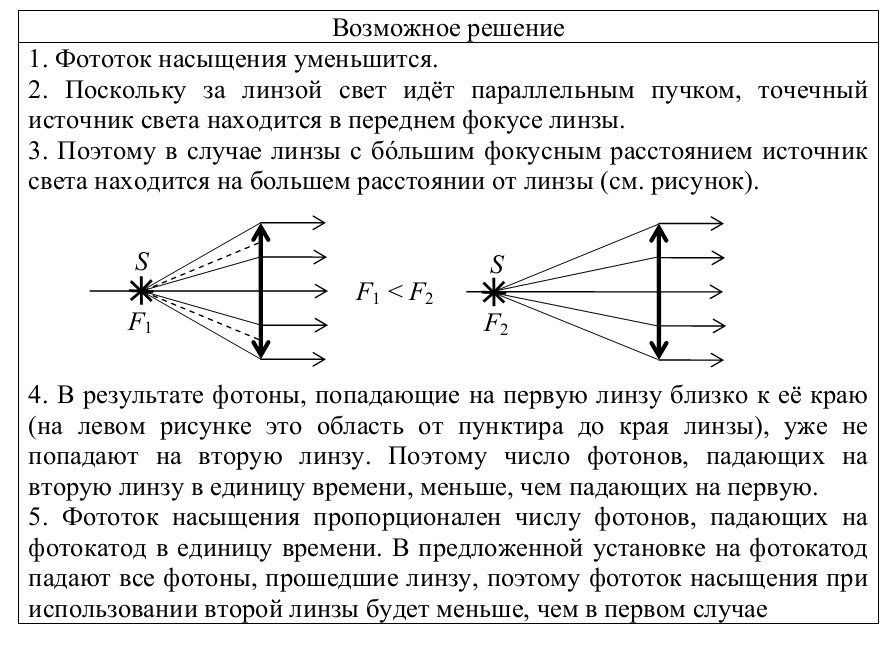

Фокус линзы — точка, в которой пересекутся лучи, которые проходят параллельно ГОО.

Обратите внимание, что точка фокуса есть и справа, и слева от линзы. Фокус, который располагается левее линзы, называют мнимым фокусом — в нем при определенных условиях могут пересечься не сами лучи, а только их продолжения, и в этой плоскости мы получим только мнимое изображение.

Фокусное расстояние — расстояние от точки F до оптического центра линзы.

На главной оптической оси располагают и точку 2F, но тут все просто — мы ставим ее на двойном фокусном расстоянии. Расстояние от объекта до линзы обозначают буквой d, а от линзы до изображения — буквой f.

В зависимости от того, как близко стоит объект перед линзой, мы будем получать разные по размеру действительные и мнимые изображения объекта. Чтобы характеризовать увеличивающую способность линзы, ввели понятие «оптическая сила».

Оптическая сила линзы — это величина, характеризующая преломляющую способность линзы. Эта величина зависит от радиусов кривизны сферических поверхностей линзы и от показателя преломления материала, из которого она сделана.

Эта физическая величина обозначается латинской буквой D и измеряется в диоптриях. Сокращенное обозначение — дптр.

Как найти оптическую силу линзы с помощью формулы

Оптическая сила — это величина, обратно пропорциональная фокусному расстоянию, следовательно ее можно рассчитать в диоптриях по формуле:

D = 1/F.

Так как фокусное расстояние измеряется в метрах, можно сделать логичное заключение:

[дптр] = [1/м] = [м_–1].

Обратите внимание!

Мы уже знаем, что собирающая и рассеивающая линзы отличаются по своим основным функциям. Это значит, что и оптическая сила этих линз будет отличаться. Для собирающих линз впереди оптической силы ставится знак «+», а для рассеивающих — знак «–».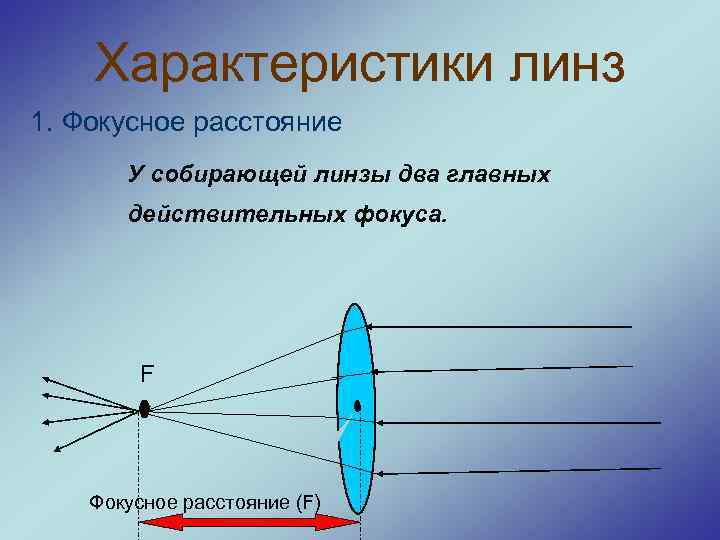

Разберем еще 3 формулы, которые помогут вам решать задачи по этой теме.

Если необходимо рассчитать оптическую силу системы двух линз, воспользуйтесь формулой:
D = D1 + D2 – dD1D2, где:D — конечная оптическая сила,D1 — оптическая сила первой линзы,
D2 — оптическая сила второй линзы,d — расстояние между линзами.
Для системы тонких линз оптическая сила рассчитывается как алгебраическая сумма оптических сил каждой линзы:
D = D1 + D2 + D3 + … + Dn.
Оптическую силу линзы также можно рассчитать через формулу тонкой линзы:
1/F = 1/f + 1/d или D = 1/f + 1/d, так как D = 1/F, где:F — фокусное расстояние,D — оптическая сила линзы,f — расстояние от линзы до изображения,d — расстояние от объекта до линзы.

Проверьте себя

Чтобы закрепить пройденный материал, давайте подведем промежуточные итоги в виде обсуждения в стиле «вопрос-ответ». С помощью этой таблицы вы можете подготовиться к контрольной работе по теме: закройте правую часть рукой и ответьте на вопросы.

Фокусное расстояние — Энциклопедия Нового Света

Фокусное расстояние F и фокусное расстояние f положительной (выпуклой) линзы, отрицательной (вогнутой) линзы, вогнутого зеркала и выпуклого зеркала.

Фокусное расстояние оптической системы — это свойство, которое обеспечивает меру того, насколько сильно система сводит (фокусирует) или расходит (рассеивает) свет. Оптическая система может состоять из линзы или зеркала или некоторой комбинации линз и зеркал. Система с более коротким фокусным расстоянием имеет большую оптическую силу, чем система с большим фокусным расстоянием.

Содержимое

1 Аппроксимация тонкой линзы
2 Общие оптические системы
3 В фотографии
4 Примечания
5 Каталожные номера
6 кредитов

Знание этого свойства полезно для создания различных оптических устройств, таких как очки, фотоаппараты, телескопы и микроскопы.

Аппроксимация тонкой линзы

Для тонкой линзы в воздухе фокусное расстояние — это расстояние от центра линзы до главных фокусов (или фокусных точек) линзы. Для собирающей линзы (например, выпуклой линзы) фокусное расстояние положительно и представляет собой расстояние, на котором пучок коллимированного света будет сфокусирован в одном месте. Для рассеивающей линзы (например, вогнутой линзы) фокусное расстояние отрицательно и представляет собой расстояние до точки, из которой коллимированный луч кажется расходящимся после прохождения через линзу.

Общие оптические системы

Для линзы толщиной (имеющей незначительную толщину) или системы формирования изображения, состоящей из нескольких линз и/или зеркал (например, фотографического объектива или телескопа), фокусное расстояние часто называют эффективным фокусным расстоянием (EFL), чтобы отличить его от других часто используемых параметров:

Переднее фокусное расстояние (FFL) или Переднее фокусное расстояние (FFD) — это расстояние от переднего фокуса системы до вершины первая оптическая поверхность. ^[1]
Заднее фокусное расстояние (BFL) или Заднее фокусное расстояние (BFD) — это расстояние от вершины последней оптической поверхности системы до задней фокусной точки. ^[1]

Для оптической системы в воздухе эффективное фокусное расстояние представляет собой расстояние от передней и задней главных плоскостей до соответствующих фокусных точек. Если окружающая среда не воздух, то расстояние умножается на показатель преломления среды. Некоторые авторы называют это расстояние передним (задним) фокусным расстоянием, отличая его от переднего (заднего) фокусного

расстояние, \, определенное выше. ^[1]

В общем, фокусное расстояние или EFL — это значение, которое описывает способность оптической системы фокусировать свет, и это значение используется для расчета увеличения системы. Другие параметры используются для определения того, где будет формироваться изображение для данного положения объекта.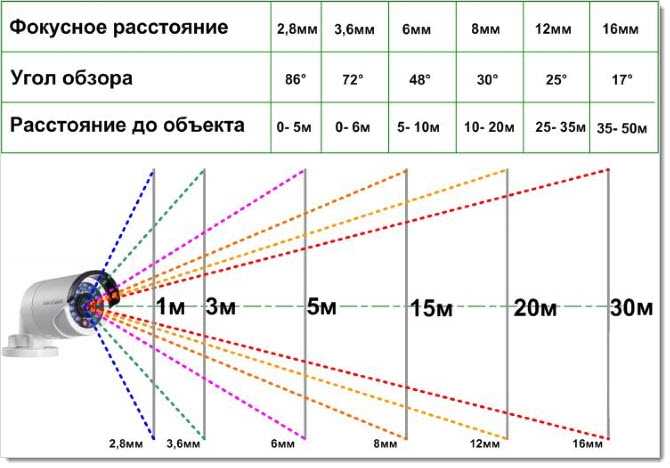

Для случая линзы толщиной d в воздухе и поверхностей с радиусом кривизны R ₁ и R ₂ эффективное фокусное расстояние f определяется по формуле:

1f = (n−1) [1R1−1R2 + (n−1) dnR1R2], {\ displaystyle {\ frac {1} {f}} = (n-1) \ left [{\ frac {1} {R_ {1}}} — {\ frac {1} {R_ {2}}} + {\ frac {(n-1) d} {nR_ {1} R_ {2}}} \ right],}

, где n — показатель преломления среды линзы. Величина 1/

f также известна как оптическая сила линзы.

Соответствующее переднее фокусное расстояние:

FFD = f (1+ (n−1) dnR2), {\ displaystyle {\ mbox {FFD}} = f \ left (1 + {\ frac {(n-1) d} {nR_ {2} }}\справа),}

и заднее фокусное расстояние:

BFD = f (1−(n−1)dnR1).{\displaystyle {\mbox{BFD}}=f\left(1-{\frac {(n-1)d}{nR_{1} }}\right).}

В используемом здесь соглашении о знаках значение R ₁ будет положительным, если первая поверхность линзы выпуклая, и отрицательным, если она вогнутая. Значение R ₂ положительно, если вторая поверхность вогнута, и отрицательно, если выпуклая. Обратите внимание, что соглашения о знаках различаются у разных авторов, что приводит к разным формам этих уравнений в зависимости от используемого соглашения.

Для сферически изогнутого зеркала в воздухе величина фокусного расстояния равна радиусу кривизны зеркала, деленному на два. Фокусное расстояние положительно для вогнутого зеркала и отрицательно для выпуклого зеркала. В соглашении о знаках, используемом в оптических схемах, вогнутое зеркало имеет отрицательный радиус кривизны, поэтому

f = −R2{\displaystyle f=-{R \over 2}},

, где R{\displaystyle R} — радиус кривизны поверхности зеркала. ^[2]

В фотографии

Как фокусное расстояние влияет на композицию фотографии: регулируя расстояние камеры от основного объекта при изменении фокусного расстояния, главный объект может оставаться одного размера, а другой на другом расстоянии изменять размер. На этом эффекте основан кукольный зум.

Когда фотообъектив установлен на «бесконечность», его задняя узловая точка отделяется от сенсора или пленки в фокальной плоскости на фокусное расстояние объектива. Объекты, находящиеся далеко от камеры, затем создают четкие изображения на датчике или пленке, которые также находятся в плоскости изображения. Фотографы иногда называют плоскость изображения фокальной плоскостью; эти плоскости совпадают, когда объект находится в бесконечности, но для более близких объектов фокальная плоскость фиксирована относительно линзы, а плоскость изображения перемещается в соответствии со стандартными оптическими определениями.

Фокусное расстояние объектива определяет степень увеличения, с которой он отображает удаленные объекты. Фокусное расстояние объектива равно расстоянию между плоскостью изображения и точечным отверстием (см. модель камеры-обскуры), которое отображает удаленные небольшие объекты того же размера, что и рассматриваемый объектив. Сочетание этого определения с предположением о прямолинейности изображения (то есть без искажения изображения) приводит к простой геометрической модели, которую фотографы используют для вычисления угла обзора камеры.

Чтобы сделать более близкие объекты в резком фокусе, необходимо отрегулировать объектив, чтобы увеличить расстояние между задней узловой точкой и пленкой, чтобы поместить пленку в плоскость изображения. Фокусное расстояние f {\ displaystyle f}, расстояние от передней узловой точки до фотографируемого объекта S1 {\ displaystyle S_ {1}} и расстояние от задней узловой точки до плоскости изображения S2 {\ displaystyle S_ { 2}} затем связаны:

1S1 + 1S2 = 1f {\ displaystyle {\ frac {1} {S_ {1}}} + {\ frac {1} {S_ {2}}} = {\ frac {1} {f}}} .

При уменьшении S1{\displaystyle S_{1}} необходимо увеличить S2{\displaystyle S_{2}}. Например, рассмотрим обычный объектив для 35-мм камеры с фокусным расстоянием f=50 мм{\displaystyle f=50{\text{мм}}}.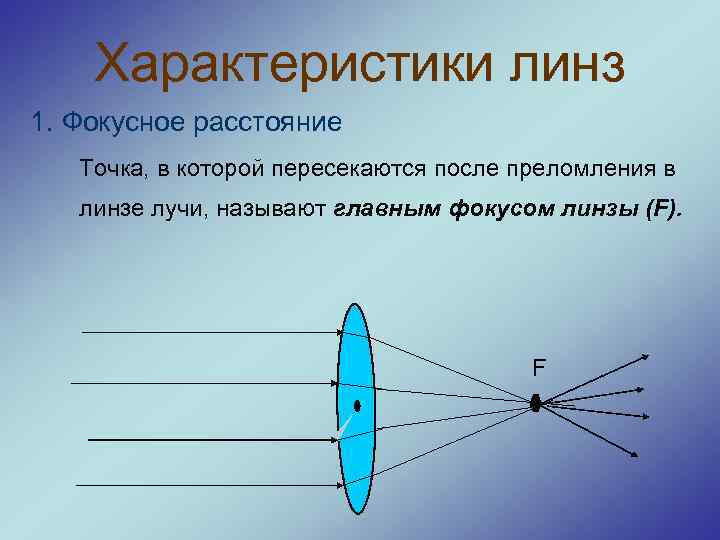 Чтобы сфокусироваться на удаленном объекте (S1≈∞{\displaystyle S_{1}\приблизительно \infty}), задняя узловая точка линзы должна находиться на расстоянии S2=50 мм{\displaystyle S_{2}=50{\displaystyle S_{2}=50мм text{ мм}}} из плоскости изображения. Чтобы сфокусировать объект на расстоянии 1 м (S1 = 1000 мм {\ displaystyle S_ {1} = 1000 {\ text {мм}}}), объектив необходимо переместить на 2,6 мм дальше от плоскости изображения, чтобы S2 = 52,6 мм. {\ displaystyle S_ {2} = 52,6 {\ text {мм}}}.

Обратите внимание, что некоторые простые и обычно недорогие камеры имеют линзы с фиксированным фокусным расстоянием, которые нельзя регулировать.

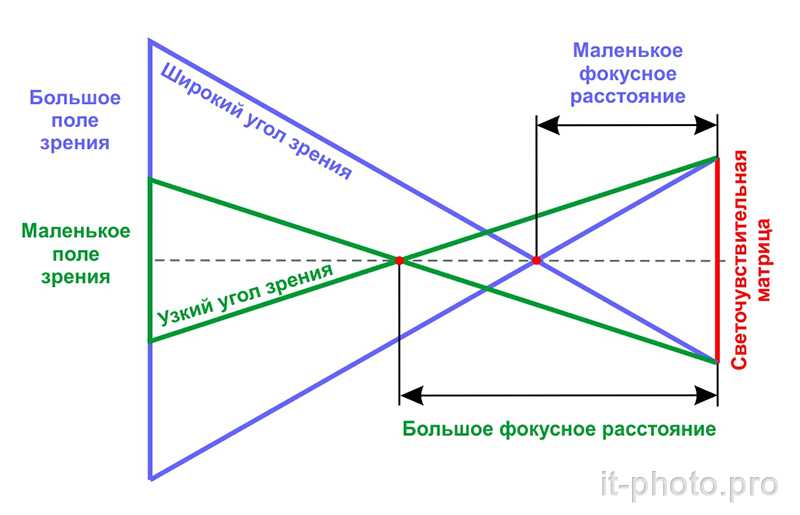
Фокусное расстояние обычно указывается в миллиметрах (мм), но старые объективы с маркировкой в сантиметрах (см) и дюймах все еще встречаются. Угол зрения зависит от соотношения между фокусным расстоянием и размером пленки.

Объектив с фокусным расстоянием, примерно равным размеру диагонали формата пленки или сенсора, называется нормальным объективом; его угол обзора аналогичен углу, образуемому достаточно большим отпечатком, рассматриваемым с типичного расстояния просмотра по диагонали отпечатка, что, следовательно, дает нормальную перспективу при просмотре отпечатка; ^[3] этот угол обзора составляет около 53 градусов по диагонали.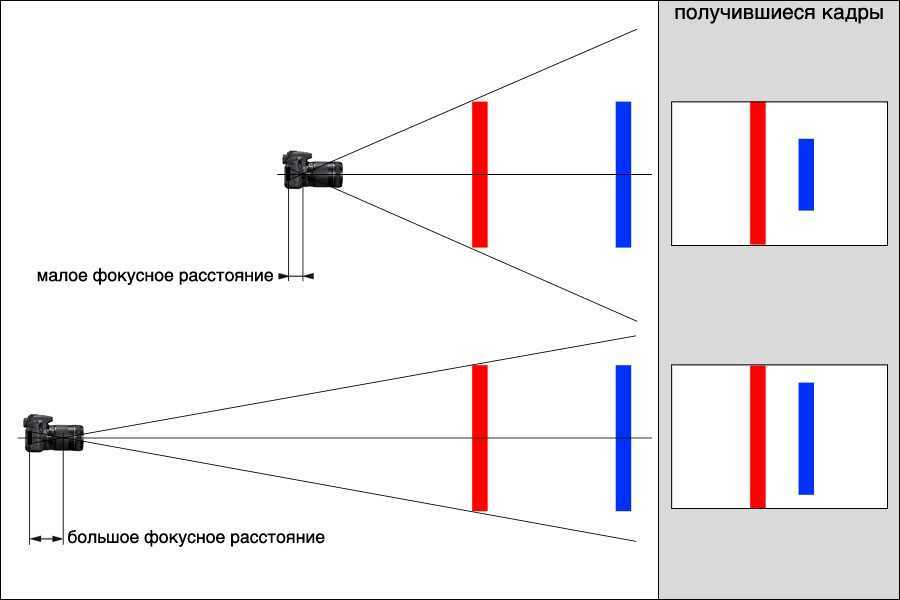 Для полнокадровых камер формата 35 мм диагональ составляет 43 мм, а типичный «обычный» объектив имеет фокусное расстояние 50 мм. Объектив с фокусным расстоянием короче обычного часто называют широкоугольным объективом (обычно 35 мм и меньше для камер формата 35 мм), в то время как объектив значительно длиннее обычного может называться телеобъективом (обычно 85 мм и более для камер формата 35 мм), хотя использование этого термина является неточным, поскольку подразумевает определенные качества оптической конструкции, которые могут применяться или не применяться к данному объективу.

Из-за популярности стандарта 35 мм комбинации камеры и объектива часто описываются с точки зрения их эквивалентного 35-мм фокусного расстояния, то есть фокусного расстояния объектива, который будет иметь такой же угол обзора или поле зрения. вид, если используется на полнокадровой 35-мм камере. Использование фокусного расстояния, эквивалентного 35 мм, особенно распространено в цифровых камерах, в которых часто используются датчики размером менее 35 мм пленки, и поэтому для достижения заданного угла обзора требуются соответственно более короткие фокусные расстояния с помощью фактора, известного как кроп-фактор.

Примечания

↑ ^1,0 ^1,1 ^1,2 Джон Э. Грейвенкамп, Guides Spie Field, v. FG01 (Bellingham, WA: Spie Press, 2004, ISBN 08194297).
↑ Уравнение, данное здесь, зависит от произвольного соглашения о знаках, как объяснено на странице. В некоторых книгах используется другое соглашение о знаках.
↑ Лесли Д. Стробель, View Camera Technique, 7-е изд. (Бостон: Focal Press, 1999, ISBN 0240803450).

Ссылки

Ссылки ISBN поддерживают NWE за счет реферальных сборов

Грейвенкамп, Джон Э. Полевое руководство по геометрической оптике. Полевые руководства SPIE, v. FG01. Беллингем, Вашингтон: SPIE Press, 2004. ISBN 0819452947
Хехт, Юджин. Оптика, 4-е изд. Рединг, Массачусетс: Аддисон-Уэсли, 2002. ISBN 0805385665
Стробель, Лесли Д. Техника камеры обзора, 7-е изд. Бостон: Focal Press, 1999. ISBN 0240803450

Кредиты

Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:

Фокусное расстояние ^{история}

История этой статьи с момента ее импорта в New World Encyclopedia :

История «Фокусное расстояние»

Примечание. На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.

Тонкие линзы и системы линз

Введение

Когда свет от объекта проходит через линзу, обычно формируется изображение объекта. расстояние, q , изображения от объектива определяется фокусным расстоянием, f , объектива и расстояние, p , объекта от линзы. Для параксиальных лучей (лучи, лежащие близко к главной оси), эти параметры связаны уравнением тонкой линзы .

( 1 )

+ =

Если известны расстояния до изображения и объекта, фокусное расстояние можно определить экспериментально. Экспериментальное определение фокусного расстояния несколько усложняется сферическим и хроматические аберрации. Сферическая аберрация возникает из-за того, что лучи света вдали от главная ось не фокусируется в той же точке, что и лучи, близкие к оси. Хроматическая аберрация Это связано с тем, что свет с разной длиной волны преломляется в разной степени и, поэтому фокусируйтесь на разных точках. Для понимания физики линз часто полезно рисовать диаграммы лучей, которые показывают, где находится линза. будет формироваться изображение, будь то прямое или перевернутое, и увеличение изображения. Свет рассеивается от объекта во все стороны, но для построения лучевой диаграммы достаточно двух Для определения местоположения изображения необходимы следующие три основных луча.

1
Луч, параллельный оптической оси и пересекающий линзу, преломится (изогнется) так, что проходит через фокус F на противоположной стороне линзы. (это определение фокус.)
2
Луч, проходящий через фокальную точку объектива со стороны объекта и пересекающий линза будет преломляться и выходить параллельно оси. (По сути, это та же физика, что и № 1, но с использованием другого фокуса.)
3
Луч, проходящий через центр линзы, не отклонится от своего пути. (Это потому что центр линзы практически плоский, так как кривизна в этой точке изменяется.)

На рисунке 1 расстояние до объекта больше, чем фокусное расстояние объектива. Диаграмма лучей показывает, что изображение формируется там, где сходятся три главных луча на дальней стороне линзы. В качестве Как видно из диаграммы, изображение больше, чем объект. Так как видимые (реальные) световые лучи сходятся, говорят, что изображение равно настоящий . Это изображение можно просмотреть на экране, расположенном рядом с изображением. должность.

Рисунок 1

На рисунке 2 расстояние до объекта меньше фокусного расстояния объектива. Обратите внимание, что реальный свет лучи, идущие от предмета, после прохождения линзы расходятся. Они кажутся исходящими из точку позади объекта. Здесь формируется образ. Поскольку видимые световые лучи не на самом деле проходят через изображение, говорят, что этот тип изображения равен виртуальный . Виртуальный образ не может быть проецируется на экран, но кажется парящим в пространстве, если смотреть справа.

Рисунок 2

Увеличение изображения определяется приведенным ниже уравнением.

(2)

M ≡

H _{Изображение}

H _Объект

Для тонких линз можно показать следующее.

( 3 )

м = —

Увеличение изображения пропорционально соотношению расстояний между изображением и объектом. Знак (+ или –) увеличения указывает на ориентацию изображения:

•
m > 0 (положительное увеличение) означает, что изображение вертикально .
•
m (отрицательное увеличение) означает, что изображение перевернутый .

Процедура

Часть 1. Измерение фокусных расстояний с помощью луча-бокса

Объектив в первую очередь характеризуется своим фокусным расстоянием , поэтому стоит научиться измерять фокусное расстояние линзы. Хотя фокусное расстояние немного различается для разных частот или цвета света, в этой лабораторной работе мы будем использовать источники видимого белого света в соответствии с тем, что производители обычно предполагают, когда продают объективы с уникальным фокусным расстоянием. Держите в помните, что по соглашению выпуклый ( собирающая ) линза имеет положительное фокусное расстояние, а вогнутая ( рассеивающая ) линза обозначается отрицательным фокусным расстоянием .

A. Выпуклая (собирающая) линза

1
Используйте лучевую коробку и черную пластиковую карту с разным количеством прорезей, чтобы сформировать 3 или 5 параллельных линий . световых лучей. Вам нужно будет переместить корпус блока лучей относительно источника света, чтобы сделать выходящие лучи параллельны (не сходящиеся и не расходящиеся). Важно, чтобы эти лучи были параллельны, иначе расстояние до изображения не будет фокусным расстоянием объектива! Какое измерение будет вы делаете, чтобы определить, параллельны ли выходящие лучи?
2
Поместите пластиковую двояковыпуклую линзу на лист бумаги и выровняйте лучи по нормали. (перпендикулярно) к линзе так, чтобы преломленные лучи сходились на противоположной стороне в точке фокуса. Перемещайте линзу и лучевой ящик по мере необходимости, чтобы центрировать линзу и фокусную точку на бумаге.
3
Проследите падающие и преломленные лучи на бумаге вместе с контуром линзы. Быть уверенным рисовать стрелки на лучах, чтобы указать их направление (без стрелок, лучей — это просто линий ).
4
С помощью линейки измерьте расстояние от центра линзы до точки, где лучи крестиком и обозначьте это фокусное расстояние f на бумаге. Не забудьте включить оценку неопределенности в этом измерении при сообщении фокусного расстояния. Соответствует ли ваше измерение фокусного расстояния с другими учениками? (Все линзы сделаны одинаково, поэтому размеры должны совпадать.)

B. Вогнутая (рассеивающая) линза

Следуйте той же процедуре, что и в части А, но на этот раз с вогнутой линзой. Так как эта линза рассеивает световых лучей, вам нужно будет найти точку фокусировки, растянув реальные лучи назад пунктирными линии, чтобы показать, где находится виртуальное изображение. Это означает, что вам нужно будет сместить объектив вперед. на бумаге, чтобы было достаточно места для размещения фокуса на передней стороне объектива. Как только вы измерьте фокусное расстояние, не забудьте использовать знак минус, чтобы указать, что это рассеивающая линза.

Примечание: Часть света отражается от передней поверхности вогнутой линзы, которая в данном случае действует как зеркало. Эти лучи формируют реальное изображение, которое является фокусом зеркала, а не линзы.

Часть 2. Проверка изображений с помощью оптической скамьи

В этом разделе вы будете использовать выпуклую линзу с фокусным расстоянием 90 228 f 90 229 = 7,5 см и исследовать, как изменения изображения для нескольких различных расстояний объекта.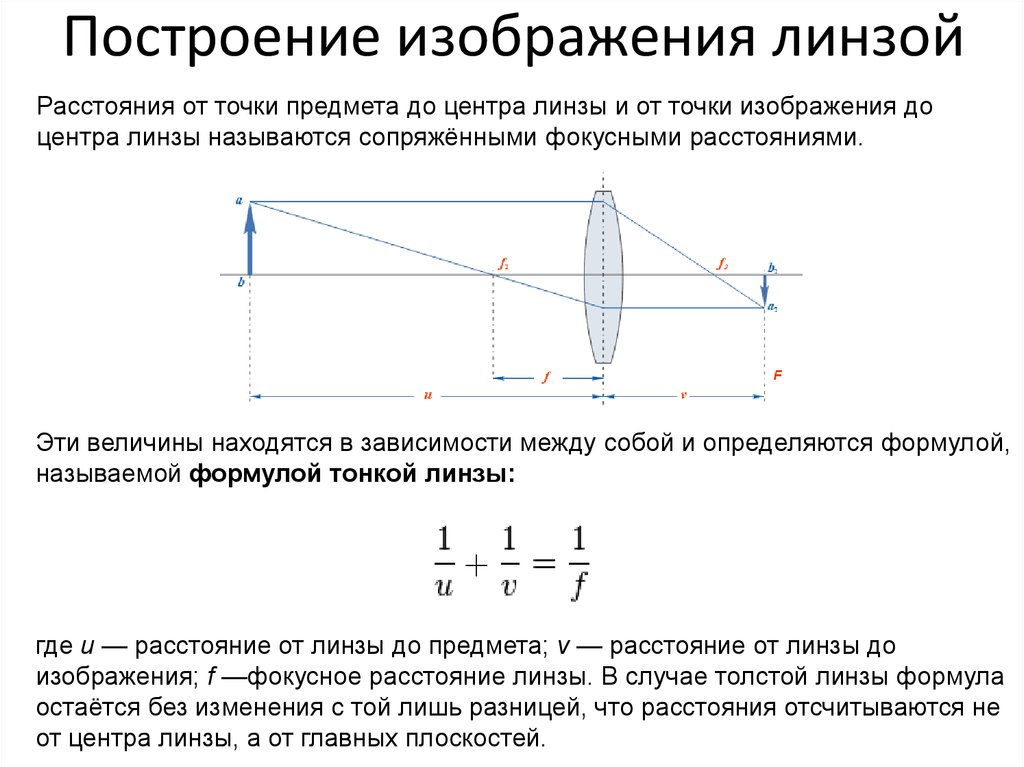 Скамья для оптики обеспечивает удобный способ просмотрите изображение и сделайте замеры.

A. Проверьте фокусное расстояние объектива с помощью удаленного объекта

Перед съемкой данных с помощью объектива рекомендуется измерить или, по крайней мере, проверить его фокусное расстояние. Самый простой способ сделать это для выпуклой линзы — найти яркий удаленный объект (например, солнце или лампочку), и результирующее расстояние изображения будет почти равно фокусному расстоянию. Используя предмет, который находится очень далеко далеко, падающие лучи почти параллельны, как и лучи, создаваемые лучевым ящиком в Части 1. Это взаимосвязь также можно увидеть с помощью тонкой линзы

уравнение (1)

+ =

когда расстояние до объекта установлено на бесконечность.

( 4 )

+ = ⇒ = ⇒ f = q

Даже если расстояние до объекта не бесконечно, а просто велико по сравнению с фокусным расстоянием, изображение расстояние очень близко к фокусному расстоянию. Например, если объект находится через лабораторию, так что расстояние до объекта 750 см, а f ≈ q = 7,5 см, то член

1/p = 1/750

отличается от терма 1/ q = 1/7,5 всего на 1%, а f = q с ошибкой всего 1%.

1
Снимите источник света с оптической скамьи. Поместите экран просмотра примерно на 10 см от объектива. Направьте оптическую скамью на удаленный источник света и медленно перемещайте поворачивайте экран к объективу до тех пор, пока изображение не станет в фокусе. Запишите расстояние изображения и приблизительное расстояние до объекта. Равно ли расстояние изображения фокусному расстоянию, отмеченному на объективе?
2
Замените источник света перед началом следующей процедуры.

B. Изучение изображений, формируемых выпуклой линзой

1
Используйте уравнение тонкой линзы, чтобы рассчитать расстояние до изображения и увеличение, которые вы должны ожидать и записывать результаты в следующую таблицу данных. Не забудьте приложить копию этого таблицу в итоговом отчете.

2
Поместите источник света с перечеркнутой стрелкой на одном конце оптической скамьи. Должность выпуклая линза перед объектом для первого расстояния до объекта в таблице 1. Найдите изображение предмета с помощью экрана, медленно отодвигая экран от объектива. изображение будет уменьшаться в размере и сфокусироваться по мере приближения экрана просмотра к изображению расположение. После этого изображение становится нечетким, а его размер увеличивается. (Обратите внимание, что из-за аберраций в объективе есть диапазон, в котором изображение попадает в фокус. Рассмотреть возможность этот диапазон, когда вы определяете неопределенность ваших измерений.) Когда изображение находится в точке оптимальной фокусировки, измерьте как можно точнее расстояние от от центра объектива до экрана и запишите это расстояние до изображения в таблицу данных.
3
Измерьте как можно точнее высоту перечеркнутой стрелки, h .
4
Измерьте как можно точнее высоту изображения, h’ . (По соглашению, h’ отрицательно, если изображение перевернуто по сравнению с объектом.)
5
Повторите вышеуказанный процесс для остальных расстояний до объектов, перечисленных в таблице 1.
6
Предсказать, что произойдет с изображением, если вы накроете верхнюю половину объекта куском бумаги. Проверьте свой прогноз и объясните свои выводы.
7
Предскажите, что произойдет с изображением, если вы накроете верхнюю половину линзы куском бумага. Проверьте свой прогноз и объясните свои выводы.

C. Изучение изображений, формируемых вогнутой линзой

1
Поместите вогнутую линзу ( f = –15,0 см) примерно в 10 см перед источником света. Переместите Отведите экран от объектива и опишите, что вы видите.
2
Посмотрите через вогнутую линзу на источник света. Увеличено ли виртуальное изображение или минифицированный? Он прямой или перевернутый?

Часть 3: Система линз и корректирующие линзы

Когда две или более линзы используются вместе для создания изображения, такая комбинация называется 9-кратной.0234 объектив система . Обычная система линз встречается, когда очки или контактные линзы используются в комбинации. с роговицей глазного яблока для коррекции близорукости или дальнозоркости. Человеческий глаз действует почти так же, как выпуклая линза в Части 2B, за исключением того, что глаз использует мышцу для изменения. фокусное расстояние линзы для фокусировки изображения на сетчатке в задней части глазного яблока. Поскольку изображение расстояние для глазного яблока фиксировано, существует ограниченный диапазон, в котором роговица может изменить свое фокусное расстояние. Большинство глазных яблок могут комфортно фокусироваться на объектах от бесконечности до 9. 0234 рядом с точкой около 25 см, но у некоторых людей глазные яблоки плохо фокусируются вблизи или вдали. Люди с близорукостью могут видеть объекты, которые находятся близко, но им трудно сфокусироваться на удаленных объектах, потому что их глазное яблоко имеет тенденцию формируют изображение перед сетчаткой. Дальнозоркость возникает, когда можно видеть удаленные предметы, но объекты, которые находятся поблизости, трудно рассмотреть четко, потому что глазное яблоко имеет тенденцию формировать изображение сзади сетчатка. Следующее упражнение покажет, как корректирующие линзы могут изменить точку фокусировки для эти два общих состояния зрения.

1
Поместите выпуклую линзу ( f = 7,5 см) на расстоянии 25 см от предмета. Эта линза представляет собой роговицу глаз. Используйте уравнение линзы, чтобы найти положение изображения этой линзы.
2
Предсказать, где должно сформироваться изображение, когда вторая выпуклая линза ( ф = 15,0 см) представляющие собой корректирующие очки, помещаются на 5 см впереди «роговицы» (между «роговицей» и объект). Для этого пусть изображение корригирующей линзы будет объектом «роговицы». (Примечание: это расстояние до объекта должно быть отрицательным, поскольку оно находится на дальней стороне «роговицы». Также не забудьте учесть расстояние между двумя линзами. Расстояние изображения для этого систему линз следует измерять от центра корректирующей линзы.)
3
Экспериментально проверьте свой прогноз. Соответствует ли ваше измерение расстояния изображения с вашим рассчитанным прогнозом в пределах неопределенности ваших измерений?
4
Повторите шаги 2 и 3 для вогнутой линзы ( f = –15,0 см).
5
Какие линзы нужны для коррекции близорукости? Объяснять.
6
Какие линзы нужны для коррекции дальнозоркости? Объяснять.

Убедитесь, что и вы, и ваш ассистент инициализировали свои данные и передали копию данные перед выходом из лаборатории. Не забудьте заявить о своей работе.